Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 639
Cuenta la leyenda que un velero pirata llegó a una remota isla perseguido por galeones
españoles y, en ella, el capitán escondió el botín que llevaba a bordo, fruto de sus abordajes. Desembarcó, con sus secuaces, en una playa desierta donde había una palmera y una roca. Clavó en la playa su espada y, desde ella, caminó en línea recta hasta la palmera. Estando en ella giró $90^\circ$ en sentido contrario de las agujas del reloj y anduvo (siempre en línea recta) la misma distancia anterior, en donde hincó una estaca. Volvió a la posición de la espada y caminó, también en línea recta hasta la roca y, girando $90^\circ$
en el sentido de las agujas del reloj, repitió la misma distancia hasta un punto en donde clavó otra estaca. Buscó el punto medio entre las dos estacas y allí ordenó enterrar el tesoro. De inmediato mandó recoger la espada y las estacas para, así, proteger la situación exacta del tesoro. Volvió al barco con su tripulación y siguió con sus fechorías hasta que pasaron diez años. Entonces volvió a la isla y desenterró el tesoro. ¿Cómo consiguió localizar el tesoro con la ayuda, únicamente, de la situación de la palmera y de la roca, que aún permanecían allí?
pistasolución 1info
Pista. Demuestra que el lugar en que se entierra el tesoro no depende de dónde se pone la espada, luego el pirata sólo tiene que hacer el mismo proceso poniendo la espada donde quiera.
Solución. Podemos poner un sistema de coordenadas de forma que la playa sea el eje $X$, de forma que la espada está colocada en el punto $E=(t,0)$. Supongamos que la palmera está en el punto $P=(x_P,y_P)$ y la roca en $R=(x_R,y_R)$, con $y_P,y_R\gt 0$. Rotando los vectores $\vec{PE}=(t-x_P,-y_P)$ y $\vec{RE}=(t-x_R,-y_R)$ un ángulo recto en sentido antihorario y horario, respectivamente, obtenemos los vectores $\vec{u}=(y_P,t-x_P)$ y $\vec{v}=(-y_R,x_R-t)$. Por tanto, sumados a los puntos $P$ y $R$, obtenemos la localización de las estacas:
\[E_1=P+\vec{u}=(x_P+y_P,y_P-x_P+t),\qquad E_2=R+\vec{v}=(x_R-y_R,x_R+y_R-t).\]
Su punto medio $M$ se calcula fácilmente como la media aritmética de las coordenadas:
\[M=\frac{E_1+E_2}{2}=\left(\frac{x_P+y_P+x_R-y_R}{2},\frac{y_P-x_P+x_R+y_R}{2}\right).\]
Este punto no depende de $t$, la localización de la espada, luego el pirata sólo tiene que repetir el mismo proceso diez años después poniendo la espada en cualquier punto de la costa.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 636
Sea $ABC$ un triángulo acutángulo, $D$, $E$ y $F$ los pies de las alturas que pasan por $A$, $B$ y $C$, respectivamente. Sea $\Gamma$ la circunferencia de diámetro $AD$, que corta a los lados $AB$ y $AC$ en los puntos $X$ e $Y$, respectivamente. Si $P$ es la intersección de $XY$ con $AD$ y $Q$ la intersección de $AD$ y $EF$, demuestra que $P$ es el punto medio de $QD$.
pistasolución 1info
Pista. Demuestra que $XY$ es paralela a $EF$ y corta a $FD$ en su punto medio.
Solución. Sea $H$ el ortocentro del triángulo $ABC$. Como los ángulos $\angle AFH$ y $\angle AEH$ son rectos, tenemos que $AEFH$ es cíclico con diámetro $AH$ (circunferencia verde en la figura). Si hacemos la homotecia con centro en $A$ que lleva $H$ en $D$, esta circunferencia se transforma en $\Gamma$ ya que $AD$ es un diámetro de $\Gamma$. Esto nos dice que $F$ se transforma en $X$ y $E$ en $Y$, así como que $EF$ es paralela a $XY$, $XD$ es paralela a $CF$ y $DY$ paralela a $BE$. Trazamos la paralela a $AB$ que pasa por $D$ (en naranja en la figura), que corta a $CF$ en cierto punto $Z$. Por el paralelismo mencionado y porque $CF$ es la altura perpendicular a $AB$, obtenemos que $XDZF$ es un rectángulo. Ahora bien, usando el arco capaz en $\Gamma$, tenemos que
\[\angle FXY=\angle ADY=90-\angle DAC=\angle ACB.\] De forma similar, usando el arco capaz en la circunferencia circunscrita a $BDHF$ (que también es cíclico), tenemos que
\[\angle XFD=\angle BFD = \angle BHD=90-\angle EBC=\angle ACB.\]
Esto asegura que $XY$ es la diagonal del rectángulo $XDZF$ y, por tanto, corta a la otra diagonal $FD$ en su punto medio $M$. En otras palabras, el vértice $Z$ está sobre $XY$, cosa que no sabíamos inicialmente.
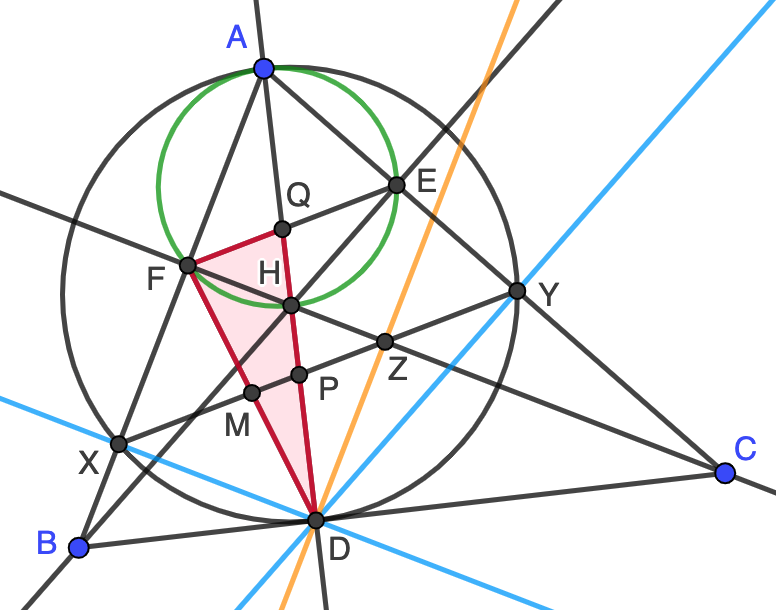
Finalmente, en el triángulo $FDQ$ (sombreado en rojo en la figura) la recta $XY$ es paralela al lado $FQ$ y pasa por el punto medio de $FD$, luego corta a $QD$ también en su punto medio, que es el punto $P$, y el problema está resuelto.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 629
OIM, 2023-P5
Una sucesión $P_1,P_2,\ldots,P_n$ de puntos en el plano (no necesariamente distintos) es carioca si existe una permutación $a_1,a_2,\ldots,a_n$ de los números $1,2,\ldots,n$ para la que los segmentos
\[P_{a_1}P_{a_2},\quad P_{a_2}P_{a_3}, \ldots\quad P_{a_n}P_{a_1}\]
son todos de la misma longitud.
Determinar el mayor número $k$ tal que para cualquier sucesión de $k$ puntos en el plano, se pueden añadir $2023-k$ puntos de modo que la sucesión de $2023$ puntos es carioca.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 628
OIM, 2023-P4
Sean $B$ y $C$ dos puntos fijos en el plano. Para cada punto $A$ del plano que no pertenece a la recta $BC$, sea $G$ el baricentro del triángulo $ABC$. Hallar el lugar geométrico de los puntos $A$ tales que $\angle BAC + \angle BGC = 180^\circ$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 623
OIM, 2022-P5
Sea $ABC$ un triángulo acutángulo con circunferencia circunscrita $\Gamma$. Sean $P$ y $Q$ puntos en el semiplano definido por $BC$ que contiene a $A$, tales que $BP$ y $CQ$ son tangentes a $\Gamma$ con $PB = BC = CQ$. Sean $K$ y $L$ puntos distintos de $A$ en la bisectriz externa del ángulo $\angle CAB$, tales que $BK = BA$ y $CL = CA$. Sea $M$ el punto de corte de las rectas $PK$ y $QL$. Demostrar que $MK = ML$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre