Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Con todo esto ya podemos calcular el área de $AECF$ puesto que esta consta de los dos triángulos equiláteros $ADM$ y $DMC$ (en azul en la figura). Ambos tienen lado $\ell=5$, luego su área es $\frac{\ell^2\sqrt{3}}{4}=\frac{25\sqrt{3}}{4}$ (esto se comprueba fácilmente usando el teorema de Pitágoras). También tenemos que contar los dos triángulos congruentes $DEC$ y $CMF$ (en amarillo en la figura), que tienen la misma altura que los equiláteros pero un tercio de su base, luego cada uno aporta un tercio del área ya calculada $\frac{25\sqrt{3}}{4}$. En resumen, tenemos que
\begin{align*}
\mathrm{Area}(AECF)&=\mathrm{Area}(ADM)+\mathrm{Area}(DMC)+\mathrm{Area}(DEC)+\mathrm{Area}(CMF)\\
&=\frac{25\sqrt{3}}{4}+\frac{25\sqrt{3}}{4}+\frac{1}{3}\cdot\frac{25\sqrt{3}}{4}+\frac{1}{3}\cdot\frac{25\sqrt{3}}{4}=\frac{50\sqrt{3}}{3}.
\end{align*}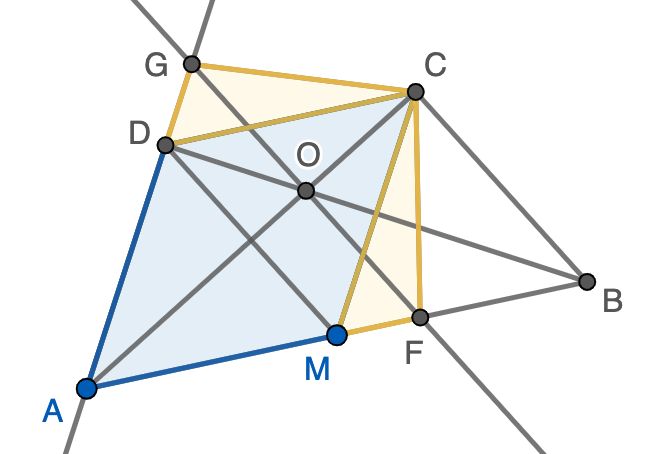
Informar de error en enunciado Informar de procedencia del problema
Para ello, sólo hay que ver que $K$ y $L$ tienen la misma potencia respecto de ambas circunferencias, lo que equivale a decir que $LB\cdot LF=LE\cdot LA$ y $KD\cdot KG=KC\cdot KH$. Sin embargo, la primera igualdad se deduce directamente de que los triángulos $LFA$ y $LEB$ son semejantes, mientras que la segunda viene de que $KGC$ y $KDH$ son semejantes. En ambos casos se trata de triángulos rectángulos con un ángulo (no recto) común.
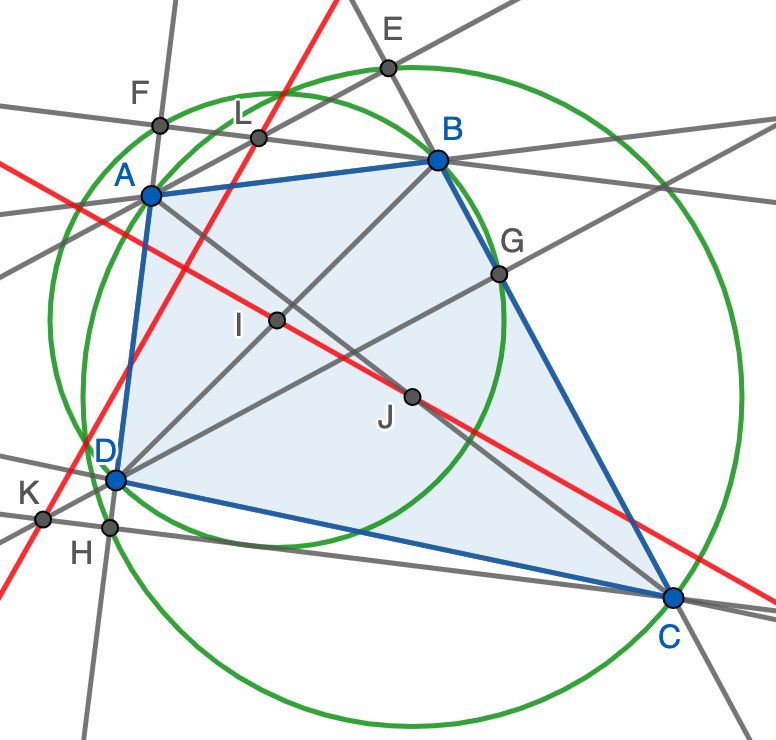
Nota. La demostración vale tanto si el cuadrilátero es cóncavo o convexo, o incluso si no hay cuadrilátero sino solo cuatro puntos dados en el plano. La única salvedad es que $ABCD$ sea un paralelogramo, en cuyo caso $I=J$ (y, por tanto, la recta $IJ$ no está definida) y $K$ y $L$ no existen ya que las rectas cuya intersección los define son paralelas.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema