Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 566
OIM, 1987-P6
Sea $ABCD$ un cuadrilátero convexo. Sean $P$ y $Q$ puntos de $AD$ y $BC$, respectivamente, tales que
$$\frac{AP}{PD}=\frac{AB}{DC}=\frac{BQ}{QC}.$$
Demostrar que los ángulos que forma la recta $PQ$ con las rectas $AB$ y $CD$ son iguales.
pistasolución 1info
Pista. Utiliza la proporcionalidad del enunciado para encontrar dos cuadriláteros semejantes, aunque para ello tendrás que dibujar algunos puntos nuevos
Solución. Construimos puntos $P'$ y $Q'$ sobre la recta $PQ$ tales que $PD=P'D$ y $CQ=C'Q$. Supondremos que $P\neq P'$ y $Q\neq Q'$ a menos que $AD$ o $BC$ sean perpendiculares a $PQ$. Observamos que $pp'D$ y $QQ'C$ son isósceles, luego se tiene que $\angle APQ=\angle P'PD=\angle Q'P'D$ y $\angle BQP=\angle Q'QC=\angle P'Q'C$. Esta igualdad de ángulos junto con las proporciones dadas en el enunciado nos dicen que $ABQP$ y $DCQ'P'$ son cuadriláteros semejantes (indicados en rojo y verde en la figura. Por tanto, el ángulo que forman los pares de lados opuestos $AB$ y $PQ$ en $ABQP$ es el mismo que el que forman los lados homólogos $CD$ y $P'Q'$ en $DCQ'P'$. Dicho de otra forma, cuando prolongamos los estos lados, obtenemos triángulos semejantes $APX$ y $DP'Y$ (representados en azul), siendo $X$ la intersección de $PQ$ y $AB$ e $Y$ la intersección de $PQ$ y $CD$. Esto concluye la demostración ya que nos dice que $\angle AXP=\angle DYP$.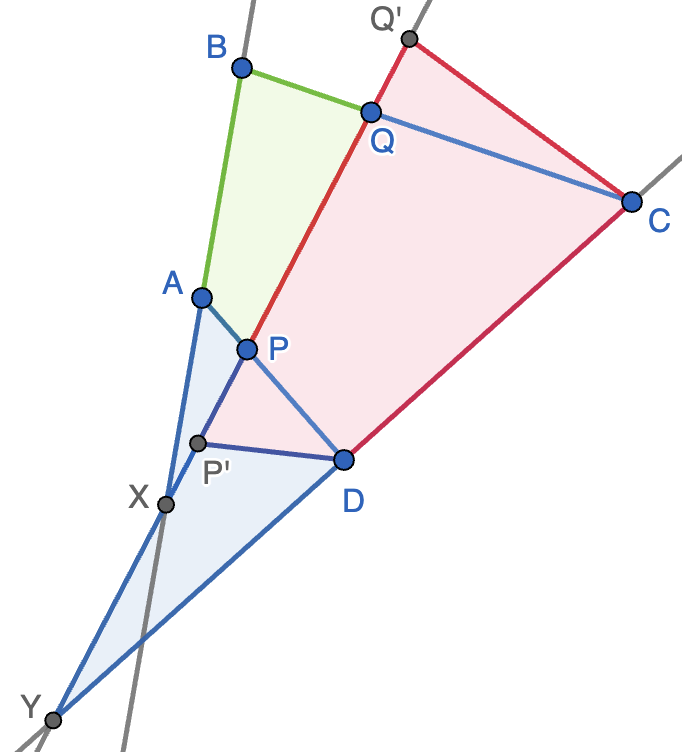

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 565
OIM, 1987-P2
En un triángulo $ABC$, $M$ y $N$ son los puntos medios de los lados $AC$ y $AB$, respectivamente, y $P$ es el punto de intersección de $BM$ y $AN$. Demostrar que, si es posible inscribir una circunferencia en el cuadrilátero $ANMP$, entonces $ABC$ es isósceles.
pistasolución 1info
Pista. Si $AMNP$ tiene circunferencia inscrita, entonces $AM+NP=AN+MP$. Observa también que $P$ no es otra cosa que el baricentro del triángulo.
Solución. En primer lugar, hay que decir que $P$ no es otra cosa que el baricentro de $ABC$. Como el baricentro dista de un vértice el doble que del punto medio del lado opuesto, tenemos que
$$MP=\frac{BM}{3}=\frac{\sqrt{2(a^2+c^2)-b^2}}{6},\quad
NP=\frac{CN}{3}=\frac{\sqrt{2(a^2+b^2)-c^2}}{6},$$
donde hemos usado la conocida expresión para las medianas del triángulo en términos de las longitudes de los lados. Con esta información, tenemos que el cuadrilátero $ANMP$ tiene una circunferencia inscrita si, y solo si, sus lados opuestos tienen la misma suma. Podemos desarrollar
\begin{eqnarray*}
AM+NP=AN+MP&\Leftrightarrow&\frac{b}{2}+\frac{\sqrt{2(a^2+b^2)-c^2}}{6}=\frac{c}{2}+\frac{\sqrt{2(a^2+c^2)-b^2}}{6}\\
&\Leftrightarrow&\frac{b}{2}-\frac{c}{2}=\frac{\sqrt{2(a^2+c^2)-b^2}}{6}-\frac{\sqrt{2(a^2+b^2)-c^2}}{6}\\
&\Leftrightarrow&b-c=\frac{(2(a^2+c^2)-b^2)-(2(a^2+b^2)-c^2)}{3(\sqrt{2(a^2+c^2)-b^2}+\sqrt{2(a^2+b^2)-c^2})}\\
&\Leftrightarrow&b-c=\frac{c^2-b^2}{\sqrt{2(a^2+c^2)-b^2}+\sqrt{2(a^2+b^2)-c^2}}
\end{eqnarray*}
En los últimos pasos, hemos multiplicado por la expresión conjugada (para eliminar las raíces del numerador) y hemos simplificado. Ahora basta observar que si $b=c$, entonces se tiene la igualdad anterior. Sin embargo, si $b\neq c$, la igualdad no es cierta ya que los dos miembros tienen signos opuestos. Deducimos entonces, que si hay circunferencia inscrita, entonces tiene que ser $b=c$, es decir, el triángulo $ABC$ tiene que ser isósceles.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 563
OIM, 2008-P5
Sea $ABC$ un triángulo y $X,Y,Z$ puntos sobre los lados $BC,AC, AB$, respectivamente. Sean $A',B',C'$ los circuncentros correspondientes a los triángulos $AZY$, $BXZ$ y $CYX$. Demostrar que
$$\mathrm{Area}(A'B'C')\geq\frac{1}{4}\mathrm{Area}(ABC)$$
y que la igualdad se cumple si, y sólo si, las rectas $AA',BB',CC'$ tienen un punto en común.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 561
OIM, 2008-P2
Sean $ABC$ un triángulo escaleno y $r$ la bisectriz externa del ángulo $\angle ABC$. Se consideran $P$ y $Q$ los pies de las perpendiculares a la recta $r$ que pasan por $A$ y $C$, respectivamente. Las rectas $CP$ y $AB$ se intersecan en $M$ y las rectas $AQ$ y $BC$ se intersecan en $N$. Demostrar que las rectas $AC$, $MN$ y $r$ tienen un punto en común.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 559
OIM, 2007-P6
Sea $F$ la familia de todos los hexágonos convexos $H$ que satsifacen las siguientes condiciones:
- los lados opuestos de $H$ son paralelos,
- tres vértices cualesquiera de $H$ se pueden cubrir con una franja de ancho $1$.
Nota: una franja de ancho $\ell$ es la región del plano comprendida entre dos rectas paralelas que están a distancia $\ell$ (incluídas ambas rectas).
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre