Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 555
OIM, 2007-P2
Sean $ABC$ un triángulo con incentro $I$ y $\Gamma$ una circunferencia de centro $I$, de radio mayor al de la circunferencia inscrita y que no pasa por ninguno de los vértices. Sean $X_1$ la intersección de $\Gamma$ con la recta $AB$ más cercano a $B$; $X_2$ y $X_3$ los puntos de intersección de $\Gamma$ con la recta $BC$, siendo $X_2$ más cercano a $B$; y $X_4$ el punto de intersección de $\Gamma$ con la recta $CA$ más cercano a $C$. Sea $K$ el punto de intersección de las rectas $X_1X_2$ y $X_3X_4$. Demostrar que $AK$ corta a $X_2X_3$ en su punto medio.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 552
OIM, 2006-P5
Dada una circunferencia $\Gamma$, se considera un cuadrilátero $ABCD$ con sus cuatro lados tangentes a $\Gamma$, con $AD$ tangente a $\Gamma$ en $P$ y $CD$ tangente a $\Gamma$ en $Q$. Sean $X$ e $Y$ los puntos donde $BD$ corta a $\Gamma$ y $M$ el punto medio de $XY$. Demostrar que $\angle AMP=\angle CMQ$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 548
OIM, 2006-P1
En un triángulo escaleno $ABC$ con $\angle BAC=90^\circ$ se consideran las circunferencias inscrita y circunscrita. La recta tangente en $A$ a la circunferencia circunscrita corta a la recta $BC$ en $M$. Sean $S$ y $R$ los puntos de tangencia de la circunferencia inscrita con los catetos $AC$ y $AB$, respectivamente. La recta $RS$ corta a la recta $BC$ en $N$. Las retas $AM$ y $SR$ se cortan en $U$. Demostrar que el triángulo $UMN$ es isósceles.
pistasolución 1info
Pista. ¡Caza de ángulos!
Solución. Llamamos $\gamma=\angle ACB$ por comodidad y supongamos que $AB\lt AC$ sin perder generalidad. Tenemos que $\angle AOC=2\gamma$ por la propiedad del ángulo central. Como $OA$ y $AM$ son perpendiculares, para que los ángulos del triángulo $AMO$ sumen $180$, tiene que ser $\angle AMO=90-2\gamma$, luego $\angle NMU=90+2\gamma$ y ya tenemos uno de los tres ángulos del triángulo $UMN$. Por otro lado, se tiene que $ARS$ es rectángulo isósceles, luego $\angle NRB=\angle ARS=45$. Como $\angle RBN=180-\angle ABC=180-(90-\gamma)=90+\gamma$, para que los ángulos de $NRB$ sumen $180$ tiene que ser $\angle RNB=45-\gamma$ y tenemos el segundo ángulo de $UMN$. Para que la suma sea $180$, el tercero tiene que ser igual a $180-(90+2\gamma)-(45-\gamma)=45-\gamma$, luego $\angle UNM=\angle MUN=45-\gamma$ y queda demostrado que el triángulo $UMN$ es isósceles.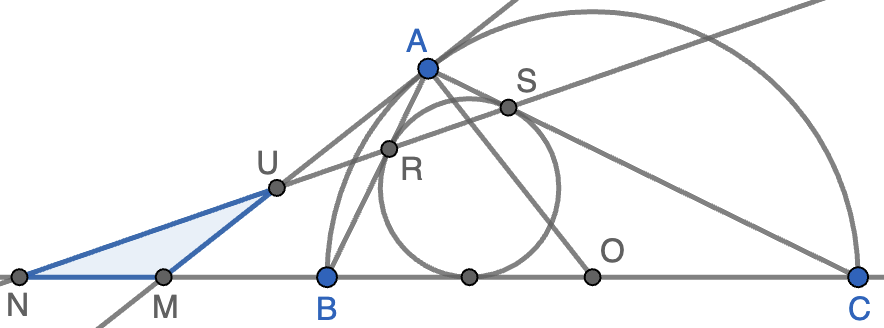

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 546
OIM, 2005-P5
Sea $O$ el circuncentro de un triángulo acutángulo $ABC$ y $A_1$ un punto en el arco menor $BC$ de la circunferencia circunscrita al triángulo $ABC$. Sean $A_2$ y $A_3$ puntos en los lados $AB$ y $AC$, respectivamente, tales que $\angle BA_1A_2=\angle OAC$ y $\angle CA_1A_3=\angle OAB$. Demostrar que la recta $A_2A_3$ pasa por el ortocentro del triángulo $ABC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 541
Sea $ABCD$ un cuadrilátero convexo cuyas diagonales son perpendiculares y se cortan en un punto $P$. Demostrar que hay una circunferencia que pasa por las proyecciones desde $P$ a los cuatro lados del cuadrilátero.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre