Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 510
OIM, 1994-P4
Sea $ABC$ un triángulo acutángulo con circunferencia circunscrita $K$. Sea $P$ un punto interior a $K$. Se trazan las rectas $AP$, $BP$ y $CP$ que cortan de nuevo a $K$ en $X$, $Y$ y $Z$, respectivamente. Determinar el punto $P$ para que el triángulo $XYZ$ sea equilátero.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 508
OIM, 1994-P2
Sea $ABCD$ un cuadrilátero inscrito en una circunferencia tal que existe una semicircunferencia con centro en $AB$ y tangente a los otros tres lados del cuadrilátero.
- Demostrar que $AB=AD+BC$.
- Calcular, en función de $x = AB$ e $y = CD$, el área máxima que puede alcanzar un cuadrilátero en estas condiciones.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 506
Sea $ABC$ un triángulo y sea $L$ la recta que pasa por $C$ y es paralela al lado $AB$. Supongamos que la bisectriz interior del ángulo $A$ corta al lado $BC$ en $D$ y a la recta $L$ en $E$ y que la bisectriz interior del ángulo $B$ corta al lado $AC$ en $F$ y a la recta $L$ en $G$. Demostrar que si $FG=DE$, entonces $AC=BC$.
pistasolución 1solución 2info
Pista. Observa que $ABF$ y $CGF$ son semejantes, con lo que puedes hallar $FC$ en términos de $a,b,c$, las longitudes de los lados de $ABC$. Utiliza esto para hallar el valor de $FG$ usando el teorema del seno.
Solución. Llamemos $2\alpha$, $2\beta$ y $2\gamma$ a los ángulos del triángulo $ABC$ en los vértices $A$, $B$ y $C$, respectivamente. Como $L$ es paralela a $AB$, se tiene que $\angle BGC=\angle ABF=\beta$, $\angle ACG=\angle BAC=2\alpha$, $\angle BCE=\angle ABC=2\beta$ y $\angle AEC=\angle BAD=\alpha$. Esto nos dice que los triángulos $BCG$ y $ACE$ son isósceles, luego $CG=BC=a$ y $CE=AC=b$. La semejanza entre $ABF$ y $CGF$ y la semejanza entre $BAD$ y $CED$ nos dicen que
\[\frac{a}{FC}=\frac{c}{AF}=\frac{a+c}{AF+FC}=\frac{a+c}{b},\qquad \frac{b}{DE}=\frac{c}{BD}=\frac{b+c}{BD+DE}=\frac{b+c}{a}.\]
Usando esto y el teorema del seno en los triángulos $CFG$ y $CDE$, llegamos a que
\[FG=\frac{\sin(2\alpha)}{\sin(\beta)}FC=\frac{ab\sin(2\alpha)}{(a+c)\sin(\beta)},\qquad DE=\frac{\sin(2\beta)}{\sin(\alpha)}CD=\frac{ab\sin(2\beta)}{(b+c)\sin(\alpha)}.\]
Igualando estas dos expresiones, llegamos a que
\[(a+c)\sin(\beta)\sin(2\beta)=(b+c)\sin(\alpha)\sin(2\alpha).\]
Usamos ahora el teorema del seno en $ABC$, que nos dice que $\sin(2\beta)=\frac{b}{a}\sin(2\alpha)$, y el hecho de que $\sin(2\alpha)\neq 0$ por ser $0\lt\alpha\lt90$, para reescribir lo anterior como
\[(a+c)b\sin(\beta)=(b+c)a\sin(\alpha)\ \Leftrightarrow\ ab(\sin(\beta)-\sin(\alpha))+c(b\sin(\beta)-a\sin(\alpha))=0.\qquad (\star)\]
La demostración habrá terminado si probamos que $\alpha=\beta$, lo que se deduce de $(\star)$ por reducción al absurdo. Si $\alpha\gt\beta\gt 0$, entonces $a\gt b\gt 0$ y $\sin(\alpha)\gt\sin(\beta)\gt 0$ (la función seno es creciente en el intervalo $[0,90]$) luego el miembro de la izquierda en $(\star)$ sería negativo y no cero (como habíamos probado). Análogamente, si $\beta\gt\alpha$, el miembro de la derecha en $(\star)$ es positivo y no cero.
Solución. Llamemos $2\alpha$, $2\beta$ y $2\gamma$ a los ángulos del triángulo $ABC$ en los vértices $A$, $B$ y $C$, respectivamente. Como $L$ es paralela a $AB$, se tiene que $\angle BGC=\angle ABF=\beta$, $\angle ACG=\angle BAC=2\alpha$, $\angle BCE=\angle ABC=2\beta$ y $\angle AEC=\angle BAD=\alpha$. Esto nos dice que los triángulos $BCG$ y $ACE$ son isósceles, luego $CG=BC=a$ y $CE=AC=b$. Si llamamos $v_a=AD$ y $v_b=BF$ a las longitudes de las bisectrices de $ABC$, entonces la semejanza entre $ABF$ y $CGF$ y la semejanza entre $BAD$ y $CED$ nos dicen que
\[\frac{a}{FG}=\frac{c}{v_b},\qquad \frac{b}{DE}=\frac{c}{v_a}.\]
Teniendo en cuenta que $FG=DE$ según el enunciado, obtenemos que $av_b=bv_a$ o bien $a^2v_b^2-b^2v_a^2=0$. Ahora vamos a usar las siguientes fórmulas para las longitudes de las bisectrices
\[v_a^2=\frac{2bc(b+c-a)}{(b+c)^2},\qquad v_b^2=\frac{2ac(a+c-b)}{(a+c)^2}.\]
Con ellas podemos transformar la condición $a^2v_b^2-b^2v_a^2=0$ en
\begin{align*}
\frac{2b^3c(b+c-a)}{(b+c)^2}-\frac{2a^3c(b+c-a)}{(a+c)^2}=0&\ \Leftrightarrow\ b^3(a+c)^2(b+c-a)-a^3(b+c)^2(a+c-b)=0\\
&\ \Leftrightarrow\ (b-a)(b^3(a+c)^2+a^3(b+c)^2)+c(b^3(a+c)^2-a^3(b+c)^2)
\end{align*}
Ahora bien, podemos sacar un factor $b-a$ del último término $b^3(a+c)^2-a^3(b+c)^2$ si lo desarrollamos:
\begin{align*}
b^3(a+c)^2-a^3(b+c)^2&=b^3a^2-b^2a^3+2c(b^3a-ba^3)+c^2(b^3-a^3)\\
&=a^2b^2(b-a)+2abc(b+a)(b-a)+c^2(b^2+ab+a^2)(b-a).
\end{align*}
Juntándolo todo, hemos podido sacar factor común $b-a$ de forma que $av_b-bv_a=0$ equivale a
\[(b-a)\left(b^3(a+c)^2+a^3(b+c)^2+ca^2b^2+2abc^2(b+a)+c^3(b^2+ab+b^2)\right)=0.\]
Obviamente, el segundo factor de la igualdad anterior es positivo ya que $a,b,c\gt 0$ y todos los coeficientes son positivos. Deducimos que $a=b$, como queríamos probar.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 503
Consideremos un paralelogramo $ABCD$. Una circunferencia $\Gamma$ que pasa por el punto $A$ corta a los lados $AB$ y $AD$ por segunda vez en los puntos $E$ y $F$, respectivamente, y a la diagonal $AC$ en el punto $G$. Las prolongaciones de $FG$ y $BC$ se cortan en $H$ y las prolongaciones de $EG$ y $CD$ se cortan en $I$. Demostrar que la recta $HI$ es paralela a $EF$.
pistasolución 1info
Pista. Considera una homotecia de centro $G$ que lleve $E$ en $I$ y demuestra que también lleva $F$ en $H$ usando que las homotecias llevan rectas en rectas paralelas.
Solución. Consideremos la homotecia $h$ de centro $G$ que lleva $E$ en $I$ (esta homotecia tiene razón negativa). Entonces, $h$ debe llevar la recta $AB$ en una recta paralela a $AB$ que pasa por $I$, es decir, $h$ lleva la recta $AB$ a la recta $CD$. Asimismo, $h$ lleva $A$ en un punto de la recta $CD$ alineado con $G$ y $A$, que no puede ser otro que el punto $C$. Finalmente, $h$ lleva la recta $AD$ en una recta paralela a $AD$ que pasa por $h(A)=C$, que no es otra que la recta $BC$. Como un punto y su imagen por $h$ están alineados con $G$, tenemos que $h(F)=G$, luego $h$ lleva la recta $EF$ en la recta $h(E)h(F)=IH$, que es por tanto paralela a $EF$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 502
- Probar que si una terna de números positivos $(a,b,c)$ verifica el sistema de ecuaciones \[\left\{\begin{array}{l}a^2+a=b^2,\\b^2+b=c^2,\\c^2+c=a^2,\end{array}\right.\] entonces $(a-b)(b-c)(c-a)=1$.
- Supongamos que $A_1A_2\ldots A_9$ es un eneágono regular tal que \[A_1A_4=1,\qquad A_1A_2=a,\qquad A_1A_3=b,\qquad A_1A_5=c.\] Probar que la terna $(a,b,-c)$ cumple el sistema del apartado anterior.
pistasolución 1info
Pista. El apartado (a) es simple manipulación con un poco de pericia desarrollando el producto $(a-b)(b-c)(c-a)$ (probar que $a+b+c=0$ y $ab+bc+cd=-1$ puede ser útil). Para el apartado (b), usa el teorema de Ptolomeo eligiendo convenientemente cuadriláteros con vértices en los vértices del $n$-gono.
Solución. Para probar el apartado (a), desarrollamos y usamos las ecuaciones para calcular
\begin{align*}
(a-b)(b-c)(c-a)&=(c^2-a^2)b+(b^2-c^2)a+(a^2-b^2)c=-(ab+bc+ac).
\end{align*}
Bastará ver que $ab+bc+ac=-1$. Ahora bien, multiplicando las tres ecuaciones del sistema obtenemos que $abc(a+1)(b+1)(c+1)=a^2b^2c^2$, donde podemos simplificar $abc$ ya que los tres números son no nulos. Esto nos da
$$(a+1)(b+1)(c+1)=abc\Leftrightarrow 1+a+b+c+ab+bc+ac=0.$$
Esto nos da la igualdad deseada ya que, sumando las tres ecuaciones originales, se tiene claramente que $a+b+c=0$.
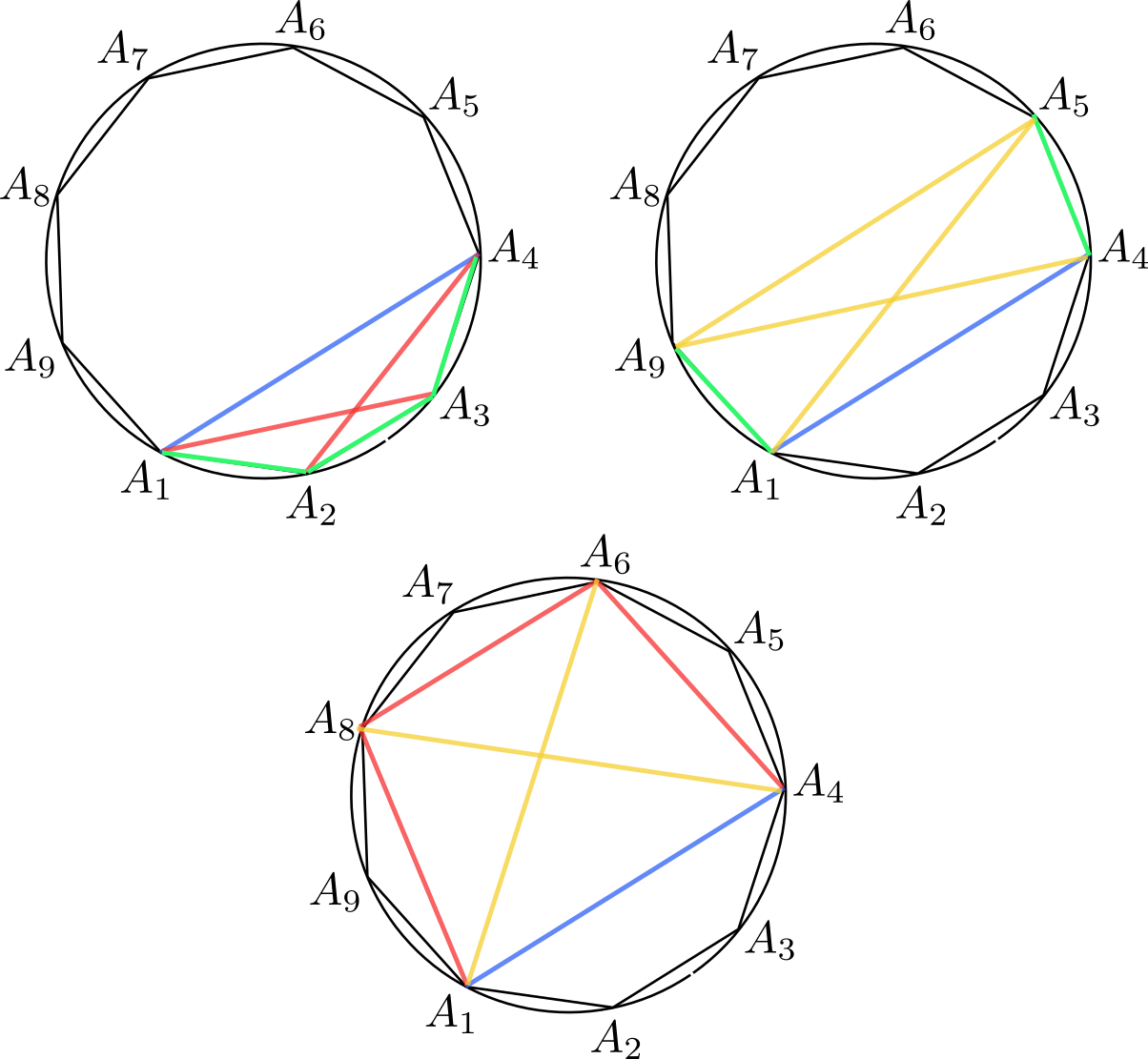
El apartado (b) es bastante estándar a partir del teorema de Ptolomeo para cuadriláteros cíclicos aplicado a cuadriláteros con vértices cuatro de los vértices del eneágono. Observemos que tenemos que probar tres relaciones: (1) $a^2+a=b^2$, (2) $b^2+b=c^2$ y (3) $c^2-c=a^2$ (hemos cambiado $c$ por $-c$ en las ecuaciones del sistema del apartado a). La primera de ellas se sigue de aplicar Ptolomeo al cuadrilátero $A_1A_2A_3A_4$, la segunda al cuadrilátero $A_1A_4A_6A_8$ y la tercera al cuadrilátero $A_1A_4A_5A_9$, como se indica en la figura (los segmentos verdes son iguales a $a$, los rojos a $b$, los azules a $1$ y los amarillos a $c$):

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre