Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Informar de error en enunciado Informar de procedencia del problema
- Probar que si una terna de números positivos $(a,b,c)$ verifica el sistema de ecuaciones \[\left\{\begin{array}{l}a^2+a=b^2,\\b^2+b=c^2,\\c^2+c=a^2,\end{array}\right.\] entonces $(a-b)(b-c)(c-a)=1$.
- Supongamos que $A_1A_2\ldots A_9$ es un eneágono regular tal que \[A_1A_4=1,\qquad A_1A_2=a,\qquad A_1A_3=b,\qquad A_1A_5=c.\] Probar que la terna $(a,b,-c)$ cumple el sistema del apartado anterior.
El apartado (b) es bastante estándar a partir del teorema de Ptolomeo para cuadriláteros cíclicos aplicado a cuadriláteros con vértices cuatro de los vértices del eneágono. Observemos que tenemos que probar tres relaciones: (1) $a^2+a=b^2$, (2) $b^2+b=c^2$ y (3) $c^2-c=a^2$ (hemos cambiado $c$ por $-c$ en las ecuaciones del sistema del apartado a). La primera de ellas se sigue de aplicar Ptolomeo al cuadrilátero $A_1A_2A_3A_4$, la segunda al cuadrilátero $A_1A_4A_6A_8$ y la tercera al cuadrilátero $A_1A_4A_5A_9$, como se indica en la figura (los segmentos verdes son iguales a $a$, los rojos a $b$, los azules a $1$ y los amarillos a $c$):
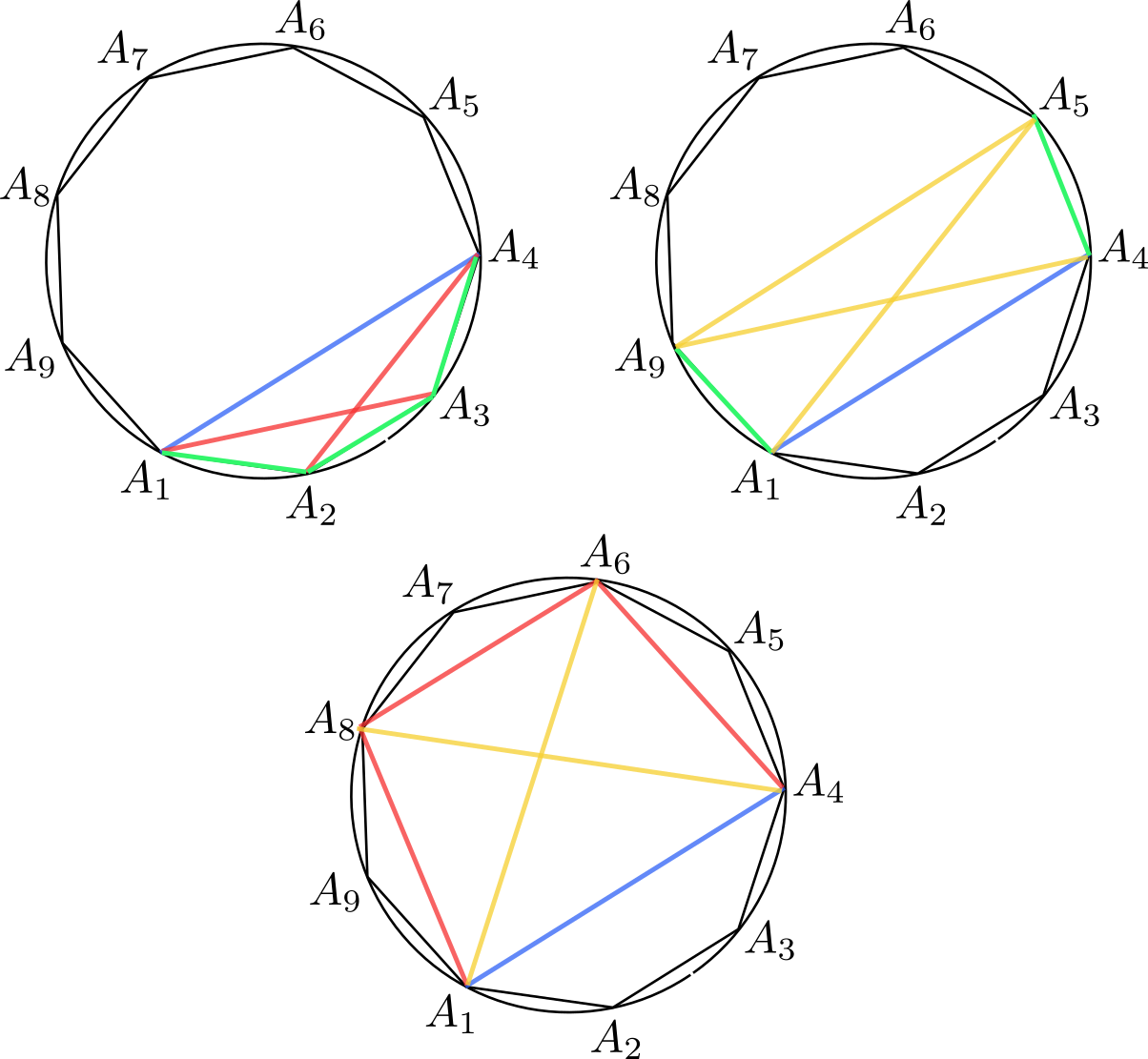
Informar de error en enunciado Informar de procedencia del problema
Para probar la otra desigualdad, prolongamos $AP$ hasta un punto $Q$ en $BC$. La desigualdad triangular en el triángulo $BPQ$ nos dice que $BP\leq PQ+BQ$ y en el triángulo $ACQ$ también nos dice que $AQ\leq AC+QC$. Entonces, podemos escribir $$AP+BP\leq AP+PQ+BQ=AQ+BQ\leq AC+QC+BQ=AC+BC.$$ De la misma forma, se prueba que $AP+CP\leq AB+BC$ y $BP+CP\leq AB+AC$. Sumando estas tres desigualdades, llegamos a que $AP+BP+CP\leq p$.
Nota. Si buscamos constantes $m$ y $M$ tales que $mp\leq AP+BP+CP\leq Mp$ (que no dependen del punto $P$ ni del triángulo $ABC$), tomar $m=\frac{1}{2}$ es una elección óptima ya que la igualdad se da en el caso límite en que $A=P$ son el punto medio del segmento $BC$. En cambio, la constante $M=1$ del enunciado no es óptima, por lo que puede que otra demostración dé de hecho una constante mejor. La obtención del valor óptimo de $M$ es un problema más difícil que puede resolverse usando el punto de Fermat del triángulo (que es el que minimiza la suma de distancias a los tres vértices).
Informar de error en enunciado Informar de procedencia del problema
Consideremos el círculo que pasa por $O$, $A$ y $B$, el círculo que pasa por $O$, $B$ y $C$ y el círculo que pasa por $O$, $A$ y $C$. Si $P\neq O$, entonces $P$ estará en el exterior en uno de estos tres círculos (ya que no tienen puntos interiores común al pasar todos por $O$). Pongamos que $P$ está en el exterior del círculo que pasa por $O$, $A$ y $B$ sin perder generalidad. Las propiedades del arco capaz y del ángulo central nos dicen que $\angle APB\lt \angle AOB=2\angle ACB$, luego no se da la igualdad y hemos terminado.
Nota. Supongamos que $P$ es un punto que se encuentra en el mismo semiplano que $O$ respecto de la recta $AB$. Hemos usado la propiedad de que si $P$ está en el exterior del círculo que pasa por $O$, $A$ y $B$, entonces $\angle APB\lt \angle AOB$. Si, por el contrario, el punto $P$ está en el interior del círculo, entonces $\angle APB\gt \angle AOB$. La igualdad $\angle APB=\angle AOB$ se da únicamente cuando $P$ es parte de la circunferencia.
Informar de error en enunciado Informar de procedencia del problema
Ahora bien, el área de $ABC$ se puede calcular como $S=\frac{1}{2}(a+b+c)r$ y también como $S=\frac{1}{2}ah$. Igualando estas dos fórmulas, tenemos que $r=\frac{1}{3}h$ si, y sólo si, $\frac{1}{6}(a+b+c)h=\frac{1}{2}ah$ y esto a su vez equivale a que $b+c=2a$. Obtenemos así que la condición buscada es que la longitud de un lado sea la media aritmética de las longitudes de los otros dos.
Nota. La condición de que el triángulo no sea equilátero es para que el baricéntro y el incentro no sean el mismo punto. ¿Sabrías demostrar por qué?
Informar de error en enunciado Informar de procedencia del problema