Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Llamemos $\Gamma_1,\Gamma_2,\Gamma_3,\Gamma_4,\Gamma_5$ a las circunferencias y supongamos por hipótesis que existen puntos $p_1,p_2,p_3,p_4,p_5$ tales que $p_i\in\Gamma_j$ siempre que $j\neq i$. Si dos de estos puntos son iguales, entonces hemos terminado (por ejemplo, si $p_1=p_2$, entonces este punto está en las cinco circunferencias puesto que $p_1$ está en todas menos en $\Gamma_1$, pero $p_2$ sí que está en $\Gamma_1$).

Supongamos entonces que los cinco puntos $p_1,p_2,p_3,p_4,p_5$ son distintos. En particular, $p_1,p_2,p_3$ son tres puntos distintos tanto en $\Gamma_4$ como en $\Gamma_5$. Como tres puntos distintos determinan una única circunferencia, deducimos que $\Gamma_4=\Gamma_5$, luego $p_5$ está también en $\Gamma_5$ y, por tanto, es un punto común a todas las circunferencias.

Solución. Si prolongamos los lados del hexágono, se formarán dos triángulos equiláteros (que contienen al hexágono) ya que sus ángulos interiores son iguales y, por tanto, iguales a $120º$ (ver figura). Si llamamos $a,b,c,d,e,f$ a las longitudes de los lados del hexágono (etiquetados de forma consecutiva), el hecho de que tales triángulos sean equiláteros se traduce en que sus lados son iguales, es decir: \begin{align*} a+b+c=c+d+e=e+f+a,\\ b+c+d=d+e+f=f+a+b. \end{align*} Para llegar a estas igualdades, también hemos usado que al prolongar los lados $a$ y $c$ se forma otro triángulo equilátero de lado $b$ (y lo mismo ocurre para el resto de lados, como se ve en la figura). De las dos ecuaciones anteriores, se llega fácilmente a que \[f-c=b-e=d-a.\] Estas diferencias se pueden suponer positivas, si tomamos $f=6$ como el mayor de los lados en nuestro etiquetado. Como $a,b,c,d,e,f$ son los números del $1$ al $6$ en cierto orden, las diferencias anteriores sólo pueden ser iguales a $1$ y $3$. Además, tras aplicar una simetría axial, podemos suponer que $b$ es mayor que $d$, lo que nos da dos posibles casos:

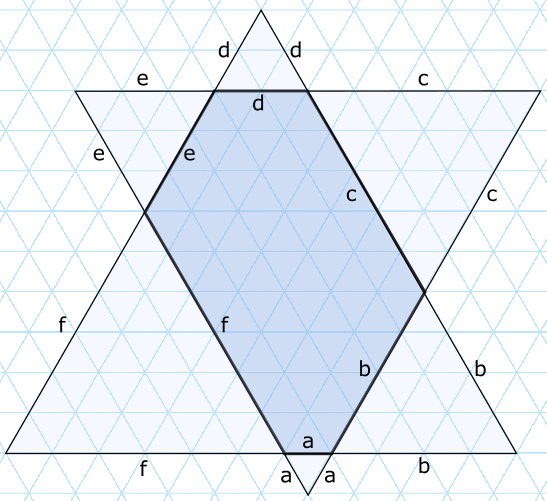
• [Diferencia 3]: $(a,b,c,d,e,f)=(1,5,3,4,2,6)$. El área del hexágono es el área de un triángulo equilátero de lado $a+b+f=12$ menos la suma de las áreas de tres triángulos equiláteros de lados $b=5$, $d=4$ y $f=6$. Como el área de un triángulo equilátero de lado $\ell$ es $\frac{\sqrt{3}}{4}\ell^2$, tenemos que el área del hexágono es \[A=\frac{\sqrt{3}}{4}(12^2-5^2-4^2-6^2)=\frac{67\sqrt{3}}{4}.\]
• [Diferencia 1]: $(a,b,c,d,e,f)=(1,4,5,2,3,6)$. Razonando de forma análoga y teniendo en cuenta que $a+b+f=11$, $b=4$, $d=2$ y $f=6$, llegamos a que \[A=\frac{\sqrt{3}}{4}(11^2-4^2-2^2-6^2)=\frac{65\sqrt{3}}{4}.\]

En la figura, hemos dibujado el segundo de estos dos hexágonos con la ayuda de una malla triangular (el primero se haría de forma similar). Estos son, por tanto, los dos únicos posibles valores del área.

Solución. Sean $P$, $Q$ y $R$ los pies de las alturas de $ABC$ sobre los lados $AB$, $AC$ y $BC$, respectivamente y llamemos $\alpha$, $\beta$ y $\gamma$ a los ángulos de $ABC$ por simplicidad. Vamos a suponer en primer lugar que el triángulo es acutángulo (primera figura). Como el cuadrilátero $APHQ$ tiene dos ángulos rectos, deducimos que $\angle PHQ=\pi-\beta$, luego $\angle CHQ=\beta$. Esto nos dice que los triángulos $CHQ$ y $ABQ$ son semejantes, luego tenemos que $\frac{CH}{HQ}=\frac{AB}{BQ}$. Por hipótesis, estamos suponiendo que $AB=CH$, luego $HQ=BQ$. Es inmediato entonces que $BHQ$ es un triángulo rectángulo isósceles, de donde $\angle HBQ=\frac{\pi}{4}$. Contando ángulos en el triángulo $BRC$, llegamos a que $\gamma=\frac{\pi}{4}$, lo que responde a la pregunta del enunciado.

Supongamos ahora que $\alpha=\frac\pi2$ (se razona igualmente para $\beta=\frac\pi2$), en cuyo caso se tiene que $A=H$ y $ABC$ es un triángulo rectángulo isósceles, de donde también tenemos que $\gamma=\frac{\pi}{4}$. Otro caso posible es que $\alpha\gt\frac\pi2$ (análogamente, se razona para $\beta=\frac\pi2$). En tal caso, la demostración del caso acutángulo se adapta a este caso, teniendo en cuenta ahora que $CHQ$ y $ABQ$ son semejantes por un motivo distinto: ambos son triángulos rectángulos y tienen el mismo ángulo en el vértice común $A$ (opuestos por el vértice).

Queda por analizar el caso en que $\gamma\geq\frac\pi2$. El caso $\gamma=\frac\pi2$ es imposible ya que se tendría que $CH=0$, por lo que supondremos $\gamma\gt\frac\pi2$ (segunda figura). En este caso, $CHQ$ y $ABQ$ vuelven a ser semejantes, lo que nos da de nuevo que $\angle HBQ=\frac{\pi}{4}$. En el triángulo $\angle HBR$, tenemos que $\angle HBR=\frac{\pi}{4}$, $\angle HRB=\frac\pi2$ y $\angle BHR=\pi-\gamma$, luego $\gamma=\frac{3\pi}{4}$.

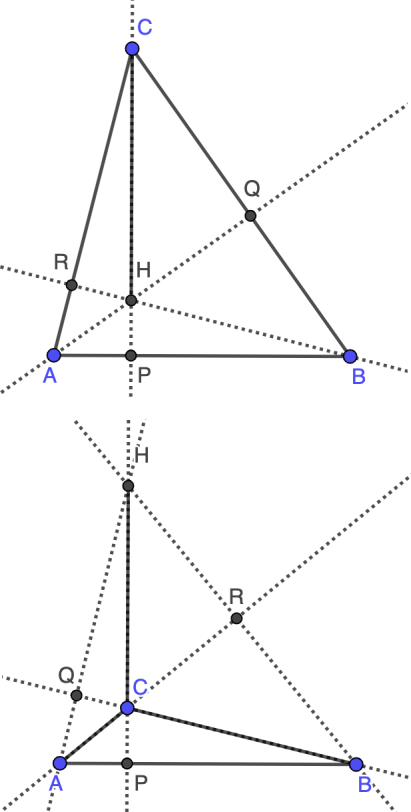
Nota. Este problema es sencillo ya que sólo hay que identificar dos triángulos semejantes en una situación estándar (involucrando al ortocentro). No obstante, se ha marcado con tres estrellas porque es difícil darse cuenta de que puede aparecer una solución distinta si el triángulo es obtusángulo.

Solución. Para cada $i$ entre $1$ y $n$, consideremos la circunferencia $\Gamma_i$ de centro $P_i$ y radio $|r_i|$. No puede haber dos de los $r_i$ que sean negativos o cero ya que entonces tendríamos una distancia negativa o cero (los puntos deben ser distintos). Distinguimos casos:

• Si todos los $r_i$ son positivos, entonces las circunferencias $\Gamma_1,\ldots,\Gamma_n$ son tangentes exteriores dos a dos. Es bien conocido que el número máximo de circunferencias mutuamente tangentes es cuatro (ver la nota), lo que nos da $n\leq 4$ en este caso.
• Si existe un $r_i$ cero y el resto son positivos, pongamos $r_1=0$, entonces las circunferencias $\Gamma_2,\ldots,\Gamma_n$ son mutuamente tangentes exteriormente y además $P_1$ pertenece a todas ellas. Como los puntos de tangencia de $\Gamma_2,\ldots,\Gamma_n$ son distintos, el punto $P_i$ no puede pertenecer a todas las circunferencias salvo que $n=3$. Esto nos dice que $n\leq 3$ en este caso.
• Si existe un $r_i$ negativo y el resto son positivos, pongamos $r_1\lt 0$, entonces las circunferencias $\Gamma_2,\ldots,\Gamma_n$ son mutuamente tangentes exteriormente, mientras que $\Gamma_1$ es tangente interior a todas las demás (siendo $r_1+r_i\gt 0$, se tiene que $|r_1|\leq |r_i|$ para todo $i$). Esto nos dice que $n\geq 2$ en este caso ya que $\Gamma_1$ no puede ser interior a dos o más circunferencias tangentes exteriormente.

Hemos probado así que el máximo buscado es $n=4$.

Nota. El hecho de que el máximo número de circunferencias mutuamente tangentes es cuatro es consecuencia, por ejemplo, del teorema de los círculos de Descartes (aunque puede razonarse independientemente de forma más elemental).

Solución. Sean $r$ y $s$ las tangentes exteriores a las circunferencias de centros $A$ y $C$ y $r'$ y $s'$ las tangentes exteriores a las circunferencias de centros $B$ y $D$. Una circunferencia tangente a $r$ y $s$ debe equidistar de ambas rectas por lo que su centro pertenece a la bisectriz del ángulo formado por estas (si $r$ y $s$ son paralelas, entonces el centro pertenece a una paralela equidistante a ambas). Esto nos dice que las circunferencias tangentes a $r$ y $s$ tienen su centro en una recta, luego esta debe ser la que contiene a la diagonal $AC$. De la misma forma, debe pertenecer a la diagonal $BD$, luego el centro ha de ser el centro del rectángulo, que denotaremos por $O$.

Consideremos $A'$, $O'$ y $C'$ los pies de las perpendiculares a $r$ que pasan por $A$, $O$ y $C$. Como $AO=OC$, se deduce del teorema de Tales (las rectas $r$ y $AC$ son cortadas por tres paralelas $AA'$, $OO'$ y $CC'$) que $OO'=\frac{1}{2}(AA'+CC')=\frac{1}{2}(a+c)$. Por tanto, la circunferencia con centro $O$ y tangente a $r$ y $s$ tiene radio $\frac{1}{2}(a+c)$. Análogamente, la circunferencia con centro $O$ y tangente a $r'$ y $s'$ tiene radio $\frac{1}{2}(b+d)$. Como $a+c=b+d$, deducimos que ambas son la misma circunferencia y, por tanto, el cuadrilátero que se forma admite una circunferencia inscrita.