Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 79
Sea \(H\) el ortocentro de un triángulo, \(P\) el pie de una altura y \(Q\) el otro punto de corte de la recta \(AP\) (distinto de \(A\)) con la circunferencia circunscrita. Demostrar que \(HP=PQ\).
pistasolución 1info
Pista. Demuestra, haciendo cálculos con ángulos, que el triángulo \(BHQ\) es isósceles.
Solución. Por fijar notación, supongamos que estamos trazando la altura desde el vértice \(A\) y sean \(B\) y \(C\) los otros dos vértices. Por la propiedad del arco capaz sobre la circunferencia circunscrita, tenemos que \(\angle HBQ=\angle ACB\) y, por otro lado, \(\angle BHQ=90-\angle HBP=\angle ACB\), usando que los triángulos \(BHP\) y \(BRC\) son rectángulos, donde \(R\) es el pie de la altura por \(B\). Hemos probado así que el triángulo \(BHQ\) es isósceles y, como \(BC\) es la altura de este triángulo relativa al vértice \(B\), tenemos que corta al segmeno \(HQ\) en su punto medio \(P\), que es lo que queríamos probar.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 78
En el triángulo \(ABC\) sea \(D\) el punto de corte de la bisectriz trazada desde \(C\) al lado \(AB\). Sabiendo que el centro de la circunferencia inscrita en el triángulo \(BCD\) coincide con el centro de la circunferencia circunscrita al triángulo \(ABC\), ¿cuáles son los ángulos de \(ABC\)?
pistasolución 1info
Pista. Demuestra que el triángulo \(ABC\) es isósceles.
Solución. Sea \(O\) el circuncentro del triángulo \(ABC\) y \(M\) y \(N\) los puntos medios de los lados \(AB\) y \(BC\), respectivamente. Entonces, \(BM=BN\) por ser ambas tangentes a la circunferencia inscrita al triángulo \(BCD\), y, como \(BM=\frac{1}{2}BC\) y \(BN=\frac{1}{2}AB\), tenemos que el triángulo original cumple que \(\angle ACB=\angle BAC\). Además, \(\frac{1}{4}\angle ACB=\angle OCN=\angle NBO=\frac{1}{2}\angle CBA\), donde se ha usado que \(\angle COB\) es isósceles. De aquí tenemos que \(\angle CBA=\frac{1}{2}\angle ACB\) y, usando finalmente que \(180=\angle CAB+\angle CBA+\angle ACB=\frac{5}{2}\angle ABC\), llegamos a que \(\angle ABC=36\) y \(\angle CAB=\angle CBA=72\).
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 77
Sea $ABC$ un triángulo. Consideremos los puntos $D$ y $E$ sobre el lado $BC$ de forma que las rectas $AD$ y $AE$ son paralelas a las tangentes a la circunferencia circunscrita al triángulo que pasan por $C$ y $B$, respectivamente. Demostrar que
\[\frac{BE}{CD}=\frac{AB^2}{AC^2}{.}\]
pistasolución 1info
Pista. Si tomamos la paralela a $BC$ que pasa por $A$ y llamamos $P$ y $Q$, respectivamente, a los puntos de corte de esta recta con la tangente por $B$ y con la tangente por $C$ definidas en el enunciado, demuestra que $ABC$, $ABP$ y $ACQ$ son semejantes.
Solución. Consideremos la recta paralela a $BC$ que pasa por $A$ y llamamos $P$ y $Q$, respectivamente, a los puntos de corte de esta recta con la tangente por $B$ y con la tangente por $C$ definidas en el enunciado. Entonces, se cumple que $BE=AP$ y $CD=AQ$, ya que los cuadriláteros $APBE$ y $AQCD$ son paralelogramos. Si denotamos por $\alpha,\beta,\gamma$ los ángulos del triángulo $ABC$, el paralelismo de $PQ$ y $BC$ también nos asegura que $\angle PAB=\beta$ y $\angle QAC=\gamma$. Por otro lado, como $\angle ACQ$ es el ángulo semiinscrito correspondiente y $AC$ está abarcado por el ángulo $\angle ABC=\beta$, se sigue que $\angle ACQ=\beta$ y, de la misma forma, $\angle ACQ=\gamma$. Así, hemos probado que los triángulos $ABC$, $ABP$ y $ACQ$ son semejantes. Por tanto, $AP/AB=AB/BC$ y $AQ/AC=AC/BC$, luego despejamos $BE=AP=AB^2/BC$ y $CD=AQ=AC^2/BC$, y obtenemos fácilmente la identidad del enunciado.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 75
OIM, 1993-P4
Sea $ABC$ un triángulo equilátero y sean $M$ y $N$ puntos de $AB$ y $AC$, respectivamente, tales que el segmento $MN$ es tangente a la circunferencia inscrita de $ABC$. Demostrar que
\[\frac{AM}{MB}+\frac{AN}{NC}=1{.}\]
pistasolución 1info
Pista. Demostrar que el triángulo $AMN$ tiene perímetro igual al lado del triángulo equilátero inicial y, de ahí, sustituir $MB=MN+AN$ y $NC=MN+AM$.
Solución. Llamemos $T$ al punto de tangencia de $MN$ con la circunferencia inscrita y $\ell$ al lado del triángulo. Observemos que la longitud de $MT$ es igual a la del segmento que une $M$ con el punto medio del lado $AB$ por la propiedad de tangencia. Por tanto, $AM+MT=\frac{\ell}{2}$ y, de la misma forma, $AN+NT=\frac{\ell}{2}$, con lo que el perímetro del triángulo $AMN$ es exactamente $\ell$. Así, podemos escribir
\[\frac{AM}{MB}+\frac{AN}{NC}=\frac{AM}{MN+AN}+\frac{AN}{MN+AM}=\frac{AM^2+AN^2+MN(AN+AM)}{MN^2+MN(AN+AM)+AM\cdot AN}{.}\]
Por lo tanto, quisiéramos demostrar que $AM^2+AN^2=MN^2+AM\cdot AN$, pero esto se deduce de forma fácil del teorema del coseno aplicado al triángulo $AMN$ teniendo en cuenta que $\angle MAN=60^\circ$.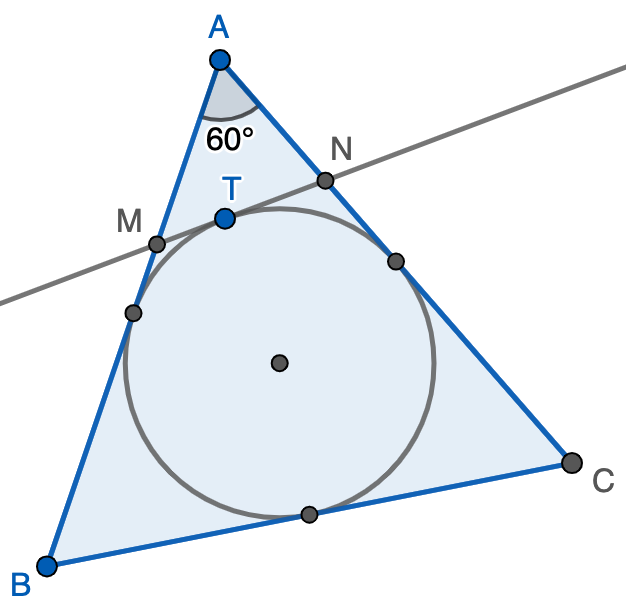

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 74
Sea $ABC$ un triángulo y $M$ el punto medio del lado $BC$. Si $r_1$ y $r_2$ son los inradios de los triángulos $ABM$ y $ACM$ respectivamente, demostrar que $r_1<2r_2$.
pistasolución 1info
Pista. Observa que el área del triángulo $ABM$ es la misma que la del triángulo $ACM$. ¿Qué relación existe entre el área de un triángulo, su perímetro y su radio inscrito?
Solución. El área del triángulo $ABM$ es la misma que la del triángulo $ACM$ ya que tienen la misma base $BM=CM$ y la misma altura. Por lo tanto, si llamamos $p_1$ y $p_2$ al semiperímetro de $ABM$ y $ACM$ respectivamente, tenemos que $r_1p_1=r_2p_2$ y deducimos que
\[\frac{r_1}{r_2}=\frac{p_2}{p_1}=\frac{AM+CM+AC}{AM+BM+MB}{.}\]
Así, tenemos que probar que $AM+CM+AC<2(AM+BM+AB)$ o, lo que es lo mismo, $AM+CM+2AB>AC$ y esta última desigualdad es consecuencia de la desigualdad triangular $AM+CM>AC$ (en el triángulo $ACM$) y de que $2AB>0$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre