Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 75
OIM, 1993-P4
Sea $ABC$ un triángulo equilátero y sean $M$ y $N$ puntos de $AB$ y $AC$, respectivamente, tales que el segmento $MN$ es tangente a la circunferencia inscrita de $ABC$. Demostrar que
\[\frac{AM}{MB}+\frac{AN}{NC}=1{.}\]
pistasolución 1info
Pista. Demostrar que el triángulo $AMN$ tiene perímetro igual al lado del triángulo equilátero inicial y, de ahí, sustituir $MB=MN+AN$ y $NC=MN+AM$.
Solución. Llamemos $T$ al punto de tangencia de $MN$ con la circunferencia inscrita y $\ell$ al lado del triángulo. Observemos que la longitud de $MT$ es igual a la del segmento que une $M$ con el punto medio del lado $AB$ por la propiedad de tangencia. Por tanto, $AM+MT=\frac{\ell}{2}$ y, de la misma forma, $AN+NT=\frac{\ell}{2}$, con lo que el perímetro del triángulo $AMN$ es exactamente $\ell$. Así, podemos escribir
\[\frac{AM}{MB}+\frac{AN}{NC}=\frac{AM}{MN+AN}+\frac{AN}{MN+AM}=\frac{AM^2+AN^2+MN(AN+AM)}{MN^2+MN(AN+AM)+AM\cdot AN}{.}\]
Por lo tanto, quisiéramos demostrar que $AM^2+AN^2=MN^2+AM\cdot AN$, pero esto se deduce de forma fácil del teorema del coseno aplicado al triángulo $AMN$ teniendo en cuenta que $\angle MAN=60^\circ$.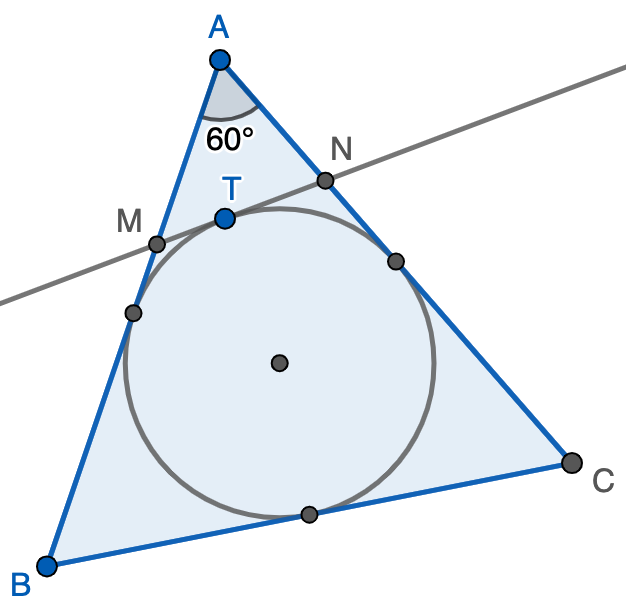

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 74
Sea $ABC$ un triángulo y $M$ el punto medio del lado $BC$. Si $r_1$ y $r_2$ son los inradios de los triángulos $ABM$ y $ACM$ respectivamente, demostrar que $r_1<2r_2$.
pistasolución 1info
Pista. Observa que el área del triángulo $ABM$ es la misma que la del triángulo $ACM$. ¿Qué relación existe entre el área de un triángulo, su perímetro y su radio inscrito?
Solución. El área del triángulo $ABM$ es la misma que la del triángulo $ACM$ ya que tienen la misma base $BM=CM$ y la misma altura. Por lo tanto, si llamamos $p_1$ y $p_2$ al semiperímetro de $ABM$ y $ACM$ respectivamente, tenemos que $r_1p_1=r_2p_2$ y deducimos que
\[\frac{r_1}{r_2}=\frac{p_2}{p_1}=\frac{AM+CM+AC}{AM+BM+MB}{.}\]
Así, tenemos que probar que $AM+CM+AC<2(AM+BM+AB)$ o, lo que es lo mismo, $AM+CM+2AB>AC$ y esta última desigualdad es consecuencia de la desigualdad triangular $AM+CM>AC$ (en el triángulo $ACM$) y de que $2AB>0$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 34
Calcular la razón entre la diagonal y el lado de un pentágono regular.
pistasolución 1info
Pista. Traza las diagonales y busca triángulos semejantes en la figura resultante.
Solución. Llamemos \(A_1\), \(A_2\), \(A_3\), \(A_4\) y \(A_5\) a los vértices del pentágono en sentido antihorario y \(l\) y \(d\) al lado y la diagonal del pentágono. Sea además \(P\) el punto de corte de las diagonales \(A_1A_3\) y \(A_2A_5\). Como cada diagonal es paralela a un lado del pentágono, se tiene que el cuadrilátero \(PA_3A_4A_5\) es un paralelogramo y, por tanto, \(PA_5=l\) y \(PA_2=d-l\). Finalmente, como los triángulos \(A_2PA_3\) y \(A_3A_4A_1\) son semejantes (tienen los lados paralelos), se cumple que \(\frac{A_2P}{A_3A_4}=\frac{A_2A_3}{A_1A_3}\) y, sustituyendo el valor de cada segmento en términos de \(l\) y \(d\), \(\frac{d-l}{l}=\frac{l}{d}\). De aquí puede deducirse fácilmente que \((\frac{d}{l})^2-\frac{d}{l}-1=0\) y, resolviendo esta ecuación de segundo grado, tenemos finalmente que
\[\frac{d}{l}=\frac{1+\sqrt{5}}{2},\]
es decir, la razón entre la diagonal de un pentágono regular y su lado es la razón áurea.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 5
IMO, 1995-P5
Sea $ABCDEF$ un hexágono convexo tal que $AB=BC=CD$, $DE=EF=AF$ y $\angle BCD=\angle EFA=\frac{\pi}{3}$. Sean $P$ y $Q$ dos puntos interiores al hexágono de forma que los ángulos $\angle APB$ y $\angle DQE$ valen ambos $\frac{2\pi}{3}$. Demostrar que
\[AP+PB+PQ+DQ+QE\geq CF.\]
pistasolución 1info
Pista. La longitud de una poligonal es siempre mayor o igual que la distancia que une sus extremos por la desigualdad triangular. Intenta relacionar $AP+PB+PQ+DQ+QE$ con la longitud de una poligonal.
Solución. Sean $M$ y $N$ puntos exteriores al hexágono tales que $ABM$ y $DEN$ sean triángulos equiláteros. Entonces, la propiedad de arco capaz nos asegura que $P$ está en la circunferencia circunscrita al triángulo $ABM$ y el teorema de Ptolomeo (aplicado al cuadrilátero $AMBP$) nos dice que $AP+PB=MP$. De la misma forma, obtenemos que $DQ+QE=NQ$ y se cumple que $AP+PB+PQ+DQ+QE=MP+PQ+QN\geq MN$ ya que $MPQN$ es una poligonal que une $M$ y $N$ y su longitud siempre es mayor que la del segmento $MN$. Ahora bien, el octógono $AMBCDNEF$ es simétrico respecto de la recta $BE$ por las condiciones del enunciado luego se tiene que $MN=CF$ y hemos terminado.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 4
Sea $ABCD$ un paralelogramo y supongamos que $AC$ es su diagonal mayor. Desde $C$ se trazan perpendiculares a las rectas $AB$ y $AD$, con pies en $E$ y $F$ respectivamente. Demostrar que
\[AB\cdot AE+AD\cdot AF=AC^2{.}\]
pistasolución 1info
Pista. Aplica el teorema de Pitágoras a los triángulos rectángulos que se forman.
Solución. Aplicando el teorema de Pitágoras a los triángulos rectángulos $ACE$ y $BCE$ y usando que $BC=AD$, obtenemos que
\begin{eqnarray*}
AC^2&=&AE^2+EC^2=AE^2+BC^2-BE^2\\
&=&(AE+BE)(AE-BE)+AD^2=AB\cdot AE+AB\cdot BE+AD^2{.}
\end{eqnarray*}
Ahora bien, como los triángulos $BCE$ y $CDF$ son semejantes (es fácil ver que tienen dos ángulos iguales), tenemos que $BE/BC=DF/CD$ y, teniendo en cuenta que $CD=AB$, deducimos que $BE\cdot AB=AD\cdot DF$. Sustituyendo esto último en la igualdad antes obtenida para $AC^2$, la fórmula del enunciado queda probada.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre