Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Informar de error en enunciado Informar de procedencia del problema
Nota. No se puede expresar el resultado final en términos de funciones trigonométricas.
En el pentágono regular de lado $1$ de la figura, los triángulos $ACD$ y $DEP$ son semejantes pues sus lados son paralelos. Si llamamos $d$ a la longitud de la diagonal del pentágono, la semejanza $\frac{AD}{CD}=\frac{DE}{PE}$ se escribe como $\frac{d}{1}=\frac{1}{d-1}$, de donde $d$ cumple la ecuación $d^2-d-1=0$, de la que nos quedamos con la única solución positiva $d=\frac{1+\sqrt{5}}{2}$, la razón áurea. Ahora bien, el triángulo $ABQ$ de la figura es rectángulo y cumple $\angle BAQ=54$, luego \begin{align*}
\mathrm{sen}(54)&=BD=\frac{d}{2}=\frac{1+\sqrt{5}}{4},\\
\cos(54)&=AQ=\sqrt{1-BQ^2}=\sqrt{1-\left(\tfrac{1+\sqrt{5}}{4}\right)^2}=\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}.
\end{align*}
De esta forma, tenemos que el área del triángulo es
\[8\,\mathrm{sen}(54)\cos(54)=8\frac{1+\sqrt{5}}{4}\cdot\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}=\sqrt{10+2\sqrt{5}}.\]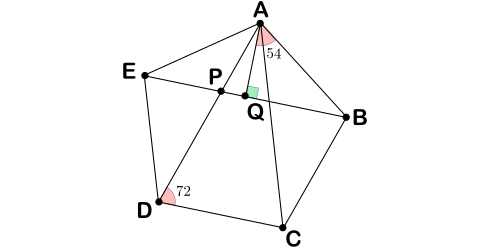
Informar de error en enunciado Informar de procedencia del problema
El área del triángulo $AOB$ se puede calcular de dos maneras equivalentes: \[\tfrac{1}{2}AB\cdot OP=\mathrm{Area}(AOB)=\tfrac{1}{2}BO\cdot AO\,\mathrm{sen}(60^\circ)=\tfrac{\sqrt{3}}{4}BO\cdot AO.\] Multiplicando por $(1+\lambda)$ y usando que \begin{align*} AC&=AO+OC=(1+\lambda)AO=7,\\ PQ&=OP+OQ=(1+\lambda)OP=4\sqrt{3}, \end{align*} según la información del enunciado, la igualdad de áreas se puede reescribir como \[AB\cdot (1+\lambda)OP=\tfrac{\sqrt{3}}{2}BO\cdot (1+\lambda)AO\ \Leftrightarrow\ \frac{BO}{AB}=\frac{8}{7}.\] Ahora bien, el teorema del coseno aplicado al triángulo $AOB$ nos dice que \[AB^2=BO^2+AO^2-2BO\cdot AO\cos(60^\circ)=BO^2+AO^2-BO\cdot AO,\] Dividiendo por $AB^2$, esto puede reescribirse como \[1=\left(\frac{BO}{AB}\right)^2+\left(\frac{AO}{AB}\right)^2-\frac{BO}{AB}\cdot \frac{AO}{AB}.\] Sustituyendo $\frac{BO}{AB}=\frac{8}{7}$ nos queda una ecuación de segundo grado en la incógnita $\frac{AO}{AB}$, que se resuelve fácilmente dando dos soluciones positivas: $\frac{AO}{AB}=\frac{3}{7}$ y $\frac{AO}{AB}=\frac{5}{7}$. Teniendo en cuenta que $AO=\frac{7}{1+\lambda}$, las soluciones anteriores nos dan $(1+\lambda)AB=\frac{49}{3}$ o bien $(1+\lambda)AB=\frac{49}{5}$.
Finalmente, como el área del trapecio está dada por $S=\frac{1}{2}(AB+CD)PQ=\frac{1}{2}(1+\lambda)AB\cdot PQ$ y que $PQ=4\sqrt{3}$ es conocido, llegamos a que las posibles soluciones son \[S=\frac{98\sqrt{3}}{3}\quad\text{y}\quad S=\frac{98\sqrt{3}}{5}.\] Las dos soluciones se corresponden con que $C$ se proyecte sobre $AB$.

Informar de error en enunciado Informar de procedencia del problema
- Si $\mathrm{sen}(\alpha)=\mathrm{sen}(\beta)$ y $\mathrm{sen}(\gamma)=\mathrm{sen}(\delta)$, hay dos posibilidades. La primera es que $\alpha+\beta=180^\circ$ o $\beta+\delta=180^\circ$ (en cuyo caso, $P$ está en la diagonal $AC$ o $BD$, respectivamente). La segunda es que $\alpha=\beta$ y $\gamma=\delta$; como $\alpha+\beta+\gamma+\delta=360^\circ$, se tiene que $\alpha+\delta=180^\circ$ y $P$ está sobre $BD$.
- Si $\mathrm{sen}(\alpha)=\mathrm{sen}(\delta)$ y $\mathrm{sen}(\gamma)=\mathrm{sen}(\beta)$, se razona de forma totalmente análoga.
Informar de error en enunciado Informar de procedencia del problema
Nota. Hemos usado la identidad de factorización \[\mathrm{sen}(x)\mathrm{sen}(y)=\frac{\cos(x-y)-\cos(x+y)}{2},\] que se deduce fácilmente sumando las fórmulas de los cosenos de la suma y la diferencia.
Informar de error en enunciado Informar de procedencia del problema