Demuestra que en un triángulo se verifica: si $r$ es una recta que pasa por su baricentro y no pasa por ningún vértice, la suma de las distancias a dicha
recta de los vértices que quedan en un mismo semiplano es igual a la distancia del tercer vértice a dicha recta.
pistasolución 1solución 2info
Pista. Usa coordenadas y recuerda que las coordenadas del baricentro son la media aritmética de las coordenadas de los vértices.
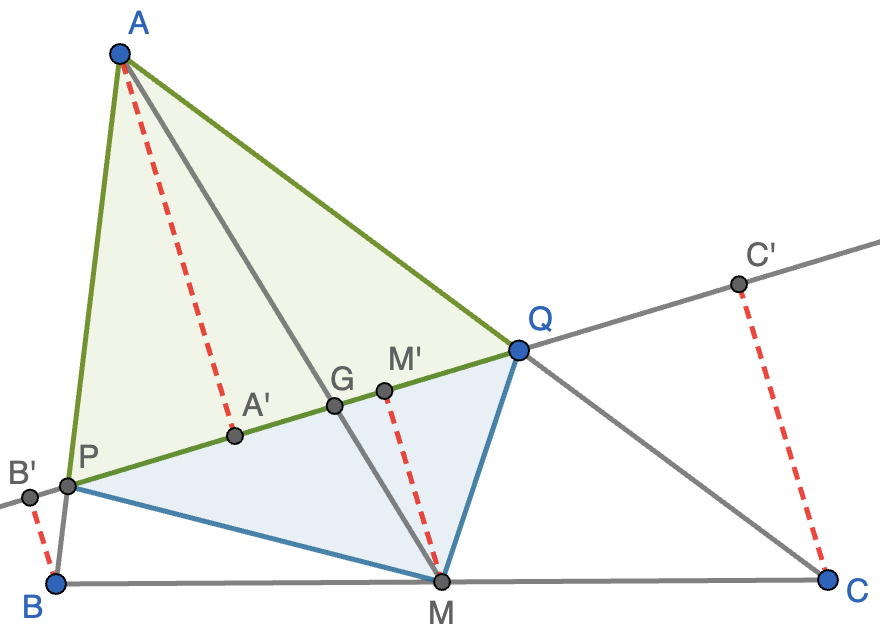
Solución. En primer lugar, nos damos cuenta de que $r$ no es una mediana y deja un vértice a un lado y dos al otro. Supondremos que es el vértice $A$ el que deja a un lado y $B$ y $C$ al otro. Sea $M$ el punto medio de $BC$, $G$ el baricentro y $P$ y $Q$ los puntos de corte de $r$ con los lados $AB$ y $BC$, respectivamente, como se muestra en la figura. También trazamos segmentos perpendiculares a $r$ por $A$, $B$, $C$ y $M$, que tienen sus pies en $A'$, $B'$, $C'$ y $M'$, respectivamente.
Sabemos que el baricentro divide a la mediana $AM$ en dos segmentos tales que $AG=2GM$, luego el triángulo $AGQ$ tiene doble de área del triángulo $GQM$ (tiene la misma altura y base doble) y el triángulo $AGP$ tiene el doble de área que el triángulo $PGM$. Por tanto, el área de $APQ$ (en verde) es también el doble que la de $PQM$ (en azul). Podemos calcular el área de $APQ$ como $\frac{1}{2}AA'\cdot PQ$ y el área de $PQM$ como $\frac{1}{2}MM'\cdot PQ$. Ahora nos damos cuenta de que $MM'=\frac{1}{2}(BB'+CC')$ por el teorema de Thales ya que $BB',MM',CC'$ son paralelas que cortan a $r$ y $BC$ con $BM=CM$. Por lo tanto, el área de $PQM$ es $\frac{1}{4}(BB'+CC')PQ$, que debe ser la mitad de $\frac{1}{2}AA'\cdot PQ$, luego necesariamente $AA'=BB'+CC'$, que es lo que queríamos demostrar.
Solución. Vamos a trabajar en coordenadas, escribiendo los vértices del triángulo como $(x_1,y_1)$, $(x_2,y_2)$ y $(x_3,y_3)$. Las coordenadas del baricentro son la media aritmética, es decir,
\[\left(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}\right).\]
Por tanto, una recta que pasa por este punto tendrá ecuación $Ax+By+C=0$, siendo $A,B,C\in\mathbb{R}$ tales que $A^2+B^2\neq 0$ y
\[A\frac{x_1+x_2+x_3}{3}+B\frac{y_1+y_2+y_3}{3}+C=0.\]
Esto último puede reescribirse como
\[\frac{Ax_1+By_1+C}{3}+\frac{Ax_2+By_2+C}{3}+\frac{Ax_3+By_3+C}{3}=0.\]
Como las tres fracciones suman cero, habrá dos de ellas con un signo y otra con el signo opuesto (no pueden ser cero porque la recta no pasa por ningún vértice). Supondremos que las dos primeras son del mismo signo y la tercera del signo opuesto, luego tomando valores absolutos, dividiendo por $\sqrt{A^2+B^2}$ y multiplicando por $3$, tenemos
\[\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}+\frac{|Ax_2+By_2+C|}{\sqrt{A^2+B^2}}=\frac{|Ax_3+By_3+C|}{\sqrt{A^2+B^2}}.\]
Cada fracción es la distancia desde el vértice correspondiente a la recta, luego el resultado está probado. El hecho de que dos fracciones tengan el mismo signo y otra el signo opuesto refleja el hecho de que la recta deja a dos puntos a un lado y al tercero al otro.
Dos esferas de radio $r$ son tangentes exteriores. Otras tres esferas de radio $R$ son tangentes exteriores entre sí dos a dos. Cada una de estas tres esferas es además tangente exterior a las dos primeras. Encuentra la relación entre $R$ y $r$.
pistasolución 1info
Pista. Encuentra un triángulo rectángulo con vértices en los centros y los puntos de tangencia.
Solución. Sea $O$ el centro de una de las esferas de radio $r$, $C$ el centro de una de las esferas de radio $R$ y $T$ el punto de tangencia de las dos esferas de radio $r$. Por la simetría de la figura, es evidente que $OCT$ es un triángulo rectángulo con ángulo recto en $T$. Como $T$ es un punto de la esfera de centro $O$, tenemos que $OT=r$; por la tangencia de las esferas de centros $O$ y $C$, tenemos que $OC=R+r$; finalmente, como los centros de las esferas de radio $R$ forman un triángulo equilátero de centro $T$ y lado $2R$, se tiene que $CT$ es $\frac{2}{3}$ de la altura de dicho triángulo, es decir $CT=\frac{2}{3}\cdot\frac{\sqrt{3}}{2}\cdot 2R=\frac{2\sqrt{3}}{3}R$. El teorema de Pitágoras nos dice entonces que
\[OC^2=OT^2+CT^2\ \Longleftrightarrow\ (R+r)^2=r^2+\tfrac{4}{3}R^2\ \Longleftrightarrow\ 2Rr=\tfrac{1}{3}R^2\ \Longleftrightarrow\ R=6r.\]
Esta es la relación buscada (observemos que se ha descartado la solución $R=0$ ya que no es posible en este problema).
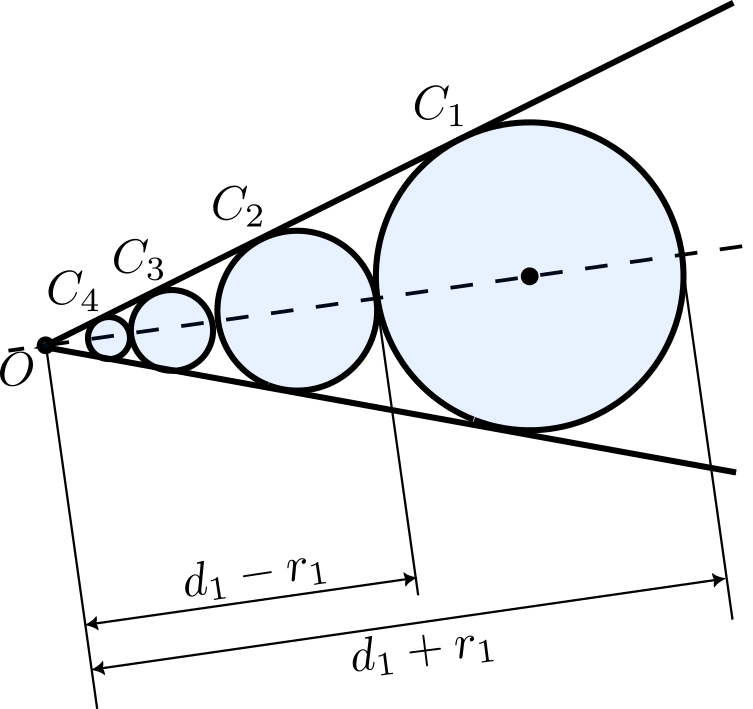
Dos semirrectas tienen su común origen en el punto $O$. Se considera una
circunferencia $C_1$ tangente a ambas semirrectas cuyo centro está situado
a distancia $d_1$ de $O$ y cuyo radio es $r_1$. Se construyen sucesivamente las circunferencias $C_n$, de modo que $C_n$ es tangente a las semirrectas, tangente exterior a $C_{n−1}$ y tal que la distancia de su centro a $O$, $d_n$, es menor que $d_{n−1}$ para $n\gt 1$. Halla la suma de las áreas de los círculos limitados por las circunferencias $C_n$ para todo $n$ en función de $r_1$ y $d_1$.
pistasolución 1info
Pista. Date cuenta de que existe una homotecia que lleva $C_k$ en $C_{k+1}$ para todo $k$. ¿Cuál es la razón de esta homotecia en términos de $r_1$ y $d_1$?
Solución. Sea $O_1$ el centro de $C_1$, que está sobre la bisectriz de las semirrectas dadas. Entonces, para pasar de la circunferencia $C_1$ a $C_2$, podemos hacer una homotecia de centro $O$ que lleva uno de los puntos de corte de $C_1$ con la bisectriz en el otro. Como el punto más alejado está a distancia $d_1+r_1$ y el más cercano a distancia $d_1-r_1$, la razón de la homotecia es $\lambda=\frac{d_1-r_1}{d_1+r_1}$. Como la homotecia transforma las áreas en un factor $\lambda^2$ y lleva cada circunferencia $C_k$ en $C_{k+1}$, tenemos que
\[\sum_{k=1}^n\mathrm{Area}(C_k)=\sum_{k=1}^n\lambda^{2k-2}\mathrm{Area}(C_1)=\frac{\pi r_1^2(1-\lambda^{2n+2})}{1-\lambda^2},\]
donde hemos usado la fórmula de la suma de los términos de una progresión geométrica. En el límite de esta suma cuando $n\to\infty$ el término $\lambda^{2n+2}$ desparece y el resultado es
\begin{align*}
\sum_{k=1}^\infty\mathrm{Area}(C_k)&=\frac{\pi r_1^2}{1-\lambda^2}=\frac{\pi r_1^2(d_1+r_1)^2}{(d_1+r_1)^2-(d_1-r_1)^2}\\
&=\frac{\pi r_1^2(d_1+r_1)^2}{4r_1d_1}=\frac{\pi r_1}{4d_1}(d_1+r_1)^2.
\end{align*}
Sea $ABCD$ un cuadrilátero cíclico cuyas diagonales $AC$ y $BD$ son perpendiculares. Sean $O$ el circuncentro de $ABCD$, $K$ la intersección de sus diagonales, $L\neq O$ la intersección de las circunferencias circunscritas a $OAC$ y $OBD$, y $G$ la intersección de las diagonales del cuadrilátero cuyos vértices son los puntos medios de $ABCD$. Probar que $O$, $K$, $L$ y $G$ están alineados.
Sin pistas
Sin soluciones
infoLa circunferencia $\Gamma$ inscrita al triángulo escaleno $ABC$ es tangente a los lados $BC$, $CA$ y $AB$ en los puntos $D$, $E$ y $F$, respectivamente. La recta $EF$ corta a la recta $BC$ en $G$. La circunferencia de diámetro $GD$ corta a $\Gamma$ en $R$ ($R\neq D$). Sean P y Q ($P\neq R$, $Q\neq R$) las intersecciones de $BR$ y $CR$ con $\Gamma$, respectivamente. Las rectas $BQ$ y $CP$ se cortan en $X$. La circunferencia circunscrita a $CDE$ corta al segmento $QR$ en $M$ y la circunferencia circunscrita a $BDF$ corta al segmento $PR$ en $N$. Demostrar que las rectas $PM$, $QN$ y $RX$ son concurrentes.
Sin pistas
Sin soluciones
info

