Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Si reflejamos repetidamente el triángulo respecto de sus lados, entonces la poligonal que forma la trayectoria del rayo se vuelve una línea recta ya que el ángulo de incidencia es el de reflexión. Como nos dicen que se refleja primero respecto de $AB$, luego $AC$ y por último $BC$, estas son las reflexiones que debemos hacer y que hemos dibujado en la figura. Vemos así que hay una única forma hacer los rebotes para que se cumpla la condición del enunciado y ahora solamente hay que calcular su longitud.

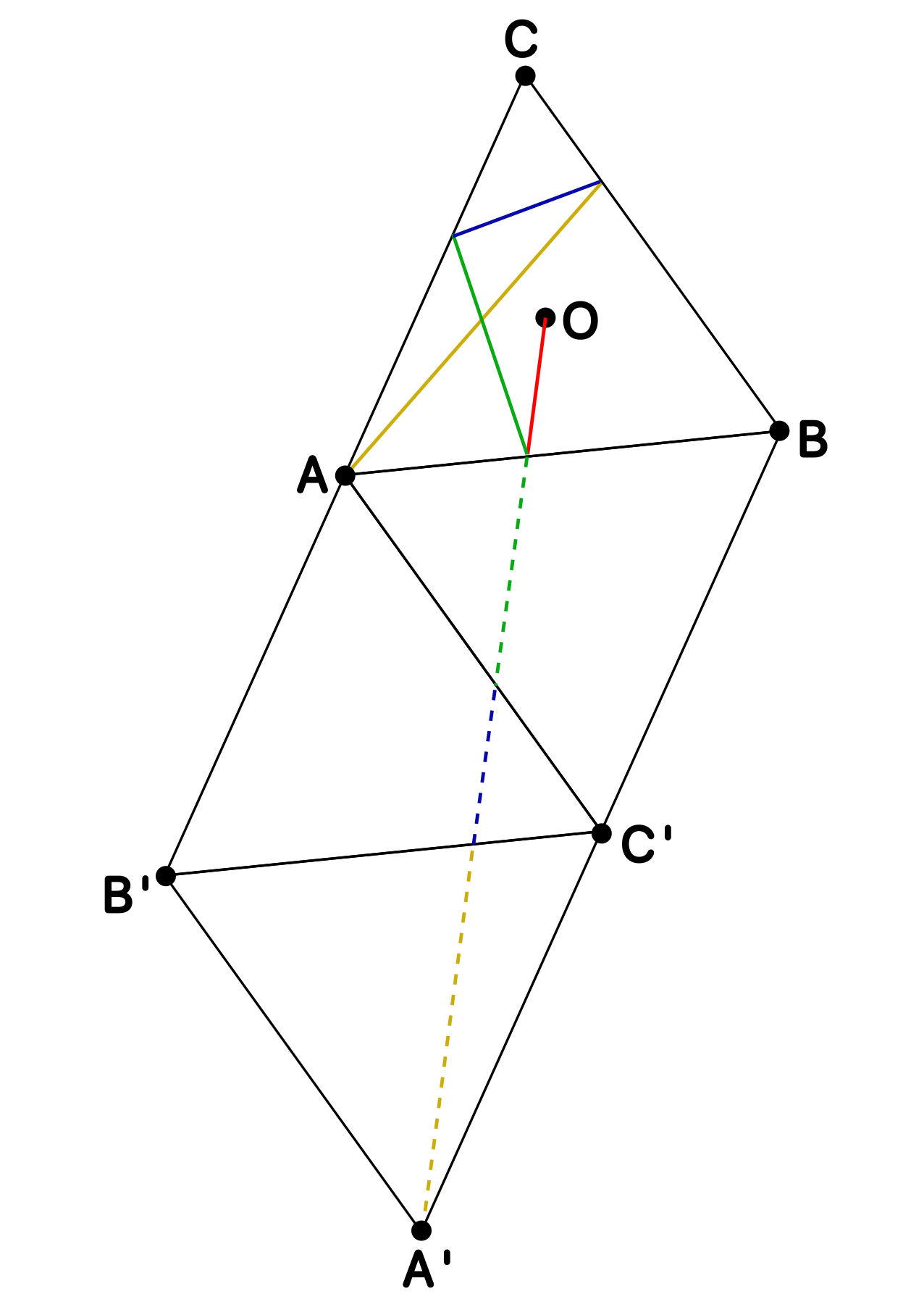
Para ello, observamos que $OBA'$ es un triángulo rectángulo ya que $OB$ es una altura del triángulo equilátero y $BA'$ es paralela al lado opuesto. Además, se tiene que $OB=\frac{2}{3}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$ (dos tercios de la altura) y $BA'=2$ (dos veces el lado), luego el teorema de Pitágoras nos da la distancia que buscamos: \[OA'=\sqrt{\left(\tfrac{\sqrt{3}}{3}\right)^2+2^2}=\frac{\sqrt{39}}{3}.\]

Solución. Sean $a$ la hipotenusa y $b$ y $c$ los catetos. Vamos a plantear un sistema de tres ecuaciones para obtener sus valores. Por un lado, tenemos la condición sobre el perímetro $a+b+c=96$ y la condición sobre la altura podemos escribirla calculando el área de dos formas distintas como base por altura entre $2$, esto es, se tiene que $\frac{1}{2}bc=\frac{1}{2}bh$. Finalemente, la tercera ecuación nos la da el teorema de Pitágoras $a^2=b^2+c^2$. Tenemos, pues, el siguiente sistema: \[\left\{\begin{array}{l}a+b+c=96\\bc=\frac{96}{5}a\\a^2=b^2+c^2\end{array}\right.\] Sumando dos veces la segunda ecuación a la tercera para completar el cuadrado y despejando $b+c$ de la primera, obtenemos una ecuación que sólo involucra a $a$: \[a^2+\frac{192}{5}a=b^2+c^2+2bc=(b+c)^2=(96-a)^2.\] Esta ecuación es de primer grado y nos da fácilmente $a=40$. Ahora las dos primeras ecuaciones del sistema nos dicen que $b+c=56$ y $bc=\frac{96}{5}\cdot 40=768$. Teniendo la suma y el producto, sabemos que $b$ y $c$ son las soluciones de la ecuación $x^2-56x+768=0$. Esta se resuelve con la fórmula de la ecuación de segundo grado y nos da las soluciones $x=24$ y $x=32$. Deducimos que los lados del triángulo rectángulo tienen longitudes 24, 32 y 56.

Solución. Consideremos los puntos $S$ y $S'$ simétricos de $P$ y $P'$ respecto del centro de la circunferencia, lo que define un rectángulo inscrito $PP'SS'$. Además, como $AP'$ es perpendicular a $PP'$, se tiene que $A$ pertenece al interior del segmento $PS'$ y $B$, por simetría, pertenece al segmento $SP'$. Por la simetría respecto de $O$ y la simetría de $B$ y $C$ respecto de $PP'$, s e tiene que $AS'=BP'=P'C$. Como los segmentos $AS'$ y $P'C$ son paralelos (están en lados opuestos del rectángulo), se tiene que $AS'P'C$ es un paralelogramo, luego $AC=P'S'=2r$. Finalmente, observamos que $QC=QB$ por simetría, luego $AQ+QB=AQ+QC=2r$ y deducimos que la suma de las distancias de $Q$ a $A$ y $B$ es constante. Esto nos asegura que $Q$ está en una elipse de focos $A$ y $B$.

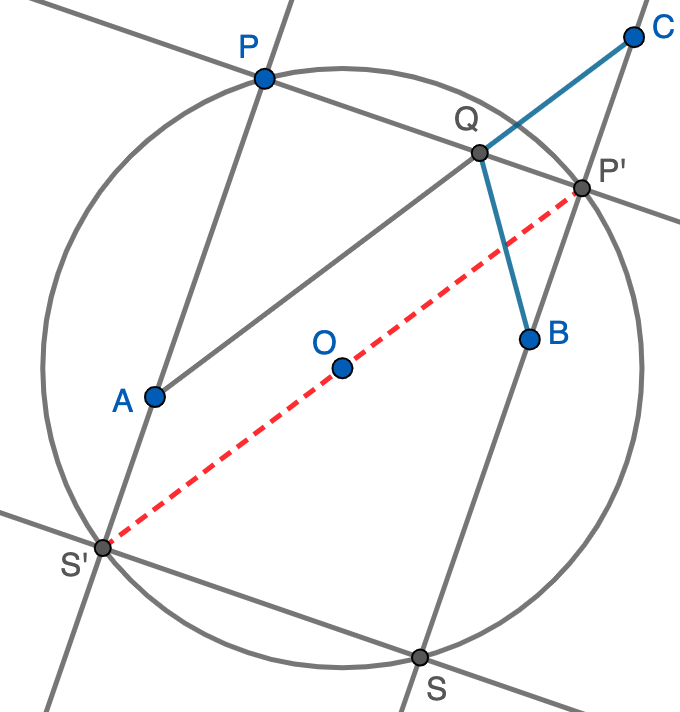
Nos queda determinar de qué elipse se trata concretamente ya que hay infinitas con focos $A$ y $B$. Si prolongamos $AB$ hasta que corte en un punto $X$ a la circunferencia, se tiene claramente que $AX+XB=2r$, luego $X$ también está en la misma elipse. Como la elipse es simétrica respecto de la recta $AB$, no queda otra que ser tangente a la circunferencia en $X$. Además, como $Q$ pertenece a la cuerda $PP'$, los puntos de la elipse siempre son interiores a la circunferencia. Concluimos que el lugar geométrico es la única elipse de focos $A$ y $B$ tangente interiormente a la circunferencia.