Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 859
OIM, 2009-P4
Sea $ABC$ un triángulo con $AB\neq AC$. Sean $I$ el incentro de $ABC$ y $P$ el otro punto de intersección de la bisectriz exterior del ángulo $A$ con el circuncírculo de $ABC$. La recta $PI$ interseca por segunda vez al circuncírculo de $ABC$ en el punto $J$. Demostrar que los circuncírculos de los triángulos $JIB$ y $JIC$ son tangentes a $IC$ y a $IB$, respectivamente.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 858
OIM, 2009-P3
Sean $C_1$ y $C_2$ dos circunferencias de centros $O_1$ y $O_2$ con el mismo radio y que se cortan en $A$ y en $B$. Sea $P$ un punto sobre el arco $AB$ de $C_2$ que está dentro de $C_1$. La recta $AP$ corta a $C_1$ en $C$, la recta $CB$ corta a $C2$ en $D$ y la bisectriz de $\angle CAD$ corta a $C_1$ en $E$ y a $C_2$ en $L$. Sea $F$ el punto simétrico a $D$ con respecto al punto medio de $PE$. Demostrar que existe un punto $X$ que satisface $\angle XFL=\angle XCD=30^\circ$ y $CX=O_1O_2$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 855
En el interior de una circunferencia de centro $O$ y radio $r$, se toman dos puntos $A$ y $B$ simétricos respecto de $O$. Se considera $P$ un punto variable sobre esta circunferencia y se traza la cuerda $PP'$ perpendicular a $AP$. Sea $C$ el punto simétrico de $B$ respecto de $PP'$. Hallar el lugar geométrico del punto $Q$, interseccion de $PP'$ con $AC$ al variar $P$ sobre la circunferencia.
pistasolución 1info
Pista. Demuestra que $AQ+BQ$ es constante cuando se mueve $P$.
Solución. Consideremos los puntos $S$ y $S'$ simétricos de $P$ y $P'$ respecto del centro de la circunferencia, lo que define un rectángulo inscrito $PP'SS'$. Además, como $AP'$ es perpendicular a $PP'$, se tiene que $A$ pertenece al interior del segmento $PS'$ y $B$, por simetría, pertenece al segmento $SP'$. Por la simetría respecto de $O$ y la simetría de $B$ y $C$ respecto de $PP'$, s e tiene que $AS'=BP'=P'C$. Como los segmentos $AS'$ y $P'C$ son paralelos (están en lados opuestos del rectángulo), se tiene que $AS'P'C$ es un paralelogramo, luego $AC=P'S'=2r$. Finalmente, observamos que $QC=QB$ por simetría, luego $AQ+QB=AQ+QC=2r$ y deducimos que la suma de las distancias de $Q$ a $A$ y $B$ es constante. Esto nos asegura que $Q$ está en una elipse de focos $A$ y $B$.
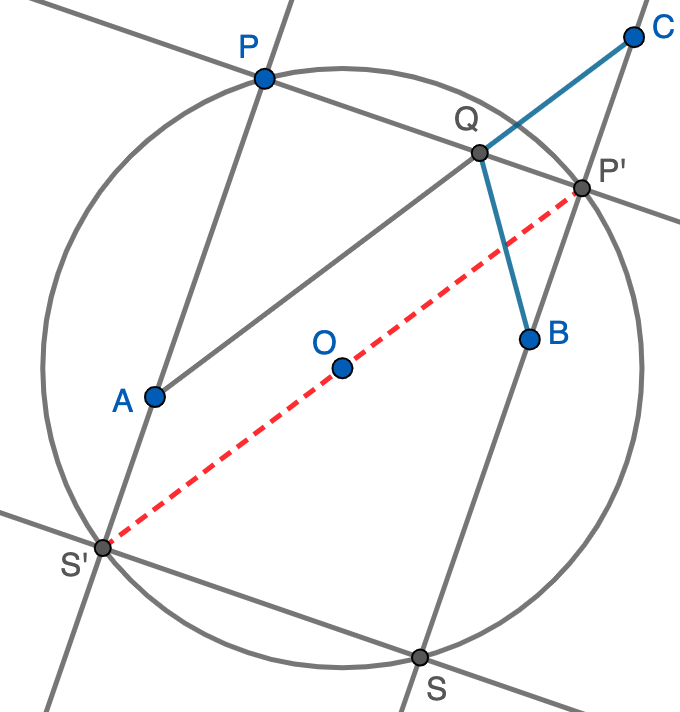
Nos queda determinar de qué elipse se trata concretamente ya que hay infinitas con focos $A$ y $B$. Si prolongamos $AB$ hasta que corte en un punto $X$ a la circunferencia, se tiene claramente que $AX+XB=2r$, luego $X$ también está en la misma elipse. Como la elipse es simétrica respecto de la recta $AB$, no queda otra que ser tangente a la circunferencia en $X$. Además, como $Q$ pertenece a la cuerda $PP'$, los puntos de la elipse siempre son interiores a la circunferencia. Concluimos que el lugar geométrico es la única elipse de focos $A$ y $B$ tangente interiormente a la circunferencia.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 851
Sean $ABC$ un triángulo acutángulo, $I$ el centro de la circunferencia inscrita, $r$ su radio y $R$ el radio de la circunferencia circunscrita. Se traza la altura $AD=h_a$, con $D$ perteneciente al lado $BC$. Demuestra que
\[DI^2=(2R-h_a)(h_a-2r).\]
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 849
OME Local, 2009-P12
Sean $C_1$ y $C_2$ dos circunferencias exteriores tangentes en el punto $P$. Por un punto $A$ de $C_2$ trazamos dos rectas tangentes a $C_1$ en los puntos $M$ y $M'$. Sean $N$ y $N'$ los puntos respectivos de corte, distintos ambos de $A$, de estas rectas con $C_2$. Probar que $PN'\cdot MN=PN\cdot M'N'$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre