Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 847
OME Local, 2009-P10
En el interior de un paralelogramo $ABCD$ se dibujan dos circunferencias. Una es tangente a los lados $AB$ y $AD$ y la otra es tangente a los lados $CD$ y $CB$. Probar que, si estas circunferencias son tangentes entre sí, el punto de tangencia está en la diagonal $AC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 841
Dado un triángulo acutángulo $ABC$, determinar para qué puntos $P$ de su interior se verifican simultáneamente las siguientes desigualdades:
\[1\leq\frac{\angle APB}{\angle ACB}\leq 2,\qquad 1\leq\frac{\angle BPC}{\angle BAC}\leq 2,\qquad 1\leq\frac{\angle CPA}{\angle CBA}\leq 2.\]
pistasolución 1info
Pista. Demuestra que se tiene necesariamente la igualdad a $2$ en las tres fracciones.
Solución. Estas tres desigualdades se pueden reescribir como
\begin{align*}
\angle ACB\leq \angle APB\leq 2\angle ACB,\\
\angle BAC\leq \angle BPC\leq 2\angle BAC,\\
\angle CBA\leq \angle CPA\leq 2\angle CBA.
\end{align*}
Sumando y usando que $\angle ACB+\angle BAC+\angle CBA=180^\circ$ (los ángulos del triángulo $ABC$ suman $180^\circ$, tenemos que
\[180^\circ\leq \angle APB+\angle BPC+\angle CPA\leq 360^\circ.\]
Sin embargo, se tiene que $\angle APB+\angle BPC+\angle CPA=360^\circ$ ya que estos tres ángulos forman un ángulo completo. Tenemos así que deben darse las siguientes tres igualdades:
\[\angle APB=2\angle ACB,\qquad\angle BPC=2\angle BAC,\qquad\angle CPA=2\angle CBA.\]
Estas igualdades se cumplen si $P$ coincide con $O$, el circuncentro de $ABC$ por la propiedad del ángulo central en la circunferencia circunscrita a $ABC$. Por la propiedad del arco capaz, la igualdad $\angle APB=\angle AOP$ nos dice que $P$ tiene que estar en la circunferencia circunscrita de $ABO$ y análogamente, tiene que estar en las circunferencias circunscritas de $BCO$ y $CAO$. Como estas tres circunferencias solo se cortan en $O$, necesariamente ha de ser $P=O$. Hemos probado así que el circuncentro es el único punto que cumple las condiciones del enunciado (observemos que el circuncentro es interior al triángulo puesto que es acutángulo).
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 839
Si la sección producida por un plano al cortar un tetraedro es un rombo, probar que necesariamente el rombo es un cuadrado.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 836
OME Local, 2008-P10
Determina el triángulo de menor perímetro de entre todos los que tienen la
circunferencia inscrita con el mismo radio y el mismo valor de un ángulo.
pistasolución 1info
Pista. El problema equivale a encontrar el triángulo de menor área. Demuestra que la solución es el triángulo isósceles con ese ángulo como ángulo desigual y ese radio inscrito viendo que otro triángulo en las mismas condiciones tiene necesariamente mayor área.
Solución. Sea $ABC$ el triángulo en cuestión y supongamos que el ángulo en $A$ está fijo y también el radio $r$ de la circunferencia inscrita, que es tangente a los lados en los puntos $X,Y,Z$, como se muestra en la figura. El área del triángulo está dada por $S=rp$, siendo $p$ el semiperímetro, luego minimizar el perímetro del triángulo equivale a minimizar su área cuando variamos $X$ en el arco mayor $YZ$. Es fácil intuir que la solución al problema es el triángulo isósceles $ARS$ tangente a la circunferencia inscrita en el punto medio $M$ de $RS$. Vamos a confirmar esta intuición viendo que cualquier otra elección de $X$ distinta de $M$ nos da un triángulo $ABC$ de área mayor que $ARS$. Si suponemos sin perder generalidad que $X$ está en el arco $MZ$ (en caso de estar en $MY$ el razonamiento es similar), probaremos que el área de $PBR$ (en verde) es menor que el área de $PCS$ (en azul), siendo $P$ el punto en de corte entre $BC$ y $RS$.
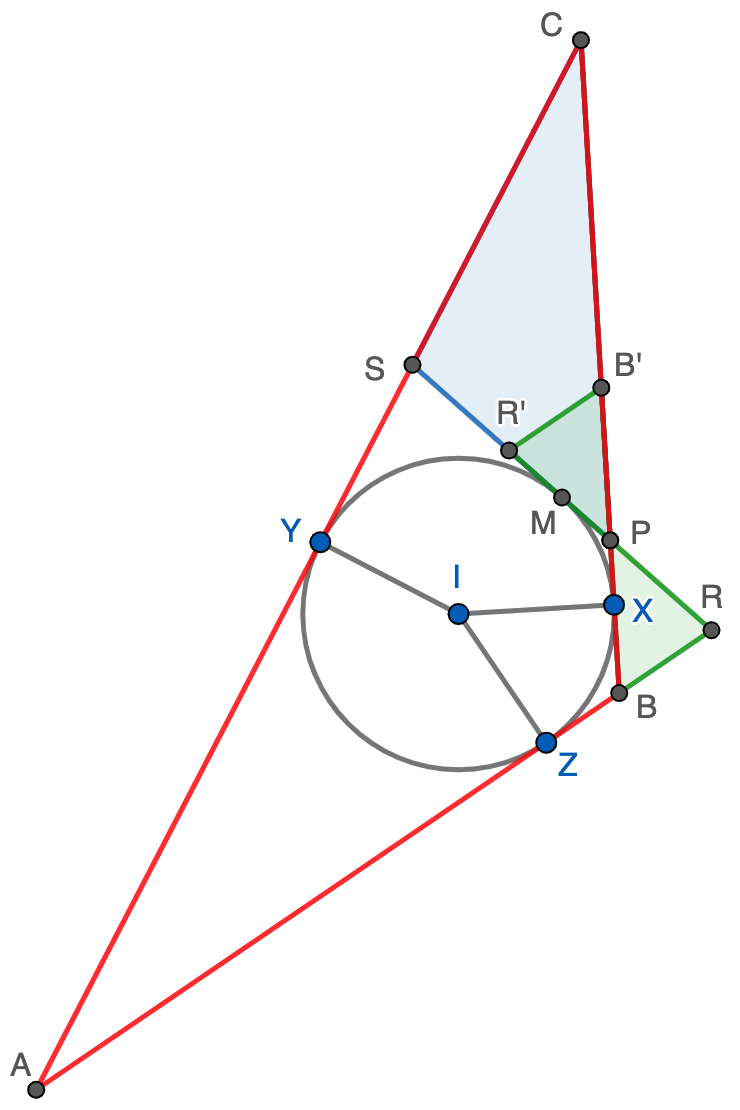
Como $P$ está en el segmento $MR$ y $M$ es el punto medio de $RS$, se sigue que $PR\lt PS$; además, se tiene que $\angle PRB$ es agudo mientras que $\angle CSR=180-\angle PRB$ es obtuso. Esto nos dice que si giramos $180^\circ$ el triángulo $PRB$ respecto de $P$ obtenemos un triángulo $PR'B'$ contenido en $PCS$, luego ciertamente el área de $PBR$ es menor que el área de $PCS$ y hemos terminado la demostración.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 834
Un cuadrilátero convexo tiene la propiedad que cada una de sus dos diagonales
biseca su área. Demostrar que este cuadrilátero es un paralelogramo.
pistasolución 1info
Pista. Usa que el área es $\frac{1}{2}$ de la base por la altura en los cuatro triángulos en que las diagonales dividen al cuadrilátero.
Solución. Sea $ABCD$ el cuadrilátero convexo y $P$ el punto de corte de las diagonales. Si llamamos $S_1,S_2,S_3,S_4$ a las áreas de los cuatro triángulos en que las diagonales dividen al cuadrilátero, como se indica en la figura, entonces la propiedad de la bisección nos dice que
\[S_1+S_2=S2+S_3=S_3+S_4=S_4+S_1\ \Longleftrightarrow\ \begin{cases}S_1=S_3,\\S_2=S_4.\end{cases}\]
Ahora bien, para que la diagonal $BD$ biseque, las distancias de $A$ y $C$ a la recta $BD$ deben ser las mismas (las alturas de los triángulos $ABD$ y $BCD$ de base común $BD$, indicadas con línea discontinua roja). Por lo tanto, tiene que ser $BP=DP$ para que se cumpla que $S_1=S_3$. Análogamente, se demuestra que $AP=CP$, luego hemos llegado a que las diagonales se cortan en su punto medio y esto implica que $ABCD$ es un paralelogramo.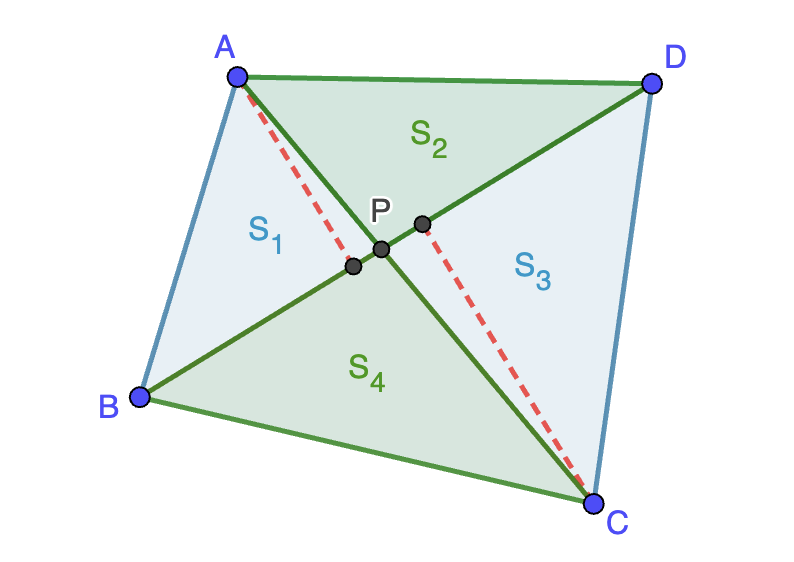

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre