Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Para terminar, vamos a expresar el resultado sin que intervenga $M$, por rizar el rizo. Tenemos que $MP=\frac{1}{2}PQ$ y que $OM$ es la mediana de $OPQ$. Usando la fórmula de la meidana, la condición que buscamos se puede escribir finalmente como \[\frac{1}{2}PQ+\sqrt{\frac{OP^2+OQ^2}{2}-\frac{PQ^2}{4}}\geq R.\]
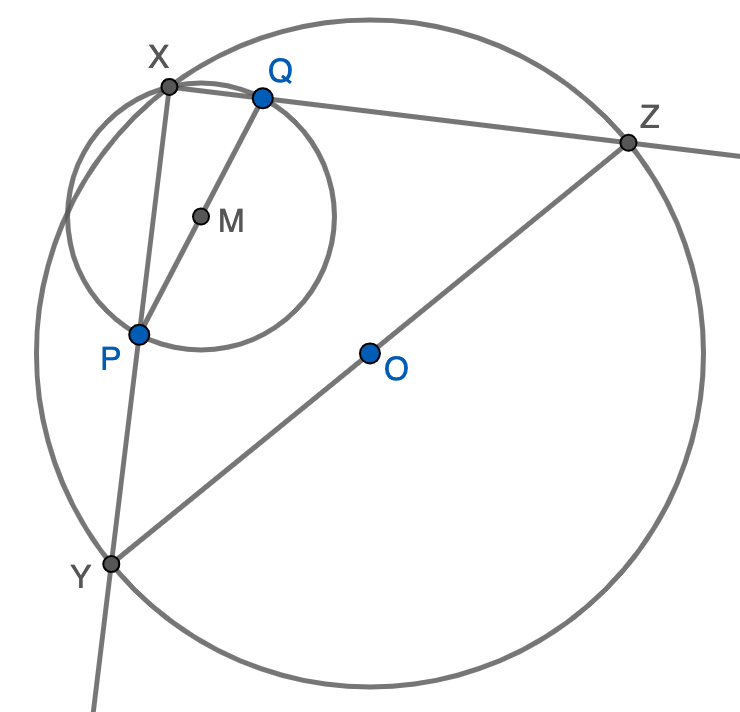
Nota. En realidad, cuando la desigualdad es estricta, hay dos soluciones ya que hay dos puntos de corte de ambas circunferencias.
Informar de error en enunciado Informar de procedencia del problema
Los triángulos $AA'P$ y $BB'P$ son semejantes porque son rectángulos y tienen un ángulo común en el vértice $P$, luego se cumple que \[\frac{AP}{BP}=\frac{A'P}{B'P},\] lo que también nos dice que $ABP$ y $A'B'P$ son semejantes. De forma similar se prueba que $BCP$ y $B'C'P$ son semejantes, que $CDP$ y $C'D'P$ son semejantes y que $DAP$ y $D'A'P$ son semejantes. La razón de semejanza es la misma para los cuatro pares de triángulos ya que se tiene que $\frac{AP}{A'P}=\frac{BP}{B'P}=\frac{CP}{C'P}=\frac{DP}{D'P}$, luego el cuadrilátero $A'B'C'D'$ es semejante a $ABCD$ ya que está formado por cuatro triángulos semejantes en disposición similar. Más aún, $A'B'C'D'$ se obtiene de $ABCD$ a partir de una reflexión respecto de una de las bisectrices de las diagonales y una homotecia.
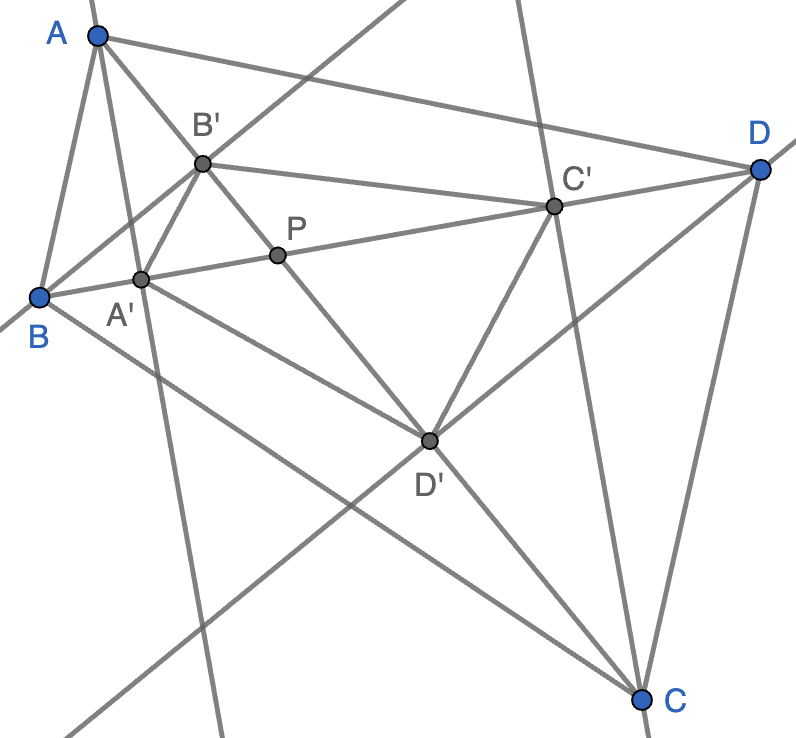
Informar de error en enunciado Informar de procedencia del problema
Nota. En realidad, es necesario que el enunciado diga que $P$ tiene al menos cuatro puntos o que los puntos de $P$ no están alineados. Por ejemplo, un conjunto $P$ formado por tres puntos alineados cumple la condición pero no todos los puntos de $P$ están en una circunferencia.
Informar de error en enunciado Informar de procedencia del problema
Es muy fácil darse cuenta de la recta $EF$ ha de ser perpendicular a $AB$: dado que los ángulos $\angle ACB$ y $\angle ADB$ son rectos por comprender al diámetro $AB$ en la semicircunferencia, se tiene que $AD$ y $BC$ son alturas del triángulo $AEB$, luego $F$ es su ortocentro y $EF$ es la tercera altura, que debe ser perpendicular al lado $AB$. Tenemos así que la dirección del segmento $EF$ no varía.
Veamos ahora que su longitud tampoco varía. Por la propiedad del arco capaz, el ángulo $\alpha=\angle CAD=\angle CBD$ sólo depende de $c$, no de la posición concreta de la cuerda $CD$. Como los ángulos $\angle ACB$ y $\angle ADB$ son rectos por comprender al diámetro $AB$ en la semicircunferencia, deducimos que $\angle AEB=90-\alpha$. Además, como la suma de los ángulos del cuadrilátero $ECFD$ es $360$, tenemos también que $\angle AFB=\angle CFD=90+\alpha$. Todo ello nos dice que los puntos $E$ y $F$ se mueven en sendos arcos de circunferencia con extremos $A$ y $B$ (al variar la cuerda $CD$ sin modificar su longitud), como puede verse en la figura. Además, como los ángulos con los que $E$ y $F$ ven al segmento $AB$ son $90-\alpha$ y $90+\alpha$, que suman $180$, estas circunferencias son simétricas respecto de $AB$. En particular, tienen el mismo radio y, al pasar por $A$ y $B$, tiene que ser una trasladada de la otra en la dirección perpendicular a $AB$. De esta forma, la longitud del segmento $EF$ es la del vector de traslación, o sea, constante.
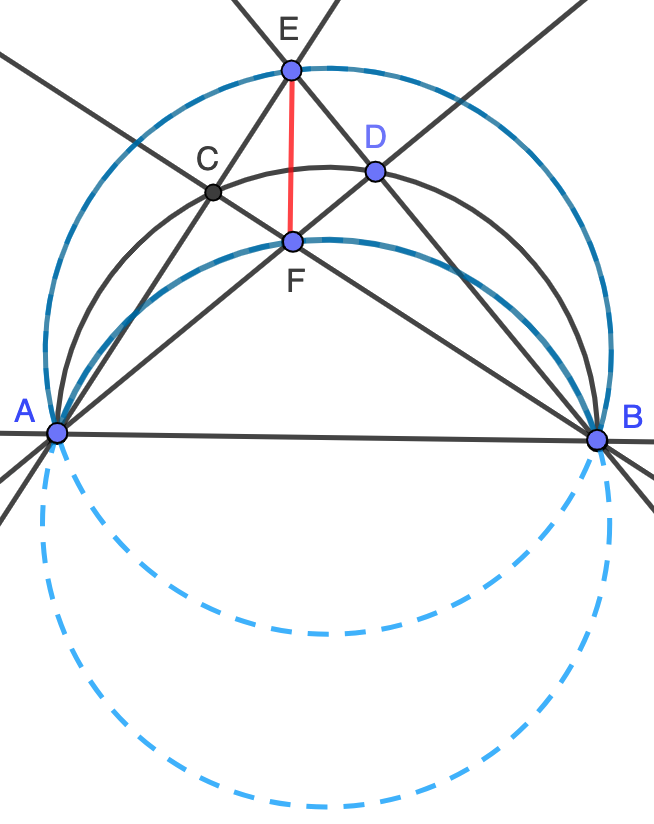
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema