Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Por simplicidad, llamamos $a=AE$, $b=BE$, $c=CE$ y $d=DE$. También llamamos $\alpha=\angle AEB=\angle CED$, con lo que $\angle BEC=\angle DEA=180-\alpha$. Usando que el área de un triángulo es el la mitad del producto de dos de sus lados por el seno del ángulo que forman y que $\mathrm{sen}(180-\alpha)=\mathrm{sen}(\alpha)$, la desigualdad del enunciado se reescribe como \[\sqrt{ab}+\sqrt{cd}\leq\sqrt{ab+bc+cd+da}.\] Elevando al cuadrado esto a su vez equivale (porque todos son positivos) a \[2\sqrt{abcd}\leq ac+bd,\] que no es más que la desigualdad entre las medias aritmética y geométrica aplicada a los números $ac$ y $bd$. Se da la igualdad si y solo si $ac=bd$. Esto equivale a que los triángulos $ABE$ y $CDE$ sean semejantes (tienen además un ángulo común $\alpha$ opuesto por el vértice), lo que nos dice que la igualdad se alcanza si y solo si $AB$ es paralela a $CD$.

Solución. Sean $X,Y,Z$ los pies de las perpendiculares desde $P$ a los lados $BC,AC,AB$, respectivamente. Vamos a demostrar que $XPY$ es semejante a $ZPX$, probando que dos de sus ángulos son iguales. Esta semejanza nos dirá que $\frac{ZP}{PX}=\frac{PX}{PY}$, que equivale a $a^2=bc$. Vamos a distinguir dos casos, suponiendo previamente que $P\neq B$ y $P\neq C$ (en tal caso la igualdad $a^2=bc$ es cierta ya que queda $0=0$).

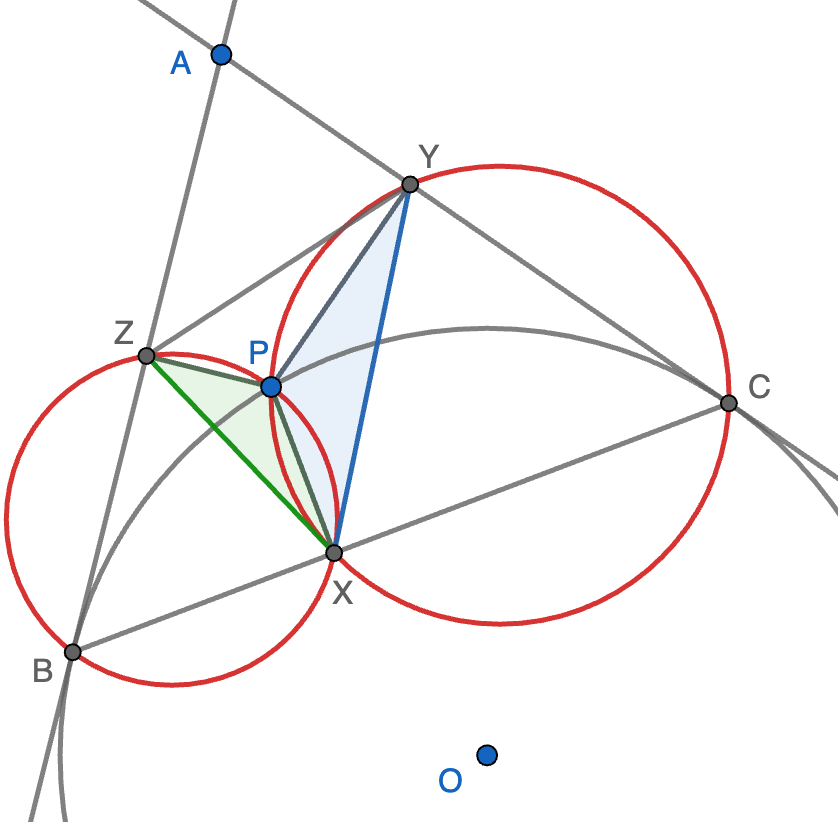
El primer caso es que $P$ sea interior al triángulo $ABC$. Los cuadriláteros $ZPBX$ e $YPXC$ son cíclicos ya que tienen dos ángulos rectos opuestos. La propiedad del arco capaz nos dice que $\angle XPY=180-\angle ACB$ y $\angle ZPX=180-\angle ABC$; como se tiene que $\angle ACB=\angle ABC$ por ser $ABC$ isósceles, se deduce que $\angle XPY=\angle ZPX$ y ya tenemos un ángulo igual. Para el segundo ángulo, calculamos de nuevo por arco capaz \begin{align*} \angle PXY-\angle ZPX&=\angle PCY-\angle PBX=\angle ACB-\angle PCX-\angle PBX\\ &=\angle ACB-180+\angle BPC. \end{align*} En el último paso hemos usado que los ángulos del triángulo $BPC$ suman $180$. Ahora bien, $\angle BOC=360-2\angle BPC$ por la propiedad del arco central, donde $O$ es el centro de la circunferencia tangente a los lados. Como en el cuadrilátero $ABCO$ los ángulos suman $360$ y dos de ellos son rectos, llegamos a que $\angle BOC=180-\angle BAC$ y, por tanto, $\angle BPC=90+\frac{1}{2}\angle BAC=180-\angle ACB$ (ya que $ABC$ es isósceles). Volviendo al cálculo anterior, tenemos que $\angle PXY-\angle ZPX=0$, lo que concluye la demostración de que $XPY$ es semejante a $ZPX$.

El segundo caso es que $P$ sea exterior al triángulo $ABC$, es decir, $P$ está en el arco mayor $BC$ de la circunferencia. La demostración se adapta pero los cálculos son ligeramente distintos. La igualdad $\angle XPY=\angle ZPX$ es cierta pero en este caso porque los dos ángulos son iguales a $180-\angle ABC$. Para la otra igualdad de ángulo, calculamos \begin{align*} \angle PXY-\angle ZPX&=\angle PCY-\angle PBX=180-\angle ACB-\angle PCX-\angle PBX\\ &=\angle ACB+\angle BPC=\angle ACB+\tfrac{1}{2}\angle BOC=\angle ACB+\tfrac{1}{2}(180-\angle BAC)=0. \end{align*}

Solución. Para resolver el primer apartado, usaremos el teorema del coseno, del que podemos despejar el coseno del ángulo $A$ como \begin{align*} \cos(A)&=\frac{b^2+c^2-a^2}{2bc}=\frac{b^2+c^2-\left(\frac{b+c}{2}\right)^2}{2bc}\\ &=\frac{3b^2+3c^2-2bc}{8bc}=\frac{3}{8}\left(\frac{b}{c}+\frac{c}{b}\right)-\frac{1}{4}\geq\frac{3}{8}\cdot 2-\frac{1}{4}=\frac{1}{2}, \end{align*} donde se ha usado que la suma de un número positivo y su inverso es siempre mayor o igual que $2$. Como $A$ es un ángulo entre $0^\circ$ y $180^\circ$, de la desigualdad anterior deducimos que $0\leq A\leq 60^\circ$.

En cuanto al apartado (b), calculamos el área del triángulo de dos formas distintas. Por un lado, $S=\frac{1}{2}(a+b+c)r$ y por otro $S=\frac{1}{2} ah_a$, siendo $h_a$ la altura relativa al vértice $A$. Sustituyendo $a=\frac{b+c}{2}$ en ambas expresiones e igualándolas, se llega directamente a que $h_a=3r$.

Finalmente, para el apartado (c) usaremos la fórmula $abc=4RS$ y la fórmula de Herón, de forma que \begin{align*} R-r&=\frac{abc}{4S}-\frac{2S}{a+b+c}=\frac{abc(a+b+c)-8S^2}{4(a+b+c)S}\\ &=\frac{abc(a+b+c)-\frac{1}{2}(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}{4(a+b+c)S}\\ &=\frac{2abc-(-a+b+c)(a-b+c)(a+b-c)}{8S}=\frac{(b+c)bc-\frac{b+c}{2}(\frac{-b+3c}{2})(\frac{3b-c}{2})}{8S}\\ &=\frac{(b+c)(3b^2-2bc+3c^2)}{64S}=\frac{abc\cos(A)}{4S}=R\cos(A). \end{align*} Si $O$ es el circuncentro y $M$ el punto medio de $BC$, entonces el triángulo $BOM$ es rectángulo y tiene $\angle COM=A$ ya que este es la mitad del ángulo central. Por tanto, en este triángulo rectángulo se cumple que $\cos(A)=\frac{OM}{OB}$, es decir, $OM=OB\cos(A)=R\cos(A)$ y hemos terminado.

Nota. Probablemente, la demostración del apartado (c) no sea la más elegante, pero es sistemática en el sentido de que expresamos $R-r$ en función únicamente de los lados $a,b,c$. Luego se puede expresar también $OM$ en términos de estos lados y usando la condición $a=\frac{b+c}{2}$ se tiene que conseguir probar el enunciado. En la solución propuesta, se ha introducido además el área y el coseno de $A$ como atajo para evitar más cálculos.

Solución. Llamamos $a_1,a_2,\ldots,a_{n-1}$ a los lados de los $n-2$ triángulos que parten de $B$ y llamamos $d_1,d_2,\ldots,d_{n-2}$ a los lados opuestos al vértice $B$, como se muestra en la figura. El ángulo en el vértice $B$ tiene el mismo valor para los $n-2$ triángulos ya que es el arco capaz que subtiende a un lado del polígono desde la circunferencia circunscrita al triángulo. Vamos a probar por inducción sobre $k$ que se cumple que $a_k\,a_{k+1}=d_k$ para todo $k$ desde $1$ hasta $n-2$, lo que demostrará que los triángulos son multiplicativos y habremos terminado.

Para $k=1$, está claro que $a_1=1$ (es un lado del polígono) y $a_2=d_2$ por simetría de este primer triángulo respecto de la mediatriz del lado $BC$. Supongamos entonces cierto que $a_{k-1}a_k=d_{k-1}$ para cierto $k$ y probemos que $a_ka_{k+1}=d_k$. Para ello, consideramos el triángulo que se obtiene al unir los triángulos $(k-1)$-ésimo y $k$-ésimo, que tiene por lados $a_{k-1}$, $a_{k+1}$ y $d_{k-1}+d_k$, de forma que $a_k$ es la longitud de una de sus bisectrices interiores. El teorema de la bisectriz (ver la nota) nos da entonces el resultado deseado: \[\frac{a_{k+1}}{d_k}=\frac{a_{k-1}}{a_{k-1}a_k}=\frac{1}{a_k}\ \Leftrightarrow\ a_ka_{k+1}=d_k.\]

Nota. El teorema de la bisectriz nos dice que la bisectriz interior de un triángulo desde un vértice divide al lado opuesto en dos segmentos proporcionales a los lados correspondientes.