Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. La desigualdad a demostrar se puede expresar como \[x_1\log(\tfrac{y_1}{x_1})+x_2\log(\tfrac{y_2}{x_2})+\ldots+x_n\log(\tfrac{y_n}{x_n})\leq 0,\] luego necesitamos una acotación inferior del logaritmo. Como se trata de una función cóncava, se quedará por debajo de la recta tangente a la gráfica en cada punto. En particular, como $y=\log(x)$ tiene recta tangente $y=x-1$ en $x=1$, se cumple que $\log(x)\leq x-1$ para todo $x\gt 0$. Esto nos permite escribir \begin{align*} x_1\log(\tfrac{y_1}{x_1})+\ldots+x_n\log(\tfrac{y_n}{x_n})&\leq x_1(\tfrac{y_1}{x_1}-1)+\ldots+x_n(\tfrac{y_n}{x_n}-1)\\ &=y_1+\ldots+y_n-x_1-\ldots-x_n=0. \end{align*}

Solución. Vamos a suponer por comodidad que el cuadrado tiene sus vértices en el plano con coordenadas $(0,0),(1,0),(1,1),(0,1)$ y vamos a parametrizar los distintos casos usando la pendiente $m$ de las rectas paralelas (observamos que, para cada pendiente, hay un único par de rectas que cumple el requisito de la trisección). Aplicando un movimiento rígido podemos suponer además que $0\leq m\leq 1$. Es interesante darse cuenta de que para $m=\frac{2}{3}$ se tiene una trisección especial (figura central) en la que las rectas pasan por vértices del cuadrado. No es difícil calcular en este caso que la distancia entre las dos rectas es $d=\frac{1}{\sqrt{10}}$. Por la simetría de las regiones respecto de la recta de pendiente $m$ que pasa por el centro $(\frac12,\frac12)$, podemos distinguir dos casos:

• Caso 1. Las rectas paralelas cortan al cuadrado en lados opuestos. Como la región que delimitan estas rectas es un paralelogramo de base $\ell$ y altura $d$ (según la figura de la izquierda), la condición sobre el área nos dice que $d\cdot\ell=\frac{1}{3}$. Además, si la recta inferior corta a los lados en $(0,a)$ y $(1,b)$ con $b\geq a$, entonces el teorema de Pitágoras nos dice que $\ell^2=1+(b-a)^2$. Además, como el área del trapecio $T$ que queda por debajo de la recta es $\frac{1}{3}$, se tiene que $1\cdot \frac{a+b}{2}=\frac{1}{3}$, o equivalentemente $a+b=\frac{2}{3}$. De todo esto inferimos que \[d=\frac{1}{3\ell}=\frac{1}{3\sqrt{1+(b-a)^2}}=\frac{1}{3\sqrt{1+4(a-\frac{1}{3})^2}}.\] Esto define a $d$ como función de $a$ y además se tiene que $0\leq a\leq\frac{1}{3}$ (si fuera $a\gt\frac{1}{3}$, entonces $b\geq a\geq \frac{1}{3}$ y $T$ contendría un rectángulo de área mayor que $\frac{1}{3}$). En este intervalo la función $1+4(a-\frac{1}{3})^2$ es decreciente, luego $d$ es una función creciente de $a$. El valor mínimo $d=\frac{1}{\sqrt{13}}$ se obtiene para $a=0$ y el máximo $d=\frac{1}{3}$ para $a=\frac{1}{3}$.
• Caso 2. Las rectas paralelas cortan al cuadrado en lados contiguos. Pongamos entonces que la recta inferior corta a los lados en los puntos $(1-a,0)$ y $(0,b)$ con $b\geq a$, lo que define un triángulo $T$ bajo dicha recta. Como el área de $T$ debe ser $\frac{1}{3}$, deducimos que $ab=\frac{2}{3}$. El área de la región entre las dos paralelas está formado por un rectángulo de base $\ell=\sqrt{a^2+b^2}$ y altura $d$ más dos triángulos rectángulos de catetos $1-a$ y $1-b$, lo que nos da un área total $\ell\cdot d+(1-a)(1-b)$. Podemos despejar entonces \begin{align*} d=\frac{\frac{1}{3}-(1-a)(1-b)}{\ell}&=\frac{a+b-\frac{4}{3}}{\sqrt{a^2+b^2}}\\ &=\frac{a+\frac{2}{3a}-\frac{4}{3}}{\sqrt{a^2+\frac{4}{9a^2}}}=\frac{3(a-\frac{2}{3})^2+\frac{2}{3}}{\sqrt{9a^4+4}}. \end{align*} Ahora bien, esto define de nuevo a $d$ como función de $a$ y en este caso $a$ se mueve en el intervalo $[\frac{2}{3},1]$ (si fuera $a\lt \frac{2}{3}$, entonces $T$ estaría contenido en un triángulo de área menor que $\frac{1}{3}$). Para hallar el mínimo de esta función consideramos su derivada, que podemos factorizar como \[d'=\frac{4 \left(9 a^4-9 a^3+6 a-4\right)}{\left(9 a^4+4\right)^{3/2}}=\frac{4(3a^2-2)(3a^2-3a+2)}{\left(9 a^4+4\right)^{3/2}}.\] El factor $3a^2-3a+2$ es siempre positivo y el factor $3a^2-2$ se anula en $a\pm\frac{\sqrt{6}}{3}$. Deducimos que $d$ es decreciente en $[\frac{2}{3},\frac{\sqrt{6}}{3}]$ y creciente en $[\frac{\sqrt{6}}{3},1]$. Por lo tanto, el valor mínimo es $d=\sqrt{2}-\frac{2\sqrt{3}}{3}$, que se obtiene para $a=\frac{\sqrt{6}}{3}$. Para el valor máximo, evaluamos los extremos del intervalo y obtenemos que $d=\frac{1}{\sqrt{13}}$ para $a=\frac{2}{3}$ y también para $a=1$.

Comparando los valores obtenidos, llegamos a que el valor mínimo de la distancia es $\frac{1}{3}$, que se obtiene para dos rectas paralelas a los lados, y que su valor mínimo es $\sqrt{2}-\frac{2\sqrt{3}}{3}$.

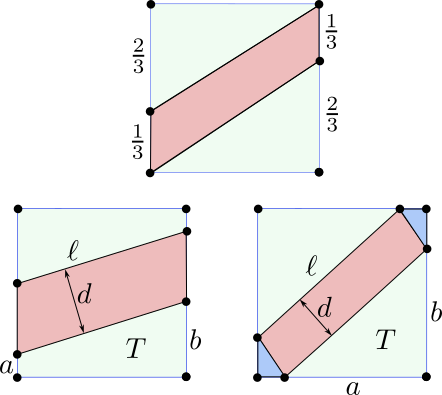
Nota. En el problema original, se precisaba no hacer uso de derivadas, lo que requería una dosis de ingenio considerable para cazar el valor $a=\frac{2\sqrt{3}}{3}$ del caso 2. En realidad, la función $d$ en este caso tiene una simetría oculta ya que $d(a)=d(\frac{2}{3a})$. Esto nos asegura que el valor de $a$ tal que $a=\frac{2}{3a}$ debe haber un punto crítico y puede probarse que la función decrece hasta este punto y luego crece. Los detalles puedes encontrarlos en la solución oficial del problema.

Solución. El logaritmo del numerador es igual a \[\frac{1}{ab}\log(a+b)+\frac{1}{bc}\log(b+c)+\frac{1}{ca}\log(c+a),\] que es una combinación de logaritmos con coeficientes positivos. Esto nos da pie a usar la desigualdad de Jensen (ver la nota) para la función $f(x)=\log(x)$, que es cóncava, aplicada a los números $x_1=a+b$, $x_2=b+c$ y $x_3=c+a$ con pesos $\frac{1}{ab}$, $\frac{1}{bc}$ y $\frac{1}{ca}$, respectivamente. Esto nos da \begin{align*} \frac{\frac{1}{ab}\log(a+b)+\frac{1}{bc}\log(b+c)+\frac{1}{ca}\log(c+a)}{\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}}&\leq\log\left(\frac{a+b}{ab}+\frac{b+c}{bc}+\frac{c+a}{ca}\right)\\ &=\log\left(2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\right). \end{align*} Por tanto, podemos despejar \begin{align*} \log\left(\frac{(a+b)^{\frac{1}{ab}}(b+c)^{\frac{1}{bc}}(c+a)^{\frac{1}{ca}}}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)&\leq \log(2)\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)\\ &=\log(2)\cdot\frac{a+b+c}{abc}=\log(2).\\ \end{align*} Haciendo la exponencial de ambos miembros, se tiene la desigualdad del enunciado.

Nota. La desigualdad de Jensen nos dice que si $f(x)$ es una función cóncava en un intervalo $[a,b]$ y tenemos puntos $x_1,\ldots,x_n\in [a,b]$ y pesos $w_1,\ldots,w_n\gt 0$, entonces \[\frac{w_1f(x_1)+w_2f(x_2)+\ldots+w_nf(x_n)}{w_1+w_2+\ldots+w_n}\leq f(\frac{w_1x_1+w_2x_2+\ldots+w_nx_n}{w_1+w_2+\ldots+w_n}).\]

Solución. La desigualdad entre las medias geométrica y cuadrática nos dice que \[\sqrt[4]{|abcd|}\leq\sqrt{\frac{a^2+b^2+c^2+d^2}{4}}=\sqrt{3},\] de donde $abcd\leq |abcd|\leq 9$ (observemos que hay que poner valor absoluto porque esta desigualdad sólo es cierta para números no negativos). Ahora bien, para que se dé la igualdad, tiene que ser $|a|=|b|=|c|=|d|=\sqrt{3}$ y la condición $a+b+c+d=0$ nos dice que exactamente dos de los números tienen que ser positivos y dos negativos. Por ejemplo, podemos poner $a=b=\sqrt{3}$ y $c=d=-\sqrt{3}$, lo que confirma que el valor máximo de $abcd$ es efectivamente $9$ y sabemos exactamente cuándo se da la igualdad.

En cuanto al mínimo,