Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Nota. La desigualdad entre las medias aritmética y geométrica con pesos se puede ver también como la desigualdad de Jensen para la función cóncava $f(t)=\ln(t)$. La pista la da el hecho de que los exponentes sumen $1$ pero puede ser difícil darse cuenta de que hay que invertir primero para que los signos de la desigualdad vayan en el sentido correcto.
Como los pesos son todos positivos, la igualdad se alcanza sólo cuando $x_1=x_2=x_3$, es decir, cuando $a=b=c$.
Informar de error en enunciado Informar de procedencia del problema
- Cuando decrece $f(0)$ mientras se fijan $f(-1)$ y $f(1)$.
- Cuando crece $f(1)$ mientras se fijan $f(-1)$ y $f(0)$.
- Cuando decrece $f(-1)$ mientras se fijan $f(0)$ y $f(1)$.
Por tanto, la parábola que toma los menores valores de $(-1,0)$ es aquella que cumple $f(-1)=f(0)=-1$ (mínimo posible) y $f(1)=1$ (máximo posible). Se obtiene fácilmente que esta parábola es $f(x)=x^2+x-1=(x+\frac{1}{2})^2-\frac{5}{4}$, lo que prueba que $f(x)\geq\frac{-5}{4}$ en $[-1,1]$ y hemos respondido así a la primera pregunta.
En cuanto a $g(x)$, comenzamos observando que \[g(x)=x^2(\tfrac{a}{x^2}+\tfrac{b}{x}+c)=x^2f(\tfrac{1}{x}).\] Por lo tanto, para acotar superiormente $|g(x)|$ en $[-1,1]$, tendremos que acotar inferiormente $|f(x)|$ en $(-\infty,-1]\cup[1,+\infty)$. Podemos seguir suponiendo que $a,b\geq 0$, luego $f(x)\geq f(-x)$ para $x\geq 1$ y solo debemos fijarnos en el caso $x\geq 1$. Un razonamiento similar al descrito más arriba nos dice que $f(x)$ crece para $x\in [1,+\infty)$ en cualquiera de las siguientes situaciones:
- Cuando decrece $f(0)$ mientras se fijan $f(-1)$ y $f(1)$.
- Cuando crece $f(1)$ mientras se fijan $f(-1)$ y $f(0)$.
- Cuando crece $f(-1)$ mientras se fijan $f(0)$ y $f(1)$.
Nota. La igualdad $|f(x)|=\frac{5}{4}$ sólo se alcanza en los siguientes casos: para los polinomios $f(x)=x^2+x-1$ y $f(x)=-x^2-x+1$ en $x=\frac{-1}{2}$ y para los polinomios $f(x)=x^2-x+1$ y $f(x)=-x^2+x-1$ en $x=\frac{1}{2}$. La igualdad $|g(x)|=2$ se alcanza sólo para los polinomios $g(x)=x^2-2$ y $g(x)=2-x^2$ en $x=0$.
Informar de error en enunciado Informar de procedencia del problema
- Si $x+y+z\geq 3$, ¿se verifica necesariamente que $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\leq 3$?
- Si $x+y+z\leq 3$, ¿se verifica necesariamente que $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq 3$?
La respuesta al apartado (b) es afirmativa. Para verlo, usamos la desigualdad entre las medias aritmética y armónica aplicada a los tres números positivos $x,y,z$: \[\frac{3}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}\leq \frac{x+y+z}{3}\leq 1\ \Longleftrightarrow\ \frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq 3.\]
Informar de error en enunciado Informar de procedencia del problema
Nota. La igualdad se alcanza si y solo si $t=0$, es decir, cuando $x=y=1$.
Informar de error en enunciado Informar de procedencia del problema
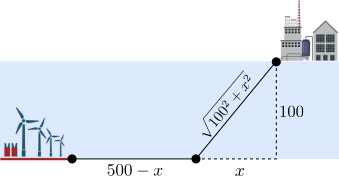
Informar de error en enunciado Informar de procedencia del problema