Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Si le aplicamos la desigualdad entre las medias aritmética y geométrica a los diez sumandos del miembro de la izquierda, tenemos que \[\tfrac{a^2+b^2+c^2+d^2+ab+ac+ad+bc+bd+cd}{10}\geq\sqrt[10]{a^2b^2c^2abacadbcbdcd}=\sqrt[10]{a^5b^5c^5d^5}=1,\] de donde deducimos de forma inmediata la desigualdad propuesta.

Nota. Si se alcanza la igualdad, entonces $a^2=b^2=c^2=d^2$, luego $a=b=c=d$ por ser números positivos y, como su producto es $1$, los cuatro números tienen que ser iguales a $1$. Recíprocamente, si los cuatro números son iguales a $1$, la igualdad se alcanza, luego este es la única situación en la que se alcanza.

Solución. Para probar la primera desigualdad, vamos a aplicar la desigualdad entre las medias aritmética y geométrica a los números $x_1=x_2=\ldots=x_n=\frac{1}{n}$ y $x_{n+1}=\frac{1}{n+1}$. Como no todos estos números son iguales, tendremos una desigualdad estricta: \begin{align*} \sqrt[n+1]{\frac{1}{n}\cdots\frac{1}{n}\cdot\frac{1}{n+1}}\lt \frac{\frac{1}{n}+\ldots+\frac{1}{n}+\frac{1}{n+1}}{n+1}&\Longleftrightarrow \sqrt[n+1]{\frac{1}{n^n(n+1)}}\lt \frac{1+\frac{1}{n+1}}{n+1}\\ &\Longleftrightarrow \frac{1}{n^n(n+1)}\lt \frac{1}{(n+1)^{n+1}}\left(1+\frac{1}{n+1}\right)^{n+1}\\ &\Longleftrightarrow \left(\frac{n+1}{n}\right)^n\lt\left(1+\frac{1}{n+1}\right)^{n+1}, \end{align*} que es la desgiualdad que buscamos.

En cuanto a la segunda desigualdad, desarrollamos por el binomio de Newton \begin{align*} \left(1+\frac{1}{n+1}\right)^{n+1}&=\sum_{k=0}^{n+1}\binom{n+1}{k}\frac{1}{(n+1)^k}=2+\sum_{k=2}^{n+1}\frac{(n+1)n\cdots(n-k+2)}{k!(n+1)^k}\\ &\leq 2+\sum_{k=2}^{n+1}\frac{1}{k!}\leq 2+\sum_{k=2}^{n+1}\frac{1}{k(k-1)}\\ &\leq 2+\sum_{k=2}^{n+1}\left(\frac{1}{k-1}-\frac{1}{k}\right)=3-\frac{1}{n+1}\lt 3. \end{align*} En primer lugar, hemos usado que cada uno de los factores en $(n+1)n\cdots(n-k+2)$ es menor o igual que $n+1$. Después hemos despreciado todos los factores de $k!$ salvo los dos primeros. Finalmente, hemos expresado la suma como una suma telescópica para poder obtener su valor explícito.

Solución. La desigualdad de Jensen con pesos $x,y\geq 0$ tales que $x+y=1$, nos dice que si $f:\mathbb{R}\to\mathbb{R}$ es una función estrictamente convexa, entonces \[f(ax+by)\leq xf(a)+yf(b).\] ya que, en el intervalo $[a,b]$, la gráfica de la función se queda por debajo del segmento de recta que une los puntos $(a,f(a)$ y $(b,f(b))$. Ahora bien, fuera del intervalo $[a,b]$, la gráfica se queda por encima de la recta, lo que nos dice que, para $x,y\in\mathbb{R}$ tales que $x+y=1$, si uno de estos dos números es negativo, se cumple la desigualdad contraria: \[f(ax+by)\gt xf(a)+yf(b).\] Por ser un poco más explícitos en este punto, basta mirar la figura y tener en cuenta que:

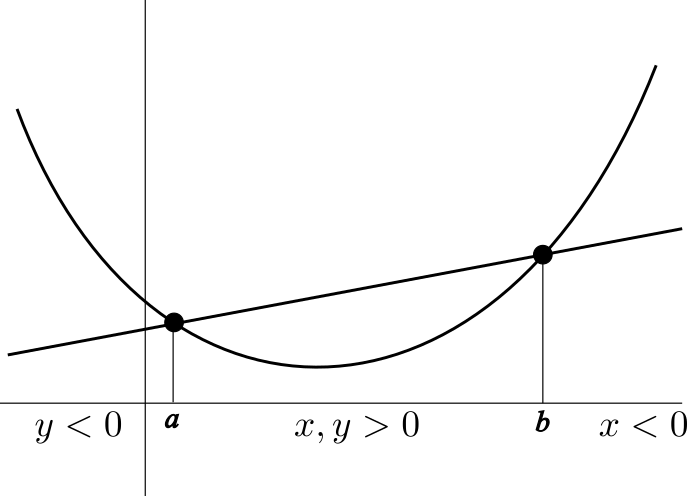
• Si $x+y=1$ y $a\lt b$, entonces el número $ax+by$ está entre $a$ y $b$ para $x,y\geq 0$, a la derecha de $b$ para $x\lt 0$ y a la izquierda de $a$ para $y\lt 0$.
• $f(ax+by)$ es el valor de la función en $ax+by$.
• $xf(a)+yf(b)$ es el valor de la recta en $ax+by$.

Aplicando este razonamiento a las funciones $f(t)=t^2$ y $f(t)=t^4$, que son ambas estrictamente convexas, deducimos que el conjunto de soluciones son los puntos $(x,y)$ que cumplen $x,y\geq 0$ y $x+y=1$. En otras palabras, son los puntos del segmento que une $(1,0)$ y $(0,1)$ en el plano.

Solución. Procedamos por inducción sobre $n$. Para el caso base $n=1$, se cumple la igualdad: $$\binom{2n}{n}=\binom{2}{1}=2=\frac{4}{2}=\frac{4^n}{n+1}.$$ Supongamos entonces que la desigualdad es cierta para $n$ y veamos qué ocurre para $n+1$. Usando la hipótesis de inducción, tenemos que \begin{align*} \binom{2(n+1)}{n+1}&=\frac{(2n+2)!}{((n+1)!)^2}=\frac{(2n+2)(2n+1)(2n)!}{(n+1)^2(n!)^2}=\frac{2(2n+1)}{n+1}\binom{2n}{n}>\frac{(2n+1)4^{n+1}}{(n+1)^2}. \end{align*} Ahora sólo falta ver que $\frac{2n+1}{(n+1)^2}\geq\frac{1}{n+2}$, lo que equivale a que $(2n+1)(n+2)\geq (n+1)^2$, esto es, $n^2+n+1\geq 0$. Ya hemos terminado porque esta última igualdad es claramente cierta (es la suma de tres números positivos).

Como la desigualdad $n^2+n+1\gt 0$ es realmente estricta, deducimos que no puede haber igualdad para ningún $n\geq 2$, luego la igualdad se alcanza sólo para $n=1$.