Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Informar de error en enunciado Informar de procedencia del problema
Consideremos la función $f:(0,+\infty)\to\mathbb{R}$ definida por $f(x)=\log\frac{x}{\sqrt{1+x^2}}$. Sus derivadas vienen dadas por \[f'(x)=\frac{1}{x(x^2+1)},\qquad f''(x)=\frac{-3x^2-1}{x^2(x^2+1)^2}.\] Como $f''(x)<0$ para todo $x>0$, deducimos que $f$ es una función cóncava, luego aplicando la desigualdad de Jensen obtenemos que \begin{eqnarray} \frac{1}{3}\log\left(\frac{xyz}{\sqrt{(1+x^2)(1+y^2)(1+z^2)}}\right)&=&\frac{f(x)+f(y)+f(z)}{3}\\ &\leq& f\left(\frac{x+y+z}{3}\right)=f\left(\frac{4}{3}\right)=\log\left(\frac{4}{5}\right). \end{eqnarray} Tomando exponenciales en ambos miembros, deducimos la desigualdad del enunciado.
Nota. Como la función $f$ es estrictamente convexa, la igualdad se alcanzará si, y sólo si, $x=y=z=\frac{4}{3}$.
Informar de error en enunciado Informar de procedencia del problema
Nota. De este razonamiento se deduce que la igualdad es cierta cuando $x$ e $y$ tienen distinto signo o bien alguno de los dos es igual a cero.
Informar de error en enunciado Informar de procedencia del problema
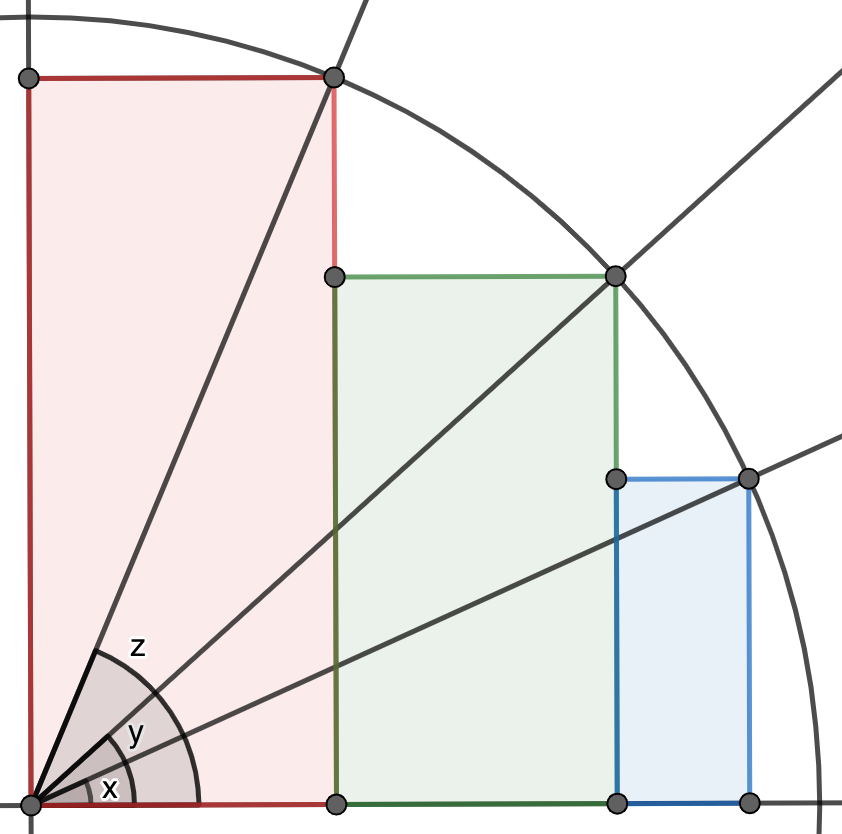
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema