En esta entrada veremos la demostración dada por Schmidt en 1939 de la desigualdad isoperimétrica en el plano:
Teorema.
Dado un dominio compacto y regular \(\Omega \subset \mathbb{R}^2\), se tiene:
$$
4\pi \mbox{Area}(\Omega )\leq \mbox{Longitud}(\partial \Omega )^2,
\quad \mbox{«=»} \Longleftrightarrow \Omega \mbox{ es un disco
redondo.}
$$
Es de destacar la sencillez de la prueba, que sólo usa geometría
elemental, y que no supone existencia de dominios isoperimétricos.
Fijamos un dominio compacto y regular \(\Omega \subset \mathbb{R}^2\). Tomamos una dirección \(v\in \mathbb{R}^2-\{ 0\} \).
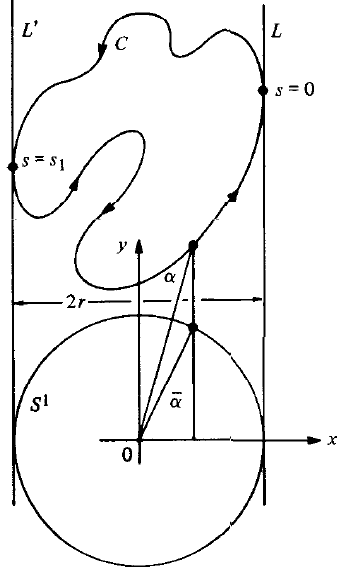
Ejercicio 1. Prueba que existen rectas \(L,L’\) paralelas a \(v\) que son tangentes a \(\partial \Omega \) y tales que \(\Omega \) está contenido en la banda cerrada con borde \(L\cup L’\).
Llamamos \(2r\gt 0\) a la distancia de \(L\) a \(L’\). Ahora consideramos una circunferencia \(S^1\) de radio \(r\) que sea tangente a \(L\) y a \(L’\). Tomamos coordenadas cartesianas en \(\mathbb{R}^2\) de forma que el centro de \(S^1\) es \((0,0)\) y las rectas \(L,L’\) vienen dadas por
$$
L=\{ x=r\} ,\qquad L’=\{ x=-r\} .
$$
Respecto de estas coordenadas, podemos parametrizar \(\partial \Omega \) por el arco mediante \(\alpha (s)=(x(s),y(s))\), \(s\in [0,B]\), de forma que \(\alpha (0)=\alpha (B)\in L\), siendo \(B=\mbox{Longitud}(\partial \Omega )\). Así, existirá \(s_1\in (0,B)\) tal que \(\alpha (s_1)\in L’\) (posiblemente \(s_1\) no es único), como en la siguiente figura:
Ejercicio 2. Demuestra que existe una función \(\overline{y}\colon [0,B]\to R \) de clase \(C^1\) tal que \(\overline{\alpha }(s)=(x(s),\overline{y}(s))\) parametriza la circunferencia \(S^1\).
De esta forma, en cada instante \(s\), los puntos \(\alpha (s)\) y \(\overline{\alpha }(s)\) están sobre la misma recta vertical, como en la figura de arriba.
En esta página vimos cómo calcular el área de los recintos encerrados por \(\alpha \) y \(\overline{\alpha }\):
$$
\mbox{Area}(\Omega )=\int _0^Bx(s)y'(s)\, ds, \qquad \pi r^2=-\int _0^B\overline{y}(s)x'(s)\, ds,
$$
luego
$$
\mbox{(a)}\hspace{2cm}
\mbox{Area}(\Omega )+\pi r^2=\int _0^B(xy’-\overline{y}x’)ds\leq \int _0^B\sqrt{(xy’-\overline{y}x’)^2}ds.
$$
Ejercicio 3. Usa la desigualdad de Schwarz para probar que \(\forall s\in [0,B]\),
$$
\left[ x(s)y'(s)-\overline{y}(s)x'(s)\right] ^2\leq \left[ x(s)^2+(\overline{y}(s))^2\right] \left[ (y'(s)^2+x'(s)^2\right] ,
$$
y deduce que
$$
\left[ xy'(s)-\overline{y}x’\right] ^2\leq r^2\qquad \mbox{ en }\ [0,B].
$$
Usando el ejercicio 3 en (a), tenemos
$$
\mbox{(b)}\hspace{2cm}\mbox{Area}(\Omega )+\pi r^2\leq \int _0^Br\, ds=rB.
$$
Por otro lado, la relación entre la media geométrica y la media aritmética de números positivos implica que
$$
\mbox{(c)}\hspace{2cm}\sqrt{\mbox{Area}(\Omega )\cdot \pi r^2}\leq \frac{1}{2}\left( \mbox{Area}(\Omega )+\pi r^2\right) ^2.
$$
De (b) y (c) deducimos que
$$
\mbox{Area}(\Omega )\cdot \pi r^2\leq \frac{1}{4}r^2B^2,
$$
que es la desigualdad isoperimétrica.
Supongamos ahora que se da la igualdad en la desigualdad isopermétrica. Entonces, tiene que darse la igualdad en cada desigualdad del desarrollo anterior. En particular:
- La igualdad en (c) implica que \(\mbox{Area}(\Omega )=\pi r^2\). De aquí deducimos que \(r\) no depende de la dirección \(v\) que tomamos al principio.
- La igualdad en (b) implica que se da la igualdad en la desigualdad de Schwarz (ejercicio 3). Por tanto, existe \(\lambda =\lambda (s)\) tal que \((x,\overline{y})=\lambda (y’,x’)\).
Ejercicio 4. En el caso 2 anterior, deduce que \(\lambda \) es constante \(\pm r\).
Acabamos de probar que \(y’=\pm \frac{1}{r}x\). Como \(r\) no depende de la dirección \(v\), podemos intercambiar los papeles de \(x,y\) con lo que obtendremos análogamente \(x’=\pm \frac{1}{r}y\). Por tanto,
$$
x^2+y^2=r^2[ (y’)^2+(x’)^2]=r^2,
$$
de donde deducimos que \(\Omega \) es un disco de radio \(r\).