Las losas tradicionalmente se arman en ELU con una red ortogonal de barras de acero. Las normativas no recogen en su articulado un método específico para dimensionar en rotura losas de HA sino que recomiendan usar un modelo tipo sándwich. Igualmente, programas como SAP© utilizan también el modelo de sándwich.
Uno de los estudios pioneros en este campo es la denominada teoría de Broundum-Nielsen (1974).
En un modelo sándwich, el elemento se supone formado por 3 capas: las capas externas resisten las fuerzas correspondientes a la descomposición del axil, flector y torsor mientras que la central se encarga de transmitir el cortante.
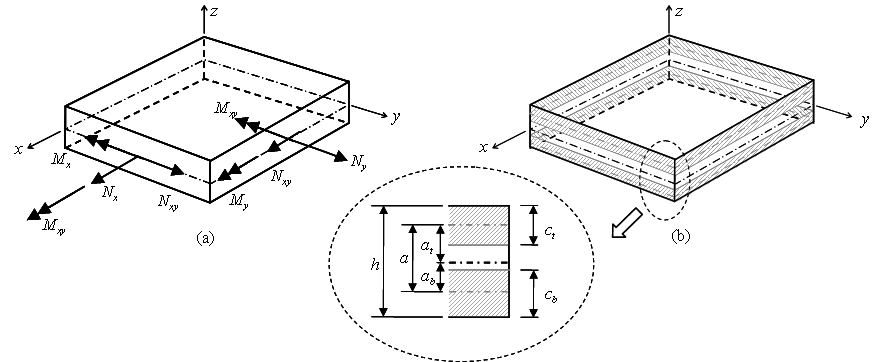
Figura 1. Modelo sándwich
Las hipótesis adoptadas son:
- La compresión se distribuye uniformemente en el espesor de la capa,
- Las barras plastificadas a tracción
- Se desprecia la tracción en el hormigón,
- Se desprecia la compresión en las barras.
Imponiendo el equilibrio sobre una porción de losa delimitada por una grieta (Figura 2) se obtienen: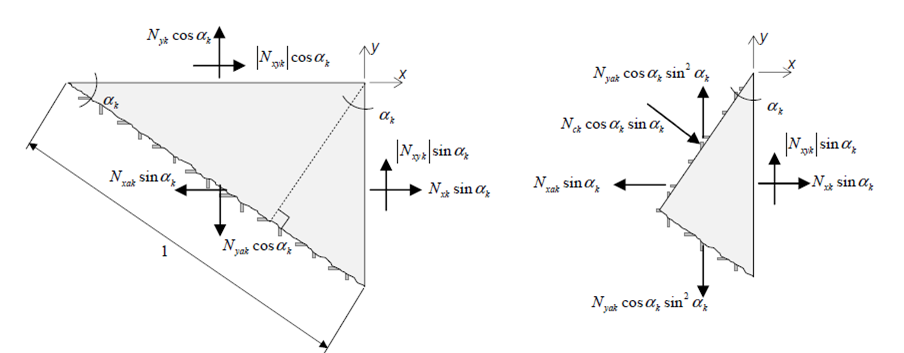
Figura 2. Porción de losa en equilibrio.
- la fuerza de compresión principal en el hormigón
- las fuerzas en las armaduras por unidad de longitud (para ambas direcciones)
El ángulo de inclinación de la grieta, α, se obtiene de imponer que la cantidad de armadura total sea MINIMA.
El procedimiento propuesto por Broundum-Nielsen empieza considerando la flexión dominante y el axil correspondiente: M y N. Y acepta que:
- el cdg de la armadura de tracción coincide con el centro del estrato exterior traccionado, y que
- la tensión de compresión es uniforme en el espesor del estrato comprimido. A partir de equilibrio a nivel de la armadura del estrato traccionado se obtiene el valor del espesor del estrato comprimido, de manera iterativa.
Conocida la geometría de los estratos se puede realizar la descomposición de acciones y obtener: las fuerzas en las armaduras por unidad de longitud (para ambas direcciones) y la fuerza de compresión principal en el hormigón: Nc.
El área de acero en la teoría de B-N se obtiene dividiendo la tracción entre el límite elástico, es decir, se supone que el acero ha plastificado.
Hdez-Montes et al. cuestionaron esta hipótesis e introdujeron una comprobación a nivel de deformaciones de la sección transversal, similar a como se hace habitualmente en vigas en las que la plastificación de la armadura se produce si la profundidad de la fibra neutra es menor que xlim .
Admitiendo que dirección principal de compresión en un estrato coincide con la dirección principal de tracción en el estrato opuesto y asumiendo que el plano de rotura viene dado por la dirección principal de compresión en el hormigón se puede obtener un espesor límite del estrato.
Por tanto, el acero en cada una de las dos direcciones de armado habrá plastificado sii el espesor c del estrato opuesto es menor que este valor límite. Si el acero no ha plastificado, el área se obtendrá dividiendo la fuerza de tracción entre la tensión correspondiente a su deformación o cambiar la geometría de la losa para forzar la plastificación del acero: cambiar posición de la armadura, espesor total de la losa, etc.
Para comprobar si la armadura plastificaba o no, se ensayaron a flexo-torsión 2 especímenes de losa en el laboratorio de estructuras de la ugr.
La máquina de ensayo fue diseñada por nosotros (araña) y las cargas eran introducidas mediante 4 gatos, uno en cada brazo. Las cargas se aplicaron manualmente, con control de fuerzas, manteniendo casi constante el torsor e introduciendo un flector claramente predominante.
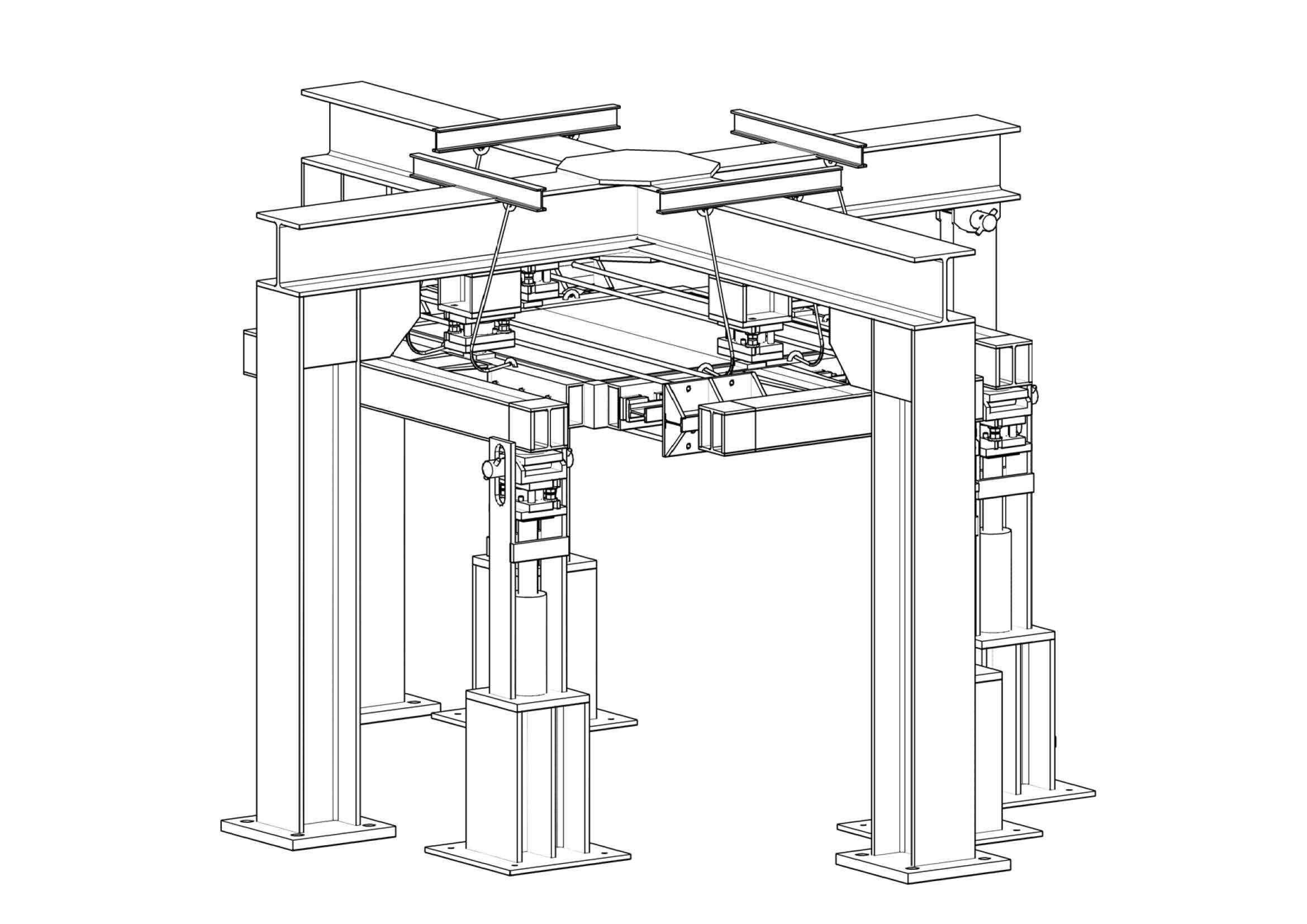

Figura 3. Aparato para ensayo de losas. “La araña”.
Además se realizó un modelo numérico que reproducía fielmente ambos ensayos.
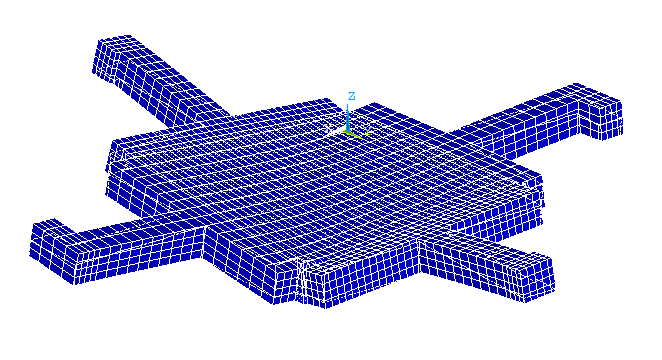
Figura 4. Modelo de elementos finitos de la losa ensayada.
La experimentación y los resultados numéricos han puesto de manifiesto que:
- La plastificación no se produce simultáneamente para las dos direcciones de armado: plastifican en x y no en y.
- El modelo de sandwich conduce a valores del momento de agotamiento del lado de la seguridad.
- Es necesario imponer una condición de compatibilidad.
