Olimpiadas de Matemáticas
Página de preparación y problemas

Elige un tema
| Aritmética |
| Geometría |
| Polinomios |
| Desigualdades |
| Álgebra |
| Combinatoria |
| Invariantes |
Lección 0. Distancias, ángulos y áreas
La geometría clásica, llamada así por tener sus orígenes en la Antigüedad, es una rama de las matemáticas que estudia distintos objetos del plano y el espacio mediante la comparación de longitudes y ángulos (ejemplos de tales objetos son los puntos, las rectas o los polígonos). Este tipo de geometría es uno de los temas centrales en el currículo de olimpiadas por basarse en el razonamiento geométrico puro, al estilo de los Elementos de Euclides. En esta lección introductoria presentaremos los ingredientes básicos que vamos a utilizar para estudiar la geometría del plano; más adelante, se tratarán algunas características de la geometría del espacio. Esta introducción no pretende ser rigurosa ni exhaustiva sino presentar definiciones y propiedades elementales que aparecerán más adelante (como recordatorio, ya que todos estamos familiarizados con ellas).
Puntos, rectas y segmentos
Los puntos son las unidades indivisibles de la geometría y todas las demás figuras se componen de ellos. Una recta es una colección unidimensional de puntos y un plano es una colección bidimensional de puntos. Definir rigurosamente una recta o un plano puede ser complejo, así que simplemente diremos que son figuras ilimitadas cuyos puntos son indistinguibles unos de otros: si nos colocaran en un punto de una recta o un plano sin referencia alguna, no sabríamos decir en qué punto estamos (piensa que otras figuras como una circunferencia o un triángulo no cumplen estas propiedades).
Si un punto pertenece a una recta, diremos que la recta pasa por el punto, en cuyo caso la separa en dos subconjuntos disjuntos llamados semirrectas con extremo en dicho punto. Por dos puntos distintos pasa una única recta, aunque esto no es cierto para tres o más puntos (en caso de que ocurra, tales puntos se dice que están alineados o que son colineales). Dos puntos en una recta la dividen en tres subconjuntos: dos semirrectas (ilimitadas) y un segmento (limitado), como se muestra en la figura más abajo. Estos dos puntos se llaman extremos del segmento. Normalmente supondremos que los segmentos y semirrectas contienen a sus extremos salvo que se diga lo contrario.
En la siguiente figura se muestra la recta que pasa por dos puntos distintos $A$ y $B$, recta que suele representarse por $\overline{AB}$:
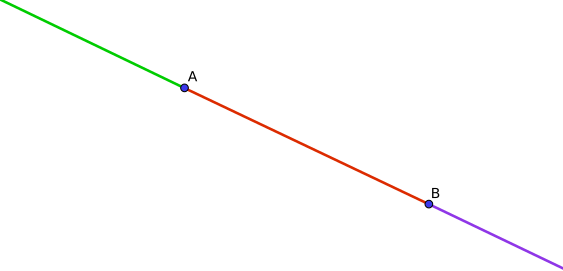
- El segmento con extremos $A$ y $B$, se escribe simplemente como $AB$ y se corresponde con la parte roja de la recta, incluyendo los puntos $A$ y $B$.
- La semirrecta con extremo en $A$ que pasa por $B$ se escribe como $\overrightarrow{AB}$ y se corresponde con las partes roja y morada. Esta semirrecta es distinta de $\overrightarrow{BA}$, que se corresponde con las partes roja y verde.
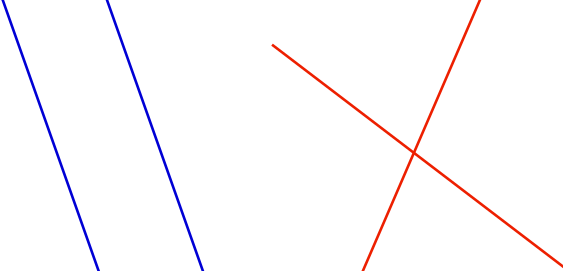
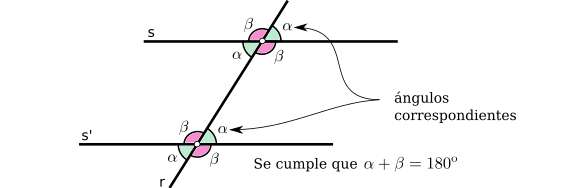
Dos rectas distintas en el plano pueden cortarse o no en algún punto. Si no se cortan, se dice que son paralelas y, si se cortan, se dice que son secantes. Dos rectas secantes se cortan en un único punto (¿por qué?). En la siguiente figura se puede ver un par de rectas secantes (en rojo) y un par de rectas paralelas (en azul):
Ángulos
Dos semirrectas en el plano con vértice común en un punto $O$ dividen al plano en dos regiones, llamadas ángulos con vértice en $O$. Cuando las dos semirrectas son la misma, una de estas dos regiones "desaparece" y a la otra se le llama ángulo completo y se le asigna el valor 360º. Este es un valor arbitrario que resulta de haber elegido los grados sexagesimales (º) como unidad. Más adelante también trabajaremos con otra unidad, el radián, de forma que el ángulo completo mide $2\pi$ radianes. A cada ángulo del plano se le puede asignar un valor entre 0º y 360º, de forma que cumple las siguientes propiedades:
- Si un ángulo está contenido en otro, entonces su valor es menor o igual que el de este último.
- Si un ángulo se descompone como unión de dos ángulos, entonces su valor es la suma de estos dos ángulos.
Esta última propiedad permite sumar y restar ángulos geométricamente, como se muestra en la figura más abajo. Observemos que una semirrecta $r$ y un número real $\alpha$ entre $0$ y $360$, distinto de $180$, existen dos semirrectas con el mismo extremo que $r$ que determinan con $r$ un ángulo de valor $\alpha$, una en sentido de las agujas del reloj y otra en sentido contrario. En el caso de $\alpha=180$ estas dos semirrectas coinciden (no son más que la prolongación de $r$).
Dos rectas secantes determinan cuatro semirrectas con vértice en el punto de intersección y, por tanto, cuatro ángulos. De estos cuatro ángulos, los que sólo comparten el vértice se llaman opuestos por el vértice y son iguales. Los que comparten una semirrecta se llaman suplementarios y suman 180º. Si los cuatro ángulos formados por dos rectas son iguales, su valor es $90º$ y las rectas se llaman perpendiculares. Los ángulos de $90º$ se llaman rectos, los de más de $90º$ obtusos y los de menos de $90º$ agudos. Si una recta divide a un ángulo $\alpha$ en dos ángulos iguales, éstos tendrán un valor $\frac{\alpha}{2}$ y dicha recta se llama bisectriz (interior) del ángulo. Suele hablarse de bisectriz exterior para referirse a la bisectriz del ángulo suplementario, como puede verse en la figura. La bisectriz interior y exterior de un ángulo son perpendiculares (¿sabrías demostrarlo?).
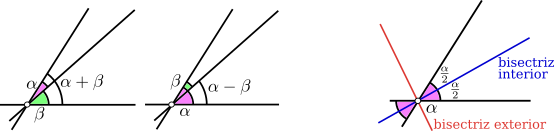
Dada una recta $r$, por todo punto $P$ pasa una única recta perpendicular a $r$ y una única recta paralela a $r$. Además, la perpendicular es secante con $r$ en un punto $P'$ que suele llamarse pie de la perpendicular por $P$ a $r$. Lo representamos en la siguiente figura:

Todas estas propiedades para ángulos se pueden aplicar normalmente a rectas, semirrectas y segmentos, siempre que haya un extremo o punto común. Por ejemplo, cuando hablemos de los ángulos de un triángulo, estos serán ángulos formados por segmentos (lados del triángulo) con un extremo en común (vértice del triángulo).
Longitudes
La longitud es un número mayor o igual que cero que se le asigna a cada segmento del plano y que representa la distancia entre los extremos del segmento. Si el segmento es $AB$, suele usarse la misma notación $AB$ para hacer referencia a la dicha longitud. La longitud puede ser cero en el caso degenerado en que $A=B$ y el segmento se reduce a un único punto. Algunas propiedades de la longitud son las siguientes:
- Si un segmento de longitud $a$ está contenido en otro de longitud $b$, entonces $a\leq b$.
- Dados dos puntos $A$ y $B$, se tiene que $AB=BA$. Dado un punto $P$ en el segmento $AB$, se cumple que $AB=AP+PB$.
De la misma forma que ocurría con los ángulos, esta última propiedad nos permite sumar y restar longitudes de forma geométrica:
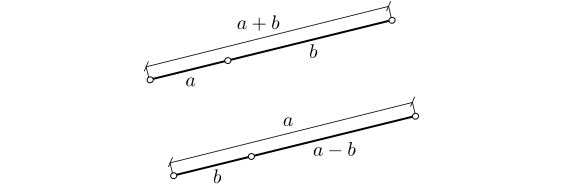
Una propiedad más interesante es la siguiente desigualdad, que nos dice que para ir de un punto $A$ a un punto $B$ seguir el segmento $AB$ es más corto que pasar por un tercer punto $C$ que no está en el segmento $AB$.
Circunferencias
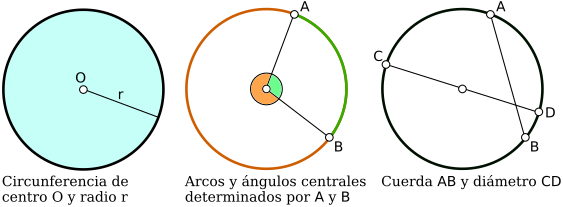
Dado un punto $O$ y un número real $r>0$, existen muchos puntos del plano a distancia $r$ de $O$. Al conjunto de todos estos puntos se le llama circunferencia de centro $O$ y radio $r$. Dos puntos $A$ y $B$ en una circunferencia la dividen en dos trozos curvilíneos llamados arcos de la circunferencia, mientras que el segmento que los une se llama cuerda. Una cuerda que pasa por el centro de la circunferencia se llama diámetro. El ángulo $\angle AOB$ se llama ángulo central correspondiente al arco $AB$. Esto nos permite identificar ángulos con vértice en el centro de la circunferencia y arcos de la misma. Además, a la región delimitada por el arco $AB$ y los segmentos $OA$ y $OB$ se le llama sector circular de ángulo $\angle AOB$. Por otro lado, una circunferencia divide al plano en dos regiones, una limitada llamada círculo o interior y la otra no limitada llamada exterior.
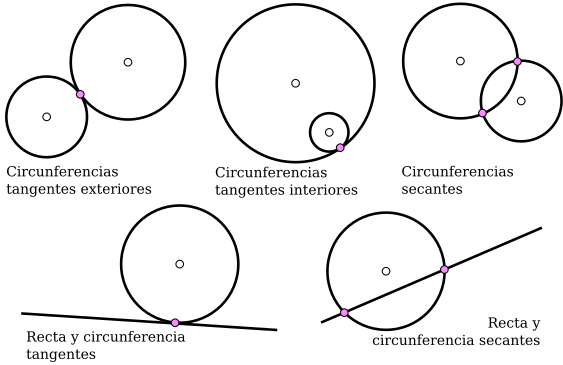
Por tres puntos no alineados pasa una única circunferencia (esto se justificará cuando se hable de circunferencia circunscrita a un triángulo), por lo que dos circunferencias distintas se cortan en como mucho dos puntos. Si se cortan en dos puntos, se dicen secantes y si se cortan en un punto tangentes. Dos circunferencias tangentes pueden serlo interiormente si una está contenida en el interior de la otra, o exteriormente en caso contrario. De la misma forma, una circunferencia y una recta se cortan en un máximo de dos puntos. Si se cortan en dos puntos, se dicen secantes y si se cortan en un punto tangentes. En la siguiente figura mostramos estas posibilidades, indicando en color rosa los puntos de intersección y en blanco los centros de las circunferencias:
Si por cada tres puntos del plano no alineados pasa una única circunferencia, esto no es cierto en general para cuatro o más puntos. Se dice que ciertos puntos son concíclicos si por ellos pasa una circunferencia. Determinar si ciertos puntos están alineados o son concíclicos es un problema que puede llegar a ser muy complejo y que trataremos bastante a lo largo de estas lecciones.
Para terminar con hechos generales de la circunferencia, hemos de decir que su longitud es igual a $2\pi r$, siendo $r$ su radio. Esto nos permite calcular la longitud $\ell$ de un arco entre dos puntos $A$ y $B$ ya que ésta debe ser proporcional al correspondiente ángulo central $\alpha=\angle AOB$. Como un ángulo central de $360$ corresponde a la circunferencia completa de longitud $2\pi r$, tenemos que \[\frac{360}{2\pi r}=\frac{\alpha}{\ell}\ \Longleftrightarrow\ \ell=\frac{\pi r\alpha}{180}.\]
Polígonos
Una línea poligonal es una curva formada por una sucesión de segmentos de forma que el extremo final de cada segmento es el extremo inicial del siguiente. Si el extremo final del último segmento es el extremo inicial del primero, entonces se dice que la poligonal es cerrada. Si además cada segmento sólo tiene intersección con el siguiente y el anterior en los mencionados extremos, entonces la poligonal bordea una región del plano llamada polígono. Cada segmento de la poligonal es un lado del polígono y cada extremo de un lado es un vértice. Un polígono tiene, por tanto, el mismo número de vértices que de lados. Además, en cada vértice de un polígono se tocan exactamente dos lados (que se dicen adyacentes a dicho vértice), que forman dos ángulos: un ángulo interior (hacia el interior del polígono) y un ángulo exterior. Los vértices de un polígono $A_1,A_2,\ldots,A_n$ escritos en orden consecutivo determinan completamente al polígono, por lo que es usual escribir simplemente $A_1A_2\ldots A_n$ para hacer referencia al polígono. Los lados de este polígono se expresan escribiendo los pares de vértices consecutivos que son sus extremos, es decir, $A_1A_2, A_2A_3,\ldots,A_nA_1$.
Un polígono es un triángulo si tiene tres lados, un cuadrilátero si tiene cuatro lados, un pentágono si tiene cinco lados, etc. En general, si queremos expresar que tiene un número $n$ de lados, suele decirse que es un $n$-ágono. Veamos algunos nombres importantes que reciben algunos polígonos destacados:
- Un triángulo se dice...
- equilátero si tiene los tres ángulos iguales,
- isósceles si tiene dos ángulos iguales,
- escaleno si tiene los tres ángulos distintos,
- acutángulo si tiene los tres ángulos agudos,
- rectángulo si tiene un ángulo recto,
- obtusángulo si tiene un ángulo obtuso.
-
Un cuadrilátero se dice...
- un paralelogramo si sus dos pares de ángulos opuestos son iguales,
- un rectángulo si todos sus ángulos son iguales,
- un cuadrado si es un rectángulo y tiene los cuatro lados iguales,
- un trapecio si dos de sus lados son paralelos,
- un rombo si tiene los cuatro lados iguales,
- Un polígono se dice regular si tiene todos sus lados iguales y todos sus ángulos interiores iguales.
- Un polígono se dice convexo si todos sus ángulos interiores son menores o iguales que un ángulo llano (180º). Esto es lo mismo que decir que, dados dos puntos del polígono, el segmento que los une está contenido en el polígono.
Estas definiciones no son excluyentes. Por ejemplo, todo triángulo equilátero es isósceles; todos los cuadrados son rectángulos; todos los rectángulos y rombos son paralelogramos; todos los paralelogramos son trapecios. En la siguiente lección, veremos que hay otras definiciones o formas de comprobar estas definiciones. Por ejemplo, un paralelogramo también es todo cuadrilátero que tiene sus lados opuestos iguales (en el caso del rectángulo, a estas dos longitudes se les llama base y altura). Por otro lado, los adjetivos acutángulo, rectángulo y obtusángulo sí que son excluyentes, como consecuencia del siguiente resultado.
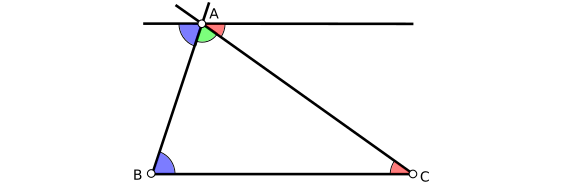
Los ángulos que tienen el mismo color son iguales por tratarse de una paralela, por lo que claramente los tres ángulos suman 180º.
- Un triángulo no puede tener dos ángulos rectos.
- Todo triángulo es acutángulo, rectángulo u obtusángulo.
- Los ángulos de un triángulo rectángulo e isósceles son $90º$, $45º$ y $45º$.
- Los ángulos de un triángulo equilátero son iguales a $60º$.
Todo polígono de se puede descomponer en triángulos de forma que dos cualesquiera de esos triángulos se toquen sólo a lo largo de un vértice o una arista y a este proceso se le llama triangulación del polígono. De hecho, un polígono de $n$-lados se puede triangular con $n-2$ triángulos. Por ejemplo, en la siguiente figura se muestra un $24$-ágono no convexo pintado de amarillo triangulado en $22$ triángulos (obviamente, la forma de triangularlo no es única):

- La suma de los ángulos internos es $180(n-2)$.
- La suma de los ángulos externos es $180(n+2)$.
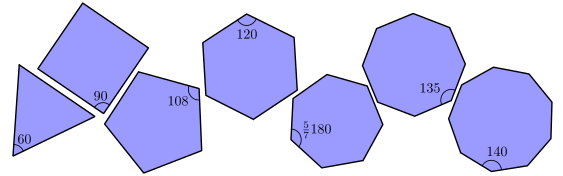
- Si el polígono es regular, entonces cada ángulo interno es igual a $180-\frac{360}{n}$ y cada ángulo externo es igual a $180+\frac{360}{n}$.
En la siguiente figura pueden verse los ángulos interiores de los polígonos regulares, desde el triángulo hasta el eneágono:
Un polígono se dice cíclico o inscriptible si hay una circunferencia que pasa por todos sus vértices, es decir, si dichos vértices son concíclicos. Se dice que tiene una circunferencia inscrita si hay una circunferencia tangente a todos los lados del polígono. Más adelante, veremos que todo triángulo admite circunferencias inscrita y circunscrita, aunque esto no es siempre cierto para polígonos con más de tres lados. En la siguiente imagen se pueden ver heptágonos con circunferencia circunscrita e inscrita:
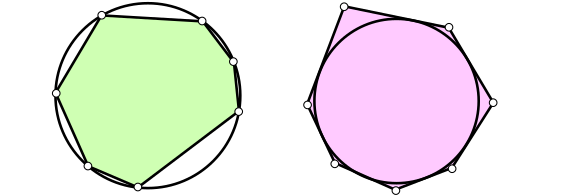
Los polígonos regulares tienen circunferencia circunscrita y también circunferencia inscrita. El centro de estas circunferencias coincide y se llama centro del polígono. Al radio de la circunferencia inscrita también se le llama apotema del polígono.
A la suma de las longitudes de todos los lados de un polígono se le llama perímetro del polígono. En un $n$-ágono regular, el perímetro es $n$ veces la longitud del lado.
Movimientos del plano
Un movimiento rígido o isometría del plano es una transformación que conserva las distancias. Sobre este tema volveremos más adelante con mucha mayor profundidad, pero conviene saber que las siguientes aplicaciones son movimientos rígidos:
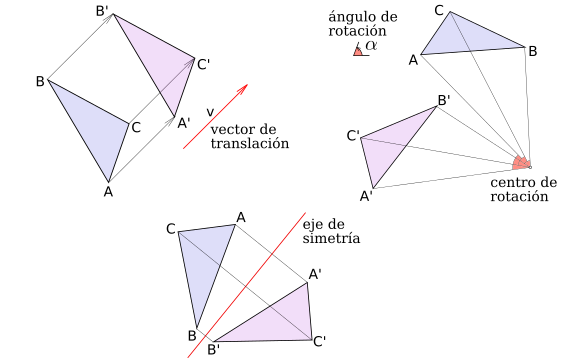
- Traslación. Consisten en moverse una longitud prefijada en una dirección y sentido prefijados, lo que puede resumirse en dar un vector de traslación.
- Rotación. Consisten en girar un cierto ángulo prefijado respecto de un punto prefijado llamado centro de rotación.
- Simetría. Consisten en reflejar respecto de una recta prefijada llamada eje de simetría como si se tratara de la imagen a través del espejo.
Los movimientos conservan todos los elementos geométricos: las distancias, los ángulos y, como comentaremos a continuación, las áreas. Además, llevan rectas en rectas y circunferencias en circunferencias del mismo radio.
Si podemos pasar de una figura a otra aplicando uno o varios movimientos consecutivos, se dice que las figuras son congruentes. Intuitivamente, si el plano estuviera hecho de papel, dos figuras son congruentes cuando una puede recortarse y superponerse perfectamente sobre la otra. En la figura pueden verse ejemplos de triángulos $A'B'C'$ congruentes por los movimientos arriba mencionados con un triángulo $ABC$ (es usual utilizar $'$ para denotar los puntos correspondientes, también llamados homólogos):
Áreas
Para terminar con las generalidades, hablaremos del área de las regiones del plano. La definición matemática de área es muy sofisticada, pero aquí sólo hablaremos de regiones delimitadas por trozos de rectas y circunferencias y nos ceñiremos a la idea intuitiva del área, para lo que basta saber que se cumplen las siguientes propiedades:
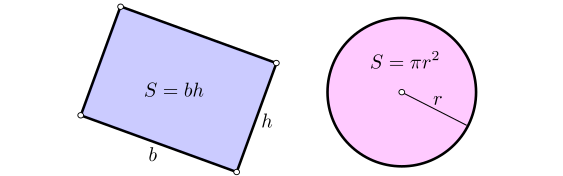
- El área de un rectángulo de base $b$ y altura $h$ es $bh$.
- El área de un círculo de radio $r$ es $\pi r^2$.
- Si una región se descompone como unión de varias trozos que no se solapan, entonces su área es la suma de las áreas de estos trozos.
- Si dos regiones son congruentes, entonces tienen la misma área.
Veamos cómo aplicar estas ideas al cálculo del área de un triángulo $ABC$. Para ello, consideraremos el segmento $AP$ perpendicular en su extremo $P$ a la recta que contiene el lado $a=BC$ . Este segmento se llama altura del triángulo respecto del vértice $A$ y $P$ se llama pie de la altura. También tomaremos la recta paralela a $BC$ que pasa por $A$ y los puntos $Q$ y $R$ que son pies de las perpendiculares a esta recta que pasan por $B$ y $C$, respectivamente.
Este cálculo tiene una particularidad que aparece frecuentemente en los problemas y es que hay que distinguir casos ya que la demostración no es idéntica si el ángulo $A$ es agudo, recto u obtuso. Estos tres casos se pueden ver en la figura siguiente:
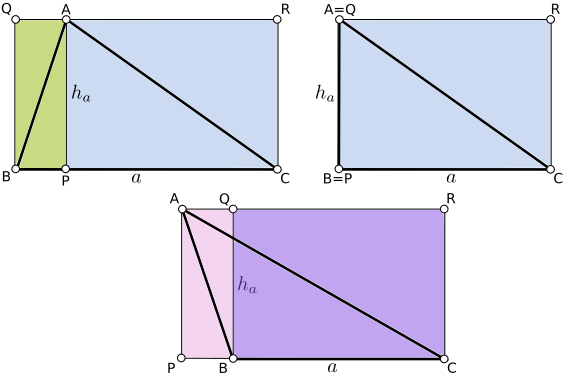
- En el caso en que $A$ es agudo, los dos triángulos verdes y los dos triángulos azules son congruentes, luego tienen la misma área. Por tanto, el área del triángulo $ABC$ es la mitad del área del rectángulo $BQRC$, que es igual a $ah_a$ (base por altura).
- En el caso en que $A$ es recto, los triángulos verdes desaparecen y el argumento es similar al anterior.
- Finalmente, si $A$ es obtuso, el área de $ABC$ es el área de $APC$ menos el área de $APB$. El área de $APC$ es la mitad del área de $APRC$ y el área de $APB$ es la mitad del área de $APBQ$ (triángulos rosas). Por tanto, el área de $ABC$ es la mitad de la diferencia entre las áreas de $APRC$ y $APBQ$, es decir, la mitad del área de $BQRC$, que es igual a $ah_a$.
El área no depende de haber elegido el ángulo $A$ y podría haberse hecho el mismo razonamiento usando $B$ ó $C$ y considerando las correspondientes alturas $h_b$ y $h_c$.
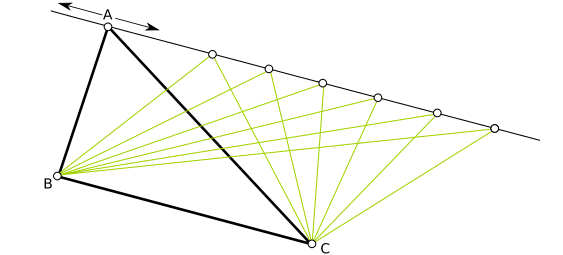
Una consecuencia importante de esta fórmula para el área de un triángulo es que si trasladamos un vértice del triángulo paralelamente al lado opuesto, entonces los triángulos resultantes tienen el mismo área que el original:
Los polígonos de más de tres lados pueden triangularse para calcular su área como la suma de las áreas de los triángulos que aparecen en la triangulación. En cuanto a un sector circular de radio $r$, el área es proporcional a su ángulo central; teniendo en cuenta que un ángulo de $360º$ corresponde a $\pi r^2$, un ángulo central $\alpha$ dará lugar a un área $S$ dada por \[\frac{360}{\pi r^2}=\frac{\alpha}{S}\ \Leftrightarrow\ S=\frac{\pi r^2\alpha}{360}.\]
Ir arribaIr al índiceInformar Problemas que puedes resolver con lo aprendido en esta lección
Nota. ¿Cuáles son los ángulos del triángulo construido? ¿Es equilátero?
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema