Olimpiadas de Matemáticas
Página de preparación y problemas

Elige un tema
| Aritmética |
| Geometría |
| Polinomios |
| Desigualdades |
| Álgebra |
| Combinatoria |
| Invariantes |
Lección 1. Congruencia y semejanza de triángulos
La herramienta geométrica más útil y que se aplica en mayor sin duda en la resolución de problemas de geometría de olimpiada es la semejanza de triángulos. Encontrar triángulos semejantes en un problema suele dar siempre información útil para su resolución. En esta lección, aprenderemos la diferencia entre triángulos iguales, triángulos congruentes y triángulos semejantes, cómo identificarlos y algunas propiedades relacionadas.
Por fijar notación para esta lección y algunas siguientes, cuando trabajamos con un triángulo $ABC$, las letras mayúsculas $A$, $B$ y $C$ denotan los vértices del triángulo, mientras que usaremos las minúsculas $a$, $b$ y $c$ para los lados opuestos a dichos vértices. También denotaremos por $\alpha$, $\beta$ y $\gamma$ los ángulos interiores en estos vértices. Todo ello queda resumido en la siguiente figura:
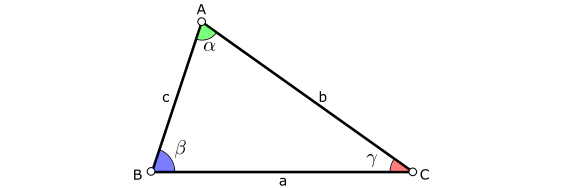
Triángulos congruentes
Dos triángulos son congruentes cuando puede pasarse de uno a otro mediante sucesivos movimientos rígidos del plano (como son las simetrías, las traslaciones o las rotaciones). Informalmente, esto quiere decir que se puede recortar uno de ellos y pegarlo sobre el otro haciéndolo coincidir de forma exacta. Aunque suele decirse que dos triángulos congruentes son triángulos iguales, esta terminología no es del todo correcta ya que no son el mismo triángulo sino que difieren en un movimiento del plano.
Supongamos que los triángulos $ABC$ y $A'B'C'$ son congruentes, donde el vértice $A'$ corresponde con $A$, el vértice $B'$ con $B$ y el vértice $C'$ con $C$. Entonces los lados y ángulos homólogos coinciden: \[a=a',\quad b=b',\quad c=c',\qquad\qquad \alpha=\alpha',\quad \beta=\beta',\quad \gamma=\gamma',\] donde $'$ denota los elementos de $A'B'C'$. Esto es consecuencia de que los movimientos rígidos conservan distancias y ángulos. Recíprocamente, si dos triángulos tienen las mismas longitudes de lados y los mismos ángulos, entonces son congruentes. No obstante, no hay que conocer estos seis datos (tres lados y tres ángulos) para saber si son congruentes ya que son sufientes tres de ellos. Esta es la filosofía de los siguientes criterios.
Criterio LLL: Dos triángulos son congruentes si, y sólo si, tienen tienen los tres lados iguales.
Criterio LAL: Dos triángulos son congruentes si, y sólo si, tienen tienen dos lados iguales y el ángulo común a estos igual.
Criterio ALA: Dos triángulos son congruentes si, y sólo si, tienen un lado igual y sus ángulos adyacentes iguales.
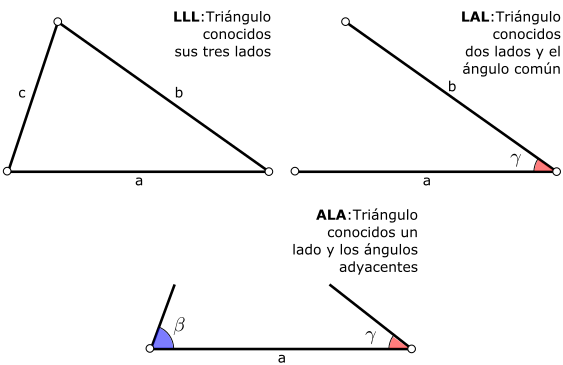
Cada uno de los criterios nos da tres datos del triángulo, lo que quiere decir que sólo hay una forma (salvo movimientos rígidos) de construir el triángulo con tales datos. Damos a continuación una justificación de estas construcciones con regla y compás, lo que debería convencernos de la veracidad de los criterios (no los demostraremos rigurosamente).
En el criterio LLL, conocemos las longitudes $a$, $b$ y $c$ de los lados del triángulo. Construimos un segmento $BC$ de longitud $a$ y circunferencias de radios $b$ y $c$ centradas en $C$ y $B$, respectivamente. Estas se cortan en dos puntos, uno a cada lado de la recta que contiene a $BC$, lo que da dos posibilidades para el vértice $A$, pero son simétricas respecto de la recta que contiene a $BC$ y, por tanto, congruentes.
En el criterio LAL, tenemos dos lados $a$ y $b$ y el ángulo $\gamma$ que definen. Para construir el triángulo, dibujamos dos semirrectas que forman un ángulo $\gamma$ y vértice un punto $C$. Ahora consideramos segmentos $AC$ y $BC$ de longitudes $b$ y $a$, respectivamente, contenidos en sendas semirrectas. Las dos posibilidades, en qué semirrecta hemos colocado $A$ y en cuál $B$, difieren en una simetría respecto de la bisectriz interior al ángulo $\gamma$ y dan dos triángulos congruentes.
Finalmente en el criterio ALA, tenemos una longitud $a$ y los dos ángulos adyacentes $\beta$ y $\gamma$. Para construir el triángulo, dibujamos un segmento $BC$ de longitud $a$ y semirrectas con vértices en $B$ y $C$ formando ángulos interiores $\beta$ y $\gamma$ con $BC$. El punto en que se corten dichas semirrectas será $A$ y está determinado salvo simetría respecto de $BC$ o de su mediatriz.
Falso criterio LAL: Dos triángulos son congruentes si, y sólo si, tienen dos lados iguales y un ángulo igual.
Falso criterio AA: Dos triángulos son congruentes si, y sólo si, tienen dos ángulos iguales (el tercero es igual también ya que suman 180º).
Triángulos semejantes
Dos triángulos son semejantes cuando puede pasarse de uno a otro usando movimientos rígidos del plano y también cambios de escala (homotecias). Esto último quiere decir que podemos multiplicar las longitudes de sus lados por una constante fija, por lo que los triángulos semejantes tienen lados proporcionales (a la constante de proporcionalidad se le llama razón de semejanza). Además, como tales transformaciones conservan los ángulos, no es difícil convencerse de que dos triángulos son semejantes cuando tienen los ángulos homólogos iguales. Por ejemplo, la siguiente figura muestra siete triángulos semejantes, con ángulos homólogos representados por el mismo color.

Criterio LLL: Dos triángulos son semejantes si, y sólo si, tienen tienen los tres lados proporcionales.
Criterio LAL: Dos triángulos son semejantes si, y sólo si, tienen tienen dos lados proporcionales y el ángulo común a estos igual.
Criterio AAA: Dos triángulos son semejantes si, y sólo si, tienen sus tres ángulos iguales.
Un resultado fundamental para trabajar la semejanza es el teorema de Tales.
Los triángulos $OAC$ y $OBD$, que pueden verse en la siguiente figura, se dice que están en posición de Tales. Observemos que si las rectas $AC$ y $BD$ son paralelas, entonces los ángulos correspondientes que forman con la recta $OB$ son iguales, es decir, $\angle OAC=\angle OBD$. De la misma forma, tenemos que $\angle OCA=\angle ODB$. Así, los triángulos $OAB$ y $OCD$ tienen sus tres ángulos iguales y son, por tanto, semejantes.
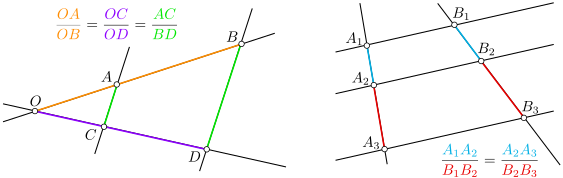
Una forma equivalente del teorema de Tales es que si tres o más paralelas cortan a dos rectas, entonces lo hacen en segmentos proporcionales, como puede verse en la figura de arriba a la derecha (su demostración se deja como ejercicio). En la resolución de problemas, siempre que aparezcan rectas paralelas, es buena idea comprobar si se puede aplicar Tales o si hay triángulos semejantes.
A partir de ahora, la congruencia y semejanza las usaremos como herramientas básicas para tratar multitud de problemas. Para facilitar la aplicación de los criterios y no confundir lados y ángulos homólogos, cuando digamos que $ABC$ es semejante (o congruente) a $DEF$, implícitamente asumiremos que $A$ se corresponde con $D$, $B$ se corresponde con $E$ y $C$ se corresponde con $F$. Se recomienda seguir esta notación.
Triángulos rectángulos
Supongamos que $ABC$ es un triángulo rectángulo con ángulo recto en el vértice $A$. Los lados $AB$ y $BC$ se llaman catetos del triángulo y el lado $BC$ hipotenusa. Si llamamos $P$ al pie de la perpendicular a $BC$ que pasa por $A$, entonces el segmento $AP$ se llama altura del triángulo y lo denotaremos por $h$. Dicha altura divide a $ABC$ en los triángulos $APB$ y $APC$, ambos rectángulos, como puede verse en la figura.

Los triángulos $ABC$ y $PBA$ son semejantes por el criterio AA ya que tienen dos ángulos iguales: uno recto $\angle BPA=\angle BAC=90º$ y otro coincidente $\angle ABP=\angle ABC$. Los ángulos iguales están representados por el mismo color en la figura. La semejanza nos da \[\frac{AB}{BP}=\frac{BC}{AB}=\frac{AC}{AP}\ \Longleftrightarrow\ \frac{c}{BP}=\frac{a}{c}=\frac{b}{h}.\] De aquí obtenemos que $h=\frac{b\cdot BP}{c}$ y $BP=\frac{c^2}{a}$. También son semejantes $ABC$ y $PAC$ por la misma razón y obtenemos que \[\frac{AB}{AP}=\frac{BC}{AC}=\frac{AC}{CP}\ \Longleftrightarrow\ \frac{c}{h}=\frac{a}{b}=\frac{b}{CP},\] de donde $h=\frac{c\cdot CP}{b}$ y $BP=\frac{b^2}{a}$. Multiplicando las dos expresiones que hemos obtenido para $h$, llegamos al conocido como teorema de la altura: \[h^2=\frac{b\cdot BP}{c}\cdot \frac{c\cdot CP}{b}=BP\cdot CP\]
En un triángulo rectángulo, la altura sobre la hipotenusa divide a esta en dos segmentos cuyo producto es el cuadrado de dicha altura.
En cambio, si sumamos las expresiones para $BP$ y $CP$, tenemos el teorema de Pitágoras: \[a=BP+CP=\frac{b^2}{a}+\frac{c^2}{a}=\frac{b^2+c^2}{a}\ \Longleftrightarrow\ a^2=b^2+c^2.\]
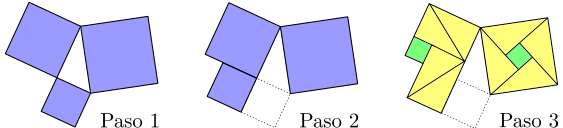
El teorema de Pitágoras nos dice que los cuadrados construidos sobre los catetos reunen un área igual a la del cuadrado construido sobre la hipotenusa. Existen más de 300 demostraciones de este resultado, muchas de ellas visuales como la siguiente (¿serías capaz de explicar cómo se ha hecho la subdivisión en el paso 3?):
Clasificación de cuadriláteros
Un cuadrilátero $ABCD$ se dice que es...
- un paralelogramo si sus lados opuestos son paralelos,
- un rectángulo si todos sus ángulos son rectos,
- un cuadrado si sus lados son iguales y sus ángulos son rectos,
- un trapecio si dos de sus lados son paralelos,
- un rombo si tiene los cuatro lados iguales,
Un cuadrado es, a la vez, un rectángulo y un rombo. Un rectángulo es siempre un paralelogramo y un paralelogramo es siempre un trapecio. Por tanto, estas definiciones no son excluyentes. Vamos a ver distintas formas de entender cada una de estas figuras.
- Los lados opuestos son paralelos ($ABCD$ es un paralelogramo).
- Las diagonales $AC$ y $BD$ se cortan en su punto medio.
- Los lados opuestos son iguales.
- Los ángulos opuestos son iguales.
(a $\Rightarrow$ b) Comencemos suponiendo que $ABCD$ es un paralelogramo, es decir, $AB$ es paralela a $CD$ y $BC$ es paralela a $AD$. Consideremos las diagonales $AC$ y $BD$, que se cortarán en un punto $O$. Los triángulos $AOB$ y $COD$ son semejantes por el criterio AA: se cumple que $\angle AOB=\angle COD$ por ser ángulos opuestos por el vértice y se cumple que $\angle OAB=\angle OCD$ por ser ángulos alternos internos respecto de las paralelas $AB$ y $CD$. La semejanza nos dice que $\frac{AO}{CO}=\frac{BO}{DO}$. Análogamente, los triángulos $BOC$ y $DOA$ son semejantes y la semejanza nos dice que $\frac{AO}{CO}=\frac{DO}{BO}$. Con estas dos igualdades llegamos a que \[\frac{BO}{DO}=\frac{AO}{CO}=\frac{DO}{BO}\ \Longrightarrow\ BO^2=DO^2\ \Longrightarrow\ BO=DO.\] De forma similar, se obtiene que $AO=CO$, lo que demuestra que las diagonales se cortan en su punto medio $O$.
(b $\Rightarrow$ c) Supongamos ahora que las diagonales se cortan en su punto medio $O$. Entonces, los triángulos $AOB$ y $COD$ son congruentes por el criterio LAL: tienen dos lados iguales y también el ángulo en el vértice común $O$ (son ángulos opuestos por el vértice). Por tanto, se deduce que el tercer lado es igual, es decir, $AB=CD$. De forma similar se demuestra que $BC=AD$.
(c $\Rightarrow$ d) Supongamos ahora que $AB=CD$ y $BC=AD$. Entonces, los triángulos $BAD$ y $DCB$ son congruentes por el criterio LLL, luego sus ángulos homólogos son iguales. Esto nos lleva a que $\angle BAD=\angle DCB$ y, de forma similar, $\angle ABC=\angle CDA$.
(d $\Rightarrow$ a) Supongamos finalmente que $\angle BAD=\angle DCB$ y $\angle ABC=\angle CDA$. Como los ángulos de un cuadrilátero suman $360º$, tenemos que $\angle BAD+\angle CDA=180º$. Esto implica que las rectas $AB$ y $CD$ son paralelas (si no lo fueran, se cortarían en un punto $P$ y el triángulo $ADP$ tendría ángulo $0º$ en el vértice $P$ ya que $\angle PAD+\angle PDA=\angle BAD+\angle CDA=180º$). Esto concluye la demostración.
En la siguiente figura, los colores iguales representan ángulos iguales, triángulos congruentes y longitudes iguales en un paralelogramo:
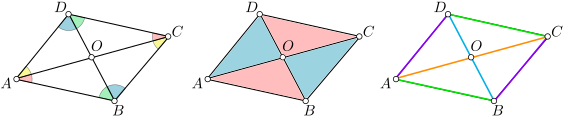
El punto $O$ de corte de las diagonales se llama centro del paralelogramo. Una consecuencia del ejercicio anterior es que todo rombo es un paralelogramo. El siguiente resultado nos dice que la suma de los cuadrados de los lados de un paralelogramo es igual a la suma de los cuadrados de sus diagonales.
Sean $P$ y $Q$ los pies de las perpendiculares a la recta que contiene a $AB$ que pasan por $C$ y $D$ respectivamente. Estas perpendiculares son paralelas entre sí, luego los triángulos $ADQ$ y $BPC$ son congruentes (tienen los ángulos iguales por paralelismo y un lado igual $AD=BC$). Los triángulos $APC$, $DQB$ y $BPC$ son rectángulos con ángulo recto en los vértices $P$ y $Q$. Aplicando el teorema de Pitágoras a estos cuatro triángulos y llamando $x=AQ=BP$ y $h=DQ=CP$, tenemos que \begin{eqnarray*} APC:\qquad&&AC^2=(AB+x)^2+h^2\\ DQB:\qquad&&BD^2=(AB-x)^2+h^2\\ BPC:\qquad&&BC^2=x^2+h^2 \end{eqnarray*} Sumando las dos primeras igualdades y restando dos veces la tercera, se eliminan las variables $x$ y $h$ y obtenemos la igualdad del enunciado teniendo en cuenta que $AB=CD$ y $BC=AD$.
- Demostrar que $ABCD$ es un rectángulo si, y sólo si, $AC=BD$.
- Demostrar $ABCD$ es un rombo si, y sólo si, $AC$ es perpendicular a $BD$.
En los problemas de olimpiada, una técnica muy útil en algunas ocasiones es encontrar paralelogramos en el problema. Por ejemplo, si encontramos dos segmentos paralelos de la misma longitud, entonces sus vértices forman un paralelogramo (¿sabrías probar por qué?).
Ir arribaIr al índiceInformar Problemas que puedes resolver con lo aprendido en esta lecciónProblemas de Geometría