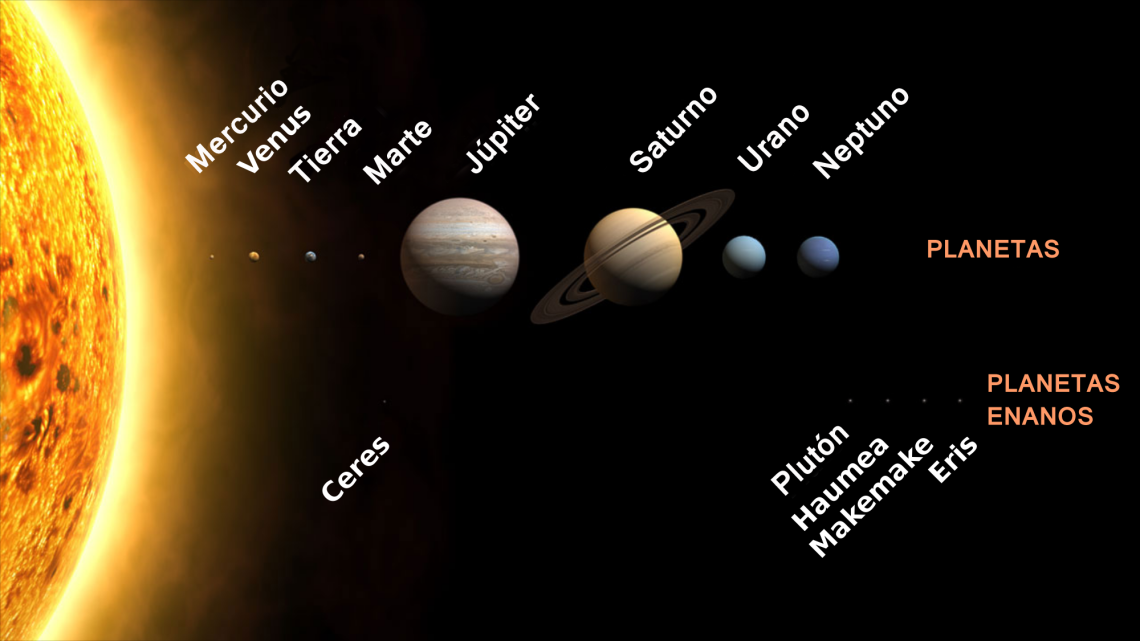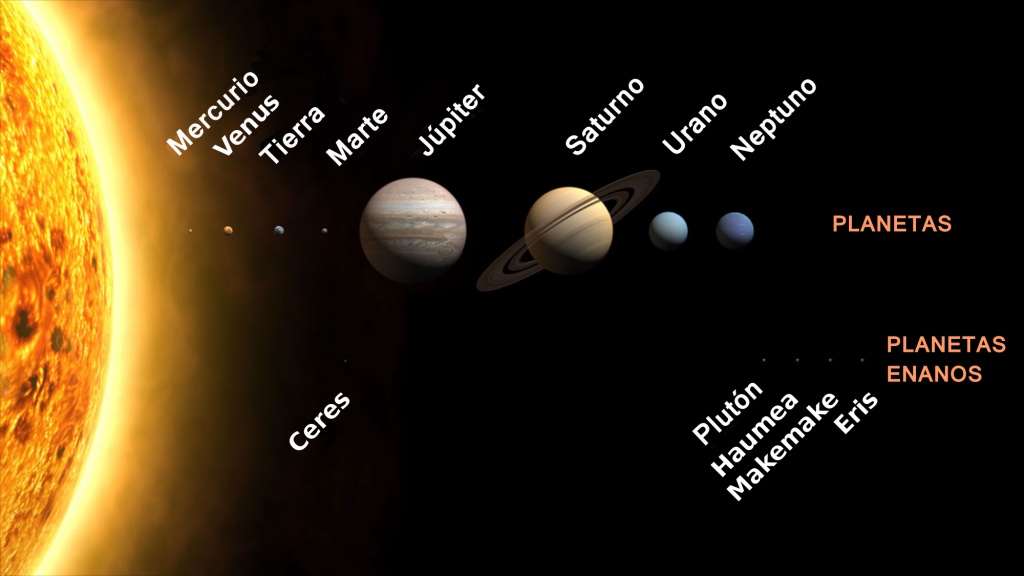
En mi libro Planetas, planteé el siguiente ejercicio:
Sea la serie de números 1, 2, 3, 4, 5, 6… ¿cuál es el siguiente?
Evidentemente, el siguiente es 1000.
En efecto, la serie 1, 2, 3, 4, 5, 6, 1000 se obtiene con la fórmula:
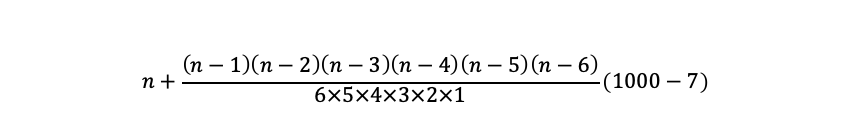
Y se podrían haber buscado muchas fórmulas más. Se me dirá que esta solución es posible, pero no es la más sencilla ni la más estética… que es «rebuscada». Sin embargo, se trataba de un problema de lógica, no de estética. En realidad, por dos puntos pasa (al menos) una recta; por tres puntos, una parábola…; por 6 puntos, un polinomio de grado 6. Si en lugar de poner 1000 en el último paréntesis, hubiera puesto cualquier número, ese mismo número hubiera sido la solución.
Esto muestra la falacia de muchos “test de inteligencia” que se basan en series de números o series de figuras. Este tipo de series tiene infinitas soluciones, en particular, la que elija caprichosamente el examinando.
En el libro de “Planetas” este problema se incluía a propósito de la ley de Titius-Bode. No es difícil encontrar una regla para determinar las distancias de los planetas. Esa regla resulta interesante si tiene un número mínimo de parámetros.