VARIABLE ALEATORIA
Introducción
En el capítulo anterior hemos tratado la teoría de la probabilidad, herramienta necesaria para hacer predicciones, obtener conclusiones sobre una población con base en una muestra extráida de ella. Pero aún no hemos mostrado cómo puede utilizarse la teoría de la probabilidad para obtener estas conclusiones. Para ello, necesitamos una nueva herramienta que nos va a servir de nexo entre la Teoría de la Probabilidad y la Estadístca Inferencial, nos referimos a la noción de Variable Aleatoria.
Variable aleatoria unidimensional
En este capítulo nos vamos a centrar en los experimentos aleatorios cuyos resultados son cuantificables o bien se pueden cuantificar. Consideremos, por ejemplo:
- Un experimento consistente en el lanzamiento de una moneda y observar si sale “cara” o “cruz”, es un dato cualitativo que puede convertirse en numérico, dato discreto, asignándole a la moneda el valor “1” si sale cara y el valor “0” si sale cruz,
- o bien este otro experimento consistente en el lanzamiento de dos dados y en cada lanzamiento anotamos el máximo de los dos números obtenidos (dato discreto),
- o este otro referido a un proceso de fabricación de piezas de automóviles y de cada pieza medimos su diámetro en cm (dato continuo).
En cada una de estas situaciones estamos asignando a cada suceso elemental del espacio muestral un valor numérico y el resultado es impredecible.
Recibe el nombre de Variable Aleatoria la función X que asigna a cada lanzamiento de la moneda el valor “1” si sale cara o el valor “0” si sale cruz, a cada lanzamiento de los dos dados el máximo de los dos números obtenidos o que asocia cada pieza con su diámetro en cm. Por tanto, la función X convierte la muestra de observaciones (monedas, dados, piezas de automóviles) en número reales (“1″ o “0″; “1, 2, 3, 4, 5 o 6”; “diámetro en cm.”) que pueden tratarse matemáticamente.
Intuitivamente, una variable aleatoria es una variable cuyo valor numérico se determina al azar, su comportamiento depende del azar y es impredecible. Por ejemplo:
- Sea la variable X el tamaño que alcanzan las lagartijas adultas, X es una variable aleatotoria ya que no todas las lagartijas adultas tienen el mismo diámetro de cuerpo. La variabilidad de X es debida a diversos factores, genéticos, medio donde viven…
- Consideremos la variable Y, cantidad de sangre perdida por un paciente durante el transcurso de una operación. Esta variable cambia de valor en el mismo paciente a lo largo del tiempo; por tanto debe ser considerada como una variable aleatoria.
- Sea Z el tiempo de latencia de SIDA en pacientes sero-positivos. Esta variable cambia de valor de paciente a paciente como resultado de diferencias de edad, sexo, categorías de transmisión…. El tiempo de latencia se considera una variable aleatoria.
Definición: Dada una función de probabilidad P definida en el espacio muestral E. Se llama Variable Aleatoria (en adelante v.a.) a una función de valor real, X, definida en E de forma que transforma los resultados de E en números reales. Las variables aleatorias se representan por letras mayúsculas y sus valores numéricos observados por letras minúsculas.
Consideremos, de nuevo los ejemplos anteriores:
Ejemplo 5.1: En el experimento del lanzamiento de una moneda le asignamos a la moneda el valor “1” si sale cara y el valor “0” si sale cruz.
El espacio muestral está formado por dos posibles resultados “cara” y “cruz”: E≡{cara, cruz}.
La v.a. X es una función tal que: X(cara)=1; X(cruz)=0.
Ejemplo 5.2: Al lanzar dos dados, consideramos el máximo de los dos números obtenidos.
El espacio muestral está formado por los siguientes sucesos:
\( E \left \{ \begin{array} (1,1), (1,2), (1,3), (1,4), (1,5), (1,6) \\ (2,1), (2,2), (2,3), (2,4), (2,5), (2,6) \\ \ddots \ddots \ddots \ddots \ddots \\ (6,1), (6,2), (6,3), (6,4), (6,5), (6,6) \end{array} \right. \)
La v. a. X que representa el máximo de los dos números obtenidos está formada por los siguientes resultados:
\( \begin{array}\\ X\{(1,1)\}=1 \\ X\{(1,2),(2,2),(2,1) \}=2 \\ X\{(1,3),(2,3),(3,3),(3,2),(3,1)\}=3 \\ X\{(1,4),(2,4),(3,4),(4,4),(4,3),(4,2),(4,1)\}=4 \\ X\{(1,5),(2,5),(3,5),(4,5),(5,5),(5,4),(5,3),(5,2)(5,1)\}=5 \\ X\{(1,6),(2,6),(3,6),(4,6),(5,6),(6,6),(6,5),(6,4),(6,3),(6,2),(6,1)\}=6 \end{array} \)
Tipos de variables aleatorias. Variable aleatoria discreta y continua
Al igual que en las variables estadísticas distinguíamos entre variable estadística discreta y continua aquí hablaremos de Variables Aleatorias Discretas y Continuas.
Se dice que una Variable Aleatoria es Discreta si el conjunto de valores que puede tomar es contable o bien si la variable toma un número finito de valores determinados. En los ejemplos 5.1 y 5.2, los valores que pueden tomar las variables son {1,0} y {1,2,3,4,5,6} respectivamente, siendo por tanto, ambas variables aleatorias discretas.
Se dice que una Variable Aleatoria es Continua si el conjunto numérico es el conjunto de los números reales o bien si la variable toma un número infinito de valores.
Ejemplo 5.3: En el proceso de fabricación de piezas de automóviles, a cada pieza le medimos su diámetro en cm. Estos diámetros están comprendidos ente 1.20 cm y 1.70 cm.
En este caso la v.a. X, como puede tomar todos los valores posibles del intervalo [1.20, 1.70], es una v.a. continua.
Se llama Recorrido de X, y se denota por R_{X}, al espacio formado por todos los posibles valores de X. Así, en los ejemplos 5.1 y 5.2, los recorridos de las variables aleatorias son {1,0} y {1,2,3,4,5,6} respectivamente.
Función masa de probabilidad y Función de distribución de una variable aleatoria
Una variable aleatoria no está perfectamente definida si no se conocen los valores que puede tomar (recorrido), pero dichos valores son impredecibles. Puesto que el comportamiento de una variable aleatoria está gobernado por el azar, debemos determinar dicho comportamiento en términos de probabilidades. Para ello se utilizan dos funciones: la Función Masa de Probabilidad y la Función de Distribución.
Variable aleatoria discreta
Función masa de probabilidad
La función masa de probabilidad de una v.a. discreta es una función que a cada valor posible de dicha v.a. le asigna una probabilidad. Así en los ejemplos:
1) Ejemplo 5.1: La v.a. \( X \)=“cara superior de una moneda ” puede tomar los valores \( X=\{1, 0 \} \) con probabilidades \( P(X)=\{1/2, 1/2 \} \). Así, la probabilidad de que la v.a.
∗) \( X \) tome el valor 1, que se denota por \( P[X=1] \), vale \( 1/2 \hspace{.2cm} ( P[X=1]=1/2) \) y que
∗) \( X \) tome el valor 0, que se denota por, \( P[X=0] \), vale \( 1/2 \hspace{.2cm} (P[X=0]=1/2) \).
2) Ejemplo 5.2: La v.a. \( X \)=“máximo de los dos números obtenidos” puede tomar los valores \( X= \{1, 2, 3, 4, 5, 6 \} \) con probabilidades \( P(X)= \{ 1/36, 3/36, 5/36, 7/36, 9/36, 11/36 \} \). Así, por ejemplo, \( P[X=2]=3/36 \) o \( P[X=6]=11/36 \).
Sea \( X \) una v.a. discreta que puede tomar los valores \( \{x_1, x_2, ⋯, x_{k} \} \) con probabilidades \( P(X) =\{p_1, p_2, ⋯, p_{k}\} \), es decir \( P[X=x_{i}]=p_{i} \) con \( i=1, 2, \cdots, k \). Se define la Función Masa de Probabilidad de la variable aleatoria \( X \), y se denota por \( p_{i} \), como la probabilidad de que la v.a. \( X \) tome un valor \( x_{i} \)
\( p_{i}=P[X=x_{i}] \)
si verifica las siguientes propiedades: \( \displaystyle \sum_{i=1}^{k}p_{i}=1 \) y \( p_{i} \geq 0 \hspace{.2cm} \forall i \)
La función masa de probabilidad se suele expresar en forma de tabular de la siguiente manera:
\( \begin{array} {|c|c|c|c|c|c|c|} \hline x_{i} & x_1 & x_2 & \cdots & x_{i} & \cdots & x_{k} \\ \hline p_{i} & p_1 & p_2 & \cdots & p_{i} & \cdots & p_{k} \\ \hline \end{array} \)
Ejemplo: En el Ejemplo 5.2 el recorrido de la v.a. y las probabilidades correspondientes se expresan en forma tabular como se muestra a continuación
\( \begin{array} {|c|c|c|c|c|c|c|} \hline x_{i} & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline p_{i} & 1/36 & 3/36 & 5/36 & 7/36 & 9/36 & 11/36 \\ \hline \end{array} \)
y gráficamente, mediante el siguiente diagrama de barras
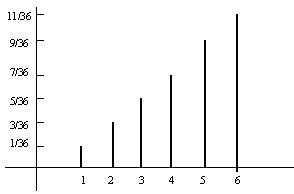 Figura 5.1: Diagramas de barras
Figura 5.1: Diagramas de barras
Ejemplo 5.4: En un hospital se está realizando un estudio sobre el número de personas por día que solicitan un tratamiento innecesario en el servicio de urgencias. Sea X la v.a. número de personas por día. La siguiente tabla muestra los valores que toma la v.a. y las probabilidades correspondientes
\( \begin{array} {|c|c|c|c|c|c|c|c|} \hline x_{i} & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline p_{i} & 0.02 & 0.09 & 0.2 & 0.4 & 0.1 & 0.04 & ? \\ \hline \end{array} \)
Calcular las probabilidades de que soliciten el servicio: a) Seis personas ; b) A lo sumo dos personas; c) Por lo menos dos personas; d) más de tres personas; d) Mayor o igual que tres personas.
Respuesta:
a) \( P[X=6]=1-0.02-0.09-0.2-0.4-0.1-0.04=0.15 \)
b) \( P[X \leq 2]=P[X=0]+P[X=1]+P[X=2]=0.02+0.09+0.2=0.31 \)
c) \( P[X \geq 2]=1-P[X<2]=1-0.02-0.09=0.89 \)
d) \( P[X>3]=P[X=4]+P[X=5]+P[X=6]=0.1+0.04+0.15=0.29 \)
f) \( P[X \geq 3]=P[X=3]+P[X=4]+P[X=5]+P[X=6]=0.4+0.29=0.69 \)
Función de distribución
Se define la Función de Distribución de la variable aleatoria \( X \), y se denota por \( F_{X} \), como la probabilidad de que la v.a. \( X \) tome un valor menor o igual que \( (x) \)
Nota: La notación que utilizamos es representar a las vv.aa. por letras mayúsculas \( (X) \) y a sus valores por letras minúsculas \( (x) \).
\( F_{X}(x)=P[X \leq x] \hspace{.2cm} \forall x \)
Es decir, \( F_{X}\) es una función de los números reales, \( R \), en el intervalo \( [0,1] \)
\( F_{X}: R \rightarrow [0,1] \) de forma que
\( \forall x \in R, \hspace{.2cm} F_{X}(x)=P[X \leq x] \)
Hemos dicho que una v.a. discreta está caracterizada por la función masa de probabilidad. Conocidos los valores \( p_{i}\) se puede conocer la función de distribución. En efecto,
\( \begin{array} {l} F(x_1) = P[X \leq x_1]=P[X=x_1]=p_1 \\F(x_2) = P[X \leq x_2]=P[X=x_1]+P[X=x_2]=p_1+p_2 \hspace{2cm} [5.1] \\
\vdots \\
F(x_{i}) = P[X \leq x_{i}]= \displaystyle \sum_{j=1}^{i}P[X=x_{j}]=p_1+p_2+ \cdots +p_{i} \\ \end{array} \)
Nota: Utilizamos la notación \( F(x) \) en vez de \( F_{X}(x) \) cuando en el contexto no es necesario especificar la variable aleatoria.
Propiedades
P1) \( F_{X}(.) \) es una función no-decreciente
P2) \( F_{X}(.) \) es continua a la derecha
P3) \( F_{X}(+ \infty) =+1 \hspace{.2cm} \) y \( \hspace{.2cm F_{X}(-\infty)=0 \)
Propiedades que se deducen fácilmente de la definición
P4) \( P[x_1 <X \leq x_2]=F(x_2)-F(x_1) \) (Se deduce de ([5.1])
P5) \( P[X>x]=1-F(x) \)
Ejemplo: Determinar la función de distribución en el Ejemplo 5.2.
Respuesta:
\( F(0) = P[X \leq 0]=0 \)\( F(1) = P[X \leq 1]= \displaystyle \frac{1}{36} \)
\( F(2) = P[X \leq 2]= \displaystyle \frac{1}{36}+ \displaystyle \frac{3}{36}= \displaystyle \frac{4}{36} \)
\( F(3) = P[X \leq 3]= \displaystyle \frac{1}{36}+ \displaystyle \frac{3}{36}+ \displaystyle \frac{5}{36}= \displaystyle \frac{9}{36} \)
\( F(4) = P[X \leq 4]= \displaystyle \frac{1}{36}+ \displaystyle \frac{3}{36}+ \displaystyle \frac{5}{36} + \displaystyle \frac{7}{36}= \displaystyle \frac{16}{36} \)
\( F(5) = P[X \leq 5]= \displaystyle \frac{1}{36}+ \displaystyle \frac{3}{36}+ \displaystyle \frac{5}{36}+ \displaystyle \frac{7}{36} + \displaystyle \frac{9}{36}= \displaystyle \frac{25}{36} \)
\( F(6) = P[X \leq 6]=\displaystyle \frac{1}{36}+ \displaystyle \frac{3}{36}+ \displaystyle \frac{5}{36}+ \displaystyle \frac{7}{36} + \displaystyle \frac{9}{36}+ \displaystyle \frac{11}{36}= \displaystyle \frac{36}{36}=1 \)
Gráficamente
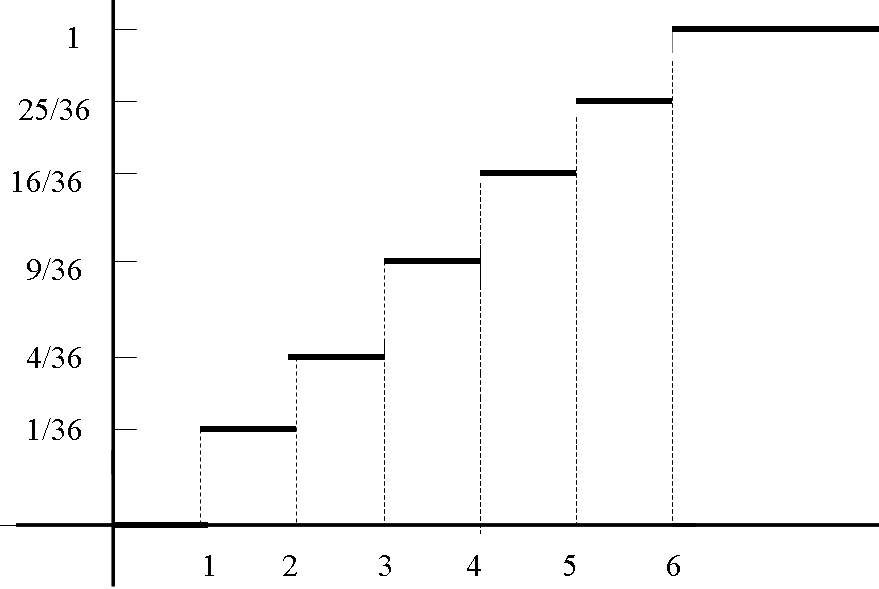
Figura 5.2: Curva acumulativa
Ejemplo 5.5: Una urna contiene 10 bolas de las que 8 son blancas. Se sacan al azar dos bolas. Sea X el número de bolas blancas obtenidas. Calcular: a) La distribución de probabilidad; b) La función de distribución de X
Respuesta:
a) \( p_0=P[X=0]= \displaystyle \frac{2}{10} \displaystyle \frac{1}{9}= \displaystyle \frac{1}{45} \)
\( p_1=P[X=1]= \displaystyle \frac{8}{10} \displaystyle \frac{2}{9}+ \displaystyle \frac{2}{10} \displaystyle \frac{8}{9}= \displaystyle \frac{16}{45} \)
\( p_2=P[X=2]= \displaystyle \frac{8}{10} \displaystyle \frac{7}{9}= \displaystyle \frac{28}{45}\)
Resuelto aplicando combinatoria
\( p_0= \displaystyle \frac{ \displaystyle {8 \choose 0 } \displaystyle {2 \choose 2 }}{ \displaystyle {10 \choose 2 }}= \displaystyle \frac{1}{45} \hspace{.4cm} ; \hspace{.4cm} p_1= \displaystyle \frac{ \displaystyle {8 \choose 1 }\displaystyle {2 \choose 1 }}{ \displaystyle {10 \choose 2 }}= \displaystyle \frac{16}{45} \hspace{.4cm} ; \hspace{.4cm} p_2= \displaystyle \frac{ \displaystyle {8 \choose 2 }\displaystyle {2 \choose 0 }}{ \displaystyle {10 \choose 2 }}= \displaystyle \frac{28}{45} \)
b)
\( \left. \begin{array} \\ F(0) =P[X \leq 0]=P[X=0]=1/45 \\
F(1)=P[X \leq 1]=p_0+p_1=17/45 \\
F(2)=P[X \leq 2]=p_0+p_1+p_2=1 \end{array} \right \} \Rightarrow \) \( F(x) = \left \{ \begin{array} \\
0 \hspace{.4cm} si \hspace{.4cm} x<0 \\
1/45 \hspace{.4cm} si \hspace{.4cm} 0 \leq x<1 \\
17/45 \hspace{.4cm}si \hspace{.4cm} 1 \leq x <2 \\ 1 \hspace{.4cm} si \hspace{.4cm} x \geq 2 \end{array} \right. \)
Ejemplo 5.6: En un hospital se realiza un estudio sobre células situadas en secciones de tejidos dañados. Dichas celulas se clasifican, con respecto a la extensión del daño, mediante la siguiente escala: 0 (no dañadas); 1 (débilmente dañadas); 2 (moderadamente dañadas) y 3 (extremadamente dañadas). En determinado tejido dañado se obtienen los siguientes resultados:
\( \begin{array}{|c|c|c|c|} \hline x_{i} & 0 & 1 & 2 & 3 \\ \hline p_{i} & 0.2 & 0.35 & 0.4 & 0.05 \\ \hline \end{array} \)
Se pide: a) Función de distribución; b) Utilizar F para determinar la probabilidad de que una célula seleccionada aleatoriamente esté sólo ligeramente dañada o no dañada; c) Utilizar F para determinar la probabilidad de que en una célula seleccionada aleatoriamente se obverve al menos un daño débil.
Respuesta:
a)
\( \begin{array}{|c|c|c|c|} \hline x_{i} & 0 & 1 & 2 & 3 \\ \hline F & 0.2 & 0.55 & 0.95 & 1 \\ \hline \end{array} \)
b) \( F(1)=P[X \leq 1]=0.55 \)
c) \( P[X \geq 1]=1-P[X\leq 0]=1-F(0)=1-0.2=0.8 \)
Variable aleatoria continua
Función de densidad
En una v.a. continua no tiene sentido determinar una función, como en las vv.aa. discretas, que asigne a cada valor posible de dicha v.a. una probabilidad; puesto que la v.a. continua puede tomar infinitos valores y la probabilidad de que la v.a. tome un valor determinado vale cero. Por ello, en el caso continuo definiremos una función que nos permita calcular la probabilidad de que la v.a. esté comprendida en un intervalo de valores específico.
Sea \( X \) una v.a. continua. La Función de Densidad de probabilidad, \( f(x) \), es una función definida para todos los números reales tal que satisface las siguientes condiciones:
1. \( f(x) \geq 0 \) (no negativa) \( \forall x \)
2. \( \int_{- \infty }^{+ \infty}f(x)dx=1 \) (El área comprendida entre la gráfica de \( f \) y el eje \( x \) es igual a 1)
3. \( P[a<X<b]= \int_{a}^{b}f(x)dx \) (Para cualquier valor real entre los números \( a \) y \( b \) , \( P[a<X<b] \) representa el área comprendida entre la gráfica de \( f(x) \), el eje \( OX \) y las rectas \( x=a \) y \( x=b \) ). La interpretación de esta condición se muestra en la figura 5.3
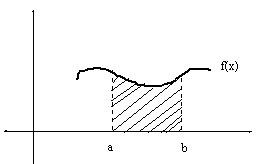
Figura 5.3
Ejemplo: En el Ejemplo 5.3 las medidas de los diámetros de las piezas de los automóviles es una variable aleatoria continua con la siguiente función de densidad
\( f(x) = \left \{ \begin{array} \\ kx \hspace{.5cm} 0 \leq x<2 \\ 0 \hspace{.3cm} para \hspace{.2cm} cualquier \hspace{.2cm} otro \hspace{.2cm} caso \end{array} \right. \)
Comprobar que es una función de densidad y representar su gráfica.
Respuesta:
Se tiene que verificar que \( \displaystyle \int_{- \infty}^{+ \infty}f(x)dx=1 \)
\( \displaystyle \int_{- \infty}^{+ \infty}f(x)dx = \displaystyle \int_{0}^{2}kx dx=k \left [ \displaystyle \frac{x^{2}}{2} \right]_{o}^{2}=2k=1 \Rightarrow k=(1/2) \)
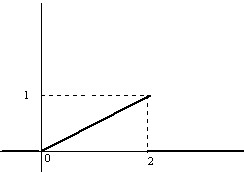
Figura 5.4
La función de densidad contiene toda la información sobre la variabilidad del experimento en estudio, en este caso, sobre la variabilidad de medidas de los diámetros de las piezas de los automóviles. En efecto, conocida f(x) se pueden contestar preguntas como:
1. ¿Qué proporción de piezas tendrán diámetros entre a y b?
2. ¿Qué proporción de piezas tendrán diámetros inferiores a a?
3. ¿Qué proporción de piezas tendrán diámetros superiores a b?
Las correspondientes respuestas son:
1) \( \int_{a}^{b}f(x)dx \)
2) \( \int_{- \infty}^{a}f(x)dx \)
3) \( \int_{b}^{\infty}f(x)dx \)
Para cada una de las respuestas es necesario calcular el área bajo la curva \( f(x) \), problema que se puede solventar mediante la Función de Distribución.
Función de distribución
Dada una variable aleatoria continua \( X \), recibe el nombre de Función de Distribución, y se denota por \( F_{X} \) (o \( F \) cuando en el contexto está claro a la v.a. que se refiere), la función \( F: R \longrightarrow [0,1] \) definida por:
\( F(x_{i})=P[X \leq x_{i}]= \displaystyle \int_{- \infty}^{x_{i}}f(x)dx \)
La función de densidad y la función de distribución de una v.a. continua están relacionadas:
\( F(x)= \displaystyle \int_{-\infty}^{x}f(x)dx \hspace{.5cm}; \hspace{.5cm} f(x)= \displaystyle \frac{\partial F(x)}{ \partial x}=F^′(x) \)
Por lo tanto respuestas a las preguntas anteriores son:
1. \( P[a<X<b]=F(b)-F(a) \)
2. \( P[X<a]=F(a) \)
3. \( P[X>b]=1-F(b) \)
La función de distribución es monótona no-decreciente, continua por lo menos a la derecha y tal que \( \lim_{x→- \infty}F(x)=0 \hspace{.3cm} \) y \( \hspace{.3cm} \lim_{x→+ \infty}F(x)=1 \).
Comentario: Se comprueba fácilmente que si \( X \) es una v.a. continua entonces la probabilidad del suceso \( X \) igual a constante es cero, \( P[X=a]=0 \), aunque no es el suceso imposible. En efecto,
\( P[X=a]= \displaystyle \int_{a}^{a}f(x)dx=0 \)
Ejemplo: Calcular, en el Ejemplo 5.3, la función de distribución y las siguientes probabilidades: \( P(X \leq 1.2) \hspace{.3cm}; \hspace{.3cm} P(0.8 \leq X) \hspace{.3cm}; \hspace{.3cm} P(1 \leq X \leq 1.5) \)
Respuesta:
a)
– Para \( x<0⇒F(x)=0 \)
– Para \( 0 \leq x < 2 \Rightarrow F(x) = \displaystyle \int_{- \infty}^{0}0 \, dt + \displaystyle \int_{0}^{x} \displaystyle \frac{t}{2}dt= \displaystyle \frac{1}{2} \left [ \displaystyle \frac{t^2}{2} \right ]_{0}^{x}= \displaystyle \frac{x^2}{4} \)
– Para \( x \geq 2 \Rightarrow F(x)= \displaystyle \int_{- \infty}^0 0 \, dt+ \displaystyle \int_{0}^{2} \displaystyle \frac{t}{2}dt+ \displaystyle \int_{2}^{x}0 \, dt= \displaystyle \frac{1}{2} \left[ \displaystyle \frac{t^2}{2} \right]_{0}^{2} =1 \)
Por lo tanto la función de distribución es:
\( F(x) = \left \{ \begin{array}{cc} 0 & x<0 \\ \displaystyle \frac{x^2}{4} & 0 \leq x <2 \\ 1 & x \geq 2 \end{array} \right. \)
b) \( P[X \leq 1.2]=F(1.2)= \displaystyle \frac{1.2^2}{4}=0.36 \)
c) \( P[X \geq 0.8]=1-P[X \leq 0.8]=1-F(0.8)=1- \displaystyle \frac{0.8^2}{4}=0.84 \)
d) \( P[1 \leq X \leq 1.5]=P[X \leq 1.5]-P[X \leq 1]=F(1.5)-F(1)=0.3125 \)
Ejemplo 5.7: Sea \( X \) la v.a. que representa la duración en segundos de un tipo de bombillas. Dicha v.a. puede tomar todos los valores comprendidos entre \( 0 \) y \( + \infty \). Supongamos que la función de densidad es:
\( f(x) = \left \{ \begin{array}{cc} a/x^2 & 100<x<1000 \\ 0 & para \hspace{.1cm} cualquier \hspace{.1cm} otro \hspace{.1cm} caso \end{array} \right. \)
Se pide:
a) El valor de a para que \( f(x) \) sea una función de densidad
b) La probabilidad de que la bombilla dure 200 días
c) \( P[200<X<300] \)
Respuesta:
a)
\( \displaystyle \int_{100}^{1000} \displaystyle \frac{a}{x^2} dx=1 \hspace{.3cm} ; \hspace{.3cm} \displaystyle \int_{100}^{1000} \displaystyle \frac{a}{x^2} dx =-a \left [ \displaystyle \frac{1}{x} \right ]_{100}^{1000}=-a \displaystyle \frac{9}{1000}\Rightarrow a= \displaystyle \frac{1000}{9} \)
b)
\( P[X=200]= \displaystyle \int_{200}^{200} \displaystyle \frac{a}{x^2} dx=0 \)
c)
\( P[200<X<300]=\displaystyle \int_{200}^{300} \displaystyle \frac{1000}{9} \displaystyle \frac{1}{x^2} dx=- \displaystyle \frac{1000}{9} \left [ \displaystyle \frac{1}{x} \right ]_{200}^{300}=0.1851 \)
Características de una variable aleatoria unidimensional
Al igual que en una muestra, parte de la variabilidad puede venir sintetizada a través de medidas de posición y de dispersión, en las variables aleatorias también vamos a estudiar características que proporcionan información sobre determinados aspectos de la distribución de dichas variables. Como se puede apreciar, en las siguientes secciones, los aspectos que se desarrollan son generalizaciones al caso de variables aleatorias de las nociones análogas expuestas para las variables estadísticas. Las características que se van a estudiar son: Esperanza Matemática, Varianza, Desviación Típica y Momentos.
Esperanza matemática
Variable aleatoria discreta
Consideremos una variable aleatoria discreta, \( X \), que toma los valores \( x_1, x_2, \cdots \) con probabilidades \( p_1, p_2, \cdots \)
Se define la Esperanza Matemática o Media de la v.a. \( X \), y se representa por \( E[X] \) o \( \mu \) como
\( E[X]= \displaystyle \sum_{i}x_{i}p_{i} \)
La Esperanza matemática existe si y sólo sí la suma es absolutamente convergente, es decir \( \displaystyle \sum_{i}∣x_{i}∣p_{i}< \infty \)
En el caso en que la v.a. \( X \) tome un número finito de valores \( x_1, x_2, \cdots x_{n} \) con probabilidades \( p_1, p_2, \cdots, p_{n} \), la esperanza matemática existe siempre y viene definida por
\( E[X]=\displaystyle \sum_{i=1}^{n} x_{i}p_{i} \)
Ejemplo: Determinar la esperanza matemática en el Ejemplo 5.2
\( E[X]=\displaystyle \sum_{i=1}^{6} x_{i}p_{i}=1 \times \displaystyle \frac {1}{36} +2 \times \displaystyle \frac {3}{36}+3 \times \displaystyle \frac {5}{36}+4 \times \displaystyle \frac {7}{36}+5 \times \displaystyle \frac {9}{36}+6 \times \displaystyle \frac {11}{36}= \displaystyle \frac {161}{36} \)
Esperanza Matemática de una función de variable aleatoria
Dada una v.a. discreta, \( X \), que toma los valores \( x_1, x_2, \cdots \). Consideramos una función real, \( g(X) \), de la variable aleatoria \( X \). La función \( g(X) \) es una v.a. discreta y su esperanza matemática se define como
\( E[g(X)]= \displaystyle \sum_{i}p_{i}g(x_{i}) \)
con la exigencia \( \displaystyle \sum_{i} \left | g(x_{i}) \right | p_{i}< \infty \)
Ejemplo 5.8: En unos laboratorios se están realizando unas pruebas con un fármaco nuevo, para ello se ha realizado un test a unos ratones. Los resultados del test pueden ser positivo, nulo o negativo, asociando el valor 1 si el test da positivo, 0 si es nulo y -1 si es negativo. La función masa de probabilidad asociada es \( P[X=-1]=P[X=0]=P[X=1]=1/3 \). Calcula la esperanza de \( Y=X^{2}\)
Respuesta
\( E[Y]= \displaystyle \sum_{i} p_{i}g(x_{i})= \displaystyle \sum_{i}p_{i}x_{i}^{2}= \displaystyle \frac{1}{3} \left [(-1)^{2}+1^{2}+0^{2} \right]= \displaystyle \frac{2}{3} \)
Variable aleatoria continua
Consideremos una variable aleatoria continua, \( X \), con función de densidad \( f(x) \)
Se define la Esperanza Matemática o Media de la v.a. \( X \), y se representa por \( E[X] \) o \( \mu \) como
\( E[X]= \displaystyle \int_{- \infty}^{ \infty}xf(x)dx \)
La Esperanza matemática existe si y sólo sí la integral es absolutamente convergente, es decir \( \displaystyle \int_{- \infty}^{ \infty} \left |x \right | f(x)dx < \infty \)
Propiedades:
P1) Si todos los valores de una v.a., \( X \), se multiplican o se dividen por una constante, \( a \), su esperanza queda multiplicada o dividida por dicha constante
\( E[aX]=aE[X] \)
En efecto:
– En las vv.aa. discretas
\( E[aX]= \displaystyle \sum_{i}ax_{i}p_{i}=a \displaystyle \sum_{i}x_{i}p_{i}=aE[X] \)
– En las vv.aa. continuas
\( E[aX]= \displaystyle \int_{- \infty}^{+ \infty}axf(x)dx=a \displaystyle \int_{- \infty}^{ +\infty}xf(x)dx=aE[X] \)
P2) Si a todos los valores de una v.a., \( X \), se les suma una constante, \( a \), su esperanza queda aumentada por dicha constante
\( E[X+a]=E[X]+a \)
Por tanto la esperanza de una constante es la constante: \( E[a]=a \)
P3) Las dos propiedades anteriores se pueden resumir en una sola
\( E[aX+b]=aE[X]+b \)
donde a y b son dos constantes arbitrarias.
P4) La esperanza matemática de la suma de dos variables aleatorias, \( X \) e \( Y \), es la suma de las esperanzas de las variables aleatorias
\( E[X+Y]=E[X]+E[Y] \)
P5) Las propiedades anteriores se pueden resumir en una sola
\( E[aX+bY+c]=aE[X]+bE[Y]+c \)
donde a, b, y c son constantes arbitrarias
Nota: En todas las propiedades se supone que las correspondientes sumas o integrales son absolutamente convergentes.
Las demostraciones de las propiedades 2, 3, 4 y 5 se dejan como ejercicio.
Ejemplo: Determinar la esperanza matemática en el Ejemplo 5.3.
\( E[X]= \displaystyle \int_{- \infty}^{+ \infty}xf(x)dx= \displaystyle \int_{0}^{2} \displaystyle \frac{1}{2}x^2dx= \displaystyle \frac{1}{2}\left [ \displaystyle \frac{x^{3}}{3}\right]_{0}^{2}= \displaystyle \frac{4}{3} \)
Esperanza Matemática de una función de variable aleatoria
Sea \( X \) una v.a.continua con función de densidad \( f(x) \) y sea \( g(X) \) una función real de la v.a. \( X \). La función \( g(X) \) es una v.a. continua y su esperanza matemática se define de la siguiente forma:
\( E[g(X)]= \displaystyle \int_{- \infty}^{+ \infty}g(x)f(x)dx \)
Ejemplo 5.9: En unos viveros se está realizando un estudio sobre la altura de los bonsais. Se comprueba que la altura sigue una v.a. con función de densidad \( f(x)=3x \) para \( 0<x<1 \). Calcular la esperanza matemática de \( g(X)= \sqrt {X} \)
Respuesta
\( E[g(X)]= \displaystyle \int_{- \infty}^{+ \infty}g(x)f(x)dx= \displaystyle \int_{- \infty}^{+ \infty} \sqrt{x}3xdx=3 \displaystyle \int_{0}^{1}x^{3/2}dx=3 \displaystyle \frac{2}{5} \left [x^{5/2}\right]_{0}^{1}= \displaystyle \frac{6}{5}\)
Varianza y desviación típica
Variable aleatoria discreta
Se define la Varianza de la v.a. \( X \), y se representa por \( Var(X) \) o \( \sigma^2 \), como
\( Var(X)=E \left [(X-E(X))^2 \right]= \displaystyle \sum_{i}p_{i} \left (x_{i}-E(X) \right)^2 \)
que también se puede expresar de la siguiente forma
\( Var(X)=E[X^2]-[E(X)]^2= \displaystyle \sum_{i}p_{i}x_{i}^{2}- \left ( \displaystyle \sum_{i}p_{i}x_{i} \right )^{2} \)
La demostración se deja como ejercicio. (Se desarrolla el cuadrado del binomio y se aplican las propiedades de los sumatorios).
Se define la Desviación Típica de la v.a. \( X \), y se representa por \( \sigma \), como la raíz cuadrada positiva de la varianza
\( \sigma=+ \displaystyle \sqrt{E \left [(X-E(X))^{2} \right]}=+ \displaystyle \sqrt{ \displaystyle \sum_{i}p_{i}(x_{i}-E(X))^{2} } \)
Ejemplo: Determinar la varianza en el Ejemplo 5.2.
\( Var(X) = \displaystyle \sum_{i=1}^{6}p_{i}x_{i}^{2}- \left ( \displaystyle \sum_{i=1}^{6}p_{i}x_{i} \right )^{2}= \)
\( = 1^{2} \times \displaystyle \frac{1}{36}+2^{2} \times \displaystyle \frac{3}{36}+3^{2} \times \displaystyle \frac{5}{36}+4^{2} \times \displaystyle \frac{7}{36}+5^{2} \times \displaystyle \frac{9}{36}+6^{2} \times \displaystyle \frac{11}{36}= \displaystyle \frac {791^{2}}{36} \)
Variable aleatoria continua
Se define la Varianza como
\( Var(X)=E \left [ \left ( X-E(X) \right)^{2} \right]=\displaystyle \int_{- \infty}^{+ \infty} \left (x-E[X] \right )^{2}f(x)dx \)
que también se puede expresar de la siguiente forma
\( Var(X)=E[X^{2}]- \left (E[X] \right )^{2}= \displaystyle \int_{- \infty}^{+ \infty}x^{2}f(x)dx- \left ( \displaystyle \int_{- \infty}^{+ \infty} xf(x)dx \right )^{2} \)
La demostración se deja como ejercicio.
Se define la Desviación Típica como
\( \sigma =+ \sqrt { E \left [(X-E(X))^{2}\right ] }=+ \sqrt { \displaystyle \int_{- \infty}^{+ \infty} \left (x-E[X] \right)^{2}f(x)dx } \)
Propiedades:
P1) Si todos los valores de una v.a., \( X \), se multiplican o se dividen por una constante, a, su varianza queda multiplicada o dividida por dicha constante al cuadrado
\( Var[aX]=a^{2} Var[X] \)
En efecto:
\( Var[aX] = E \left [(aX-E(aX)) \right ]^{2}=E \left [(aX-aE(X)) \right]^{2}= E \left [a(X-E(X)) \right]^{2}=a^{2} E \left [(X-E(X)) \right]^{2}=a^{2}Var[X] \)
P2) Si a todos los valores de una v.a., \( X \), se les suma una constante, a, su varianza permanece constante
\( Var[X+a]=Var[X] \)
Por tanto la varianza de una constante es cero: \( Var[a]=0 \)
P3) Las dos propiedades anteriores se pueden resumir en una sola
\( Var[aX+b]=a^{2}Var[X] \)
donde a y b son dos constantes arbitrarias.
Las demostraciones de las propiedades 2 y 3 se dejan como ejercicio.
Comentario: La propiedad referente a la varianza de la suma de dos variables aleatorias, X e Y, se estudia en la siguiente sección cuando se introduzca el concepto de independencia de variables aleatorias.
Ejemplo: Determinar la varianza en el Ejemplo 5.3.
\( Var[X] = \displaystyle \int_{- \infty}^{+ \infty} x^{2}f(x)dx- \left ( \displaystyle \int_{- \infty}^{+ \infty}xf(x)dx \right)^{2}= \displaystyle \int_{o}^{2} \displaystyle \frac{1}{2} x^{3}dx- \left ( \displaystyle \int_{0}^{2} \displaystyle \frac{1}{2} x^{2}dx \right )^{2}= \)
\( = \displaystyle \frac{1}{2} \left [ \displaystyle \frac{x^{4}}{4} \right]_{0}^{2}- \left (\displaystyle \frac{1}{2}\left [ \displaystyle \frac{x^{3}}{3} \right ]_{0}^{2} \right)^{2}= \displaystyle \frac{2}{9} \)
Momentos
Variable aleatoria discreta
a) Momentos no-centrales o respecto al origen
Se definen los Momentos No-Centrales de orden r o Momentos de orden \( r \) respecto del Origen de una v.a. \( X \), y se denotan por \( m_{r} \), como
\( m_{r}=E[X^{r}]=∑_{i}p_{i}x_{i}^{r} \)
Casos particulares:
– Si \( r=0 \Rightarrow m_{0}=E[X^{0}]=\displaystyle \sum_{i}p_{i}x_{i}^{0}=1 \)
– Si \( r=1 \Rightarrow m_{1}=E[X]=\displaystyle \sum_{i}p_{i}x_{i}^{1}=\displaystyle \sum_{i}p_{i}x_{i} \)
– Si \( r=2 \Rightarrow m_{2}=E[X^{2}]= \displaystyle \sum_{i}p_{i}x_{i}^{2} \Rightarrow Var(X)=m_{2}-m_{1}^{2} \)
b) Momentos centrales o respecto de la media
Se definen los Momentos Centrales de orden \( r \) o Momentos de orden \( r \) respecto de la media de una v.a. \( X \), y se denotan por \( \mu_{r} \), como
\( \mu_{r}=E \left [(X-E(X))^{r} \right ]= \displaystyle \sum_{i}p_{i} \left (x_{i}-E(X) \right)^{r} \)
Casos particulares:
– Si \( r=0 \Rightarrow \mu_{0}=E \left [(X-E(X))^{0}\right ]= \displaystyle \sum_{i}p_{i} \left (x_{i}-E(X) \right)^{0}=1 \)
– Si \( r=1 \Rightarrow \mu_{1} =E \left [(X-E(X))^{1} \right ]= \displaystyle \sum_{i}p_{i} \left (x_{i}-E(X) \right)^{1}=0 \)
– Si \( r=2 \Rightarrow \mu_{2} =E \left [(X-E(X))^{2} \right ]= \displaystyle \sum_{i}p_{i} \left (x_{i}-E(X) \right)^{2}=Var(X) \)
Variable aleatoria continua
a) Momentos no-centrales o respecto al origen
\( m_{r}=E[X^{r}]= \displaystyle \int_{- \infty}^{+ \infty} x^{r}f(x)dx \)
Casos particulares:
– Si \( r=0 \Rightarrow m_{0}=E[X^{0}]=\displaystyle \int_{- \infty}^{+ \infty}x^{0}f(x)dx=1 \)
– Si \( r=1 \Rightarrow m_{1}=E[X]=\displaystyle \int_{- \infty}^{+ \infty} x^{1}f(x)dx \)
– Si \( r=2 \Rightarrow m_{2}=E[X^{2}]=\displaystyle \int_{- \infty}^{+ \infty}x^{2}f(x)dx \Rightarrow Var(X)=m_{2} -m_{1}^{2} \)
b) Momentos centrales o respecto de la media
\( μ_{r}=E[(X-E(X))]^{r}=\displaystyle \int_{- \infty}^{+ \infty}(x-E[X])^{r}f(x)dx \)
Casos particulares:
– Si \( r=0 \Rightarrow \mu{0}=E \left [(X-E(X))^{0} \right]=\displaystyle \int_{- \infty}^{+ \infty} \left (x-E[X] \right)^{0}f(x)dx=1 \)
– Si \( r=1 \Rightarrow \mu{1}=E \left [(X-E(X))^{1} \right]=\displaystyle \int_{- \infty}^{+ \infty} \left (x-E[X] \right)^{1}f(x)dx=0 \)
– Si \( r=2 \Rightarrow \mu_{2}=E \left [(X-E(X))^{2} \right ]=\displaystyle \int_{- \infty}^{+ \infty} \left (x-E[X] \right)^{2}f(x)dx=Var(X) \)
La expresión de la relación entre los momentos centrales y no-centrales es la misma que estudiamos en las variables estadísticas. (Su desarrollo se deja como ejercicio).
Función generatriz de momentos
Se define la Función Generatriz de Momentos de una v.a. \( X \), y se denota por ψ(t), como
\( \psi (t)=E[e^{tX}] \hspace{.4cm} ; \hspace{.4cm} t \in R \)
Variable aleatoria discreta
\( \psi (t)=E[e^{tX}]= \displaystyle \sum_{i}p_{i}e^{tx_{i}} \)
Variable aleatoria continua
\( \psi (t) =E[e^{tX}]=\displaystyle \int_{- \infty}^{+ \infty} e^{tx}f(x)dx \)
Relación entre la función generatriz de momentos y los momentos respecto al origen
Si existe la función generatriz de momentos y es continuamente derivable en un entorno del origen, tenemos:
a) Variable aleatoria discreta:
\( \begin{array} {ccc} \psi ^{′}(t) = & \displaystyle \sum_{i}p_{i}x_{i}e^{tx_{i}} \Rightarrow & \displaystyle \psi ^{′}(0)= \displaystyle\sum_{i}p_{i}x_{i}=m_{1} \\ \psi ^{′′} (t) = & \displaystyle \sum_{i}p_{i}x_{i}^{2}e^{tx_{i}}\Rightarrow & \psi ^{′′}(0)= \displaystyle \sum_{i}p_{i}x_{i}^{2}=m_{2} \\ \vdots & \vdots & \vdots \\ \psi ^{r}(t) = & \displaystyle \sum_{i}p_{i}x_{i}^{r}e^{tx_{i}} \Rightarrow & \psi ^{r} (0)= \displaystyle \sum_{i}p_{i}x_{i}^{r}=m_{r} \\ \end{array} \)
b) Variable aleatoria continua:
\( \begin{array} {ccc} \psi ^{′}(t) = & \displaystyle \int_{- \infty}^{+ \infty}x e^{tx}f(x)dx \Rightarrow & \psi ^{′}(0) =\displaystyle \int_{- \infty}^{+ \infty}xf(x)dx=m_{1} \\ \psi ^{′′} (t) = & \displaystyle \int_{- \infty}^{+ \infty}x^{2} e^{tx}f(x)dx \Rightarrow & \psi^{′′}(0)=\displaystyle \int_{- \infty}^{+ \infty}x^{2}f(x)dx=m_{2} \\ \vdots & \vdots & \vdots \\ \psi ^{r}(t) = & \displaystyle \int_{- \infty}^{+ \infty}x^{r}e^{tx}f(x)dx \Rightarrow & \psi^{r} (0)=\displaystyle \int_{- \infty}^{+ \infty}x^{r}f(x)dx=m_{r} \\ \end{array} \)
El momento de orden r respecto del origen es igual a la derivada \(r \)-ésima de la función generatriz de momentos particularizada para \( t=0 \).
Ejemplo 5.10: Sea X una v.a. cuya f. de densidad de probabilidad está dada por:
\( f(x) \left \{ \begin{array} {cc} \displaystyle \frac{1}{8}x^{-1/2}e^{- \displaystyle \frac{x^{1/2}}{4}} & 0<x \\ 0 & para \hspace{.1cm} cualquier \hspace{.1cm} otro \hspace{.1cm} caso \\ \end{array} \right. \)
Determinar: a) Función de distribución; b) Media;c) Varianza;d) Probabilidad de que \( X \) exceda su valor medio.
Respuesta:
a)
\( F(x)= \displaystyle \frac{1}{8} \displaystyle \int_{0}^{x}t^{-1/2}e^{- \displaystyle \frac{t^{1/2}}{4}}dt= \displaystyle \int_{0}^{x}e^{-u}du=\left [-e^{- \displaystyle \frac{t^{1/2}}{4}} \right ]_{0}^{x}=1-e^{- \displaystyle \frac{x^{1/2}}{4}} \)
con \( u= \displaystyle \frac{t^{1/2}}{4} \hspace{.3cm} ; \hspace{.3cm} t=16u^{2} \hspace{.3cm}; \hspace{.3cm} dt=32udu \)
b)
\( \mu=E[X]= \displaystyle \frac{1}{8} \displaystyle \int_{0}^{ \infty}x^{1/2}e^{- \displaystyle \frac{t^{1/2}}{4}}dx= \) \( \left \{ \begin{array} {c} t= \displaystyle \frac{x^{1/2}}{4} \hspace{.3cm} ; \hspace{.3cm} x=16t^{2} \\ dx=32tdt \\ \end{array} \right \} \)
\( = \displaystyle \frac{1}{8} \displaystyle \int_{0}^{ \infty} 4te^{-t}32tdt= =16 \displaystyle \int_{0}^{ \infty}t^{2}e^{-t}dt= \) \( \left \{ \begin{array} {c} u=t^{2} \hspace{.3cm} ; \hspace{.3cm} du=2tdt \\ dv=e^{-t}dt \hspace{.3cm} ; \hspace{.3cm} v=-e^{-t} \\ \end{array} \right \} \)
\( =16 \left [ \left [-t^{2}e^{-t}\right ]_{0}^{\infty}+ \displaystyle \int_{0}^{ \infty}2te^{-t}dt \right ]= \) \( \left \{ \begin{array} {c} u=2t \hspace{.3cm} ; \hspace{.3cm} du=2dt \\ dv=e^{-t}dt \hspace{.3cm} ; \hspace{.3cm} v=-e^{-t} \\ \end{array} \right \} \)
\( =16 \left [ \left [-t^{2} e^{-t}\right ]_{0}^{∞}- \left [2te^{-t} \right ]_{0}^{∞}+ \displaystyle \int_{0}^{ \infty}2e^{-t}dt \right]= 16 \left [ \left[-t^{2}e^{-t} \right ]_{0}^{∞}- \left [2te^{-t} \right ]_{0}^{∞}- \left [2e^{-t} \right ]_{0}^{∞}\right ]=16(0+0+2)=32 \)
c)
\( Var[X]=E[X^{2}]- \left (E[X] \right)^{2}= \displaystyle \frac{1}{8} \displaystyle \int_{0}^{ \infty}x^{2}x^{-1/2} e^{- \displaystyle \frac{x^{1/2}}{4}}dx-(32)^{2}=6144-1024=5120 \)
d) \( P[X>32]=1-F(32)=1-1+e^{- \displaystyle \frac{32^{1/2}}{4}}=e^{ \sqrt{2}} \)
Independencia de variables aleatorias
En esta sección se plantea una generalización, de lo anteriormente desarrollado, a la situación de estudiar simultáneamente dos fenómenos aleatorios. Sólo mostraremos las nociones que son imprescindibles para los desarrollos posteriores.
Variable aleatoria bidimensional
Dadas dos variables aleatorias unidimensionales, \( X \) e \( Y \) , llamamos Variable Aleatoria Bidimensional al par \( (X,Y) \) . Es decir, una variable aleatoria bidimensional es un par donde cada una de las componentes es una v. a. unidimensional.
Cada una de las componentes \( X \) e \( Y \) puede ser una v.a. discreta o continua. Nosotros sólo consideramos dos situaciones
1. Las dos variables son discretas : Variable Aleatoria Bidimensional Discreta
2. Las dos variables son continuas : Variable Aleatoria Bidimensional Continua
Función de distribución conjunta
Se define la Función de Distribución Conjunta de la v.a. \( (X,Y) \) como:
\( F(x,y)=P(X \leq x; Y \leq y) \)
Función de densidad
1. Variable aleatoria bidimensional discreta
Consideramos la v.a. bidimensional \( (X,Y) \), pudiendo \( X \) e \( Y \) tomar los valores \( x_{1}, x_{2}, \cdots, x_{n} \) e \( y_1, y_2, ⋯, y_{m} \), respectivamente.
Función de Probabilidad Conjunta
Se define la Función de Probabilidad Conjunta de \( (X,Y) \), y se denota por \( p_{ij} \), como la probabilidad de que simultáneamente \( X \) tome el valor \( x_{i}\) e \( Y \) el valor \( y_{j} \),
\( P[X=x_{i} ; Y=y_{j}]=p_{ij} \hspace{.2cm} \) con \( \hspace{.2cm} i=1,2, \cdots, n \hspace{.2cm}; \hspace{.2cm} j=1,2, \cdots, m \)
que satisface las condiciones
a) \( p_{ij} \geq 0 \hspace{.2cm} \) con \( \hspace{.2cm} i=1,2, \cdots, n \hspace{.2cm}; \hspace{.2cm} j=1,2, \cdots, m \)
b) \( \displaystyle \sum_{i=1}^{n} \displaystyle \sum_{j=1}^{m}p_{ij}=1 \)
2. Variable aleatoria bidimensional continua
Función de Densidad
Se define la Función de Densidad de \( (X,Y) \), y se denota por \( f(x,y) \), como
\( P[a_1<X \leq a_2 \hspace{.2cm}; \hspace{.2cm} b_1<Y \leq b_2]= \displaystyle \int_{a₁}^{a₂} \displaystyle \int_{b₁}^{b₂}f(x,y)dxdy \)
que satisface las condiciones
a) \( f(x,y) \geq 0 \hspace{.3cm} \forall(x,y)\in R×R \)
b) \( \displaystyle \int_{a₁}^{a₂} \displaystyle \int_{b₁}^{b₂}f(x,y)dxdy=1 \)
Por lo tanto
\( f(x,y) = \displaystyle \frac{ \partial^{2}F(x)}{\partial x \partial y} \)
Distribuciones marginales
Se define la Función de Distribución marginal de \( X \) , y se denota por \( F_1(x) \), como
\( F_1(x)=F(x,+ \infty)=P[X \leq x ; Y \leq + \infty] \)
Se define la Función de Distribución marginal de \( Y \), y se denota por \( F_2(y) \), como
\( F_2(y)=F(+ \infty, y)=P[X \leq +\infty; Y \leq y] \)
Variable aleatoria bidimensional discreta
a) Distribución marginal de \( X \)
\( P[X=x_{i} ]=P[X=x_{i} ; Y= arbitrario]= \displaystyle \sum_{j=1}^{m}p_{ij}=p_{i.} \)
por tanto la función de distribución marginal se puede expresar
\( F_1(x)= \displaystyle \sum_{X_{i}<x} \displaystyle \sum_{j=1}^{m}p_{ij}= \displaystyle \sum_{X_{i}<x}p_{i.} \)
b) Distribución marginal de \( Y \)
\( P[Y=y_{j} ]=P[X=arbitrario; Y=y_{j}]= \displaystyle \sum_{i=1}^{n}p_{ij}=p_{.j} \)
por tanto la función de distribución marginal se puede expresar
\( F_2(y)= \displaystyle \sum_{i=1}^{n} \displaystyle \sum_{Y_{j}<y}p_{ij}= \displaystyle \sum_{Y_{j}<y}p_{.j} \)
Variable aleatoria bidimensional continua
a) Función de distribución marginal de \( X \)
\( F_1(x)= \displaystyle \int_{- \infty}^{x} \displaystyle \int_{- \infty}^{+ \infty}f(u,v)dudv= \displaystyle \int_{- \infty}^{x}du \displaystyle \int_{- \infty}^{+ \infty}f(u,v)dv= \displaystyle \int_{- \infty}^{x}f_1(u)du \)
siendo \( f_1(x) \) la Función de Densidad Marginal de \( X \) que viene dada por,
\( f_1(x) = \displaystyle \int_{- \infty}^{+ \infty}f(x,v)dv \)
b) Función de distribución marginal de \( Y \)
\( F_2(y)= \displaystyle \int_{- \infty}^{y} \displaystyle \int_{- \infty}^{+ \infty}f(u,v)dudv= \displaystyle \int_{- \infty}^{y}dv \displaystyle \int_{- \infty}^{+ \infty}f(u,v)du= \displaystyle \int_{- \infty}^{y}f_2(v)dv \)
siendo \( f_2(y) \) la Función de Densidad Marginal de \( Y \) que viene dada por,
\( f_2(y)= \displaystyle \int_{- \infty}^{+ \infty}f(u,y)du \)
Distribuciones condicionadas
En el Capítulo 4, correspondiente a la probabilidad, definimos la probabilidad del suceso A condicionada al suceso B de la siguiente forma:
\( P(A/B)= \displaystyle \frac{P(A \cap B)}{P(B)} \hspace{.3cm} \) con \( \hspace{.3cm} P(B)>0 \)
Una situación análoga se plantea en las variables aleatorias bidimensionales, en las que vamos a distinguir, como en toda la sección, entre variables aleatorias bidimensionales discretas y continuas.
Variable aleatoria bidimensional discreta
a) Se define la Función de Distribución de \( X \) Condicionada al valor \( y_{j} \) de \( Y \) como:
\( F(x/y_{j})=P[X \leq x / Y=y_{j} ]= \displaystyle \frac{P[X \leq x ; Y=y_{j} ] }{P[Y=y_{j} ]}= \displaystyle \frac{ \displaystyle \sum_{x_{i}<x}p_{ij}}{p_{.j}} \)
b) Se define la Función de Distribución de \( Y \) Condicionada al valor \( x_{i} \) de \( X \) como:
\( F(y/x_{i})=P[Y \leq y/X=x_{i} ]= \displaystyle \frac{P[X=x_{i} ; Y \leq y ]}{P[X=x_{i} ]}= \displaystyle \frac{ \displaystyle \sum_{y_{j}<y}p_{ij}}{p_{i.}} \)
Variable aleatoria bidimensional continua
a) Se define la Función de Distribución de \( X \) Condicionada a \( Y \) como:
\( F(x/y)= \displaystyle \frac{F(x,y)}{f_2(y)} \)
b) Se define la Función de Distribución de \( Y \) Condicionada a \( X \) como:
\( F(y/x)= \displaystyle \frac{F(x,y)}{f_1(x)} \)
Análogamente, se define
a) la Función de Densidad de \( X \) Condicionada a \( Y \) como:
\( f(x/y)= \displaystyle \frac{f(x,y)}{f_2(y)} \)
b) la Función de Densidad de \( Y \) Condicionada a \( X \) como:
\( f(y/x)= \displaystyle \frac{f(x,y)}{f_1(x)} \)
Variables aleatorias independientes
De la misma forma que definíamos el concepto de independencia entre dos sucesos \( A \) y \( B \) como \( P(A \cap B)=P(A)P(B) \), definimos, a continuación, este concepto en las variables aleatorias bidimensionales
Intuitivamente dos variables aleatorias \( X \) e \(Y \) son independientes si el resultado de una no influye en el resultado de la otra.
Decimos que las variables aleatorias \( X \) e \( Y \) son independientes si:
a) Variable aleatoria bidimensional discreta
\( P[X=x_{i} ; Y=y_{j}]=P[X=x_{i} ]P[ Y=y_{j}] \hspace{.3cm} \forall x_{i},y_{j}\hspace{.3cm} o \hspace{.3cm} p_{ij}=p_{i.}p_{.j} \hspace{.3cm} \forall i,j \)
siendo \( p_{i.} \) y \( p_{.j} \) las funciones de probabilidad marginales
b) Variable aleatoria bidimensional continua
\( f(x,y)=f_1(x)f_2(y) \)
siendo \( f_1(x) \) y \( f_2(y) \) las funciones de densidad marginales
Integrando la expresión anterior se obtiene:
\( F(x,y)=F_1(x)F_2(y) \)
siendo \( F_1(x) \) y \( F_2(y) \) las funciones de distribución marginales.
Esperanza matemática
En la Sección 5 definimos la esperanza matemática de \( g(X) \) (función real de la v.a. \( X \) de la siguiente forma:
a) Variable aleatoria discreta: \( E[g(X)]= \displaystyle \sum_{i}p_{i}g(x_{i}) \)
b) Variable aleatoria continua: \( E[g(X)]= \displaystyle \int_{- \infty}^{+ \infty}g(x)f(x)dx \)
Estas expresiones se pueden aplicar a funciones de más de una variable. Así, dada una función real \( g(X,Y) \) de dos variables aleatorias \( X \) e \( Y \) , se define la Esperanza Matemática de \( g(X,Y) \) como
a) Variable aleatoria bidimensional discreta:
\( E[g(X,Y)]= \displaystyle \sum_{i,j}p_{ij}g(x_{i},y_{j}) \)
b) Variable aleatoria bidimensional continua
\( E[g(X,Y)]= \displaystyle \int_{- \infty}^{+ \infty} \displaystyle \int_{- \infty}^{+ \infty}g(x,y)f(x,y)dxdy \)
siendo, en todos los casos, la suma y la integral absolutamente convergentes.
Propiedades:
Dadas las variables aleatorias \( X \) e \( Y \) y las constantes arbitrarias \( a \) y \( b \) . Se verifican las siguientes propiedades:
P1) \( E[aX+b]=a E[X]+b \)
P2) \( E[aX+bY]=a E[X]+bE[Y] \)
P3) Si \( X \) e \( Y \) son dos variables aleatorias independientes entonces: \( E[XY]=E[X]E[Y] \)
Varianza
Dada una función real \( g(X,Y) \) de dos variables aleatorias \( X \) e \( Y \) , se define la Varianza de \( g(X,Y) \) como
\( Var[g(X,Y)]=E \left \{g(X,Y)-E \left [g(X,Y) \right ] \right \}^{2} \)
a) Variable aleatoria bidimensional discreta:
\( Var[g(X,Y)]= \displaystyle \sum_{i,j}[g(x_{i},y_{j})- E \left [g(X,Y)] \right]^{2}p_{ij} \)
b) Variable aleatoria bidimensional continua
\( Var[g(X,Y)]= \displaystyle \int_{- \infty}^{+ \infty} \displaystyle \int_{- \infty}^{+ \infty} \left [g(x,y)-E \left [g(X,Y) \right ] \right ]^{2}f(x,y)dxdy \)
siendo, en todos los casos, la suma y la integral absolutamente convergentes.
Propiedades:
P1) Sean \( X \) e \( Y \) dos variables aleatorias entonces:
\( Var(X \pm Y)=Var(X)+Var(Y) \pm 2Cov(X,Y) \)
P2) Si \( X \) e \( Y \) son dos variables aleatorias independientes entonces:
\( Var(X+Y)=Var(X)+Var(Y) \hspace{.4cm} \) y \( \hspace{.4cm} Var(X-Y)=Var(X)+Var(Y) \)
Ejercicios propuestos: Relación V
1. En el Registro Andaluz del SIDA se están estudiando el número de casos nuevos de SIDA diagnosticado en un determinado hospital durante un día. Sea \( X \) la v.a. que representa dicho número de casos y \( F(X) \) la función de distribución dada por:
\( \begin{array} {|c|c|c|c|c|c|c|c|} \hline x & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline F(x) & 0.1 & 0.2 & 0.4 & 0.6 & 0.8 & 0.9 & 1 \\ \hline \end{array} \)
a) Calcular la probabilidad de que en un día cualquiera se diagnostiquen: a1) A lo sumo cuatro casos nuevos; a2) Por lo menos un caso; a3) Ningún caso nuevo; a4) No más de un caso; a5) Entre tres y cinco casos, ambos inclusive. (Sol: a1) 0.8; a2) 0.9; a3) 0.1; a4) 0.2; a5) 0.3 )
b) Hallar la función masa de probabilidad (Sol: 0.1; 0.1; 0.2; 0.2; 0.2; 0.1; 0.1 )
c) Calcular la media y la varianza. (Sol: \( E[x]=3=Var[x] \))
d) Calcular la desviación típica de los casos diagnosticados en un día. ¿Qué magnitud física podemos asociar a \( \sigma \)? (Sol: \( + \sqrt {3} \) casos de SIDA).
2. Se comprueba en unos laboratorios que los ratones blancos no reaccionan igual que los negros a determinados estímulos. Se selecciona al azar una muestra de 3 ratones de una jaula que contiene 12 de los cuales tres son blancos. Hallar la distribución de probabilidad de la v. a. \( X \) que representa el número de ratones blancos. (Sol: 21/55; 27/55; 27/220; 1/220 ).
3. Supongamos un juego con dos jugadores \( A \) y \( B \). Se lanza un dado, la ganancia \( X \) del jugador \( A \) depende del resultado del dado
\( \begin{array} {|c|c|c|c|c|c|c|} \hline Resultados & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline X & 3 & -2 & -2 & 5 & 1 & a \\ \hline \end{array} \)
¿Qué valor debe de tener \( a \) si el jugador \( A \) no espera ninguna ganancia? \( ( a=-5) \) .
4. La variable aleatoria \( X \) representa el intervalo de tiempo entre dos llegadas consecutivas a una tienda y su función de densidad de probabilidad está dada por:
\( f(x)= \left \{ \begin{array} {cc} K exp(-x/2) & si \hspace {.2cm} x>0 \\ 0 & para \hspace {.2cm} cualquier \hspace {.2cm} otro \hspace {.2cm} caso \\
\end{array} \right. \)
para una constante \( K \) apropiada. Determinar: a) El valor de \( K \); b) La función de distribución acumulativa; c) La probabilidad de que un intervalo entre 2 llegadas consecutivas se encuentre entre 2 y 6; d) La probabilidad de que transcurran menos de 8 minutos entre 2 llegadas consecutivas; e) La probabilidad de que ésta exceda los 8 minutos. (Sol: a) 1/2; b) \( 1-e^{-x/2} \); c) 0.3181; d) 0.9817; e) 0.0183 ).
5. Sea la v.a. \( X \) los gramos de hidrocarburos emitidos por un automóvil por cada kilómetro recorrido y \( f(x) \) su función de densidad:
\( f(x)= \left \{ \begin{array} {cc} Kx & 0 \leq x<2 \\ 0 & para \hspace {.2cm} cualquier \hspace {.2cm} otro \hspace {.2cm} caso \end{array} \right. \)
Calcular: a) El valor de \( K \); b) \( F(x) \); c) \( P(X \leq 1.2) \) ; d) \( P(0.8 \leq X) \) ; e) \( P(1 \leq X \leq 1.5) \) . (Sol: a) 1/2; b) \( x^{2} /4 \); c) 0.36; d) 0.84; e) 0.3125 ).
6. Supongamos que un jugador tiene 3 oportunidades para que al lanzar una moneda aparezca una “cara”. Si en el primer, segundo o tercer lanzamiento aparece cara el jugador recibe 2$, 4$, y 8$ respectivamente. Si no sale cara en ninguno de los 3 lanzamientos, pierde 20$. Determinar la ganancia o pérdida (Sol: 0.50).
7. Un inversionista dispone de 100.000$ para una inversión de un año. El inversionista está considerando dos opciones: colocar el dinero en el mercado de valores, lo que le garantiza una ganancia anual fija del 15% y un plan de inversión cuya ganancia anual puede considerarse como una v.a. cuyos valores dependen de las condiciones económicas que prevalezcan. Con base en la historia pasada del segundo plan, una analista ha determinado los posibles valores de la ganancia y ha calculado sus probabilidades como muestra la tabla . Con base a la ganancia esperada ¿Cuál de los dos planes debe seleccionarse? (Sol. El segundo).
\( \begin{array} {|c|c|c|c|c|c|c|} \hline Ganancia & 30 & 25 & 20 & 15 & 10 & 5 \\ \hline Probabilidad & 0.2 & 0.2 & 0.3 & 0.15 & 0.1 & 0.05 \\ \hline \end{array} \)
8. En unos estudios recientes se ha descubierto que unas determinadas aves padecían contaminación por mercurio. Dicha contaminación podía deberse a que habían comido semillas de plantas que fueron tratadas durante su crecimiento con metilo de mercurio. Sea \( X \) el nivel de mercurio en un pájaro en partes por millón. Supóngase que la v.a. \( X \) tiene la siguiente función de distribución
\( F(x)= \left \{ \begin{array} {cc} 0 & x \leq 2 \\ (x-2)^{2}/8 & 2<x<4 \\ 1 & 4 \leq x \end{array} \right. \)
Se pide calcular: a) La función de densidad; b) \( P(3 \leq x); P(1<x<3); P(x<3); P(x>4) \). (Sol: \( a) 3/8(x-2)^{2}; b) 1/8; 7/8; 7/8; 1/8; 0; 0 \)).
9. Sea \( X \) una v.a. continua con la siguiente función de densidad. Calcular \(E[|x|] \) y \( E[x] \). (Sol: \( E[|x|]= 1; E[x]= 0 \)).
\( f(x)= \left \{ \begin{array} {cc} \displaystyle \frac{e^{x}}{2} & x \leq 0 \\ \displaystyle \frac{e^{-x}}{2} & x>0 \end{array} \right. \)
10. Sea \( X \) una v.a. que representa el tiempo de duración es horas de un cierto componente eléctrico. Si la función de densidad de probabilidad de \( X \) está dada por:
\( f(x)= \left \{ \begin{array} {cc} \displaystyle \frac{e^{-x/1000}}{1000} & 0<x \\ 0 & para \hspace {.2cm} cualquier \hspace {.2cm} otro \hspace {.2cm} caso \\ \end{array} \right. \)
Se pide: a) La media; b) Probabilidad de que un componente rebaje más que el valor medio. (Sol.: \( a) \mu \) =1000; b) 0.3679 ).
11. Lanzamos un proyectil con un cierto ángulo de tiro, y medimos la distancia a la que cae. Esta distancia es una v. a. con función de densidad:
\( f(Z)=k \displaystyle \frac{ 500}{500+x^{2}} \hspace {.2cm} si \hspace {.2cm} 0 \leq x \)
Determinar: a) El valor de \( k \); b) \( F(X) \); c) \( P(X<50) \). (Sol: \( a) 2/ ( \pi \sqrt{500} \); b) \( (2/ \ pi) \arctan x/ \sqrt {500} \); c) \( (2/ \pi ) \arctan \sqrt{5} \)).
12. Una v. a. tiene como función de densidad:
\( f(x)= \left \{ \begin{array} {cc} k(x+1) & x \in [0,4] \\ mx^{2} & x\in [4,6] \\ 0 & para \hspace {.2cm} cualquier \hspace {.2cm} otro \hspace {.2cm} caso
\\ \end{array} \right. \)
Se sabe que \( P(0<x<4)=2/3 \), determinar \( k \) y \( m \). (Sol: k=1/18; m= 1/152).
13. Una v.a. tiene como función de densidad
\( f(x)= \left \{ \begin{array} {cc} \displaystyle \frac{7+x}{k } & -7<x \leq 0 \\ \displaystyle \frac{7-x}{k} & 0<x \leq 7 \\ 0 & en \hspace {.2cm} el \hspace {.2cm} resto \\ \end{array} \right. \)
a) Determinar el valor de \( k \) ; b) \( P[X>0] \). (Sol: a) k=49; b) 1/2 ).
14. El número de unidades vendidas mensualmente de un artículo sigue la ley de probabilidad definida por la función:
\( f(x)= \left \{ \begin{array} {cc} \displaystyle \frac{x} {25} & 0 \leq x \leq 5 \\ \displaystyle \frac{10-x}{25} & 5<x \leq 10 \\ 0 & en \hspace {.2cm} el \hspace {.2cm} resto \\ \end{array} \right. \)
Se pide: a) La función de distribución; b) La probabilidad de que las ventas sean superiores a 5 unidades; c) La probabilidad de que las ventas estén entre 5 y 7 unidades. (Sol: b) 1/2); c) 0.375 ).
15. Calcular la esperanza y varianza de la variable \( Z \) , \( Z=X+Y \) , donde \( X \) e \( Y \) son variables independientes y tienen como función de densidad cada una:
\( f(x)= \left \{ \begin{array} {cc} 1 & 0 \leq x \leq 1 \\ 0 & para \hspace {.2cm} cualquier \hspace {.2cm} otro \hspace {.2cm} caso \\ \end{array} \right. \)
(Sol: \( E[Z]=1; Var[Z]=1/6 \) ).
Autora: Ana María Lara Porras. Universidad de Granada
Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.