ALGUNAS DISTRIBUCIONES CONTINUAS

Introducción

En la teoría de la probabilidad existen muchos modelos teóricos que resultan de utilidad en una gran variedad de situaciones prácticas. El objetivo de este capítulo es presentar los modelos más relevantes desde un punto de vista conceptual. El lector interesado en los aspectos matemáticos involucrados en la deducción de dichos modelos y sus principales características puede dirigirse a los textos de estadística matemática mencionados en la bibliografía.

Distribución Normal N(μ, σ)

La Distribución Normal fue descubierta por Abraham de Moivre en 1753 como límite de un modelo binomial cuando el número de ensayos es infinito, pero su uso fue potenciado en el siglo XIX por Pierre Simon Laplace y especialmente por Carl Friedrich Gauss. Ambos estudiaban problemas de astronomía y cada uno de ellos “redescubrió” la distribución normal como la distribución que describía el comportamiento de los errores en las medidas astronómicas. Es por ello, por lo que esta distribución también se le conoce con el nombre de Distribución de Gauss-Laplace.

La distribución normal es la distribución continua de gran importancia en el análisis y cálculo de todos los aspectos relacionados con datos experimentales en ciencias y en medicina. Este hecho lo vamos a ver reflejado en los próximos capítulos donde la mayoría de los métodos estadísticos básicos que presentamos se apoyan en el modelo normal. Dicho modelo probabilístico desempeña un papel esencial en la teoría y la práctica de la Estadística, así como en la teoría de la Probabilidad.

Recibe el nombre de Normal  porque está presente en multitud de experimentos físicos, biológicos, etc. Su importancia fue tal, que durante mucho tiempo se creyó que la mayoría de las variables aleatorias continuas de la Naturaleza seguían distribuciones normales, es decir que la mayoría de las distribuciones eran normales, llamándoles a las restantes distribuciones anormales. Aún habiendo comprobado que esto no es cierto, esta distribución mantiene su importancia.

Función de densidad

Se dice que la variable aleatoria continua, \( X \), se distribuye según una Normal de parámetros \(  \mu, \sigma \) y se denota por \( X \rightarrow N(\mu, \sigma) \), cuando su función de densidad viene dada por la siguiente expresión:

\(  f(x)= \displaystyle \frac {1}{\sigma \sqrt{2 \pi }}e^{- \displaystyle \frac{(x-\mu)^{2}}{2 \sigma ^{2}}} \hspace {.9cm} [7.1 ]    \)

para     \( – \infty <x< \infty \),  \( – \infty< \mu < \infty \)  y \( \sigma >0 \).

Posteriormente veremos que los parámetros \( \mu  \) y \( \sigma  \) son la media y la desviación típica respectivamente, de la v.a. \( X \).

Existen muchas distribuciones normales diferentes y en cada una de ellas la función de densidad tiene la forma ([7.1]) donde \( \mu \) es la media y \( \sigma \) es la desviación típica. Para identificar una determinada distribución hay que hallar los valores de \( \mu \) y  \( \sigma  \).

Comprobamos, a continuación, que \( f(x)  \) es una función de densidad es decir que verifica las condiciones:

1) \( f(x) \geq 0  \) (En efecto, de la expresión ([7.1]) se deduce que \( f(x) \) no toma valores negativos).

2)  \( \int_{- \infty}^{+ \infty}f(x)dx=1 \)

En efecto

 \( \displaystyle \int_{- \infty}^{+ \infty}f(x)dx = \displaystyle \int_{- \infty}^{+ \infty} \displaystyle \frac {1}{ \sigma \sqrt {2\pi}} e^{- \displaystyle \frac{(x-\mu)^{2} }{2 \sigma^{2}}}dx= \)

\(   \left \{  \begin{array} \\ t = \displaystyle \frac {x- \mu} {\sigma} \\ dt = dx/ \sigma \\ \end{array} \right \}  \)

 =  \( \displaystyle \frac {1}{ \sigma \sqrt {2\pi}}\displaystyle \int_{- \infty}^{+ \infty} e^{-t^{2}/2}dt= ^{(1)} \displaystyle \frac {1}{ \sigma \sqrt {2\pi}} \sigma \sqrt {2\pi} = 1 \)

(1) La integral \( \displaystyle \int_{- \infty}^{+ \infty} e^{-t^{2}/2}dt  \) se llama Integral de Gauss y su valor es \( \sqrt{2 \pi}\).

Representación gráfica

Desde un punto de vista geométrico, la función de densidad de la distribución Normal tiene forma campaniforme, por lo que también recibe el nombre de Campana de Gauss, como se presenta en la Figura 7.1

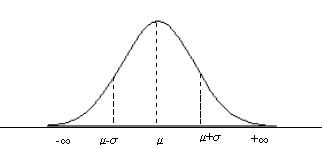
Figura 7.1: Curva de densidad de la distribución Normal N(μ, σ)

Es fácil comprobar las siguiente características más relevantes:

1) Campo de existencia: \( (- \infty, + \infty) \)

2) La curva es simétrica respecto a la vertical trazada en \(  \mu \). Por tanto, la recta \(  x= \mu \) divide a la curva en dos partes iguales cuyas áreas valen 0.5.

3) La gráfica de \( f(x) \) alcanza un máximo relativo en el punto \(  (\mu, 1/(\sigma \sqrt{2 \pi})) \)

4) De los apartados anteriores se deduce que la media \( \mu \) coincide con la moda (por el apartado 3) y con la mediana (por el apartado 2)

5) Puntos de inflexión \(   (\mu + \sigma, 1/(\sigma \sqrt{2 \pi e })) \) y \(   (\mu – \sigma, 1/(\sigma \sqrt{2 \pi e })) \). Es decir, los puntos de inflexión en la curva son los valores de \(  X \) iguales a una desviación típica a cada lado de la media \(   (x= \mu \pm \sigma) \). (La distancia entre la recta \( x= \mu \) y el punto de inflexión es \(  \sigma \) ). La situación de estos puntos determina la forma de la curva. Cuanto mayor sea el valor de \( \sigma \), más lejos de la media estarán los puntos de inflexión y más achatada será la curva. Es decir, su mayor o menor aplastamiento lo determina \(  \sigma \).

6) Tiene una asíntota horizontal en el eje de abcisas.

Es interesante observar, como se muestra en la figura 7.2, que la curva de densidad de la distribución Normal

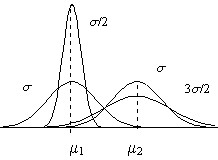
Figura 7.2: Efectos de μ y σ sobre la curva de densidad de la distribución N(μ, σ)

 

• Cambia de posición cuando varia el valor del parámetro \( \mu \) pero no cambia su forma
• Modifica su forma cuando varía el valor del parámetro \( \sigma \), (un aumento del valor de \( \sigma \) produce un alejamiento de los puntos de inflexión del eje \( x= \mu \) y por tanto una disminución de la ordenada del máximo relativo dando lugar a una curva más achatada), pero dicha variación no afecta a la posición de la curva.

Los efectos que producen las variaciones de los valores de los parámetros \( \mu \) y \( \sigma \) sobre la curva de densidad de la distribución Normal son perfectamente razonables ya que, como mostraremos posteriormente \( \mu \) y \( \sigma \) son la Esperanza Matemática y la Varianza respectivamente, de la variable aleatoria \( X \). Por lo tanto, \( \mu \) es un parámetro de posición, de situación, afecta a la localización de la curva en el sentido de que indica dónde está centrada o localizada la curva a lo largo del eje de abcisas, mientras que \(\sigma \) es un parámetro de dispersión, afecta a la forma de la curva.

Características

En primer lugar calculamos la función generatriz de momentos.

Función generatriz de momentos

   \(   \begin{array}{cc} \psi(t) & = E[e^{tX}]= \displaystyle \int_{- \infty}^{+ \infty}e^{tx}f(x)dx=\displaystyle \int_{- \infty}^{+ \infty}e^{tx} \displaystyle \frac{1}{\sigma \sqrt{2 \pi}}e^- { \displaystyle \frac{(x- \mu)^{2}}{2 \sigma^{2}}} dx =\displaystyle \frac{1}{\sigma \sqrt{2 \pi}} \displaystyle \int_{- \infty}^{+ \infty} e^{tx-  \displaystyle \frac{ (x- \mu)^{2}}{2 \sigma^{2}}}dx= \\ \end{array}  \)

\(   \left \{  \begin{array} \\ t = \displaystyle \frac {x- \mu} {\sigma} \\ dt = dx/ \sigma \\ \end{array} \right \}  \)

  \(   \begin{array}{cc}  & = \displaystyle \frac{1}{ \sqrt {2 \pi}} \displaystyle \int_{- \infty}^{+ \infty} e^{ \displaystyle \frac{2t \sigma y+2t \mu-y^{2}}{2}}dy= \displaystyle \frac{e^{t \mu}}{ \sqrt {2 \pi}} \displaystyle \int_{- \infty}^{+ \infty}e^{ \displaystyle \frac{2t \sigma y-y^{2}}{2}}dy=e^{t \mu+ \displaystyle \frac{t^{2} \sigma^{2}}{ \sqrt{2 \pi}}} \displaystyle \int_{- \infty}^{+ \infty}e^{- \displaystyle \frac{(y-t \sigma)^{2}}{2}}dy= \\ \end{array}  \)

\(   \left \{  \begin{array} \\ y-t \sigma=u \\  dy=du \\ \end{array} \right \}  \)

  \(   \begin{array}{cc}  & =  \displaystyle \frac{   e^{    t \mu+ \displaystyle \frac{  t^{2} \sigma^{2}}{2} }}{ \sqrt{2 \pi} }     \displaystyle \int_{- \infty}^{+ \infty} e^{-u^{2}/2}du=   \displaystyle \frac {    e^{      t \mu+ \displaystyle \frac{  t^{2} \sigma^{2}}{2}}}{ \sqrt{2 \pi}} \sqrt {2 \pi}= e^{t \mu+ \displaystyle \frac{t^{2} \sigma^{2}}{2}  } \\ \end{array}  \)

La media y la varianza se van a obtener a partir de la función generatriz de momentos, para ello se calculan las dos primeras derivadas de dicha función y se particulariza para t=0

 \( \psi^{´}(t)=(\mu+t \sigma^{2})e^{t \mu+ \displaystyle \frac{t^{2}\sigma^{2}}{2}} \Rightarrow \psi{´}(0)= \mu=m_{1} \)

 \(  \psi^{´´} (t)= \sigma^{2}e^{t \mu + \displaystyle \frac{t^{2}\sigma^{2}}{2}}+(\mu+t \sigma^{2})^{2}e^{t \mu+\displaystyle \frac{t^{2}\sigma^{2}}{2}} \Rightarrow \psi{´´}(0)= \sigma^{2}+ \mu^{2}=m_2 \)

Por lo tanto:

• Esperanza matemática  \( E[X]= \mu  \)
• Varianza  \( Var[X]=m_2-m_1^{2}= \sigma^{2}+ \mu^{2}- \mu^{2}= \sigma^{2}  \)

Función de distribución

La función de distribución de una v.a. \( X \) que sigue una distribución \( N(\mu, \sigma) \) tiene la siguiente expresión:

 

\(  F(x)=P[X \leq x]= \displaystyle \int_{- \infty}^{x}f(t)dt= \displaystyle \int_{- \infty}^{x} \displaystyle \frac {1}{\sigma \sqrt{2 \pi}} e^{ – \displaystyle \frac {(t-\mu)^{2}}{2\sigma^{2}}} dt \)

donde \( f(t) \) es la función de densidad.

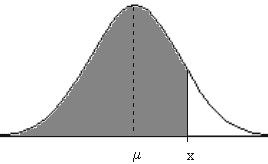
Figura 7.3

Gráficamente representa el área encerrada entre la curva \( y=f(t) \), función de densidad, el eje OX y la recta \( X=x \).

La función de densidad f(x) depende de dos parámetros μ y σ. Por lo tanto, hay un número infinito de variables normales cada una de las cuales se caracteriza por los valores de los parámetros  μ y σ. Es decir, f(x) no tiene función primitiva, no existe expresión analítica para F(x) y, en consecuencia, la función de densidad de la ley normal aparece en forma de tablas o programada en muchas de las calculadoras existentes en el mercado. El lector interesado en las distintas aproximaciones para el cálculo numérico de F(x) puede encontrar abundante material en Abramowitz y Stegun (1964), Johnson y Kotz (1970) o Patel y Read (1982) entre otros.

Al depender la ley Normal de μ (que varia de \( – \infty \) a  \( + \infty \)) y de \( \sigma^{2} \) (que varía de 0 a \(  + \infty \)) serían necesarias una infinidad de tablas, una para cada pareja de valores de \( \mu \) y \( \sigma^{2} \). En consecuencia, para calcular las probabilidades asociadas a una curva normal específica se utiliza, como veremos a continuación, una transformación algebraica,  \( Z=(X- \mu)/ \sigma \), conocida como procedimiento de tipificación que convierte cualquier v.a. \( X \rightarrow N( \mu, \sigma) \) en una v.a. \( Z \rightarrow N(0, 1) \) que recibe el nombre de Normal Tipificada o Normal Estándar por lo que solamente hay que tabular esta última. La tabla proporciona las probabilidades \( P[Z>z] \) para valores determinados de z.

Tipificación

Dada una v.a. \(  X \rightarrow N(\mu, \sigma) \), recibe el nombre Tipificación el proceso de restarle la media \( \mu \) a la v.a. X y dividir esta diferencia por la desviación típica \( \sigma \).

Si \( Z \) es una v.a. definida por la relación \( Z= \displaystyle \frac {X- \mu}{\sigma} \), donde \( X  \rightarrow N(\mu, \sigma) \), entonces \(  Z \rightarrow N(0, 1)  \) y se dice que la v.a. \( X \) se ha tipificado o estandarizado.

Veamos, que en efecto, la media de \( Z \) es cero y la varianza de \( Z \) es uno

• La media de \( Z \) es cero

\( E[Z]=E \left [ \displaystyle \frac {X- \mu}{\sigma}\right ]= \displaystyle \frac {1}{\sigma} E[X- \mu] = \displaystyle \frac {1}{\sigma}[E[X]- \mu] = \displaystyle \frac {1}{\sigma}(\mu -\mu)=0 \)

• La varianza de \( Z \) es uno

\( \sigma^{2}[Z]=E[Z-E[Z]]^{2}=E[Z-0]^{2}=E \left [ \displaystyle \frac {X- \mu}{\sigma} \right ]^{2}= \displaystyle \frac {1}{\sigma^{2}} E[X-\mu]^{2}= \displaystyle \frac {1}{\sigma^{2}}\sigma^{2}=1 \)

Distribución Normal N(0, 1)

Función de densidad

La Función de Densidad de la distribución N(0,1) se obtiene haciendo μ=0 y σ=1 en la Función de Densidad de la N(μ, σ) y resulta la siguiente expresión

\( f(z)= \displaystyle \frac {1}{\sigma \sqrt{2 \pi}}e^{- \displaystyle \frac {z^{2}}{2}} con – \infty <z<+ \infty \hspace{2cm}\)  [4.2]

Representación gráfica

La figura 7.4 nos muestra la curva de densidad de la distribución N(0, 1). Es fácil comprobar las siguiente características más relevantes:

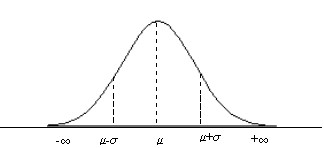
Figura 7.4

∗ Campo de existencia: (-∞, +∞)

∗ La curva es simétrica respecto al eje de ordenadas

∗ La curva tiene un máximo relativo en \( (0, 1/ \sqrt{2 \pi}\)

∗ La Media coincide con la Moda y con la Mediana

∗ Puntos de inflexión \( (1, 1/( \sqrt{2 \pi e}) \) y \( (-1, 1/( \sqrt{2 \pi e}) \)

∗ Tiene una asíntota horizontal en el eje de abcisas.

Características

En primer lugar calculamos la función generatriz de momentos.

Función generatriz de momentos

\(   \begin{array}{cc} \Psi(t) & = E[e^{tZ}]= \displaystyle \int_{- \infty}^{+ \infty}e^{tz}f(z)dz=\displaystyle \int_{- \infty}^{+ \infty}e^{tz} \displaystyle \frac{1}{\sigma \sqrt{2 \pi}}e^- { \displaystyle \frac{z^{2}}{2 }} dz = \displaystyle \frac{1}{\sqrt{2 \pi}} \displaystyle \int_{- \infty}^{+ \infty} e^{ \displaystyle \frac{2tz- z^{2}}{2}}dz \\  & =  \displaystyle \frac{1}{ \sqrt {2 \pi}} \displaystyle \int_{- \infty}^{+ \infty} e^{ \displaystyle \frac{2t z- t^{2}-z^{2}}{2}} e ^{ \displaystyle \frac{t^{2}}{2} } dz = \displaystyle \frac{   e^{    \displaystyle \frac {t^{2}}{2}} }    { \sqrt {2 \pi}}  \displaystyle \int_{- \infty}^{+ \infty}e^{- \displaystyle \frac{(z-t)^{2}}{2}}dz= \\  \end{array}  \)

\(   \left \{  \begin{array} \\ y = z-t \\  dy=dz \\ \end{array} \right \}  \)

\(   \begin{array}{cc}  & = \displaystyle \frac{e^{\displaystyle \frac {t^{2}}{2}}}{ \sqrt {2 \pi}} \displaystyle \int_{- \infty}^{+ \infty}e^{-\displaystyle \frac{y^{2}}{2}}dy=  \displaystyle \frac{e^{\displaystyle \frac{t^{2}}{2}}}{ \sqrt{2 \pi}}\sqrt{2 \pi}= e^{\displaystyle \frac{t^{2}}{2}} \\ \end{array}  \)

Conocida la función generatriz de momentos, a partir de ella determinamos la media y la varianza, para ello se calculan las dos primeras derivadas de dicha función y se particulariza para t=0

\(   \begin{array}{cc}  \psi^{´}(t)  & = t e^{\displaystyle \frac {t^{2}}{2}} \Rightarrow  \psi^{´}(0)=0=m_1 \\ & & \\ \psi^{′′}(t) & =e^{\displaystyle \frac {t^{2}}{2}} +t^{2}e^{\displaystyle \frac {t^{2}}{2}} \Rightarrow \psi^{′′}(0)=1=m_2 \\ \end{array}  \)

• Esperanza matemática \(  E[Z]=0 \)
• Varianza \(  Var[Z]=m_2-m_{1}^{2}=1-0=1 \)

Función de distribución

La Función de Distribución de la distribución N(0, 1) viene dada por la expresión

\(  F(z)=P[Z \leq z]= \displaystyle \int_{- \infty}^{z}f(t)dt= \displaystyle \int_{- \infty}^{z} \displaystyle \frac {1}{ \sqrt{2 \pi}}e^{- \displaystyle \frac {t^{2}}{2}}dt \)

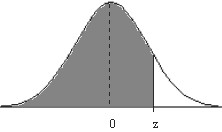Figura 7.5

Gráficamente representa el área encerrada entre la curva y=f(t), función de densidad, el eje OX y la recta X=z.

Las tablas nos permiten conocer las áreas bajo la curva N(0,1), entre las diversas tablas de áreas existentes nosotros vamos a utilizar la tabla III del Apéndice B que muestra las probabilidades siguientes. (Llamadas tablas de colas a la derecha).

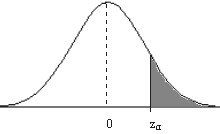
Figura 7.6

\(  P[Z>z_{α}]= \displaystyle \int_{z_{α}}^{\infty } \displaystyle \frac {1}{ \sqrt{2 \pi}} e^{- \displaystyle \frac {z^{2}}{2}}dz = \alpha  \)

Veamos, mediante algunos ejemplos, como se utiliza esta tabla.

Ejemplo: Dada \(  X \rightarrow N(\mu, \sigma) \)  obtener P[X>a] y aplicarlo para determinar P[X>9] cuando  \( X \rightarrow N(6, 3) \)

Hay que tipificar la variable para ello efectuamos el cambio de variable  \( Z= \displaystyle \frac {X- \mu}{\sigma} \)

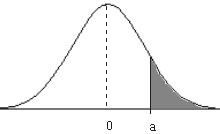
Figura 7.7

\(  P[X>a]=P \left [ \displaystyle \frac {X-\mu}{\sigma} > \displaystyle \frac {a- \mu}{\sigma} \right ]=P \left [Z > \displaystyle \frac {a- \mu}{\sigma} \right ] \)

\(  P[X>9]= P \left [ Z > \displaystyle \frac {9-6}{3} \right ]=P[Z>1]=0.1597 \)

La tabla III del Apéndice B nos muestra las probabilidades P[Z>a]. Para hallar P[Z>1], en la tabla III, en la columna encabezada por z se buscan los dos primeros dígitos, en este caso 1.0 y el tercer dígito, que en este caso es 0, se busca en la columna rotulada por 0.00. La probabilidad pedida es la que muestra la tabla III al hacer coincidir la fila 1.0 con la columna 0.00. En este caso, dicha probabilidad es 0.1597.

Ejemplo: Dada \(  X \rightarrow N(\mu, \sigma) \)  obtener P[X>-a] y aplicarlo para determinar P[X>-9] cuando \(  X \rightarrow N(6, 3) \)

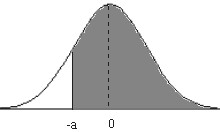
Figura 7.8

\( P[X>-a]=1-P[X<-a]=1-P[X>a]= 1-P \left [Z > \displaystyle \frac {a- \mu}{\sigma} \right ] \)

\( P[X>-3]=1-P \left [Z<\displaystyle \frac {-3-6}{3} \right]=1-P[Z<-3]=1-P[Z>3]=1-0.00135=0.99865 \)

Ejemplo: Dada \(  X \rightarrow N(\mu, \sigma) \)  obtener P[X<a] y aplicarlo para determinar P[X<9] cuando  \(  X \rightarrow N(6 , 3) \)

Figura 7.9

\(  P[X<a]=1-P[X>a]=1-P \left [Z > \displaystyle \frac {a- \mu}{\sigma} \right ] \)

\( P[X<9]=1-P[Z> \displaystyle \frac {9-6}{3}]=1-P[Z>1]= 1-0.1597=0.8403 \)

Ejemplo: Dada \(  X \rightarrow N(\mu, \sigma) \)  obtener P[a<X<b] y aplicarlo para determinar P[6<X<8] cuando \(  X \rightarrow N(5, 2) \)

Figura 7.10

\(  P[a<X<b]=P[X>a]-P[X>b] \)

\(  P[6<X<8]=P[Z>0.5]-P[Z>1.5]= 0.3085-0.0668=0.2417 \)

Regla de la probabilidad normal

Dada una variable aleatoria X con distribución Normal de media μ y desviación típica σ, \(  X \rightarrow N(\mu, \sigma) \), entonces:

• La probabilidad de que X tome un valor a una distancia máxima de su media de una desviación típica es 0.68

\(   \begin{array}{ll} P[\mu – \sigma <X< \mu + \sigma] & = P \left [ \displaystyle \frac {\mu – \sigma- \mu}{ \sigma} <Z <  \displaystyle \frac {\mu + \sigma- \mu}{ \sigma}  \right ] = \\ & = P[-1<Z<1]= 1-2P[Z>1]=1-2×0.1597=0.6806 \\ \end{array}  \)

• La probabilidad de que X tome un valor a una distancia máxima de su media de dos veces la desviación típica es 0.95

\( P[\mu – 2 \sigma <X< \mu + 2 \sigma] \simeq 0.95 \)

• La probabilidad de que X tome un valor a una distancia máxima de su media de tres veces la desviación típica es 0.99

\( P[\mu – 3 \sigma <X< \mu + 3 \sigma]  \simeq 0.99 \)

La regla de la probabilidad normal se puede considerar como una regla rápida de tanteo que permite saber si un determinado valor de una variable aleatoria normal es habitual o por el contrario es inusualmente grande o pequeño, todo ello basádonos exclusivamente en el conocimiento de la media y de la desviación típica de dicha variable.

Una de las aplicaciones más frecuente es en el contexto médico, en concreto en los análisis de sangre donde se miden los niveles de potasio, proteina, calcio, colesterol…. Del banco de datos de las mediciones realizadas durante varios años a un gran número de personas se ha podido establecer con bastante precisión los niveles medios y la cantidad de variabilidad esperada en los individuos sanos. De la regla de la probabilidad normal sabemos que:

• Aproximadamente un 68% de las personas sanas estarán dentro de los límites μ±σ y un 32% de la población está fuera de ellos, de los cuales un 16% presentará niveles anormalmente más altos y el 16% restante presentará niveles anormalmente más bajos.
• Aproximadamente un 95% de las personas sanas estarán dentro de los límites μ±2σ y un 5% de la población está fuera de ellos, de los cuales un 2.5% presentará niveles anormalmente más altos y el 2.5% restante presentará niveles anormalmente más bajos.
• Aproximadamente un 99% de las personas sanas estarán dentro de los límites μ±3σ y un 1% de la población está fuera de ellos, de los cuales un 0.5% presentará niveles anormalmente más altos y el 0.5% restante presentará niveles anormalmente más bajos.

Los informes médicos habitualmente presentan una lista de los “límites 2-sigma”, μ±2σ,  para cada variable y marcan los valores considerados anómalos. Cualquier valor que se encuentra en esta región se considera aceptable mientras que los que se encuentran fuera de la región no se consideran aceptables.

Ejemplo 7.1. En una ciudad se ha medido la cantidad de lluvia media caída durante el mes de mayo, esta medición ha dado 26cc y una desviación típica de 4cc. Se supone que la cantidad de lluvia caida se distribuye aproximadamente normal. ¿Se podría considerar un mes de mayo inusualmente húmedo si cayeran más de 34 cc?

Respuesta:

Aplicando la regla de la probabilidad normal, sabemos que existe un 95% de posibilidades de que la cantidad de lluvia total caida se encuentre dentro del intervalo μ±2σ, en este caso 26±8. Por lo tanto, podemos decir que hay una probabilidad alta de que la cantidad de lluvia esté entre los 18cc y los 34cc, y alrededor de un 5% de posibilidades de que se encuentre fuera de estos valores, de los cuales alrededor sólo de un 2.5% de posibilidades de un valor superior a los 34cc. Por lo tanto, la probabilidad de que en el mes de mayo caigan 34cc tiene una probabilidad realmente pequeña, es decir, podemos considerar un mes de mayo inusualmente húmedo.

Ejemplo 7.2. En una cierta población de primates, el volumen de la cavidad craneal X se distribuye aproximadamente según una curva normal con media 100 u.c. y desviación típica 10 u.c., \(  X \rightarrow N(100, 10) \).

Calcular la probabilidad de que un miembro de la población seleccionado aleatoriamente tenga una cavidad craneal: 

a) Mayor que 100

b) Menor que 85

c) A lo más 112

d) Por lo menos 108

e) Más grande que 90

f) Entre 95 y 120

g) Encontrar un punto x₀ tal que el 70 % de los primates tengan una cavidad craneal más pequeña que él

h) Encontrar un punto x₀ tal que el 10 % de los primates tengan una cavidad craneal superior a él.

Respuesta:

a) \( P[X>100]=0.5 \)

La función de densidad es simétrica respecto a su media.

b)\( P[X<85]=1-P[X>85]=1-P[Z> \displaystyle \frac{85-100}{10}]=1-P[Z>-1.5]=P[Z>1.5]=0.0668 \)

c) \(  P[X \leq 112]=1-P[X>112]=1-P[Z>1.2]=1-0.1151=0.8849 \)

d) \(  P[X \geq 108]=P[Z> \displaystyle \frac{108-100}{10}]=P[Z>0.8]=0.2119 \)

e) \(  P[X>90]=P[Z> \displaystyle \frac{90-100}{10}]=P[Z>-1]=1-P[Z>1]=1-0.1597=0.8403 \)

f)  \( P[95<X<120]=P[Z>0.5]-P[Z>2]=0.3085-0.0228=0.2857 \)

g) \(  P[X<x₀]=0.7; P[Z< \displaystyle \frac{x_0-100}{10}]=0.7; 1-P[Z> \displaystyle \frac{x_0-100}{10}]=0.7; \)

\( P[Z>\displaystyle \frac{x_0-100}{10}]=0.3;  \displaystyle \frac{x_0-100}{10}=0.52; x_0=105.2 \)

La abcisa \( (x_0-100)/10 \) es el punto de la curva normal tipificada que deja un 30% del área a la derecha y el 70% restante a la izquierda. En este apartado estamos trabajando a la inversa del apartado anterior, es decir, a partir de una probabilidad tenemos que hallar el valor numérico asociado a ella. En la tabla III del Apéndice B, encontramos las probabilidades 0.3015 y 0.2981, la más próxima a 0.3 es la probabilidad 0.3015 que corresponde al valor númerico 0.52.

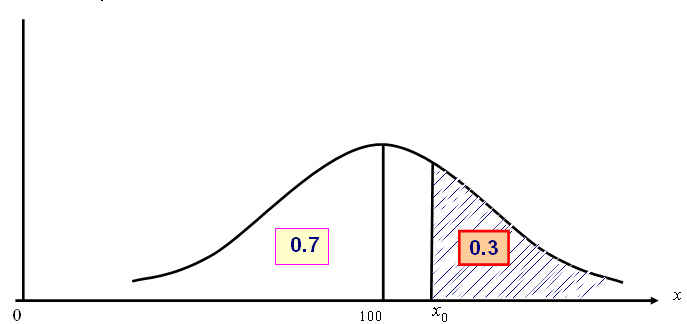
Figura: 7.11

h)   \( P[X>x_0]=0.1; P[Z> \displaystyle \frac{x_0-100}{10}]=0.1;  \displaystyle \frac{x_0-100}{10}=1.28; x_0=112.8   \)

Ejemplo 7.3. En una ciudad compuesta por 5 millones de personas, la probabilidad de ser mujer es igual al 48% de la población de esa ciudad. La estatura, en metros de los mujeres, se distribuye aproximadamente según una N(1.68; 0.2). Se pide:

a) ¿Cuántas mujeres hay con estatura comprendida entre 1.6 y 1.75 m.?
b) ¿Cuántas con estatura inferior a 1.65?
c) ¿Cuántas con estatura superior a 1.8?
d) Si el 15% de los mujeres quieren realizar un determinado trabajo y sólo serán admitidas aquellas que tengan una estatura superior a 1.65. Determinar cuántas son rechazadas, suponiendo que en este 15% la distribución de las estaturas es N(1.72; 0.14).

Respuesta:

El número de mujeres de la ciudad es 5000000×0.48=2400000.

Sea \( X  (Estatura) \rightarrow N(1.68; 0.2) \)

a)

   \(   \begin{array}{ll} P[1.6<X<1.75] &  =P \left [Z> \displaystyle \frac{1.6-1.68}{0.2}\right ]-P[Z> \displaystyle \frac{1.75-1.68}{0.2}]= \\ & = 1-P[Z>0.4]-P[Z>0.35]=1-0.3446-0.3632=0.2922 \\ \end{array}  \)

El 29.22% de las mujeres tienen una estatura comprendida entre 1.6 y 1.75. El número total de mujeres con esa estatura es el 29.22% de 2400000 igual a 701280.

b)   \(  P[X<1.65]=P[Z< \displaystyle \frac{1.65-1.68}{0.2}]=P[Z<-0.15]=P[Z>0.15]=0.4404 \)

El número de mujeres con estatura inferior a 1.65 es 0.4404×2400000=1056960.

c) \( P[X>1.8]=P \left [Z> \displaystyle \frac{1.8-1.68}{0.2}\right ]=P[Z>0.6]=0.2743 \)

El número de mujeres con estatura superior a 1.8 es 0.2743×2400000=658320

d) El número de mujeres que quieren realizar el trabajo es 0.15×2400000=360000

Sea Y (Estatura de mujeres que quieren realizar el trabajo); \(  Y  \rightarrow N(1.72; 0.14) \)

\(  P[ser \hspace{.2cm} rechazada]=P[Y \leq 1.65]=P \left [Z \leq \displaystyle \frac{1.65-1.72}{0.14} \right ]=P[Z>0.5]=0.3085 \)

El número pedido es 0.3085×360000=11060.

Aproximación de una Binomial por una Normal

La distribución Binomial se puede aproximar mediante una distribución Normal, cuando n es grande y p no toma valores extremos, aplicando el Teorema de Moivre.

Teorema de Moivre: Si X es una v.a. discreta Binomial de parámetros n y p,  \(  X \rightarrow B(n, p) \), con función  de probabilidad

\(  P[X=k]=\displaystyle { n \choose k} p^{k}q^{n-k} \)

entonces la variable aleatoria Z definida por

\( Z= \displaystyle \frac{X-np}{ \sqrt{npq}}\rightarrow N(0, 1) \hspace {.5cm}si \hspace{.5cm} n \rightarrow \infty \)

Las condiciones bajo las cuales esta aproximación conduce a resultados correctos varían según distintos autores. Nosotros consideramos que las condiciones más aceptables son cuando n >30 y  0.1<p<0.9. Cuanto mayor sea n y el valor de p esté más próximo a 0.5 mejor será la aproximación.

Ejemplo 7.4. Una organización política planea llevar a cabo una encuesta para detectar la preferencia de los votantes con respecto a los candidatos A y B que ocuparán un puesto en la administración pública. Supóngase que toma una muestra aleatoria de 1000 ciudadanos. ¿Cuál es la probabilidad de que 550 o más de los votantes indiquen una preferencia por el candidato A si la población, con respecto a los candidatos, se encuentra igualmente dividida?

Respuesta:

Sea X la v.a. que representa el número de ciudadanos que tienen preferencia por el candidato A.

\(  X \rightarrow  B(1000, 0.5) \) como n es suficientemente grande y  p=0.5 se puede aproximar la distribución Binomial mediante una distribución Normal; \( X \rightarrow N(np, \sqrt{npq} \Rightarrow X \rightarrow N(500, 15.81) \)

\( P[X \geq 550] \sim P[Z> \displaystyle \frac{550-500}{15.81}]=P[Z>3.16]=0.00079 \)

Distribuciones asociadas a la ley normal

En esta sección presentamos tres familias de variables aleatorias continuas muy importantes asociadas a la ley normal. Estas variables aleatorias, llamadas χ² de Pearson, t de Student y F de Snedecor, se utilizan en muchos de los distintos entornos estadísticos.

Distribución χ² de Pearson

Sean   \( X_1, X_2, \cdots , X_{n}   \) , n variables aleatorias independientes entre sí e idénticamente distribuidas según una N(0, 1). Definimos la variable aleatoria X como la suma de los cuadrados de las vv.aa.   \(  X_{i }   \) , es decir, como

   \(  X=X_1^{2}+X_2^{2}+ \cdots +X_{n}^{2}   \)

La distribución que sigue la v.a. X se le denomina Distribución χ² (Chi-Cuadrado) de Pearson con n grados de libertad y se denota,   \(  X \rightarrow  \chi_n^{2} \).

Por lo tanto, la distribución \(  \chi_{n}^{2} \) es la distribución de la suma de los cuadrados de n variables aleatorias independientes entre sí y todas ellas con distribución N(0, 1).

Obsérvese que los grados de libertad de la distribución Chi-cuadrado, n (también se denotan por υ) son el número de sumandos es decir, el número de variables aleatorias independientes que intervienen en la distribución.

Función de densidad

Se dice que una v.a. X se distribuye según una \(  \chi_{n}^{2} \) si la función de densidad de probabilidad de dicha v.a. viene dada por

\( f(x)= \displaystyle \frac{1}{2^{n/2}\Gamma ( \frac{n}{2})}e^{-x/2}x^{(n/2)-1} \hspace{.3cm} \) para \hspace{.3cm}  \( x>0 \)

donde \( \Gamma(.) \) se le conoce como función gamma y se define como:

\( \Gamma(P)= \displaystyle \int_{0}^{\infty}x^{P-1}e^{-x}dx \)

Nota: \( \Gamma (P)=(P-1) \Gamma(P-1) \)

Características generales

• Las variables aleatorias \(  \chi^{2} \) se identifican cada una por un parámetro, n o (υ), llamado grados de libertad. Este parámetro es siempre un entero positivo.
• Hay un número infinito de variables aleatorias \(  \chi^{2} \) identificadas cada una por los grados de libertad (n).  El número de grados de libertad es el número de variables aleatorias independientes que intervienen en la distribución
• Cada variable aleatoria \(  \chi^{2} \) es una variable aleatoria continua
• La función de densidad de la distribución χ² depende del número de grados de libertad. La gráfica de dicha función para cada variable aleatoria \(  \chi^{2} \) con n≥2 es:
  • Una curva asimétrica positiva que presenta la forma que aparece en la Figura 7.12, correspondiente a n=4, n=6, n=10, n=20 y n=30 grados de libertad
  • El campo de variabilidad es (0, +∞)
  • Las variables \(  \chi^{2} \) no pueden tomar valores negativos
  • Depende del parámetro n, por lo que no hay una curva única, como sucede con la distribución Normal tipificada.
  • El parámetro n es, al mismo tiempo, un parámetro de posición afecta a la localización de la curva y un parámetro de dispersión afecta a la forma de la curva.

\( E[\chi_{n}^{2}]=n   \hspace{.5cm} \) y \( \hspace{.5cm} Var[\chi_{n}^{2}]=2n \)

Es decir, la esperanza matemática de una v.a. \(  \chi^{2} \) coincide con sus grados de libertad y su varianza es el doble de sus grados de libertad.

Figura 7.12: Gráficas de densidades de χ²  para n=4,6,10,20 y 30

Función de distribución

La función de distribución de la v.a. X viene dada por

\(  F(x)=P[X \leq x]=\displaystyle \int_{0}^{x} \displaystyle \frac{1}{2^{n/2} \Gamma ( \frac{n}{2})}e^{-x/2}x^{(n/2)-1} dx \)

La distribución \(  \chi^{2} \) está parcialmente tabulada en la Tabla (IV) del Apéndice B. Esta tabla es de doble entrada, en la fila figuran los valores de α y en las columnas los grados de libertad denotados por ν. Los valores de esta tabla representan:

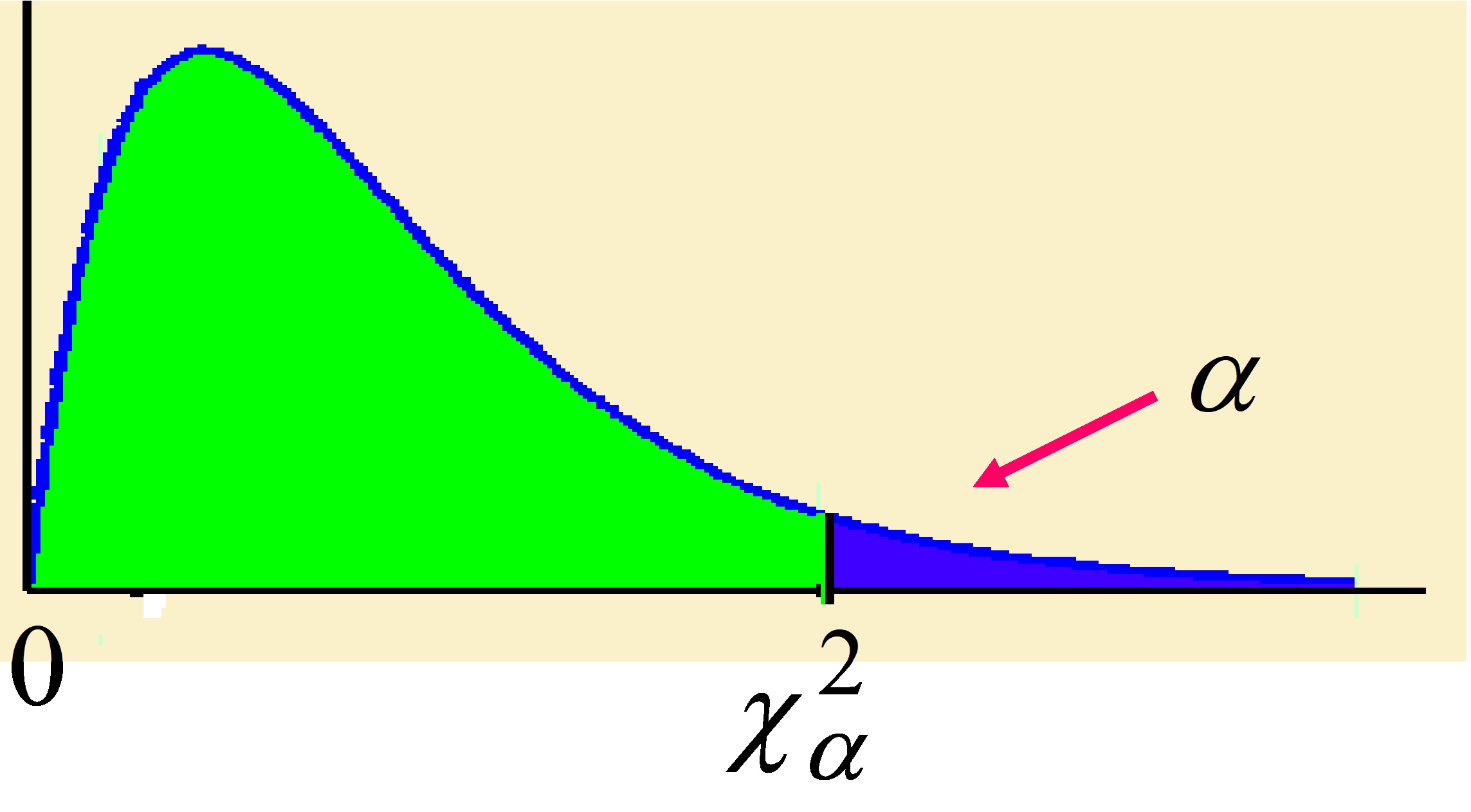
Figura 7.13

 \( P [ \chi_{n}^{2} > \chi_{\alpha; n}^{2}] = \displaystyle \int_{\chi_{\alpha;n}^{2}}^{\infty}\displaystyle \frac{1}{2^{n/2} \Gamma ( \frac{n}{2})}e^{-x/2}x^{(n/2)-1} dx \)

Para valores grandes de n, la distribución \(  \chi^{2} \) se aproxima a la distribución Normal. La aproximación se considera aceptable para n>30, para este valor existen diversas aproximaciones:

• Para  \( 30<n \leq 200 \hspace{.3cm}; \hspace{.3cm} \displaystyle \sqrt {2 \chi_{n}^{2}} \rightarrow N( \sqrt{2n-1}, 1) \)
• Para \(  n>200  \hspace{.3cm}; \hspace{.3cm} \chi_{n}^{2} \rightarrow N(n, \sqrt{2n}) \)

Teorema de adición

Si  \( X_1  \) y  \( X_2  \) son dos variables aleatorias independientes y cada una tiene una distribución chi-cuadrado con  \( n_1  \) y  \( n_2  \) grados de libertad respectivamente, entonces  \( X_1+X_2  \) también tiene una distribución chi-cuadrado con n₁+n₂ grados de libertad.
Este resultado se puede generalizar al caso de n variables aleatorias independientes.

Ejemplo 7.5. Dada una variable aleatoria que se distribuye según una χ² de Pearson. Se pide calcular:

a) Los puntos críticos: \( \chi_{0.9;5}^{2}\hspace{.3cm}; \hspace{.3cm} \chi_{0.01;26}^{2}\hspace{.3cm}; \hspace{.3cm} \chi_{0.025;8}^{2}\hspace{.3cm}; \hspace{.3cm}\chi_{0.08;10}^{2}\hspace{.3cm}; \hspace{.3cm} \chi_{0.01;61}^{2} \)

b) Las probabilidades: \( P[\chi_{8}^{2} \geq 3.49] \hspace{.3cm}; \hspace{.3cm} P[\chi_{8}^{2} \leq 15.51] \hspace{.3cm}; \hspace{.3cm} P[\chi_{10}^{2} \geq 4] \hspace{.3cm}; \hspace{.3cm} P[\chi_{20}^{2} \leq 29]  \)

Respuesta:.

a) \( \chi_{0.9;5}^{2}=1.61 \hspace{.3cm}; \hspace{.3cm} \chi_{0.01;26}^{2}=45.6 \hspace{.3cm}; \hspace{.3cm} \chi_{0.025;8}^{2}=17.5 \)

\( \chi_{0.08;10}^{2} =16.92 \left \{  \begin{array}{ll}  & 0.10 \rightarrow  16 \\ & 0.08 \rightarrow x \\ & 0.05  \rightarrow 18.3 \\  \end{array} \right \} \Rightarrow  \) \( \left. \begin{array} \\  0.05 \rightarrow -2.3 \\  0.03 \rightarrow  x-18.3 \\  \end{array} \right \} \Rightarrow  x=16.92 \)

\( \chi_{0.01;61}^{2}\): Al ser n=61 la distribución \( \chi_{0.01;61}^{2}\) se puede aproximar mediante una distribución Normal de la siguiente forma:

\( \displaystyle \sqrt {2 \chi_{n}^{2}} \sim N( \sqrt{2n-1}, 1) \Rightarrow \displaystyle \sqrt {2 \chi_{n}^{2}}  – \displaystyle \sqrt {2 n-1} \rightarrow N(0, 1) \)

\(  P[Z>z_1]=0.01 \Rightarrow z_1=2.33 \)

\(  Z= \displaystyle \sqrt {2 \chi_{0.01;61}^{2}} –  \displaystyle \sqrt {2×61-1}=2.33 \Rightarrow χ_{0.01;61}^{2}=88.844 \)

b) \( P[ \chi_{8}^{2} \geq 3.49]=0.9\hspace{.3cm}; \hspace{.3cm} P[\chi_{8}^{2} \leq 15.51]=1-0.05=0.95 \)

\( P[ \chi_{10}^{2} \geq 4]=0.946; \left \{  \begin{array} {ll} & 3.94 \rightarrow  0.95 \\ &  4 \rightarrow x \\ & 4.87 \rightarrow 0.90 \\ \end{array} \right \} \Rightarrow  \) \( \left. \begin{array} \\  0.93 \rightarrow -0.05 \\ 0.87 \rightarrow 0.90-x \\  \end{array} \right \} \Rightarrow x=0.946 \)

\( P[ \chi_{20}^{2} \leq 29]=1-0.09 = 0.91; \left \{  \begin{array} {ll} & 28.4 \rightarrow 0.1 \\ & 29 \rightarrow x \\ & 31.4 \rightarrow 0.05 \\ \end{array} \right \} \Rightarrow  \) \( \left. \begin{array} \\  3 \rightarrow -0.05 \\ 2.4 \rightarrow 0.05-x \\  \end{array} \right \} \Rightarrow x=0.09 \)

Distribución t de Student

La distribución t de Student fue descubierta por William Sealey Gosset que utilizaba el seudónimo de “A Student” (Un Estudiante).

A William Sealey Gosset le interesaba estudiar la relación existente entre la calidad de ciertas materias primas que intervienen en la fabricación de la cerveza, como la cebada y la calidad del producto final, pero sólo disponía de muestras pequeñas. El tamaño de las muestras fue lo que “obligó” a Gosset a descubrir la distribución que se conoce con el nombre de distribución t-Student.

Nota: La teoría estadística que se estudiaba era teoría asintótica y, en consecuencia, válida únicamente para muestras de tamaño grande.

Comentario: William Sealey Gosset utilizaba el seudónimo de “A Student” (Un estudiante) cuando trabajaba en la empresa cervecera Guiness en Dublin, debido a que dicha empresa no permitía que sus empleados divulgaran los procesos utilizados en la fábrica. Gosset desarrolló la prueba t para manejar muestras pequeñas para control de calidad en la elaboración de cerveza. Por tanto, su logro más famoso se conoce ahora como la distribución t de Student, que de otra manera hubiera sido la distribución t de Gosset.

Gosset obtuvo la ley t-Student con n grados de libertad como distribución del siguiente estadístico:

\( t_{n}= \displaystyle \frac{Z}{ \sqrt{Y/n}} \)

donde:

∗) Z y Y son dos variables aleatorias independientes

∗) \( Z \rightarrow N(0, 1) \)

∗) \( Y \rightarrow  \chi_{n}^{2} \)

Es decir, \( t_{n}\) se define como el cociente entre dos variables aleatorias independientes, una variable normal estándar, N(0, 1), y la raíz cuadrada de una variable chi-cuadrado dividida por sus grados de libertad.

Función de densidad

La función de densidad de la distribución t-Student depende del parámetro n y tiene la siguiente expresión:

 \( f(t_{n})= \displaystyle \frac{1}{\sqrt{n \pi}} \displaystyle \frac{ \Gamma \left ( \displaystyle \frac{n+1}{2}\right )}{ \Gamma \left ( \displaystyle \frac{n}{2}\right )} \displaystyle \frac{1}{ \left( 1+ \displaystyle \frac{t^{2}}{n} \right )^{\displaystyle \frac{n+1}{2}}} \hspace{.3cm} ; \hspace {.3cm} para -\infty <t< \infty \hspace{.5cm} y \hspace{.5cm} n>0  \)

Características generales

• Las variables aleatorias T se identifican cada una por un parámetro, n o (υ), llamado grados de libertad. Este parámetro es siempre un entero positivo. El número de grados de libertad es el número de variables aleatorias independientes que intervienen en la distribución, por lo que hay un número infinito de variables aleatorias T identificadas cada una por los grados de libertad (n).
• Cada variable aleatoria T es una variable aleatoria continua.
• La  gráfica de la función de densidad de la distribución T es una curva simétrica respecto del eje de ordenadas con forma de campana centrada en cero.
  ∗ El campo de variabilidad es  \( (- \infty , + \infty)  \)
  ∗ La Media coincide con la Moda y con la Mediana en la abcisa x=0
  ∗ Depende del parámetro n, por lo que no hay una curva única, como sucede con la distribución Normal tipificada. (La figura 7.14 muestra algunas densidades de la distribución t-Student).

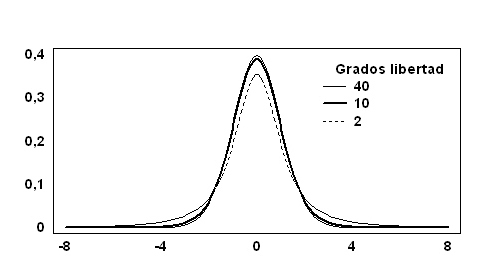Figura 7.14

• La curva de densidad de la t-Student tiene las colas más extensas que la distribución Normal. (La Figura 7.15 muestra las curvas de densidad de las distribuciones t-Student y N(0, 1)).
• Tiene una asíntota horizontal en el eje de abcisas
• El parámetro n de la distribución t-Student es un parámetro de forma en el sentido de que cuando n crece, la varianza de la v.a. T decrece. Por lo tanto, cuanto más grande es el número de grados de libertad, más apuntamiento presenta la curva. Cuando  \( n→ \infty \) (en la práctica cuando n>30), la función de densidad se puede aproximar mediante la distribución Normal tipificada.

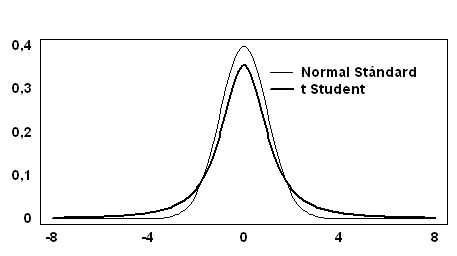
Figura 7.15

La distribución t-Student se encuentra parcialmente tabulada en la Tabla V del Apéndice B. En esta tabla se muestran los valores de las abcisas \( t_{\alpha; \nu}  \) (también se denotan por \( t_{\alpha} \) ) para los distintos valores de α y ν, la lectura se realiza como en la tabla de la distribución \( \chi^{2} \) . Los valores de dicha tabla representan:

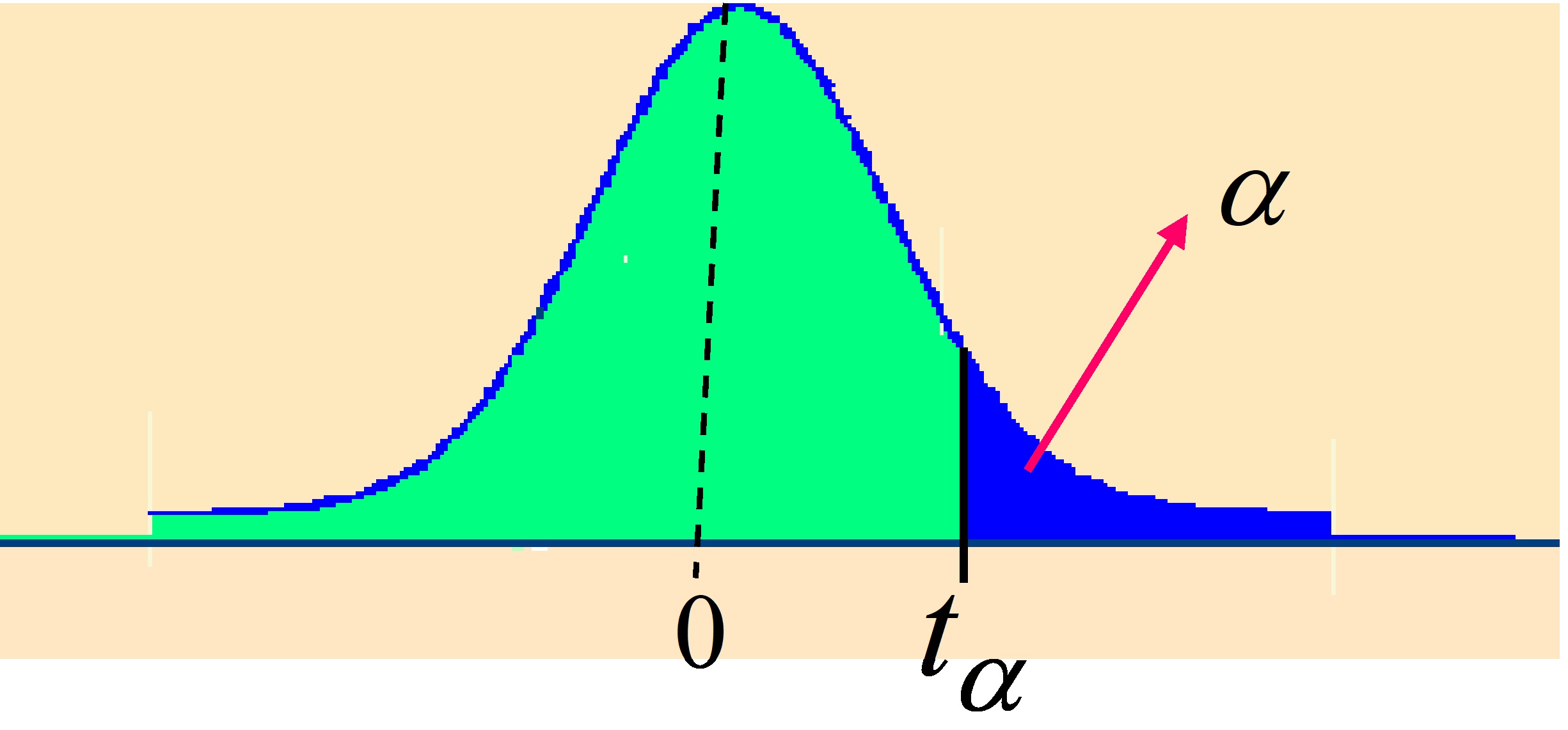
Figura 7.16

 \( P[t_{n} \geq t_{ \alpha; n}]= \alpha \hspace{.5cm} o  \hspace{.5cm} P[t \geq t_{\alpha}]=\alpha  \)

Se cumplen las siguientes relaciones:

 \( P[t \leq -t_{\alpha}]=P[t \geq t_{\alpha}]=\alpha  \)

 \( P[t \geq -t_{\alpha}]=1-P[t \leq -t_{\alpha}]=1-\alpha  \)

 \( t_{\alpha ; n}=-t_{1-\alpha;n}  \)

Ejemplo 7.6. Dada una variable aleatoria que sigue una distribución t de Student. Se pide calcular:

a) Los puntos críticos:  \( t_{0.25;10} \hspace{.3cm}; \hspace{.3cm} t_{0.99;10}\hspace{.3cm}; \hspace{.3cm} t_{0.2;20}  \)
b) Las probabilidades:  \( P[t_{10} \geq 1.372] \hspace{.3cm}; \hspace{.3cm} P[t_8 \leq 1.2] \hspace{.3cm}; \hspace{.3cm} P[-0.5 \leq t_6 \leq 0.6] \hspace{.3cm}; \hspace{.3cm} P[∣t_{24}∣>2]  \)

Respuesta:

a)  \( t_{0.25;10}=0.7 \hspace{.3cm}; \hspace{.3cm} t_{0.99;10}=-t_{0.01;10}=-2.764  \)

\( t_{0.2;20}=0.899;  \left \{  \begin{array} {ll} & 0.687 \rightarrow 0.25 \\ & x \rightarrow 0.20 \\ & 1.325 \rightarrow 0.10 \\ \end{array} \right \} \Rightarrow  \) \( \left. \begin{array} \\  0.638 \rightarrow -0.15 \\  x-1.325 \rightarrow 0.1 \\  \end{array} \right \} \Rightarrow x=0.899 \)

b) \( P[_{10} \geq 1.372]=0.1 \)

\( P[t_8 \leq 1.2]=1-0.1427=0.8573  \left \{  \begin{array} {ll} & 0.706 \rightarrow 0.25   \\ & 1.2 \rightarrow x   \\ & 1.397  \rightarrow 0.10 \\ \end{array} \right \} \Rightarrow    x=0.1427    \)

 

  \(  P[-0.5≤ t_6≤0.6]=1-P[t_6 ≥0.5]-P[t_6 ≥0.6]=1-0.322-0.289=0.389 \)

\(  \left \{  \begin{array} {ll} & 0.265 \rightarrow 0.4 \\ &  0.5 \rightarrow x \\ & 0.718 \rightarrow 0.25 \\ \end{array} \right \} \Rightarrow    x=0.322 \hspace{.3cm}; \hspace{.3cm}  \)  \(  \left \{  \begin{array} {ll} & 0.265 \rightarrow 0.4 \\ & 0.6 \rightarrow x \\ & 0.718 \rightarrow 0.25 \\ \end{array} \right \}  \Rightarrow x=0.289 \)

\( P[∣t_{24}∣>2]=2P[t_{24}>2]=0.029; \left \{  \begin{array} {ll} & 1.711 \rightarrow 0.05 \\ & 2 \rightarrow x \\ & 2.064 \rightarrow 0.025 \\ \end{array} \right \} \Rightarrow x=0.029 \)

Ejemplo 7.7. La probabilidad de que una t con 12 grados de libertad esté comprendida entre dos valores simétricos respecto del origen es igual a 0.80. ¿Cuánto vale la abcisa del extremo positivo?

Respuesta:

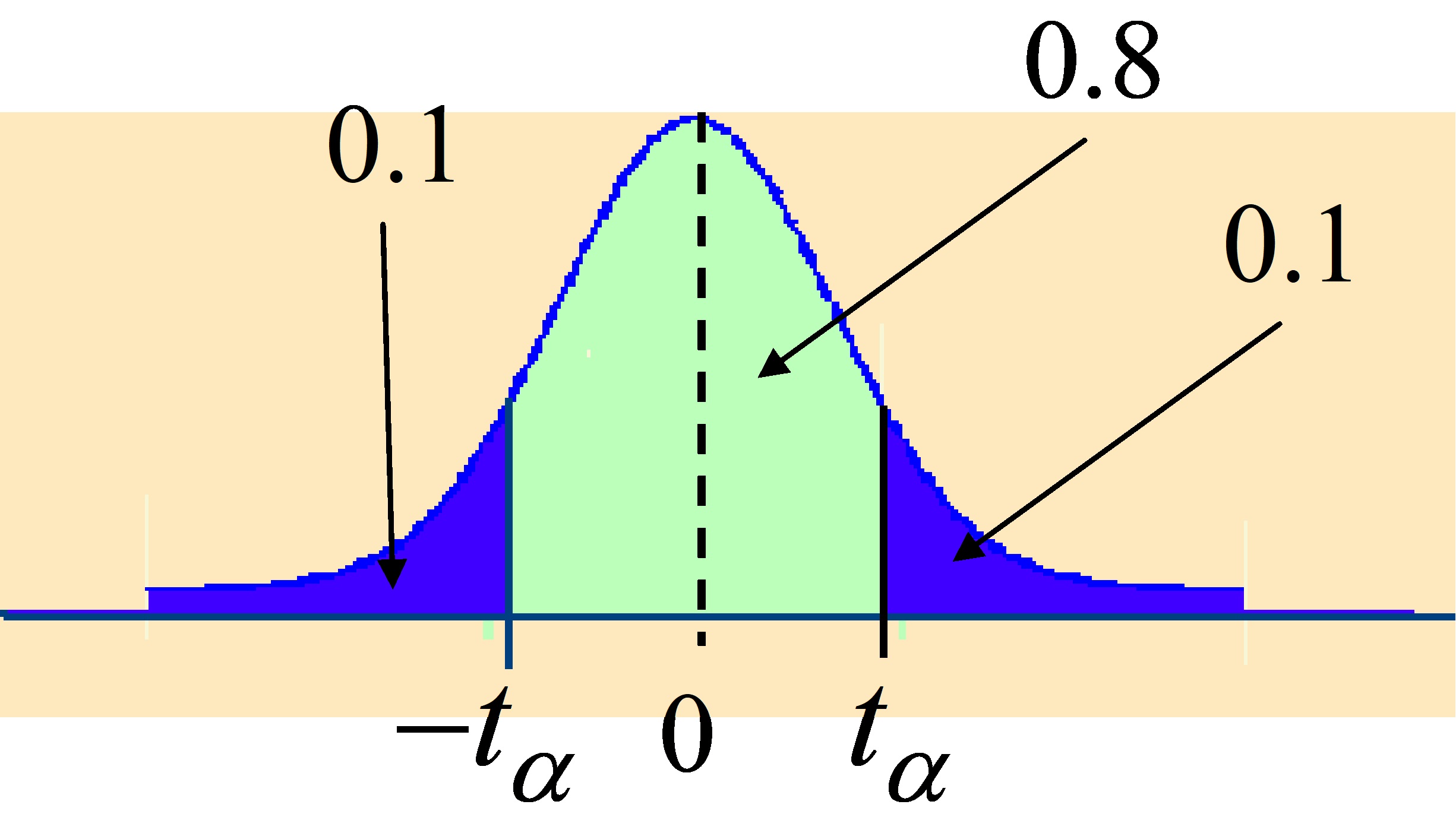
Figura 7.17

\(  P[t_{12} ≥t_{\alpha}]=0.1 \hspace{.3cm }; \hspace{.3cm} t_{0.1;12}=1.356 \)

Distribución F de Snedecor

Se define la variable aleatoria F-Snedecor como el cociente:

\(  F= \displaystyle \frac{X_1/n_1}{X_2/n_2} \)

donde

∗) X₁ y X₂ son dos variables aleatorias independientes entre sí

∗) \( X_1 \rightarrow \chi_{n_1}^{2} \)  y \(  X_2  \rightarrow  \chi_{n_2}^{2} \)

Entonces F se distribuye  según una F-Snedecor con n₁ y n₂ grados de libertad y se denota \( F \rightarrow F_{n_1,n_2} \)

Es decir, la variable aleatoria F es el cociente de dos variables aleatorias chi-cuadradas independientes, cada una dividida por sus grados de libertad.

Función de densidad

La función de densidad de la distribución F-Snedecor depende de los parámetros \( n_1 \) y \( n_2 \) y tiene la siguiente expresión:

\( f(F_{n_1,n_2})=  \displaystyle \frac{ \Gamma \left ( \displaystyle \frac{n_1+n_2}{2} \right ) \left ( \displaystyle \frac{n_1}{n_2} \right )^ { \displaystyle \frac{n_1}{2}} } { \Gamma \left ( \displaystyle \frac{n_1}{2} \right )  \Gamma \left ( \displaystyle \frac{n_2}{2} \right ) }    \displaystyle \frac{   x^{ \displaystyle \frac{n_1}{2}-1 }} { \left ( 1 + \displaystyle \frac{n_1}{n_2}x \right ) ^{ \displaystyle \frac{n_1 +n_2}{2}}  } \)

Características generales

• Las variables aleatorias F se identifican cada una por dos parámetros, \( n_1 \) y \( n_2 \), llamados grados de libertad. Estos parámetros son siempre enteros positivos: n₁ está asociado con la v.a. \( \chi^{2} \) del numerador de la v.a. F y \(  n_{2 } \) está asociado con la v.a. \( \chi^{2} \) del denominador
• Hay un número infinito de variables aleatorias F identificadas cada una por los grados de libertad (\( n_1 \) y \( n_2 \))
• Cada variable aleatoria F es una variable aleatoria continua
• La función de densidad de la distribución F depende del número de grados de libertad. La gráfica de dicha función para cada variable aleatoria F es:
  • Una curva asimétrica positiva que presenta la forma que aparece en la Figura 7.18 correspondiente a \( n_1=n_2=10 \hspace{.2cm} ;  \hspace{.2cm} n_1=25 \hspace{.2cm},  \hspace{.2cm} n_2=30 \hspace{.2cm};  \hspace{.2cm} n_1=35 \hspace{.2cm},  \hspace{.2cm} n_2=40  \hspace{.2cm} ;  \hspace{.2cm} n_1=45 \hspace{.2cm},  \hspace{.2cm} n_2=50 \) grados de libertad. La asimetría de la curva va disminuyendo conforme  \( n_1   \) y  \( n_2  \) toman valores cada vez más grandes
  • El campo de variabilidad es \(  (0, + \infty) \)
  • Las variables F no pueden tomar valores negativos
  • Depende de los parámetros \( n_1 \) y \(  n_2 \) por lo que no hay una curva única, como sucede con la distribución Normal tipificada.

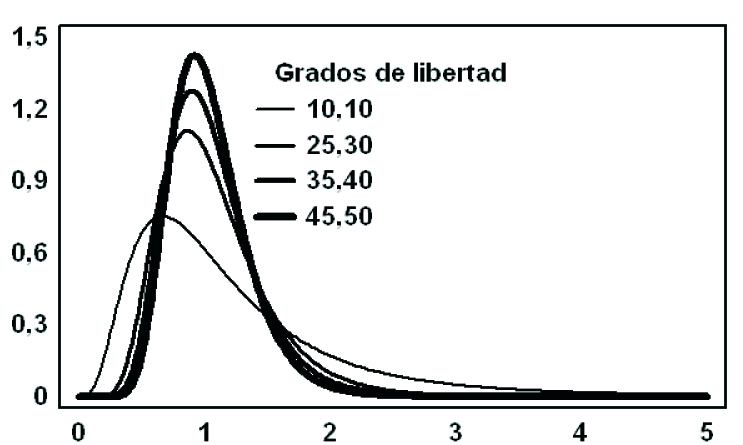
Figura 7.18

En la Tabla VI del Apéndice B están tabulados los valores \( F_{\alpha ;n_1,n_2} \)  para algunos valores de α. Siendo \(   F_{\alpha;n_1,n_2} \)  el valor crítico de la distribución F-Snedecor, con \(   n_1 \)  y \(  n_2 \)  grados de libertad, que deja un área de valor α a su derecha.

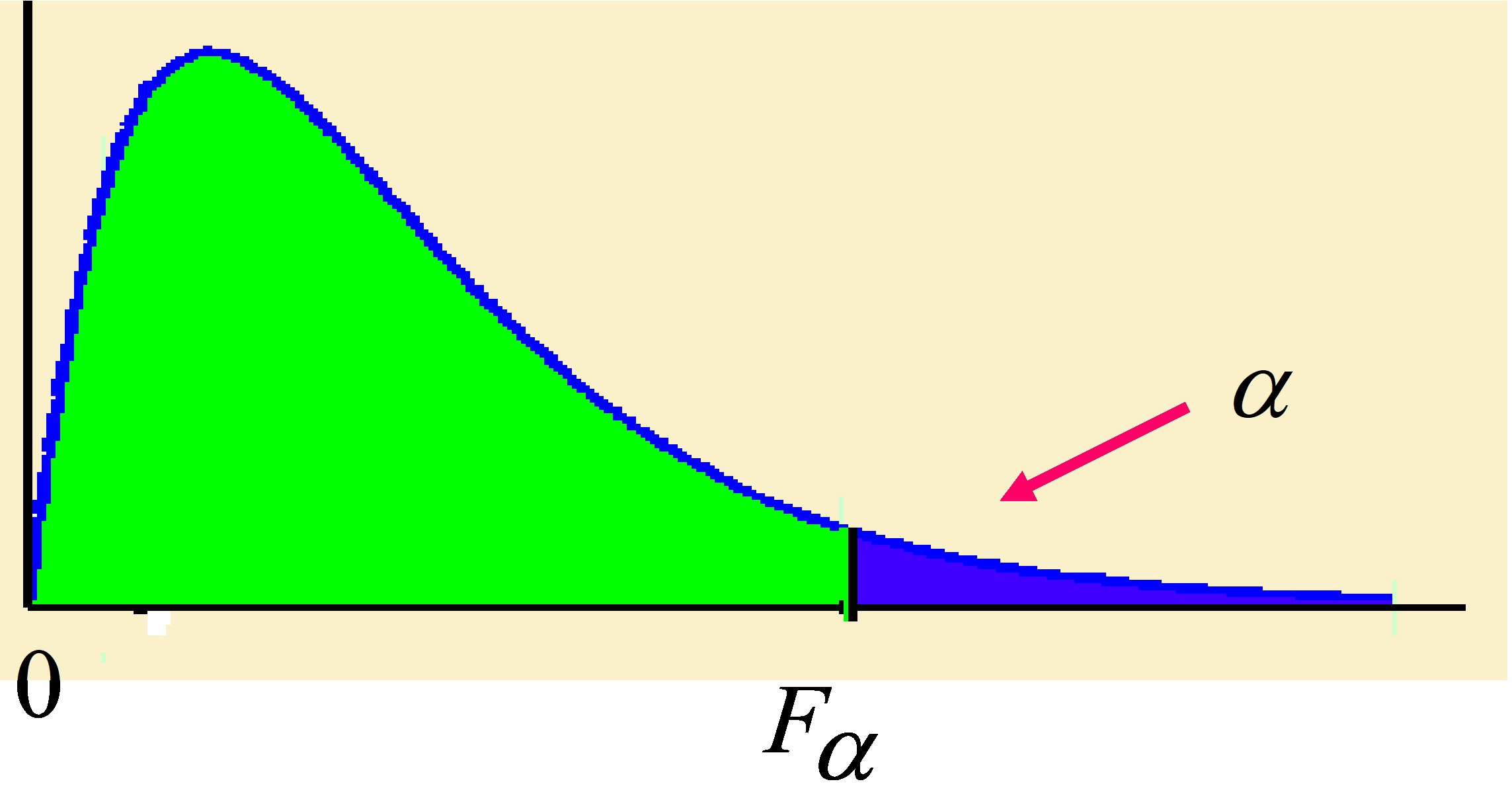
Figura 7.19

∗) \( P[F_{n_1,n_2}≥F_{ \alpha ;n_1,n_2}]= \alpha \) ó \( P[F≥F_{\alpha }]=\alpha \)

∗) Las tablas contienen valores de \( F_{\alpha;n_1,n_2} \) para  \( \alpha <0.5 \)

∗) Si  \( \alpha >0.5 \) se busca en las tablas \( F_{1-\alpha;n_2,n_1} \)

verificándose que:

\( F_{\alpha ;n_1,n_2}=  \displaystyle \frac{1}{F_{1-\alpha;n_2,n_1}} \)

Ejemplo 7.8. Dada una variable aleatoria que sigue la distribución F de Fisher-Snedecor. Se pide:

a) Los puntos críticos: \( F_{0.1;10,12} \hspace{.2cm}; \hspace{.2cm} F_{0.05;5,24}  \hspace{.2cm}; \hspace{.2cm} F_{0.9;28,30} \)

b) La probabilidad: \( P[2≤F_{10;20}≤2.25] \)

Respuesta:

a) \( F_{0.1;10,12}=2.19  \hspace{.2cm}; \hspace{.2cm}  F_{0.05;5,24}=2.62 \)

\( F_{0.9;28,30}=  \displaystyle \frac{1}{F_{1-\alpha;n_2,n_1}} =  \displaystyle \frac{1} {F_{0.1;30,28}}= \displaystyle \frac{1}{1.63}=0.613 \)

b) \( P[2≤F_{10;20}≤2.25]=P[F_{10;20}≥2]-P[F_{10;20}≥2.25]=0.092-0.062=0.03 \)

\(  \left \{  \begin{array} {ll} & 1.94 \rightarrow 0.1 \\ &  2 \rightarrow x \\ & 2.35 \rightarrow 0.05  \\ \end{array} \right \} \Rightarrow    x=0.092 \hspace{.3cm}; \hspace{.3cm}  \)  \(  \left \{  \begin{array} {ll} & 1.94 \rightarrow 0.1 \\ & 2.25 \rightarrow x\\ & 2.35 \rightarrow 0.05  \\ \end{array} \right \}  \Rightarrow x=0.062 \)

Ejercicios propuestos: Relación VII

1. Sea X una v.a. que representa la inteligencia medida por medio de pruebas CI. Si  X se distribuye según una N(100,10), obtener las probabilidades de que X sea:

a) mayor que 100

b) menor que 85

c) a lo más 112

d) por lo menos 108

e) más grande que 90;

f) entre 95 y 120.

(Soluciones: a) 0.5; b)  0.0668; c) 0.8849; d) 0.2119; e) 0.8413; f) 0.6687)

2. Determinar los extremos del intervalo simétrico respecto a la media que contiene al:

a) 50% de las observaciones de la dist. N(μ,σ)

b) 95% de las observaciones de la dist. N(μ,σ)?

(Soluciones: a) [μ-0.68σ, μ+0.68σ]; b) [μ-1.96σ, μ+1.96σ])

3. Suponiendo que las variables que se dan a continuación son normales con media y varianza indicadas en cada apartado, calcular:

a) P(-2<Z<-1), si  Z→N(0,1)

b) P(∣z∣>2), si  Z → N(0,1)

c) P(∣z∣<2.5), si Z→ N(0,1)

d) P(1.5<X<3.5), si  X→ (2,1)

e) P(∣X-3∣>2), si X→ N(3,2)

f) P(∣X-5∣<2.8), si X→ N(5,1)

g) P(X<-4), si X→ N(2,3)

h) P(X²>1.21), si X → N(2,3)

(Soluciones: a) 0.1359; b) 0.0456; c) 0.9876; d) 0.6247; e) 0.3174; f) 0.9948; g) 0.0228; h) 0.7694).

4. En unos estudios realizados a un determinado tipo de aves rapaces. Se comprueba que la longitud de las alas extendidas, X, es una variable aleatoria que se distribuye aproximadamente según una curva normal, de media 110 cm. y desviación típica 4 cm.

a) Calcular la probabilidad de que la longitud de las alas de un ave elegida al azar sea: a1) Mayor de 105 cm; a2) Menor de 100 cm; a3) Esté comprendido entre 110 y 115 cm;

b) Encontrar un punto x₀ tal que el 15 % de las aves tengan una longitud de alas superior a él.

(Soluciones: a1) 0.8994; a2) 0.00621; a3) 0.3944; b)114.16)

5. En unos laboratorios se realizan unos estudios sobre la concentración de NH3 en sangre. Por estudios anteriores, se sabe que la concentración media de NH3 en sangre venosa de individuos sanos es de 110 mgr/mm y que la concentración de NH3 del 99% de los individuos se encuentra entre 85 y 135 mgr/mm. (La concentración de NH3 en sangre tiene una distribución aproximadamente normal). Calcular:

a) La desviación típica de la distribución

b) Si un individuo tiene concentración de 115 mgr/mm, ¿a qué porcentaje de la población es superior este individuo?

c) Los límites del intervalo, simétrico respecto a la media, que contiene el 70% de los valores de dicha población

d) Si un individuo tiene concentración de 100 mgr/mm, ¿a qué porcentaje de la población es inferior este individuo

e) Si un individuo tiene concentración de 125 mgr/mm. ¿A qué porcentaje de la población es superior este individuo?

(Soluciones: a) 9.708; b) 69.5%; c) [100, 120]; d) 84.85%; e) 93.8%)

6. Se observó que el número de glóbulos rojos (en millones por microlitro) de un grupo de individuos sigue una distribución normal de media 4,5 y desviación típica 0,5. Se pide:

a) Probabilidad de que una persona elegida al azar tenga entre 4,25 y 4,75 millones de glóbulos rojos por microlitro

b) Si se desea estudiar los hábitos alimenticios del 20% de personas con mayor número de glóbulos rojos, ¿cuál es el número mínimo de glóbulos rojos de dichas personas?

(Soluciones: a) 0.383; b) 4.92)

7. En un laboratorio se está estudiando el crecimiento de cierto cultivo, se supone que la aparición de nuevas células sigue una ley de Poisson de media 16 células cada minuto. Obtener:

a) La probabilidad de que en un minuto aparezcan al menos 10 células

b) La probabilidad de que aparezcan entre 10 y 20

c) El número mínimo de células nuevas en un minuto con una probabilidad de 0.95.

(Soluciones: a) 0.9332; b) 0.7795; c) 9.4)

8. Si se clasifican los cráneos en “dodicacéfalos” cuando el índice longitud-anchura es menor que 75, “mesocéfalos” si está entre 75 y 80, y “branquicéfalos” si es superior a 80. Hallar la media y la desviación típica de una serie en la que el 65% son dodicacéfalos, el 34% mesocéfalos y el 1% branquicéfalos. Suponiendo que la distribución es normal. (Soluciones μ=73.99; σ=2.6)

9. La probabilidad de que un individuo reaccione favorablemente a un tratamiento es de 0.5. Si dicho tratamiento se prueba en 100 individuos. Hallar:

a) La probabilidad de que a lo sumo 40 individuos reaccionen favorablemente al tratamiento

b) El número máximo de individuos que reaccionan favorablemente al tratamiento con una probabilidad de 0.8

10. La media de ganancias obtenidas por las industrias cerveceras de una determinada región fue durante un año igual a 500 unidades monetarias, y la desviación típica 100. Si las ganancias obedecen aproximadamente a una distribución normal. Se pide:

a) Calcular el % de industrias cuyas ganancias están comprendidas entre 400 y 600 unidades monetarias

b) Probabilidad de que en una industria elegida al azar, su ganancia difiera de la media menos de 150 u.m.

(Soluciones: a) 68.26%; b) 0.8664)

11. El tiempo necesario para reparar la transmisión de un automóvil en un taller se distribuye según una normal con media 45 m. y desviación típica 8 m. El mecánico planea comenzar la reparación del auto de un cliente 10 minutos después de que el vehículo sea entregado y le comunica al cliente que el auto estará listo en una hora en total. Se pide:

a) ¿Cuál es la probabilidad de que el mecánico esté equivocado?

b) ¿Cuál es el tiempo requerido de trabajo para que haya un 90% de posibilidades de que la reparación se termine dentro de ese tiempo?

(Soluciones: a) 0.0307; b) 55.25)

12. La media de las calificaciones obtenidas en un test de aptitud por los alumnos de un centro fue 400 y la desviación típica 100. Si las calificaciones siguen un distribución normal, calcular la proporción de alumnos que obtuvieron una calificación:

a) Superior a 500 puntos

b) Inferior a 300

c) Comprendida entre 300 y 500 puntos

d) Determinar la probabilidad de que la calificación, de un alumno elegido al azar, difiera de la media en menos de 150 puntos.

(Soluciones: a) 15.87%; b) 15.87%; c) 68.26%; d) 8664)

13. En una industria el proceso de elaboración del producto se compone de 3 fases. Los tiempos de duración de cada fase son v.a. independientes distribuidas según:

Fase 1:    N(μ₁=5; σ₁=0.5)
Fase 2:    N(μ₂=3; σ₂=0.5)
Fase 3:    N(μ₃=2; σ₃=0.7)

Se pide:

a) ¿A qué distribución obedece el tiempo total de fabricación?

b) ¿Cuál es la probabilidad de que el tiempo total de fabricación no sea superior a 9.8?

c) ¿Cómo se distribuye el tiempo medio de duración de una fase?

(Soluciones: a) N(10; 0.99); b) 0.420; c) N(10/3; 0.3316))

14. La concentración en plomo en partes por millón en la corriente sanguinea de un individuo tiene una media de 0.25 y una desviación tipica de 0.11. Supongamos que dicha concentración sigue una ley Normal. Se pide:

a) Una concentración superior o igual a 0.6 partes por millón se considera extremadamente alta. ¿Cuál es la probabilidad de que un individuo seleccionado aleatoriamente esté incluido en esta categoría?

b) ¿Cuál es la concentración mínima del 30% de los individuos con mas concentración?

c) Determinar la mediana de esta distribución.

(Soluciones: a) 0.00074; b) 0.30775; c) 0.25)

15. La cantidad de radiación que puede ser absorbida por un individuo antes de que le sobrevenga la muerte tiene una media de 500 roentgen y una desviación tipica de 150 roentgen. Supongamos que la distribución de la cantidad de radición sigue una ley Normal. Se pide:

a) ¿Por encima de que nivel de dosificación sobreviviría solamente el 5% de los expuestos?

b) ¿Cuál es el porcentaje de supervivientes para un nivel de radiación de 800 roentgen?

c) Obtener los cuartiles de esta distribución.

(Soluciones: a) 746.75; b) 2.28%; c) 398.75; 500: 601.25)

16. En un laboratorio se está estudiando el crecimiento de cierto cultivo, se supone que la aparición de nuevas células sigue una ley de Poisson de media 16 células cada minuto. Obtener:

a) La probabilidad de que en un minuto aparezcan al menos 10 células

b) La probabilidad de que aparezcan entre 10 y 20

c) El número mínimo de células nuevas en un minuto con una probabilidad de 0.95.

(Soluciones: a) 0.9332; b) 0.7795; c) 9.4)

Autora: Ana María Lara Porras. Universidad de Granada

Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.