DISEÑO ESTADÍSTICO DE EXPERIMENTOS
Objetivos
- Identificar un diseño unifactorial de efectos fijos.
- Plantear y resolver el contraste sobre las medias de los tratamientos.
- Saber aplicar los procedimientos de comparaciones múltiples.
- Identificar un diseño unifactorial de efectos aleatorios.
- Estimar los componentes de la varianza.
- Identificar un diseño en bloque completo aleatorizado con efectos fijos.
- Identificar un diseño en bloque incompleto aleatorizado con efectos fijos.
- Identificar un diseño en bloque incompleto balanceado (BIB).
- Identificar un diseño en cuadrados latinos.
- Identificar un diseño en cuadrados greco-latinos.
- Identificar un diseño en cuadrados de Jouden.
- Plantear y resolver los contrastes de igualdad de tratamientos y de igualdad de bloques.
- Identificar un diseño bifactorial de efectos fijos y estudiar las interacciones entre los factores.
- Identificar un diseño trifactorial de efectos fijos y estudiar las interacciones entre los factores
- Estudiar la influencia de los factores.
- Analizar en qué sentido se producen las interacciones mediante el gráfico de medias.
- Aplicar los procedimientos de comparaciones múltiples: Obtener conclusiones sobre el experimento planteado y las interacciones.
- Analizar la idoneidad de los modelos planteados.
Introducción al Diseño Estadístico de Experimentos
En la práctica 6 hemos descrito métodos de inferencias sobre la media y la varianza de una población y de dos poblaciones. En esta práctica 7 ampliamos dichos métodos a más de dos poblaciones e introducimos algunos aspectos elementales del Diseño Estadístico de Experimentos y del Análisis de la Varianza.
El diseño estadístico de experimentos incluye un conjunto de técnicas de análisis y un método de construcción de modelos estadísticos que, conjuntamente, permiten llevar a cabo el proceso completo de planificar un experimento para obtener datos apropiados, que puedan ser analizados con métodos estadísticos, con objeto de obtener conclusiones válidas y objetivas.
El análisis de la varianza o abreviadamente ANOVA (del inglés analysis of variance) es un procedimiento estadístico que permite dividir la variabilidad observada en componentes independientes que pueden atribuirse a diferentes causas de interés. Es una técnica estadística para comparar más de dos grupos, es decir un método para comparar más de dos tratamientos y la variable de estudio o variable respuesta es numérica.
En esta práctica presentamos el Diseño Completamente Aleatorio con efectos fijos y con efectos aleatorios, el Diseño en Bloques Completos Aleatorizados, Diseño en Bloques Incompletos Balanceados (BIB), el Diseño en Cuadrados Latinos, el Diseño en Cuadrados Greco-Latinos, el Diseño en Cuadrados de Jouden, el Diseño Bifactorial de efectos fijos y el Diseño Trifactorial de efectos fijos.
Diseño Completamente Aleatorio con efectos fijos (Diseño unifactorial de efectos fijos)
El primer diseño que presentamos es el diseño completamente aleatorio de efectos fijos y la técnica estadística es el análisis de la varianza de una vía o un factor. La descripción del diseño así como la terminología subyacente la vamos a introducir mediante el siguiente supuesto práctico.
Supuesto práctico 1
Un fabricante de calzado desea mejorar la calidad de las suelas, las cuales se pueden hacer con uno de los cuatro tipos de cuero A, B, C, y D disponibles en el mercado. Para hacer ello, prueba los cueros con una máquina que hace pasar los zapatos por una superficie abrasiva; la suela de los zapatos se desgasta al pasarla por dicha superficie. Como criterio de desgaste se usa la pérdida de peso después de un número fijo de ciclos. Se prueban en orden aleatorio 24 zapatos, seis de cada tipo de cuero.
\( \begin{array} {|c|cccccc|} \hline \text { Tipo de cuero} & & & \text{Pérdida de peso} & & \\ \hline A & 264 & 260 & 258 & 241 & 262 & 255 \\ \hline B & 208 & 220 & 216 & 200 & 213 & 206 \\ \hline C & 220 & 263 & 219 & 225 & 230 & 228 \\ \hline D & 217 & 226 & 215 & 224 & 220 & 222 \\ \hline \end{array} \)
Figura1: Tabla de datos del Supuesto Práctico 1
En el ejemplo disponemos de una colección de 24 unidades experimentales y queremos estudiar el efecto de cinco tipos de cuero en la pérdida de peso de la suela del zapato. Es decir, estamos interesados en contrastar el efecto de un solo factor (tipo de cuero), que se presenta con cinco niveles, sobre la variable respuesta (pérdida de peso de la suela del zapato).
Por lo que nos interesa saber si las medias de las pérdidas de peso son iguales en los cinco tipos de cuero, para ello realizamos el siguiente contraste de hipótesis:
\( \begin{array}{c} H_0 \equiv \mu_1 = \mu_2 = \cdots = \mu_5 ~~~ vs ~~~ H_1 \equiv \mu_i \neq \mu_j \hspace{.2cm} \text {para algún } i\neq j \end{array} \)
Expresión 1: Contraste de hipótesis
Es decir, contrastamos que no hay diferencia en las medias de los cinco tratamientos frente a la alternativa de que al menos una media difiere de otra.
En este modelo, que estudia el efecto que produce un solo factor en la variable respuesta, la asignación de las unidades experimentales a los distintos niveles del factor se debe realizar de forma completamente al azar. Este modelo, junto con este procedimiento de asignación, recibe el nombre de Diseño Completamente Aleatorizado y está basado en el modelo estadístico de Análisis de la Varianza de un Factor o una Vía. Esta técnica estadística, Análisis de la Varianza de un factor, se utiliza cuando se tienen que comparar más de dos grupos y la variable respuesta es una variable numérica. Para aplicar este diseño adecuadamente las unidades experimentales deben ser lo más homogéneas posible.
Todo este planteamiento se puede formalizar de manera general para cualquier experimento unifactorial. Supongamos un factor con niveles y para el nivel i-ésimo se obtienen observaciones de la variable respuesta. Entonces podemos postular el siguiente modelo:
\( y_{ij}=\mu+\tau_i+u_{ij},~~~~ i=1,…,I; ~~~ j=1,…,n_i \)
Expresión 2: Ecuación del modelo unifactorial
donde:
- \( y_{ij} \): es la variable aleatoria que representa la observación j-ésima del i-ésimo tratamiento (Variable respuesta).
- \( \mu \): Es un efecto constante, común a todos los niveles del factor, denominado media global.
- \( \tau_i \): es la parte de debida a la acción del nivel i-ésimo, que será común a todos los elementos sometidos a ese nivel del factor, llamado efecto del tratamiento i-ésimo.
- \( u_{ij} \): son variables aleatorias que engloban un conjunto de factores, cada uno de los cuales influye en la respuesta sólo en pequeña magnitud pero que de forma conjunta debe tenerse en cuenta. Es decir, se pueden interpretar como las variaciones causadas por todos los factores no analizados y que dentro del mismo tratamiento variarán de unos elementos a otros. Reciben el nombre de perturbaciones o error experimental.
Nuestro objetivo es estimar el efecto de los tratamientos y contrastar la hipótesis de que todos los niveles del factor producen el mismo efecto, frente a la alternativa de que al menos dos difieren entre sí. Para ello, se supone que los errores experimentales son variables aleatorias independientes igualmente distribuidas según una Normal de media cero y varianza constante.
En este modelo se distinguen dos situaciones según la selección de los tratamientos: modelo de efectos fijos y modelo de efectos aleatorios.
En el modelo de efectos fijos el experimentador decide qué niveles concretos se van a considerar y las conclusiones que se obtengan sólo son aplicables a esos niveles, no pudiéndose hacer extensivas a otros niveles no incluidos en el estudio.
En el modelo de efectos aleatorios, los niveles del factor se seleccionan al azar; es decir los niveles estudiados son una muestra aleatoria de una población de niveles y las conclusiones que se obtengan se generalizan a todos los posibles niveles del factor, hayan sido explícitamente considerados en el estudio o no.
En cuanto a los tamaños muestrales de los tratamientos, los modelos se clasifican en: modelo equilibrado o balanceado si todas las muestras son del mismo tamaño = n y modelo no-equilibrado o no-balanceado si los tamaños muestrales son distintos.
El contraste de hipótesis planteado anteriormente está asociado a la descomposición de la variabilidad de la variable respuesta. Dicha variabilidad se descompone de la siguiente forma:
\( SCT = SCTr + SCR \)
Donde:
\( SCT \): es la suma de cuadrados total o variabilidad total de \( Y \):
\( SCT= \displaystyle \sum_{i=1}^I \displaystyle \sum_{j=1}^{n_i} (y_{ij}- \overline{y}_{..})^2 \)
\( SCTr \): es la suma de cuadrados entre tratamientos o variabilidad explicada:
\( SCTr = \displaystyle \sum_{i=1}^{I} n_i ( \overline{y}_{i.}- \overline{y}_{..})^2 \)
\( SCR \): es la suma de cuadrados dentro de los tratamientos, variabilidad no explicada o residual:
\( SCR= \displaystyle \sum_{ij} (y_{ij}-\overline{y}_{i.})^2 \)
La tabla de análisis de la varianza (tabla ANOVA) se construye a partir de esta descomposición y proporciona el valor del estadístico \( F \) que permite contrastar la hipótesis nula planteada anteriormente.
\( \begin{array}{c} H_0 \equiv \mu_1 = \mu_2 = \cdots = \mu_5 ~~~ vs ~~~ H_1 \equiv \mu_i \neq \mu_j \hspace{.2cm} \text {para algún } i\neq j \end{array} \)
En el Supuesto práctico 1:
- Variable respuesta: Pérdida de peso de la suela del zapato.
- Factor: Tipo de cuero, que tiene cuatro niveles. Es un factor de efectos fijos ya que viene decidido que niveles concretos se van a utilizar (4 tipos de cuero).
- Modelo equilibrado: Los niveles de los factores tienen el mismo número de elementos (6 elementos).
- Tamaño del experimento: Número total de observaciones, en este caso 24 unidades experimentales.
El problema planteado se modeliza a través de un diseño unifactorial totalmente aleatorizado de efectos fijos equilibrado.
Para realizar este supuesto en RStudio debemos introducir primero los datos. Para ello. En el menú principal de RStudio elegir Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, elegir el directorio de trabajo donde están los datos. En mi caso dicho archivo está en la dirección: “C:/Users/Usuario/Desktop/Datos”. Se muestra la siguiente salida
elegimos el fichero “supuesto1.txt y se muestra la siguiente ventana de RStudio donde se muestran los datos
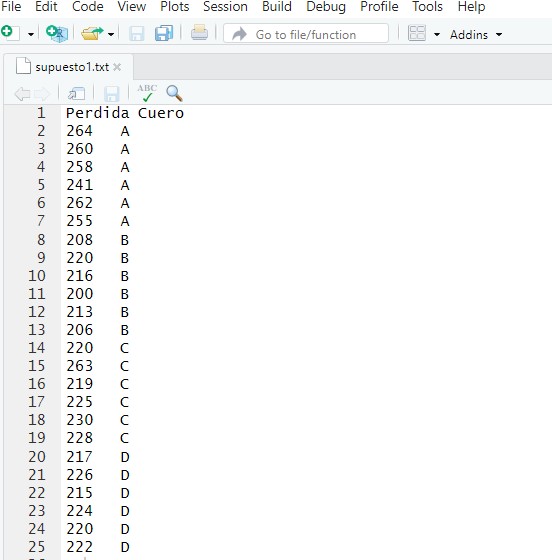
En primer lugar describimos los cuatro grupos que tenemos que comparar, los cuatro tipos de cuero, la variable respuesta es la pérdida de peso en la suela del zapato. Cada tipo de cuero tiene seis unidades, en total tenemos 24 observaciones. La hipótesis nula es que el promedio de las pérdidas de peso es igual para cada tipo de cuero diferente. Es decir, no hay diferencias en las pérdidas de peso con respecto a los tipos de cuero y la alternativa es que las pérdidas de peso son diferentes al menos en dos tipos de cuero.
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en Figura 1, es decir, las observaciones en una sola columna y a continuación especificado su tratamiento y su bloque correspondiente.
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
perdida <- read.table(“supuesto1.txt”, header = TRUE)
perdida
Ejecutar la sentencia, para ello Click en la tecla Run o bien presionar las teclas Ctrl+ Enter y se ejecuta, mostrándose en la Consola de RStudio
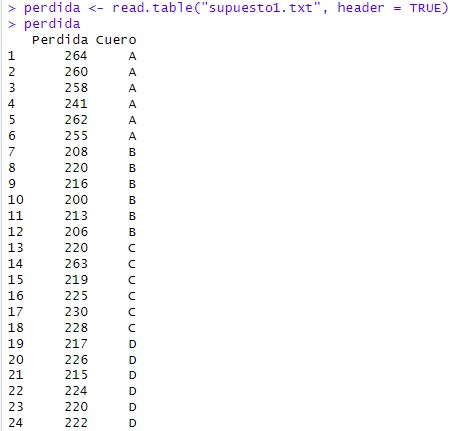
Debemos de transformar la variable factor (llamada “cuero” en nuestro problema). Se puede hacer de dos maneras:
- Transformar la variable referente a los niveles del factor fijo como factor (función “factor”)
perdida$Cuero<-factor(perdida$Cuero)
perdida$Cuero (Ejecutar sentencia Ctrl+ Enter)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
mod <- aov(Perdida ~ Cuero, data = perdida)
mod
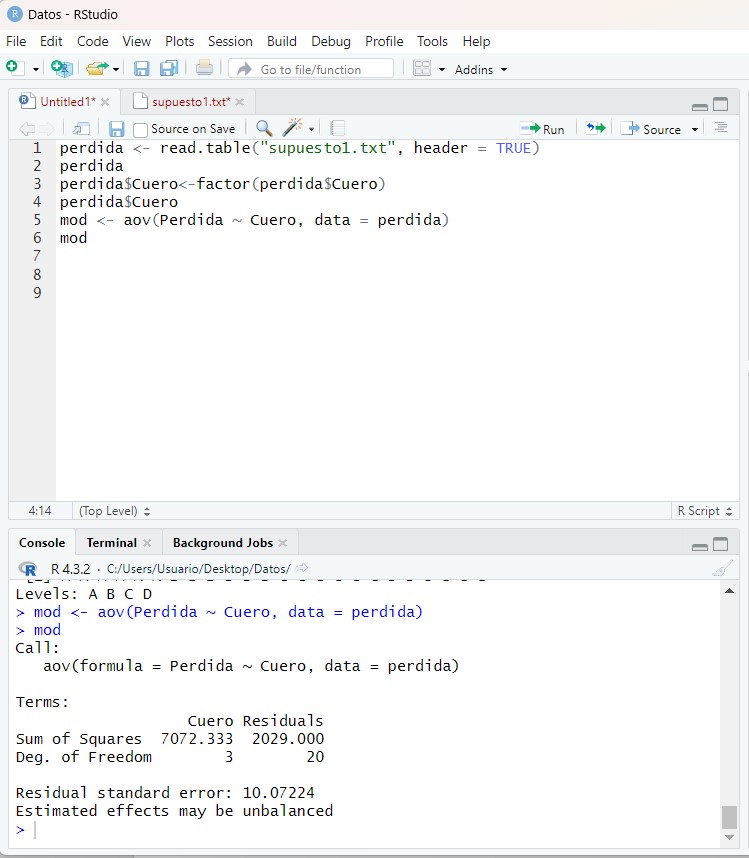
donde:
- Perdida = nombre de la columna de las observaciones.
- Cuero = nombre de la columna en la que están representados los tratamientos.
- data= data.frame en el que están guardados los datos.
Se puede mostrar un resumen de los resultados con la función “summary” (verdadera tabla ANOVA)
summary(mod)
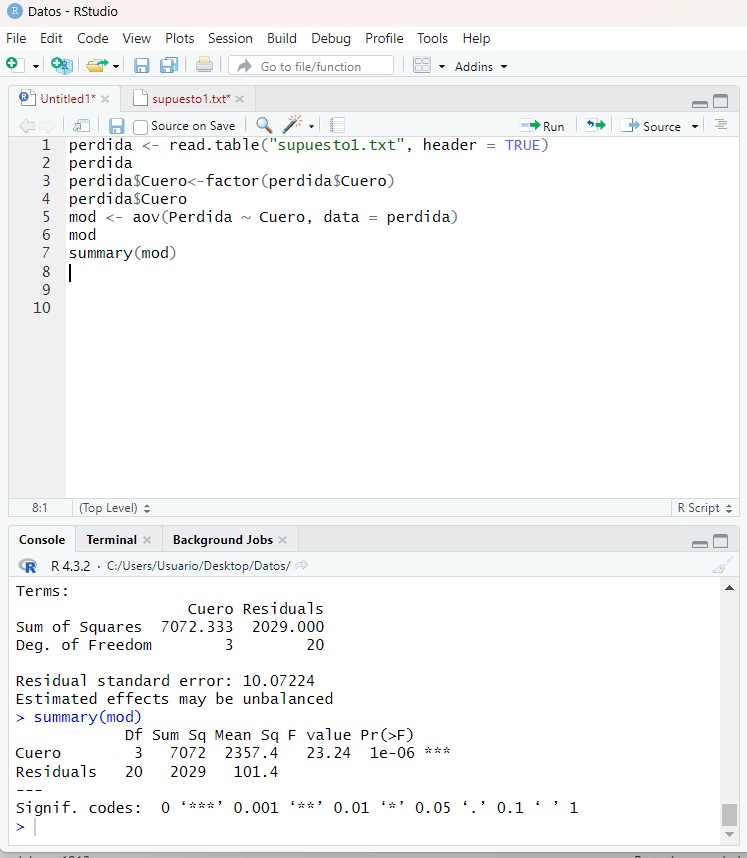
Si el valor de F es mayor que uno quiere decir que hay un efecto positivo del factor tipo de cuero. Se observa que el P-valor (Sig.) tiene un valor de 1e-06 (0.000001), que es menor que el nivel de significación 0.05 (normalmente se toma como nivel de significación 5%). Por lo tanto, hemos comprobado estadísticamente que estos cinco grupos son distintos. Es decir, existen diferencias significativas en las pérdidas de peso medias entre los cinco tipos de cuero. Por lo tanto no se puede rechazar la hipótesis alternativa que dice que al menos dos grupos son diferentes, pero ¿Cuáles son esos grupos? ¿Los cinco grupos son distintos o sólo alguno de ellos? Pregunta que resolveremos más adelante mediante los contrastes de comparaciones múltiples.
- En la expresión del comando “aov” indicar el factor. Directamente en la función “aov” se puede indicar que variable es de tipo factor.
mod1 <- aov(Perdida ~ factor(Cuero), data = perdida)
mod1
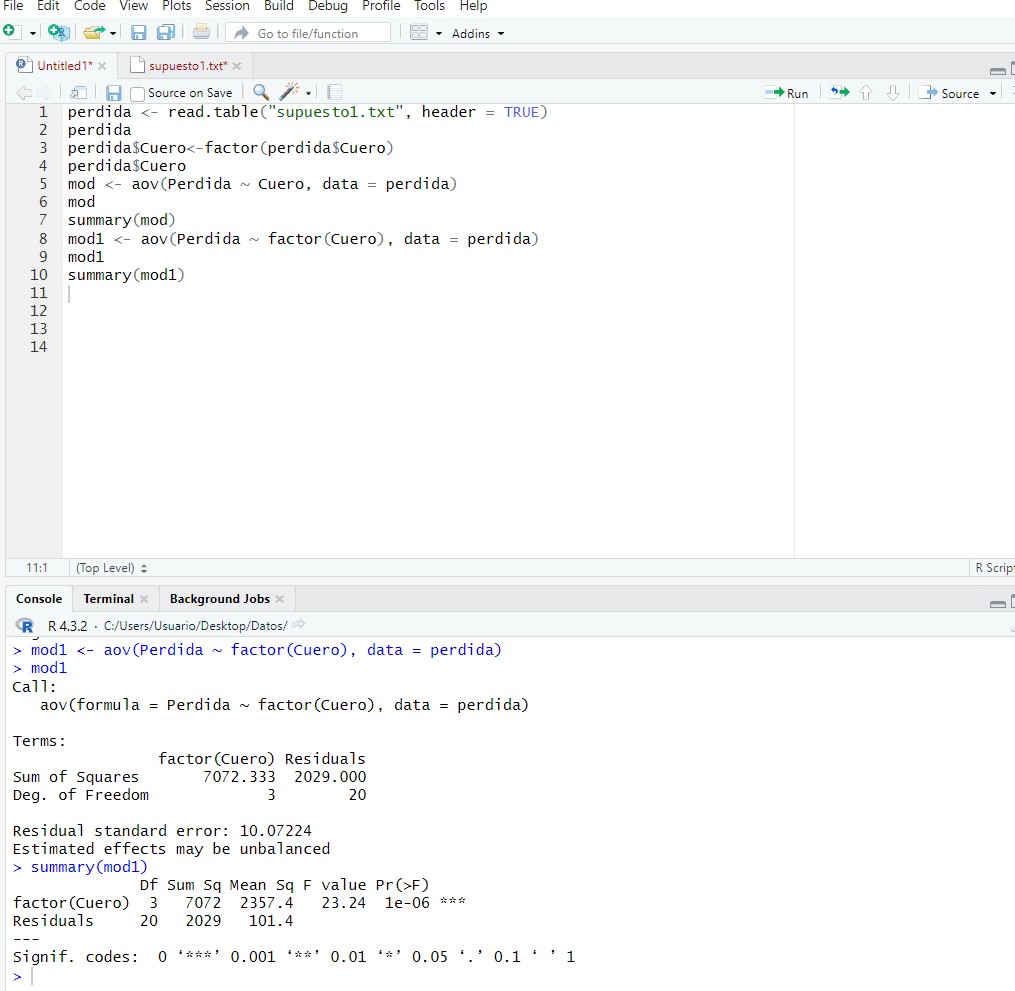
Observamos como obtenemos los mismos resultados. También se puede utilizar el comando “anova” y no es necesario usar la función “summary”:
mod2 <- anova(lm (Perdida ~ factor(Cuero), data= perdida))
mod2

Obteniendo de nuevo los mismos resultados.
Destacar que los datos del problema pueden venir en otro formato al visto anteriormente (en un archivo de texto):
1. Los datos se muestran agrupados por cada nivel del factor principal, como se muestra a continuación:
\( \begin{array} {cccc} A & B & C & D \\ 264 & 208 & 220 & 217 \\ 260 & 220 & 263 & 226 \\ 258 & 216 & 219 & 215 \\ 241 & 200 & 225 & 224 \\ 262 & 213 & 230 & 220 \\ 255 & 206 & 228 & 222 \end{array} \)
De nuevo en el menú principal de RStudio elegir Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, elegir el directorio de trabajo donde están los datos y elegir el fichero supuesto1-1
perdida <- read.table(“supuesto1-1.txt”, header = TRUE)
perdida
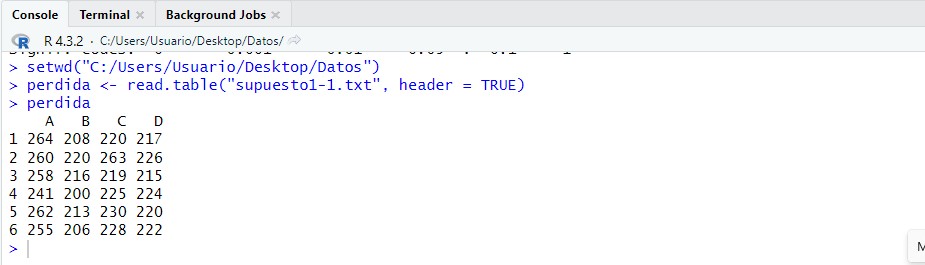
En primer lugar apilaremos las columnas, para ello utilizamos el comando “stack” de la siguiente forma
trats <- stack(perdida)
trats
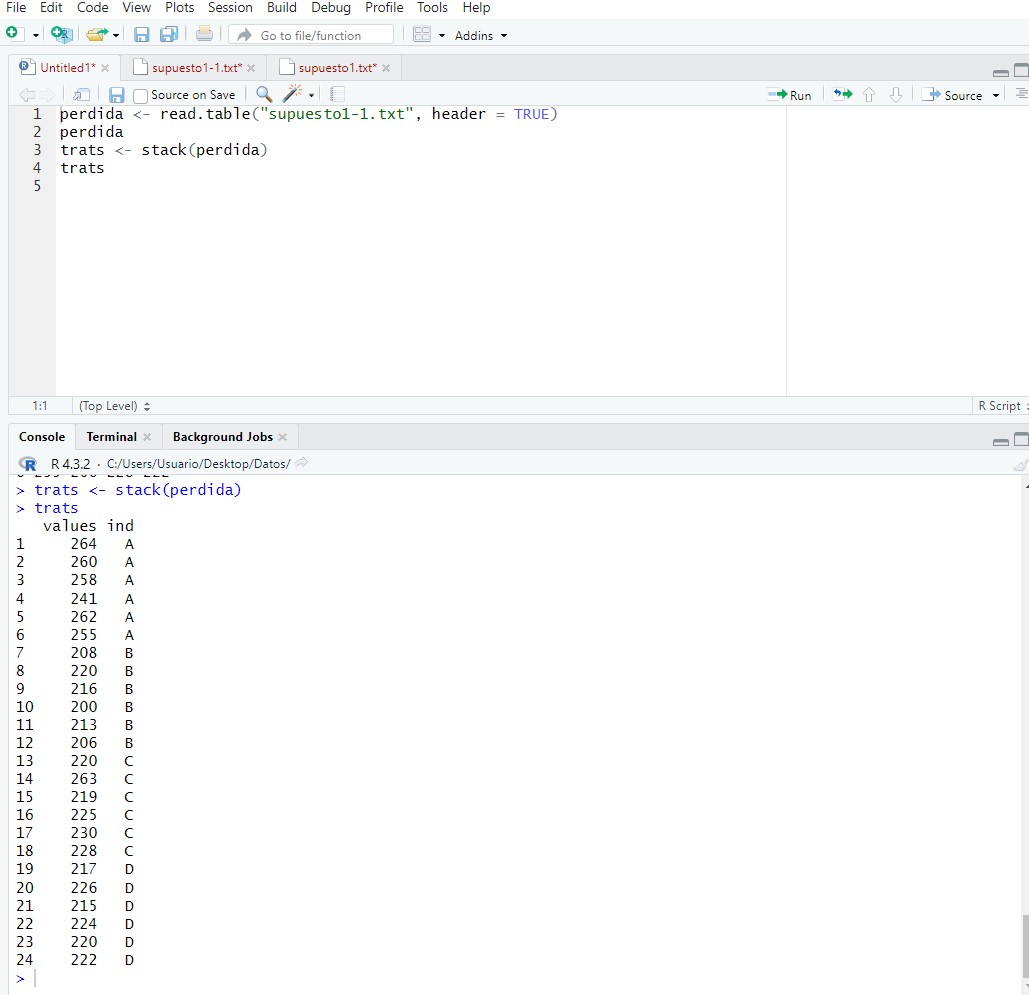
Nos muestra dos columnas:
- La primera columna: “values” nos muestra los valores de la variable respuesta. En este caso la pérdida de peso.
- La segunda columna: ”ind” nos muestra los diferentes tratamientos.
Podemos realizar el Análisis de la varianza utilizando el comando “anova”:
anova(lm(values ~ ind, data = trats))
2. Los datos vienen dados en forma de vectores de la siguiente forma:
>A <- c(264, 260, 258, 241, 262, 255)
B <- c(208, 220, 216, 200, 213, 206)
C <- c(220, 263, 219, 225, 230, 228)
D <- c(217, 226, 215, 224, 220, 222)
Primero creamos un data.frame para poder resolver el ANOVA:
De esta forma hemos creado una nueva base de datos que hemos llamado “datos“. Para resolver el ANOVA tenemos primero que apilar las columnas con el comando “stack” como en el caso anterior:
datos1 = stack(datos)
datos1
Una vez tenemos los datos en este formato resolvemos el ANOVA como en el caso anterior:
anova(lm(values ~ ind, data = trats))
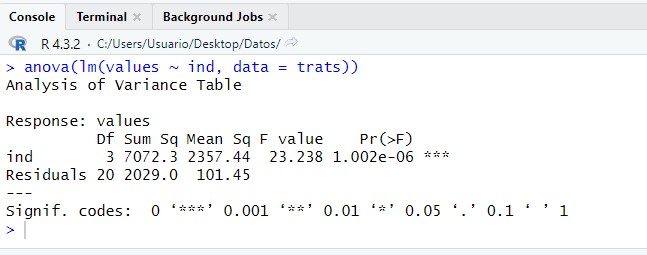 3. Los datos se muestren en un solo vector que contiene toda la información, de la forma:
3. Los datos se muestren en un solo vector que contiene toda la información, de la forma:
perdida = c(A,B,C,D)
perdida

Este vector está formado por los 24 datos que podemos comprobarlo con el comando “length”
length(perdida)

Para realizar el ANOVA, ya tenemos los datos de la variable respuesta y a continuación tenemos que crear el factor tratamiento, para ello vamos a utilizar la función generador de niveles “gl”, y le decimos que nos genere 4 niveles que son los cuatro tratamientos, cada uno repetido 6 veces con un total de 24 datos. Para identificar qué nivel es cada uno, creamos las etiquetas A,B,C,D:
trat = gl(4,6,24, labels = c(“A”, “B”, “C”, “D”))
trat

Y realizamos el ANOVA con la función “lm”:
anova(lm(perdida ~ trat))
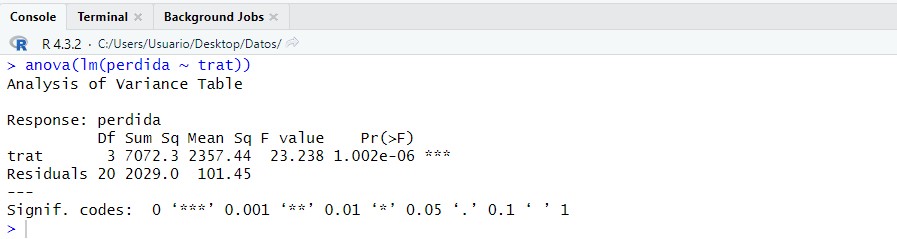
Sin embargo, el modelo que hemos propuesto hay que validarlo, para ello hay que comprobar si se verifican las hipótesis básicas del modelo, es decir, si las perturbaciones son variables aleatorias independientes con distribución normal de media 0 y varianza constante (homocedasticidad).
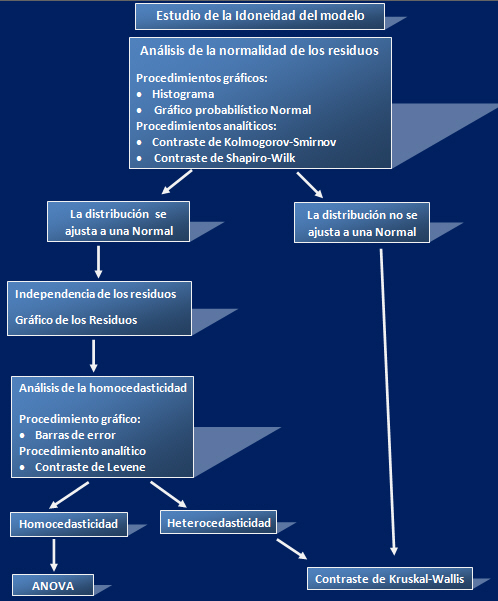
Estudio de la Idoneidad del modelo
Como hemos dicho anteriormente, validar el modelo propuesto consiste en estudiar si las hipótesis básicas del modelo están o no en contradicción con los datos observados. Es decir si se satisfacen los supuestos del modelo: Normalidad, Independencia, Homocedasticidad. Para ello utilizamos procedimientos gráficos y analíticos.
Figura 3: Estudio de la idoneidad del modelo
Figura 3: Estudio de la Idoneidad del modelo
Hipótesis de normalidad
En primer lugar, analizamos la normalidad de las observaciones y continuamos con el análisis de la normalidad de los residuos. Para analizar la normalidad de las observaciones utilizamos el test de Shapiro-Wilks (n<50):
De nuevo seleccionamos el fichero: supuesto1.txt
perdida <- read.table(“supuesto1.txt”, header = TRUE)
perdida
shapiro.test(mod$residuals)
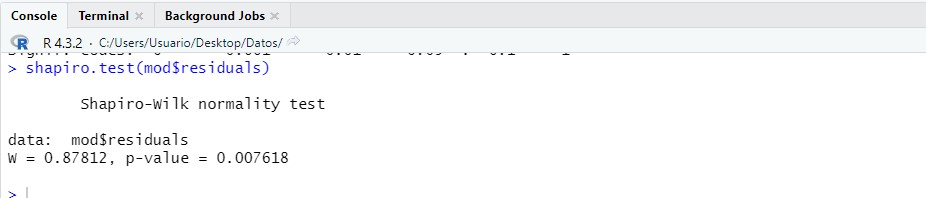
Observamos el contraste de Shapiro-Wilk que es adecuado cuando las muestras son pequeñas (n < 50) y es una alternativa más potente que el test de Kolmogorov-Smirnov. El p-valor es menor que el nivel de significación del 5%, concluyendo que las muestras de las observaciones no se distribuyen de forma normal para cada tipo de cuero.
Podemos verlo también gráficamente con la orden “qqnorm”
qqnorm (mod$residuals)
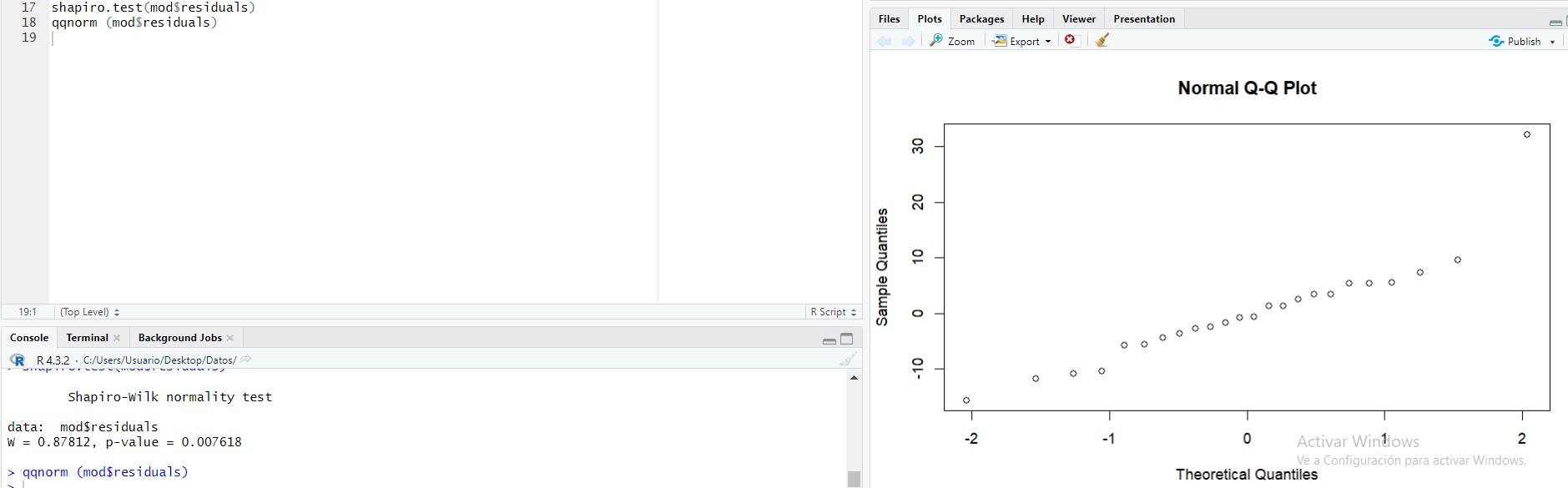
Figura 4: Gráfico Q-Q plot
Si los puntos del gráfico aparecen próximos a la línea diagonal sería una prueba de que exista normalidad en las observaciones, pero como vemos en el gráfico se aprecia una línea diagonal salvo por la última observación.
Hipótesis de homocedasticidad
Para comprobar la hipótesis de igualdad entre las varianzas del factor utilizamos el Test de Barlett “bartett.test”
bartlett.test(perdida$Perdida, perdida$Cuero)

El p-valor es del 0.03 que al ser menor del nivel significación usual del 5% podemos rechazar la hipótesis de igualdad de varianzas, es decir, se rechaza la igualdad de varianzas en el factor.
Hipótesis de independencia
Para comprobar que se satisface el supuesto de independencia entre los residuos analizamos el gráfico de los residuos frente a los valores pronosticados o predichos por el modelo. El empleo de este gráfico es útil puesto que la presencia de alguna tendencia en el mismo puede ser indicio de una violación de dicha hipótesis. En R obtenemos varios gráficos a la vez que están incluidos en la estimación del modelo. Para verlos de forma correcta hacemos uso de las siguientes órdenes:
layout(matrix(c(1,2,3,4),2,2)) # para que salgan en la misma pantalla
plot(mod)
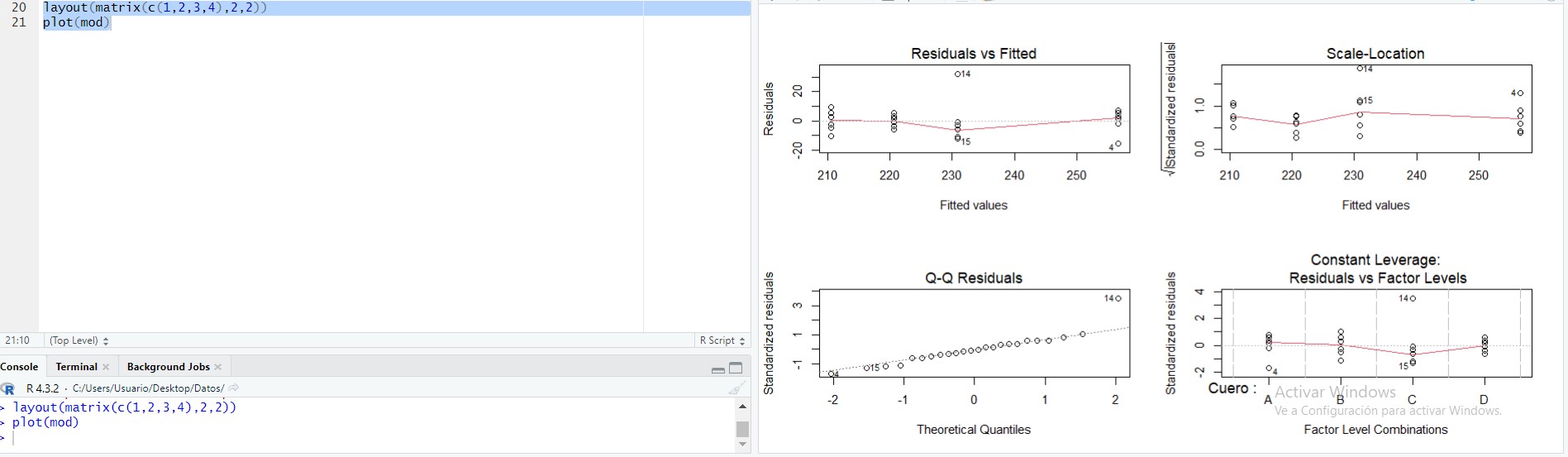
Figura 5: Estudio gráfico de la hipótesis de independencia
En la Figura 5 se muestran cuatro gráficos, en el primero de ellos que se representan los residuos en el eje de ordenadas y los valores pronosticados en el eje de abscisas. No observamos, en dicho gráfico, ninguna tendencia sistemática que haga sospechar del incumplimiento de la suposición de independencia.
Hemos visto como se incumplen la hipótesis de Normalidad y de Homocedasticidad, por lo cual el ANOVA no se podría aplicar y deberíamos usar el contraste de Kruskal-Wallis. Este es un método no paramétrico, por lo que no necesita de supuestos previos para funcionar. En esta la Hipótesis Nula considera que todas las muestras provienen de la misma población (sin diferencia entre tratamientos) y como Hipótesis Alternativa considera que al menos una muestra proviene de una población distinta (existen diferencias entre tratamientos). Para más información sobre el test: https://rpubs.com/Joaquin_AR/219504
Si deseamos aplicar dicho test debemos usar la función “kruskal.test”:
kruskal.test(Perdida ~ Cuero, data = perdida)

Observamos como el p-valor es menor que el nivel de significación usual (5%), por lo tanto rechazamos la hipótesis nula. Es decir, los tipos de cuero influyen significativamente en la pérdida de peso de la suela del zapato. Obtenemos las mismas conclusiones que con la ANOVA pero está es la forma ideal de proceder si se incumplen las hipótesis del modelo.
Anteriormente, hemos comprobado estadísticamente que estos cuatro grupos (tipos de cuero) son distintos. Es decir no se puede rechazar la hipótesis alternativa que dice que al menos dos grupos son diferentes, pero ¿Cuáles son esos grupos? ¿Los cuatro grupos son distintos o sólo alguno de ellos? Pregunta que resolveremos más adelante mediante los contrastes de comparaciones múltiples.
Comparaciones múltiples
Para saber entre que parejas de días las diferencias entre concentraciones medias de CO son significativas aplicamos la prueba Post-hoc de Tukey (“TukeyHSD”)
mod.tukey <- TukeyHSD(mod, ordered = TRUE)
mod.tukey
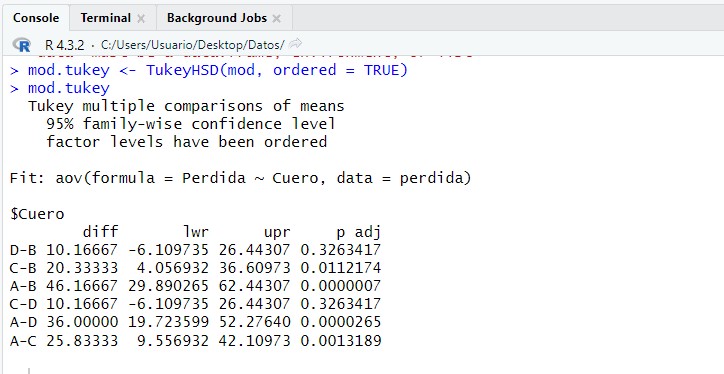
Esta salida nos muestra los intervalos de confianza simultáneos construidos por el método de Tukey. En la tabla se muestra un resumen de las comparaciones de cada tratamiento con los restantes. Es decir, aparecen comparadas dos a dos las cinco medias de los tratamientos.
En esta tabla, las columnas:
- diff: muestra las medias de cada par
- p adj: muestra los p-valores de los contrastes, que permiten conocer si la diferencia entre cada pareja de medias es significativa al nivel de significación considerado (en este caso 0.05)
- lwr y upr: proporcionan los intervalos de confianza al 95% para cada diferencia.
Así por ejemplo, si comparamos la pérdida de peso media del tipo de cuero D con el B, tenemos una diferencia entre ambas medias de 10.17, un p-valor (Sig.) de 0.3263 no significativo (p-valor > 5%) por lo que la pérdida de peso no difiere significativamente entre el tipo de cuero D y el B. Además el intervalo de confianza tiene un límite inferior negativo y un límite superior positivo, por lo tanto contiene al cero de lo que también deducimos que no hay diferencias significativas entre los dos grupos que se comparan o que ambos grupos son homogéneos (la diferencia entre medias puede tomar el valor cero). Por lo tanto la tabla se interpreta observando los valores de “p adj” menores que el 5%, o si el intervalo de confianza contiene al cero.
Siguiendo esto, concluimos que se detectan diferencias significativas en las pérdidas de peso de la suela del zapato entre los tipos de cuero: C-B, A-B, A-C y A-D. Es decir, en dichas parejas de tipos de cuero es donde se aprecian diferencias significativas en la pérdida de peso de la suela del zapato.
Comandos y funciones utilizadas para resolver el supuesto práctico 1
perdida <- read.table(“supuesto1.txt”, header = TRUE)
perdida
perdida$Cuero<-factor(perdida$Cuero)
perdida$Cuero
mod <- aov(Perdida ~ Cuero, data = perdida) # Obtener la tabla ANOVA
mod
summary(mod) # mostrar resumen de resultados
mod1 <- aov(Perdida ~ factor(Cuero), data = perdida) # en la función “aov” indicar el factor
mod1
mod2 <- anova(lm (Perdida ~ factor(Cuero), data= perdida)) # el comando “anova” no necesita la función “summary”
mod2
shapiro.test(mod$residuals) # Hipótesis de normalidad
qqnorm (mod$residuals) # Representación Q-Q plot
bartlett.test(perdida$Perdida, perdida$Cuero) # Hipótesis de homocedasticidad
layout(matrix(c(1,2,3,4),2,2)) # para que salgan en la misma pantalla
plot(mod) # Hipótesis de independencia
kruskal.test(Perdida ~ Cuero, data = perdida) #método no paramétrico
mod.tukey <- TukeyHSD(mod, ordered = TRUE) # Comparaciones múltiples
mod.tukey
Diseño Unifactorial de efectos aleatorios
En el modelo de efectos aleatorios, los niveles del factor son una muestra aleatoria de una población de niveles. Este modelo surge ante la necesidad de estudiar un factor que presenta un número elevado de posibles niveles, que en algunas ocasiones puede ser infinito. En este modelo las conclusiones obtenidas se generalizan a toda la población de niveles del factor, ya que los niveles empleados en el experimento fueron seleccionados al azar. El estudio de este diseño lo vamos a realizar mediante el siguiente supuesto práctico.
Supuesto práctico 2
Se desea analizar un alimento para gatos, en tanto se sabe que existen muchas marcas comerciales en un país. Para ello, primero se selecciona una muestra de cinco marcas comerciales aleatoriamente y luego se mide el aumento de peso en gramos de 45 gatos cachorros, alimentados de la misma manera durante un mes con uno de los productos seleccionados, como se muestra en la siguiente tabla
\( \begin{array} {|c|cccccccc|} \hline \text { Marca} & & & \text{Aumento} & \text{ de } & \text{ peso} & & &\\ \hline 1 & 120 & 240 & 300 & 360 & 240 & 180 & 144 & 300 & 240 \\ \hline 2 & 240 & 360 & 180 & 180 & 300 & 240 & 360 & 360 & 300 \\ \hline 3 & 240 & 270 &300 & 360 & 360 & 300 & 360 & 360 & 300 \\ \hline 4 & 300 & 240 & 300 & 360 & 360 & 360 & 360 & 360 & 300 \\ \hline 5 & 300 & 360 & 240 & 360 & 360 & 360 & 360 & 300 & 360 \\ \hline \end{array} \)
Figura 6: Tabla de datos del Supuesto Práctico 2
Supuestos del modelo:
- Las cinco muestras representan muestras aleatorias independientes extraídas de \( I \) poblaciones seleccionadas aleatoriamente de un conjunto mayor de poblaciones.
- Todas las poblaciones del conjunto más amplio tienen distribución Normal, de modo que cada una de las 5 poblaciones muestreadas se distribuyen según una Normal.
- Todas las poblaciones del conjunto más amplio tienen la misma varianza, y por lo tanto, cada una de las 5 poblaciones muestreadas tiene también varianza \( \sigma^2 \) .
- Las variables son variables aleatorias normales independientes, cada una con media 0 y varianza común \( \sigma^2_\tau \).
El modelo matemático de este diseño y los tres primeros supuestos del modelo son semejantes a los del modelo de efectos fijos. Sin embargo, el supuesto 4 expresa matemáticamente una importante diferencia entre los dos. En el modelo de efectos fijos, el experimentador elige los tratamientos o niveles del factor utilizados en el experimento. Si se replicase el experimento, se utilizarían los mismos tratamientos. Es decir, se muestrearían las mismas poblaciones cada vez y los \( I \) efectos del tratamiento \( \tau_i = \mu_i – \mu \) no variarían. Esto implica que en el modelo de efectos fijos, estos \( I \) términos se consideran constantes desconocidas. En el modelo de efectos aleatorios se seleccionan aleatoriamente \( I \) poblaciones, las elegidas variarán de replicación en replicación. De este modo, en este modelo los \( I \) términos \( \mu_i – \mu \) no son constantes, son variables aleatorias, cuyos valores para una determinada réplica depende de la elección de las \( I \) poblaciones a estudiar. En este modelo estas variables \( \tau_i \) se suponen variables aleatorias normales independientes con media 0 y varianza común \( \sigma^2_\tau \). Además este modelo requiere que las variables \( \tau_i \) y \( u_{ij} \) sean independientes. Así, por la independencia de estas variables, la varianza de cualquier observación de la muestra, es decir, la varianza total, vale
\( \sigma_T^2=\sigma_{\tau}^2+\sigma^2 \)
La mecánica del Análisis de la Varianza es la misma que en el modelo de efectos fijos. En este modelo, carece de sentido probar la hipótesis que se refiere a los efectos de los tratamientos individuales. Si las medias poblacionales en el conjunto mayor son iguales, no variarán los efectos del tratamiento \( \tau_i \), es decir, \( \sigma^2_\tau = 0 \). Así en el modelo de efectos aleatorios, la hipótesis de medias iguales se contrasta considerando
\( H_0 \equiv \sigma_{\tau}^2 = 0~~vs~~H_1 \equiv \sigma_{\tau}^2 \neq 0 \)
Si no se rechaza \( H_0 \), significa que no hay variedad en los efectos de los tratamientos.
En el Supuesto práctico 2:
- Variable respuesta: Aumento de peso en gatos.
- Factor: Marca de alimento, que tiene cinco niveles. Es un factor de efectos aleatorios, se han elegido aleatoriamente cinco marcas, que constituyen únicamente una muestra de todas las marcas y el propósito no es comparar estas cinco marcas sino contrastar el supuesto general de que el aumento de peso en los gatos difiere en función de la marca de alimento.
- Modelo equilibrado: Los niveles de los factores tienen el mismo número de elementos (9 elementos).
- Tamaño del experimento: Número total de observaciones, en este caso 45 unidades experimentales.
El problema planteado se modeliza a través de un diseño unifactorial totalmente aleatorizado de efectos aleatorios equilibrado. En este se quiere comprobar el aumento de peso en gatos depende de la marca de alimento.
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio. En este caso lo hacemos en un archivo de texto:
Figura 7: Tabla de datos del Supuesto Práctico 2
Recordemos que en el menú principal de RStudio tenemos que elegir Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos. En ese directorio elegimos el fichero “supuesto2.txt y se muestran los datos en la siguiente ventana de RStudio

perros<-read.table(“supuesto2.txt”, header = TRUE)
perros
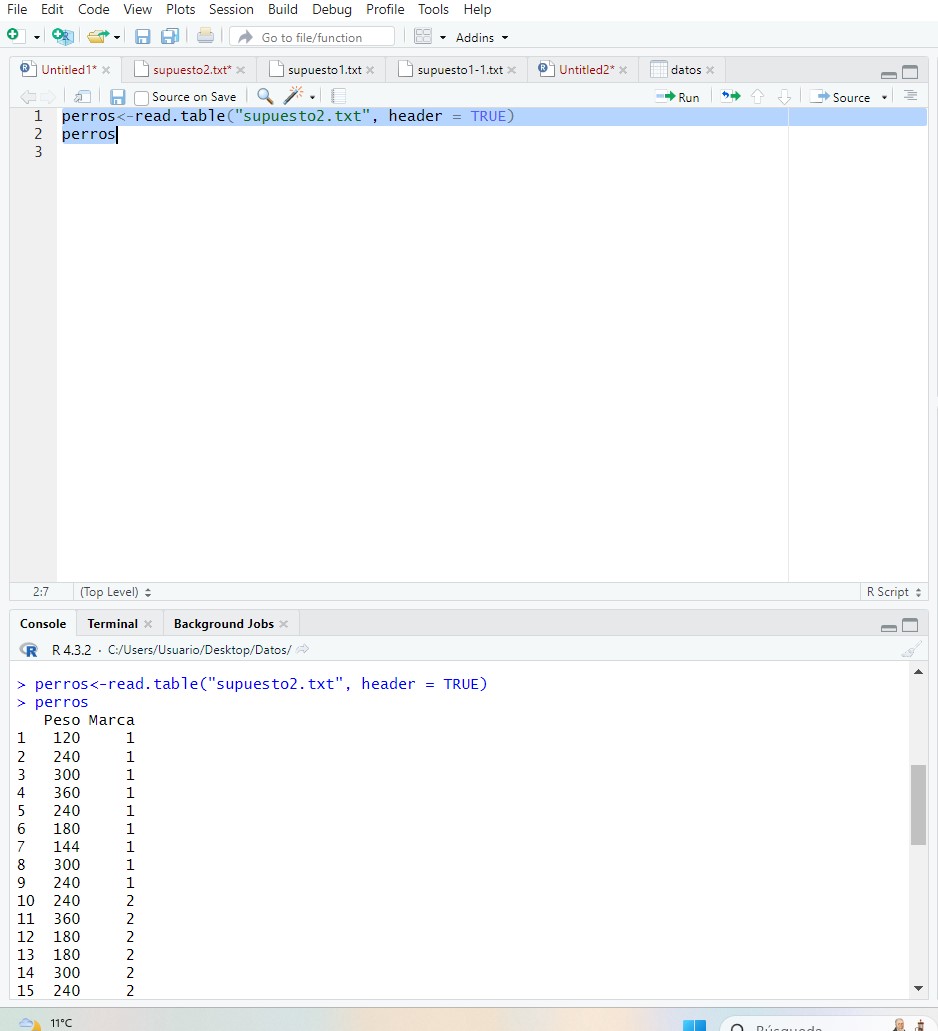
Debemos transformar la variable referente a los niveles del factor fijo como factor para poder hacer los cálculos de forma adecuada
perros$Marca<- factor(perros$Marca)
perros$Marca
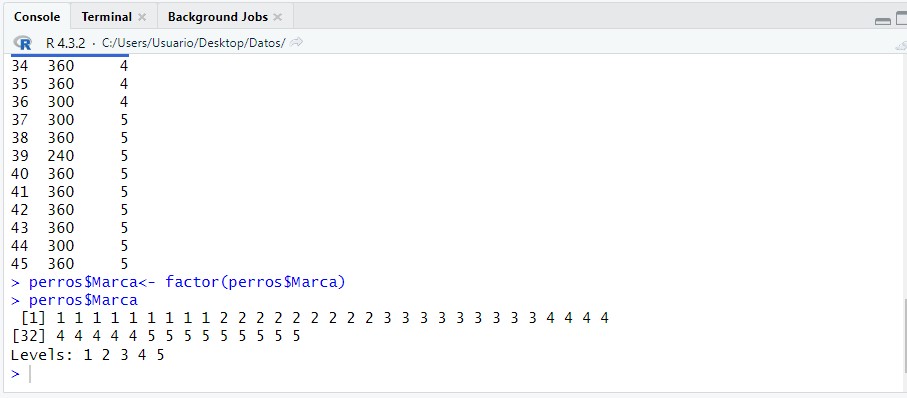
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
mod <- aov(Peso ~ Marca, data = perros)
mod
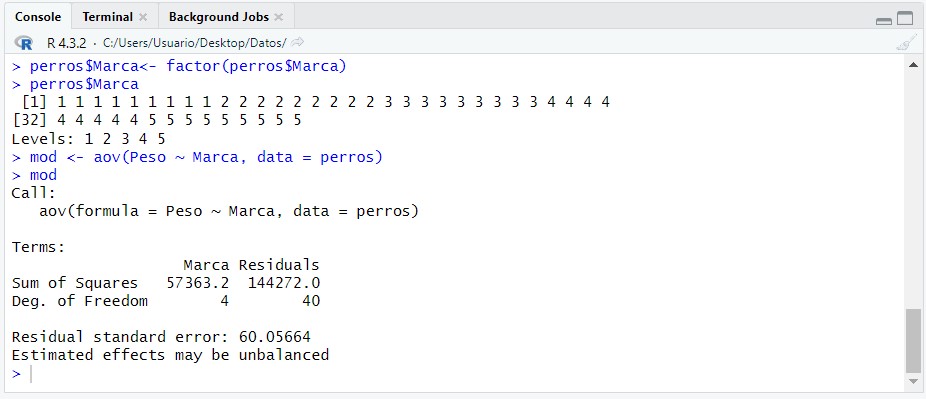
donde:
- Peso = nombre de la columna de las observaciones.
- Marca =nombre de la columna en la que están representados los tratamientos.
- data = data.frame en el que están guardados los datos.
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
summary(mod)
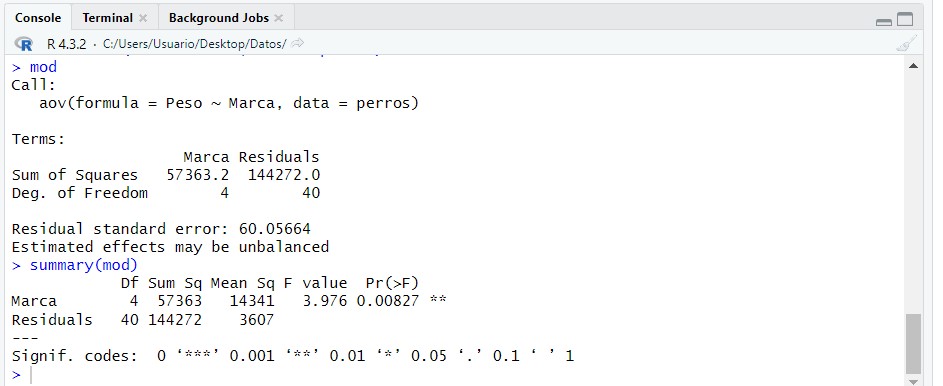
Esta tabla muestra los resultados del contraste planteado. El valor del estadístico de contraste es igual a 3.976 que deja a la derecha un p-valor de 0.00827, así que la respuesta dependerá del nivel de significación que se fije. Si fijamos un nivel de significación de 0.05 se concluye que hay evidencia suficiente para afirmar la existencia de alguna variabilidad en el aumento de peso de los gatos según las diferentes marcas de alimentación.
En el modelo de efectos aleatorios no se necesitan llevar a cabo más contrastes incluso aunque la hipótesis nula sea rechazada. Es decir, en el caso de rechazar \( H_0 \) no hay que realizar comparaciones múltiples para comprobar que medias son distintas, ya que el propósito del experimento es hacer un planteamiento general relativo a las poblaciones de las que se extraen las muestras.
En este caso, R no tiene ninguna función que nos permita calcular la varianza de tratamientos, por lo que tenemos que calcularla a mano:
En el modelo de efectos aleatorios las variables \( \tau_i \) y \( u_{ij} \) son independientes, por lo tanto la varianza de cualquier observación de la muestra, es decir, la varianza total, vale:
\( \sigma_T^2=\sigma_{\tau}^2+\sigma^2 \)
La varianza dentro de los factores (varianza residual):
\( \widehat{\sigma}^2 = S^2_R = 3607 \)
La varianza entre los factores:
\( \widehat{ \sigma }^2_\tau = \displaystyle \frac {N(I-1)}{N^2- \sum_i n_i^2}(S^2_{Tr}-S^2_R) = \displaystyle \frac {45 \times 4} {45^2-5 \times 9^2} (1431-3067) = 1192.667 \)
Obteniendo por tanto que la varianza total vale:
\( \widehat{\sigma}^2_T = \widehat{ \sigma }^2_\tau + \widehat{\sigma}^2 = 1192.667 + 3607 = 4799.67 \)
Por lo tanto, la varianza total (4799.467) se descompone en una parte atribuible a la diferencia entre las marcas de alimentos (1192.667) y otra procedente de la variabilidad existente dentro de ellas (3606.8). Comprobamos que en dicha varianza tiene mayor peso la variación dentro de las marcas, en porcentaje un 75.15 % frente a la variación entre fabricantes, que representa el 24.85 % del total.
Comandos y funciones utilizadas para resolver el supuesto práctico 2
perros<-read.table(“supuesto2.txt”, header = TRUE)
perros
perros$Marca<- factor(perros$Marca)
perros$Marca
mod <- aov(Peso ~ Marca, data = perros)
mod
summary(mod)
Diseño en Bloques Aleatorizados
En los diseños estudiados anteriormente hemos supuesto que existe bastante homogeneidad entre las unidades experimentales. Pero puede suceder que dichas unidades experimentales sean heterogéneas y contribuyan a la variabilidad observada en la variable respuesta. Si en esta situación se utiliza un diseño completamente aleatorizado, no sabremos si la diferencia entre dos unidades experimentales sometidas a distintos tratamientos se debe a una diferencia real entre los efectos de los tratamientos o a la heterogeneidad de dichas unidades. Como resultado, el error experimental reflejará esta variabilidad. En esta situación se debe sustraer del error experimental la variabilidad producida por las unidades experimentales y para ello el experimentador puede formar bloques de manera que las unidades experimentales de cada bloque sean lo más homogéneas posible y los bloques entre sí sean heterogéneos.
En el diseño en bloques Aleatorizados, primero se clasifican las unidades experimentales en grupos homogéneos, llamados bloques, y los tratamientos son entonces asignados aleatoriamente dentro de los bloques. Esta estrategia de diseño mejora efectivamente la precisión en las comparaciones al reducir la variabilidad residual.
Distinguimos dos tipos de diseños en bloques aleatorizados:
- Los diseños en bloques completos aleatorizados (Todos los tratamientos se prueban en cada bloque exactamente vez).
- Los diseños por bloques incompletos aleatorizados (Todos los tratamientos no están representados en cada bloque, y aquellos que sí están en uno en particular se ensayan en él una sola vez).
Diseño en Bloques Completos Aleatorizados
En esta sección presentamos el diseño en Bloques Completos Aleatorizados. La palabra bloque se refiere al hecho de que se ha agrupado a las unidades experimentales en función de alguna variable extraña; aleatorizado se refiere al hecho de que los tratamientos se asignan aleatoriamente dentro de los bloques; completo implica que se utiliza cada tratamiento exactamente una vez dentro de cada bloque y el término efectos fijos se aplica a bloques y tratamientos. Es decir, se supone que ni los bloques ni los tratamientos se eligen aleatoriamente. Además una caracterización de este diseño es que los efectos bloque y tratamiento son aditivos; es decir no hay interacción entre los bloques y los tratamientos.
La descripción del diseño así como la terminología subyacente la vamos a introducir mediante el siguiente supuesto práctico.
Supuesto práctico 3
Se realiza un experimento para determinar el efecto de cuatro sustancias químicas diferentes sobre la resistencia de una tela. Las sustancias se emplean como parte del proceso terminal de planchado permanente. Para ello, se escogen cinco muestras de tela y se aplica un diseño aleatorizado por bloques completos mediante la prueba de cada sustancia en un orden aleatorio sobre cada una de las muestras de tela.
\( \begin{array} {|c|ccccc|} \hline \text {Sustancias} & & \text{Muestras} & \text{ de } & \text{ tela} & \\ \text{ Químicas} & 1 & 2 & 3 & 4 & 5 \\ \hline A & 1.3 & 1.6 & 0.5 & 1.2 & 1.1 \\ \hline B & 2.2 & 2.4 & 0.4 & 2.0 & 1.8 \\ \hline C & 1.8 & 1.7 & 0.6 & 1.5 & 1.3 \\ \hline D & 3.9 & 4.4 & 2.0 & 4.1 & 3.4 \\ \hline \end{array} \)
Figura 8: Tabla de datos del Supuesto Práctico 3
En el Supuesto práctico 3:
- Variable respuesta: Resistencia de la tela
- Factor: Sustancia química, que tiene 4 niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Bloque: Muestra de tela, que tiene 5 niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Modelo completo: Los tres tratamientos se prueban en cada bloque exactamente una vez.
- Tamaño del experimento: Número total de observaciones (20).
En este caso se trata de un diseño en bloques completos aleatorizados. El objetivo del estudio es comparar cuatro sustancias químicas en la resistencia de una tela, por lo que se trata de un factor con cuatro niveles. Sin embargo, es posible que influya la muestra de tela que se seleccione, por lo que al no ser directamente motivo de estudio, las muestras de tela son un factor secundario que recibe el nombre de bloque.
Nos interesa saber si los distintas sustancias químicas influyen en la resistencia de la tela, para ello realizamos el siguiente contraste de hipótesis:
\( H_0\equiv\tau_1=\tau_2=\tau_3=\tau_4~~vs~~H_1\equiv\tau_i\neq\tau_j~~~para~algún~~i\neq j \)
Es decir, contrastamos que no hay diferencia en las medias de las cuatro sustancias químicas frente a la alternativa de que al menos una media difiere de otra.
Pero, previamente hay que comprobar si la presencia del factor bloque (muestras de tela) está justificada. Para ello, realizamos el siguiente contraste de hipótesis:
\( H_0\equiv\beta_1=…=\beta_5=~~vs~~H_1\equiv\beta_i\neq\beta_j~~~para~algún~~i\neq j \)
Es decir, contrastamos que no hay diferencia en las medias de los cinco bloques frente a la alternativa de que al menos una media difiere de otra.
Este experimento se modeliza mediante un diseño en bloques completos al azar. El modelo matemático es:
\( y_{ij}=\mu+\tau_i+ \beta_j + u_{ij},~~~~ i=1,…,4; ~~~ j=1,…,5 \)
Expresión 3: Ecuación del diseño en bloques completos al azar
La fórmula expresa simbólicamente la idea de que cada observación \( y_{ij} \) (resistencia de la tela medida con la sustancia química \( i \), de la muestra de tela \( j \)), puede subdividirse en cuatro componentes: un efecto medio global \( \mu \), un efecto tratamiento \( \tau_i \) (efecto del factor principal sobre la resistencia de la tela), un efecto bloque \( \beta_j \) (efecto del factor secundario sobre sobre la resistencia de la tela) y una desviación aleatoria debida a causas desconocidas \( u_{ij} \) (Perturbaciones o error experimental). Este modelo tiene que verificar los siguientes supuestos:
- Las 20 observaciones constituyen muestras aleatorias independientes, cada una de tamaño 4, de 20 poblaciones con medias \( \mu_{ij}, \hspace{.1cm} i=1, 2,3,4 \hspace{.1cm} y \hspace{.1cm} j = 1, 2, .., 5 \) .
- Cada una de las 20 poblaciones es normal.
- Cada una de las 20 poblaciones tiene la misma varianza.
- Los efectos de los bloques y tratamientos son aditivos; es decir, no existe interacción entre los bloques y tratamientos. Esto significa que si hay diferencias entre dos tratamientos cualesquiera, estas se mantienen en todos los bloques (abetos).
Los tres primeros supuestos coinciden con los supuestos del modelo unifactorial, con la diferencia de que en el modelo unifactorial se examinaban I poblaciones y en este modelo se examinan \( IJ \). El cuarto supuesto es característico del diseño en bloques. La no interacción entre los bloques y los tratamientos significa que los tratamientos tienen un comportamiento consistente a través de los bloques y que los bloques tienen un comportamiento consistente a través de los tratamientos. Expresado matemáticamente significa que la diferencia de los valores medios para dos tratamientos cualesquiera es la misma en todo un bloque y que la diferencia de los valores medios para dos bloques cualesquiera es la misma para cada tratamiento.
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio. En este caso lo hacemos en un archivo de texto: En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos. En ese directorio elegimos el fichero “supuesto3.txt y se muestran los datos en la siguiente ventana de RStudio
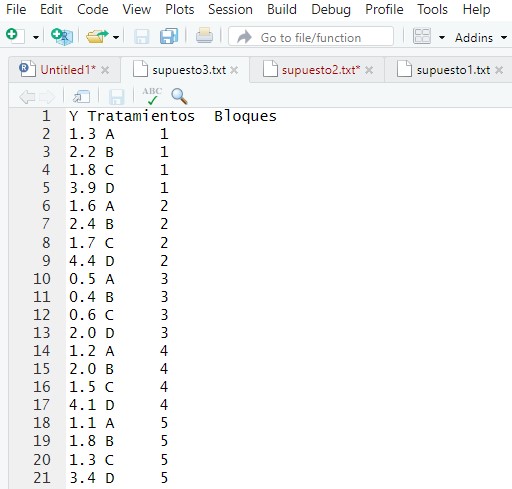
Figura 9: Tabla de datos del Supuesto Práctico 3
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
telas<-read.table(“supuesto3.txt”, header = TRUE)
telas
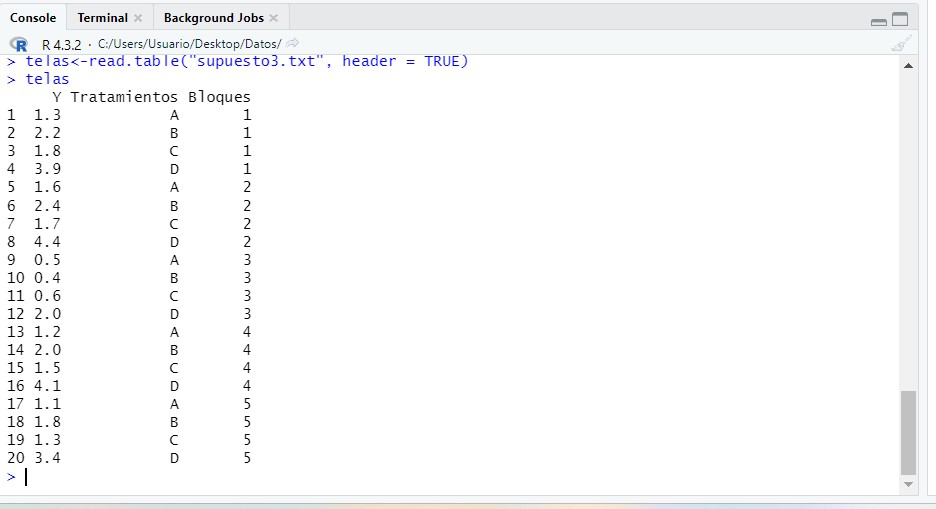
A continuación debemos transformar tanto la columna de los tratamientos como la de los bloques en un factor para podemos realizar los cálculos posteriores adecuadamente. Para hacerlo en en RStudio debemos:
telas$Tratamientos=factor(telas$Tratamientos)
telas$Bloques=factor(telas$Bloques)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
mod <- aov(Y ~ Tratamientos+Bloques, data = telas)
mod
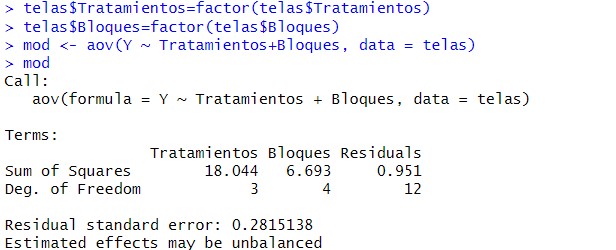
donde:
- Y = nombre de la columna de las observaciones (Resistencia de la tela).
- Tratamientos = nombre de la columna en la que están representados los tratamientos (Sustancias químicas).
- Bloques = nombre de la columna en la que están representados los bloques (Muestras de tela).
- data = data.frame en el que están guardados los datos
y a continuación mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
summary(mod)
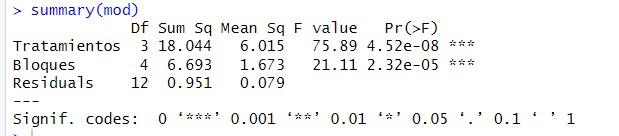
Puesto que la construcción de bloques se ha diseñado para comprobar el efecto de una variable, nos preguntamos si ha sido eficaz su construcción. En caso afirmativo, la suma de cuadrados de bloques explicaría una parte sustancial de la suma total de cuadrados. También se reduce la suma de cuadrados del error dando lugar a un aumento del valor del estadístico de contraste experimental utilizado para contrastar la igualdad de medias de los tratamientos y posibilitando que se rechace la Hipótesis nula, mejorándose la potencia del contraste.
La construcción de bloques puede ayudar cuando se comprueba su eficacia pero debe evitarse su construcción indiscriminada. Ya que, la inclusión de bloques en un diseño da lugar a una disminución del número de grados de libertad para el error, aumenta el punto crítico para contrastar la Hipótesis nula y es más difícil rechazarla. La potencia del contraste es menor.
La Tabla ANOVA, muestra que:
- El valor del estadístico de contraste de igualdad de bloques, \( F = 21.11 \) deja a su derecha un \( p-valor = 0.00002 \), menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de bloques. La eficacia de este diseño depende de los efectos de los bloques. Un valor grande de \( F \) de los bloques (21.11) implica que el factor bloque tiene un efecto grande. En este caso el diseño es más eficaz que el diseño completamente aleatorizado ya que si el cuadrado medio entre bloques es grande (1.673), el término residual será mucho menor (0.079) y el contraste principal de las medias de los tratamientos será más sensible a las diferencias entre tratamientos. Por lo tanto la inclusión del factor bloque en el modelo es acertada. Así, la resistencia de la tela depende de las muestras usadas en el experimento.
Si los efectos de los bloques son muy pequeños, el análisis de bloque quizás no sea necesario y en caso extremo, cuando el valor de \( F \) de los bloques es próximo a 1, puede llegar a ser perjudicial, ya que el número de grados de libertad, \( (I-1)(J-1) \), del denominador de la comparación de tratamientos es menor que el número de grados de libertad correspondiente, \( IJ-I \), en el diseño completamente aleatorizado. Pero, ¿Cómo saber cuándo se puede prescindir de los bloques? La respuesta la tenemos en el valor de la \( F \) experimental de los bloques, se ha comprobado que si dicho valor es mayor que 3, no conviene prescindir de los bloques para efectuar los contrastes.
- El valor del estadístico de contraste de igualdad de tratamiento, F = 9.228 deja a su derecha un p-valor=4.52e-08, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de tratamientos. Así, las sustancias químicas influyen en la resistencia de la tela. Es decir, existen diferencias significativas en el resistencia de la tela entre las cuatro sustancias químicas.
El modelo que hemos propuesto hay que validarlo, para ello hay que comprobar si se verifican los cuatros supuestos expresados anteriormente.
Estudio de la Idoneidad del modelo
Como hemos dicho anteriormente, validar el modelo propuesto consiste en estudiar si las hipótesis básicas del modelo están o no en contradicción con los datos observados. Es decir si se satisfacen los supuestos del modelo: Normalidad, Independencia, Homocedasticidad. Para ello utilizamos procedimientos gráficos y analíticos.
En este modelo se ha supuesto otra hipótesis adicional: Aditividad de los efectos de tratamiento y bloque (no existe interacción entre tratamiento y bloque). Por lo que hay que contrastar la hipótesis de aditividad de los efectos de tratamiento y bloque.
Hipótesis de aditividad entre los bloques y tratamientos
La interacción entre el factor bloque y los tratamientos vamos a estudiarla analíticamente mediante el Test de Interacción de un grado de Tukey. Para realizar este test en R tenemos que utilizar la library “daewr” y dentro de ella la función “Tukey1df”. Primero hay que instalar el paquete “daewr”. Para ello, seleccionar “Paquetes/Instalar paquetes” y de la lista escoger “daewr”. O bien utilizar la siguiente orden:
utils:::menuInstallPkgs()
Para realizar este contraste hay que utilizar la librería “daewr” y usar la función “Tukey1df”, para ello realizamos la siguiente orden:
library(daewr)
Tukey1df(telas)
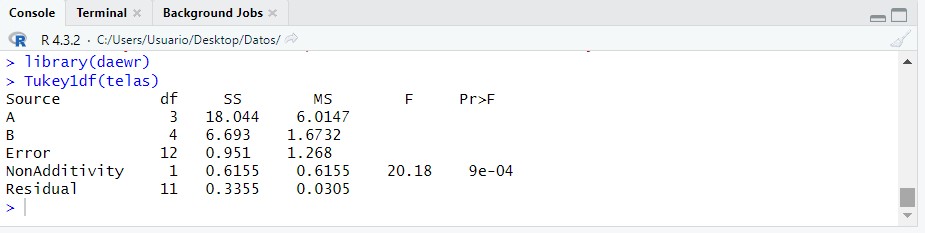
Puesto que el p-valor (Pr > F) es menor que 0.05, rechazamos la hipótesis nula de no interacción, es decir, hay interacción entre las sustancias químicas y las muestras de tela.
Hipótesis de Normalidad
La normalidad las vamos a comprobar analíticamente y gráficamente. Analíticamente mediante el contraste de Shapiro-Wilk que es adecuado cuando las muestras son pequeñas (n<50):
shapiro.test(mod$residuals)
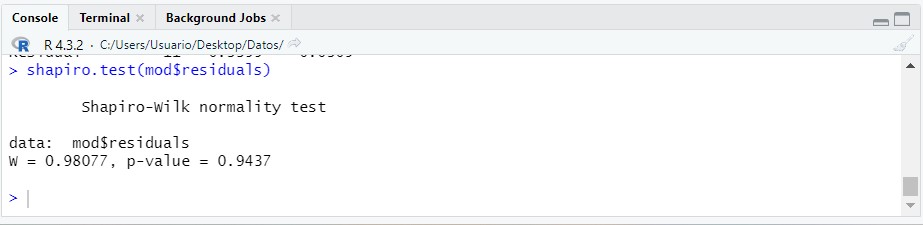
Como podemos observar tenemos un p-valor de 0.9437 que aceptaría la hipótesis de normalidad por ser mayor al 5% (nivel de significación usual).
Gráficamente mediante el gráfico probabilístico normal. Para ello utilizamos la orden “qqnorm”:
qqnorm (mod$residuals)
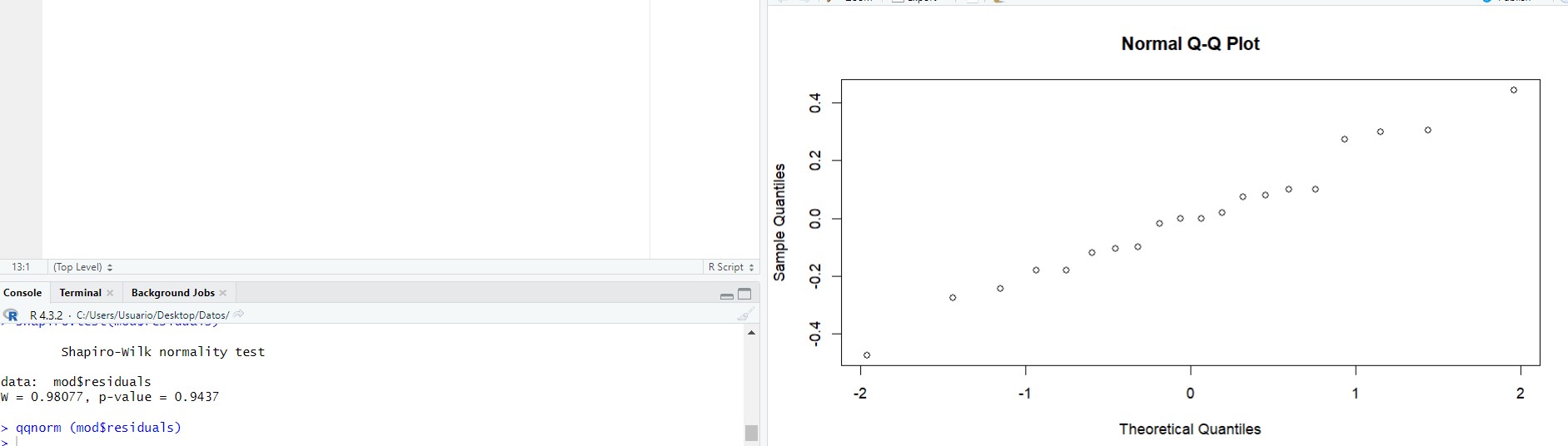
En esta gráfica observamos que prácticamente todos los puntos se encuentran sobre la diagonal por lo tanto podemos decir que no muestra una desviación marcada de la normalidad.
Hipótesis de Homogeneidad de Varianzas
Para comprobar la hipótesis de homocedasticidad utilizamos el Test de Barlett distinguiendo entre la igualdad entre varianzas del factor principal y la igualdad de varianzas del factor bloque.
En nuestro ejemplo, el test para igualdad de varianzas (“bartlett.test”) del factor principal sería:
bartlett.test(telas$Y, telas$Tratamiento)
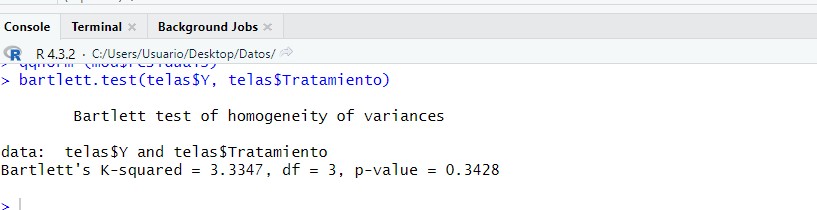
El p-valor es del 0.343 que al ser mayor del nivel significación usual (5%) no podemos rechazar la hipótesis de igualdad de varianzas en el factor principal.
De la misma manera procedemos para el factor bloque:
bartlett.test(telas$Y, telas$Bloques)
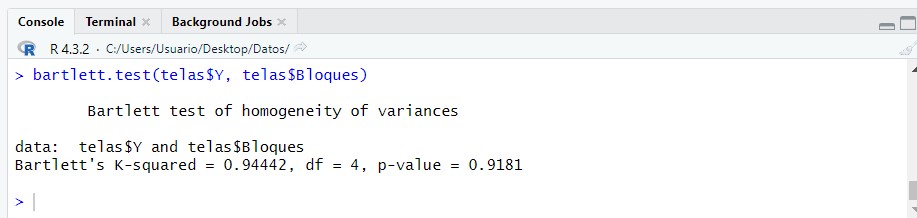
El p-valor es del 0.918 que al ser mayor del nivel de significación usual (5%) no podemos rechazar la hipótesis de igualdad de varianzas en el factor bloque.
Hipótesis de Independencia
Comprobaremos si se satisface el supuesto de independencia entre los residuos. Para ello tenemos que representar un gráfico de los residuos tipificados frente a los pronosticados. En R obtenemos varios gráficos a la vez que están incluidos en la estimación del modelo.
Para verlos de forma correcta hacemos uso de las siguientes órdenes:
layout(matrix(c(1,2,3,4),2,2))
plot(mod)
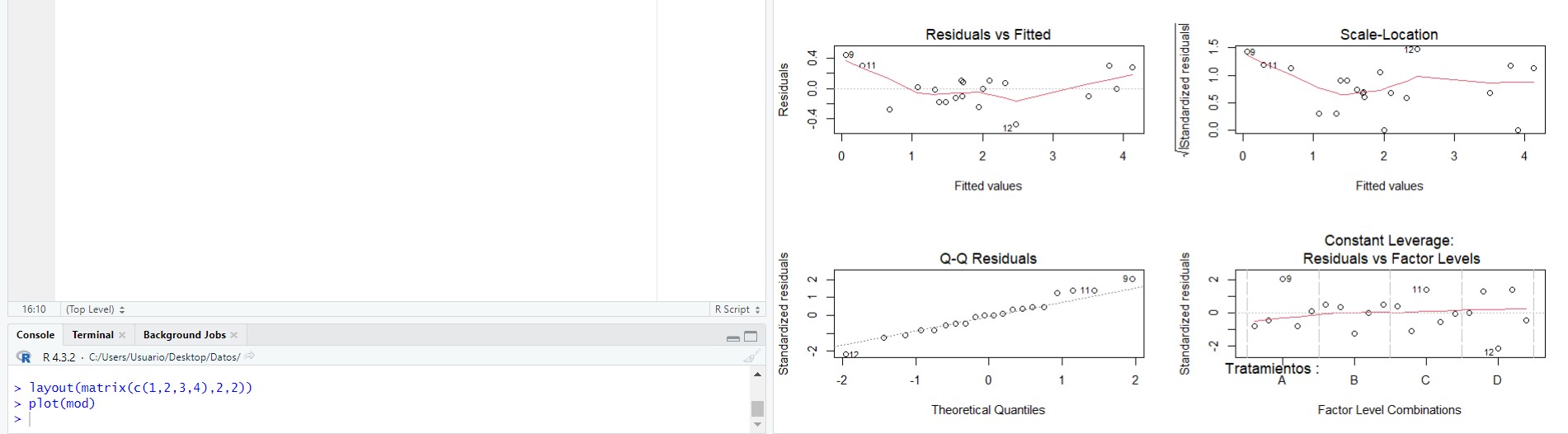
Figura 7: Estudio gráfico de la hipótesis de independencia de los residuos
Nos fijamos en el primer gráfico que representa los residuos frente a los valores ajustados y observamos que no hay ninguna tendencia sistemática. Concluimos que no hay sospechas para que se incumpla la hipótesis de independencia.
Comparaciones múltiples
Hemos probado anteriormente que se rechaza la Hipótesis nula de igualdad de tratamientos y de bloques. Así, las sustancias químicas influyen en la resistencia de la tela. Es decir, existen diferencias significativas en la resistencia de la tela entre las cuatro sustancias químicas. Para saber entre que parejas de sustancias estas diferencias son significativas aplicamos una prueba Post-hoc. Lo mismo ocurre para los bloques.
El contraste de Comparaciones múltiples que vamos a utilizar es el Test de Duncan. Para poder hacer uso de él en R tenemos que instalar en primer lugar el paquete “agricolae” y dentro de él usar la función “duncan.test”. Destacar que este test hace las comparaciones especificándole si es para el factor principal o el factor bloque.
Comenzamos con el factor principal:
install.packages(“agricolae”)
library(“agricolae”)
(duncan=duncan.test(mod, “Tratamiento” , group = T))
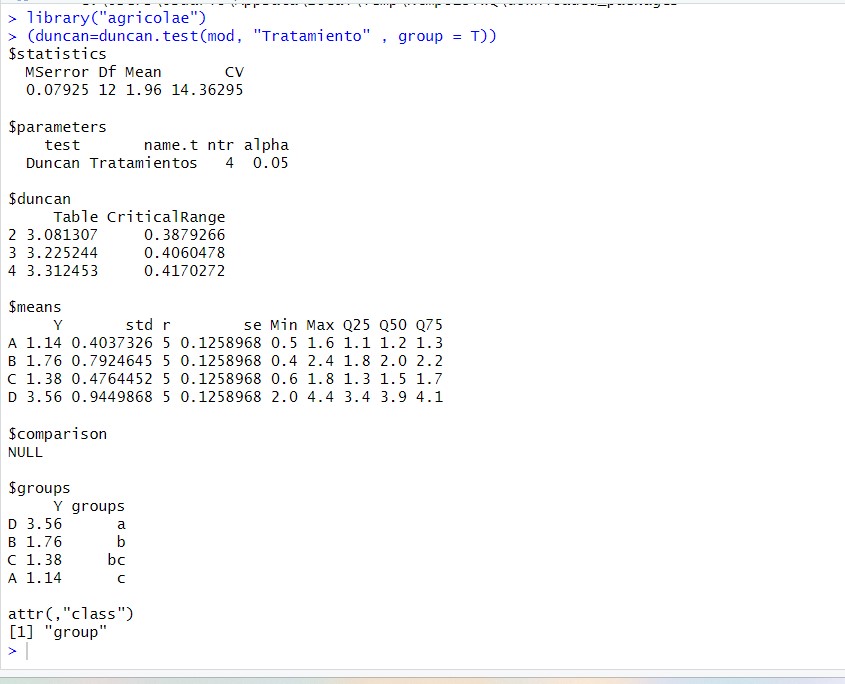
En el apartado “$groups” concluimos que tres sustancias químicas difieren significativamente entre sí (grupos a, b y c para cada sustancia). Vemos como la sustancia “C” comparte subgrupo con la sustancia “A” y la sustancia “B”, es decir, dicha sustancia estaría entre ambos subgrupos (podría pertenecer a ambos), por lo tanto no se diferencia tanto de dichas sustancias.
Se observa que la resistencia media de la tela es mayor con la sustancia química “D” (3.56) y menor con la sustancia “A” (1.14).
Para el factor bloque
(duncan=duncan.test(mod, “Bloques” , group = T))
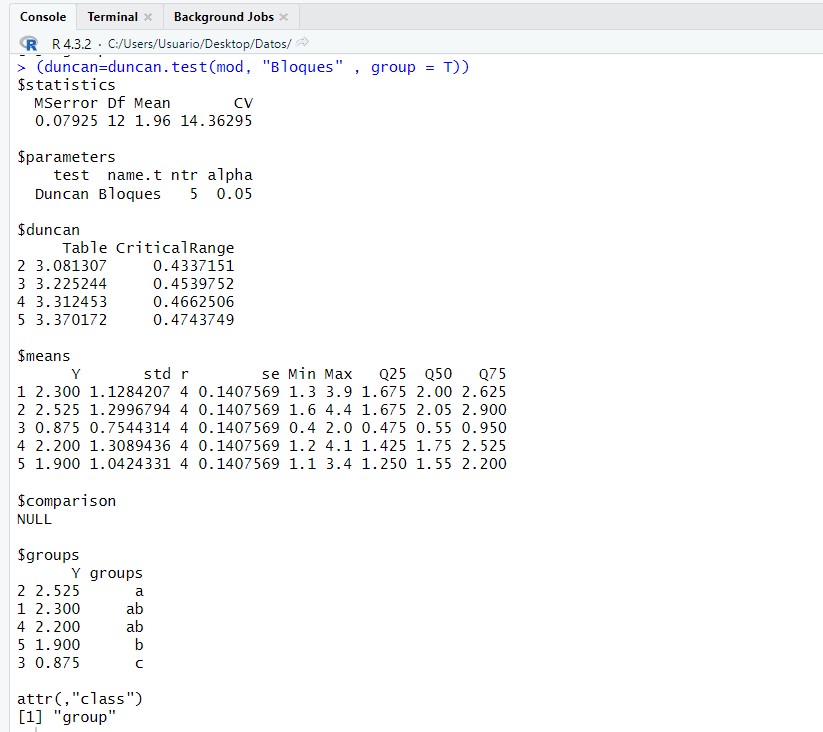
Se observa que la prueba de Duncan ha agrupado las muestras de tela 2,1,4 en un mismo grupo; 1,4,5 en otro grupo y un tercer está formada únicamente por la muestra de tela número 3. Esta difiere de todos los demás, siendo en esta muestra donde se produce la menor resistencia (0.875) y la mayor en la segunda muestra (2.525).
Comandos y funciones utilizadas para resolver el supuesto práctico 3
telas<-read.table(“supuesto3.txt”, header = TRUE)
telas
telas$Tratamientos=factor(telas$Tratamientos)
telas$Bloques=factor(telas$Bloques)
mod <- aov(Y ~ Tratamientos+Bloques, data = telas)
mod
summary(mod)
utils:::menuInstallPkgs()
library(daewr)
Tukey1df(telas)
shapiro.test(mod$residuals)
qqnorm (mod$residuals)
bartlett.test(telas$Y, telas$Tratamiento)
bartlett.test(telas$Y, telas$Bloques)
layout(matrix(c(1,2,3,4),2,2))
plot(mod)
install.packages(“agricolae”)
library(“agricolae”)
(duncan=duncan.test(mod, “Tratamiento” , group = T))
(duncan=duncan.test(mod, “Bloques” , group = T))
Diseño en bloques Incompletos Aleatorizados
En los diseños en bloques Aleatorizados, puede suceder que no sea posible realizar todos los tratamientos en cada bloque. En estos casos es posible usar diseños en bloques Aleatorizados en los que cada tratamiento no está presente en cada bloque. Estos diseños reciben el nombre de diseño en bloque incompleto aleatorizado siendo uno de los más utilizados el diseño en bloque incompleto balanceado (BIB)
El diseño de bloques incompletos balanceado (BIB) compara todos los tratamientos con igual precisión.
Este diseño experimental debe verificar:
-
Cada tratamiento ocurre el mismo número de veces en el diseño.
-
Cada par de tratamientos ocurren juntos el mismo número de veces que cualquier otro par.
Supongamos que se tienen \( I \) tratamientos de los cuales sólo pueden experimentar \( K \) tratamientos en cada bloque \( (K < I) \). Los parámetros que caracterizan este modelo son:
-
\( I \), \( J \) y \( K \) son el número de tratamientos, el número de bloques y el número de tratamientos por bloque, respectivamente.
-
\( R \), número de veces que cada tratamiento se presenta en el diseño, es decir el número de réplicas de un tratamiento dado.
-
\( \lambda \), número de bloques en los que un par de tratamientos ocurren juntos.
-
\( N \), número de observaciones.
Estos parámetros deben verificar las siguientes relaciones:
\( \lambda = R \displaystyle \frac {K-1}{I-1} = \)
Expresión 4: Relación en Bloques Incompletos
donde \( J \geq I \) y \( N = IR = JK \)
- Si \( J = I \) el diseño recibe el nombre de simétrico.
Al igual que en el diseño en bloques completo, la asignación de los tratamientos a las unidades experimentales en cada bloque se debe realizar en forma aleatoria.
Este diseño lo estudiaremos a continuación mediante el supuesto práctico 4
Supuesto práctico 4
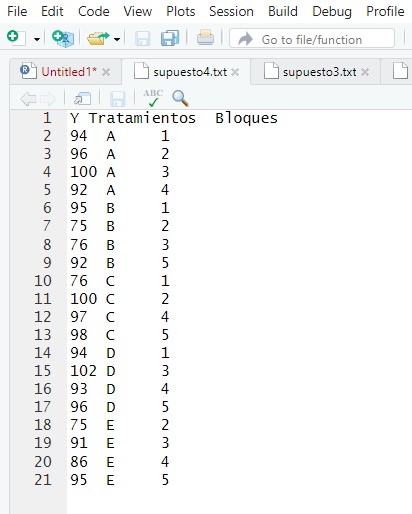
Una industria algodonera, interesada en maximizar el rendimiento de la semilla de algodón, quiere comprobar si dicho rendimiento depende del tipo de fertilizante utilizado para tratar la planta. A su disposición tiene 5 tipos de fertilizantes. Como se cree que el tipo de terreno puede influir también en el rendimiento de la semilla de algodón se considera el terreno dividido en bloques. Para ello, divide el terreno en 5 bloques y cada bloque en 4 parcelas, fumigando dentro de cada bloque cada una de las parcelas con un fertilizante, pero debido a la extensión de los bloques y a la falta de recursos, no se pueden aplicar todos los fertilizantes en cada bloque, sino que sólo se pueden aplicar 4 de los 5 fertilizantes en cada uno de ellos. Al recoger la cosecha se mide el rendimiento de la semilla, obteniéndose las siguientes observaciones que se muestran a continuación :
\( \begin{array} {|c|ccccc|} \hline \text {Tipo de } & & \text{Bloques} & \text{ de } & \text{ terreno} & \\ \text{Fertilizante} & 1 & 2 & 3 & 4 & 5 \\ \hline A & 94 & 96 & 100 & 92 & \\ \hline B & 95 & 75 & 76 & & 92 \\ \hline C & 76 & 100 & & 97 & 98 \\ \hline D & 94 & & 102 & 93 & 96 \\ \hline E & & 75 & 91 & 86 & 95 \\ \hline \end{array} \)
Figura 8: Tabla de datos del Supuesto Práctico 4
En el Supuesto práctico 4:
- Variable respuesta: Rendimiento de la semilla de algodón
- Factor: Tipo de Fertilizante, que tiene 5 niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Bloque: Bloque de terreno, que tiene 5 niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Modelo incompleto: Todos los tratamientos no se prueban en cada bloque.
- Tamaño del experimento: Número total de observaciones (20).
El objetivo principal es estudiar el rendimiento de la semilla de algodón utilizando cuatro tipos de fertilizantes. Sin embrago, como los bloques de terreno son una fuente de variabilidad potencial, consideramos un factor bloque con cinco niveles. Además en este caso:
\( N = I R = J K \) . En efecto, ya que \( N= 20; I = 5 = J ; R = K = 4 \).
\( \lambda = R \displaystyle \frac {K-1}{I-1} = 4 \displaystyle \frac {3}{4} = 3 \)
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio. En este caso lo hacemos en un archivo de texto: En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos. En ese directorio elegimos el fichero “supuesto4.txt y se muestran los datos en la siguiente ventana de RStudio
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
algodon <-read.table(“supuesto4.txt”, header = TRUE)
algodon
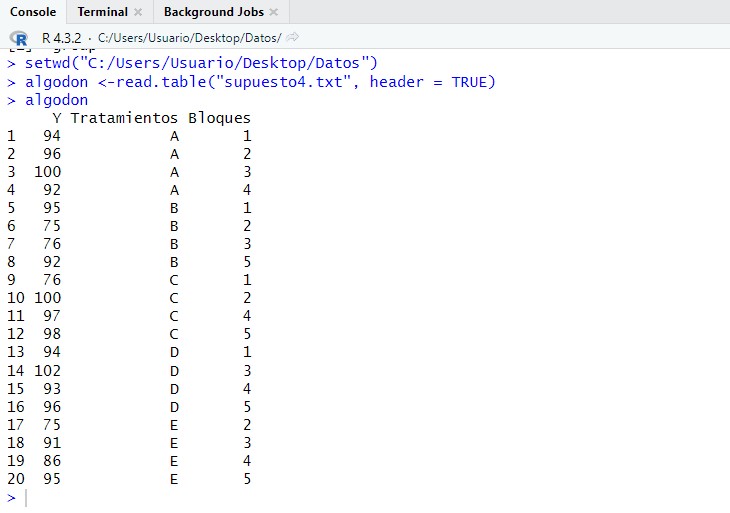
A continuación debemos transformar tanto la columna de los tratamientos como la de los bloques en un factor para poder realizar los cálculos posteriores adecuadamente.
algodon$Tratamientos = factor(algodon$Tratamientos)
algodon$Bloques = factor(algodon$Bloques)
Para poder analizar los datos mediante un diseño BIB debemos instalar y cargar dos paquetes de R especializados en este tipo de diseños:
library(daewr)
library(AlgDesign)
La función “BIBsize(t , k)” de la librería daewr nos permite saber si el diseño puede realizarse. Calcula los parámetros del diseño donde: t = número de niveles del factor tratamiento; k = número de tratamientos por bloque. Ejecutamos:
BIBsize(t = 5 , k = 4)
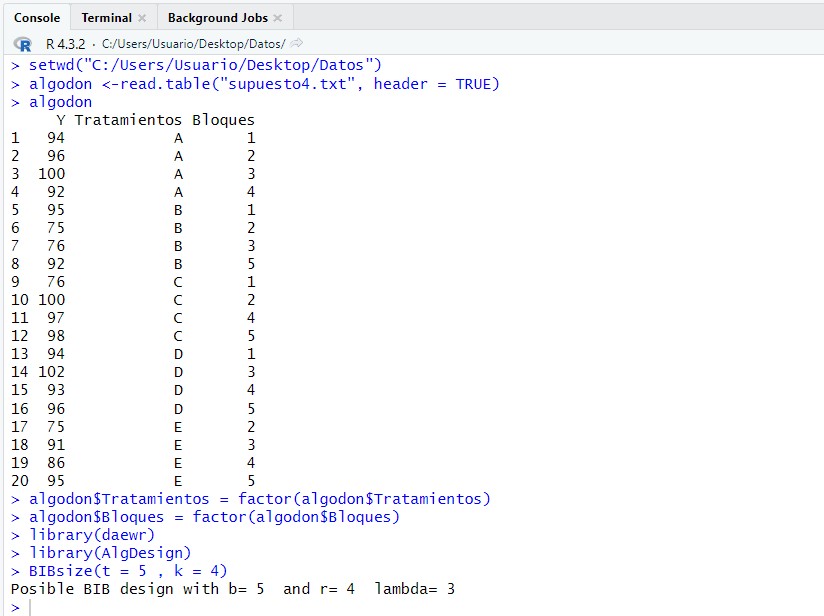
El análisis de este modelo lo podemos realizar en R de dos formas:
1. Realizaremos el análisis evaluando primero el efecto de los tratamientos y después el de los bloques utilizando dos funciones diferentes.
Para evaluar el efecto de los tratamientos, la suma de cuadrados de tratamientos debe ajustarse por bloques, por lo tanto primero se introducen los bloques y después los tratamientos.
Para calcular la tabla ANOVA hacemos uso de la función “aov” (aov(y ~ A + B, data=mydataframe) asume suma de cuadrados tipo I) de la siguiente forma:
mod1 <- aov(Y ~ Bloques + Tratamientos, data = algodon)
mod1
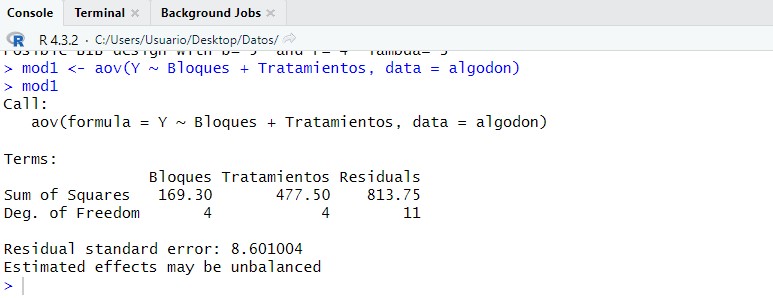
donde:
- Y = nombre de la columna de las observaciones (Rendimiento de la semilla de algodón).
- Tratamientos = nombre de la columna en la que están representados los tratamientos (Tipo de Fertilizante).
- Bloques = nombre de la columna en la que están representados los bloques (Bloque de terreno).
- data = data.frame en el que están guardados los datos
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA)
summary(mod1)
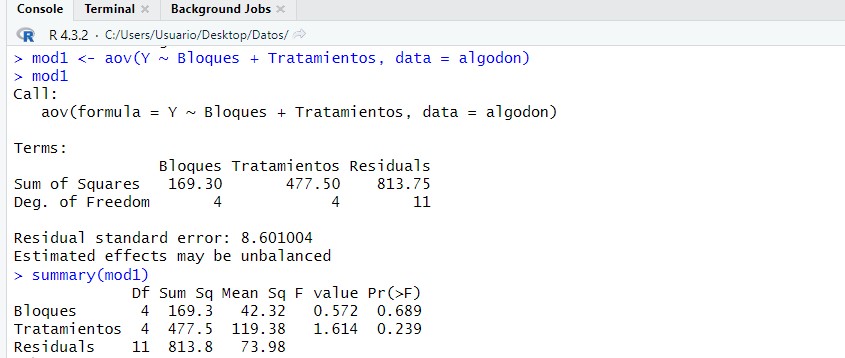
El valor del estadístico de contraste de igualdad, F = 1.614, deja a su derecha un p-valor=0.239, mayor que el nivel de significación del 5%, por lo que no se rechaza la Hipótesis Nula de igualdad de tratamientos. Por lo tanto el tipo de fertilizante no influye en el rendimiento de la semilla de algodón.
Para evaluar el efecto de los bloques, la suma de cuadrados de bloques debe ajustarse por los tratamientos, por lo tanto primero se introducen los tratamientos y después los bloques:
mod2 <- aov(Y ~ Tratamientos + Bloques, data = algodon)
mod2
summary(mod2)
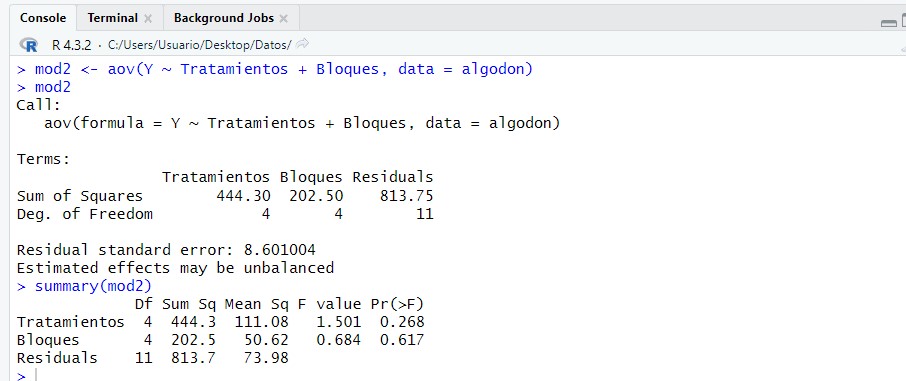
El valor del estadístico de contraste de igualdad, F = 0.684, deja a su derecha un p-valor=0.617, mayor que el nivel de significación del 5%, por lo que no se rechaza la Hipótesis Nula de igualdad de tratamientos. Por lo tanto el bloque de terreno no influye en el rendimiento de la semilla de algodón.
Concluimos por tanto que ni el tipo de fertilizante ni el bloque de terreno influye significativamente en el rendimiento de la semilla de algodón.
Con este ejemplo se ilustra el hecho de decidir si se prescinde o no de los bloques. Hay situaciones en las que, aunque los bloques no resulten significativamente diferentes no es conveniente prescindir de ellos. Pero ¿cómo saber cuándo se puede prescindir de los bloques? La respuesta la tenemos en el valor de la F de los bloques, experimentalmente se ha comprobado que si dicho valor es mayor que 3, no conviene prescindir de los bloque para efectuar los contrastes.
En esta situación si se puede prescindir del efecto de los bloques y estudiar el modelo unifactorial correspondiente, cuyo único factor sería: Tipo de fertilizante.
2. Realizaremos el análisis evaluando tanto para los tratamientos como para los bloques ejecutando solo una función.
Para ello necesitamos instalar y cargar el paquete “car”, mediante la función “install.packages” para instalarlo y “library” para cargarlo. Una vez instalado cargado el paquete realizamos el ANOVA usando la función “lm”.
mod3 <- lm(Y ~ Tratamientos + Bloques, data = algodon)
mod3
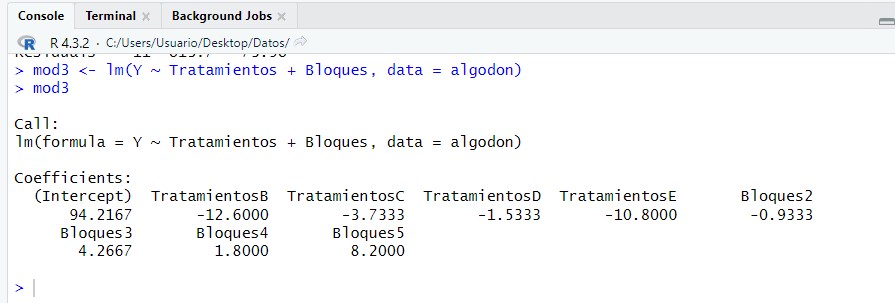
Para mostrar el resumen de los resultados, que antes hacíamos con la función “summary”, debemos usar la función “Anova” de la siguiente manera:
install.packages(“car”)
library(car)
car::Anova(mod3, type=”III”)
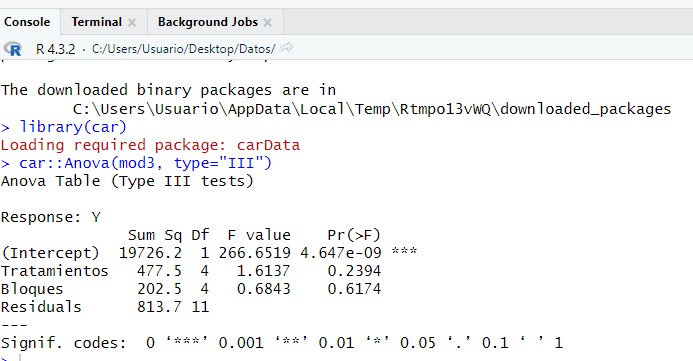
Obteniendo de esta manera los mismos resultados que con el anterior procedimiento.
Comandos y funciones utilizadas para resolver el supuesto práctico 4
algodon <-read.table(“supuesto4.txt”, header = TRUE)
algodon
algodon$Tratamientos = factor(algodon$Tratamientos)
algodon$Bloques = factor(algodon$Bloques)
library(daewr)
library(AlgDesign)
BIBsize(t = 5 , k = 4)
mod1 <- aov(Y ~ Bloques + Tratamientos, data = algodon)
mod1
summary(mod1)
mod2 <- aov(Y ~ Tratamientos + Bloques, data = algodon)
mod2
summary(mod2)
mod3 <- lm(Y ~ Tratamientos + Bloques, data = algodon)
mod3
install.packages(“car”)
library(car)
car::Anova(mod3, type=”III”)
Diseño en Cuadrados Latinos
Hemos estudiado en el apartado anterior que los diseños en bloques completos aleatorizados utilizan un factor de control o variable de bloque con objeto de eliminar su influencia en la variable respuesta y así reducir el error experimental. Los diseños en cuadrados latinos utilizan dos variables de bloque para reducir el error experimental.
Un inconveniente que presentan a veces los diseños es el de requerir excesivas unidades experimentales para su realización. Un diseño en bloques completos con un factor principal y dos factores de bloque, con \( K1 \), \( K2 \) y \( K3 \) niveles en cada uno de los factores, requiere \( K1 \times K2 \times K3 \) unidades experimentales. En un experimento puede haber diferentes causas, por ejemplo de índole económico, que no permitan emplear demasiadas unidades experimentales, ante esta situación se puede recurrir a un tipo especial de diseños en bloques incompletos aleatorizados. La idea básica de estos diseños es la de fracción es decir, seleccionar una parte del diseño completo de forma que, bajo ciertas hipótesis generales, permita estimar los efectos que interesan.
Uno de los diseños en bloques incompletos aleatorizados más importante con dos factores de control es el modelo en cuadrado latino, dicho modelo requiere el mismo número de niveles para los tres factores.
En general, para \( K \) niveles en cada uno de los factores, el diseño completo en bloques aleatorizados utiliza \( K^2 \) bloques, aplicándose en cada bloque los \( K \) niveles del factor principal, resultando un total de \( K^3 \) unidades experimentales.
Los diseños en cuadrado latino reducen el número de unidades experimentales a \( K^2 \) utilizando los \( K^2 \) bloques del experimento, pero aplicando sólo un tratamiento en cada bloque con una disposición especial. De esta forma, si \( K \) fuese 4, el diseño en bloques completos necesitaría \( 4^3 = 64 \) observaciones, mientras que el diseño en cuadrado latino sólo necesitaría \( 4^2 = 16 \) observaciones.
Los diseños en cuadrados latinos son apropiados cuando es necesario controlar dos fuentes de variabilidad. En dichos diseños el número de niveles del factor principal tiene que coincidir con el número de niveles de las dos variables de bloque o factores secundarios y además hay que suponer que no existe interacción entre ninguna pareja de factores.
Recibe el nombre de cuadrado latino de orden \( K \) a una disposición en filas y columnas de \( K \) letras latinas, de tal forma que cada letra aparece una sola vez en cada fila y en cada columna.
En resumen, podemos decir que un diseño en cuadrado latino tiene las siguientes características:
-
Se controlan tres fuentes de variabilidad, un factor principal y dos factores de bloque.
-
Cada uno de los factores tiene el mismo número de niveles, \( K \).
-
Cada nivel del factor principal aparece una vez en cada fila y una vez en cada columna.
-
No hay interacción entre los factores.
En el Fichero-Adjunto se muestran algunos cuadrados latinos estándares para los órdenes 3, 4, 5, 6, 7, 8 y 9.
Este diseño lo estudiaremos a continuación mediante el supuesto práctico 5
Supuesto práctico 5
Un laboratorio utiliza 4 hornos en la fabricación de un determinado producto. Se sospecha que la temperatura afecta a la dureza del producto obtenido. Cada horno puede operar a 4 temperaturas distintas. Se sabe que cada horno tiene sus propias características de operación, de modo que los hornos se consideran una variable influyente en la fabricación de dicho producto. Además el analista piensa que 4 procedimientos de fabricación (A, B, C, D) pueden ser una fuente de variabilidad, por ello decide utilizar un cuadrado latino que se muestra a continuación.
\( \begin{array} {|c|cccc|} \hline \text {Temperatura } & & & \text{Hornos} & \\ & 1 & 2 & 3 & 4 \\ \hline 80 & B6 & C10 & D8& A5 \\ \hline 90 & C7 & D11 & A13& B8 \\ \hline 100 & D7 & A15 & B11 & C8 \\ \hline 110 & A8 & B12 & C10 & D9 \\ \hline \end{array} \)
Figura 10: Tabla de datos del Supuesto Práctico 5
En el Supuesto práctico 5:
- Variable respuesta: Dureza del producto.
- Factor: Temperatura, que tiene 4 niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Bloque: Tipo de horno y procedimiento de fabricación, ambos con 4 niveles y son factores de efectos fijos.
- Tamaño del experimento: Número total de observaciones (16).
El objetivo principal es estudiar la influencia de las distintas temperaturas en la dureza del producto. Sin embargo, como los hornos y las procedimientos de fabricación son dos fuentes de variabilidad potencial, consideramos dos factores de bloque con cuatro niveles cada uno.
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio. En este caso lo hacemos en un archivo de texto:
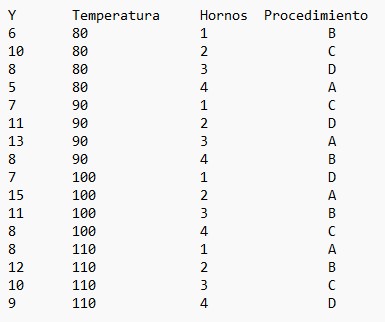
Figura 11: Tabla de datos del Supuesto Práctico 5
En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos. En ese directorio elegimos el fichero “supuesto5.txt y se muestran los datos en la siguiente ventana de RStudio
dureza <- read.table(“supuesto5.txt”, header = TRUE)
dureza
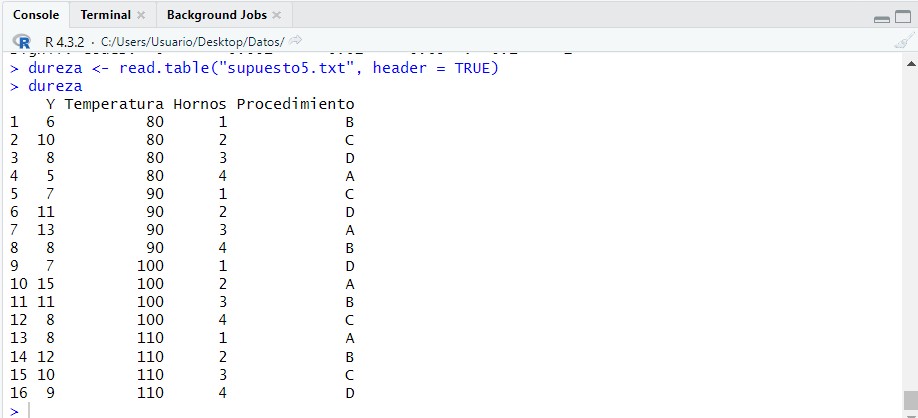
A continuación debemos transformar tanto la columna de los tratamiento como la de los bloques en un factor para podemos realizar los cálculos posteriores adecuadamente.
dureza$Temperatura <- factor(dureza$Temperatura)
dureza$Hornos <- factor(dureza$Hornos)
dureza$Procedimiento <- factor(dureza$Procedimiento)
Para calcular la tabla ANOVA en RStudio, primero hacemos uso de la función “aov” de la siguiente forma:
mod <- aov(Y ~ Temperatura + Hornos + Procedimiento, data = dureza)
mod
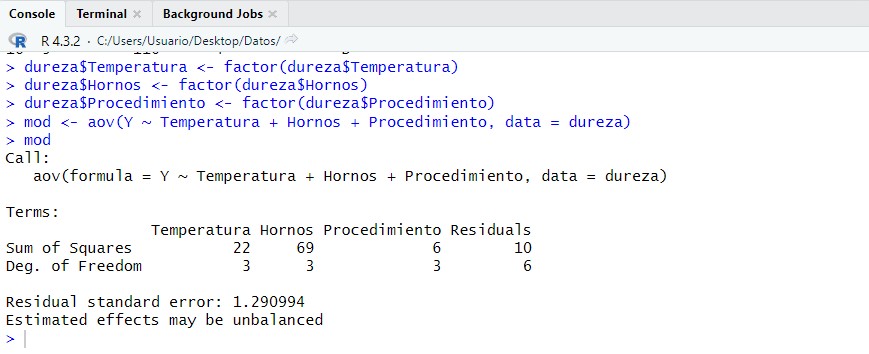
donde:
- Y: Nombre de la columna de las observaciones (Dureza del producto).
- Temperatura: Nombre de la columna en la que está representado el factor principal.
- Hornos: Nombre de la columna en la que está representado el primer bloque.
- Procedimiento: Nombre de la columna en la que está representado el segundo bloque.
- data: data.frame en el que están guardados los datos.
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
summary(mod)
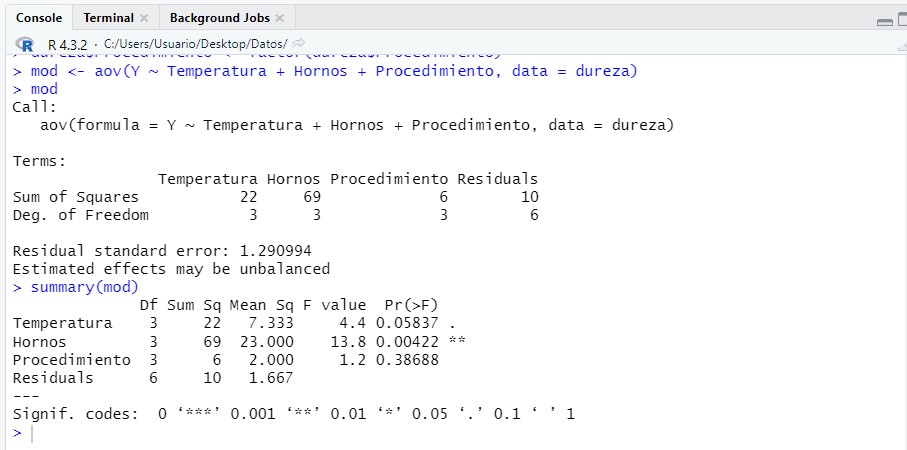
Observando los resultados de los p-valores, 0.058, 0.004, 0.387, deducimos que el único efecto significativo, al nivel de significación del 5%, es el asociado al bloque tipo de hornos. También vemos como el factor Temperatura también podría ser influyente (mayor que 5% pero muy cercano). Probamos a simplificar el modelo eliminando los factores no significativos, que en este caso es el referente al procedimiento de fabricación.
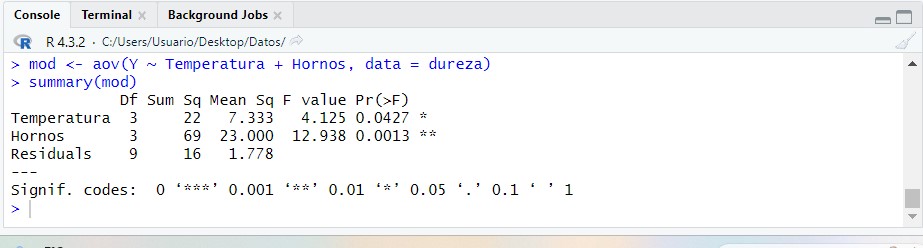
En este nuevo modelo simplificado observamos como ambos factores son significativos, al nivel de significación del 5%, ya que sus p-valores son menores que 0.05. Es decir, tanto la temperatura como el tipo de horno influye significativamente en la dureza del producto fabricado.
Comandos y funciones utilizadas para resolver el supuesto práctico 5
dureza <- read.table(“supuesto5.txt”, header = TRUE)
dureza
dureza$Temperatura <- factor(dureza$Temperatura)
dureza$Hornos <- factor(dureza$Hornos)
dureza$Procedimiento <- factor(dureza$Procedimiento)
mod <- aov(Y ~ Temperatura + Hornos + Procedimiento, data = dureza)
mod
summary(mod)
mod <- aov(Y ~ Temperatura + Hornos, data = dureza)
summary(mod)
Diseño en Cuadrados Greco-Latinos
El modelo en cuadrado greco-latino se puede considerar como una extensión del modelo en cuadrado latino en el que se incluye una tercera variable control o variable de bloque. En este modelo como en el diseño en cuadrado latino, todos los factores deben tener el mismo número de niveles, \( K \), y el número de observaciones necesarias sigue siendo \( K^2 \). Este diseño es, por tanto, una fracción del diseño completo en bloques aleatorizados con un factor principal y tres factores secundarios que requeriría \( K^4 \) observaciones.
Los cuadrados greco-latinos se obtienen por superposición de dos cuadrados latinos del mismo orden y ortogonales entre sí, uno de los cuadrados con letras latinas el otro con letras griegas. Dos cuadrados reciben el nombre de ortogonales si, al superponerlos, cada letra latina y griega aparecen juntas una sola vez en el cuadrado resultante.
En el Fichero-Adjunto se muestra una tabla de cuadrados latinos que dan lugar, por superposición de dos de ellos, a cuadrados greco-latinos. Notamos que no es posible formar cuadrados greco-latinos de orden 6.
La Tabla siguiente ilustra un cuadrado greco-latino para \( K= 4 \),
\( \begin{array} {|c|c|c|c|} \hline A & B & C & D \\ \alpha & \beta & \gamma & \delta \\ \hline D & C & B & A \\ \gamma & \delta & \alpha & \beta \\ \hline B & A & D & C \\ \delta & \gamma & \beta & \alpha \\ \hline C & D & A & B \\ \beta & \alpha & \delta & \gamma \\ \hline \end{array} \)
Figura 12: Ejemplo de un cuadrado greco-latino para K=4
Este diseño lo estudiaremos a continuación mediante el supuesto práctico 6.
Supuesto práctico 6
El rendimiento de un determinado cultivo se midió utilizando 4 tipos de abonos, 4 tipos de terreno, 4 insecticidas (A, B, C, y D) y 4 tipos de semillas (α, ẞ, γ y δ). Se utilizo un diseño en cuadrado greco-latino que proporcionó las siguientes observaciones.
\( \begin{array} {|c|c|c|c|c|} \hline \text { Tipo de } & \text {Cuatro} & \text {Tipos } & \text {de} & \text {terreno} \\ \text {Abono } & 1 & 2 & 3 & 4 \\ \hline 1 & 12 & 11 & 15 & 11 \\ & \alpha B & \delta C & \gamma A & \beta D \\ \hline 2 & 17 & 18 & 15 & 16 \\ & \delta A & \alpha D & \beta B & \gamma C \\ \hline 3 & 19 & 15 & 17 & 10 \\ & \gamma D & \beta A & \alpha C & \delta B \\ \hline 4 & 11 & 12 & 19 & 18 \\ & \beta C & \gamma B & \delta D & \alpha A \\ \hline \end{array} \)
Figura 13: Tabla de datos del Supuesto Práctico 6
En el Supuesto práctico 6:
- Variable respuesta: Rendimiento del cultivo.
- Factor: Insecticida, que tiene 4 niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Bloque: Abono, Tipo de terreno y tipo de semilla, cada uno con 4 niveles y son factores de efectos fijos.
- Tamaño del experimento: Número total de observaciones (16).
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio. En este caso lo hacemos en un archivo de texto.
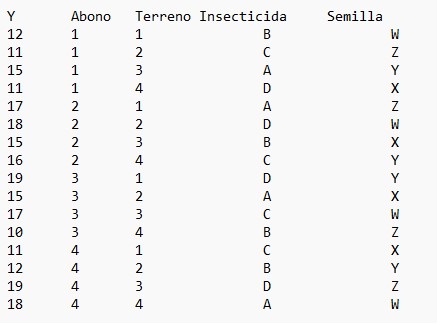
Figura 14: Tabla de datos del Supuesto Práctico 6
En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos.
En ese directorio elegimos el fichero “supuesto5.txt y se muestran los datos en la siguiente ventana de RStudio
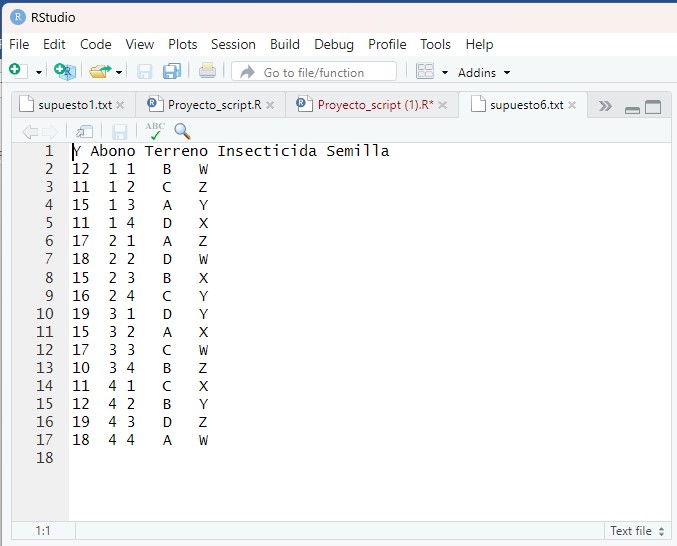
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
cultivo <- read.table(“supuesto6.txt”, header = TRUE)
A continuación debemos transformar tanto la columna de los tratamiento como la de los bloques en un factor para podemos realizar los cálculos posteriores adecuadamente
cultivo$Abono = factor(cultivo$Abono)
cultivo$Terreno = factor(cultivo$Terreno)
cultivo$Insecticida = factor(cultivo$Insecticida)
cultivo$Semilla = factor(cultivo$Semilla)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
mod <- aov(Y ~ Abono + Terreno + Insecticida + Semilla, data = cultivo)
mod
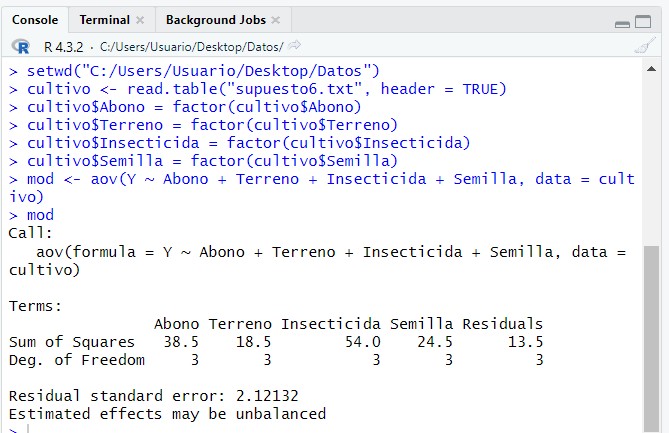
donde:
- Y: Nombre de la columna de las observaciones (Rendimiento del cultivo).
- Abono: Nombre de la columna en la que está representado el primer bloque.
- Terreno: Nombre de la columna en la que está representado el segundo bloque.
- Semilla: Nombre de la columna en la que está representado el tercer bloque.
- Insecticida: Nombre de la columna en la que está representado el factor principal.
- data: data.frame en el que están guardados los datos.
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
summary(mod)
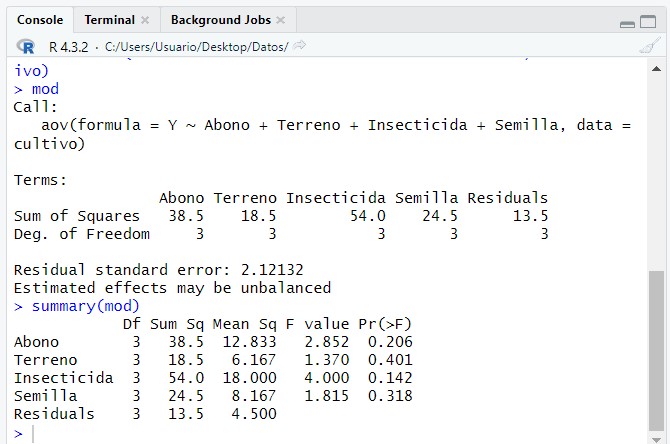
Observando los resultados de los p-valores, 0.206, 0.401, 0.142 y 0.318, deducimos que no hay ningún efecto significativo, al nivel de significación del 5%. Es decir, ninguno de los factores estudiados influyen significativamente en el rendimiento de los cultivos.
Comandos y funciones utilizadas para resolver el supuesto práctico 6
cultivo <- read.table(“supuesto6.txt”, header = TRUE)
cultivo$Abono = factor(cultivo$Abono)
cultivo$Terreno = factor(cultivo$Terreno)
cultivo$Insecticida = factor(cultivo$Insecticida)
cultivo$Semilla = factor(cultivo$Semilla)
mod <- aov(Y ~ Abono + Terreno + Insecticida + Semilla, data = cultivo)
mod
summary(mod)
Diseño en Cuadrados de Youden
Hemos estudiado que en el diseño en cuadrado latino se tiene que verificar que los tres factores tengan el mismo número de niveles, es decir que hay el mismo número de filas, de columnas y de letras latinas. Sin embargo, puede suceder que el número de niveles disponibles de uno de los factores de control sea menor que el número de tratamientos, en este caso estaríamos ante un diseño en cuadrado latino incompleto. Estos diseños fueron estudiados por W.J. Youden y se conocen con el nombre de cuadrados de Youden.
Este diseño lo estudiaremos a continuación mediante el supuesto práctico 7.
Supuesto práctico 7
Una empresa de ingeniería industrial está estudiando el efecto de 5 niveles de iluminación (A, B, C, D, E) en la presencia de defectos en un ensamblado. El tiempo puede ser un factor de variación, por eso decide hacer el experimento en 5 días. Pero el departamento que realiza el experimento solo posee 4 estaciones de trabajo que a su vez pueden ser una fuente de variación. Los datos se muestran en la siguiente tabla.
\( \begin{array} {|c|c|c|c|c|} \hline & \text {Cuatro} & \text {estaciones} & \text {de } & \text {trabajo} \\ \hline \text { Días } & 1 & 2 & 3 & 4 \\ \hline 1 & A 3 & B 1 & C 2 & D 0 \\ \hline 2 & B 0 & C 0 & D 1 & E 7 \\ \hline 3 & C 1 & D 0 & E 5 & A 3 \\ \hline 4 & D 1 & E 6 & A 4 & B 0 \\ \hline 5 & E 5 & A 2 & B 1 & C 1 \\ \hline \end{array} \)
Figura 15: Tabla de datos del Supuesto Práctico 7
En el Supuesto práctico 7:
- Variable respuesta: Número de defectos en un ensamblado.
- Factor: Niveles de iluminación, que tiene 5 niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Bloque: Día y Estación de trabajo, con 5 y 4 niveles, respectivamente, y ambos son factores de efectos fijos.
- Tamaño del experimento: Número total de observaciones (20).
El objetivo principal es estudiar la influencia de cinco niveles de iluminación en la presencia de defectos en un ensamblado. Sin embargo, como los días en los que se realiza el experimento y las estaciones de trabajo son dos fuentes de variabilidad potencial, consideramos dos factores de bloque con cinco y cuatro niveles, respectivamente.
Recordamos que los parámetros que caracterizan este modelo son:
- \( I, J \) y \( K \) son el número de tratamientos, el número de bloques y el número de tratamientos por bloque, respectivamente.
- \( R \), número de veces que cada tratamiento se presenta en el diseño, es decir el número de réplicas de un tratamiento dado.
- \( \lambda \), número de bloques en los que un par de tratamientos ocurren juntos.
- \( N \), número de observaciones.
Por lo cual los valores de los parámetros del modelo en este ejemplo son:
\( N = I R = J K \) . En efecto, ya que \( N= 30; I = 5 = J ; R = K = 4 \).
\( \lambda = R \displaystyle \frac {K-1}{I-1} = 4 \displaystyle \frac {3}{4} = 3 \)
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio.
En este caso lo hacemos en un archivo de texto:
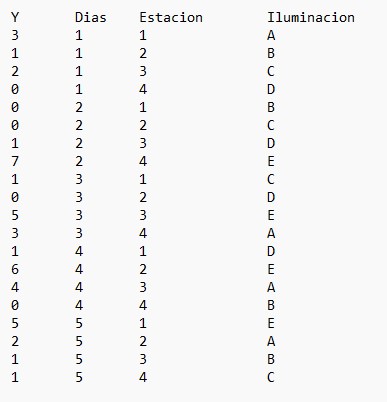
Figura 16: Tabla de datos del Supuesto Práctico 7
En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos.
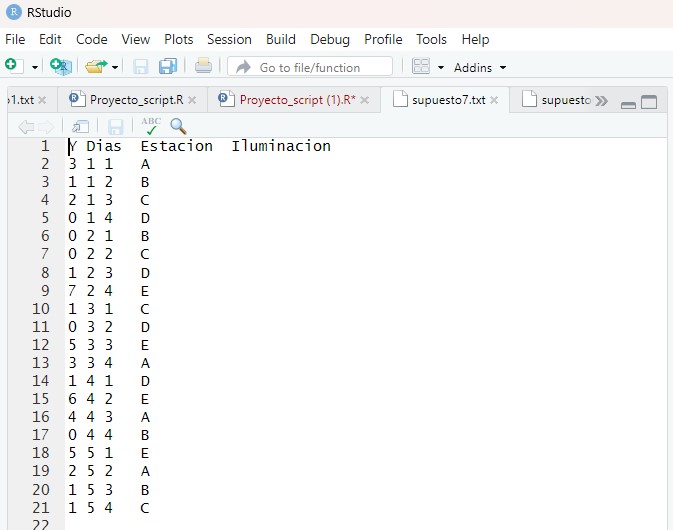
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
defectos <- read.table(“supuesto7.txt”, header = TRUE)
A continuación debemos transformar tanto la columna de los tratamiento como la de los bloques en un factor para podemos realizar los cálculos posteriores adecuadamente:
defectos$Dias = factor(defectos$Dias)
defectos$Estacion = factor(defectos$Estacion)
defectos$Iluminación = factor(defectos$Iluminacion)
Para cada factor realizamos una tabla ANOVA:
- Factor principal: Niveles de iluminación.
Para evaluar el efecto de los tratamientos, la suma de cuadrados de tratamientos debe ajustarse por bloques, por lo tanto primero se introducen los bloques y después los tratamientos.
Para calcular la tabla ANOVA hacemos uso de la función “aov” (asume suma de cuadrados tipo I) de la siguiente forma:
mod1 <- aov(Y ~ Dias + Estacion + Iluminación, data = defectos)
mod1
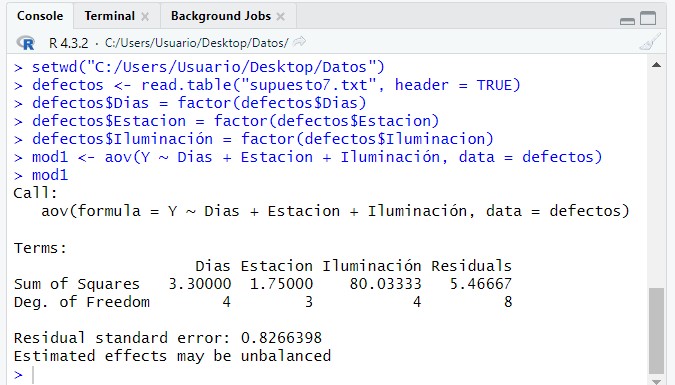
donde:
- Y: Nombre de la columna de las observaciones (Número de defectos en un ensamblado).
- Días: Nombre de la columna en la que está representado el primer bloque.
- Estación: Nombre de la columna en la que está representado el segundo bloque.
- Iluminación: Nombre de la columna en la que está representado el factor principal.
- data: data.frame en el que están guardados los datos.
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
summary(mod1)
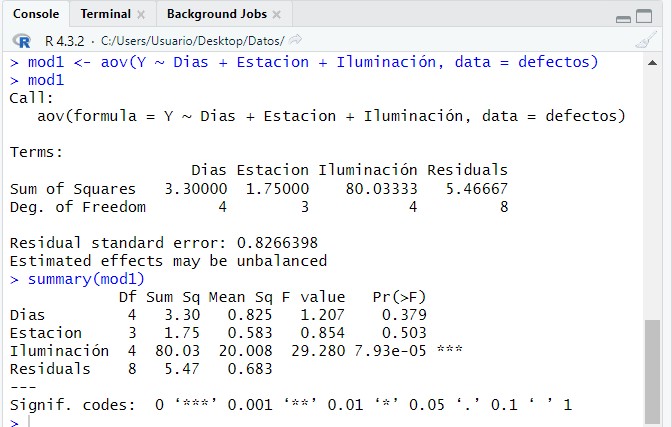
El p-valor=0.00007, es menor que el nivel de significación del 5%, por lo que deducimos que el factor principal: niveles de iluminación es significativo. Es decir, los niveles de iluminación influyen significativamente en el número de defectos del ensamblado.
- Factor Bloques: Días
Para evaluar el efecto del primero de los bloques en RStudio, la suma de cuadrados de bloques debe ajustarse por los tratamientos, por lo tanto primero se introducen los tratamientos (y el resto de bloques) y después los bloques en estudio:
mod2 <- aov(Y ~ Iluminación + Estacion + Dias, data = defectos)
mod2
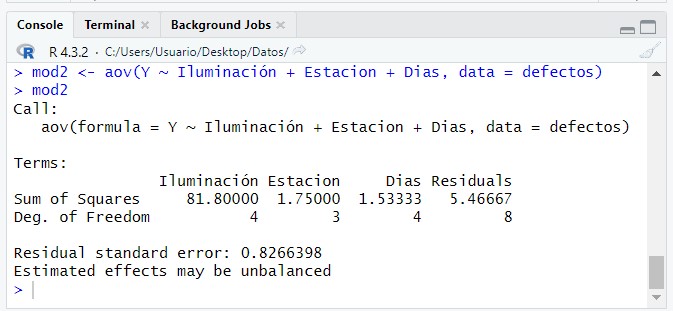
summary(mod2)
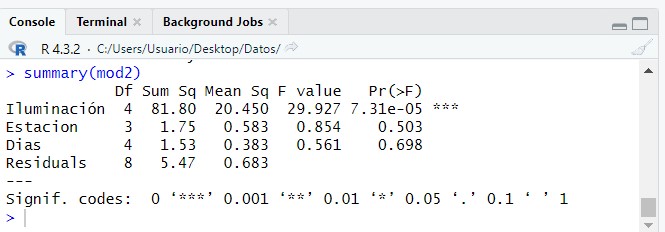
El p-valor=0.698, es mayor que el nivel de significación del 5%, por lo que deducimos que el factor bloque: días no es significativo. Es decir, los días en los que se realiza el experimento no influyen significativamente en el número de defectos del ensamblado.
- Factor Bloques: Estación de Trabajo
Para evaluar el efecto del primero de los bloques, la suma de cuadrados de bloques debe ajustarse por los tratamientos, por lo tanto primero se introducen los tratamientos (y el resto de bloques) y después los bloques en estudio:
mod3 <- aov(Y ~ Iluminación + Dias + Estacion, data = defectos)
mod3
summary(mod3)
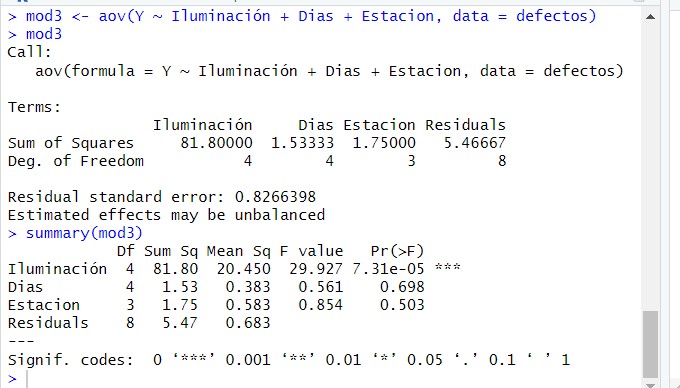
El p-valor=0.503, es mayor que el nivel de significación del 5%, por lo que deducimos que el factor bloque: estación de trabajo no es significativo. Es decir, las estaciones de trabajo en las que se realiza el experimento no influyen significativamente en el número de defectos del ensamblado.
Viendo estos resultados concluimos que en el número de defectos del ensamblado estudiado solo influyen significativamente los distintos niveles de iluminación.
Comandos y funciones utilizadas para resolver el supuesto práctico 7
defectos <- read.table(“supuesto7.txt”, header = TRUE)
defectos$Dias = factor(defectos$Dias)
defectos$Estacion = factor(defectos$Estacion)
defectos$Iluminación = factor(defectos$Iluminacion)
mod1 <- aov(Y ~ Dias + Estacion + Iluminación, data = defectos)
mod1
summary(mod1)
mod2 <- aov(Y ~ Iluminación + Estacion + Dias, data = defectos)
mod2
summary(mod2)
mod3 <- aov(Y ~ Iluminación + Dias + Estacion, data = defectos)
mod3
summary(mod3)
Diseños Factoriales
En muchos experimentos es frecuente considerar dos o más factores y estudiar el efecto conjunto que dichos factores producen sobre la variable respuesta. Para resolver esta situación se utiliza el Diseño Factorial.
Se entiende por diseño factorial aquel diseño en el que se investigan todas las posibles combinaciones de los niveles de los factores en cada réplica del experimento. En estos diseños, los factores que intervienen tienen la misma importancia a priori y se supone por tanto, la posible presencia de interacción. En este epígrafe vamos a considerar únicamente modelos de efectos fijos.
Diseños factoriales con dos factores
En primer lugar vamos a estudiar los diseños más simples, es decir aquellos en los que intervienen sólo dos factores. Supongamos que hay \( a \) niveles para el factor \( A \) y \( b \) niveles del factor \( B \), cada réplica del experimento contiene todas las posibles combinaciones de tratamientos, es decir contiene los \( ab \) tratamientos posibles.
El modelo sin replicación
El modelo estadístico para este diseño es:
\( y_{ij}=\mu+\tau_i+ \beta_j + (\tau \beta)_{ij} + u_{ij},~~~~ i=1,…,a; ~~~ j=1,…,b ~~~~, ~~~~ \) donde
Expresión 16: Modelo estadístico del diseño factorial de dos factores sin replicación
- \( y_{ij} \): Representa la observación correspondiente al nivel (i) del factor \( A \) y al nivel (j) del factor \( B \).
-
\( \mu \): Efecto constante, común a todos los niveles de los factores, denominado media global.
-
\( \tau_i \): Efecto producido por el nivel i-ésimo del factor \( A \), ( \( \sum_i \tau_i = 0 \)).
-
\( \beta_j \): Efecto producido por el nivel j-ésimo del factor \( B \), \( \sum_j \beta_j = 0 \) ).
-
\( (\tau \beta)_{ij} \): Efecto producido por la interacción entre \( A \times B \), ( \( \sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij} = 0 \) ).
-
\( u_{ij} \) son vv aa. independientes con distribución N(0,σ).
Supondremos que se toma una observación por cada combinación de factores, por tanto, hay un total de \( N = ab \) observaciones.
Parámetros a estimar:
\( \begin{array} {|c|c|} \hline \text {Parámetros} & \text {Número} \\ \hline \mu & 1 \\ \hline \tau_i & a-1 \\ \hline \beta_j & b-1 \\ \hline (\tau \beta)_{ij} & (a-1)(b-1) \\ \hline \sigma^2 & 1 \\ \hline Total &ab -1 \\ \hline \end{array} \)
Figura 17: Tabla del número de parámetros a estimar
A pesar de las restricciones impuestas al modelo,
\( \sum_i \tau_i = \sum_j \beta_j = \sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij} = 0 \)
el número de parámetros \( (ab + 1) \) supera al número de observaciones \( (ab) \). Por lo tanto, algún parámetro no será estimable.
Los residuos de este modelo son nulos, \( e_{ij} = 0 \), por lo tanto no es posible estimar la varianza del modelo y no se pueden contrastar la significatividad de los efectos de los factores. Dichos contrates sólo pueden realizarse si:
- Suponemos que la interacción entre \( A \times B \) es cero.
- Replicamos el experimento (Tomamos varias observaciones por cada combinación de factores).
Supuesto práctico 8
En unos laboratorios se está estudiando los factores que influyen en la resistencia de un tipo particular de fibra. Se eligen al azar cuatro máquinas y tres operarios y se realiza un experimento factorial usando fibras de un mismo lote de producción. Los resultados obtenidos se muestran en la tabla adjunta. Analizar los resultados y obtener las conclusiones apropiadas.
\( \begin{array} {|c|c|c|c|c|} \hline & \text {Cuatro} & \text {Tipos } & \text {de} & \text {máquinas} \\ \hline \text {Operario } & A & B & C & D \\ \hline 1 & 109 & 110 & 108 & 110 \\ \hline 2 & 110 & 110 & 111 & 114 \\ \hline 3 & 116 & 112 & 114 & 120 \\ \hline \end{array} \)
Figura 18: Tabla de datos del Supuesto Práctico 8
En el Supuesto práctico 8:
- Variable respuesta: Resistencia de una fibra.
- Factor: Operario, que tiene tres niveles.
- Factor: Tipo de máquina, que tiene cuatro niveles.
- Ambos factores de efectos fijos, ya que viene decidido qué niveles concretos se van a utilizar.
- Tamaño del experimento: Número total de observaciones (24).
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio.
En este caso lo hacemos en un archivo de texto:
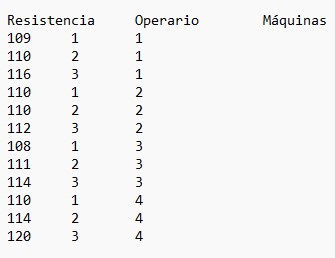
Figura 19: Tabla de datos del Supuesto Práctico 8
En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos.
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
factorial <- read.table(“supuesto8.txt”, header = TRUE)
A continuación debemos transformar todas las columnas que contienen a los factores en un factor para podemos realizar los cálculos posteriores adecuadamente.
factorial$Operario = factor(factorial$Operario)
factorial$Máquinas = factor(factorial$Máquinas)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma
mod3 <- aov(Resistencia ~ Operario + Máquinas, data = factorial)
mod3
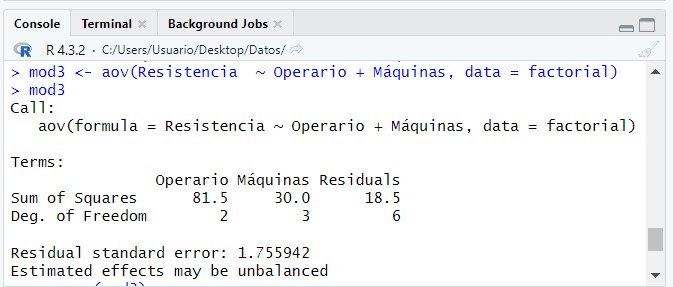
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
summary(mod3)
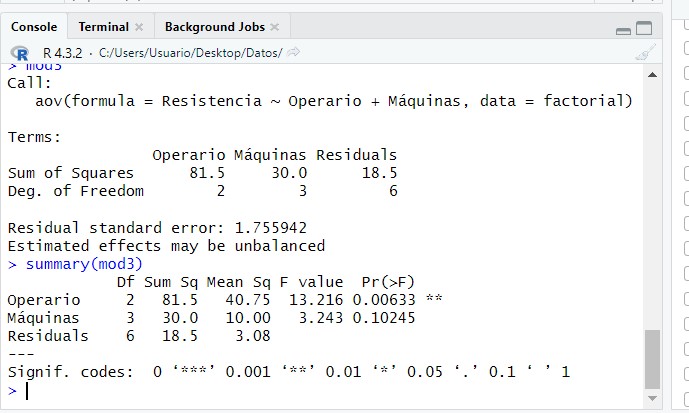
Esta Tabla ANOVA recoge la descomposición de la varianza considerando como fuente de variación los doce tratamientos o grupos que se forman al combinar los niveles de los dos factores. En dicha Tabla se indica que, para un nivel de significación del 5%, los efectos que son significativos del modelo planteado son los referentes al factor tipo de operario (p-valor=0.00633). Descartamos por tanto el efecto del factor tipo de máquinas.
Concluimos por tanto que la resistencia de la fibra dependerá exclusivamente del tipo operario que la produzca.
Comandos y funciones utilizadas para resolver el supuesto práctico 8
factorial <- read.table(“supuesto8.txt”, header = TRUE)
factorial$Operario = factor(factorial$Operario)
factorial$Máquinas = factor(factorial$Máquinas)
mod3 <- aov(Resistencia ~ Operario + Máquinas, data = factorial)
mod3
summary(mod3)
El modelo con replicación
El modelo estadístico para este diseño es:
\( y_{ijk}=\mu+\tau_i+ \beta_j + (\tau \beta)_{ij} + u_{ijk},~~~~ i=1,…,a; ~~~ j=1,…,b, ~~~k=1,…,r ~~~~, ~~~~ \) donde
Expresión 17: Modelo estadístico del diseño factorial de dos factores con replicación
donde \( r \) es el número de replicaciones y \( N = abr \) es el número de observaciones.
El número de parámetros de este modelo es, como en el modelo de dos factores sin replicación, \( ab+1 \) pero en este caso el número de observaciones es \( abr \).
La descripción del diseño así como la terminología subyacente la vamos a introducir mediante el siguiente supuesto práctico.
Supuesto práctico 9
Consideremos el supuesto práctico anterior en el que realizamos dos réplicas por cada tratamiento. En unos laboratorios se está estudiando los factores que influyen en la resistencia de un tipo particular de fibra. Se eligen al azar cuatro máquinas y tres operarios y se realiza un experimento factorial usando fibras de un mismo lote de producción. Los resultados obtenidos se muestran en la tabla adjunta. Analizar los resultados y obtener las conclusiones apropiadas.
\( \begin{array} {|c|c|c|c|c|} \hline & \text {Cuatro} & \text {Tipos } & \text {de} & \text {máquinas} \\ \hline \text {Operario } & A & B & C & D \\ \hline 1 & 109 & 110 & 108 & 110 \\ & 110 & 115 & 109 & 108 \\ \hline 2 & 110 & 110 & 111 & 114 \\ & 112 & 111 & 109 & 112 \\ \hline 3 & 116 & 112 & 114 & 120 \\ & 114 & 115 & 119 & 117 \\ \hline \end{array} \)
Figura 20: Tabla de datos del Supuesto Práctico 9
En el Supuesto práctico 9:
- Variable respuesta: Resistencia de una fibra.
- Factor: Operario, que tiene tres niveles.
- Factor: Tipo de máquina, que tiene cuatro niveles.
- Ambos factores de efectos fijos, ya que viene decidido qué niveles concretos se van a utilizar.
- Tamaño del experimento: Número total de observaciones (24).
En este caso, el modelo matemático del experimento que planteamos es el siguiente:
\( y_{ijk}=\mu+\tau_i+ \beta_j + (\tau \beta)_{ij} + u_{ijk},~~~~ i=1, 2, 3; ~~~ j=1, 2, 3, 4; ~~~k=1, 2; \)
donde
- \( y_{ijk}\) : Representa la resistencia de la fibra \( k \) con el operario \( i \) y la máquina \( j \).
- \( \mu \): Efecto constante, común a todos los niveles de los factores, denominado media global.
- \( \tau_i \): Efecto medio producido por el operario i, \( (\sum_i \tau_i = 0 ) \).
- \( \beta_j \): Efecto medio producido por la máquina j, \( (\sum_j \beta_j = 0 ) \).
- \( (\tau \beta)_{ij} \): Efecto medio producido por la interacción entre el operario i y la máquina j, \( (\sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij} = ) \).
- \( u_{ijk} \): Vv aa. independientes con distribución \( N(0,σ) \).
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio.
En este caso lo hacemos en un archivo de texto:
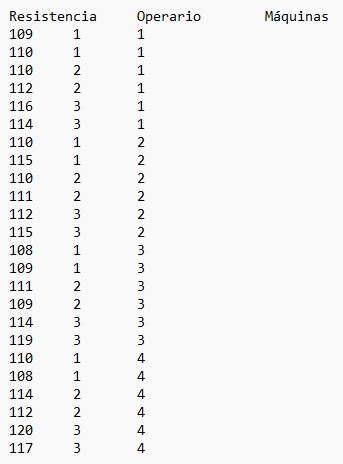
Figura 21: Tabla de datos del Supuesto Práctico 9
En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos.
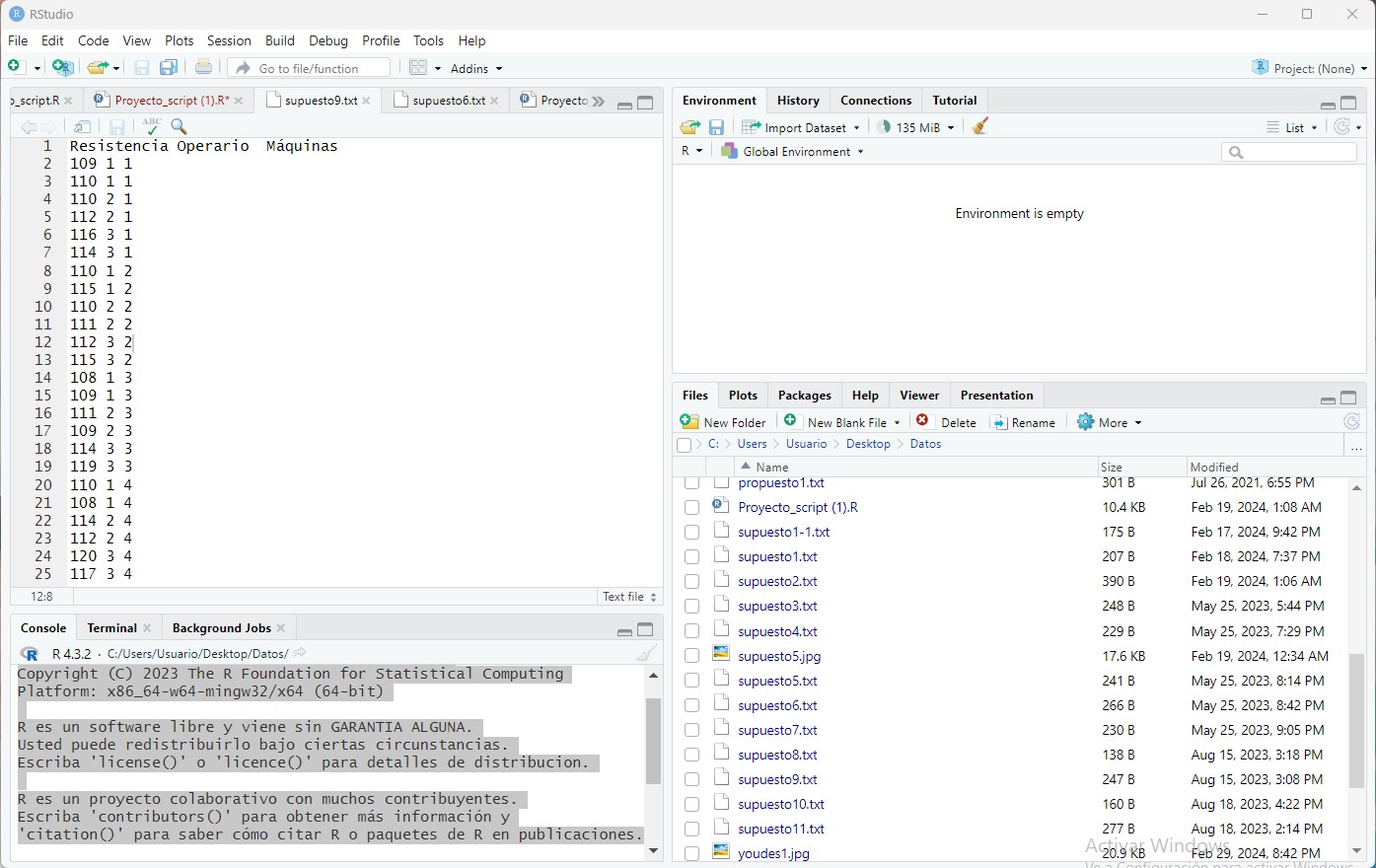
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
factorial <- read.table(“supuesto9.txt”, header = TRUE)
A continuación debemos transformar todas las columnas que contienen a los factores en un factor para podemos realizar los cálculos posteriores adecuadamente.
factorial$Operario = factor(factorial$Operario)
factorial$Máquinas = factor(factorial$Máquinas)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
mod4 <- aov(Resistencia ~ Operario * Máquinas, data = factorial)
mod4
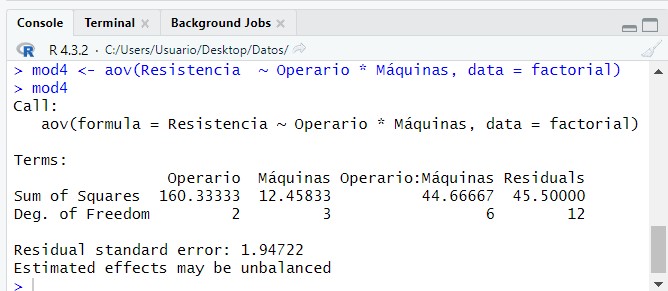
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA)
summary(mod4)
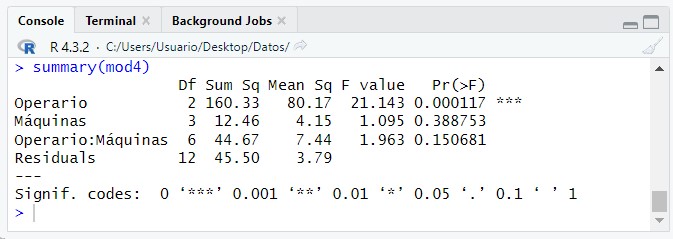
En dicha Tabla se indica que, para un nivel de significación del 5%, los efectos que son significativos del modelo planteado son los referentes al factor tipo de operario (p-valor=0.0001). Descartamos por tanto el efecto del factor tipo de máquinas y de la interacción entre factores.
Concluimos por tanto que la resistencia de la fibra dependerá exclusivamente del tipo operario que la produzca. Por lo tanto, el modelo matemático del experimento que planteamos es el siguiente:
\( y_{ijk}=\mu+\tau_i + u_{ijk},~~~~ i=1, 2, 3; ~~~ j=1, 2, 3, 4; ~~~k=1, 2; \)
Comandos y funciones utilizadas para resolver el supuesto práctico 9
factorial <- read.table(“supuesto9.txt”, header = TRUE)
factorial$Operario = factor(factorial$Operario)
factorial$Máquinas = factor(factorial$Máquinas)
mod4 <- aov(Resistencia ~ Operario * Máquinas, data = factorial)
mod4
summary(mod4)
Diseños factoriales con tres factores
Supongamos que hay \( a \) niveles para el factor \( A \), \( b \) niveles del factor \( B \) y \( c \) niveles para el factor \( C \) y que cada réplica del experimento contiene todas las posibles combinaciones de tratamientos, es decir contiene los \( abc \) tratamientos posibles.
El modelo sin replicación
El modelo estadístico para este diseño es:
\( y_{ijk}=\mu+\tau_i+ \beta_j + \gamma_k * (\tau \beta)_{ij} + (\tau \gamma)_{ik} + (\beta \gamma)_{jk}+ (\tau \beta \gamma)_{ijk} + u_{ijk},~~~~ i=1,…,a; ~~~ j=1,…,b, ~~~k=1,…,c ~~~~, ~~~~ \)
Expresión 18: Modelo estadísticodel diseño factorial de tres factores sin replicación
donde
- \( y_{ijk} \): Representa la observación correspondiente al nivel (i) del factor \( A \), al nivel (j) del factor \( B \) y al nivel (k) del factor \( C \).
-
\( \mu \): Efecto constante, común a todos los niveles de los factores, denominado media global.
-
\( \tau_i \): Efecto producido por el nivel i-ésimo del factor \( A \), ( \( \sum_i \tau_i = 0 \)).
-
\( \beta_j \): Efecto producido por el nivel j-ésimo del factor \( B \), \( \sum_j \beta_j = 0 \) ).
-
\( \gamma_k \): Efecto producido por el nivel k-ésimo del factor \( C \), \( \sum_k \gamma_k = 0 \) ).
-
\( (\tau \beta)_{ij} \): Efecto producido por la interacción entre \( A \times B \), ( \( \sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij} = 0 \) ).
-
\( (\tau \gamma)_{ik} \): Efecto producido por la interacción entre \( A \times C \), ( \( \sum_i (\tau \gamma)_{ik} = \sum_k (\tau \gamma)_{ik} = 0 \) ).
-
\( (\beta \gamma)_{jk} \): Efecto producido por la interacción entre \( B \times C \), ( \( \sum_j (\beta \gamma)_{jk} = \sum_k (\beta \gamma)_{jk} = 0 \) ).
-
\( (\tau \beta \gamma)_{ijk} \): Efecto producido por la interacción entre \( A \times B \times C \), ( \( \sum_i (\tau \beta \gamma)_{ijk} = \sum_j (\tau \beta \gamma)_{ijk} = \sum_k (\tau \beta \gamma)_{ijk} = 0 \) ).
-
\( u_{ij} \) son vv aa. independientes con distribución N(0,σ).
Supondremos que se toma una observación por cada combinación de factores, por tanto, hay un total de \( N = ab c \) observaciones.
Parámetros a estimar:
\( \begin{array} {|c|c|} \hline \text {Parámetros} & \text {Número} \\ \hline \mu & 1 \\ \hline \tau_i & a-1 \\ \hline \beta_j & b-1 \\ \hline \gamma_k & c-1 \\ \hline (\tau \beta)_{ij} & (a-1)(b-1) \\ \hline (\tau \gamma)_{ij} & (a-1)(c-1) \\ \hline ( \beta \gamma)_{jk} & (b-1)(c-1) \\ \hline (\tau \beta \gamma)_{ijk} & (a-1)(b-1)(c-1) \\ \hline \sigma^2 & 1 \\ \hline Total & abc +11 \\ \hline \end{array} \)
Figura 22: Tabla del número de parámetros a estimar
A pesar de las restricciones impuestas al modelo,
\( \sum_i \tau_i = \sum_j \beta_j = \sum_k \gamma_k = \sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij}= , \cdots , = \sum_k (\tau \beta \gamma)_{ijk} = 0 \)
el número de parámetros \( (abc + 1) \) supera al número de observaciones \( (abc) \). Por lo tanto, algún parámetro no será estimable.
Expresión de la descomposición de la variabilidad de la variable respuesta.
\( SCT=SCA+SCB+SCC+SC(AB)+SC(AC)+SC(BC)+SC(ABC)+SCR \)
Que representan:
- \( SCT \) : Suma de Cuadrados Total,
- \( SCA, SCB, SCC \): Suma de Cuadrados entre los niveles de \( A \), de \( B \) y de \( C \), respectivamente
- \( SC(AB), SC(AC), SC(BC), SC(ABC), SCR \): Suma de Cuadrados de las interacciones \( A×B, A×C, B×C, A×B×C \) y del error, respectivamente.
A partir de la ecuación básica del Análisis de la Varianza se pueden construir los cuadrados medios definidos como:
-
Cuadrado medio total: \( CMT=(SCT)/(n-1) \)
-
Cuadrado medio de \( A \) : \( CMA=(SCA)/(a-1) \)
-
Cuadrado medio de \( B \) : \( CMB=(SCB)/(b-1) \)
-
Cuadrado medio de \( C \) : \( CMC=(SCC)/(c-1) \)
-
Cuadrado medio de las interacciones:
-
Cuadrado medio residual: \(CMR=(SCR)/((a-1)(b-1(c-1)) \)
Supuesto práctico 10
Se están investigando los efectos sobre la resistencia del papel que producen la concentración de fibra de madera (factor A), la presión del tanque (factor B) y el tiempo de cocción de la pulpa (factor C). Se seleccionan dos niveles de la concentración de madera (A1, A2), tres niveles de la presión (B1 , B2 , B3) y dos niveles del tiempo de cocción (C1 , C2). Pueden considerarse todos los factores fijos. Analizar los resultados y obtener las conclusiones apropiadas.
\( \begin{array} {|c|ccc|ccc|} \hline & & \text {C1 } & & & \text {C2} & \\ \hline & \text {B1 } & \text {B2 }& \text {B3 } & \text {B1 } & \text {B2 } & \text {B3 } \\ \hline \text {A1 } & 10 & 20 & 2 & 6 & 23 & -2 \\ \hline \text {A2 } & 26 & 28 & 30 & 30 & 34 & 32 \\ \hline \end{array} \)
Figura 22: Tabla de datos del Supuesto Práctico 10
En el Supuesto práctico 10:
- Variable respuesta: Resistencia del papel.
- Factor: Tipo de fibra de madera, que tiene dos niveles.
- Factor: Presión del tanque, que tiene tres niveles.
- Factor: Tiempo de cocción, que tiene dos niveles.
- Todos los factores son de efectos fijos, ya que viene decidido qué niveles concretos se van a utilizar.
- Tamaño del experimento: Número total de observaciones (12), y el número de tratamientos es 2x3x2=12.
En este caso, el modelo matemático del experimento que planteamos es el siguiente:
\( y_{ijk}=\mu+\tau_i+ \beta_j + \gamma_k + (\tau \beta)_{ij} + (\tau \gamma)_{ik} + (\beta \gamma)_{jk}+ u_{ijk},~~~~ i=1,2; ~~~ j=1,2,3; ~~~k=1,2; \)
donde:
- \( y_{ijk} \): Representa la resistencia del papel con la fibra i, presión del tanque j, y tiempo de cocción k.
-
\( \mu \): Efecto constante, común a todos los niveles de los factores, denominado media global.
-
\( \tau_i \): Efecto medio producido por tipo de fibra i.
-
\( \beta_j \): Efecto medio producido por la presión del tanque j.
-
\( \gamma_k \):Efecto producido por el tiempo de cocción k.
-
\( (\tau \beta)_{ij} \): Efecto medio producido por la interacción entre el tipo de fibra i y la presión del tanque j.
-
\( (\tau \gamma)_{ik} \): Efecto producido por la interacción entre el tipo de fibra i y el tiempo de cocción k.
-
\( (\beta \gamma)_{jk} \): Efecto producido por la interacción entre la presión del tanque j y el tiempo de cocción k.
-
\( u_{ij} \) son vv aa. independientes con distribución N(0,σ).
Estos efectos son parámetros a estimar, con las condiciones:
\( \sum_i \tau_i= \sum_j \beta_j= \sum_k \gamma_k=\sum_i (\tau\beta)_{ij}=\sum_j (\tau\beta)_{ij}=…=\sum_k (\beta\gamma)_{jk}=0.\)
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio.
En este caso lo hacemos en un archivo de texto:
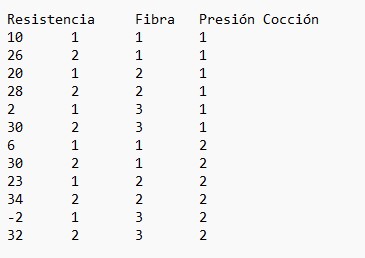
Figura 23: Tabla de datos del Supuesto Práctico 9
En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos.
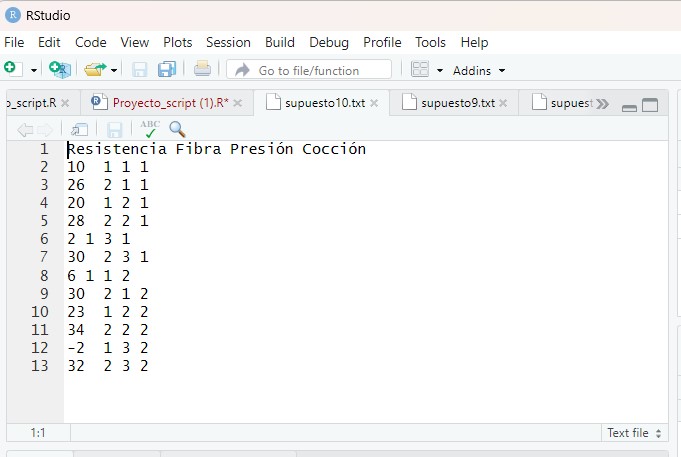
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
factorial <- read.table(“supuesto10.txt”, header = TRUE)
A continuación debemos transformar la tres columnas en factores para poder realizar los cálculos posteriores adecuadamente.
factorial$Fibra = factor(factorial$Fibra)
factorial$Presión = factor(factorial$Presión)
factorial$Cocción = factor(factorial$Cocción)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
mod5 <- aov(Resistencia ~ Fibra + Presión + Cocción + Fibra * Presión + Fibra * Cocción + Presión * Cocción, data = factorial)
donde:
- Resistencia: Nombre de la columna de las observaciones.
- Fibra: Nombre de la columna en la que está representado el primer factor.
- Presión: Nombre de la columna en la que está representado el segundo factor.
- Cocción: Nombre de la columna en la que está representado el tercer factor.
- Fibra*Presión, Fibra*Cocción, Presión*Cocción: hacen referencia a las distintas interacciones.
- data: data.frame en el que están guardados los datos.
mod5
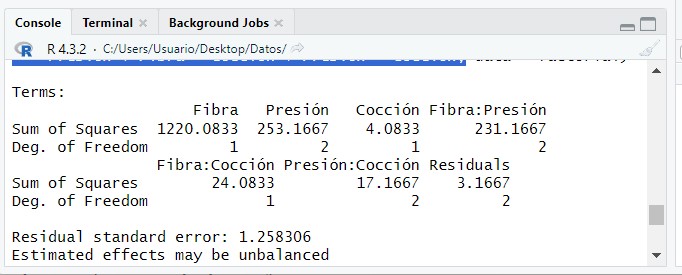
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
summary(mod5)
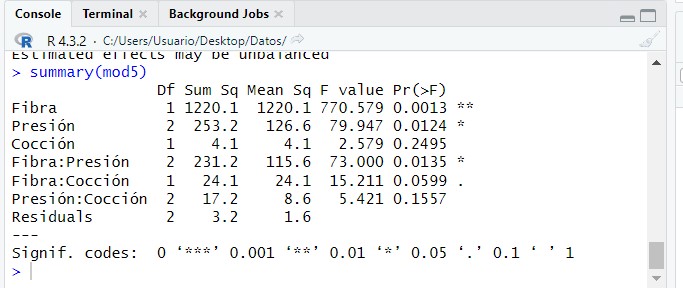
En dicha Tabla se indica que para un nivel de significación del 5% los efectos que son significativos del modelo planteado son los referentes al factor tipo de fibra (p-valor=0.001), al factor presión del tanque (p-valor=0.012), y a la interacción entre ambos factores (p-valor=0.0135) que son menores que el nivel de significación.
Como consecuencia de este resultado, replanteamos el modelo suprimiendo los efectos con mayor significación. Probamos a dejar solo la interacción entre Fibra y Presión, junto con los efectos de dichos factores. Para hacerlo en RStudio debemos:
mod6 <- aov(Resistencia ~ Fibra * Presión, data = factorial)
summary(mod6)
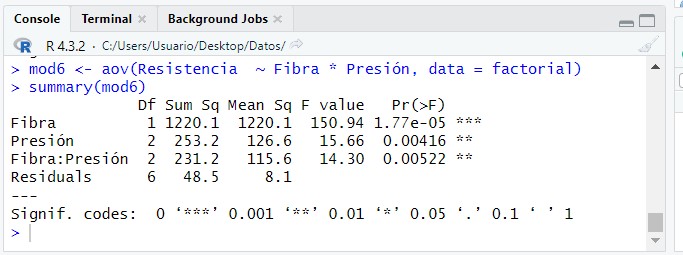
Todos los efectos de este último modelo planteado son significativos y por lo tanto es en este modelo donde vamos a realizar el estudio. Concluimos diciendo que la resistencia del papel dependerá exclusivamente del tipo de fibra que se use, de la presión del tanque, y de la interacción entre ambos factores (el tipo de fibra influya en la resistencia del papel de distinta forma en función de la presión del tanque). Por lo tanto, el modelo matemático del experimento que planteamos es el siguiente:
\( y_{ijk}=\mu+\tau_i+\beta_j+(\tau\beta)_{ij}+u_{ijk},~~i=1,2;~j=1,2,3;~k=1,2. \)
Comandos y funciones utilizadas para resolver el supuesto práctico 10
factorial <- read.table(“supuesto10.txt”, header = TRUE)
factorial$Fibra = factor(factorial$Fibra)
factorial$Presión = factor(factorial$Presión)
factorial$Cocción = factor(factorial$Cocción)
mod5 <- aov(Resistencia ~ Fibra + Presión + Cocción + Fibra * Presión + Fibra * Cocción + Presión * Cocción, data = factorial)
mod5
summary(mod5)
mod6 <- aov(Resistencia ~ Fibra * Presión, data = factorial)
summary(mod6)
El modelo con replicación
El modelo estadístico para este diseño es:
\( y_{ijkl}= \mu+\tau_i+ \beta_j + \gamma_k + (\tau \beta)_{ij} + (\tau \gamma)_{ik} + (\beta \gamma)_{jk}+ (\tau \beta \gamma)_{ijk} + u_{ijkl} \)
\( i=1,…,a; ~~~ j=1,…,b, ~~~k=1,…,c ~~~~, l = 1,2,…,r \)
Expresión 19: Modelo estadístico del diseño factorial de tres factores con replicación
donde r es el número de replicaciones y \( N=abcr \) y es el número de observaciones. El número de parámetros de este modelo es, como en el modelo de tres factores sin replicación, \( abc + 1 \) pero en este caso el número de observaciones es \( abcr \). El objetivo del análisis de este modelo es realizar los contrastes sobre los efectos principales, las interacciones de orden dos y la interacción de orden tres.
Supuesto práctico 11
Consideremos el supuesto práctico anterior en el que realizamos dos réplicas por cada tratamiento. Se están investigando los efectos sobre la resistencia del papel que producen la concentración de fibra de madera (factor A), la presión del tanque (factor B) y el tiempo de cocción de la pulpa (factor C). Se seleccionan dos niveles de la concentración de madera (A1, A2), tres niveles de la presión (B1 , B2 , B3) y dos niveles del tiempo de cocción (C1 , C2). Pueden considerarse todos los factores fijos. Analizar los resultados y obtener las conclusiones apropiadas.
\( \begin{array} {|c|ccc|ccc|} \hline & & \text {C1 } & & & \text {C2} & \\ \hline & \text {B1 } & \text {B2 }& \text {B3 } & \text {B1 } & \text {B2 } & \text {B3 } \\ \hline \text {A1 } & 10 & 20 & 2 & 6 & 23 & -2 \\ & 7 & 10 & 0 & 2 & 11 & -1 \\ \hline \text {A2 } & 26 & 28 & 30 & 30 & 34 & 32 \\ & 14 & 17 & 13 & 14 & 18 & 16 \\ \hline \end{array} \)
Figura 23: Tabla de datos del Supuesto Práctico 11
En el Supuesto práctico 11:
- Variable respuesta: Resistencia del papel.
- Factor: Tipo de fibra de madera, que tiene dos niveles.
- Factor: Presión del tanque, que tiene tres niveles.
- Factor: Tiempo de cocción, que tiene dos niveles.
- Todos los factores son de efectos fijos, ya que viene decidido qué niveles concretos se van a utilizar.
- Tamaño del experimento: Número total de observaciones (24), y el número de tratamientos es 2x3x2=12.
En este caso, el modelo matemático del experimento que planteamos es el siguiente:
\( y_{ijkl}=\mu+\tau_i+\beta_j+\gamma_k+(\tau\beta)_{ij}+(\tau\gamma)_{ik}+(\beta\gamma)_{jk}+(\tau\beta\gamma)_{ijk}+u_{ijkl},~~i=1,2;~j=1,2,3;~k=1,2;~l=1,2. \)Donde la variable respuesta y los efectos de los factores se definieron en el Supuesto práctico 10. Aunque debemos de añadir que es el efecto producido por la interacción entre el tipo de fibra i, la presión del tanque j, y el tiempo de cocción k.
Las restricciones para este modelo son:
\( \sum_i\tau_i=\sum_j \beta_j=\sum_k \gamma_k=\sum_i (\tau\beta)_{ij}=\sum_j (\tau\beta)_{ij}=…=\sum_k (\tau\beta\gamma)_{ijk}=0. \)
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio.
En este caso lo hacemos en un archivo de texto:
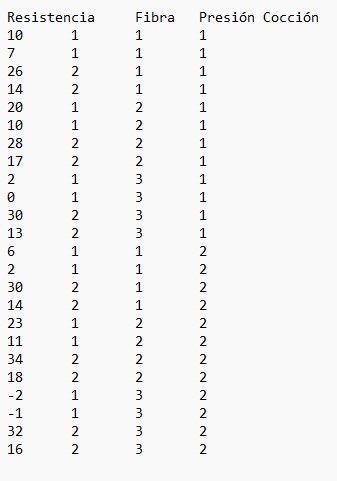
Figura 24: Tabla de datos del Supuesto Práctico 11
En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos.
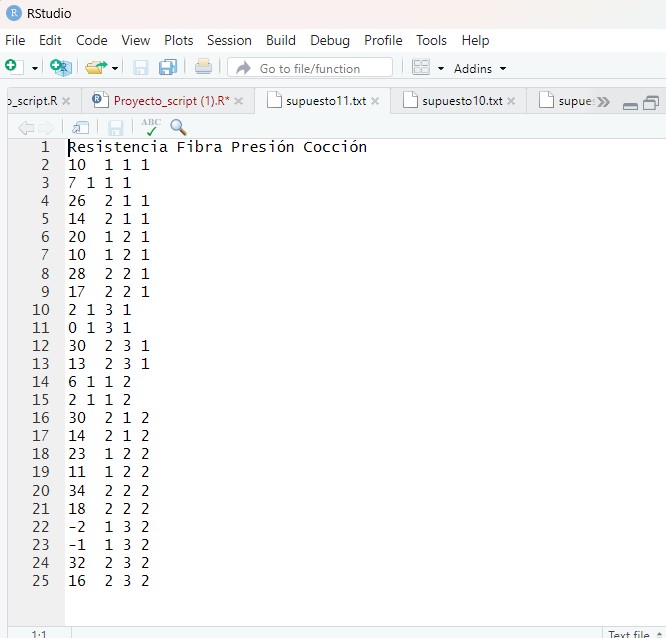
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
factorial <- read.table(“supuesto11.txt”, header = TRUE)
A continuación debemos transformar las tres columnas en factores para poder realizar los cálculos posteriores adecuadamente.
factorial$Fibra = factor(factorial$Fibra)
factorial$Presión = factor(factorial$Presión)
factorial$Cocción = factor(factorial$Cocción)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
mod6 <- aov(Resistencia ~ Fibra + Presión + Cocción + Fibra * Presión + Fibra * Cocción + Presión * Cocción + Fibra * Presión*Cocción, data = factorial)
donde:
- Resistencia: Nombre de la columna de las observaciones.
- Fibra: Nombre de la columna en la que está representado el primer factor.
- Presión: Nombre de la columna en la que está representado el segundo factor.
- Cocción: Nombre de la columna en la que está representado el tercer factor.
- Fibra*Presión, Fibra*Cocción, Presión*Cocción y Fibra*Presión*Cocción: hacen referencia a las distintas interacciones.
- data: data.frame en el que están guardados los datos
mod6
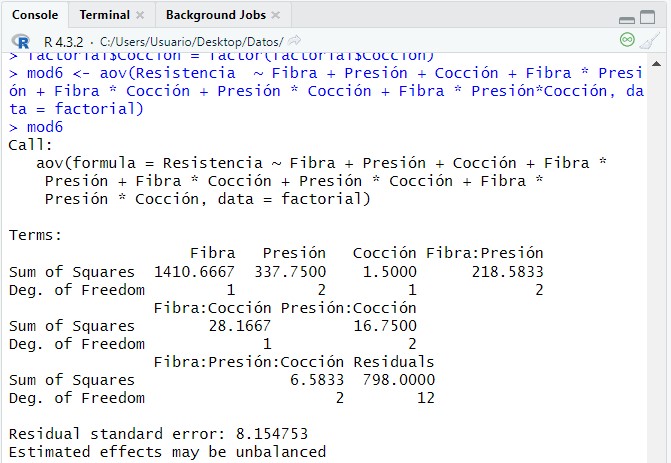
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
summary(mod6)
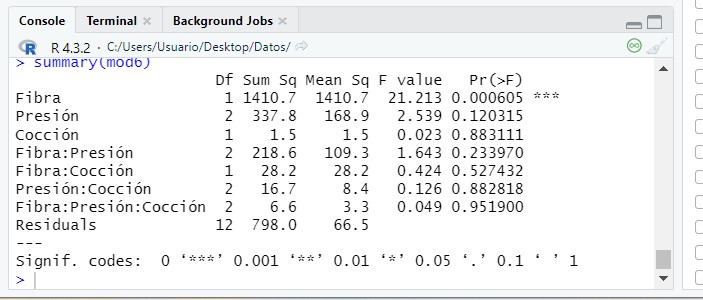
En dicha Tabla se indica que para un nivel de significación del 5% los efectos que son significativos del modelo planteado son los referentes al factor tipo de fibra, ya que su p-valor=0.0006 que es menor que el nivel de significación.
Como consecuencia de este resultado, replanteamos el modelo suprimiendo los efectos con mayor significación. Probamos a dejar solo la interacción entre Fibra y Presión, junto con los efectos de dichos factores:
mod7 <- aov(Resistencia ~ Fibra * Presión, data = factorial)
summary(mod7)
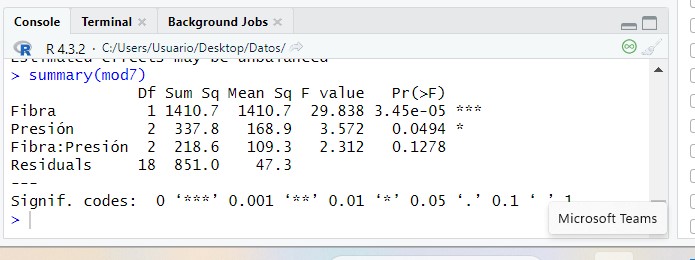
En dicha Tabla se indica que para un nivel de significación del 5% los efectos que son significativos del modelo planteado son los referentes al factor tipo de fibra y al factor tipo de presión, ya que sus p-valores son 0.00003 y 0.049 respectivamente, que son menores que el nivel de significación.
Por lo cual replanteamos el modelo suprimiendo los efectos entre ambos factores (mayor significación). Dejamos solo los efectos de los factores tipo de Fibra y tipo de Presión:
mod8 <- aov(Resistencia ~ Fibra + Presión, data = factorial)
summary(mod8)
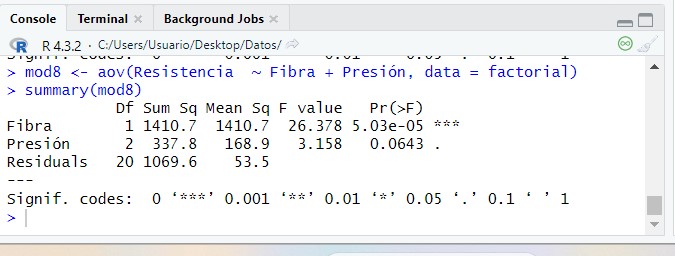
En dicha Tabla se indica que para un nivel de significación del 5% los efectos que son significativos del modelo planteado son los referentes al factor tipo de fibra, ya que su p-valor=0.00005, que es menor que el nivel de significación. Vemos como el efecto del factor tipo de presión es ligeramente superior al nivel de significación, por lo que lo eliminamos del modelo y así obtenemos el modelo final que sería aquel que solo depende del factor tipo de fibra:
mod9 <- aov(Resistencia ~ Fibra, data = factorial)
summary(mod9)
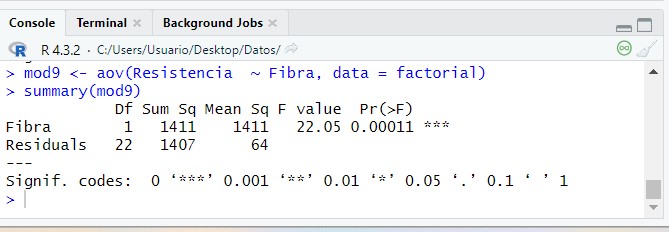
Concluimos diciendo que la resistencia del papel dependerá exclusivamente del tipo de fibra que se use, es decir, el tipo de fibra tiene un efecto significativo en la resistencia del papel. Por lo tanto, el modelo matemático del experimento que planteamos es el siguiente:
\( y_{ijkl}=\mu+\tau_i+\beta_j+\gamma_k+(\tau\beta)_{ij}+(\tau\gamma)_{ik}+(\beta\gamma)_{jk}+(\tau\beta\gamma)_{ijk}+u_{ijkl},~~i=1,2;~j=1,2,3;~k=1,2;~l=1,2. \)
Comandos y funciones utilizadas para resolver el supuesto práctico 11
factorial <- read.table(“supuesto11.txt”, header = TRUE)
factorial$Fibra = factor(factorial$Fibra)
factorial$Presión = factor(factorial$Presión)
factorial$Cocción = factor(factorial$Cocción)
mod6 <- aov(Resistencia ~ Fibra + Presión + Cocción + Fibra * Presión + Fibra * Cocción + Presión * Cocción + Fibra * Presión*Cocción, data = factorial)
mod6
summary(mod6)
mod7 <- aov(Resistencia ~ Fibra * Presión, data = factorial)
summary(mod7)
mod8 <- aov(Resistencia ~ Fibra + Presión, data = factorial)
summary(mod8)
mod9 <- aov(Resistencia ~ Fibra, data = factorial)
summary(mod9)
Ejercicios
Ejercicios Guiados
Ejercicio Guiado1
La contaminación es uno de los problemas ambientales más importantes que afectan a nuestro mundo. En las grandes ciudades, la contaminación del aire se debe a los escapes de gases de los motores de explosión, a los aparatos domésticos de la calefacción, a las industrias,… El aire contaminado nos afecta en nuestro vivir diario, manifestándose de diferentes formas en nuestro organismo. Con objeto de comprobar la contaminación del aire en una determinada ciudad, se ha realizado un estudio en el que se han analizado las concentraciones de monóxido de carbono (CO) durante cinco días de la semana (lunes, martes, miércoles, jueves y viernes).
\( \begin{array} {|c|cccccccc|} \hline \text { Día} & & \text{Concentración} & \text{ de } & \text{ monóxido} & \text{de} & \text{carbono} & & \\ \hline \text{Lunes} & 420 & 390 & 480 & 430 & 440 & 324 & 450 &460 \\ \hline \text{Martes} & 450 & 390 & 430 & 521 & 320 & 360 & 342 & 423 \\ \hline \text{Miércoles} & 355 & 462 & 286 & 238 & 344 & 423 & 123 & 196 \\ \hline \text{Jueves} & 321 & 254 & 412 & 368 & 340 & 258 & 433 & 489 \\ \hline \text{Viernes} & 238 & 255 & 366 & 389 & 198 & 256 & 248 & 324 \\ \hline \end{array} \)
cc
Para un nivel de significación del 5%:
- ¿Se puede confirmar que la contaminación es la misma en los diferentes días de la semana?
- Si se rechaza la hipótesis nula (misma contaminación los diferentes días), determinar que días difieren entre sí utilizando el método de comparaciones múltiples de Tukey.
- Estudiar las hipótesis de modelo: Homocedasticidad (Homogeneidad de las varianzas por grupo), Independencia y Normalidad.
Ejercicio Guiado 2
Abeto blanco o Abeto del Pirineo, es un árbol de gran belleza por la elegancia de sus formas y el exquisito perfume balsámico que destilan sus hojas y cortezas. Destilando hojas y madera se obtiene aceite de trementina muy utilizado en medicina contra torceduras y contusiones. En estos últimos años se ha observado que la producción de semillas ha descendido y con objeto de conseguir buenas producciones se proponen tres tratamientos (A,B,C). Se observa que árboles diferentes tienen distintas características naturales de reproducción, este efecto de las diferencias entre los árboles se debe de controlar y este control se realiza mediante bloques. En el experimento se utilizan 10 abetos, dentro de cada abeto se seleccionan tres ramas semejantes. Cada rama recibe exactamente uno de los tres tratamientos que son asignados aleatoriamente. Constituyendo cada árbol un bloque completo. Los datos obtenidos se presentan en la siguiente tabla donde se muestra el número de semillas producidas por rama.
\( \begin{array} {|c|cccccccc|} \hline & & & & & & \text{Abetos} & & & & & \\ \hline \text{Tratamientos} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline \text{A} & 7 & 8 & 9 & 10 & 11& 8 & 7 & 8 & 7 & 8 \\ \hline \text{B} & 9 & 9 & 9 & 9 & 12 & 10 & 8 & 8 & 9 & 9 \\ \hline \text{C} & 10 & 10 & 12 & 12 & 14 & 9 & 7 & 7 & 10 & 10 \\ \hline \end{array} \)
Figura 26: Tabla de datos del Ejercicio Guiado 2
Para un nivel de significación del 5%:
- ¿ Se puede afirmar que los diferentes tratamientos no influyen en el número de semillas? ¿Se puede concluir que los distintos árboles no afectan a la producción de semillas?
- En caso de que influyan significativamente alguno de los dos factores, extraer conclusiones utilizando el método de Duncan.
- Estudiar las hipótesis de modelo: Homocedasticidad, Independencia y Normalidad.
Ejercicio Guiado 3
En unos laboratorios se está investigando sobre el tiempo de supervivencia de unos animales a los que se le suministra al azar tres tipos de venenos (V1,V2,V3) y cuatro antídotos distintos (A1,A2,A3,A4). Se pretende estudiar si los tiempos de supervivencia de los animales varían en función de las combinaciones veneno-antídoto. Los datos que se recogen en la tabla adjunta son los tiempos de supervivencia en horas.
\( \begin{array} {|c|cccc|} \hline & & \text{Antídoto} & & \\ \hline \text{Veneno} & \text{A1} & \text{A2} & \text{A3} & \text{A4} \\ \hline \text{V1} & 4.5 & 11.0 & 4.5 & 7.1 \\ & 4.3 & 7.2 & 7.6 & 6.2 \\ \hline \text{V2} & 2.9 & 6.1 & 3.5 & 10.2 \\ & 2.3 & 12.4 & 4.0 & 3.8 \\ \hline \text{V3} & 2.1 & 3.7 & 2.5 & 3.6 \\ & 2.3 & 2.9 & 2.2 & 3.3 \\ \hline \end{array} \)
Figura 27: Tabla de datos del Ejercicio Guiado 3
Para un nivel de significación del 5%:
- ¿Se puede afirmar que los diferentes tipos de veneno influyen en la supervivencia de los animales? ¿Y los diferentes antídotos?
- ¿La efectividad del antídoto es la misma para los tres tipos de veneno?
- Estudia, utilizando el método de Newman-Keuls, qué antídoto es más efectivo.
Ejercicio Guiado 1 (Resuelto)
La contaminación es uno de los problemas ambientales más importantes que afectan a nuestro mundo. En las grandes ciudades, la contaminación del aire se debe a los escapes de gases de los motores de explosión, a los aparatos domésticos de la calefacción, a las industrias,… El aire contaminado nos afecta en nuestro vivir diario, manifestándose de diferentes formas en nuestro organismo. Con objeto de comprobar la contaminación del aire en una determinada ciudad, se ha realizado un estudio en el que se han analizado las concentraciones de monóxido de carbono (CO) durante cinco días de la semana (lunes, martes, miércoles, jueves y viernes).
\( \begin{array} {|c|cccccccc|} \hline \text { Día} & & \text{Concentración} & \text{ de } & \text{ monóxido} & \text{de} & \text{carbono} & & \\ \hline \text{Lunes} & 420 & 390 & 480 & 430 & 440 & 324 & 450 &460 \\ \hline \text{Martes} & 450 & 390 & 430 & 521 & 320 & 360 & 342 & 423 \\ \hline \text{Miércoles} & 355 & 462 & 286 & 238 & 344 & 423 & 123 & 196 \\ \hline \text{Jueves} & 321 & 254 & 412 & 368 & 340 & 258 & 433 & 489 \\ \hline \text{Viernes} & 238 & 255 & 366 & 389 & 198 & 256 & 248 & 324 \\ \hline \end{array} \)
Figura 25: Tabla de datos del Ejercicio Guiado 1
Para un nivel de significación del 5%:
- ¿Se puede confirmar que la contaminación es la misma en los diferentes días de la semana?
- Si se rechaza la hipótesis nula (misma contaminación los diferentes días), determinar que días difieren entre sí utilizando el método de comparaciones múltiples de Tukey.
- Estudiar las hipótesis de modelo: Homocedasticidad (Homogeneidad de las varianzas por grupo), Independencia y Normalidad.
Solución:
El problema planteado se modeliza a través de un diseño unifactorial totalmente aleatorizado de efectos fijos equilibrado.
- Variable respuesta: Concentraciones de monóxido de carbono.
- Factor: Días de la semana con cinco niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Modelo equilibrado: Los niveles de los factores tienen el mismo número de elementos.
- Tamaño del experimento: Número total de observaciones (40).
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio. En este caso lo hacemos en un archivo de texto
En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos.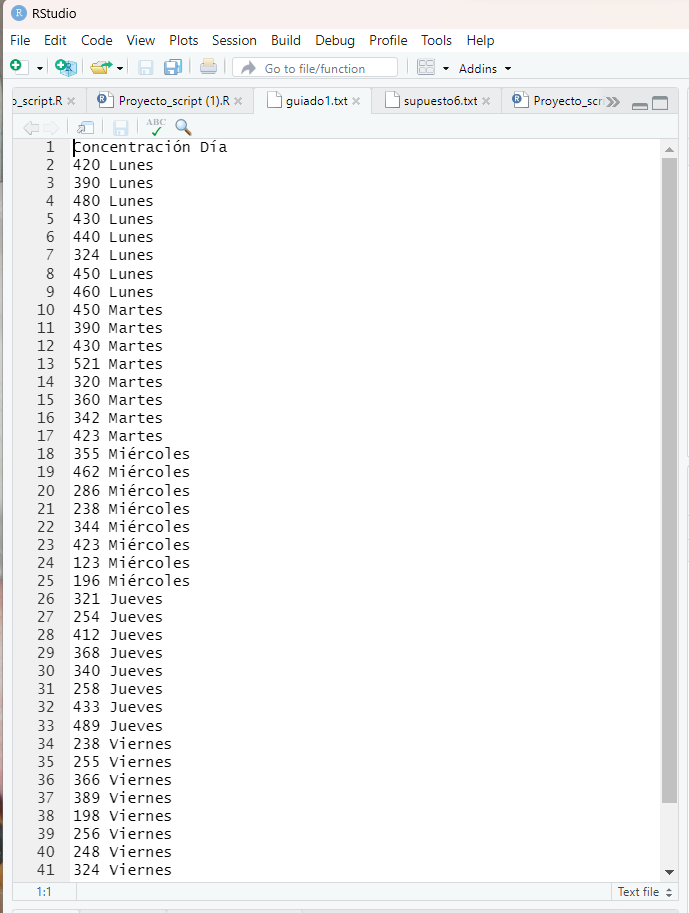
Figura 26: Tabla de datos del Ejercicio Guiado 1
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
contaminacion <- read.table(“guiado1.txt”, header = TRUE)
Transformamos todas las columnas que contienen a los factores en un factor para poder realizar los cálculos posteriores adecuadamente.
contaminacion$Día = factor(contaminacion$Día)
1 ¿Se puede confirmar que la contaminación es la misma en los diferentes días de la semana? Para responder a este apartado debe resolverse el contraste de igualdad de medias para el factor día de la semana:
\( \begin{array}{c} H_0 \equiv \mu_1 = \mu_2 = \cdots = \mu_5 ~~~ vs ~~~ H_1 \equiv \mu_i \neq \mu_j \hspace{.2cm} \text {para algún } i\neq j \end{array} \)
Para calcular la tabla ANOVA en RStudio primero hacemos uso de la función “aov”:
mod <- aov(Concentración ~ Día, data = contaminacion)
mod
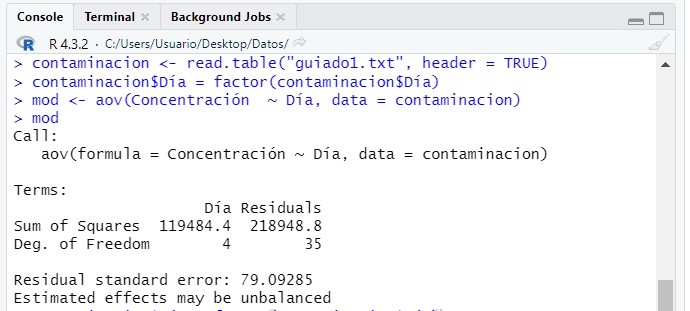
Y a continuación “summary” para mostrar un resumen de los resultados, de la siguiente forma:
summary(mod)
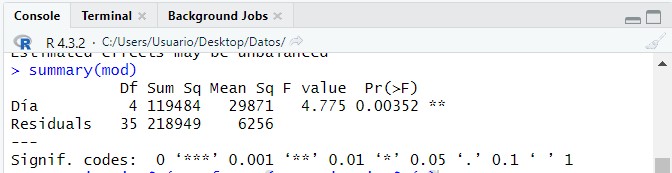
El valor del estadístico de contraste de igualdad de medias del factor día de la semana, F=4.775 deja a su derecha un p-valor=0.0035, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias de los niveles del factor día de la semana Es decir, existen diferencias significativas en la contaminación (concentración de monóxido de carbono) dependiendo del día de la semana.
2. Si se rechaza la hipótesis nula (misma contaminación los diferentes días), determinar que días difieren entre sí utilizando el método de comparaciones múltiples de Tukey.
mod.tukey <- TukeyHSD(mod, ordered = TRUE)
mod.tukey
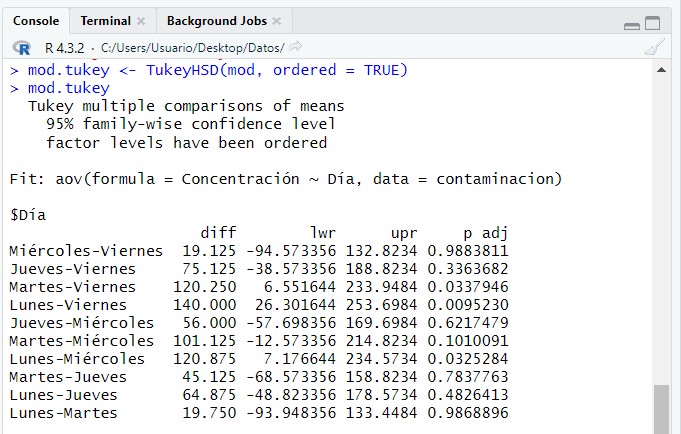
Solo se detectan diferencias significativas entre los Martes-Viernes, Lunes-Viernes, y Lunes-Miércoles. Para ello nos fijamos en las significaciones (menores que 0.05) o en los límites de los intervalos (dos medias se declaran iguales si el cero pertenece al intervalo de confianza construido para la diferencia de ellas).
3. Estudiar las hipótesis de modelo: Homocedasticidad (Homogeneidad de las varianzas por grupo), Independencia y Normalidad.
bartlett.test(contaminacion$Concentración, contaminacion$Día)

El estadístico de contraste experimental, B= 5.494, deja a la derecha un p-valor = 0.24, que nos indica que no se debe rechazar la igualdad entre las varianzas (no podemos rechazar la hipótesis nula).
Hipótesis de Independencia: Esta hipótesis la comprobaremos gráficamente mediante la representación de los residuos frente a los valores pronosticados por el modelo.
layout(matrix(c(1,2,3,4),2,2))
plot(mod)
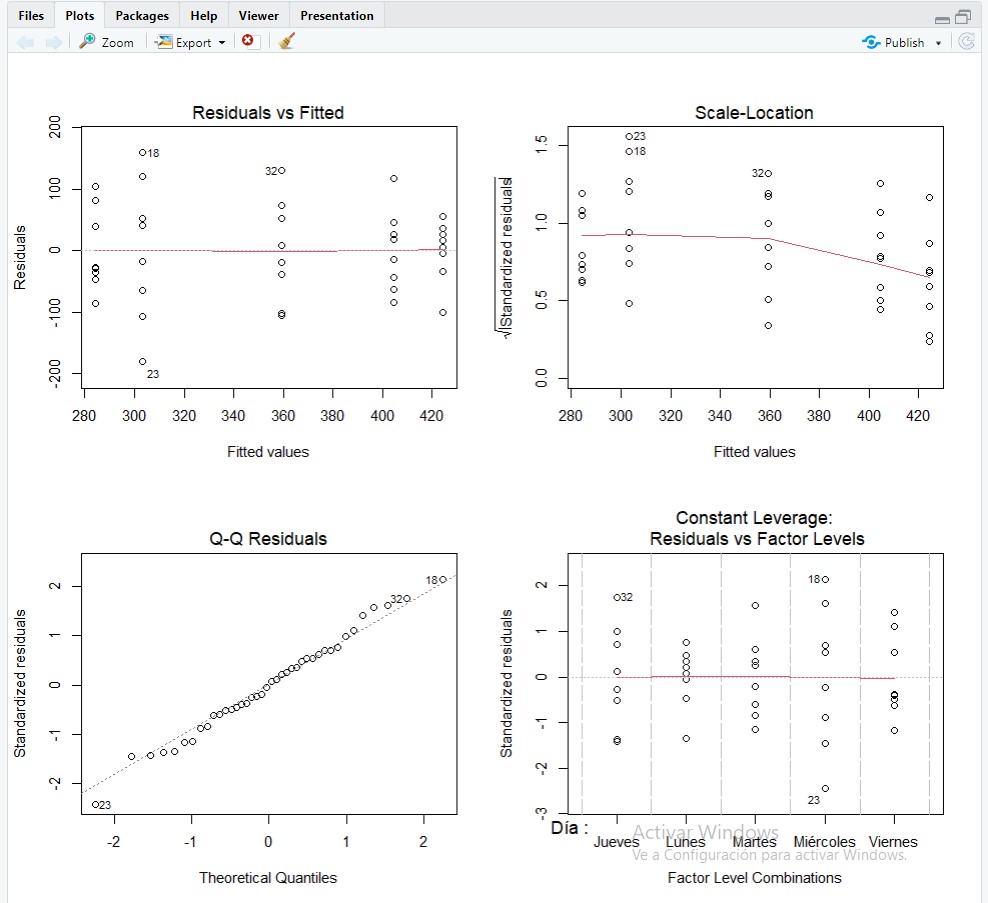
En esta salida interpretamos el gráfico que se muestra en la Fila 1, Columna 1. Es decir, el gráfico el que se representan los residuos en el eje de ordenadas y los valores ajustados por el modelo en el eje de abscisas. Este gráfico no muestra ningún aspecto que haga sospechar de la hipótesis de independencia de los residuos.
Estudiamos la Normalidad gráficamente mediante el gráfico probabilístico normal y analíticamente mediante el contraste de Shapiro-Wilk: Observamos el gráfico que se muestra en la Fila 2, Columna1. Es decir, el gráfico el que se representan los residuos estandarizados en el eje de ordenadas y cuantiles teóricos en el eje de abscisas. En dicho gráfico se aprecian leves desviaciones a la normalidad, pero el contraste ANOVA es robusto frente a desviaciones pequeñas de la normalidad. Realizaremos a continuación el contraste de Shapiro-Wilk para comprobar analíticamente la normalidad de los residuos.
shapiro.test(mod$residuals)
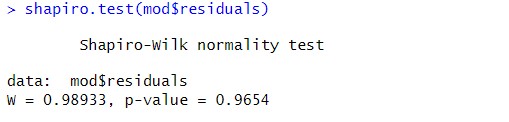
El valor del p-valor es de 0.9654, no pudiéndose rechazar la hipótesis de normalidad.
Comandos y funciones utilizadas para resolver el ejercicio guiado 1
contaminacion <- read.table(“guiado1.txt”, header = TRUE)
contaminacion$Día = factor(contaminacion$Día)
mod <- aov(Concentración ~ Día, data = contaminacion)
mod
summary(mod)
mod.tukey <- TukeyHSD(mod, ordered = TRUE)
mod.tukey
bartlett.test(contaminacion$Concentración, contaminacion$Día)
layout(matrix(c(1,2,3,4),2,2))
plot(mod)
shapiro.test(mod$residuals)
Ejercicio Guiado 2 (Resuelto)
Abeto blanco o Abeto del Pirineo, es un árbol de gran belleza por la elegancia de sus formas y el exquisito perfume balsámico que destilan sus hojas y cortezas. Destilando hojas y madera se obtiene aceite de trementina muy utilizado en medicina contra torceduras y contusiones. En estos últimos años se ha observado que la producción de semillas ha descendido y con objeto de conseguir buenas producciones se proponen tres tratamientos (A,B,C). Se observa que árboles diferentes tienen distintas características naturales de reproducción, este efecto de las diferencias entre los árboles se debe de controlar y este control se realiza mediante bloques. En el experimento se utilizan 10 abetos, dentro de cada abeto se seleccionan tres ramas semejantes. Cada rama recibe exactamente uno de los tres tratamientos que son asignados aleatoriamente. Constituyendo cada árbol un bloque completo. Los datos obtenidos se presentan en la siguiente tabla donde se muestra el número de semillas producidas por rama.
\( \begin{array} {|c|cccccccc|} \hline & & & & & & \text{Abetos} & & & & & \\ \hline \text{Tratamientos} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline \text{A} & 7 & 8 & 9 & 10 & 11& 8 & 7 & 8 & 7 & 8 \\ \hline \text{B} & 9 & 9 & 9 & 9 & 12 & 10 & 8 & 8 & 9 & 9 \\ \hline \text{C} & 10 & 10 & 12 & 12 & 14 & 9 & 7 & 7 & 10 & 10 \\ \hline \end{array} \)
Figura 26: Tabla de datos del Ejercicio Guiado 2
Para un nivel de significación del 5%:
- ¿ Se puede afirmar que los diferentes tratamientos no influyen en el número de semillas? ¿Se puede concluir que los distintos árboles no afectan a la producción de semillas?
- En caso de que influyan significativamente alguno de los dos factores, extraer conclusiones utilizando el método de Duncan.
- Estudiar las hipótesis de modelo: Homocedasticidad, Independencia y Normalidad.
Solución:
El problema planteado se modeliza a través de un diseño en bloques completos aleatorizados.
- Variable respuesta: Número de semillas.
- Factor: Tipo de tratamiento con tres niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Bloque: Tipo de abeto con diez niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Modelo completo: Los tres tratamientos se prueban en cada bloque exactamente una vez.
- Tamaño del experimento: Número total de observaciones (30).
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio. En este caso lo hacemos en un archivo de texto
En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos.
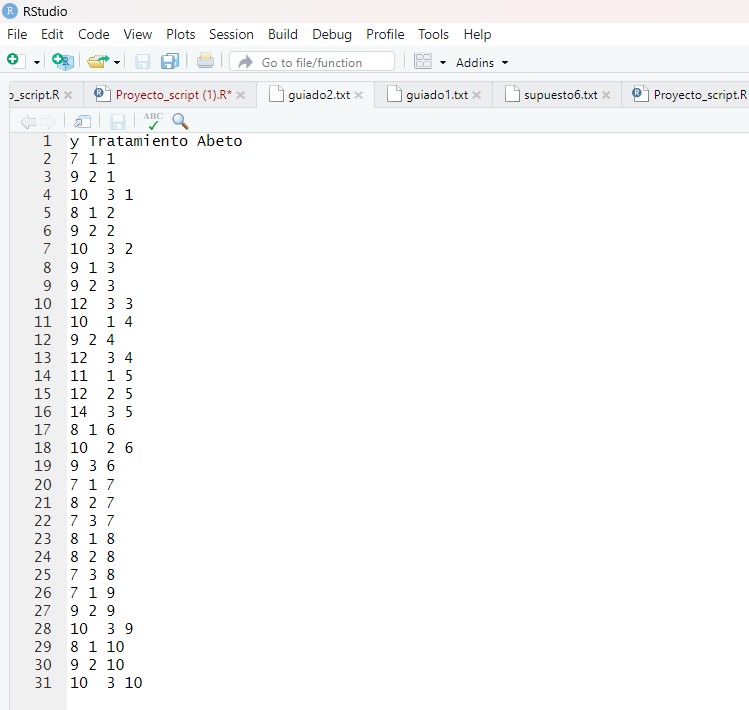
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
semillas <- read.table(“guiado2.txt”, header = TRUE)
Transformamos todas las columnas que contienen a los factores en un factor para poder realizar los cálculos posteriores adecuadamente.
semillas$Tratamiento = factor(semillas$Tratamiento)
semillas$Abeto= factor(semillas$Abeto)
- ¿ Se puede afirmar que los diferentes tratamientos no influyen en el número de semillas? ¿Se puede concluir que los distintos árboles no afectan a la producción de semillas?
Para responder a este apartado debe resolverse el contraste de igualdad de medias para el factor tipo de tratamiento:
\( \begin{array}{c} H_0 \equiv \mu_1 = \mu_2 = \mu_3 ~~~ vs ~~~ H_1 \equiv \mu_i \neq \mu_j \hspace{.2cm} \text {para algún } i\neq j \end{array} \)
y para el factor Abeto
\( \begin{array}{c} H_0 \equiv \mu_1 = \mu_2 = \cdots = \mu_10 ~~~ vs ~~~ H_1 \equiv \mu_i \neq \mu_j \hspace{.2cm} \text {para algún } i\neq j \end{array} \)
Para calcular la tabla ANOVA en R primero hacemos uso de la función “aov”:
mod <- aov(y ~ Tratamiento + Abeto, data = semillas)
mod
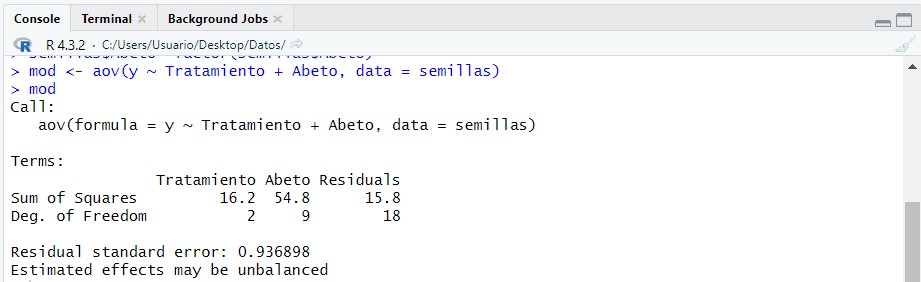
Y a continuación “summary” para mostrar un resumen de los resultados, de la siguiente forma:
summary(mod)
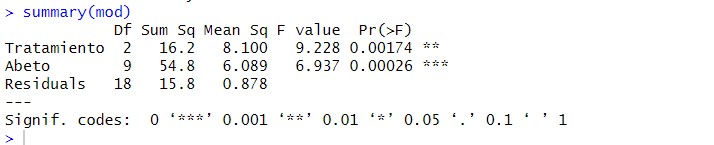
- El valor del estadístico de contraste de igualdad de medias del factor tipo de tratamiento, F=9.23 deja a su derecha un p-valor=0.0017, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias de los niveles del factor tipo de tratamiento. Es decir, existen diferencias significativas en el número de semillas dependiendo del tipo de tratamiento.
- El valor del estadístico de contraste de igualdad de medias del factor tipo de abeto, F=6.94 deja a su derecha un p-valor=0.0003, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias de los niveles del factor tipo de abeto. Es decir, existen diferencias significativas en el número de semillas dependiendo del tipo de abeto.
2. En caso de que influyan significativamente alguno de los dos factores, extraer conclusiones utilizando el método de Duncan.
Primero vamos a hacer el contraste de Duncan para los tratamientos, previa lectura del paquete “agricolae”. Para hacerlo en RStudio debemos:
library(agricolae)
(duncan=duncan.test(mod, “Tratamiento” , group = T))
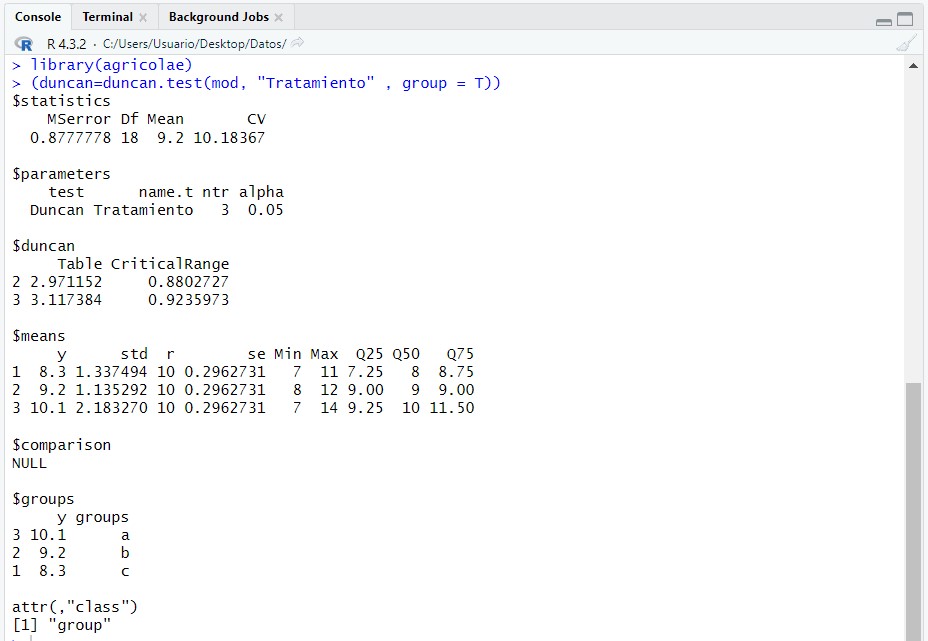
En la tabla del factor Tipo de tratamiento hay tres subconjuntos que se diferencian entre sí, donde cada tratamiento pertenece a un subconjunto distinto. Y dentro de cada subconjunto no se aprecian diferencias significativas entre las medias. También se observa que en el tercer tratamiento se produce el mayor número de semillas (10.1) y en el primero se produce el menor número de semillas (8.3).
Hacemos el contraste de Duncan para los bloques:
(duncan=duncan.test(mod, “Abeto” , group = T))
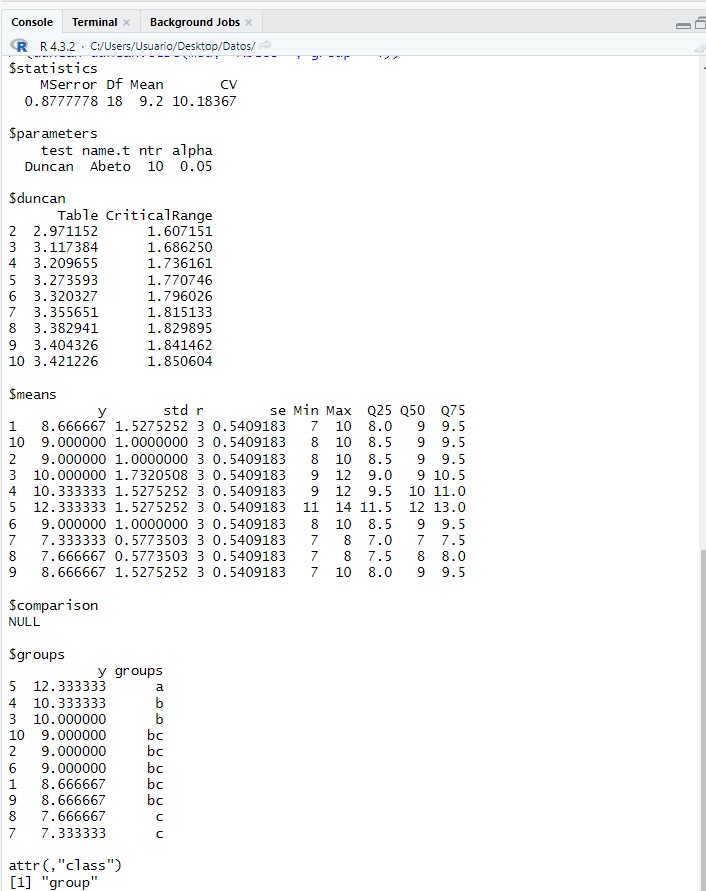
En la tabla del factor Tipo de abeto hay tres subconjuntos que se diferencian entre sí: en el primer subconjunto se encuentra el quinto abeto; en el segundo subconjunto se encuentra el primer, segundo, tercero, cuarto, sexto, noveno y décimo abeto; en el tercer subconjunto se encuentra el primer, segundo, sexto, séptimo, octavo, noveno y décimo abeto. También se observa que en el quinto tratamiento se produce el mayor número de semillas (12.33) y en el séptimo se produce el menor número de semillas (7.3).
3. Estudiar las hipótesis de modelo: Homocedasticidad, Independencia y Normalidad.
Estudiamos la homocedasticidad mediante el test de Barlett:
bartlett.test(semillas$y, semillas$Tratamiento)

bartlett.test(semillas$y, semillas$Abeto)
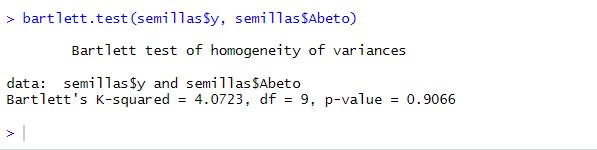
Las Tablas muestran los resultados del contraste de Barlett de igualdad de varianzas en todos los grupos del factor tipo de tratamiento y en todos los grupos del factor tipo de abeto. Los p-valores, 0.1241 y 0.9066 indican que no se debe rechazar la igualdad entre las varianzas ni en el factor tipo de tratamiento ni en el factor tipo de abeto.
Estudiamos la independencia gráficamente:
layout(matrix(c(1,2,3,4),2,2))
plot(mod)
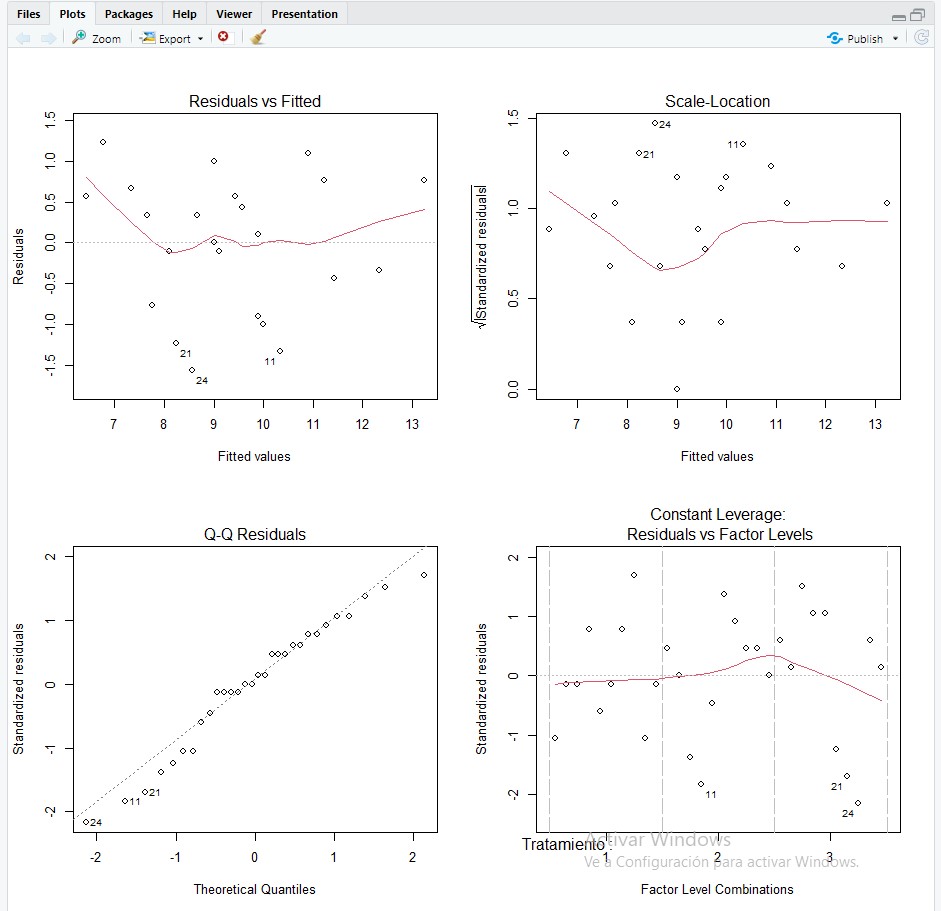
En esta salida, interpretamos el gráfico que se muestra en la Fila 1, Columna 1. Es decir, el gráfico el que se representan los residuos en el eje de ordenadas y los valores predichos por el modelo en el eje de abscisas. Este gráfico no muestra ningún aspecto que haga sospechar de la hipótesis de independencia de los residuos.
Estudiamos la Normalidad gráficamente mediante el gráfico probabilístico normal y analíticamente mediante el contraste de Shapiro-Wilk:
Observamos el gráfico que se muestra en la Fila 2, Columna1. Es decir, el gráfico el que se representan los residuos estandarizados en el eje de ordenadas y cuantiles teóricos en el eje de abscisas. En dicho gráfico se aprecian algunas desviaciones a la normalidad, pero el contraste ANOVA es robusto frente a desviaciones pequeñas de la normalidad. Realizaremos a continuación el contraste de Shapiro-Wilk para comprobar analíticamente la normalidad de los residuos.
shapiro.test(mod$residuals)
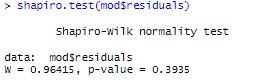
El p-valor es de 0.3935, no pudiéndose rechazar la hipótesis de normalidad.
Comandos y funciones utilizadas para resolver el ejercicio guiado 2
semillas <- read.table(“guiado2.txt”, header = TRUE)
semillas$Tratamiento = factor(semillas$Tratamiento)
semillas$Abeto= factor(semillas$Abeto)
mod <- aov(y ~ Tratamiento + Abeto, data = semillas)
mod
summary(mod)
library(agricolae)
(duncan=duncan.test(mod, “Tratamiento” , group = T))
(duncan=duncan.test(mod, “Abeto” , group = T))
bartlett.test(semillas$y, semillas$Tratamiento)
bartlett.test(semillas$y, semillas$Abeto)
layout(matrix(c(1,2,3,4),2,2))
plot(mod
shapiro.test(mod$residuals))
Ejercicio Guiado 3 (Resuelto)
En unos laboratorios se está investigando sobre el tiempo de supervivencia de unos animales a los que se le suministra al azar tres tipos de venenos (V1,V2,V3) y cuatro antídotos distintos (A1,A2,A3,A4). Se pretende estudiar si los tiempos de supervivencia de los animales varían en función de las combinaciones veneno-antídoto. Los datos que se recogen en la tabla adjunta son los tiempos de supervivencia en horas.
\( \begin{array} {|c|cccc|} \hline & & \text{Antídoto} & & \\ \hline \text{Veneno} & \text{A1} & \text{A2} & \text{A3} & \text{A4} \\ \hline \text{V1} & 4.5 & 11.0 & 4.5 & 7.1 \\ & 4.3 & 7.2 & 7.6 & 6.2 \\ \hline \text{V2} & 2.9 & 6.1 & 3.5 & 10.2 \\ & 2.3 & 12.4 & 4.0 & 3.8 \\ \hline \text{V3} & 2.1 & 3.7 & 2.5 & 3.6 \\ & 2.3 & 2.9 & 2.2 & 3.3 \\ \hline \end{array} \)
Figura 27: Tabla de datos del Ejercicio Guiado 3
Para un nivel de significación del 5%:
- ¿Se puede afirmar que los diferentes tipos de veneno influyen en la supervivencia de los animales? ¿Y los diferentes antídotos?
- ¿La efectividad del antídoto es la misma para los tres tipos de veneno?
- Estudia, utilizando el método de Newman-Keuls, qué antídoto es más efectivo.
Solución:
El problema planteado se modeliza a través de un diseño de dos factores con replicación, donde:
- Variable respuesta: Tiempo de supervivencia de unos animales
- Factor Veneno: Tipo de veneno con tres niveles. Es un factor de efectos fijos.
- Factor Antídoto: Tipo de antídoto con cuatro niveles. Es un factor de efectos fijos.
- Tamaño del experimento: Número total de observaciones (24).
Para realizar este supuesto en RStudio debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en RStudio de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en RStudio. En este caso lo hacemos en un archivo de texto
En el menú principal de RStudio elegimos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, seleccionamos el directorio de trabajo donde están los datos.
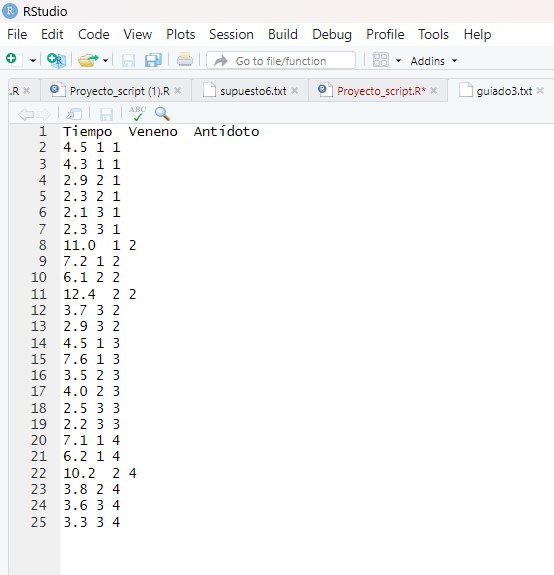
Para cargar los datos utilizamos la función “read.table” indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
factorial <- read.table(“guiado3.txt”, header = TRUE)
Transformamos todas las columnas que contienen a los factores en un factor para poder realizar los cálculos posteriores adecuadamente.
factorial$Veneno=factor(factorial$Veneno)
factorial$Antídoto=factor(factorial$Antídoto)
1. ¿Se puede afirmar que los diferentes tipos de veneno influyen en la supervivencia de los animales? ¿Y los diferentes antídotos?
Para responder a este apartado debe resolverse el contraste de igualdad de medias para el factor Veneno:
\( \begin{array}{c} H_0 \equiv \mu_1 = \mu_2 = \mu_3 ~~~ vs ~~~ H_1 \equiv \mu_i \neq \mu_j \hspace{.2cm} \text {para algún } i\neq j \end{array} \)
y para el factor Antídoto
\( \begin{array}{c} H_0 \equiv \mu_1 = \mu_2 = \cdots = \mu_4 ~~~ vs ~~~ H_1 \equiv \mu_i \neq \mu_j \hspace{.2cm} \text {para algún } i\neq j \end{array} \)
Para calcular la tabla ANOVA en R primero hacemos uso de la función “aov”:
mod <- aov(Tiempo ~ Veneno * Antídoto, data = factorial)
mod
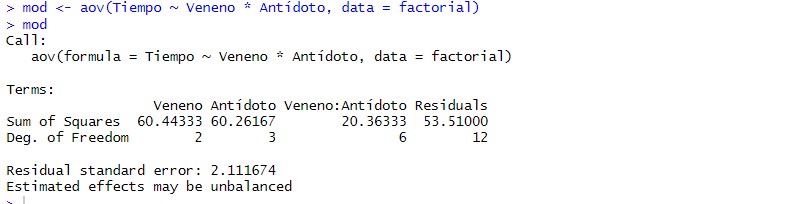
Y a continuación “summary” para mostrar un resumen de los resultados, de la siguiente forma:
summary(mod)
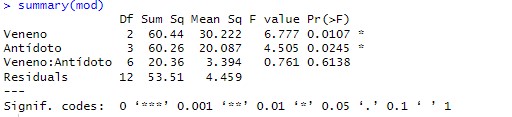
- El valor del estadístico de contraste de igualdad de medias del factor tipo de veneno, F=6.78 deja a su derecha un p-valor=0.0107, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias de los niveles del factor tipo de veneno. Es decir, existen diferencias significativas en el tiempo de supervivencia de los animales dependiendo del tipo de veneno.
- El valor del estadístico de contraste de igualdad de medias del factor tipo de antídoto, F=4.505 deja a su derecha un p-valor=0.0245, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias de los niveles del factor tipo de antídoto. Es decir, existen diferencias significativas en el tiempo de supervivencia de los animales dependiendo del tipo de antídoto.
2. ¿La efectividad del antídoto es la misma para los tres tipos de veneno?
Para responder a esta pregunta, realizamos el contraste de hipótesis sobre la interacción de los dos factores
\( \begin{array}{c} H_0 \equiv (\tau \beta)_{ij} = 0 \text {no existe interacción} ~~~ vs ~~~ H_1 \equiv (\tau \beta)_{ij} \neq 0 \text { existe interacción} \end{array} \)
En la Tabla ANOVA mostrada anteriormente, el valor del estadístico de contraste de la interacción de los dos factores, F= 0.761 deja a su derecha un p-valor=0.6138, mayor que el nivel de significación del 5%, por lo que no se puede rechazar la Hipótesis nula de no interacción entre los factores. Por lo tanto la efectividad del antídoto sí es la misma para los diferentes tipos de veneno. Es decir, no puede ocurrir que el tipo de antídoto influya en el tiempo de supervivencia de los animales de distinta forma en función del tipo de veneno.
3. Estudia, utilizando el método de Newman-Keuls, qué antídoto es más efectivo.
Usamos la función “SNK.test” del paquete “agricolae”. Leemos dicho paquete y aplicamos la función para el factor “antídoto”.
library(agricolae)
contraste <- SNK.test(mod, “Antídoto”, console = TRUE, main = “Contraste de Newman-Keuls para el factor tipo de antídoto”)
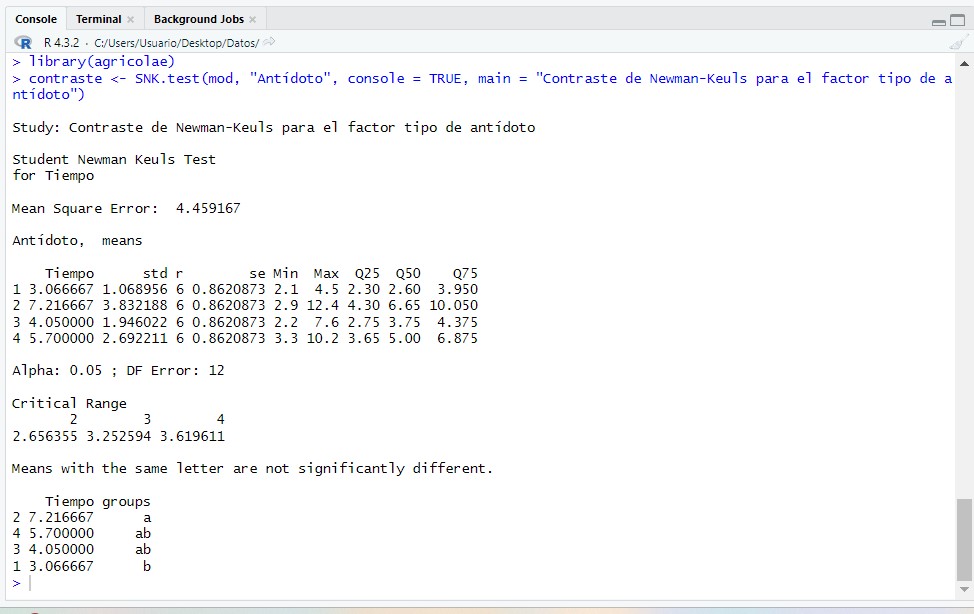
En la tabla se muestran los subgrupos formados de medias iguales al utilizar el método de Newman-Keuls. Hay dos subconjuntos que se diferencian entre sí, el primero formado por los antídotos A2, A3 y A4, y el segundo conjunto formado por los antídotos A1, A3 y A4. También se observa que con segundo antídoto se produce un mayor tiempo de supervivencia (7.22), y con el primer antídoto se produce el menor tiempo de supervivencia (3.07).
Comandos y funciones utilizadas para resolver el ejercicio guiado 3
factorial <- read.table(“guiado3.txt”, header = TRUE)
factorial$Veneno=factor(factorial$Veneno)
factorial$Antídoto=factor(factorial$Antídoto)
mod <- aov(Tiempo ~ Veneno * Antídoto, data = factorial)
mod
summary(mod)
library(agricolae)
contraste <- SNK.test(mod, “Antídoto”, console = TRUE, main = “Contraste de Newman-Keuls para el factor tipo de antídoto”)
Ejercicios Propuestos
Ejercicio Propuesto 1
Los medios de cultivo bacteriológico en los laboratorios de los hospitales proceden de diversos fabricantes. Se sospecha que la calidad de estos medios de cultivo varía de un fabricante a otro. Para comprobar esta teoría, se hace una lista de fabricantes de un medio de cultivo concreto, se seleccionan aleatoriamente los nombres de cinco de los que aparecen en la lista y se comparan las muestras de los instrumentos procedentes de éstos. La comprobación se realiza colocando sobre una placa dos dosis, en gotas, de una suspensión medida de un microorganismo clásico, Escherichia coli, dejando al cultivo crecer durante veinticuatro horas, y determinando después el número de colonias (en millares) del microorganismo que aparecen al final del período. Se quiere comprobar si la calidad del instrumental difiere entre fabricantes.
\( \begin{array} {|c|ccccccccc|} \hline \text{Fabricantes} & & \text{Número} & \text{de} & \text{colonias} & \text{en } & \text{millares} & & \\ \hline \text{Fabricante 1} & 120 & 240 & 300 & 360 & 240 & 180 & 144 & 300 & 240 \\ \hline \text{Fabricante 2} & 240 & 360 & 180 & 180 & 300 & 240 & 360 & 360 & 360 \\ \hline \text{Fabricante 3} & 240 & 270 & 300 & 360 & 360 &300 & 360 & 360 & 300 \\ \hline \text{Fabricante 4} & 300 & 240 & 300 & 360 & 360 & 360 & 360 & 360 & 300 \\ \hline \text{Fabricante 5} &300 & 360 & 240 & 360 & 360 & 360 & 360 & 300 & 360 \\ \hline \end{array} \)
Figura 28: Tabla de datos del Ejercicio Propuesto 1
Para un nivel de significación del 5% , ¿Qué conclusiones se deducen de este experimento?
Ejercicio Propuesto 2
Un laboratorio utiliza 4 hornos en la fabricación de un determinado producto. Se sospecha que la temperatura afecta a la dureza del producto obtenido. Cada horno puede operar a 4 temperaturas distintas. Se sabe que cada horno tiene sus propias características de operación, de modo que los hornos se consideran una variable influyente en la fabricación de dicho producto. Se utiliza un diseño en bloques aleatorizados, considerando los hornos como bloque. Los resultados se muestran en la siguiente tabla.
\( \begin{array} {|c|cccc|} \hline & & \text{Hornos} & & \\ \hline \text{Temperatura} & 1& 2 & 3 & 4 \\ \hline 80 & 7 & 6 & 10 & 5 \\ \hline 90 & 9 & 7 & 12 & 8 \\ \hline 100 & 7 & 15 & 10 & 7 \\ \hline 110 & 12 & 6 & 5 & 10 \\ \hline \end{array} \)
Figura 29: Tabla de datos del Ejercicio Propuesto 2
Para un nivel de significación del 5%:
- ¿Existe alguna evidencia de que la temperatura influye en la dureza del producto? ¿Y el tipo de horno?
- Estudiar las interacciones de los factores.
Ejercicio Propuesto 3
Se realiza un estudio para comprobar la efectividad en el retraso del crecimiento de bacterias utilizando cuatro soluciones diferentes para lavar los envases de la leche. El análisis se realiza en el laboratorio y sólo se pueden realizar seis pruebas en un mismo día. Como los días son una fuente de variabilidad potencial, el investigador decide utilizar un diseño aleatorizado por bloques, pero al recopilar las observaciones durante seis días no ha sido posible aplicar todos los tratamientos en cada día, sino que sólo se han podido aplicar dos de las cuatro soluciones cada día.
\( \begin{array} {|c|cccccc|} \hline & & & \text{Días} & & & \\ \hline \text{Soluciones} & 1& 2 & 3 & 4 & 5 & 6\\ \hline 1 & 12 & 24 & 31 & & & \\ \hline 2 & 21 & & & & 20 & 21 \\ \hline 3 & & & 19 & 18 & & 19 \\ \hline 4 & & 15 & & 19 & 47 & \\ \hline \end{array} \)
Figura 30: Tabla de datos del Ejercicio Propuesto 2
Para un nivel de significación del 5%:
- ¿Son las diferentes soluciones fuente de variación? ¿Y los días?
- Utilizando el método de Newman-Keuls, ¿qué tipo de solución produce un mayor efecto en el crecimiento de bacterias?
Ejercicio Propuesto 1 (Resuelto)
El fabricante del medio de cultivo sí influye significativamente (p-valor=0.008<0.05, rechazamos la hipótesis nula) en el número de colonias. Por lo que concluimos que existe una diferencia entre en la calidad del instrumental en función del fabricante.
Ejercicio Propuesto 1 (Resuelto)
Ejercicio Propuesto 2 (Resuelto)
En la tabla ANOVA observamos como ni la temperatura (p-valor=0.685>0.05, ni el tipo de horno (p-valor=0.893>0.05) influyen significativamente en la dureza del producto.
Respecto a la interacción, como el p-valor (0.9037) es mayor que el nivel de significación (0.05) no podemos rechazar la hipótesis de no interacción, es decir, no existe interacción entre los factores.
Ejercicio Propuesto 2 (Resuelto)
Ejercicio Propuesto 3 (Resuelto)
-
Observamos cómo ni el tipo de solución (p-valor=0.818>0.05, no podemos rechazar la hipótesis nula) ni los diferentes días (p-valor=0.7118>0.05) influyen significativamente en el crecimiento de bacterias.
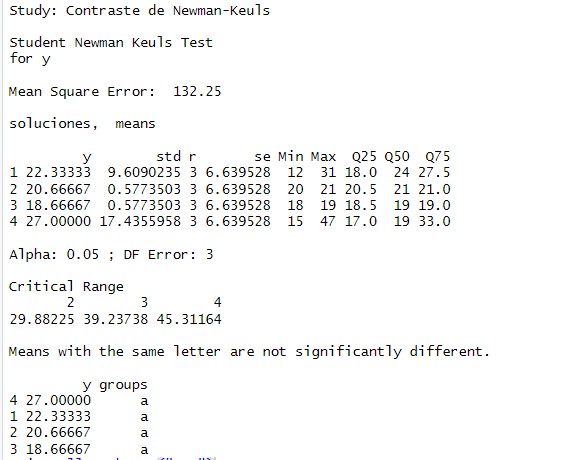
Ejercicio Propuesto 3 (Resuelto)
Autores: Jorge Luis Rueda Sánchez y Ana María Lara Porras. Universidad de Granada. (2024)