DISEÑO FACTORIAL CON DOS FACTORES 

Objetivos

• Identificar un diseño bifactorial  y estudiar las interacciones entre los factores.
• Realizar un análisis de la varianza de dos vías a través de una tabla ANOVA que permita estudiar simultáneamente los efectos de dos fuentes de variación sobre una variable respuesta.
• Emitir juicios sobre la validación del modelo en vista de los gráficos residuales.
• Contrastar la igualdad de varianzas a partir del test de Bartlett
• Realizar comparaciones múltiples de medias a través del test HSD de Tukey.

Introducción

En muchos experimentos es frecuente considerar dos factores y estudiar el efecto conjunto que producen sobre la variable respuesta. Para resolver esta situación se utiliza el diseño factorial con dos factores.

Se entiende por diseño factorial aquel en el que se investigan todas las posibles combinaciones de los niveles de los factores en cada réplica del experimento. En estos diseños, los factores que intervienen tienen la misma importancia a priori y puede suponerse o no la presencia de interacción.

Supongamos que tenemos un factor \( A \) con \( a \) niveles y un factor \( B \) con \( b \) niveles, en cuyo caso cada réplica del experimento puede contener todas las posibles combinaciones de tratamientos, es decir, los \( ab \) tratamientos posibles.

Si se toma una observación para cada combinación de niveles de los dos factores el modelo se conoce como modelo sin replicación (\( N=ab \)). En caso de tomar \( r \) observaciones para cada combinación de los niveles de los dos factores, el modelo se conoce como modelo con replicación \( (N=abr) \).

El modelo sin replicación

El modelo estadístico para este diseño es:

\( y_{i j}= \mu + \tau_i + \beta_j + (\tau \beta)_{i j}+ u_{i j} \hspace{.2cm}; \hspace{.2cm} i: 1, \ldots, a \hspace{.2cm}; \hspace{.2cm} j: 1, \ldots, b \hspace{.2cm}, \hspace{.2cm} \) donde

Expresión 1: Modelo estadístico del diseño factorial de dos factores sin replicación

• \( y_{i j}  \): Representa la observación correspondiente al nivel (i) del factor \( A \)  y al nivel (j) del factor \( B \).
• \( \mu  \): Efecto constante, común a todos los niveles de los factores, denominado media global.
• \( \tau_i  \): Efecto producido por el nivel i-ésimo del factor \( A \), \( ( \sum_i \tau_i = 0 ) \).
• \( \beta_j  \): Efecto producido por el nivel j-ésimo del factor \( B \), \( ( \sum_j \beta_j = 0 ) \).
• \( (\tau \beta)_{i j}  \): Efecto producido por la interacción entre \( A \times B \), \( ( \sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij} = 0 ) \).
• \(  u_{i j}  \) son vv aa. independientes con distribución \( N(0,σ)  \).

Supondremos que se toma una observación por cada combinación de factores, por tanto, hay un total de \( N = ab \) observaciones.

Parámetros a estimar:

\( \begin{array}{|c|c|} \hline \text { Parámetros } & \text { Número } \\  \hline \mu & 1 \\  \hline \tau_i & \mathrm{a}-1 \\ \hline \beta_j & \mathrm{~b}-1 \\  \hline(\tau \beta)_{i j} & (\mathrm{a}-1)(\mathrm{b}-1) \\  \hline \sigma^2 & 1 \\ \hline \text { Total } & \mathrm{ab}+1 \\ \hline  \end{array} \)

Figura 1: Tabla del número de parámetros a estimar

A pesar de las restricciones impuestas al modelo, \( ( \sum_i \tau_i =\sum_j \beta_j =  \sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij} = 0 ) \), el número total de parámteros a estimar \( ab+1 \), es superior al número de observaciones \( ab \). Por lo tanto, algún parámetro no será estimable.

Los residuos de este modelo son \( e_{i j}=y_{i j}-y_{i j}=0 \), por lo tanto, al ser nulos, no es posible estimar la varianza del modelo y no se puede contrastar la significatividad de los efectos de los factores. Dichos contrastes sólo pueden realizarse si:

1. Suponemos que la interacción entre los factores  \( A  \) y \( B \) es cero o
2. Replicamos el experimento (tomamos varias observaciones por cada combinación de factores)

 Supuesto práctico 1

En unos laboratorios se está investigando sobre el tiempo de supervivencia de unos animales a los que se les suministra al azar tres tipos de venenos y cuatro antídotos distintos. Se pretende estudiar si los tiempos de supervivencia de los anímales varían en función de las combinaciones veneno-antídoto. Los datos que se recogen en la tabla adjunta son los tiempos de supervivencia en horas.

\( \begin{array}{|c|c|c|c|} \hline   \text {Veneno } &  \text { Antídoto 1 } &  \text { Antídoto 2 } &  \text { Antídoto 3 }  &  \text { Antídoto 4} \\  \hline  \text { Veneno 1 } &  4.5 & 11.0 & 4.5 & 7.1 \\ \hline  \text { Veneno 2 } & 2.9 & 6.1 & 3.5 & 10.2   \\  \hline  \text { Veneno 3} & 2.1 & 3.7 & 2.5 & 3.6 \\   \hline  \end{array} \)

Figura 2: Tabla de datos del Supuesto Práctico1. txt

El objetivo principal es estudiar la influencia de tres tipos de venenos y 4 tipos de antídotos sobre el tiempo de supervivencia de unos determinados animales, por lo que se trata de un modelo con dos factores: el veneno (con tres niveles) y el antídoto (con cuatro niveles). La variable que va a medir las diferencias entre los tratamientos es el tiempo que sobreviven los animales. Se combinan todos los niveles de los dos factores por lo que tenemos en total doce tratamientos, como el número total de observaciones también es 12 supondremos que no hay interacción entre los factores ya que si la hubiera el número de parámetros del modelo superaría al número de observaciones y como consecuencia los residuos del modelo serían nulos y no se podrían contrastar la significatividad de los efectos de los factores.

• Variable respuesta: Tiempo de supervivencia
• Factor: Tipo de veneno que tiene tres niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.

• Factor: Tipo de antídoto que tiene cuatro niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.

• Tamaño del experimento: Número total de observaciones (12).

El modelo estadístico para este diseño es:

\( y_{i j}= \mu + \tau_i + \beta_j + (\tau \beta)_{i j}+ u_{i j} \hspace{.2cm}; \hspace{.2cm} i: 1, 2,3 \hspace{.2cm}; \hspace{.2cm} j: 1, 2,3,4 \hspace{.2cm}, \hspace{.2cm} \) donde

• \( y_{i j}  \): tiempo de supervivencia del animal al que se le suministró el veneno \( i \) y el antídoto \( j  \)
• \( \mu  \): Efecto constante, común a todos los niveles de los factores, denominado media global.
• \( \tau_i  \): Efecto producido por el veneno \(  i  \), \( ( \sum_i \tau_i = 0 ) \).
• \( \beta_j  \): Efecto producido por el antídoto \( j \), \( ( \sum_j \beta_j = 0 ) \).
• \(  u_{i j}  \): Errores experimentales. Son vv aa. independientes con distribución \( N(0,σ)  \).

Denotaremos los tres venenos como \( A_1 \),  \( A_2 \) y \( A_3 \) y a los cuatro antídotos como  \( B_1 \), \( B_2 \), \( B_3 \) y \( B_4 \)

Para realizar este supuesto con BrailleR, ejecutamos R y cargamos el paquete BrailleR

>  library(“BrailleR”)

Leemos el fichero que contiene los datos. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.

En este caso lo hacemos en un archivo de texto:

Figura 3: Tabla de datos del Supuesto Práctico1.txt

Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado sus factores correspondientes.

Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.

> setwd(“C:/Users/Usuario/Desktop/Datos”)
> supuesto= read.table(“supuesto1.txt”,header=TRUE)
> supuesto
tiempo veneno antidoto
1             4.5      1 1
2             2.9      2 1
3             2.1      3 1
4            11.0     1 2
5             6.1      2 2
6            3.7      3 2
7            4.5      1 3
8            3.5      2 3
9            2.5      3 3
10          7.1      1 4
11         10.2      2 4
12         3.6       3 4

Hay que tener en cuenta que cuando R lee el fichero de datos interpreta que éste contiene tres variables numéricas por lo que es necesario decirle que interprete las variables veneno y antídoto como factores para lo cual utilizamos las siguientes sentencias:

> supuesto$veneno=as.factor(supuesto$veneno)
> supuesto$antidoto=as.factor(supuesto$antidoto)

Realizamos el análisis de la varianza mediante la función TwoFactors

> TwoFactors(Response=’tiempo’,Factor1=’veneno’,Factor2=’antidoto’,Data=supuesto, Inter=’False’, HSD=’TRUE’)

Nótese que hemos especificado Inter= FALSE por la razón que se ha comentado anteriormente de ser un modelo sin interacción entre los factores.

Entonces, se muestra una salida en html con los siguientes resultados:

a) Un análisis descriptivo de la variable respuesta para cada combinación de valores de los dos factores (dado que solo tenemos una observación para cada combinación de los valores, no se calcula la desviación típica).

Analysis of the supuesto data, using tiempo as the response variable and the variables veneno and antidoto as factors.

Prepared by BrailleR

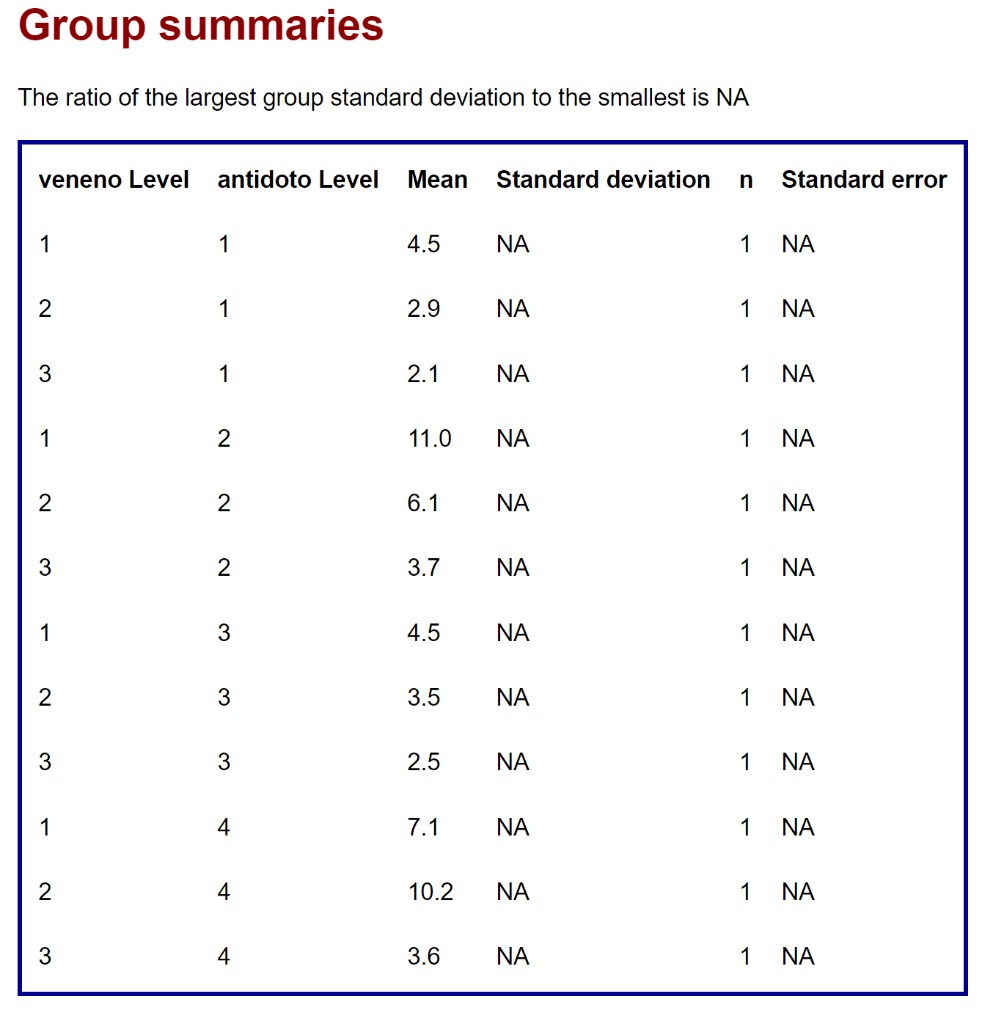
b) Diagramas de puntos comparativos para cada uno de los factores.

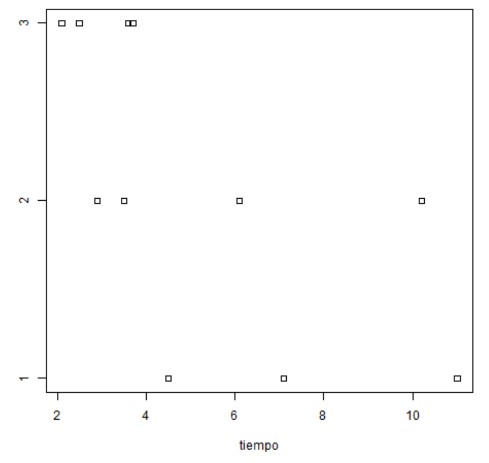
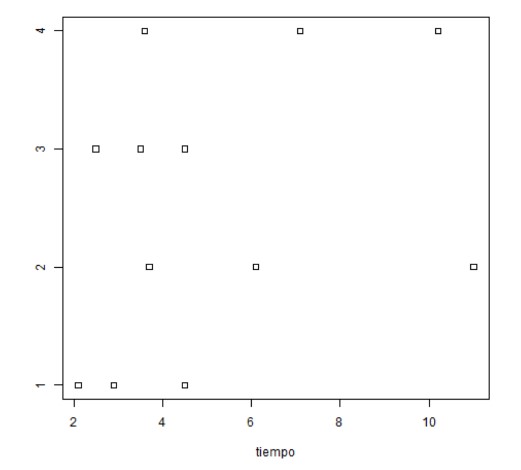
c) Tabla ANOVA para el análisis de la varianza de dos factores

Esta Tabla ANOVA recoge la descomposición de la varianza considerando como fuente de variación los doce tratamientos o grupos que se forman al combinar los niveles de los dos factores. Mediante esta tabla se puede estudiar sí varían los tiempos que sobreviven los animales en función de las combinaciones veneno-antídoto. Es decir, se pueden estudiar si existen diferencias significativas entre los tiempos medios de supervivencia con los distintos tipos de venenos

\( \begin{array}{ll}  H_0: & \text { Efecto veneno }=0 \equiv \tau_1=\tau_2=\tau_3=0 \\  H_1: & \text { Efecto veneno } \neq 0 \equiv \tau_i \neq 0 \text { para algún } i=1,2,3 \end{array} \)

y si existen diferencias significativas entre los tiempos medios de supervivencia con los distintos tipos de antídotos

\( \begin{array}{ll}  H_0:  & \text { Efecto antídoto }=0 \equiv \beta_1=\beta_2=\beta_3=0 \\  H_1: & \text { Efecto antídoto } \neq 0 \equiv \beta_j \neq 0 \text { para algún } j=1,2,3,4 \end{array} \)

Pero no se puede estudiar si la efectividad de los antídotos es la misma para todos los venenos. Observando los p-valores, 0.084 y 0.099; mayores respectivamente que el nivel de significación del 5%, deducimos que ningún efecto es significativo. Por lo tanto, no existen diferencias en los tiempos medios de supervivencia de los animales, en función de la pareja veneno-antídoto que se les suministra.

Para comprobar la idoneidad del modelo propuesto, se muestran los siguientes gráficos:

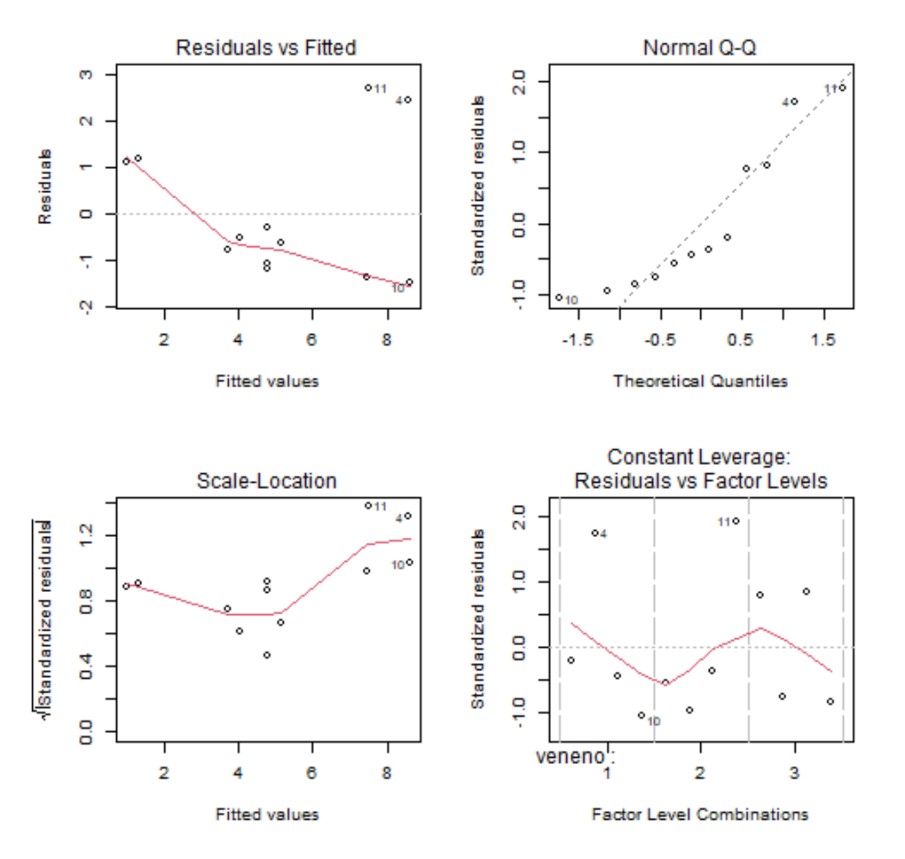
1. Valores predichos frente a residuos
2. Gráfico Q-Q de normalidad
3. Valores predichos frente a raíz cuadrada de los residuos estandarizados (en valor absoluto)
4. Residuos estandarizados frente a leverages

Los gráficos 1 y 3 se utilizan para contrastar gráficamente la independencia, la homocedasticidad y la linealidad de los residuos. Idealmente, los residuos deben estar aleatoriamente distribuidos a lo largo del gráfico, sin formar ningún tipo de patrón.

El gráfico de leverages frente a los residuos estandarizados se utiliza para detectar puntos con una influencia importante en el cálculo de las estimaciones de los parámetros. En caso de detectarse algún punto fuera de los límites que establecen las líneas discontinuas debe estudiarse este punto de forma aislada para detectar, por ejemplo, si la elevada importancia de esa observación se debe a un error.

d) Test para la homogeneidad de varianzas de la variable respuesta según los distintos niveles de factor, para cada uno de los factores.

Los resultados del test de Barlett indican que se aceptan la hipótesis nulas de igualdad de varianzas tanto para los diferentes niveles del factor veneno  (p-valor =0.1143)

\(  H_0: \sigma_{A_1}^2=\sigma_{A_2}^2=\sigma_{A_3}^2  \hspace{.3cm} \text { vs } \hspace{.3cm} H_1: \sigma_{A_i}^2 \neq \sigma_{A_j}^2 \text { para algún } i \neq j \)

como para los diferentes niveles del factor antídoto  (p-valor=0.2917)

\(  H_0: \sigma_{B_1}^2=\sigma_{B_2}^2=\sigma_{B_3}^2=\sigma_{B_4}^2 \hspace{.3cm} \text { vs }  \hspace{.3cm} H_1: \sigma_{B_i}^2 \neq \sigma_{B_j}^2 \text { para algún } i \neq j \)

 d) Test HSD de Tukey para la comparación múltiple de medias, así como el gráfico de diferencia de medias.

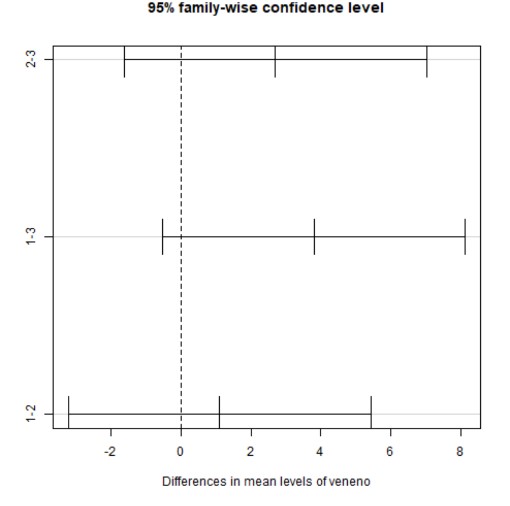
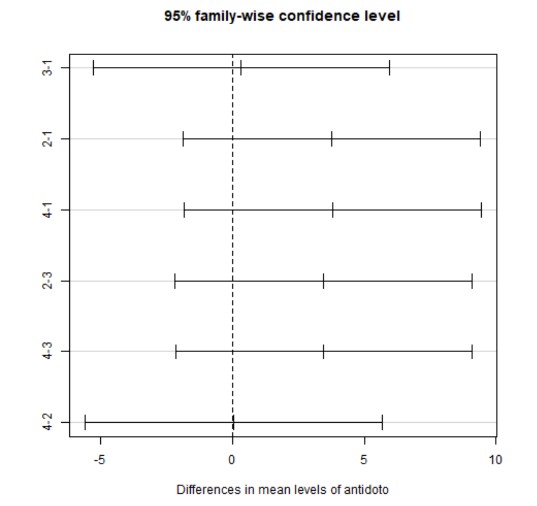
Los tres pares de hipótesis para ver si los tres venenos son igual de peligrosos son:

\( \begin{array}{lll} H_0: \mu_{A _1}= \mu_{A_2}  & H_0: \mu_{A_1}= \mu_{A_3}  & H_0: \mu_{A_2}= \mu_{A_3} \\ H_1: \mu_{A_1} \neq \mu_{A_2} & H_1: \mu_{A _1} \neq \mu_{A_3} & H_1: \mu_{A_2} \neq \mu_{A_3} \end{array} \)

Mientras que para estudiar si los cuatro antídotos son igual de efectivos se tienen los seis pares de hipótesis,

\(  \begin{array}{lll} H_0: \mu_{B_1}=\mu_{B_2} & H_0: \mu_{B_1}=\mu_{B_3} & H_0: \mu_{B_1}=\mu_{B_4} \\  H_1: \mu_{B_1} \neq \mu_{B_2}{ }^{\prime} & H_1: \mu_{B_1} \neq \mu_{B_3} & H_1: \mu_{B_1} \neq \mu_{B_4} \\  H_0: \mu_{B_2}=\mu_{B_3} ; & H_0: \mu_{B_2}=\mu_{B_4} & H_0: \mu_{B_3}=\mu_{B_4} \\ H_1: \mu_{B_2} \neq \mu_{B_3}{ }^{\prime} & H_1: \mu_{B_2} \neq \mu_{B_4} & H_1: \mu_{B_3} \neq \mu_{B_4} \end{array} \)

Dado que anteriormente ya hemos visto que ninguno de los efectos era significativo, es lógico que ahora ninguno de los test sea significativo, se acepten todas las hipótesis nulas y no haya diferencias ni en las peligrosidades de los venenos ni en las efectividades de los antídotos.

Los test de Tukey tiene sentido hacerlos cuando al hacer el Anova se rechaza la hipótesis nula obteniéndose que los factores son significativos.

El modelo con replicación

El modelo estadístico para este diseño es:

\( y_{i j k}=\mu+\tau_i+\beta_j+(\tau \beta)_{i j}+u_{i j k} ; \quad i: 1, \ldots, a \quad ; \quad j: 1, \ldots, b  \quad ; \quad \mathrm{k}: 1, \ldots, \mathrm{r} \)

Expresión 2: Modelo estadístico del diseño factorial de dos factores con replicación

donde \( r \) es el número de replicaciones y \( N=abr \) es el número de observaciones.

El número de parámetros de este modelo es, como en el modelo de dos factores sin replicación, \(  ab+1 \) pero en este caso el número de observaciones es \(  abr \).

Estimación de los parámetros del modelo

Los estimadores máximo verosímiles de los parámetros del modelo son:

\(  \hat{\mu}=\bar{y}_{\ldots,}, \quad \hat{\tau}_i=\bar{y}_{i ..}-\bar{y}_{\ldots,}, \quad \hat{\beta}_j=\bar{y}_{\cdot j \cdot}-\bar{y}_{\ldots,} \quad  (\widehat{\tau \beta})_{i j}=\bar{y}_{i j \cdot}-\bar{y}_{i \cdot}-\bar{y}_{\cdot j \cdot}+\bar{y}_{\ldots} \)

donde

\( \bar{y}_{i j.} \) es la media de las \( r \) observaciones del nivel i-ésimo del factor \( A \) y del nivel j-ésimo del factor \( B \) (celdilla ij):  \( \bar{y}_{i j.}=\left(\sum_k y_{i j k}\right) / r \)

\( \bar{y}_{i..} \) es la media de las observaciones del nivel i-ésimo del factor \( A \): \( \bar{y}_{i..}=\left(\sum_{j, k} y_{i j k}\right) / b r \);  \( \mathrm{i}=1, \ldots, \mathrm{a}\)

\( \bar{y}_{.j.} \) es la media de las observaciones del nivel j-ésimo del factor \( B\): \( \bar{y}_{.j.}=\left(\sum_{i, k} y_{i j k}\right) / a r \);  \( \mathrm{j}=1, \ldots, \mathrm{b} \)

 \( \bar{y}_{. . .} \) es la media total de las observaciones: \( \bar{y}_{.. .}=\left(\sum_{i, j, k} y_{i j k}\right) / r \).

Los residuos de este modelo son:

\( e_{i j k}=y_{i j k}-\hat{y}_{i j k}=y_{i j}-\hat{\mu}-\hat{\tau}_i-\hat{\beta}_j-(\widehat{\tau \beta})_{i j}=y_{i j k}-\bar{y}_{ij.} \)

Se verifica que todos los residuos de una celdilla deben sumar cero, es decir, en cada celdilla hay \( r-1 \) residuos independientes. Por lo tanto, en total habrá \( ab(r-1) \) residuos independientes.

La varianza residual tiene la siguiente expresión:

\(  \hat{S}_R^2=\frac{\displaystyle \sum_{i=1}^a \displaystyle \sum_{j=1}^b  \displaystyle \sum_{k=1}^r e_{i j k}^2}{a b(r-1)} \)

Descomposición de la variabilidad

La ecuación básica del análisis de la varianza es:

\(  \begin{gathered} \sum_{i, j, k}\left(y_{i j k}-\bar{y}_{…}\right)^2=b r \sum_{i=1}^a \left(\bar{y}_{i..}-\bar{y}_{…} \right)^2+a r \sum_{j=1}^b \left(\bar{y}_{.j.}-\bar{y}_{…}\right)^2 \\  +r \sum_{i, j} \left(y_{i j k}-\bar{y}_{i..}-\bar{y}_{.j.}+\bar{y}_{…}\right)^2 + \sum_{i, j, k} \left(y_{i j k} – \bar{y}_{i j.} \right)^2 \end{gathered} \)

que simbólicamente escribimos como: \( SCT = SCA + SCB + SC(AB)+SCR \), siendo:

\( SCT =\sum_{i, j, k}\left(y_{i j k}-\bar{y}_{\ldots}\right)^2 \) : Suma total de cuadrados

\( SCA= =\operatorname{br} \sum_{i=1}^a\left(\bar{y}_{i . .}-\bar{y}_{…}\right)^2  \):  Suma de cuadrados entre niveles de  \( A \)

\( SCB = =\operatorname{ar} \sum_{j=1}^b\left(\bar{y}_{. j .}-\bar{y}_{…}\right)^2 \): Suma de cuadrados entre niveles de \( B \)

\( SC(AB)= =r \sum_{i, j}\left(y_{i j k}-\bar{y}_{i . .}-\bar{y}_{. j .}+\bar{y}_{…}\right)^2 \): Suma de cuadrados de la intersección \( A \times B \)

\( SCR = \sum_{i, j, k}\left(y_{i j k}-\bar{y}_{i j}\right)^2 \): Suma de cuadrados residual, donde \( SCR = SCT-SCA-SCB-SC(AB) \)

A partir de estas sumas de cuadrados pueden calcularse los cuadrados medios como:

\(  CMT = SCT / (n-1)  \): Cuadrado medio total

\(  CMA = SCA / (a-1)  \): Cuadrado medio de \( A  \)

\(  CMB = SCB / (b-1)  \): Cuadrado medio de \( B  \)

\(  CM(AB) = (SC(AB))/((a-1)(b-1))  \): Cuadrado medio de la interacción  \( A \times B  \)

\( CMR = SCR/(ab(r-1))  \): Cuadrado medio residual

 Análisis estadístico

El objetivo es realizar los siguientes contrastes de hipótesis nula:

1) Considerando la presencia de las interacciones con el factor \( B \), contrastar si los efectos de los niveles del factor \( A \) son nulos, siendo el estadístico de contraste \( F_A \)

  \(    H_{0}: \tau_{1}=\tau_{2}=\ldots=\tau_{a}= 0 \quad ;  \quad F_A = \frac{CMA}{CMR} \rightarrow F_{(a-1), ab(r-1)} \)

Se rechaza la hipótesis nula si  \( F_A> F_{(a-1), a b ( r – 1 )} \) al nivel de significación considerado.

2) Considerando la presencia de las interacciones con el factor \( A \), contrastar si los efectos de los niveles del factor \(  B \)  son nulos. El estadístico de contraste es \( F_B \)

\(  H_{0}:\beta_{1} = \beta_2 = \ldots = \beta_b = 0 \quad ; \quad F_B = \frac{C M B}{C M R} \rightarrow F_{(b-1), ab(r-1)} \)

Se rechaza la hipótesis nula si \( F_B>F_{(b-1), a b(r-1)} \) al nivel de significación considerado

3. Contrastar si los efectos de las interacciones entre los factores  \( A \) y \( B \) son nulos. El estadístico de contraste es \( F_{AB} \)

\( H_{0}:\tau_{i j} = 0 \quad ; \quad F_{A B} = \frac{C M(A B)}{C M R} \rightarrow F_{(a-1)(b-1), a b(r-1)} \)

Se rechaza la hipótesis nula si \( F_{A B}>F_{(a-1)(b-1), ab(r-1)} \) al nivel de significación considerado.

La tabla ANOVA para el modelo bifactorial con replicación queda de la siguiente forma:

\( \begin{array}{|l|l|l|l|l|} \hline F.V. & S.C & G.L. & C.M. & F_{exp} \\ \hline Factor A & SCA & a-1 & CMA & CMA/CMR \\ \hline Factor B & SCB & b-1 & CMB & CMB/CMR \\ \hline Interacción & SC(AB) & (a-1)(b-1) & CM(AB) & CM(AB)CMR \\ \hline Residual & SCR & ab(r-1) & CMR & \\ \hline TOTAL & SCT & Abr-1 & CMT & \\ \hline \end{array} \)

Validación del modelo

La diagnosis y validación del modelo consiste en estudiar si las hipótesis básicas del modelo están o no en contradicción con los datos observados. Es decir, si se satisfacen los supuestos del modelo: Normalidad, Independencia y Homocedasticidad.

Hipótesis de normalidad. Para contrastar esta hipótesis se puede utilizar el histograma de los residuos, debiendo mostrar éste  una distribución normal con centro en cero o el gráfico probabilístico normal (Normal Q-Q), siendo lo deseable que los residuos estandarizados estén lo más cerca posible a la línea punteada que aparece en el gráfico. También suelen utilizarse métodos analíticos como el de test de Kolmogorov-Smirnov o el de Shapiro-Wilk. Hay que tener en cuenta que las pruebas ANOVA son robustas ante leves desviaciones de la normalidad.

Hipótesis de independencia. Para comprobar que se satisface el supuesto de independencia entre los residuos se utiliza el gráfico de los residuos frente a los valores ajustados o predichos, la presencia de alguna tendencia en el mismo puede ser indicio de una violación de dicha hipótesis. Para contrastar la independencia de los residuos también se puede utilizar el test de Durbin-Watson.

Hipótesis de homocedasticidad. Para detectar heterocedasticidad se pueden usar gráficas de dispersión de los valores ajustados frente a los predicho o de los valores ajustados frente al valor absoluto de los residuos estandarizados o la raíz positiva de éstos, la presencia de algún patrón indicaría la violación del supuesto de homocedasticidad. Para confirmar las conclusiones obtenidas con los métodos gráficos se puede utilizar, por ejemplo, el test de Levene.

Test de Barlett 

Para estudiar si son iguales las varianzas de los niveles de cada uno de los factores, es decir, para decidir entre las hipótesis

 \( \begin{aligned} & H_0: \sigma_{A_1}^2=\sigma_{A_2}^2=\cdots=\sigma_{A_\alpha}^2 \text { vs } H_1: \sigma_{A_1}^2 \neq \sigma_{A_j}^2 \text { para algún } i \neq j \\ & H_0: \sigma_{B_1}^2=\sigma_{B_2}^2=\cdots=\sigma_{B_{\Delta}}^2 \text { vs } H_1: \sigma_{B_i}^2 \neq \sigma_{B_j}^2 \text { para algún } i \neq j \end{aligned}  \)

se puede utilizar el test de Barlett que demostró que si se consideran  \( I  \) muestras aleatorias provienen de poblaciones normales independientes, el estadístico

 \( B= \displaystyle \frac{1}{C}\left[(N-1) \ln \left( \displaystyle  \frac{\sum_{i=1}^I\left(n_i-1\right) s_i^2}{N-I}\right)-\sum_{i=1}^I\left(n_i-1\right) \ln s_i^2\right]  \)

se distribuye bajo la hipótesis nula y para tamaños de muestra grandes y suficientemente grandes, aproximadamente como una   \( \chi^2  \) con  \( I-1  \) grados de libertad donde

 \(  C=1+\displaystyle  \frac{1}{3(I-1)}\left(\sum_{i=1}^I\left(n_i-1\right)^{-1}-(N-I)^{-1}\right)  \)

Así, fijado un nivel \( \alpha \) se rechaza \( H_0  \) si \( B_{\exp }>\chi_{\alpha, I-1}^2  \), donde \( \chi_{\alpha, I-1}^2  \) es el valor crítico de la distribución \( \chi^2  \) con \( I-1  \) grados de libertad.

Comparaciones múltiples de medias: Test HSD de Tukey

Si el análisis de la varianza confirma la existencia de diferencias significativas entre los niveles de un factor, es conveniente investigar qué medias son distintas. Para ello se emplean diversas técnicas que se engloban bajo la denominación de contrastes para comparaciones múltiples. Uno de estos contraste es el test HSD (Honestly-significant-difference) de Tukey que se basa en la distribución del rango estudentizado que se define como el cociente

\(  \displaystyle \frac{\max \left(y_i\right)-\min _{i n}\left(y_i\right)}{S}= \displaystyle  \frac{R}{S} \)

y se denota por \( q_{k, \nu} \). En este procedimiento se rechaza \( H_0 \) si \( \left | \underline {y}_{i.} – \underline {y}_{j.} \right | > HSD  \)  siendo

• En el modelo equilibrado  \( HSD = q_{\alpha,I,N-I}    \displaystyle \sqrt{\displaystyle \frac { \widehat{S}^2_{R}}{n}} \)
• En el modelo no-equilibrado se reemplaza \( n \) por la media armónica, \( n_h \), de los tamaños de los grupos, es decir:

\(  n_h= \displaystyle \frac{2}{\displaystyle \sum_{i=1}^2  \displaystyle \frac{1}{n_i}} \)

La descripción del diseño así como la terminología subyacente la vamos a introducir mediante el siguiente supuesto práctico.

Supuesto práctico 2

Consideremos el supuesto práctico anterior en el que realizamos dos réplicas por cada tratamiento. Los datos que se recogen en la tabla adjunta son los tiempos de supervivencia en horas de unos animales a los que se les suministra al azar tres venenos y cuatro antídotos. El objetivo es estudiar qué antídoto es el adecuado para cada veneno. 

\(  \begin{array}{|c|c|c|c|c|}  \hline & & \text { Antídoto } & &  \\ \hline \text { Veneno } & \text { Antídoto 1 } & \text { Antídoto 2 } & \text { Antídoto 3 } & \text { Antídoto 4 } \\ \hline \text { Veneno 1 } & 4.5 & 11.0 & 4.5 & 7.1 \\ & 4.3 & 7.2 & 7.6 & 6.2 \\ \hline \text { Veneno 2 } & 2.9 & 3.1 & 3.5 & 10.2 \\ & 2.3 & 12.4 & 4.0 & 3.8 \\ \hline \text { Veneno 3 } & 2.1 & 3.7 & 2.5 & 3.6 \\ & 2.3 & 2.9 & 2.2 & 3.3 \\ \hline \end{array} \)

Figura 4: Tabla de datos del Supuesto Práctico 2.txt

El modelo matemático que planteamos es el siguiente:

\( y_{i j k}=\mu+\tau_i+\beta_j+(\tau \beta)_{i j}+u_{i j k} ; \quad i: 1,2,3 ; \quad j: 1,2,3,4 ; \quad k=1,2  \quad \), donde

Expresión 18: Modelo estadístico del diseño factorial de dos factores con replicación (Supuesto práctico 2)

• \( y_{i j k} \): Representa el tiempo de supervivencia del animal k al que se le suministró el veneno i y el antídoto j.

• \( \mu \):  Efecto constante, común a todos los niveles de los factores, denominado media global.
• \( \tau_i \): Efecto medio producido por el veneno \( i \), \( ( \sum_i \tau_i = 0 ) \).
• \( \beta_j \): Efecto medio producido por antídoto \( j \), \( ( \sum_i \beta_j = 0 ) \).
• \( (\tau \beta) _{ij} \): Efecto medio producido por la interacción entre el veneno \( i \),  y el antídoto \( j \), ( \(  \sum_i (\tau \beta)_{ij} = \sum_i (\tau \beta)_{ij} =0 \) ).
• \( u_{ijk} \) : Vv aa. independientes con distribución  \( N(0, \sigma)  \).

• Variable respuesta: Tiempo de supervivencia;
• Factor: Tipo de veneno (tres niveles).
• Factor: Tipo de antídoto (cuatro niveles).
• Ambos factores de efectos fijos.

• Tamaño del experimento: Número total de observaciones (24).

Función TwoFactors

Para realizar el análisis de la varianza de los diseños factoriales con el paquete BrailleR se utiliza la función TwoFactors cuya sintaxis es la siguiente:

TwoFactors(Response, Factor1, Factor2, Inter=FALSE, HSD=TRUE, Data=NULL)

donde:

Response es el nombre de la variable respuesta tipo continuo.

Factor1, Factor2 es el nombre de los dos factores incluidos en el análisis.

Inter es una variable lógica cuyo valor sebe ser “FALSE” dependiendo de si queremos que se incluya o no la interacción entre los dos factores. El valor por defecto de esta variable es FALSE.

HSD es una variable lógica al igual que la anterior, con los valores “TRUE” o “FALSE” dependiendo de si se quiere que se incluya la prueba HSD de Tukey en los resultados del análisis. Su valor por defecto es TRUE.

Data es el nombre de los datos

Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.

En este caso lo hacemos en un archivo de texto:

Figura 5: Tabla de datos del Supuesto Práctico 2.txt

Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado sus factores correspondientes.

Para realizar este supuesto con BrailleR, ejecutamos R y cargamos el paquete BrailleR

>  library(“BrailleR”)

Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.

> setwd(“C:/Users/Usuario/Desktop/Datos”)

> supuesto= read.table(“supuesto2.txt”,header=TRUE)
> supuesto
Tiempo Veneno Antidoto
1 4.5 1 1
2 4.3 1 1
3 2.9 2 1
4 2.3 2 1
5 2.1 3 1
6 2.3 3 1
7 11.0 1 2
8 7.2 1 2
9 6.1 2 2
10 12.4 2 2
11 3.7 3 2
12 2.9 3 2
13 4.5 1 3
14 7.6 1 3
15 3.5 2 3
16 4.0 2 3
17 2.5 3 3
18 2.2 3 3
19 7.1 1 4
20 6.2 1 4
21 10.2 2 4
22 3.8 2 4
23 3.6 3 4
24 3.3 3 4

A continuación debemos transformar todas las columnas que contienen a los factores en un factor para podemos realizar los cálculos posteriores adecuadamente.

> supuesto$Veneno=as.factor(supuesto$Veneno)
> supuesto$Antidoto=as.factor(supuesto$Antidoto)

Para realizar el análisis de la varianza de los diseños factoriales con el paquete BrailleR se utiliza la función TwoFactors

> TwoFactors(Response=’Tiempo’,Factor1=’Veneno’,Factor2=’Antidoto’,Data=supuesto, Inter=’TRUE’, HSD=’TRUE’)

Lo que muestra una salida html con la siguiente información:

En primer lugar, nos da el análisis descriptivo con la media y desviación típica del tiempo de supervivencia para cada combinación de nivel entre los dos factores:

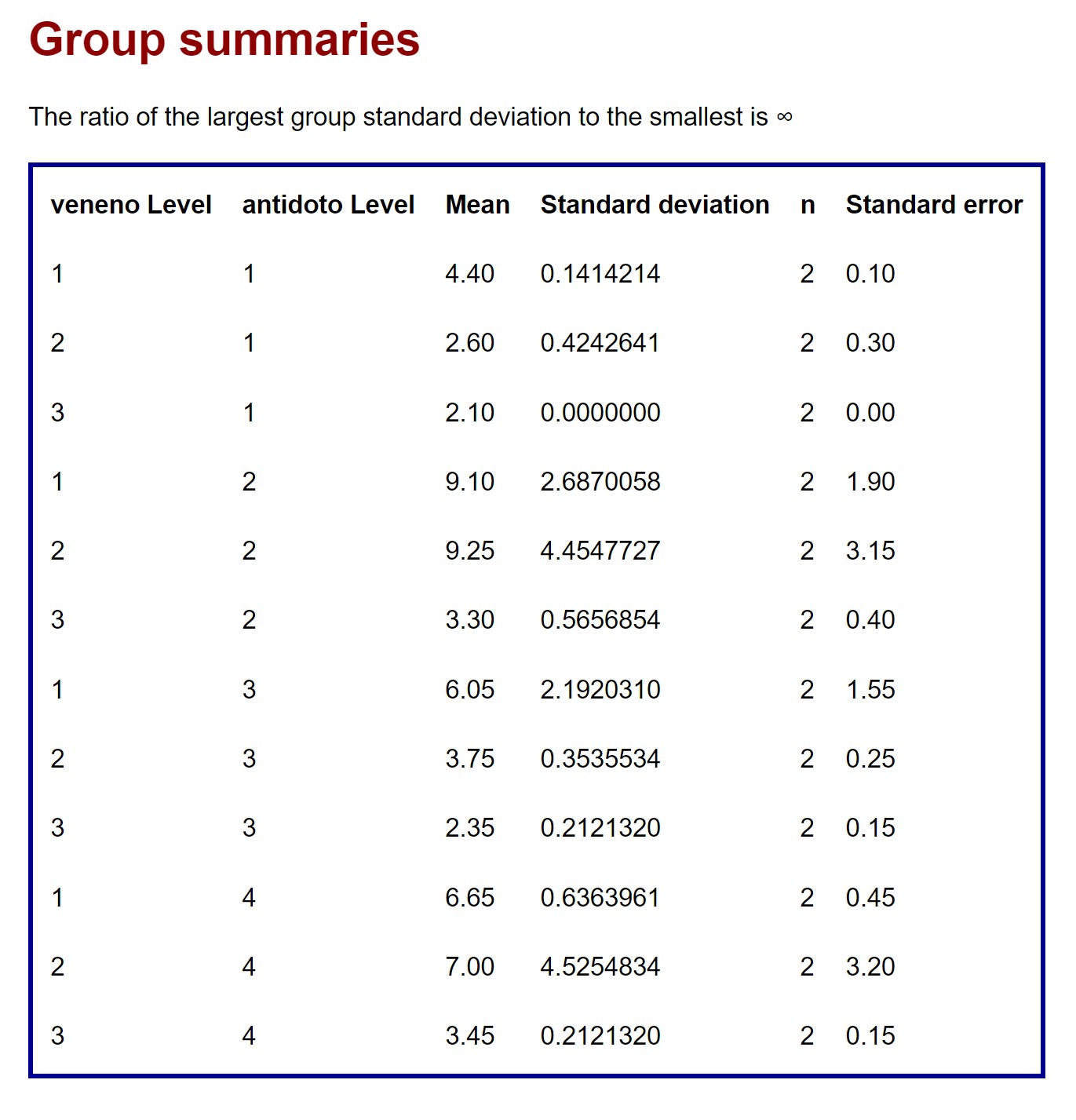
A continuación, nos muestra los diagramas de puntos para cada uno de los factores y el gráfico de interacción:

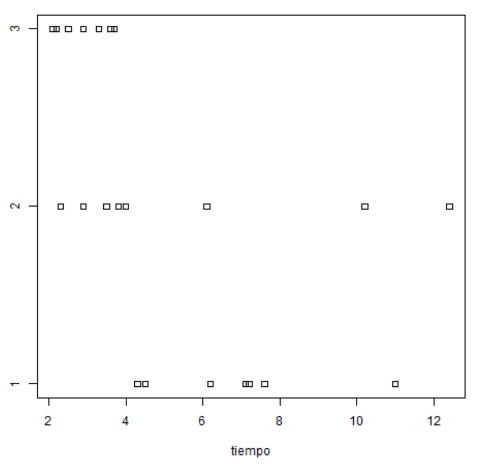
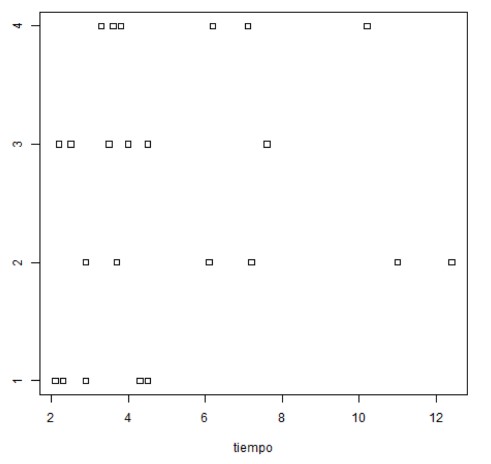
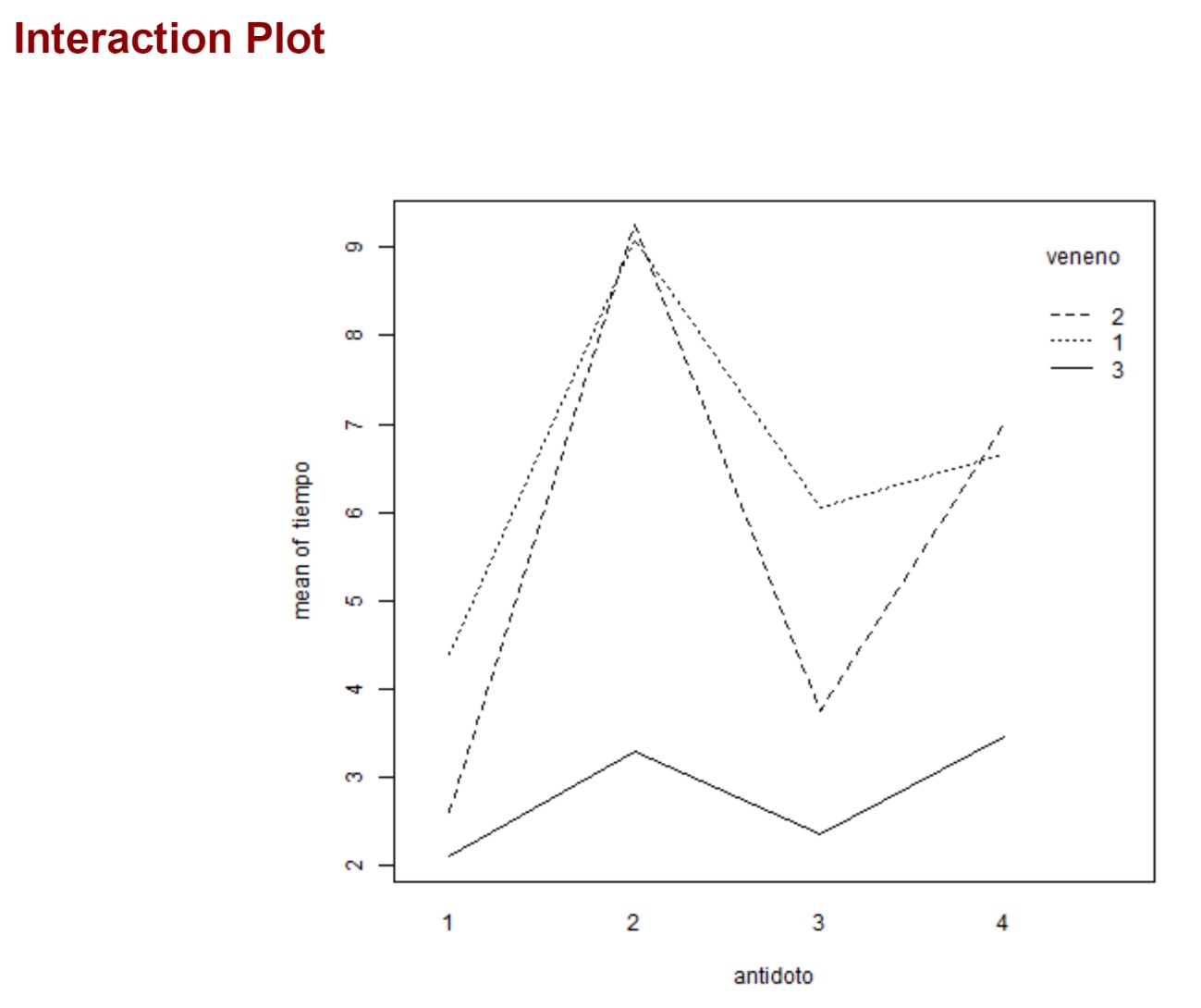
En tercer lugar, tenemos la tabla ANOVA para el análisis de la varianza:

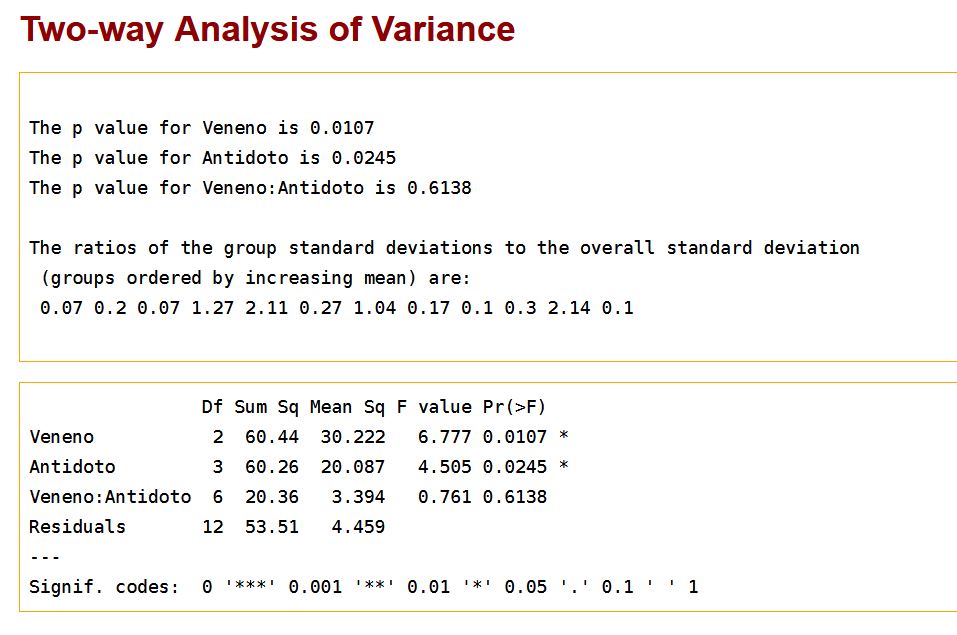
Las hipótesis de interés para los tres efectos del modelo que estamos considerando son:

 \( \begin{aligned} & H_0: \text { Efecto veneno }=0 \equiv \tau_1=\tau_2=\tau_3=0 \\ & H_1: \text { Efecto veneno } \neq 0 \equiv \tau_i \neq 0 \text { para algún } i=1,2,3 \end{aligned} \)

 \(  \begin{aligned} & H_0: \text { Efecto antídoto }=0 \equiv \beta_1=\beta_2=\beta_3=0 \\ & H_1: \text { Efecto antídoto } \neq 0 \equiv \beta_j \neq 0 \text { para algún } j=1,2,3,4 \end{aligned} \)

\(  \begin{aligned} & H_0: \text { veneno } \times \text { antídoto }=0 \equiv(\tau \beta)_{i j}=0  \text { para todo } i, j \\  & H_1: \text { veneno } \times \text { antídoto }=0 \equiv(\tau \beta)_{i j} \neq 0  \text { para algún } i, j  \end{aligned} \)

Comenzamos comprobando si el efecto de los antídotos es el mismo para todos los venenos. Para ello observamos el valor del estadístico (F_exp= 0.761) que contrasta la hipótesis correspondiente a la interacción entre ambos factores (\( H_0: (\tau \beta)_{ij} = 0 \) ) (H_0: (τβ)_ij = 0). Dicho valor deja a la derecha un Sig. = 0.6138, mayor que el nivel de significación 0.05. Por lo tanto, la interacción entre ambos factores no es significativa y debemos eliminarla del modelo que ahora será

\( y_{i j k}=\mu+\tau_i+\beta_j+u_{i j k} ; \quad i: 1,2,3 ; \quad j: 1,2,3,4 ; \quad k=1,2  \)

Por lo que debemos construir una nueva Tabla ANOVA en la que sólo figuren los efectos principales.

> TwoFactors(Response=’Tiempo’,Factor1=’Veneno’,Factor2=’Antidoto’,Data=supuesto, Inter=’FALSE’, HSD=’TRUE’)

Analysis of the supuesto data, using Tiempo as the response variable and the variables Veneno and Antidoto as factors.

Prepared by BrailleR

Group summaries

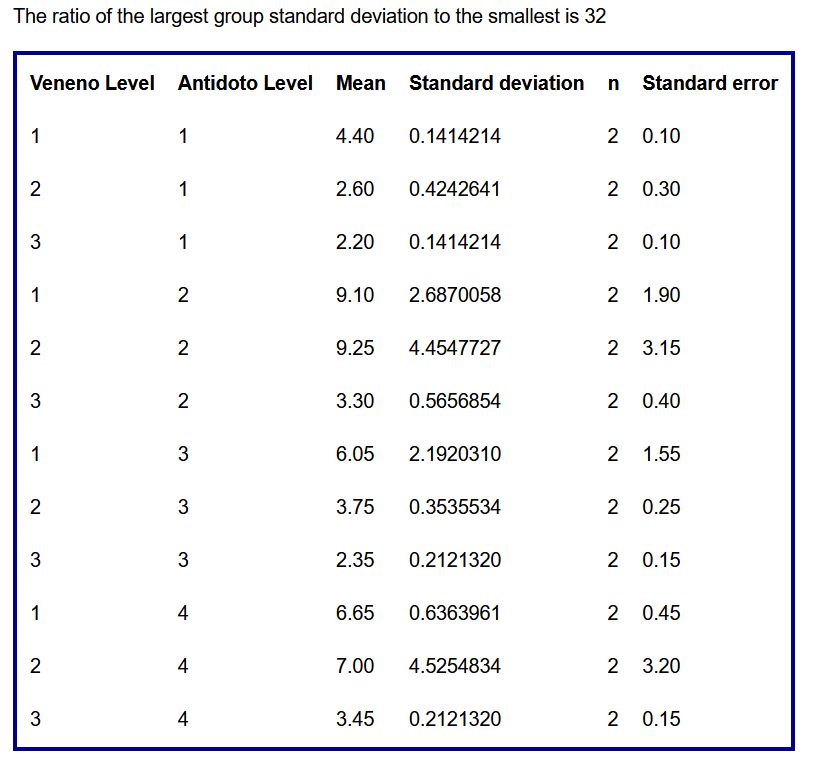
A continuación, nos muestra los diagramas de puntos para cada uno de los factores

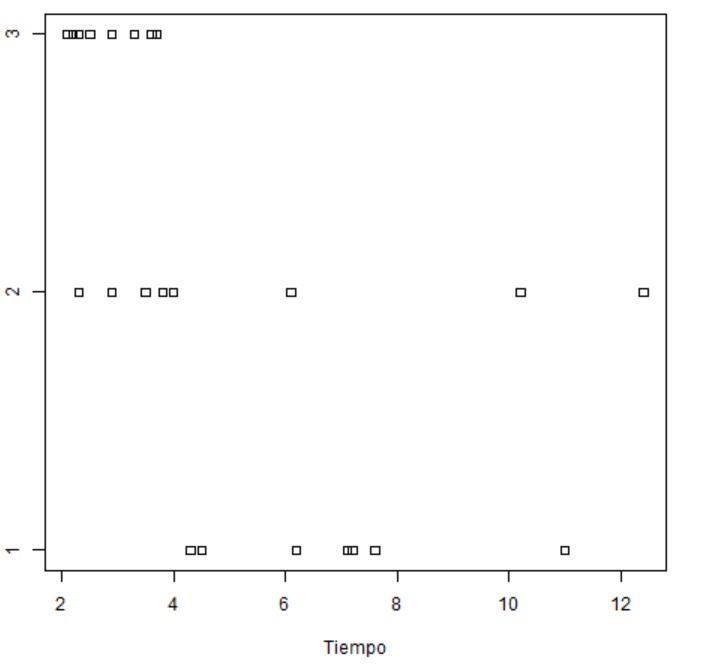
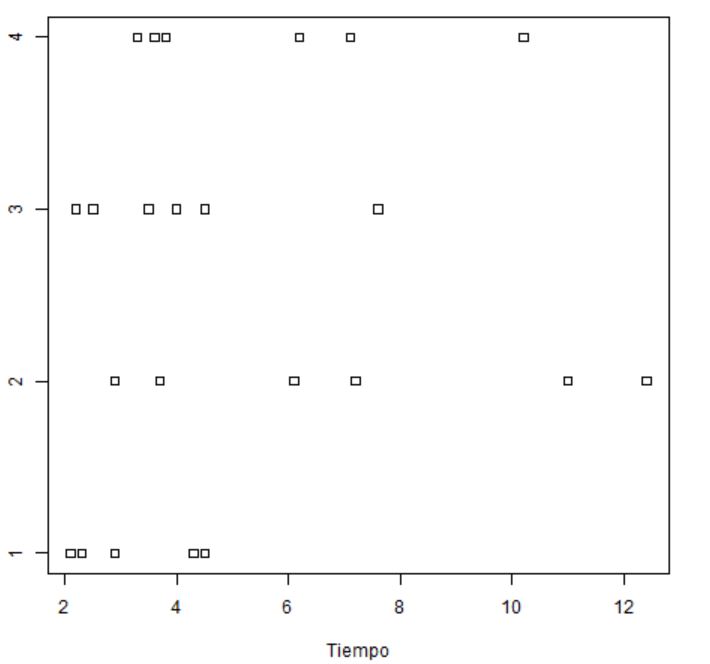
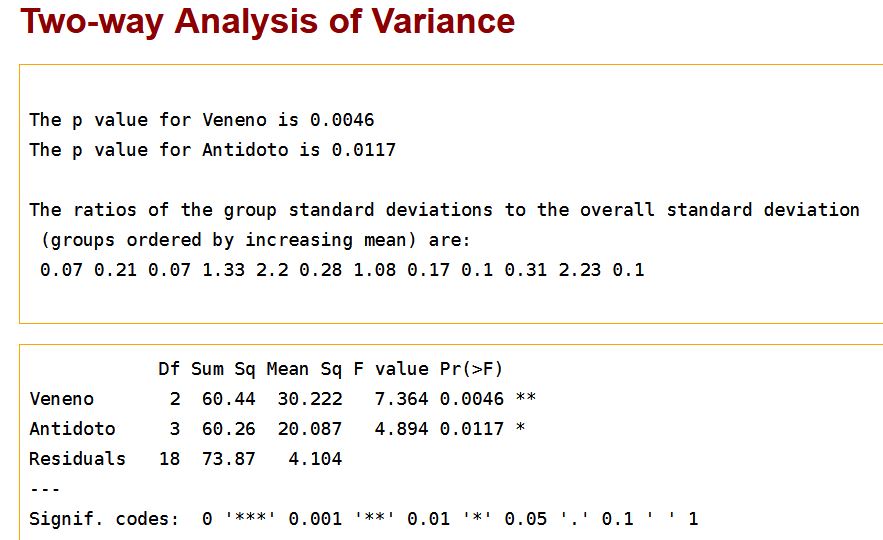
Esta tabla muestra dos únicas fuentes de variación, lo efectos principales de los dos factores (Tipo_veneno y Tipo_antídoto), y se ha suprimido la interacción entre ambos. Se observa que el valor de la Suma de Cuadrados del error de este modelo (73.87) se ha formado con los valores de las Sumas de cuadrados del error y de la interacción del modelo anterior (20.36 + 53.51 = 73.87). Observando los valores de los p-valores, 0.0046 y 0.0117 asociados a los contrastes principales, se deduce que los dos efectos son significativos a un nivel de significación del 5%. Deducimos que ni la gravedad de los venenos es la misma, ni la efectividad de los antídotos, pero dicha efectividad no depende del tipo de veneno con el que se administre ya que la interacción no es significativa.

A continuación, habría que comprobar la idoneidad del modelo viendo si se cumplen las hipótesis de normalidad, homocedasticidad e independencia de los residuos, para lo que se aportan los siguientes cuatro gráficos, si bien es conveniente acompañarlos de pruebas analíticas.

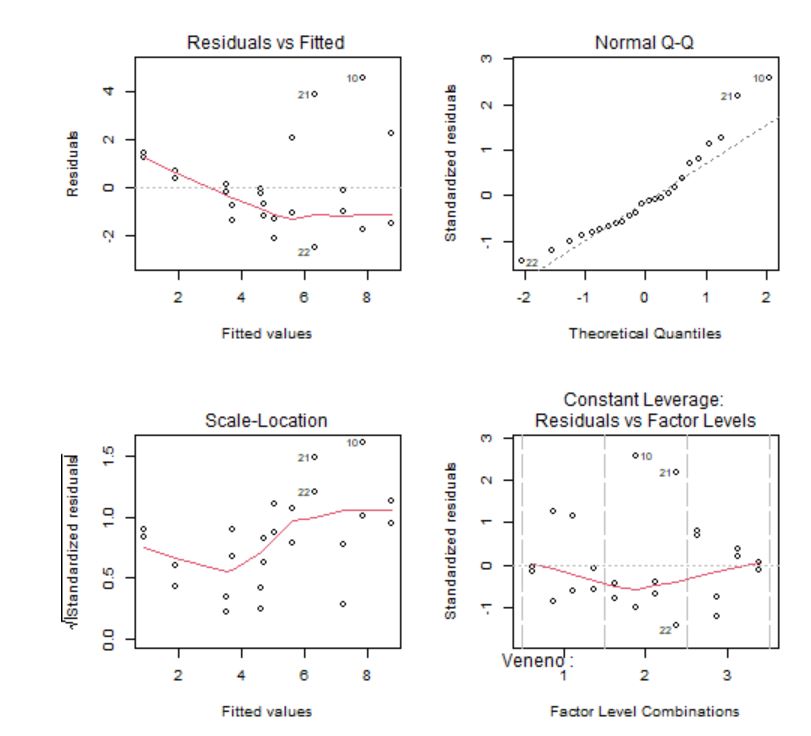
Para contrastar la homogeneidad de varianzas nos centraremos en los resultados de la prueba de Bartlett:

El estadístico de contraste para esta prueba es \( \chi^2 \) igual a 14.557 con un p-valor igual a 0.0006904 para el contraste de varianzas del tiempo de supervivencia según los distintos tipos de veneno, por lo que se rechazaría la igualdad de varianzas en este caso, al ser el p-valor menor de 0.05 (significación del 5%),  y \( \chi^2 \) igual a 6.8554 con un p-valor igual a 0.07665 para el contraste de varianzas del tiempo de supervivencia según los distintos antídotos, así pues se acepta la igualdad de varianzas.

Por último, se realiza la prueba HST de Tukey.

Los tres pares de hipótesis para comprobar si los tres venenos son igual de peligrosos son:

\( \begin{array}{lll} H_0: \mu_{A_1}=\mu_{A_2} ; & H_0: \mu_{A_1}=\mu_{A_3} ; & H_0: \mu_{A_2}=\mu_{A_3} \\ H_1: \mu_{A_1} \neq \mu_{A_2} ; & H_1: \mu_{A_1} \neq \mu_{A_3} ; & H_1: \mu_{A_2} \neq \mu_{A_3} \end{array} \)

Observado los p-valores de los tres test llegamos a la conclusión de que el veneno que tiene una media distinta es el tercero.

Para estudiar si los cuatro antídotos son igual de efectivos se tienen los seis pares de hipótesis,

\(  \begin{array}{lll} H_0: \mu_{B_1}=\mu_{B_2} ; & H_0: \mu_{B_1}=\mu_{B_3} ; & H_0: \mu_{B_1}=\mu_{B_4} \\ H_1: \mu_{B_1} \neq \mu_{B_2} ; & H_1: \mu_{B_1} \neq \mu_{B_3} ; & H_1: \mu_{B_1} \neq \mu_{B_4} \\ H_0: \mu_{B_2}=\mu_{B_3} ; & H_0: \mu_{B_2}=\mu_{B_4} ; & H_0: \mu_{B_3}=\mu_{B_4} \\ H_1: \mu_{B_2} \neq \mu_{B_3} ; & H_1: \mu_{B_2} \neq \mu_{B_4} ; & H_1: \mu_{B_3} \neq \mu_{B_4} \end{array} \)

Con respecto a los antídotos, solamente dos tipos de antídotos proporcionan medias del tiempo de supervivencia significativamente diferentes, son las correspondientes a los antídotos 2 y 1.

---

---

---

Ejercicios

Ejercicios Guiados

 Ejercicio Guiado1

Se tiene una base de datos de los trabajadores de una empresa (empleados.txt). En concreto se tiene información de 474 empleados y de las siguientes variables:

Id: Representa el código de empleado

Sexo: Representa el sexo (hombre o mujer).

Educ: Nivel educativo con valores del 8 al 21

Catlab: Categoría laboral (administrativo, seguridad o directivo)

Salario: Salario en euros anuales

Salini: Salario inicial en euros anuales

Tiempemp: Número de meses desde el contrato del empleado en la empresa.

Expprev: Experiencia previa en meses

Minoría: Toma los valores sí y no dependiendo de si el empleado pertenece o no a una minoría.

Se quiere estudiar el efecto del sexo de los empleados y el hecho de pertenecer o no a una minoría sobre su salario, para lo que se pide realizar un análisis de la varianza del salario de los empleados en función del sexo y de la variable Minoría, con lo que se tendría un modelo con dos factores y dos niveles de factor cada uno.

Nótese que este ejercicio no corresponde con un diseño de tipo balanceado o equilibrado, ya que no se produce el mismo número de réplicas para cada combinación de factores.

Ejercicio Guiado2 

Se realiza un estudio sobre el efecto del fotoperiodo y del genotipo en el periodo latente de infección del moho de cebada aislado AB3. Se obtienen cincuenta hojas de cuatro genotipos distintos. Cada grupo es infectado y posteriormente expuesto a diferente fotoperiodo.  La respuesta anotada es el número de días hasta la aparición de síntomas visibles.

\( \begin{array}{|l|cccccc|}  \hline & & & Fotoperiodo & &  \\ \hline Genotipo & \hspace{.6cm} 0 & \hspace{.6cm} 2 & \hspace{.5 cm}  4 & \hspace{.6cm} 8 & \hspace{.6cm} 16 \\ \hline Armelle & \hspace{.5cm} 630 & \hspace{.5cm} 610  & \hspace{.5cm} 560 & \hspace{.5cm} 570 & \hspace{.5cm} 590 \\ \hline Golden & \hspace{.5cm} 640 & \hspace{.5cm} 630 &\hspace{.5cm} 600 & \hspace{.5cm} 620 & \hspace{.5cm} 620  \\ \hline Promise & \hspace{.5cm} 640 & \hspace{.5cm} 630 & \hspace{.5cm} 650  & \hspace{.5cm} 620 & \hspace{.5cm} 580  \\ \hline Emir & \hspace{.5cm}  660 & \hspace{.5cm}  660 & \hspace{.5cm} 620  & \hspace{.5cm} 610 & \hspace{.5cm} 630 \\ \hline \end{array} \)

Figura 6: Tabla de datos del Ejercicio Guiado2.txt

1. ¿Se puede afirmar que los diferentes genotipos no influyen en el número de días hasta la aparición de la infección? ¿Se puede concluir que los distintos fotoperiodos no afectan al tiempo de aparición de los síntomas de infección del moho?
2. En caso de que influyan significativamente alguno de los dos factores, extraer conclusiones utilizando el método de Tukey.
3. Estudiar las hipótesis de modelo: Homocedasticidad, Independencia y Normalidad.

Ejercicio Guiado3 

Se realiza un estudio para determinar el efecto del nivel del agua y del tipo de planta sobre la longitud global del tallo de las plantas de guisantes. Para ello, se utilizan tres niveles de agua (bajo, medio y alto) y dos tipos de plantas (sin hojas y convencional). Se dispone para el estudio de dieciocho plantas sin hojas y dieciocho plantas convencionales. Se dividen aleatoriamente los dos tipos de plantas en tres subgrupos y después se asignan los niveles de agua aleatoriamente a los dos grupos de plantas. Los datos sobre la longitud del tallo de los guisantes (en centímetros) se muestran en la siguiente tabla:

\(  \begin{array}{|c|c|c|c|}  \hline & & \text { Nivel agua } &   \\ \hline \text { Tipo de planta } & \text {Bajo } & \text { Medio } & \text { Alto } \\ \hline  & 69.50 & 96.10 & 121.00 \\  & 69.00 & 102.30 & 122.90 \\  & 75.00 & 107.50 & 123.10  \\ \text { Sin hojas }& 70.00 & 103.60 & 125.70 \\  & 74.40 & 100.70 & 125.20 \\ & 75.00 & 101.80 & 120.10 \\ \hline  & 71.10 & 81.00 & 101.10 \\ & 69.20 & 85.80 & 103.10  \\  \text { Convencional } &  70.40 & 86.00 & 106.10 \\ & 73.20 & 87.50 & 109.70 \\ & 71.20 & 88.10 & 110.00 \\ & 70.90 & 87.60 & 99.00 \\ \hline \end{array} \)

Figura 7: Tabla de datos del Ejercicio Guiado3.txt

Para un nivel de significación del 5%.

1. ¿Se puede afirmar que los distintos niveles de agua influyen en la longitud del tallo de los guisantes? ¿Y el tipo de planta?
2. ¿La efectividad del nivel del agua es la misma para los dos tipos de plantas?
3. Estudia, utilizando el método de Tukey, qué nivel de agua es más efectivo.

---

Ejercicio Guiado 1 (Resuelto)

Se tiene una base de datos de los trabajadores de una empresa (empleados.txt). En concreto se tiene información de 474 empleados y de las siguientes variables:

Id: Representa el código de empleado

Sexo: Representa el sexo (hombre o mujer).

Educ: Nivel educativo con valores del 8 al 21

Catlab: Categoría laboral (administrativo, seguridad o directivo)

Salario: Salario en euros anuales

Salini: Salario inicial en euros anuales

Tiempemp: Número de meses desde el contrato del empleado en la empresa.

Expprev: Experiencia previa en meses

Minoría: Toma los valores sí y no dependiendo de si el empleado pertenece o no a una minoría.

Se quiere estudiar el efecto del sexo de los empleados y el hecho de pertenecer o no a una minoría sobre su salario, para lo que se pide realizar un análisis de la varianza del salario de los empleados en función del sexo y de la variable Minoría, con lo que se tendría un modelo con dos factores y dos niveles de factor cada uno.

Nótese que este ejercicio no corresponde con un diseño de tipo balanceado o equilibrado, ya que no se produce el mismo número de réplicas para cada combinación de factores.

---

Solución: 

Para realizar este supuesto con BrailleR, ejecutamos R y cargamos el paquete BrailleR 
library(“BrailleR”)

Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.

> setwd(“C:/Users/Usuario/Desktop/Datos”)
> empleados=read.table(“empleados.txt”,header=TRUE)
> empleados
id sexo educ catlab salario salini tiempemp expprev minoria
1 1 hombre 15 directivos 57000 27000 98 144 no
2 2 hombre 16 administrativos 40200 18750 98 36 no
3 3 mujer 12 administrativos 21450 12000 98 381 no
4 4 mujer 8 administrativos 21900 13200 98 190 no
5 5 hombre 15 administrativos 45000 21000 98 138 no
6 6 hombre 15 administrativos 32100 13500 98 67 no
7 7 hombre 15 administrativos 36000 18750 98 114 no

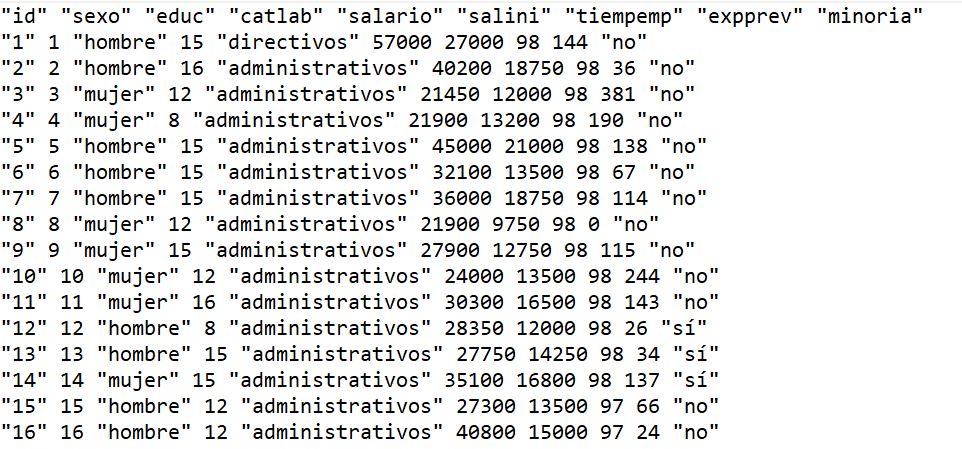
Figura 8: Tabla de datos del Ejercicio Guiado1.txt

A continuación, hay que indicar qué factores vamos a considerar en nuestro análisis y decir a R que interprete esas variables como factores, para lo que escribimos:

> empleados$sexo=as.factor(empleados$sexo)
> empleados$minoria=as.factor(empleados$minoria)

Por último, llamamos a la función TwoFactors de la siguiente forma:

> TwoFactors(‘salario’,’sexo’,’minoria’, Data=empleados, Inter=TRUE,)

Lo que nos creará un html con la siguiente información:

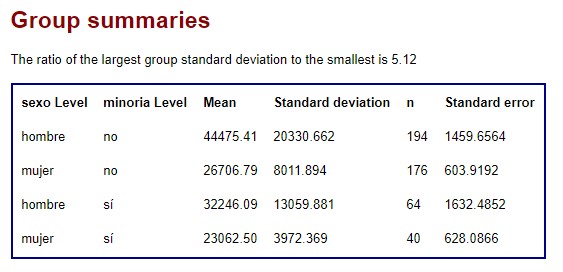
Lo primero que nos muestra es una tabla con la media, desviación típica, tamaño de muestra y error estándar de cada combinación posible entre los factores. Así vemos que el mayor tamaño de muestra corresponde a los hombres que no pertenecen a una minoría y el menor a las mujeres que sí pertenecen. Ocurre igual para el salario medio, que es mayor para los hombres que no pertenecen a una minoría, seguido por el de los hombres que sí pertenecen, en tercer lugar el de las mujeres que no pertenecen a una minoría, siendo el salario medio más bajo el de las mujeres que pertenecen a una minoría.

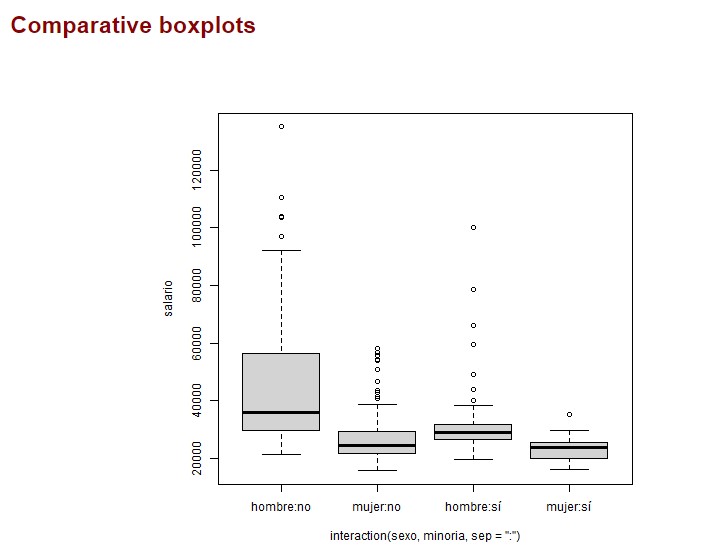
En el gráfico comparativo de caja y bigotes puede observarse el valor de la mediana de cada uno de estos grupos, así como rango intercuartílico, salario mínimo y máximo, valores atípicos, etc. Así vemos que el salario de los hombres que no pertenecen a una minoría es el que presenta mayor dispersión y donde se alcanzan los valores atípicos más altos. Este gráfico también permite realizar otras comparaciones, por ejemplo, podemos apreciar que el primer cuartil del salario de los hombres que no pertenecen a una minoría está por encima de la mediana (y casi también del tercer cuartil) del salario del resto de grupos.

R Braille ofrece la siguiente interpretación del gráfico en formato texto:

A continuación, realiza diagramas de puntos comparativos para cada uno de los factores:

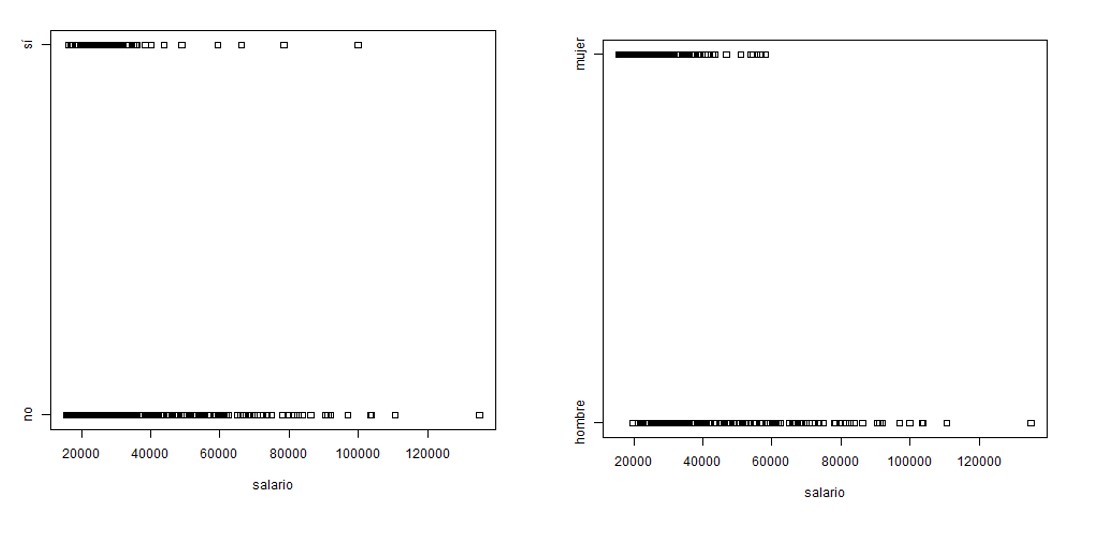
Y el gráfico de interacción:

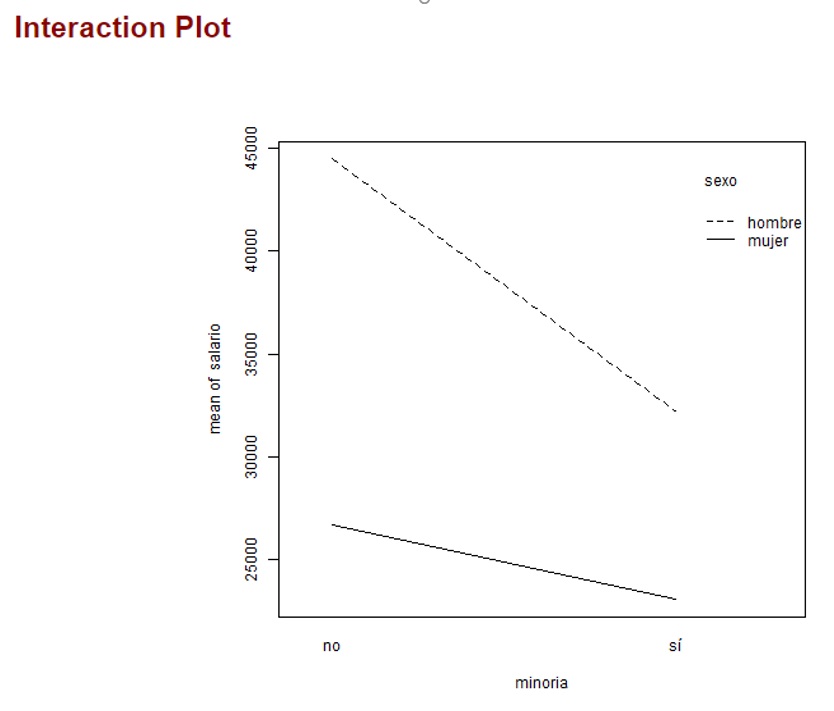
Realiza un doble análisis de la varianza, en primer lugar, tomando sexo como primer factor y minoría como segundo y a continuación alternando el orden de los factores. A su vez, acompaña estos análisis con una breve interpretación en formato texto, indicando los p-valores.

Vemos que, independientemente del orden en que se tomen los factores, tanto el primer factor como el segundo resultan significativos al 5% (p-valor < 0,05), como también lo es la intersección entre ambos.

Para la validación del modelo, nos muestra en primer lugar gráficos para contrastar visualmente la independencia, homocedasticidad y normalidad de los residuos. Adicionalmente, sería recomendable acompañar estos gráficos mediante test analíticos, como el test de Kolmogorov-Smirnov (para normalidad) o el de Durbin-Watson (para independencia).

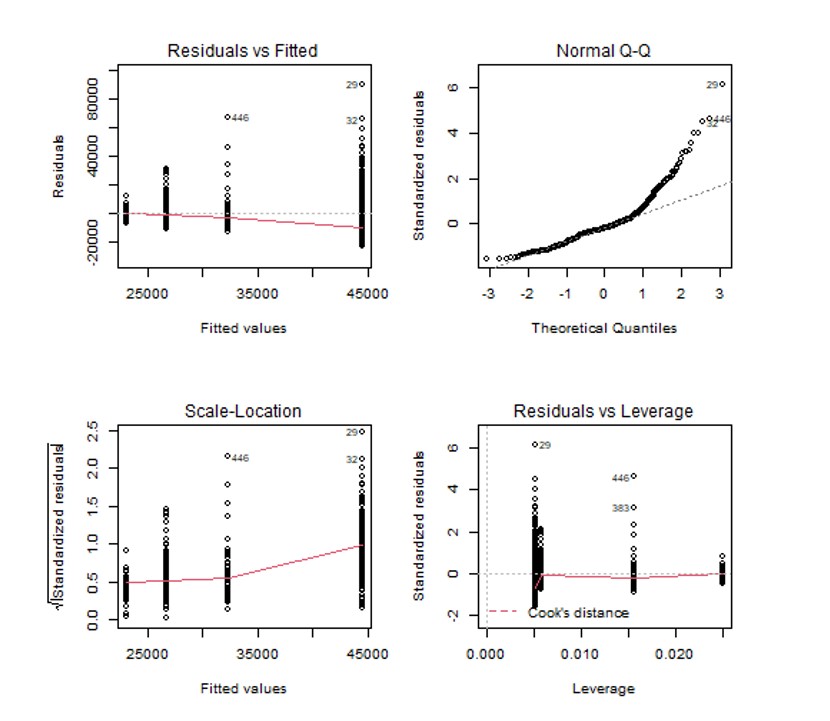
El test para contrastar la homocedasticidad lo proporciona directamente la función TwoFactors, que nos muestra los resultados del test de Bartlett y del test de Fligner-Killeen. Centraremos nuestro interés únicamente en el test de Bartlett.

Como el p-valor es inferior a 0.05, se rechaza la hipótesis nula de homocedasticidad, por lo que no se cumple homogeneidad de varianzas al 5% de significación.

Para terminar, la función TwoFactors realiza el test HSD de Tukey, para la comparación múltiple de medias y acompaña el test con una breve interpretación en formato texto, donde se especifica qué diferencias entre las medias resultan significativas y el p-valor de estas diferencias

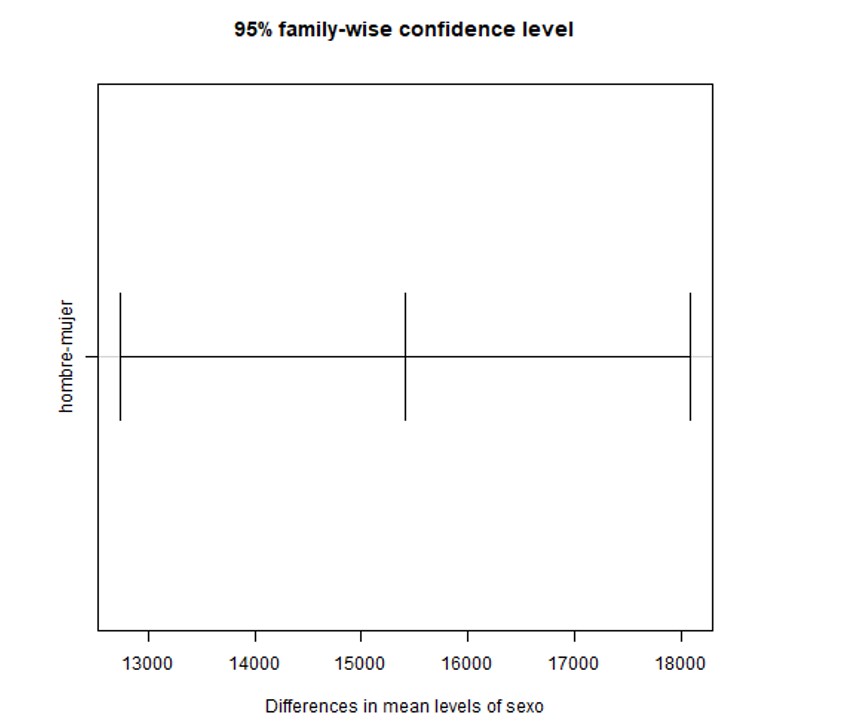
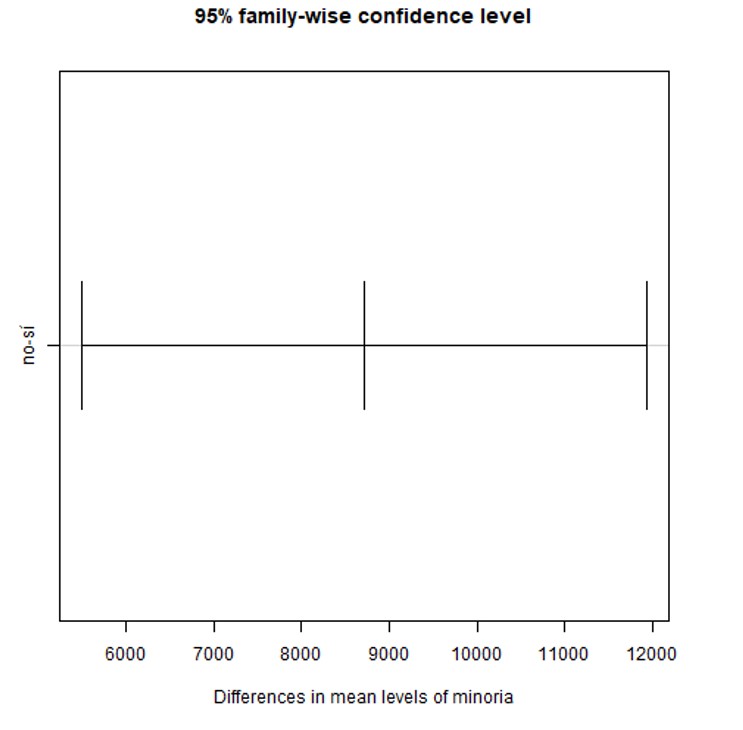
Como podemos ver, primero se muestran los resultados de la comparación de medias de la variable respuesta, “salario”, para las categorías de cada factor independientemente, así vemos que la media del salario de los hombres difiere de la media del salario de las mujeres (p-valor=0) y lo mismo ocurre para el salario medio de los que pertenecen a una minoría en comparación con los que no pertenecen (p-valor=0).

Posteriormente, se realiza una comparación de medias de la variable respuesta según los valores del factor intersección, comparando dos a dos estos posibles valores. Así vemos por ejemplo que no existe diferencia entre el salario medio de las mujeres que no pertenecen a una minoría y aquellas que sí pertenecen (p-valor=0.493844), pero sí existe diferencia entre el salario medio de los hombres que pertenecen a una minoría y el de las mujeres que también pertenecen (p-valor=0.0114553).

Por último, se muestran los gráficos con los intervalos al 95% de confianza para la diferencia entre las medias, primero para un factor, luego para el otro y en tercer lugar para la interacción.

---

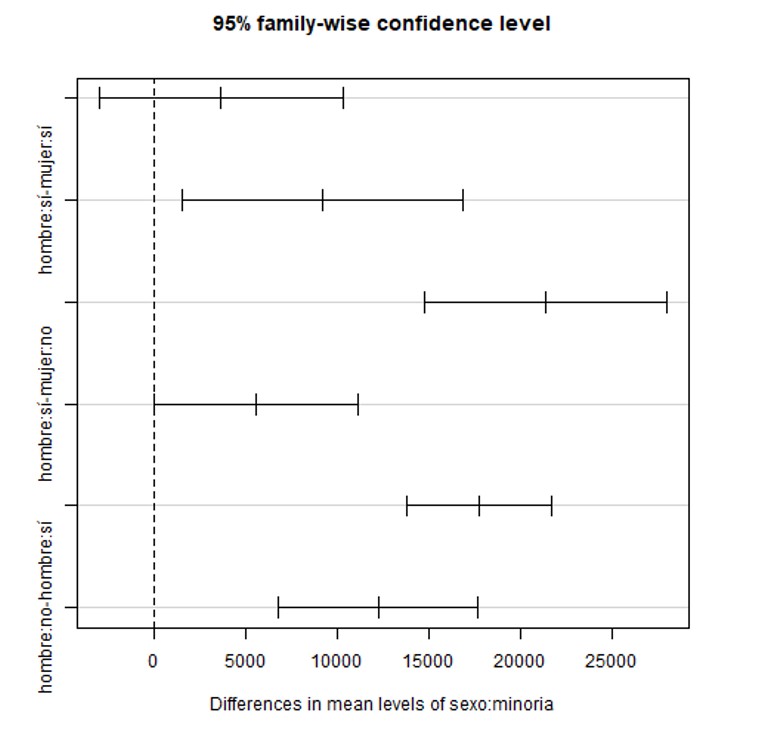
Ejercicio Guiado 2 (Resuelto) 

Se realiza un estudio sobre el efecto del fotoperiodo y del genotipo en el periodo latente de infección del moho de cebada aislado AB3. Se obtienen cincuenta hojas de cuatro genotipos distintos. Cada grupo es infectado y posteriormente expuesto a diferente fotoperiodo. La respuesta anotada es el número de días hasta la aparición de síntomas visibles.

\( \begin{array}{|l|cccccc|}  \hline & & & Fotoperiodo & &  \\ \hline Genotipo & \hspace{.6cm} 0 & \hspace{.6cm} 2 & \hspace{.5 cm}  4 & \hspace{.6cm} 8 & \hspace{.6cm} 16 \\ \hline Armelle & \hspace{.5cm} 630 & \hspace{.5cm} 610  & \hspace{.5cm} 560 & \hspace{.5cm} 570 & \hspace{.5cm} 590 \\ \hline Golden & \hspace{.5cm} 640 & \hspace{.5cm} 630 &\hspace{.5cm} 600 & \hspace{.5cm} 620 & \hspace{.5cm} 620  \\ \hline Promise & \hspace{.5cm} 640 & \hspace{.5cm} 630 & \hspace{.5cm} 650  & \hspace{.5cm} 620 & \hspace{.5cm} 580  \\ \hline Emir & \hspace{.5cm}  660 & \hspace{.5cm}  660 & \hspace{.5cm} 620  & \hspace{.5cm} 610 & \hspace{.5cm} 630 \\ \hline \end{array} \)

Figura 9: Tabla de datos del Ejercicio Guiado2.txt

1. ¿Se puede afirmar que los diferentes genotipos no influyen en el número de días hasta la aparición de la infección? ¿Se puede concluir que los distintos fotoperiodos no afectan al tiempo de aparición de los síntomas de infección del moho?
2. En caso de que influyan significativamente alguno de los dos factores, extraer conclusiones utilizando el método de Tukey.
3. Estudiar las hipótesis de modelo: Homocedasticidad, Independencia y Normalidad.

---

Solución:

1. ¿Se puede afirmar que los diferentes genotipos no influyen en el número de días hasta la aparición de la infección? ¿Se puede concluir que los distintos fotoperiodos no afectan al tiempo de aparición de los síntomas de infección del moho?

• Variable respuesta: Número de días hasta la aparición de síntomas visibles
• Factor: Genotipo que tiene cuatro niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
• Factor: Fotoperiodo que tiene cinco niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
• Modelo completo: Los cuatro tratamientos se prueban exactamente una vez.
• Tamaño del experimento: Número total de observaciones (20).

Para realizar este supuesto con BrailleR, ejecutamos R y cargamos el paquete BrailleR 

>  library(“BrailleR”)

Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.

> setwd(“C:/Users/Usuario/Desktop/Datos”)

Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.

En este caso lo hacemos en un archivo de texto:

Figura 10: Tabla de datos del Ejercicio Guiado2.txt

Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.

> guiado2= read.table(“guiado2.txt”,header=TRUE)
> guiado2
dias Genotipo Fotoperiodo
1 630 1 1
2 640 2 1
3 640 3 1
4 660 4 1
5 610 1 2
6 630 2 2
7 630 3 2
8 660 4 2
9 560 1 3
10 600 2 3
11 650 3 3
12 620 4 3
13 570 1 4
14 620 2 4
15 620 3 4
16 610 4 4
17 590 1 5
18 620 2 5
19 580 3 5
20 630 4 5

> dias<-read.table(“guiado2.txt”, header = TRUE)
> dias
  Días Fotoperiodo Genotipo
1   630           1        1
2   640           1        2
3   640           1        3
4   660           1        4
5   610           2        1
6   630           2        2
7   630           2        3
8   660           2        4
9   560           3        1
10  600           3        2
11  650           3        3
12  620           3        4
13  570           4        1
14  620           4        2
15  620           4        3
16  610           4        4
17  590           5        1
18  620           5        2
19  580           5        3
20  630           5        4

Hay que tener en cuenta que cuando R lee este fichero de datos interpreta que éste contiene tres variables numéricas por lo que es necesario decirle que interprete las variables veneno y antídoto como factores para lo cual utilizamos las siguientes sentencias:

> guiado2$Genotipo=as.factor(guiado2$Genotipo)
> guiado2$Fotoperiodo=as.factor(guiado2$Fotoperiodo)
> guiado2$Genotipo
[1] 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
Levels: 1 2 3 4
> guiado2$Fotoperiodo
[1] 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5
Levels: 1 2 3 4 5

Realizamos el análisis de la varianza mediante la función TwoFactors

> TwoFactors(Response=’dias’,Factor1=’Genotipo’,Factor2=’Fotoperiodo’,Data=guiado2, Inter=’False’, HSD=’TRUE’)
se muestra una salida en html con los siguientes resultados:

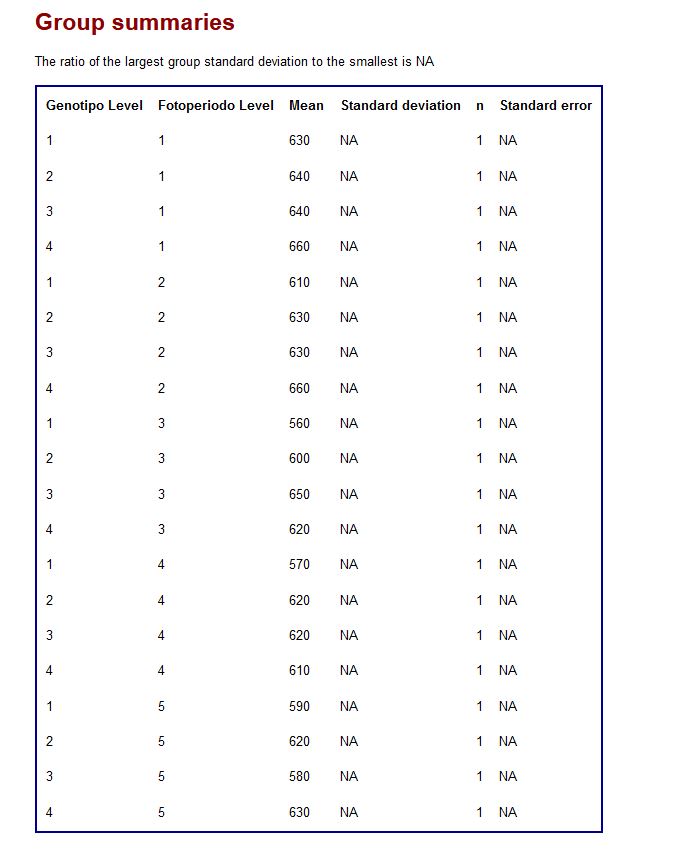
a) Un análisis descriptivo de la variable respuesta para cada combinación de valores de los dos factores (dado que solo tenemos una observación para cada combinación de los valores, no se calcula la desviación típica).

Analysis of the guiado2 data, using dias as the response variable and the variables Genotipo and Fotoperiodo as factors.

Prepared by BrailleR

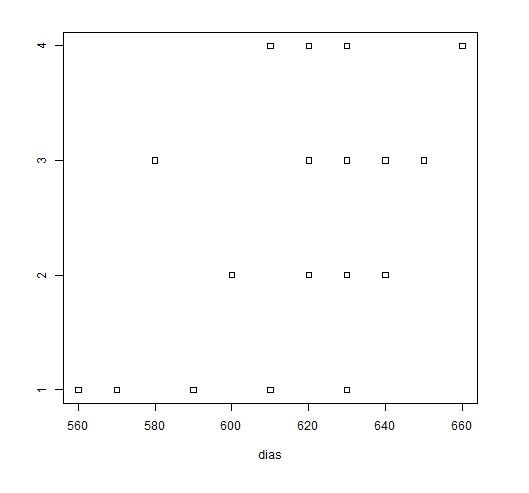
b) Diagramas de puntos comparativos para cada uno de los factores.

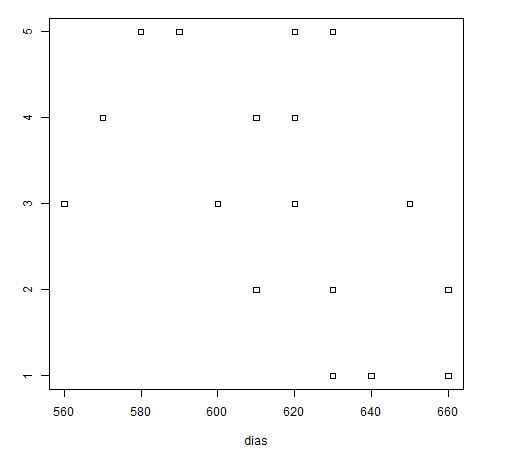
c)  Tabla ANOVA para el análisis de la varianza de dos factores.

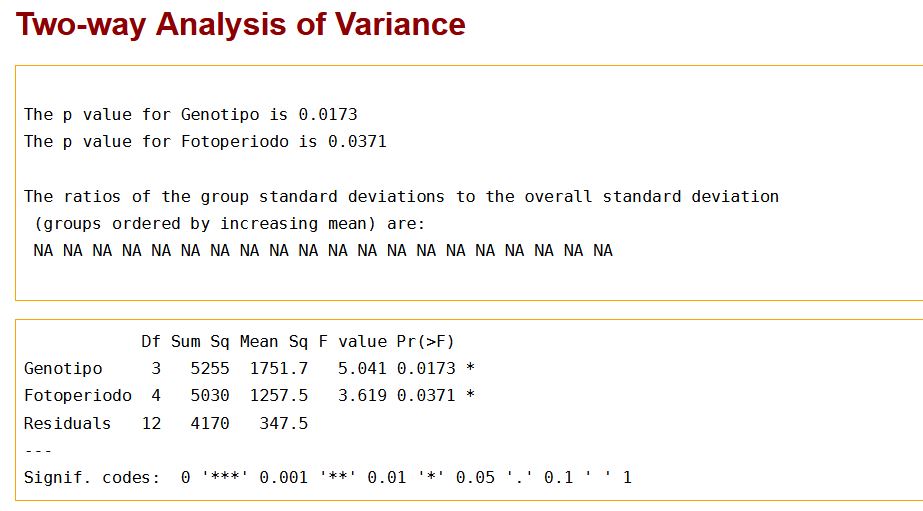
En la Tabla ANOVA, el valor del estadístico de contraste de igualdad de medias del factor genotipo, F = 5.041 deja a su derecha un p-valor igual a 0.0173, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias. Es decir, existen diferencias significativas en el número de días hasta la aparición de la infección entre los cuatro genotipos.

En esta Tabla ANOVA, también se observa que el valor del estadístico de contraste de igualdad de medias del factor fotoperiodo, F = 3.619 deja a su derecha un p-valor igual a 0.0371, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias del factor fotoperiodo. Es decir, existen diferencias significativas en el número de días hasta la aparición de la infección entre los cinco tipos de fotoperiodos. Por lo tanto, se concluye que los niveles de ambos factores influyen de forma significativa en el número de días hasta la aparición de los síntomas de infección del moho.

2. En caso de que influyan significativamente alguno de los dos factores, extraer conclusiones utilizando el método de Tukey.

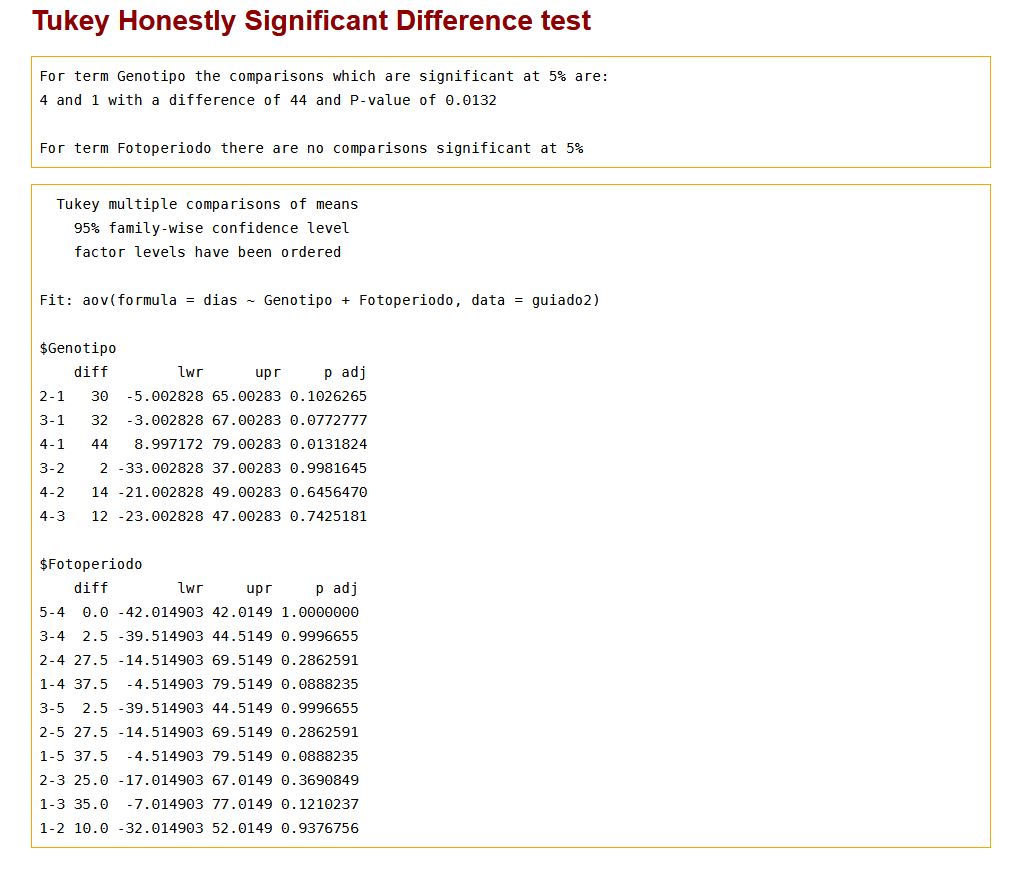
En la tabla sel factor Tipo de genotipo: Se observan diferencias entre los genotipos 4 y 1 ( Emir y Armelle) con una diferencia de 44 y un p-valor de 0.0132

En la tabla del factor Tipo de fotoperiodo no hay diferencias significativas entre los subconjuntos al 5%

3. Estudiar las hipótesis de modelo: Homocedasticidad, Independencia y Normalidad.

Para comprobar la idoneidad del modelo propuesto, se muestran los siguientes gráficos:

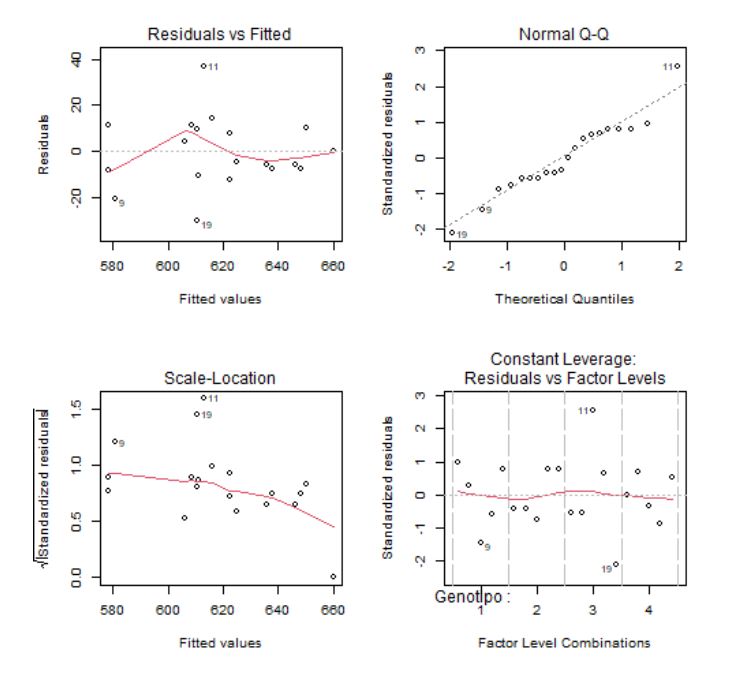
1. Valores predichos frente a residuos
2. Gráfico Q-Q de normalidad
3. Valores predichos frente a raíz cuadrada de los residuos estandarizados (en valor absoluto)
4. Residuos estandarizados frente a leverages

Los gráficos 1 y 3 se utilizan para contrastar gráficamente la independencia, la homocedasticidad y la linealidad de los residuos. Idealmente, los residuos deben estar aleatoriamente distribuidos a lo largo del gráfico, sin formar ningún tipo de patrón.

El gráfico que se muestra en la Fila 1, Columna 1. Es decir, el gráfico el que se representan los residuos en el eje de ordenadas y los valores predichos por el modelo en el eje de abscisas. Este gráfico no muestra ningún aspecto que haga sospechar de la hipótesis de independencia de los residuos

El gráfico de leverages frente a los residuos estandarizados se utiliza para detectar puntos con una influencia importante en el cálculo de las estimaciones de los parámetros. En caso de detectarse algún punto fuera de los límites que establecen las líneas discontinuas debe estudiarse este punto de forma aislada para detectar, por ejemplo, si la elevada importancia de esa observación se debe a un error.

d) Test para la homogeneidad de varianzas de la variable respuesta según los distintos niveles de factor, para cada uno de los factores.

Los resultados del test de Barlett indican que se aceptan la hipótesis nulas de igualdad de varianzas tanto para los diferentes niveles del factor Genotipo  (p-valor =0.6537)

\( H_0: \sigma_{A_1}^2=\sigma_{A_2}^2=\sigma_{A_3}^2 = \sigma_{A_4}^2  \text { vs } H_1: \sigma_{A_i}^2 \neq \sigma_{A_j}^2 \hspace{.2cm} \text { para algún } \hspace{.2cm} i \neq j  \hspace{.2cm} (p \text {-valor }=0.6537) \)

como para los diferentes niveles del factor Fotoperiodo  (p-valor=0.5474)

\( H_0: \sigma_{A_1}^2=\sigma_{A_2}^2=\sigma_{A_3}^2 = \sigma_{A_4}^2 = = \sigma_{A_5}^2  \text { vs } H_1: \sigma_{A_i}^2 \neq \sigma_{A_j}^2 \hspace{.2cm} \text { para algún } \hspace{.2cm} i \neq j  \hspace{.2cm} (p \text {-valor }=0.5474) \)

---

Ejercicio Guiado 3 (Resuelto) 

Se realiza un estudio para determinar el efecto del nivel del agua y del tipo de planta sobre la longitud global del tallo de las plantas de guisantes. Para ello, se utilizan tres niveles de agua (bajo, medio y alto) y dos tipos de plantas (sin hojas y convencional). Se dispone para el estudio de dieciocho plantas sin hojas y dieciocho plantas convencionales. Se dividen aleatoriamente los dos tipos de plantas en tres subgrupos y después se asignan los niveles de agua aleatoriamente a los dos grupos de plantas. Los datos sobre la longitud del tallo de los guisantes (en centímetros) se muestran en la siguiente tabla:

\(  \begin{array}{|c|c|c|c|}  \hline & & \text { Nivel agua } &   \\ \hline \text { Tipo de planta } & \text {Bajo } & \text { Medio } & \text { Alto } \\ \hline  & 69.50 & 96.10 & 121.00 \\  & 69.00 & 102.30 & 122.90 \\  & 75.00 & 107.50 & 123.10  \\ \text { Sin hojas }& 70.00 & 103.60 & 125.70 \\  & 74.40 & 100.70 & 125.20 \\ & 75.00 & 101.80 & 120.10 \\ \hline  & 71.10 & 81.00 & 101.10 \\ & 69.20 & 85.80 & 103.10  \\  \text { Convencional } &  70.40 & 86.00 & 106.10 \\ & 73.20 & 87.50 & 109.70 \\ & 71.20 & 88.10 & 110.00 \\ & 70.90 & 87.60 & 99.00 \\ \hline \end{array} \)

Figura 11: Tabla de datos del Ejercicio Guiado3.txt

Para un nivel de significación del 5%. 

1. ¿Se puede afirmar que los distintos niveles de agua influyen en la longitud del tallo de los guisantes? ¿Y el tipo de planta?
2. ¿La efectividad del nivel del agua es la misma para los dos tipos de plantas?
3. Estudia, utilizando el método de Tukey, qué nivel de agua es más efectivo.

> longitud$agua <- factor(longitud$Nivel_agua)
> longitud$agua
[1] 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
Levels: 1 2 3

> longitud$Tipo <- factor(longitud$Tipo_planta)
> longitud$Tipo
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
Levels: 1 2

Realizamos el análisis de la varianza mediante la función TwoFactors

 > TwoFactors(Response=’longitud_tallo’,Factor1=’agua’,Factor2=’Tipo’, Data=longitud, Inter=’True’, HSD=’TRUE’)

En primer lugar, se muestra un análisis descriptivo de las variables.

Analysis of the longitud data, using longitud_tallo as the response variable and the variables agua, Tipo, and their interaction as factors.

Prepared by BrailleR

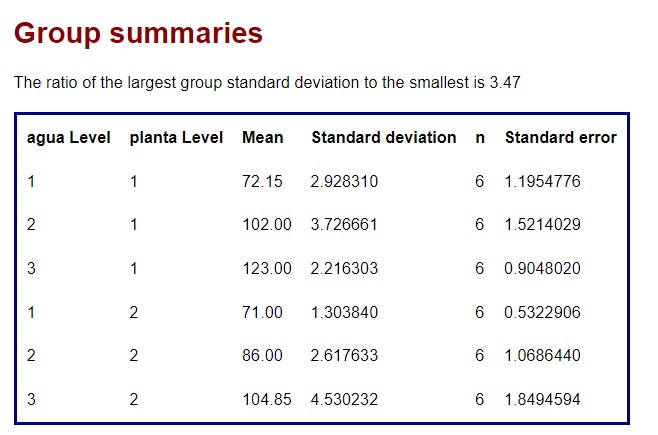
Mediante esta tabla se puede estudiar si varía la longitud de los tallos en función de las combinaciones tipo de planta y nivel de agua. Es decir, se puede estudiar si existen diferencias significativas entre los tiempos medios de supervivencia con los distintos tipos de venenos

\( \begin{aligned} & H_0: \text { Nivel de agua }=0 \equiv \tau_1=\tau_2=\tau_3=0 \\ & H_1: \text { Nivel de agua } \neq 0 \equiv \tau_i \neq 0 \text { para algún } i=1,2,3  \end{aligned} \) \( \begin{aligned} & H_0: \text {Tipo planta }=0 \equiv \tau_1=\tau_2=0 \\ & H_1: \text { Tipo planta} \neq 0 \equiv \tau_i \neq 0 \text { para algún } i=1,2 \end{aligned} \)

 

• El valor del estadístico de contraste de igualdad de medias del factor Nivel_agua, F= 572.56 deja a su derecha un p-valor menor que 0.001, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias de los niveles del factor Nivel_agua. Es decir, existen diferencias significativas en la longitud del tallo de guisantes dependiendo del nivel del agua.
• El valor del estadístico de contraste de igualdad de medias del factor Tipo_planta, F= 132.445 deja a su derecha un p-valor menor que 0.001, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias del factor Tipo_planta.  Es decir, el tipo de planta afecta significativamente a la longitud del tallo de guisantes.

2. ¿La efectividad del nivel del agua es la misma para los dos tipos de plantas?

Para responder a esta pregunta, realizamos el contraste de hipótesis sobre la interacción de los dos factores

 \( \begin{array}{ll} H_0: \text { Nivel agua } \times \text { Tipo planta }=0 \equiv(\tau \beta)_{i j}=0 & \text { para todo } i, j \\ H_1: \text { Nivel agua } \times \text { Tipo planta }=0 \equiv(\tau \beta)_{i j} \neq 0 & \text { para algún } i, j \end{array} \)

En la Tabla Two-way Analisys of variance mostrada anteriormente, el valor del estadístico de contraste de la interacción de los dos factores, F= 27.32 deja a su derecha un p-valor menor que 0.001, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de no interacción entre los factores. Por lo tanto, la efectividad del nivel de agua no es la misma para los dos tipos de plantas. Es decir, puede ocurrir que un nivel de agua influya en el crecimiento de la longitud del tallo con un tipo de planta pero no con el otro o influya de distinta forma.

3. Estudia, utilizando el método de Tukey, qué nivel de agua es más efectivo.

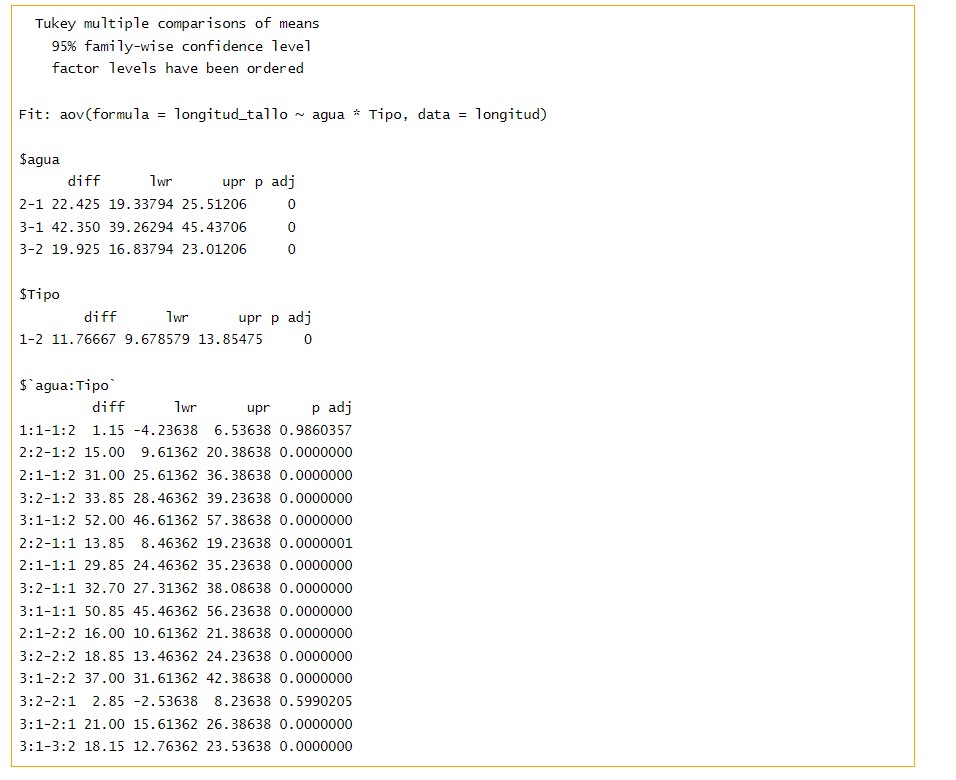
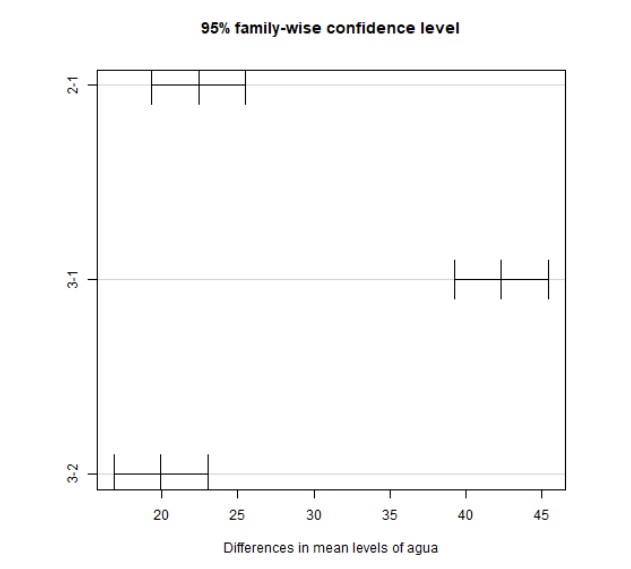
Se puede comprobar que la diferencia entre los tres niveles de agua es significativa, y la diferencia mayor se observa entre el tipo 1 y 3.

---

---

Ejercicios Propuestos

Ejercicio Propuesto 1 

Se realiza un estudio sobre el efecto que produce la descarga de aguas residuales de una planta sobre la ecología del agua natural de un río. En el estudio se utilizaron dos lugares de muestreo. Un lugar está aguas arriba del punto en el que la planta introduce aguas residuales en la corriente; el otro está aguas abajo. Se tomaron muestras durante un periodo de cuatro semanas y se obtuvieron los datos sobre el número de diatomeas halladas. Los datos se muestran en la tabla adjunta (disponibles en el fichero propuesto 1.txt):

\( \begin{array}{|c|c|c|c|c|} \hline & &   Semana  & & \\ \hline Luqar &  Semana 1 &  Semana 2 & Semana 3 & Semana 4 \\ \hline  Aguas   & 78 \hspace{.5cm} 94 & 620 \hspace{.5cm} 760 & 204 \hspace{.5cm} 333 & 890 \hspace{.5cm} 6555 \\  arriba & 43 \hspace{.5cm} 58 & 420\hspace{.5cm} 913 & 98 \hspace{.5cm} 89 & 763 \hspace{.5cm} 562 \\ \hline  Aguas   & 79 \hspace{.5cm} 87 & 546 \hspace{.5cm} 652 &  45 \hspace{.5cm} 69 & 254 \hspace{.5cm} 86 \\  abajo & 145 \hspace{.5cm} 522 & 76 \hspace{.5cm} 94 & 59 \hspace{.5cm}  62 & 789 \hspace{.5cm} 267 \\ \hline \end{array} \)

Figura 13 : Tabla de datos del Ejercicio Propuesto1.txt

Responder a las siguientes cuestiones:

1. Identificar el diseño adecuado a este experimento, escribir el modelo matemático y explicar los distintos elementos que intervienen.
2. Estudiar si la semana y el lugar son factores determinantes en el número de diatomeas halladas en el agua del río. ¿Hay posibilidad que una semana sea más recomendable en un lugar del río en concreto y no lo sea en el otro lugar?
3. Estudiar en qué semana se producen menos contaminación en el río, utilizando el método de HSD de Tukey.
4. Estudiar en qué lugar del río se producen menos diatomeas, utilizando el método de HSD de Tukey.

Ejercicio Propuesto 2 

Consideremos un experimento en el que se quiere estudiar el efecto de los factores A: profundidad de corte y B: velocidad de alimentación sobre el acabado de un metal. Aunque los factores son de naturaleza continua, en este proceso sólo se puede trabajar en 4 y 3 niveles, respectivamente.

\( \begin{array}{|ccccc|} \hline & & &  Velocidad  & \\ \hline Profund. & & 0.2 & 0.25 & 0.3 \\ \hline & &  74 & 92 & 99 \\   0.15 & & 64 & 86 & 98 \\  & & 60 & 88 & 102 \\  \hline & & 79 & 98 & 104 \\   0.18 & & 68 & 104 & 99 \\  & & 73 & 88 & 95 \\ \hline & & 82 & 99 & 108 \\   0.21 & & 88 & 108 & 110 \\  & & 92 & 95 & 99  \\  \hline & & 99   & 104 & 114 \\   0.24 & & 104 & 110 & 111 \\  & & 96 & 99 & 107 \\ \hline \end{array} \)

Figura 14 : Tabla de datos del Ejercicio Propuesto2.txt

Realizar un análisis de la varianza del acabado del metal en función de la profundidad de corte y la velocidad de alimentación mediante la función TwoFactors.

Ejercicio Propuesto 3 

Sobre la misma base de datos de empleados del ejercicio guiado 1 (empleados.txt) 

Se tiene una base de datos de los trabajadores de una empresa (empleados.txt). En concreto se tiene información de 474 empleados y de las siguientes variables:

Id: Representa el código de empleado

Sexo: Representa el sexo (hombre o mujer).

Educ: Nivel educativo con valores del 8 al 21

Catlab: Categoría laboral (administrativo, seguridad o directivo)

Salario: Salario en euros anuales

Salini: Salario inicial en euros anuales

Tiempemp: Número de meses desde el contrato del empleado en la empresa.

Expprev: Experiencia previa en meses

Minoría: Toma los valores sí y no dependiendo de si el empleado pertenece o no a una minoría.

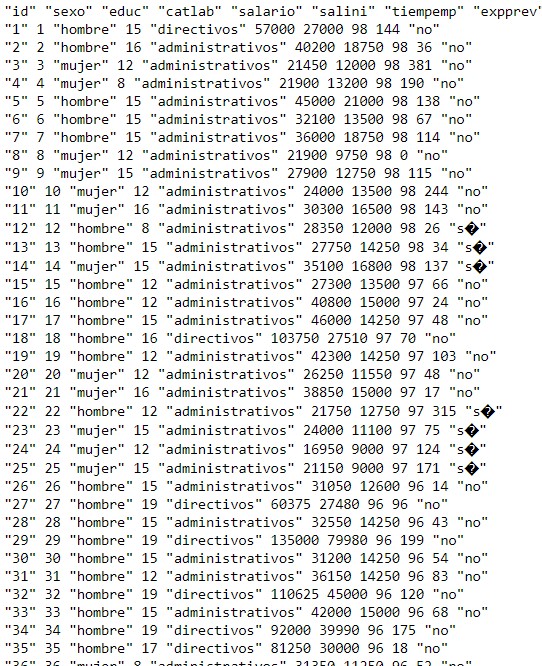
Figura 15 : Tabla de datos del Ejercicio Propuesto3.txt

Realizar un análisis de la varianza de dos factores para comprobar el efecto del sexo (factor A) y la categoría laboral (factor B) de los empleados sobre su experiencia previa en meses (variable respuesta).

Ejercicio Propuesto 4 

Utilizamos una nueva base de datos (propuesto4.csv). Supongamos que deseamos analizar la influencia que tienen sobre los ingresos anuales brutos del cliente (en decenas de miles de euros):

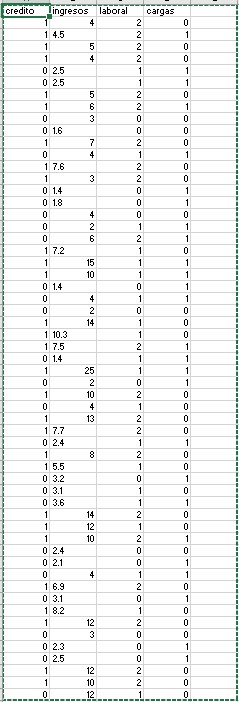
Figura 16 : Tabla de datos del Ejercicio Propuesto4.csv

Factor A: la situación laboral del cliente (0 en paro, 1 contrato temporal, 2 contrato fijo), y

Factor B: las cargas familiares (1 si el cliente tiene cargas familiares),

En este caso tenemos un diseño factorial con dos factores, el primero de los cuales tiene tres niveles y el segundo dos

Ejercicio propuesto 5 

Utilizando la base de datos propuesto5.txt, realizar un análisis de la varianza de dos factores para comprobar el efecto del género (factor A) y el tipo de medicamento (factor B) en el paciente después de cuatro unidades de tiempo (tiempo4) tras habérselo administrado.

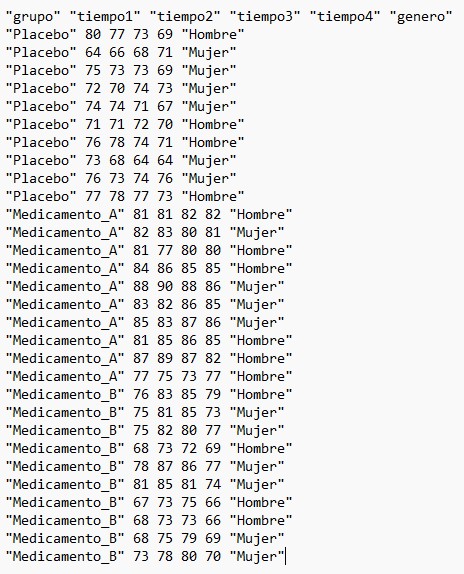
Figura 17 : Tabla de datos del Ejercicio Propuesto5.txt

Tenemos un diseño factorial con dos factores, en el que el primero tiene dos niveles (mujer y hombre) y el segundo tiene tres niveles (medicamentoA, medicamentoB y placebo). 

---

Ejercicio Propuesto 1 Resuelto

Se realiza un estudio sobre el efecto que produce la descarga de aguas residuales de una planta sobre la ecología del agua natural de un río. En el estudio se utilizaron dos lugares de muestreo. Un lugar está aguas arriba del punto en el que la planta introduce aguas residuales en la corriente; el otro está aguas abajo. Se tomaron muestras durante un periodo de cuatro semanas y se obtuvieron los datos sobre el número de diatomeas halladas. Los datos se muestran en la tabla adjunta:

\( \begin{array}{|c|c|c|c|c|} \hline & &   Semana  & & \\ \hline Luqar &  Semana 1 &  Semana 2 & Semana 3 & Semana 4 \\ \hline  Aguas   & 78 \hspace{.5cm} 94 & 620 \hspace{.5cm} 760 & 204 \hspace{.5cm} 333 & 890 \hspace{.5cm} 6555 \\  arriba & 43 \hspace{.5cm} 58 & 420\hspace{.5cm} 913 & 98 \hspace{.5cm} 89 & 763 \hspace{.5cm} 562 \\ \hline  Aguas   & 79 \hspace{.5cm} 87 & 546 \hspace{.5cm} 652 &  45 \hspace{.5cm} 69 & 254 \hspace{.5cm} 86 \\  abajo & 145 \hspace{.5cm} 522 & 76 \hspace{.5cm} 94 & 59 \hspace{.5cm}  62 & 789 \hspace{.5cm} 267 \\ \hline \end{array} \)

Figura 13 : Tabla de datos del Ejercicio Propuesto 1.txt

Responder a las siguientes cuestiones:

1. Identificar el diseño adecuado a este experimento, escribir el modelo matemático y explicar los distintos elementos que intervienen.
2. Estudiar si la semana y el lugar son factores determinantes en el número de diatomeas halladas en el agua del río. ¿Hay posibilidad que una semana sea más recomendable en un lugar del río en concreto y no lo sea en el otro lugar?
3. Estudiar en qué semana se producen menos contaminación en el río, utilizando el método de HSD de Tukey
4. Estudiar en qué lugar del río se producen menos diatomeas, utilizando el método de HSD de Tukey

---

Solución

1. Identificar el diseño adecuado a este experimento, escribir el modelo matemático y explicar los distintos elementos que intervienen.

El modelo estadístico para este diseño es:

\( y_{i j k}=\mu+\tau_i+\beta_j+(\tau \beta)_{i j}+u_{i j k} \quad ; \quad i: 1,2,3,4 \quad ; \quad j: 1,2  \quad ; \quad \mathrm{k}=1,2,3,4 \)

donde:

\( y_{i j k}\): Número de diatomeas halladas en la observación \( k\) en la semana \( i \) y lugar \( j \)

\( \mu \): Efecto constante, común a todos los niveles de los factores, denominado media global

\( \tau_i \): Efecto producido por la semana  \( i \), \( \left(\sum_{i=1}^4 \tau_i=0\right) \)

\( \beta_j \): Efecto producido por el lugar \( j \), \( \left(\sum_{j=1}^2 \beta_j=0\right) \)

\( (\tau \beta)_{i j} \): Efecto medio producido por la interacción entre la semana i y el lugar \( j \), \( \left(\sum_i(\tau \beta)_{i j}=\sum_j(\tau \beta)_{i j}=0\right) \)

\( u_{i j k} \): Errores experimentales \( u_{ij} \): v. a. independientes \( \rightarrow N(0 ; \sigma) \)

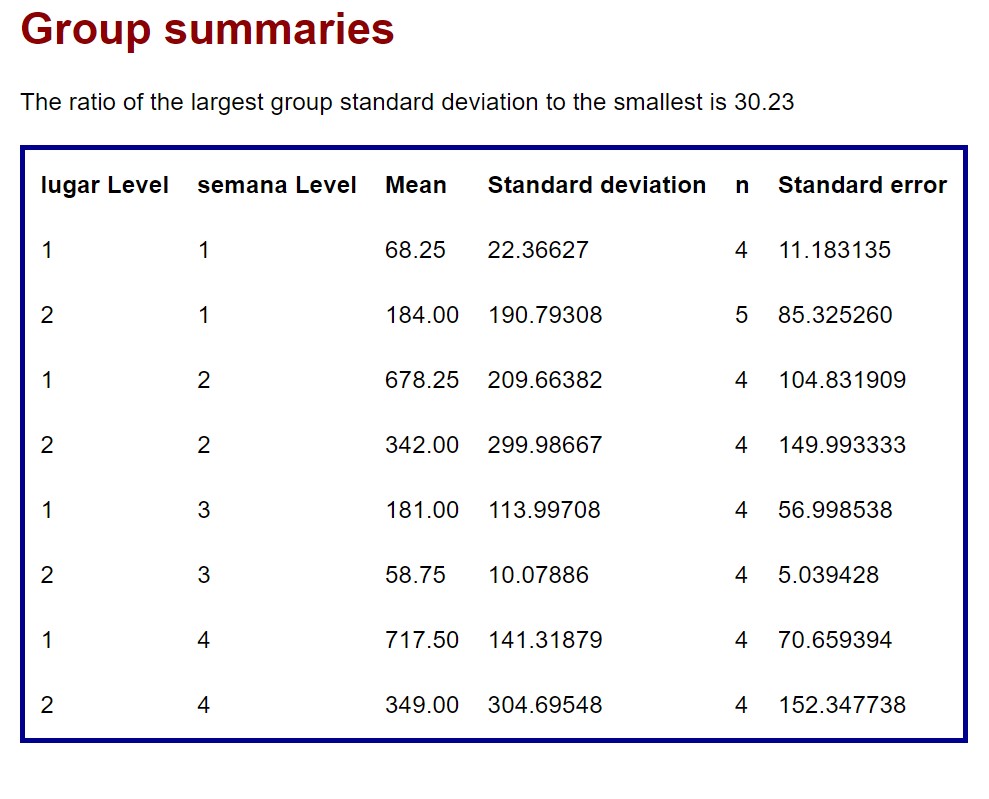
Solución del Ejercicio Propuesto1

---

Ejercicio Propuesto 2 Resuelto

Consideremos un experimento en el que se quiere estudiar el efecto de los factores A: profundidad de corte y B: velocidad de alimentación sobre el acabado de un metal. Aunque los factores son de naturaleza continua, en este proceso sólo se puede trabajar en 4 y 3 niveles, respectivamente.

\( \begin{array}{|ccccc|} \hline & & &  Velocidad  & \\ \hline Profund. & & 0.2 & 0.25 & 0.3 \\ \hline & &  74 & 92 & 99 \\   0.15 & & 64 & 86 & 98 \\  & & 60 & 88 & 102 \\  \hline & & 79 & 98 & 104 \\   0.18 & & 68 & 104 & 99 \\  & & 73 & 88 & 95 \\ \hline & & 82 & 99 & 108 \\   0.21 & & 88 & 108 & 110 \\  & & 92 & 95 & 99  \\  \hline & & 99   & 104 & 114 \\   0.24 & & 104 & 110 & 111 \\  & & 96 & 99 & 107 \\ \hline \end{array} \)

Figura 14 : Tabla de datos del Ejercicio Propuesto2.txt

Realizar un análisis de la varianza del acabado del metal en función de la profundidad de corte y la velocidad de alimentación mediante la función TwoFactors.

---

Solución

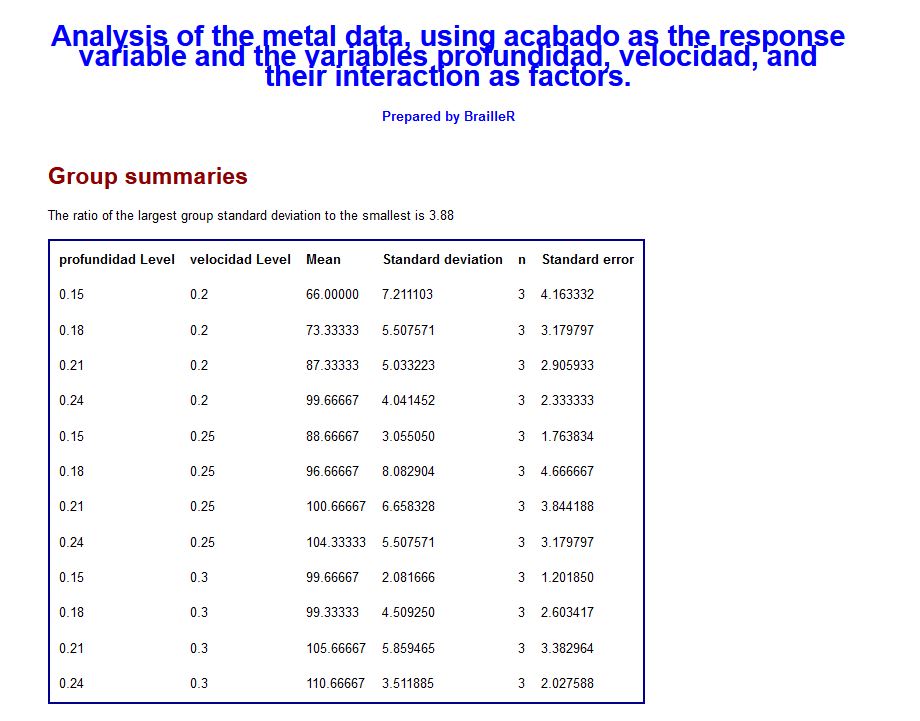
Solución del Ejercicio Propuesto 2

---

Ejercicio Propuesto 3 Resuelto 

Sobre la misma base de datos de empleados del ejercicio guiado 1 (empleados.txt) 

Se tiene una base de datos de los trabajadores de una empresa (empleados.txt). En concreto se tiene información de 474 empleados y de las siguientes variables:

Id: Representa el código de empleado

Sexo: Representa el sexo (hombre o mujer).

Educ: Nivel educativo con valores del 8 al 21

Catlab: Categoría laboral (administrativo, seguridad o directivo)

Salario: Salario en euros anuales

Salini: Salario inicial en euros anuales

Tiempemp: Número de meses desde el contrato del empleado en la empresa.

Expprev: Experiencia previa en meses

Minoría: Toma los valores sí y no dependiendo de si el empleado pertenece o no a una minoría.

Figura 15 : Tabla de datos del Ejercicio Propuesto3.txt

Realizar un análisis de la varianza de dos factores para comprobar el efecto del sexo (factor A) y la categoría laboral (factor B) de los empleados sobre su experiencia previa en meses (variable respuesta).

---

Solución

En este ejercicio tenemos un diseño factorial con dos factores, el primero de los cuales tiene dos niveles (hombre y mujer) y el segundo tres (administrativos, seguridad, directivos).

> TwoFactors(‘expprev’,’sexo’,’catlab’, Data=empleados, Inter=TRUE)

---

Ejercicio Propuesto 4 

Utilizamos una nueva base de datos (propuesto4.csv). Supongamos que deseamos analizar la influencia que tienen sobre los ingresos anuales brutos del cliente (en decenas de miles de euros):

Figura 16 : Tabla de datos del Ejercicio Propuesto4.csv

Factor A: la situación laboral del cliente (0 en paro, 1 contrato temporal, 2 contrato fijo), y

Factor B: las cargas familiares (1 si el cliente tiene cargas familiares),

En este caso tenemos un diseño factorial con dos factores, el primero de los cuales tiene tres niveles y el segundo dos

---

Solución

> TwoFactors(‘ingresos’,’laboral’,’carga’, Data=datos, Inter=TRUE)

Como podemos ver, el factor interacción no es significativo (p-valor = 0.8442), por lo que lo eliminamos del modelo

> TwoFactors(‘ingresos’,’laboral’,’carga’, Data=datos, Inter=FALSE)

Solución del Ejercicio Propuesto 4

---

Ejercicio propuesto 5 Resuelto

Utilizando la base de datos propuesto5.txt, realizar un análisis de la varianza de dos factores para comprobar el efecto del género (factor A) y el tipo de medicamento (factor B) en el paciente después de cuatro unidades de tiempo (tiempo4) tras habérselo administrado.

Tenemos un diseño factorial con dos factores, en el que el primero tiene dos niveles (mujer y hombre) y el segundo tiene tres niveles (medicamentoA, medicamentoB y placebo).

---

Solución

Como podemos ver, el factor interacción no es significativo, su p-valor es 0.451, por lo que quitamos la interacción del modelo y obtenemos el siguiente resultado

Sólo uno de los factores es significativo, el grupo, por lo que podemos decir que el efecto en el paciente en el tiempo4 depende del medicamento suministrado, pero no del género del paciente.

Mediante el test de Bartlett se comprueba la igualdad de varianzas para los distintos niveles de ambos factores, p-valores mayores de 0.05.

Solución del Ejercicio Propuesto 5

Autores: Sandra González Gallardo, Alessio Gaggero y Ana María Lara Porras. Universidad de Granada. (2024).