ESTADÍSTICA DESCRIPTIVA UNIDIMENSIONAL
La Estadística es una rama de las matemáticas que trata de la recopilación, el análisis, la interpretación y la presentación de una gran cantidad de datos numéricos. Definición dada por el New Collegiate Dictionary de Webster, que:
- Implica una recopilación de datos teniendo como objetivo la inferencia
- Requiere una selección de un subconjunto de una gran colección de datos, con el propósito de hacer inferencias con respecto a las características del conjunto completo.
En este capítulo tomaremos un primer contacto con las técnicas estadísticas que se utilizan para recoger, clasificar, representar y resumir un determinado conjunto de datos que forman una muestra obtenida de una población, (objeto de la Estadística Descriptiva), sin pretender obtener conclusiones o hacer inferencias a partir de los datos experimentales, (objeto de la Estadística Inductiva o Inferencia Estadística).
La Estadística, por tanto, puede considerarse dividida en dos grandes bloques: Estadística Descriptiva y Estadística Inductiva.
Generalidades
Población y muestra
Recibe el nombre Población cualquier colección de datos que tienen ciertas características comunes. Así, una población puede estar constituida por un colectivo de personas de una determinada profesión, por un conjunto de automóviles, por las calificaciones obtenidas por un grupo de estudiantes o por el número de piezas producidas por una fábrica en un día determinado. A cada uno de los elementos que componen la población se les denomina Unidad estadística, Individuo o Dato estadístico; así cada persona, cada automóvil, cada calificación o cada pieza es una unidad estadística de las poblaciones citadas anteriormente.
El número de elementos que componen o integran la población se llama Tamaño de la población.
Es a menudo imposible o poco práctico estudiar la totalidad de elementos que componen la población y en lugar de examinar el grupo entero, se examina un subconjunto representativo seleccionado de la población llamado Muestra.
Caracteres
Llamamos Caracteres de los elementos de una población a las características desde el punto de vista de las cuales se estudia dicha población. Así, en la población formada por los estudiantes de un determinado curso de una facultad los caracteres pueden ser: sexo, color del pelo, edad, estatura, peso etc. A cada uno de los posibles estados que puede presentar un carácter se denomina Modalidad. Así: Mujer y hombre; Pelirrojo, rubio y moreno; 18, 19, 20 y 21 etc. son las modalidades de los caracteres sexo, color del pelo y edad, respectivamente. Las modalidades de un carácter deben ser incompatibles y exhaustivas, es decir, cada individuo de la población presenta una y sólo una de las modalidades del carácter. Los caracteres de los elementos de una población se clasifican en Cualitativos (o atributos) y Cuantitativos.
Variable estadística
Introducimos el término de variable estadística, que denotaremos por v.e., para refe-renciar a un símbolo (X, Y, Z, A, B, ⋯) que puede tomar cualquier modalidad de un conjunto determinado, que llamaremos dominio de la variable o rango. Dependiendo del tipo de dominio, las variables estadísticas se clasifican en:
Variables cualitativas
La variable estadística se dice Cualitativa si sus diversas modalidades son de tipo nominal (no son cuantificables, no son medibles). Ejemplos: sexo, color del pelo, grupo sanguíneo, profesión, estado civil, nacionalidad, etc. Dentro de este tipo de variable podemos mencionar las variables ordinales cuyas modalidades siguen siendo de tipo nominal pero se puede establecer un orden entre ellas. Por ejemplo el estamento militar (sargento, brigada, teniente, capitán, comandante, teniente coronel, coronel.)
Variables cuantitativas
La variable estadística se dice Cuantitativa si sus diversas modalidades son susceptibles de ser medidas numéricamente, es decir, si a cada una de las modalidades se le asigna un número. Ejemplos: edad, peso, estatura, coeficiente intelectual, etc. Según los distintos va-lores que pueden tomar las variables estadísticas se clasifican en Discretas y Continuas.
Variables estadísticas discretas
Una variable estadística es discreta si sus posibles valores están aislados, en número finito o infinito numerable, por ejemplo: número de hijos en una familia, número de alumnos en una facultad.
Variables estadísticas continuas
Una variable estadística es continua si puede tomar todos los valores de un intervalo, por ejemplo: el peso de un individuo, la estatura de un individuo, la temperatura de un cuerpo, la velocidad de un coche, etc.
La teoría estadística puede utilizarse únicamente para fines descriptivos: Se ha recogido un conjunto grande de datos y sólo interesa describir las características particulares de dicho conjunto de la forma más breve y concisa posible. Para ello, en primer lugar, organizamos los datos en una tabla conveniente y efectuamos representaciones gráficas apropiadas.
Tablas estadísticas y Representaciones gráficas
Tablas estadísticas
Se denomina Frecuencia absoluta de la modalidad \( c_i \), y se denota por \( n_i \), al número de veces que se presenta dicha modalidad en la población en estudio. Si suponemos que el carácter C tiene k modalidades, \( c_1, …, c_i, …, c_k \), como éstas deben ser incompatibles y exhaustivas se verifica que \( n = \sum_{i=1}^{k}n_i \), siendo n el número total de observaciones.
Se define la Frecuencia relativa de la modalidad \( c_i \), que notamos por \( f_i \), como la proporción de individuos de la población que presentan dicha modalidad es decir, como el cociente entre la frecuencia absoluta y el número total de observaciones.
\( f_i= \displaystyle \frac{n_i}{n} \)
Se verifica que: \( n = \sum_{i=1}^{k}f_i = 1 \).
Ejemplo 1.1: Se lanza un dado 25 veces obteniendo los siguientes resultados: 2, 3, 6, 1, 2, 5, 1, 2, 4, 5, 1, 2, 4, 3, 6, 3, 6, 5, 5, 4, 1, 5, 6, 1, 3.
La tabla estadística que describe esta población se muestra a continuación:
\(
\begin{matrix} \hline
{\bf x_i } & {\bf n_i } & {\bf f_i }\\
\hline 1 & 5 & 0.20 \\ 2 & 4 & 0.16 \\ 3 & 4 & 0.16 \\ 4 & 3 & 0.12 \\ 5 & 5 & 0.20 \\ 6 & 4 & 0.16 \\ \hline \end{matrix} \)
donde hemos denotado por \( x_i \) a los valores de la variable.
Se define la Frecuencia absoluta acumulada correspondiente a \( x_i \), que notaremos por \( N_i \), como el número de elementos de la población con un valor de la variable menor o igual que el considerado. Es decir, es la suma de las frecuencias absolutas hasta un valor determinado de la variable.
\( N_i =n_1+n_2+⋯+n_i = \sum_{j=1}^{i} n_j \),
supuesto que los valores de la variable están ordenados en forma ascendente.
Llamamos Frecuencia relativa acumulada correspondiente a \( x_i \), que notaremos por \( F_i \), al cociente entre la frecuencia absoluta acumulada y el número total de observaciones o a la suma de las frecuencias relativas hasta un valor determinado de la variable.
\( F_i= \displaystyle \frac{N_i}{n } =f_1+f_2+⋯+f_i =\sum_{j=1}^{i}f_j \),
supuesto que los valores de la variable están ordenados en forma ascendente.
Recibe el nombre de Distribución de frecuencias al conjunto de los valores que presenta la variable junto con sus frecuencias. Dependiendo del tipo de frecuencias que se consideren hablaremos de Distribución de frecuencias absolutas; Distribución de frecuencias relativas acumuladas etc.
Considerando una variable estadística discreta \( x_i \), que puede tomar los valores \( x_1, ⋯, x_i, ⋯, x_k \), una tabla estadística con los tipos de frecuencias estudiados se muestra a continuación.
\(
\begin{array}{||l|l|l|l|l||} \hline
{\bf x_i } & {\bf n_i } & {\bf f_i } & {\bf N_i } & {\bf F_i } \\
\hline \hline x_1 & n_1 & f_1 & N_1=n_1 & F_1=f_1 \\ x_2 & n_2 & f_2 & N_2=n_1+n_2 & F_2=f_1+f_2 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\
x_i & n_i & f_i & N_i=n_1+⋯+n_i & F_i=f_₁+⋯+f_i \\
⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\
x_k & n_k & f_k & N_k = n_1+⋯+n_k=n & F_k=f_1+⋯+f_k =1 \\ x_1 & n_1 & f_1 & N_1=n_1 & F_1=f_1 \\ x_2 & n_2 & f_2 & N_2=n_1+n_2 & F_2=f_1+f_2 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\
x_1 & n_1 & f_1 & N_1=n_1 & F_1=f_1 \\ x_2 & n_2 & f_2 & N_2=n_1+n_2 & F_2=f_1+f_2 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\
\hline \hline
& n & 1 & & \\ \hline \end{array} \)
No siempre realizamos un estudio en el que la variable toma valores aislados, como en el ejemplo anterior, es decir en el que la variable es discreta, sino que en muchas situaciones la variable puede tomar todos los valores de un intervalo, es decir que la variable es de tipo continuo.
En las variables de tipo continuo se agrupan los valores de la variable en intervalos o clases que notaremos como \( e_{i-1}- e_i \), (cuyos extremos son \( [e_{i-1}, e_i) \)). Cada clase está representada por su punto medio, que recibe el nombre de Marca de clase, y se denota por \( x_i \)
\( x_i= \displaystyle \frac{e_i+e_{i-1}} {2} \) ,
este valor juega un papel análogo al valor \( x_i \) de las variables estadísticas discretas.
Llamamos Amplitud del intervalo, y se denota por \( a_i \), a la diferencia entre los extremos del intervalo
\( a_i=e_i – e_{i-1} \).
Los intervalos de una población pueden elegirse de la misma o de distinta amplitud.
La tabla de frecuencias correspondiente a las variables de tipo continuo con las frecuencias estudiadas, se muestra a continuación
\(
\begin{array} {||l|l|l|l|l|l|l||} \hline {\bf e_{i-1}-e_i } & {\bf n_i } & {\bf x_i } & {\bf a_i } & {\bf f_i } & {\bf N_i } & {\bf F_i } \\
\hline \hline e_0 – e_1 & n_1 & x_1 & a_1 & f_1 & N_1 = n_1 & F_1 = f_1 \\ e_1 – e_2 & n_2 & x_2 & a_2 & f_2 & N_2 = n_1 + n_2 & F_2 = f_1 + f_2 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ e_{i-1}-e_i & n_i & x_i & a_i & f_i & N_i=n_1+⋯+n_i & F_i = f_1+⋯+f_i \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ e_{k-1}-e_k & n_k & x_k & a_k & f_k & N_k=n_1+⋯+n_k = n & F_k = f_1+⋯+f_k =1 \\ \hline \hline & n & & & 1 & & \\ \hline \end{array} \)
Ejemplo 1.2: La siguiente tabla muestra los precios, en euros, de los objetos que hay en una estantería de una tienda
\(
\begin{matrix} \hline {\bf Precios} & n_{i} \\
40-70 & 2 \\
70-80 & 5 \\
80-100 & 10 \\
100-200 & 35 \\
200-300 & 43 \\
300-350 & 5 \\ \hline \hline
& 100 \\ \hline \end{matrix} \)
La tabla de frecuencias correspondiente es:
\(
\begin{array}{||l|c|c|c|c|c|c||} \hline
{\bf Precios} & {\bf n_i } & {\bf x_i } & {\bf a_i } & {\bf f_i } & {\bf N_i } & {\bf F_i } \\
\hline \hline
40-70 & 2 & 55 & 30 & 0.02 & 2 & 0.02 \\
70-80 & 5 & 75 & 10 & 0.05 & 7 & 0.07 \\
80-100 & 10 & 90 & 20 & 0.10 & 17 & 0.17 \\
100-200 & 35 & 150 & 100 & 0.35 & 52 & 0.52 \\
200-300 & 43 & 250 & 100 & 0.43 & 95 & 0.95 \\
300-350 & 5 & 325 & 50 & 0.05 & 100 & 1.00 \\ \hline \hline
& 100 & & & 1.00 & & \\ \hline \end{array} \)
Recibe el nombre de Función de distribución de una variable x, y se denota por F(x), a la proporción de individuos de la población cuyo carácter es inferior o igual a x,
\( F(x)=\sum_{x_i <=x } f_i \)
es decir, es la función que hace corresponder a cada valor de la variable su frecuencia relativa acumulada.
\( F(x_i) = \sum_{j=1}^{i } f_j =F_{i} \)
Representaciones gráficas
Aunque las tablas estadísticas contienen toda la información que disponemos de una población de forma que ésta se puede analizar de una forma más sistemática y resu-mida, es conveniente, muchas veces, traducir dicha información mediante un gráfico con el que realizar una síntesis visual. Atendiendo al tipo de variable estadística en estudio se utilizan varios tipos de representación.
Variables estadísticas cualitativas
Los gráficos más usuales para representar las variables de tipo nominal son: Diagrama de rectángulos y Diagrama de sectores.
Diagrama de rectángulos: En unos ejes cartesianos se sitúan sobre el eje de abscisas las distintas modalidades de la v.e. y sobre el eje de ordenadas los valores de las frecuencias. A continuación, en el eje de abscisas se levantan rectángulos de base constante y de altura proporcional a la frecuencia absoluta correspondiente.
Ejemplo 1.3: El número de alumnos de los primeros cursos de las distintas facultades de una Universidad se muestran en la siguiente tabla
\(
\begin{array}{||l|c||} \hline
{\bf Sección} & {\bf N^{o} de \hspace {1mm } matriculados } \\
\hline \hline Químicas & 800 \\
Matemáticas & 400 \\
Estadística & 200 \\
Ambientales & 100 \\
Físicas & 500 \\
Biológicas & 700 \\
Geológicas & 300 \\ \hline \hline
Total & 3000 \\ \hline
\end{array} \)
El diagrama de rectángulos correspondiente es
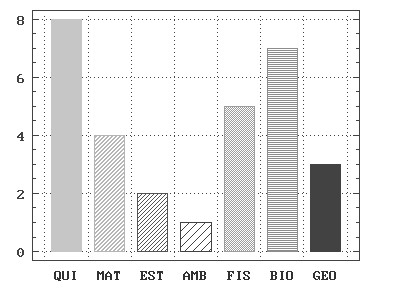
Figura 1: Diagrama de rectángulos
Diagrama de sectores: En esta representación un círculo se divide en tantos sectores circulares como modalidades tenga la variable estadística, teniendo cada sector el área proporcional a la frecuencia absoluta correspondiente. Los grados de cada sector se obtienen resolviendo la proporción
\( \displaystyle \frac{360º} {n} = \displaystyle \frac{xº_i} {n_i} \) ,
Considerando el ejemplo anterior, los grados de cada sector se obtienen de la siguiente forma:
\( \begin{matrix} \hline
QUI = \displaystyle \frac{360º \times 800} {3000}=96º & & MAT = \displaystyle \frac{360º \times 400} {3000} = 48º \\ & & \\ EST = \displaystyle \frac{360º \times 200} {3000} =24º & & AMB = \displaystyle \frac{360º \times 100} {3000} =12º \\ & & \\ FIS = \displaystyle \frac{360º \times 500} {3000} = 60º & & BIO = \displaystyle \frac{360º \times 700} {3000}=84º \\ & & \\ GEO = \displaystyle \frac{360º \times 300} {3000}=36º & & \\ \hline
\end{matrix} \)
El diagrama de sectores correspondiente es:
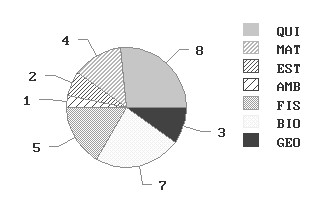
Figura 2: Diagrama de sectores
Variables estadísticas cuantitativas
En el caso de las variables estadísticas cuantitativas distinguiremos entre
a) Gráficos de variable estadística discreta: Diagrama de barras, Polígono de frecuencias y Curva acumulativa o de distribución.
b) Gráficos de variable estadística continua: Histograma, Polígono de frecuencias y Curva acumulativa o de distribución.
a) Gráficos de variable estadística discreta:
a1) Diagrama de barras: Sobre unos ejes cartesianos, se toman en el eje de abscisas los valores de la variable y sobre cada uno de estos valores se levantan barras de altura igual a su frecuencia absoluta (Diagrama de barras de frecuencias absolutas) o a su frecuencia relativa (Diagrama de barras de frecuencias relativas). Si se utilizan las frecuencias (absolutas o relativas) acumuladas el gráfico recibe el nombre de Diagrama de barras acumulativo.
a2) Polígono de frecuencias: Se construye uniendo con segmentos, en el diagrama de barras, los extremos superiores de las barras. La línea quebrada abierta que se obtiene recibe el nombre de Polígono de frecuencias.
Ejemplo 1.4: Se inició una investigación para averiguar el número de bacterias que aparecen en determinados cultivos. Para ello, se tomaron 40 de estos cultivos y se contó el número de bacterias, \( x_{i} \), que apareceiron en cada uno de ellos.
\( \begin{matrix} \hline {\bf x_i} & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
{\bf n_i} & 2 & 5 & 6 & 12 & 9 & 5 & 1 \\
\hline
\end{matrix} \)
El diagrama de barras correspondiente es:
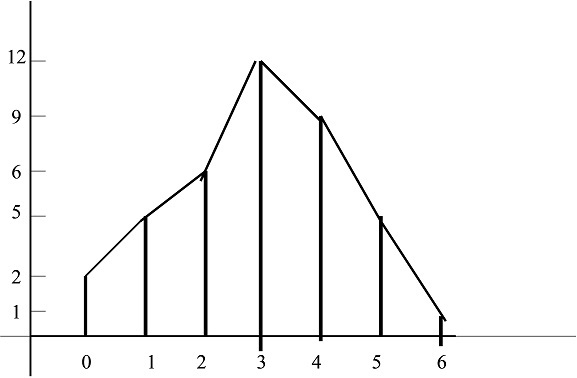
Figura 3: Diagrama de barras y polígono de frecuencias
El polígono de frecuencias es la línea quebrada en el diagrama de barras anterior.
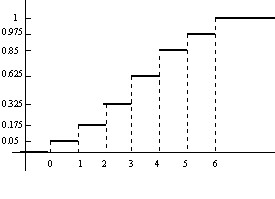
a3) Curva acumulativa o de distribución: Sobre unos ejes cartesianos, se toman en el eje de abscisas los valores de la variable y sobre cada uno de estos valores se levantan barras de altura igual a su frecuencia relativa acumulada. A continuación, se trazan paralelas al eje de abscisas sobre el extremo de cada barra hasta cortar a la barra siguiente, obteniéndose una representación escalonada, cuyos saltos, que corresponden a los posibles valores de \( x_{i} \), son iguales a las frecuencias relativas correspondientes, \( f_{i} \). Dicha curva es la representación gráfica de la función de distribución F(x).
Utilizando los datos del Ejemplo 1.4 completamos la tabla de frecuencias añadiendo las frecuencias relativas acumuladas
\( \begin{matrix} \hline {\bf x_i} & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \\ \hline
{\bf n_{i} } & 2 & 5 & 6 & 12 & 9 & 5 & 1 & 40 \\ \hline
{\bf f_{i} } & 0.05 & 0.125 & 0.15 & 0.3 & 0.225 & 0.125 & 0.025 & 1 \\ \hline
{\bf F_{i}} & 0.05 & 0.175 & 0.325 & 0.625 & 0.85 & 0.975 & 1 & \\
\hline
\end{matrix} \)
La curva acumulativa correspondiente es:
b) Gráficos de variable estadística continua:
b1) Histograma: Sobre unos ejes cartesianos, se marcan en el eje de abscisas los extremos de los intervalos de clase de la variable y sobre cada uno de estos intervalos se levantan rectángulos de altura igual a
– \( n_{i} \) o \( f_{i} \) en el caso de que los intervalos tengan la misma amplitud. Si se utilizan las frecuencias (absolutas o relativas) acumuladas el gráfico recibe el nombre de Histograma de frecuencias (absolutas o relativas) acumuladas
– \( \displaystyle \frac{n_{i}}{a_{i} } \) o \( \displaystyle \frac{ f_{i}} {a_{i}} \) en el caso de que los intervalos no tengan la misma amplitud.
b2) Polígono de frecuencias: Se construye uniendo los puntos medios, mediante segmentos, de los lados superiores de los rectángulos que forman el histograma. La línea quebrada que se obtiene recibe el nombre de Polígono de frecuencias.
Ejemplo 1.5: Las alturas de 40 estudiantes, obtenidas de una lista alfabética de una universidad, son:
\( \begin{array}{||l|c|c|c||} \hline {\bf Alturas} &
{\bf 160-165 } & {\bf 165-170 } & {\bf 170-175} & {\bf 175-180 } & {\bf 180-185 } \\ \hline
{\bf n_{i} } & 4 & 7 & 10 & 13 & 6 \\ \hline
\end{array} \)
El histograma correspondiente es:
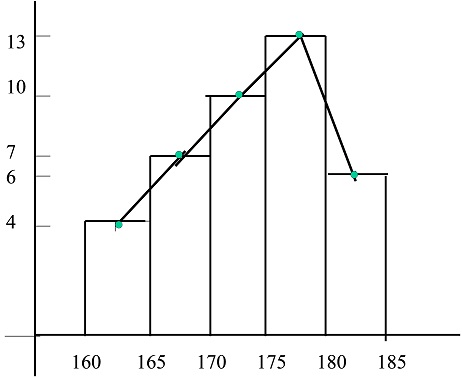
Figura 5: Histograma y polígono de frecuencias
El Polígono de frecuencias es la línea quebrada en el histograma.
Ejemplo 1.6: Las edades de 40 jóvenes que acuden a un concierto son:
\( \begin{matrix} \hline {\bf Edades} & {\bf 14-15 } & {\bf 15-17 } & {\bf 17-18 } & {\bf 18-20 } & {\bf 20-23 } \\ \hline
{\bf n_{i} } & 6 & 14 & 11 & 6 & 3 \\ \hline \end{matrix} \)
Los intervalos tienen distintas amplitudes, denotamos por \( h_{i} \) a la altura correspondiente a cada uno y construimos la siguiente tabla:
\( \begin{matrix} \hline {\bf Edades} & {\bf 14-15 } & {\bf 15-17 } & {\bf 17-18 } & {\bf 18-20 } & {\bf 20-23 } \\ \hline
{\bf n_{i} } & 6 & 14 & 11 & 6 & 3 \\ \hline
{\bf a_{i} } & 1 & 2 & 1 & 2 & 3 \\ \hline
{\bf h_{i}= \displaystyle \frac{ n_{i} } {a_{i} }} & 6 & 7 & 11 & 3 & 1 \\ \hline
\end{matrix} \)
El histograma y el polígono de frecuencias correspondientes son:
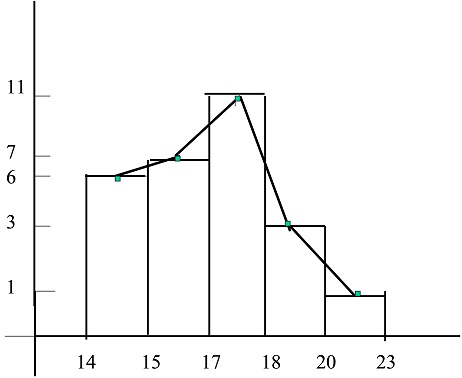
Figura 6: Histograma y polígono de frecuencias
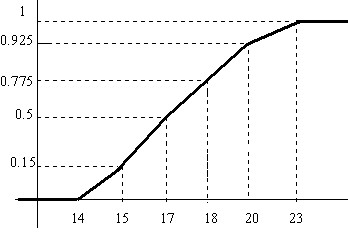
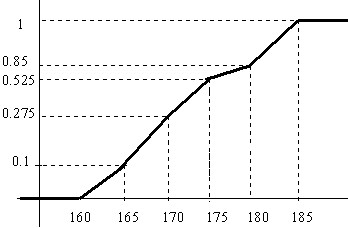
b3) Curva acumulativa o de distribución: Se construye uniendo con segmentos los vértices superiores de los rectángulos que forman el histograma realizado con las frecuencias relativas acumuladas. En este caso, la representación gráfica de la función de distribución no será continua a trozos sino una curva regular que pasa por los puntos \( (e_{i},F(e_{i})) \).
Utilizando los datos de los ejemplos 1.5 y 1.6 completamos las tablas de frecuencias añadiendo las frecuencias relativas acumuladas y representamos las curvas acumulativas correspondientes
En el ejemplo 1.5
\( \begin{matrix} \hline {\bf Alturas} & {\bf n_i } & {\bf f_i } & {\bf F_i } \\ \hline 160-165 & 4 & 0.100 & 0.1 \\ \hline
165-170 & 7 & 0.175 & 0.275 \\ \hline
170-175 & 10 & 0.250 & 0.525 \\ \hline
175-180 & 13 & 0.325 & 0.85 \\ \hline
180-185 & 6 & 0.150 & 1 \\ \hline
& 40 & 1.000 & \\ \hline \end{matrix} \)
En el ejemplo 1.6
\( \begin{matrix} \hline {\bf Edades} & {\bf n_i } & {\bf a_i } & {\bf f_i } & {\bf F_i } \\ \hline 15-17 & 14 & 2 & 0.350 & 0.5 \\ \hline 17-18 & 11 & 1 & 0.275 & 0.775 \\ \hline
18-20 & 6 & 2 & 0.150 & 0.925 \\ \hline
20-23 & 3 & 3 & 0.075 & 1 \\ \hline
& 40 & & 1.000 & \\ \hline \end{matrix} \)
Descripción numérica de una variable estadística unidimensional
En la sección anterior se han planteado técnicas gráficas, tablas estadísticas y representaciones gráficas, que han proporcionado una representación visual de las variables estadísticas. Dichas técnicas gráficas nos dan una idea de la composición de la población en estudio. En esta sección tratamos de resumir todos los datos recogidos en una tabla estadística en unos valores, medidas numéricas, llamadas Características o Medidas, que representen o sinteticen el conjunto de datos.
Los fenómenos biológicos no suelen ser constantes, es necesario que junto a una medida que indique el valor alrededor del cual se agrupan los datos, se asocie una medida que haga referencia a la variabilidad que refleje dicha fluctuación. Por tanto, el objeto de estudio, como hemos dicho anteriormente, consistirá en definir algunos tipos de medidas que sinteticen los datos aún más, que los describan mediante unas cantidades numéricas.
Entre las medidas que pueden describir los datos, comenzaremos por estudiar los valores alrededor de los cuales se agrupa la muestra, la mayor o menor fluctuación alrededor de esos valores. Nos interesaremos en ciertos valores que marcan posiciones características de una distribución, así como su simetría y su forma.
Estudiaremos las Características o Medidas de posición, de dispersión, de asimetría y de apuntamiento o curtosis.
Medidas de posición
Las Medidas de posición tratan de resumir y sintetizar el conjunto de datos mediante un valor numérico, si este valor numérico se sitúa hacia el centro de la distribución se habla, entonces, de Medidas de posición central o de Tendencia central.
Las principales medidas de posición central son: Media aritmética, Mediana y Moda. Estudiaremos también otras medidas de posición “no central” llamadas Cuantiles.
Media aritmética
Dada una variable estadística discreta \( x_{i} \) , que puede tomar los valores \( x_1,x_2, ⋯ x_{k} \) con frecuencias \( n_1,n_2,⋯n_{k} \) se define la Media aritmética, y se denota por \( \bar{x} \) , como el cociente
\( \bar{x} = \displaystyle \frac{1} {n} = \sum_{1=1}^{k }n_{i}x_{i} = \sum_{i=1}^{k }f_{i}x_{i} \)
siendo n el número total de observaciones.
Ejemplo 1.7: En un experimento de germinación se sembraron 80 filas con 10 semillas de col cada una. La distribución del número de semillas de col que germinaron por cada fila se muestra en tabla adjunta.
\( \begin{matrix} \hline {\bf N^{o} de \hspace {1mm } semillas \hspace {1mm } germinadas \hspace {1mm } por \hspace {1mm } filas: x_{i}} & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline
{\bf N^{o} de \hspace {1mm } filas \hspace {1mm }con \hspace {1mm } x \hspace {1mm } semillas \hspace {1mm }germinadas: n_{i} } & 6 & 20 & 28 & 12 & 8 & 6 \\ \hline \end{matrix} \)
Calcular la media.
Respuesta:
\( \begin{matrix} \hline {\bf x_i } & {\bf n_i } & {\bf n_i x_i } \\ \hline 0 & 6 & 0 \\ \hline
1 & 20 & 20 \\ \hline
2 & 28 & 56 \\ \hline
3 & 12 & 36 \\ \hline
4 & 8 & 32 \\ \hline
5 & 6 & 30 \\ \hline
& 80 & 174 \\ \hline \end{matrix} \) \( \hspace {10 mm }\) \( \bar{x} = \displaystyle \frac{1} {n} \sum_{1=1}^{6 }n_{i}x_{i}= \displaystyle \frac{174}{80}= 2.175 \)
Si la variable estadística es continua, las clases se representan por su marca de clase \( x_{i} \), definiéndose la media de forma análoga al caso de variable estadística discreta.
Ejemplo 1.8: En un cierto barrio se ha constatado que las familias residentes se han distribuido, según su tamaño de la siguiente forma:
\( \begin{matrix} \hline {\bf Tamaño \hspace {1mm } familias} & {\bf 0-2} & {\bf 2-4 } & {\bf 4-6 } & {\bf 6-8 } & {\bf 8-10 } \\ \hline
{\bf N^{o} familias } & 110 & 200 & 90 & 75 & 25
\\ \hline \end{matrix} \)
Calcular la media.
Respuesta:
\( \begin{array}{||l|c|c|c|c|c|c||} \hline {\bf Tamaño \hspace {1mm } familias} & {\bf n_{i} } & {\bf x_{i} } & {\bf n_{i}x_{i} } \\ \hline
0-2 & 110 & 1 & 110 \\ \hline
2-4 & 200 & 3 & 600 \\ \hline
4-6 & 90 & 5 & 450 \\ \hline
6-8 & 75 & 7 & 525 \\ \hline
8-10 & 25 & 9 & 225 \\ \hline
& 500 & & 1910 \\ \hline \end{array} \) \( \hspace {10 mm }\) \( x= \displaystyle \frac{1} {n} \sum_{i=1} ^{5} n_{i}x_{i}= \displaystyle \frac{1910}{500}= 3.82 \)
Cálculo abreviado de la media: Si los valores que toma la variable estadística \( x_{i} \) (discreta o continua) son grandes se utiliza otra variable \( x^´_{i} \), para simplificar los cálculos, cuyos valores se obtienen de la siguiente forma:
\( x^´_{i} = \displaystyle \frac{x_{i}-x_0}{a} \)
siendo:
- \( x_0 \): Un valor cualquiera del recorrido de la variable (aunque puede estar fuera del recorrido). Es recomendable que sea el valor central si el número de modalidades es impar o uno de los valores centrales si el número de modalidades es par. Recibe el nombre de origen de trabajo
- \( a \): El máximo común divisor de \( x_{i}-x_0 \). Recibe el nombre de escala.
En este caso, la media \( \bar{x}^´ \) adopta la expresión
\( \bar{x}^´ = \displaystyle \sum_{i=1} ^{k}f_{i}x^´_{i} = \displaystyle \sum_{i=1} ^{k}f_{i} \left ( \displaystyle \frac{x_{i}-x_0} {a} \right) = \displaystyle \frac{1}{a} \left ( \sum_{i=1} ^{k}f_{i} x_{i} – \sum_{i=1} ^{k}f_{i}x_0 \right) = \displaystyle \frac{1}{a} \left (\bar{x}- x_0 \sum_{i=1} ^{k}f_{i} \right) = \displaystyle \frac{\bar{x}-x_0} {a} \)
Por lo tanto, a la media aritmética le afecta un cambio de origen y de escala de la misma forma que le afecta a la variable.
Ejemplo 1.9: Dada la siguiente distribución, calcular la media efectuando un cambio de origen y escala.
\( \begin{array}{|l||c|c|c|c|c|c|} \hline {\bf e_{i-1}-e_{i} } & {\bf n_{i} } & {\bf a_{i} } & {\bf x_{i} } & {\bf x_{i}-300 } & {\bf x^´_{i}= \displaystyle \frac{ x_{i}-300} {5} } & {\bf n_{i}x^´_i } \\ \hline 20-30 & 20 & 10 & 25 & -275 & -55 & -1100 \\
30-100 & 30 & 70 & 65 & -235 & -47 & -1410 \\
100-500 & 10 & 400 & 300 & 0 & 0 & 0 \\
500-600 & 30 & 100 & 550 & 250 & 50 & 1500 \\
600-1000 & 10 & 400 & 800 & 500 & 100 & 1000 \\ \hline
& 100 & & & & & -10 \\ \hline \end{array} \)
Se ha tomado \( x_0 =300 \) y \( a = 5 \). Entonces la media \( \bar{ x}^′ \) es: \(\bar{ x}^′ = \displaystyle \frac{-10}{100}= – 0.1 \)
Por lo tanto
\( \bar {x} =x_0+a \bar{ x}^′=300+5×(-0.1)=299.5 \)
Observación: Uno de los principales inconvenientes de la media es que muy sensible a los valores extremos de la variable, ya que al intervenir en su cálculo todas las observaciones la aparición de una observación extrema hará que la media se desplace en esa dirección. Por tanto, no es recomendable utilizar la media como medida central en las distribuciones muy asimétricas.
Mediana
Se define la Mediana, que notaremos por Me, de un conjunto de observaciones, como el valor de la variable estadística que divide a los elementos de la población (supuestos ordenados creciente o decrecientemente) en dos partes iguales. La mediana ocupa el punto central de la serie numérica, supuesto la serie ordenada creciente o decrecientemente.
También se define la mediana de un conjunto de observaciones como el valor de la variable estadística, supuesto todas las observaciones ordenadas de manera creciente, para el cual la mitad de las observaciones son inferiores a este valor y la otra mitad son superiores a él.
En general, dada una variable estadística x con función de distribución \( F(x) \), se define la mediana como el valor de la variable estadística, \( x_{1/2}\), tal que la ordenada en la curva de distribución vale 1/2; \( F(x_{1/2}) =1/2 \).
Dependiendo del valor de las frecuencias de las observaciones y del tipo de variable la mediana de calcula de las siguientes formas:
Variable estadística discreta
a) Frecuencias son unitarias
a1) Número impar de observaciones: La mediana, en este caso, es única, es el término que ocupa la posición central.
Ejemplo 1.10: Dada la serie numérica \( {\bf x_i :11,8,5,2,13} \) . Calcular la mediana.
Respuesta:
Ordenamos los datos en orden creciente: 2,5,8,11,13⇒ Me=8.
a2) Número par de observaciones: La mediana, en este caso, está indeterminada. La mediana es siempre un valor de la variable estadística y en el caso de un número par de observaciones no hay un único valor central.
Ejemplo 1.11: Dada la serie numérica \( {\bf x_i:13,9,5,2,12,1} \) . Calcular la mediana
Respuesta:
Ordenamos los datos en orden creciente: 1,2,5,9,12,13 ⇒ La mediana está indeterminada entre 5 y 9.
b) Las frecuencias no son unitarias. Se calculan las frecuencias absolutas acumuladas y la mitad de las observaciones, n/2. A continuación, se busca el valor n/2 en las \( N_{i}\), pudiendo haber dos situaciones:
b1) El valor n/2 se encuentre entre dos valores de la frecuencias absolutas acumuladas, es decir: \( N_{i-1}<n/2<N_{i} \). En este caso se toma como mediana el valor de la variable estadística que corresponde a \( N_{i} \), es decir: \( Me = x_{i} \) .
Ejemplo: Calcular la mediana del ejemplo 1.7
\( \begin{matrix} \hline {\bf x_{i} } & {\bf 0} & {\bf 1 } & {\bf 2 } & {\bf 3 } & {\bf 4 } & {\bf 5 } \\ \hline {\bf n_{i} } & 6 & 20 & 28 & 12 & 8 & 6 \\ \hline
{\bf N_{i}} & 6 & 26 & 54 & 66 & 74 & 80 \\ \hline \end{matrix} \)
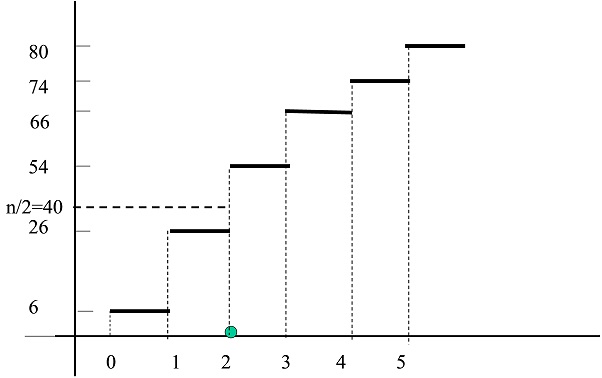
Figura 9: Cálculo gráfico de la Mediana en una variable estadística discreta
\( \begin{matrix} {\bf n/2 = 40 } \\ N_{i-1}<n/2<N_{i}⇒26<40<54 \\ M_{e}=x_{i}⇒M_{e}=2 \\ \end{matrix} \)
b2) El valor n/2 coincida con una frecuencia absoluta acumulada, es decir \( n/2=N_{i} \). En este caso, (estamos ante una situación similar al caso de un número par de observaciones), la mediana está indeterminada entre los valores \( x_{i} \) y \( x_{i+1} \).
Ejemplo 1.12: Calcular la mediana de la siguiente distribución
\( \begin{matrix} \hline {\bf x_{i} } & {\bf 1 0} & {\bf 20 } & {\bf 30 } & {\bf 40 } & {\bf 50 } \\ \hline {\bf n_{i}} & 6 & 20 & 14 & 26 & 8 & 6 \\ \hline
{\bf N_{i} } & 6 & 26 & 40 & 66 & 74 & 80
\\ \hline \end{matrix} \)
Respuesta:
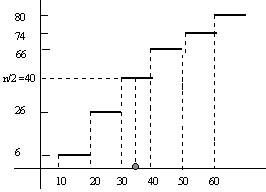
Figura 10: Cálculo gráfico de la Mediana en una variable estadística discreta
\( \begin{matrix}{\bf n/2=40} \\ {\bf n/2=40=N_{i}} \\ \end{matrix} \)
La mediana está indeterminada entre 30 y 40
Variable estadística continua
Cuando las variables son continuas se determina el intervalo mediano, es decir el intervalo \( (e_{i-1} , e_{i}) \) tal que
\( N_{i-1}<(n/2)<N_{i} \)
y en dicho intervalo se selecciona un representante que recibirá el nombre de mediana. Esta mediana se obtiene por interpolación lineal. Pueden ocurrir dos casos:
∗) El valor n/2 se encuentre entre dos valores de la frecuencia absoluta acumulada, es decir: \( N_{i-1}<n/2<N_{i} \). Para determinar Me se representa el polígono de frecuencias absolutas acumuladas y por interpolación lineal se obtiene la mediana
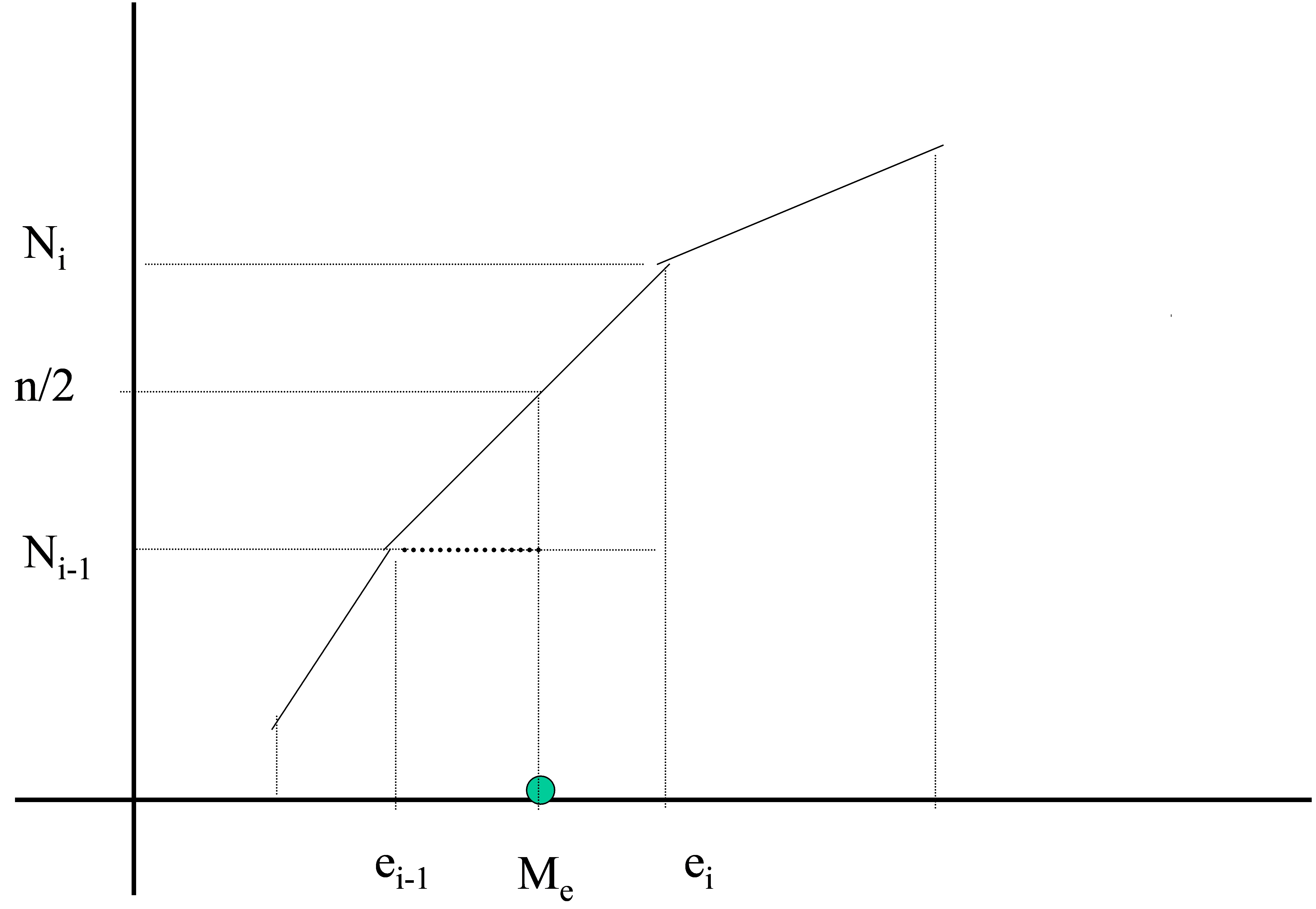 Figura 11: Cálculo gráfico de la Mediana en una variable estadística continua
Figura 11: Cálculo gráfico de la Mediana en una variable estadística continua
\( \begin{matrix} e_{i}-e_{i-1}→N_{i}-N_{i-1} \\ M_{e}-e_{i-1}→(n/2)-N_{i-1} \\ \end{matrix} \)
\( M_{e}=e_{i-1}+ \displaystyle \frac{ \displaystyle \frac{n} {2}-N_{i-1}}{N_{i}-N_{i-1}}(e_{i}-e_{i-1})= e_{i-1}+ \displaystyle \frac{1/2-F_{i-1}}{f_{i}}a_{i} \)
Ejemplo: En el ejemplo 1.8 calcular la mediana
\( \begin{matrix} \hline {\bf Tamaño \hspace {1mm } familias} & {\bf 0-2} & {\bf 2-4 } & {\bf 4-6 } & {\bf 6-8 } & {\bf 8-10 } \\ \hline
{\bf n_i } & 110 & 200 & 90 & 75 & 25 \\ \hline {\bf N_i } & 110 & 310 & 400 & 475 & 500
\\ \hline \end{matrix} \)
Respuesta:
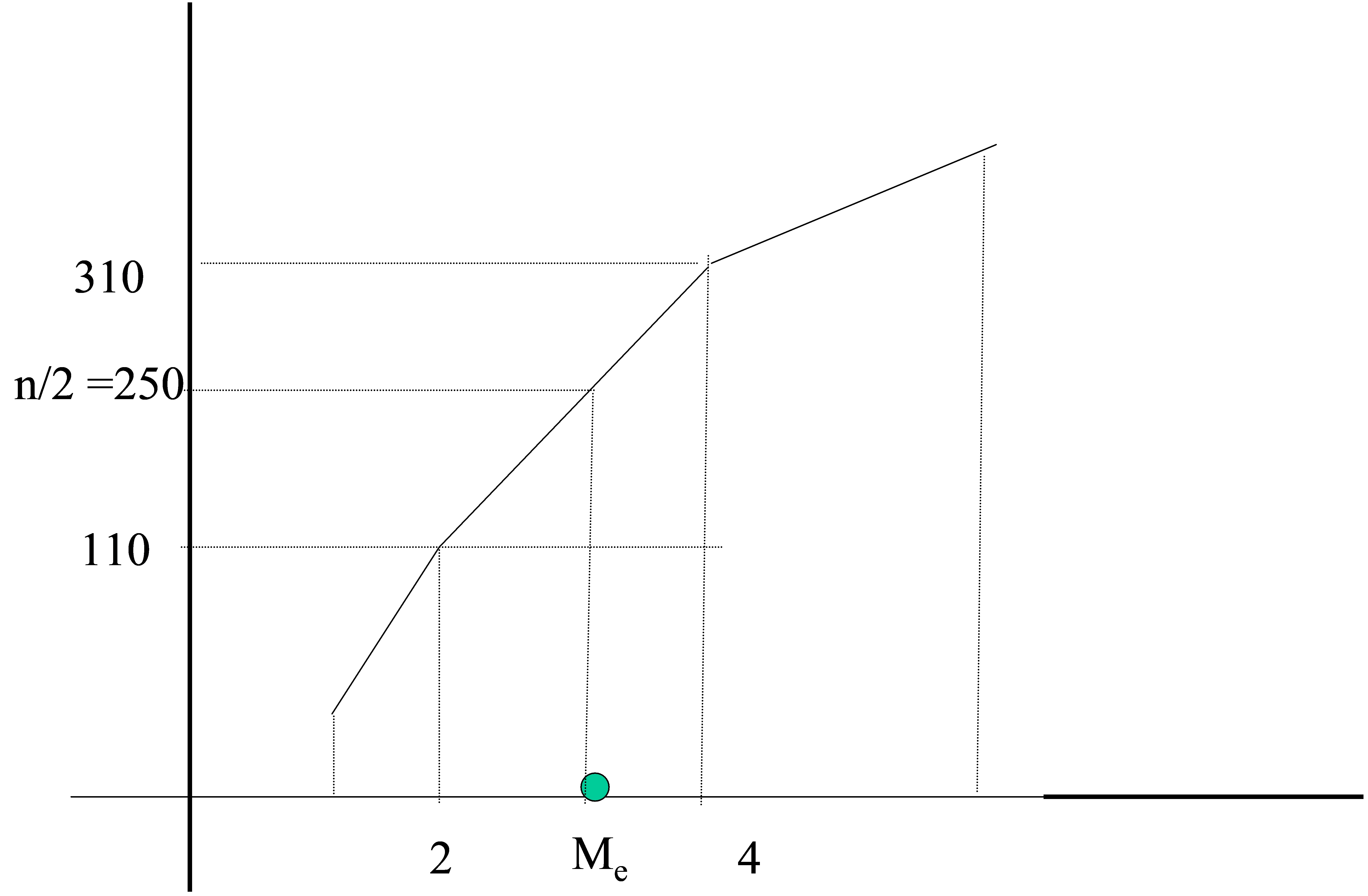
Figura 12: Cálculo gráfico de la Mediana en una variable estadística continua
\( \displaystyle \frac{n} {2}= 250 \)
\( N_{i-1}<n/2<N_{i}⇒110<250<310 \)
El intervalo mediano es: (2 , 4)
\( Me=e_{i-1}+ \displaystyle \frac{(n/2)-N_{i-1} } {N_{i}-N_{i-1}}(e_{i}-e_{i-1})=2 + \displaystyle \frac{250-110} {310-110} (4-2)= 3.4 \)
∗) El valor n/2 coincida con una frecuencia absoluta acumulada, es decir \( n/2=N_{i} \). Entonces \( Me=e_{i} \) (el extremo superior del intervalo que le corresponde). En efecto
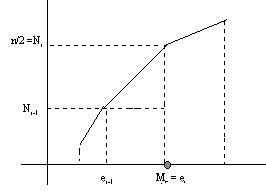 Figura 13: Cálculo gráfico de la Mediana en una variable estadística continua
Figura 13: Cálculo gráfico de la Mediana en una variable estadística continua
\( Me=e_{i-1}+ \displaystyle \frac{(n/2)-N_{i-1} } {N_{i}-N_{i-1}}(e_{i}-e_{i-1}) = e_{i-1}+ \displaystyle \frac{N_i-N_{i-1} } {N_{i}-N_{i-1}}(e_{i}-e_{i-1}) = e_i \)
Ejemplo: En el ejemplo 1.9 calcular la mediana
\( \begin{matrix} \hline {\bf e_{i-1}-e_{i} } & {\bf 20-30 } & {\bf 30-100 } & {\bf 100-500 } & {\bf 500-600 } & {\bf 600-1000 } \\ \hline
{\bf n_{i} } & 20 & 30 & 10 & 30 & 10 \\ \hline
{\bf N_{i}} & 20 & 50 & 60 & 90 & 100 \\ \hline
\\ \end{matrix} \)
Respuesta:
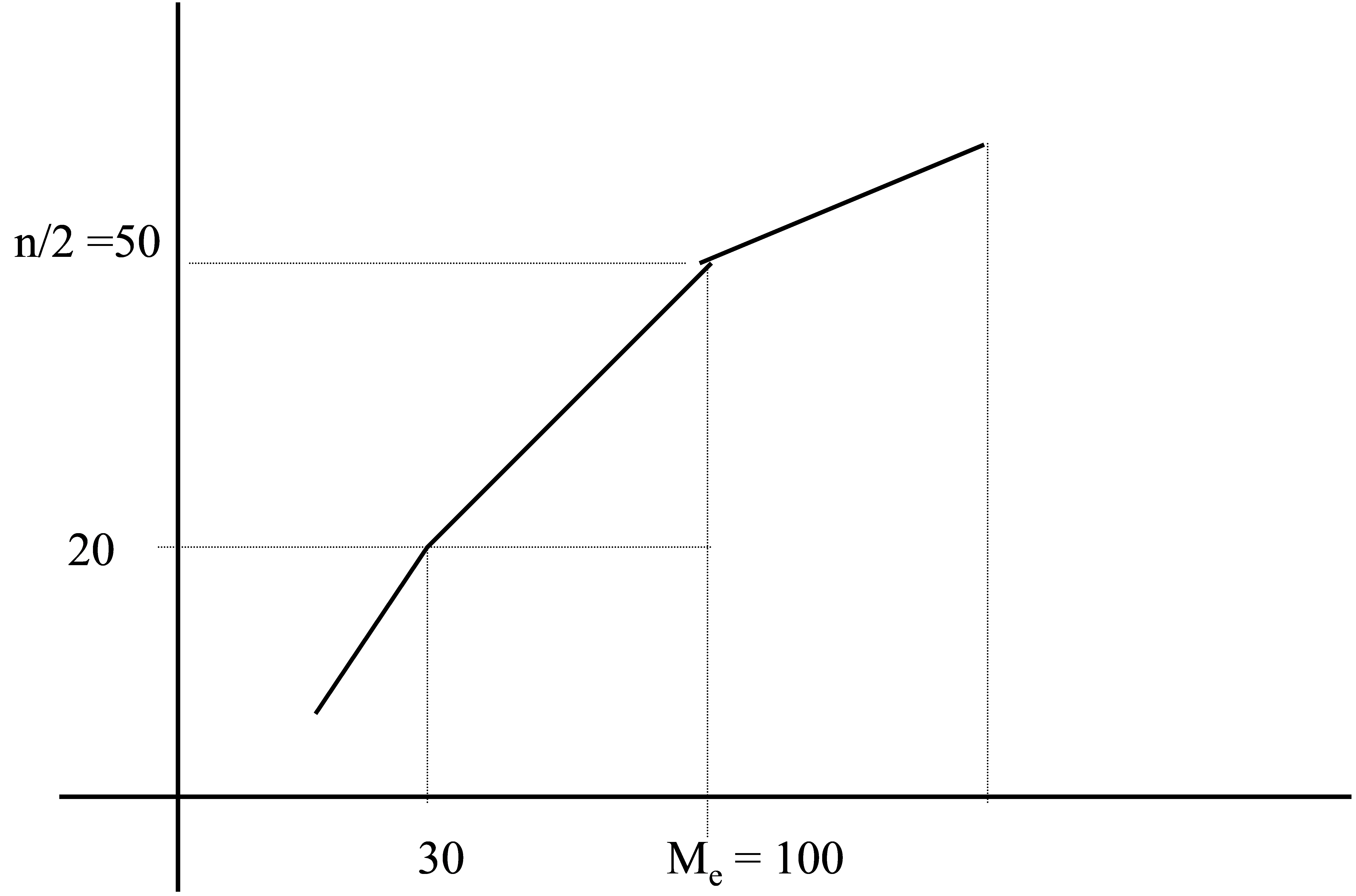
Figura 14: Cálculo gráfico de la Mediana en una variable estadística continua
\( \displaystyle \frac{ n} { 2} = \displaystyle \frac{ 100} { 2}=50 \)
El intervalo mediano: (30 , 100)
\( M_{e}=e_{i-1}+ \displaystyle \frac{(n/2)-N_{i-1} } {N_{i}-N_{i-1}}(e_{i}-e_{i-1}) = 30 + \displaystyle \frac{50-20 } {50-20}(100-30)= 100 \)
Observaciones:
∗ La mediana no depende de los valores que toma la variable sino del orden de las mismas por lo tanto no está afectada por observaciones extremas y es adecuado su uso, como medida descriptiva de tendencia central, en distribuciones asimétricas.
∗ A diferencia de la media, la mediana de una variable discreta es un valor de la variable. Por ejemplo, en el número de hijos de las familias de una ciudad la mediana toma un valor entero pero el valor de la media puede no pertenecer al conjunto de valores de la variable (\( \bar{x}=2.3 \)).
Moda
Llamamos Moda, y se denota por Mo, al valor de la variable estadística que se presenta con mayor frecuencia.
Variable estadística discreta
El cálculo de la moda es inmediato (Aplicar la definición)
Ejemplo: En el ejemplo 1.7 la Moda es 2.
Variable estadística continua
En este tipo de variables se determina el intervalo modal, es decir el intervalo en el que las observaciones tienen mayores frecuencias y en dicho intervalo se selecciona un representante que recibirá el nombre de moda. Se distinguen dos casos:
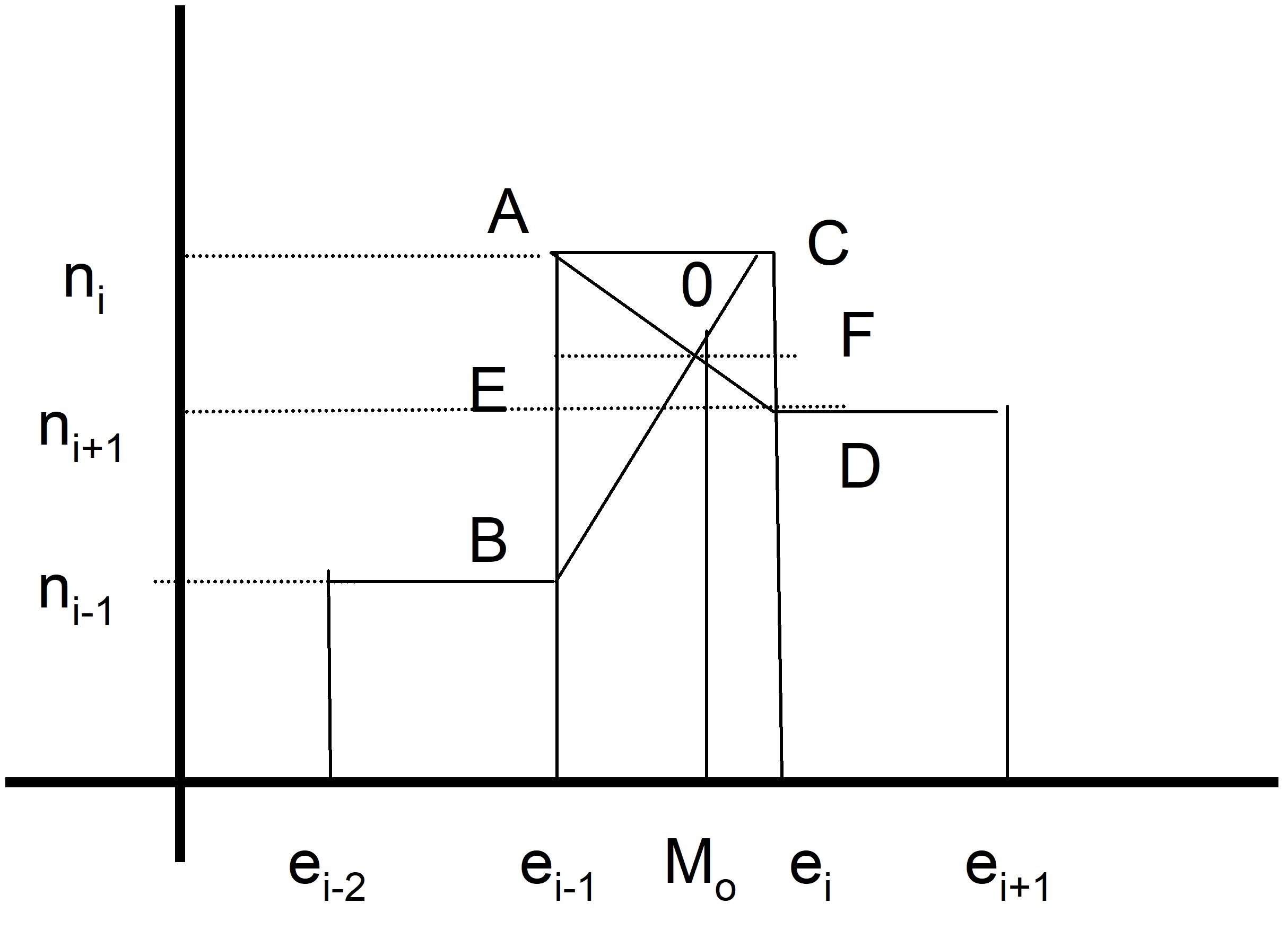
a) Si los intervalos tienen la misma amplitud entonces la moda se obtiene de la siguiente forma:
\( Mo = e_{i-1}+EO \)
Por la semejanza de los triángulos AOB y COD tenemos que:
\( \displaystyle \frac{OF } {OE } = \displaystyle \frac{CD} {AB } \Rightarrow \displaystyle \frac{ a_i- OE } {OE} = \displaystyle \frac { n_{i}-n_{i+1} } {n_{i}-n_{i-1}} \Rightarrow \) \( (a_{i}-OE) (n_{i}-n_{i-1}) = (n_{i}-n_{i+1}) × OE \Rightarrow \) \( ((n_{i}-n_{i-1})+ (n_{i}-n_{i+1})) × OE = (n_{i}-n_{i-1}) × a_{i} \Rightarrow \)
\( OE= \displaystyle \frac { n_{i}-n_{i-1} } {(n_{i}-n_{i-1}) + (n_{i}-n_{i+1})}×a_{i} \)
Por lo tanto
\( Mo = e_{i-1} + \displaystyle \frac { n_{i}-n_{i-1} } { (n_{i}-n_{i+1}) + (n_{i}-n_{i-1})}×a_{i} \)
Ejemplo: En el ejemplo 1.8 calcular la moda
\( \begin{matrix} \hline {\bf Tamaño \hspace {1mm } familias} & {\bf 0-2} & {\bf 2-4 } & {\bf 4-6 } & {\bf 6-8 } & {\bf 8-10 } \\ \hline
{\bf n_i } & 110 & 200 & 90 & 75 & 25 \\ \hline \end{matrix} \)
Respuesta:
El intervalo modal es (2 , 4)
\( M_o = e_{i-1} + \displaystyle \frac {( e_{i}-e_{i-1} ) (n_{i}-n_{i-1}) } { (n_{i}-n_{i+1}) + (n_i – n_{i-1})} = 2+ \displaystyle \frac {200-110} {(200-90)+(200-110) }×2=2.9 \)
b) Si los intervalos no tienen la misma amplitud entonces el intervalo modal es aquel que tiene la mayor densidad de frecuencia, es decir el mayor valor \( n_{i}/a_{i} \) y la moda se obtiene de la misma forma que en el caso anterior, pero sustituyendo \( n_{i} \) por \( n_{i}/a_{i} \), obteniendo por tanto, la siguiente expresión
\( M_o = e_{i-1} + \displaystyle \frac { \displaystyle \frac {n_{i}}{a_i} – \displaystyle \frac {n_{i-1}}{a_{i-1} } } { \left ( \displaystyle \frac {n_{i}}{a_i} + \displaystyle \frac {n_{i+1}}{a_{i+1}}\right) – \left ( \displaystyle \frac {n_{i}}{a_i} – \displaystyle \frac {n_{i-1}}{a_{i-1}}\right)} × a_{i} \)
Ejemplo 1.13: Calcular la moda de la siguiente distribución
\( \begin{array}{||l|c|c|c|c||} \hline e_{i-1}-e_{i} & 5-7 & 7-9 & 9-12 & 12-16 \\ \hline n_{i} & 20 & 36 & 48 & 20 \\ \hline a_{i} & 2 & 2 & 3 & 4 \\ \hline
n_{i}/a_{i} & 10 & 18 & 16 & 5
\\ \hline \end{array} \)
Respuesta:
El intervalo modal es (7 , 9)
\( M_o = e_{i-1} + \displaystyle \frac { (e_{i} – e_{i-1}) \left ( \displaystyle \frac {n_{i}}{a_i} – \displaystyle \frac {n_{i-1}}{a_{i-1}}\right) } { \left (\displaystyle \frac {n_{i}}{a_i} – \displaystyle \frac {n_{i+1}}{a_{i+1}} \right) + \left (\displaystyle \frac {n_{i}}{a_{i } } – \displaystyle \frac {n_{i-1}}{a_{i-1}}\right) } = 7 + \displaystyle \frac { (9-7)(18-10)}{(18-16)(18-10)} = 8.6 \)
Percentiles
Los Percentiles son aquellos valores de la variable estadística que dividen a los elementos de la población (supuestos ordenados crecientemente) en intervalos con igual número de observaciones. En general no van a reflejar ninguna posición central, salvo la mediana que es un caso particular de percentil.
Se define el Percentil de orden k, (k=1,2,⋯,99), como el valor de la variable que deja por debajo el k % de los valores de la variable.
Los percentiles se clasifican en distintos tipos dependiendo del número de intervalos en que dividan a la población, los más importantes son:
∗ Cuartiles
Dividen a los elementos de la población en cuatro intervalos con igual número de observaciones. Se denotan por: \( Q_1 \) , \( Q_2 \) , \( Q_3 \).
⋄ \( Q_1= P_{25} \) Cuartil 1º
⋄ \( Q_2 = P_{50} \) Cuartil 2º = Mediana
⋄ \( Q_3 = P_{75} \) Cuartil 3º
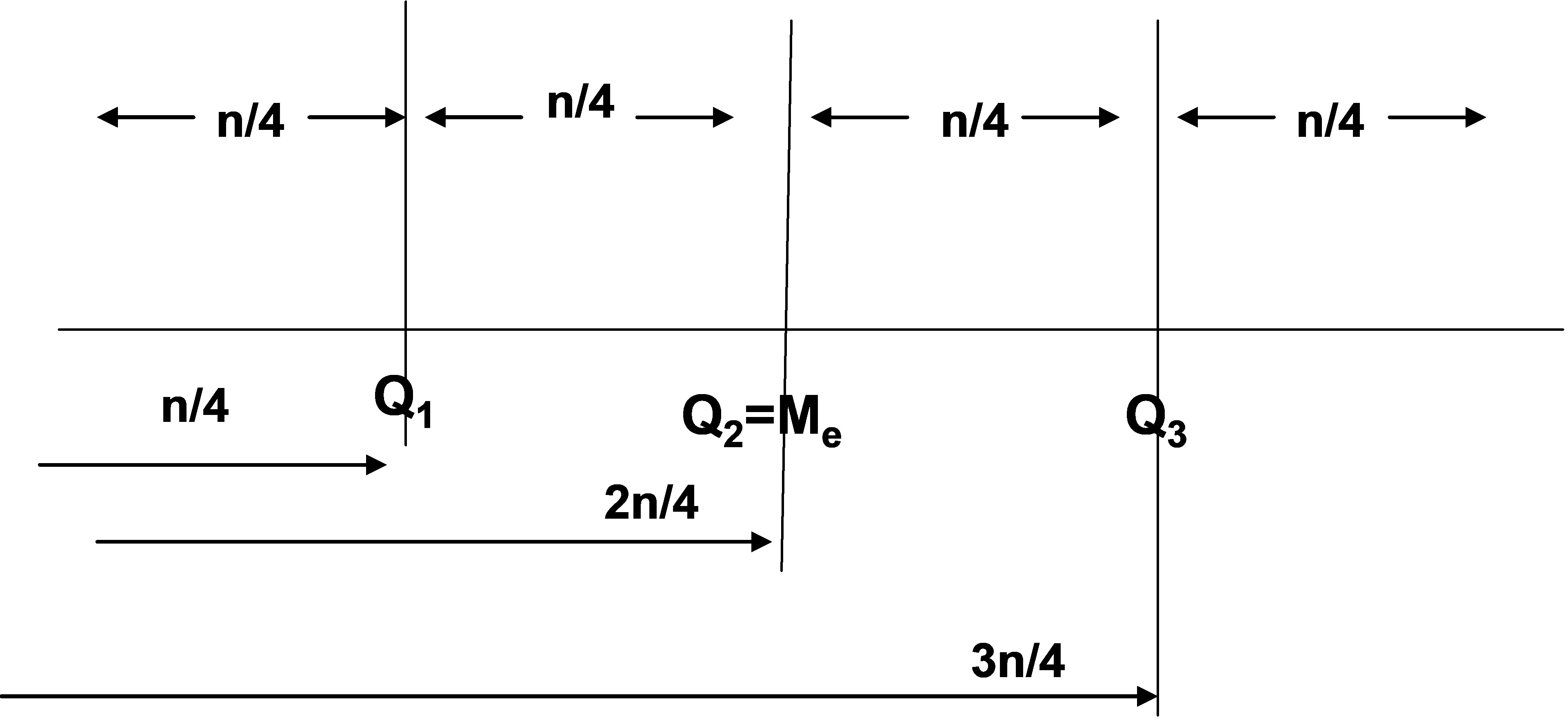 Figura 16: Representación de los Cuartiles en la recta real
Figura 16: Representación de los Cuartiles en la recta real
∗ Deciles
Dividen a los elementos de la población en diez intervalos con igual número de observaciones. Se denotan por: \( D_1 \) , \( D_2 \) , … \( D_9 \).
\( D_{i} = P_{10i}; \hspace {10mm } i=1,2,⋯,9 \).
El cálculo de los percentiles se efectúa siguiendo el mismo procedimiento que en la mediana, cambiando n/2 por nk/100.
Variable estadística discreta
∗ El valor \( n_{\alpha}=nk/100 \) se encuentra entre dos valores de la frecuencia absoluta acumulada, es decir: \( N_{i-1}<n_{α}<N_{i} \). En este caso se toma como percentil el valor de la variable estadística que corresponde a \( N_{i} \), es decir: \( P_{k}=x_{i} \).
Ejemplo: Calcular el primer cuartil y el tercer cuartil del ejemplo 1.7
\( \begin{matrix} \hline x_i & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline n_i & 6 & 20 & 28 & 12 & 8 & 6 \\ \hline N_{i} & 6 & 26 & 54 & 66 & 74 & 80
\\ \hline \end{matrix} \)
Respuesta:
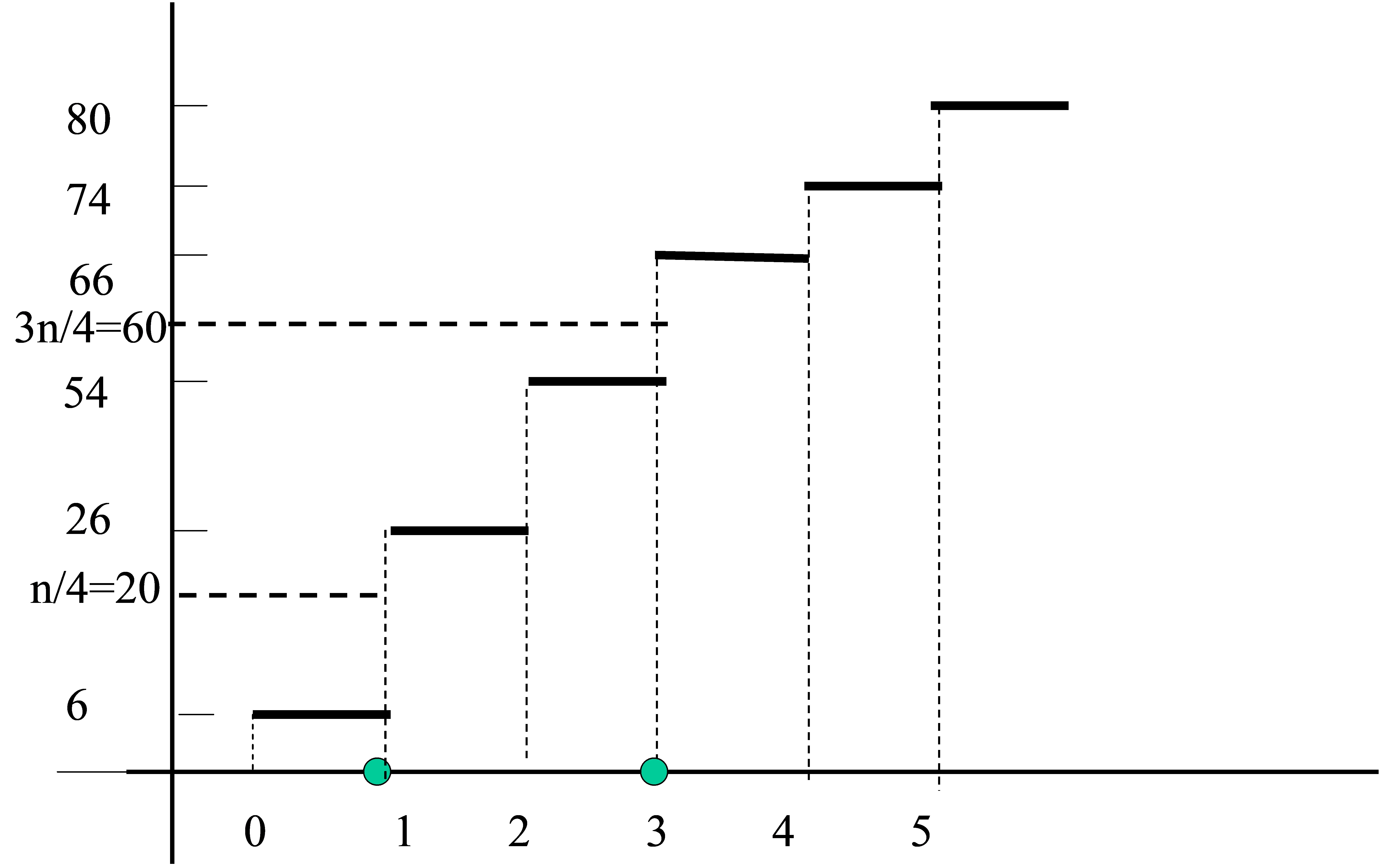 Figura 17: Cálculo gráfico del primer y tercer cuartil en una variable estadística discreta
Figura 17: Cálculo gráfico del primer y tercer cuartil en una variable estadística discreta
\( \begin{matrix} n/4 =80/4=20 \\
N_{i-1}<n/4<N_{i}; \hspace {5mm } 6<20<26 \\
Q_1=x_{i}⇒Q_1=1\\ & \\ (3n)/4=(3×80)/4=60 \\ \end{matrix} \)
\( \begin{matrix} N_{i-1}<3n/4<N_{i}; \hspace {5mm } 54<60<66 \\
Q_3=x_{i}⇒Q_3=3 \\ \end{matrix} \)
* El valor \( n_{α} \) coincide con una frecuencia absoluta acumulada, es decir \( n_{α}=N_{i} \). En este caso, (estamos ante una situación similar al caso de un número par de observaciones), el percentil está indeterminado entre los valores \( x_{i} \) y \( x_{i+1}\).
Ejemplo 1.14: Calcular el tercer cuartil de la siguiente distribución
\( \begin{matrix} \hline x_i & 15 & 25 & 35 & 45 & 55 & 65 \\ \hline n_i & 6 & 20 & 34 & 6 & 8 & 6 \\ \hline N_{i} & 6 & 26 & 60 & 66 & 74 & 80
\\ \hline \end{matrix} \)
Respuesta:
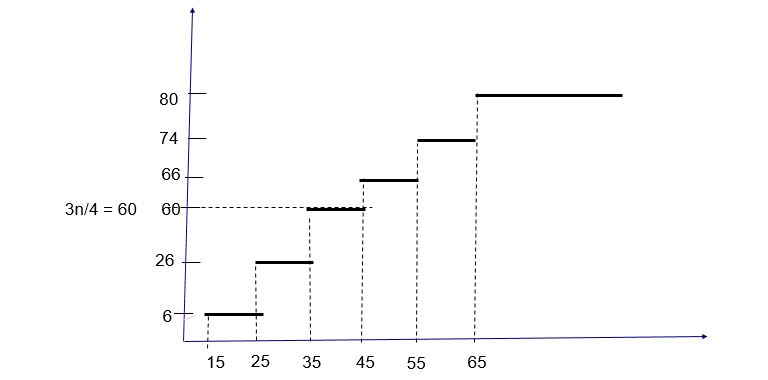 Figura 18: Cálculo gráfico del tercer cuartil en una variable estadística discreta
Figura 18: Cálculo gráfico del tercer cuartil en una variable estadística discreta
\( \displaystyle \frac{3n}{4} = \displaystyle \frac{3×80}{4} = 60 ; \hspace{2cm} \displaystyle \frac{3n}{4} = 60 = N_i \)
Q₃ está indeterminado entre 35 y 45
Variable estadística continua
∗ El valor \( n_{α}=nk/100 \) se encuentra entre dos valores de la frecuencia absoluta acumulada, es decir: \( N_{i-1}<n_{α}<N_{i} \). El percentil se obtiene, como en la mediana, interpolando.
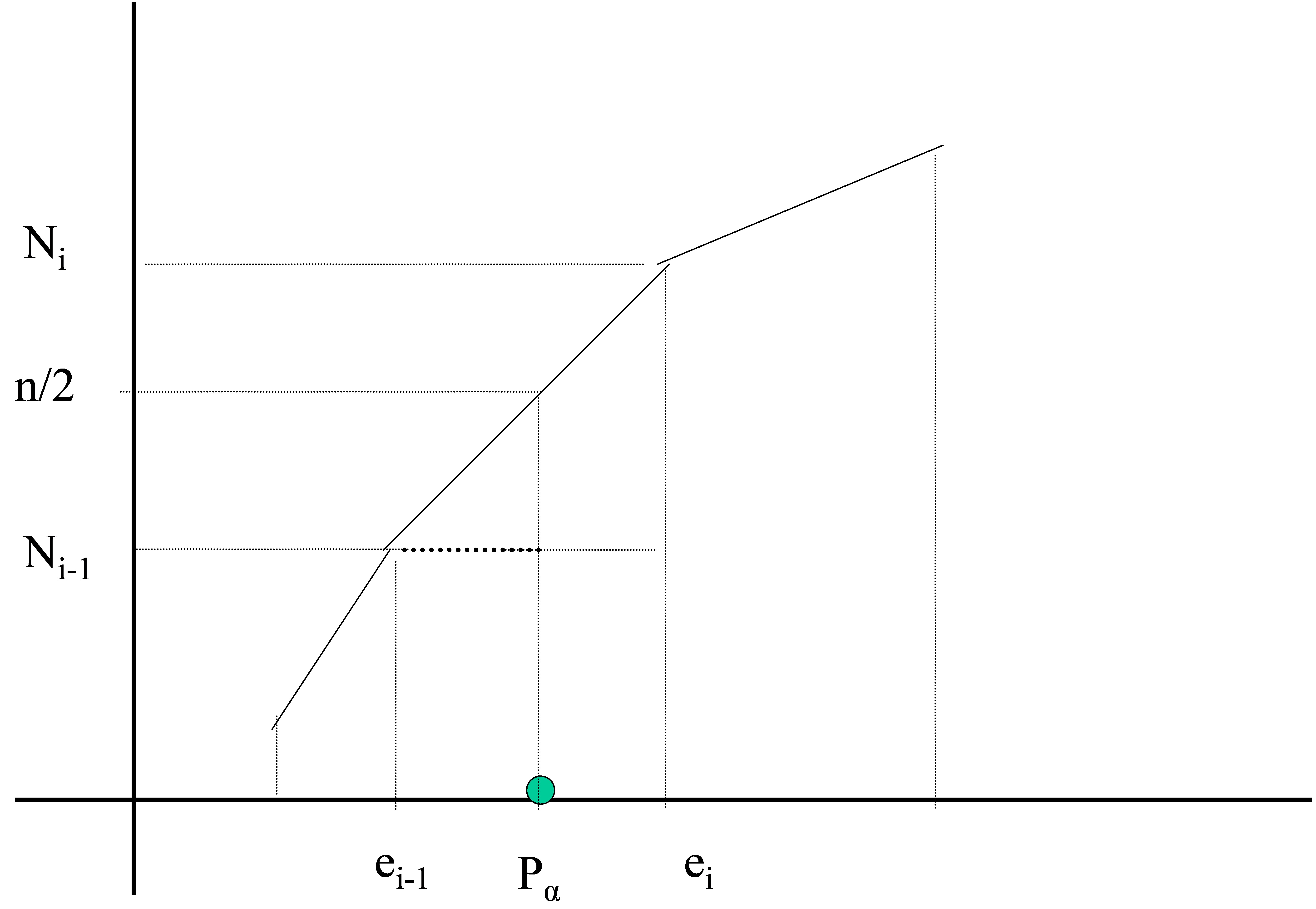 Figura 19: Cálculo gráfico de los percentiles en una variable estadística continua
Figura 19: Cálculo gráfico de los percentiles en una variable estadística continua
\( \begin{matrix} e_{i}-e_{i-1}→N_{i}-N_{i-1 } \\ P_{k}-e_{i-1}→n_{α}-N_{i-1} \\ \end{matrix} \) \( \hspace{1cm}\)
\( P_{k}=e_{i-1}+ \displaystyle \frac{\displaystyle \frac{nk}{100} – N_{i-1}}{N_{i}-N_{i-1} } (e_{i}-e_{i-1}) \)
Ejemplo: En el ejemplo 1.8 calcular el percentil 60
\( \begin{array}{||l|c|c|c|c|c||} \hline {\bf Tamaño \hspace {1mm } familias} & 0-2 & 2-4 & 4-5 & 6-8 & 8-10 \\ \hline
n_i & 110 & 200 & 90 & 75 & 25 \\ \hline
N_{i} & 110 & 310 & 400 & 475 & 500 \\ \hline
\end{array} \)
Respuesta:
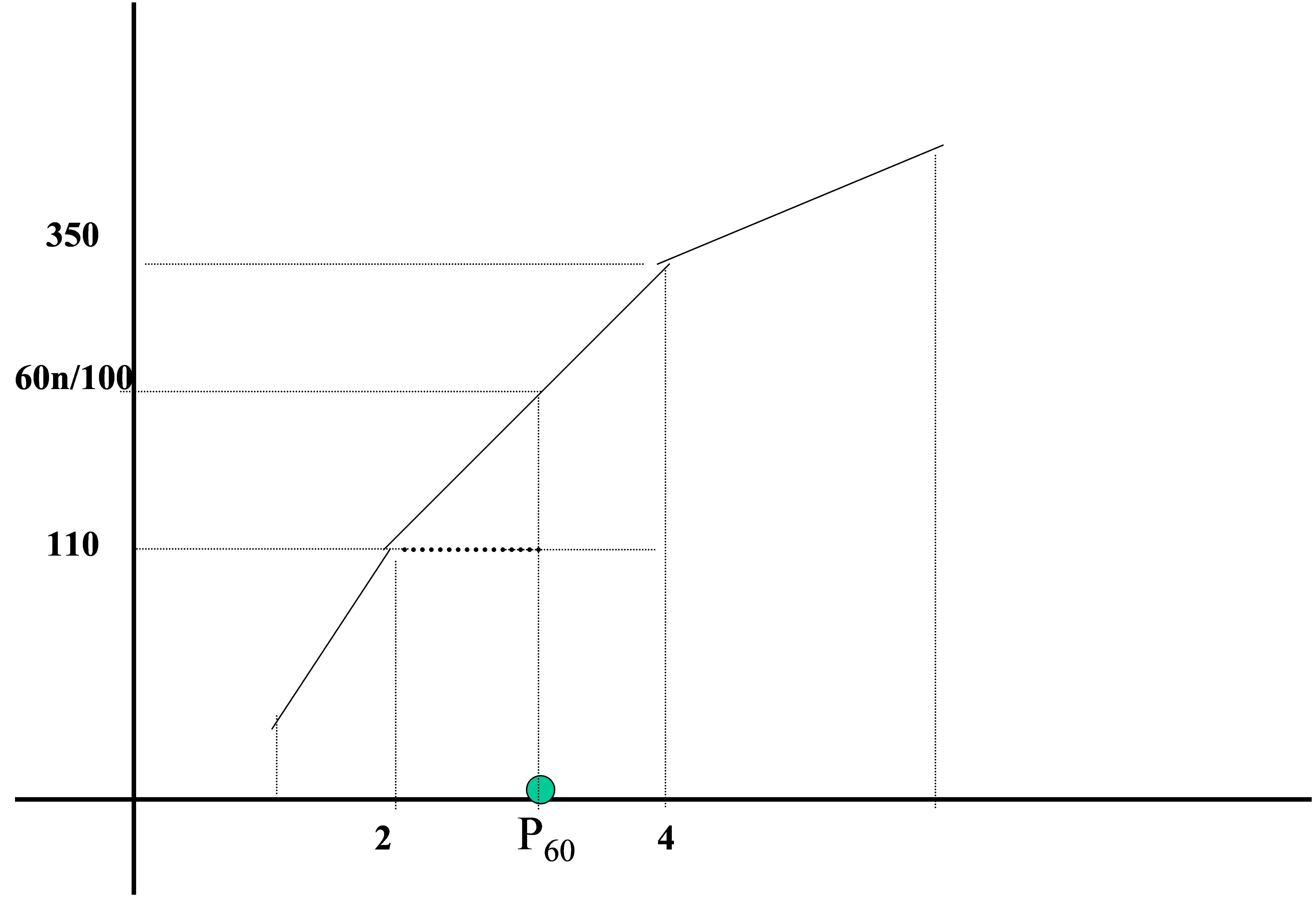 Figura 20: Cálculo gráfico del percentil 60 en una variable estadística continua
Figura 20: Cálculo gráfico del percentil 60 en una variable estadística continua
El intervalo es: (2 , 4)⇒
\( P_{60} = e_{i-1}+ \displaystyle \frac{ (60n/100) – N_{i-1}}{N_i – N_ {i-1}} (e_{i}-e_{i-1}) =2 + \displaystyle \frac{300 – 110}{310 – 110}(4-2)=3.9 \)
∗ El valor \( n_{α}=nk/100 \) coincide con una frecuencia absoluta acumulada, es decir \( n_{α}=N_{i} \). Entonces \( P_{k}=e_{i} \). En efecto
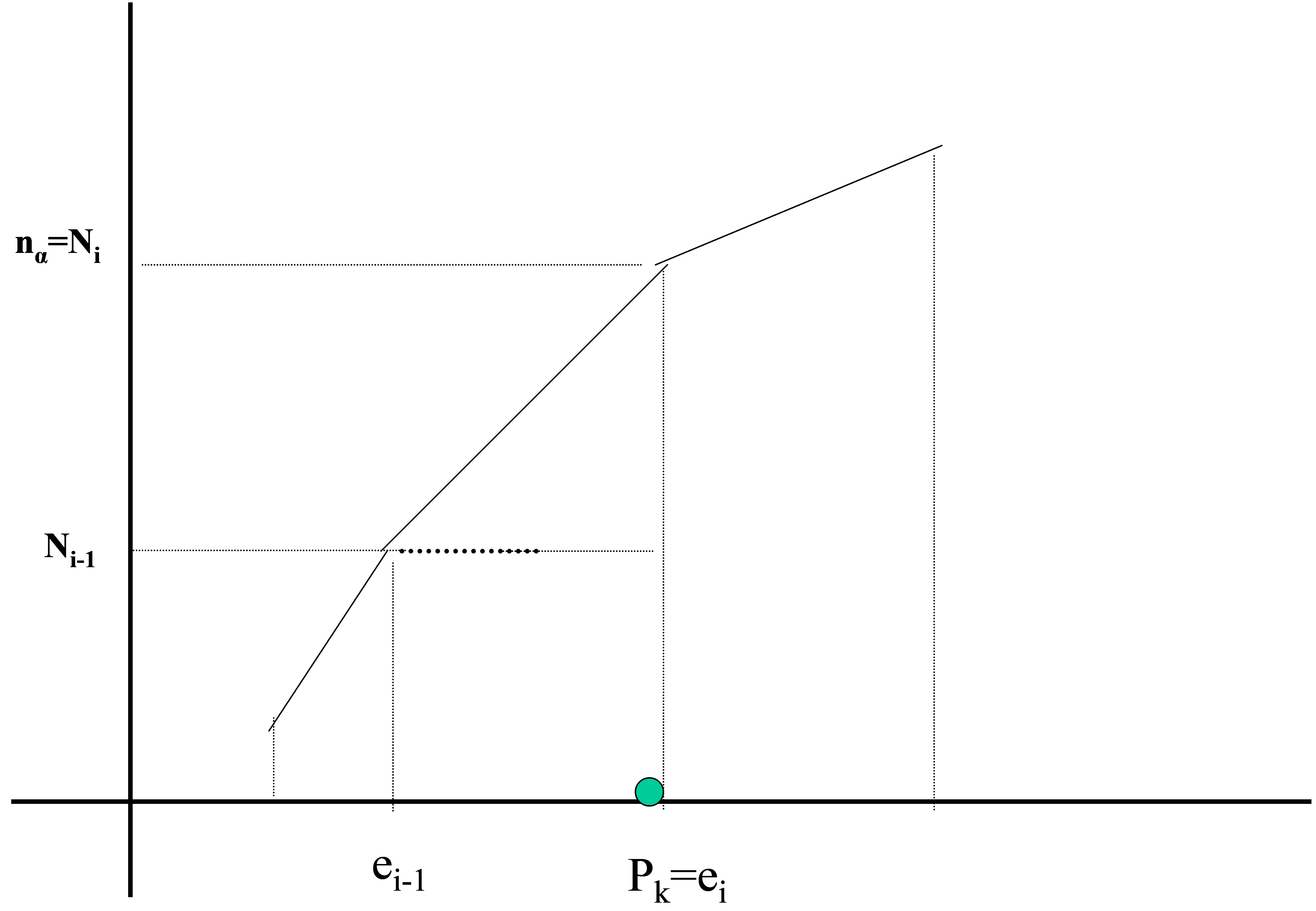 Figura 21: Cálculo gráfico de los percentiles en una variable estadística continua
Figura 21: Cálculo gráfico de los percentiles en una variable estadística continua
\( P_{k}=e_{i-1} + \displaystyle \frac{n_{α}-N_{i-1}}{N_{i}-N_{i-1} } (e_{i}-e_{i-1}) = e_{i-1} + \displaystyle \frac{N_{i}-N_{i-1}}{N_{i}-N_{i-1}} (e_{i}-e_{i-1}) = e_{i} \)
Ejemplo: En el ejemplo 1.9 calcular el percentil 90
\( \begin{array}{||l|c|c|c|c|c||} \hline e_{i-1}-e_{i} & 20-30 & 30-100 & 100-500 & 500-600 & 600-1000 \\ \hline
n_{i} & 20 & 30 & 10 & 30 & 10 \\ \hline
N_{i} & 20 & 50 & 60 & 90 & 100 \\ \hline
\end{array} \)
Respuesta:
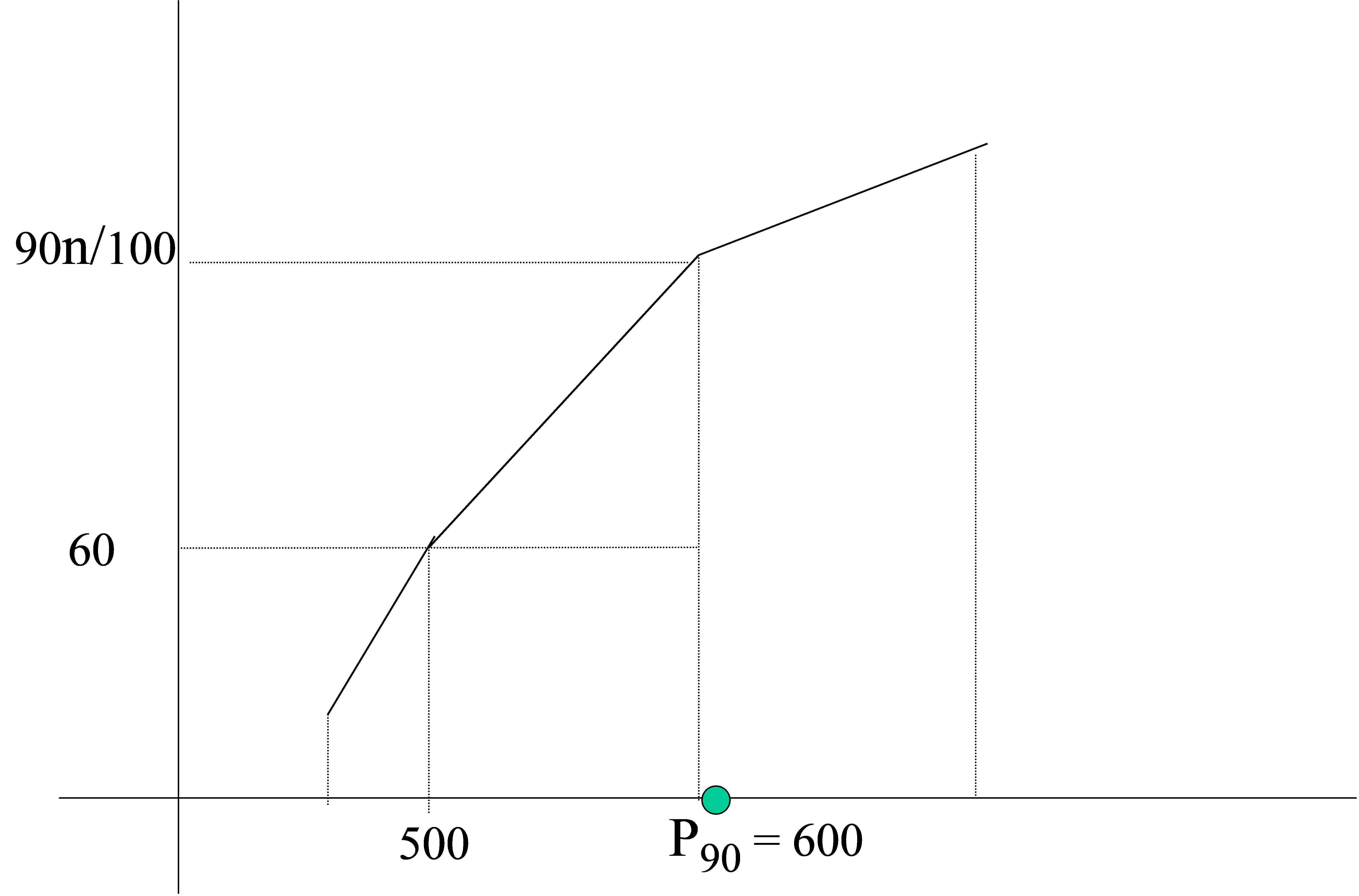 Figura 22: Cálculo gráfico del percentil 90 en una variable estadística continua
Figura 22: Cálculo gráfico del percentil 90 en una variable estadística continua
El intervalo es: (500 , 600)⇒
\( P_{90}=e_{i-1}+ \displaystyle \frac { \displaystyle \frac {90n}{100} – N_{i-1}} {N_{i}-N_{i-1}}(e_{i}-e_{i-1}) = 500 + \displaystyle \frac{90-60}{90-60} (600-500)=600 \)
Medidas de dispersión
Las medidas de dispersión tratan de cuantificar la variabilidad o esparcimiento de un conjunto de observaciones informando acerca de la mayor o menor representatividad de las medidas de tendencia central.
Presentamos únicamente las medidas de dispersión más comunes: Rango o Recorrido, Recorrido intercuartílico, Desviación absoluta media, Varianza, Desviación típica y Coeficiente de variación.
Rango o Recorrido
Se define el Rango o Recorrido, que se denota por R, como la diferencia entre el mayor y el menor valor de la variable estadística.
\( R = x_{n}-x_1 \)
Recorrido intercuartílico
Se define el Recorrido intercuartílico, que se denota por \( R_{I} \) , como la diferencia entre el tercer cuartil y el primer cuartil.
\( R_{I}=Q_3 – Q_1 \)
Desviación absoluta media
Se define la Desviación absoluta media respecto de un valor \( p \) , y se denota por \( D_{M} \), como la media aritmética de las desviaciones en valor absoluto entre los valores de la variable estadística y \( p \)
\( D_{M}= \sum_{i=1}^{k}f_{i}∣ x_{i}-p ∣ \)
- Si \( p \) es la Mediana, entonces se denomina Desviación absoluta media respecto de la Mediana y se representa por \( D_{M_{e}} \)
\( D_{M_{e}}= \sum_{i=1}^{k} f_{i}∣x_{i}-M_{e}∣ \)
- Si \( p \) es la Media, entonces se denomina Desviación absoluta media respecto de la Media y se representa por \( D_{\bar {x}} \)
\( D_{\bar {x}}=\sum_{i=1}^{k}f_{i}∣x_{i}- \bar {x}∣ \)
Ejemplo: En el ejemplo 1.7 calcular el recorrido, recorrido intercuartílico, la desviación absoluta media respecto de la mediana y respecto de la media.
\( \begin{array}{||l|c|c|c||} \hline x_i & n_{i} & n_i | x_i – M_e| & n_{i}∣x_{i}-\bar {x}∣ \\ \hline
0 & 6 & 12 & 13.056 \\ \hline
1 & 20 & 20 & 23.500 \\ \hline 2 & 28 & 0 & 4.900 \\ \hline
3 & 12 & 12 & 9.900 \\ \hline
4 & 8 & 16 & 14.600 \\ \hline
5 & 6 & 18 & 16.950 \\ \hline
& 80 & 78 & 82.906 \\ \hline \end{array} \)
\( \begin{matrix} \bar {x} =2.175 \hspace {5mm } M_{e}=2 \hspace {5mm } Q_1=1 \hspace {5mm } Q_3=3 \\ & \\ R=x_{n}-x_1= 5-0 = 5 \\ & \\ R_{I}=Q_3-Q_1= 3 – 1 = 2 \end{matrix} \)
\( D_{M_{e}}= \sum_{i=1}^{6 } \displaystyle \frac{n_{i}}{n} ∣x_{i}-M_{e}∣= \displaystyle \frac{78}{80}=0.975 \)
\( D_{\bar {x}}=\sum_{i=1}^{6} \displaystyle \frac{n_{i}}{n}∣x_{i}-\bar {x}∣ = \displaystyle \frac{82.906}{80}=1.036 \)
Varianza
Se define la Varianza, y se denota por \( σ^{2}\), como la media aritmética de los cuadrados de las desviaciones entre los valores de la variable estadística y la media aritmética
\( σ^{2} = \sum_{i=1}^{k}f_{i}(x_{i}-\bar{x})^2 = \sum_{i=1}^{k} \displaystyle \frac{n_{i}}{n}(x_{i}- \bar{x})^2 \)
La varianza también se puede expresar de la siguiente forma
\( σ^{2} = \sum_{i=1}^{k}f_{i}(x_{i}- \bar{x})^2 = \sum_{i=1}^{k}f_{i}(x_{i}^2+\bar{x}^2 -2x_{i}\bar{x}) = \sum_{i=1}^{k}f_{i}x_{i}^2 + \bar{x} ^2 \sum_{i=1}^{k}f_{i}-2\bar{x} \sum_{i=1}^{k}f_{i}x_{i}= \)
\( = \sum_{i=1}^{k}f_{i}x_{i}^2+\bar{x} ^2-2\bar{x}^2 = \sum_{i=1}^{k}f_{i}x_{i}^2-\bar{x}^2 \)
que se conoce como el Teorema de König.
Cálculo abreviado de la varianza: Con objeto de simplificar el cálculo de la varianza se puede realizar un cambio de origen y escala. Utilizando el mismo cambio de variable que el realizado para el cálculo abreviado de la media aritmética, se tiene
\( σ^{´2} = \displaystyle \sum_{i=1}^{k}f_{i}(x_{i}′-\bar{x}′)^2= \displaystyle \sum_{i=1}^{k}f_{i}( \displaystyle \frac{x_{i}-x_0}{a} – \displaystyle \frac{\bar{x}-x_0}{a})^2 = \displaystyle \frac{1}{a^2} \sum_{i=1}^{k}f_{i}(x_{i}-\bar{x})^2= \displaystyle \frac{σ^2}{a^2}\)
Como puede observarse la varianza es invariante frente a los cambios de origen, sólo le afecta el cambio de escala al cuadrado.
Desviación típica
Se define la Desviación típica, y se denota por \( σ \), como la raíz cuadrada positiva de la varianza.
\( σ=+ \sqrt{ \displaystyle \sum _{i=1}^{k}f_{i}(x_{i}-\bar{x})^2} = + \sqrt{ \displaystyle \sum_{i=1}^{k} \displaystyle \frac {n_i}{n}(x_{i}-\bar{x} )^2 }\)
El cambio de origen y escala anterior le afecta a la desviación típica de la siguiente forma: \( σ′=σ/a \).
Ejemplo: En el ejemplo 1.7 calcular la varianza y la desviación típica.
\( \begin{array}{||l|l|l|l||} \hline x_i & n_{i} & \sum n_i x_i & \sum n_{i} x_{i}^2 \\ \hline
0 & 6 & 0 & 0 \\ \hline
1 & 20 & 20 & 20 \\ \hline 2 & 28 & 56 & 112 \\ \hline
3 & 12 & 36 & 108 \\ \hline
4 & 8 & 32 & 128 \\ \hline
5 & 6 & 30 & 150 \\ \hline
& 80 & 174 & 519 \\ \hline \end{array} \) \( \begin{matrix}\bar{x}=2.175 \\ & \\ σ^2 = \displaystyle \frac{518}{80}-(2.175)^2=1.744 \\ & \\ σ=+ \sqrt{1.744}=1.320 \\ \end{matrix} \)
Ejemplo: En el ejemplo 1.9 calcular la varianza y la desviación típica efectuando un cambio de origen y escala.
\( \begin{array}{||l|c|c|c|c|c||} \hline e_{i-1}-e_{i} & n_{i} & x_{i} & x_{i}^′= \displaystyle \frac{x_i – 300}{5} & n_{i}x_{i}^′ & n_{i}x_{i}^{′2} \\ \hline
20-30 & 20 & 25 & -55 & -1100 & 60500 \\ \hline
30-100 & 30 & 65 & -47 & -1410 & 66270 \\ \hline
100-500 & 10 & 300 & 0 & 0 & 0 \\ \hline
500-600 & 30 & 550 & 50 & 1500 & 75000 \\ \hline
600-1000 & 10 & 800 & 100 & 1000 & 100000 \\ \hline
& 100 & & & -10 & 3017700 \\ \hline \end{array} \)
\( σ^{′2}=\sum_{i=1}^5 \displaystyle \frac{n_{i}x_{i}^{′2}}{n}- \bar{x}^{′2}= \displaystyle \frac{301770}{100}-(-0.1)^2 = 3017.69 \)
Por lo tanto
\( σ^{2}=a^2σ^{′2}=5^2×3017.69=75442.25; \hspace{5 mm} σ=aσ^′=5 \sqrt{3017.69}=274.66 \)
Coeficiente de variación de Pearson
Las medidas de centralización y dispersión nos dan información sobre una muestra, pero ¿tiene sentido utilizar estas medidas para comparar dos poblaciones? Por ejemplo, sí queremos comparar la dispersión de las estaturas de dos poblaciones diferentes, la desviación típica nos proporcionará información útil. ¿Pero qué ocurre si queremos comparar la estatura con respecto al peso? Comparar una medida en metros con otra en kilogramos no tiene ningún sentido.
Los problemas surgen cuando se quiere comparar dos poblaciones con distintas unidades de medidas, el Coeficiente de variación de Pearson nos permite evitar estos problemas, es un coeficiente adimensional, elimina la dimensionalidad de las variables y tiene en cuenta la proporción existente entre media y desviación típica.
Se define el Coeficiente de variación de Pearson, y se denota por CV, como el cociente entre la desviación típica y la media aritmética,
\( CV= \displaystyle \frac{σ}{|\bar{x}|} \)
se utiliza para comparar la variabilidad de un conjunto de datos con la de otro, en situaciones en las que la comparación directa de desviaciones típicas no es conveniente o suficientemente realista o en ocasiones en que los conjuntos de datos vienen expresados en unidades distintas.
∗ No es invariante ante cambios de origen. Es decir, si a los resultados de una medida le sumamos una cantidad positiva, \( Y=X+b; (b>0) \) entonces \( CV_{Y} < CV_{X} \)
∗ Permanece invariante si se efectúa un cambio de escala, es una cantidad adimensional. El coeficiente de variación de una variable medida en kilómetros no cambia si la medición se hace en metros.
El coeficiente de variación representa el número de veces que la desviación típica contiene a la media aritmética, por tanto, cuanto mayor sea el coeficiente de variación significa que mayor número de veces contiene la desviación típica a la media aritmética y por lo tanto la media aritmética es menos representativa.
- Si \( \bar{x}<σ ⇒ \) la media no tendrá representatividad
- Si \( σ=0⇒CV=0 ⇒ \) la máxima representatividad de la media \( ⇒ \) No hay dispersión
- Si \( \bar{x} = 0 \) este coeficiente no se puede utilizar.
Es un coeficiente muy utilizado en Biología para comparar la variabilidad de las dimensiones de ciertos órganos en distintas clases de animales. Por ejemplo, si la media de las longitudes de las alas de una muestra de águilas es igual a 1.30 m, y la desviación típica es de 0.20 m, mientras que la media y la desviación típica de las alas de una muestra de colibríes son iguales a 0.05 m y 0.01 m, respectivamente. A primera vista parece que las dimensiones de las alas de las águilas son más dispersas, \( σ=0.20 \), que las alas de los colibríes, \( σ^{´}=0.01 \); pero si calculamos los coeficientes de variabilidad relativa, es decir los coeficientes de variación de Pearson, se obtiene:
\( CV_{Aguilas}= \displaystyle \frac{0.20}{1.30}=0.154; \hspace{5mm} CV_{Colibríes}= \displaystyle \frac{0.01}{0.05}=0.20 \)
que pone de manifiesto que la variabilidad relativa es más alta (0.20) en las alas de los colibríes que en las alas de las águilas.
Ejemplo 1.15: En un Instituto se ha aplicado el mismo test de inteligencia a dos grupos de alumnos y se han obtenido los siguientes resultados:
\( \begin{matrix} Grupo A: \bar{x} = 30; \hspace {5mm} σ = 6 \\ & \\ Grupo B: \bar{x} = 62; \hspace{5mm} σ =9 \\ \end{matrix} \)
¿En qué grupo hay mayor dispersión?
Respuesta:
Observando los resultados, una respuesta rápida sería que en el Grupo B hay mayor dispersión ya que la desviación típica es mayor. Veámoslo
\( CV_{A}= \displaystyle \frac{6}{30}=0.2; \hspace{5mm} CV_{B}= \displaystyle \frac{9}{62}=0.145 \)
Los resultados de los coeficientes de variación nos muestran que hay mayor dispersión en el Grupo A ya que el coeficiente de variación es mayor que el del Grupo B.
Tipificación
Recibe el nombre de Tipificación al proceso de restarle la media \( \bar{x} \) a la v.e. X y dividir esta diferencia por la desviación típica σ. La nueva variable obtenida, se denota por Z, y se caracteriza por tener de media 0 \( (\bar{z} = 0 ) \) y desviación típica 1 \( (σ_{Z}=1) \)
\( Z= \displaystyle \frac{X – \bar{x}}{σ } \)
Esta nueva variable es una cantidad adimensional y permite comparar:
- Dos medidas, expresadas en unidades distintas, en una misma población. Por ejemplo, comparar los pesos y las tallas de una población
- Individuos semejantes de poblaciones diferentes. Por ejemplo, si deseamos comparar el nivel académico de dos estudiantes de diferentes Universidades, se debe tener en cuenta que la dificultad para conseguir una buena calificación puede ser mayor en un centro que en el otro por lo que comparar únicamente las medias de ambos estudiantes no sería correcto. En este caso se debe comparar las calificaciones de ambos, pero tipificadas cada una de ellas por las medias y las desviaciones típicas.
Observaciones:
- Los coeficientes de variación se utilizan para comparar las variabilidades de dos conjuntos de valores (muestras o poblaciones)
- Los valores tipificados se utilizan para comparar dos medidas en una misma población y dos individuos semejantes en poblaciones diferentes.
Momentos
Los Momentos son unos valores, medidas numéricas, que caracterizan la distribución de frecuencias y resumen la información recogida en la tabla estadística respecto a alguna propiedad de la variable estadística.
A continuación, veremos que algunas características de tendencia central y dispersión, como la media y la varianza, son casos particulares de momentos.
Distinguiremos entre dos tipos de momentos: Momentos no-centrales o respecto del origen y Momentos centrales o respecto de la media.
Momentos no-centrales o respecto del origen
Se definen los Momentos no-centrales de orden r o Momentos de orden r respecto del origen, y se denotan por \( m_{r} \), como
\( m_{r}=\sum_{i=1}^{k}f_{i}x_{i}^{r}=\sum_{i=1}^{k} \displaystyle \frac{n_{i}}{n}x_{i}^{r} \)
Casos particulares:
- Si \( r = 0 \Rightarrow m_0 = \sum_{i=1}^{k}f_{i}x_{i}^0 =1\)
- Si \( r= 1 \Rightarrow m_1=\sum_{i=1}^{k}f_{i}x_{i}^1=\bar{x} \)
- Si \( r = 2 \Rightarrow m_2 = \sum_{i=1}^{k}f_{i}x_{i}^2 \Rightarrow σ^2=m_2-m_1^2 \)
Momentos centrales o respecto de la media
Se definen los Momentos centrales de orden r o Momentos de orden r respecto de la media, y se denotan por \( μ_{r}\), como
\( μ_{r}=∑_{i=1}^{k}f_{i}(x_{i}-\bar{x})^{r}=∑_{i=1}^{k}\displaystyle \frac{n_{i}}{n}(x_{i}- \bar{x})^{r}\)
Casos particulares:
- Si \( r = 0 \Rightarrow μ_0=\sum_{i=1}^{k}f_{i}(x_{i}- \bar{x})^0=1 \)
- Si \( r =1 \Rightarrow μ_1=\sum_{i=1}^{k}f_{i}(x_{i}- \bar{x})^1 = \sum_{i=1}^{k}f_{i}x_{i}-\bar{x} \sum_{i=1}^{k}f_{i}=\bar{x} – \bar{x} =0 \)
- Si \( r = 2 \Rightarrow μ_2=\sum_{i=1}^{k}f_{i}(x_{i}-\bar{x})^2=σ^2 \)
Relación entre los momentos centrales y no-centrales
Los momentos centrales y los no-centrales están relacionados mediante la siguiente expresión:
\( μ_{r}=\sum_{t=0}^{r}(-1)^{t} {r\choose t}m_1^{t}m_{r-t} \)
En efecto
\( μ_{r} = \sum_{i=1}^{k}f_{i}(x_{i}-\bar{x})^{r}= \)
\( = \sum_{i=1}^{k}f_{i}(x_{i}-m_1)^{r}= \sum_{i=1}^{k}f_{i}[ {r\choose 0}x_{i}^{r}m_1^0 {r\choose 1}x_{i}^{r-1}m_1^1+ {r\choose 2}x_{i}^{r-2}m_1^2 -⋯± {r\choose r}m_1^{r}] = \)
\( = \sum_{i=1}^{k}f_{i}\sum_{t=0}^{r}(-1)^{t} {r\choose t}m_1^{t}x_{i}^{r-t}=\sum_{t=0}^{r}(-1)^{t} {r\choose t}m₁^{t}\sum_{i=1}^{k}f_{i}x_{i}^{r-t}= \sum_{t=0}^{k}(-1)^{t} {r\choose t}_1^{t}m_{r-t} \)
Cálculo abreviado de los momentos: Con objeto de simplificar el cálculo de los momentos centrales se puede realizar un cambio de origen y escala. Utilizando el mismo cambio de variable que el realizado para el cálculo abreviado de la media aritmética y de la varianza, se tiene
\( μ_{r}^′ = \displaystyle \sum_{i=1}^{k}f_{i}(x_{i}^′-x^′)^{r}= \displaystyle \sum_{i=1}^{k}f_{i} ( \displaystyle \frac{x_i-x_0}{a}- \displaystyle \frac{\bar{x}-x_0}{a})^{r}= \displaystyle \frac{1}{a^{r}}\sum_{i=1}^{k}f_{i}(x_{i}- \bar{x})^{r}= \displaystyle \frac {μ_{r}}{a^{r}} \)
Como puede observarse los momentos centrales de orden r son invariantes frente a los cambios de origen, sólo les afecta el cambio de escala elevado a r.
Comentario. La transformación, mediante un cambio de origen y escala, de los momentos no-centrales, excepto el caso de la media, tiene una expresión complicada por lo que en la práctica no se suele utilizar.
Ejemplo: En el ejemplo 1.7 calcular los momentos centrales y no-centrales de orden tres.
\( \begin{array}{||l|l|l|l||} \hline x_{i} & n_{i} & \sum n_{i}(x_i-\bar{x})^3 & \sum n_{i}x_{i}^3 \\ \hline 0 & 6 & -61.73 & 0 \\ \hline 1 & 20 & -32.44 & 20 \\ \hline 2 & 28 & -0.15 & 224 \\ \hline 3 & 12 & 6.73 & 324 \\ \hline 4 & 8 & 48.62 & 512 \\ \hline 5 & 6 & 135.27 & 750 \\ \hline & 80 & 96.30 & 1830 \\ \hline \end{array} \)\(
\begin{matrix} \bar{x} =2.175 \\ & \\ μ_3=\sum_{i=1}^6 \displaystyle \frac{n_{i}}{n} (x_{i}-\bar{x})^3= \displaystyle \frac{96.30}{80}=1.20 \\ & \\ m_3=\sum_{i=1}^6 \displaystyle \frac{n_{i}}{n} x_{i}^3= \displaystyle \frac{1830}{80}=22.875 \\ \end{matrix} \)
En las secciones anteriores hemos sintetizado la información de una distribución de frecuencias mediante medidas de posición y de dispersión. Es decir, hemos calculado los valores alrededor de los cuales se distribuyen las observaciones y la dispersión de dichos valores respecto a un valor central. Del análisis de los datos se pueden obtener otras muchas medidas que resumen características del fenómeno en estudio. En esta sección nos proponemos avanzar más en el análisis de los datos. En primer lugar, vamos a comprobar si los datos se distribuyen de forma simétrica con respecto a un valor central y una vez que hemos determinado su simetría estudiaremos si la curva es más o menos apuntada. Para medir este apuntamiento tendremos que compararlo con una cierta distribución de frecuencias que consideraremos Normal.
Medidas de asimetría
Una distribución de frecuencias decimos que es simétrica cuando lo es su representación gráfica respecto al eje vertical o equivalentemente cuando son iguales las frecuencias correspondientes a valores de la variable equidistantes de un punto central. Dicho eje vertical o dicho punto central en el caso de:
⋄ Variables discretas es la media \( (x= \bar{x}) \)
⋄ Variables continuas es la mediana \( (x=Me) \). (La mediana es la medida que divide al histograma de frecuencias en dos partes de igual área).
Si la distribución es simétrica coinciden la media, la mediana y la moda \( (x=Me=Mo) \). (En el caso de distribuciones bimodales o con más de una moda sólo coinciden la media y la mediana).
Cuando no hay simetría se dice que la distribución es asimétrica, entre los tipos de asimetría posibles los dos fundamentales son:
- Asimetría positiva o a la derecha: Mayor desplazamiento de las observaciones hacía la derecha (las frecuencias más altas se encuentran en el lado izquierdo de la media y las más bajas en el lado derecho)
- Asimetría negativa o a la izquierda: Mayor desplazamiento de las observaciones hacía la izquierda (la cola de la distribución está a la izquierda)
Para interpretar la asimetría de una distribución se utilizan una serie de coeficientes entre los que destacamos el Coeficiente de asimetría de Pearson y el Coeficiente de asimetría de Fisher
Coeficiente de asimetría de Pearson
Se define el Coeficiente de asimetría de Pearson, y se denota por \( A_{p} \), como el siguiente cociente
\( A_{p}= \displaystyle \frac {\bar{x}-Mo} {σ} \)
Es un coeficiente adimensional por lo que se puede utilizar para comparar el grado de asimetría de variables medidas en distintas unidades correspondientes a poblaciones distintas.
- \( A_{p}=0 \) : Distribuciones unimodales y simétricas ya que \( \bar{x}=Mo \)
- \( A_{p}>0 \) : Distribuciones asimétricas positivas. La media como representante del comportamiento global de la variable se desplazará, como las observaciones, hacía la derecha y por tanto \( \bar{x} >Mo \Rightarrow A_{p}>0 \)
- \( A_{p}<0 \): Distribuciones asimétricas negativas. La media se desplazará hacía la izquierda y por tanto \( \bar{x}<Mo \Rightarrow A_{p}<0 \)
En el coeficiente de asimetría de Pearson el signo del numerador es el que informa del tipo de asimetría, (la desviación típica es siempre positiva por definición). Por lo tanto, podría pensarse en definir este coeficiente como \( \bar{x}-Mo \) pero entonces no sería un coeficiente invariante frente a los cambios de origen y escala.
Este coeficiente de asimetría de Pearson no puede utilizarse en distribuciones con más de una moda, en este caso se utiliza un segundo coeficiente de asimetría de Pearson que se denota por \( A_{p}^{´}\) y se define como el cociente
\( A_{p}^{´}= \displaystyle \frac{3(\bar{x}-Me)}{σ} \)
Es un coeficiente, como el anterior, invariante frente a los cambios de origen y escala y diremos que hay asimetría positiva si \( A_{p}^{´}>0 \) y asimetría negativa si \( A_{p}^{´}<0 \) .
Coeficiente de asimetría de Fisher
Se define el Coeficiente de asimetría de Fisher, y se denota por \( γ_1 \) , como el siguiente cociente
\( γ_1= \displaystyle \frac{m_3}{σ^3} \)
Es un coeficiente adimensional e invariante ante los cambios de origen y de escala
- Si la distribución es simétrica: \( m_3=0 \Rightarrow γ_1=0 \)
- Si la distribución es asimétrica a la derecha: \( m_3 >0 \Rightarrow γ_1 >0 \)
- Si la distribución es asimétrica a la izquierda: \( m_3<0 \Rightarrow γ_1 < 0 \)
Medidas de apuntamiento o curtosis
La mayor o menor concentración de observaciones alrededor de la media dará lugar a una representación más o menos apuntada (larga y estrecha). Par medir el apuntamiento o curtosis es necesario referirlo a un apuntamiento de referencia. Este apuntamiento de referencia es el de la curva Normal. Diremos que una distribución es:
- Platicúrtica si es menos apuntada que la curva Normal
- Leptocúrtica si es más apuntada que la curva Normal
- Mesocúrtica si es tan apuntada como la curva Normal
Para medir el apuntamiento de una distribución se utiliza el Coeficiente de curtosis de Fisher
Coeficiente de curtosis de Fisher
Se define el Coeficiente de curtosis de Fisher, y se denota por \( γ_2 \) , como el siguiente cociente
\( γ_2 = \displaystyle \frac{m_4} {σ^4}-3 \)
Es un coeficiente adimensional e invariante ante los cambios de origen y de escala.
En la distribución Normal se verifica que
\( \displaystyle \frac{m_4} {σ^4}=3 \Rightarrow γ_2 = 0 \)
por lo tanto diremos que una distribución es:
- Platicúrtica si \( γ_2<0 \)
- Leptocúrtica si \( γ_2>0 \)
- Mesocúrtica si \( γ_2=0 \)
Ejercicios propuestos: Relación I
1. Se inició una investigación para averiguar el número de bacterias que aparecen en determinados cultivos. Para ello, se tomaron 40 de estos cultivos y se contó el número de bacterias, \( x_{i} \) , que aparecieron en cada uno de ellos.
\( \begin{matrix} \hline x_{i} & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
n_{i} & 1 & 12 & 22 & 34 & 26 & 14 & 0 \\ \hline \end{matrix} \)
a) Obtener las frecuencias relativas, relativas acumuladas y absolutas acumuladas
b) Representar la distribución de frecuencias absolutas
c) Porcentaje de valores menores o iguales a 3. (Sol. 62.38%)
d) Porcentaje de valores mayores que 5. (Sol. 0%).
2. Se ha desarrollado una nueva vacuna contra la difteria para aplicarla a niños. El nivel de protección estándar obtenidos por la antiguas vacuna era de 1 μg/mL, un mes después de la inmunización. Transcurrido un mes, se han obtenido estos datos del nivel de protección de la nueva vacuna:
\( \begin{matrix} \hline 12.5 & 13.8 & 13.0 & 13.5 & 13.2 \\ \hline
11.2 & 13.1 & 14.0 & 13.3 & 13.6 \\ \hline
12.6 & 14.1 & 14.6 & 13.2 & 13.1 \\ \hline
13.3 & 12.5 & 12.0 & 11.5 & 13.2 \\ \hline
13.7 & 12.0 & 12.8 & 13.2 & 12.7 \\ \hline \end{matrix} \)
Se pide:
a) Elaborar la muestra presentándola en forma de tabla de distribución de frecuencias
b) Dibujar el diagrama de barras de las frecuencias no acumuladas y acumuladas y los polígonos de frecuencias.
3. Completa los datos que aparecen en la siguiente distribución
\( \begin{array} {|l||c|c|c|c|c|c|c|} \hline x_{i} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline
n_{i} & 4 & 4 & & 7 & 5 & & 7 & \\ \hline
N_{i} & & & 16 & & 28 & 38 & 45 & \\ \hline
f_{i} & 0.08 & & 0.16 & 0.14 & & & 0.14 & \\ \hline \end{array} \)
4. En un estudio sobre el pH de la sangre de un grupo de personas adultas, se tomó una muestra de 50 de tales personas y mediante un análisis se obtuvieron los siguientes resultados:
\( \begin{matrix} \hline 7.40 & 7.41 & 7.40 & 7.39 & 7.42 & 7.42 & 7.43 & 7.42 & 7.41 & 7.40 \\ \hline
7.39 & 7.38 & 7.39 & 7.42 & 7.40 & 7.41 & 7.42 & 7.41 & 7.38 & 7.39 \\ \hline
7.43 & 7.41 & 7.40 & 7.43 & 7.41 & 7.40 & 7.40 & 7.43 & 7.41 & 7.43 \\ \hline
7.38 & 7.39 & 7.41 & 7.39 & 7.38 & 7.43 & 7.41 & 7.39 & 7.40 & 7.40 \\ \hline
7.42 & 7.40 & 7.43 & 7.42 & 7.41 & 7.41 & 7.39 & 7.39 & 7.40 & 7.40 \\ \hline \end{matrix} \)
Se pide:
a) Construir la tabla completa de distribución de frecuencias
b) Dibujar el histograma, el polígono de frecuencias y la curva acumulativa (Supon-gamos que la variable está agrupada en intervalos de clase de amplitud 0.01, siendo las marcas de clase los valores dados de la variable
c) Hallar el porcentaje de personas con pH menor que 7.40. (Sol. 26%)
d) Hallar el porcentaje de personas con pH mayor que 7.41. (Sol. 28%)
e) Hallar el porcentaje de personas con pH comprendido entre 7.39 y 7.42, incluido el extremo inferior y excluido el superior. (Sol. 64%).
5. Para obtener información acerca del porcentaje de albúmina en el suero proteico de personas normales se analizaron muestras de 40 personas, entre 2 y 40 años de edad, con los siguientes resultados:
\( \begin{matrix} \hline 70.2 & 62.4 & 72.3 & 63.3 & 62.8 & 60.4 \\ \hline
73.4 & 72.4 & 68.4 & 67.0 & 70.1 & 69.4 \\ \hline
65.2 & 62.9 & 70.0 & 71.3 & 66.3 & 65.9 \\ \hline
68.3 & 70.2 & 70.7 & 67.5 & 65.0 & 70.4 \\ \hline
72.8 & 66.6 & 72.1 & 64.1 & 68.7 & 67.8 \\ \hline
66.1 & 69.1 & 71.9 & 73.5 & 65.5 & 66.4 \\ \hline
64.4 & 63.1 & 62.0 & 65.2 & & \\ \hline \end{matrix} \)
Se pide:
a) Suponiendo que un error del 0.5 % en el porcentaje de albúmina no es importante, agrupar las medidas de la muestra en intervalos de clase de amplitud igual a la unidad y organizar los datos de la muestra en una tabla completa de distribución de frecuencias: Extremos de los intervalos de clase, marcas de clase, frecuencias acumuladas, frecuencias relativas, frecuencias absolutas acumuladas y frecuencias relativas acumuladas
b) Hallar el tanto por ciento de personas cuyo porcentaje de albúmina en el suero proteico está comprendido entre el 62% y 72%. En este caso, como la variable es continua y está agrupada en intervalos de clase, es indiferente incluir o no estos valores. (Sol. 82.5%)
c) Hallar el % de personas de la muestra cuyo porcentaje de albúmina es superior al 72%. (Sol. 1.45 %)
d) Calcular la media, mediana, desviación absoluta media respecto de la media, varianza, desviación típica y el coeficiente de variación de Pearson.
(Sol.: \( \bar{x} =67.7; Me=67.62; D_{\bar{x}}=3.0125; σ^2=12.24; σ=3.49; CV=0.051 \)).
6. Se realiza un estudio con objeto de detectar las variables que constituyen el estrés en pacientes clínicos cardíacos. El estrés se midió mediante la puntuación de ansiedad de Hamilton. Estas marcas se encuentran en una escala de 1 a 25, donde el número 18 denota un estrés moderado y el 25, un estrés grave. Se trataba de comparar los dos grupos de pacientes. Se obtuvieron los siguientes datos.
Viven solos
\( \begin{matrix} \hline 8.6 & 9.1 & 9.3 & 9.6 \\ \hline
8.3 & 13.5 & 9.5 & 8.3 \\ \hline
10.2 & 11.0 & 10.3 & 9.4 \\ \hline
8.9 & 10.5 & 10.7 & 9.5 \\ \hline
14.3 & 11.7 & 12.3 & 8.5 \\ \hline \end{matrix} \)
Viven con otras personas
\( \begin{matrix} \hline 7.6 & 18.1 & 19.3 & 13.6 \\ \hline
14.3 & 16.5 & 19.5 & 15.3 \\ \hline
13.2 & 15.0 & 17.3 & 19.4 \\ \hline
18.9 & 13.5 & 14.7 & 19.5 \\ \hline
14.3 & 16.7 & 15.3 & 18.5 \\ \hline \end{matrix} \)
Se pide:
a) La media, mediana, moda, varianza y desviación típica de cada grupo
b) Coeficientes de variación de Pearson, asimetría de Fisher y apuntamiento de Fisher de cada grupo
c) La distribución de los datos en cada grupo ¿sugiere forma de campana?
d) ¿Alguna de estas distribuciones es sesgada? Si es así, ¿en qué dirección?
e) ¿Qué grupo tiende a tener una menor puntuación media de estrés?
7. En un parque natural se está realizando un estudio sobre el recorrido que realizan los pájaros. Para ello se estudió la distancia de vuelo desde el punto en que se soltó un pájaro recién anillado hasta su primera posada. Los siguientes datos corresponden a dos tipos de pájaros
Estorninos
\( \begin{matrix} \hline 108.6 & 119.1 & 99.3 & 109.6 \\ \hline
98.3 & 103.5 & 119.5 & 148.3 \\ \hline
120.2 & 131.0 & 140.3 & 89.4 \\ \hline
82.9 & 180.5 & 210.7 & 119.5 \\ \hline
134.3 & 101.7 & 132.3 & 208.5 \\ \hline \end{matrix} \)
Vencejos
\( \begin{matrix} \hline 107.6 & 108.1 & 119.3 & 153.6 \\ \hline
134.3 & 106.5 & 109.5 & 95.3 \\ \hline
133.2 & 145.0 & 127.3 & 109.4 \\ \hline
188.9 & 213.5 & 134.7 & 199.5 \\ \hline
214.3 & 106.7 & 205.3 & 3218.5 \\ \hline \end{matrix} \)
Se pide:
a) La media, mediana de cada grupo ¿Son semejantes los conjuntos con respecto a alguna de las medidas?
b) Obsérvese que el último dato del segundo grupo es muy diferente al resto; este dato recibe el nombre de outlier o dato atípico. Para comprobar su efecto: eliminar el dato y calcular la media y mediana para los restantes. ¿Qué medida está menos afectada por la presencia del dato atípico?
c) La varianza y desviación típica de cada grupo. ¿Son estas medidas de variabi-lidad resistentes al dato atípico?
d) ¿Alguna de estas distribuciones es sesgada? Si es así, ¿en qué dirección?
e) ¿Qué grupo tiene el rango intercuartílico más grande?
f) ¿Qué grupo posee variabilidad más grande?
g) ¿Qué grupo es más simétrico?
8. En un laboratorio farmacéutico se acaba de instalar una nueva máquina automática, “de gran precisión”, para dosificar y tabletear ciertos productos. Si el director del laboratorio quiere investigar la exactitud de la máquina no le queda otro camino que probarla. Supongamos que la máquina se utiliza para fabricar tabletas de 200 mg del producto y se extraen dos muestras:
La primera muestra dio los resultados: 300,100, 250 y 150 mg.
La segunda muestra dio los resultados: 202,198, 201 y 199 mg.
Se pide:
a) Calcular la media en ambos casos. (Sol. \( \bar{x}_{A}=200= \bar{ x}_{B} \))
b) Desviaciones absolutas medias (Sol. \( D_{\bar{x}_{A}}=75; D_{\bar{x}_{B}}=1.5 \))
c) ¿En qué caso se considerará la máquina aceptable? (Sol. b)
9. Se aplicó un test de inteligencia a 456 estudiantes del primer curso de Biológicas. Las puntuaciones obtenidas, agrupadas en intervalos de clase de 4 unidades de amplitud, figuran en la siguiente tabla de distribución de frecuencias:
\( \begin{array}{|l||c|c|c|c|c|c|c|} \hline e_{i-1}-e_{i} & 78-82 & 82-86 & 86-90 & 90-94 & 94-98 & 98-102 & 102-106 \\ \hline
n_{i} & 1 & 2 & 6 & 42 & 54 & 75 & 92 \\ \hline
e_{i-1}-e_{i} & 106-110 & 110-114 & 114-118 & 118-122 & 122-126 & 126-130 & 130-134 \\ \hline
n_{i} & 96 & 38 & 27 & 12 & 8 & 2 & 1 \\ \hline \end{array} \)
Calcular: \( P_{25}; P_{75}; P_{90} \) . (Sol. \( P_{25}=98.48; P_{75} =108.92; P_{90} =114.65 \) ).
10. En una clínica infantil se han ido anotando, durante un mes, el número de metros que el niño anda seguido y sin caerse el primer día que comienza a caminar. Obteniéndose así la tabla de información adjunta:
\( \begin{matrix} \hline N^{o} \hspace{1mm} de \hspace{1mm} niños & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline
N^{o} \hspace{1mm} de \hspace{1mm} metros & 2 & 6 & 10 & 5 & 10 & 3 & 2 & 2 \\ \hline \end{matrix} \)
Se pide:
a) Tabla de frecuencias. Diagrama de barras para frecuencias absolutas y para las frecuencias absolutas acumuladas
b) Mediana, moda y cuartiles (Sol: \( Me=4; M₀= 3; M₀^´ = 5; Q_1=3; Q_2=4; Q_3=5 \) )
c) Recorrido Intercuartílico (Sol: \( R_{I}=2 \) )
d) Momentos respecto al origen de primer, segundo y tercer orden. (Sol: \( m_1=4.05; m_2=19.5; m_3=106.2 \) )
e) Momentos centrales de primer y tercer orden (Sol:\( μ_1=0; μ_3=2.135 \) )
f) ¿Es simétrica la distribución?
g) Determinar el coeficiente de curtosis
11. La siguiente tabla muestra la distribución del coeficiente intelectual de 120 alumnos.
\( \begin{array}{|l||c|c|c|c|} \hline C.I. & 60-70 & 70-80 & 80-90 & 90-100 \\ \hline
n_{i} & 2 & 3 & 25 & 46 \\ \hline
C.I. & 100-110 & 110-120 & 120-130 & 130-140 \\ \hline
n_{i} & 35 & 5 & 3 & 1 \\ \hline \end{array} \)
a) Si se consideran bien dotados a los alumnos cuya puntuación está por encima del percentil 95 ¿A partir de que coeficiente intelectual mínimo los consideramos bien dotados? (Sol: \( P_{95} \)).
b) Si se consideran atrasados los alumnos cuya puntuación sea inferior al percentil 5 ¿Qué puntuación máxima pueden tener los atrasados? (Sol: 80.4)
c) Si el coeficiente intelectual es 109. Determinar el percentil correspondiente. (Sol: \( P_{90} \)).
12. Un profesor califica a sus alumnos siguiendo el siguiente criterio: suspensos 40%, aprobados 30%, notables 15%, sobresalientes 10%, matrículas 5%. Si las notas vienen dadas por la siguiente tabla:
\( \begin{matrix} \hline Notas & 0-1 & 1-2 & 2-3 & 3-4 & 4-5 & 5-6 & 6-7 & 7-8 & 8-9 & 9-10 \\ \hline
n_{i} & 34 & 74 & 56 & 81 & 94 & 70 & 41 & 28 & 16 & 4 \\ \hline \end{matrix} \)
Calcula la nota máxima para conseguir suspenso, aprobado, notable, sobresaliente y matrícula. (Sol: Suspenso ≤3.43; 3.43< Aprobado ≤ 5.13; 5.13< Notable ≤ 6.34; 6.34< Sobresaliente ≤ 7.57; Matrícula >7.57).
13. Una especie de mamíferos tiene en cada cría un número variable de hijos. Se observa durante un año la cría de 35 familias, anotándose el número de hijos obtenidos por las familias en dicha cría.
\( \begin{matrix} \hline N^{o} \hspace{1mm} hijos & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline N^{o} \hspace{1mm} familias & 2 & 3 & 10 & 10 & 5 & 0 & 5 & 0 \\ \hline \end{matrix} \)
a) Hallar los cuartiles de primer y tercer orden. (Sol: \( Q_1=2; Q_3= 4 \))
b) Hallar la moda. (Sol: \( M₀=2; M₀^′= 3 \)).
14. Un curso está dividido en 4 grupos de los cuales tenemos los datos:
\( \begin{matrix} \hline Grupo & N^{o} \hspace{1mm} alumnos & Nota \hspace{1mm} media & Varianza \\ \hline A & 30 & 6 & 1 \\ \hline
B & 40 & 6.5 & 1.69 \\ \hline
C & 50 & 5 & 0.81 \\ \hline
D & 60 & 4 & 0.64 \\ \hline \end{matrix} \)
a) Calcular los coeficientes de variación de cada grupo. (Sol: \( CV_{A}= 0.17; CV_{B}=0.2; CV_{C}=0.18; CV_{D}= 0.2 \))
b) ¿Qué grupo resulta más homogéneo? (Sol: A)
c) Calcular la varianza de todas las notas del curso. (Sol: 1.7983).
15. Se han medido mediante pruebas adecuadas los coeficientes intelectuales de un grupo de 20 alumnos, presentando los resultados agrupados en 6 intervalos de amplitud variable. Estas amplitudes son: \( a_1=12, a_2=12, a_3=4, a_4=4, a_5=12, a_6=20 \). Si las frecuencias relativas acumuladas correspondientes a cada uno de los intervalos son: \( F_1=0.15, F_2=0.15, F_3=0.55, F_4=0.8, F_5=0.95, F_6=1.00 \).
Se pide:
a) Formar la tabla de distribución de frecuencias, sabiendo que el extremo inferior del primer intervalo es 70
b) Dibujar el histograma y polígono de frecuencias absolutas. Calcular la moda
c) ¿Entre qué dos percentiles está comprendido un coeficiente intelectual de 98.4? Encontrar el valor ambos percentiles.
Al mismo grupo de alumnos se les hace una prueba de rendimiento y los resultados vienen dados en la Figura 1
d) Formar la tabla de distribución de frecuencias y calcular la mediana
e) ¿Qué medidas están más dispersas, los coeficientes intelectuales o las puntuaciones del rendimiento?
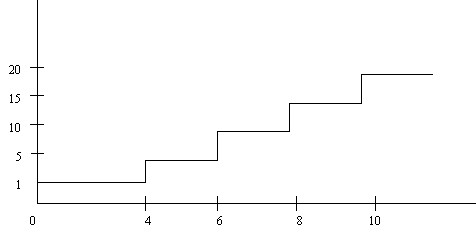 Figura 1
Figura 1
Soluciones: \( b) Mo=96.9; \hspace{1mm} c) P_{57}=98.32 \hspace{1mm} y \hspace{1mm} P_{58} =98.48; \hspace{1mm} d) Me=7 \); \hspace{1mm} e) Las puntuaciones del rendimiento. \( (CV_{I}=0.11;\hspace{1mm} CV_{R}=0.38) \).
16. En una empresa el 20% es personal “no cualificado”, el 50% es personal “cualificado” y el resto es personal “técnico”. La plantilla consta de 1000 empleados. Se ha estimado la productividad para cada uno de estos grupos en unos coeficientes que van de 1 a 5. Los resultados se muestran en la tabla adjunta.
\( \begin{matrix} \hline Coeficiente & Personal \hspace{1mm} no & Personal & Personal & \% \hspace{1mm} total \\ \hline
productividad & cualificado & cualificado & técnico & de \\ \hline
x_{i} & en \hspace{1mm} \% & en \hspace{1mm} \% & en \hspace{1mm} \% & trabajadores \\ \hline
1 & 10 & 5 & 0 & 4.5 \\ \hline
2 & 20 & 20 & 10 & 17 \\ \hline
3 & 30 & 20 & 40 & 28 \\ \hline
4 & 30 & 40 & 30 & 35 \\ \hline
5 & 10 & 15 & 20 & 15.5 \\ \hline \end{matrix} \)
a) Hállese la productividad media de los 1000 empleados. (Sol: \( \bar{x}=3.4 \))
b) ¿Qué nivel de productividad es el más corriente en esta empresa? (Sol \( Mo=4 \))
c) ¿Bajo qué coeficiente están el 50% de los trabajadores menos productivos? (Sol: \( Me=4 \)).
d) Comparando las productividades medias del personal no cualificado y del personal cualificado, ¿Cuál de ellas corresponde a una distribución de frecuencias más homogénea? (Sol: Personal cualificado (\( CV_{N}=0.37; CV_{C}=0.339 \)).
17. En un cierto barrio se ha constatado que las familias residentes se han distribuido, según su tamaño, de la siguiente forma:
\( \begin{matrix} \hline Tamaño \hspace{1mm} familias & 0-2 & 2-4 & 4-6 & 6-8 & 8-10 \\ \hline N^{o}\hspace{1mm} familias & 110 & 200 & 90 & 75 & 25 \\ \hline \end{matrix} \)
Se pide:
a) ¿Cuál es el número medio de personas por familia? (Sol: \( \bar{x} =3.82 \))
b) ¿Cuál es el tipo de familia más frecuente? (Sol: \( Mo= 2.9 \))
c) Si sólo hubiera plaza de aparcamiento para el 50% de las familias y éstas se atendieran por familias de mayor a menor tamaño, ¿Qué componentes tendría que tener una familia para entrar en el cupo? Se supone que cada familia sólo tiene un vehículo. (Sol: \( Me=3.4 \))
d) Si el coeficiente de variación de Pearson de otro barrio es 1.8, ¿Cuál de los dos barrios puede ajustar mejor sus previsiones en base al diferente tamaño de las familias que lo habitan. (Sol: \( CV_1=0.59; CV_2=1.8. \) El primer barrio).
18. Una variable X puede someterse a una transformación denominada Tipificación que consiste en restarle la media \( \bar{x} \) y dividir por la desviación típica σ. Una variable tipificada así obtenida, \( Z, Z= \displaystyle \frac{X-\bar{x}{σ}\), tiene dos propiedades fundamentales: Su media es cero y su desviación típica es uno. Aplicar este concepto a la distribución.
\( \begin{matrix} \hline x_{i} & 4 & 6 & 9 & 10 & 12 \\ \hline \end{matrix} \)
(Solución: \( \bar{x} =8 ; σ_{x}=21.83; z=0; σ_{z}=1 \) )
Autora: Ana María Lara Porras. Universidad de Granada
Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.