ALGUNAS DISTRIBUCIONES DISCRETAS DE PROBABILIDAD
Introducción
En el capítulo anterior hemos estudiado propiedades generales de las variables aleatorias discretas, en este capítulo vamos a desarrollar tipos específicos de variables aleatorias dis-cretas. En primer lugar estudiamos la variable aleatoria de Bernouilli: “Cualquier variable aleatoria que represente la presencia o ausencia de una determinada condición de un fenómeno observado tendrá una distribución de Bernouilli”. El nombre de Bernouilli lo recibe del probabilista suizo Jacques Bernouilli (1645-1705) que desarrolló por primera vez el concepto de ensayos independientes. La extensión a n ensayos independendientes nos conduce a la variable aleatoria discreta binomial. Por último estudiamos la distribución de Poisson, llamada así en honor al matemático francés Simeón Denis Poisson (1781-1840).
Distribución de Bernouilli
La distribución de Bernouilli (o distribución dicotómica), nombrada así por el matemático y científico suizo Jacques Bernoulli, es una distribución de probabilidad discreta, que toma valor 1 para la probabilidad de éxito p y valor 0 para la probabilidad de fracaso q = 1 – p. Es decir, si consideramos un experimento aleatorio E en el que observamos si se presenta o no un suceso A. Llamamos “éxito” a la ocurrencia del suceso A y “fracaso” a la no ocurrencia del suceso A. A su vez, llamamos p a la Probabilidad de Éxito, P(A)=p, y q a la Probabilidad de Fracaso, P(A)=q.
\( \left. \begin{array} \\ P(A) =p \\ P(A)=1-P(A)=q \\ \end{array} \right \} \Rightarrow p+q=1 \)
Sea \( X \) una variable aleatoria discreta que representa el número de éxitos (nº de veces que ocurre el suceso A) y toma dos valores 0 y 1
\( X = \left \{ \begin{array}{cc} 1 & si \hspace{.2cm} ocurre \hspace{.2cm} el \hspace{.2cm} suceso A \\ 0 & si \hspace{.2cm} no \hspace{.2cm} ocurre \hspace{.2cm} el \hspace{.2cm} suceso \hspace{.2cm} A \\ \end{array} \right. \hspace{.2cm} \) o \( \hspace{.2cm} X = \left \{ \begin{array}{cc} 1 & con \hspace{.2cm} probabilidad \hspace{.2cm} p \\ 0 & con \hspace{.2cm} probabilidad \hspace{.2cm} q \\ \end{array} \right. \)
Por lo tanto \( P[X=1]=p \) y \( P[X=0]=q \) .
En estas condiciones se dice que \( X \) tiene una Distribución de Bernouilli de parámetros 1 y p, y se denota \( X \rightarrow B(1, p) \), donde 1 es el número de veces que se realiza el experimento y p es la probabilidad de éxito.
Características
Esperanza matemática
\( E[X]= \displaystyle \sum_{i}p_{i}x_{i}=p \times 1 + q \times 0=p \)
Varianza
\( Var[X]=E[X^{2}]- \left [E[X] \right ]^{2}=p \times 1^{2}+q \times 0^{2}-p^{2}= p-p^{2}=p(1-p)=pq \)
Función generatriz de momentos
\( \psi (t)=E[e^{tX}]= \displaystyle \sum_{i}p_{i}e^{tx_{i}}=p \times e^{t}+q \times e^{t0}=pe^{t}+q \)
La media y la varianza también se pueden obtener a partir de la función generatriz de momentos
\( \left. \begin{array} \\ \psi {´}(t)=pe^{t} \Rightarrow \psi {´}(0)=p=m_1=E[X] \\ \psi {´´}(t)=pe^{t} \Rightarrow \psi {´´}(0)=p=m_2 \\ \end{array} \right \} \)
Por lo tanto
\( \begin{array} {l} \\ E[X]=p \\ Var[X]=m_2-m_1^{2}=p-p^{2}=pq \\ \end{array} \)
Distribución binomial
La distribución binomial es una distribución de probabilidad discreta, mide el número de éxitos en una secuencia de n ensayos independientes de Bernoulli, con una probabilidad fija p de ocurrencia del éxito entre los ensayos. La distribución binomial es una generalización de la distribución de Bernoulli, a la que puede llegarse nuevamente haciendo n = 1.
Supongamos que el experimento aleatorio \( E \), definido en la sección anterior, se realiza \( n \) veces en las mismas condiciones y se anotan los valores para \( X_1,X_2, \cdots ,X_{n} \), donde
\( X_{i}= \left \{ \begin{array} {ll} \ 1 & si \hspace{.2cm} ocurre \hspace{.2cm} el \hspace{.2cm} suceso \hspace{.2cm} A \hspace{.2cm} en \hspace{.2cm} el \hspace{.2cm} i-ésimo \hspace{.2cm} ensayo \\ 0 & si \hspace{.2cm} no \hspace{.2cm} ocurre \\ \end{array} \right. \hspace{.4cm} i=1,2, \cdots ,n \)
o
\( X_{i}= \left \{ \begin{array} {ll} 1 & con \hspace{.2cm} probabilidad \hspace{.2cm} p \\ 0 & con \hspace{.2cm} probabilidad \hspace{.2cm} q \\ \end{array} \right. \hspace{.4cm} i=1,2, \cdots , n \)
Por tanto, se tiene una sucesión de n variables aleatorias de Bernouilli. Una función de interés especial de \( X_1,X_2,⋯,X_{n} \) es la suma, \( X₁+X₂+ \cdots +X_{n} \), que denotamos por \( X= \displaystyle \sum_{i=1}^{n}X_{i} \). Es decir, consideramos una v.a. \( X \) suma de \( n \) variables aleatorias independientes, \( X=X_1+X_2+ \cdots + X_{n} \), distribuidas cada una de ellas según una distribución de Bernouilli de parámetros \(1 \) y \( p \), \( X_{i} \rightarrow B(1, p), (i=1, 2, \cdots , n) \).
Veamos qué distribución tiene la variable aleatoria \( X \).
Sabemos que la función generatriz de momento de cada v.a. \( X_{i} \) es:
\( \psi_{X_{i}}(t)=E[e^{tX_{i}}]=pe^{t}+q \)
Por lo tanto la función generatriz de la variable aleatoria \( X=X_1+X_2+ \cdots +X_{n} \) es
\( \psi_{X}(t) = E[e^{tX}]=E[e^{t(X_1+X_2+ \cdots +X_{n})}]=E[e^{t(X_1)}.e^{t(X_2)} \cdots e^{t(X_{n})}]=^{(1)} \)
\( = E[e^{t(X_1)}].E[e^{t(X_2)}] \cdots E[e^{t(X_{n})}]=(pe^{t}+q) \cdots(pe^{t}+q)=(pe^{t}+q)^{n} \)
De donde deducimos que \( X \rightarrow B(n, p) \)
(1): \( X_{i} \) son vv.aa. independientes \( \Rightarrow E[X_1.X_2 \cdots X_{n}]=E[X_1].E[X_2] \cdots E[X_{n}] \)
La variable aleatoria discreta \( X \), que representa el número de éxitos en n ensayos independientes y toma todos los valores correspondientes entre 0 y n \( (0, 1, 2, \cdots, n) \) se dice que se distribuye según una Distribución Binomial de parámetros n y p, y se denota \( X \rightarrow B(n, p) \) , (donde \( n \) es el número de veces que se realiza el experimento y \( p \) es la probabilidad de éxito).
\( X = \left \{ \begin{array}{ll} 1 & si \hspace{.2cm} ocurre \hspace{.2cm} el \hspace{.2cm} suceso A \\ 0 & si \hspace{.2cm} no \hspace{.2cm} ocurre \hspace{.2cm} el \hspace{.2cm} suceso \hspace{.2cm} A \\ \end{array} \right. \hspace{.2cm} \) o \( \hspace{.2cm} X = \left \{ \begin{array}{cc} 1 & con \hspace{.2cm} probabilidad \hspace{.2cm} p \\ 0 & con \hspace{.2cm} probabilidad \hspace{.2cm} q \\ \end{array} \right. \)
Por lo tanto \( P[X=1]=p \) y \( P[X=0]=q \)
Fácilmente se determina la distribución de probabilidad para \( X \) con la hipótesis de que \( P[X_{i}=1]=p \), donde \( p \) es constante en todos los intentos.
Función de probabilidad
Supongamos que una de las realizaciones del experimento aleatorio \( E \) es la siguiente
\( AAAA \bar{A}\bar{A} \bar{A}AA \cdots⋯A\bar{A}A \)
y supongamos también que el suceso \( A \) se presenta \( k \) veces y, por tanto, el suceso \( \bar{A} \) se presenta \( n-k \) veces, siendo \( k \) un entero positivo comprendido entre \( 0 \) y\( n \). Como los resultados obtenidos, cada vez que se repite el experimento aleatorio, son independientes unos de otros la probabilidad de la secuencia anterior es
\( P[AAAA \bar{A}\bar{A} \bar{A}AA \cdots⋯A\bar{A}A]=ppppqqqpp⋯pqp=p^{k}q^{n-k} \)
Pero, ¿cuántas formas posibles hay de obtener \( k \) éxitos y \( n-k \) fracasos? o ¿de cuántas formas diferentes se pueden ordenar los \( n \) elementos en los que la \( A \) se repite \( k \) veces y \( \bar{A} \) se repite \( n-k veces? \). El número posibles ordenaciones viene dado por el número de permutaciones con repetición de \( n \) elementos siendo, por un lado \( k \) iguales entre sí y por otro lado \( n-k \) también iguales entre sí, por lo tanto:
\( P_{n}^{k,(n-k)}= \displaystyle \frac{n!} {k!(n-k)! }= \displaystyle \frac {n} {k} \)
En definitiva, la probabilidad de obtener \( k \) éxitos en \( n \) ensayos independientes es
\( P[X=k]= \displaystyle{ n \choose k } p^{k}q^{n-k} \hspace{.9cm} [1] \)
donde \( \displaystyle { n \choose k } \) es el número de combinaciones sin repetición de orden \( k \) entre \( n \) elementos y su valor es \( \displaystyle \frac{n!}{k!(n-k)!} \) .
Comprobamos que [1] es una función de probabilidad, para ello se tiene que verificar que
\( \displaystyle \sum_{k=0}^{n}P[X=k]=1 \)
En efecto,
\( \displaystyle \sum_{k=0}^{n}P[X=k] =\displaystyle \sum_{k=0}^{n} { n \choose k } p^{k}q^{n-k}=(p+q)^{n}=1 \)
Definición: Sea \( X \) una v.a. discreta que representa el número de éxitos en \( n \) ensayos independientes entre sí y toma todos los valores posibles entre \( 0 \) y \( n \). Sean \( p \) y \( q \) las probabilidades de éxito y fracaso, respectivamente, de cualquiera de estos ensayos. Se dice que \( X \) tiene una Distribución Binomial de parámetros \( n \) y \( p \), y se denota \( X \rightarrow B(n, p) \) con función de probabilidad
\( P[X=k]=b[k; n,p] = \left \{ \begin{array}{ll} \displaystyle { n \choose k } p^{k}q^{n-k} & k=0,1,2, \cdots n \hspace{.3cm} ; \hspace{.3cm} n \in Z \hspace{.3cm} ; \hspace{.3cm} 0 \leq p \leq 1 \\ 0 & para \hspace{.2cm} cualquier \hspace{.2cm} otro \hspace{.2cm} valor \\ \end{array} \right. \)
Ejemplos:
1. Número de hijos con ojos verdes en una familia de 4 hijos
2. Número de plantas enfermas seleccionadas de un total de 10 plantas
3. Número de personas contagiadas de una enfermedad de un total de 20 que han estado en contacto con el portador, con un 10% de posibilidades de transmitir la enfermedad
4. Número de reacciones negativas a un fármaco administrado a 30 pacientes.
En estos ejemplos, que aparentemente pueden parecer que no guardan ninguna relación, podemos observar los siguientes puntos comunes:
a) Cada uno de estos experimentos se puede considerar formado por un número fijo de pruebas o ensayos idénticos. En el ejemplo 1 hay cuatro pruebas y cada nacimiento será una prueba. En el ejemplo 2, la prueba consiste en seleccionar una planta y comprobar si está enferma, en total se hacen 10 ensayos idénticos. En el ejemplo 3, el ensayo consiste en observar a un individuo que entra en contacto con el portador de una enfermedad y comprobar si se ha contagiado, se hacen 20 ensayos idénticos. En el ejemplo 4, la prueba consiste en comprobar si la reacción a un fármaco es negativa, se hacen 30 pruebas idénticas.
b) Cada ensayo sólo puede tener un resultado de dos posibles, que reciben el nombre de “éxito” y “fracaso”. Así, en los ejemplos anteriores el éxito consiste en: tener un niño con ojos verdes, la planta seleccionada esté enferma, el individuo observado esté contagiado, la reacción al fármaco sea negativa, respectivamente.
c) La probabilidad de éxito, p, permanece constante en cada ensayo. En los ejemplos anteriores las probabilidades de éxito permanecen constantes en cada ensayo y sus valores son: 1/4 en el Ejemplo 1; p=0.1 en los ejemplos 2 y 3 y p=0.3 en el Ejemplo 4.
d) Los ensayos son independientes entre sí (el resultado de un ensayo no tiene efecto sobre el resultado de cualquier otro ensayo). En el Ejemplo 1 los nacimientos son obviamente independientes entre sí, en los ejemplos 2, 3 y 4 también se satisface la independencia ya que el hecho de que una planta, una persona seleccionada esté enferma no influye en que lo esté otra, o el hecho de que un paciente tenga reacción negativa a un fármaco no tiene influencia sobre la susceptibilidad de otro paciente.
e) La variable de interés es el número de éxitos en n ensayos.
Resumiendo: Una variable aleatoria discreta \( X \) tiene una distribución \( B(n, p) \) si cumple las siguientes condiciones:
1. El experimento consiste en un número fijo de ensayos idénticos.
2. Cada ensayo sólo puede tener un resultado de dos posibles, que reciben el nombre de “éxito” y “fracaso”.
3. La probabilidad de éxito, p, permanece constante en cada ensayo.
4. Los n ensayos son independientes entre sí.
5. Se define \( X \) como el número de éxitos en \( n \) ensayos.
La función de distribución de la v.a. \( X \rightarrow B(n, p) \), se define de la siguiente manera:
\( P[X \leq k] = \displaystyle \sum_{i=0}^{k}b[i; n,p] \)
su gráfica es la de una función escalonada, continua por la derecha y monótona no decreciente.
La distribución \( b[k; n,p] \) se encuentra tabulada para algunos valores de \( n \) y \( p \) en la Tabla de la Distribución Binomial.
Ejemplo 6.1: Supongamos el experimento consistente en el lanzamiento de diez monedas, siendo, en cada una de ellas, la probabilidad de cara 0.7, P(cara)=0.7. Se pide la probabilidad de que:
a) El número de caras sea menor o igual a 2
b) El número de caras esté entre 5 y 7 ambos inclusive.
Respuesta:
Suceso \( A: \) “Obtener cara en el lanzamiento de una moneda”.
La variable aleatoria discreta \( X: \) “Número de caras en el lanzamiento de 10 monedas” se distribuye según una distribución Binomial \( B(10, 0.7) \) y su función de probabilidad es
\( P[X=k]= \displaystyle { 10 \choose k } (0.7)^{k}(0.3)^{10-k} \)
a)
\( \begin{array}{ll} P[X \leq 2] & =P[X=0]+P[X=1]+P[X=2]= \\ & \\ & = \displaystyle { 10 \choose 0 }(0.7)^{0}(0.3)^{10}+ \displaystyle { 10 \choose 1 }(0.7)^{1} (0.3)^{9} + \displaystyle { 10 \choose 2 }(0.7)^{2}(0.3)^{3}= \\ & \\ & =(0.3)^{10}+10(0.7){1}(0.3)^{9}+45(0.7)^{2}(0.3)^{8} \\ \end{array} \)
b)
\( \begin{array}{ll} P[5 \leq X \leq 7] & = P[X=7]+P[X=6]+P[X=5]= \\ & \\ & = \displaystyle { 10 \choose 7 } (0.7)^{7}(0.3)^{3}+ \displaystyle { 10 \choose 6 }(0.7)^{6}(0.3)^{4}+ \displaystyle { 10 \choose 5 }(0.7)^{5}(0.3)^{5} \\ \end{array} \)
Características
En primer lugar calculamos la función generatriz de momentos.
Función generatriz de momentos
\( \begin{array}{ll} \psi (t) & = E[e^{tX}]= \displaystyle \sum_{k=0}^{n} e^{tk}P[X=k]= \displaystyle \sum_{k=0}^{n} e^{tk} \displaystyle { n \choose k } p^{k}q^{n-k}= \\ & \\ & = \displaystyle \sum_{k=0}^{n} \displaystyle { n \choose k } (pe^{t})^{k}q^{n-k}= \left (pe^{t}+q \right )^{n} \\ \end{array} \)
La media y la varianza se van a obtener a partir de la función generatriz de momentos, para ello se calculan las dos primeras derivadas de dicha función y se particulariza para \( t=0 \)
\( \begin{array}{ll} \psi^{´} (t) & = n (pe^{t}+q )^{n-1}pe^{t} \Rightarrow \psi^{´} (0)=n(p+q)^{n} p=np=m_{1} \\ & \\ \psi^{´´}(t) & = n(n-1)(pe^{t}+q)^{n-2}(pe^{t})^{2}+npe^{t}(pe^{t}+q)^{n-1}\Rightarrow \\ & \\ & \Rightarrow \psi^{´´}(0) =n(n-1)p^{2}+np=m_{2} \\ \end{array} \)
Por lo tanto:
Esperanza matemática
\( E[X]=np \)
Varianza
\( Var[X] = m_2-m_1^{2}=n(n-1)p^{2}+np -n^{2}p^{2}= n^{2}p^{2}-np^{2}+np-n^{2}p^{2}=np(-p+1)=npq \)
Propiedad aditiva
Sean \( X_1,X_2,⋯,X_{k} \), \( k \) variables aleatorias independientes, distribuidas cada una de ellas según una distribución Binomial, \( X_{i} \rightarrow B(n_{i}, p) \), \( (i=1, 2, \cdots , k) \). Entonces la v.a. formada por la suma de las vv.aa. \( X_{i}, X_1+X_2+ \cdots +X_{k} \), se distribuye según una Binomial de parámetros \( n_1+n_2+⋯+n_{k} \) y \( p \).
En efecto, sabemos que la función generatriz de momento de cada v.a. \( X_{i} \) es:
\( \begin{array}{ll} X_1: & \psi_{X_1}(t)=E[e^{tX_1}]=(pe^{t}+q)^{n_1} \\ X_2: & \psi_{X_2}(t)=E[e^{tX_2}]=(pe^{t}+q)^{n_2} \\ \vdots & \vdots \\
X_{k}: & \psi_{X_{k}}(t)=E[e^{tX_{k}}]=(pe^{t}+q)^{n_{k}} \\ \end{array} \)
Por lo tanto la función generatriz de la variable aleatoria \( X_1+X_2+ \cdots +X_{k} \) es
\( \begin{array}{ll} \psi_{X_1+X_2+⋯X_{k}}(t) & = E[e^{t(X_1+X_2+⋯+X_{k})}]=E[e^{t(X_1)}.e^{t(X_2)}.⋯.e^{t(X_{k})}]=^{(1)} = \\ & = E[e^{t(X_1)}].E[e^{t(X_2)}] \cdots E[e^{t(X_{k})}]= \\ & = (pe^{t}+q)^{n_1} \times (pe^{t}+q)^{n_2} \cdots (pe^{t}+q)^{n_{k}}=(pe^{t}+q)^{n_1+n_2+ \cdots +n_{k}} \\ \end{array} \)
de donde deducimos que \( X_1+X_2+⋯+X_{k} \rightarrow B(n_1+n_2+⋯+n_{k}, p) \). Se dice que la distribución Binomial es aditiva en el parámetro \( n \). No sucede lo mismo con el parámetro \( p \).
(1): \( X_{i} \) son vv.aa. independientes \( \Rightarrow E[X_1X_2 \cdots X_{n}]=E[X_1].E[X_2] \cdots E[X_{n}] \).
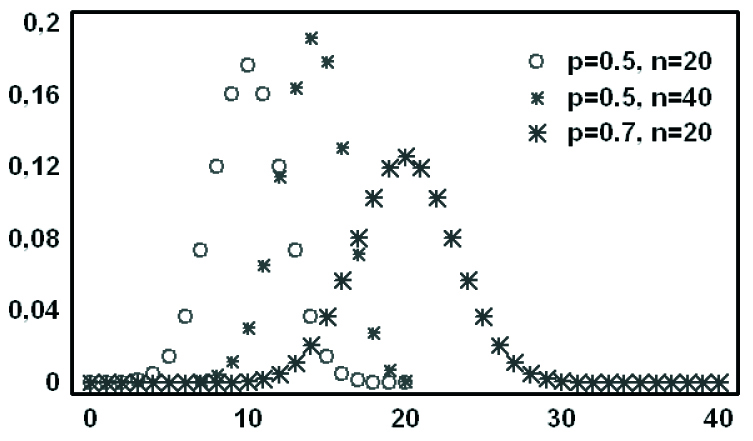Figura 6.1: Función masa de probabilidad
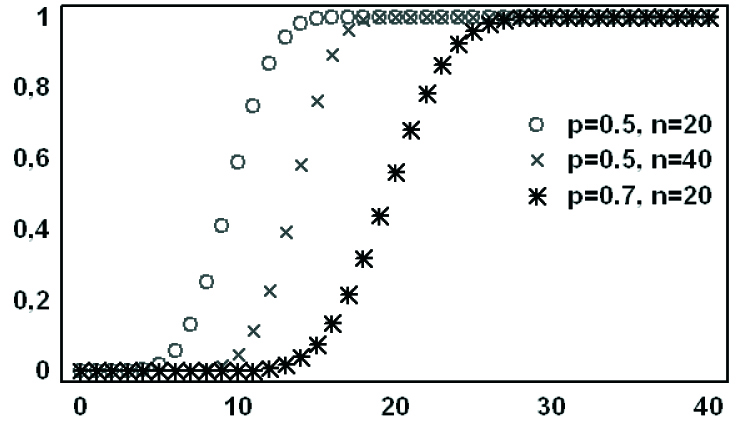
Figura 6.2: Función de distribución
Ejemplo 6.2: Una pareja formada por un hombre y una mujer ambos con un gen recesivo y uno dominante para el color de los ojos, son padres de cuatro hijos. El gen recesivo es el color verde en los ojos y el gen dominante es el color marrón. Sea X el número de hijos con los ojos verdes. Determinar: a) La función de probabilidad; b) Tengan exactamente dos hijos con ojos verdes; c) Ningún hijo tenga los ojos verdes; d) más de dos hijos tengan los ojos verdes; e) entre uno y dos hijos tengan los ojos verdes; f) menos de tres hijos tengan los ojos verdes; g)La media; h) La varianza.
Respuesta:
Sean los sucesos V: “Color de ojos verdes” y M: “Color de ojos marrones”.
El Espacio muestral \( E: \displaystyle \{(VV),(VM),(MV),(MM) \} \hspace{.2cm} \); \( \hspace{.2cm} P(VV)=1/4 \hspace{.2cm} \); \( \hspace{.2cm}n=4 \)
\( X \): “Nº de hijos con ojos verdes de un total de 4 hijos” es una variable aleatoria discreta Binomial \( B(4, p) \), con \( P(VV)=(1/4) \). Por tanto \( X \rightarrow B(4, 1/4) \)
a) \( P[X=k]= \displaystyle { 4 \choose k } \left ( \displaystyle \frac{1}{4} \right )^{k} \left ( \displaystyle \frac{3}{4} \right)^{4-k} \)
b) \( P[X=2]= \displaystyle { 4 \choose 2 } \left ( \displaystyle \frac{1}{4} \right )^{2} \left ( \displaystyle \frac{3}{4} \right) ^{4-2}=0.2109 \)
c) \( P[X=0]= \displaystyle { 4 \choose 0 } \left ( \displaystyle \frac{1}{4} \right )^{0} \left ( \displaystyle \frac{3}{4} \right )^{4-0} =0.3164 \)
d)
\( \begin{array}{ll} P[X>2]= & P[X=3]+P[X=4]= \displaystyle { 4 \choose 3 } \left ( \displaystyle \frac{1}{4} \right )^{3} \left ( \displaystyle \frac{3}{4} \right )^{4-3}+ \displaystyle { 4 \choose 4 } \left ( \displaystyle \frac{1}{4} \right )^{4} \left ( \displaystyle \frac{3}{4} \right)^{4-4}= \\
& = 0.4609+0.0039=0.4648 \\ \end{array} \)
e) \( P[X=1]+P[X=2]=0.4219+0.2109=0.6328 \)
f) \( P[X<3]=1-P[X \geq 3]=1- \left (P[X=3]+P[X=4] \right )=1-0.4648=0.5352 \)
g) \( E[X]=np=4 \times \displaystyle \frac{1}{4}=1 \)
h) \( Var[X]=npq=4 \times \displaystyle \frac{1}{4} \times \displaystyle \frac{3}{4}= \displaystyle \frac{3}{4} \)
Ejemplo 6.3: Un portador de una determinada enfermedad contagiosa tiene un 10% de posibilidades de transmitir la enfermedad. Durante el transcurso de un día el portador entra en contacto con 20 personas cada una de ellas propensa a la enfermedad. ¿Cuántos individuos se espera que contraigan la enfermedad?
Respuesta:
\( X: \) “Nº de personas que contraen la enfermedad” es una v.a. discreta Binomial \( B(20; 0.1) \). Por tanto \( X \rightarrow B(20; 0.1) \).
Cada individuo que entra en contacto con el portador tiene un 10% de posibilidades de contraer la enfermedad, por lo tanto se espera que se contagien un 10% de las personas que entran en contacto con el portador, es decir 10% de 20, (0.1×20=2). O bien aplicando la expresión de la Esperanza matemática
\( E[X]=np=20 \times 0.1=2 \)
Distribución de Poisson
La distribución de Poisson fue descubierta por Siméon-Denis Poisson (1781–1840). En el trabajo publicado en 1838, “Recherches sur la probabilité des jugements en matières criminelles et matière civile” (“Investigación sobre la probabilidad de los juicios en materias criminales y civiles”), estudia unas variables aleatorias discretas que cuentan el número de ocurrencias que tiene lugar durante un intervalo de tiempo de duración determinada. Si el número esperado de ocurrencias en este intervalo es \( \lambda \), entonces la probabilidad de que haya exactamente \( r \) ocurrencias (siendo \( r \) un entero no negativo, \( r = 0, 1, 2, \cdots) \) es igual a \( P[X=r]=p(r, \lambda )= \displaystyle \frac { \lambda^{r}}{r!}e^{- \lambda} \).
Definición: Se dice que una variable aleatoria discreta, \( X \) , sigue una distribución de Poisson de parámetro \( \lambda \) no negativo, y se denota por \( X \rightarrow P( \lambda) \) , cuando puede tomar todos los valores enteros positivos \( 0, 1, 2, \dots, n, \cdots \) siendo la probabilidad de \( X=r \) la siguiente:
\( P[X=r]=p(r, \lambda)= \displaystyle \frac{ \lambda^{r}}{r!}e^{- \lambda} \hspace{.3cm} , \hspace{.3cm}r=0, 1, 2, \cdots , n, \cdots \hspace{.3cm} ; \hspace{.3cm} \lambda >0 \hspace{.7cm} [6.2] \)
dónde:
- \( e \) es el base del logaritmo natural o neperiano \( (e = 2.71828 \cdots) \)
- \( r! \) es el factorial de \( r \)
- \( r \) es el número de ocurrencias de un evento
- \( \lambda \) es un número real positivo, equivalente al número esperado de ocurrencias durante un intervalo dado.
Veamos que efectivamente la expresión ([6.2]) define una función de probabilidad. Para ello hay que comprobar que
\( \displaystyle \sum_{r=0}^{ \infty}P[X=r]=1 \)
En efecto,
\( \displaystyle \sum_{r=0}^{ \infty}P[X=r]=\displaystyle \sum_{r=0}^{ \infty} \displaystyle \frac{ \lambda^{r}}{r!}e^{- \lambda}=e^{- \lambda}\displaystyle \sum_{r=0}^{ \infty} \displaystyle \frac{ \lambda^{r}}{r!}=e^{ \lambda}e^{- \lambda}=1 \)
La función de distribución de la ley de Poisson viene dada por
\( P[X \leq r]= \displaystyle \sum_{i=0}^{r}p(i, \lambda) \)
Dicha función de distribución está tabulada en la Tabla II y su gráfica, como en la distribución Binomial, es la de una función escalonada, continua por la derecha y monótona no decreciente.
La distribución Poisson, Se aplica a varios fenómenos discretos de la naturaleza (esto es, aquellos fenómenos que ocurren 0, 1, 2, 3, … veces durante un periodo definido de tiempo o en una área determinada) cuando la probabilidad de ocurrencia del fenómeno es constante en el tiempo o el espacio. Ejemplos de estos eventos que pueden ser modelados por la distribución Poisson incluyen:
- El número de coches que pasan a través de un cierto punto en un tramo determinado de una vía (con los semáforos suficientemente distantes) durante un periodo definido de tiempo
- El número de errores de ortografía que una persona comete al escribir una única página
- El número de llamadas telefónicas en una central telefónica por minuto
- El número de servidores Web accedidos por minuto
- El número de leucocitos en una gota de sangre
- El número de animales muertos encontrados por unidad de longitud
- El número de mutaciones de determinada cadena de ADN después de cierta cantidad de radiación
- El número de estrellas en un determinado volumen de espacio.
Ejemplo 6.4: En una gasolinera la llegada de vehículos sigue la distribución de Poisson de parámetro 1,6. Calcúlese la probabilidad de que:
a) El número de vehículos que lleguen sea superior a tres.
b) El número de vehículos que lleguen esté comprendido entre 2 y 5.
c) Llegue algún vehículo.
Respuesta:
Se trata de una distribución de Poisson de parámetro \( \lambda=1.6 \hspace{.3cm} \) ; \( \hspace{.3cm} X \rightarrow P(\lambda =1.6) \)
a)
\( \begin{array}{ll}P[X>3] & = 1-P[X \leq 3]=1-P[X=0]-P[X=1]-P[X=2]-P[X=3]= \\ & = 1-0.2019-0.3230-0.2584-0.1378=0.0789 \\ \end{array} \)
b)
\( \begin{array}{ll}P[2 \leq X \leq 5] & =P[X=2]+P[X=3]+P[X=4]+P[X=5]= \\ & = 0.2584+0.1378+0.0551+0.0176=0.4689 \\ \end{array} \)
c)
\( P[X \geq 1]=1-P[X<1]=1-P[X=0]=1-0.2019=0.7981 \)
Características
La ley de Poisson viene caracterizada por un único parámetro \( \lambda \) y es sencillo de probar que \( E[X ]= \lambda \) y \( Var[X]= \lambda \), es decir, que la media y la varianza de una ley de Poisson coinciden y que las dos son iguales a \( \lambda \). Para ello, en primer lugar calculamos la función generatriz de momentos y a partir de ella obtenemos la media y la varianza.
Función generatriz de momentos
\( \begin{array}{ll} \psi(t) & = E[e^{tX}]= \displaystyle \sum_{r=0}^{ \infty}e^{tr}P[X=r]= \displaystyle \sum_{r=0}^{ \infty}e^{tr} \displaystyle \frac{ \lambda ^{r}}{r!} e^{- \lambda}= \\ & = e^{- \lambda } \displaystyle \sum_{r=0}^{ \infty} \displaystyle \frac{(e^{t}λ)^{r}}{r!}=e^{- \lambda}e^{ \lambda e^{t}}=e^{ \lambda (e^{t}-1)} \\ \end{array} \)
La media y la varianza, como en la distribución Binomial, se van a obtener a partir de la función generatriz de momentos, para ello se calculan las dos primeras derivadas de dicha función y se particularizan para t=0
\( \begin{array}{ll} \psi^{´}(t) & = \lambda e^{t}e^{ \lambda (e^{t}-1)} \Rightarrow \psi^{´}(0)= \lambda =m_1 \\ \psi^{´´}(t) & = \lambda e^{t}e^{ \lambda (e^{t}-1)}+ \lambda ^{2} e^{2t}e^{ \lambda (e^{t}-1)} \Rightarrow \psi^{´´}(0)= \lambda + \lambda ^{2}=m_2 \\ \end{array} \)
Por lo tanto
Esperanza matemática
\( E[X]= \lambda \)
Varianza
\( Var[X]=m_2-m_1^{2}= \lambda + \lambda^{2}- \lambda ^{2}= \lambda \)
Comentario
En la distribución de Poisson la media y la varianza coinciden entre sí y con el parámetro que la caracteriza.
Propiedad aditiva
Sean \( X_1,X_2, \cdots ,X_{k} \) , \( k \) variables aleatorias independientes, distribuidas cada una de ellas según una distribución de Poisson, \( X_{i} \rightarrow P(\lambda_{i}) \hspace{.2cm}, \hspace{.2cm} ( i=1, 2, \cdots , k) \). Entonces la v.a. formada por la suma de las vv.aa. \( X_{i}, X_1+X_2+ \cdots +X_{k} \), se distribuye según una distribución de Poisson de parámetros \( \lambda_1+ \lambda_2+ \cdots +\lambda_{k} \). En efecto: Sabemos que la función generatriz de momento de cada v.a. \( X_{i} \) es:
\( \begin{array}{ll} X_1 : & \psi_{X_1}(t)=E[e^{tX_1}]=e^{ \lambda_1(e^{t}-1)} \\ X_2: & \psi_{X_2}(t)=E[e^{tX_2}]=e^{ \lambda_2(e^{t}-1)} \\
\vdots & \vdots \\ X_{k}: & \psi_{X_{k}}(t)=E[e^{tX_{k}}]=e^{\lambda_{k}(e^{t}-1)} \\ \end{array} \)
Por lo tanto la función generatriz de la variable aleatoria \( X_1+X_2+ \cdots +X_{k} \) es
\( \begin{array}{ll} \psi_{X_1+X_2+⋯X_{k}}(t) & = E[e^{t(X_1+X_2+ \cdots +X_{k})}]=E[e^{t(X_1)}.e^{t(X_2)} \cdots e^{t(X_{k})}]=^{(1)} \\ & = E[e^{t(X_1)}].E[e^{t(X_2)}] \cdots E[e^{t(X_{k})}]= \\ & = e^{ \lambda_1(e^{t}-1)} \times e^{\lambda_2(e^{t}-1)} \times \cdots \times e^{ \lambda_{k}(e^{t}-1)}=e^{(\lambda_1+ \lambda_2+ \cdots + \lambda_{k})(e^{t}-1)} \\ \end{array} \)
De donde deducimos que \( X_1+X_2+⋯+X_{k} \rightarrow P (\lambda_1+ \lambda_2+ \cdots + \lambda_{k}) \) . Se dice que la distribución de Poisson es aditiva en el parámetro \( \lambda \).
(1): \( X_{i} \) son vv.aa. independientes \( \Rightarrow E[X_1.X_2 \cdots X_{n}]=E[X_1].E[X_2] \cdots E[X_{n}] \).
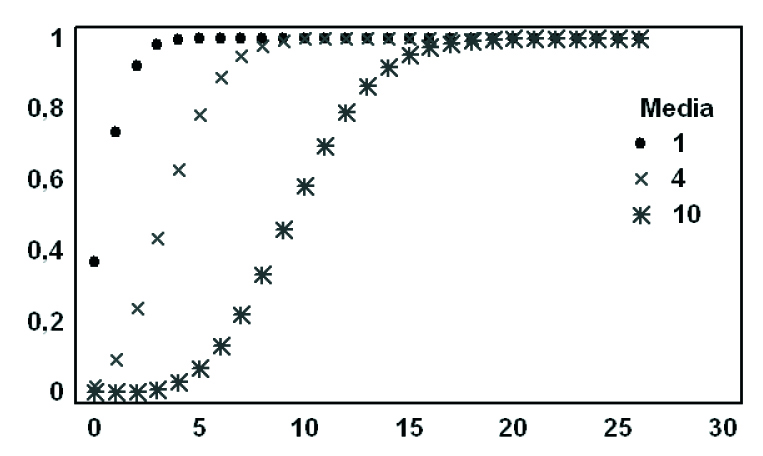
Figura 6.3: Función masa de probabilidad
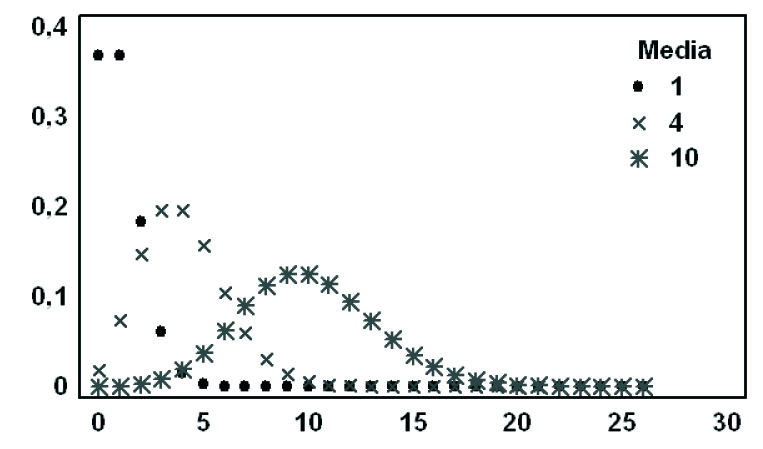
Figura 6.4: Función de distribución
Aproximación de una distribución binomial por una Poisson
Consideremos la función de probabilidad de una distribución Binomial de parámetros \( n \) y \( p \), \( B(n, p) \), vamos a comprobar que cuando \( n \rightarrow \infty \) y \( p \rightarrow 0 \) ( \( \lim_{n \rightarrow \infty }(np) \) es finito o constante) entonces la distribución de Poisson se puede obtener como una aproximación de la distribución Binomial. Así, vamos a examinar el límite de la distribución Binomial de probabilidad cuando \( n \rightarrow \infty \) y \( p \rightarrow 0 \). En la expresión de la función de probabilidad de una distribución Binomial
Nota: Para simplificar se estima el límite con la restricción de que el promedio \( np \) , en el caso binomial, permanece constante en un valor que llamaremos \( λ \).
\( P[X=k]= \displaystyle { n \choose k } p^{k}q^{n-k} \hspace{.5cm} [6.3] \)
llamamos: \( np= \lambda \Rightarrow p= \displaystyle \frac{\lambda}{n} \) y \(q=1- \displaystyle \frac{\lambda}{n} \), por lo tanto, sustituyendo en [6.3].
\( \begin{array}{ll} P[X=k] & = \displaystyle { n \choose k } \left ( \displaystyle \frac{\lambda}{n} \right )^{k} \left (1- \displaystyle \frac{\lambda}{n} \right )^{n-k}= \\ & = \displaystyle \frac{ n(n-1)(n-2) \cdots (n-k+1)}{k!} \times \displaystyle \frac{ \lambda^{k}}{n^{k}} \times \displaystyle \frac{ \left (1- \displaystyle \frac{ \lambda} {n} \right )^{n}}{ \left ( 1- \displaystyle \frac{ \lambda }{n} \right)^{k}}= \\ & = \displaystyle \frac{ \lambda^{k}}{k! } \times \left (1- \displaystyle \frac{ \lambda}{n} \right )^{n} \times \displaystyle \frac{n(n-1)(n-2) \cdots (n-k+1)}{n^{k} \left (1- \displaystyle \frac{ \lambda} {n} \right)^{k}} \\ \end{array} \)
dividiendo el numerador y denominador por \( n^{k} \), la expresión anterior queda de la siguiente forma:
\( P[X=k]= \displaystyle \frac{ \lambda^{k}}{k!} \times \left (1- \displaystyle \frac{ \lambda }{n} \right)^{n} \times \displaystyle \frac{1 \left (1- \displaystyle \frac{1}{n} \right ) \left (1- \displaystyle \frac{2}{n} \right ) \cdots \left (1- \displaystyle \frac{k-1}{n}\right ) }{ \left ( 1- \displaystyle \frac{ \lambda}{n} \right )^{k}}\)
A continuación calculamos el límite cuando \( n \rightarrow \infty \)
\( \begin{array}{ll} \lim_{n \to \infty}P[X=k] & = \lim_{n \to \infty} \displaystyle \frac{ \lambda^{k}}{k!} \times \left( 1- \displaystyle \frac{\lambda}{n} \right )^{n} \times \displaystyle \frac{ 1 \left (1- \displaystyle \frac{1}{n} \right ) \left (1- \displaystyle \frac{2}{n} \right ) \cdots \left (1- \displaystyle \frac{k-1}{n} \right ) }{ \left (1- \displaystyle \frac{\lambda}{n}) \right )^{k}}= \\ & = \displaystyle \frac{ \lambda^{k}}{k!} \times \lim_{n \to \infty} \left(1- \displaystyle \frac{ \lambda}{n} \right)^{n} \times \lim_{n \to \infty} \displaystyle \frac{ 1 \left (1- \displaystyle \frac{1}{n} \right ) \left (1- \displaystyle \frac{2}{n} \right ) \times \left (1- \displaystyle \frac{k-1}{n} \right) }{ \left (1- \displaystyle \frac{\lambda }{n}\right )^{k}}= \\ & = \displaystyle \frac{\lambda ^{k}}{k!}e^{- \lambda} \times 1= \displaystyle \frac{\lambda λ^{k}}{k!}e^{- \lambda} \\ \end{array} \)
que es la función de probabilidad de una distribución de Poissson de parámetro \( \lambda \).
Nota: La distribución de Poisson se puede utilizar para modelizar conteos en áreas o volúmenes, así como en el tiempo. Por ejemplo, el número de accidentes que ocurren en un determinado cruce de una carretera en el periodo de una semana, el número de colonias de bacterias en un cc. de agua, el número de veces que falla una máquina en el transcurso de un día de trabajo.
Comentario: En el cálculo del límite anterior hemos utilizado
\( \lim_{n \to \infty} \left (1-\displaystyle \frac{\lambda }{n} \right)^{n} =lim_{n→∞} \left [ \left (1+ \displaystyle \frac{1}{-\displaystyle \frac{n}{\lambda}} \right )^{- \displaystyle \frac{n}{\lambda}} \right ]^{-\lambda }=e^{- \lambda} \)
y
\( \lim_{n \to \infty} \left [ \left (1- \displaystyle \frac{1}{n} \right ) \left (1- \displaystyle \frac{2}{n} \right ) \cdots \left (1- \displaystyle \frac{k-1}{n} \right ) \right ]=1= \lim_{n \to \infty} \left (1- \displaystyle \frac{\lambda}{n} \right)^{k} \)
En general, cuando en la distribución binomial, \( B(n, p), n \geq 50 \) y \( p \leq 0.1 \) o cuando \( np<5 \), dicha distribución se puede sustituir por la distribución de Poisson, \( P( \lambda=np) \), para el cálculo de las probabilidades de los valores de la v.a. \( X \).
Ejemplo 6.5: El 2% de los libros encuadernados en cierto taller tiene encuadernación defectuosa, obtener la probabilidad de que 5 de 400 libros encuadernados en este taller tengan encuadernaciones defectuosas.
Respuesta:
Si consideramos la v.a. \( X \) que contabiliza el número de libros defectuosos encuadernados en cierto taller, esta v.a. sigue una disribución binomial \( B(n=400, p=0.02) \). Como \( n\geq 50 \) y \( p \leq 0.1\), se puede aproximar la distribución binomial por una distribución de Poisson de parámetro \( \lambda =np=400 \times 0.02=8; X \rightarrow P( \lambda =8) \)
\( P[X=5]= \displaystyle \frac{\lambda^{r}}{r!}e^{-\lambda }= \displaystyle \frac{8^{5}}{5!}e^{-8}=0.092 \)
Ejemplo 6.6: Cierta enfermedad tiene una probabilidad muy baja de ocurrir, p=1/100.000. Calcular la probabilidad de que en una ciudad con 500.000 habitantes haya más de 3 personas con dicha enfermedad. Calcular el número esperado de habitantes que la padecen.
Respuesta:
Si consideramos la v.a. \( X \) que contabiliza el número de personas que padecen la enfermedad, es claro que sigue un modelo binomial, pero que puede ser muy bien aproximado por un modelo de Poisson, de modo que
\( X \rightarrow B(n=500.000, p=1/100.000) \Rightarrow X \rightarrow P(\lambda =5) \)
\( \begin{array}{ll} P[X>3] = 1-P[X \leq 3] & = 1-P[X=0]-P[X=1]-P[X=2]-P[X=3]= \\ & = 1-0.0067-0.0337-0.0842-0.1404=0.735 \\ \end{array} \)
El número esperado de personas que padecen la enfermedad es \( E[X]=5 \).
Ejercicios propuestos: Relación VI
1. Una compañía de telefonía comienza una campaña con el propósito de aumentar el número de miembros. Con base en experiencia previa, se sabe que una de cada 20 personas que reciben la llamada se une a la compañía. Si en un día 25 personas reciben la llamada telefónica ¿Cuál es la probabilidad de que por lo menos dos de ellas se inscriban en la compañía? ¿Cuál es el número esperado? (Sol: a) 0.3576; b) 1.25).
2. En un proceso de manufactura se seleccionan todos los días, de manera aleatoria, 15 unidades con el propósito de verificar el porcentaje de unidades defectuosas en la producción. Con base en la información previa, la probabilidad de tener una unidad defectuosa es de 0.05. La producción se detiene cada vez que una muestra de 15 unidades tenga 2 o más defectuosas. Determinar la probabilidad de que la producción se detenga. (Sol: 0.1709).
3. Un comprador de circuitos integrados ha adoptado un plan para aceptar un envio de éstos y que consiste en inspeccionar una muestra aleatoria de 100 circuitos provenientes del lote. Si el comprador encuentra no más de dos circuitos defectuosos en la muestra, acepta el lote; de otra forma, lo rechaza. Si se envía al comprador un lote que contiene 1% de circuitos defectuosos, ¿Cuál es la probabilidad de que éste sea aceptado? (Sol.: 0.9197).
4. Una máquina automática dedicada a la fabricación de comprimidos laxantes, produce defectuosos a razón de 1%. Calcular: a) Si los comprimidos se colocan en tubos de 25 unidades, ¿Cuál es la probabilidad de que el tubo tenga 0 defectuosos? b) Si los tubos se colocan en cajas de 10, ¿Cuál es la probabilidad de que una caja contenga los 10 tubos con ningún comprimido defectuoso? (Sol: a) 0.778; b) 0.0812).
5. Una compañia de seguros ha determinado que 1 de cada 5000 personas fallecen anualmente por accidente laboral. La compañía tiene 50000 seguros de vida de este tipo en todo el país teniendo que abonar a los afectados por cada póliza 6000 euros. Determinar la probabilidad de que la compañía tenga que pagar en un año por lo menos 72.000 euros a los familiares de los asegurados. (Sol: 0.303).
6. Sabiendo que el número medio de enfermos recibidos cada 10 minutos en un centro sanitario entre las 10 h. y las 15 h. es 1.8. Suponiendo que dicho número de enfermos sigue una distribución de Poisson. Calcular la probabilidad de que entre las 12 h. y las 12 h. 10 m. haya: a) Ningún enfermo; b) un enfermo; c) Dos enfermos; d) Al menos dos enfermos; e) Más de 2 enfermos. (Sol: a) 0.1653; b) 0.2975; c) 0.2678; d) 0.5372; e) 0.2694).
7. La probabilidad de que se rompa la lámpara de un televisor en un mes es 0.02. Si tenemos 5 años el televisor: Calcular: a) La distribución del número de roturas, X; b) Esperanza y varianza de X; c) Probabilidad de que no haya ninguna rotura; d) Probabilidad de que haya más de una rotura. (Sol: a) \( {60 \choose r }(0.02)^{r}(0.98)^{60-r} \); b) 1.2; 1.176; c) 0.301; d) 0.3376).
8. El delegado de zona de una casa dedicada a la fabricación de calculadoras electrónicas vende, el mismo día a distintas empresas de una misma localidad, 5 máquina iguales. La probabilidad de que este tipo de calculadoras estén en funcionamiento 3 años después es 0.8. Calcular la probabilidad de que: a) Las cinco calculadoras estén fuera de servicio 3 años más tarde; b) Estén en servicio 3 años más tarde; c) Dos calculadoras a lo sumo estén fuera de servicio; d) Tres calculadoras estén fuera de servicio. (Sol: a) 3.2×10⁻⁴ ; b) 0.3277; c) 0.9421; d) 0.0512).
9. Una solución contiene virus bacteriófagos T₄ en una concentración de 6×10⁶ por mm³. En la misma solución hay 3×10⁶ bacterias E. coli por mm³. Suponiendo que los virus se distribuyen al azar entre las bacterias, se pide el porcentaje de bacterias que: a) No están infectadas por virus; b) Están infectadas; c) Tengan al menos 2 virus fijados sobre ellas; d) Tengan exactamente 2 virus fijados sobre ellas. (Sol: a) 13.5%; b) 86.5%; c) 59.4%; d) 27.1%).
10. Por larga experiencia se ha determinado que la meningitis por salmonelas, enfermedad rara, pero muy grave de los lactantes, produce una mortalidad aproximada del 60%, aún cuando sean tratados con cloranfenicol, seguido de tetraciclinas. En un hospital ingresaron 16 niños lactantes atacados por la enfermedad, en un brote epidémico en una gran ciudad. Se pide la probabilidad de que: a) Sobrevivan más de la mitad; b) Sobrevivan todos; c) Mueran todos; d) El número de sobrevivientes esté comprendido entre 6 y 10, incluidos estos extremos. (Sol: a) 0.142; b) 0.000000429; c) 0.0002821; d) 0.652).
11. La incidencia de una enfermedad en un determinado país fue de aproximadamente 25 casos por cada 100000 habitantes, se pide la probabilidad de que: a) En una ciudad de 60000 habitantes se dieran 6 casos o menos; b) En una ciudad de 80000 habitantes se dieran: b1) 6 casos o menos; b2) 10 casos o menos. (Sol: a) 0.007632; b1) 0.000255122; b2) 0.0108116).
12. El número de capturas diarias de loros en la cuenca del Amazonas para su utilización como animales domésticos sigue una distribución de Poisson de parámetro 5. Se pide las probabilidades: a) En un día no se produzcan más de 4 capturas; b) En una semana no se produzcan más de 4 capturas ningún día (Sol: a) 0.4405; b) 0.003218) (Examen 2006).
13. Para estudiar la regulación hormonal de una línea metabólica se les inyecta a ratas albinas un fármaco que inhibe la síntesis de proteínas del organismo. En general, cuatro de cada veinte ratas mueren a causa del fármaco antes de que el experimento haya concluido. Si se trata a 10 animales con el fármaco, calcular las probabilidades: a) Al menos 8 lleguen vivas al final del experimento; b) El número de muertes no se separe en más de una unidad de la media. (Sol: a) 0.6778; b) 0.7717).
14. En unos laboratorios se preparan los tres fármacos que se están utilizando contra una enfermedad. Las probabilidades de obtener en el mercado cada uno de ellos son, 1/6 para el fármaco A; 1/3 para el fármaco B y 1/2 para el fármaco C. Las probabilidades de curación con cada uno de ellos son: 0.9 con el fármaco A; 0.94 con el fármaco B y 0.88 con el fármaco C. Determinar: a) la probabilidad de que utilizando cualquiera de ellos, el sujeto administrado resulte curado; b) Si el sujeto se ha curado calcula la probabilidad de que se le haya administrado el fármaco B; c) Se sabe por experiencia que una de cada 5000 personas fallece al año por ingestión de cierto contaminante fatal. Si se exponen 50000 personas a dicho contaminante y se ha de indemnizar con 3000 euros si una persona fallece, calcula la probabilidad de que se tenga que pagar al año al menos 36000 euros. (Sol: a) 0.903; b) 0.3486; c) 0.3032) .
15. Un grupo de investigadores está estudiando la concentración de bacterias de un cierto tipo (A) en la cuenca de un río. Han detectado una concentración media de 3 bacterias de tipo A por cada cc de agua y se sabe que las bacterias están aleatoriamente distribuidas. Se pide: a) ¿Qué distribución de probabilidad se puede aplicar en esta situación?; b) Obtener la probabilidad de que en un cc de agua se encuentren: b1) cuatro bacterias de tipo A; b2) al menos 2 bacterias de tipo A; c) En un punto determinado se une al río un afluente que aporta otro tipo distinto de bacterias (B), con una concentración media de dos bacterias por cada cc de agua. Obtener las probabilidades de que en un cc de agua se encuentren: c1) seis bacterias de tipo A o B; c2) como máximo tres bacterias de tipo A o B. (Sol: b1) 0.1680; b2) 0.8008; c1) 0.1462; c2) 0.265).
Autora: Ana María Lara Porras. Universidad de Granada
Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.