INTRODUCCIÓN A LA INFERENCIA ESTADÍSTICA
Conceptos generales. Breve introducción al muestreo
Uno de los aspectos más importante de la Estadística es la obtención de conclusiones basadas en los datos experimentales. Este proceso, como ya hemos mencionado anteriormente, se conoce como Inferencia Estadística. Para comprender la esencia de la inferencia estadística es necesario entender las nociones de Población y Muestra (Conceptos estudiados en el Capítulo 1).
En este capítulo se establecerán algunos conceptos teóricos básicos con respecto al muestreo y a la inferencia estadística. La aplicación de estos conceptos se mostrará en capítulos posteriores.
Consideramos una población formada por N objetos en los que se selecciona una muestra de tamaño n, el proceso de muestreo debe asegurar que cada elemento de la población tiene la misma probabilidad de ser seleccionado para formar parte de la muestra y cada muestra del mismo tamaño tiene la misma probabilidad de ser seleccionada. Este procedimiento nos conduce al concepto de Muestra Aleatoria Simple.
Una muestra extraída de una población se dice que es una Muestra Aleatoria Simple (m.a.s.), cuando todo elemento de dicha población tiene la misma probabilidad de ser seleccionado para formar parte de la muestra.
Sea una población donde observamos la variable aleatoria X. Una muestra aleatoria simple (m.a.s.) de tamaño n, es un conjunto de n variables aleatorias \( X_1, X_2, \cdots, X_{n} \), tales que:
a) Las variables aleatorias \( X_1, X_2, \cdots, X_{n} \) son independientes entre sí
b) Cada v.a. \( X_{i} \), para \( i=1, 2, \cdots, n \), tiene idénticas características que la v.a. X.
De acuerdo con lo anterior, cada una de las observaciones \( X_1, X_2, \cdots, X_{n} \) es una variable aleatoria cuya distribución de probabilidad es idéntica a la de la población de la que ha sido obtenida
Comentario 8.1: Si se va a tomar una m.a. sus valores serán vv. aa., ya que aún no se ha tomado la muestra, y por tanto la notación que se debe de utilizar es \( X_1, X_2, \cdots, X_{n} \) y su media se debe notar por \( \overline {X} \) ya que también es una v.a.. Pero cuando se obtienen los valores de la muestra éstos dejan de ser vv.aa. para pasar a ser constantes, y la notación sería \( x_1, x_2, \cdots, x_{n} \), y su media, \( \overline {x} \), también es un valor.
En poblaciones finitas el muestreo aleatorio simple se realiza con reemplazamiento, es decir: Se selecciona un elemento de la población al azar, se observa el valor de la v.a. X, se devuelve a la población y se vuelve a seleccionar otro elemento. Así hasta obtener los n elementos. Este procedimiento garantiza la independencia de las observaciones.
Consideremos una población cualquiera con N objetos y todas las muestras de tamaño n que se pueden extraer aleatoriamente de dicha población. Cada una de estas muestras tiene una distribución estadística de la que se puede obtener alguna característica como la media, varianza, mediana etc. Evidentemente, estas características variarán con cada muestra.
Las características muestrales reciben el nombre de Estadísticos (o Estadísticas) y se utilizan para hacer inferencias con respecto a las características poblaciones llamadas Parámetros.
En el caso de que la característica que obtengamos de la totalidad de las muestras extraídas de la población sea:
- La media, los valores obtenidos forman una distribución que recibe el nombre de Distribución Muestral de las Medias
- La varianza, los valores obtenidos forman una distribución que recibe el nombre de Distribución Muestral de las Varianzas.
En la población considerada, X, donde denotamos cada elemento por \( X_{i} \) y designamos por \( \mu \) y \( \sigma^{2} \) a la media y la varianza poblacional, respectivamente.
\( E[X]= \mu \hspace{.3cm}\) y \( \hspace{.3cm} Var[X]= \sigma^{2} \)
Formamos todas las muestras posibles de tamaño n de dicha población y designamos por \( \overline{X}_1, \overline{X}_2, \overline{X}_3, \cdots \) y por \( \widehat{\sigma}_{1}^{2}, \widehat{\sigma}_{2}^{2}, \widehat{\sigma}_{3}^{2}, \cdots \) a las medias y varianzas muestrales, respectivamente.
Dichas medias \( \overline{X}_1, \overline {X}_2, \overline{X}_3, \cdots \) forman una Distribución Muestral de las Medias en donde denotamos por \( \mu_{ \overline{X}}, \sigma_{ \overline{X}}^{2} \) a su media y varianza, respectivamente.
\( E[ \overline{X}]= \mu_{ \overline{X}}\hspace{.3cm}\) y \( \hspace{.3cm} Var[ \overline{X}]= \sigma_{ \overline{X}}^{2} \)
y dichas varianzas \( \widehat {\sigma}_{1}^{2}, \widehat {\sigma}_{2}^{2}, \widehat {\sigma}_{3}^{2}, \cdots \) forman una Distribución Muestral de las Varianzas.
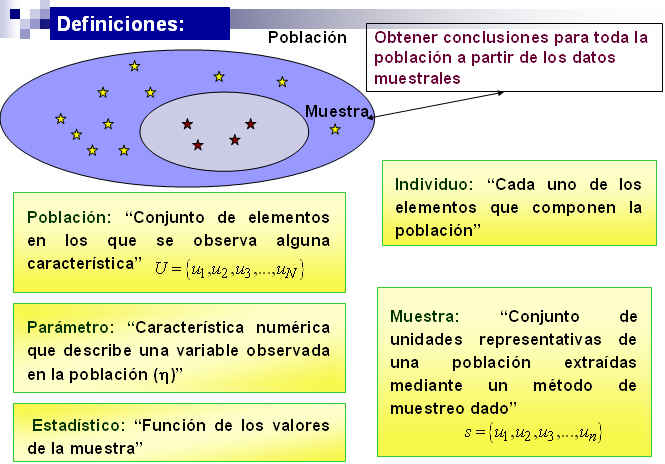
Figura 1: Conceptos básicos
Ejemplo 8.1. Para realizar un estudio sobre el nivel de colesterol de los alumnos de un centro de enseñanza se decide extraer una muestra aleatoria simple de tamaño 10. Los niveles de colesterol de los alumnos seleccionados son: 110, 120, 133, 140, 130, 220, 131, 203, 112, 149.
Población: Alumnos del centro de enseñanza
Variable aleatoria: X: {Nivel del colesterol}
Muestra aleatoria simple: \( X_1, X_2, \cdots , X_{10} \)
Nivel de colesterol del i-ésimo alumno seleccionado: \( X_{i} \)
Valores observados de las variables aleatorias: \( X_1, X_2, \cdots , X_{10} \)
\( x_1=110 \hspace{.2cm}; \hspace{.2cm} x_2=120 \hspace{.2cm}; \hspace{.2cm} x_3=133 \hspace{.2cm}; \hspace{.2cm} x_4=140 \hspace{.2cm}; \hspace{.2cm} \cdots \hspace{.2cm}; \hspace{.2cm} x_{10}=149 \)
Ejemplo 8.2. De una población P formada por 4 elementos P={1,2,3,4} se extraen muestras de tamaño 2. Calcular:
a) Media y desviación típica de la población
b) Media y desviación típica de la distribución muestral de las medias.
Respuesta:
a)
\( \mu = \displaystyle \frac {1+2+3+4} {4}=2.5 \hspace{.4cm}; \hspace{.4cm} \sigma = \displaystyle \sqrt { \displaystyle \frac {(1-2.5)^{2}+\cdots +(4-2.5)^{2} }{4}}= \displaystyle \frac { \sqrt{5}}{2} \)
b) Formemos todas las muestras posibles de tamaño 2
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_1 & 1 & 1 & 1 & 1 & 2 & 2 & 2 & 2 & 3 & 3 & 3 & 3 & 4 & 4 & 4 & 4 \\ \hline x_2 & 1 & 2 & 3 & 4 & 1 & 2 & 3 & 4 & 1 & 2 & 3 & 4 & 1 & 2 & 3 & 4 \\ \hline \overline {x}_{i} & 1 & 1.5 & 2 & 2.5 & 1.5 & 2 & 2.5 & 3 & 2 & 2.5 & 3 & 3.5 & 2.5 & 3 & 3.5 & 4 \\ \hline \end{array} \)
Formemos la distribución de las medias de cada muestra
\( \begin{array} {|l|c|c|c|c|c|c|c|c|} \hline \overline{x}_{i} & 1 & 1.5 & 2 & 2.5 & 3 & 3.5 & 4 & 4 \\ \hline n_{i} & 1 & 2 & 3 & 4 & 3 & 2 & 1 & 16 \\ \hline n_{i} \overline{x}_{i} & 1 & 3 & 6 & 10 & 9 & 7 & 4 & 40 \\ \hline n_{i}( \overline{x}_{i}-\mu_{ \overline{x}})^{2} & 2.5 & 2& 0.75 & 0 & 0.75 & 2& 2.25 & 10 \\ \hline \end{array} \)
\( \mu_{ \overline{X}}= \displaystyle \frac{40}{16}=2.5 \hspace{.4cm}; \hspace{.4cm} \sigma_{ \overline{X}}= \displaystyle \sqrt { \displaystyle \frac {10}{16}}= \displaystyle \frac { \sqrt {5}}{2 \sqrt{2}} \)
Observamos que:
i) La media poblacional μ coincide con la media \( \mu_{ \overline{X}} \) de la distribución muestral de las medias
ii) La desviación típica poblacional \( \sigma \) y la desviación típica \( \sigma_{ \overline{X}} \) de la distribución muestral de las medias están relacionadas de la forma siguiente:
\( \sigma_{ \overline{X}}= \displaystyle \frac{ \sigma }{ \sqrt{n}} \hspace{.3cm} \) , siendo n el tamaño de la muestra.
Vamos a comprobar que efectivamente se verifican i) e ii)
Consideremos de nuevo la población formada por N objetos de la que extraemos una m.a.s. \( X_1, X_2, \cdots, X_{n} \) que consiste en n variables aleatorias independientes e idénticamente distribuidas tales que
\( E(X_{i})= \mu \hspace{.3cm}; \hspace{.3cm} Var(X_{i})= \sigma^{2} \hspace{.3cm}; \hspace{.3cm}i=1,2, \cdots , n \)
donde \( \mu \) y \( \sigma^{2} \) son la media y la varianza de la distribución de la población.
Denotemos por \( \overline{X} \) a la media muestral
\( \overline{X} = \displaystyle \frac{ \displaystyle \sum_{i=1}^{n} X_{i}}{n} \)
Entonces la esperanza y la varianza de la media muestral son:
i)
\( \begin{array} {ll} \\ E[ \overline{X}] = & E \left [ \displaystyle \frac{X_1+X_2+ \cdots +X_{n}} {n} \right]=\displaystyle \frac{1}{n} E[X_1+X_2+\cdots +X_{n}]= \\
& = \displaystyle \frac{1}{n} [E(X_1)+E(X_2)+\cdots +E(X_{n})]=\displaystyle \frac{1}{n} (\mu+ \mu + \cdots + \mu) = \\ & = \displaystyle \frac{1}{n}n \mu= \mu \end{array} \)
ii)
\( \begin{array} {ll} \\ Var[ \overline{X}] = & Var \left [\displaystyle \frac{X_1+X_2+\cdots +X_{n}}{n)}\right ] = \displaystyle \frac{1}{n^{2}}\left [Var(X_1)+Var(_2₂)+\cdots +Var(X_{n}) \right]= \\
& = \displaystyle \frac{1}{n^{2}}(\sigma^{2}+ \sigma^{2}+\cdots + \sigma^{2})=\displaystyle \frac{1}{n^{2}}n \sigma^{2}= \displaystyle \frac{ \sigma^{2}}{n} \end{array} \)
En definitiva, se tiene el siguiente teorema:
Teorema 8.1. Sea X una v.a cualquiera con media \( \mu \) y varianza \( \sigma^{2} \), entonces la media, \( \overline{X} \), de una muestra aleatoria simple, \( X_2, \cdots, X_{n} \), de tamaño n es otra v.a. cuya media es \( \mu \) y cuya varianza es \( \sigma^{2}/n \)
\( E[ \overline{X}]= \mu \hspace{.3cm} \) y \( \hspace{.3cm} Var[ \overline{X}]= \displaystyle \frac{ \sigma^{2}}{n} \)
Comentario 8.2: Es importante resaltar que siempre se va a verificar que \( E[ \overline{X}]= \mu \) y \( Var[ \overline{X}]= \sigma^{2}/n \) sin importar la distribución de probabilidad de la población de la que se obtuvo la muestra, siempre que la varianza tenga un valor finito. La cantidad \( \sigma / \sqrt{n} \) recibe el nombre de error estándar.
Comentario 8.3: Se observa que cuando aumenta el tamaño de la muestra el error estándar disminuye y por tanto aumenta la precisión de la media muestral para estimar la media poblacional.
Tanto la media muestral \( \overline {X} \) como la varianza muestral \( \widehat {\sigma}^{2} \) son variables aleatorias y uno de los objetivos de este capítulo es obtener las densidades de probabilidad de \( \overline{X} \) y de \( \widehat {\sigma}^{2} \).
Distribuciones de estadísticos muestrales
En esta sección se estudiarán las distribuciones en el muestreo de las características muestrales \( \overline{X} \) y \( \widehat {\sigma}^{2} \).
Distribución en el muestreo de la media muestral \( \overline{X} \)
La media muestral es uno de los estadísticos más importante y juega un papel fundamental en situaciones en las cuales las medias poblacionales son desconocidas.
Se comprueba que para un valor grande del tamaño muestral la distribución de muestreo de la media muestral es aproximadamente Normal. Este resultado no es exclusivo de unos determinados ejemplos, sino el hecho de que las distribuciones de muestreo de la media muestral siempre tiendan a ser de forma aproximadamente Normal es una consecuencia del Teorema Central del Límite.
Teorema 8.2. Teorema Central del Límite: Sea ( \( X_1, X_2, \cdots , X_{n} \)) una m.a.s. de tamaño n de una población, con una distribución de probabilidad no especificada, cuya media es μ y su desviación típica es σ. Entonces la media muestral \( \overline {X} \) tiene una distribución aproximadamente Normal cuya media es μ y su desviación típica es σ/√n. La aproximación mejora a medida que aumenta el tamaño de la muestra.
Nota: La demostración de este teorema se deja para cursos más avanzados.
Comentario 8.4: El Teorema Central del Límite es un resultado muy útil para formular inferencias sobre la media poblacional. La esencia de este teorema reside en el hecho de que para un tamaño muestral grande, n>30, la distribución de la v.a.
\( \displaystyle \frac { \overline {X}- \mu }{\sigma / \sqrt{n}} \)
es aproximadamente N(0, 1) sin importar el tipo de modelo probabilístico que tiene la población. Dicha variable aleatoria se utiliza para formular inferencias sobre el parámetro poblacional μ cuando la varianza poblacional es conocida.
Teorema 8.3: Sea (\( X_1, X_2, \cdots, X_{n} \)) una m.a.s. de tamaño \( n \) de una población Normal X de media \( \mu \) y desviación típica \( σ \), \( ( X \rightarrow N(\mu, \sigma) ) \). Entonces la distribución de la media muestral \( \overline {X} \) es Normal con media es \( \mu \) y desviación típica \( σ/ \sqrt {n} \), \( \overline {X} \rightarrow N(\mu, \sigma/ \sqrt{n}) \)
\( X \rightarrow N(\mu, \sigma) \Rightarrow \overline {X} \rightarrow N(\mu, \sigma/ \sqrt{n}) \)
En efecto: dado que \( \overline {X} = \displaystyle \sum_{i=1}^{n} X_{i}/n \), se tiene que:
La distribución de \( \overline {X} \) será Normal ya que \( \overline {X} \) es una combinación lineal de las v.a. \( X_{i} \) que son normales y la \( E[X]= \mu \) y \( Var[X]= \sigma^{2}/n \) (Como se ha demostrado anteriormente).
También se puede demostrar este teorema utilizando la función generatriz de momentos de la distribución \( N( \mu, \sigma) \), ya que \( X \rightarrow N(\mu, \sigma) \), cuya expresión es:
\( \Psi_{X}(t)= e^{t \mu+\displaystyle \frac{t^{2} \sigma^{2}}{2}} \hspace {2cm} \) [8.1]
Para determinar la ley que sigue la distribución muestral de las medias, la expresión ( [8.1]) adopta la siguiente forma:
\( \begin{array}{ll} \Psi_{ \overline {x}}(t) & = E \left [e^{t \overline {X}}\right]=E \left [ e^{t \left [ \displaystyle \frac{X_1+X_2+ \cdots +X_{n}}{n} \right ] } \right] =E \left [e^{\displaystyle \frac {t}{n} \left [X_1+X_2+ \cdots +X_{n}\right]} \right] = \\ & = E \left [e^{\displaystyle \frac {t}{n}X_1} \times e^{\displaystyle \frac {t}{n}X_2}\times \cdots \times e^{\displaystyle \frac {t}{n}X_{n}} \right] = ^{(1)}E \left [e^{\displaystyle \frac {t}{n}X_1} \right] \times E \left [e^{\displaystyle \frac {t}{n}X_2}\right] \times \cdots \times E \left[e^{\displaystyle \frac {t}{n}X_{n}} \right]=^{(2)} \\ & = \left [e^{ \displaystyle \frac {t}{n} \mu+ \displaystyle \frac {t^{2} \sigma^{2}}{2n^{2}}}\right] \times \left [e^{ \displaystyle \frac {t}{n} \mu+ \displaystyle \frac {t^{2} \sigma^{2}}{2n^{2}}}\right] \times \cdots × \left [e^{ \displaystyle \frac {t}{n} \mu+ \displaystyle \frac {t^{2} \sigma^{2}}{2n^{2}}}\right] = \left [e^{ \displaystyle \frac {t}{n} \mu+ \displaystyle \frac {t^{2} \sigma^{2}}{2n^{2}}}\right]^{n} = \\ & = e^{ \left (\displaystyle \frac {t}{n} \mu+ \displaystyle \frac {t^{2} \sigma^{2}}{2n^{2}} \right) n}=e^{ t \mu+ \displaystyle \frac {t^{2} \sigma^{2}}{2n}} \\ \end{array} \)
que es la función generatriz de momentos de una v.a. normalmente distribuida con media \( \mu \) y desviación típica \( \sigma/ \sqrt{n} \), por lo tanto, \( X \rightarrow N(\mu, \sigma/ \sqrt{n}) \).
(1): Las variables aleatorias \( X_1, X_2, ⋯, X_{n} \) son independientes, (es una m.a.s.)
(2): Cualquier v.a. \( X_{i}\) tiene la misma distribución de probabilidad que la v.a. \( X \).
Ejemplo 8.3. En un estudio sobre la utilización de agua en una ciudad pequeña, se extrae una muestra aleatoria de 49 casas. Supongamos que la variable de interés X: “Número de litros de agua utilizados por día” es una v.a. con distribución no especificada. Del estudio realizado en el consumo de las 49 casas se obtiene que la desviación típica del nº de litros de agua consumido por día es 17.5. Obtener la probabilidad de que la media muestral se encuentre a no más de 5 litros del verdadero valor del consumo medio diario.
Respuesta:
\( X_1 \): “Nº de litros en la casa 1”
\( X_2 \): “Nº de litros en la casa 2”
…
\( X_{i} \): “Nº de litros en la casa i”
…
\( X_{49} \): “Nº de litros en la casa 49”
\( n=49>30 \Rightarrow \overline {X} \rightarrow N(\mu; \sigma/ \sqrt {n})=N(\mu; 17.5/\sqrt {49})=N(\mu; 2.5) \)
\( Z= \displaystyle \frac{\overline{X}- \mu}{ \sigma/ \sqrt {n}}= \displaystyle \frac{\overline{X}- \mu} {2.5} \rightarrow N(0, 1) \)
\( \begin{array}{ll} P[| \overline {X}- \mu| \leq 5] & = P(-5 \leq \overline{X} – \mu \leq 5)=P \left ( \displaystyle \frac{-5}{2.5} \leq \displaystyle \frac{ \overline {X}- \mu}{17.5/ \sqrt{49}} \right) \leq \displaystyle \frac{5}{2.5} = \\ & = P(-2 \leq Z \leq 2)=1-2P(Z \geq 2)=1-2 \times 0.0228=0.9544 \\ \end{array} \)
Nota: La distribución de la media muestral cuando la varianza poblacional es desconocida se estudiará en la siguiente subsección.
Teorema 8.4: Sea \( X_1, X_2, \cdots , X_{n} \) un conjunto de n variables aleatorias independientes tales que
\( \left. \begin{array} \\ X_1 \rightarrow N( \mu_1, \sigma_1) \\ \vdots \\ X_{n} \rightarrow N(\mu_{n}, \sigma_{n}) \\ \end{array} \right \} \)
Entonces
\( X_1+X_2+⋯+X_{n} \rightarrow N(\mu_1+\mu_2+⋯+\mu_{n}, \sqrt{\sigma_{1}^{2}+ \sigma_{2}^{2}+ \cdots + \sigma_{n}^{2} }) \)
\( X_1-X_2- ⋯- X_{n} \rightarrow N(\mu_1- \mu_2 -⋯- \mu_{n}, \sqrt{\sigma_{1}^{2}+ \sigma_{2}^{2}+ \cdots + \sigma_{n}^{2} }) \)
Teorema 8.5: Sea \( X_1, X_2, \cdots , X_{n} \) un conjunto de n variables aleatorias independientes normalmente distribuidas con \( E[X_{i}]= \mu_{i} \) y \( Var[X_{i}]= \sigma_{i}^{2} \) para \( i=1, 2, \cdots , n \) y sea la v.a. \( Y \) dada por
\( Y=a_1X_1+a_2X_2+ \cdots +a_{n}X_{n} \hspace{.2cm} \) con \( \hspace{.2cm} a_1, a_2, \cdots ,a_{n} \) constantes
Entonces
\( Y \rightarrow N \left ( \displaystyle \sum_{i=1}^{n} a_{i} \mu_{i}, \displaystyle \sqrt { \displaystyle \sum_{i=1}^{n}a_{i}^{2} \sigma_{i}^{2}} \right ) \)
Este resultado se conoce, generalmente, como la propiedad aditiva de la distribución Normal.
Comentario 8.5: Es importante notar que la hipótesis de normalidad no es necesaria para que la v.a. \( Y \) tenga de media \( E[Y]= \displaystyle \sum_{i=1}^{n} a_{i} \mu_{i} \) y de varianza \( Var[Y]= \displaystyle \sum_{i=1}^{n} a_{i}^{2} \sigma_{i}^{2} \).
Teorema 8.6: Si \( X_1, X_2, \cdots , X_{n} \) es un conjunto de n variables aleatorias independientes e idénticamente distribuidas según \( N(\mu, \sigma) \) . Es decir, \( X_{i} \rightarrow N(\mu, \sigma) \) para \( i=1, 2, \cdots, n \). Entonces
\( X_1+X_2+ \cdots +X_{n} \rightarrow N(n \mu, \sigma \sqrt{n}) \)
Las demostraciones de estos teoremas se dejan como ejercicios.
Ejemplo 8.4. La mayor parte de las especies de coníferas tiene piñas de polen y piñas de semilla. El polen desprendido por la piña macho es transportado por el viento hasta la piña hembra, donde se fertilizan los huevos. Se estudia el tiempo transcurrido entre la polinización y la fertilización, X. Supongamos que la variable X está normalmente distribuida con una media de 6 meses y una desviación típica de 2 meses y extraemos una muestra aleatoria simple de 25 piñas hembras. Determinar:
a) \( E[ \overline{X}] \hspace {.2cm} \) y \( \hspace {.2cm} Var[\overline{X}] \)
b) La probabilidad de que el tiempo medio transcurrido entre la polinización y la fertilización sea como mínimo de 6.5 meses
Respuesta:
a) \( E[\overline{X}]=6 \hspace{.3cm}; \hspace{.3cm} Var[\overline{X}]= \displaystyle \frac{ \sigma^{2}}{n}= \displaystyle \frac {4}{25} \)
b) X:{ Tiempo transcurrido entre la polinización y la fertilización};
\( \overline {X} \rightarrow N \left ( \mu, \displaystyle \frac{ \sigma} { \sqrt{n}} \right )=N \left (6, \displaystyle \frac{2}{5} \right) \)
\( P[ \overline {X} \geq 6.5]=P \left [ \displaystyle \frac{ \overline {X}-6}{0.4} \geq \displaystyle \frac{6.5-6}{0.4} \right ] =P[Z \geq 1.25]=0.1056 \)
Ejemplo 8.5. Las distribuciones de las calificaciones obtenidas por un grupo de alumnos es aproximadamente normal. Si la media es 5.2 y la desv. típica es 0.5. Se pide:
a) La media y la desv. típica de las sumas y de las medias muestrales para muestras de tamaño 4
b) La probabilidad de que la suma de las calificaciones obtenidas por 4 alumnos elegidos al azar sea superior a 22
c) La probabilidad. de que la media de las calificaciones de 4 alumnos elegidos al azar sea menor que 4.5.
Respuesta:
a) Sea \( X_1, X_2, X_3, X_4 \) una m.a.s. de tamaño 4 y sea \( T=X_1+X_2+X_3+X_4 \)
\( E[T]=E[X_1+X_2+X_3+X_4]=E[X_1]+E[X_2]+E[X_3]+E[X_4]=4 \times 5.2=20.8 \)
\( \sigma^{2}[T]= \sigma^{2}[X_1+X_2+X_3+X_4]=4 \sigma^{2}[X_{i}]=4×0.5^{2} \Rightarrow \sigma [T]= \sqrt{4} \times 0.5=1 \)
Por lo tanto:
\( X_1+X_2+X_3+X_4 \rightarrow N(n \mu, \sigma \sqrt{n}) \Rightarrow X_1+X_2+X_3+X_4 \rightarrow N(20.8; 1) \)
\( \left. \begin{array} {ll} \\ E[ \overline {X}]= \mu=5.2 & \\ & \\ \sigma_{\overline{X}}= \displaystyle \frac{ \sigma}{\sqrt{n}}= \displaystyle \frac{ 0.5}{2}=0.25 \\ \end{array} \right \} \Rightarrow \overline{X} \rightarrow N \left (\mu; \displaystyle \frac{ \sigma}{\sqrt{n}} \right)=N(5.2; 0.25) \)
b) \( P[T>22]=P \left [Z > \displaystyle \frac{22-20.8}{1} \right]=P[Z>1.2]=0.1151 \)
c) \( P[X<4.5]= P \left [Z< \displaystyle \frac{4.5-5.2}{0.25} \right]=P[Z<-2.8]=P[Z>2.8]=0.0026 \)
Distribución en el muestreo de la varianza muestral \( \widehat{\sigma}^{2} \)
La varianza muestral, denotada por \( \sigma^{2}\), es otro estadístico muy importante y se utiliza para formular inferencias con respecto a las varianzas poblacionales desconocidas.
Sea (\( X_1, X_2, ⋯, X_{n}\)) una m.a.s. de tamaño \( n \) de una población \( X \rightarrow N(\mu, \sigma) \). Vamos a obtener las distribuciones en el muestreo de \( \sigma^{2} \) y para ello vamos a considerar distintas situaciones:
a) La media poblacional, \( \mu \), es conocida
En este caso, la varianza muestral, \( \sigma^{2} \), se define como
\( \widehat {\sigma}^{2}= \displaystyle \frac{\displaystyle \sum_{i=1}^{n}(X_{i}- \mu)^{2}}{n} \hspace{2cm} \) [8.3]
El estadístico apropiado para formular inferencias sobre la varianza poblacional con base en la varianza muestral, es
\( \displaystyle \frac{n \widehat {\sigma} ^{2}} {\sigma^{2}}= \displaystyle \frac{\displaystyle \sum_{i=1}^{n}(X_{i}- \mu)^{2}} { \sigma^{2}} \)
que sigue una chi-cuadrada con n grados de libertad, \( \chi_{n}^{2} \).
b) La media poblacional, \( \mu \), es desconocida
En general la media poblacional, μ, será desconocida por lo que la expresión de la varianza muestral dada por ([8.2]) no será de utilidad. En su lugar, para estimar \( \sigma^{2} \), se utiliza la varianza muestral \( \widehat {\sigma}^{2} \) o la cuasivarianza muestral, \( S^{2} \), dadas por las expresiones:
Nota: En el capítulo 9 se justificará la presencia del divisor n-1 en lugar de n.
\( \widehat {\sigma}^{2} = \displaystyle \frac{ \displaystyle \sum_{i=1}^{n} \left ( X_{i}- \overline{X} \right )^{2}}{n} \hspace{1cm} ; \hspace{1cm} S^{2}= \displaystyle \frac{ \displaystyle \sum_{i=1}^{n} \left ( X_{i}- \overline{X} \right )^{2}}{n-1} \)
y la distribución en el muestreo para formular inferencias, en este caso, será la distribución del estadístico
\( \displaystyle \frac{(n-1)S^{2}}{\sigma^{2}}= \displaystyle \frac{n \widehat {\sigma}^{2}}{\sigma^{2}}= \displaystyle \frac{ \displaystyle \sum_{i=1}^{n} \left ( X_{i}- \overline{X} \right )^{2}}{\sigma^{2}} \)
que sigue una chi-cuadrada con n-1 grados de libertad, \( \chi_{n-1}^{2} \).
Ejemplo 8.6. Se investiga la resistencia a la presión de botellas de vidrio recicladas. El fabricante envía lotes de estas botellas a la embotelladora. Se sabe que la resistencia a la presión de estas botellas es una v.a. con distribución Normal y desviación típica 3 unidades. Se selecciona una m.a. de 25 botellas. Obtener la probabilidad de que el valor de la varianza muestral sea mayor de 15.48 unidades cuadradas.
Respuesta:
X: {Resistencia a la presión de botellas de vidrio recicladas}; \( X \rightarrow N(\mu, 3) \hspace{.2cm}; \hspace{.2cm} n=25 \)
\( \displaystyle \frac{(n-1)S^{2}}{\sigma^{2}}= \displaystyle \frac{n \widehat{\sigma}{2}}{\sigma^{2}} \rightarrow \chi_{n-1}^{2} \hspace{.2cm}; \hspace{.2cm} \displaystyle \frac{n \widehat{\sigma}{2}}{\sigma^{2}} \rightarrow \chi_{24}^{2} \)
\( P[ \widehat{\sigma}^{2}>15.48]=P \left [ \displaystyle \frac{n \widehat{\sigma}{2}}{\sigma^{2}} > \displaystyle \frac{n \times 5.48}{ \sigma^{2}} \right ]=P \left [ \displaystyle \frac{n \widehat{\sigma}{2}}{\sigma^{2}} > \displaystyle \frac{25×15.48}{9} \right ]= P[ \chi_{24}^{2} >43]=0.01 \)
Caso particular de la distribución de la \( X \) cuando la varianza poblacional, \( \sigma^{2} \), es desconocida.
En general, la varianza poblacional será desconocida por lo que el estadístico dado por
\( Z= \displaystyle \frac{ \overline{X} – \mu }{ \sigma/ \sqrt{n}} \)
no se puede utilizar. En esta situación, para determinar el estadístico apropiado, se tiene en cuenta que:
\( \left. \begin{array} \\ \displaystyle \frac{ \overline{X} – \mu }{ \sigma/ \sqrt{n}} \rightarrow N(0,1) \\ \\ \displaystyle \frac{(n-1)S^{2}}{\sigma^{2}}= \displaystyle \frac{n \widehat{\sigma}{2}}{\sigma^{2}} \rightarrow \chi_{n-1}^{2} \\ \end{array} \right \} \Rightarrow \displaystyle \frac{ \displaystyle \frac{\overline{X} – \mu}{\sigma / \sqrt{n}}}{ \displaystyle \sqrt {\displaystyle \frac{(n-1) S^{2}}{\sigma^{2} (n-1)} }} = \displaystyle \frac{\overline{X} – \mu}{S/ \sqrt{n}} \rightarrow t_{n-1} \)
Por lo tanto, la distribución en el muestreo para formular inferencias con respecto a μ, cuando la varianza poblacional es desconocida, es la distribución del siguiente estadístico
\( \displaystyle \frac{ \overline{X} – \mu }{S / \sqrt{n}} = \displaystyle \frac{ \overline{X} – \mu }{ \widehat {\sigma} / \sqrt{n-1}} \rightarrow t_{n-1} \)
Comentario 8.5. Para tamaños muestrales grandes los valores de la varianza muestral (o de la cuasivarianza muestral) estarán próximos a \( \sigma \) y por tanto el estadístico
\( \displaystyle \frac{ \overline{X} – \mu }{S / \sqrt{n}} \rightarrow N(0, 1) \)
Ejemplo 8.7: La leucemia mieloblástica aguda es uno de los cánceres más mortales. Se estudia la v.a. X, el tiempo en meses que sobrevive un paciente después del diagnótico inicial de la enfermedad. Se supone que X está normalmente distribuida. Se realizan 11 mediciones y se obtiene una cuasidesviación típica de 18 meses. Obtener la probabilidad de que la media no difiera de la media poblacional en más de 4 unidades.
Respuesta:
X: {Tiempo en meses que sobrevive un paciente después del diagnótico inicial de la enfermedad}
\( \displaystyle \frac{ \overline{X} – \mu }{S / \sqrt{n}} = \displaystyle \frac{ \overline{X} – \mu }{18 / \sqrt{11}} \rightarrow t_{10} \)
\( \begin{array}{ll} \\ P(| \overline{X}- \mu| \leq 4) & = P(-4 \leq \overline {X}- \mu \leq 4)=P \left ( \displaystyle \frac{-4}{18/ \sqrt{11}} \leq \displaystyle \frac{ \overline {X} – \mu }{18/ \sqrt{11}} \leq \displaystyle \frac{4}{18/ \sqrt{11}} \right) = \\ & = P(-0.73 \leq t_{10} \leq 0.73)=1-2P(t_{10} \geq 0.73)=1-2 \times 0.25=0.5 \\ \end{array} \)
Distribución de la diferencia de medias de dos poblaciones normales independientes
Todas las distribuciones estudiadas en la sección anterior sólo tenían en cuenta el caso en el que se seleccionaba únicamente una muestra aleatoria para estimar un sólo parámetro. En muchas situaciones intervienen más de una población y, por lo tanto, más de una muestra. Por ejemplo, supóngase que se desea comparar el número medio de tornillos producidos por dos máquinas distintas, o el número de piezas defectuosas que se producen en dos turnos de trabajadores, etc.
Un problema que se suele plantear, con frecuencia, es la comparación de dos medias poblacionales, esta comparación se realiza estimando la diferencia entre las dos medias y para ello se formula la inferencia con base en la diferencia entre las dos medias muestrales \( \overline{X}- \overline {Y} \). Por lo que se necesita obtener la distribución de \( \overline{X}- \overline {Y} \) cuando el muestreo se realiza sobre dos poblaciones normales independientes con:
∙ Varianzas poblacionales conocidas
∙ Varianzas poblacionales desconocidas pero iguales y tamaños muestrales pequeños
∙ Varianzas poblacionales desconocidas y tamaños muestrales grandes
∙ Varianzas poblacionales desconocidas y tamaños muestrales pequeños (que no estudiamos en este curso).
Supongamos que \( X \) e \( Y \) son dos variables aleatorias independientes y tales que \( X \rightarrow N(μ_{X}, σ_{X}) \hspace {.2cm} \) e \( \hspace{.2cm} Y \rightarrow N(μ_{Y}, σ_{Y}) \).
∙ Sea \( (X_1, X_2, \cdots , X_{n_{X}}) \) una m.a.s. de tamaño \( n_{X} \) extraída de la población \( N(μ_{X}, σ_{Y}) \) y denotamos por \( \overline{X} \) y \( \widehat{ σ}_{X}^{2} \), a la media muestral y a la varianza muestral, respectivamente.
∙ Sea \( (Y_1, Y_2, \cdots, Y_{n_{Y}}) \) una m.a.s. de tamaño \( n_{Y} \) extraída de la población \( N(μ_{Y}, σ_{Y}) \) y denotamos por \( \overline {Y} \) y \( \widehat{σ}_{Y}^{2} \), a la media muestral y a la varianza muestral, respectivamente.
Vamos a determinar la distribución de la diferencia entre las dos medias muestrales, \( \overline {X}- \overline {Y} \)
1) Las varianzas poblacionales \( σ_{X}^{2} \) y \( σ_{Y}^{2} \) son conocidas
Se comprueba fácilmente que:
\( \overline {X} – \overline {Y} \rightarrow N \left (μ_{X}-μ_{Y}, \displaystyle \sqrt { \displaystyle \frac {σ_{X}^{2}}{n_{X}}+\displaystyle \frac {σ_{Y}^{2}}{n_{Y}} } \right ) \)
En efecto:
Como \( \overline{X} \rightarrow N(μ_{X}, σ_{X}/\sqrt{n_{X}} ) \Rightarrow \Psi_{\overline{X}}(t)=E[e^{t \overline{X}}]=e^{tμ_{X}+\displaystyle \frac {t^{2}σ_{X}^{2}}{2n_{X}}} \)
Como \( \overline{Y} \rightarrow N(μ_{Y}, σ_{Y}/\sqrt{n_{Y}} ) \Rightarrow \Psi_{\overline{Y}}(t)=E[e^{t \overline{Y}}]=e^{tμ_{Y}+\displaystyle \frac {t^{2}σ_{Y}^{2}}{2n_{Y}}} \)
Entonces la función generatriz de \( X-Y \) viene dada por
\( \begin{array} {ll} \\ \Psi_{ \overline{X}- \overline{Y}}(t) = & E \left [e^{t( \overline {X}- \overline {Y})} \right] = E \left [e^{t \overline{X}} \cdotp e^{-t \overline {Y}}\right ] = ^{(1)} E \left [e^{t \overline {X}} \right ] \cdotp E \left [e^{-t \overline {Y}} \right ] = \\ & = \left [e^{tμ_{X}+ \displaystyle \frac {t^{2}σ_{X}^{2}}{2n_{X}}} \right ] \times \left [e^{- tμ_{Y}+ \displaystyle \frac {t^{2}σ_{Y}^{2}}{2n_{Y}}} \right ] = e^{t (μ_{X}-μ_{Y})+ \displaystyle \frac {t^{2}}{2} \left ( \displaystyle \frac {σ_{X}^{2}}{n_{X}} + \displaystyle \frac {σ_{Y}^{2}}{n_{Y}}\right ) } \\ \end{array} \)Por lo tanto, \( ( \overline {X}- \overline {Y}) \rightarrow N \left (\mu_{X}- \mu_{Y}, \displaystyle \sqrt {\displaystyle \frac {σ_{X}^{2}}{n_{X}}+ \displaystyle \frac {σ_{Y}^{2}}{n_{Y}} } \right ) \)
(1): X e Y independientes.
Ejemplo 8.8. Dos máquinas dedicadas a producir tornillos lo hacen: la 1^{a} con una media de 150 mm y una desviación típica de 10 mm y la 2^{a}con una media de 100 mm y una desviación típica de 5 mm. Se toman muestras de tamaño 10. Se pide:
a) Distribución muestral de la diferencia de medias
b) La probabilidad de que la longitud media de los tornillos fabricados por la 1ª máquina no sea superior en más de 45 mm a la longitud media de los tornillos fabricados por la 2ª máquina.
c) La probabilidad de que la longitud media de los tornillos fabricados por la 1ª máquina sea superior en más de 55 mm, a la longitud media de los tornillos fabricados por la 2ª máquina.
Respuesta:
a)
\( N \left (\mu_{X}- \mu_{Y} \hspace {.2cm} ; \hspace {.2cm} \displaystyle \sqrt { \displaystyle \frac { σ_{X}^{2}}{(n_{X}}+ \displaystyle \frac { σ_{Y}^{2}}{n_{Y}}} \right )=N \left (150-100) \hspace {.1cm} ; \hspace {.1cm} \displaystyle \sqrt { \displaystyle \frac {10^{2}} {10}+ \displaystyle \frac {5^{2}} {10} } \right ) =N(50; 3.54) \)
b)
\( P[ \overline {X}- \overline {Y}<45]=P \left [Z< \displaystyle \frac {45-50}{3.54} \right ]=P [Z<-1.41]=P[Z>1.41]=0.0793 \)
c)
\( P[ \overline {X} – \overline {Y} >55]=P \left [Z> \displaystyle \frac {55-50}{3.54} \right ]=P[Z>1.41]=0.0793 \)
2) El caso anterior es más de tipo teórico que práctico, pues su aplicación requiere el conocimiento de las varianzas poblacionales y estas usualmente son desconocidas. Por lo tanto, se debe obtener la distribución de \( \overline {X} – \overline {Y} \) en el caso en que el muestreo se realice sobre dos poblaciones normales independientes con varianzas desconocidas, distinguiendo dos situaciones: 2a) Las varianzas sean iguales y los tamaños muestrales pequeños. 2b) Los tamaños muestrales son grandes.
2a) Las varianzas poblacionales son desconocidas pero iguales, \( \sigma_{X}^{2}= \sigma_{Y}^{2}=\sigma^{2} \) y los tamaños de muestras son pequeños
Sabemos que:
\( ( \overline {X}- \overline {Y}) \rightarrow N \left( \mu_{X}-\mu_{Y}, \sigma \displaystyle \sqrt { \displaystyle \frac {1}{n_{X}}+ \displaystyle \frac {1} {n_{Y}}}\right ) \)
Tipificando tenemos
\( Z= \displaystyle \frac {( \overline {X}- \overline {Y})-( \mu_{X}-\mu_{Y} )} { \sigma \displaystyle \sqrt { \displaystyle \frac {1} {n_{X}}+ \displaystyle \frac {1}{n_{Y} }} } \rightarrow N(0, 1) \)
Al ser la varianza común σ² desconocida hay que determinar un buen estimador de dicha varianza que será función de las varianzas muestrales \( \widehat {σ}_{ X}^{2} \) y \( \widehat {\sigma}_{Y}^{2} \). Dicho estimador recibe el nombre de Estimador combinado de la varianza común \( σ_{X}^{2} \), se va a denotar por \( S_{p}^{2}\) y se obtiene como una media ponderada, según los grados de libertad, de las dos varianzas muestrales, siendo su expresión
\( S_{p}^{2}= \displaystyle \frac {n_{X}\widehat{\sigma}_{X}^{2}+n_{Y} \widehat{\sigma}_{Y}^{2}} {n_{X}+n_{Y}-2} \)
De esta forma, la distribución muestral para formular inferencias con respecto a la diferencia entre \( \mu_{X} \) y \( \mu_{Y} \), es la correspondiente a la variable aleatoria:
\( t= \displaystyle \frac { ( \overline {X} – \overline {Y})-(\mu_{X}-\mu_{Y})} {S_{p} \displaystyle \sqrt { \displaystyle \frac {1}{n_{X}}+ \displaystyle \frac {1} {n_{Y}} }}\)
que vamos a comprobar que sigue una distribución \( t_{n_{x}+n_{y}-2}\). En efecto, como:
\( \left. \begin{array} {ll} \\ \displaystyle \frac {n_{X} \widehat{σ}_{X}^{2}} { \sigma ^{2}} \rightarrow \chi_{n_{X}-1} & \\ \displaystyle \frac {n_{Y} \widehat {\sigma}_{Y}^{2}} { \sigma^{2}} \rightarrow \chi_{n_{Y}-1} & \\ \end{array} \right \} \Rightarrow \displaystyle \frac {n_{X} \widehat{\sigma}_{X}^{2}} { \sigma ^{2}}+ \displaystyle \frac {n_{Y} \widehat {\sigma}_{Y}^{2}} { \sigma^{2}} \rightarrow \chi_{n_{X}+n_{Y}-2} \)
y el cociente
\( \displaystyle \frac {\displaystyle \frac { ( \overline {X}- \overline {Y}) – (\mu_{X}- \mu_{Y})} { \sigma \displaystyle \sqrt { \displaystyle \frac {1} {n_{X}}+ \displaystyle \frac {1} {n_{Y}} } } } { \displaystyle \sqrt { \displaystyle \frac { \displaystyle \frac {n_{X} \widehat{\sigma}_{X}^{2}} {\sigma ^{2}}+ \displaystyle \frac {n_{Y} \widehat{σ}_{Y}^{2}} { \sigma^{2}} } { n_{X}+n_{Y}-2 } } } = \displaystyle \frac {\displaystyle \frac { ( \overline {X}- \overline {Y}) – (\mu_{X}- \mu_{Y})} { \displaystyle \sqrt { \displaystyle \frac {1} {n_{X}}+ \displaystyle \frac {1} {n_{Y}} } } } { \displaystyle \sqrt { \displaystyle \frac { n_{X} \widehat{\sigma}_{X}^{2} + n_{Y} \widehat{σ}_{Y}^{2}} { n_{X}+n_{Y}-2 } } } = \displaystyle \frac {( \overline {X}- \overline {Y}) – (\mu_{X}- \mu_{Y}) } { S_{p} \displaystyle \sqrt {\displaystyle \frac {1} {n_{X}}+ \displaystyle \frac {1} {n_{Y}}}} \rightarrow t_{n_{X}+n_{Y}-2} \)
Ejemplo 8.9. De dos poblaciones que siguen una ley normal de igual media y desviación típica, se toman muestras de tamaño 5 y cuyos valores son:
Muestra1: 4, 6, 7, 8, 10;Muestra 2: 9, 11, 12, 13, 15. Se pide:
a) Media y desviación típica muestral
b) Calcular el valor del estadístico para la distribución muestral de las diferencias de medias, según la t de Student con 8 grados de libertad.
Respuesta:
a)
\( \overline {x} = \displaystyle \frac{4+6+7+8+10}{5}=7 \hspace{.3cm} ; \hspace{.3cm} \overline{y}= \displaystyle \frac {9+11+12+13+15}{5}=12 \)
\( \widehat{σ}_{X}= \displaystyle \sqrt {\displaystyle \frac {(4-7)^{2}+ \cdots + (10-7)^{2}}{5} }=2 \hspace{.3cm} ; \hspace{.3cm} \widehat {σ}_{Y}= \displaystyle \sqrt {\displaystyle \frac {(9-12)^{2}+ \cdots + (15-12)^{2}}{5}}=2 \)
b)
\( \displaystyle \frac { ( \overline {X}- \overline {Y}) – (\mu_{X}- \mu_{Y})} { \displaystyle \sqrt { \displaystyle \frac { n_{X} \widehat{\sigma}_{X}^{2} + n_{Y} \widehat{σ}_{Y}^{2}} { n_{X}+n_{Y}-2 } } \displaystyle \sqrt { \displaystyle \frac {1} {n_{X}}+ \displaystyle \frac {1} {n_{Y}} } } = \displaystyle \frac {12-7-0 }{ \displaystyle \sqrt { \displaystyle \frac {5×4+5×4}{8 }} \displaystyle \sqrt { \displaystyle \frac {1}{5}+\displaystyle \frac {1}{5}} }=3.538 \)
2b) Las varianzas son desconocidas y los tamaños de muestras son grandes. En este caso las varianzas poblacionales se pueden estimar mediante las varianzas muestrales, de la siguiente forma
\( σ_{X}^{2} \simeq \widehat{σ}_{X}^{2}= \displaystyle \frac { \displaystyle \sum_{i=1}^{n_{x}}(x_{i}-\overline {X})^{2}}{n_{X}} \hspace{.4cm} \) y \( \hspace{.4cm} σ_{Y}^{2} \simeq \widehat{σ}_{Y}^{2}= \displaystyle \frac { \displaystyle \sum_{j=1}^{n_{y}}(y_{j}-\overline {Y})^{2}}{n_{Y}} \)
y la variable aleatoria \( \overline {X}- \overline {Y} \rightarrow N \left ( \mu_{X}-\mu_{Y}, \displaystyle \sqrt { \displaystyle \frac { \widehat{σ}_{X}^{2}}{n_{X}}+\displaystyle \frac { \widehat{σ}_{Y}^{2}}{n_{Y}}} \right ) \)
Ejemplo 8.10. Dos poblaciones normales poseen de medias 17 y 15 siendo sus desviaciones típicas desconocidas. Se toman dos muestras de tamaños 50 y 80, respectivamente y de desviaciones típicas 5 y 7. Obtener la distribución de las diferencias de medias muestrales.
Respuesta:
\( N \left ( \mu_{X}-\mu_{Y}, \displaystyle \sqrt { \displaystyle \frac { \widehat{σ}_{X}^{2}}{n_{X}}+\displaystyle \frac { \widehat{σ}_{Y}^{2}}{n_{Y}} } \right ) = N \left ( 17 – 15, \displaystyle \sqrt { \displaystyle \frac { 5^{2}}{50}+\displaystyle \frac { 7^{2}}{80} } \right )= N(2, 105) \)
Distribución del cociente de varianzas de dos poblaciones normales independientes
Cuando se dispone de dos poblaciones normales a veces interesa comparar las dos varianzas poblacionales, esta comparación se realiza estimando el cociente entre las dos varianzas y para ello se formula la inferencia con base en el cociente entre las dos varianzas (o cuasivarianzas) muestrales.
Por lo tanto, se necesita obtener la distribución de \( \widehat{σ}_{X}^{2}/ \widehat{σ}_{Y}^{2} \) (o de \( S_{X}^{2}/S_{Y}^{2} \) ) cuando el muestreo se realiza sobre dos poblaciones normales independientes con:
∙ Medias poblacionales conocidas
∙ Medias poblacionales desconocidas.
Supongamos que \( X \) e \( Y \) son dos variables aleatorias independientes y tales que \( X \rightarrow N(\mu_{X},σ_{X}) \) e \( Y \rightarrow N(\mu_{Y},σ_{Y}) \).
∙ Sea \( (X_1, X_2, \cdots , X_{n_{X}}) \) una m.a.s. de tamaño\( n_{X} \) extraída de la población \( N(\mu_{X},σ_{X}) \) y denotamos por \( \overline {X} \) y \( \widehat {σ}_{X}^{2} \) , a la media muestral y a la varianza muestral, respectivamente.
∙ Sea \( (Y_1, Y_2, \cdots , Y_{n_{Y}}) \) una m.a.s. de tamaño\( n_{Y} \) extraída de la población \( N(\mu_{Y},σ_{Y}) \) y denotamos por \( \overline {Y} \) y \( \widehat {σ}_{Y}^{2} \) , a la media muestral y a la varianza muestral, respectivamente.
1) Las medias poblacionales \( \mu_{X} \) y \( \mu_{Y} \) son conocidas
Sabemos que
\( \left. \begin{array} \\ \displaystyle \sum_{i=1}^{n_{x}} \left ( \displaystyle \frac {X_{i}- \mu_{X}}{σ_{X}} \right ) ^{2} \rightarrow \chi_{n_{X}}^{2} \\ \displaystyle \sum_{j=1}^{n_{y}} \left ( \displaystyle \frac {Y_{j}- \mu_{Y}}{σ_{Y}} \right ) ^{2} \rightarrow \chi_{n_{Y}}^{2} \\ \end{array} \right \} \Rightarrow \displaystyle \frac { \displaystyle \frac {\displaystyle \sum_{i=1}^{n_{x}} \left ( \displaystyle \frac {X_{i}- \mu_{X}}{σ_{X}} \right ) ^{2} }{n_{X}}} { \displaystyle \frac {\displaystyle \sum_{j=1}^{n_{y}} \left ( \displaystyle \frac {Y_{j}- \mu_{Y}}{σ_{Y}} \right ) ^{2} }{n_{Y}}} = \displaystyle \frac {n_Y}{n_X} \displaystyle \frac { \sigma^{2}_{Y}}{\sigma^{2}_{X}} \displaystyle \frac { \displaystyle \sum_{i=1}^{n_{x}} (X_i – \mu_X)^{2}}{\displaystyle \sum_{j=1}^{n_{y}} (Y_j – \mu_Y)^{2}} \)
sigue una distribución F- Snedecor con \( n_{X} \) y \( n_{Y} \) grados de libertad \((F_{n_{X},n_{Y}}) \)
Por lo tanto, el estadístico apropiado para formular la inferencia es
\( \displaystyle \frac {n_Y}{n_X} \displaystyle \frac { \sigma^{2}_{Y}}{\sigma^{2}_{X}} \displaystyle \frac { \displaystyle \sum_{i=1}^{n_{x}} (X_i – \mu_X)^{2}}{\displaystyle \sum_{j=1}^{n_{y}} (Y_j – \mu_Y)^{2}} \rightarrow F_{n_{X}, n_{Y}} \)
2) Las medias poblacionales \( \mu_{X} \) y \( \mu_{Y} \) son desconocidas
Sabemos que
\( \left. \begin{array} \\ \displaystyle \frac { (n_{X}-1) S_{X}^{2}}{σ_{X}^{2}} \rightarrow \chi_{n_{X}-1}^{2} \\ \displaystyle \frac { (n_{Y}-1) S_{Y}^{2}}{σ_{Y}^{2}} \rightarrow \chi_{n_{Y}-1}^{2} \\ \end{array} \right \} \Rightarrow \displaystyle \frac { \displaystyle \frac {\displaystyle \frac { (n_{X}-1) S_{X}^{2}}{σ_{X}^{2}}}{n_{X}-1}}{ \displaystyle \frac {\displaystyle \frac { (n_{Y}-1) S_{Y}^{2}}{σ_{Y}^{2}}}{n_{Y}-1}} = \displaystyle \frac {\displaystyle \frac {S_{X}^{2}}{\sigma_{X}^{2}}}{\displaystyle \frac {S_{Y}^{2}}{\sigma_{Y}^{2}}} \)
sigue una distribución F- Snedecor con \( n_{X}-1 \) y \( n_{Y}-1 \) grados de libertad \( (F_{n_{X}-1,n_{Y}-1}) \)
Por lo tanto, el estadístico apropiado para formular la inferencia es
\( \displaystyle \frac {S_{X}^{2}} {S_{Y}^{2}} \displaystyle \frac { \sigma_{Y}^{2}}{ \sigma_{X}^{2}} \rightarrow F_{n_{X}-1,n_{Y}-1} \)
∙ Caso particular: \( \sigma_{X}^{2}= \sigma_{Y}^{2} \), entonces el estadístico F se reduce a
\( F= \displaystyle \frac {S_{X}^{2}}{S_{Y}^{2}} \rightarrow F_{n_{X}-1,n_{Y}-1} \)
Ejemplo 8.11. En dos ciudades, A y B, próximas a una central nuclear se están analizando los niveles de radiación. Los niveles de radiación, \( X_{A} \) y \( X_{B} \), siguen distribuciones normales de varianzas 6.2 y 5.3 respectivamente. Se realizan 16 mediciones en la ciudad A y 21 en la ciudad B. Unos análisis previos han detectado que el índice en la Ciudad A está aumentando de forma alarmante. Por ello, se realizará un plan de evacuación de la ciudad A si la varianza muestral en dicha ciudad es por lo menos el triple que la varianza muestral de la ciudad B. Obtener la probabilidad de que se realice el plan de evacuación de la ciudad.
Respuesta:
\( \displaystyle \frac {S_{X}^{2}} {S_{Y}^{2}} \displaystyle \frac { \sigma_{Y}^{2}}{ \sigma_{X}^{2}} \rightarrow F_{n_{X}-1,n_{Y}-1} \)
\( \begin{array}{ll} P[S_{X}^{2} \geq 3 S_{Y}^{2}] & = P \left [\displaystyle \frac {S_{X}^{2}} {S_{Y}^{2}} \geq 3 \right ]=P \left [ \displaystyle \frac {S_{X}^{2}} {S_{Y}^{2}}\displaystyle \frac {σ_{Y}^{2}}{σ_{X}^{2}} \geq 3 \displaystyle \frac {σ_{Y}^{2}}{σ_{X}^{2}} \right ] \\ & \\ & = P \left [F_{15.20} \geq 3 \times \displaystyle \frac {5.3}{6.2} \right ]=P[F_{15.20} \geq 2.564]=0.025 \\ \end{array} \)
Distribuciones en el muestreo para distribuciones Binomiales
En esta sección estudiamos la distribución muestral de una proporción y de dos proporciones. El Teorema central del límite, estudiado en la Sección 2, proporcionará la justificación teórica para los procedimientos que utilizamos. En toda la sección supondremos que los tamaños muestrales son lo suficientemente grandes para justificar el uso de dicho teorema.
Distribución de la proporción muestral
En estudios médicos, biólogos,… es frecuente estudiar en una población determinada una característica particular, (una determinada enfermedad, un determinado hábito (ejemplo fumar),…) y cada miembro de la población puede clasificarse según que posea o no esa característica. Las inferencias se hacen con respecto al parámetro p, proporción de la población que tiene la característica.
Consideramos una variable aleatoria X con distribución B(n, p), donde “p” es la proporción de “éxitos” en la población.
Sea \( (X_1, X_2, \cdots , X_{n}) \) una m.a.s. de tamaño n de una población \( X \rightarrow B(n, p) \). Se denota por p a la proporción muestral y se define como:
\( \widehat {p} = \displaystyle \frac{X}{n} \)
Para tamaños muestrales grandes, la proporción muestral \( \widehat {p} \) tiene una distribución aproximadamente normal, con media p y varianza \( p(1-p)/n \)
\( p \rightarrow N \left ( p, \displaystyle \sqrt { \displaystyle \frac {p(1-p)}{n} } \right ) \)
Nota: En la Sección 3 del Capítulo 7 estudiamos que en el caso de tamaños muestrales grandes, n > 30 y p no tome valores extremos, la distribución Binomial se puede aproximar mediante una distribución Normal aplicando el Teorema de Moivre: \( X \rightarrow N(np, \displaystyle \sqrt { np(1-p) }) \).
Por lo tanto, el estadístico para formular inferencias sobre la proporción poblacional con base en la proporción muestral es :
\( Z= \displaystyle \frac { \widehat{p}-p}{ \displaystyle \sqrt { \displaystyle \frac {p(1-p)}{n} }} \rightarrow N(0,1) \)
Ejemplo 8.12. El virus del herpes simple produce una de las formas mas molestas de enfermedad venérea. Un estudio reciente probó una pomada sobre 36 mujeres con infecciones genitales de herpes. En el transcurso de cuatro días, los síntomas disminuyeron en 32 de los 36 casos. Encontrar una estimación puntual para la proporción de mujeres para las que este tratamiento se mostrará eficaz.
Respuesta:
\( \widehat{p} = \displaystyle \frac {X}{n}= \displaystyle \frac {32}{36}=0.889 \)
Ejemplo 8.13. Los excesos del botellón ha llevado a una asociación de alcohólicos ha realizar una terapia a los jóvenes para que dejen de beber. Se sabe que las personas que llevan al menos 5 años bebiendo tienen más dificultades para dejar de beber, y que el 29% de los jóvenes llevan al menos 5 años bebiendo. Para realizar el estudio se toma una m.a.s. de 60 jóvenes y se decide separar los que se consideran alcohólicos de los otros si entre los bebedores elegidos más de un 18% llevan más de 5 años bebiendo. Determinar la probabilidad de que se decida separarlos.
Respuesta:
\( p \) : {Proporción de bebedores con al menos 5 años bebiendo} (Poblacional)
\( \widehat{p} \) : {Proporción de bebedores con al menos 5 años bebiendo} (Muestral)
\( \widehat{p} \rightarrow N \left ( p, \displaystyle \sqrt {\displaystyle \frac {p(1-p)}{n} } \right ) =N \left ( 0.29, \displaystyle \sqrt {\displaystyle \frac {0.29 \times 0.71}{60} } \right )= N(0.29; 0.0586) \)
\( Z= \displaystyle \frac { \widehat{p}-p}{ \displaystyle \sqrt { \displaystyle \frac {p(1-p)}{n} }} = \displaystyle \frac { \widehat{p}-0.29}{ 0.0586} \rightarrow N(0,1) \)
\( \begin{array}{ll} P[ \widehat {p} \geq 0.18] & = P \left [ \displaystyle \frac { \widehat {p} -0.29 }{0.0586 } \geq \displaystyle \frac { 0.18-0.29 }{0.0586} \right ]=P[Z \geq -1.877]=1-P[Z \geq 1.877] = \\ & = 1-0.0307=0.9693 \\ \end{array} \)
Distribución de la diferencia de proporciones muestrales
En diversos estudios surge frecuentemente el problema de comparar dos proporciones. En general, tenemos dos poblaciones de interés y en cada población se estudia la misma característica. De esta forma, cada miembro de la población se clasifica según posea o no la característica y en cada población es conocida la proporción de los individuos que poseen la característica. Las inferencias se hacen sobre \( p_{X}-p_{Y}\), siendo \( p_{X} \) y \( p_{Y} \) las proporciones de individuos que presentan la característica en la primera población y en la seguna población, respectivamente.
Supongamos que X e Y son dos variables aleatorias independientes y tales que \( X \rightarrow B(n_{X}, p_{X}) \) e \( Y \rightarrow B(n_{Y}, p_{Y}) \)
∙ Sea \( (X_1, X_2, \cdots , X_{n_{X}}) \) una m.a.s. de tamaño \( n_{X} \) extraída de la población \( B(n_{X}, p_{X}) \) y denotamos por \( \widehat {p}_{X}= \displaystyle \frac {X} {n_{X}} \) a la proporción muestral
∙ Sea \( (Y_1, Y_2, \cdots , Y_{n_{Y}}) \) una m.a.s. de tamaño \( n_{Y} \) extraída de la población \( B(n_{Y}, p_{Y}) \) y denotamos por \( \widehat{p}_{Y}= \displaystyle \frac {Y}{n_{Y}} \) a la proporción muestral
Cuando los tamaños muestrales son lo suficientemente grandes (>30) se pueden aproximar por distribuciones normales, por tanto para \( n_{X} \) y \( n_{Y} \) mayores que 30, se verifica:
\( X \rightarrow N \left ( n_{X}p_{X}, \displaystyle \sqrt {n_{X}p_{X}(1-p_{X}) }\right) \)
\( Y \rightarrow N \left ( n_{Y}p_{Y}, \displaystyle \sqrt {n_{Y}p_{Y}(1-p_{Y}) } \right) \)
Por lo tanto, el estadístico para formular inferencias sobre diferencia de proporciones poblacionales con base en la diferencia de las proporciones muestrales es :
\( \widehat{p}_{X}- \widehat{p}_{Y}= \displaystyle \frac {X} {n_{X}}- \displaystyle \frac {Y} {n_{Y}} \rightarrow N \left ( p_{X}-p_{Y} , \displaystyle \sqrt { \displaystyle \frac {p_{X}(1-p_{X}}{n_{X}}+ \displaystyle \frac {p_{Y}(1-p_{Y})} {n_{Y}} } \right ) \)
Ejemplo 8.14. Ante la ley antitabaco muchos españoles han dejado de fumar, o fuman menos. A pesar de la ley, el 30% de las mujeres y el 27% de los hombres son fumadores. Queremos saber la probabilidad de que las mujeres fumadoras superan a los hombres fumadores en al menos 5%. Para ello se toma una muestra de 50 mujeres y 45 hombres.
Respuesta:
\( p_{X} \) : {Proporción de mujeres fumadoras en la población}
\( p_{Y} \) : {Proporción de hombres fumadores en la población}
\( \widehat {p}_{X} \) : {Proporción de mujeres fumadoras en la muestra}
\( \widehat{p}_{Y} \) : {Proporción de hombres fumadores en la muestra}
\( Z= \displaystyle \frac {( \widehat{p}_{X}- \widehat {p}_{Y})-(p_{X}-p_{Y}) }{ \displaystyle \sqrt { \displaystyle \frac {p_{X}(1-p_{X})}{n_{X}}+ \displaystyle \frac {p_{Y}(1-p_{Y}) } {n_{Y}}}} = \displaystyle \frac { ( \widehat {p}_{X}- \widehat {p}_{Y})-(0.30-0.27) }{ \displaystyle \sqrt {\displaystyle \frac {0.30 \times 0.90 } {50}+ \displaystyle \frac {0.27 \times 0.73 } {45} }}= \displaystyle \frac { ( \widehat {p}_{X}- \widehat {p}_{Y})-0.03 } {0.099} \)
\( \begin{array}{ll} P[ \widehat {p}_{X} \geq \widehat {p}_{Y}+0.05] & = P[ \widehat {p}_{X}- \widehat {p}_{Y} \geq 0.05]= P \left [\displaystyle \frac {( \widehat {p}_{X}- \widehat {p}_{Y})-0.03 } {0.099} \geq \displaystyle \frac {0.05-0.03 } {0.099} \right ] = \\ & = P[Z≥0.2020]=0.4207 \\ \end{array} \)
Ejercicios propuestos: Relación VIII
1. Unos grandes almacenes han calculado que el 1% de los artículos le son sustraídos en las rebajas. Se disponen en una sección controlar 200 piezas rebajadas. Se pide: a) Probabilidad de que roben menos de 0.5% ; b) Probabilidad de que roben más de 1%. (Soluciones: a) 23.89%; b) 50%)
2. En una reunión una droga fue tomada por 14 personas, de las cuales 6 lo hacen por 1ª vez y 8 ya son habituales a ellas. La droga produjo en el primer grupo sueños de duración; 11, 12, 13, 16, 17 y 15 horas, mientras que en el segundo grupo: 8, 7, 9, 10, 6, 7, 9, 8, horas. Se pide: a) Media y desviación típica de cada grupo; b) Calcular el valor del estadístico de la dist. muestral de las diferencias de medias, que se distribuye según una t de Student de 12 grados de libertad, sabiendo que las poblaciones tienen la misma media y desviación típica (Soluciones: a) 14; 2.16; 8; 1.2); b) 6.084)
3. Las manadas de lobos son territoriales, con territorios de 130 Km² o más. Se piensa que los aullidos de los lobos, que comunican información tanto de la situación como de la composición de la manada, están relacionados con la territorialidad. Consideramos la variable X, duración en minutos de una sesión de aullidos de una determinada manada sometida a estudio. Supongamos que X está normalmente distribuida. Se pide: a) Se realizan 16 mediciones en las que se obtiene una cuasidesviación típica de 0.2 segundos. Obtener la probabilidad de que la media muestral no difiera de la media poblacional en más de 0.08765 segundos; b) Se realizan 64 mediciones en las que se obtiene una cuasidesviación típica de 4 segundos. Obtener la probabilidad de que la media muestral no difiera de la media poblacional en más de 0.6 segundos. (Soluciones: a) ; b) 0.7698)
4. El peso medio de los pasajeros de un avión es de 75 kg y la desv. típica es de 7.5 kg. ¿Cuántos pasajeros debe admitir un avión para que la probabilidad de que su carga total supere a los 3000 kg sea igual a 0,05? (Sol: \( 19 \leq n \))
5. De una población N(μ,σ), de media y desviación típica desconocidas, se toma una muestra de tamaño 10 y de varianza \( σ^{2} \). Hallar las siguientes probabilidades. (Soluciones: a) 0.982; b) 0.419; c) 0.98).
a) \( P \left [ \displaystyle \frac {\widehat{σ}^{2}} {σ^{2}} \leq 2 \right] \)
b) \( P \left [1 \leq \displaystyle \frac {\widehat{σ}^{2}} {σ^{2}} \leq 1.8 \right ] \)
c) \( P[σ \leq 2]\hspace {.2cm} (con \hspace {.2cm} \widehat {σ}^{2}=1) \)
6. De una población normal N(0,σ) se toma una muestra de tamaño 5, de media x y desviación típica σ. Calcúlense las siguientes probabilidades. (Soluciones: a) 0.008; b) 0.053; c) 0.994).
a) \( P \left [ \displaystyle \frac { \overline{X}} { \widehat{σ}}>2 \right] \)
b) \( P \left [0.9 \leq \displaystyle \frac { \overline {X}} { \widehat{σ}} \leq 1.4 \right ] \)
c) \( P \left [ \left | \displaystyle \frac { \overline {X}} { \widehat{σ}} \right | <3 \right ] \)
7. Las planchas metálicas de un gran conjunto están compuestas por 3 clases de láminas superpuestas A, B, y C elegidas al azar de 3 poblaciones de láminas. Cada plancha tiene 3 láminas de la clase A, 2 de la clase B y 4 de la clase C. Los espesores de las láminas son variables aleatorias con las medias y desviaciones típicas que se indican: \( \mu_{A}=0,20 , σ_{A}=0,030 \hspace{.2cm} ; \hspace{.2cm} \mu_{B}=0,30,σ_{B}=0,02 ; \hspace{.2cm} \mu_{C}=0,01,σ_{C}=0,001\). Se pide: a) La media y desviación típica de los espesores de todas las planchas; b) La probabilidad de que una plancha elegida al azar del conjunto tenga un espesor comprendido entre 1.10 y 1.30. (Soluciones: a) 1.24; 0.098; b) 0.6535).
8. De una población normal de media μ y varianza 4,5, se extraen 2 muestras al azar de tamaño n de las que se calculan sus medias \( \overline {X}_1 \) y \( \overline {X}_2 \). ¿Qué valor debe tener n para que \( \overline {X}_1 \) y \( \overline {X}_2 \) difieran entre sí en menos de 2 unidades con una probabilidad igual a 0,95 ? (Sol: n=9).
9. Se llevó a cabo un estudio para investigar el efecto producido por el desagüe de una zona de aparcamientos en la densidad de la vegetación circundante. Se estudiaron dos áreas. Una era objeto de desagüe de una zona de aparcamientos; la otra no estaba cerca de ningún aparcamiento y se utilizó de control. Cada área se subdividió en una serie de paneles de 2 metros por 20 metros y se contó el número de plantas encontradas en cada uno, obteniéndose los siguientes datos:
X: {Área de drenaje}: 62, 76, 58, 57, 79, 82, 72, 77, 64, 74, 71, 59, 54, 49, 53
Y: {Área de control}: 72, 77, 60, 59, 61, 64, 69, 65, 59, 64, 62, 75, 69, 64, 71
Se pide: a) Estimar el número medio de plantas por panel encontradas en cada área; b) Se supone que las varianzas poblacionales son iguales. Obtener la probabilidad de que la diferencia de medias muestrales no difiera de la diferencia de medias poblacionales en más de 1.5 unidades. (Soluciones. a) \( \overline {x}=65.80, \widehat {σ}_{X}=10.645 \hspace{.2cm}; \hspace{.2cm} \overline {y} =66.07, \widehat {σ}_{Y}=5.788 \hspace{.2cm}; \hspace{.2cm} b) 0.0712) \).
10. Un determinado fármaco disponible en el mércado para el tratamiento de la gota, está siendo estudiado para utilizarlo en la prevención de muertes súbitas por una segunda crisis cardíaca, entre pacientes que ya sufrieron un primer ataque. En el estudio, 72 pacientes recibieron el fármaco y a 80 se les dio un placebo. Después de ocho meses, se observó que de 32 muertes por un segundo ataque al corazón, 14 se produjeron en el grupo del placebo y 18 en el grupo de fármaco. Determinar la probabilidad de que las muertes súbitas entre los pacientes tratados con el placebo superen a los tratados con el fármaco en al menos un 8%. (Sol: 0.1112).
Autora: Ana María Lara Porras. Universidad de Granada
Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.