DISTRIBUCIONES ESTADÍSTICAS BIDIMENSIONALES
Concepto de variable estadística bidimensional
En el Tema 1 se ha estudiado, sobre cada uno de los individuos que forman la población, un sólo carácter. En este capítulo se estudiarán sobre cada uno de los individuos dos caracteres, que se notarán por X e Y, (por ejemplo: estatura y peso de los estudiantes de una facultad, edad y peso de los niños de un colegio, ⋯). La variable que representa el estudio conjunto de esos dos caracteres se denota por (X,Y) y recibe el nombre de Variable Estadística Bidimensional.
Consideremos que se realiza el estudio de dos caracteres, X e Y, sobre cada uno de los n individuos que integran una población.
Denotemos por \( x_1, ⋯, x_i, ⋯, x_k \), las k modalidades del carácter X y por \( y_1, ⋯, y_j, ⋯, x_p \), las p modalidades del carácter Y. Por lo tanto, a cada individuo de la población le corresponden un par de valores \( (x_{i},y_{j}) \).
Se llama Frecuencia absoluta del par de valores \( (x_{i},y_{j}) \), y se denota por \( n_{ij} \), al número de individuos de la población que presentan el valor \( x_{i} \) de X y el valor \( y_{j} \) de Y.
Las modalidades de cada uno de los caracteres deben ser incompatibles y exhaustivas, por tanto
\( n = \sum_{i=1}^{k} \sum_{j=1}^{p}n_{ij} = \sum_{j=1}^{p} \sum_{i=1}^{k}n_{ij}\)
Se define la Frecuencia Relativa del par de valores \( (x_{i},y_{j}) \), y se denota por \( f_{ij} \) , como la proporción de individuos de la población que presentan simultáneamente los valores \( x_{i} \) de X e \( y_{j} \) de Y, es decir
\( f_{ij}= \displaystyle \frac {n_{ij}}{n} \)
Se comprueba que la suma de las frecuencias relativas de todos los pares de valores es igual a la unidad
\( \sum_{i=1}^{k}\sum_{j=1}^{p}f_{ij}=1 \)
El conjunto de valores denotados por \( ((x_{i},y_{j}),n_{ij} ; i=1,⋯,k; j=1,⋯,p) \) recibe el nombre de Distribución Bidimensional de Frecuencias.
Tablas estadísticas
La forma usual de representar a los n individuos de la población, descrita anteriormente, es mediante una tabla de doble entrada, llamada Tabla de Correlación, en cuyas filas figuran las k modalidades del carácter X y en las columnas las p modalidades del carácter Y. Obteniéndose, por lo tanto, una tabla formada por k filas y p columnas.
\(
\begin{array} {|c|c|c|c|c|c|c|} \hline & e^´_0-e^´_1 & \cdots & e^´_{j-1}-e^´_j & \cdots & e^´_{p-1}- e^´_p & n_{i.} \\ X/Y & y_1 & & y_j & & y_p & \\
\hline e_0 – e_1 & n_{11} &\cdots & n_{1j} & \cdots & n_{1p} & n_{1.} \\ x_1 & & & & & & \\ \hline \vdots & \vdots & \cdots & \vdots & \cdots & \vdots & \vdots \\ \hline e_{i-1} – e_i & n_{i1} & … & n_{ij} & \cdots & n_{ip} & n_{i.} \\ x_i & & & & & & \\ \hline \vdots & \vdots & \cdots & \vdots & \cdots & \vdots & \vdots \\ \hline e_{k-1} – e_k & n_{k1} & \cdots & n_{kj} & \cdots & n_{kp} & n_{k.} \\ x_k & & & & & & \\ \hline n_{.j} & n_{.1} & \cdots & n_{.j} & \cdots & n_{.p} & n_{..} \\ \hline \end{array} \)
Tabla 2.1
En la última columna y en la ultima fila aparecen las notaciones \( n_{1.}, ⋯, n_{i.}, ⋯, n_{k.} \) y \( n_{.1}, ⋯, n_{.j}, ⋯, n_{.p} \), respectivamente, y el valor \( n_{..} \), donde
- La frecuencia absoluta \( n_{i.} \) representa el número de veces que se ha observado el valor \( x_{i} \) de X independientemente del valor presentado por Y. Por lo tanto, \( n_{i.}\) es la suma de todas las frecuencias absolutas de la fila correspondiente al valor \( x_{i} \) de X.
\( n_{i1}+n_{i2}+⋯+n_{ij}+⋯+n_{ip}=\sum_{j=1}^{p}n_{ij}=n_{i.} \hspace{1cm} \) (i fijo)
- La frecuencia absoluta \( n_{.j} \) representa el número de veces que se ha observado el valor \( y_{j} \) de Y independientemente del valor presentado por X. Por lo tanto, \( n_{.j} \) es la suma de todas las frecuencias absolutas de la columna correspondiente al valor \( y_{j} \) de Y.
\( n_{1j}+n_{2j}+⋯+n_{ij}+⋯+n_{kj}= \sum_{i=1}^{k}n_{ij}=n_{.j} \hspace{1cm} \) (j fijo)
- La frecuencia absoluta \( n_{..} \) (también n) representa el número total de observaciones. Es decir, es el total de las frecuencias absolutas \( n_{ij} \) correspondiente a los valores \( x_{i} \) de X e \( y_{j} \) de Y, o también la suma de la columna correspondiente a las frecuencias \( n_{i.}, i=1, 2, ⋯, k \) o la suma de la fila correspondiente a las frecuencias \( n_{.j}, j=1, 2, ⋯, p \).
\( n=n_{..}=\sum_{i=1}^{k}\sum_{j=1}^{p}n_{ij}=\sum_{i=1}^{k}n_{i.}=\sum_{j=1}^{p}n_{.j} \)
También se emplea la notación de punto en las frecuencias relativas para sus sumas parciales, así
\( f_{i.}=\sum_{j=1}^{p}f_{ij}= \displaystyle \frac {n_{i.}} {n} \hspace{10 mm} , \hspace{10 mm} f_{.j}=\sum_{i=1}^{k}f_{ij}= \displaystyle \frac{n_{.j}} {n} \)
Se comprueba que:
\( \sum_{i=1}^{k}\sum_{j=1}^{p}f_{ij}=\sum_{i=1}^{k}f_{i.}=\sum_{j=1}^{p}f_{.j}=1 \)
Ejemplo 2.1: Se han estudiado los pesos (Kg.) y las tallas (cm.) correspondientes a un grupo de individuos, obteniendo la siguiente información:
\( \begin{array} {|c|c|c|c|c|c|c|c|} \hline X/Y & 159-161 & 161-163 & 163-165 & 165-167 & 167-169 & 169-171 & n_{i.} \\ \hline
48 & 3 & 2 & 2 & 1 & 0 & 0 & 8 \\
51 & 2 & 3 & 4 & 2 & 2 & 1 & 14 \\
54 & 1 & 3 & 6 & 8 & 5 & 1 & 24 \\
57 & 0 & 0 & 1 & 2 & 8 & 3 & 14 \\
{34}0 & 0 & 0 & 0 & 2 & 4 & 4 & 10 \\ \hline
n_{.j} & 6 & 8 & 13 & 15 & 19 & 9 & 70 \\ \hline \end{array} \)
- \( n_{34}=8 \); significa que 8 de los 70 individuos pesan 54 Kg y miden entre 165 y 167 cm.
- \( n_{4.}=n_{41} +n_{42}+n_{43}+n_{44}+n_{45}+n_{46}=0+0+1+2+8+3=14 \); significa que 14 de los 70 individuos pesan 57 Kg independientemente de la talla que tengan.
- \( n_{.5}= n_{15}+ n_{25}+ n_{35}+ n_{45}+ n_{55}=0+2+5+8+4=19 \); significa que 19 de los 70 individuos miden entre 167 y 169 cm independientemente de sus pesos.
- \( n=\sum_{i=1}^5 \sum_{j=1}^6 n_{ij}=3+2+2+1+0+0+2+3+⋯+0+0+0+2+4+4=70 \)
- \( n=\sum_{i=1}^5 n_{i.}=8+⋯+14+10=70 \hspace{10 mm}; \hspace{10 mm}n=\sum_{j=1}^6 n_{.j}=6+8+⋯+19+9=70 \)
Distribuciones marginales y condicionadas
Distribuciones marginales
Consideramos que en los n individuos de la población, descrita anteriormente, solamente estudiamos uno de los dos caracteres, la distribución resultante de este estudio es una distribución unidimensional que recibe el nombre de Distribución Marginal de X o de Y (dependiendo del carácter implicado en el estudio).
- Distribución Marginal de X: Las frecuencias absolutas \( n_{i.} \) (columna marginal en la tabla de doble entrada) definen la Distribución Marginal según el carácter X. Por tanto, la Distribución Marginal según el carácter X expresa cómo se distribuye la variable X independientemente de los valores presentados por la variable Y.
\( \begin{array} {|c|c|c|} \hline x_{i} & n_{i.} & f_{i.} \\ \hline
x_1 & n_{1.} & f_{1.} \\ x_2 & n_{2.} & f_{2.} \\ ⋮ & ⋮ & ⋮ \\ x_{i} & n_{i.} & f_{i.} \\ ⋮ & ⋮ & ⋮ \\ x_{k} & n_{k.} & f_{k.} \\ \hline & n & 1 \\ \hline \end{array} \)
\( n_{i.} \) representa la frecuencia absoluta marginal de X \( \hspace{5 mm} \sum_{i=1}^{k}n_{i.}=n \)
\( f_{i.}\) representa la frecuencia relativa marginal de X
\( f_{i.}=\displaystyle \frac{n_{i.}}{n} \hspace{5 mm} \) o \( \hspace{5 mm} f_{i.}=\sum_{j=1}^{p}f_{ij} \hspace{5 mm} \) (i fijo); \( \hspace{5 mm}\sum_{i=1}^{k}f_{i.}=1\)
- Distribución Marginal de Y: Las frecuencias absolutas \( n_{.j} \) (fila marginal en la tabla de doble entrada) definen la Distribución marginal según el carácter Y. Por tanto, la Distribución Marginal según el carácter Y expresa cómo se distribuye la variable Y independientemente de los valores presentados por la variable X.
\( \begin{array} {|c|c|c|} \hline y_{j} & n_{.j} & f_{.j} \\ \hline
y_1 & n_{.1} & f_{.1} \\
y_2 & n_{.2} & f_{.2} \\
⋮ & ⋮ & ⋮ \\
y_{j} & n_{.j} & f_{.j} \\
⋮ & ⋮ & ⋮ \\
y_{p} & n_{.p} & f_{.p} \\ \hline
& n & 1 \\ \hline \end{array} \)
\( n_{.j} \) representa la frecuencia absoluta marginal de Y \( \hspace{5 mm} \sum_{j=1}^{p}n_{.j}=n \)
\( f_{.j} \) representa la frecuencia relativa marginal de Y \( \hspace{5 mm} f_{.j}= \displaystyle \frac{n_{.j}}{n} \hspace{5 mm} \) o \( \hspace{5 mm} f_{.j}=\sum_{i=1}^{k}f_{ij} \hspace{5 mm} \) (j fijo); \( \hspace{5 mm} \sum_{j=1}^{p}f_{.j}=1 \)
Características de las distribuciones marginales
En el capítulo 1 estudiamos la media y la varianza de las distribuciones unidimensionales, a estas características, en las distribuciones marginales, se les añade el calificativo de “marginal” y se utiliza una notación que indica el carácter que se estudia.
Media marginal de X
\( \bar{\bar{ x}}= \bar{x} = \displaystyle \frac {1}{n} \sum_{i=1}^{k}n_{i.}x_{i}=\sum_{i=1}^{k}f_{i.}x_{i} \)Media marginal de Y
\( \bar{\bar{y}} = y = \displaystyle \frac {1}{n}\sum_{j=1}^{p}n_{.j}y_{j} = \sum_{j=1}^{p}f_{.j}y_{j} \)Varianza marginal de X
\( σ_{x}^2= \sum_{i=1}^{k}f_{i.}(x_{i}- \bar{x})^2=\sum_{i=1}^{k} \displaystyle \frac{n_{i.}}{n}(x_{i}-\bar{x})^2=\sum_{i=1}^{k} \displaystyle \frac{n_{i.}x_{i}^2}{n}- \bar {x}^2 \)Varianza marginal de Y
\( σ_{y}^2=\sum_{j=1}^{p}f_{.j}(y_{j}- \bar{y})^2=\sum_{j=1}^{p} \displaystyle \frac{n_{.j}}{n}(y_{j}-\bar{y})^2=\sum_{j=1}^{p} \displaystyle \frac{n_{.j}y_{j}^2}{n}- \bar{y}^2 \)Ejemplo 2.2: Se han lanzado dos dados varias veces. Designando X el resultado del primer dado e Y el resultado del segundo dado. La información obtenida se dispone en la siguiente tabla:
\( \begin{array} {|c|cccccccccccccc|} \hline X & 1 & 2 & 2 & 3 & 5 & 4 & 1 & 3 & 3 & 4 & 1 & 2 \\ \hline Y & 2 & 3 & 1 & 4 & 3 & 2 & 6 & 4 & 1 & 6 & 6 & 5 \\ \hline X & 5 & 4 & 3 & 4 & 4 & 5 & 3 & 1 & 6 & 5 & 4 & 6 \\ \hline Y & 1 & 2 & 5 & 1 & 1 & 2 & 6 & 6 & 2 & 1 & 2 & 5 \\ \hline \end{array} \)
La tabla bidimensional correspondiente es:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|} \hline X / Y & 1 & 2 & 3 & 4 & 5 & 6 & n_{i.} & n_{i.}x_{i} & n_{i.}x_{i}^2 \\ \hline 1 & 0 & 1 & 0 & 0 & 0 & 3 & 4 & 4 & 4 \\ \hline 2 & 1 & 0 & 1 & 0 & 1 & 0 & 3 & 6 & 12 \\ \hline 3 & 1 & 0 & 0 & 2 & 1 & 1& 5 & 15 & 45 \\ \hline 4 & 2 & 3 & 0 & 0 & 0 & 1 & 6 & 24 & 96 \\ \hline 5 & 2 & 1 & 1 & 0 & 0 & 0 & 4 & 20 & 100 \\ \hline 6 & 0 & 1 & 0 & 0 & 1 & 0 & 2 & 12 & 72 \\ \hline n_{.j} & 6 & 6 & 2 & 2 & 3 & 5 & 24 & 81 & 329 \\ \hline n_{.j}y_{j} & 6 & 12 & 6 & 8 & 15 & 30 & 77 & &\\ \hline
n_{.j}y_{j}^2 & 6 & 24 & 18 & 32 & 75 & 180 & 335 & & \\ \hline \end{array} \)
\( \bar {x} = \displaystyle \frac {1}{n} \sum_{i=1}^6 n_{i.}x_{i}= \displaystyle \frac {81}{24}=3.375 \hspace{5 mm}\) ; \( \hspace{5 mm}y= \displaystyle \frac{1}{n} \sum_{j=1}^6n_{.j}y_{j}= \displaystyle \frac{77}{24}=3.2083 \)
\( σ_{x}^2=\sum_{i=1}^6 \displaystyle \frac{n_{i.}x_{i}^2}{n}- \bar{x}^2= \displaystyle \frac{329}{24}-3.375^2=2.318 \)
\( σ_{y}^2=\sum_{j=1}^6 \displaystyle \frac{n_{.j}y_{j}^2}{n}-y^2= \displaystyle \frac{335}{24}-3.2083^2=3.667 \)
Cálculo abreviado de la media y de la varianza: Con objeto de simplificar el cálculo de ambas características se pueden realizar cambios de origen y escala.
Ejemplo: Calcular las medias y varianzas marginales, efectuando un cambio de origen y escala, en el Ejemplo 2.1
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline X / Y & 160 & 162 & 164 & 166 & 168 & 170 & n_{i.} & x_{i}^′= \displaystyle \frac {x_{i}-54}{3} & n_{i.}x_{i}^´ & n_{i.}x_{i}^{′2} \\ \hline 48 & 3 & 2 & 2 & 1 & 0 & 0 & 8 & -2 & -16 & 32 \\ \hline 51 & 2 & 3 & 4 & 2 & 2 & 1 & 14 & -1 & -14 & 14 \\ \hline 54 & 1 & 3 & 6 & 8 & 5 & 1 & 24 & 0 & 0 & 0 \\ \hline 57 & 0 & 0 & 1 & 2 & 8 & 3 & 14 & 1 & 14 & 14 \\ \hline 60 & 0 & 0 & 0 & 2 & 4 & 4 & 10 & 2 & 20 & 40 \\ \hline n_{.j} & 6 & 8 & 13 & 15 & 19 & 9 & 70 & & 4 & 100 \\ \hline y_{j}^´= \displaystyle \frac{y_{j}-164}{2} & -2 & -1 & 0 & 1 & 2 & 3 & & & & \\ \hline n_{.j}y_{j}^´ & -12 & -8 & 0 & 15 & 38 & 27 & 60 & & & \\ \hline n_{.j}y_{j}^{′2} & 24 & 8 & 0 & 15 & 76 & 81 & 204 & & & \\ \hline \end{array} \)
\( \begin{array}{l} x^′= \displaystyle \frac{1}{n} \sum_{i=1}^5 n_{i.}x_{i}^′= \displaystyle \frac {4}{70}=0.057 \Rightarrow x=3×0.057+54=54.171 \\ \\ y^′= \displaystyle \frac{1}{n} \sum_{j=1}^6 n_{.j}y_{j}^′= \displaystyle \frac{60}{70}=0.857 \Rightarrow y=2×0.857+164=165.714 \\ \\ σ_{x}^{′2}=∑_{i=1}^5 \displaystyle \frac{n_{i.}x_{i}^{′2}}{n}-x^{′2}= \displaystyle \frac{100}{70}-0.057^2=1.4253 \Rightarrow σ_{x}^2=1.4253×3^2=12.8277 \\ \\ σ_{y}^{′2}=\sum_{j=1}^6 \displaystyle \frac {n_{.j}y_{j}^{′2}}{n}-y^{′2}= \displaystyle \frac{204}{70}-0.857^2=2.1798 \Rightarrow σ_{y}^2=2.1798×2^2=8.7192 \end{array} \)Distribuciones condicionadas
Son distribuciones unidimensionales obtenidas a partir de las distribuciones bidimensionales, que expresan la distribución de una de las dos variables para un valor o conjunto de valores de la otra variable. Son distribuciones unidimensionales en las cuales previamente se define una condición, por ejemplo: la distribución según el carácter X de los individuos de la población que presentan los valores\( y_2 \) e \( y_3 \) del carácter Y.
- La j-ésima columna de la tabla de doble entrada (Tabla 2.1) representa el número de individuos, \( n_{.j \), de los n que integran la población que presentan la modalidad \( y_{j} \) del carácter Y y de esos \( n_{.j} \) individuos, \( n_{ij} \) presentan la modalidad \( x_{i} \) del carácter X. Dicha j-ésima columna define la Distribución Condicionada según el carácter X de los individuos que presentan la modalidad \( y_{j} \) del carácter Y. Esta distribución condicionada se denota por \( X/y_{j}\).
Se define la Frecuencia Relativa Condicionada de la distribución \( X/y_{j} \), y se denota por \( f_{i/j} \), como el cociente
\( f_{i/j}= \displaystyle \frac {n_{ij}}{n_{.j}} \)
- La i-ésima fila de la Tabla 2.1 representa el número de individuos, \( n_{i.}\), de los n que integran la población que presentan la modalidad \( x_{i} \) del carácter X y de esos \( n_{i.} \) individuos, \( n_{ij}\) presentan la modalidad \( y_{j} \) del carácter Y. Dicha i-ésima fila define la Distribución Condicionada según el carácter Y de los individuos que presentan la modalidad \( x_{i} \) del carácter X. Esta distribución condicionada se denota por \(Y/x_{i} \).
Se define la Frecuencia Relativa Condicionada de la distribución \( Y/x_{i} \), y se denota por \( f_{j/i}\), como el cociente
\( f_{j/i}= \displaystyle \frac{n_{ij}}{n_{i.}} \)
Las tablas numéricas de dichas distribuciones condicionadas son, respectivamente
\( \begin{array} {|c|c|c|} \hline X/y_{j} & n_{i/j} & f_{i/j}\\ \hline x_1 & n_{1j} & f_{1/j} \\ x_2 & n_{2j} & f_{2/j} \\ ⋮ & ⋮ & ⋮ \\ x_{i} & n_{ij} & f_{i/j} \\ ⋮ & ⋮ & ⋮ \\ x_{k} & n_{kj} & f_{k/j} \\ & n_{.j} & 1 \\ \hline \end{array} \) \( \hspace {20 mm} \begin{array} {l} \sum_{i=1}^{k}n_{i/j}=n_{.j} \\ \\ \sum_{i=1}^{k}f_{i/j}=1 \\ \end{array} \)
\( \begin{array} {|c|c|c|} \hline Y/x_{i} & n_{j/i} & f_{j/i} \\ \hline y_1 & n_{i1} & f_{1/i} \\ y_2 & n_{i2} & f_{2/i} \\ ⋮ & ⋮ & ⋮ \\ y_{j} & n_{ij} & f_{j/i} \\ ⋮ & ⋮ & ⋮ \\ y_{p} & n_{ip} & f_{p/i} \\ & n_{i.} & 1 \\ \hline \end{array} \) \( \hspace {20 mm} \begin{array} {l} \sum_{j=1}^{p}n_{j/i}=n_{i.} \\ \\ \sum_{j=1}^{p}f_{j/i}=1 \\ \end{array} \)
Cada una de las filas (columnas) de la tabla de doble entrada definen una distribución condicionada para la variable Y (X).
Ejemplo: Determinar, en el Ejemplo 2.1, las distribuciones siguientes:
a) Distribución según las tallas de los individuos que pesan 54 Kg
b) Distribución según los pesos de los individuos que miden entre 161 cm. y 167 cm.
Respuesta
a) Distribución según las tallas de los individuos que pesan 54 Kg
\( \begin{array} {|c|c|c|c|c|c|c|c|} \hline Y/x_3 & 160 & 162 & 164 & 166 & 168 & 170 & \\ \hlinen_{j/i=3} & 1 & 3 & 6 & 8 & 5 & 1 & 24 \\ \hline \end{array} \)
b) Distribución según los pesos de los individuos que miden entre 161 cm. y 167 cm.
\( \begin{array} {|c|c|c|c|c|c|c|} \hline X/y_{j=2,3,4} & 48 & 51 & 54 & 57 & 60 & \\ \hlinen_{i/j=2,3,4} & 5 & 9 & 17 & 3 & 2 & 36 \\ \hline \end{array} \)
Características de las distribuciones condicionadas
Distribución condicionada \( X/y_{j} \)
- Se define la Media condicionada de la distribución \( X/y_{j} \), que se denota por \( \bar{x}_{j} \), como
\( \bar{x}_{j}= \displaystyle \frac{1}{n_{.j}} \sum_{i=1}^{k}x_{i}n_{i/j}= \sum_{i=1}^{k}x_{i}f_{i/j} \)
- Se define la Varianza condicionada de la distribución \( X/y_{j} \), que se denota por \( σ_{j}^2(x) \), mediante la siguiente expresión
\( σ_{j}^2(x)= \displaystyle \frac{1}{n_{.j}} \sum_{i=1}^{k}(x_{i}- \bar{x}_{j})^2 n_{i/j}= \sum_{i=1}^{k}(x_{i}- \bar{x}_{j})^2 f_{i/j} \)
Distribución condicionada \( Y/x_{i} \)
- Se define la Media condicionada de la distribución \( Y/x_{i} \), que se denota por \( \bar{ y}_{i} \), como
\( \bar{ y}_{i}= \displaystyle \frac{1}{n_{i.}} \sum_{j=1}^{p}y_{j}n_{j/i}=\sum_{j=1}^{p}y_{j}f_{j/i} \)
- Se define la Varianza condicionada de la distribución \( Y/x_{i} \), que se denota por \( σ_{i}^2(y) \), mediante la siguiente expresión
\( σ_{i}^2(y) = \displaystyle \frac{1}{n_{i.}} \sum_{j=1}^{p}(y_{j}- \bar{y}_{i})^2 n_{j/i}=\sum_{j=1}^{p}(y_{j}- \bar{y}_{i})^2f_{j/i}\)
Relación entre las distribuciones marginales y las condicionadas
- Las distribuciones marginales y condicionadas están relacionadas por la siguiente expresión:
\( f_{ij}=f_{j/i}f_{i.}=f_{i/j}f_{.j} \)
En efecto
\( f_{ij}= \displaystyle \frac{n_{ij}}{n}= \displaystyle \frac{n_{ij}}{n_{i.}} \displaystyle \frac{n_{i.}}{n}=f_{j/i}f_{i.} \hspace{5 mm} ; \hspace{5 mm} f_{ij}= \displaystyle \frac{n_{ij}}{n}= \displaystyle \frac{n_{ij}}{n_{.j}} \displaystyle \frac{n_{.j}}{n}=f_{i/j}f_{.j} \)
- Las medias marginales y condicionadas se relacionan de la siguiente forma:
\(\bar{x}= \sum_{j=1}^{p} \bar{x}_{j}f_{.j} \hspace{10 mm} ; \hspace{10 mm}\bar{y}=\sum_{i=1}^{k} \bar{y}_{i}f_{i.} \)
En efecto
\( \bar{x}=\sum_{i=1}^{k}x_{i}f_{i.}=\sum_{i=1}^{k}x_{i}\sum_{j=1}^{p}f_{ij}=\sum_{j=1}^{p}\sum_{i=1}^{k}x_{i}f_{i/j}f_{.j}=\sum_{j=1}^{p} \bar{x}_{j}f_{.j} \)
De forma análoga se comprueba la otra relación (expresión de \( \bar{y} \))
- Las varianzas marginales y condicionadas se relacionan de la siguiente forma:
\( σ_{x}^2=\sum_{j=1}^{p}σ_{j}^2(x)f_{.j}+\sum_{j=1}^{p} (\bar{x}_{j}- \bar{x})^2 f_{.j} \)
\( σ_{y}^2=\sum_{i=1}^{k}σ_{i}^2(y)f_{i.}+\sum_{i=1}^{k}(\bar{y}_{i}-\bar{y})^2 f_{i.} \)
En efecto
\( \begin{array} {l} σ_{x}^2 = \sum_{i=1}^{k}(x_{i}-\bar{x})^2 f_{i.}=\sum_{i=1}^{k}(x_{i}-\bar{x})^2 \sum_{j=1}^{p}f_{ij}=\sum_{i=1}^{k}(x_{i}- \bar{x})^2 \sum_{j=1}^{p}f_{i/j}f_{.j} \\ \\ = \sum_{i=1}^{k}\sum_{j=1}^{p} \left ((x_{i}-\bar{x}_{j})+(\bar{x}_{j}- \bar {x}) \right)^2f_{i/j}f_{.j}= \\ \\ = \sum_{i=1}^{k}\sum_{j=1}^{p} \left [(x_{i}-\bar{x}_{j})^2+(\bar{x}_{j}- \bar{x})^2+2(x_{i}-\bar{x}_{j})(\bar{x}_{j}- \bar{x}) \right ] f_{i/j}f_{.j}= \\ \\ = \sum_{j=1}^{p}\left [\sum_{i=1}^{k}(x_{i}-\bar{x}_{j})^2 f_{i/j} \right ]f_{.j}+\sum_{j=1}^{p}(\bar{x}_{j}- \bar{x})^2f_{.j}(\sum_{i=1}^{k}f_{i/j})+ \\ \\ +2\sum_{j=1}^{p}(\bar{x}_{j}- \bar{x}) f_{.j}\sum_{i=1}^{k}(x_{i}- \bar{x}_{j})f_{i/j} \\ \end{array} \)
Como
∗ \( \sum_{i=1}^{k}f_{i/j}=1 \)
∗ \( \sum_{i=1}^{k}(x_{i}-\bar{x}_{j})f_{i/j}=\sum_{i=1}^{k}x_{i}f_{i/j}-\sum_{i=1}^{k}\bar{x}_{j}f_{i/j}= \bar{x}_{j}- \bar{x}_{j}\sum_{i=1}^{k}f_{i/j}=\bar{x}_{j} – \bar{x}_{j} =0 \)
Entonces
\( σ_{x}^2=\sum_{j=1}^{p}σ_{j}^2(x)f_{.j}+\sum_{j=1}^{p}(\bar{x}_{j}- \bar{x})^2 f_{.j} \)
Análogamente se comprueba la relación
\( σ_{y}²=\sum_{i=1}^{k}σ_{i}^2(y)f_{i.}+\sum_{i=1}^{k}(\bar{y}_{i}-\bar{y})^2 f_{i.} \)
Ejemplo: Determinar, en el Ejemplo 2.1, la media y la varianza de la distribución de los individuos que miden entre 163 cm. y 165 cm.
Respuesta:
\( \begin{array} {|c|c|c|c|} \hline X/y_3 & n_{i/j=3} & x_{i}n_{i/j} & x_{i}^2 n_{i/j} \\ \hline 48 & 2 & 96 & 4608 \\ \hline 51 & 4 & 204 & 10404 \\ \hline 54 & 6 & 324 & 17496 \\ \hline 57 & 1 & 57 & 3249 \\ \hline 60 & 0 & 0 & 0 \\ \hline & 13 & 681 & 35757 \\ \hline \end{array} \)
\( \begin{array} {l} \bar{x}_{j}= \displaystyle \frac{1}{n_{.j}}\sum_{i=1}^{k}x_{i}n_{i/j}= \displaystyle \frac{681}{13}=52.38 \\ \\ σ_{j}^2(x)= \displaystyle \frac {1}{n_{.j}}\sum_{i=1}^{k}x_{i}^2n_{i/j}-\bar{x }_{j}^2= \displaystyle \frac{35757}{13}-52.38^2=6.874 \end{array} \)
Representaciones gráficas
En las distribuciones bidimensionales la representación gráfica más usual es el Diagrama de Dispersión o Nube de Puntos, que consiste en representar, en unos ejes cartesianos rectangulares, los pares de valores \( (x_{i},y_{j}) \) mediante puntos que tienen esas coordenadas. Cuando la frecuencia con que aparece \( (x_{i},y_{j}) \) es mayor que uno, junto al punto se coloca el valor de dicha frecuencia o bien el tamaño del punto se hace proporcional a la frecuencia.
Ejemplo: Representar mediante un diagrama de dispersión el Ejemplo 2.2
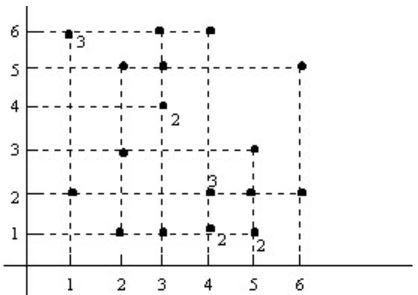
Figura 2.1: Diagrama de dispersión
Covarianza. Comportamiento frente a cambios de origen y escala
En primer lugar estudiamos los Momentos de las distribuciones bidimensionales y al igual que hicimos en la distribuciones unidimensionales distinguimos entre Momentos No-Centrales o respecto del Origen y Momentos Centrales o respecto de la Media.
Momentos no-centrales o respecto del origen
Se definen los Momentos No-Centrales de órdenes r y s o Momentos de orden r y s respecto del Origen, y se denotan por \( m_{rs} \) , como
\( m_{rs}=\sum_{i=1}^{k}\sum_{j=1}^{p}x_{i}^{r}y_{j}^{s}f_{ij}= \displaystyle \frac{1}{n}\sum_{i=1}^{k}∑_{j=1}^{p}x_{i}^{r}y_{j}^{s}n_{ij} \)
Casos particulares:
- Si \( r=1 \hspace{3mm} y \hspace{3mm} s=0 \Rightarrow m_{10}=\sum_{i=1}^{k}\sum_{j=1}^{p}x_{i}^1y_{j}^0 f_{ij}= \bar{x} \)
- Si \( r=0 \hspace{3mm} y \hspace{3mm} s=1 \Rightarrow m_{01}=\sum_{i=1}^{k}\sum_{j=1}^{p}x_{i}^0y_{j}^1f_{ij}= \bar{y} \)
- Si \( r=2 \hspace{3mm} y \hspace{3mm} s=0 \Rightarrow m_{20}=\sum_{i=1}^{k}\sum_{j=1}^{p}x_{i}^2f_{ij} \Rightarrow σ_{x}^2=m_{20}-m_{20}-m_{10}^2 \)
- Si \( r=0 \hspace{3mm} y \hspace{3mm} s=2 \Rightarrow m_{02}=\sum_{i=1}^{k}\sum_{j=1}^{p}y_{j}^2f_{ij} \Rightarrow σ_{y}^2=m_{02}-m_{01}^2 \)
Los momentos bidimensionales en los que uno de los subíndices es cero se corresponden con los momentos de las distribuciones marginales, son momentos unidimensionales.
Uno de los momentos, respecto al origen, más utilizado es el momento de órdenes r=1 y s=1, es decir el momento
\( m_{11}= \sum_{i=1}^{k}\sum_{j=1}^{p}x_{i}y_{j}f_{ij}= \displaystyle \frac{1}{n}\sum_{i=1}^{k}\sum_{j=1}^{p}x_{i}y_{j}n_{ij} \)
Momentos Centrales o respecto de la Media
Se definen los Momentos Centrales de órdenes r y s o Momentos de órdenes r y s respecto de la Media, y se denotan por \( μ_{rs} \), como
\( μ_{rs}=\sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}- \bar{x})^{r}(y_{j}- \bar{y})^{s}f_{ij}= \displaystyle \frac{1}{n}\sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}-\bar{x})^{r}(y_{j}- \bar{y})^{s}n_{ij} \)
Casos particulares:
- Si \( r=1 \hspace{3mm} y \hspace{3mm} s=0 \Rightarrow μ_{10}=\sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}-\bar{x})^1(y_{j}-\bar{y})^0 f_{ij}=0 \)
- Si \( r=0 \hspace{3mm} y \hspace{3mm} s=1 \Rightarrow μ_{01}=\sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}-\bar{x})^0(y_{j}-\bar{y})^1f_{ij}=0 \)
- Si \( r=2 \hspace{3mm} y \hspace{3mm} s=0 \Rightarrow μ_{20}=\sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}-\bar{x})^2(y_{j}-\bar{y})^0f_{ij}=σ_{x}^2 \)
- Si \( r=0 \hspace{3mm} y \hspace{3mm} s=2 \Rightarrow μ_{02}=\sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}-\bar{x})^0(y_{j}-\bar{y})^2f_{ij}=σ_{y}^2 \)
El momento bidimensional respecto a la media más interesante es el momento de órdenes r=1 y s=1, que recibe el nombre de Covarianza y se puede notar por Cov(x,y) o \( σ_{xy} \)
\( μ_{11}=σ_{xy}=\sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}-\bar{x})(y_{j}-\bar {y})f_{ij}= \displaystyle \frac{1}{n}\sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}-\bar {x})(y_{j}-\bar {y})n_{ij} \)
La Covarianza es una medida de la variabilidad conjunta de las variables X e Y. El signo de la covarianza indica el sentido en el que varían conjuntamente las dos variables:
- Si la \( σ_{xy}>0 \Rightarrow \) Las variables X e Y varían en el mismo sentido. Las dos variables crecen o decrecen a la vez (nube de puntos creciente)
- Si la \( σ_{xy}<0 \Rightarrow \) Las variables X e Y varían en sentido opuesto. Cuando una variable crece, la otra variable tiene tendencia a decrecer (nube de puntos decreciente)
Relación entre los momentos centrales y no-centrales
Veamos las relaciones sólo para los momentos bidimensionales más usuales
\( μ_{20} = \sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}- \bar{x})^2f_{ij}=\sum_{i=1}^{k}(x_{i}-\bar{x})^2f_{i.}=\sum_{i=1}^{k}x_{i}^2f_{i.}-2\bar{x}\sum_{i=1}^{k}x_{i}f_{i.}+\bar{x}^2\sum_{i=1}^{k}f_{i.}= m_{20}- m_{10}^2 \)
\( μ_{02} = \sum_{i=1}^{k}\sum_{j=1}^{p}(y_{j}-\bar{y})^2f_{ij}=m_{02}-m_{01}^2 \)
\( μ_{11}= \sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}-\bar{x})(y_{j}-\bar{y})f_{ij}=\sum_{i,j}x_{i}y_{j}f_{ij}-\bar{y}\sum_{i,j}x_{i}f_{ij}- \bar{x}\sum_{i,j}y_{j}f_{ij}+ \bar{x}\bar{y}\sum_{i,j}f_{ij}= \)
\( =\sum_{i,j}x_{i}y_{j}f_{ij}-\bar{x}\bar{y}-\bar{x}\bar{y}+\bar{x}\bar{y}=\sum_{i,j}x_{i}y_{j}f_{ij}-\bar{x}\bar{y} \)
Ejemplo: Calcular la covarianza del Ejemplo 2.2
\( \begin{array} {|l|c|c|c|c|c|c|c|c|c|r|} \hline X / Y & 1 & 2 & 3 & 4 & 5 & 6 & n_{i.} & n_{i.}x_{i} & n_{i.}x_{i}^2 & \sum_{j=1}^6x_{i}y_{j}n_{ij} \\ \hline 1 & 0 & 1 & 0 & 0 & 0 & 3 & 4 & 4 & 4 & 0+2+0+0+0+18=20 \\ \hline 2 & 1 & 0 & 1 & 0 & 1 & 0 & 3 & 6 & 12 & 2+0+6+0+10+0=18 \\ \hline 3 & 1 & 0 & 0 & 2 & 1 & 1 & 5 & 15 & 45 & 3+24+15+18=60 \\ \hline 4 & 2 & 3 & 0 & 0 & 0 & 1 & 6 & 24 & 96 & 8+24+15+18=56 \\ \hline 5 & 2 & 1 & 1 & 0 & 0 & 0 & 4 & 20 & 100 & 10+10+15=35 \\ \hline 6 & 0 & 1 & 0 & 0 & 1 & 0 & 2 & 12 & 72 & 12+30=42 \\ \hline n_{.j} & 6 & 6 & 2 & 2 & 3 & 5 & 24 & 81 & 329 & 231 \\ \hline n_{.j}y_{j} & 6 & 12 & 6 & 8 & 15 & 30 & 77 & & & \\ \hline n_{.j}y_{j}^2 & 6 & 24 & 18 & 32 & 75 & 180 & 335 & & & \\ \hline \end{array} \)\( σ_{xy}=\sum_{i,j}x_{i}y_{j}f_{ij}-\bar{x}\bar{y}= \displaystyle \frac{231}{24}-3.3×3.2=-0.9 \)
Las variables x e y varían en sentido opuesto. Cuando una variable crece, la otra tiende a decrecer. (La nube de puntos es decreciente)
Cálculo abreviado de los momentos: Realizamos los siguientes cambios de origen y escala en los momentos centrales bidimensionales
\( x_{i}^′= \displaystyle \frac{x_{i}-x_0}{a} \hspace{2mm}; \hspace{2mm}y_{j}^′= \displaystyle \frac{y_{j}-y_0}{b} \)Por lo tanto
\( \begin{array}{ccl} μ_{r,s}^′ & = & \sum_{i=1}^{k}\sum_{j=1}^{p}(x_{i}^′- \bar{x}^′)^{r}(y_{j}^′- \bar{y}^′){s}f_{ij} \\ & & \\ & = & \sum_{i,j}f_{ij} \left ( \displaystyle \frac {x_{i}-x_0}{a} – \displaystyle \frac{\bar{x}-x_0}{a} \right)^{r} \left ( \displaystyle \frac{y_{j}-y_0}{b}- \displaystyle \frac{\bar{y}-y_0}{b} \right)^{s}\\ & & \\ & = & \displaystyle \frac {1}{a^{r}b^{s}} \sum_{i,j}f_{ij}(x_{i}-\bar{x})^{r}(y_{j}-\bar{y})^{s}= \displaystyle \frac{μ_{rs}}{a^{r}b^{s}} \end{array} \)
Como puede observarse los momentos centrales son invariantes frente a los cambios de origen, sólo les afecta los cambios de escala elevados a r y s.
En el caso de la covarianza
\( σ_{xy}=abσ_{xy}^′ \)
Ejemplo 2.3: Se han medido dos caracteres simultáneamente sobre cada uno de los miembros de un colectivo, obteniéndose los datos de la tabla:
\( \begin{array}{|c|c|c|c|} \hline
X/Y & 90-100 & 100-120 & 120-140 \\ \hline
10-15 & 6 & 3 & 1 \\ \hline
15-20 & 5 & 10 & 2 \\ \hline
20-25 & 4 & 1 & 7 \\ \hline
25-30 & 2 & 2 & 4 \\ \hline \end{array} \)
Calcular la covarianza.
\( \begin{array}{|c|c|c|c|c|c|c|r|} \hline & y_{j}^′= \displaystyle \frac{y_{j}-110}{5} & -3 & 0 & 4 & & & \\ \hline x_{i}^′= \displaystyle \frac{x_{i}-17.5}{5} & x_{i}/y_{j} & 95 & 110 & 130 & n_{i.} & x_{i}^′n_{i.} & \sum x_{i}^′y_{j}^′n_{ij} \\ \hline -1 & 12.5 & 6 & 3 & 1 & 10 & -10 & 18+0-4=14 \\ \hline 0 & 17.5 & 5 & 10 & 2 & 17 & 0 & 0 & \\ \hline 1 & 22.5 & 4 & 1 & 7 & 12 & 12 & -12+0+28=16 \\ \hline 2 & 27.5 & 2 & 2 & 4 & 8 & 16 & -12+0+32=20 \\ \hline & n_{.j} & 17 & 16 & 14 & 47 & 18 & 50 \\ \hline & n_{.j}y_{j}^′ & -51 & 0 & 56 & 5 & & \\ \hline \end{array} \)
\( x^′= \displaystyle \frac{18}{47} \Rightarrow x= \displaystyle \frac{18}{47}×5+17.5=19.41 \)
\( y^′= \displaystyle \frac {5}{47} \Rightarrow y= \displaystyle\frac{5}{47}×5+110=110.53 \)
\( σ_{xy}^′= \displaystyle \frac{50}{47}- \displaystyle \frac{18}{47}× \displaystyle \frac{5}{47}=1.023 \Rightarrow σ_{xy}=5×5×1.023=25.575 \)
Dependencia e Independencia estadística
Dependencia funcional
a) Se dice que X Depende Funcionalmente Y si a cada valor \( y_{j} \) de Y le corresponde un único valor de X, es decir para todo j la frecuencia absoluta \( n_{ij}=0 \) salvo para un i fijo. De esta forma en cada columna de la tabla de doble entrada sólo hay un término distinto de cero pero en cada fila pueden figurar varios términos distintos de cero. Un ejemplo, puede ser el dado por la siguiente tabla
\( \begin{array}{|c|c|c|c|c|} \hline X /Y & 50 & 60 & 70 & 80 \\ \hline 12 & 10 & 0 & 6 & 0 \\ \hline 13 & 0 & 7 & 0 & 0 \\ \hline 15 & 0 & 0 & 0 & 1 \\ \hline \end{array} \)
b) Se dice que Y Depende Funcionalmente X si a cada valor \( x_{i} \) de X le corresponde un único valor de Y, es decir para todo i la frecuencia absoluta \( n_{ij}=0 \) salvo para un j fijo. De esta forma en cada fila de la tabla de doble entrada sólo hay un término distinto de cero pero en cada columna pueden figurar varios términos distintos de cero. Un ejemplo, puede ser el dado por la siguiente tabla
\( \begin{array}{|c|c|c|c|} \hline X / Y & 15 & 25 & 35 \\ \hline 5 & 0 & 6 & 0 \\ \hline 7 & 0 & 8 & 0 \\ \hline 14 & 0 & 3 & 0 \\ \hline 16 & 0 & 0 & 1 \\ \hline \end{array} \)
- La Dependencia Funcional se dice Recíproca cuando a cada valor \( y_{j} \) de Y le corresponde un único valor de X y a cada valor \( x_{i} \) de X le corresponde un único valor de Y. Así, en cada fila y en cada columna de la tabla de doble entrada sólo hay un número distinto de cero. Un ejemplo, puede ser el dado por la siguiente tabla
\( \begin{array}{|c|c|c|c|c|} \hline X / Y & 15 & 25 & 30 & 35 \\ \hline 5 & 0 & 6 & 0 & 0 \\ \hline 7 & 7 & 0 & 0 & 0 \\ \hline 10 & 0 & 0 & 2 & 0 \\ \hline 18 & 0 & 0 & 0 & 1 \\ \hline \end{array} \)
La dependencia funcional no es siempre recíproca, para que sea recíproca es condición necesaria pero no suficiente que la tabla de doble entrada sea cuadrada.
Independencia estadística
a) Se dice que X es Independiente de Y si las distribuciones condicionadas de X a los distintos valores de Y (X/ y_{j}) son idénticas entre sí, por lo tanto las frecuencias relativas de esas distribuciones condicionadas son iguales. Por ejemplo
\( \begin{array}{|c|c|c|c|c|c|} \hline X / Y & 15 & 24 & 27 & 30 & n_{i.} \\ \hline 12 & 3 & 6 & 9 & 12 & 30 \\ \hline 15 & 2 & 4 & 6 & 8 & 20 \\ \hline 19 & 1 & 2 & 3 & 4 & 10 \\ \hline n_{.j} & 6 & 12 & 18 & 24 & 60 \\ \hline \end{array} \)
\( \displaystyle \frac{3}{6}= \displaystyle \frac{6}{12}= \displaystyle \frac{9}{18} = \displaystyle \frac{12}{24} = \displaystyle \frac{30}{60} \hspace{2mm} ; \hspace{2mm} \displaystyle \frac{2}{6}= \displaystyle \frac{4}{12} = \displaystyle \frac{6}{18} = \displaystyle \frac{8}{24}= \displaystyle \frac{20}{60} \hspace{2mm}; \hspace{2mm} \displaystyle \frac{1}{6} = \displaystyle \frac{2}{12}= \displaystyle \frac{3}{18}= \displaystyle \frac{4}{24}= \displaystyle \frac{10}{60} \)
Es decir,
- X es independiente de Y si \( f_{i/j} \) no depende de j para todo valor de i. Por tanto, si X es independiente de Y las columnas de la tabla de doble entrada son proporcionales entre sí.
- X es independiente de Y si \( f_{i/j}=f_{i.}\)
En efecto
\( f_{i.} = \sum_{j=1}^{p}f_{ij}=⁽¹⁾∑_{j=1}^{p}f_{i/j}f_{.j}=⁽²⁾f_{i/j}\sum_{j=1}^{p}f_{.j}=⁽³⁾f_{i/j} \Rightarrow \)
\( \Rightarrow f_{i/j}=f_{i.}⁽⁴⁾⇒f_{ij}=f_{i.}f_{.j} \)
\( (1): f_{ij}=f_{i/j}f_{.j} \hspace{2mm} ;\hspace{2mm} (2): f_{i/j} \) no depende de \( j \hspace{2mm}; \hspace{2mm}(3): \sum_{j=1}^{p}f_{.j}=1 \hspace{2mm}; \hspace{2mm}(4): f_{ij}=f_{i/j}f_{.j} \)
Es decir, X es independiente de Y
- si \( f_{i/j} \) no depende de j, \( ∀i \hspace{2mm} (f_{i/j}=f_{i.}) \) o
- Si \( f_{ij}=f_{i.}f_{.j} \)
b) Se dice que Y es Independiente de X si las distribuciones condicionadas de Y a los distintos valores de X \( (Y/ x_{i}) \) son idénticas entre sí, por lo tanto las frecuencias relativas de esas distribuciones condicionadas son iguales. Por ejemplo
\( \begin{array}{|c|c|c|c|c|c|} \hline X / Y & 15 & 24 & 27 & 30 & n_{i.} \\ \hline 12 & 3 & 4 & 2 & 5 & 14 \\ \hline 15 & 6 & 8 & 4 & 10 & 28 \\ \hline 19 & 9 & 12 & 6 & 15 & 42 \\ \hline n_{.j} & 18 & 24 & 12 & 30 & 84 \\ \hline \end{array} \)
\( \displaystyle \frac{3}{14}= \displaystyle \frac{6}{28}= \displaystyle \frac{9}{42}= \displaystyle \frac{18}{84} \hspace{2mm} ;\hspace{2mm} \displaystyle \displaystyle \frac{4}{14}= \displaystyle \frac{8}{28} = \displaystyle \frac{12}{42} = \displaystyle \frac{24}{84} \)
\( \displaystyle \frac{2}{14} = \displaystyle \frac{4}{28}= \displaystyle \frac{6}{42}= \displaystyle \frac{12}{84} \hspace{2mm} ;\hspace{2mm} \displaystyle \frac{5}{14} = \displaystyle \frac{10}{28}= \displaystyle \frac{15}{42} = \displaystyle \frac{30}{84} \)
Es decir,
- Y es Independiente de X si \( f_{j/i} \) no depende de i para todo valor de j. Por tanto, si Y es independiente de X las filas de la tabla de doble entrada son proporcionales entre sí.
- Y es independiente de X si \( f_{j/i}=f_{.j} \Rightarrow f_{ij}=f_{i.}f_{.j} \)
Demostración análoga al caso en que X es independiente de Y.
∗) La Independencia es una propiedad Recíproca
En efecto
- Si X es independiente de Y \( \Rightarrow f_{i/j}=f_{i.} \)
Como
\( f_{i/j}f_{.j}=f_{j/i}f_{i.} \Rightarrow ⁽¹⁾f_{.j}=f_{j/i} \Rightarrow \) Y es independientede X
(1) X es independiente de Y
De forma análoga se comprueba el recíproco.
∗) La condición necesaria y suficiente para que X e Y sean independientes es que la frecuencia relativa conjunta \( f_{ij} \) sea igual al producto de las frecuencias marginales
\( f_{ij}=f_{i.}f_{.j} \)
La demostración se deja como ejercicio.
Concluimos diciendo que si los dos caracteres son independientes entre sí tanto las filas como las columnas de la tabla de doble entrada son proporcionales entre sí.
Comprobar la propiedad recíproca en los dos ejemplos anteriores.
Ejercicios propuestos: Relación II
1. Se han estudiado los pesos (Kg) y las tallas (cm) correspondientes a un grupo de individuos, obteniendo la siguiente información:
\( \begin{array}{|c|c|c|c|c|c|c|} \hline X / Y & 160 & 162 & 164 & 166 & 168 & 170 \\ \hline 48 & 3 & 2 & 2 & 1 & 0 & 0 \\ \hline 51 & 2 & 3 & 4 & 2 & 2 & 1 \\ \hline 54 & 1 & 3 & 6 & 8 & 5 & 1 \\ \hline 57 & 0 & 0 & 1 & 2 & 8 & 3 \\ \hline 60 & 0 & 0 & 0 & 2 & 4 & 4 \\ \hline \end{array} \)
a) El peso y la talla media. (Sol. \( \bar{x}=54.171; \bar{ y}=165.71 \))
b) El porcentaje de alumnos que pesan menos de 55 Kg y miden más de 165. (Sol. 28.57).
c) Dentro del conjunto de los que miden más de 165 ¿Cuál es el porcentaje de los que pesan más de 52 Kg? (Sol. 86.046%)
d) ¿Cuál es la altura más frecuente entre los individuos cuyo peso oscila entre 51 Kg y 57 Kg?.(Sol. Mo=168)
e) ¿Qué peso medio es más representativo, el de los individuos que miden 164 o el de los que miden 168? (Sol. 164 cm (\( CV_164=0.0483; CV_168=0.0486 \))
2. En una encuesta sobre el número de individuos que componen una familia (X) y el número de personas activas en ella (Y) se han obtenido los resultados indicados en la siguiente tabla:
\( \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline Y/X & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline 1 & 7 & 10 & 11 & 10 & 8 & 1 & 1& 0 \\ \hline 2 & 0 & 2 & 5 & 6 & 6 & 2 & 0 & 0 \\ \hline 3 & 0 & 0 & 1 & 6 & 4 & 3 & 0 & 1 \\ \hline 4 & 0 & 0 & 0 & 0 & 2 & 1 & 1 & 1 \\ \hline
\end{array} \)
a) Calcular el número medio de miembros de las familias encuestadas. (Sol. \( \bar{x} =4 \))
b) Cuantificar la dispersión que presenta la distribución del número de personas activas entorno a su medio. (Sol. \( σ_{y}=0.9304 \))
c) ¿Cuál es el número de miembros activos más frecuente en las familias formadas por 5 personas? (Sol. Mo=1)
d) En el grupo de familias donde las personas activas son 3, calcular el número medio de miembros que las forman. (Sol. \( \bar{x}_{j=3}=5 \))
e) Comprobar las relaciones que ligan las medias y varianzas marginales y condicionadas
f) Calcula la covarianza. (Sol.\( σ_{xy}=0.7908 \)).
3. Se han lanzado dos dados varias veces. Designando X el resultado del primer dado e Y el resultado del segundo dado, la información obtenida se dispone en la siguiente tabla:
\( \begin{array}{|c|cccccccccccc|} \hline X & 1 & 2 & 2 & 3 & 5 & 4 & 1 & 3 & 3 & 4 & 1 & 2 \\ \hline Y & 2 & 3 & 1 & 4 & 3 & 2 & 6 & 4 & 1 & 6 & 6 & 5 \\ \hline X & 5 & 4 & 3 & 4 & 4 & 5 & 3 & 1 & 6 & 5 & 4 & 6 \\ \hline Y & 1 & 2 & 5 & 1 & 1 & 2 & 6 & 6 & 2 & 1 & 2 & 5 \\ \hline \end{array} \)
a) Construir la tabla bidimensional. (Realizado en el Ejemplo 2.2)
b) Calcular las puntuaciones medias obtenidas con cada dado. (Sol. 3.375; 3.2083)
c) ¿Qué puntuaciones son más homogéneas, las obtenidas con el primer dado o con el segundo? (Sol. \( CV_{x}=0.45 \) ; \( CV_{y}=0.597 \) (primer dado))
d) Calcular la puntuación más frecuente obtenida con el segundo dado si con el primero se obtuvo 3. (Sol, Mo=4)
e) Calcula la puntuación máxima del 50% de las puntuaciones más bajas obtenidas con el primer dado si con el segundo se obtiene un 2 o un 5. (Sol. Me=4)
4. Se han medido dos caracteres simultáneamente sobre cada uno de los miembros de un colectivo, obteniéndose los datos de la tabla adjunta. Se pide:
\( \begin{array}{|c|c|c|c|} \hline
X/Y & 90-100 & 100-120 & 120-140 \\ \hline
10-15 & 6 & 3 & 1 \\ \hline
15-20 & 5 & 10 & 2 \\ \hline
20-25 & 4 & 1 & 7 \\ \hline
25-30 & 2 & 2 & 4 \\ \hline \end{array} \)
a) La media de Y si X toma valores superiores a 20. (Sol. \( \bar {y}_{3,4}= 116.5 \) )
b) La media de X si Y toma valores entre 100 y 120. (Sol. \( \bar{ x}_2=18.125 \) )
c) Las medias y las varianzas marginales. (Sol. \( \bar {x}=19.41 \) ; \( σ_{x}^2= 25.05 \) ; \( \bar {y}=110.53\) ; \( σ_{y}^2=200.25 \) )
d) En el conjunto de individuos que presentan valores de Y inferiores a 120, calcular el valor de X mínimo del 30% de las observaciones más altas. (Sol. 19.7)
e) En el conjunto de individuos que presentan valores de X entre 15 y 25, calcular el porcentaje de éstos que presentan valores inferiores a 117. (Sol. 63.28%)
f) Calcular la covarianza. (Sol. \( σ_{xy}=25.575 \) ).
5. Con los datos de la tabla adjunta, obtener:
\( \begin{array}{|c|c|c|c|} \hline X/Y & 1 & 2 & 4 \\ \hline 5 & 1 & 0 & 2 \\ \hline 10 & 2 & 1 & 0 \\ \hline 15 & 0 & 1 & 3 \\ \hline \end{array} \)
a) Media marginal de X y de Y. (Sol. \( \bar{x}=10.5; \bar{y}=2.7 \) );
b) Varianza marginal de X y de Y. (Sol. \( σ_{x}^2= 17.25; σ_{y}^2=1.81 \) );
c) Covarianza. (Sol: \( σ_{xy}=1.15 \) ). ¿Son X e Y independientes?. (Sol. No son independientes).
6. En una región se observó durante algunos años el precio de la leche y la cantidad de leche que consumían, obteniéndose los resultados que muestra la siguiente tabla:
\( \begin{array}{|ccccccccccc|} \hline X & 36 & 31 & 42 & 61 & 52 & 49 & 61 & 51 & 56 & 58 \\ \hline
Y & 100 & 140 & 120 & 140 & 200 & 200 & 110 & 160 & 120 & 200 \\ \hline \end{array} \)
donde X denota el precio de la leche e Y la cantidad de leche en miles de litros. Considerando X agrupada en intervalos de amplitud 5 y siendo 30 el límite inferior del primer intervalo. Construir la tabla bidimensional.
a) ¿Cuál es el precio medio de la leche? ¿Y la producción media? (Sol. \( \bar{x}=50.5; \bar{y} =149000 \) )
b) ¿Cuál es el precio más habitual de la leche cuando la producción es superior a 120000 l.? (Sol. Mo=52.5)
c) ¿Cuál es el porcentaje de años en que el precio de la leche fue superior a 47? (Sol. 66%)
d) En los años en que el precio de la leche oscila entre 35 y 55, ¿Cuál es la cantidad máxima de litros del 30% de las menores producciones? (Sol. 120.000).
7. Se considera la siguiente distribución bidimensional.
\( \begin{array}{|cccccc|} \hline X/Y & 1 & 2 & 3 & 4 & 5 \\ \hline 100 & 2 & 4 & 6 & 10 & 8 \\ \hline 200 & 1 & 2 & 3 & 5 & 4 \\ \hline 300 & 3 & 6 & 9 & 15 & 12 \\ \hline 400 & 4 & 8 & 12 & 20 & 16 \\ \hline \end{array} \)
a) Calcular las medias y varianzas marginales. ¿ Qué distribución está más agrupada alrededor de su media? (Sol. \( \bar{ x}=290; \bar{y}=3.6; CV_{x}=0.39164; CV_{y}=0.333 \) ( La distribución de Y))
b) Calcular las medias de X condicionada a todos los valores de Y. (Sol. \( \bar{x}_1=290= \bar{x}_2=⋯ = \bar{x}_5 \) )
c) Calcular las medias de Y condicionadas a todos los valores de X. (Sol. \( \bar{y}_1=3.6= \bar{y}_2=⋯= \bar{y}_4 \) )
d) ¿Son X e Y independientes? (Sol. SI)
e) Calcula la covarianza. (Sol. \( σ_{xy}=0 \).)
8. Dada la distribución bidimensional:
\( \begin{array}{|c|ccc|} \hline X/Y & 1 & 2 & 3 \\ \hline -1 & 0 & 1 & 0 \\ \hline 0 & 1 & 0 & 1 \\ \hline 1 & 0 & 1 & 0 \\ \hline \end{array} \)
a) Calcular las medias marginales y la covarianza (Sol. \( \bar{x}=0; \bar{y}=2; σ_{xy}=0 \))
c) ¿Dependen las medias de Y condicionadas a los valores de X del valor de la variable al cuál se condicionan? (Sol. NO)
d) ¿Dependen las medias de X condicionadas a los valores de Y del valor de la variable al cuál se condicionan? (Sol. NO)
e) ¿Son X e Y independientes? (Sol. NO)
Autora: Ana María Lara Porras. Universidad de Granada
Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.