TEORÍA DE LA ESTIMACIÓN
Introducción
Como ya hemos dicho anteriormente la Inferencia Estadística es el conjunto de métodos mediante los cuales se puede obtener una conclusión sobre una población a través de la información proporcionada por una muestra. En el caso de que la información que se desea obtener de la población es el valor de alguno de sus parámetros, la técnica que se utiliza es la estimación. Siendo dicha técnica una forma de Inferencia Estadística.
En este capítulo se estudiará la estimación de los parámetros poblaciones desconocidos y se especificarán algunas propiedades deseables de los Estimadores (funciones de los valores de la muestra).
La estimación de los parámetros se llevará a cabo de dos formas: la Estimación Puntual y la Estimación por Intervalo.
- Estimación Puntual. Mediante los estadísticos muestrales se estiman los parámetros de la población, como por ejemplo, la media o la varianza. Es decir, se busca un estimador que, con base en los datos muestrales, más se aproxime al valor verdadero del parámetro.
- Estimación por Intervalo. Mediante la distribución en el muestreo de la característica estadística utilizada se determina un intervalo aleatorio que, de forma probable, contiene el verdadero valor del parámetro. Este intervalo recibe el nombre de Intervalo de Confianza.
Estimación puntual
Supongamos una variable aleatoria X que sigue una ley de probabilidad con función de densidad f(x,θ), siendo θ el parámetro poblacional desconocido. El objetivo es encontrar una función de los valores muestrales que proporcione la “mejor” estimación de θ.
Para ello, tomamos una muestra aleatoria, \( X_1, X_2, \cdots, X_{n} \), de tamaño n y sea \( u(X_1, X_2, \cdots, X_{n} ) \) una función de los valores de la muestra. Recibe el nombre de Estimador u de θ la función que hace corresponder los valores de la muestra con el valor del parámetro θ
\( u(X_1, X_2, \cdots, X_{n})= \theta \)
Un estimador de un parámetro \( \theta \), que vamos a denotar por \( \theta\) (o \( \theta^{∗} \)), es una variable aleatoria pues varía de muestra a muestra, así a cada muestra de tamaño n le corresponde un valor de u.
El método descrito proporciona estimadores, pero no asegura que estos sean los mejores, ni tan siquiera que sean buenos. A continuación mostramos una propiedad interesante de los estimadores puntuales, como es la Insesgadez.
Estimadores insegados o centrados
Un estimador se dice que es Insesgado o Centrado si la esperanza del estimador, \( E( \widehat{\theta}) \), coincide con el valor del parámetro θ que se desea estimar
\( E( \widehat{\theta}) = \theta \)
La media muestral es un estimador insesgado de la media poblacional
En efecto, sea \( X_1, X_2, \cdots, X_{n} \) una muestra aleatoria de tamaño n de una distribución X con media μ. \( ( E(X_{i})= \mu \hspace {.2cm} \)para todo \( i=1,2, \cdots, n ) \).
Comprobemos que: \( E( \overline{X})= \mu \)
En efecto,
\( E(\overline{X})=E \left ( \displaystyle \frac {1} {n} \displaystyle \sum_{i=1}^{n}X_{i} \right )= \displaystyle \frac {1}{n}E \left ( \displaystyle \sum_{i=1}^{n}X_{i} \right)= \displaystyle \frac {1}{n} \displaystyle \sum_{i=1} ^{n} E(X_{i})= \displaystyle \frac{1}{n} \displaystyle \sum_{i=1}^{n} \mu= \displaystyle \frac{1}{n}n \mu= \mu \)
El estimador X de μ tiene algunas buenas propiedades. En particular, que en un muestreo repetido de una población con media μ los valores de el estimador X fluctuarán alrededor de μ. También que para muestras de tamaño grande, los valores del estimador X variarán muy poco de una muestra a otra. Así los valores del estimador X están centrados en μ, valor que se pretende estimar a través de este estadístico, y para muestras grandes, se espera que la mayoría de los valores observados caigan cerca de μ.
Estimadores segados o descentrados
Un estimador se dice que es Sesgado o Descentrado si la esperanza del estimador, \( E( \widehat{\theta}) \), no coincide con el valor del parámetro θ que se desea estimar
\( E( \widehat{\theta}) \neq \theta \hspace{.3cm} \) o \( \hspace{.3cm}E( \widehat{\theta}) =\theta+b(\theta) \)
donde \( b(\theta) \) recibe el nombre de Sesgo o Excentricidad.
-La varianza muestral es un estimador sesgado de la varianza poblacional
En efecto, sea \( X_1, X_2, \cdots, X_{n} \) una muestra aleatoria de tamaño n de una distribución X con media \( \mu \) y varianza \( σ^{2} \), \( (E(X_{i})= \mu \hspace{.2cm}; \hspace{.2cm}Var(X_{i})=σ^{2} \hspace{.2cm} \)para todo \( \hspace{.2cm} i=1,2, \cdots n) \).
Comprobemos que: \( E( \widehat{\sigma}{2}) \neq \widehat{\sigma}{2} \)
En efecto, como
\( \begin{array}{ll} \\ \widehat {\sigma}^{2} & = \displaystyle \frac {1} {n} \displaystyle \sum_{i=1}^{n} (X_{i}- \overline {X})^{2}= \displaystyle \frac {1} {n} \displaystyle \sum_{i=1}^{n} \left [(X_{i}- \mu)-( \overline {X}- \mu) \right]^{2}=\displaystyle \sum_{i=1}^{n} \displaystyle \frac {(X_{i}-\mu)^{2}} {n} + \\ & + \displaystyle \frac { (\overline {X}-\mu)^{2}}{n}-2 \displaystyle \frac {(X_{i}- \mu) ( \overline{X}- \mu)} {n} = \displaystyle \sum_{i=1}^{n} \displaystyle \frac {(X_{i}-\mu)^{2}} {n}+( \overline {X}- \mu)^{2} – \\ & –
2( \overline {X}- \mu) \displaystyle \sum_{i=1}^{n} \displaystyle \frac {(X_{i}- \mu) } {n}=\displaystyle \sum_{i=1}^{n} \displaystyle \frac {(X_{i}-\mu)^{2}} {n} -( \overline {X}- \mu)^{2} \\ \end{array} \)
Entonces
\( \begin{array}{ll} \\ E(\widehat {\sigma}^{2} ) & = E \left [ \displaystyle \sum_{i=1}^{n} \displaystyle \frac {(X_{i}- \mu)^{2} } {n} -( \overline {X} – \mu)^{2} \right ]= \displaystyle \frac {1}{n} \displaystyle \sum_{i=1}^{n} E(X_{i}- \mu)^{2}-E( \overline{X}- \mu)^{2}= \\ & = \displaystyle \frac {1}{n} \displaystyle \sum_{i=1}^{n} σ^{2}- \displaystyle \frac{σ^{2}} {n}=σ ^{2}-\displaystyle \frac{σ^{2}} {n} \\ \end{array} \)
Por lo tanto, \( \widehat {\sigma}^{2} \) es un estimador sesgado de la varianza poblacional y su sesgo es \( -σ^{2}/n \).
-La cuasivarianza muestral es un estimador insesgado de la varianza poblacional
En efecto
\( \begin{array}{ll} \\ E( S^{2} ) & = E \left [ \displaystyle \frac {1}{n-1} \displaystyle \sum_{i=1}^{n}(X_{i}- \overline {X})^{2} \right]=E \left [ \displaystyle \frac {n}{n-1} \displaystyle \sum_{i=1}^{n} \displaystyle \frac {(X_{i}-\overline {X})^{2}} {n} \right ] = \\ & = \displaystyle \frac {n}{n-1}E( \widehat{σ}^{2})= \displaystyle \frac {n}{n-1} \left (σ^{2} – \displaystyle \frac {σ^{2}}{n} \right )= \displaystyle \frac {n}{n-1} \left ( \displaystyle \frac {n-1}{n} σ^{2} \right)=σ^{2} \\ \end{array} \)
Vamos a fijar, a continuación una serie de conceptos: Un estadístico utilizado para aproximar un parámetro de la población se denomina estimador del parámetro. El número obtenido cuando se evalúa el estimador para una muestra en particular, es una estimación del parámetro. Por ejemplo, el estadístico \( \overline {X} \) es un estimador de \( \mu \); el valor que obtenemos al sustituir los valores de la muestra es la estimación basada en dicha muestra. El estadístico \( \overline {X} \) se denomina estimador puntual de \( \mu \) porque al evaluarlo para una muestra en concreto da un solo número.
El estimador \( \widehat {\theta} \) del parámetro \( \theta \) debe tener una distribución concentrada alrededor de \( \theta \) y la varianza debe ser lo menor posible. Para estudiar la variabilidad de los valores del parámetro utilizaremos una cantidad llamada error cuadrático medio.
Definición: Sea \( \widehat {\theta} \) el estimador de \( \theta \). Se define el error cuadrático medio, que se denota por ECM, como:
\( ECM (\widehat {\theta} )=E \left [(\widehat {\theta}- \theta)^{2} \right ]=Var[\widehat {\theta}]+ \left [(\theta-E[\widehat {\theta}] \right]^{2} \)
Veamos que: \( ECM( \overline {X})=Var[ \overline {X}] \)
\( \begin{array}{ll} \\ ECM( \overline {X}) & = Var[\overline {X}]+ \left [(\mu -E[\overline {X}] \right]^{2}=^{(1)}Var[\overline {X}]=Var \left ( \displaystyle \frac {1}{n} \displaystyle \sum_{i=1}^{n} X_{i} \right) = \\ & = \displaystyle \frac {1}{n^{2}} \displaystyle \sum_{i=1}^{n}Var(X_{i})= \displaystyle \frac {n \sigma^{2}}{n^{2}} = \displaystyle \frac {σ^{2}}{n} \\ \end{array} \)(1): La media muestral es un estimador insesgado de la media poblacional ( \( E(\overline {X})= \mu \) )
Estimación por intervalos de confianza: Intervalos de confianza para una población Normal
Ya hemos dicho, en la sección anterior, que los estimadores puntuales sólo proporcionan el “mejor” valor que se puede proponer como valor del parámetro poblacional desconocido que se desea estimar, es decir dan una idea aproximada del verdadero valor del parámetro poblacional pero no se sabe cómo de buena es dicha aproximación. Hemos visto que la media muestral es un buen estimador de la media poblacional, pero un único valor observado \( \overline {X} \) generalmente no es exactamente igual a μ, habrá una cierta diferencia entre \( \overline {x} \) y \( \mu \). Sería conveniente poder tener una idea de lo cerca que está nuestra estimación del verdadero valor de la media poblacional y también poder dar información de los seguros o confiados que estamos de la precisión de la estimación. Por medio de los intervalos de confianza podemos no sólo tener una idea del valor de la media, sino también de la precisión del estimador (cuanto de alejado está el valor del estimador del verdadero valor del parámetro).
El propósito es determinar un intervalo que con cierta seguridad contenga el parámetro a estimar. Los extremos del intervalo son funciones \( \theta_1^{∗}(X_1,X_2, \cdots, X_{n}) \) y \( \theta_2^{∗}(X_1,X_2,\cdots ,X_{n}) \) de la muestra y por tanto variables aleatorias, siendo el objetivo de los intervalos de confianza encontrar tales funciones de forma que con cierta seguridad se pueda afirmar que \( \theta_1^{∗} \leq \theta \leq \theta_2^{∗} \).
En término generales, la construcción de un intervalo de confianza para un parámetro desconocido \( \theta \) consiste en encontrar dos funciones \( \theta_1^{∗}(X_1,X_2, \cdots, X_{n}) \) y \( \theta_2^{∗}(X_1,X_2,⋯,X_{n}) \) de los valores muestrales (estadísticos) \( (\theta_1^{∗} \leq \theta_2^{∗}) \) tales que
\( P[\theta_1^{∗}\leq \theta \leq \theta_2^{∗}]=1-α \) . para algún \( α>0 \),
entonces se puede decir que \( \theta_1^{∗} \) y \( \theta_2^{∗} \) determina un intervalo que tiene la probabilidad \( 1-α \) de contener al parámetro poblacional \( \theta \).
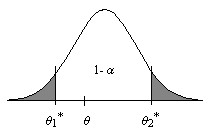 Figura 9.1
Figura 9.1
donde
∙ 1-α recibe el nombre de coeficiente de confianza o nivel de confianza. Es la probabilidad de que un intervalo de confianza contenga el verdadero valor del parámetro
∙ α es un número pequeño comprendido entre 0 y 1, 0 < α < 1 (usualmente próximo a 0). Es el riesgo de que el intervalo no contenga el valor del parámetro a estimar θ, por lo que α recibe el nombre de riesgo del error del intervalo, nivel del error del intervalo o nivel de significación del intervalo.
∙ \( \theta_1^{∗} \) y \( \theta_2^{∗} \) reciben el nombre de límite inferior y superior de confianza, respectivamente
Este intervalo recibe el nombre Intervalo de confianza con coeficiente de confianza 1-α. Se desea que el coeficiente de confianza sea próximo a la unidad y que la amplitud del intervalo sea lo más pequeña posible.
En esta sección vamos a estudiar, dentro de la distribución Normal, los intervalos de confianza para los parámetros μ, σ y p.
Intervalo de confianza para la media de una distribución N(μ, σ) con varianza conocida
Supongamos que interesa estimar la media poblacional μ para una población N(μ, σ) cuya varianza es conocida. Para ello, se selecciona de esta población una m.a.s., \( X_1,X_2, \cdots ,X_{n}\), y se calcula su media muestral, \( \overline {X} \), como “mejor” estimador puntual de μ. La construcción del intervalo se hace tomando como base este estimador.
Dado un nivel de significación α, buscamos dos funciones de la media muestral, \( \theta_1^{∗}( \overline {X}) \) y \( \theta_2^{∗}(\overline {X}) \), de modo que se verifique:
\( P[\theta_1^{∗}( \overline {X}) \leq \mu \leq \theta_2^{∗}( \overline {X})]=1- \alpha \)
Dado que
\( \overline {X } \rightarrow N(\mu, σ/ \sqrt{n}) \Rightarrow Z= \displaystyle \frac { \overline{X} – \mu}{σ/ \sqrt{n}} \rightarrow N(0, 1) \)
Entonces
\( \begin{array}{ll} P[\theta_1^{∗}( \overline {X}) \leq \mu \leq \theta_2^{∗}( \overline {X})] & = P[- \theta_1^{∗}( \overline {X}) \geq – \mu \geq -\theta_2^{∗}( \overline {X})] = \\ \\ & = P[- \theta_2^{∗}( \overline {X}) \leq -\mu \leq -\theta_1^{∗}( \overline {X})] = \\ \\ & = P[\overline {X}- \theta_2^{∗}( \overline {X}) \leq \overline{X}- \mu \leq \overline {X} -\theta_1^{∗}( \overline {X})] = \\ \\ & = P \left [ \displaystyle \frac { \overline {X}- \theta_2^{∗}( \overline {X}) }{σ/ \sqrt{n}} \leq \displaystyle \frac { \overline {X}- \mu }{σ/ \sqrt{n}} \leq \displaystyle \frac { \overline {X}- \theta_1^{∗}( \overline {X}) }{σ/ \sqrt{n}} \right] = \\ \\ & = P \left [ \displaystyle \frac { \overline {X}- \theta_2^{∗}( \overline {X}) }{σ/ \sqrt{n}} \leq Z \leq \displaystyle \frac { \overline {X}- \theta_1^{∗}( \overline {X}) }{σ/ \sqrt{n}} \right] =1- \alpha \\ \end{array} \hspace{1cm} \) [9.1]
Para un nivel de significación dado, se determina, mediante la Tabla III del Apéndice B, un valor \( z_{α/2} \) tal que
\( P[-z_{α/2} \leq Z \leq z_{α/2}]=1-α \Rightarrow \left \{ \begin{array} \\ \displaystyle \frac { \overline {X}- \theta_2^{∗}( \overline {X}) }{σ/ \sqrt{n}} = -z_{α/2} \\ \displaystyle \frac { \overline {X}- \theta_1^{∗}( \overline {X}) }{σ/ \sqrt{n}}=z_{α/2} \end{array} \right. \)
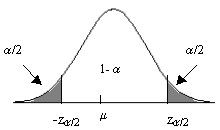
Figura 9.2
Por tanto las funciones muestrales \( \theta_1^{∗}( \overline {X}) \) y \( \theta_2^{∗}( \overline {X}) \) tienen las siguientes expresiones
\( \theta_1^{∗}( \overline {X}) = \overline {X} – z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \hspace{.5cm} \) y \( \hspace{.5cm} \theta_2^{∗}( \overline {X}) =\overline {X} +z_{α/2}\displaystyle \frac {σ} { \sqrt{n}}\)
Sustituyendo estas expresiones en el primer miembro de la expresión ([9.1]) se tiene
\( P \left [ \overline {X} – z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \leq \mu \leq \overline {X} + z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \right]=1-α \hspace{1cm} \) [9.2]
Por lo tanto, la probabilidad de que el intervalo aleatorio
\( \left [\overline {X} – z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} , \overline {X} + z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \right ] \hspace{1cm} \) [9.2]
contenga el verdadero valor de la media \( μ \) es \(1-α \).
\( \overline {X} – z_{α/2}(σ/ \sqrt {n}) \) y \( \overline {X} + z_{α/2}(σ/ \sqrt {n}) \) reciben el nombre de límites de confianza inferiores y superiores, respectivamente, para μ.
Ejemplo 9.1. De una cierta población se ha extraído una muestra de 64 individuos, cuyo valor medio es \( \overline {x}=1012 \). Se sabe por otras experiencias del mismo tipo, que la desviación típica vale 25. Hallar intervalos de confianza para el valor medio de la población a los niveles de confianza del 0.90,0.95 y 0.99.
Respuesta:
a) Para un nivel de confianza del 90%
\( \Rightarrow 1- \alpha =0.90 \Rightarrow \alpha =0.1 \Rightarrow \alpha/2=0.05 \)\( \begin{array}{ll} P \left [ \overline {X} – z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \leq \mu \leq \overline {X} + z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \right] & = P \left [1012-1.645 \displaystyle \frac {25}{ \sqrt{64}} \leq \mu \leq 1012+1.645 \displaystyle \frac {25}{ \sqrt{64}} \right] \\ & = P[1006.86 \leq \mu \leq 1017.14]=0.90 \\ \end{array} \)
Entonces, hay un 90% de confianza de que el valor medio de la población se encuentre entre 1006.86 y 1017.14.
b) Para un nivel de confianza del 95%
\( \Rightarrow 1- \alpha =0.95 \Rightarrow \alpha =0.05 \Rightarrow \alpha/2=0.025 \)\( \begin{array}{ll} P \left [ \overline {X} – z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \leq \mu \leq \overline {X} + z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \right] & = P \left [1012-1.96 \displaystyle \frac {25}{ \sqrt{64}} \leq \mu \leq 1012+1.96 \displaystyle \frac {25}{ \sqrt{64}} \right] \\ & = P[1005.875 \leq \mu \leq 1018.125]=0.95 \\ \end{array} \)
Por tanto, se tiene el 95% de confianza de que el intervalo [1005.875 , 1018.125] comprenda al valor medio de la población.
En la expresión ([9.3]) del intervalo de confianza para μ observamos que:
i) Al aumentar el tamaño de la muestra disminuye la amplitud del intervalo, este resultado es lógico ya que un tamaño grande de la muestra disminuirá el error estándar, \( σ/ \sqrt{n} \).
Por lo tanto, una cuestión que se plantea es cuál debe ser el tamaño mínimo de la muestra para obtener una estimación de la media con una precisión establecida de antemano. Para determinar dicho tamaño muestral escribamos la expresión ([9.3]) de la siguiente forma
\( \begin{array}{ll} P \left [-z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \leq \overline {X} -μ \leq z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \right] & = P \left [∣\overline {X}-μ∣≤z_{α/2} \displaystyle \frac {σ} { \sqrt{n}}\right] \\ & = P[∣\overline {X}-μ∣ \leq \epsilon]=1-α \\ \end{array} \)
donde \( \epsilon \) es la precisión de la estimación o error.
\( \epsilon =z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \Rightarrow n= \left (z_{α/2} \displaystyle \frac {σ}{ \epsilon} \right)^{2} \)
Ejemplo 9.2. Determinar el tamaño muestral correspondiente al apartado a) del Ejemplo 9.1 con una precisión de la estimación igual a 4.
Respuesta:
\( n= \left (z_{α/2} \displaystyle \frac {σ}{ \epsilon} \right )^{2}= \left (1.645 \displaystyle \frac {25}{4} \right)^{2}=105.704 \simeq 106 \)Se necesita una muestra de 106 individuos para estimar el valor medio de la población con un error igual a 4.
ii) Al aumentar el coeficiente de confianza aumenta la amplitud del intervalo ya que un nivel de confianza grande incrementa el valor del cuantil \( z_{α/2} \) dando como resultado un intervalo más amplio.
Situación que se puede observar en el Ejemplo 9.1, donde la amplitud del intervalo
– para un coeficiente de confianza del 95% es: 1018.125-1005.875=12.25 mientras que
– para un coeficiente de confianza del 90% es: 1017.14-1006.86=10.28.
Ejemplo 9.3. Ante la sospecha de una diferencia sistemática entre dos laboratorios A y B en la determinación de la cantidad de albúmina sérica, expresada en gr./100ml., se ha realizado una experiencia consistente en la extracción de sangre a 10 pacientes. Para cada muestra de sangre se midió la albúmina sérica en ambos laboratorios y las diferencias entre laboratorios (A–B) fueron las siguientes:
0.6, 0.7, 0.8, 0.9, 0.3, 0.5, –0.5, 1.3, 0.4, 0.8
Considerando normalidad. Se pide, al nivel de confianza 0.9:
a) Calcular un intervalo de confianza para la diferencia media de medición considerando que la desviación típica de las diferencias poblacionales es 0.22.
b) ¿Qué tamaño mínimo de muestra deberíamos tomar para que la amplitud del intervalo fuese menor o igual que la mitad del anterior?
Respuesta:
X: {Diferencia albúmina entre A y B} ; n=10; x=0.58; σ=0.22; \( X \rightarrow N(μ, 0.22) \)
a) \(1-α=0.90; α=0.10; α/2=0.05; z_{α/2}=z_{0.05}=1.645 \)
\( \begin{array}{ll} P \left [ \overline {X} – z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \leq μ \leq \overline {X} + z_{α/2} \displaystyle \frac {σ} { \sqrt{n}} \right] & = P \left [0.58-1.645 \displaystyle \frac {0.22} { \sqrt{10}} \leq μ \leq 0.58+1.645\displaystyle \frac {0.22} { \sqrt{10}} \right] \\ & = P[0.4656 \leq μ \leq 0.6944]=0.90 \\ \end{array} \)
b) Amplitud actual: 0.6944-0.4656=0.2288
Amplitud teórica: \( \overline {X}+z_{α/2}\displaystyle \frac {σ} { \sqrt{n}} – \left (\overline {X}-z_{α/2}\displaystyle \frac {σ} { \sqrt{n}}\right )=2z_{α/2}\displaystyle \frac {σ} { \sqrt{n}} \)
Se tiene que determinar \( n \) de forma que la amplitud del intervalo sea menor o igual que la mitad de la amplitud del intervalo calculado en el apartado a)
\( 2z_{α/2}\displaystyle \frac {σ} { \sqrt{n}} \leq \displaystyle \frac {0.2288}{2} \Rightarrow \displaystyle \frac {2σ} {0.114} z_{α/2} \leq \sqrt {n} \Rightarrow n \geq \left (\displaystyle \frac {2σ} {0.1144} z_{α/2} \right )^{2} \Rightarrow \)
\( \Rightarrow n \geq \left (\displaystyle \frac {2 \times 0.22} {0.114} 1.645 \right)^{2} \Rightarrow n \geq 40.3 \Rightarrow n=40 \)
El tamaño mínimo de muestra pedido es 40.
Intervalo de confianza para la media de una distribución N(μ, σ) con varianza desconocida
Supongamos una muestra aleatoria, \( X_1,X_2, \cdots ,X_{n} \), de una distribución Normal con media \( μ \), y varianza \( σ^{2} \), ambas desconocidas y vamos a hallar un intervalo de confianza para la media poblacional \( μ \). Para ello, consideremos la variable aleatoria
\( T= \displaystyle \frac {\overline{X}-μ }{ \widehat {σ} / \sqrt {n-1}} \)
que tiene una distribución t-Student con n-1 grados de libertad.
Tenemos que determinar el valor del cuantil \( t_{α/2;n-1} \) tal que
\( \begin{array}{ll} P \left [ – t_{α/2; n-1} \leq \displaystyle \frac {\overline{X}-μ }{ \widehat {σ} / \sqrt {n-1}} \leq t_{α/2; n-1} \right] = & \\ = P \left [ \overline {X} – t_{α/2; n-1} \displaystyle \frac { \widehat{σ}} { \sqrt{n -1}} \leq μ \leq \overline {X} + t_{α/2; n-1} \displaystyle \frac { \widehat {σ}} { \sqrt{n-1}} \right] = 1-α \\ \end{array} \)
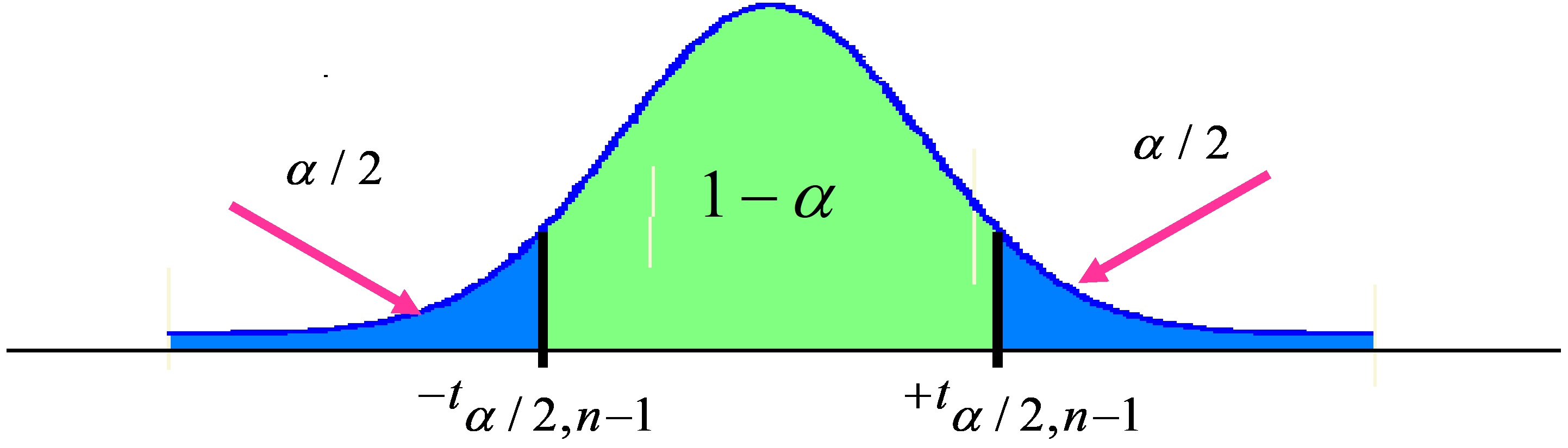
Figura 9.3
También se puede expresar en función de la cuasidesviación típica muestral S.
Dado que, la relación entre \( σ^{2} \) y \( S^{2} \) es:
\( n \widehat{σ}^{2}=(n-1)S^{2} \)
Tenemos la siguiente expresión del intervalo de confianza para μ
\( P \left [ \overline {X} – t_{α/2; n-1} \displaystyle \frac { S} { \sqrt{n }} \leq μ \leq \overline {X} + t_{α/2; n-1} \displaystyle \frac { S} { \sqrt{n}} \right] =1-α \)
Por lo tanto, la probabilidad de que el intervalo aleatorio
\( \left [ \overline {X} – t_{α/2; n-1} \displaystyle \frac { \widehat{σ}} { \sqrt{n -1}} , \overline {X} + t_{α/2; n-1} \displaystyle \frac { \widehat {σ}} { \sqrt{n-1}} \right] \)
o
\( \left [ \overline {X} – t_{α/2; n-1} \displaystyle \frac { S} { \sqrt{n}} , \overline {X} + t_{α/2; n-1} \displaystyle \frac { S} { \sqrt{n}} \right] \)
contenga el verdadero valor de la media μ es 1-α.
Ejemplo 9.4. En una muestra de 9 preparados de jugo de tomate se ha obtenido una media de 22 mg/100 cc y una cuasidesviación típica de 6.3 mg/100 cc. Supuesto que el contenido de vitamina C del jugo de tomate se distribuye normalmente. Se pide:
a) Estimar el contenido medio, en vitamina C, del jugo de tomate
b) Calcular un intervalo de confianza al 95% para dicha cantidad.
Respuesta:
a) El estimador pedido es la media muestral \( \overline {x} =22 \)
b) Para \( 1-α=0.95 \Rightarrow α/2=0.025 \hspace{.2cm}; \hspace{.2cm} t_{α/2;n-1}=t_{0.025;8}=2.307 \)
\( \begin{array}{ll} P \left [ \overline {X} – t_{α/2; n-1} \displaystyle \frac { S} { \sqrt{n }} \leq μ \leq \overline {X} + t_{α/2; n-1} \displaystyle \frac { S} { \sqrt{n}} \right] = & \\ = P \left [22-2.307 \displaystyle \frac {6.3}{ \sqrt{9}} \leq μ \leq 22+2.307\displaystyle \frac {6.3}{ \sqrt{9}} \right ]= P[17.1553 \leq μ \leq 26.8447]=0.95
\\ \end{array} \)
Por lo tanto, hay un 95% de confianza de que el intervalo [17.1553, 26.8447] contenga al contenido medio, en vitamina C, del jugo de tomate.
Intervalo de confianza para una proporción
Dada una variable aleatoria \( X \rightarrow B(n, p) \) con p desconocido, el objetivo es determinar un intervalo de confianza para el parámetro p. El Teorema de Moivre, (Capítulo 7), dice que para un tamaño muestral grande (n>30), la distribución Binomial se aproxima a una Normal
\( X \rightarrow N(np, \sqrt {npq}) \)
Denotamos por \( \widehat {p} \) al estadístico proporción muestral que lo definimos como: \( \widehat {p} =X/n \).
\( \widehat {p} \) es un estimador insesgado de p y se demuestra que la distribución de \( \widehat {p} \)
\( \widehat {p} = \displaystyle \frac {X} {n} \rightarrow N \left (p, \displaystyle \sqrt{ \displaystyle \frac {pq}{n}} \right ) \)
o que la distribución de
\( \displaystyle \frac { \widehat {p} – p} { \displaystyle \sqrt { \displaystyle \frac { \widehat {p}\widehat {q} } {n} } } \rightarrow N(0,1) \hspace {1cm} \) para n grande
De esta forma el intervalo de confianza para el parámetro desconocido p viene dado por
\( P \left [ \widehat {p }-z_{α/2}\displaystyle \sqrt { \displaystyle \frac { \widehat {p}\widehat {q} } {n} } \leq p \leq \widehat {p } + z_{α/2}\displaystyle \sqrt { \displaystyle \frac { \widehat {p}\widehat {q} } {n} } \right ]=1-α \hspace {1cm} \) [9.7]
en donde \( \widehat {p} =X/n \) se obtiene a partir de la muestra aleatoria de tamaño n.
El intervalo
\( \left [ \widehat {p }-z_{α/2}\displaystyle \sqrt { \displaystyle \frac { \widehat {p}\widehat {q} } {n} } , \widehat {p } + z_{α/2}\displaystyle \sqrt { \displaystyle \frac { \widehat {p}\widehat {q} } {n} } \right ] \)
es un intervalo aleatorio, para tamaño de muestra grande, que contiene a p con una probabilidad \( 1-α \) , donde \( \widehat {p}=X/n \) .
Ejemplo 9.5. Una encuesta de 100 votantes para conocer sus opiniones respecto a dos candidatos muestra que 55 apoyan a A y 45 a B. Se pide: Calcular un intervalo de confianza para la proporción de votos de cada candidato, al nivel de confianza del 95%.
Respuesta:
a) Intervalo de confianza para el candidato A
\( \begin{array}{ll} P \left [ \widehat {p }-z_{α/2}\displaystyle \sqrt { \displaystyle \frac { \widehat {p}\widehat {q} } {n} } \leq p \leq \widehat {p } + z_{α/2}\displaystyle \sqrt { \displaystyle \frac { \widehat {p}\widehat {q} } {n} } \right ] = & \\ = P \left [ \displaystyle \frac {55} {100}-1.96 \displaystyle \sqrt { \displaystyle \frac { 0.55 \times 0.45} {100} } \leq p \leq \displaystyle \frac {55} {100}+1.96 \displaystyle \sqrt { \displaystyle \frac { 0.55 \times 0.45} {100} } \right ] = & \\ = P[0.45 \leq p \leq 0.65]=0.95 \\ \end{array} \)
Hay un 95% de confianza de que la proporción de votos del candidato A se encuentre entre 0.45 y 0.65.
b) Intervalo de confianza para el candidato B
\( \begin{array}{ll} P \left [ \widehat {p }-z_{α/2}\displaystyle \sqrt { \displaystyle \frac { \widehat {p}\widehat {q} } {n} } \leq p \leq \widehat {p } + z_{α/2}\displaystyle \sqrt { \displaystyle \frac { \widehat {p}\widehat {q} } {n} } \right ] = & \\ = P \left [ \displaystyle \frac {45} {100}-1.96 \displaystyle \sqrt { \displaystyle \frac { 0.55 \times 0.45} {100} } \leq p \leq \displaystyle \frac {45} {100}+1.96 \displaystyle \sqrt { \displaystyle \frac { 0.55 \times 0.45} {100} } \right ] = & \\ = P[0.35 \leq p \leq 0.55]=0.95 \\ \end{array} \)
Por tanto, el intervalo de confianza para la proporción de votos del candidato B, al 95%, es [0.35 , 0.55].
Un problema que puede plantearse es el correspondiente a la estimación del tamaño muestral necesario de manera que, con una confianza de 100(1-α)% aproximadamente, el estimador p de la proporción p se encuentre a no más de \( \epsilon \) unidades de p.
Para determinar el tamaño muestral escribamos la expresión ([9.7]) de la siguiente forma
\( P \left [| \widehat {p}-p| \leq z_{α/2}\displaystyle \sqrt { \displaystyle \frac {\widehat {p}\widehat {q}}{n}} \right ]=P [| \widehat {p} -p| \leq \epsilon]=1-α \)
donde \( \epsilon \) es la precisión de la estimación o el error.
\( \epsilon = z_{α/2} \displaystyle \sqrt { \displaystyle \frac {\widehat {p}\widehat {q}}{n}} \Rightarrow n=\left (z_{α/2}\displaystyle \frac { \sqrt {\widehat {p}\widehat {q} }} {\epsilon} \right )^{2} \hspace{.3cm} \) con \( \hspace{.3cm} \widehat {p} =X/n \)
Ejemplo 9.6. Unos grandes almacenes desean estimar la proporción de empleados que están a favor de cambiar el convenio laboral. Para ello se realiza una encuesta a 100 trabajadores y resulta que la mitad está a favor del cambio y la otra mitad no. La estimación debe quedar a menos de 0.05 de la proporción verdadera de los que están a favor del cambio del convenio, con un coeficiente de confianza del 90 %. ¿Cuántos empleados se debe muestrear?.
Respuesta: El tamaño muestral se determina de la siguiente forma
\( n= \left (z_{0.05}\displaystyle \frac { \sqrt {\widehat {p}\widehat {q} }} {\epsilon} \right )^{2} =\left (1.645 \displaystyle \frac { \sqrt {0.5 \times 0.5 }} {0.05}\right )^{2}=270.6 \simeq 271 \)Es necesario una muestra de 271 empleados para estimar la proporción verdadera, que está a favor del cambio del convenio laboral, con una exactitud de ±0.05.
Ejemplo 9.7. Un equipo de investigadores realiza unos estudios para estimar la proporción de personas que padecen gripe A, en una región española, mediante un intervalo con un error máximo de 0.015 y nivel de confianza 0.95. ¿A cuántas personas deben analizar para alcanzar aproximadamente este objetivo, sabiendo que en un pequeño sondeo orientativo (muestra piloto) resultó que el 15% de las personas estaban afectadas por la enfermedad?
Respuesta:
X: “Número de personas con gripe A”; \( p=0.15; z_{α/2}=z_{0.025}=1.96; \epsilon =0.015 \)
\( n = \left (z_{0.05} \displaystyle \frac { \sqrt {\widehat {p}\widehat {q} }} {\epsilon} \right )^{2} =\left (1.96 \displaystyle \frac { \sqrt {0.15 \times 0.85 }} {0.015}\right )^{2}=2176.9 \)
Es necesario una muestra de 2177 personas para estimar la proporción de ellas que padecen gripe A, con una exactitud de ±0.015.
Intervalo de confianza para la varianza de una distribución N(μ, σ) con media conocida
Consideremos la variable aleatoria
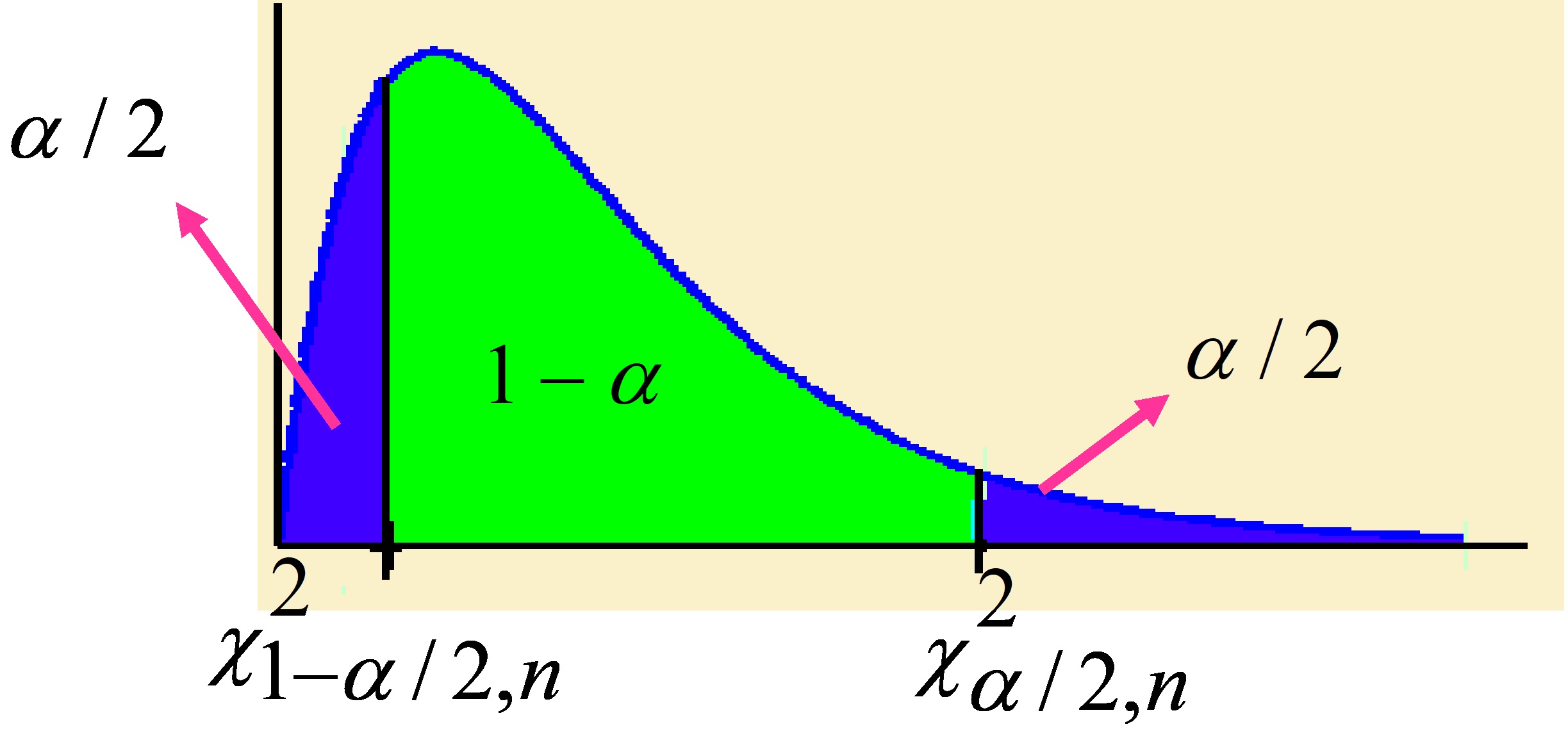
\( \displaystyle \frac {\displaystyle \sum_{i=1}^{n} (X_i – \mu )^{2} } { \sigma^{2}} \rightarrow \chi_{n}^{2} \)
Se determinan los cuantiles \( \chi_{\alpha/2; n}^{2} \) y \( \chi_{1- \alpha/2; n}^{2} \), tales que:
 Figura
Figura
\( P[\chi_{1-\alpha/2;n}^{2} \leq \chi_{n}^{2} \leq \chi_{\alpha/2;n}^{2}]=1- \alpha \)
Por tanto,
\( P \left [\chi_{1-\alpha/2;n}^{2} \leq \displaystyle \frac {\displaystyle \sum_{i=1}^{n} (X_i – \mu )^{2} } { \sigma^{2}} \leq \chi_{\alpha/2;n}^{2} \right]= P \left [ \displaystyle \frac {\displaystyle \sum_{i=1}^{n} (X_i – \mu )^{2} } {\chi_{\alpha/2;n}^{2}} \leq \sigma^{2} \leq \displaystyle \frac {\displaystyle \sum_{i=1}^{n} (X_i – \mu )^{2} } { \chi_{1 – \alpha/2;n}^{2}} \right ]=1- \alpha \)
Entonces el intervalo aleatorio
\( \left [ \displaystyle \frac {\displaystyle \sum_{i=1}^{n} (X_i – \mu )^{2} } {\chi_{\alpha/2;n}^{2}} \hspace{.2cm}, \hspace{.2cm} \displaystyle \frac {\displaystyle \sum_{i=1}^{n} (X_i – \mu )^{2} } {\chi_{1- \alpha/2;n}^{2}} \right] \)
contiene a \( σ^{2} \) con una probabilidad \( 1- \alpha \).
Ejemplo 9.8. Se estudia un nuevo proceso de fabricación de bombillas que se supone reduce la dispersión de la duración de las mismas. Sabiendo que la duración media de las bombillas es 1100 horas y suponiendo que su distribución es normal, construir intervalos de confianza para la dispersión a los niveles del 90% y 98% a partir de una muestra de tamaño 20 que ha dado \( \displaystyle \sum_{i}x_{i}=22160 \) y \( \displaystyle \sum_{i}x_{i}^{2}=25000000 \).
Respuesta: Como \( \displaystyle \sum_{i}x_{i}=22160 \) y \( \displaystyle \sum_{i}x_{i}^{2}=25000000 \) entonces
\( \begin{array}{ll} \\ \displaystyle \sum_{i=1}^{20}(x_{i}- \mu)^{2} & = \displaystyle \sum_{i=1}^{20} x_{i}^{2} +20 μ^{2}-2μ \displaystyle \sum_{i=1}^{20} x_{i}= \\ & = 25000000+20(1100)^{2}-2 \times 1100 \times 22160=448000 \\ \end {array} \)
a) \( 1- \alpha =0.90 \Rightarrow α/2=0.05 \hspace{.2cm} ; \hspace{.2cm} \chi_{0.05;20}^{2}=31.4 \hspace{.2cm}; \hspace{.2cm} \chi_{0.95;20}^{2}=10.9 \)
\( \begin{array}{ll} \\ P \left [ \displaystyle \frac {\displaystyle \sum_{i=1}^{n} (x_i – \mu )^{2} } {\chi_{\alpha/2;n}^{2}} \leq \sigma^{2} \leq \displaystyle \frac {\displaystyle \sum_{i=1}^{n} (x_i – \mu )^{2} } {1- \chi_{\alpha/2;n}^{2}} \right ] = & P \left [ \displaystyle \frac {448000}{31.4} \leq \sigma^{2} \leq \displaystyle \frac {448000}{10.9} \right ] = \\ & = P[14262.97 \leq \sigma^{2} \leq 41290.32]=0.90 \\ \end{array} \)
Por lo tanto el intervalo confianza para la desviación típica es:
\( I=[119.42 ; 203.2] \)
b) \( 1- \alpha=0.98 \Rightarrow α/2=0.01 \hspace{.2cm} ; \hspace{.2cm} \chi_{0.01;20}^{2}=37.6 \hspace{.2cm} ; \hspace{.2cm} \chi_{0.99;20}^{2}=8.26 \)
\( P \left [ \displaystyle \frac { 448000} {37.6} \leq σ^{2} \leq \displaystyle \frac { 448000} {8.26} \right ]=P[11925.67 \leq σ^{2} \leq 54237.28]=0.98 \)
Por lo tanto el intervalo confianza para la desviación típica es:
\( I=[109.20 ; 232.88] \)
Intervalo de confianza para la varianza de una distribución N(μ, σ) con media desconocida
Consideremos las variables aleatorias
\( \displaystyle \frac {n \widehat{σ}^{2}}{σ^{2}} \rightarrow \chi_{n-1}^{2} \hspace{1cm} \) o \( \hspace{1cm} \displaystyle \frac {(n-1)S^{2}} {σ^{2}} \rightarrow \chi_{n-1}^{2} \)
donde
\( \widehat{σ}^{2}= \displaystyle \frac { \displaystyle \sum_{i=1}^{n} (X_{i}- \overline {X})^{2}} {n} \hspace{1cm} \) y \( \hspace{1cm} S^{2}= \displaystyle \frac { \displaystyle \sum_{i=1}^{n} (X_{i}- \overline {X})^{2}} {n-1} \)
Siguiendo el mismo razonamiento que en el caso anterior, tenemos que
\( P \left [χ_{1-α/2;n-1}^{2} \leq \displaystyle \frac { n \widehat{σ}^{2}}{σ^{2}} \leq χ_{α/2;n-1}^{2} \right ] = P \left [ \displaystyle \frac {n \widehat{σ}^{2}}{χ_{α/2;n-1}^{2}} \leq σ^{2} \leq \displaystyle \frac {n \widehat{σ}^{2}}{χ_{1- α/2;n-1}^{2}} \right ]=1-α \)
o
\( P \left [χ_{1-α/2;n-1}^{2} \leq \displaystyle \frac { (n- 1) S^{2}}{σ^{2}} \leq χ_{α/2;n-1}^{2} \right ]=P \left [ \displaystyle \frac { (n- 1) S^{2}} {χ_{α/2;n-1}^{2}} \leq σ^{2} \leq \displaystyle \frac { (n- 1) S^{2}} {χ_{1- α/2;n-1}^{2}} \right ]=1-α \)
De esta manera, un intervalo de confianza que contenga a σ² con una probabilidad 1-α está dado por
\( \left [ \displaystyle \frac {n \widehat{σ}^{2}}{χ_{α/2;n-1}^{2}} , \displaystyle \frac {n \widehat{σ}^{2}}{χ_{1- α/2;n-1}^{2}} \right ] \hspace{1cm} \) o \( \hspace{1cm} \left [ \displaystyle \frac {(n -1 ) S^{2}}{χ_{α/2;n-1}^{2}} , \displaystyle \frac { (n – 1) S^{2}}{χ_{1- α/2;n-1}^{2}} \right ] \)
Ejemplo 9.9. En unos laboratorios se realizan unos estudios para determinar el nivel de nistamina que hay en un determinado ungüento. Se sabe que su distribución sigue una ley Normal. Se toma una muestra de 16 ungüentos y se calcula su varianza resultando ser de 30. Estimar la varianza mediante un intervalo de confianza del 80%.
Respuesta: \( 1-α=0.80 \Rightarrow α/2=0.1 \hspace{.2cm} ; \hspace{.2cm} χ_{0.1;15}^{2}=22.3 \hspace{.2cm}: \hspace{.2cm} χ_{0.9;15}^{2}=8.55 \)
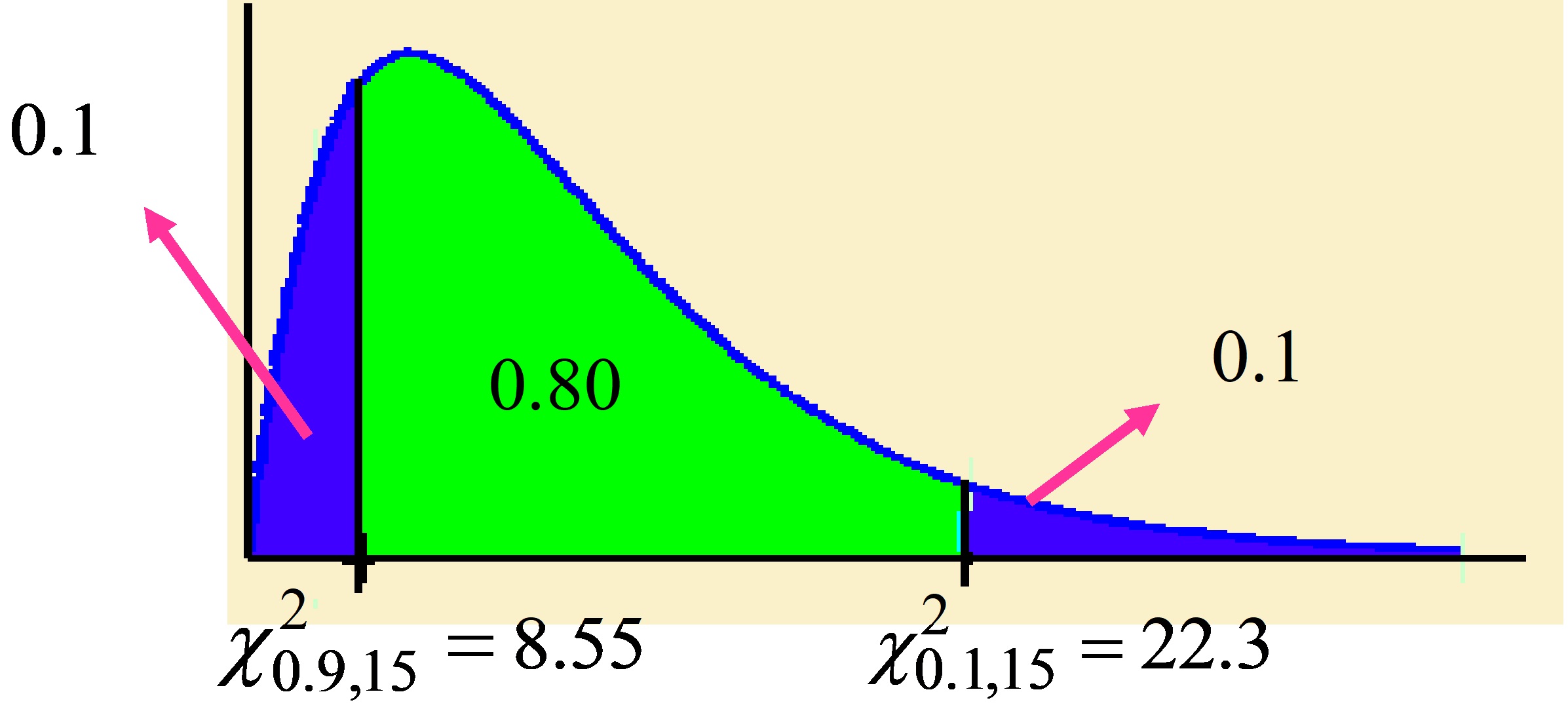
Figura
\( \begin{array}{ll} \\ P \left [ \displaystyle \frac {n \widehat{σ}^{2}}{χ_{α/2;n-1}^{2}} \leq σ^{2} \leq \displaystyle \frac {n \widehat{σ}^{2}}{χ_{1- α/2;n-1}^{2}} \right ] & = P \left [ \displaystyle \frac {16 \times 30}{22.3} \leq σ^{2} \leq \displaystyle \frac {16 \times 30}{8.55} \right ] \\ & = P[21.40 \leq σ ^{2} \leq 56.14]=0.80 \\ \end{array} \)
Intervalos de confianza para dos poblaciones normales: Muestras independientes y muestras apareadas
En las sesiones siguientes los intervalos de confianza se efectuarán bajo dos tipos de muestreo: muestras independientes y muestra apareadas.
Muestras independientes: Dos muestras se dicen que son independientes cuando las observaciones de una de ellas no condicionan a las observaciones de la otra.
Muestras apareadas: Dos muestras se dicen apareadas cuando cada dato de una muestra tiene su homónimo en la otra con el que está relacionado, cada observación de una muestra está emparejada con una observación de la otra muestra. Ejemplos de esta clase de emparejamiento ocurren por ejemplo en estudios en los que se suministra dos tratamientos al mismo sujeto.
Intervalos de confianza para dos poblaciones normales independientes
Supongamos que X e Y son dos variables aleatorias independientes y tales que \( X \rightarrow N(μ_{X}, σ_{X}) \) e \( Y \rightarrow N(μ_{Y}, σ_{Y}) \) .
∙ Sea \( ( X_1, X_2, \cdots , X_{n_{X}}) \) una m.a.s. de tamaño \( n_{X} \) extraída de la población \( N(μ_{X}, σ_{X}) \) y denotamos por \( \overline {X} \) y \( \widehat {σ}_{X}^{2} \), a la media muestral y a la varianza muestral, respectivamente.
∙ Sea \( (Y_1, Y_2, \cdots, Y_{n_{Y}}) \) una m.a.s. de tamaño \( n_{Y} \) extraída de la población \( N(μ_{Y}, σ_{Y}) \) y denotamos por \( \overline {Y} \) y \( \widehat {σ}_{Y}^{2} \) , a la media muestral y a la varianza muestral, respectivamente.
Vamos a construir intervalos de confianza para la diferencia de medias, diferencia de proporciones y cociente de varianzas.
Intervalos de confianza para la diferencia de medias
Supongamos que interesa comparar las dos medias poblaciones, para ello construyamos intervalos de confianza para \( μ_{X}-μ_{Y} \) para cada una de las situaciones siguientes:
- Conocidas las varianzas \( σ_{X}^{2} \) y \( σ_{Y}^{2} \)
- Desconocidas las varianzas pero supuestas iguales \( σ_{X}^{2}=σ_{Y}^{2} \) , y tamaños muestrales pequeños
- Desconocidas las varianzas y tamaños muestrales grandes.
1) Conocidas las varianzas \( σ_{X}^{2} \) y \( σ_{Y}^{2} \)
Sabemos (Capítulo 8) que la diferencia de las medias muestrales \( \overline {X} \) e \( \overline {Y} \)
\( \overline {X} – \overline {Y} \rightarrow N \left ( μ_{X}-μ_{Y}; \displaystyle \sqrt { \displaystyle \frac {σ_{X}^{2}} {n_{X}}+ \displaystyle \frac {σ_{Y}^{2}} {n_{Y}} } \right ) \)
Por lo tanto, el intervalo de confianza para la diferencia de medias se determina de la siguiente forma:
\( \begin{array} \\ P \left [ -Z_{α/2} \leq \displaystyle \frac { ( \overline {X}- \overline {Y})-(μ_{X}-μ_{Y}) }{ \displaystyle \sqrt { \displaystyle \frac {σ_{X}^{2}} {n_{X}} + \displaystyle \frac {σ_{Y}^{2}} {n_{Y}} } } \leq Z_{α/2} \right ] \\ = P \left [ ( \overline {X}- \overline {Y}) -Z_{α/2} \displaystyle \sqrt { \displaystyle \frac {σ_{X}^{2}} {n_{X}}+ \displaystyle \frac {σ_{Y}^{2}} {n_{Y}} } \leq μ_{X}-μ_{Y} \leq ( \overline {X}- \overline {Y}) + Z_{α/2} \displaystyle \sqrt { \displaystyle \frac {σ_{X}^{2}} {n_{X}}+ \displaystyle \frac {σ_{Y}^{2}} {n_{Y}} } \right ] =1-α \\ \end{array} \)
De esta forma, se tiene que un intervalo de confianza del 100(1-α)% para \( μ_{X}-μ_{Y} \) es
\( \left [ ( \overline {X}- \overline {Y}) -Z_{α/2} \displaystyle \sqrt { \displaystyle \frac {σ_{X}^{2}} {n_{X}}+ \displaystyle \frac {σ_{Y}^{2}} {n_{Y}} } , ( \overline {X}- \overline {Y}) + Z_{α/2} \displaystyle \sqrt { \displaystyle \frac {σ_{X}^{2}} {n_{X}}+ \displaystyle \frac {σ_{Y}^{2}} {n_{Y}} } \right ] \)
Ejemplo 9.10. En una vaquería se utilizan dos tipos de piensos para alimentar a las vacas. Se desea comparar la media de engorde con ambos piensos. Para ello, se alimenta a 10 vacas durante un cierto tiempo con el pienso A obteniéndose una ganancia media de peso de 2 Kg por vaca. Simultáneamente a otras 12 vacas se les alimenta con el pienso B y se obtiene un engorde medio de 2.4 Kg. Por experiencias anteriores se sabe que las variables objeto de estudio, engorde con cada uno de los piensos siguen distribuciones normales con desviación típica de 0.06 para el pienso A y 0.1 para el pienso B. Estimar la diferencia de engorde a un nivel de confianza del 95%.
Respuesta:
\( P \left [ ( \overline {X}_{A}- \overline {X}_{B}-Z_{α/2} \displaystyle \sqrt { \displaystyle \frac {σ_{A}^{2} }{n_{A}}+ \displaystyle \frac {σ_{B}^{2}} {n_{B}} } \leq μ_{A}-μ_{B} \leq ( \overline {X_{A}}- \overline {X_{B}} + Z_{α/2} \displaystyle \sqrt { \displaystyle \frac {σ_{A}^{2}} {n_{A}}+ \displaystyle \frac {σ_{B}^{2}} {n_{B}} } \right ] \Rightarrow \)
\( \Rightarrow I= \left [(2-2.4) \pm 1.96 \displaystyle \sqrt { \displaystyle \frac {0.06^{2}} {10}+\displaystyle \frac {0.1^{2}} {12}} \right ]=[-0.4677 , -0.3323] \)
Por lo tanto, hay el 95% de confianza de que \( μ_{A}-μ_{B} \) se encuentre entre -0.4577 y -0.3323. El intervalo no contiene al cero, por lo tanto hay diferencia de engorde con cada uno de los piensos, siendo el engorde medio mayor con el pienso B.
2) Desconocidas las varianzas pero supuestas iguales \( σ_{X}^{2}=σ_{Y}^{2} \) , y tamaños muestrales pequeños, entonces la variable aleatoria
\( T= \displaystyle \frac { ( \overline {X}- \overline {Y})-(μ_{X}-μ_{Y}) } {S_{p} \displaystyle \sqrt { \displaystyle \frac {1 } {n_{X}}+ \displaystyle \frac {1} {n_{Y}} } } \rightarrow t_{n_{X}+n_{Y}-2} \)
donde \( S_{p}^{2}= \displaystyle \frac { (n_{X}-1)S_{X}^{2}+(n_{Y}-1)S_{Y}^{2} } {n_{X}+n_{Y}-2 } \)
Por lo tanto, el intervalo de confianza para la diferencia de medias se determina de la siguiente forma
\( P \left [-t_{α/2;n_{X}+n_{Y}-2} \leq \displaystyle \frac { ( \overline {X}- \overline {Y})-(μ_{X}-μ_{Y}) } {S_{p} \displaystyle \sqrt { \displaystyle \frac {1 } {n_{X}}+ \displaystyle \frac {1} {n_{Y}} } } \leq t_{α/2;n_{X}+n_{Y}-2} \right] = 1-α \Rightarrow \)
\( \Rightarrow I= \left [ ( \overline {X}- \overline {Y}) \pm t_{α/2;n_{X}+n_{Y}-2}S_{p} \displaystyle \sqrt { \displaystyle \frac {1 }{n_{X}}+ \displaystyle \frac {1} {n_{Y}} } \right ] \)
Ejemplo 9.11. Dos laboratorios A y B realizan determinaciones de nicotina en 4 unidades de tabaco, con los resultados siguientes:
Laboratorio A: 16, 14, 13, 17
Laboratorio B: 18, 21, 18, 19
Suponiendo que las dos poblaciones examinadas son normales e independientes con igual varianza, estimar la diferencia del contenido medio en nicotina del tabaco a un nivel de confianza del 95%.
Respuesta:
\( A: n_{X}=4 \hspace{.3cm}; \hspace{.3cm} \overline {x} = \displaystyle \frac {16+ \cdots +17} {4}=15 \hspace{.3cm}; \hspace{.3cm}σ_{X}^{2}= \displaystyle \frac {(16-15)^{2}+ \cdots + (17-15)^{2}} {4}=3.34 \)
\( B: n_{Y}=4 \hspace{.3cm} ; \hspace{.3cm} \overline {y}= \displaystyle \frac {18+ \cdots +19 } {4}=19 \hspace{.3cm} ; \hspace{.3cm} σ_{Y}^{2}= \displaystyle \frac {(18-19)^{2}+ \cdots + (19-19)^{2} }{4}=2 \)
\( S_{p}= \displaystyle \sqrt { \displaystyle \frac {n_{X} \widehat {σ}_{X}^{2}+n_{Y} \widehat {σ}_{Y}^{2} } {n_{X}+n_{Y}-2} }= \displaystyle \sqrt { \displaystyle \frac {4 \times 3.34+ 4 \times 2 } {6}}=1.88 \)
\( t_{α/2;n_{X}+n_{Y}-2} =t_{0.025;6}=2.447 \)\( I= \left [( \overline {X} – \overline {Y}) \pm t_{α/2;n_{X}+n_{Y}-2}S_{p} \displaystyle \sqrt { \displaystyle \frac { 1} {n_{X}}+ \displaystyle \frac {1} {n_{Y}} }\right ] \Rightarrow \)
\( \Rightarrow P \left [(15-19) -2.447 \times 1.88 \displaystyle \sqrt { \displaystyle \frac {2} {4}} \leq μ_{X}-μ_{Y} \leq (15-19)+2.447 \times 1.88 \displaystyle \sqrt { \displaystyle \frac {2} {4}} \right ] \Rightarrow \)
\( \Rightarrow P[-7.253 \leq μ_{X}-μ_{Y} \leq -0.747]=0.95 \)
Por tanto, el contenido medio de nicotina difiere de un laboratorio a otro, siendo dicho contenido mayor en el laboratorio B que en laboratorio A.
3) Desconocidas las varianzas y tamaños muestrales grandes, entonces el intervalo de confianza para la diferencia de medias se determina de la siguiente forma:
\( \begin{array} \\ P \left [ -Z_{α/2} \leq \displaystyle \frac { ( \overline {X}- \overline {Y})-(μ_{X}-μ_{Y}) }{ \displaystyle \sqrt { \displaystyle \frac {S_{X}^{2}} {n_{X}} + \displaystyle \frac {S_{Y}^{2}} {n_{Y}}} } \leq Z_{α/2} \right ] = \\ = P \left [ ( \overline {X}- \overline {Y})-Z_{α/2} \displaystyle \sqrt { \displaystyle \frac {S_{X}^{2}} {n_{X}}+ \displaystyle \frac {S_{Y}^{2}} {n_{Y}} } \leq μ_{X}-μ_{Y} \leq ( \overline {X}- \overline {Y}) + Z_{α/2} \displaystyle \sqrt { \displaystyle \frac {S_{X}^{2}} {n_{X}}+ \displaystyle \frac {S_{Y}^{2}} {n_{Y}} }\right ] = \\ = 1-α \\ \end {array} \)
Ejemplo 9.12. Un fabricante de juguetes desea comparar el tiempo de producción medio de dos máquinas que hacen soldaditos de plomo y se encuentran en dos fábricas distintas. Los registros de la compañía, para 100 días seleccionados al azar para cada una de las máquinas, dieron los siguientes resultados:
Máquina 1: \( n_{1}=100 \hspace{.2cm}; \hspace{.2cm} \overline {x}_{1}=12 \hspace{.2cm}; \hspace{.2cm} s_{1}^{2}=6 \hspace{.2cm} ; \hspace{.6cm} \) Máquina 2: \( \hspace{.2cm} n_{2}=100 \hspace{.2cm}; \hspace{.2cm} \overline {x}_{2}=9 \hspace{.2cm}; \hspace{.2cm} s_{2}^{2}=4 \)
Construir un intervalo de confianza al 95% para la diferencia de medias.
Respuesta:
\( \begin{array} \\ P \left [ ( \overline {X}_{1}- \overline {Y}_{2}) -Z_{α/2} \displaystyle \sqrt { \displaystyle \frac {S_{1}^{2}} {n_{1}} + \displaystyle \frac {S_{2}^{2}} {n_{2}} } \leq μ_{1}-μ_2 \leq ( \overline {X}_{1}- \overline {Y}_{2}) + Z_{α/2} \displaystyle \sqrt { \displaystyle \frac {S_{1}^{2}} {n_{1}} + \displaystyle \frac {S_{2}^{2}} {n_{2}} } \right ] = \\ = P \left [(12-9)-1.96 \displaystyle \sqrt { \displaystyle \frac {6} {100}+ \displaystyle \frac {4} {100} } \leq μ_1-μ_2 \leq (12-9)+1.96 \displaystyle \sqrt { \displaystyle \frac {6} {100}+ \displaystyle \frac {4} {100} } \right] = \\ = P[2.38 \leq μ_1-μ_2 \leq 3.62]=0.95 \end{array} \)
Por lo tanto, se tiene el 95% de confianza de que \( μ_1-μ_2 \) esté entre 2.38 y 3.62. Esto sugiere que \( μ_1 \) debe ser mayor que \( μ_{2} \).
Intervalo de confianza para la diferencia de proporciones
Supongamos dos variables aleatorias independientes X e Y tales que \( X \rightarrow B(n_1, p_1) \) e \( Y \rightarrow B(n_2, p_2) \) con \( p_1 \) y \( p_2 \) desconocidos y los tamaños muestrales grandes.
Sean \( \widehat {p}_1= \displaystyle \frac {X} {n_1} \) y \( \widehat{p}_2= \displaystyle \frac {Y} {n_2} \) los valores estimados de \( p_1 \) y \( p_2 \) , respectivamente.
Entonces
\( \widehat {p}_1- \widehat {p}_2 \rightarrow N \left (p_1-p_2, \displaystyle \sqrt { \displaystyle \frac { \widehat {p}_1 \widehat {q}_1}{n_1}+ \displaystyle \frac { \widehat {p}_2 \widehat {q}_2}{n_2} } \right ) \)
o
\( \displaystyle \frac { ( \widehat {p}_1 – \widehat {p}_2 ) -(p_1-p_2) } { \displaystyle \sqrt { \displaystyle \frac { \widehat {p}_1 \widehat {q}_1}{n_1}+ \displaystyle \frac { \widehat {p}_2 \widehat {q}_2}{n_2} }} \rightarrow N(0,1) \) para \( n_1 \) y \( n_2 \) grandes
De esta forma el intervalo de confianza para la diferencia de proporciones se construye de la siguiente manera:
\( P \left [( \widehat {p}_{1}- \widehat {p}_{2} ) -z_{α/2} \displaystyle \sqrt { \displaystyle \frac { \widehat {p}_{1} \widehat {q}_{1}}{n_{1}}+ \displaystyle \frac { \widehat {p}_{2 }\widehat {q}_{2}}{n_{2}} } \leq p_1-p_2 \leq ( \widehat {p}_{1}- \widehat {p}_{2} ) + z_{α/2} \displaystyle \sqrt { \displaystyle \frac { \widehat {p}_{1} \widehat {q}_{1}}{n_{1}}+ \displaystyle \frac { \widehat {p}_{2 } \widehat {q}_{2}}{n_{2} }} \right ]=1-α \)Ejemplo 9.12. Unos estudios sobre las ranas tigres en dos regiones de Méjico tienen como objetivo comparar las proporciones de dichas ranas en cada una de las regiones. Para ello, se toma una muestra al azar de 100 ranas observando que 5 son ranas tigres en la zona A, mientras que de una muestra de 150 ranas en la zona B, 9 son ranas tigres. Construir un intervalo de confianza al 95% para la diferencia entre las verdaderas proporciones de ranas tigres en las dos regiones.
Respuesta: El intervalo de confianza pedido es:
\( \begin{array} \\ I = \left [(0.05-0.06) \pm 1.96 \displaystyle \sqrt { \displaystyle \frac {0.05 \times 0.95} {100}+\displaystyle \frac {0.06 \times 0.94 } {150}} \right ] =[-0.01 \pm 0.05717] = \\ = [-0.06717;0.04714] \\ \end {array} \)
Por tanto, hay un 95% de confianza de que la diferencia entre las verdaderas proporciones de ranas tigres en las dos regiones se encuentre entre -0.06717 y 0.04714. Como el intervalo contiene al cero, no parece haber diferencia significativa entre las cantidades de ranas tigres en las dos regiones.
Intervalos de confianza para el cociente de varianzas
Supongamos que interesa comparar las dos varianzas poblaciones, para ello construyamos intervalos de confianza para \( σ_{X}^{2} /σ_{Y}^{2} \) para cada una de las situaciones siguientes
∙ Las medias \( μ_{X} \) y \( μ_{Y} \) conocidas
∙ Las medias \( μ_{X} \) y \( μ_{Y} \) desconocidas
1) Las medias \( μ_{X} \) y \( μ_{Y} \) conocidas
Del Capítulo 8 se recordará que las variables aleatorias
\( \left. \begin{array} \\ \displaystyle \sum_{i=1}^{n_{x}} \left ( \displaystyle \frac {X_{i}- \mu_{X}}{σ_{X}} \right ) ^{2} \rightarrow \chi_{n_{X}}^{2} \\ \displaystyle \sum_{j=1}^{n_{y}} \left ( \displaystyle \frac {Y_{j}- \mu_{Y}}{σ_{Y}} \right ) ^{2} \rightarrow \chi_{n_{Y}}^{2} \\ \end{array} \right \} \Rightarrow \displaystyle \frac { \displaystyle \frac {\displaystyle \sum_{i=1}^{n_{x}} \left ( \displaystyle \frac {X_{i}- \mu_{X}}{σ_{X}} \right ) ^{2} }{n_{X}}} { \displaystyle \frac {\displaystyle \sum_{j=1}^{n_{y}} \left ( \displaystyle \frac {Y_{j}- \mu_{Y}}{σ_{Y}} \right ) ^{2} }{n_{Y}}} = \displaystyle \frac {n_Y}{n_X} \displaystyle \frac { \sigma^{2}_{Y}}{\sigma^{2}_{X}} \displaystyle \frac { \displaystyle \sum_{i=1}^{n_{x}} (X_i – \mu_X)^{2}}{\displaystyle \sum_{j=1}^{n_{y}} (Y_j – \mu_Y)^{2}} \rightarrow F_{n_{X},n_{Y}} \)
Vamos a determinar los cuantiles \( F_{α/2;n_{X},n_{Y}} \) y \( F_{1-α/2;n_{X},n_{Y}} \), tales que:
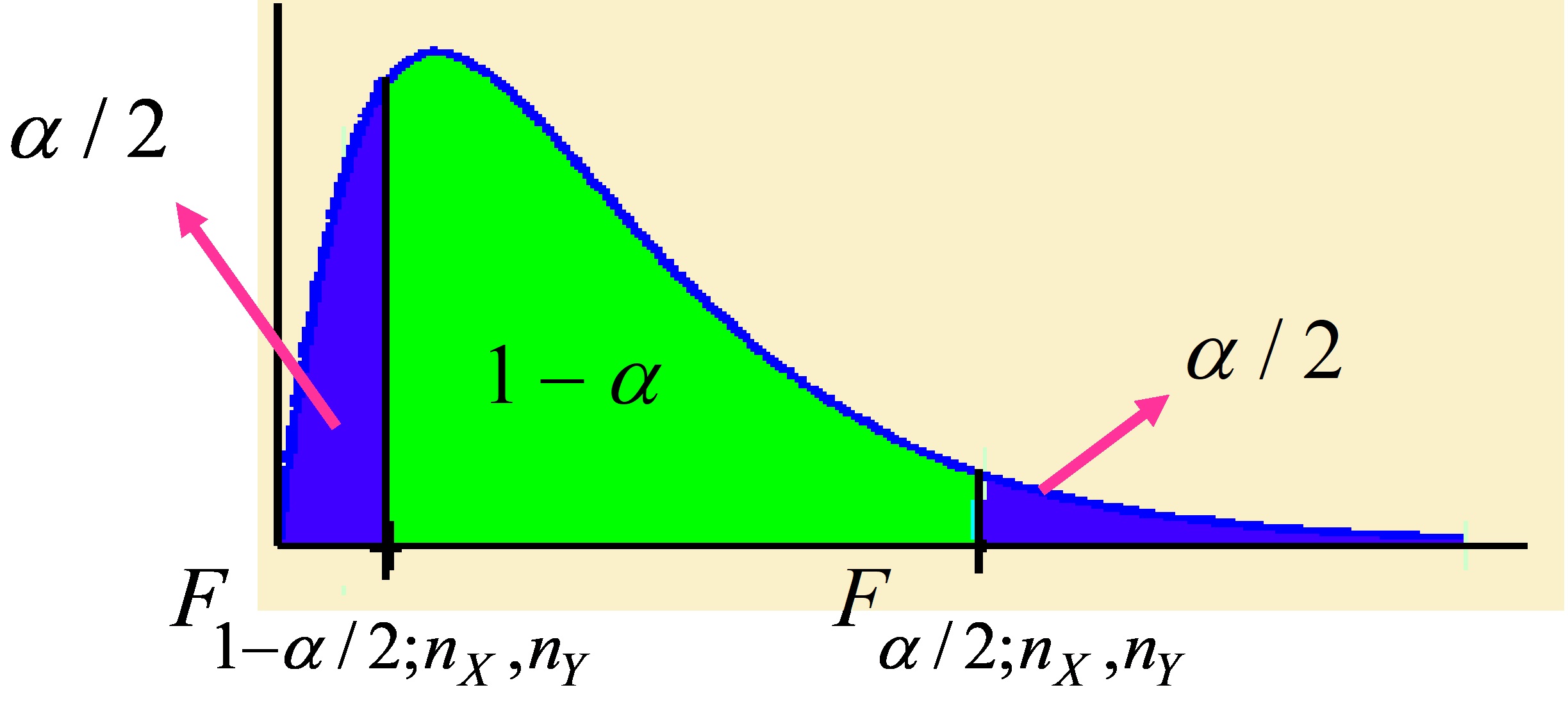
Figura
\( P[F_{1-α/2;n_{X},n_{Y}} \leq F_{n_{X},n_{Y}} \leq F_{α/2;n_{X},n_{Y}}]=1-α \)
Entonces, el intervalo de confianza para el cociente de varianzas se determina de la siguiente forma:
\( P \left [F_{1-α/2;n_{X},n_{Y}} \displaystyle \frac {n_{X}} {n_{Y}} \displaystyle \frac { \displaystyle \sum_{j=1}^{n_{y}}(Y_{j}-μ_{Y})^{2}} { \displaystyle \sum_{i=1}^{n_{x}}(X_{i}-μ_{X})^{2}} \leq \displaystyle \frac {σ_{Y}^{2}} {σ_{X}^{2}} \leq F_{α/2;n_{X},n_{Y}} \displaystyle \frac {n_{X}} {n_{Y}} \displaystyle \frac { \displaystyle \sum_{j=1}^{n_{y}}(Y_{j}-μ_{Y})^{2}} { \displaystyle \sum_{i=1}^{n_{x}}(X_{i}-μ_{X})^{2}} \right ]=1-α \)
2) Las medias \( μ_{X} \) y \( μ_{Y} \) desconocidas
Del Capítulo 8 se recordará que las variables aleatorias
\( \left. \begin{array} \\ \displaystyle \frac { (n_{X}-1) S_{X}^{2}}{σ_{X}^{2}} \rightarrow \chi_{n_{X}-1}^{2} \\ \displaystyle \frac { (n_{Y}-1) S_{Y}^{2}}{σ_{Y}^{2}} \rightarrow \chi_{n_{Y}-1}^{2} \\ \end{array} \right \} \Rightarrow \displaystyle \frac { \displaystyle \frac {\displaystyle \frac { (n_{X}-1) S_{X}^{2}}{σ_{X}^{2}}}{n_{X}-1}}{ \displaystyle \frac {\displaystyle \frac { (n_{Y}-1) S_{Y}^{2}}{σ_{Y}^{2}}}{n_{Y}-1}} = \displaystyle \frac {\displaystyle \frac {S_{X}^{2}}{\sigma_{X}^{2}}}{\displaystyle \frac {S_{Y}^{2}}{\sigma_{Y}^{2}}} \rightarrow F_{n_{X}-1,n_{Y}-1} \)
Por tanto
\( P \left [F_{1-α/2;n_{X}-1,n_{Y}-1} \displaystyle \frac {S_{Y}^{2}} {S_{X}^{2}} \leq \displaystyle \frac {σ_{Y}^{2}} {σ_{X}^{2}} \leq F_{α/2;n_{X}-1,n_{Y}-1}\displaystyle \frac {S_{Y}^{2}} {S_{X}^{2}} \right ]=1-α \)
Ejemplo 9.13. De dos poblaciones normales \( X \) e \(Y \) se han extraído muestras de tamaño \( n_{X}=15 \) y \( n_{Y}=10 \) cuyas cuasivarianzas valen \( s_{X}^{2} =69 \) y \( s_{Y}^{2}=44 \). Construir intervalos de estimación para el cociente de las varianzas poblacionales a los niveles de confianza del 90% y 98%.
Respuesta:
a) \(1-α=0.90 \Rightarrow α/2=0.05 \)
\( F_{α/2;n_{X}-1,n_{Y}-1}=F_{0.05;14,9}=3.03 \hspace{1cm} ; \) \( \hspace{1cm} F_{1-α/2;n_{X}-1,n_{Y}-1}=F_{0.95;14,9}= \displaystyle \frac {1} {F_{0.05;9,14}}= \displaystyle \frac{1} {2.65}=0.38 \)\( \begin{array} \\ P \left [F_{1-α/2;n_{X}-1,n_{Y}-1} \displaystyle \frac {S_{Y}^{2}} {S_{X}^{2}} \leq \displaystyle \frac {σ_{Y}^{2}} {σ_{X}^{2}} \leq F_{α/2;n_{X}-1,n_{Y}-1} \displaystyle \frac {S_{Y}^{2} }{S_{X}^{2}} \right] = \\ = P \left [0.38 \times \displaystyle \frac {44} {69} \leq \displaystyle \frac {σ_{Y}^{2}} {σ_{X}^{2}} \leq 3.03 \times \displaystyle \frac {44} {69} \right] = P[0.242 \leq \displaystyle \frac {σ_{Y}^{2}} {σ_{X}^{2}} \leq 1.932]=0.90 \end{array} \)
Por tanto, se tiene el 90% de seguridad de que la relación de \( σ_{Y}^{2} /σ_{X}^{2} \) se encuentra entre 0.242 y 1.932. Como el uno pertenece al intervalo, en realidad no hay razón para sospechar que \( σ_{X}^{2} \) es distinto de \( σ_{Y}^{2} \).
b) \( 1-α=0.98 \Rightarrow α/2=0.01 \)
\( F_{α/2;n_{X}-1,n_{Y}-1}=F_{0.01;14,9}=5.01 \hspace{1cm} ; \hspace{1cm} \) \( F_{1-α/2;n_{X}-1,n_{Y}-1}=F_{0.99;14,9}= \displaystyle \frac {1} {F_{0.01;9,14}}= \displaystyle \frac{1} {4.03}=0.29 \)\( P \left [0.29 \times \displaystyle \frac {44} {69} \leq \displaystyle \frac {σ_{Y}^{2}} {σ_{X}^{2}} \leq 5.01 \times \displaystyle \frac {44} {69} \right ] = P \left [ 0.184 \leq \displaystyle \frac {σ_{Y}^{2}} {σ_{X}^{2}} \leq 3.194 \right ]=0.98 \)
Se llega a la misma conclusión que en apartado anterior pero con una confianza del 98%.
Intervalo de confianza para dos poblaciones normales: Muestras apareadas
En las muestras apareadas, cada observación de una muestra está emparejado con una observación de la otra muestra, por lo tanto consideramos parejas de valores (x,y).
Supongamos que \( X \) e \( Y \) son dos variables aleatorias tales que \( X \rightarrow N(μ_{X}, σ_{X}) \) e \( Y \rightarrow N(μ_{Y}, σ_{Y}) \) y consideremos la diferencia de poblaciones \( D=X-Y \). Entonces, \( D \rightarrow N(μ_{D}, σ_{D}) \)
Se selecciona una muestra aleatoria de diferencias, \( D_{i}=X_{i}-Y_{i} \hspace{.2cm } \); \( \hspace{.2cm } i=1,2, \cdots , n \)
El valor medio de \( D \) es la diferencia de los valores medios de \( X \) e \( Y\) :
\( μ_{D}=E(D)=E(X-Y)=E(X)-E(Y)=μ_{X}-μ_{Y} \)
La varianza de \( D \) es:
\( σ_{D}^{2}=Var(D)=Var(X-Y) \)
Por lo tanto el problema original de realizar una inferencia sobre dos muestras se reduce al problema de realizar la inferencia sobre una muestra que consiste en construir un intervalo de confianza para la media de la población de diferencias. Para la realización de este intervalo de confianza recurrimos a los métodos utilizados en la Sección 9.2.
En particular, construyamos el intervalo de confianza para \( μ_{X}-μ_{Y}=μ_{D} \). Para ello, consideremos la variable aleatoria
\( T= \displaystyle \frac { \overline {D} -μ_{D}} {S_{D}/ \sqrt{n}} \)
que tiene una distribución t-Student con n-1 grados de libertad.
Tenemos que determinar el valor del cuantil \( t_{α/2;n-1} \) tal que
\( \begin{array} \\ P \left [-t_{α/2;n-1} \leq \displaystyle \frac { \overline {D} -μ_{D}} {S_{D}/ \sqrt{n}} \leq t_{α/2;n-1} \right ] = \\ =P \left [ \overline {D} -t_{α/2;n-1} \displaystyle \frac { S_{D}}{ \displaystyle \sqrt {n}} \leq μ_{D} \leq \overline {D} + t_{α/2;n-1} \displaystyle \frac { S_{D}}{ \displaystyle \sqrt {n}} \right]=1-α \\ \end{array} \)
donde \( \overline {D } \) y \( S_{D} \) son la media muestral y la cuasidesviación típica muestral de la muestra de diferencias, respectivamente.
Ejemplo 9.14. Se realiza un estudio, en el que participan 10 individuos, para investigar el efecto del ejercicio físico en el nivel de colesterol en plasma. Antes del ejercicio se tomaron muestras de sangre para determinar el nivel de colesterol de cada individuo. Después, los participantes fueron sometidos a un programa de ejercicios. Al final de los ejercicios se tomaron nuevamente muestras de sangre y se obtuvo una segunda lectura del nivel de colesterol. Los resultados se muestran a continuación:
\( \begin{array} {|l|cccccccccc|} \hline Nivel \hspace{.2cm}previo & 182 & 230 & 160 & 200 & 160 & 240 & 260 & 480 & 263 & 240 \\ \hline Nivel \hspace{.2cm} posterior & 190 & 220 & 166 & 150 & 140 & 220 & 156 & 312 & 240 & 250 \\ \hline \end{array} \)
Construir un intervalo de confianza de \( μ_{D} \) para un nivel de confianza del 90%.
Respuesta:
\( \begin{array} {|l|cccccccccc|} \hline Nivel \hspace{.2cm}previo & 182 & 230 & 160 & 200 & 160 & 240 & 260 & 480 & 263 & 240 \\ \hline Nivel \hspace{.2cm} posterior & 190 & 220 & 166 & 150 & 140 & 220 & 156 & 312 & 240 & 250 \\ \hline d=x-y & -8 & 10 & -6 & 50 & 20 & 20 & 44 & 168 & 20 & -10 \\ \hline \end{array} \)
\( \overline {d} = \displaystyle \frac { 268} {10} =30.8 \hspace{.2cm}; \hspace{.2cm} s_{d}= \displaystyle \frac { \displaystyle \sum_{i=1}^{10} (d_{i}- \overline {d}) } {n-1}=52.36 \)Para \( 1-α=0.90 \Rightarrow α/2=0.05 \hspace{.2cm}; \hspace{.2cm} t_{α/2;n-1}=t_{0.05;9}=1.833 \)
\( \begin{array} \\ P \left [ \overline {D} -t_{α/2;n-1} \displaystyle \frac {S_{D}} { \displaystyle \sqrt {n}} \leq μ_{D} \leq \overline {D} + t_{α/2;n-1} \displaystyle \frac {S_{D}} { \displaystyle \sqrt {n}} \right]= \\ =P \left [ 30.8-1.833 \displaystyle \frac {52.36} { \displaystyle \sqrt {10}} \leq μ \leq 30.8+1.833 \displaystyle \frac {52.36} { \displaystyle \sqrt {10}} \right]=P[0.4497 \leq μ \leq 61.150]=0.90 \\ \end{array} \)
Por lo tanto, podemos tener un 90% de confianza en que la diferencia media de niveles de colesterol en plasma está entre 0.4497 y 61.150. Es decir, podemos tener un 90% de confianza de que el nivel medio de colesterol se reducirá como mínimo en 0.45 unidades.
Ejercicios propuestos: Relación IX
1. En el análisis de un pigmento contenido en una cierta flor de una planta vegetal se obtuvieron los siguientes resultados experimentales, expresados como mg de pigmento por gramo de flor: 2.08; 2.11; 2.39; 2.08; 2.12; 2.23; 2.17 y 2.11.
Considerando normalidad, calcular un intervalo de confianza para el número medio de mg de pigmento por gramo de flor, así como para su varianza a un nivel de confianza del 99%. (Soluciones: (2.0313, 2.2913); (0.003808, 0.0782))
2. Para evaluar la viabilidad de un proyecto de reforestación de una zona sometida a stress turístico, para el que se ha solicitado una subvención pública, se analiza la composición en mg. por cm³ de desechos orgánicos del territorio. Los datos que se obtienen son:
10.87; 9.01; 22.50; 12.35; 17.39; 31.05; 17.19; 16.74; 20.33; 19.32; 23.18; 25.15; 15.49; 20.30; 2.38; 13.55; 9.33; 22.72; 10.96; 25.90; 27.66; 9.74; 18.65; 9.31; 24.60; 17.41; 24.86; 15.34; 23.34; 22.81; 17.86
Considerando normalidad, estimar mediante un intervalo de confianza la dispersión de la distribución de los datos al nivel de confianza del 95%. (Sol: (27.9543, 78.2054).
3. Si la desviación típica de la duración de los tubos de televisión se estima en 100 horas, ¿Qué tamaño de muestra deberá tomarse para que la amplitud del intervalo de confianza de la duración media no exceda de 40 horas a los niveles de confianza del 90, 95 y 99%? (Sol: 68; 97; 167).
4. Para investigar el coeficiente intelectual medio de una cierta población estudiantil, se propuso un test a 400 estudiantes. La media y cuasidesviación típica de ese estudio fueron, respectivamente, 86 y 10.2. A partir de estos datos, determinar intervalos de estimación para el coeficiente de inteligencia medio a los niveles de confianza del 90, 95 y 98%. (Sol: [86±0.83895]; [86±0.9996]; [86±1.3158])
5. La siguiente tabla proporciona datos sobre la precipitación total registrada en 11 estaciones meteorológicas de dos provincias españolas. Suponiendo independencia y normalidad, dar una estimación mediante un intervalo de confianza al nivel de con-fianza de 0.8 para:
a) Cociente de varianzas de la pluviosidad entre las dos provincias
b) Diferencia de las medias de la pluviosidad entre las dos provincias
c) Diferencia de las medias de pluviosidad si se sabe por experiencia previa que la varianza de las precipitaciones en la provincia A es de 475 y en la provincia B de 350.
\( \begin{array} {|l|ccccccccccc|} \hline Prov. \hspace {.1cm} A & 100 & 89 & 84 & 120 & 130 & 105 & 60 & 70 & 90 & 108 & 130 \\ Prov. \hspace {.1cm} B & 120 & 115 & 96 & 115 & 140 & 120 & 75 & 90 & 108 & 130 & 135 \\ \hline \end{array} \)
(Soluciones: a) (0.5808,3.1261); b) (-26.4436, -2.2836); c) (-28.6097. -0.1175))
6. En una muestra aleatoria de 900 personas con pelo oscuro se encontró que 150 de ellas tenían los ojos azules. Construir un intervalo de confianza al 95% para la proporción de individuos que teniendo pelo oscuro en la población poseen ojos azules. ¿Son compatibles estos resultados con la suposición de que dicha proporción vale 1/4? (Sol: [0.1423,0.191]; No es compatible)
7. ¿Entre qué margénes oscilará el cociente de las cuasivarianzas de muestras independientes de tamaño 10 y 20 de una población Normal al nivel de 90% ? y ¿ al 98% ? (Supongamos que las varianzas son iguales). (Sol: [0.34,2.4]; [0.2,3.46]).
8. En una piscifactoría hay una proporción desconocida de peces de una especie A. Para obtener información sobre esa proporción se sacan 145 peces de los cuales 29 son tipo A. Estimar dicha proporción mediante un intervalo de confianza al nivel de confianza 0.95. (Sol: (0.1349, 0.2651))
9. En una experiencia genética se extraen 20 moscas de una caja experimental. Medida la longitud del ala en cada mosca se obtuvieron los siguientes valores: 93; 90; 97; 90; 93; 91; 96; 94; 91; 91; 88; 93; 95; 91; 89; 92; 87; 88; 90; 86.
Suponiendo que la longitud del ala sigue una distribución normal, hallar un intervalo de confianza de nivel 0.9 para los parámetros μ y σ². (Soluciones: (89.8761, 92.6239); (4.9772, 18.3780))
10. Se desea comparar dos métodos rápidos para estimar la concentración de una hormona en una solución. Para ello, se dispone de 10 dosis preparadas en el laboratorio y se mide la concentración de cada una con los dos métodos. Se obtienen los siguientes resultados:
\( \begin{array} {|l|cccccccccc|} \hline Dosis & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline Método \hspace{.1cm} A & 10.7 & 11.2 & 15.3 & 14.9 & 13.9 & 15 & 15.6 & 15.7 & 14.3 & 10.8 \\ \hline Método \hspace{.1cm} B & 11.1 & 11.4 & 15 & 15.1 & 14.3 & 15.4 & 15.4 & 16 & 14.3 & 11.2 \\ \hline \end{array} \)
.Calcular un intervalo de confianza al nivel 0.9 para el cociente de varianzas y la diferencia de concentraciones medias (considerar normalidad e independencia). (Soluciones: (0.3531, 3.5709); (-1.7158, 1.3558))
11. Se estudian dos tipos de neumáticos con los resultados siguientes:
A: \( n_1=121 \hspace{.3cm} ; \hspace{.3cm} \overline {x}_1=27465 Km \hspace{.3cm} : \hspace{.3cm} s_1=2.500 \)
B: \( n_2=121 \hspace{.3cm} ; \hspace{.3cm} \overline {x}_2=27572 Km \hspace{.3cm} ; \hspace{.3cm} s_2=3.000 \)
Calcular, para α=0.01, los intervalos de confianza para
a) \( σ_{1}^{2}/σ_{2}^{2} \)
b) \( μ_1-μ_2 \)
(Soluciones: a) [0.4325, 1.1149]);b) [107±916])
12. En una piscifactoría se desea comparar el porcentaje de peces adultos que miden menos de 20 cm con los que miden más de 40 cm. Para ello, se toma una muestra de 200 peces observando que 40 de ellos miden menos de 20 cm y una muestra de 200 peces de los que 57 miden más de 40 cm. Hallar un intervalo de confianza para la diferencia de proporciones al nivel de confianza del 0.95.(Sol: (-0.1686, 0.001409))
13. Una compañía contrata 10 tubos con filamentos de tipo A y 10 con filamentos de tipo B. Las duraciones de vida observadas, han sido:
A: 1614; 1094; 1293; 1643; 1466; 1270; 1340; 1380; 1028; 1497
B: 1383; 1138; 1092; 1143; 1017; 1061; 1627; 1021; 1711; 1065
Encontrar un intervalo de confianza para la diferencia de medias. Con α=0,05. (Sol: [-80.33,353.73]).
14. Se desea comprobar el efecto de 2 fertilizantes (A y B) sobre la producción de árboles frutales, para ello se toman dos grupos de 8 y 10 árboles seleccionados aleatoriamente y se le añade al agua de riego de cada uno de los grupos de árboles el fertilizante A y B, respectivamente. La producción en ese año fue la siguiente (en Kg):
Fertilizante A: 30 25 28 29 30 31 24 22 25 27
Fertilizante B: 28 27 28 28 26 27 26 29
Se pide:
a) Obtener un intervalo de confianza al 99% para la producción media de los árboles tratados con el Fertilizante A y para la producción media de los árboles tratados con el Fertilizante B;
b) Obtener un intervalo de confianza al 98% para la diferencia entre la producción media de los árboles tratados con el Fertilizante A y con el Fertilizante B;
c) La producción de los árboles tratados con el Fertilizante A en el año anterior viene reflejada en la siguiente tabla.
\( \begin{array} {|l|cccccccccc|} \hline Antes & 25 & 20 & 25 & 28 & 30 & 30 & 26 & 15 & 18 & 22 \\ \hline Después & 30 & 25 & 28 & 29 & 30 & 31 & 24 & 22 & 25 & 27 \\ \hline \end{array} \)
Obtener un intervalo de confianza al 99% para la diferencia de medias, en la producción antes y después de tratar los árboles con dicho fertilizante. (Soluciones: a) (24.02, 30.18) y (26.06, 28.69) ; b) (–3.020, 2.470); c) (-6.369, -0.031) )
Autora: Ana María Lara Porras. Universidad de Granada
Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.