EJERCICIOS RESUELTOS: ESTADÍSTICA DESCRIPTIVA UNIDIMENSIONAL
1. Se inició una investigación para averiguar el número de bacterias que aparecen en determinados cultivos. Para ello, se tomaron 40 de estos cultivos y se contó el número de bacterias, \( x_{i} \) , que aparecieron en cada uno de ellos.
\( \begin{matrix} \hline x_{i} & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline n_{i} & 1 & 12 & 22 & 34 & 26 & 14 & 0 \\ \hline \end{matrix} \)
a) Obtener las frecuencias relativas, relativas acumuladas y absolutas acumuladas
b) Representar la distribución de frecuencias absolutas
c) Porcentaje de valores menores o iguales a 3. (Sol. 62.38%)
d) Porcentaje de valores mayores que 5. (Sol. 0%).
2. Se ha desarrollado una nueva vacuna contra la difteria para aplicarla a niños. El nivel de protección estándar obtenidos por la antiguas vacuna era de 1 μg/mL, un mes después de la inmunización. Transcurrido un mes, se han obtenido estos datos del nivel de protección de la nueva vacuna:
\( \begin{matrix} \hline 12.5 & 13.8 & 13.0 & 13.5 & 13.2 \\ \hline
11.2 & 13.1 & 14.0 & 13.3 & 13.6 \\ \hline
12.6 & 14.1 & 14.6 & 13.2 & 13.1 \\ \hline
13.3 & 12.5 & 12.0 & 11.5 & 13.2 \\ \hline
13.7 & 12.0 & 12.8 & 13.2 & 12.7 \\ \hline \end{matrix} \)
Se pide:
a) Elaborar la muestra presentándola en forma de tabla de distribución de frecuencias
b) Dibujar el diagrama de barras de las frecuencias no acumuladas y acumuladas y los polígonos de frecuencias.
3. Completa los datos que aparecen en la siguiente distribución
\( \begin{array} {|l||c|c|c|c|c|c|c|} \hline x_{i} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline
n_{i} & 4 & 4 & & 7 & 5 & & 7 & \\ \hline
N_{i} & & & 16 & & 28 & 38 & 45 & \\ \hline
f_{i} & 0.08 & & 0.16 & 0.14 & & & 0.14 & \\ \hline \end{array} \)
4. Para obtener información acerca del porcentaje de albúmina en el suero proteico de personas normales se analizaron muestras de 40 personas, entre 2 y 40 años de edad, con los siguientes resultados:
\( \begin{matrix} \hline 70.2 & 62.4 & 72.3 & 63.3 & 62.8 & 60.4 \\ \hline
73.4 & 72.4 & 68.4 & 67.0 & 70.1 & 69.4 \\ \hline
65.2 & 62.9 & 70.0 & 71.3 & 66.3 & 65.9 \\ \hline
68.3 & 70.2 & 70.7 & 67.5 & 65.0 & 70.4 \\ \hline
72.8 & 66.6 & 72.1 & 64.1 & 68.7 & 67.8 \\ \hline
66.1 & 69.1 & 71.9 & 73.5 & 65.5 & 66.4 \\ \hline
64.4 & 63.1 & 62.0 & 65.2 & & \\ \hline \end{matrix} \)
Se pide:
a) Suponiendo que un error del 0.5 % en el porcentaje de albúmina no es importante, agrupar las medidas de la muestra en intervalos de clase de amplitud igual a la unidad y organizar los datos de la muestra en una tabla completa de distribución de frecuencias: Extremos de los intervalos de clase, marcas de clase, frecuencias acumuladas, frecuencias relativas, frecuencias absolutas acumuladas y frecuencias relativas acumuladas
b) Hallar el tanto por ciento de personas cuyo porcentaje de albúmina en el suero proteico está comprendido entre el 62% y 72%. En este caso, como la variable es continua y está agrupada en intervalos de clase, es indiferente incluir o no estos valores. (Sol. 82.5%)
c) Hallar el % de personas de la muestra cuyo porcentaje de albúmina es superior al 72%. (Sol. 1.5 %)
d) Calcular la media, mediana, desviación absoluta media respecto de la media, varianza, desviación típica y el coeficiente de variación de Pearson.
(Sol.: \( \bar{x} =67.7; Me=67.62; D_{\bar{x}}=3.0125; σ^2=12.24; σ=3.49; CV=0.051 \)).
5. Se realiza un estudio con objeto de detectar las variables que constituyen el estrés en pacientes clínicos cardíacos. El estrés se midió mediante la puntuación de ansiedad de Hamilton. Estas marcas se encuentran en una escala de 1 a 25, donde el número 18 denota un estrés moderado y el 25, un estrés grave. Se trataba de comparar los dos grupos de pacientes. Se obtuvieron los siguientes datos.
Viven solos
\( \begin{matrix} \hline 8.6 & 9.1 & 9.3 & 9.6 \\ \hline
8.3 & 13.5 & 9.5 & 8.3 \\ \hline
10.2 & 11.0 & 10.3 & 9.4 \\ \hline
8.9 & 10.5 & 10.7 & 9.5 \\ \hline
14.3 & 11.7 & 12.3 & 8.5 \\ \hline \end{matrix} \)
Viven con otras personas
\( \begin{matrix} \hline 7.6 & 18.1 & 19.3 & 13.6 \\ \hline
14.3 & 16.5 & 19.5 & 15.3 \\ \hline
13.2 & 15.0 & 17.3 & 19.4 \\ \hline
18.9 & 13.5 & 14.7 & 19.5 \\ \hline
14.3 & 16.7 & 15.3 & 18.5 \\ \hline \end{matrix} \)
Se pide:
a) La media, mediana, moda, cuasivarianza y cuasidesviación típica de cada grupo
b) Coeficientes de variación de Pearson, asimetría de Fisher y apuntamiento de Fisher de cada grupo
c) La distribución de los datos en cada grupo ¿sugiere forma de campana?
d) ¿Alguna de estas distribuciones es sesgada? Si es así, ¿en qué dirección?
e) ¿Qué grupo tiende a tener una menor puntuación media de estrés?
6. En un parque natural se está realizando un estudio sobre el recorrido que realizan los pájaros. Para ello se estudió la distancia de vuelo desde el punto en que se soltó un pájaro recién anillado hasta su primera posada. Los siguientes datos corresponden a dos tipos de pájaros
Estorninos
\( \begin{matrix} \hline 108.6 & 119.1 & 99.3 & 109.6 \\ \hline
98.3 & 103.5 & 119.5 & 148.3 \\ \hline
120.2 & 131.0 & 140.3 & 89.4 \\ \hline
82.9 & 180.5 & 210.7 & 119.5 \\ \hline
134.3 & 101.7 & 132.3 & 208.5 \\ \hline \end{matrix} \)
Vencejos
\( \begin{matrix} \hline 107.6 & 108.1 & 119.3 & 153.6 \\ \hline
134.3 & 106.5 & 109.5 & 95.3 \\ \hline
133.2 & 145.0 & 127.3 & 109.4 \\ \hline
188.9 & 213.5 & 134.7 & 199.5 \\ \hline
214.3 & 106.7 & 205.3 & 321.8 \\ \hline \end{matrix} \)
Se pide:
a) La media, mediana de cada grupo ¿Son semejantes los conjuntos con respecto a alguna de las medidas?
b) Obsérvese que el último dato del segundo grupo es muy diferente al resto; este dato recibe el nombre de outlier o dato atípico. Para comprobar su efecto: eliminar el dato y calcular la media y mediana para los restantes. ¿Qué medida está menos afectada por la presencia del dato atípico?
c) La cuasivarianza y cuasidesviación típica de cada grupo. ¿Son estas medidas de variabi-lidad resistentes al dato atípico?
d) ¿Alguna de estas distribuciones es sesgada? Si es así, ¿en qué dirección?
e) ¿Qué grupo tiene el rango intercuartílico más grande?
f) ¿Qué grupo posee variabilidad más grande?
g) ¿Qué grupo es más simétrico?
7. En un laboratorio farmacéutico se acaba de instalar una nueva máquina automática, “de gran precisión”, para dosificar y tabletear ciertos productos. Si el director del laboratorio quiere investigar la exactitud de la máquina no le queda otro camino que probarla. Supongamos que la máquina se utiliza para fabricar tabletas de 200 mg del producto y se extraen dos muestras:
La primera muestra dio los resultados: 300,100, 250 y 150 mg.
La segunda muestra dio los resultados: 202,198, 201 y 199 mg.
Se pide:
a) Calcular la media en ambos casos. (Sol. \( \bar{x}_{A}=200= \bar{ x}_{B} \))
b) Desviaciones absolutas medias (Sol. \( D_{\bar{x}_{A}}=75; D_{\bar{x}_{B}}=1.5 \))
c) ¿En qué caso se considerará la máquina aceptable? (Sol. b)
8. Se aplicó un test de inteligencia a 456 estudiantes del primer curso de Biológicas. Las puntuaciones obtenidas, agrupadas en intervalos de clase de 4 unidades de amplitud, figuran en la siguiente tabla de distribución de frecuencias:
\( \begin{array}{|l||c|c|c|c|c|c|c|} \hline e_{i-1}-e_{i} & 78-82 & 82-86 & 86-90 & 90-94 & 94-98 & 98-102 & 102-106 \\ \hline
n_{i} & 1 & 2 & 6 & 42 & 54 & 75 & 92 \\ \hline
e_{i-1}-e_{i} & 106-110 & 110-114 & 114-118 & 118-122 & 122-126 & 126-130 & 130-134 \\ \hline
n_{i} & 96 & 38 & 27 & 12 & 8 & 2 & 1 \\ \hline \end{array} \)
Calcular: \( P_{25}; P_{75}; P_{90} \) . (Sol. \( P_{25}=98.48; P_{75} =108.92; P_{90} =114.65 \) ).
9. En una clínica infantil se han ido anotando, durante un mes, el número de metros que el niño anda seguido y sin caerse el primer día que comienza a caminar. Obteniéndose así la tabla de información adjunta:
\( \begin{matrix} \hline N^{o} \hspace{1mm} de \hspace{1mm} niños & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline
N^{o} \hspace{1mm} de \hspace{1mm} metros & 2 & 6 & 10 & 5 & 10 & 3 & 2 & 2 \\ \hline \end{matrix} \)
Se pide:
a) Tabla de frecuencias. Diagrama de barras para frecuencias absolutas y para las frecuencias absolutas acumuladas
b) Mediana, moda y cuartiles (Sol: \( Me=4; M₀= 3; M₀^´ = 5; Q_1=3; Q_2=4; Q_3=5 \) )
c) Recorrido Intercuartílico (Sol: \( R_{I}=2 \) )
d) Momentos respecto al origen de primer, segundo y tercer orden. (Sol: \( m_1=4.05; m_2=19.5; m_3=106.2 \) )
e) Momentos centrales de primer y tercer orden (Sol:\( μ_1=0; μ_3=2.135 \) )
10. La siguiente tabla muestra la distribución del coeficiente intelectual de 120 alumnos.
\( \begin{array}{|l||c|c|c|c|} \hline C.I. & 60-70 & 70-80 & 80-90 & 90-100 \\ \hline
n_{i} & 2 & 3 & 25 & 46 \\ \hline
C.I. & 100-110 & 110-120 & 120-130 & 130-140 \\ \hline
n_{i} & 35 & 5 & 3 & 1 \\ \hline \end{array} \)
a) Si se consideran bien dotados a los alumnos cuya puntuación está por encima del percentil 95 ¿A partir de que coeficiente intelectual mínimo los consideramos bien dotados? (Sol: \( P_{95} \)).
b) Si se consideran atrasados los alumnos cuya puntuación sea inferior al percentil 5 ¿Qué puntuación máxima pueden tener los atrasados? (Sol: 80.4)
c) Si el coeficiente intelectual es 109. Determinar el percentil correspondiente. (Sol: \( P_{90} \)).
11. Un profesor califica a sus alumnos siguiendo el siguiente criterio: suspensos 40%, aprobados 30%, notables 15%, sobresalientes 10%, matrículas 5%. Si las notas vienen dadas por la siguiente tabla:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|} \hline Notas & 0-1 & 1-2 & 2-3 & 3-4 & 4-5 & 5-6 & 6-7 & 7-8 & 8-9 & 9-10 \\ \hline n_{i} & 34 & 74 & 56 & 81 & 94 & 70 & 41 & 28 & 16 & 4 \\ \hline\end{array} \)
Calcula la nota máxima para conseguir suspenso, aprobado, notable, sobresaliente y matrícula. (Sol: Suspenso ≤3.43; 3.43< Aprobado ≤ 5.13; 5.13< Notable ≤ 6.34; 6.34< Sobresaliente ≤ 7.57; Matrícula >7.57).
12. Una especie de mamíferos tiene en cada cría un número variable de hijos. Se observa durante un año la cría de 35 familias, anotándose el número de hijos obtenidos por las familias en dicha cría.
\( \begin{matrix} \hline N^{o} \hspace{1mm} hijos & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline N^{o} \hspace{1mm} familias & 2 & 3 & 10 & 10 & 5 & 0 & 5 & 0 \\ \hline \end{matrix} \)
a) Hallar los cuartiles de primer y tercer orden. (Sol: \( Q_1=2; Q_3= 4 \))
b) Hallar la moda. (Sol: \( M₀=2; M₀^′= 3 \))
c) Coeficiente se asimetría de Fisher
d) Recorrido intercuartílico
13. Un curso está dividido en 4 grupos de los cuales tenemos los datos:
\( \begin{matrix} \hline Grupo & N^{o} \hspace{1mm} alumnos & Nota \hspace{1mm} media & Varianza \\ \hline A & 30 & 6 & 1 \\ \hline
B & 40 & 6.5 & 1.69 \\ \hline
C & 50 & 5 & 0.81 \\ \hline
D & 60 & 4 & 0.64 \\ \hline \end{matrix} \)
a) Calcular los coeficientes de variación de cada grupo. (Sol: \( CV_{A}= 0.17; CV_{B}=0.2; CV_{C}=0.18; CV_{D}= 0.2 \))
b) ¿Qué grupo resulta más homogéneo? (Sol: A)
c) Calcular la varianza de todas las notas del curso. (Sol: 1.7983).
14. Se han medido mediante pruebas adecuadas los coeficientes intelectuales de un grupo de 20 alumnos, presentando los resultados agrupados en 6 intervalos de amplitud variable. Estas amplitudes son: \( a_1=12, a_2=12, a_3=4, a_4=4, a_5=12, a_6=20 \). Si las frecuencias relativas acumuladas correspondientes a cada uno de los intervalos son: \( F_1=0.15, F_2=0.15, F_3=0.55, F_4=0.8, F_5=0.95, F_6=1.00 \).
Se pide:
a) Formar la tabla de distribución de frecuencias, sabiendo que el extremo inferior del primer intervalo es 70
b) Dibujar el histograma y polígono de frecuencias absolutas. Calcular la moda
c) ¿Entre qué dos percentiles está comprendido un coeficiente intelectual de 98.4? Encontrar el valor ambos percentiles.
Al mismo grupo de alumnos se les hace una prueba de rendimiento y los resultados vienen dados en la Figura 1
d) Formar la tabla de distribución de frecuencias y calcular la mediana
e) ¿Qué medidas están más dispersas, los coeficientes intelectuales o las puntuaciones del rendimiento?
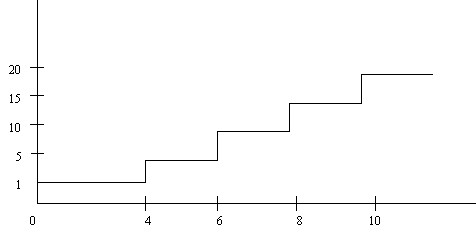Figura 1
Soluciones: \( b) Mo=96.9; \hspace{1mm} c) P_{57}=98.32 \hspace{1mm} y \hspace{1mm} P_{58} =98.48; \hspace{1mm} d) Me=7 \); \hspace{1mm} e) Las puntuaciones del rendimiento. \( (CV_{I}=0.11;\hspace{1mm} CV_{R}=0.38) \).
15. En una empresa el 20% es personal “no cualificado”, el 50% es personal “cualificado” y el resto es personal “técnico”. La plantilla consta de 1000 empleados. Se ha estimado la productividad para cada uno de estos grupos en unos coeficientes que van de 1 a 5. Los resultados se muestran en la tabla adjunta.
\( \begin{matrix} Coeficiente & Personal \hspace{1mm} no & Personal & Personal & \% \hspace{1mm} total \\ \hline
productividad & cualificado & cualificado & técnico & de \\ \hline
x_{i} & en \hspace{1mm} \% & en \hspace{1mm} \% & en \hspace{1mm} \% & trabajadores \\ \hline
1 & 10 & 5 & 0 & 4.5 \\ \hline
2 & 20 & 20 & 10 & 17 \\ \hline
3 & 30 & 20 & 40 & 28 \\ \hline
4 & 30 & 40 & 30 & 35 \\ \hline
5 & 10 & 15 & 20 & 15.5 \\ \hline \end{matrix} \)
a) Hállese la productividad media de los 1000 empleados. (Sol: \( \bar{x}=3.4 \))
b) ¿Qué nivel de productividad es el más corriente en esta empresa? (Sol \( Mo=4 \))
c) ¿Bajo qué coeficiente están el 50% de los trabajadores menos productivos? (Sol: \( Me=4 \)).
d) Comparando las productividades medias del personal no cualificado y del personal cualificado, ¿Cuál de ellas corresponde a una distribución de frecuencias más homogénea? (Sol: Personal cualificado (\( CV_{N}=0.37; CV_{C}=0.339 \)).
16. En un cierto barrio se ha constatado que las familias residentes se han distribuido, según su tamaño, de la siguiente forma:
\( \begin{matrix} \hline Tamaño \hspace{1mm} familias & 0-2 & 2-4 & 4-6 & 6-8 & 8-10 \\ \hline N^{o}\hspace{1mm} familias & 110 & 200 & 90 & 75 & 25 \\ \hline \end{matrix} \)
Se pide:
a) ¿Cuál es el número medio de personas por familia? (Sol: \( \bar{x} =3.82 \))
b) ¿Cuál es el tipo de familia más frecuente? (Sol: \( Mo= 2.9 \))
c) Si sólo hubiera plaza de aparcamiento para el 50% de las familias y éstas se atendieran por familias de mayor a menor tamaño, ¿Qué componentes tendría que tener una familia para entrar en el cupo? Se supone que cada familia sólo tiene un vehículo. (Sol: \( Me=3.4 \))
d) Si el coeficiente de variación de Pearson de otro barrio es 1.8, ¿Cuál de los dos barrios puede ajustar mejor sus previsiones en base al diferente tamaño de las familias que lo habitan. (Sol: \( CV_1=0.59; CV_2=1.8. \) El primer barrio).
e) ¿Se pueden hacer previsiones en base al número medio de componentes por familia?
17. Una variable X puede someterse a una transformación denominada Tipificación que consiste en restarle la media \( \bar{x} \) y dividir por la desviación típica σ. Una variable tipificada así obtenida, \( Z, Z= \displaystyle \frac{X-\bar{x}{σ}\), tiene dos propiedades fundamentales: Su media es cero y su desviación típica es uno. Aplicar este concepto a la distribución.
\( \begin{matrix} \hline x_{i} & 4 & 6 & 9 & 10 & 12 \\ \hline \end{matrix} \)
(Solución: \( \bar{x} =8 ; σ_{x}=21.83; z=0; σ_{z}=1 \) )
Soluciones
1. Se inició una investigación para averiguar el número de bacterias que aparecen en determinados cultivos. Para ello, se tomaron 40 de estos cultivos y se contó el número de bacterias, \( x_{i} \) , que aparecieron en cada uno de ellos.
\( \begin{matrix} \hline x_{i} & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline n_{i} & 1 & 12 & 22 & 34 & 26 & 14 & 0 \\ \hline \end{matrix} \)
a) Obtener las frecuencias relativas, relativas acumuladas y absolutas acumuladas
b) Representar la distribución de frecuencias absolutas
c) Porcentaje de valores menores o iguales a 3. (Sol. 62.38%)
d) Porcentaje de valores mayores que 5. (Sol. 0%).
Solución
a) Obtener las frecuencias relativas, relativas acumuladas y absolutas acumuladas
\(
\begin{array} {||c|c|c|c|c|c||} \hline
{\bf x_i } & {\bf n_i } & {\bf N_i } & {\bf f_i } & {\bf f_i } ascendente & {\bf f_i } descendente \\ \hline 0 & 1 & 1& 0.0092 & 0.0092 & 0.9999 \\ 1 & 12 & 13 & 0.1101 & 0.1193 & 0.9907 \\
2 & 22 & 35 & 0.2018 & 0.3211 & 0.8806 \\ 3 & 34 & 69 & 0.3119 & 0.6238 & 0.6788 \\ 4 & 26 & 95 & 0.2385 & 0.8716 & 0.3669 \\ 5 & 14 & 109 & 0.1284 & 1.0000 & 0.1284 \\ 6 & 0 & 109 & 0.0000 & 1.0000 & 0.0000 \\ \hline \end{array} \)
b) Representar la distribución de frecuencias absolutas
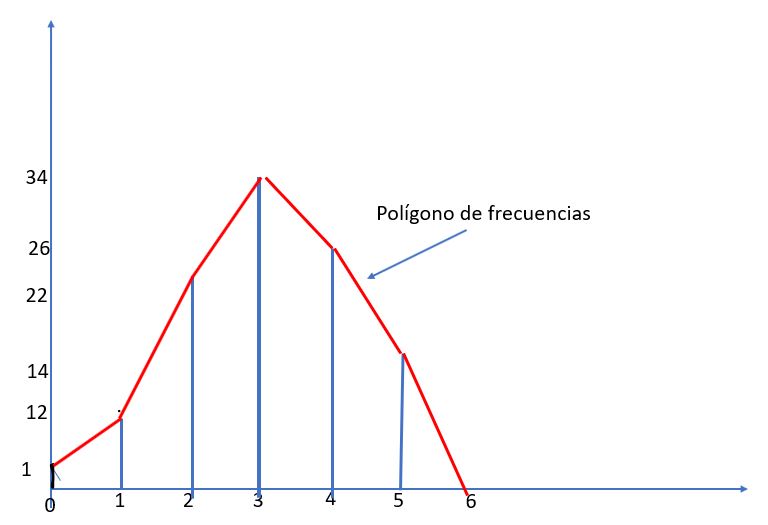
c) Porcentaje de valores menores o iguales a 3
Las \( F_i \) ascendentes indican la proporción de individuos de la población que presentan un valor de x menor o igual que. En la columna de las \( F_i \) el valor correspondiente a 3 es 0.6238. Por lo tanto, el 62.38% de nacimientos de ratas blancas machos en camadas de 6 crias es \( \leq 3 \) .
d) Porcentaje de valores mayores que 5
Las \( F_i \) descendentes indican la proporción de individuos de la población que presentan un valor de x mayor o igual que. En la columna de las \( F_i \) el valor correspondiente a 5 es 0.1284. Pero nos piden el porcentaje que sea mayor que 5.
Por lo tanto nos están pidiendo \( (-1 \leq 5) = (1- 1.0000) = 0.000 = 0.00 \% \)
2. Se ha desarrollado una nueva vacuna contra la difteria para aplicarla a niños. El nivel de protección estándar obtenidos por la antiguas vacuna era de 1 μg/mL, un mes después de la inmunización. Transcurrido un mes, se han obtenido estos datos del nivel de protección de la nueva vacuna:
\( \begin{matrix} \hline 12.5 & 13.8 & 13.0 & 13.5 & 13.2 \\ \hline
11.2 & 13.1 & 14.0 & 13.3 & 13.6 \\ \hline
12.6 & 14.1 & 14.6 & 13.2 & 13.1 \\ \hline
13.3 & 12.5 & 12.0 & 11.5 & 13.2 \\ \hline
13.7 & 12.0 & 12.8 & 13.2 & 12.7 \\ \hline \end{matrix} \)
Se pide:
a) Elaborar la muestra presentándola en forma de tabla de distribución de frecuencias
b) Dibujar el diagrama de barras de las frecuencias no acumuladas y acumuladas y los polígonos de frecuencias.
3. Completa los datos que aparecen en la siguiente distribución
\( \begin{array} {|l||c|c|c|c|c|c|c|} \hline x_{i} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline
n_{i} & 4 & 4 & & 7 & 5 & & 7 & \\ \hline
N_{i} & & & 16 & & 28 & 38 & 45 & \\ \hline
f_{i} & 0.08 & & 0.16 & 0.14 & & & 0.14 & \\ \hline \end{array} \)
Solución
\( \begin{array} {|l||c|c|c|c|c|c|c|} \hline x_{i} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline
n_{i} & 4 & 4 & 8 & 7 & 5 & 10 & 7 & 5 \\ \hline
N_{i} & 4 & 8 & 16 & 23 & 28 & 38 & 45 & 50 \\ \hline
f_{i} & 0.08 & 0.08 & 0.16 & 0.14 & 0.1 & 0.2 & 0.14 & 0.1 \\ \hline \end{array} \)
4. Para obtener información acerca del porcentaje de albúmina en el suero proteico de personas normales se analizaron muestras de 40 personas, entre 2 y 40 años de edad, con los siguientes resultados:
\( \begin{matrix} \hline 70.2 & 62.4 & 72.3 & 63.3 & 62.8 & 60.4 \\ \hline
73.4 & 72.4 & 68.4 & 67.0 & 70.1 & 69.4 \\ \hline
65.2 & 62.9 & 70.0 & 71.3 & 66.3 & 65.9 \\ \hline
68.3 & 70.2 & 70.7 & 67.5 & 65.0 & 70.4 \\ \hline
72.8 & 66.6 & 72.1 & 64.1 & 68.7 & 67.8 \\ \hline
66.1 & 69.1 & 71.9 & 73.5 & 65.5 & 66.4 \\ \hline
64.4 & 63.1 & 62.0 & 65.2 & & \\ \hline \end{matrix} \)
Se pide:
a) Suponiendo que un error del 0.5 % en el porcentaje de albúmina no es importante, agrupar las medidas de la muestra en intervalos de clase de amplitud igual a la unidad y organizar los datos de la muestra en una tabla completa de distribución de frecuencias: Extremos de los intervalos de clase, marcas de clase, frecuencias acumuladas, frecuencias relativas, frecuencias absolutas acumuladas y frecuencias relativas acumuladas
b) Hallar el tanto por ciento de personas cuyo porcentaje de albúmina en el suero proteico está comprendido entre el 62% y 72%. En este caso, como la variable es continua y está agrupada en intervalos de clase, es indiferente incluir o no estos valores. (Sol. 82.5%)
c) Hallar el % de personas de la muestra cuyo porcentaje de albúmina es superior al 72%. (Sol. 1.5 %)
d) Calcular la media, mediana, desviación absoluta media respecto de la media, varianza, desviación típica y el coeficiente de variación de Pearson.
(Sol.: \( \bar{x} =67.7; Me=67.62; D_{\bar{x}}=3.0125; σ^2=12.24; σ=3.49; CV=0.051 \)).
Solución
a) Construir la tabla completa de distribución de frecuencias
\( \begin{array} {|c|c|c|c|c|c|} \hline e_{i-1}- e{i} & x_{i} & n_i & f_i & N_i & F_{ia} \\ \hline 59.95-60.95 & 60.45 & 1 & 0.025 & 1 & 0.025 \\ \hline 60.95-61.95 & 61.45 & 0 & 0.0000 & 1 & 0.025 \\ \hline 61.95-62.95 & 62.45 & 4 & 0.1 & 5 & 0.125 \\ \hline 62.95-63.95 & 63.45 & 2 & 0.05 & 7 & 0.175 \\ \hline 63.95-64.95 & 64.45 & 2 & 0.05 & 9 & 0.225 \\ \hline 64.95-65.95 & 65.45 & 5 & 0.125 & 14 & 0.350 \\ \hline 65.95-66.95 & 66.45 & 4 & 0.10 & 18 & 0.450 \\ \hline 66.95-67.95 & 67.45 & 3 & 0.075 & 21 & 0.525 \\ \hline 67.95-68.95 & 68.45 & 3 & 0.075 & 24 & 0.600 \\ \hline 68.95-69.95 & 69.45 & 2 & 0.05 & 26 & 0.650 \\ \hline 69.95-70.95 & 70.45 & 6 & 0.150 & 32 & 0.800 \\ \hline 70.95-71.95 & 71.45 & 2 & 0.05 & 34 & 0.850 \\ \hline 71.95-72.95 & 72.45 & 4 & 0.1 & 38 & 0.950 \\ \hline 72.95-73.95 & 73.45 & 2 & 0.05 & 40 & 1.000 \\ \hline
\end{array} \)
b) Hallar el tanto por ciento de personas cuyo porcentaje de albúmina en el suero proteico está comprendido entre el 62% y 72%. En este caso, como la variable es continua y está agrupada en intervalos de clase, es indiferente incluir o no estos valores.
\( \begin{array} {ccc} 72.95-71.95 & \longrightarrow & 0.950-0.850 \\ 72-71.95 & \longrightarrow & x – 0.850 \\ \end{array} \)
\( x = 0.850 + \displaystyle \frac {0.05×0.1}{1}= 0.855 \)
Por lo tanto, el % de personas con el 72% o menos de albúmina es: 85.5%
\( \begin{array} {ccc} 62.95-61.95 & \longrightarrow & 0.125-0.025 \\ 62-61.95 & \longrightarrow & x – 0.025 \\ \end{array} \)
\( x = 0.025 + \displaystyle \frac {0.1×0.05}{1}= 0.03 \)
Por lo tanto, el % de personas con el 62% o más de albúmina es: 3%
El % pedido es 85% – 3% = 82.5%
c) Hallar el % de personas de la muestra cuyo porcentaje de albúmina es superior al 72%. (Sol. 1.5 %)
\( \% > 72 \% = (1- \leq 72) = (1-0.85) = 0.15 \)
d) Calcular la media, mediana, desviación absoluta media respecto de la media, varianza, desviación típica y el coeficiente de variación de Pearson.
\( \begin{array} {|c|c|c|c|c|c|} \hline x_{i} & \sum n_i & \sum x_i n_i & N_i & |x_i – \bar{x}| & \sum n_i |x_i – \bar{x}| & \sum (x_i – \bar{x})^{2} \times n_{i} \\ \hline 60.45 & 1 & 60.45 & 1 & 7.25 & 7.25 & 52.5625 \\ \hline 61.45 & 0 & 0 & 1 & 6.25 & 0 & 0 \\ \hline 62.45 & 4 & 249.8 & 5 & 5.25 & 21 & 110.25 \\ \hline 63.45 & 2 & 126.9 & 7 & 4.25 & 8.5 & 36.125 \\ \hline 64.45 & 2 & 128.9 & 9 & 3.25 & 6.5 6 & 21.125 \\ \hline 65.45 & 5 & 327.25 & 14 & 2.25 & 11.25 & 25.3125 \\ \hline 66.45 & 4 & 265.8 & 18 & 1.25 & 5 & 6.25 \\ \hline 67.45 & 3 & 202.35 & 21 & 0.25 & 0.75 & 3.0625 \\ \hline 68.45 & 3 & 205.35 & 24 & 0.75 & 2.25 & 1.6875 \\ \hline 69.45 & 2 & 138.9 & 26 & 1.75 & 3.5 & 6.125 \\ \hline 70.45 & 6 & 422.7 & 32 & 2.75 & 16.5 & 3.84 \\ \hline 71.45 & 2 & 142.9 & 34 & 3.75 & 7.5 & 28.125 \\ \hline 72.45 & 4 & 289.8 & 38 & 4.75 & 19 & 90.25 \\ \hline 73.45 & 2 & 146.9 & 40 & 5.75 & 11.5 & 66.125 \\ \hline & 40 & 2708 & & & 120.5 & 489.6 \\ \hline
\end{array} \)
\( \bar{x} = \displaystyle \frac{n_i x_i}{n} = \displaystyle \frac{2708}{40} = 67.6 \)
La variable variable en estudio es de tipo continuo, por lo tanto la mediana la obtenemos interpolando
\( n/2 = 40/ 2 = 20 \Rightarrow 18 < 20 < 21 \Rightarrow M_e \in (66.95-67.95) \)
\( \begin{array} {ccc} 67.95-66.95 & \longrightarrow & 21-18 \\ M_e – 66.95 & \longrightarrow & 20-18 \\ \end{array} \)
\( M_e = 66.95 + \displaystyle \frac {2×1}{3}= 67.62 \)
\( D_{ \bar{x}} = \displaystyle \frac{\sum |x_i – \bar{x}|}{n} = \displaystyle \frac{120.5}{40} = 3.0125 \)
\( \sigma^{2} = \displaystyle \frac{\sum (x_i – \bar{x})^{2} \times n_{i}}{n} = \displaystyle \frac{489.6}{40} = 12.24 \)
\( \sigma = + \sqrt 112.24 = 3.49 \)
\( CV = \displaystyle \frac {\sigma}{\bar{x}} = \displaystyle \frac {3.49}{67.6}= 0.051 \)
5. Se realiza un estudio con objeto de detectar las variables que constituyen el estrés en pacientes clínicos cardíacos. El estrés se midió mediante la puntuación de ansiedad de Hamilton. Estas marcas se encuentran en una escala de 1 a 25, donde el número 18 denota un estrés moderado y el 25, un estrés grave. Se trataba de comparar los dos grupos de pacientes. Se obtuvieron los siguientes datos.
Viven solos
\( \begin{matrix} \hline 8.6 & 9.1 & 9.3 & 9.6 \\ \hline
8.3 & 13.5 & 9.5 & 8.3 \\ \hline
10.2 & 11.0 & 10.3 & 9.4 \\ \hline
8.9 & 10.5 & 10.7 & 9.5 \\ \hline
14.3 & 11.7 & 12.3 & 8.5 \\ \hline \end{matrix} \)
Viven con otras personas
\( \begin{matrix} \hline 7.6 & 18.1 & 19.3 & 13.6 \\ \hline
14.3 & 16.5 & 19.5 & 15.3 \\ \hline
13.2 & 15.0 & 17.3 & 19.4 \\ \hline
18.9 & 13.5 & 14.7 & 19.5 \\ \hline
14.3 & 16.7 & 15.3 & 18.5 \\ \hline \end{matrix} \)
Se pide:
a) La media, mediana, moda, cuasivarianza y cuasidesviación típica de cada grupo
b) Coeficientes de variación de Pearson, asimetría de Fisher y apuntamiento de Fisher de cada grupo
c) La distribución de los datos en cada grupo ¿sugiere forma de campana?
d) ¿Alguna de estas distribuciones es sesgada? Si es así, ¿en qué dirección?
e) ¿Qué grupo tiende a tener una menor puntuación media de estrés?
Solución
a) La media, mediana, moda, varianza y desviación típica de cada grupo
VIVEN SOLOS
\( \bar{x} = \displaystyle \frac{x_i}{n} = \displaystyle \frac{203.5}{20} = 10.175 \hspace{2cm}\) \( M_e = 9.55 \)\( M_o = 8.3 \) Existen varias modas, se muestra el menor de los valores
\( \sigma^{2} = \displaystyle \frac{\sum (x_i – \bar{x})^{2} }{n-1} = \displaystyle \frac{53.6978}{19} = 2.8262 \hspace{2cm} \) \( \sigma = + \sqrt 2.8262 = 1.68113 \)ACOMPAÑADOS
\( \bar{x} = \displaystyle \frac{x_i}{20} = \displaystyle \frac{320.5}{20} = 16.025 \hspace{2cm} \) \( M_e = 15.9 \)\( M_o = 14.3 \) Existen varias modas, se muestra el menor de los valores
\( \sigma^{2} = \displaystyle \frac{\sum (x_i – \bar{x})^{2} }{n-1} = \displaystyle \frac{168.302}{20} = 8.858 \hspace{2cm} \) \( \sigma = + \sqrt 8.858 = 2.976 \)b) Coeficientes de variación de Pearson, asimetría de Fisher y apuntamiento de Fisher de cada grupo
VIVEN SOLOS
\( CV = \displaystyle \frac {\sigma}{\bar{x}} = \displaystyle \frac {1.68113}{10.175}= 0.165 \hspace{2cm} \) \( \gamma = \displaystyle \frac{m_3 }{\sigma^{3}} = \displaystyle \frac{5.48289}{4.75120} = 1.154 \)ACOMPAÑADOS
\( CV = \displaystyle \frac {\sigma}{\bar{x}} = \displaystyle \frac {2.976}{16.025}= 0.1857 \hspace{2cm} \) \( \gamma = \displaystyle \frac{m_3 }{\sigma^{3}} = \displaystyle \frac{-26.75743}{26.362} = -1.015 \)c) La distribución de los datos en cada grupo ¿sugiere forma de campana? NO
d) ¿Alguna de estas distribuciones es sesgada? Si es así, ¿en qué dirección?
viven solos es sesgada a la derecha, el coeficiente de asimetría es positivo
acompañados es sesgada a la izquierda, el coeficiente de asimetría es negativo
e) ¿Qué grupo tiende a tener una menor puntuación media de estrés?
Viven solos
6. En un parque natural se está realizando un estudio sobre el recorrido que realizan los pájaros. Para ello se estudió la distancia de vuelo desde el punto en que se soltó un pájaro recién anillado hasta su primera posada. Los siguientes datos corresponden a dos tipos de pájaros
Estorninos
\( \begin{matrix} \hline 108.6 & 119.1 & 99.3 & 109.6 \\ \hline
98.3 & 103.5 & 119.5 & 148.3 \\ \hline
120.2 & 131.0 & 140.3 & 89.4 \\ \hline
82.9 & 180.5 & 210.7 & 119.5 \\ \hline
134.3 & 101.7 & 132.3 & 208.5 \\ \hline \end{matrix} \)
Vencejos
\( \begin{matrix} \hline 107.6 & 108.1 & 119.3 & 153.6 \\ \hline
134.3 & 106.5 & 109.5 & 95.3 \\ \hline
133.2 & 145.0 & 127.3 & 109.4 \\ \hline
188.9 & 213.5 & 134.7 & 199.5 \\ \hline
214.3 & 106.7 & 205.3 & 321.8 \\ \hline \end{matrix} \)
Se pide:
a) La media, mediana de cada grupo ¿Son semejantes los conjuntos con respecto a alguna de las medidas?
b) Obsérvese que el último dato del segundo grupo es muy diferente al resto; este dato recibe el nombre de outlier o dato atípico. Para comprobar su efecto: eliminar el dato y calcular la media y mediana para los restantes. ¿Qué medida está menos afectada por la presencia del dato atípico?
c) La cuasivarianza y cuasidesviación típica de cada grupo. ¿Son estas medidas de variabi-lidad resistentes al dato atípico?
d) ¿Alguna de estas distribuciones es sesgada? Si es así, ¿en qué dirección?
e) ¿Qué grupo tiene el rango intercuartílico más grande?
f) ¿Qué grupo posee variabilidad más grande?
g) ¿Qué grupo es más simétrico?
Solución
a) La media, mediana de cada grupo ¿Son semejantes los conjuntos con respecto a alguna de las medidas?
Estorninos:
\( \bar{x} = \displaystyle \frac{x_i}{20} = \displaystyle \frac{2557.5}{20} = 127.875 \hspace{2cm} \) \( M_e = 119.5 \)Vencejos
\( \bar{x} = \displaystyle \frac{x_i}{20} = \displaystyle \frac{5930.5}{20} = 296.525 \hspace{2cm} \) \( M_e = 133.75 \)b) Obsérvese que el último dato del segundo grupo es muy diferente al resto; este dato recibe el nombre de outlier o dato atípico. Para comprobar su efecto: eliminar el dato y calcular la media y mediana para los restantes. ¿Qué medida está menos afectada por la presencia del dato atípico?
\( \bar{x} = \displaystyle \frac{x_i}{20} = \displaystyle \frac{2712}{19} = 142.7368 \hspace{2cm} \) \( M_e = 133.20 \)Está menos afectada la Mediana
c) La cuasivarianza y cuasidesviación típica de cada grupo. ¿Son estas medidas de variabilidad resistentes al dato atípico?
Estorninos:
\( \sigma^{2} = \displaystyle \frac{\sum (x_i – \bar{x})^{2} }{n-1} = \displaystyle \frac{24227.204}{19} = 1275.116 \hspace{2cm} \) \( \sigma = + \sqrt 1275.116 = 35.70876 \)Vencejos
\( \sigma^{2} = \displaystyle \frac{\sum (x_i – \bar{x})^{2} }{n-1} = \displaystyle \frac{90173448.795}{19} = 474597.305 \hspace{2cm} \) \( \sigma = + \sqrt 474597.305 = 688.91023 \) \( \sigma^{2}_1 = \displaystyle \frac{\sum (x_i – \bar{x})^{2} }{n-1} = \displaystyle \frac{30045.744}{18} = 1669.208 \hspace{2cm} \) \( \sigma_1 = + \sqrt 1669.208 = 40.85594 \)No son estas medidas de variabilidad resistentes al dato atípico
d) ¿Alguna de estas distribuciones es sesgada? Si es así, ¿en qué dirección?
Estorninos:
Coeficiente de asimetría = 1.289
Vencejos
Coeficiente de asimetría = 4.447
Ambas distribuciones son sesgadas, son asimétricas a la derecha. La cola de la distribución es mas larga por la derecha
e) ¿Qué grupo tiene el rango intercuartílico más grande?
Estorninos:
Rango intercuartílico \( = Q_3 – Q_1 = 119.5- 102.15 = 17.35 \)
Vencejos
Rango intercuartílico \( = Q_3 – Q_1 = 133.75 – 108.10 = 25.65 \)
f) ¿Qué grupo posee variabilidad más grande?
La variabilidad podemos medirla, por ejemplo mediante la Amplitud. Pero unos de los inconvenientes que plantea esta medida es su limitación al utilizar únicamente los valores extremos de la distribución; de esta forma, no recoge la poca o mucha dispersión que pueda existir entre los restantes valores, que son la mayoría de las puntuaciones. Aún así se recomienda incluir éste valor como complementario de otras medidas de dispersión.
Estorninos:
\( A_T = X_{max} – X_{min} = 210.7 – 82.9 = 127.8 \)
Vencejos
\( A_T = X_{max} – X_{min} = 3218.50 – 95.30 = 3123.2 \)
La variabilidad se puede basar en la distancia observada entre las puntuaciones y un valor central de la distribución como la media aritmética. De modo que, una distribución con poca variabilidad es en la que la mayoría de las puntuaciones están próximas a la media, mientras que con mucha variabilidad, las puntuaciones se alejan del valor medio de la variable. Una de estas medidas que utilizamos es la varianza o la cuasivarianza. Que ya la hemos calculado anteriormente
Es frecuente que uno de los objetivos del análisis descriptivo de los datos sea la comparación del grado de variabilidad o dispersión entre dos conjuntos de puntuaciones en una misma o distintas variables. Debido a que, por lo general, las variables objeto de estudio se miden en unidades distintas no tiene sentido compararlas en base a los valores de sus varianzas o desviaciones típicas. Para paliar este inconveniente es necesario definir un índice de variabilidad relativa que no dependa de las unidades de medida. Un coeficiente que cumple con estos requisitos es el coeficiente de variación de Pearson, que se expresa en porcentajes:
Estorninos:
\( CV = \displaystyle \frac {\sigma}{\bar{x}} = \displaystyle \frac {35.70876}{127.8750}= 0.27924 \)
Vencejos
\( CV = \displaystyle \frac {\sigma}{\bar{x}} = \displaystyle \frac {688.91023}{296.5250}= 2.32327 \)
Los Vencejos poseen una variabilidad mas grande que los Estorninos
g) ¿Qué grupo es más simétrico?
Estorninos:
Asimetría = 1.289
Vencejos
Asimetría = 4.447
Los estorninos es el grupo mas simétrico
7. En un laboratorio farmacéutico se acaba de instalar una nueva máquina automática, “de gran precisión”, para dosificar y tabletear ciertos productos. Si el director del laboratorio quiere investigar la exactitud de la máquina no le queda otro camino que probarla. Supongamos que la máquina se utiliza para fabricar tabletas de 200 mg del producto y se extraen dos muestras:
La primera muestra dio los resultados: 300,100, 250 y 150 mg.
La segunda muestra dio los resultados: 202,198, 201 y 199 mg.
Se pide:
a) Calcular la media en ambos casos. (Sol. \( \bar{x}_{A}=200= \bar{ x}_{B} \))
b) Desviaciones absolutas medias (Sol. \( D_{\bar{x}_{A}}=75; D_{\bar{x}_{B}}=1.5 \))
c) ¿En qué caso se considerará la máquina aceptable? (Sol. b)
8. Se aplicó un test de inteligencia a 456 estudiantes del primer curso de Biológicas. Las puntuaciones obtenidas, agrupadas en intervalos de clase de 4 unidades de amplitud, figuran en la siguiente tabla de distribución de frecuencias:
\( \begin{array}{|l||c|c|c|c|c|c|c|} \hline e_{i-1}-e_{i} & 78-82 & 82-86 & 86-90 & 90-94 & 94-98 & 98-102 & 102-106 \\ \hline
n_{i} & 1 & 2 & 6 & 42 & 54 & 75 & 92 \\ \hline
e_{i-1}-e_{i} & 106-110 & 110-114 & 114-118 & 118-122 & 122-126 & 126-130 & 130-134 \\ \hline
n_{i} & 96 & 38 & 27 & 12 & 8 & 2 & 1 \\ \hline \end{array} \)
Calcular: \( P_{25}; P_{75}; P_{90} \) . (Sol. \( P_{25}=98.48; P_{75} =108.92; P_{90} =114.65 \) ).
Solución
\( \begin{array}{|c|c|c|c|} \hline e_{i-1}-e_{i} & n_{i} & N_i & x_i \\ \hline 78-82 & 1 & 1 & 80 \\ \hline 82-86 & 2 & 3 & 84 \\ \hline 86-90 & 6 & 9 & 88 \\ \hline 90-94 & 42 & 51 & 92 \\ \hline 94-98 & 54 & 105 & 96 \\ \hline 98-102 & 75 & 180 & 100 \\ \hline 102-106 & 92 & 272 & 104 \\ \hline 106-110 & 96 & 368 & 108 \\ \hline 110-114 & 38 & 406 & 112 \\ \hline 114-118 & 27 & 433 & 116 \\ \hline 118-122 & 12 & 445 & 120 \\ \hline 122-126 & 8 & 453 & 124 \\ \hline 126-103 & 2 & 455 & 128 \\ \hline 130-134 & 1 & 456 & 132 \\ \hline \end{array} \)
\( P_{25} \)
\( \displaystyle \frac {25n}{100} = \displaystyle \frac {25 \times 456 } {100} = 114 \)
\( N_{i-1} < \displaystyle \frac {25n}{100} < Ni \Longrightarrow 105 < 114 < 180 \)
El intervalo es: \( (98, 102 ) \)
\( P_{25} = e_{i-1} + \displaystyle \frac { \displaystyle \frac {25n}{100} – N_{i-1} } { N_i – N_{i-1}} (e_i – e_{i-1}) = 98 + \displaystyle \frac {114 – 105} { 180-105} (102-98) = 98 + \displaystyle \frac {9}{75} \times 4 = 98.48 \)
\( P_{75} \)
\( \displaystyle \frac {75n}{100} = \displaystyle \frac {75 \times 456 } {100} = 342 \)
\( N_{i-1} < \displaystyle \frac {75n}{100} < Ni \Longrightarrow 272 < 342 < 368 \)
El intervalo es: \( (106, 110 ) \)
\( P_{75} = e_{i-1} + \displaystyle \frac { \displaystyle \frac {75n}{100} – N_{i-1} } { N_i – N_{i-1}} (e_i – e_{i-1}) = 106 + \displaystyle \frac {342 – 272} { 368 – 272} (110- 106) = 106 + \displaystyle \frac {70}{96} \times 4 = 108.92 \)
\( P_{90} \)
\( \displaystyle \frac {90n}{100} = \displaystyle \frac {90 \times 456 } {100} = 410.4 \)
\( N_{i-1} < \displaystyle \frac {90n}{100} < Ni \Longrightarrow 406 < 410.4 < 433 \)
El intervalo es: \( (114 , 118 ) \)
\( P_{90} = e_{i-1} + \displaystyle \frac { \displaystyle \frac {75n}{100} – N_{i-1} } { N_i – N_{i-1}} (e_i – e_{i-1}) = 114 + \displaystyle \frac {410.4 – 406} { 433 – 406} (118- 114) = 114 + \displaystyle \frac {4.4}{27} \times 4 = 114.65 \)
9. En una clínica infantil se han ido anotando, durante un mes, el número de metros que el niño anda seguido y sin caerse el primer día que comienza a caminar. Obteniéndose así la tabla de información adjunta:
\( \begin{matrix} \hline N^{o} \hspace{1mm} de \hspace{1mm} niños & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline
N^{o} \hspace{1mm} de \hspace{1mm} metros & 2 & 6 & 10 & 5 & 10 & 3 & 2 & 2 \\ \hline \end{matrix} \)
Se pide:
a) Tabla de frecuencias. Diagrama de barras para frecuencias absolutas y para las frecuencias absolutas acumuladas
b) Mediana, moda y cuartiles (Sol: \( Me=4; M₀= 3; M₀^´ = 5; Q_1=3; Q_2=4; Q_3=5 \) )
c) Recorrido Intercuartílico (Sol: \( R_{I}=2 \) )
d) Momentos respecto al origen de primer, segundo y tercer orden. (Sol: \( m_1=4.05; m_2=19.5; m_3=106.2 \) )
e) Momentos centrales de primer y tercer orden (Sol:\( μ_1=0; μ_3=2.135 \) )
Solución
a) Tabla de frecuencias. Diagrama de barras para frecuencias absolutas y para las frecuencias absolutas acumuladas
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|} \hline x_{i} & n_i & N_i & f_i & F_i & lg x_i & n_i log x_i & n_i/x_i & n_i x_i \\ \hline 1 & 2 & 2 & 0.05 & 0.05 & 0 & 0 & 2 & 2 \\ 2 & 6 & 8 & 0.15 & 0.2 & 0.3010 & 1.8060 & 3 & 12 \\ 3 & 10 & 18 & 0.25 & 0.45 & 0.4771 & 4.7710 & 3.33 & 30 \\ 4 & 5 & 23 & 0.12 & 0.5 & 0.6020 & 3.01100 & 1.25 & 20 \\ 5 & 10 & 33 & 0.25 & 0.82 & 0.6989 & 6.9890 & 2 & 50 \\ 6 & 3 & 36 & 0.08 & 0.90 & 0.7781 & 2.3343 & 0.5 & 18 \\ 7 & 2 & 38 & 0.05 & 0.95 &0.8450 & 1.69 & 0.28 & 14 \\ 8 & 2 & 40 & 0.05 & 1 & 0.9030 & 1.8060 & 0.25 & 16 \\ \hline & 40 & & & & & 22.4063 & 12.61 & 162 \\ \hline
\end{array} \)
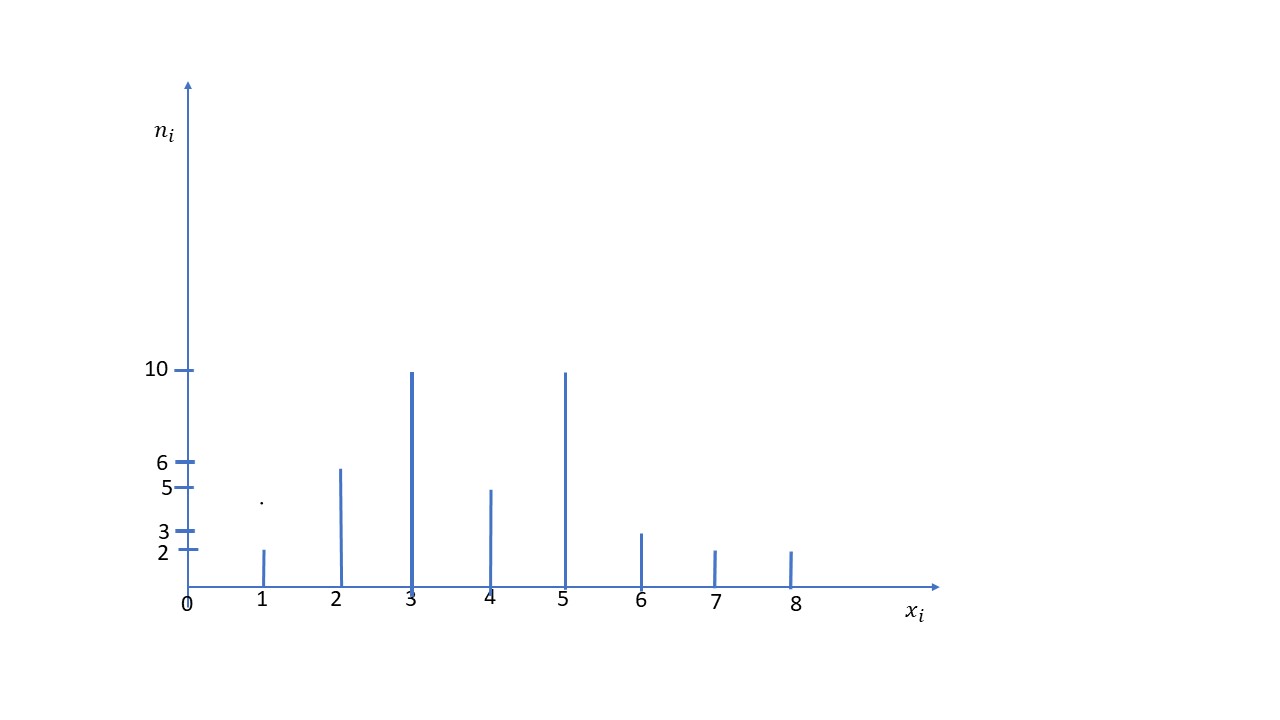
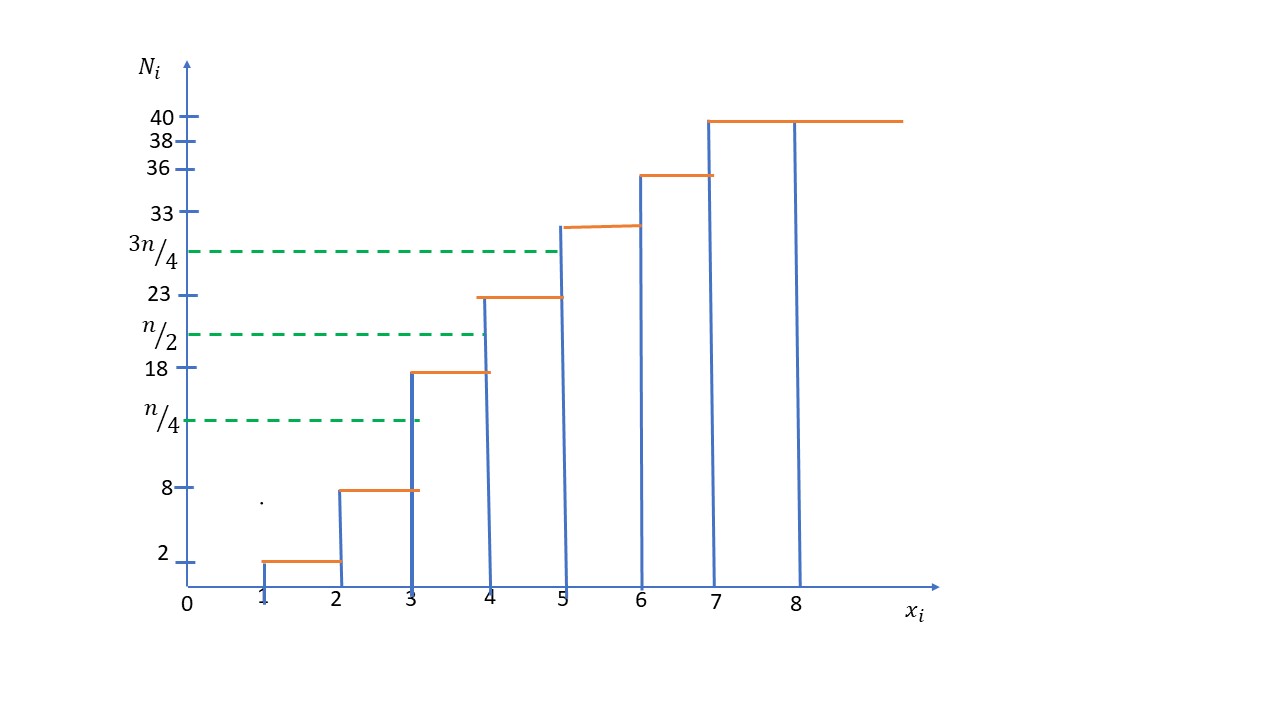
b) Mediana, moda y cuartiles (Sol: \( Me=4; M₀= 3; M₀^´ = 5; Q_1=3; Q_2=4; Q_3=5 \) )
\( M_e \)
\( \displaystyle \frac {n}{2} = \displaystyle \frac {40 } {2} = 20 \)
\( N_{i-1} < \displaystyle \frac {n}{2} < Ni \Longrightarrow 18 < 20 < 23 \)
\( M_e = x_i \Longrightarrow M_e = 4 \)La distribución es bimodal \( M_o = 3 \) y \( M_o = 5 \)
\( Q_1: \displaystyle \frac {n}{4} = 10 \Longrightarrow 8 < 10 < 18 \Longrightarrow Q_1 = 3 \hspace {1cm}\) \( Q_2: \displaystyle \frac {n}{2} = 20 \Longrightarrow 18 < 20 < 23 \Longrightarrow Q_2 = M_e = 4 \hspace {1cm} \) \( Q_3: \displaystyle \frac {3n}{4} = 30 \Longrightarrow 23 < 30 < 33 \Longrightarrow Q_3 = 5 \)c) Recorrido Intercuartílico (Sol: \( R_{I}=2 \) )
\( R_{I} = Q_3 – Q_1 =5 -3 = 2 \)d) Momentos respecto al origen de primer, segundo y tercer orden. (Sol: \( m_1=4.05; m_2=19.5; m_3=106.2 \) )
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|} \hline n_i x_{i} & x^{2}_i & n_i x^{2}_i & x^{3}_i & x^{3}_i n_i & (x_i – \bar{x})n_i & (x_i – \bar{x})^{3}n_i \\ \hline 2 & 1 & 2 & 1 & 2 & -6.1 & -56.745 \\ 12 & 4 & 24 & 8 & 48 & -12.30 & -51.690 \\ 30 & 9 & 90 & 27 & 2.70 & -10.50 & -11.576 \\ 20 & 16 & 80 & 64 & 3.20 & -0.25 & -0.001 \\ 50 & 25 & 250 & 125 & 1250 & 9.50 & 8.573 \\ 18 & 36 & 108 & 216 & 648 & 5.85 & 22.244 \\ 14 & 49 & 98 & 343 & 686 & 5.90 & 51.344 \\ 16 & 64 & 128 & 5.12 & 1024 & 71.90 & 123.259 \\ \hline 162 & & 780 & & 4.248 & 0 & 85.41 \\ \hline \end{array} \)
\( a_1= \displaystyle \frac {\sum x_i n_i}{n}= \displaystyle \frac {162 }{40}= 4.05 \hspace {1cm} \)
\( a_2= \displaystyle \frac {\sum x_i^{2} n_i}{n}= \displaystyle \frac {780 }{40}= 19.5 \hspace {1cm} \)
\( a_3= \displaystyle \frac {\sum x_i^{3} n_i}{n}= \displaystyle \frac {4248 }{40}= 106.2 \)
e) Momentos centrales de primer y tercer orden (Sol:\( μ_1=0; μ_3=2.135 \) )
\( m_1= \displaystyle \frac {\sum (x_i – \bar{x}) n_i}{n}= \displaystyle \frac {0 }{40}= 0 \hspace {1cm} \)
\( m_3= \displaystyle \frac {\sum (x_i – \bar{x})^{3} n_i}{n}= \displaystyle \frac {85.41 }{40}= 2.135 \)
10. La siguiente tabla muestra la distribución del coeficiente intelectual de 120 alumnos.
\( \begin{array}{|l||c|c|c|c|} \hline C.I. & 60-70 & 70-80 & 80-90 & 90-100 \\ \hline
n_{i} & 2 & 3 & 25 & 46 \\ \hline
C.I. & 100-110 & 110-120 & 120-130 & 130-140 \\ \hline
n_{i} & 35 & 5 & 3 & 1 \\ \hline \end{array} \)
a) Si se consideran bien dotados a los alumnos cuya puntuación está por encima del percentil 95 ¿A partir de que coeficiente intelectual mínimo los consideramos bien dotados? (Sol: \( P_{95} \)).
b) Si se consideran atrasados los alumnos cuya puntuación sea inferior al percentil 5 ¿Qué puntuación máxima pueden tener los atrasados? (Sol: 80.4)
c) Si el coeficiente intelectual es 109. Determinar el percentil correspondiente. (Sol: \( P_{90} \)).
11. Un profesor califica a sus alumnos siguiendo el siguiente criterio: suspensos 40%, aprobados 30%, notables 15%, sobresalientes 10%, matrículas 5%. Si las notas vienen dadas por la siguiente tabla:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|} \hline Notas & 0-1 & 1-2 & 2-3 & 3-4 & 4-5 & 5-6 & 6-7 & 7-8 & 8-9 & 9-10 \\ \hline n_{i} & 34 & 74 & 56 & 81 & 94 & 70 & 41 & 28 & 16 & 4 \\ \hline\end{array} \)
Calcula la nota máxima para conseguir suspenso, aprobado, notable, sobresaliente y matrícula. (Sol: Suspenso ≤3.43; 3.43< Aprobado ≤ 5.13; 5.13< Notable ≤ 6.34; 6.34< Sobresaliente ≤ 7.57; Matrícula >7.57).
Solución
\( \begin{array}{|c|c|c|} \hline Notas & n_i & N_i \\ \hline
0-1 & 34 & 34 \\ \hline
1-2 & 74 & 108 \\ \hline
2-3 & 56 & 164 \\ \hline 3-4 & 81 & 145 \\ \hline 4-5 &94 &339 \\ \hline 5-6 & 70 & 409 \\ \hline 6-7 & 41 & 450 \\ \hline 7-8 & 28 & 478 \\ \hline 8-9 & 16 & 494 \\ \hline 9-10 & 4 & 498 \\ \hline\end{array} \)
a) Suspensos 40% \( \Longrightarrow P_{40} \)
\( P_{40} \)
\( \displaystyle \frac {40n}{100} = \displaystyle \frac {40 \times 4.98 } {100} = 199.2 \)
\( N_{i-1} < \displaystyle \frac {40n}{100} < Ni \Longrightarrow 164 < 199.2 < 245 \)
El intervalo es: \( (3, 4 ) \)
\( P_{40} = e_{i-1} + \displaystyle \frac { \displaystyle \frac {40n}{100} – N_{i-1} } { N_i – N_{i-1}} (e_i – e_{i-1}) = 3 + \displaystyle \frac {199.2-164} {245-164} (4-3) = 3.43 \)
Notas menores que 3.43 \( \Longrightarrow \) suspenso
b) Aprobados 30% \( \Longrightarrow P_{70} \)
\( P_{70} \)
\( \displaystyle \frac {70n}{100} = \displaystyle \frac {70 \times 4.98 } {100} = 348.6 \)
\( N_{i-1} < \displaystyle \frac {70n}{100} < Ni \Longrightarrow 339 < 348.6 < 409 \)
El intervalo es: \( (5, 6 ) \)
\( P_{70} = e_{i-1} + \displaystyle \frac { \displaystyle \frac {70n}{100} – N_{i-1} } { N_i – N_{i-1}} (e_i – e_{i-1}) = 5 + \displaystyle \frac {348.6-339} {409-339} (6 – 5) = 5.13 \)
Para conseguir aprobado \( 3.43 < aprobado \leq 5.13 \)
c) Notables 15% \( \Longrightarrow P_{85} \)
\( P_{85} \)
\( \displaystyle \frac {85n}{100} = \displaystyle \frac {85 \times 4.98 } {100} = 423.3 \)
\( N_{i-1} < \displaystyle \frac {85n}{100} < Ni \Longrightarrow 409 < 423.3 < 450 \)
El intervalo es: \( (6, 7 ) \)
\( P_{85} = e_{i-1} + \displaystyle \frac { \displaystyle \frac {85n}{100} – N_{i-1} } { N_i – N_{i-1}} (e_i – e_{i-1}) = 6 + \displaystyle \frac {423.3 – 409} {450 – 409} (7 – 6) = 6.34 \)
Para conseguir notable \( 5.13 < Not \leq 6.34 \)
d) Sobresalientes 10% \( \Longrightarrow P_{95} \)
\( P_{95} \)
\( \displaystyle \frac {95n}{100} = \displaystyle \frac {95 \times 4.98 } {100} = 473.1 \)
\( N_{i-1} < \displaystyle \frac {95n}{100} < Ni \Longrightarrow 450 < 473.1 < 478 \)
El intervalo es: \( (7, 8 ) \)
\( P_{95} = e_{i-1} + \displaystyle \frac { \displaystyle \frac {95n}{100} – N_{i-1} } { N_i – N_{i-1}} (e_i – e_{i-1}) = 7 + \displaystyle \frac {473.1 – 450} {478 – 450} (8 – 7) = 7.57 \)
Para conseguir notable \( 6.34 < Sob \leq 7.57 \)
e) Matrículas 5% \( \Longrightarrow P_{100} \)
\( P_{100} \)
\( \displaystyle \frac {100n}{100} = \displaystyle \frac {100 \times 498 } {100} = 498 \Longrightarrow P_{100} = 10 \)
Para conseguir Matrícula > 7.57
12. Una especie de mamíferos tiene en cada cría un número variable de hijos. Se observa durante un año la cría de 35 familias, anotándose el número de hijos obtenidos por las familias en dicha cría.
\( \begin{matrix} \hline N^{o} \hspace{1mm} hijos & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline N^{o} \hspace{1mm} familias & 2 & 3 & 10 & 10 & 5 & 0 & 5 & 0 \\ \hline \end{matrix} \)
a) Hallar los cuartiles de primer y tercer orden. (Sol: \( Q_1=2; Q_3= 4 \))
b) Hallar la moda. (Sol: \( M₀=2; M₀^′= 3 \))
c) Coeficiente se asimetría de Fisher
d) Recorrido intercuartílico
Solución
a) Hallar los cuartiles de primer y tercer orden. (Sol: \( Q_1=2; Q_3= 4 \))
\( \begin{array} {|c|c|c|c|c|c|c|c|} \hline x_{i} & n_i & N_i & n_ix_i & (x_i – \bar{x}) & (x_i – \bar{x})^{2}n_i & (x_i – \bar{x})^{3}n_i \\ \hline 0 & 2 & 2 & 0 & -2.94 & 17.28 & -50.82 \\ 1 & 3 & 5 & 3 & -1.94 & 11.29 & -21.90 \\ 2 & 10 & 15 & 20 & -0.94 & 8.83 & -8.30 \\ 3 & 10 & 25 & 30 & 0.06 & 0.03 & 0.002 \\ 4 & 5 & 30 & 20 & 1.06 & 5.61 & 5.9 \\ 5 & 0 & 30 & 0 & 2.06 & 0 & 0 \\ 6 & 5 & 35 & 30 & 3.06 & 46.81 & 143.26 \\ 7 & 0 & 35 & 0 & 4.06 & 0 & 0 \\ \hline & 35 & & 103 & & 89.85 & 6815 \\ \hline\end{array} \)
\( Q_1: \displaystyle \frac {n} {4} = {35}{4} = 8.75 \)
\( 5 <8.75 < 15 \Longrightarrow Q_1 \in [1,2) \Longrightarrow Q_1 = 2 \)
\( Q_3: \displaystyle \frac {3n} {4} = {3 \times 35}{4} = 26.25 \)
\( 25 < 26.25 < 30 \Longrightarrow Q_3 \in (3 , 4 ] \Longrightarrow Q_3 = 4 \)
b) Hallar la moda. (Sol: \( M₀=2; M₀^′= 3 \))
Es bimodal \( M₀=2 \hspace {.2m} y \hspace {.2m} M₀^′= 3 \)
c) Coeficiente se asimetría de Fisher
\( \bar{x}= \displaystyle \frac { \displaystyle \sum n_i x_i } {n} = \displaystyle \frac {103}{35} = 2.94 \hspace {3cm} \) \( m_3= \displaystyle \frac { \displaystyle \sum n_i (x_i – \bar{x})^{3} } {n} = \displaystyle \frac {68.15}{35} = 1.94 \)
\( \gamma_1 = \displaystyle \frac {m_3} {\sigma^3} = \displaystyle \frac {1.94} {1.63^3} = 0.45 \Longrightarrow \hspace{.3cm} \) Hay simetría a la derecha
d) Recorrido intercuartílico
\( R_I = Q_3 – Q_1 = 4 – 2 = 2 \)
13. Un curso está dividido en 4 grupos de los cuales tenemos los datos:
\( \begin{matrix} \hline Grupo & N^{o} \hspace{1mm} alumnos & Nota \hspace{1mm} media & Varianza \\ \hline A & 30 & 6 & 1 \\ \hline
B & 40 & 6.5 & 1.69 \\ \hline
C & 50 & 5 & 0.81 \\ \hline
D & 60 & 4 & 0.64 \\ \hline \end{matrix} \)
a) Calcular los coeficientes de variación de cada grupo. (Sol: \( CV_{A}= 0.17; CV_{B}=0.2; CV_{C}=0.18; CV_{D}= 0.2 \))
b) ¿Qué grupo resulta más homogéneo? (Sol: A)
c) Calcular la varianza de todas las notas del curso. (Sol: 1.7983).
Solución
a) Calcular los coeficientes de variación de cada grupo. (Sol: \( CV_{A}= 0.17; CV_{B}=0.2; CV_{C}=0.18; CV_{D}= 0.2 \))
\( \begin{matrix} \hline Grupo & N^{o} \hspace{1mm} alumnos & Nota \hspace{1mm} media & Varianza & Desviación \hspace{1mm} Típica\\ \hline A & 30 & 6 & 1 & 1\\ \hline
B & 40 & 6.5 & 1.69 & 1.3 \\ \hline
C & 50 & 5 & 0.81 & 0.9 \\ \hline
D & 60 & 4 & 0.64 & 0.8 \\ \hline \end{matrix} \)
\( CV_A = \displaystyle \frac { \sigma_A } {\bar{x}_A} = \displaystyle \frac { 1}{6} = 0.17 \hspace{2cm} CV_B = \displaystyle \frac { \sigma_B } {\bar{x}_B} = \displaystyle \frac { 1.3}{6.5} = 0.2 \)
\( CV_C = \displaystyle \frac { \sigma_C } {\bar{x}_C} = \displaystyle \frac { 0.9}{5} = 0.18 \hspace{2cm} CV_D = \displaystyle \frac { \sigma_D } {\bar{x}_D} = \displaystyle \frac { 0.8}{4} = 0.2 \)
b) ¿Qué grupo resulta más homogéneo? (Sol: A)
\( CV_A = 0.17 \hspace {.3cm}\) es el más pequeño, por lo tanto el Grupo A resulta ser el más homogéneo. Las notas varían muy poco en torno a la media. Sin embargo, podemos observar que en conjunto todos los coeficientes de variación presentan diferencias pequeñas, por lo que los grupos tienen una homogeneidad parecida y más representativa es la media
c) Calcular la varianza de todas las notas del curso. (Sol: 1.7983)
\( \sigma^{2} =\displaystyle \sum f_i x_i^{2} – \bar{x}^{2} \)
\( \begin{array} {ll} \bar{x} & = \displaystyle \frac {\bar{x}_A \times n_a + \bar{x}_B \times n_B + \bar{x}_C \times n_C + \bar{x}_D \times n_D}{n} = \\ & = \displaystyle \frac {30 \times 6 + 40 \times 6.5 + 50 \times 5 + 60 \times 4} {180} = 5.13 \end{array} \)
\( \sigma^{2}_A = \displaystyle \sum f_ix_{iA}^{2} – \bar{x}^{2}_{A} \Longrightarrow 1 = \displaystyle \sum f_ix_{iA}^{2} – 6^{2} \Longrightarrow \displaystyle \sum f_ix_{iA}^{2} = 37 \)
\( \sigma^{2}_B = \displaystyle \sum f_ix_{iB}^{2} – \bar{x}^{2}_{B} \Longrightarrow 1.69 = \displaystyle \sum f_ix_{iB}^{2} – 6.5^{2} \Longrightarrow \displaystyle \sum f_ix_{iB}^{2} = 43.94 \)
\( \sigma^{2}_C = \displaystyle \sum f_ix_{iC}^{2} – \bar{x}^{2}_{C} \Longrightarrow 0.81 = \displaystyle \sum f_ix_{iC}^{2} – 5^{2} \Longrightarrow \displaystyle \sum f_ix_{iC}^{2} = 25.81 \)
\( \sigma^{2}_D = \displaystyle \sum f_ix_{iD}^{2} – \bar{x}^{2}_{D} \Longrightarrow 0.64 = \displaystyle \sum f_ix_{iD}^{2} – 4^{2} \Longrightarrow \displaystyle \sum f_ix_{iD}^{2} = 16.64 \)
\( \begin{array} {ll} \displaystyle \sum f_i x_i^{2} & = \displaystyle \frac { \displaystyle \sum f_ix_{iA}^{2} \times n_A + \displaystyle \sum f_ix_{iB}^{2} \times n_B + \displaystyle \sum f_ix_{iD}^{2} \times n_D }{n} = \\ & = \displaystyle \frac {37 \times 30 + 43.94 \times 40 + 25.81 \times 50 + 16.64 \times 60 } {180} = 28.52 \end{array} \)
\( \sigma^{2} =\displaystyle \sum f_i x_i^{2} – \bar{x}^{2} = 28.52 – 5.13 = 1.7983 \)
14. Se han medido mediante pruebas adecuadas los coeficientes intelectuales de un grupo de 20 alumnos, presentando los resultados agrupados en 6 intervalos de amplitud variable. Estas amplitudes son: \( a_1=12, a_2=12, a_3=4, a_4=4, a_5=12, a_6=20 \). Si las frecuencias relativas acumuladas correspondientes a cada uno de los intervalos son: \( F_1=0.15, F_2=0.15, F_3=0.55, F_4=0.8, F_5=0.95, F_6=1.00 \).
Se pide:
a) Formar la tabla de distribución de frecuencias, sabiendo que el extremo inferior del primer intervalo es 70
b) Dibujar el histograma y polígono de frecuencias absolutas. Calcular la moda
c) ¿Entre qué dos percentiles está comprendido un coeficiente intelectual de 98.4? Encontrar el valor ambos percentiles.
Al mismo grupo de alumnos se les hace una prueba de rendimiento y los resultados vienen dados en la Figura 1
d) Formar la tabla de distribución de frecuencias y calcular la mediana
e) ¿Qué medidas están más dispersas, los coeficientes intelectuales o las puntuaciones del rendimiento?
Figura 1
Soluciones: \( b) Mo=96.9; \hspace{1mm} c) P_{57}=98.32 \hspace{1mm} y \hspace{1mm} P_{58} =98.48; \hspace{1mm} d) Me=7 \); \hspace{1mm} e) Las puntuaciones del rendimiento. \( (CV_{I}=0.11;\hspace{1mm} CV_{R}=0.38) \).
Solución
a) Formar la tabla de distribución de frecuencias, sabiendo que el extremo inferior del primer intervalo es 70
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline e_{i-1}-e_i & n_i & N_i & f_i & F_i & a_i & h_i = n_i/a_i & x_i & f_ix_i & f_ix_i^{2}\\ \hline 70-82 & 3 & 3 & 0.15 & 0.15 & 12 & 0.25 & 76 & 11.4 & 866.4 \\ 82-94 & 0 & 3 & 0 & 0.15 & 12 & 0 & 88 & 0 & 0 \\ 94-98 & 8 & 11 & 0.4 & 0.55 & 4 & 2 & 96 & 38.4 & 3686.4 \\ 98-102 & 5 & 16 & 0.25 & 0.8 & 4 & 1.25 & 100 & 25 & 2500 \\ 102-114 & 3 & 19 & 0.15 & 0.95 &12 & 0.25 & 108 & 16.2 & 1749.6 \\ 114-134 & 1 & 20 & 0.05 & 1 & 20 & 0.05 & 124 & 96.2 & 768.8 \\ \hline & 20 & & & & & & & 97.2 & 9571.2 \\ \hline\end{array} \)
b) Dibujar el histograma y polígono de frecuencias absolutas. Calcular la moda
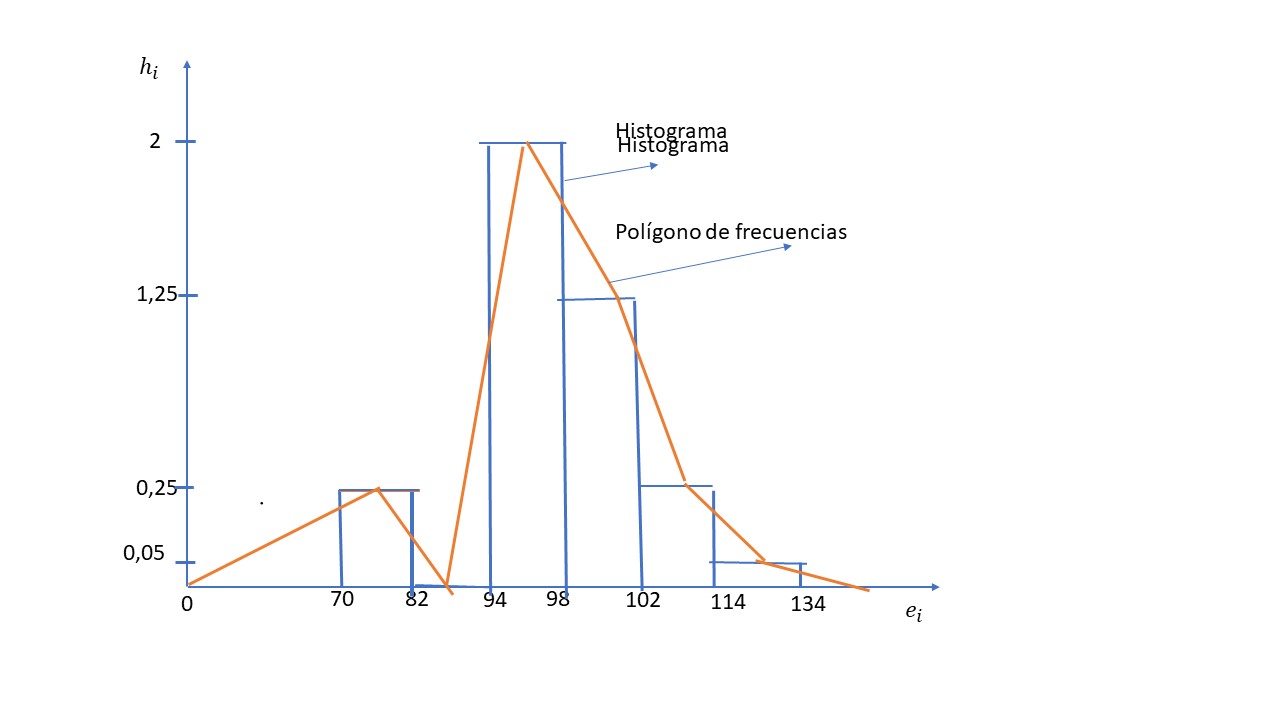
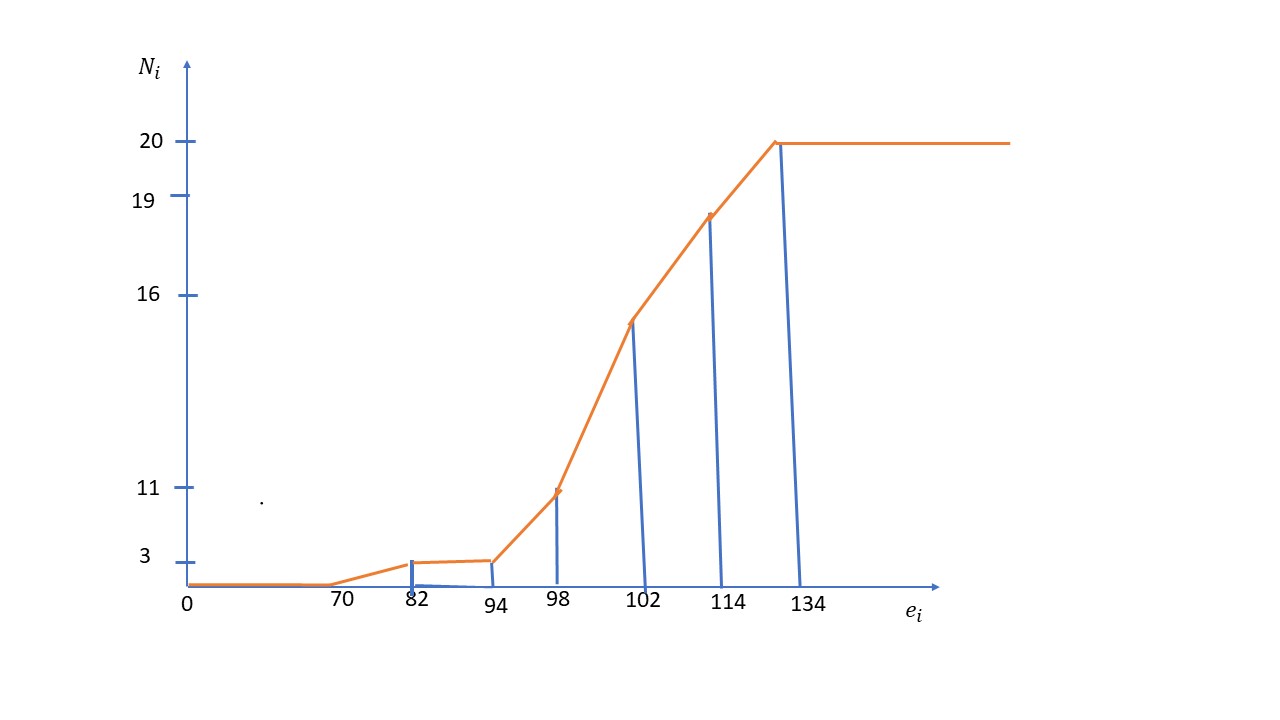
El intervalo modal es [94, 98)
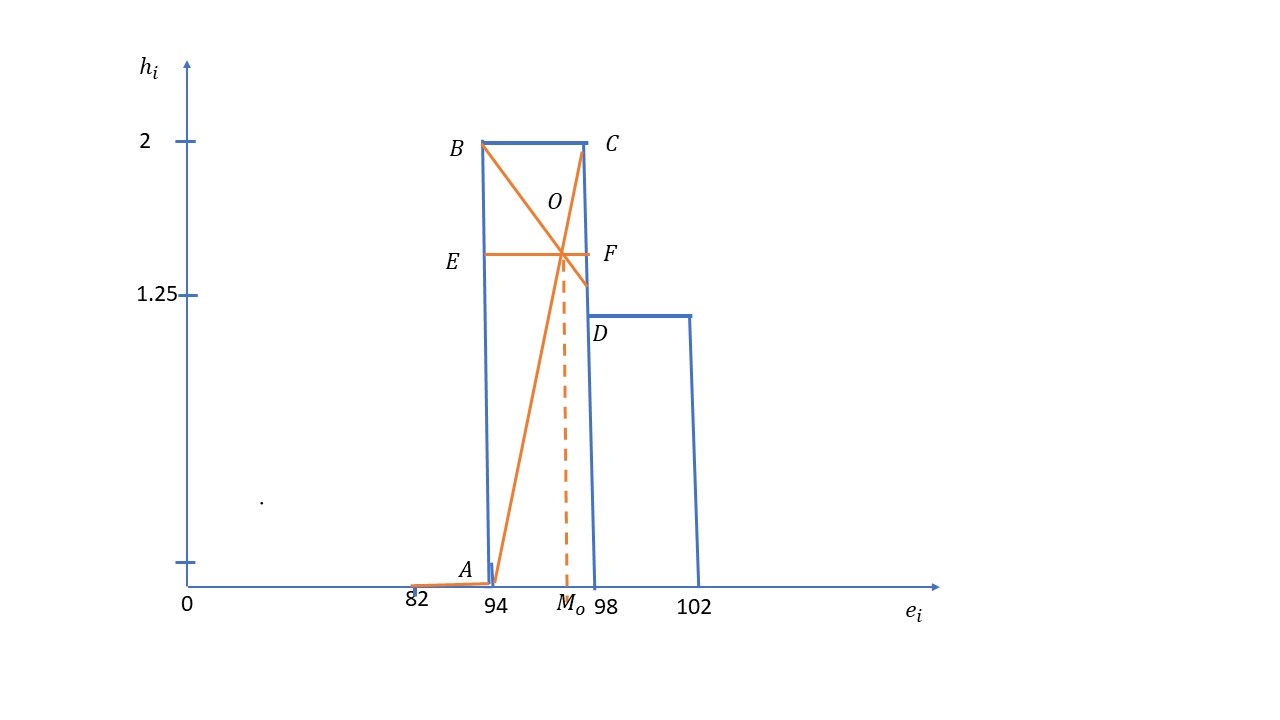
\( OE = \displaystyle \frac {BA \times EF}{CD + BA} = \displaystyle \frac {(2-0)(98-94)}{(2-1.25) + (2-0)} = 2.9 \Longrightarrow M_{O} = 94 + 2.9 = 96.9 \)
c) ¿Entre qué dos percentiles está comprendido un coeficiente intelectual de 98.4? Encontrar el valor ambos percentiles.
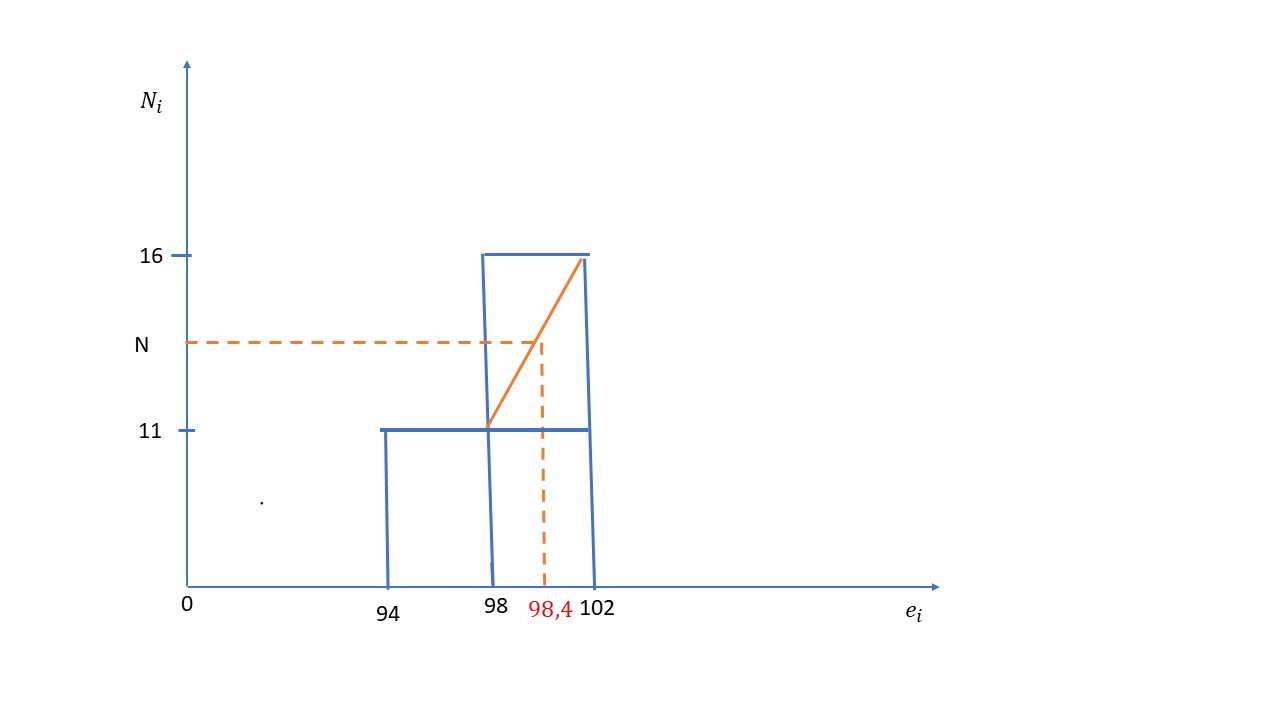
\( \begin{array} {ccc} 102 – 98 & \longrightarrow & 16 – 11 \\ 98.4 – 98 & \longrightarrow & N – 11 \\ \end{array} \longrightarrow N = 11 + 0.5 = 11.5 \)
Calculamos el porcentaje correspondiente
\( \displaystyle \frac {n \times i }{100} = 11.5 \Longrightarrow \displaystyle \frac {20 \times i }{100} = 11.5 \Longrightarrow i = 57.5 \)
Como \( \hspace{.5cm} 57 < 57.5 < 58 \Longrightarrow i = 57.5 \Longrightarrow 98.4 \) está entre los percentiles \( P_{57} \hspace{.2 cm} y \hspace{.2 cm} P_{58} \)
\( P_{57} \hspace{1cm} \displaystyle \frac {57}{100} \times n = \displaystyle \frac {57}{100} \times 20 = 11.4 \Longrightarrow \begin{array} {ccc} 102 – 98 & \longrightarrow & 16 – 11 \\ P_{57}-98 & \longrightarrow & 11.4 – 11 \\ \end{array} \Longrightarrow P_{57} = 98 + 0.38 = 98.32 \)
\( P_{58} \hspace{1cm} \displaystyle \frac {58}{100} \times 20 = 11.6 \Longrightarrow \begin{array} {ccc} 102 – 98 & \longrightarrow & 16 – 11 \\ P_{58}-98 & \longrightarrow & 11.6 – 11 \\ \end{array} \Longrightarrow P_{58} = 98 + 0.48 = 98.48 \)
\( P_{57} < 98.4 < P_{58} \Longrightarrow 98.32 < 98.4 <98.48 \)
El coeficiente intelectual de 98.4 está entre los percentiles \( P_{57} \hspace{.2cm} y \hspace{.2cm} P_{58} \hspace{.2cm} \) cuyos valores respectivos son 98.32 y 98.48
Al mismo grupo de alumnos se les hace una prueba de rendimiento y los resultados vienen dados en la Figura 1
Figura 1
El diagrama es de frecuencias absolutas, puesto que son valores mayores que la unidad.
La variable es discreta puesto que su diagrama acumulativo de frecuencias es escalonado, por lo tanto cada salto nos dará la frecuencia absoluta de cada valor de la variable
d) Formar la tabla de distribución de frecuencias y calcular la mediana
\( \begin{array} {|c|c|c|c|c|c|c|c|} \hline x_i & n_i & N_i & f_i & F_i & f_ix_i & f_ix_i^{2}\\ \hline 0 & 1 & 1 & 0.05 & 0.05 & 0 & 0 \\ 4 & 4 & 5 & 0.2 & 0.25 & 0.8 & 3.2 \\ 6 & 5 & 10 & 0.25 & 0.5 & 1.5& 9 \\ 8 & 6 & 16 & 0.3 & 0.8 & 2.4 & 19.2 \\ 10 & 4 & 20 & 0. & 1 & 2 & 20 \\ \hline & 20 & & & & 6.7 & 51.40 \\ \hline\end{array} \)
Mediana: \( \hspace{.3cm} \displaystyle \frac{n}{2} = \displaystyle \frac {20}{2} = 10 \hspace{.3cm} \) Observando la figua vemos que la ordenada 10 corresponde a la abcisa comprendida entre 6 y 8. Por lo tanto la mediana se puede considerar \( \hspace{.3cm} M_e = \displaystyle \frac{6+7}{2} = 7 \)
e) ¿Qué medidas están más dispersas, los coeficientes intelectuales o las puntuaciones del rendimiento?
Para comprobar las dispersiones calculamos los coeficientes de variación de Pearson
\( CV = \displaystyle \frac{\sigma}{\bar{x}} \)
\( \bar{x}_1 = \displaystyle \frac{\displaystyle \sum n_i x_i}{n} = \displaystyle \sum f_i x_i = 97.2 \)
\( \sigma_1^{2} = \displaystyle \sum f_i x_i^{2} – \bar{x}^{2} = 9571.2 – 97.2^{2} = 123.2 \Longrightarrow \sigma_1 = 11.1 \)
\( CV_1 = \displaystyle \frac{\sigma_1}{\bar{x}_1} = \displaystyle \frac {11.1}{97.2} = 0.11 \)
\( \bar{x}_2 = \displaystyle \sum f_i x_i = 6.7 \)
\( \sigma_2^{2} = \displaystyle \sum f_i x_i^{2} – \bar{x}^{2} = 51.40 – 6.7^{2} = 6.51 \Longrightarrow \sigma_2 = 2.55 \)
\( CV_2 = \displaystyle \frac{\sigma_2}{\bar{x}_2} = \displaystyle \frac {2.55}{6.7} = 0.38 \)
El CV de los coeficientes intectuales es 0.11 y el de las puntuaciones del rendimiento es 0.38. Por lo tanto los coeficientes intelectuales están menos dispersos que las puntuaciones del rendimiento
15. En una empresa el 20% es personal “no cualificado”, el 50% es personal “cualificado” y el resto es personal “técnico”. La plantilla consta de 1000 empleados. Se ha estimado la productividad para cada uno de estos grupos en unos coeficientes que van de 1 a 5. Los resultados se muestran en la tabla adjunta.
\( \begin{matrix} Coeficiente & Personal \hspace{1mm} no & Personal & Personal & \% \hspace{1mm} total \\ \hline
productividad & cualificado & cualificado & técnico & de \\ \hline
x_{i} & en \hspace{1mm} \% & en \hspace{1mm} \% & en \hspace{1mm} \% & trabajadores \\ \hline
1 & 10 & 5 & 0 & 4.5 \\ \hline
2 & 20 & 20 & 10 & 17 \\ \hline
3 & 30 & 20 & 40 & 28 \\ \hline
4 & 30 & 40 & 30 & 35 \\ \hline
5 & 10 & 15 & 20 & 15.5 \\ \hline \end{matrix} \)
a) Hállese la productividad media de los 1000 empleados. (Sol: \( \bar{x}=3.4 \))
b) ¿Qué nivel de productividad es el más corriente en esta empresa? (Sol \( Mo=4 \))
c) ¿Bajo qué coeficiente están el 50% de los trabajadores menos productivos? (Sol: \( Me=4 \)).
d) Comparando las productividades medias del personal no cualificado y del personal cualificado, ¿Cuál de ellas corresponde a una distribución de frecuencias más homogénea? (Sol: Personal cualificado (\( CV_{N}=0.37; CV_{C}=0.339 \)).
Solución
a) Hállese la productividad media de los 1000 empleados. (Sol: \( \bar{x}=3.4 \))
\( \begin{array}{|c|c|c|c|c|} \hline Coef. & \% \hspace{1mm} total & n^{o} \hspace{1mm} trabaj & & & \\
prod. \hspace{1mm} x_{i} & p_i & trabaj. \hspace{1mm} n_i & n_ix_i & p_ix_i & N_i \\ \hline
1 & 4.5 & 45 & 45 & 4.5 & 45 \\
2 & 17 & 170 & 340 & 34 & 215 \\
3 & 28 & 280 & 840 & 84 & 495 \\
4 & 35 & 350 & 1400 & 140 & 845 \\
5 & 15.5 & 155 & 475 & 77.5 & 1000 \\ \hline & 100 & 1000 & 3400 & 340 & \\ \hline \end{array} \)
\( \begin{array} {cc} 4.5 & \longrightarrow 100 \\ x & \longrightarrow 1000 \\ \end{array} \Longrightarrow x = 45 \hspace{1cm} \) \( \begin{array} {cc} 17 & \longrightarrow 100 \\ x & \longrightarrow 1000 \\ \end{array} \Longrightarrow x = 170 \)
\( \bar{x} = \displaystyle \frac{\displaystyle \sum n_i x_i}{n} = \displaystyle \frac{3400}{1000} = 3.4 \)
También
\( \bar{x} = \displaystyle \frac{\displaystyle \sum p_i x_i}{\displaystyle \sum p_i} = \displaystyle \frac{340}{100} = 3.4 \)
b) ¿Qué nivel de productividad es el más corriente en esta empresa? (Sol \( Mo=4 \))
La productividad modal \( \hspace{.5cm} M_o = 4 \)
c) ¿Bajo qué coeficiente están el 50% de los trabajadores menos productivos? (Sol: \( Me=4 \))
Mediana
También
\( \displaystyle \frac{n}{2}= 50 \Longrightarrow 49.5 < 50 < 84.5 \Longrightarrow M_e = 4 \)d) Comparando las productividades medias del personal no cualificado y del personal cualificado, ¿Cuál de ellas corresponde a una distribución de frecuencias más homogénea? (Sol: Personal cualificado (\( CV_{N}=0.37; CV_{C}=0.339 \)).
Consideramos las siguientes distribuciones de las que construimos las siguientes tablas:
Personal no cualificado
\( \begin{array}{|c|c|c|c|c|} \hline Coef. & \% \hspace{1mm} total & n^{o} \hspace{1mm} trabaj & & \\
prod. \hspace{1mm} x_{i} & p_i & trabaj. \hspace{1mm} n_i & p_ix_i & x_i^{2}p_i \\ \hline
1 & 10 & 100 & 10 & 10 \\
2 & 20 & 200 & 40 & 80 \\
3 & 30 & 300 & 90 & 270 \\
4 & 35 & 300 & 120 & 480 \\
5 & 10 & 100 & 50 & 250 \\ \hline & 100 & 1000 & 310 & 1090 \\ \hline \end{array} \)
\( CV = \displaystyle \frac{\sigma}{\bar{x}} \)
\( \bar{x} = \displaystyle \frac{\displaystyle \sum x_i p_i}{\displaystyle \sum p_i} = \displaystyle \frac {310}{100} = 3.1 \)
\( \sigma^{2} = \displaystyle \frac{\displaystyle \sum x_i^{2} p_i}{\displaystyle \sum p_i} – \bar{x}^{2} = \displaystyle \frac{1090}{100}- (3.1)^{2} = 1.9 \Longrightarrow \sigma = 1.1358 \)
\( CV = \displaystyle \frac{1.1358}{3.1} = 0.37 \)
Personal cualificado
\( \begin{array}{|c|c|c|c|} \hline Coef. & \% \hspace{1mm} total & & \\
prod. \hspace{1mm} x_{i} & p_i & p_ix_i & x_i^{2}p_i \\ \hline
1 & 5 & 5 & 5 \\
2 & 20 & 40 & 80 \\
3 & 10 & 60 & 180 \\
4 & 40 & 160 & 640 \\
5 & 15 & 75 & 375 \\ \hline & & 340 & 1280 \\ \hline \end{array} \)
\( CV = \displaystyle \frac{\sigma}{\bar{x}} \)
\( \bar{x} = \displaystyle \frac{\displaystyle \sum x_i p_i}{\displaystyle \sum p_i} = \displaystyle \frac {340}{100} = 3.4 \)
\( \sigma^{2} = \displaystyle \frac{\displaystyle \sum x_i^{2} p_i}{\displaystyle \sum p_i} – \bar{x}^{2} = \displaystyle \frac{1280}{100}- (3.4)^{2} = 1.24 \Longrightarrow \sigma = 1.1135 \)
\( CV = \displaystyle \frac{1.1135}{3.4} = 0.33 \)
El coeficiente de variación del personal cualificado es menor que el del personal cualificado, por lo tanto la distribución del personal cualificado es más homogénea y en consecuencia una productividad media más representativa.
16. En un cierto barrio se ha constatado que las familias residentes se han distribuido, según su tamaño, de la siguiente forma:
\( \begin{matrix} \hline Tamaño \hspace{1mm} familias & 0-2 & 2-4 & 4-6 & 6-8 & 8-10 \\ \hline N^{o}\hspace{1mm} familias & 110 & 200 & 90 & 75 & 25 \\ \hline \end{matrix} \)
Se pide:
a) ¿Cuál es el número medio de personas por familia? (Sol: \( \bar{x} =3.82 \))
b) ¿Cuál es el tipo de familia más frecuente? (Sol: \( Mo= 2.9 \))
c) Si sólo hubiera plaza de aparcamiento para el 50% de las familias y éstas se atendieran por familias de mayor a menor tamaño, ¿Qué componentes tendría que tener una familia para entrar en el cupo? Se supone que cada familia sólo tiene un vehículo. (Sol: \( Me=3.4 \))
d) Si el coeficiente de variación de Pearson de otro barrio es 1.8, ¿Cuál de los dos barrios puede ajustar mejor sus previsiones en base al diferente tamaño de las familias que lo habitan. (Sol: \( CV_1=0.59; CV_2=1.8. \) El primer barrio).
e) ¿Se pueden hacer previsiones en base al número medio de componentes por familia?
Solución
\( \begin{array}{|c|c|c|c|c|c|} \hline e_{i-1} – e_i & n_{i} & N_i & x_i & x_i n_i & x_i^{2}n_i \\ \hline
0-2 & 110 & 110 & 1 & 110 & 110 \\
2-4 & 200 & 310 & 3 & 600 & 1800 \\
4-6 & 90 & 400 & 5 & 450 & 2250 \\
6-8 & 75 & 475 & 7 & 525 & 3675 \\
8-10 & 25 & 500 & 9 & 225 & 2025 \\ \hline & 500 & & & 1910 & 9860 \\ \hline \end{array} \)
Se pide:
a) ¿Cuál es el número medio de personas por familia? (Sol: \( \bar{x} =3.82 \))
\( \bar{x} = \displaystyle \frac{\displaystyle \sum x_i n_i}{\displaystyle \sum n_i} = \displaystyle \frac {1910}{500} = 3.82 \)
b) ¿Cuál es el tipo de familia más frecuente? (Sol: \( Mo= 2.9 \))
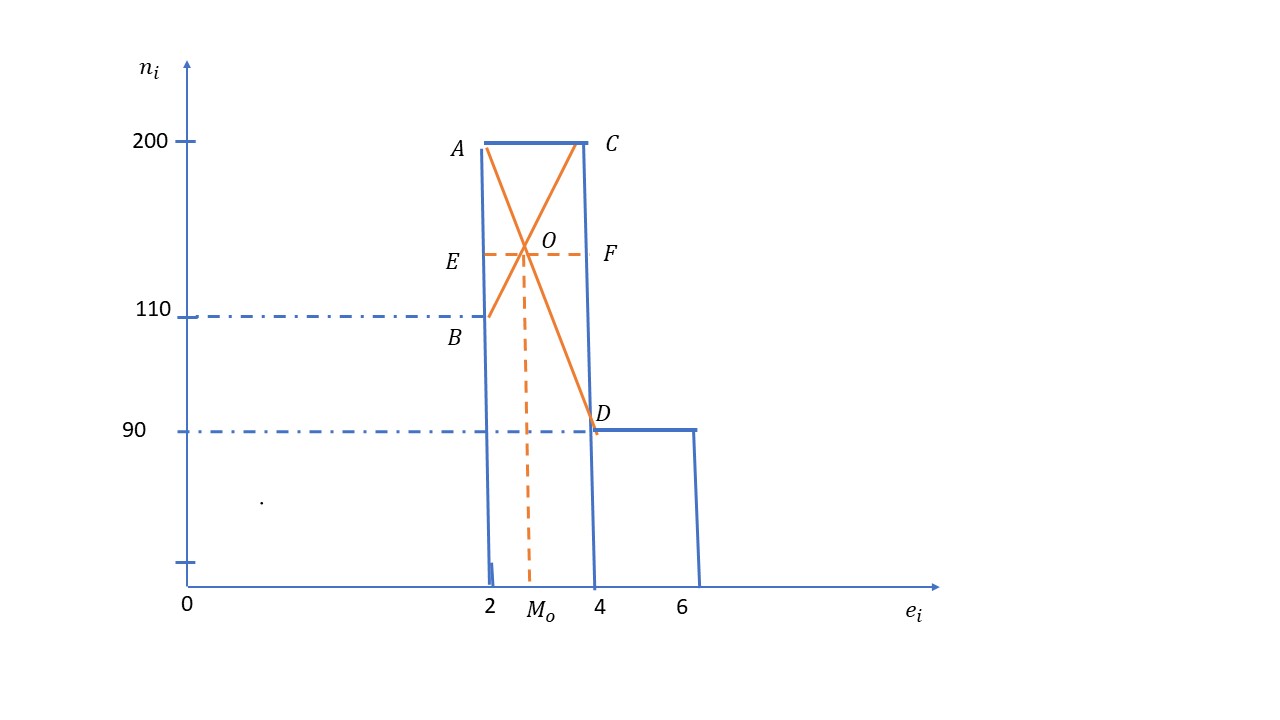
\( OE = \displaystyle \frac {AB \times EF}{CD + AB} = \displaystyle \frac {(200-110)(4-2)}{(200-90) + (200- 110)} = 0.9 \Longrightarrow M_{O} = 2 + 0.9 = 2.9 \)
El tipo de familia modal será aquella que se compone de tres personas
c) Si sólo hubiera plaza de aparcamiento para el 50% de las familias y éstas se atendieran por familias de mayor a menor tamaño, ¿Qué componentes tendría que tener una familia para entrar en el cupo? Se supone que cada familia sólo tiene un vehículo. (Sol: \( Me=3.4 \))
Para calcular los componentes que tendría que tener una familia para que estuviera encluida en el 50%, calculamos la mediana
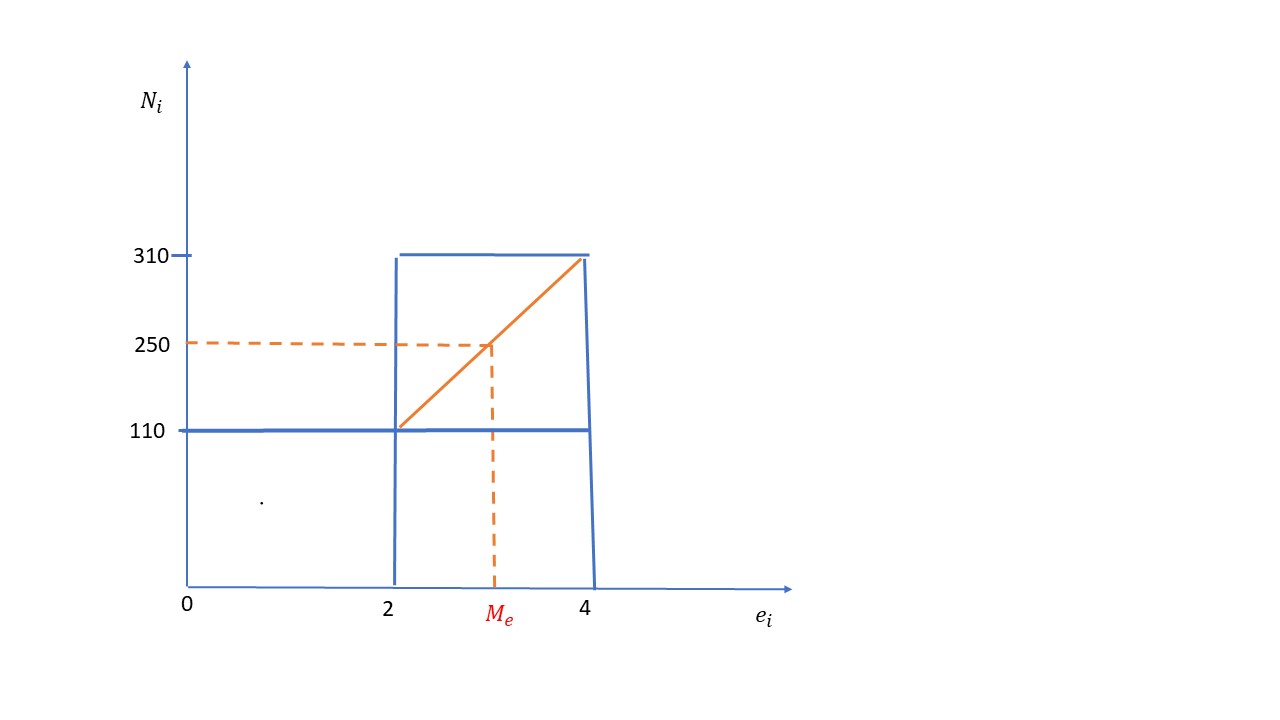
\( \displaystyle \frac {n}{2} = \displaystyle \frac {500}{2} = 250 \Longrightarrow 110 < 250 < 310 \Longrightarrow n/2 \in [2,4] \)
\( \begin{array} {ccc} 4 – 2 & \longrightarrow & 310- 110 \\ M_e – 2 & \longrightarrow & 250 – 110 \\ \end{array} \Longrightarrow M_e = 2 + 1.4 = 3.4 \)
d) Si el coeficiente de variación de Pearson de otro barrio es 1.8, ¿Cuál de los dos barrios puede ajustar mejor sus previsiones en base al diferente tamaño de las familias que lo habitan. (Sol: \( CV_1=0.59; CV_2=1.8. \) El primer barrio).
\( CV_{1} = \displaystyle \frac{\sigma}{\bar{x}} \)
\( \bar{x} = \displaystyle \frac{\displaystyle \sum x_i n_i}{\displaystyle \sum n_i} = \displaystyle \frac {1910}{500} = 3.82 \)
\( \sigma^{2} = \displaystyle \frac{\displaystyle \sum x_i^{2} n_i}{n} – \bar{x}^{2} = \displaystyle \frac{9860}{500}- (3.82)^{2} = 5.13 \Longrightarrow \sigma = 2.26 \)
\( CV = \displaystyle \frac{2.26}{3.82} = 0.59 \)
El otro barrio tiene un coeficiente de variación de 1.8, por lo tanto el tamaño de sus familias presentará una mayor variabilidad, y por tanto, serán menos fiables sus previsiones. Concluimos que el barrio que mejor se ajusta es el que tiene un CV=.59
e) ¿Se pueden hacer previsiones en base al número medio de componentes por familia?
Para poder hacer previsiones en base al número medio de personas por familia, la media debe ser representativa. La desviación típica es:
\( \sigma^{2} = 5.13 \Longrightarrow \sigma = 2.26 \)
17. Una variable X puede someterse a una transformación denominada Tipificación que consiste en restarle la media \( \bar{x} \) y dividir por la desviación típica σ. Una variable tipificada así obtenida, \( Z, Z= \displaystyle \frac{X-\bar{x}{σ}\), tiene dos propiedades fundamentales: Su media es cero y su desviación típica es uno. Aplicar este concepto a la distribución.
\( \begin{matrix} \hline x_{i} & 4 & 6 & 9 & 10 & 12 \\ \hline \end{matrix} \)
(Solución: \( \bar{x} =8 ; σ_{x}=21.83; z=0; σ_{z}=1 \) )
Solución
\( \begin{array}{|c|c|c|c|c|} \hline x_i & n_{i} & n_ix_i^{2} & z_i = \displaystyle \frac {x_i – \bar{x}}{\sigma} & n_iz_i^{2} \\ \hline
4 & 1 & 16 & -1.41 & 1.96 \\
6 & 1 & 36 & -0.7 & 0.49 \\
10 & 1 & 100 & 0.7 & 1.96 \\
12 & 1 & 144 & 1.41 & 0.49 \\
\hline 40 & 5 & 360 & 0 & 4.9 \\ \hline \end{array} \)
\( \sigma^{2} = \displaystyle \frac{\displaystyle \sum x_i^{2} n_i}{n} – \bar{x}^{2} = \displaystyle \frac{360}{5}- 8^{2} = 8 \Longrightarrow \sigma = 2.83 \)
La variable tipificada es \( \hspace{1cm} z_i = \displaystyle \frac {x_i – \bar{x}}{\sigma} \)
\( \bar{z} = \displaystyle \frac{\displaystyle \sum z_i n_i}{n} = \displaystyle \frac {0}{n} = 0 \)\( \sigma^{2} = \displaystyle \frac{\displaystyle \sum z_i^{2} n_i}{n} – \bar{z}^{2} = \displaystyle \frac{4.9}{5} \approx 1 \Longrightarrow \sigma \approx 1 \)
Autora: Ana María Lara Porras. Universidad de Granada
Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.