EJERCICIOS RESUELTOS: ESTADÍSTICA BIDIMENSIONAL

1. Se han estudiado los pesos (Kg) y las tallas (cm) correspondientes a un grupo de individuos, obteniendo la siguiente información:

\( \begin{array}{|c|c|c|c|c|c|c|} \hline X / Y & 160 & 162 & 164 & 166 & 168 & 170 \\ \hline 48 & 3 & 2 & 2 & 1 & 0 & 0 \\ \hline 51 & 2 & 3 & 4 & 2 & 2 & 1 \\ \hline 54 & 1 & 3 & 6 & 8 & 5 & 1 \\ \hline 57 & 0 & 0 & 1 & 2 & 8 & 3 \\ \hline 60 & 0 & 0 & 0 & 2 & 4 & 4 \\ \hline \end{array} \)

a) El peso y la talla media. (Sol. \( \bar{x}=54.171; \bar{ y}=165.71 \))
b) El porcentaje de alumnos que pesan menos de 55 Kg y miden más de 165. (Sol. 28.57).
c) Dentro del conjunto de los que miden más de 165 ¿Cuál es el porcentaje de los que pesan más de 52 Kg? (Sol. 86.046%)
d) ¿Cuál es la altura más frecuente entre los individuos cuyo peso oscila entre 51 Kg y 57 Kg?.(Sol. Mo=168)
e) ¿Qué peso medio es más representativo, el de los individuos que miden 164 o el de los que miden 168? (Sol. 164 cm (\( CV_164=0.0483; CV_168=0.0486 \))

2. En una encuesta sobre el número de individuos que componen una familia (X) y el número de personas activas en ella (Y) se han obtenido los resultados indicados en la siguiente tabla:

\( \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline Y/X & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline 1 & 7 & 10 & 11 & 10 & 8 & 1 & 1& 0 \\ \hline 2 & 0 & 2 & 5 & 6 & 6 & 2 & 0 & 0 \\ \hline 3 & 0 & 0 & 1 & 6 & 4 & 3 & 0 & 1 \\ \hline 4 & 0 & 0 & 0 & 0 & 2 & 1 & 1 & 1 \\ \hline
\end{array} \)

a) Calcular el número medio de miembros de las familias encuestadas. (Sol. \( \bar{x} =4 \))
b) Cuantificar la dispersión que presenta la distribución del número de personas activas entorno a su medio. (Sol. \( σ_{y}=0.9304 \))
c) ¿Cuál es el número de miembros activos más frecuente en las familias formadas por 5 personas? (Sol. Mo=1)
d) En el grupo de familias donde las personas activas son 3, calcular el número medio de miembros que las forman. (Sol. \( \bar{x}_{j=3}=5 \))
e) Calcula la covarianza. (Sol.\( σ_{xy}=0.7908 \)).

3. Se han lanzado dos dados varias veces. Designando X el resultado del primer dado e Y el resultado del segundo dado, la información obtenida se dispone en la siguiente tabla:

\( \begin{array}{|c|cccccccccccc|} \hline X & 1 & 2 & 2 & 3 & 5 & 4 & 1 & 3 & 3 & 4 & 1 & 2 \\ \hline Y & 2 & 3 & 1 & 4 & 3 & 2 & 6 & 4 & 1 & 6 & 6 & 5 \\ \hline X & 5 & 4 & 3 & 4 & 4 & 5 & 3 & 1 & 6 & 5 & 4 & 6 \\ \hline Y & 1 & 2 & 5 & 1 & 1 & 2 & 6 & 6 & 2 & 1 & 2 & 5 \\ \hline \end{array} \)

a) Construir la tabla bidimensional. (Realizado en el Ejercicio 2)
b) Calcular las puntuaciones medias obtenidas con cada dado. (Sol. 3.375; 3.2083)
c) ¿Qué puntuaciones son más homogéneas, las obtenidas con el primer dado o con el segundo? (Sol. \( CV_{x}=0.45 \) ; \( CV_{y}=0.597 \) (primer dado))
d) Calcular la puntuación más frecuente obtenida con el segundo dado si con el primero se obtuvo 3. (Sol, Mo=4)
e) Calcula la puntuación máxima del 50% de las puntuaciones más bajas obtenidas con el primer dado si con el segundo se obtiene un 2 o un 5. (Sol. Me=4)

4. Se han medido dos caracteres simultáneamente sobre cada uno de los miembros de un colectivo, obteniéndose los datos de la tabla adjunta. Se pide:

\( \begin{array}{|c|c|c|c|} \hline
X/Y & 90-100 & 100-120 & 120-140 \\ \hline
10-15 &   6   & 3 & 1 \\ \hline
15-20 &   5 & 10 &   2 \\ \hline
20-25 &   4 &   1 & 7 \\ \hline
25-30 & 2 & 2 & 4 \\ \hline \end{array} \)

a) La media de Y si X toma valores superiores a 20. (Sol. \( \bar {y}_{3,4}= 116.5 \) )
b) La media de X si Y toma valores entre 100 y 120. (Sol. \( \bar{ x}_2=18.125 \) )
c) Las medias y las varianzas marginales. (Sol. \( \bar {x}=19.41 \) ; \( σ_{x}^2= 25.05 \) ; \( \bar {y}=110.53\) ; \( σ_{y}^2=200.25 \) )
d) En el conjunto de individuos que presentan valores de Y inferiores a 120, calcular el valor de X mínimo del 30% de las observaciones más altas. (Sol. 19.7)
e) En el conjunto de individuos que presentan valores de X entre 15 y 25, calcular el porcentaje de éstos que presentan valores inferiores a 117. (Sol. 63.28%)
f) Calcular la covarianza. (Sol. \( σ_{xy}=25.575 \) ).

5. Con los datos de la tabla adjunta, obtener:

\( \begin{array}{|c|c|c|c|} \hline X/Y & 1 & 2 & 4 \\ \hline 5 & 1 & 0 & 2 \\ \hline 10 & 2 & 1 & 0 \\ \hline 15 & 0 & 1 & 3 \\ \hline \end{array} \)

a) Media marginal de X y de Y. (Sol. \( \bar{x}=10.5; \bar{y}=2.7 \) );
b) Varianza marginal de X y de Y. (Sol. \( σ_{x}^2= 17.25; σ_{y}^2=1.81 \) );
c) Covarianza. (Sol: \( σ_{xy}=1.15 \) ). ¿Son X e Y independientes?. (Sol. No son independientes).

6. En una región se observó durante algunos años el precio de la leche y la cantidad de leche que consumían, obteniéndose los resultados que muestra la siguiente tabla:

\( \begin{array}{|ccccccccccc|} \hline X & 36 & 31 & 42 & 61 & 52 & 49 & 61 & 51 & 56 & 58 \\ \hline
Y & 100 & 140 & 120 & 140 & 200 & 200 & 110 & 160 & 120 & 200 \\ \hline \end{array} \)

donde X denota el precio de la leche e Y la cantidad de leche en miles de litros. Considerando X agrupada en intervalos de amplitud 5 y siendo 30 el límite inferior del primer intervalo. Construir la tabla bidimensional.
a) ¿Cuál es el precio medio de la leche? ¿Y la producción media? (Sol. \( \bar{x}=50.5; \bar{y} =149000 \) )
b) ¿Cuál es el precio más habitual de la leche cuando la producción es superior a 120000 l.? (Sol. Mo=52.5)
c) ¿Cuál es el porcentaje de años en que el precio de la leche fue superior a 47? (Sol. 66%)
d) En los años en que el precio de la leche oscila entre 35 y 55, ¿Cuál es la cantidad máxima de litros del 30% de las menores producciones? (Sol. 120.000).

e) ¿Es simétrica la distribución de los precios de la leche? ¿Y de las producciones?

f) Determinar la concentración cuando la producción es como mínimo 140.00 litros y cuando ésta es como máximo de 160.00 litros. ¿Mayor aplastamiento?

7. Se considera la siguiente distribución bidimensional.

\( \begin{array}{|cccccc|} \hline X/Y & 1 & 2 & 3 & 4 & 5 \\ \hline 100 & 2 & 4 & 6 & 10 & 8 \\ \hline 200 & 1 & 2 & 3 & 5 & 4 \\ \hline 300 & 3 & 6 & 9 & 15 & 12 \\ \hline 400 & 4 & 8 & 12 & 20 & 16 \\ \hline \end{array} \)

a) Calcular las medias y varianzas marginales. ¿ Qué distribución está más agrupada alrededor de su media? (Sol. \( \bar{ x}=290; \bar{y}=3.6; CV_{x}=0.39164; CV_{y}=0.333 \) ( La distribución de Y))
b) Calcular las medias de X condicionada a todos los valores de Y. (Sol. \( \bar{x}_1=290= \bar{x}_2=⋯ = \bar{x}_5 \) )
c) Calcular las medias de Y condicionadas a todos los valores de X. (Sol. \( \bar{y}_1=3.6= \bar{y}_2=⋯= \bar{y}_4 \) )
d) ¿Son X e Y independientes? (Sol. SI)
e) Calcula la covarianza. (Sol. \( σ_{xy}=0 \).)

8. Dada la distribución bidimensional:

\( \begin{array}{|c|ccc|} \hline X/Y & 1 & 2 & 3 \\ \hline -1 & 0 & 1 & 0 \\ \hline 0 & 1 & 0 & 1 \\ \hline 1 & 0 & 1 & 0 \\ \hline \end{array} \)

a) Calcular las medias marginales y la covarianza (Sol. \( \bar{x}=0; \bar{y}=2; σ_{xy}=0 \))
c) ¿Dependen las medias de Y condicionadas a los valores de X del valor de la variable al cuál se condicionan? (Sol. NO)
d) ¿Dependen las medias de X condicionadas a los valores de Y del valor de la variable al cuál se condicionan? (Sol. NO)
e) ¿Son X e Y independientes? (Sol. NO)

Soluciones

1. Se han estudiado los pesos (Kg) y las tallas (cm) correspondientes a un grupo de individuos, obteniendo la siguiente información:

Solución

\( \begin{array}{|c|c|c|c|c|c|c|} \hline X / Y & 160 & 162 & 164 & 166 & 168 & 170 & n_{i.} & x{´}_{i} = \displaystyle \frac {x_i-54}{3} & x^{´}_i.n_{i} \\ \hline 48 & 3 & 2 & 2 & 1 & 0 & 0 & 8 & -2 & -16 \\ 51 & 2 & 3 & 4 & 2 & 2 & 1 & 14 & -1 & -14 \\ 54 & 1 & 3 & 6 & 8 & 5 & 1 & 24 & 0 & 0 \\ 57 & 0 & 0 & 1 & 2 & 8 & 3 & 14 & 1 & 14 \\ 60 & 0 & 0 & 0 & 2 & 4 & 4 & 10 & 2 & 20 \\ \hline n_{.j} & 6 & 8 & 13 & 15 & 19 & 9 & 70 & & 4 \\ \hline y{´}_{j} = \displaystyle \frac {y_j- 164}{2} & -2 & -1 & 0 & 1 & 2 & 3 & & & \\ \hline y^{´}_j.n_{j} & -12 & -8 & 0 & 15 & 38 & 27 & 60 & & \\ \hline \end{array} \)

a) El peso y la talla media. (Sol. \( \bar{x}=54.171; \bar{ y}=165.71 \))

\( \bar{x}^{´} = \displaystyle \frac{\displaystyle \sum n_i x^{´}_i}{n} = \displaystyle \frac{4}{70} = 0.057 \Longrightarrow \bar{x} = 3 \bar{x}^{´} + 54 = 54.171 \) \( \bar{y}^{´} = \displaystyle \frac{ \displaystyle \sum n_j y^{´}_j}{n} = \displaystyle \frac{60}{70} = 0.857 \Longrightarrow \bar{y} = 2 \bar{y}^{´} + 164 = 165.714 \)

b) El porcentaje de alumnos que pesan menos de 55 Kg y miden más de 165. (Sol. 28.57)

\( \begin{array}{|c|c|c|c|c|} \hline X / Y & 166 & 168 & 170 & \\ \hline 48 & 1 & 0 & 0 & 1 \\ 51 & 2 & 2 & 1 & 5 \\ 54 & 8 & 5 & 1 & 14 \\ \hline & 11 & 7 & 2 & 20 \\ \hline \end{array} \)

Hay 20 alumnos que miden más de 165 y pesan menos de 55 kg

\( \displaystyle \frac {20}{70} = \displaystyle \frac {y}{100} \Longrightarrow y = \displaystyle \frac {20 \times 100}{70} = 28.57 \Longrightarrow \) 28.57 %
c) Dentro del conjunto de los que miden más de 165 ¿Cuál es el porcentaje de los que pesan más de 52 Kg? (Sol. 86.046%)

8+5+1+2+8+3+2+4+4 = 37

\( \displaystyle \frac {37 \times 100}{43} = 86.046 \Longrightarrow \) 86.046 %
d) ¿Cuál es la altura más frecuente entre los individuos cuyo peso oscila entre 51 Kg y 57 Kg?.(Sol. Mo=168)

\( \begin{array}{|c|c|} \hline y_{j} & n_{j/i}=2,3,4 \\ \hline 160 & 3 \\ 162 & 6 \\ 164 & 11 \\ 166 & 12 \\ \textbf {168} & \textbf{15} \\ 170 & 5 \\ \hline \end{array} \)

\( M_o = 168 \)
e) ¿Qué peso medio es más representativo, el de los individuos que miden 164 o el de los que miden 168? (Sol. 164 cm (\( CV_164=0.0483; CV_168=0.0486 \))

Tenemos que calcular el coeficiente de variación de pearson. A menor C.V. hay menos dispersión y por lo tanto más representativa es la media

\( \begin{array}{|c|c|c|c|c|c|c|c|} \hline x_{j} & n_{i/j =3} & x^{´}_i & x^{´}_i n_{i/j=3} & x^{´2}_i n_{i/j=3} & n_{i/j =5} & x^{´}_i n_{i/j=5} & x^{´2}_i n_{i/j=3} \\ \hline 48 & 2 & -2 & -4 & 8 & 0 & 0 & 0 \\ 51 & 4 &-1 & -4 & 4 & 2 & -2 & 2 \\ 54 & 6 & 0 & 0 & 0 & 5 & 0 & 0 \\ 57 & 1 & 1 & 1 & 1 & 8 & 8 & 8 \\ 60 & 0 & 2 & 0 & 0 & 4 & 8 & 16 \\ \hline & 13 & & -7 & 13 & 19 & 14 & 26 \\ \hline \end{array} \)

\( \sigma^{´2}_{x/y = 3 } = \displaystyle \frac{\sum x^{´2}_i n_{i/j = 3}}{n_{.3}} – \bar{x}^{´2}_{/y=3} = \displaystyle \frac{13}{3}- ( \displaystyle \frac {-7}{13})^{2} = 1-0.29 = 0.71 \Longrightarrow \sigma^{´}_{x/y = 3 } = 0.84 \)

\( \sigma_{x/y = 3 } = 3 \times 0.84 = 2.527 \hspace {1cm} ; \hspace {1cm} \bar{x}_{/y=3}= 3 \times \displaystyle \frac {-7}{13} + 54 = 52.38 \)

\( CV_{/y=3} = \displaystyle \frac {2.527}{52.38} = 0.0483 \)

\( \sigma^{´2}_{x/y = 5 } = \displaystyle \frac{\sum x^{´2}_i n_{i/j = 5}}{n_{.5}} – \bar{x}^{´2}_{/y=5} = \displaystyle \frac{26}{19}- ( \displaystyle \frac {14}{19})^{2} = 0.825 \Longrightarrow \sigma^{´}_{x/y = 5 } = 0.90 \)

\( \sigma_{x/y = 5 } = 3 \times 0.90 = 2.725 \hspace {1cm} ; \hspace {1cm} \bar{x}_{/y=5} = 3 \times \displaystyle \frac {14}{19} + 54 = 56.22 \)

\( CV_{/y=5} = \displaystyle \frac {2.725}{56.22} = 0.0486 \)

Es más representativo el peso de los que miden 164

2. En una encuesta sobre el número de individuos que componen una familia (X) y el número de personas activas en ella (Y) se han obtenido los resultados indicados en la siguiente tabla:

a) Calcular el número medio de miembros de las familias encuestadas. (Sol. \( \bar{x} =4 \))

b) Cuantificar la dispersión que presenta la distribución del número de personas activas entorno a su medio. (Sol. \( σ_{y}=0.9304 \))
c) ¿Cuál es el número de miembros activos más frecuente en las familias formadas por 5 personas? (Sol. Mo=1)
d) En el grupo de familias donde las personas activas son 3, calcular el número medio de miembros que las forman. (Sol. \( \bar{x}_{j=3}=5 \))
e) Calcula la covarianza. (Sol.\( σ_{xy}=0.7908 \)).

Solución

\( \begin{array}{|c|c|c|c|c|c|c|} \hline X / Y & 1 & 2 & 3 & 4 & n_{i.} & x{´}_{i} = x_i- 4 & x^{´}_i.n_{i.} & x^{´2}_i.n_{i.} & \displaystyle \sum x{´}_{i} y{´}_{j} n_{ij} \\ \hline 1 & 7 & 0 & 0 & 0 & 7 & -3 & -21 & 63 & 21 \\ 2 & 10 & 2 & 0 & 0 & 12 & -2 & -24 & 48 & 20 \\ 3 & 11 & 5 & 1 & 0 & 17 & -1 & -17 & 17 & 11 – 1 = 10 \\ 4 & 10 & 6 & 6 & 0 & 22 & 0 & 0 & 0 & 0 \\ 5 & 8 & 6 & 4 & 2 & 20 & 1 & 20 & 20 & -8+4+4 = 0 \\ 6 & 1 & 2 & 3 & 1 & 7 & 2 & 14 & 28 & -2+6+4=8 \\ 7 & 1 & 0 & 0 & 1 & 2 & 3 & 6 & 18 & -3+6 = 3 \\ 8 & 0 & 0 & 1 & 1 & 2 & 4 & 8 & 32 & 4 + 8 =12 \\ \hline n_{.j} & 48 & 21 & 15 & 5 & 89 & & -14 & 226 & 74 \\ \hline y{´}_{j} = y_j- 2 & -1 & 0 & 1 & 2 & & & & \\ \hline y^{´}_j.n_{j} & -48 & 0 & 10 & -23 & & & & \\ \hline y^{´2}_j.n_{j} & 48 & 0 & 15 & 20 & 83 & & & \\ \hline \end{array} \)

a) Calcular el número medio de miembros de las familias encuestadas. (Sol. \( \bar{x} =4 \))

\( \bar{x}^{´} = \displaystyle \frac{\displaystyle \sum n_i x^{´}_i}{n} = \displaystyle \frac{-14}{89} =-0.157 \Longrightarrow \bar{x} = 3 \bar{x}^{´} + 44 = 3.828 \)

El número medio de las familias encuestadas es 4

b) Cuantificar la dispersión que presenta la distribución del número de personas activas entorno a su medio. (Sol. \( σ_{y}=0.9304 \))

\( \sigma^{2}_{y^{´}} = \displaystyle \sum y^{´2}_j \displaystyle \frac{ n_{.j}}{n} – \bar{y}^{´2} \)

\( \bar{y}^{´} = \displaystyle \frac{\displaystyle \sum n_{.j} y^{´}_j}{n} = \displaystyle \frac{-23}{89} =-0.2584 \)

\( \sigma^{2}_{y^´} = \displaystyle \frac{83}{89} – (-0.2584)^2 = 0.8657 \Longrightarrow \sigma_{y^´} = 0.9304 \)

\( \sigma_{y} = 0.9304 \) (El cambio de origen no le afecta a la desviación típica

c) ¿Cuál es el número de miembros activos más frecuente en las familias formadas por 5 personas? (Sol. Mo=1)

\( \begin{array}{|c|c|} \hline y_{j} & n_{j/i=5} \\ \hline \textbf {1 } & \textbf {8 } \\ 2 & 6 \\ 3 & 4 \\ 4 & 2 \\ \hline \end{array} \)

\( M_o = 1 \)

d) En el grupo de familias donde las personas activas son 3, calcular el número medio de miembros que las forman. (Sol. \( \bar{x}_{j=3}=5 \))

\( \begin{array}{|c|c|c|} \hline x_{i} & n_{i/j}=3 & x_{i}n_{i/j=3} \\ \hline 1 & 0 & 0 \\ 2 & 0 & 0 \\ 3 & 1 & 3 \\ 4 & 6 & 24 \\ 5 & 4 & 20 \\ 6 & 3 & 18 \\ 7 & 0 & 0 \\ 8 & 1 & 8 \\ \hline & 15 & 73 \\ \hline \end{array} \)

\( \bar{x}_3 = \bar{x}/_{y=3} = \displaystyle \frac{\displaystyle \sum n_{i/j} x_i}{n_{.3}} = \displaystyle \frac{73}{15} = 4.866 \Longrightarrow \bar{x}/_{y=3} = 4.866 \simeq \hspace{.3cm} \) 5 miembros

e) Calcula la covarianza. (Sol.\( σ_{xy}=0.7908 \)).

\( Cov (X,Y) = \displaystyle \sum_{i} \displaystyle \sum_{j} (x_i – \bar{x}) (y_j – \bar{y}) \displaystyle \frac{n_{ij}}{n} = \displaystyle \sum_{i} \displaystyle \sum_{j} x_i y_j \displaystyle \frac{n_{ij}}{n}- \bar{x} \bar{y} = \displaystyle \frac{74}{89}-0.157 \times 0.2584 = 0.7908312 \)

La covarianza sólo cambia ante el cambio de escala

3. Se han lanzado dos dados varias veces. Designando X el resultado del primer dado e Y el resultado del segundo dado, la información obtenida se dispone en la siguiente tabla:

a) Construir la tabla bidimensional. (Realizado en el Ejemplo 2.2)
b) Calcular las puntuaciones medias obtenidas con cada dado. (Sol. 3.375; 3.2083)
c) ¿Qué puntuaciones son más homogéneas, las obtenidas con el primer dado o con el segundo? (Sol. \( CV_{x}=0.45 \) ; \( CV_{y}=0.597 \) (primer dado))
d) Calcular la puntuación más frecuente obtenida con el segundo dado si con el primero se obtuvo 3. (Sol, Mo=4)
e) Calcula la puntuación máxima del 50% de las puntuaciones más bajas obtenidas con el primer dado si con el segundo se obtiene un 2 o un 5. (Sol. Me=4)

Solución

a) Construir la tabla bidimensional. (Realizado en el Ejercicio 2)

\( \begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline X / Y & 1 & 2 & 3 & 4 & 5 & 6 & n_{i.} & x_{i}n_{i.} & x^{2}_i.n_{i.} \\ \hline 1 & 0 & 1 & 0 & 0 & 0 & 3 & 4 & 4 & 4 \\ 2 & 1 & 0 & 1 & 0 & 1 & 0 & 3 & 6 & 12 \\ 3 & 1 & 0 & 0 & 2 & 1 & 1 & 5 & 15 & 45 \\ 4 & 2 & 3 & 0 & 0 & 0 & 1 & 6 & 24 & 96 \\ 5 & 2 & 1 & 1 & 0 & 0 & 0 & 4 & 20 & 100 \\ 6 & 0 & 1 & 0 & 0 & 1 & 0 & 2 & 12 & 72 \\ \hline n_{.j} & 6 & 6 & 2 & 2 & 3 & 5 & 24 & 81 & 329 \\ \hline y_j.n_{.j} & 6 & 12 & 6 & 8 & 15 & 30 & 77 & & \\ \hline y^{2}_j.n_{.j} & 6 & 24 & 18 & 32 & 75 & 180 & 335 & \\ \hline \end{array} \)

b) Calcular las puntuaciones medias obtenidas con cada dado. (Sol. 3.375; 3.2083)

\( \bar{x} = \displaystyle \frac{\displaystyle \sum n_{i.} x_i}{n} = \displaystyle \frac{81}{24} = 3.375 \) \( \bar{y} = \displaystyle \frac{ \displaystyle \sum n_{.j} y_j}{n} = \displaystyle \frac{77}{24} =3.2083 \)

c) ¿Qué puntuaciones son más homogéneas, las obtenidas con el primer dado o con el segundo? (Sol. \( CV_{x}=0.45 \) ; \( CV_{y}=0.597 \) (primer dado))

Para comprobar la homogeneidad de un conjunto de datos hay que obtener el Coeficinte de Variación de Pearson

\( \sigma^{2}_{x} = \displaystyle \frac {\displaystyle \sum x_i^{2}n_{i.}}{n}-\bar{x}^{2} = \displaystyle \frac {329}{24}- (3.375)^{2} = 2.318 \Longrightarrow \sigma_{x} = \displaystyle \sqrt {2.318} = 1.522 \)

\( \sigma^{2}_{y} = \displaystyle \frac {\displaystyle \sum y_j^{2}n_{.j}}{n}-\bar{y}^{2} = \displaystyle \frac {335}{24}- (3.2083)^{2} = 3.667 \Longrightarrow \sigma_{y} = \displaystyle \sqrt {3.667} = 1.915 \)

\( CV_{x} = \displaystyle \frac {\sigma_{x}}{\bar{x}} = \displaystyle \frac {1.522}{3.375} = 0.45 \)

\( CV_{y} = \displaystyle \frac {\sigma_{y}}{\bar{y}} = \displaystyle \frac {1.915}{3.2083} = 0.597 \)

Son mas hogéneas las puntuaciones del primer dado ya que \( CV_{x} = 0.45 < CV_{y} = 0.597 \)

d) Calcular la puntuación más frecuente obtenida con el segundo dado si con el primero se obtuvo 3. (Sol, Mo=4)

\( \begin{array}{|c|c|c|c|c|c|c|} \hline y_{j} & 1 & 2 & 3 & \textbf { 4 } & 5 & 6 \\ \hline n_{j/i=3} & 1 & 0 & 0 & \textbf { 2} & 1 & 1 \\ \hline \end{array} \) \( M_o = 4 \)

e) Calcula la puntuación máxima del 50% de las puntuaciones más bajas obtenidas con el primer dado si con el segundo se obtiene un 2 o un 5. (Sol. Me=4)

Hay que calcular la Mediana de \( X/_{y=2 ó y=5} \)

\( \begin{array}{|c|c|c|} \hline x_{i} & n_{i/j=2,5} & N_{i/j=2,5} \\ \hline 1 & 1 & 1 \\ 2 & 1 & 2 \\ 3 & 1 & 3 \\ 4 & 3 & 6 \\ 5 & 1 & 7 \\ 6 & 2 & 9 \\ \hline & 9 & \\ \hline \end{array} \)

\( M_e: \displaystyle \frac {n_{i/j}}{2} = \displaystyle \frac {9}{2} = 4.5 \)

\( 3<4.5<6 \Longrightarrow M_e = 4 \)

4. Se han medido dos caracteres simultáneamente sobre cada uno de los miembros de un colectivo, obteniéndose los datos de la tabla adjunta. Se pide:

Solución

\( \begin{array}{|c|c|c|c|c|c|} \hline X / Y & 90-100 & 100-120 & 120-140 & n_{i.} & x{´}_{i} & x^{´}_i.n_{i} & x^{´2}_i.n_{i} & \displaystyle \sum x{´}_{i} y{´}_{j}n_{ij} \\ \hline 10-15 & 6 & 3 & 1 & 10 & -1 & -10 & 10 & 18+0-4 = 14 \\ 15-20 & 5 & 10 & 2 & 17 & 0 & 0 & 0 & 0 \\ 20-25 & 4 & 1 & 7 & 12 & 1 & 12 & 12 & -12+0+28 = 16 \\ 25-30 & 2 & 2 & 4 & 8 & 2 & 16 & 32 & -12+0+32=20 \\ \hline n_{.j} & 17 & 16 & 14 & 47 & & 18 & 54 & 50 \\ \hline y{´}_{j} & -3 & 0 & 4 & & & & \\ \hline y^{´}_j.n_{.j} & -51 & 0 & 56 & 5 & & & \\ \hline y^{´2}_{j} n_{.j} & 153 & 0 & 224 & 377 & & & \\ \hline \end{array} \)

\( x{´}_{i} = \displaystyle \frac {x_i-17.5}{5}\)

\( y{´}_{j} = \displaystyle \frac {y_j- 110}{5} \)

a) La media de Y si X toma valores superiores a 20. (Sol. \( \bar {y}_{3,4}= 116.5 \) )

\( \begin{array}{|c|c|c|c|c|} \hline Y & y_j & y{´}_{j} & n_{j/i=3,4} & y{´}_{j} n_{j/i=3,4} \\ \hline 90-100 & 95 & -3 & 6 & -18 \\ 100-120 & 110 & 0 & 3 & 0 \\ 120-140 & 130 & 4 & 11 & 44 \\ \hline & & & 20 & 26 \\ \hline \end{array} \)

\( \bar{y}^{´}_{3,4} = \displaystyle \frac{\displaystyle \sum y^{´}_jn_{j/3,4} }{n} = \displaystyle \frac{26}{20} = 1.3 \)

\( \bar{y}_{3,4} = 1.3 \times 5 +110 =116.5 \)

b) La media de X si Y toma valores entre 100 y 120. (Sol. \( \bar{ x}_2=18.125 \) )

\( \begin{array}{|c|c|c|c|c|} \hline X & x_i & x{´}_{i} & n_{i/j= 2} & x{´}_{i} n_{i/j=2} \\ \hline 10-15 & 12.5 & -1 & 3 & -3 \\ 15-20 & 17.5 & 0 & 10 & 0 \\ 20-25 & 22.5 & 1 & 1 & 1 \\ 25-30 & 27.5 & 2 & 2 & 4 \\ \hline & & & 16 & 2 \\ \hline \end{array} \)

\( \bar{x}^{´}_{2} = \displaystyle \frac{\displaystyle \sum x^{´}_in_{i/j=2} }{n_{i/j=2}} = \displaystyle \frac{2}{16} \Longrightarrow \bar{x}_{2} = \displaystyle \frac{2}{16} \times 5 +17.5 =18.125 \)

c) Las medias y las varianzas marginales. (Sol. \( \bar {x}=19.41 \) ; \( σ_{x}^2= 25.05 \) ; \( \bar {y}=110.53\) ; \( σ_{y}^2=200.25 \) )

\( \bar{x}^{´} = \displaystyle \frac{\displaystyle \sum x^{´}_in_{i.} }{n} = \displaystyle \frac{18}{47} = 0.383 \Longrightarrow \bar{x} = 0.383 \times 5 + 17.5 = 19.415 \)

\( \bar{y}^{´} = \displaystyle \frac{\displaystyle \sum y^{´}_jn_{.j} }{n} = \displaystyle \frac{5}{47} = 0.106 \Longrightarrow \bar{y} = 0.106 \times 5 + 17.5 = 110.53 \)

\( \sigma^{2}_{x^{´}} = \displaystyle \frac {\displaystyle \sum x_i^{´2}n_{i.}}{n}-\bar{x}^{´2} = \displaystyle \frac {54}{47}- (0.383)^{2} = 1.002 \Longrightarrow \sigma^{´}_{x} = 1.0009 \Longrightarrow \sigma^{2}_{x} = 5^{2} \times 1.0009^{2} = 25.05 \)

\( \sigma^{2}_{y^{´}} = \displaystyle \frac {\displaystyle \sum y_j^{´2}n_{.j}}{n}-\bar{y}^{´2} = \displaystyle \frac {377}{47}- (0.106)^{2} = 8.01 \Longrightarrow \sigma^{´}_{y} = 2.83 \Longrightarrow \sigma^{2}_{y} = 5^{2} \times 2.83^{2} = 200.25 \)

d) En el conjunto de individuos que presentan valores de Y inferiores a 120, calcular el valor de X mínimo del 30% de las observaciones más altas. (Sol. 19.7)

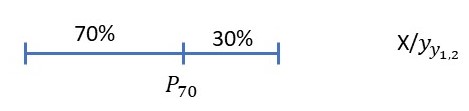
\( \begin{array}{|c|c|c|} \hline
X & n_{i/j=1,2} & N_{i/j=1,2} \\ \hline
10-15 & 9 & 9 \\
15-20 & 15 & 24 \\
20-25 & 5 & 29 \\
25-30 & 4 & 33 \\ \hline & 33 & \\ \hline \end{array} \)

\( P_{70} : \displaystyle \frac{70}{100} \times 33 = 2.31 \Longrightarrow 9 <23.1 <24 \Longrightarrow P_{70} \in (15,20) \)

\( \left. \begin{array}{ccc}
20-15 & \longrightarrow & 24-9 \\
P_{70} – 15 & \longrightarrow & 23.1-9 \\ \end{array}\right \} \Longrightarrow P_{70} = 15 + 4.7 = 19.7 \)

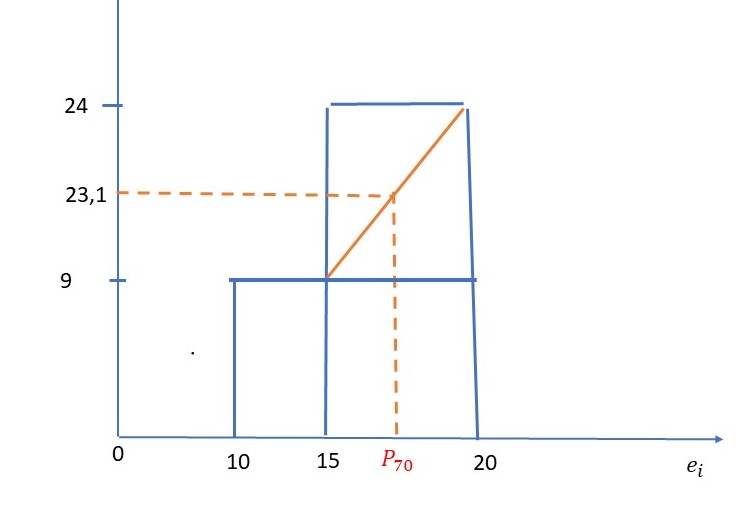
e) En el conjunto de individuos que presentan valores de X entre 15 y 25, calcular el porcentaje de éstos que presentan valores inferiores a 117. (Sol. 63.28%)

\( Y/x=x_2,x_3 \hspace{1cm} \) Calcular \( N_{j/i=2,3} \)

\( \begin{array}{|c|c|c|} \hline
Y & n_{j/i=2,3} & N_{j/i=2,3} \\ \hline
90-100 & 9 & 9 \\
100-120 & 11 & 20 \\
120-140 & 9 & 29 \\
\hline & 29 & \\ \hline \end{array} \hspace{1cm} \) \( 117 \in (100-120) \)

\( \left. \begin{array}{ccc}
120-100 & \longrightarrow & 20-9 \\
117 – 100 & \longrightarrow & N_{.j}-9 \\ \end{array}\right \} \Longrightarrow N_{.j} = 18.35 \hspace{1cm} ; \hspace{1cm} \displaystyle \frac{29}{18.85} = \displaystyle \frac{100}{x} \Longrightarrow x = \displaystyle \frac{18.35 \times 100}{29} = 63.28 \)

\( 63.28 \% \)

f) Calcular la covarianza. (Sol. \( σ_{xy}=25.575 \) )

\( Cov(x^{´},y^{´}) =\displaystyle \sum _{i}\displaystyle \sum _{j}x^{´}_i y^{´}_j \displaystyle \frac{n_{ij}}{n}-\bar{x}^{´}\bar{y}^{´} = \displaystyle \frac{50}{47}-\displaystyle \frac{18}{47} \displaystyle \frac{5}{47} = 1.023 \)

\( Cov(x,y) = a^{2}Cov(x^{´},y^{´}) = 25 \times 1.023 = 25.575 \)

5. Con los datos de la tabla adjunta, obtener:

\( \begin{array}{|c|c|c|c|} \hline X/Y & 1 & 2 & 4 \\ \hline 5 & 1 & 0 & 2 \\ \hline 10 & 2 & 1 & 0 \\ \hline 15 & 0 & 1 & 3 \\ \hline \end{array} \)

a) Media marginal de X y de Y. (Sol. \( \bar{x}=10.5; \bar{y}=2.7 \) )
b) Varianza marginal de X y de Y. (Sol. \( σ_{x}^2= 17.25; σ_{y}^2=1.81 \) )
c) Covarianza. (Sol: \( σ_{xy}=1.15 \) ). ¿Son X e Y independientes?. (Sol. No son independientes).

Solución

\( \begin{array}{|c|c|c|c|c|c|} \hline X / Y & 1 & 2 & 4 & n_{i.} & x{´}_{i} = \displaystyle \frac {x_i-10}{5} & x^{´}_i.n_{i.} & x^{´2}_i.n_{i.} & \displaystyle \sum _j x{´}_{i} y{´}_{j}n_{ij} \\ \hline 5 & 1 & 0 & 2 & 3 & -1 & -3 & 3 & 1+0-4 = -3 \\ 10 & 2 & 1 & 0 & 3 & 0 & 0 & 0 & 0 \\ 15 & 0 & 1 & 3 & 4 & 1 & 4 & 4 & 0+0+6 = 6 \\ \hline n_{.j} & 3 & 2 & 5 & 10 & & 1 & 7 & 3 \\ \hline y{´}_{j} = y_{j}-2 & -1 & 0 & 2 & & & & \\ \hline y^{´}_j.n_{.j} & -3 & 0 &10 & 7 & & & \\ \hline y^{´2}_{j} n_{.j} &3 & 0 & 20 & 23 & & & \\ \hline \end{array} \)

a) Media marginal de X y de Y. (Sol. \( \bar{x}=10.5; \bar{y}=2.7 \) )

\( \bar{x}^{´} = \displaystyle \frac{\displaystyle \sum x^{´}_in_{i.} }{n} = \displaystyle \frac{1}{10} \Longrightarrow \bar{x} = 5 \times \displaystyle \frac{1}{10} + 10 = 10.5 \hspace{1cm} \) \( \bar{y}^{´} = \displaystyle \frac{\displaystyle \sum y^{´}_jn_{.j} }{n} = \displaystyle \frac{7}{10} \Longrightarrow \bar{y} = \displaystyle \frac{7}{10} +2 = 2.7 \)

b) Varianza marginal de X y de Y. (Sol. \( σ_{x}^2= 17.25; σ_{y}^2=1.81 \) )

\( \sigma^{2}_{x^{´}} = \displaystyle \frac {\displaystyle \sum x_i^{´2}n_{i.}}{n}-\bar{x}^{´2} = \displaystyle \frac {7}{10}- (\displaystyle \frac{1}{10})^{2} = 0.69 \Longrightarrow \sigma_{x} = 5^{2} \times 0.69 = 17.25 \Longrightarrow \sigma^{2}_{x} = 17.25 \)

\( \sigma^{2}_{y^{´}} = \displaystyle \frac {\displaystyle \sum y_j^{´2}n_{.j}}{n}-\bar{y}^{´2} = \displaystyle \frac {23}{10}- (\displaystyle \frac{7}{10})^{2} = 1.81 \Longrightarrow \sigma^{2}_{y} = 1.81 \)

c) Covarianza. (Sol: \( σ_{xy}=1.15 \) ). ¿Son X e Y independientes?. (Sol. No son independientes).

\( Cov (x^{´},y^{´}) = \displaystyle \frac { \displaystyle \sum_{j} x^{´}_i y^{´}_j n_{ij}}{n} – \bar{x^{´}} \bar{y^{´}} = \displaystyle \frac{3}{10} – \displaystyle \frac{1}{10} \displaystyle \frac{7}{10} = 0.23 \Longrightarrow Cov (x,y) = 5 \times 0.23 = 1.15 \)

No son independientes ya que las filas no son proporcionales entre sí ni tampoco las columnas. Además \( \hspace{.2cm} X \hspace{.2cm} \) e \( \hspace{.2cm} Y \hspace{.2cm} \) independientes \( \hspace{.2cm} \Longrightarrow Cov(x,y) = 0 \)

6. En una región se observó durante algunos años el precio de la leche y la cantidad de leche que consumían, obteniéndose los resultados que muestra la siguiente tabla:

\( \begin{array}{|ccccccccccc|} \hline X & 36 & 31 & 42 & 61 & 52 & 49 & 61 & 51 & 56 & 58 \\ \hline
Y & 100 & 140 & 120 & 140 & 200 & 200 & 110 & 160 & 120 & 200 \\ \hline \end{array} \)

e) ¿Es simétrica la distribución de los precios de la leche? ¿Y de las producciones?

f) Determinar la concentración cuando la producción es como mínimo 140.00 litros y cuando ésta es como máximo de 160.00 litros. ¿Mayor aplastamiento?

Solución

\( \begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline X / Y & 100 & 110 & 120 & 140 & 160 & 200 & n_{i.} & x{´}_{i} & x^{´}_i.n_{i} & x^{´2}_i.n_{i} & x^{´3}_i.n_{i} & x^{´4}_i.n_{i} \\ \hline 30-35 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & -3 & -3 & 9 & -27 & 81 \\ 35-40 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & -2 & -2 & 4 & -8 & 16 \\ 40-45 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & -1 & -1 & 1 & -1 & 1 \\ 45-50 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 50-55 & 0 & 0 & 0 & 0 & 1 & 1 & 2 & 1 & 2 & 2 & 2 & 2 \\ 55-60 & 0 & 0 & 1 & 0 & 0 & 1 & 2 & 2 & 4 & 8 & 16 & 32 \\ 60-65 & 0 & 1 & 0 & 1 & 0 & 0 & 2 & 3 & 6 & 18 & 54 & 162 \\ \hline n_{.j} & 1 & 1 & 2 & 2 & 1 & 3 & 10 & & 6 & 42 & 36 & 294 \\ \hline y{´}_{j} & -2 & -1 & 0 & 2 & 4 & 8 & & & & & \\ \hline y^{´}_j.n_{.j} & -2 & -1 & 0 & 4 & 4 & 24 & 29 & & & & \\ \hline y^{´2}_{j} n_{.j} & 4 & 1 & 0 & 8 & 16 & 192 & 221 & & & & \\ \hline y^{´3}_{j} n_{.j} & -8 & -1 & 0 & 16 & 64 & 1536 & 1607 & & & & \\ \hline y^{´4}_{j} n_{.j} & 16 & 1 & 0 & 32 & 256 & 1288 & 12693 & & & & \\ \hline \end{array} \)

\( x{´}_{i} = \displaystyle \frac {x_i-47.5}{5}\)

\( y{´}_{j} = \displaystyle \frac {y_j- 120}{10} \)

a) ¿Cuál es el precio medio de la leche? ¿Y la producción media? (Sol. \( \bar{x}=50.5; \bar{y} =149000 \) )

\( \bar{x}^{´} = \displaystyle \frac{\displaystyle \sum x^{´}_in_{i.} }{n} = \displaystyle \frac{6}{10} \Longrightarrow \bar{x} = 5 \times \displaystyle \frac{6}{10} + 47.5 = 50.5 \hspace{.3cm} \) pts

\( \bar{y}^{´} = \displaystyle \frac{\displaystyle \sum y^{´}_jn_{.j} }{n} = \displaystyle \frac{29}{10} \Longrightarrow \bar{y} = \displaystyle \frac{29}{10} \times 10 +120 = 149 \hspace{.3cm}; \) 149.000 litros
b) ¿Cuál es el precio más habitual de la leche cuando la producción es superior a 120000 l.? (Sol. Mo=52.5)

\( \begin{array}{|c|c|c|} \hline
X & n_{i/j=4,2,6} & N_{i/j=4,5,6} \\ \hline
30-35 & 1 & 1 \\
35-40 & 0 & 1 \\
40-45 & 0 & 1 \\
45-50 & 1 & 2 \\ 50-55 & 2 & 4 \\ 55-60 & 1 & 5 \\ 60-65 & 1 & 6 \\ \hline & 6 & \\ \hline \end{array} \)

\( M_0 \hspace{.3cm} \) en \( \hspace{.3cm} X/y=y_4,y_5,y_6 \)

Intervalo modal es \( \hspace{.3cm} (50,55) \)

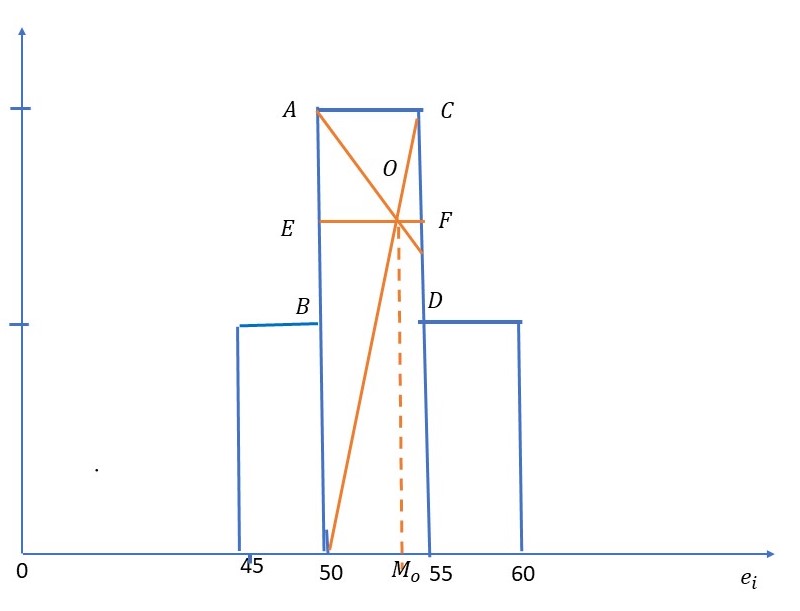
\( \displaystyle \frac {AB}{CD} + 1 = \displaystyle \frac {EO}{OF} + 1 \)

\( \displaystyle \frac {AB +CD} {CD} = \displaystyle \frac {EO + OF}{OF} = \displaystyle \frac {AC}{OF} \)

\( OF = \displaystyle \frac {DC.AC}{AB+CD} \Longrightarrow OF = \displaystyle \frac{(2-1)(55-50)}{(2-1)+ (2-1) } = \displaystyle \frac {5}{2} = 2.5 \Longrightarrow M_o = 50+ 2.5 = 52.5 \hspace{.3cm} \) pts

c) ¿Cuál es el porcentaje de años en que el precio de la leche fue superior a 47? (Sol. 66%)

\( \begin{array}{|c|c|c|} \hline
X & n_{i.} & N_{i.} \\ \hline
30-35 & 1 & 2 \\
35-40 & 1 & 2 \\
40-45 & 1 & 3 \\
45-50 & 1 & 4 \\ 50-55 & 2 & 6 \\ 55-60 & 2 & 8 \\ 60-65 & 2 & 10 \\ \hline & 10 & \\ \hline \end{array} \)

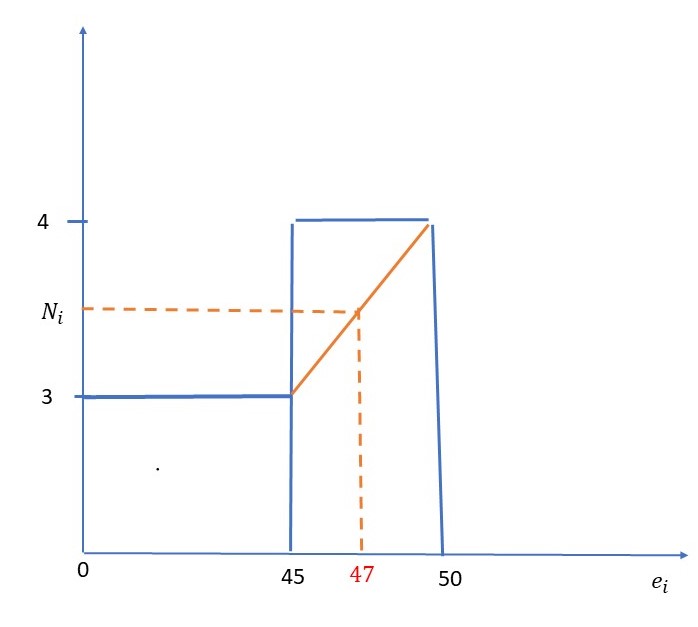
\( \left. \begin{array}{ccc}
50-45 & \longrightarrow & 4-3 \\
47 – 45 & \longrightarrow & N_i – 3 \\ \end{array}\right \} \Longrightarrow N_i = 3 + \displaystyle \frac {2}{5} = 3.4 \)

\( \displaystyle \frac {10}{3.4} = \displaystyle \frac {100}{x} \Longrightarrow x = 34 \)

El 34 % es el porcentaje en años en que el precio de la leche fue 47 pts o menos. Ya que hemos utilizado las frecuencias absolutas acumuladas que significan el número de individuos que tienen esa \( x_i \) o menos. Por lo tanto lo que tenemos que calcular en vex de > 47 es \( (1- \leq 47 ) \). Al tratarse de variables continuas es los mismo \( < \hspace{.3cm} \) o \( \hspace{.3cm} \leq \).

\( > 47 = (100 – 34) = 66 \% \)

El % de años en que el precio de la leche fue superior a 47 es el 66%.

d) En los años en que el precio de la leche oscila entre 35 y 55, ¿Cuál es la cantidad máxima de litros del 30% de las menores producciones? (Sol. 120.000).

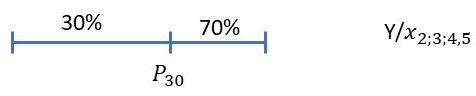
\( ¿ P_{30} ? \)

\( \begin{array}{|c|c|c|} \hline
Y & n_{j/i=2,3,4,5} & N_{j/i=2,3,4,5} \\ \hline
100 & 1 & 1 \\
110 & 0 & 1 \\
120 & 1 & 2 \\
150 & 0 & 2 \\ 160 & 1 & 3 \\ 200 & 2 & 5 \\ \hline & 5 & \\ \hline \end{array} \)

\( \displaystyle \frac {30}{100}n = \displaystyle \frac {30}{100}5 = 1.5 \)

\( 1<1.5<2 \Longrightarrow P_{30} = 120.000 \hspace{.3cm} \)

e) ¿Es simétrica la distribución de los precios de la leche? ¿Y de las producciones?

Calculamos el coeficiente de asimetría de Fisher de cada una de las distribuciones

\( \gamma = \displaystyle \frac {m_3}{\sigma^3} \)

\( m_{3X^´} = m_{3X} = a_3-3a_1a_2+2a_1^3 \)

\( a^´_1 = \displaystyle \frac{ \sum { n_{i.}x^´_i}}{n}= \displaystyle \frac{6}{10} =0.6 \)

\( a^´_2 = \displaystyle \frac{ \sum { n_{i.}x^{´2}_i}}{n}= \displaystyle \frac{42}{10} = 4.2 \)

\( a^´_3 = \displaystyle \frac{ \sum { n_{i.}x^{´3}_i}}{n}= \displaystyle \frac{36}{10} = 3.6 \)

\( m_{3X^´} = m_{3X} = a_3-3a_1a_2+2a_1^3 = 3.6 – 3 \times 0.6 \times 4.2 + 2 \times 0.6^2 = -3.5238 \)

\( \sigma ^{2}_{X^´} = \displaystyle \frac{ \sum x_i^{´2} n_{i.}}{n} – \bar{x}^{´2} = a_2 – a_1^2 = 4.2 – 0.6^2 = 3.84 \Longrightarrow \sigma_{X^´} = \displaystyle \sqrt{3.84} = 1.959 \)

\( \gamma_{1X} = \displaystyle \frac {m_{3X}}{\sigma^3_{X}} = \displaystyle \frac {m_{3X^{´}}}{\sigma^3_{X^´}} = \displaystyle \frac {-3.528}{(1.959)^3} = -0.4688 \)

\( \gamma_{1X} <0 \Longrightarrow \) Distribución asimétrica negativa por lo tanto Asimetría a la izquierda. La distribución del precio de la leche es asimétrica negativa.

\( \gamma_{1Y} = \displaystyle \frac {m_{3Y}}{\sigma^3_{Y}} = \displaystyle \frac {m_{3Y^{´}}}{\sigma^3_{Y^´}} \)

\( m_{3Y^´} = m_{3Y} = a_3-3a_1a_2+2a_1^3 = \displaystyle \frac {1607}{10}-3 \times \displaystyle \frac {29}{10} \times \displaystyle \frac {221}{10} +2 \left( \displaystyle \frac {29}{10} \right)^{3} = 17.208 \)

\( \sigma ^{2}_{Y^´} = a_2 – a_1^2 = \displaystyle \frac {221}{10}- \left( \displaystyle \frac {29}{10} \right)^{2} = 13.69 \Longrightarrow \sigma_{Y^´} = \displaystyle \sqrt{13.69} = 3.7 \)

\( \gamma_{1Y} = \displaystyle \frac {17.208}{(3.7)^{2}}= 0.3397 \)

\( \gamma_{1Y} >0 \Longrightarrow \) Distribución asimétrica positiva por lo tanto Asimetría a la derecha. La distribución de la cantidad de litros es asimétrica positiva.

f) Determinar la concentración cuando la producción es como mínimo 140.00 litros y cuando ésta es como máximo de 160.00 litros. ¿Mayor aplastamiento?

Concentración cuando la producción es como mínimo de 140.000 litros: puede ser 140.000, 160.000 0 200.000 litros \( \hspace{.3cm} X/y=y_4,y_5,y_6 \)

\( \begin{array}{|c|c|c|c|c|c|c|c|} \hline x^´_{i} & n_{i/j =4,5,6} & x^{´}_i n_{i/j} & x^{´2}_i n_{i/j} & x^{´3}_i n_{i/j} & x^{´4}_i n_{i/j} \\ \hline -3 & 1 & -3 & 9 & -27 &81 \\ -2 & 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 1 &2 & 2 & 2 & 2 & 2 \\ 2 & 1 & 2 & 4 & 8 & 16 \\ 3 & 1 & 3 & 9 & 27 & 81 \\ \hline & 6 & 4 & 24 & 10 & 180 \\ \hline \end{array} \)

Hay que calcular el coeficiente de apuntamiento o curtosis de Fisher

\( \gamma_{2} = \displaystyle \frac {m_{4}}{\sigma^4}-3 \)

\( m_{4} = a_4-4a_3a_1+6a_1^2 a_2 -3 a_{1}^4 = \displaystyle \frac {180}{6}-4 \times \displaystyle \frac {10}{6} \times \displaystyle \frac {4}{6} +6 \left( \displaystyle \frac {4}{6} \right)^{2} \times \displaystyle \frac{24}{6} – 3 \times \left( \displaystyle \frac {4}{6} \right)^{3} = 35.629629 \)

\( \sigma ^{2}_{x/y} = a_2 – a_1^2 = \displaystyle \frac {24}{6}- \left( \displaystyle \frac {4}{6} \right)^{2} = 3.5 \Longrightarrow \sigma_{x/y} = \displaystyle \sqrt{3.5} = 1.885 \Longrightarrow \sigma^{4}_{x/y} = 12.64 \)

\( \gamma_{2} = \displaystyle \frac {m_{4}}{\sigma^4}-3 = \displaystyle \frac {35.62}{12.64}-3 = -0.181639 \Longrightarrow \hspace{.3cm} \) La distribución es menos apuntada que la Normal, es decir más aplastada que la Normal, es Platicúrtica

Concentración cuando la producción es como máximo de 160.000 litros: puede ser 100.000, 110.00,…, 160.000 litros \( \hspace{.3cm} X/y=y_1,y_2,y_3,y_4,y_5 \)

\( \begin{array}{|c|c|c|c|c|c|c|c|} \hline x^´_{i} & n_{i/j =1,2,3,4,5} & x^{´}_i n_{i/j} & x^{´2}_i n_{i/j} & x^{´3}_i n_{i/j} & x^{´4}_i n_{i/j} \\ \hline -3 & 1 & -3 & 9 & -27 &81 \\ -2 & 1 & -2 & 4 & -8 & 16 \\ -1 & 1 & -1 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 2 & 1 & 2 & 4 & 8 & 6 \\ 3 & 2 & 6 & 18 & 54 & 162 \\ \hline & 7 & 3 & 37 & 27 & 277 \\ \hline \end{array} \)

\( m_{4} = a_4-4a_3a_1+6a_1^2 a_2 -3 a_{1}^4 = \displaystyle \frac {277}{7}-4 \times \displaystyle \frac {27}{7} \times \displaystyle \frac {3}{7} +6 \left( \displaystyle \frac {3}{7} \right)^{2} \times \displaystyle \frac{37}{7} – 3 \times \left( \displaystyle \frac {3}{7} \right)^{3} = 38.6753 \)

\( \sigma ^{2}_{x/y} = a_2 – a_1^2 = \displaystyle \frac {37}{7}- \left( \displaystyle \frac {3}{7} \right)^{2} = 5.1018 \Longrightarrow \sigma_{x/y} = \displaystyle \sqrt{5.1018} = 2.258 \Longrightarrow \sigma^{4}_{x/y} = 26.028 \)

\( \gamma_{2} = \displaystyle \frac {m_{4}}{\sigma^4}-3 = \displaystyle \frac {38.6753}{26.028}-3 = -1.068 \Longrightarrow \hspace{.3cm} \) La distribución es menos apuntada que la Normal, es decir más aplastada que la Normal, es Platicúrtica. Esta distribución es más aplastada que la anterior.

7. Se considera la siguiente distribución bidimensional.

Solución

\( \begin{array}{|c|c|c|c|c|c|} \hline X / Y & 1 & 2 & 3 & 4 & 5 & n_{i.} & x{´}_{i} & x^{´}_i.n_{i} & x^{´2}_i.n_{i} & \displaystyle \sum x{´}_{i} y{´}_{j}n_{ij} \\ \hline 100 & 2 & 4 & 6 & 10 & 8 & 30 & -1 & -30 & 30 & 4+4+10-10-16 = -18 \\ 200 & 1 & 2 & 3 & 5 & 4 & 15 & 0 & 0& 0 & 0 \\ 300 & 3 & 6 & 9 & 15 & 12 & 45 & 1 & 45 & 45 & -6-6+0+15+24 = 27 \\ 400 & 4 & 8 & 12 & 20 & 16 & 60 & 2 & 120 & 240 & -16-16+0+40+64=72 \\ \hline n_{.j} & 10 & 20 & 30 & 50 & 40 & 150 & & 135 & 315 & 81 \\ \hline y{´}_{j} & -2 & -1 & 0 & 1 & 2 & & & & & \\ \hline y^{´}_j.n_{.j} & -20 & -20 & 0 & 50 & 80 & 90 &&& \\ \hline y^{´2}_{j} n_{.j} & 40 & 20 & 0 & 50 & 160 & 270 & & & & \\ \hline \end{array} \)

\( x{´}_{i} = \displaystyle \frac {x_i-200}{100}\)

\( y{´}_{j} = y_j- 3 \)

\( \bar{x}^{´} = \displaystyle \frac{\displaystyle \sum x^{´}_in_{i.} }{n} = \displaystyle \frac{135}{150} \Longrightarrow \bar{x} = 100 \times \displaystyle \frac{135}{150} + 200 = 290 \hspace{1cm} \) \( \bar{y}^{´} = \displaystyle \frac{\displaystyle \sum y^{´}_jn_{.j} }{n} = \displaystyle \frac{90}{150} \Longrightarrow \bar{y} = \displaystyle \frac{90}{150} +3 = 3.6 \)

Para comprobar que distribución está más agrupada en torno a la media tenemos que calcular el Coeficiente de Variación de Pearson

\( \sigma^{2}_{x^{´}} = \displaystyle \frac {\displaystyle \sum x_i^{´2}n_{i.}}{n}-\bar{x}^{´2} = \displaystyle \frac {315}{150}- (0.9)^{2} = 1.29 \Longrightarrow \sigma_{x^´} = 1.135 \Longrightarrow \sigma_{x}= 100 \times 1.235 = 113.5 \)

\( \sigma^{2}_{y^{´}} = \displaystyle \frac {\displaystyle \sum y_j^{´2}n_{.j}}{n}-\bar{y}^{´2} = \displaystyle \frac {270}{150}- (0.6)^{2} = 1.44 \Longrightarrow \sigma^{2}_{y^´} = 1.2 \Longrightarrow \sigma^{2}_{y} = 1.2 \)

\( CV_{x} = \displaystyle \frac {\sigma_x}{\bar{x}}= \displaystyle \frac {113.5}{290} = 0.39164 \)

\( CV_{y} = \displaystyle \frac {\sigma_y}{\bar{y}}= \displaystyle \frac {1.2}{3.6} = 0.3 \)

Como \( \hspace{.3cm} CV_{x} < CV_{y} \Longrightarrow \hspace{.3cm} \) La distribución de frecuencias \( \hspace{.1cm} Y \hspace{.1cm} \) es más agrupada en torno a su media, es mas homogénea, la media de \( \hspace{.1cm} Y \hspace{.1cm} \) es más representativa.

b) Calcular las medias de X condicionada a todos los valores de Y. (Sol. \( \bar{x}_1=290= \bar{x}_2=⋯ = \bar{x}_5 \) )

\( \begin{array}{|c|c|c|c|c|c|c|} \hline x_i & x^{´}_i & n_{i/j=1} & x^{´}_i n_{i/j=1} & n_{i/j=2} & x^{´}_in_{i/j=2} & n_{i/j=3} & x{´}_{i} n_{i/j=3} & n_{i/j=4} & x^{´}_i.n_{i/j=4} & n_{i/j=5} & x{´}_{i} n_{i/j=5} \\ \hline 100 & -1 & 2 & -2 & 4 & -4 & 6 & -6 & 10 & -10 & 8 & -8 \\ 200 & 0 & 1 & 0 & 2 & 0 & 3 & 0 & 5 & 0 & 4 & 0 \\ 300 & 1 & 3 & 3 & 6 & 6 & 9 & 9 & 15 & 15 & 12 & 12 \\ 400 & 2 & 4 & 8 & 8 & 16 & 12 & 24 & 20 & 45 & 16 & 32 \\ \hline & & 10 & 9 & 20 & 18 & 30 & 27 & 50 & 45 & 40 & 36 \\ \hline \end{array} \)

\( X/y=1 : \bar {X}^{´}_{1} = \displaystyle \frac {9}{10} \Longrightarrow \bar {X}_{1} = \displaystyle \frac {9}{10} \times 100 + 200 =290 \) \( X/y=2 : \bar {X}^{´}_{2} = \displaystyle \frac {18}{20} \Longrightarrow \bar {X}_{2} = \displaystyle \frac {18}{20} \times 100 + 200 = 290 \) \( X/y=3 : \bar {X}^{´}_{3} = \displaystyle \frac {27}{30} \Longrightarrow \bar {X}_{3} = \displaystyle \frac {27}{30} \times 100 + 200 = 290 \) \( X/y=4 : \bar {X}^{´}_{4} = \displaystyle \frac {45}{50} \Longrightarrow \bar {X}_{4} = \displaystyle \frac {45}{50} \times 100 + 200 = 290 \) \( X/y=5 : \bar {X}^{´}_{5} = \displaystyle \frac {36}{40} \Longrightarrow \bar {X}_{5} = \displaystyle \frac {26}{40} \times 100 + 200 = 290 \)

Todas las medias condicionadas de \( X \) son iguales e iguales a la media marginal.

c) Calcular las medias de Y condicionadas a todos los valores de X. (Sol. \( \bar{y}_1=3.6= \bar{y}_2=⋯= \bar{y}_4 \) )

\( \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline y^{´}_j & n_{j/i=1} & y^{´}_j n_{j/i=1} & n_{j/i=2} & y^{´}_j n_{j/i=2} & n_{j/i=3} & y^{´}_j n_{j/i=3} & n_{j/i=4} & y^{´}_j n_{j/i=4} \\ \hline -2 & 2 & -4 & 1 & -2 & 3 & -6 & 4 & -8 \\ -1 & 4 & -4 & 2 & -2 & 6 & -6 & 8 & -8 \\ 0 & 6 & 0 & 3 & 0 & 9 & 0 & 12 & 0 \\ 1 & 10 & 10 & 4 & 5 & 15 & 15 & 20 & 20 \\ 2 & 8 & 16 & 5 & 8 & 12 & 24 & 16 & 32 \\ \hline & 30 & 18 & 15 & 9 & 45 & 27 & 60 & 36 \\ \hline \end{array} \) \( Y/x=1 : \bar {Y}^{´}_{1} = \displaystyle \frac {18}{30} \Longrightarrow \bar {Y}_{1} = \displaystyle \frac {18}{20} +3 = 3.6 \hspace{5cm} \) \( Y/x=2 : \bar {Y}^{´}_{2} = \displaystyle \frac {9}{15} \Longrightarrow \bar {Y}_{2} = \displaystyle \frac {9}{15} +3 = 3.6 \hspace{5cm} \) \( Y/x=3 : \bar {Y}^{´}_{3} = \displaystyle \frac {27}{45} \Longrightarrow \bar {Y}_{3} = \displaystyle \frac {27}{45} +3 = 3.6 \hspace{5cm} \) \( Y/x=4 : \bar {Y}^{´}_{4} = \displaystyle \frac {36}{60} \Longrightarrow \bar {Y}_{4} = \displaystyle \frac {36}{60} +3 = 3.6 \)

Todas las medias condicionadas de \( Y \) son iguales e iguales a la media marginal.

d) ¿Son X e Y independientes? (Sol. SI)

\( X \) es independiente de \( Y \) \( \Leftrightarrow f_{i/j} = f_{i.} \)

\( X \) es independiente de \( Y \) si las distribuciones \( X/y_{j} \) son idénticas a las distrubuciones marginales de \( X \): Las columnas de la tabla de doble entrada som proporcionales entre sí y proporcionales a la columna marginal.

La independencia es recíproca. Si \( X \) es independiente de \( Y \) ; \( Y \) es independiente de \( X \)

La indendencia se traduce en la tabla por una relación simétrica: \( n_{ij} = \displaystyle \frac{n_{i.}n_{.j}}{n_{..}} \) ; \( f_{ij} =f_{i.}f_{.j} \)

Observando la tabla de doble entrada, comprobamos que las filas son proporcionales entre sí, así como las columnas, por lo tanto \( X \) e \( Y \) son independientes.

\( X \) e \( Y \) son independientes \( \Longrightarrow Cov(x,y) = 0 \)

e) Calcula la covarianza. (Sol. \( σ_{xy}=0 \).)

\( \begin{array}{cc} Cov (x^{´},y^{´}) &= \displaystyle \sum_{i} \displaystyle \sum_{j} (x^{´}_i – \bar{x}^´) (y^{´}_j – \bar{y}^´) \displaystyle \frac {n_{ij}}{n} = \displaystyle \sum_{i} \displaystyle \sum_{j} x^{´}_i y^{´}_j \displaystyle \frac {n_{ij}}{n} – \bar{x^{´}} \bar{y^{´}} = \\ & = \displaystyle \frac{81}{150} – 0.9 \times 0.6 = 0.54 – 0.54 = 0 \Longrightarrow \\ & \Longrightarrow Cov (x,y) = 100 Cov (x^{´},y^{´}) = 0 \end{array} \)

8. Dada la distribución bidimensional:

\( \begin{array}{|c|ccc|} \hline X/Y & 1 & 2 & 3 \\ \hline -1 & 0 & 1 & 0 \\ \hline 0 & 1 & 0 & 1 \\ \hline 1 & 0 & 1 & 0 \\ \hline \end{array} \)

a) Calcular las medias marginales y la covarianza (Sol. \( \bar{x}=0; \bar{y}=2; σ_{xy}=0 \))

b) ¿Dependen las medias de Y condicionadas a los valores de X del valor de la variable al cuál se condicionan? (Sol. NO)
c) ¿Dependen las medias de X condicionadas a los valores de Y del valor de la variable al cuál se condicionan? (Sol. NO)
d) ¿Son X e Y independientes? (Sol. NO)

Solución

\( \begin{array}{|c|c|c|} \hline X / Y & 1 & 2 & 3 & n_{i.} & x_i.n_{i} & x^{2}_i.n_{i} & \displaystyle \sum_j x_{i} y_{j}n_{ij} \\ \hline -1 & 0 & 1 & 0 & 1 & -1 & 1 & 0 – 2 + 0 = -2 \\ 0 & 1 & 0 & 1 & 2 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 1 & 1 & 0 +2 +0 = 2 \\ \hline n_{.j} & 1 & 2 & 1 & 4 & 0 & 0 & 0 \\ \hline y_j.n_{.j} & 1 & 4 & 3 & 8 & & & \\ \hline y^{2}_{j} n_{.j} & 1 & 8 & 9 & 18 & & & \\ \hline \end{array} \)

a) Calcular las medias marginales y la covarianza (Sol. \( \bar{x}=0; \bar{y}=2; σ_{xy}=0 \))

\( \bar{x} = \displaystyle \frac{\displaystyle \sum x_in_{i.} }{n} = \displaystyle \frac{0}{4} = 0 \hspace{1cm}; \hspace{1cm} \) \( \bar{y} = \displaystyle \frac{\displaystyle \sum y_jn_{.j} }{n} = \displaystyle \frac{8}{4} = 2 \)

\( Cov (x,y) = \displaystyle \sum_{i} \displaystyle \sum_{j} (x_i – \bar{x}) (y_j – \bar{y}) \displaystyle \frac {n_{ij}}{n} = \displaystyle \sum_{i} \displaystyle \sum_{j} x_i y_j \displaystyle \frac {n_{ij}}{n} – \bar{x} \bar{y} = \displaystyle \frac{0}{4} – 0 \times 2 = 0 \)
b) ¿Dependen las medias de Y condicionadas a los valores de X del valor de la variable al cuál se condicionan? (Sol. NO)

\( \begin{array}{|c|c|c|c|c|c|c|} \hline y_j & n_{j/i=1} & y_{j} n_{j/i=1} & n_{j/i=2} & y_{j} n_{j/i=2} & n_{j/i=3} & y_{j} n_{j/i=3} \\ \hline 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ 2 & 1 & 2 & 0 & 0 & 1 & 2 \\ 3 & 0 & 0 & 1 & 3 & 0 & 0 \\ \hline &1 & 2 & 2 & 4 & 1 & 2 \\ \hline \end{array} \)

\( \bar{y}_{x=x_1} = \displaystyle \frac{2}{1} = 2 \hspace{.4cm}; \hspace{.4cm} \) \( \bar{y}_{x=x_2} = \displaystyle \frac{4}{2} = 2 \hspace{.4cm}; \hspace{.4cm} \) \( \bar{y}_{x=x_3} = \displaystyle \frac{2}{1} = 2 \)

Las medias de las distribuciones de Y condicionadas a los valores de X son independientes de los valores a los que se condicionan.
d) ¿Dependen las medias de X condicionadas a los valores de Y del valor de la variable al cuál se condicionan? (Sol. NO)

\( \begin{array}{|c|c|c|c|c|c|c|} \hline x_i & n_{i/j=1} & x_{i} n_{i/j=1} & n_{i/j=2} & x_{i} n_{i/j=2} & n_{i/j=3} & x_{i} n_{i/j=3} \\ \hline -1 & 0 & 0 & 1 & -1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ \hline &1 & 0 & 2 & 0 & 1 & 0 \\ \hline \end{array} \)

\( \bar{x}_{y=y_1} = \displaystyle \frac{0}{1} = 0 \hspace{.4cm}; \hspace{.4cm} \) \( \bar{x}_{y=y_2} = \displaystyle \frac{0}{2} = 0 \hspace{.4cm}; \hspace{.4cm} \) \( \bar{x}_{y=y_3} = \displaystyle \frac{0}{1} = 0 \)

Las medias de las distribuciones de X condicionadas a los valores de Y son independientes de los valores a los que se condicionan.
e) ¿Son X e Y independientes? (Sol. NO)

Las columnas no son proporcionales ni tampoco las filas por lo tanto X e Y no son independientes.

Autora: Ana María Lara Porras. Universidad de Granada

Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.

Bioestadística: Ejercicios Resueltos: Tema 2

EJERCICIOS RESUELTOS: ESTADÍSTICA BIDIMENSIONAL

Soluciones

Solución

Solución

Solución

Solución

Solución

Solución

Solución

8. Dada la distribución bidimensional:

Solución