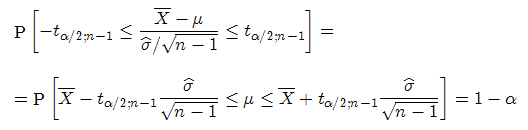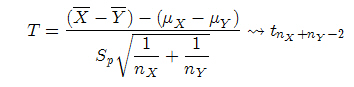INTERVALOS DE CONFIANZA
Objetivos
-
Obtener un intervalo de confianza para la media de una población normal.
-
Obtener un intervalo de confianza para la diferencia de medias de dos poblaciones normales independientes.
- Obtener un intervalo de confianza para la diferencia de medias de dos poblaciones normales relacionadas.
Introducción
El objetivo de la estimación por intervalos de confianza es obtener un intervalo, en el cual se encuentra el verdadero valor del parámetro con una determinada probabilidad. Dicha probabilidad se denomina nivel de confianza (1−α), donde α es el nivel de significación.
En término generales, la construcción de un intervalo de confianza para un parámetro desconocido θ consiste en encontrar dos funciones de los valores muestrales
t ales que
donde:
- 1- α recibe el nombre de coeficiente de confianza o nivel de confianza. Es la probabilidad de que un intervalo de confianza contenga el verdadero valor del parámetro
- α es un número pequeño comprendido entre 0 y 1, 0 < α <1 (usualmente próximo a 0). Es el riesgo de que el intervalo no contenga el valor del parámetro a estimar θ, por lo que α recibe el nombre de riesgo del error del intervalo, nivel del error del intervalo o nivel de significación del intervalo.
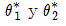reciben el nombre de límite inferior y superior de confianza, respectivamente
Este intervalo recibe el nombre Intervalo de confianza con coeficiente de confianza 1- α. Se desea que el coeficiente de confianza sea próximo a la unidad y que la amplitud del intervalo sea lo más pequeña posible.
SPSS proporciona intervalos de confianza para:
- Media poblacional con varianza desconocida
- Diferencia de medias en poblaciones independientes con varianzas desconocidas
- Diferencia de medias en poblaciones relacionadas.
Intervalo de confianza para la media de una población normal
SPSS construye intervalos de confianza para la media en el caso de varianza desconocida.
Intervalo de confianza para la media de una distribución N(μ, σ) con varianza desconocida
Supongamos una muestra aleatoria, X1, X2, …, X{n}, de una distribución Normal con media μ, y varianza σ², ambas desconocidas y vamos a hallar un intervalo de confianza para la media poblacional μ. Para ello, consideremos la variable aleatoria
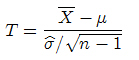que tiene una distribución t-Student con n-1 grados de libertad.
Tenemos que determinar el valor del cuantil t{α/2; n-1} tal que
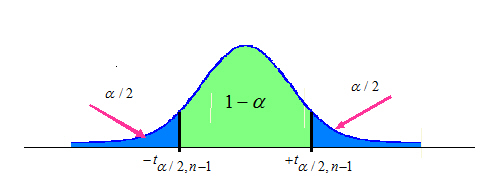También se puede expresar en función de la cuasidesviación típica muestral S.
Dado que se verifica la siguiente realción:
Tenemos la siguiente expresión del intervalo de confianza para μ
Por lo tanto, la probabilidad de que el intervalo aleatorio
o
contenga el verdadero valor de la media μ es 1-α.
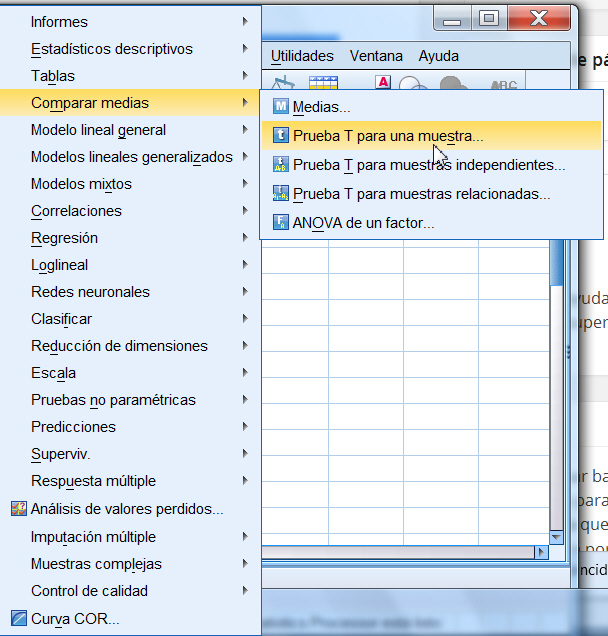
Para realizar un intervalo de confianza para la media de una población normal mediante SPSS se selecciona, en el menú principal, Analizar/Estadísticos descriptivos/Explorar…
Se muestra el siguiente Cuadro de diálogo
donde la variable a analizar, en este caso VAR1, se pasa a la ventana Dependientes:
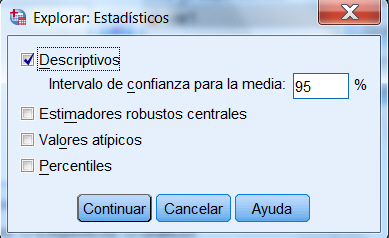
Por defecto SPSS calcula el intervalo de confianza a un nivel del 95%, para modificar este nivel se pulsa Estadísticos…
Para obtener el intervalo se pulsa Continuar y seguidamente Aceptar.
Alternativamente este intervalo de confianza también puede obtenerse seleccionando en el menú principal Analizar/Comparar medias/Prueba T para una muestra…
Se muestra el siguiente Cuadro de diálogo
donde se pasa la variable a la ventana Contrastar variables: y en el campo Valor de prueba se deja el valor 0 que viene por defecto (en la Práctica 6 sobre contrastes de hipótesis se aclarará este valor)
El nivel de confianza se puede modificar pulsando el botón Opciones…
Para obtener el intervalo se pulsa Continuar y seguidamente Aceptar.
Supuesto práctico 1
En una muestra de 9 preparados de jugo de tomate se ha obtenido los siguientes datos del contenido de vitamina C en mg/100 cc.
21,60; 19,72; 18,92; 23,01; 17,98; 22,06; 25,01; 21,98; 20,80
Supuesto que el contenido de vitamina C del jugo de tomate se distribuye normalmente. Se pide:
a) Estimar el contenido medio, en vitamina C, del jugo de tomate
b) Calcular un intervalo de confianza al 95% para dicha cantidad.
Respuesta:
a) Estimar el contenido medio, en vitamina C, del jugo de tomate
El estimador pedido es la media muestral
b) Calcular un intervalo de confianza al 95% para dicha cantidad.
Seleccionar en el menú principal Analizar/Comparar medias/Prueba T para una muestra…
En el campo Contrastar variables: se introduce la variable Conte_VitaminaC y en el campo Valor de prueba se deja el valor 0 que viene por defecto. Se pulsa Aceptar y se obtienen las siguientes salidas
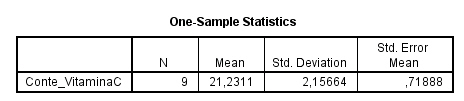
Por lo tanto, hay un 95% de confianza de que el intervalo [19.5734, 22.8888] contenga al contenido medio, en vitamina C, del jugo de tomate.
Intervalo de Confianza para la diferencia de medias en muestras independientes
Dos muestras se dicen que son independientes cuando las observaciones de una de ellas no condicionan a las observaciones de la otra.
Supongamos que X e Y son dos variables aleatorias independientes y tales que X→N(μX, σX) e Y→N(μY, σY)
Sea (X1, X2, …, Xnx) una m.a.s. de tamaño nx extraída de la población N(N(μX, σX) y denotamos por 
, a la media muestral y a la varianza muestral, respectivamente.
Sea (Y1, Y2, …, Yny) una m.a.s. de tamaño ny extraída de la población N(μY, σY) y denotamos por 
, a la media muestral y a la varianza muestral, respectivamente.
Supongamos que interesa comparar las dos medias poblaciones, podemos construir un intervalo de confianza para μX − μY para el caso de varianzas poblacionales desconocidas. Entonces la variable aleatoria
donde 
Por lo tanto, el intervalo de confianza para la diferencia de medias se determina de la siguiente forma
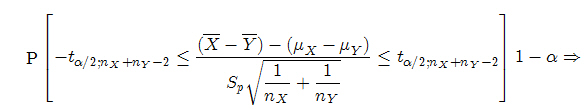
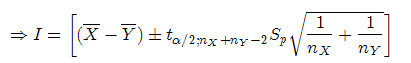SPSS construye intervalos de confianza para la diferencia de medias en el caso de varianzas poblacionales desconocidas.
Para la realización de dichos intervalos los datos se deben introducir de la siguiente forma: Se crean dos variables, una de ellas contiene todas las observaciones y la otra variable es una variable indicadora del grupo al que pertenece cada uno de los valores observados.
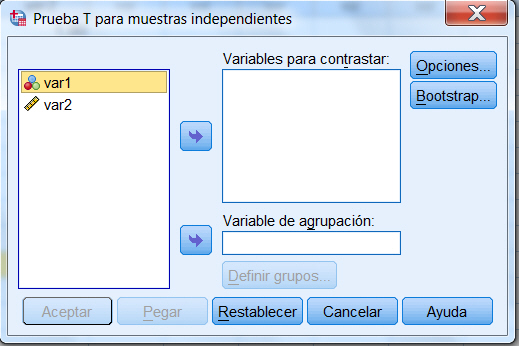
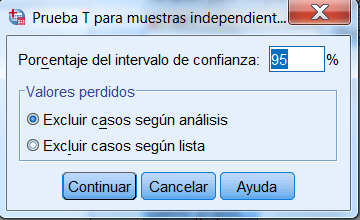
Se selecciona, en el menú principal, Analizar/Comparar medias/Prueba T para muestras independientes…
Se muestra el siguiente Cuadro de diálogo
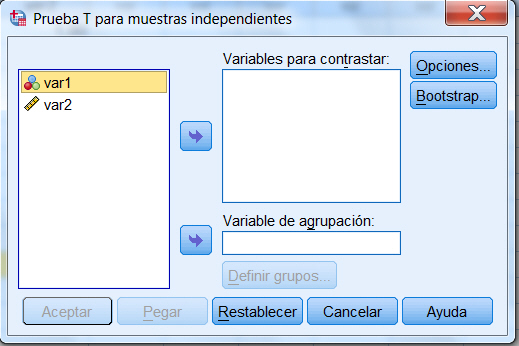Se introduce en el campo Contrastar variables: la variable que contiene los valores observados y en el campo Variable de Agrupación: la variable que indica la muestra a la que pertenece cada uno de los valores
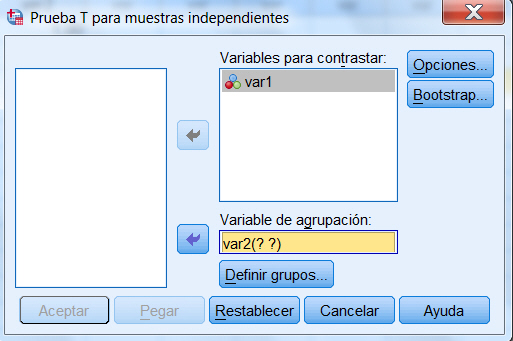A continuación se definen los dos grupos que determinan cada una de las muestras, para ello se pulsa el botón Definir grupos…
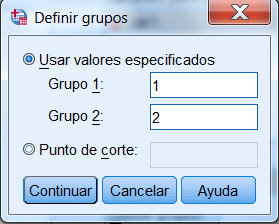Se introducen los valores asignados a cada muestra y se pulsa Continuar. El nivel de confianza, se puede modificar en Opciones..
Se pulsa Continuar y Aceptar
Supuesto práctico 2
Dos laboratorios A y B realizan determinaciones de nicotina en 4 unidades de tabaco, con los resultados siguientes:
Lab. A: 16, 14, 13, 17 Lab. B: 18, 21, 18, 19
Suponiendo que las dos poblaciones examinadas son normales e independientes con igual varianza, estimar la diferencia del contenido medio en nicotina del tabaco a un nivel de confianza del 95%.
Respuesta:
Se introducen los datos
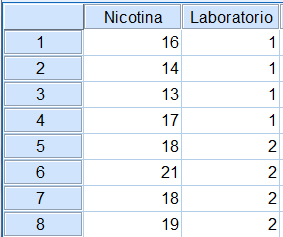Se selecciona, en el menú principal, Analizar/Comparar medias/Prueba T para muestras independientes… 
Se pulsa Definir grupos….
Se introducen los valores asignados a cada muestra y se pulsa Continuar y Aceptar. Se obtienen las siguientes salidas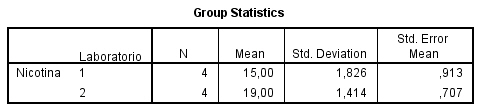 
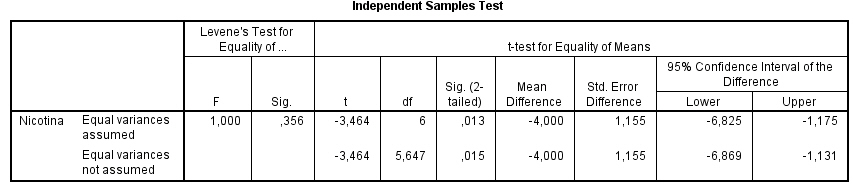En este caso la prueba de Levene nos muestra un p-valor igual a 0.356, al ser mayor que el nivel de significación 0.05, indica que no se debe rechazar la igualdad de varianzas con un nivel de confianza del 95%. Por tanto, el intervalo de confianza resultante es aquel en el que “Se han asumido varianzas iguales” (-6.825, -1.175). De este resultado se deduce que el contenido medio de nicotina difiere de un laboratorio a otro, (el intervalo no contiene al 0), siendo dicho contenido mayor en el laboratorio B que en laboratorio A.
Intervalo de Confianza para la diferencia de medias en muestras relacionadas
En las muestras apareadas, cada observación de una muestra está emparejado con una observación de la otra muestra, por lo tanto consideramos parejas de valores (x,y).
Supongamos que X e Y son dos variables aleatorias tales que X→N(μX, σX) e Y→N(μY, σY) y consideremos la diferencia de poblaciones D = X−Y. Entonces, D→N(μD, σD)
Se selecciona una muestra aleatoria de diferencias, Di = Xi−Yi ; i = 1, 2, ⋯, n
El valor medio de D es la diferencia de los valores medios de X e Y:
La varianza de D es:
Por lo tanto el problema original de realizar una inferencia sobre dos muestras se reduce al problema de realizar la inferencia sobre una muestra que consiste en construir un intervalo de confianza para la media de la población de diferencias. Para la realización de este intervalo de confianza recurrimos a los métodos utilizados anteriormente. En particular, construyamos el intervalo de confianza para μX−μY=μD. Para ello, consideremos la variable aleatoria
que tiene una distribución t-Student con n−1 grados de libertad.
Tenemos que determinar el valor del cuantil tα/2;n−1 tal que
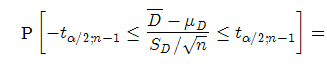
donde 
son la media muestral y la cuasidesviación típica muestral de la muestra de diferencias, respectivamente.
Para realizar un intervalo de confianza para la diferencia de medias en muestras relacionadas mediante SPSS.
En este caso las observaciones se introducen de forma que cada muestra esté en una columna del Editor de Datos de SPSS
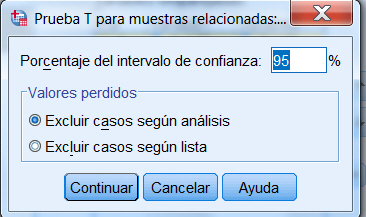
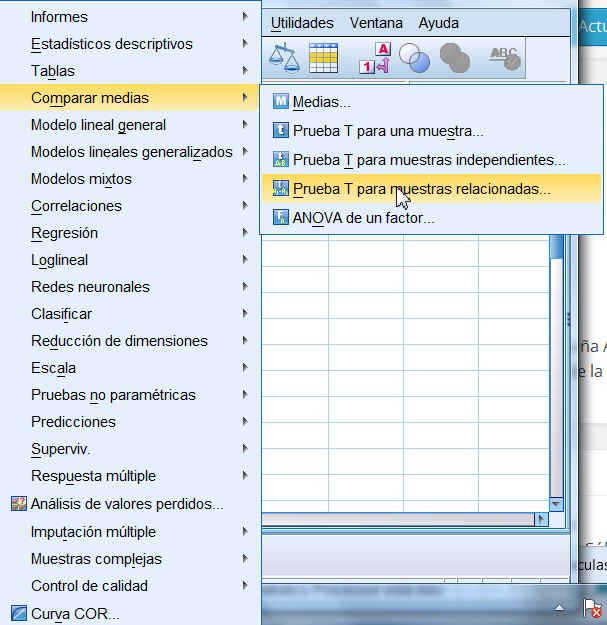
Se selecciona, en el menú principal, Analizar/Comparar medias/Prueba T para muestras relacionadas…
Se muestra el siguiente Cuadro de diálogo
Se seleccionan simultáneamente los pares de variables que se desean comparar y se pasan a Variables relacionadas:
En Opciones… se puede cambiar el nivel de confianza
Se pulsa Continuar y Aceptar.
Supuesto práctico 3
Se realiza un estudio, en el que participan 10 individuos, para investigar el efecto del ejercicio físico en el nivel de colesterol en plasma. Antes del ejercicio se tomaron muestras de sangre para determinar el nivel de colesterol de cada individuo. Después, los participantes fueron sometidos a un programa de ejercicios. Al final de los ejercicios se tomaron nuevamente muestras de sangre y se obtuvo una segunda lectura del nivel de colesterol. Los resultados se muestran a continuación:
Construir un intervalo de confianza de μD para un nivel de confianza del 95%
Respuesta:
Se introducen los datos
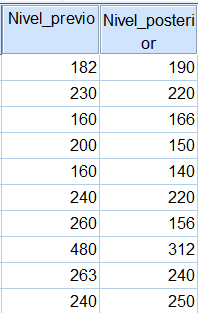Se selecciona, en el menú principal, Analizar/Comparar medias/Prueba T para muestras relacionadas… Y en el cuadro de diálogo resultante se seleccionan simultáneamente los pares de variables que se desean comparar y se pasan a Variables relacionadas:
Se pulsa Aceptar y se muestran las siguientes salidas
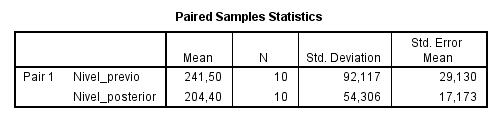
Por lo tanto, podemos tener un 95% de confianza en que la diferencia media de niveles de colesterol en plasma está entre -3.789 y 77.989. Es decir, podemos tener un 95% de confianza de que el nivel medio de colesterol se reducirá como mínimo en 0.475 unidades.
Ejercicios
Ejercicios Guiados
| A continuación se va a proceder a iniciar una aplicación Java, comprueba que tengas instalada la Máquina Virtual Java para poder ejecutar aplicaciones en Java.Si no tienes instalada la Máquina Virtual Java (Java Runtime Environment – JRE) pincha en uno de los enlaces para descargarla: |
|
| Instalación directa de la JRE 7 para WindowsPágina oficial de Sun Microsystems, descarga de la JRE para cualquier plataforma |
| Si ya tienes instalada la Máquina Virtual Java pincha en el siguiente enlace para proceder a la ejecución de los ejercicios guiados | Ejercicio 1  |
IMPORTANTE: Si al descargar el archivo *.JAR del ejercicio tu gestor de descargas intenta guardarlo como *.ZIP debes cambiar la extensión a .JAR para poder ejecutarlo.
Enunciado del Ejercicio 1
Se desea comprobar el efecto de 2 fertilizantes (A y B) sobre la producción de unos árboles frutales, para ello se toman dos grupos de 8 y 10 árboles seleccionados aleatoriamente y se le añade al agua de riego de cada uno de los grupos de árboles el fertilizante A y B, respectivamente. La producción en ese año fue la siguiente (en Kg):
Se pide:
- Obtener un intervalo de confianza al 99% para la producción media de los árboles tratados con el Fertilizante A y para la producción media de los árboles tratados con el Fertilizante B
- Obtener un intervalo de confianza al 98% para la diferencia entre la producción media de los árboles tratados con el Fertilizante A y con el Fertilizante B
- La producción de los árboles tratados con el Fertilizante A en el año anterior viene reflejada en la siguiente tabla. Obtener un intervalo de confianza al 99% para la diferencia de medias, en la producción antes y después de tratar los árboles con dicho fertilizante.
Ejercicios Propuestos
Ejercicio Propuesto 1
Se desea estudiar si la longitud del pico en una especie de loro es distinta entre los machos y las hembras. Para ello se selecciona una muestra de 14 machos y 12 hembras, cuyos resultados, expresados en milímetros, se muestran en la siguiente tabla:
Se pide:
- Obtener un intervalo de confianza a un nivel del 99%
- para la longitud media del pico en los machos
- para la longitud media del pico en las hembras
- Obtener un intervalo de confianza a un nivel del 99% para la diferencia entre la longitud media del pico de los machos y de las hembras.
Ejercicio Propuesto 2
Para comprobar si un determinado pienso puede mejorar la producción de lana de las ovejas, se selecciona una muestra aleatoria simple de 10 ovejas para ser alimentadas con dicho pienso. En la tabla siguiente se muestra el peso (en Kgr) de la lana producida antes y después del experimento
Obtener un intervalo de confianza al 98% para la diferencia de los pesos medios de la lana producida antes y después del experimento.
Ejercicio Propuesto 1(Resuelto)
Se desea estudiar si la longitud del pico en una especie de loro es distinta entre los machos y las hembras. Para ello se selecciona una muestra de 14 machos y 12 hembras, cuyos resultados, expresados en milímetros, se muestran en la siguiente tabla:
Se pide:
- Obtener un intervalo de confianza a un nivel del 99%
- para la longitud media del pico en los machos
- para la longitud media del pico en las hembras
- Obtener un intervalo de confianza a un nivel del 99% para la diferencia entre la longitud media del pico de los machos y de las hembras.
Solución:
1. Obtener un intervalo de confianza a un nivel del 99%
- para la longitud media del pico en los machos
- para la longitud media del pico en las hembras
Los datos se introducen de la siguiente forma
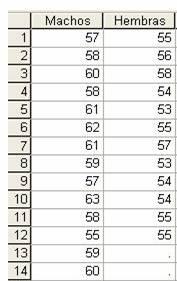
Para obtener el intervalo de confianza pedido se selecciona en el menú principal Analizar/Estadísticos descriptivos/Explorar…
En el Cuadro de diálogo se introducen las variables Machos y Hembras en el campo Dependientes:
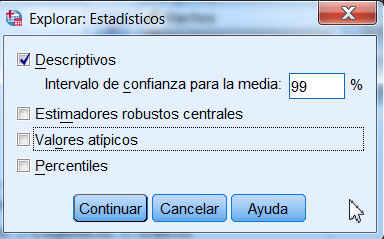
Se pulsa Estadísticos… para modificar el nivel de confianza
se selecciona en el botón Opciones… la opción de Excluir casos según pareja (las muestras tienen distinto tamaño)
Para obtener los resultados se pulsa Continuar y Aceptar.
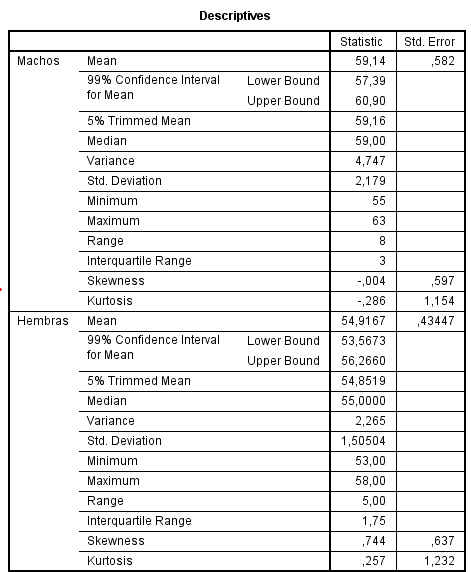
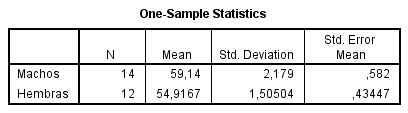
Los intervalos de confianza para la longitud media del pico de los machos y de las hembras, a un nivel del 99%, son (57.39, 60.90) y (53.57, 56.27), respectivamente. Como se puede apreciar la longitud del pico en los machos es mayor que en las hembras.
Alternativamente estos intervalos de confianza también pueden determinarse seleccionando en el menú principal Analizar/Comparar medias/Prueba T para una muestra… En el Cuadro de diálogo se introducen las variables Machos y Hembras en el campo Contrastar variables:
Se pulsa Opciones… para establecer el nivel de confianza
Se pulsa Continuar y Aceptar y se muestran las siguientes salidas
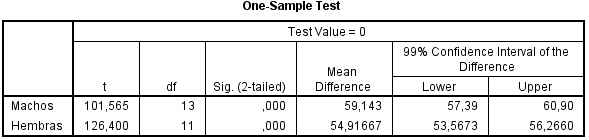
Los intervalos de confianza para la longitud media del pico de los machos y de las hembras, a un nivel del 99%, son (57.39, 60.90) y (53.57, 56.27), respectivamente.
2. Obtener un intervalo de confianza a un nivel del 99% para la diferencia entre la longitud media del pico de los machos y de las hembras.
Para obtener el intervalo de confianza pedido, en primer lugar se definen las variables: Ambos y Niveles y a continuación se introducen los valores
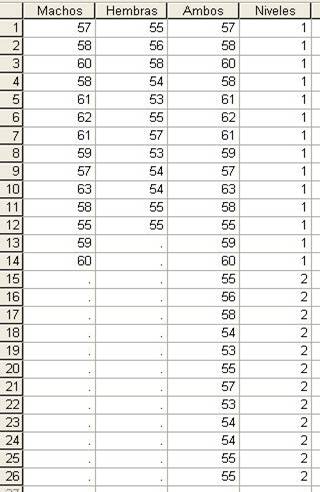y se selecciona Analizar/Comparar medias/Prueba T para muestras independientes... En el Cuadro de diálogo se introduce: la variable Ambos en el campo Contrastar variables: y la variable Niveles en el campo Variable de agrupación:
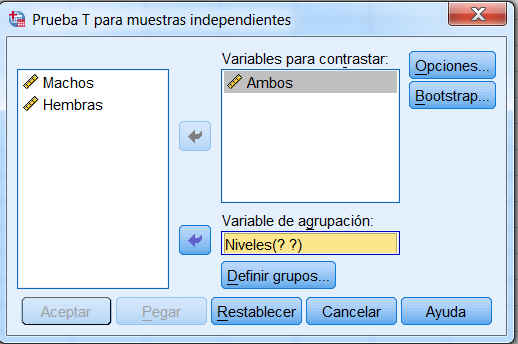
Se pulsa sobre Definir grupos…, donde se indican las etiquetas asignadas y que determinan el grupo al que pertenece cada uno de los valores de la variable Ambos
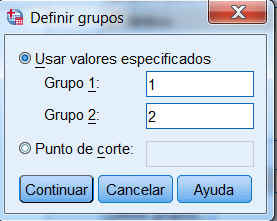Se pulsa Continuar y se establece el nivel de confianza
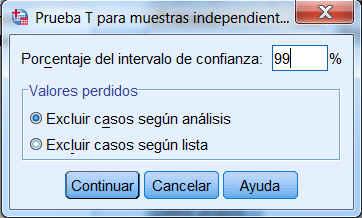Se pulsa Continuar y Aceptar y se obtienen los siguientes resultados.
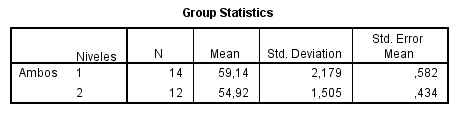
En este caso la prueba de Levene nos muestra un p-valor igual a 0.161, al ser mayor que el nivel de significación 0.01, indica que no se debe rechazar la igualdad de varianzas con un nivel de confianza del 99%. Por tanto, el intervalo de confianza resultante es aquel en el que “Se han asumido varianzas iguales”: (2.136, 6.317).
Ejercicios Propuesto 2 (Resuelto)
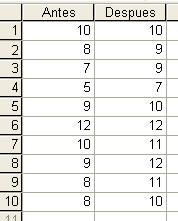
Para comprobar si un determinado pienso puede mejorar la producción de lana de las ovejas, se selecciona una muestra aleatoria simple de 10 ovejas para ser alimentadas con dicho pienso. En la tabla siguiente se muestra el peso (en Kgr) de la lana producida antes y después del experimento
Obtener un intervalo de confianza al 98% para la diferencia de los pesos medios de la lana producida antes y después del experimento.
Solución:
Los datos se introducen de la siguiente forma:
Se selecciona en el menú principal Analizar/Comparar medias/Prueba T para muestras relacionadas…
En el Cuadro de diálogo se marcan las dos variables que se desean comparar y se pasan al campo de Variables relacionadas:
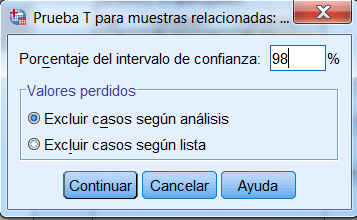
Se pulsa Opciones y se selecciona el nivel de confianza del 98%
Se pulsa Continuar y Aceptar, y se obtienen los resultados siguientes
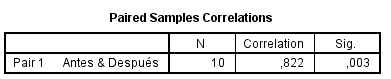
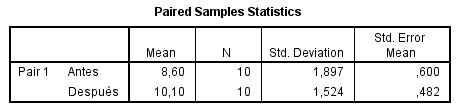El intervalo de confianza para la diferencia de los pesos medios de la lana producida antes y después del experimento, a un nivel del 98%, es (–2.464, –0.536). Como el intervalo de confianza no contiene el 0 podemos deducir que existen diferencias significativas entre las medias. Se puede apreciar que el peso de la lana es mayor después del tratamiento.