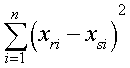MÉTODOS DE ANÁLISIS MULTIVARIANTE: ANÁLISIS CLÚSTER
Objetivos
- Identificar grupos de objetos homogéneos.
- Determinar el criterio de similitud.
- Distinguir los Métodos de clasificación Jerárquicos y los Métodos de clasificación No-Jerárquicos o Repartición.
- Plantear y aplicar el Análisis Clúster Jerárquico.
- Distinguir los Métodos Jerárquicos Aglomerativos y los Métodos Jerárquicos Divisivos.
- Entender y aplicar el proceso algorítmico del Análisis Clúster Jerárquico Aglomerativo.
- Saber construir una matriz de distancias.
- Representar e Interpretar un dendograma.
- Plantear y aplicar el Análisis Clúster de K medias.
- Entender y aplicar el proceso algorítmico del Análisis Clúster de K medias.
- Plantear y aplicar el Análisis Clúster en dos etapas o bietápico.
Introducción al Análisis Clúster
El análisis clúster es una técnica multivariante cuya idea básica es clasificar objetos formando grupos/conglomerados (clúster) que sean lo más homogéneos posible dentro de si mismos y heterogéneos entre sí.
Surge ante la necesidad de diseñar una estrategia que permita definir grupos de objetos homogéneos. Este agrupamiento se basa en la idea de distancia o similitud entre las observaciones y la obtención de dichos clusters depende del criterio o distancia considerados, por ejemplo, una baraja de carta española se podría dividir de distintas formas: en dos clusters (figuras y números), en cuatro clusters (los cuatro palos), en ocho clusters (los cuatro palos y según sean figuras o números). Es decir, el número de clusters depende de lo que consideremos como similar.
El análisis clúster es una tarea de clasificación. Por ejemplo
- Clasificar grupos de consumidores respecto a sus preferencias en nuevos productos
- Clasificar las entidades bancarias donde sería más rentable invertir
- Clasificar las estrellas del cosmos en función de su luminosidad
- Identificar si hay grupos de municipios en una determinada comunidad con una tendencia similar en el consumo de agua con el fin de identificar buenas prácticas para la sostenibilidad y zonas problemáticas por alto consumo.
Como se puede comprender fácilmente el análisis clúster tiene una extraordinaria importancia en la investigación científica, en cualquier rama del saber. La clasificación es uno de los objetivos fundamentales de la Ciencia y en la medida en que el análisis clúster nos proporciona los medios técnicos para realizarla, se nos hará imprescindible en cualquier investigación.
\( E=m^2 \)
Planteamiento del problema
Consideremos una muestra X formada por n individuos sobre los que se miden p variables, X1,…,Xp (p variables numéricas observadas en n objetos). Sea xij el valor de la variable Xj en el i -ésimo objeto i = 1,…,n; j = 1,…,p.
Este conjunto X de valores numéricos se pueden ordenar en una matriz
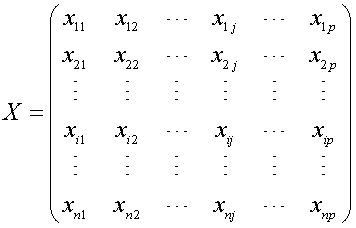 La i-ésima fila de la matriz X contiene los valores de cada variable para el i-ésimo individuo, mientras que la j-ésima columna muestra los valores pertenecientes a la j-ésima variable a lo largo de todos los individuos de la muestra.
La i-ésima fila de la matriz X contiene los valores de cada variable para el i-ésimo individuo, mientras que la j-ésima columna muestra los valores pertenecientes a la j-ésima variable a lo largo de todos los individuos de la muestra.
Se trata, fundamentalmente, de resolver el siguiente problema: Dado un conjunto de n individuos caracterizados por la información de p variables Xj, (j = 1,2,…, p), nos planteamos clasificarlos de manera que los individuos pertenecientes a un grupo (clúster) (y siempre con respecto a la información disponible de las variables) sean lo más similares posibles entre sí y los distintos grupos sean entre ellos tan disimilares como sea posible.
El proceso completo puede estructurarse de acuerdo con el siguiente esquema:
-
Partimos de un conjunto de n individuos de los que se dispone de una información cifrada por un conjunto de p variables (una matriz de datos de n individuos y p variables).
-
Establecemos un criterio de similaridad y construimos una matriz de similaridades que nos permita relacionar la semejanza de los individuos entre sí. Para medir lo similares (o disimilares) que son los individuos existe una gran cantidad de índices de similaridad y de disimilaridad o divergencia. Todos ellos tienen propiedades y utilidades distintas y habrá que ser consciente de ellas para su correcta aplicación.
-
Elegimos un algoritmo de clasificación para determinar la estructura de agrupación de los individuos.
-
Especificamos esa estructura mediante diagramas arbóreos.
El análisis clúster: Técnica de agrupación de variables y de casos
-
Como técnica de agrupación de variables, el análisis clúster es similar al análisis factorial. Pero, mientras que el análisis factorial es poco flexible en algunos de sus supuestos (linealidad, normalidad, variables cuantitativas, etc.) y estima de la misma manera la matriz de distancias, el análisis clúster es menos restrictivo en sus supuestos (no exige linealidad, ni simetría, permite variables categóricas, etc.) y admite varios métodos de estimación de la matriz de distancias.
-
Como técnica de agrupación de casos, el análisis clúster es similar al análisis discriminante. Pero mientras que el análisis discriminante se centra en la agrupación de variables, es decir efectúa la clasificación tomando como referencia un criterio o variable dependiente (los grupos de clasificación), el análisis clúster se centra en agrupar objetos, es decir permite detectar el número óptimo de grupos y su composición únicamente a partir de la similaridad existente entre los casos; además, el análisis de clúster no asume ninguna distribución específica para las variables.
Inconvenientes del Análisis Clúster: Es un análisis descriptivo, a teórico y no inferencial. Habitualmente se utiliza como una técnica exploratoria que no ofrece soluciones únicas, las soluciones dependen de las variables consideradas y del método de análisis clúster utilizado.
Aplicabilidad: Las técnicas de análisis clúster han sido tradicionalmente utilizadas en muchas disciplinas, por ejemplo, Astronomía (Clúster = galaxia, súper galaxias, etc.), Marketing (segmentación de mercados, investigación de mercados), Psicología, Biología (Taxonomía. Microarrays), Ciencias Ambientales (Clasificación de ríos para establecer tipologías según la calidad de las aguas), Sociología, Economía, Ingeniería, ….
JAIN and DUBES (1988) definen el Análisis de Clúster como una herramienta de exploración de datos que se complementa con técnicas de visualización de los mismos.
Resumiendo
-
El objetivo del Análisis Clúster es obtener grupos de objetos de forma que, por un lado, los objetos pertenecientes a un mismo grupo sean muy semejantes entre sí y, por el otro, los objetos pertenecientes a grupos diferentes tengan un comportamiento distinto con respecto a las variables analizadas.
-
Es una técnica exploratoria puesto que la mayor parte de las veces no utiliza ningún tipo de modelo estadístico para llevar a cabo el proceso de clasificación.
-
Conviene estar siempre alerta ante el peligro de obtener, como resultado del análisis, no una clasificación de los datos sino una disección de los mismos en distintos grupos. El conocimiento que el analista tenga acerca del problema decidirá que grupos obtenidos son significativos y cuáles no.
-
Una vez establecidas las variables y los objetos a clasificar el siguiente paso consiste en establecer una medida de proximidad o de distancia entre ellos que cuantifique el grado de similaridad entre cada par de objetos.
- Las medidas de proximidad, similitud o semejanza miden el grado de semejanza entre dos objetos de forma que, cuanto mayor (menor) es su valor, mayor (menor) es el grado de similaridad existente entre ellos y mayor (menor) la probabilidad de que los métodos los asignen en el mismo grupo.
-
Las medidas de disimilitud, desemejanza o distancia miden la distancia entre dos objetos de forma que, cuanto mayor (menor) sea su valor, más (menos) diferentes son los objetos y menor (mayor) la probabilidad de que los métodos de clasificación los asignen en el mismo grupo.
Métodos de clasificación
Se distinguen dos grandes categorías de métodos clusters: Métodos jerárquicos y Métodos no-jerárquicos
- Métodos Jerárquicos: En cada paso del algoritmo sólo un objeto cambia de grupo y los grupos están anidados en los de pasos anteriores. Si un objeto ha sido asignado a un grupo ya no cambia más de grupo. La clasificación resultante tiene un número creciente de clases anidadas.
- Métodos No jerárquico o Repartición: Comienzan con una solución inicial, un número de grupos g fijado de antemano y agrupa los objetos para obtener los g grupos.
Los métodos jerárquicos se subdividen a su vez en aglomerativos y divisivos:
- Los métodos jerárquicos aglomerativos comienzan con tantos clusters como objetos tengamos que clasificar y en cada paso se recalculan las distancias entre los grupos existentes y se unen los dos grupos más similares o menos disimilares. El algoritmo acaba con un clúster conteniendo todos los elementos.
- Los métodos jerárquicos divisivos comienzan con un clúster que engloba a todos los elementos y en cada paso se divide el grupo más heterogéneo. El algoritmo acaba con tantos clusters (de un elemento cada uno) como objetos se hayan clasificado.
Indepedientemente del proceso de agrupamiento, hay diversos criterios para ir formando los clusters; todos estos criterios se basan en una matriz de distancias o similitudes. Por ejemplo, dentro de los métodos:
Jerárquicos aglomerativos:
- Método del Linkage Simple, Enlace Simple o Vecino más próximo
- Método del Linkage Completo, Enlace Completo o Vecino más alejado
- Método del Promedio entre grupos
- Método del Centroide
- Método del la Mediana
- Método de Ward
Jerárquicos divisivos o disociativos
- Método del Linkage Simple
- Método del Linkage Completo
- Método del Promedio entre grupos
- Método del Centroide
- Método del la Mediana
- Análisis de Asociación
Proceso que se debe seguir en un análisis clúster
Paso 1: Selección de variables
La clasificación dependerá de las variables elegidas. Introducir variables irrelevantes aumenta la posibilidad de errores. Hay que utilizar algún criterio de selección:
- Seleccionar sólo aquellas variables que caracterizan los objetos que se van agrupando, y referentes a los objetivos del análisis clúster que se va a realizar
- Si el número de variables es muy grande se puede realizar previamente un Análisis de Componentes Principales y resumir el conjunto de variables.
Paso 2: Detección de valores atípicos. El análisis clúster es muy sensible a la presencia de objetos muy diferentes del resto (valores atípicos).
Paso 3. Seleccionar la forma de medir la distancia/disimilitud entre objetos dependiendo de si los datos con cuantitativos o cualitativos
- Datos métricos: Medidas de correlación y medidas de distancia
- Datos no métricos: Medidas de asociación.
Paso 4: Estandarización de los datos (Decidir si se trabaja con los datos según se miden o estandarizados). El orden de las similitudes puede cambiar bastante con sólo un cambio de escala de una de las variables por lo que sólo se realizará una tipificación cuando resulte necesario.
Paso 5: Obtención de los clusters y valoración de la clasificación realizada
- Elegir el algoritmo para la formación de clúster (Procedimientos jerárquicos o procedimientos no jerárquicos)
- Número de clusters: Regla de parada. Existen diversos métodos de determinación del número de clusters, algunos están basados en reconstruir la matriz de distancias original, otros en los coeficientes de concordancia de Kendall y otros realizan análisis de la varianza entre los grupos obtenidos. No existe un criterio universalmente aceptado. Dado que la mayor parte de los paquetes estadísticos proporciona las distancias de aglomeración, es decir, las distancias a las que se forma cada clúster, una forma de determinar el número de grupos consiste en localizar en qué iteraciones del método utilizado dichas distancias dan grandes saltos
- Adecuación del modelo. Comprobar que el modelo no ha definido clúster con un solo objeto, clúster con tamaños desiguales,…
Análisis clúster en SPSS
El programa SPSS dispone de tres tipos de análisis clúster:
- Análisis de conglomerados de bietápico
- Análisis de conglomerados de K medias
- Análisis de conglomerados jerárquicos.
Cada uno de estos procedimientos utiliza un algoritmo distinto en la creación de clusters y contiene opciones que no están disponibles en los otros.
- Análisis de conglomerados de bietápico. El clúster en dos etapas está pensado para minería de datos, es decir para estudios con un número de individuos grande que pueden tener problemas de clasificación con los otros procedimientos. Se puede utilizar tanto cuando el número de clúster es conocido a priori y cuando es desconocido. Permite trabajar conjuntamente con variables de tipo mixto (cualitativas y cuantitativas).
- Análisis de conglomerados de K medias. Es un método de clasificación No Jerárquico (Repartición). El número de clusters que se van a formar es fijado de antemano (requiere conocer el número de clusters a priori) y se agrupan los objetos para obtener esos grupos. Comienzan con una solución inicial y los objetos se reagrupan de acuerdo con algún criterio de optimalidad. El clúster no jerárquico sólo puede ser aplicado a variables cuantitativas. Este procedimiento puede analizar archivos de datos grandes.
- Análisis de conglomerados jerárquicos. En el método de clasificación Jerárquico en cada paso del algoritmo sólo un objeto cambia de grupo y los grupos están anidados en los pasos anteriores. Si un objeto ha sido asignado a un grupo ya no cambia más de grupo. El método jerárquico es idóneo para determinar el número óptimo de conglomerados existente en los datos y el contenido de los mismos. Se utiliza cuando no se conoce el número de clusters a priori y cuando el número de objetos no es muy grande. Permite trabajar conjuntamente con variables de tipo mixto (cualitativas y cuantitativas). Siempre que todas las variables sean del mismo tipo, el procedimiento Análisis de Conglomerados Jerárquico podrá analizar variables de intervalo (continuas), de recuento o binarias.
Los tres métodos de análisis que vamos a estudiar son de tipo aglomerativo, en el sentido de que, partiendo del análisis de los casos individuales, intentan ir agrupando casos hasta llegar a la formación de grupos o conglomerados homogéneos.
Todos los métodos de análisis clúster son métodos exploratorios de datos
- Para cada conjunto de datos podemos tener diferentes agrupaciones, dependiendo del método
- Lo importante es identificar una solución que nos enseñe cosas relevantes de los datos.
En esta práctica estudiamos primero el Análisis clúster Jerárquico, seguido del Análisis Clúster de K medias y por último el Análisis Clúster en dos etapas.
Análisis clúster jerárquico
Este procedimiento intenta identificar grupos relativamente homogéneos de casos (o de variables) basándose en las características seleccionadas. Permite trabajar conjuntamente con variables de tipo mixto (cualitativas y cuantitativas), siendo posible analizar las variables brutas o elegir de entre una variedad de transformaciones de estandarización. Se utiliza cuando no se conoce el número de clusters a priori y cuando el número de objetos no es muy grande. Como hemos dicho anteriormente, los objetos de análisis de agrupamiento jerárquico pueden ser casos o variables, dependiendo de si desea clasificar los casos o examinar las relaciones entre las variables.
Al trabajar con variables que pueden ser cuantitativas, binarias o datos de recuento (frecuencias), el escalamiento de las variables es un aspecto importante, ya que las diferentes escalas en que están medidas las variables pueden afectar a las soluciones de conglomeración. Si las variables muestran grandes diferencias en el escalamiento (por ejemplo, una variable se mide en dólares y la otra se mide en años), se debe considerar la posibilidad de estandarizarlas. Esto puede llevarse a cabo automáticamente mediante el propio procedimiento Análisis de conglomerados jerárquico.
Estudiaremos fundamentalmente los Métodos Jerárquicos Aglomerativos. En estos métodos se utilizan diversos criterios para determinar, en cada paso del algoritmo, qué grupos se deben unir.
- Enlace simple o vecino más próximo: Mide la proximidad entre dos grupos calculando la distancia entre sus objetos más próximos o la similitud entre sus objetos más semejantes
- Enlace completo o vecino más alejado: Mide la proximidad entre dos grupos calculando la distancia entre sus objetos más lejanos o la similitud entre sus objetos menos semejantes
- Enlace medio entre grupos: Mide la proximidad entre dos grupos calculando la media de las distancias entre objetos de ambos grupos o la media de las similitudes entre objetos de ambos grupos
- Enlace medio dentro de los grupos: Mide la proximidad entre dos grupos con la distancia media existente entre los miembros del grupo unión de los dos grupos
- Métodos del centroide y de la mediana: Ambos métodos miden la proximidad entre dos grupos calculando la distancia entre sus centroides. Los dos métodos difieren en la forma de calcular los centroides:Método de Ward
- El método del centroide utiliza las medias de todas las variables
- En el método de la mediana, el nuevo centroide es la media de los centroides de los grupos que se unen
Comparación de los diversos métodos aglomerativos
- El enlace simple conduce a clusters encadenados
- El enlace completo conduce a clusters compactos
- El enlace completo es menos sensible a outliers que el enlace simple
- El método de Ward y el método del enlace medio son los menos sensibles a outliers
- El método de Ward tiene tendencia a formar clusters más compactos y de igual tamaño y forma en comparación con el enlace medio
- Todos los métodos salvo el método del centroide satisfacen la desigualdad ultramétrica
Decisiones que hay que tomar para hacer un clúster
- Elegir el método clúster que se va a utilizar
- Decidir si se estandarizan los datos
- Seleccionar la forma de medir la distancia/disimilitud entre los individuos
- Elegir un criterio para unir grupos, distancia entre grupos.
Proceso que se debe seguir en un Análisis Clúster Jerárquico Aglomerativo
Paso 1: Selección de las variables. Se recomienda que las variables sean del mismo tipo (continuas, categóricas,..)
Paso 2: Detección de valores atípicos. El análisis clúster es muy sensible a la presencia de objetos muy diferentes del resto (valores atípicos).
Paso 3: Elección de una medida de similitud entre objetos y obtención de la matriz de distancias. Mediante estas medidas se determinan los clusters iniciales.
Paso 4: Buscar los clusters más similares
Paso 5: Unir estos dos clusters en un nuevo clúster que tenga al menos dos objetos, de forma que el número de clúster decrece en una unidad.
Paso 6: Calcular la distancia entre este clúster y el resto. Los distintos métodos para el cálculo de las distancias entre los clusters producen distintas agrupaciones, por lo que no existe una agrupación única.
Paso 7: Repetir desde el paso 4 hasta que todos los objetos estén en un único clúster.
El proceso de agrupación jerárquico se puede resumir gráficamente mediante una representación gráfica en forma de árbol que recibe el nombre de Dendograma. Los objetos similares se enlazan y su posición en el diagrama está determinada por el nivel de similitud/disimilitud entre los objetos.
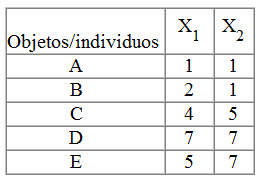
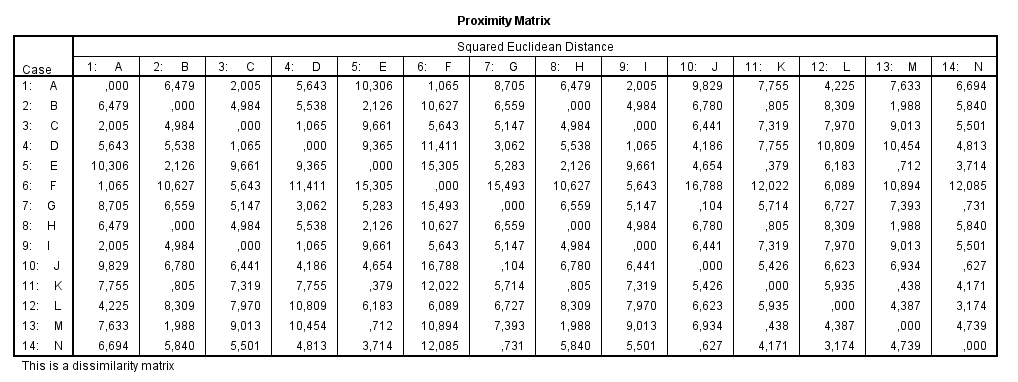
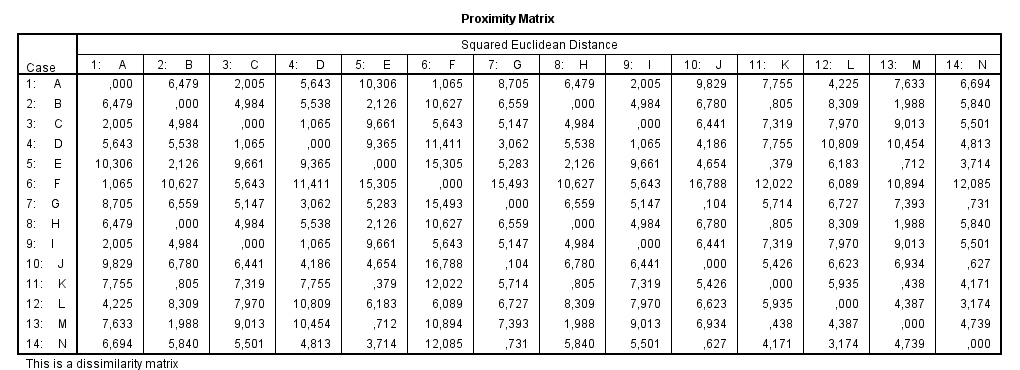
Vamos a realizar el proceso descrito y para ello utilizamos un ejemplo sencillo. Dicho ejemplo está formado por 5 objetos (A, B, C, D, E) y 2 variables (X1, X2). Los datos se presentan en la siguiente tabla
Paso 1 y 2: Para detectar valores atípicos podemos representar los puntos en el plano
No detectamos valores atípicos
Paso 3: La medida de distancia que vamos a tomar entre los objetos va a ser la distancia euclídea cuya expresión es:
![]() Así, por ejemplo, la distancia entre el clúster A y el clúster B es:
Así, por ejemplo, la distancia entre el clúster A y el clúster B es:
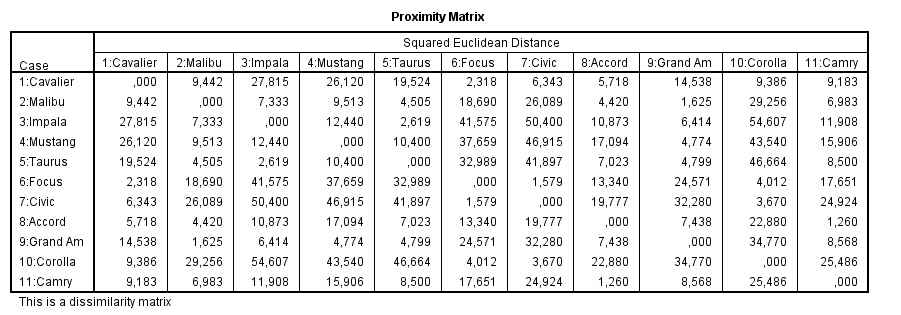
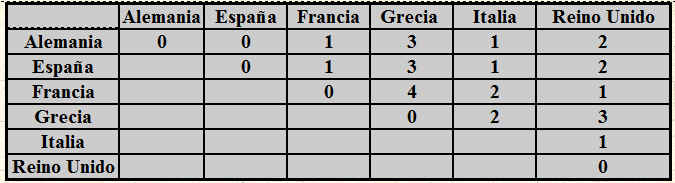
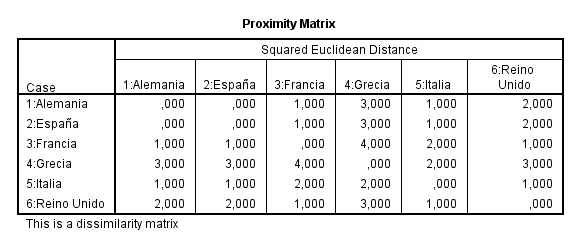
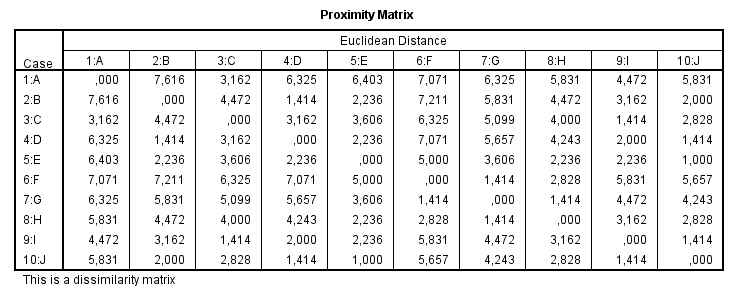
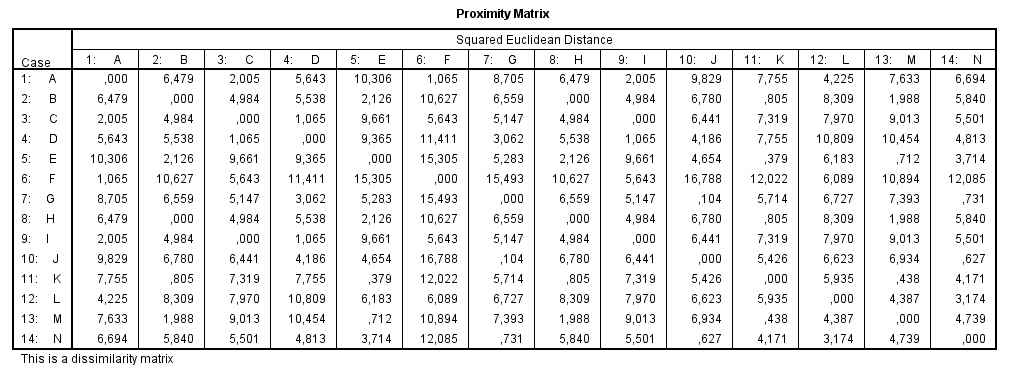
Realizamos la distancia euclídea entre todos los puntos y obtenemos la siguiente matriz de distancias euclídeas entre los objetos
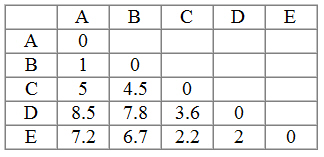 Estamos realizando el método jerárquico aglomerativo, por lo que inicialmente tenemos 5 clusters, uno por cada uno de los objetos a clasificar.
Estamos realizando el método jerárquico aglomerativo, por lo que inicialmente tenemos 5 clusters, uno por cada uno de los objetos a clasificar.
Paso 4: Observamos en la matriz de distancias cuales son los objetos más similares, en nuestro ejemplo son el A y B que tienen la distancia menor (1).
Paso 5: Fusionamos los clusters más similares construyendo un nuevo clúster que contiene A y B. Se han formado los clusters: AB, C, D y E.
Paso 6: Calculamos la distancia entre el clúster AB y los objetos C, D y E. Para medir esta distancia tomamos como representante del clúster AB el centroide, es decir, el punto que tiene como coordenadas las medias de los valores de las componentes de las variables, es decir, las coordenadas de AB son: ((1+2)/2 , (1+1)/2) = (1.5, 1). La tabla de datos es la siguiente
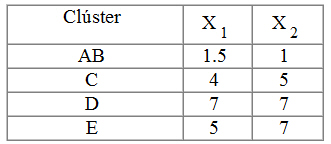 Paso 7: Repetimos desde el paso 4 hasta que todos los objetos estén en un único clúster
Paso 7: Repetimos desde el paso 4 hasta que todos los objetos estén en un único clúster
Paso 4: A partir de estos datos calculamos de nuevo la matriz de distancias
Paso 5: Los clusters más similares son el D y E con una distancia de 2, que se fusionan en un nuevo clúster DE. Se han formado tres clusters AB, C, DE
Paso 6: Calculamos el centroide del nuevo clúster que es el punto (6,7) y formamos de nuevo la tabla de datos
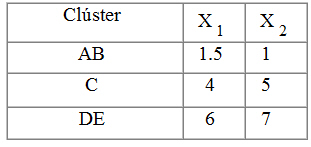 Paso 4: A partir de estos datos calculamos de nuevo la matriz de distancias
Paso 4: A partir de estos datos calculamos de nuevo la matriz de distancias
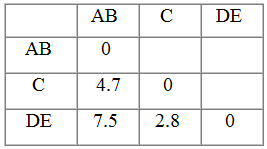 Paso 5: Los clusters más similares son el C y DE con una distancia de 2.8, que se fusionan en un nuevo clúster CDE. Se han formado dos clusters AB y CDE
Paso 5: Los clusters más similares son el C y DE con una distancia de 2.8, que se fusionan en un nuevo clúster CDE. Se han formado dos clusters AB y CDE
Paso 6. Calculamos el centroide del nuevo clúster ((4+5+7)/3 , (5+7+7)/3) = (5.3, 6.3) y formamos de nuevo la tabla de datos
 Paso 4 : A partir de estos datos calculamos de nuevo la matriz de distancias
Paso 4 : A partir de estos datos calculamos de nuevo la matriz de distancias
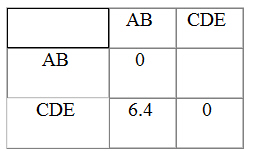 En este último paso tenemos solamente dos clusters con distancia 6.4 que se fusionarán en un único clúster en el paso siguiente terminando el proceso.
En este último paso tenemos solamente dos clusters con distancia 6.4 que se fusionarán en un único clúster en el paso siguiente terminando el proceso.
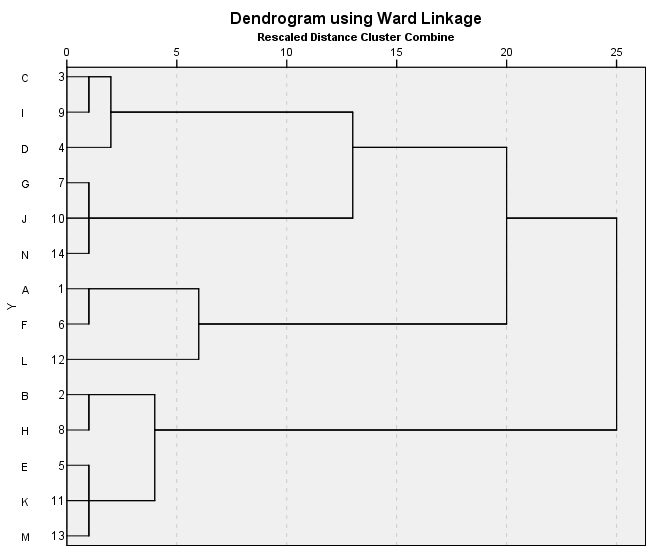
A continuación vamos a representar gráficamente el proceso de fusión mediante un dendograma
A continuación mostramos varias soluciones, para ello cortamos el dendograma por medio de líneas horizontales, así por ejemplo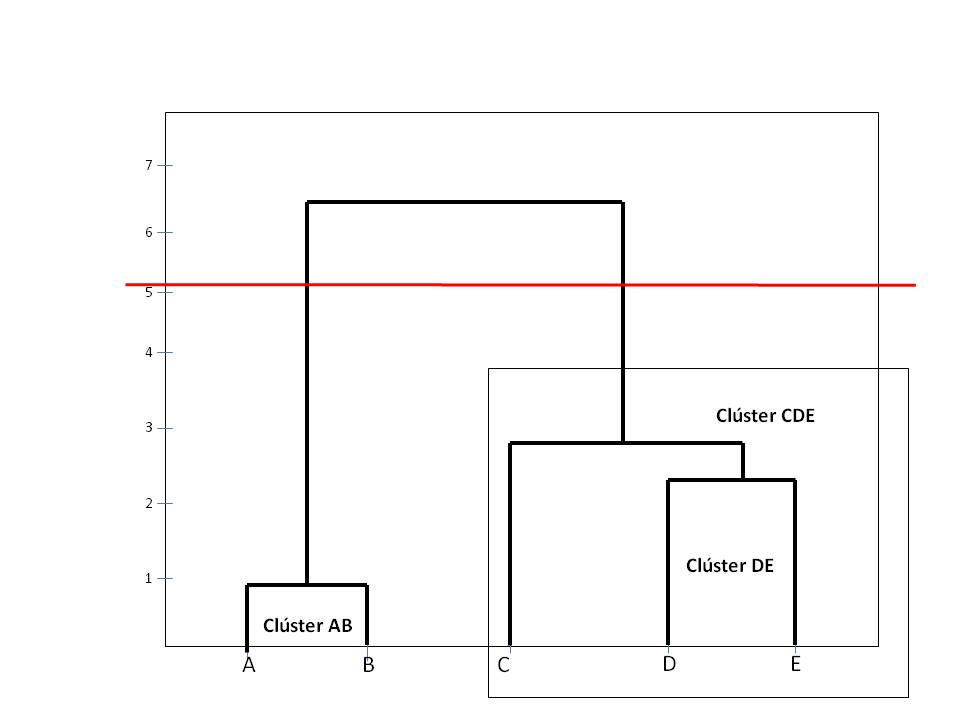
En la figura anterior se muestran 2 clusters: AB y CDE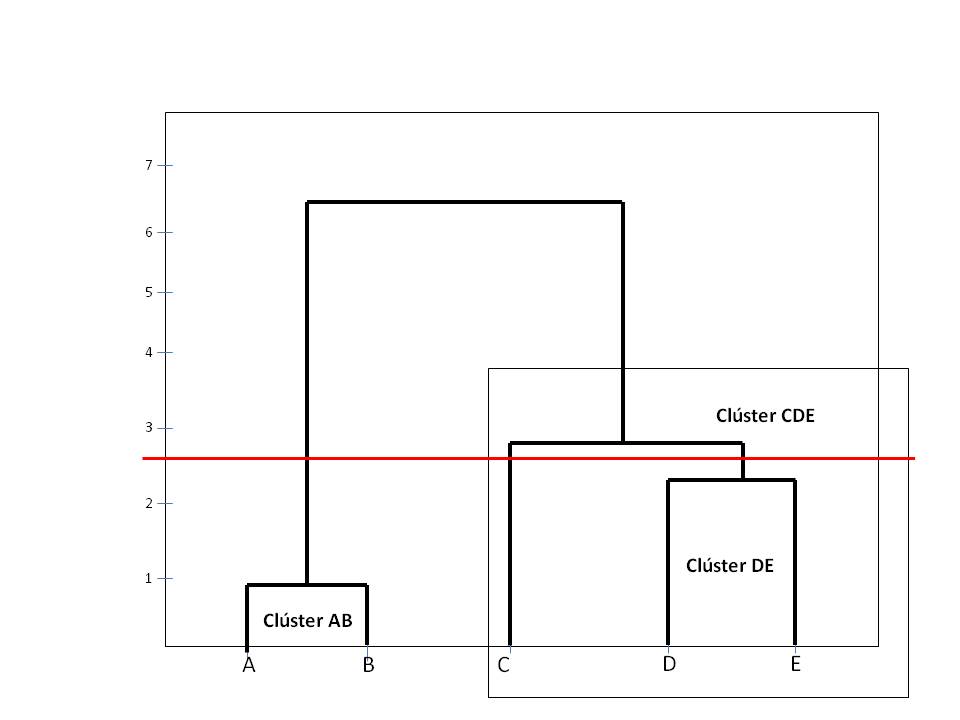
En esta figura la línea de corte nos muestra 3 clusters: AB, C y DE
El número de clusters depende del sitio donde cortemos el dendograma, por lo tanto la decisión sobre el número óptimo de clusters es subjetiva. Es conveniente elegir un número de clusters que sepamos interpretar. Para interpretar los clúster podemos utilizar:
- ANOVA
- Análisis factorial
- Análisis discriminante
- …
- Sentido común
Para decidir el número de clusters nos puede ser de gran utilidad representar los distintos pasos del algoritmo y las distancias a la que se produce la fusión de los clusters. En los primeros pasos el salto de las distancias es pequeño, mientras que esas diferencias van aumentando en los sucesivos pasos. Podemos elegir como punto de corte aquel donde comienzan a producirse saltos más bruscos. En nuestro ejemplo, el salto brusco se produce entre etapas 3 y 4, por lo tanto son dos el número de clusters óptimo.
Comentarios sobre el clúster jerárquico
-
Realizar el clúster jerárquico en conjunto de datos grande es problemático ya que un árbol con más de 50 individuos es difícil de representar e interpretar.
-
Una desventaja general es la imposibilidad de reasignar los individuos a los clusters en los casos en que la clasificación haya sido dudosa en las primeras etapas del análisis.
-
Debido a que el análisis clúster implica la elección entre diferentes medidas y procedimientos, con frecuencia es difícil juzgar la veracidad de los resultados.
-
Se recomienda comparar los resultados con diferentes métodos de conglomerados. Soluciones similares generalmente indican la existencia de una estructura en los datos. Soluciones muy diferentes probablemente indican una estructura pobre.
-
En último caso, la validez de los clusters se juzga mediante una interpretación cualitativa que puede ser subjetiva.
-
El número de clusters depende del sitio donde cortemos el dendograma.
Supuesto práctico 1
Los fabricantes de automóviles deben adaptar sus estrategias de desarrollo de productos y de marketing en función de cada grupo de consumidores para aumentar las ventas y el nivel de fidelidad a la marca. La tarea de agrupación de los coches según variables que describen los hábitos de consumo, sexo, edad, nivel de ingresos, etc. de los clientes puede ser en gran medida automática utilizando el análisis de clúster.
Se desea hacer un estudio de mercado sobre las preferencias de los consumidores al adquirir un vehículo, para ello disponemos una base de datos, ventas_vehículos.sav, de automóviles y camiones en los que figura una serie de variables como el fabricante, modelo, ventas, etc.
El archivo de datos ventas_vehículos.sav contiene 157 datos y está formado por las siguientes variables:
Variables tipo cadena: marca (Fabricante); modelo
Variables tipo numérico: ventas (en miles); reventa (Valor de reventa en 4 años); tipo (Tipo de vehículo: Valores: {0, Automóvil; 1, Camión}); precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo).
El estudio de mercado lo queremos realizar sólo en automóviles de mayor venta y para ello vamos a utilizar el procedimiento Análisis de conglomerados jerárquico para agrupar los automóviles de mayor venta en función de sus precios, fabricante, modelo y propiedades físicas.
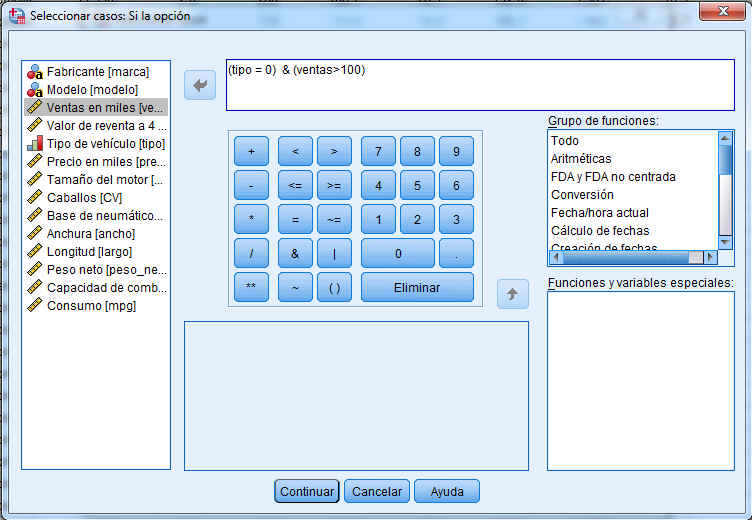
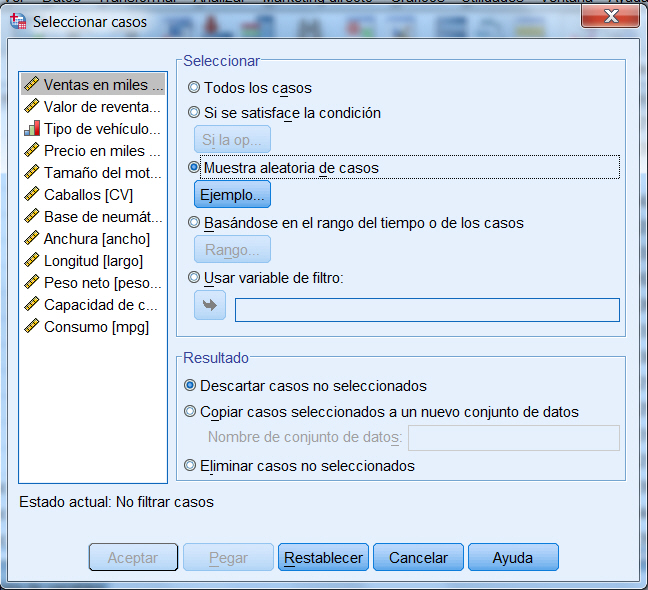
En primer lugar restringiremos el archivo de datos sólo a los automóviles de los que se vendieron al menos 100.000 unidades. Para ello seleccionamos los casos que cumplan esa condición eligiendo en los menús:
Datos/Seleccionar Casos. Seleccionar Si satisface la condición
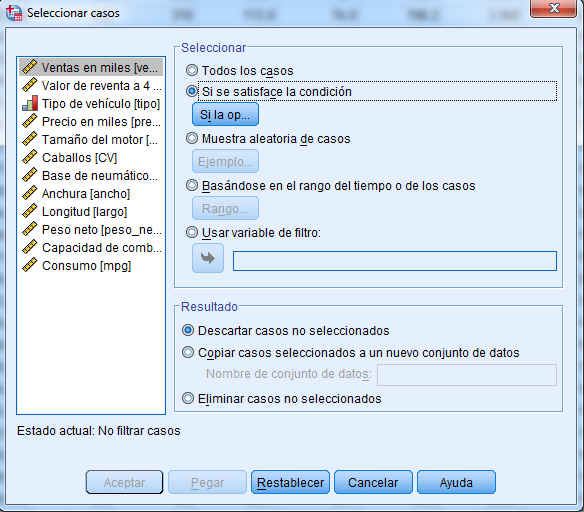 y pulsar Si la op… Como el estudio se va a realizar sólo para los automóviles de los que se vendieron al menos 100.000 unidades, en la ventana de la caja de diálogo Seleccionar casos. Si la opción escribir (tipo = 0) & (ventas>100).
y pulsar Si la op… Como el estudio se va a realizar sólo para los automóviles de los que se vendieron al menos 100.000 unidades, en la ventana de la caja de diálogo Seleccionar casos. Si la opción escribir (tipo = 0) & (ventas>100).
Pulsar Continuar. En el editor de datos (están tachados los casos para los que no se va a llevar a cabo el análisis clúster) aparece una nueva variable filter_$ con dos valores (0 = “Not Selected” y 1 = “Selected”).
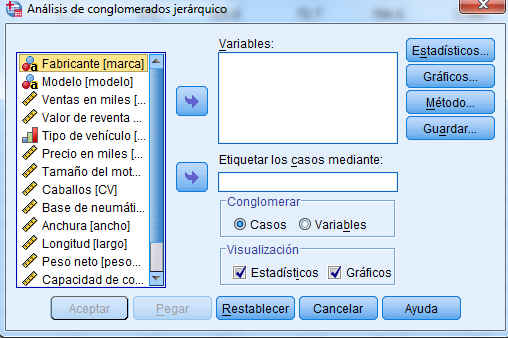
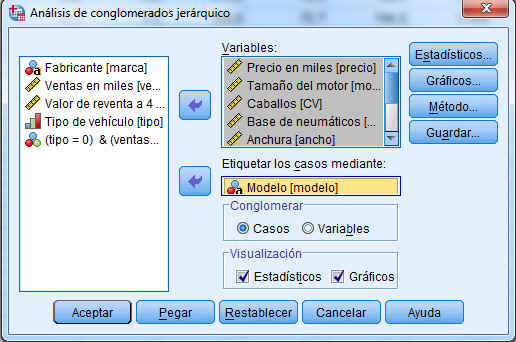
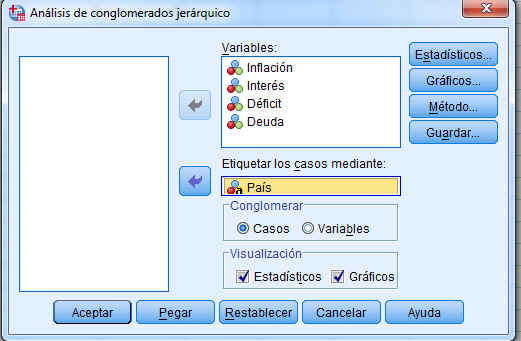
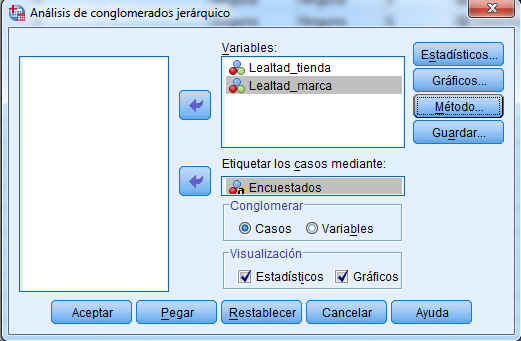
Una vez seleccionada la muestra con la que vamos a trabajar, utilizamos el Análisis de Conglomerados Jerárquicos para agrupar los automóviles de mayor venta en función de sus precios, fabricante, modelo y propiedades físicas. Para ejecutar este análisis clúster se elige en los menús: Analizar/ Clasificar/Conglomerados Jerárquicos …
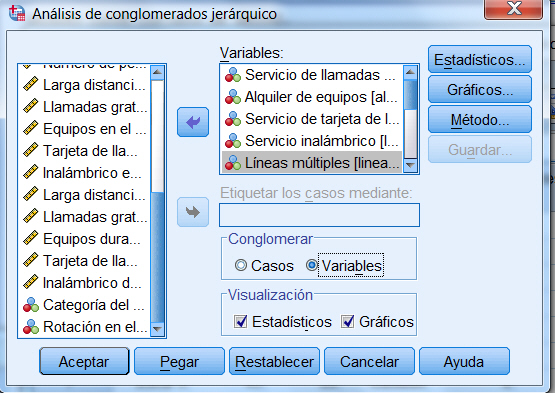
Como se observa en esta figura, se pueden realizar conglomerados para objetos (casos) o para variables (agrupar variables por el parecido que presentan en las respuestas de los individuos) y se pueden etiquetar los grupos con una de las variables del fichero.
Introducir en el campo Variables: precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo). Y elegimos una variable de identificación para etiquetar los casos (opción no obligatoria), para ello introducimos en el Campo Etiquetar los casos mediante: la variable modelo.
Nota: Si se aglomeran casos, seleccionar al menos una variable numérica. Si se aglomeran variables, seleccionar al menos tres variables numéricas.
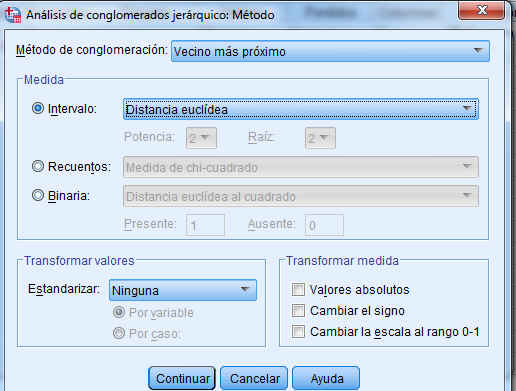
Pulsar Método.
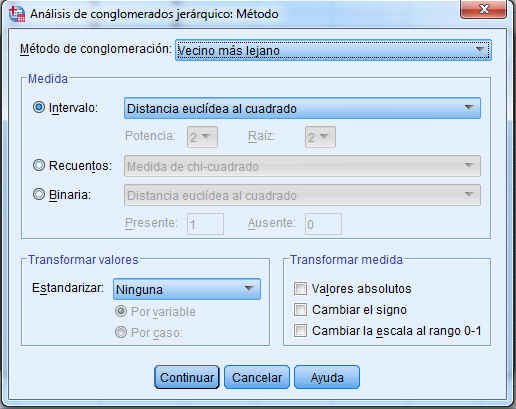
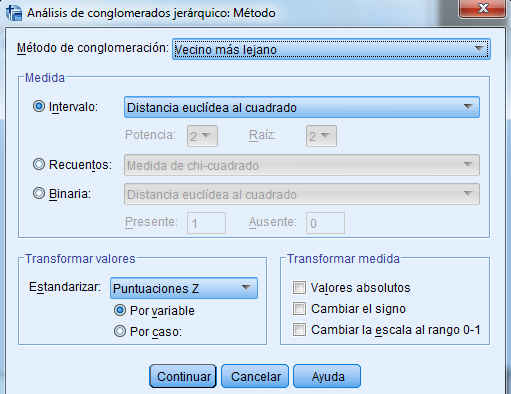
Método de conglomeración. Los métodos de enlace (linkage) utilizan la proximidad entre pares de individuos para unir grupos de individuos. Existen diversas formas de medir la distancia entre clúster que producen diferentes agrupaciones y diferentes dendogramas. No hay un criterio para seleccionar cual es el algoritmo mejor. La decisión es normalmente subjetiva y depende del método que mejor refleje los propósitos de cada estudio en particular. Las opciones disponibles en SPSS son:
- Vinculación inter-grupos. Media Intergrupos
- Vinculación intra-grupos. Media Intragrupos
-
Vecino más próximo. Enlace sencillo (salto mínimo). Utiliza la mínima distancia/disimilitud entre dos individuos de cada grupo (útil para identificar atípicos). Conduce a clusters encadenados
-
Vecino más lejano. Enlace completo (salto máximo). Utiliza la máxima distancia/disimilitud entre dos individuos de cada grupo. Conduce a clusters compactos
- Agrupación de centroides. Utiliza la distancia/disimilitud entre los centros de los grupos
- Agrupación de medianas. Utiliza la mediana de las distancias/disimilitud entre todos los individuos de los dos grupos
- Método de Ward. Tiene tendencia a formar clusters más compactos y de igual tamaño y forma, en comparación con el enlace medio
El método de Ward y el método de la media (enlace medio) son los menos sensibles a outliers.
Medida. La distancia (disimilaridad o similaridad) entre objetos es una medida que nos permite establecer el grado de semejanza entre dichos objetos. Mediante esta opción seleccionamos la medida que vamos a utilizar para ver el parecido entre individuos con distintas distancias dependiendo si la variable es binaria, frecuencia o de intervalo. La elección inicial del conjunto de medidas que describan a los elementos a agrupar es fundamental para establecer los posibles clusters. Las medidas de distancia o similaridad que utilizamos en la aglomeración se deben seleccionar dependiendo del tipo de datos. SPSS dispone de las siguientes medidas:
-
Intervalo (Opción por defecto). Las opciones disponibles son: Distancia euclídea (No es una distancia invariante por cambios de escala), Distancia euclídea al cuadrado, Coseno, Correlación de Pearson, Chebychev, Bloque, Minkowski y Personalizada.
-
Recuentos. Las opciones disponibles son: Medida de chi-cuadrado (Medida por defecto) y Medida de phi-cuadrado.
-
Binaria. Las opciones disponibles son: Distancia euclídea, Distancia euclídea al cuadrado, Diferencia de tamaño, Diferencia de configuración, Varianza, Dispersión, Forma, Concordancia simple, Correlación phi de 4 puntos, Lambda, D de Anderberg, Dice, Hamann, Jaccard, Kulczynski 1, Kulczynski 2, Lance y Williams, Ochiai, Rogers y Tanimoto, Russel y Rao, Sokal y Sneath 1, Sokal y Sneath 2, Sokal y Sneath 3, Sokal y Sneath 4, Sokal y Sneath 5, Y de Yule y Q de Yule.
Transformar valores. La mayoría de los métodos clúster con muy sensibles al hecho de que las variables no estén todas medidas en las mismas unidades y que la variabilidad sea muy diferente. Si queremos que todas las variables tengan la misma importancia en el análisis, podemos estandarizar los datos. Mediante esta opción se pueden estandarizar los valores de los datos, para los casos o las variables, antes de calcular las similaridades (no está disponible para datos binarios). Los métodos disponibles de estandarización son:
- Puntuaciones Z . Estandarizados a puntuaciones Z, con media 0 y desviación típica 1
- Rango -1 a 1. Cada valor del elemento que se tipifica se divide por el rango de los valores
- Rango 0 a 1. Sustrae el valor mínimo de cada elemento que se tipifica y lo divide por el rango
- Magnitud máxima de 1. Divide cada valor del elemento que se tipifica por el máximo de los valores
- Media de 1. Divide cada valor del elemento que se tipifica por la media de los valores
- Desviación típica 1. Divide cada valor de la variable o caso por la desviación típica.
Se puede escoger el modo de realizar la tipificación. Las opciones son Por variable o Por caso.
Transformar medidas. Mediante esta opción se pueden transformar los valores generados por la medida de distancia. Se aplican después de calcular la medida de distancia. Las opciones disponibles son: Valores absolutos, Cambiar el signo y Cambiar la escala al rango 0–1.
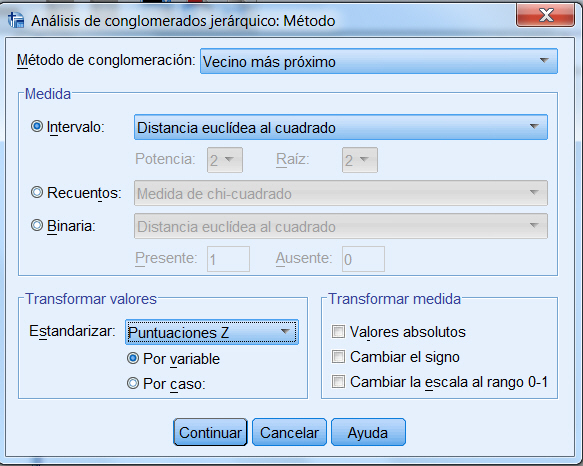
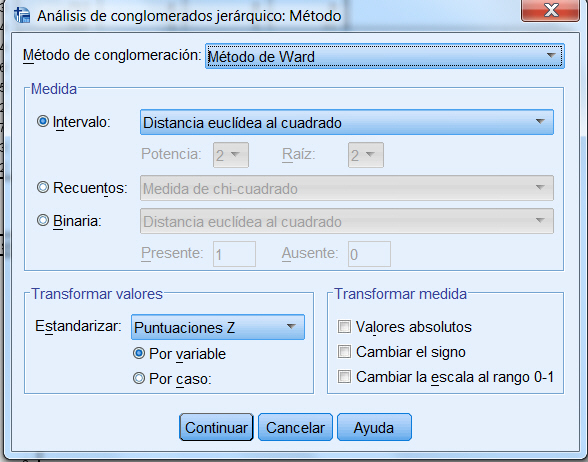
En nuestro ejemplo, dado que las variables en el análisis son variables de escala que se miden en unidades diferentes, la elección de la medida de la distancia, la medida de Intervalo (Distancia euclídea al cuadrado) y la normalización parece apropiado.
Elegimos como método de clúster Vecino más próximo, este método es apropiado para usar cuando se desea examinar los grados de similitud pero es pobre en la construcción de distintos grupos. Por lo tanto, después de examinar los resultados con este método deberíamos realizar de nuevo el estudio con un método distinto del clúster.
En la ventana de la figura anterior seleccionar como Medida: Intervalo (Distancia euclídea al cuadrado), como Método de conglomeración: Vecino más próximo y seleccionar Puntuaciones Z en Transformar valores, Estandarizar:
Pulsar Continuar y en la caja de diálogo del Análisis de conglomerados jerárquicos pulsar Gráficos…
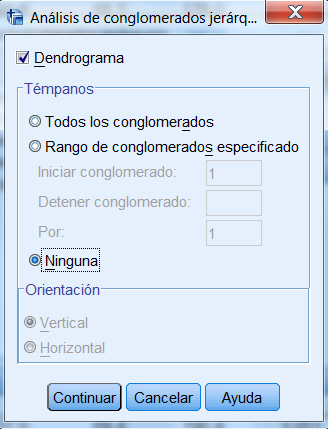
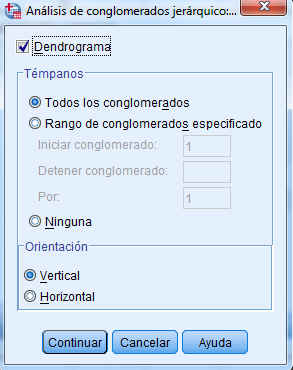
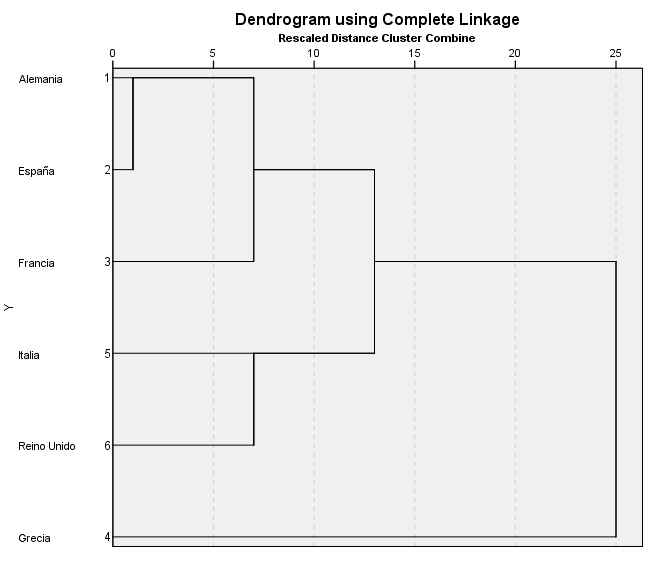
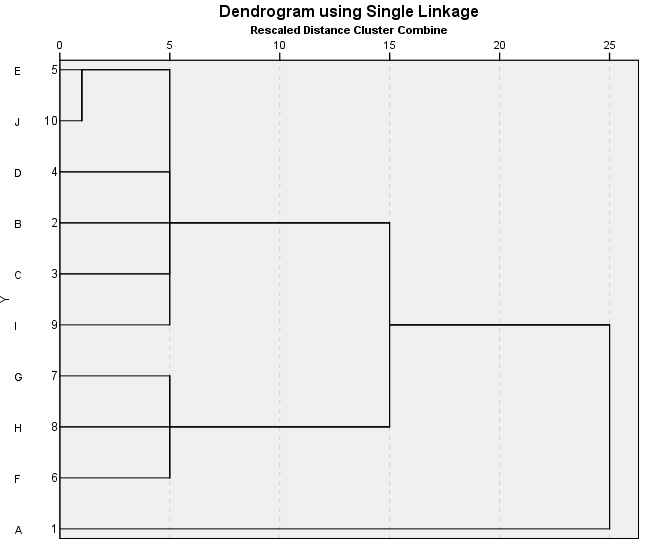
Dendrograma. Es una representación gráfica en forma de árbol, en el que los clusters están representados mediante trazos verticales (horizontales) y las etapas de fusión mediante trazos horizontales (verticales). La separación entre las etapas de fusión es proporcional a la distancia a la que están los grupos que se funden en esa etapa. SPSS representa las distancias entre grupos rescaladas, por tanto son difíciles de interpretar. Los dendrogramas pueden emplearse para evaluar la cohesión de los conglomerados que se han formado y proporcionar información sobre el número adecuado de conglomerados que deben conservarse.
Témpanos. Muestra un diagrama de témpanos, que incluye todos los conglomerados o un rango especificado de conglomerados. Los diagramas de témpanos muestran información sobre cómo se combinan los casos en los conglomerados, en cada iteración del análisis. La orientación permite seleccionar un diagrama vertical u horizontal.
Seleccionar Dendrograma y en Témpanos seleccionar Ninguna. Pulsar Continuar y Aceptar. Se obtienen las siguientes salidas
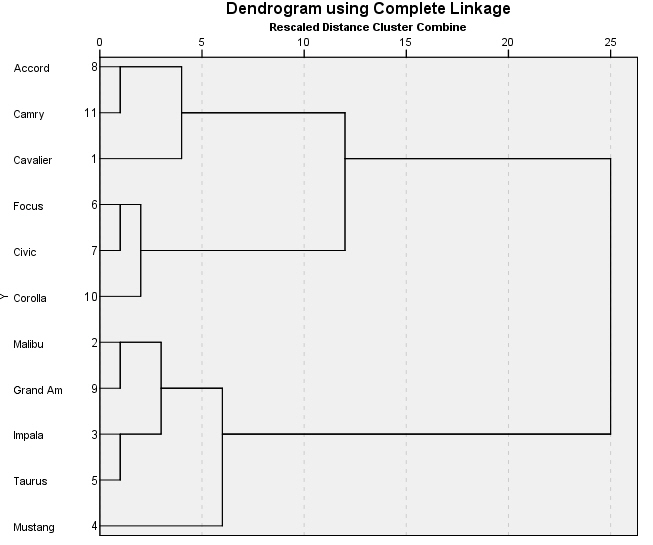
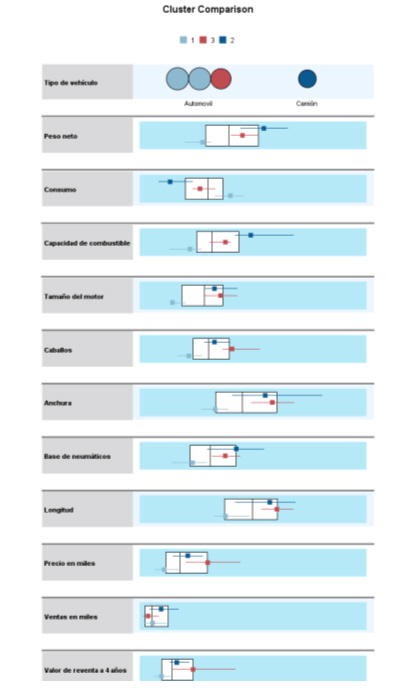
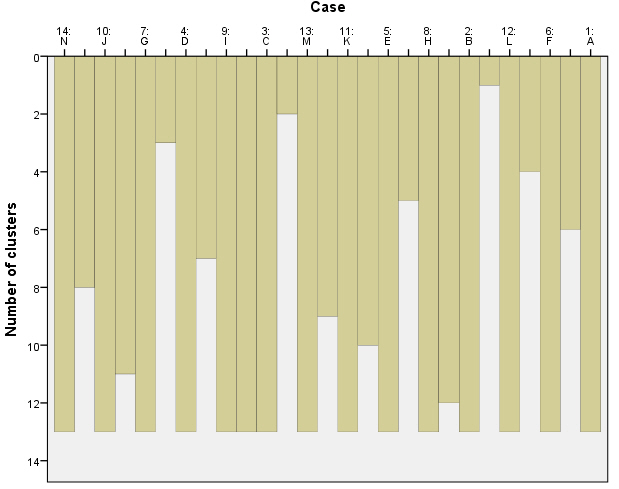
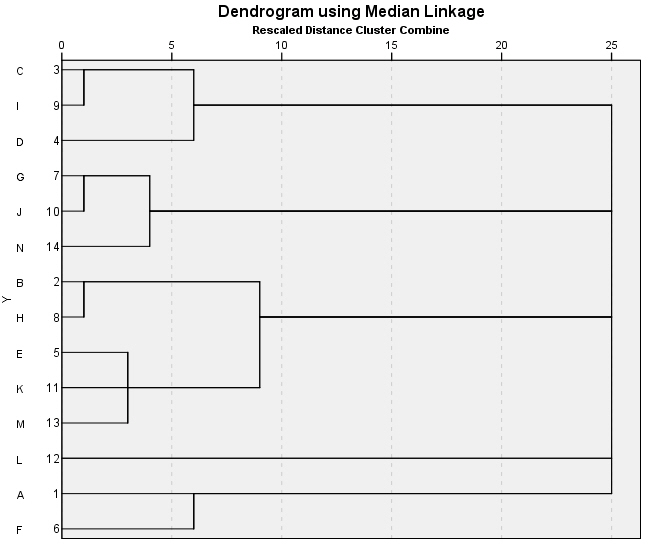
El dendrograma es un resumen gráfico de la solución de clúster. Los casos (marcas de coche) se encuentran a lo largo del eje vertical izquierdo. El eje horizontal muestra la distancia entre los grupos cuando se unieron (de 0 a 25).
Analizar el árbol de clasificación para determinar el número de grupos es un proceso subjetivo. En general, se comienza por buscar “huecos” entre uniones a lo largo del eje horizontal. De derecha a izquierda hay un hueco entre 20 y 25, que divide los coches en dos grupos:
-
Un grupo está formado por los modelos: Accord (8), Camry (11), Malibu (2), Grand Am (9), Impala (3), Taurus (5), Mustang(4) y
-
el otro grupo está formado por los modelos: Focus (6), Civic (7), Cavalier (1) y Corolla (10).
Hay otro hueco aproximadamente 15 y 20 que sugiere 5 clusters (8, 11); (2,9); (3, 5); (4); (6, 7, 1, 10).
Entre 10 y 15 hay otro hueco que sugiere 6 clusters (8, 11); (2,9); (3, 5); (4); (6, 7, 1); (10).
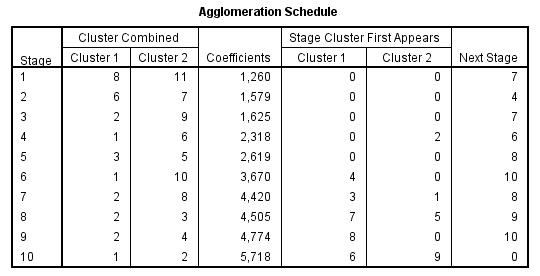
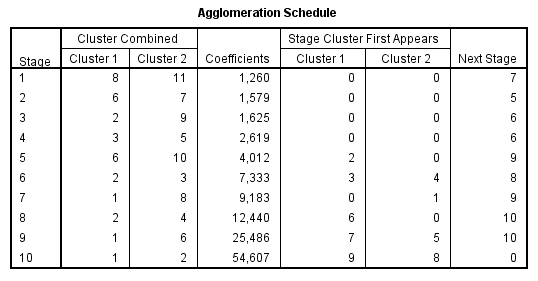
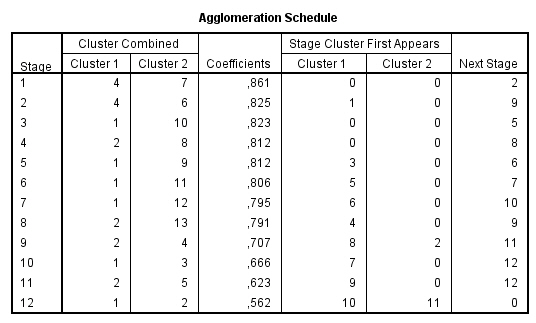
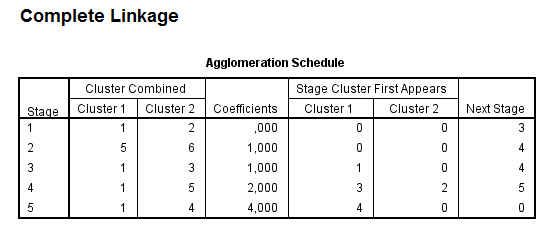
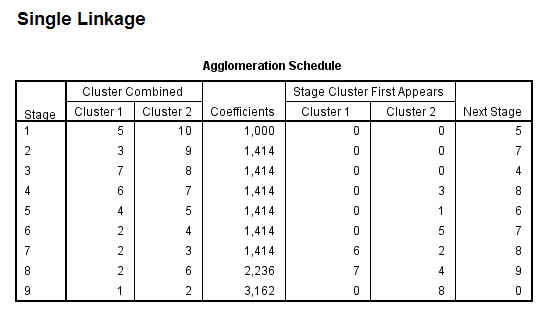
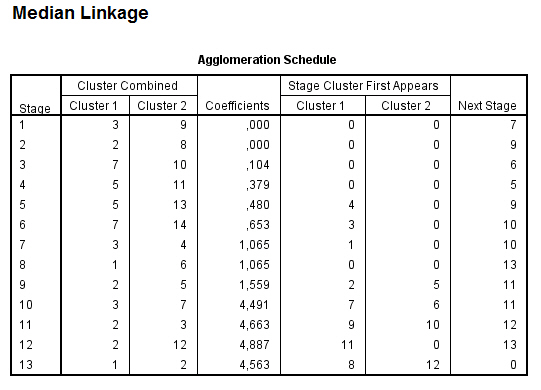
El Historial de conglomeración es una tabla que muestra un resumen numérico de la solución del método clúster utilizado. El Historial muestra los casos o conglomerados combinados en cada etapa, las distancias entre los casos o los conglomerados que se combinan (Coeficientes), así como el último nivel del proceso de conglomeración en el que cada caso (o variable) se unió a su conglomerado correspondiente. Cuando se combinan dos clusters, SPSS asigna al nuevo clúster la etiqueta menor entre las que tienen los clusters que se combinan.
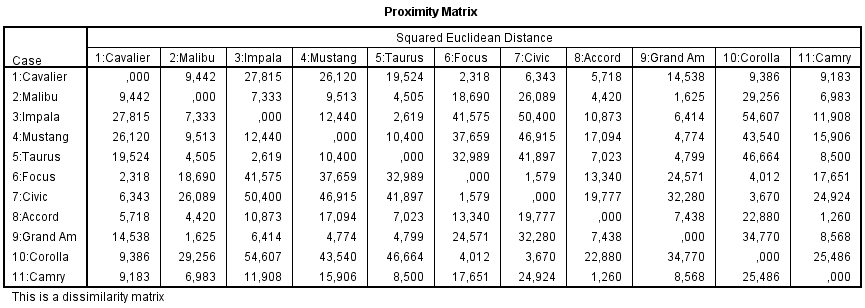
En nuestro ejemplo, en la primera etapa se unen los casos 8 y 11 (Accord (8), Camry (11)) porque son los que tienen la distancia más pequeña (1.260). El grupo creado por 8 y 11 aparece de nuevo en la etapa 7 donde se une al clúster 2 (formado en la etapa 3). Por lo tanto en esta etapa se unen los grupos creados en las etapas 1 y 3 y el grupo resultante formado por 8, 11, 2 y 9 aparece en la siguiente etapa la 8 .
Si hay muchos casos la tabla es bastante larga, pero suele ser más fácil de estudiar la columna de coeficientes para distinguir grandes distancias que analizar el dendrograma. Cuando se observa un salto inesperado en el coeficiente de distancia, la solución antes de ese hueco indica una buena elección de conglomerados .
Las mayores diferencias en la columna de los coeficientes se producen entre las etapas 5 y 6, lo que indica una solución de 6-clúster ((8, 11); (2,9); (3, 5); (4); (6, 7, 1); (10)) y entre las etapas 9 y 10, lo que indica una solución de 2-clúster. Estos son los mismos que los resultados del dendrograma.
En la caja de diálogo del Análisis de conglomerados jerárquicos pulsar Estadísticos…
Matriz de distancias. Proporciona las distancias o similaridades entre los elementos.
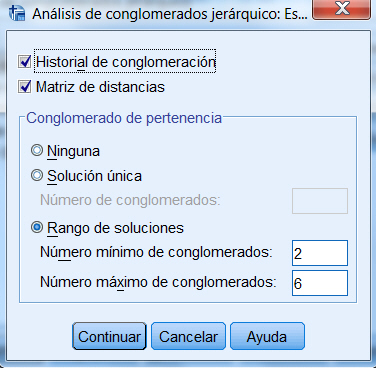
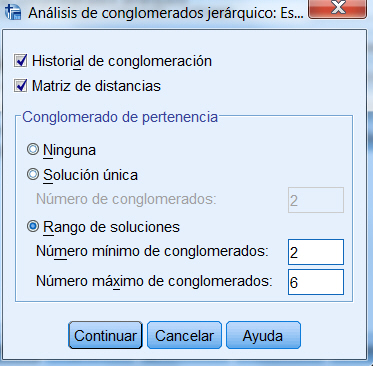
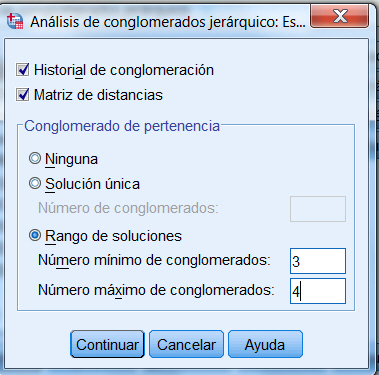
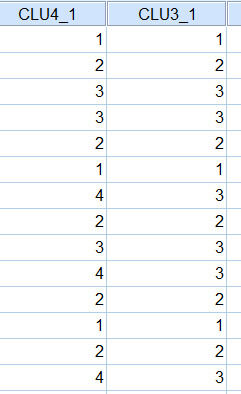
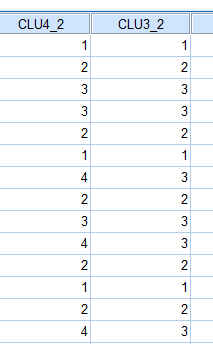
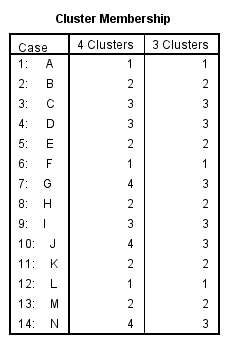
Conglomerado de pertenencia. Muestra el conglomerado al cual se asigna cada caso en una o varias etapas de la combinación de los conglomerados. Las opciones disponibles son: Solución única y Rango de soluciones.
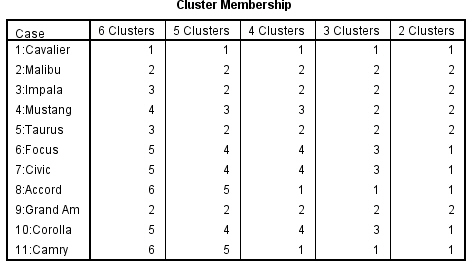
En nuestro estudio elegimos Historial de conglomeración, Matriz de distancias y en Conglomerado de pertenencia la opción Rango de soluciones (Número mínimo de conglomerados 2 y número máximo 6).
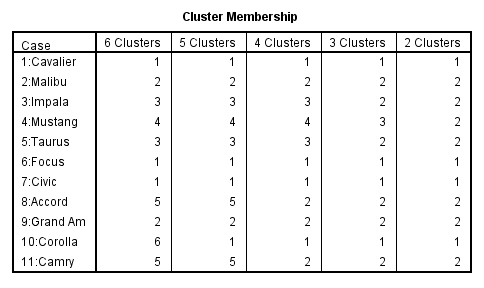 Esta tabla muestra los casos que pertenecen a cada clúster. Por ejemplo, si la solución son dos clusters, los casos Cavalier, Focus, Civic y Corolla forman el clúster 1 y los demás casos forman el clúster 2.
Esta tabla muestra los casos que pertenecen a cada clúster. Por ejemplo, si la solución son dos clusters, los casos Cavalier, Focus, Civic y Corolla forman el clúster 1 y los demás casos forman el clúster 2.
Esta tabla muestra la Matriz de distancias que proporciona las similaridades entre los casos
El programa permite guardar conglomerados de pertenencia, estas variables se pueden utilizar en análisis posteriores para explorar otras diferencias entre los grupos. Para ello en la caja de diálogo del Análisis de conglomerados jerárquicos pulsar Guardar…
Este cuadro de diálogo presenta las siguientes opciones:
-
Ninguna (opción por defecto) no guarda los conglomerados de pertenencia
-
Solución única: Guarda un número determinado de conglomerados de pertenencia
-
Rango de soluciones: Guarda un rango de soluciones de conglomerados de pertenencia.
En este estudio no hemos podido obtener unas conclusiones sólidas sobre la agrupación de los automóviles de mayor venta en función de sus precios, fabricante, modelo y propiedades físicas. Puede deberse a que hemos utilizado como método de clúster el Vecino más próximo que, aunque es aconsejable para examinar los grados de similitud es pobre en la construcción de los distintos grupos. Por ello, debemos volver a realizar de nuevo el análisis utilizando otro método de conglomerado.
Supuesto práctico 2
Realizar el supuesto práctico anterior anterior utilizando como Método de conglomerado, el Vecino más lejano.
Para ejecutar un análisis de conglomerados con vinculación completa (Vecino más lejano). En la caja de diálogo de conglomerados jerárquicos pulsar Método…
En la ventana seleccionar como Método de conglomeración: Vecino más lejano y seleccionar Puntuaciones Z . Pulsar Continuar.
En la ventana de diálogo de Análisis de conglomerados jerárquico, seleccionar Gráficos. Y dentro de esta opción: seleccionar Dendrograma y en Tempanos: Ninguna. Pulsar Continuar y Aceptar
En las primeras etapas, el Historial de conglomeración para la solución de vinculación completa (vecino más lejano) es similar a la solución de vinculación única (vecino más próximo). En cambio en las etapas finales los historiales de conglomeración son muy diferentes. Mediante el método de conglomeración del vecino más lejano se realiza una clasificación fuerte de dos o tres grupos .
La primera gran diferencia es entre las etapas 5 y 6 (6 clusters), la segunda entre 8 y 9 (3 clusters) y entre 9 y 10 (2 clusters).
La decisión de esta clasificación se refleja en el dendrograma.
- La división inicial del árbol forma dos grupos, (8, 11, 1, 6, 7, 10) y (2, 9, 3, 5, 4). El clúster primero contiene los automóviles más pequeños y el clúster segundo contiene los coches más grandes.
- El grupo de coches más pequeños se puede dividir en dos subgrupos, uno de ellos formado por los coches más pequeños y más baratos. Así la división siguiente en 3 clusters: (Accord (8), Camry (11), Cavalier (1)), (Focus (6), Civic (7), Corolla (10)), estos tres coches son más pequeños y más baratos que los tres anteriores) y (Malibu (2), Gran Am (9), Impala (3), Taurus (5), Mustang (4)).
Resumen
La solución de la vinculación completa (vecino más lejano) es satisfactoria debido a que sus grupos son diferentes, mientras que la solución del vecino más cercano es menos concluyente. Usando como Método de conglomeración la vinculación completa (Vecino más lejano), se puede determinar la competencia que hay entre los vehículos en la fase de diseño mediante la introducción de sus especificaciones como nuevos casos en el conjunto de datos y volver a ejecutar el análisis.
A continuación vamos a mostrar la Matriz de distancias y los conglomerados de pertenencia, para ello en la caja de diálogo de Conglomerados jerárquicos pulsar Estadísticos… y realizar la siguiente selección
Pulsar Continuar y Aceptar
Supuesto práctico 3
Una compañía de telecomunicaciones realiza un estudio con el fin de reducir el abandono de sus clientes. Para ello dispone de un archivo de datos, donde cada caso corresponde a un cliente distinto del que registra diversa información demográfica y del uso del servicio. El objetivo es segmentar su base de clientes por patrones de uso del servicio. Si los clientes se pueden clasificar por el uso, la empresa puede ofrecer paquetes más atractivos para sus clientes. Las variables que indican el uso y no uso de los servicios están contenidas en el archivo Telecomunicaciones1.sav.
El archivo de datos telecomunicaciones1.sav contiene 1000 datos y está formado por las siguientes variables: región, permanencia, edad, estado_civil, dirección, ingresos_familiares, nivel_educativo, empleo, género, n-pers_hogar, llamadas_gratuitas, alquiler_equipo, tarjeta_llamada, inalámbrico, larga_distancia_mes, llamadas_gratuitas_mes, equipo_mes, tarjeta_mes, inalámbrico_mes, líneas_múltiples, mensaje_voz, servicio_busca, internet, identificador_llamada, desvío_llamadas, llamada_a_tres, facturación_electrónica.
Utilizar el procedimiento Análisis de conglomerados jerárquico para estudiar las relaciones entre los distintos servicios.
Para ejecutar el análisis de conglomerados, elija en los menús: Analizar/ Clasificar/Conglomerados Jerárquicos …
Pulsar Restablecer para restaurar la configuración por defecto.
Seleccionar para Variables: Servicio de llamadas gratuitas, Alquiler de equipo, Servicio de tarjeta de llamada, Servicio inalámbrico, Líneas múltiples, mensajes de voz, servicio de busca, internet, Identificador de llamadas, llamadas en espera, Desvío de llamadas, llamadas a tres, Facturación electrónica
Seleccionar Variables en Conglomerar
Pulsar Gráficos…. Seleccionar Dendrograma y en Témpanos seleccionar Ninguna
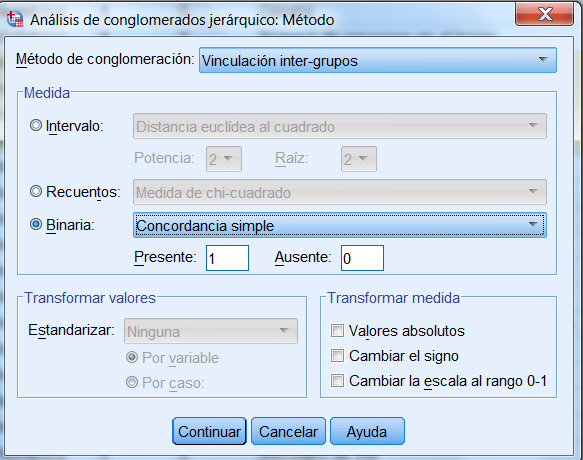
Pulsar Continuar y en el cuadro de diálogo Análisis de conglomerados jerárquico, en Método de conglomeración seleccionar Vinculación inter-grupos; en Medida seleccionar Binaria y dentro de Binaria, elegir Concordancia simple. Dado que las variables en el análisis son indicadores de si un cliente tiene un servicio, se debe elegir entre las medidas binarias.
Pulsar Continuar y Aceptar
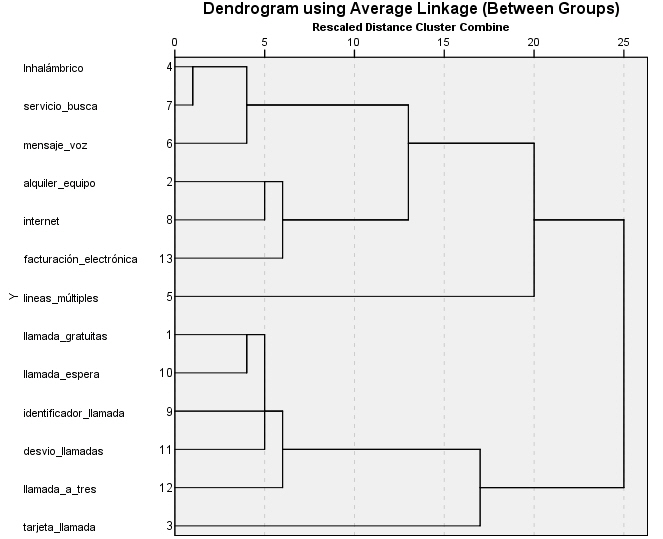
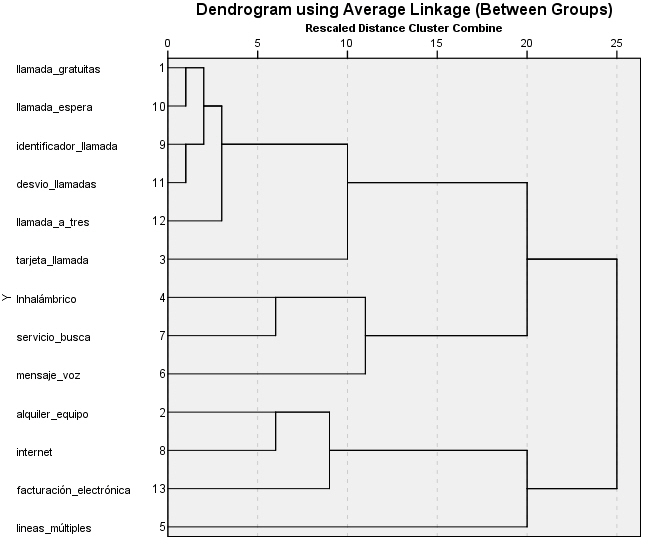
En las medidas binarias, la columna de los coeficientes informa de las medidas de similitud, por lo tanto, los valores de este coeficiente van disminuyendo en cada etapa del análisis. Es difícil interpretar los resultados, por lo que recurrimos al Dendrograma.
El dendrograma muestra que los patrones de uso de Líneas múltiples y Servicio de tarjeta de llamadas son distintos de los otros servicios. Estos otros se agrupan en tres grupos. Un grupo incluye inalámbrico, servicio_busca y mensaje_voz. Otro incluye alquiler_equipo, internet, y facturación_electrónica. El último grupo contiene las variables llamadas_gratuitas, llamadas_espera, identificador_llamada, desvío_llamadas y llamada_a_tres. El grupo servicio inalámbrico está más cerca del grupo de Internet que el grupo LlamEsp.
Supuesto práctico 4
Realizar de nuevo el estudio con la medida de distancia de Jaccard y comparar los resultados.
Para ejecutar un análisis de conglomerados con la medida de distancia de Jaccard, en el cuadro de diálogo de Análisis de Conglomerados Jerárquicos, pulsar Método y en la ventana correspondiente seleccionar Jaccard como medida binaria.
Pulsar Continuar y Aceptar en el cuadro de diálogo Análisis de conglomerados jerárquico.
Utilizando la medida de Jaccard, los tres grupos básicos son los mismos, pero el grupo servicio inalámbrico está más cerca del grupo LlamEsp que el grupo Internet.
La diferencia entre la simple adaptación y las medidas de Jaccard es que la medida Jaccard no considera dos servicios similares si una persona no está suscrita. Es decir, casación simple considera que los servicios inalámbricos y de Internet son similares cuando un cliente esté en ambos o en ninguno, mientras que Jaccard considera que son similares sólo cuando un cliente tiene dos servicios. Esto provoca una diferencia en las soluciones de clúster porque hay muchos clientes que no tienen servicios inalámbricos o Internet. Por lo tanto, estos grupos son más similares en la solución de casación simple que la solución de Jaccard. La medida que se utiliza depende de la definición de “similares” que se aplica a la situación.
Análisis clúster de k-medias
Análisis clúster de K-medias es una herramienta diseñada para asignar los casos a un número fijo de grupos, cuyas características no se conocen, pero se basan en un conjunto de variables que deben ser cuantitativas. Es muy útil cuando se quiere clasificar un gran número de casos. Es un método de agrupación de casos que se basa en las distancias existentes entre ellos en un conjunto de variables cuantitativas. Este método de aglomeración no permite agrupar variables. El objetivo de optimalidad que se persigue es “maximizar la homogeneidad dentro de los grupos.”
Es el método que se usa más habitualmente, es fácil de programar y da resultados razonables. Tiene por objetivo separar las observaciones en K clúster, de manera que cada dato pertenezca a un grupo y sólo a uno. El algoritmo busca con un método iterativo:
-
Los centroides (medias, medianas,… ) de los K clusters
-
Asigna cada individuo a un clúster.
El algoritmo requiere que se especifique el número de conglomerados, también se puede especificar los centros iniciales de los clusters si conoce de antemano dicha información.
En este método, la medida de distancia o de similaridad entre los casos se calcula utilizando la distancia euclídea. Es muy importante el tipo de escala de las variables, si las variables tienen diferentes escalas (por ejemplo, una variable se expresa en dólares y otra en años), los resultados podrían ser equívocos. En estos casos, se debería considerar la estandarización de las variables antes de realizar el análisis de conglomerados de k-medias.
Este procedimiento supone que se ha seleccionado el número apropiado de conglomerados y que se han incluido todas las variables relevantes. Si se ha seleccionado un número inapropiado de conglomerados o se han omitido variables relevantes, los resultados podrían ser equívocos.
Existen varias formas de implementarlo pero todas ellas siguen, básicamente, los siguientes pasos:
-
Paso 1. Se toman al azar k clusters iniciales y se calculan los centroides (medias) de los clusters
-
Paso 2. Se calcula la distancia euclídea de cada observación a los centroides de los clusters y se reasigna cada observación al grupo más próximo formando los nuevos clusters que se toman en lugar de los primeros como una mejor aproximación de los mismos
-
Paso 3. Se calculan los centroides de los nuevos clusters
-
Paso4. Se repiten los pasos 2) y 3) hasta que se satisfaga un criterio de parada como, por ejemplo, no se produzca ninguna reasignación, es decir, los clusters obtenidos en dos iteraciones consecutivas son los mismos.
El método suele ser muy sensible a la solución inicial dada por lo que es conveniente utilizar una que sea buena. Una forma de construirla es mediante una clasificación obtenida por un algoritmo jerárquico.
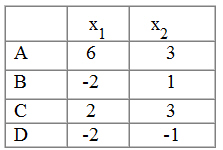
Como aclaración, vamos a realizar el procedimiento para el caso de dos variables X1 y X2 y cuatro elementos A, B, C. D. Los datos son los siguientes:
Se quiere agrupar estas observaciones en dos clusters (k = 2)
Paso 1. De forma arbitraria se agrupan las observaciones en dos clusters (AB) y (CD) y se calculan los centroides de cada clúster
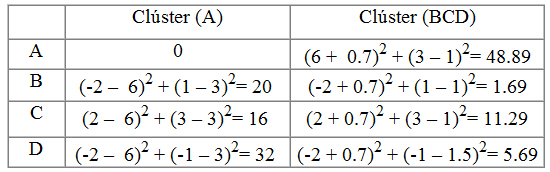
Paso 2. Calculamos la distancia euclídea de cada observación a los centroides de los clusters y reasignamos cada una de estas observaciones al clúster que esté más próximo
Como A está más próximo al clúster (AB) que al clúster (CD), no se reasigna
Como B está más próximo al clúster (CD) que al clúster (AB), se reasigna al clúster (CD) formando el clúster (BCD).
A continuación se calculan los centroides de los nuevos clusters
Paso 3. Se repite el paso 2 calculando las distancias de cada observación a los centroides de los nuevos clusters para ver si se producen cambios de nuevas reasignaciones
Como no se producen cambios en las ubicaciones de los clusters, la solución para k=2 clusters es: Clúster 1: (A) y Clúster 2: (BCD).
Existe la posibilidad de utilizar esta técnica de manera exploratoria, clasificando los casos e iterando para encontrar la ubicación de los centroides, o sólo como técnica de clasificación, clasificando los casos a partir de centroides conocidos. Cuando se utiliza como técnica exploratoria, es habitual que se desconozca el número idóneo de conglomerados, (como el ejemplo numérico que hemos hecho), por lo que es conveniente repetir el análisis con distinto número de conglomerados y comparar las soluciones obtenidas; en estos casos también se puede utilizar el método análisis de conglomerados jerárquico con una submuestra de casos.
Por último hay que interpretar la clasificación obtenida, ello requiere, en primer lugar, un conocimiento suficiente del problema analizado. Hay que estar abierto a la posibilidad de que no todos los grupos obtenidos tienen por qué ser significativos. Algunas ideas que pueden ser útiles en la interpretación de los resultados son las siguientes:
-
-
Realizar ANOVAS y MANOVAS para ver qué grupos son significativamente distintos y en qué variables lo son.
-
Realizar Análisis Discriminante.
-
Realizar un Análisis Factorial o de Componentes Principales para representar gráficamente los grupos obtenidos y observar las diferencias existentes entre ellos.
-
Calcular perfiles medios por grupos y compararlos.
-
Conviene hacer notar, finalmente, que es una técnica eminentemente exploratoria cuya finalidad es sugerir ideas al analista a la hora de elaborar hipótesis y modelos que expliquen el comportamiento de las variables analizadas identificando grupos homogéneos de objetos. Los resultados del análisis deberían tomarse como punto de partida en la elaboración de teorías que expliquen dicho comportamiento
Un buen análisis de clúster es:
-
Eficiente. Utiliza el menor número de grupos posibles.
-
Efectivo. Captura todas las agrupaciones estadísticamente y comercialmente importante. Por ejemplo, un clúster con cinco clientes puede ser estadísticamente diferente, pero no es muy rentable.
Supuesto práctico 5
Utilizamos de nuevo el archivo de datos ventas_vehículos.sav que contiene estimaciones de ventas, listas de precios y especificaciones físicas de varias marcas y modelos de vehículos. Se desea hacer un estudio de mercado para poder determinar las posibles competencias para sus vehículos, para ello agrupamos las marcas de los coches según los datos disponibles, hábitos de consumo, sexo, edad, nivel de ingresos, etc. de los clientes. Las empresas de coches adaptan sus estrategias de desarrollo de productos y de marketing en función de cada grupo de consumidores para aumentar las ventas y el nivel de fidelidad a la marca.
El archivo de datos ventas_vehículos.sav contiene 157 datos y está formado por las siguientes variables:
Variables tipo cadena: marca (Fabricante); modelo
Variables tipo numérico: ventas (en miles); reventa (Valor de reventa en 4 años); tipo (Tipo de vehículo: Valores: {0, Automóvil; 1, Camión}); precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo).
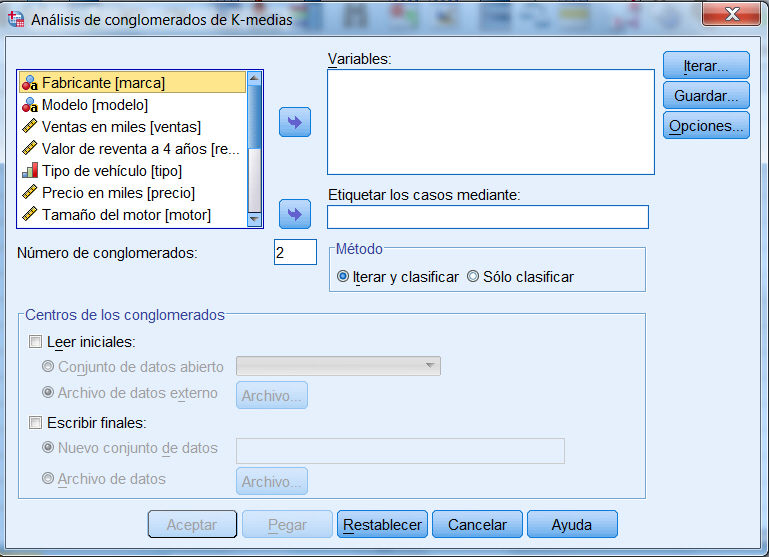
Para obtener el análisis de conglomerados de K-medias, elegir en los menús:
Analizar/Clasificar/ conglomerados de K-medias.
La lista de variables del archivo de datos ofrece un listado con todas las variables del archivo (numéricas y de cadena), pero las variables de cadena sólo pueden utilizarse para etiquetar casos.
Para obtener un análisis de conglomerados de K medias:
-
Seleccionar las variables numéricas que se desea utilizar para diferenciar a los sujetos y formar los conglomerados, y trasladarlas a la lista Variables:
-
Opcionalmente, seleccionar una variable para identificar los casos en las tablas de resultados y en los gráficos y trasladarla a la lista Etiquetar casos mediante.
Nº de conglomerados. En este cuadro de texto se encuentra seleccionada por defecto la solución de dos conglomerados. Para solicitar un número mayor de conglomerados, introducir el número deseado en el cuadro.
Método. Las opciones de este apartado permiten indicar si los centros de los conglomerados deben o no ser estimados iterativamente:
-
Iterar y clasificar. El procedimiento se encarga de estimar los centros iterativamente y de clasificar a los sujetos con respecto a los centros estimados.
-
Sólo clasificar. Se clasifica a los sujetos según los centros iniciales (sin actualizar sus valores iterativamente). Al marcar esta opción se desactiva el botón Iterar… , impidiendo esto el acceso a las especificaciones del proceso de iteración. Esta opción suele utilizarse junto con el botón Centros.
Centros de los conglomerados. Muestra dos opciones:
-
Leer iniciales de. Permite al usuario decidir qué valor deben tomar los centros de los conglomerados. El botón Archivo de datos externo sirve para indicar el nombre y ruta del archivo que contiene los valores de los centros. El nombre del archivo seleccionado se muestra junto al botón Conjunto de datos abierto. Lo habitual es designar un archivo resultante de una ejecución previa (guardado con la opción Escribir finales en) y en conjunción con la opción Sólo clasificar del apartado Método.
-
Escribir finales en. Guarda los centros de los conglomerados finales en un archivo de datos externo. Este archivo puede utilizarse posteriormente para la clasificación de nuevos casos. El botón Archivo de datos permite asignar nombre y ruta al archivo de destino. El nombre del archivo seleccionado se muestra junto al botón Nuevo conjunto de datos.
Los archivos de datos utilizados por estas dos opciones contienen variables con nombres especiales reconocidas automáticamente por el sistema. No es recomendable generar libremente la estructura de estos archivos; es preferible dejar que sea el propio procedimiento el que los genere.
El archivo ventas_vehículos.sav contiene 157 datos Para hacer más comprensible la representación gráfica de los resultados, vamos a comenzar utilizando únicamente el 20 % de los casos de la muestra.
Para ello, en el menú principal seleccionar: Datos/Seleccionar casos
Seleccionar la opción Muestra aleatoria de casos y pulsar Ejemplo…
En el apartado Tamaño de la muestra, introducir el valor 20 en recuadro de texto de la opción Aproximadamente p % de todos los casos. Pulsar el botón Continuar y Aceptar.
Aceptando estas selecciones, el archivo de datos queda filtrado, dejando disponibles sólo 36 de los 157 casos existentes.
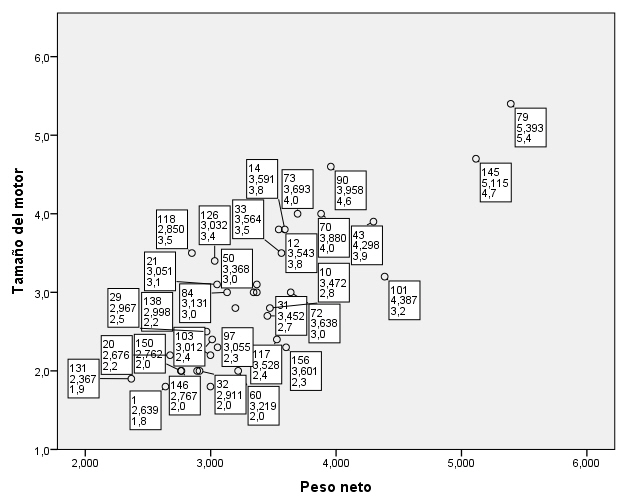
Vamos a comenzar representando la distancia existente entre los casos en dos variables de interés, hemos elegido la variable peso y la variable Tamaño del motor. Para ello, seleccionar en el menú principal Gráficos/Generador de gráficos…
En la ventana Galería, en Elija entre , seleccionar Dispersión/…
Arrastrar el gráfico de Dispersión simple a la ventana de presentación preliminar del gráfico
Desplazar la variable peso (peso total del vehículo en kg) al eje abscisas y la Tamaño del motor al eje de ordenadas
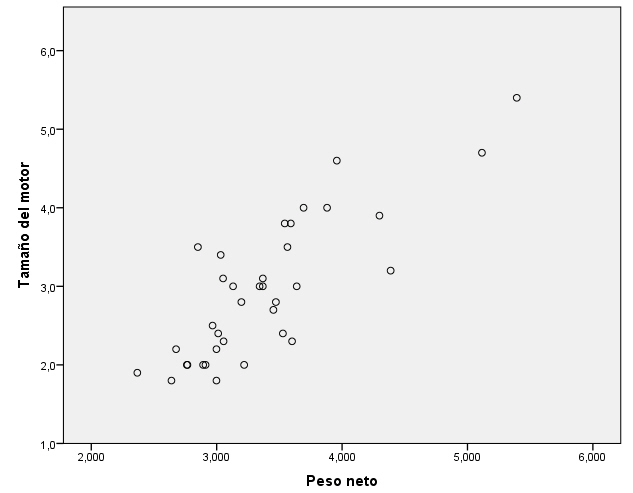
Pulsar Aceptar y se muestra el siguiente gráfico
En el diagrama de dispersión están representados los valores Peso y Tamaño motor de los 36 casos seleccionados. Se puede apreciar que existe un grupo de vehículos relativamente numeroso con peso y tamaño de motor reducidos y otro grupo más disperso de vehículos de mayor peso y mayor motor.
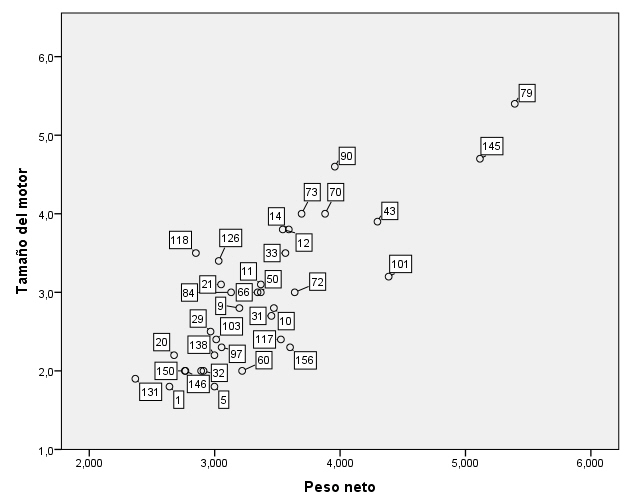
Pulsar dos veces en el gráfico y en la ventana Editor de gráficos seleccionar Elementos/Mostrar etiquetas de datos…
Se han identificado, mediante el número de caso, los dos vehículos aparentemente más alejados entre sí (el caso 79 y el caso 131). La nube de puntos, por tanto, incita a pensar que existen al menos dos grupos naturales de casos.
Para clasificar los casos en dos grupos:
Seleccionar en el cuadro de diálogo de Análisis de conglomerados de K-medias la opción Sólo Clasificar. Trasladar las variables motor y peso a la lista Variables.
Aceptando estas selecciones, el Visor ofrece los resultados que muestran las tablas siguientes
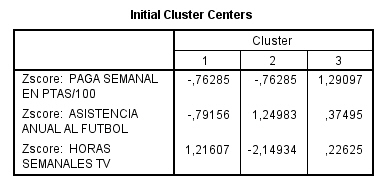
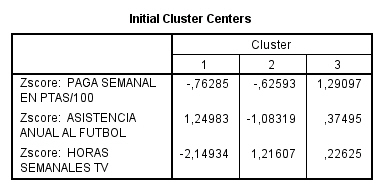
Esta tabla contiene los centros iniciales de los clusters, es decir, los valores que corresponden, en las dos variables de clasificación utilizadas, a los dos casos que han sido elegidos como centros respectivos de los dos conglomerados solicitados.
Seleccionando de nuevo, en la ventana del Editor Elementos/Mostrar etiquetas de datos… y en Propiedades pasar Peso neto y Tamaño de motor a la ventana de Mostrado:
Pulsar Aplicar
Se comprueba que los casos son el 131 (Conglomerado 1) y el 79 (Conglomerado 2), los mismos que han sido identificados en el diagrama de dispersión.
Una vez seleccionados los centros de los conglomerados, cada caso es asignado al conglomerado de cuyo centro se encuentra más próximo y comienza un proceso de ubicación iterativa de los centros. En la primera iteración se reasignan los casos por su distancia al nuevo centro y, tras la reasignación, se vuelve a actualizar el valor del centro. En la siguiente iteración se vuelven a reasignar los casos y a actualizar el valor del centro. Etc.
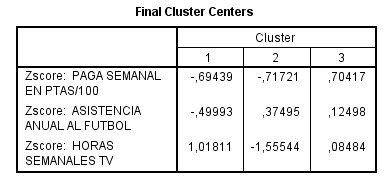
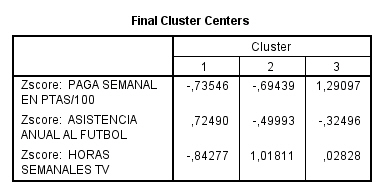
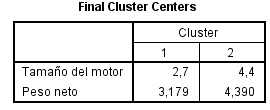 Esta tabla muestra los centros de los conglomerados finales es decir, los centros de los conglomerados tras el proceso de actualización iterativa. Comparando los centros finales (tras la iteración) de esta tabla con los centros iniciales (antes de la iteración) se puede apreciar con claridad un desplazamiento del centro del conglomerado 1 hacia la parte superior del plano definido por las dos variables de clasificación y un desplazamiento del centro del conglomerado 2 hacia la parte inferior.
Esta tabla muestra los centros de los conglomerados finales es decir, los centros de los conglomerados tras el proceso de actualización iterativa. Comparando los centros finales (tras la iteración) de esta tabla con los centros iniciales (antes de la iteración) se puede apreciar con claridad un desplazamiento del centro del conglomerado 1 hacia la parte superior del plano definido por las dos variables de clasificación y un desplazamiento del centro del conglomerado 2 hacia la parte inferior.
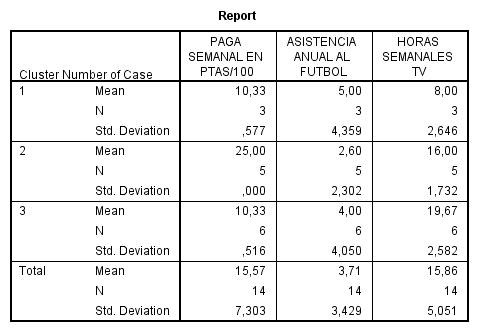
Esta tabla es de gran utilidad para interpretar la constitución de los conglomerados pues resume los valores centrales de cada conglomerado en las variables de interés. La interpretación de los resultados de nuestro ejemplo es simple: el primer conglomerado está constituido por vehículos de gran tamaño de motor y mucho peso, mientras que segundo conglomerado está constituido por los vehículos de tamaño de motor reducido y poco peso.
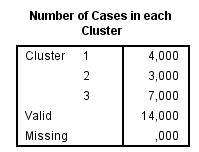
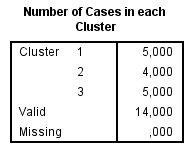
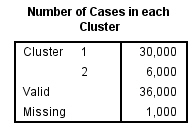 Por último, esta tabla informa sobre el Número de casos asignado a cada conglomerado. En nuestro ejemplo, los tamaños de los conglomerados son bastantes diferentes.
Por último, esta tabla informa sobre el Número de casos asignado a cada conglomerado. En nuestro ejemplo, los tamaños de los conglomerados son bastantes diferentes.
Para mostrar el Historial de iteraciones seleccionar en cuadro de diálogo de Análisis de conglomerados de K-medias la opción Iterar y Clasificar
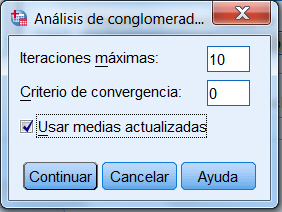
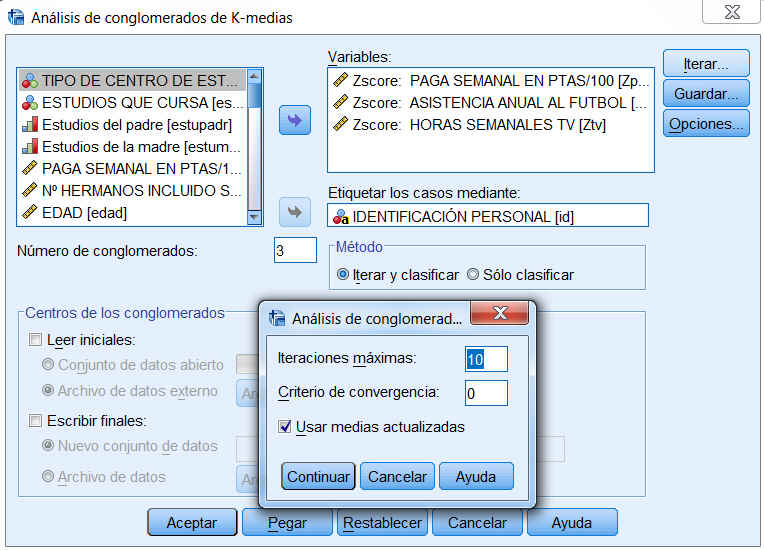
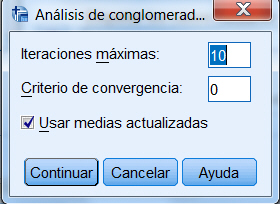 El subcuadro de diálogo Iterar permite controlar algunos detalles relacionados con el proceso de iteración utilizado para el cálculo de los centroides finales. Se puede determinar el número máximo de iteraciones o bien fijar un criterio de convergencia mayor que cero y menor que uno.
El subcuadro de diálogo Iterar permite controlar algunos detalles relacionados con el proceso de iteración utilizado para el cálculo de los centroides finales. Se puede determinar el número máximo de iteraciones o bien fijar un criterio de convergencia mayor que cero y menor que uno.
Nº máximo de iteraciones. Limita el número de iteraciones que el algoritmo k-medias puede llevar a cabo. El proceso de iteración se detiene después del número de iteraciones especificado, incluso aunque no se haya satisfecho el criterio de convergencia. Este número debe estar entre el 1 y el 999.
Criterio de convergencia. Permite modificar el criterio de convergencia utilizado por SPSS para detener el proceso de iteración, determina cuándo cesa la iteración. El valor de este criterio es, por defecto, cero, pero puede cambiarse introduciendo un valor diferente en el cuadro de texto. El valor introducido representa la proporción de la distancia mínima existente entre los centros iniciales de los conglomerados. Por tratarse de una proporción, este valor debe ser mayor o igual que cero y menor o igual que 1. Por ejemplo, si se introduce un valor igual a 0,02, el proceso de iteración cesará cuando entre una iteración y la siguiente no se consiga desplazar ninguno de los centros una distancia superior al dos por ciento de la menor de las distancias existentes entre cualquiera de los centros iniciales. La tabla del historial de las iteraciones muestra, en una nota a pie de tabla, el desplazamiento obtenido en la última iteración (se haya alcanzado o no el criterio de convergencia).
Usar medias actualizadas. Permite solicitar la actualización de los centros de los conglomerados (recalcula los centroides con cada individuo asignado al grupo). Cuando se asigna un caso a uno de los conglomerados se calcula de nuevo el valor del centro del conglomerado. Cuando se selecciona la actualización de los centros de los conglomerados, el orden de los casos en el archivo de datos puede afectar a la solución obtenida.
Si no se selecciona esta opción, los nuevos centros de los conglomerados finales se calcularán después de la clasificación de todos los casos.
Dejamos el número de iteraciones máximas que viene por defecto, 10, seleccionamos Usar medias actualizadas y pulsamos Continuar y Aceptar
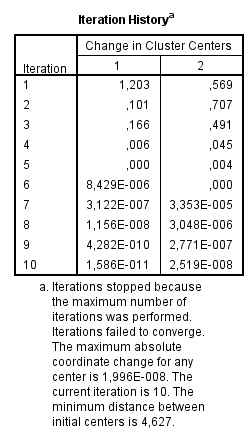 Comprobamos que no se alcanza la convergencia por lo que aumentamos las Iteraciones máximas a 20 y se muestra el siguiente Historial de iteraciones
Comprobamos que no se alcanza la convergencia por lo que aumentamos las Iteraciones máximas a 20 y se muestra el siguiente Historial de iteraciones
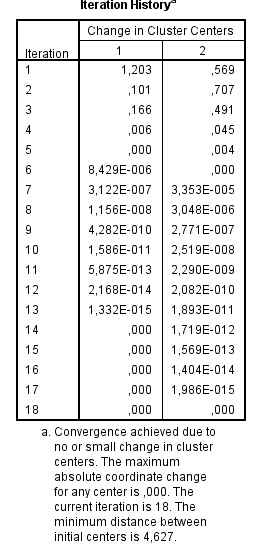
Esta tabla resume el historial de iteraciones (18 en nuestro ejemplo) con indicación del cambio (desplazamiento) experimentado por cada centro en cada iteración. Puede observarse que, conforme avanzan las iteraciones, el desplazamiento de los centros se va haciendo más y más pequeño, hasta llegar a la 18 iteración, en la que ya no existe desplazamiento alguno.
El proceso de iteración se detiene, por defecto, cuando se alcanzan 10 iteraciones o cuando de una iteración a otra no se produce ningún cambio en la ubicación de los centroides (cambio = 0). En nuestro ejemplo, el proceso ha finalizado antes de alcanzar 18 iteraciones porque en la 19 ya no se produce ningún cambio.
Supuesto práctico 6
El archivo de datos telecomunicaciones1.sav. contiene 1000 datos y está formado por las siguientes variables: región, permanencia, edad, estado_civil, dirección, ingresos_familiares, nivel_educativo, empleo, género, n-pers_hogar, llamadas_gratuitas, alquiler_equipo, tarjeta_llamada, inalámbrico, larga_distancia_mes, llamadas_gratuitas_mes, equipo_mes, tarjeta_mes, inalámbrico_mes, líneas_múltiples, mensaje_voz, servicio_busca, internet, identificador_llamada, desvío_llamadas, llamada_a_tres, facturación_electrónica.
Es conveniente unificar la escala de las variables con las que vamos a trabajar, por ello vamos a transformar algunas de ellas tomando en primer lugar logaritmo neperiano y después tipificando.
Para realizar el logaritmo neperiano, de la variable larga_distancia-mes, seleccionamos en el menú principal Transformar/Calcular Variable…
 En Grupo de funciones elegir Aritméticas, en Funciones y variables especiales elegir Ln, pulsar la flecha y en la ventana Expresión numérica pasar la variable Larga_distancia_mes.
En Grupo de funciones elegir Aritméticas, en Funciones y variables especiales elegir Ln, pulsar la flecha y en la ventana Expresión numérica pasar la variable Larga_distancia_mes.
En Variable destino poner el nombre de la nueva variable ln_larga_distanca y pulsar Aceptar.
En el Editor de datos se ha formado una nueva variable que contiene los logaritmos neperianos de la variable larga_distancia_mes.
A continuación vamos a tipificar la variable creada, para ello, seleccionar en el menú principal Analizar/Estadísticos descriptivos/Descriptivos…
 Seleccionar la variable ln_larga_distancia y elegir Guardar valores tipificados como variables. En el editor de datos se ha formado una nueva variable zln_larga_distancia que contiene los valores tipificados de la variable ln_larga_distancia.
Seleccionar la variable ln_larga_distancia y elegir Guardar valores tipificados como variables. En el editor de datos se ha formado una nueva variable zln_larga_distancia que contiene los valores tipificados de la variable ln_larga_distancia.
En el archivo de datos datos telecomunicaciones_1.sav:
-
Transformar mediante logaritmo neperiano y tipificación las siguientes variables: larga_distancia_mes, llamadas_gratuitas, equipos, tarjetas, inalámbrico
-
Transformar mediante tipificación las siguientes variables: lineas_múltiples, mensaje_voz, servicio_busca, internet, identificador_llamada, llamada_espera, desvio_llamadas, llamada_a_tres, facturación_electrónica.
El nuevo fichero de datos, lo llamamos datos telecomunicaciones_2.sav
En este nuevo fichero de datos. Se pide
- Utilizar el Análisis de conglomerados de K-medias para encontrar subconjuntos de clientes “similares”.
- Guardar el conglomerado de pertenencia y la distancia desde centro del conglomerado en nuevas variables (para 4 clusters).
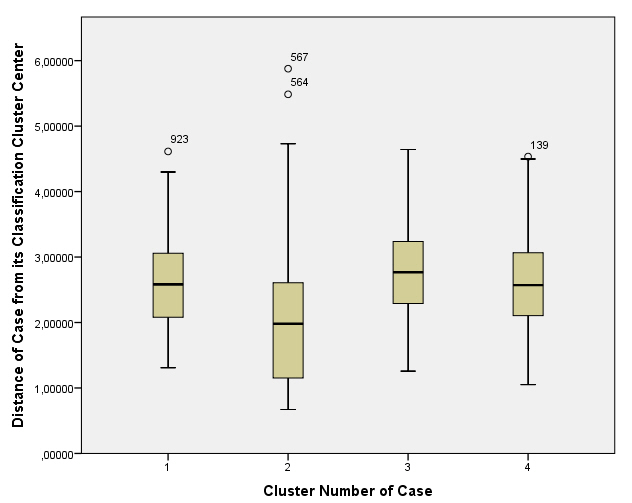
- Realizar un Diagrama de cajas con las variables conglomerado de pertenencia y la distancia desde centro. Interpretar esta representación
En primer lugar utilizamos Análisis de conglomerados de K-medias
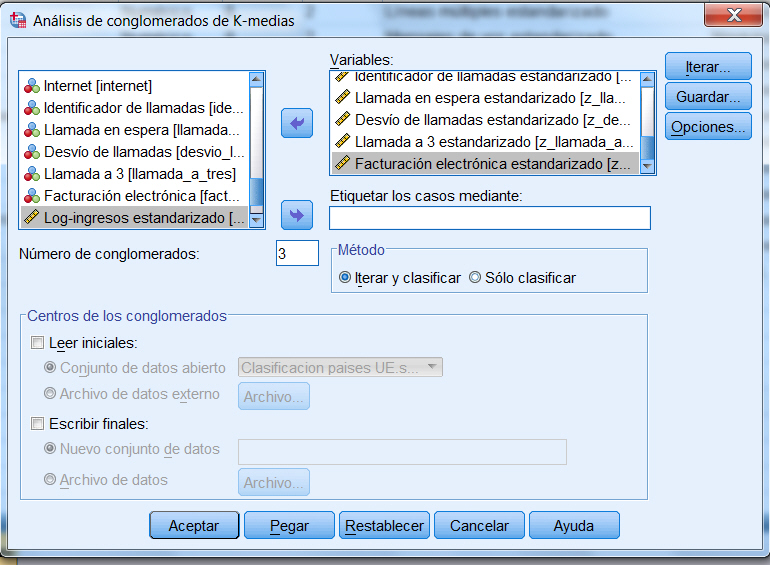
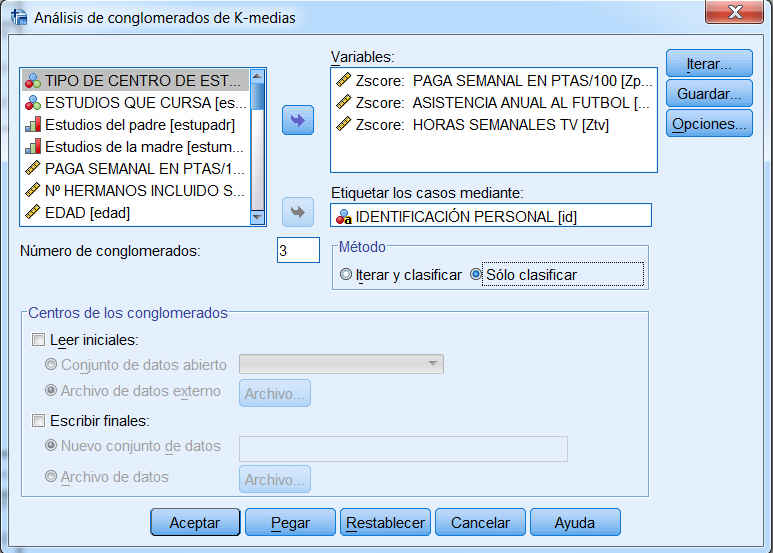
Seleccionar las variables que se van a utilizar en el análisis de conglomerados, en nuestro caso del archivo de datos telecomunicaciones_2.sav, seleccionar como variables: zln_larga_distancia, zln_llamadas_gratuitas, zln_equipos, zln_tarjetas, zln_inalámbrico, z_lineas_múltiples, z_mensaje_voz, z_servicio_busca, z_internet, z_identificador_llamada, z_llamada_espera, z_desvio_llamadas, z_llamada_a_tres, z_facturación_electrónica.
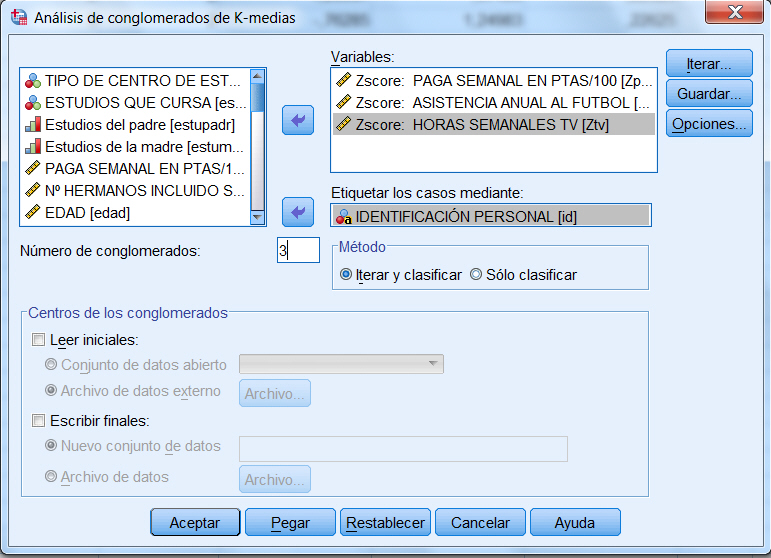
Especificar el Número de conglomerados. (Este número no debe ser inferior a 2 ni superior al número de casos del archivo de datos.) Ponemos 3
El comando de análisis de conglomerados de k-medias es eficaz principalmente porque no calcula las distancias entre todos los pares de casos, como hacen muchos algoritmos de conglomeración, como el utilizado por el comando de conglomeración jerárquica.
Pulsar Iterar… y poner 20 como número máximo de iteraciones
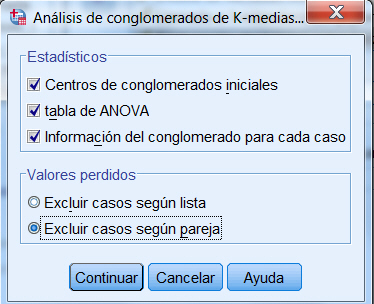
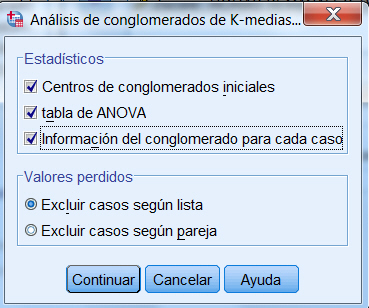
 Pulsar Continuar y en la caja de diálogo de Análisis de conglomerados K-medias pulsar Opciones. En esta ventana seleccionar, en Estadísticos, Centro de conglomerados iniciales, tabla ANOVA, Información de conglomerados para cada caso y en Valores perdidos elegir Excluir casos según pareja. Hay muchos valores perdidos debido al hecho de que la mayoría de los clientes no se suscriben a todos los servicios, así que excluir casos según pareja maximiza la información que se puede obtener de los datos a costa de posiblemente sesgar los resultados.
Pulsar Continuar y en la caja de diálogo de Análisis de conglomerados K-medias pulsar Opciones. En esta ventana seleccionar, en Estadísticos, Centro de conglomerados iniciales, tabla ANOVA, Información de conglomerados para cada caso y en Valores perdidos elegir Excluir casos según pareja. Hay muchos valores perdidos debido al hecho de que la mayoría de los clientes no se suscriben a todos los servicios, así que excluir casos según pareja maximiza la información que se puede obtener de los datos a costa de posiblemente sesgar los resultados.
El cuadro de diálogo Opciones permite obtener algunos estadísticos y controlar el tratamiento que se desea dar a los valores perdidos. Para acceder a las opciones:
Estadísticos. Las opciones de este apartado permiten seleccionar algunos estadísticos adicionales como Centros de conglomerados iniciales, Tabla de ANOVA e Información del conglomerado para cada caso.
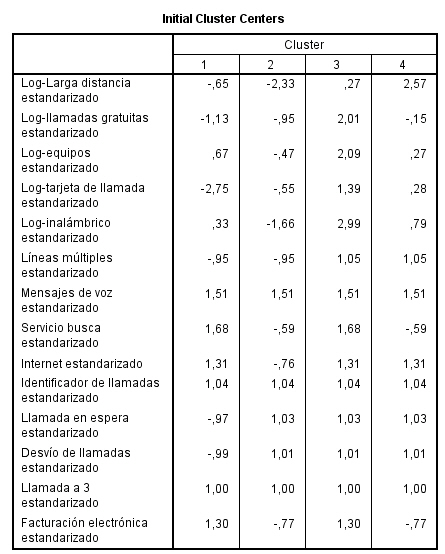
Centros de conglomerados iniciales. Primera estimación de las medias de las variables para cada uno de los conglomerados. Por defecto se selecciona entre los datos un número de casos debidamente espaciados igual al número de conglomerados. Los centros iniciales de los conglomerados se utilizan como criterio para una primera clasificación y, a partir de ahí, se van actualizando. Muestra una tabla con los casos que el procedimiento selecciona como centros iniciales de los conglomerados. Esta opción se encuentra seleccionada por defecto.
Tabla de ANOVA. Muestra una tabla de análisis de varianza que incluye las pruebas F invariantes para cada una de las variables incluidas en el análisis. Las pruebas F son sólo descriptivas y las probabilidades resultantes no se deben interpretar. La tabla de ANOVA no se mostrará si se asignan todos los casos a un único conglomerado.
El análisis de varianza se obtiene tomando los grupos definidos por los conglomerados como factor y cada una de las variables incluidas en el análisis como variable dependiente. Una nota al pie de tabla informa de que los estadísticos F sólo deben utilizarse con una finalidad descriptiva pues los casos no se han asignado aleatoriamente a los conglomerados sino que se han asignado intentando optimizar las diferencias entre los conglomerados. Además, los niveles críticos asociados a los estadísticos F no se deben interpretar de la manera habitual pues el procedimiento K-medias no aplica ningún tipo de corrección sobre la tasa de error (es decir, sobre la probabilidad de cometer errores tipo I cuando se llevan a cabo muchos contrastes).
Información del conglomerado para cada caso. Muestra un listado de todos los casos utilizados en el análisis, indicando para cada caso, el conglomerado final al que ha sido asignado y la distancia euclídea entre el caso y el centro del conglomerado utilizado para clasificar el caso. También muestra la distancia euclídea entre los centros de los conglomerados finales. Los casos se muestran en el mismo orden en el que se encuentran en el archivo de datos.
Valores perdidos. Las opciones disponibles son: Excluir casos según lista o Excluir casos según pareja.
Excluir casos según lista. Excluye los casos con valores perdidos en cualquiera de las variables incluidas en el análisis (Opción por defecto).
Excluir casos según pareja. Asigna los casos a los conglomerados en función de las distancias calculadas en todas las variables en las que no tengan valores perdidos.
Pulsar Continuar y Aceptar y se muestran las siguientes salidas
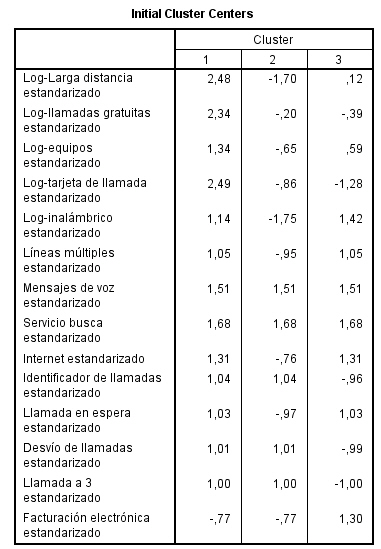
Muestra una tabla con los casos, debidamente espaciados, que el procedimiento ha seleccionado como centros iniciales de los tres conglomerados.
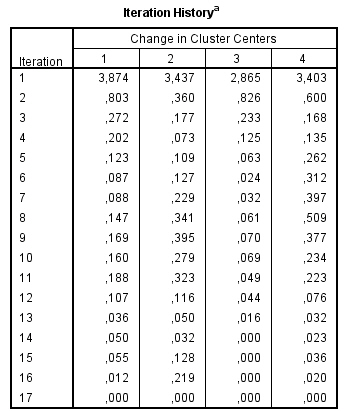
 El historial de iteraciones muestra el progreso del proceso de agrupación en cada paso.
El historial de iteraciones muestra el progreso del proceso de agrupación en cada paso.
La convergencia se consigue debido al nulo o pequeño cambio en los centros de los conglomerados. En la iteración 18 se ha conseguido que el máximo de coordenadas absolutas para cualquier centro sea, 0. La distancia mínima entre los centros iniciales es 6.611.
En las 13 primeras iteraciones, los centros de los conglomerados cambian bastante.
A partir de la iteración 14 se van estableciendo los centros y en las cuatro últimas iteraciones son ajustes menores.
Si el algoritmo se detiene porque se ha alcanzado el número máximo de iteraciones, es posible que se deba aumentar ese máximo, ya que la solución si no se aumenta puede ser inestable.
Por ejemplo, si se hubiera dejado el número máximo de iteraciones en el 10, la solución obtenida todavía estaría en un estado de flujo.
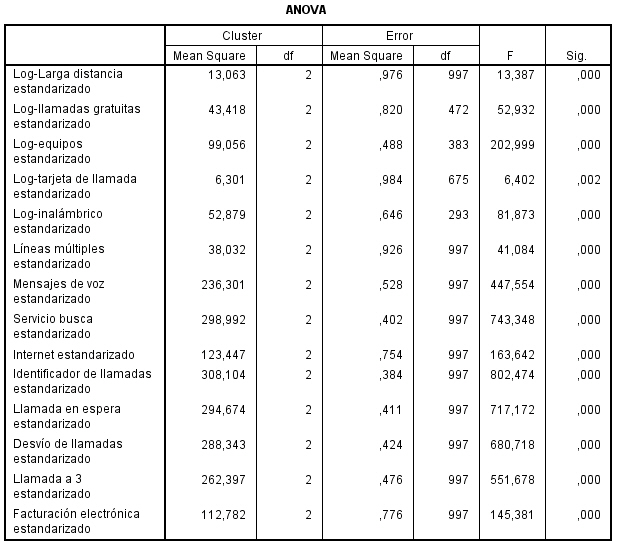
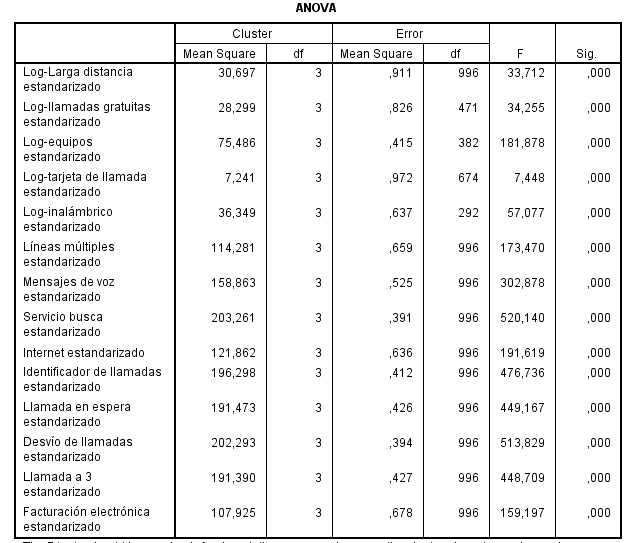
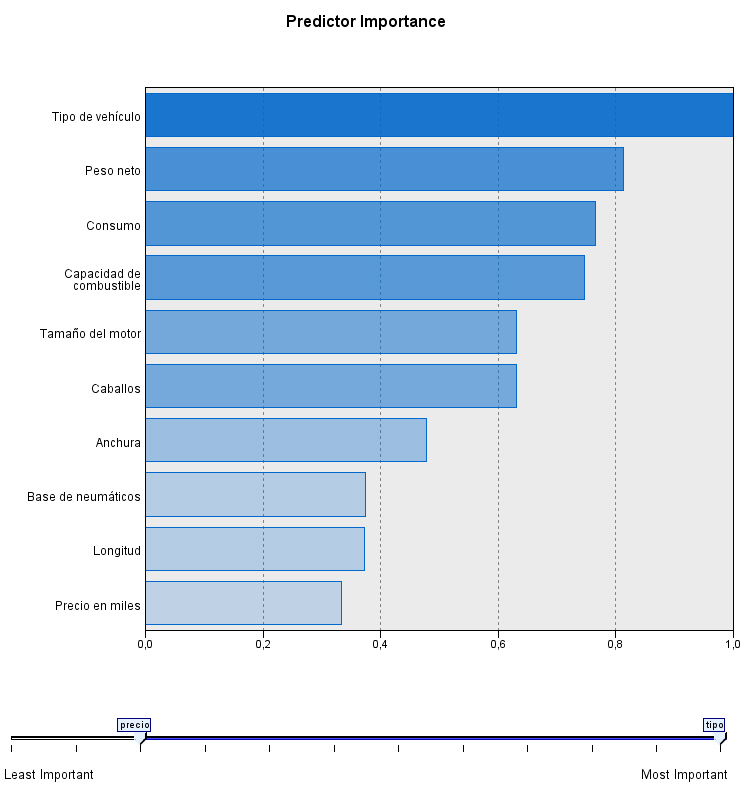
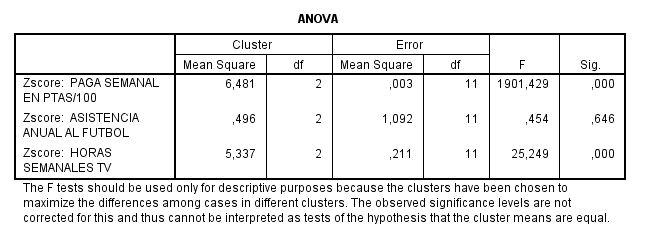
La tabla de ANOVA indica qué variables contribuyen más a la solución de clúster. Las variables con valores de F grandes proporcionan la mayor separación entre las agrupaciones. Las pruebas F sólo se deben utilizar con una finalidad descriptiva puesto que los conglomerados han sido elegidos para maximizar las diferencias entre los casos en diferentes conglomerados. Los niveles críticos no son corregidos, por lo que no pueden interpretarse como pruebas de la hipótesis de que los centros de los conglomerados son iguales.
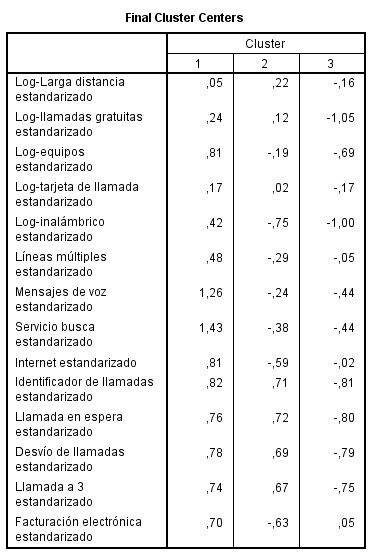
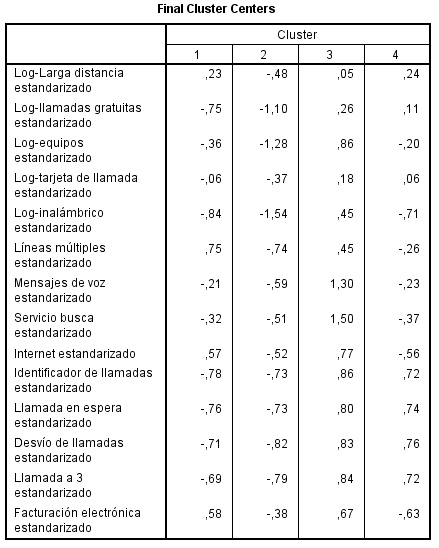
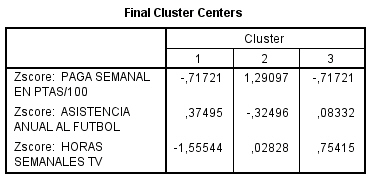
Los centros de los conglomerados finales reflejan las características del caso típico de cada clúster:
-
Los clientes del conglomerado 1 tienden a ser grandes consumidores que compran una gran cantidad de servicios.
-
Los clientes del conglomerado 2 tienden a ser derrochadores moderados que compran los servicios de “el que llama” como identificador de llamada, llamada en espera, desvío de llamada,…
-
Los clientes del conglomerado 3 tienden a gastar muy poco y no compran muchos servicios.
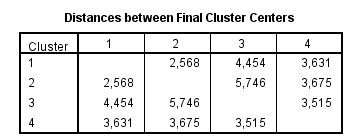
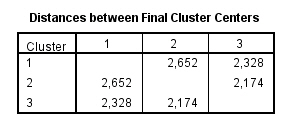
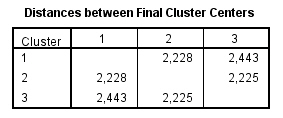
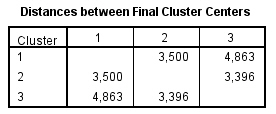 Esta tabla muestra las distancias euclideas entre los centros de los conglomerados finales. Mayores distancias entre los grupos se corresponden con mayores diferencias entre ellos.
Esta tabla muestra las distancias euclideas entre los centros de los conglomerados finales. Mayores distancias entre los grupos se corresponden con mayores diferencias entre ellos.
Los grupos 1 y 3 son los más diferentes, la distancia entre ellos es 4.863.
El grupo 2 es aproximadamente igual a los grupos 1 y 3.
Estas relaciones entre los grupos también se pueden intuir desde los centros de los conglomerados finales, pero la interpretación es más complicada ya que el número de variables es grande.
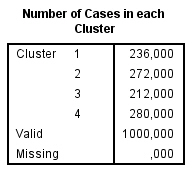
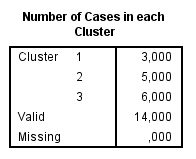
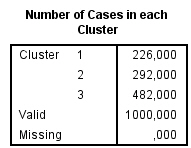 El tercer clúster es el que tiene el mayor número de casos asignados (482), que desgraciadamente es el grupo menos rentable ya que como hemos visto anteriormente es el grupo que gasta menos y compra menos servicios. Tal vez sería conveniente hacer un cuarto clúster.
El tercer clúster es el que tiene el mayor número de casos asignados (482), que desgraciadamente es el grupo menos rentable ya que como hemos visto anteriormente es el grupo que gasta menos y compra menos servicios. Tal vez sería conveniente hacer un cuarto clúster.
A continuación vamos a
-
Guardar el conglomerado de pertenencia y la distancia desde centro del conglomerado en nuevas variables (para 4 clusters)
-
Realizar un Diagrama de cajas con las variables conglomerado de pertenencia y la distancia desde centro. Interpretar esta representación
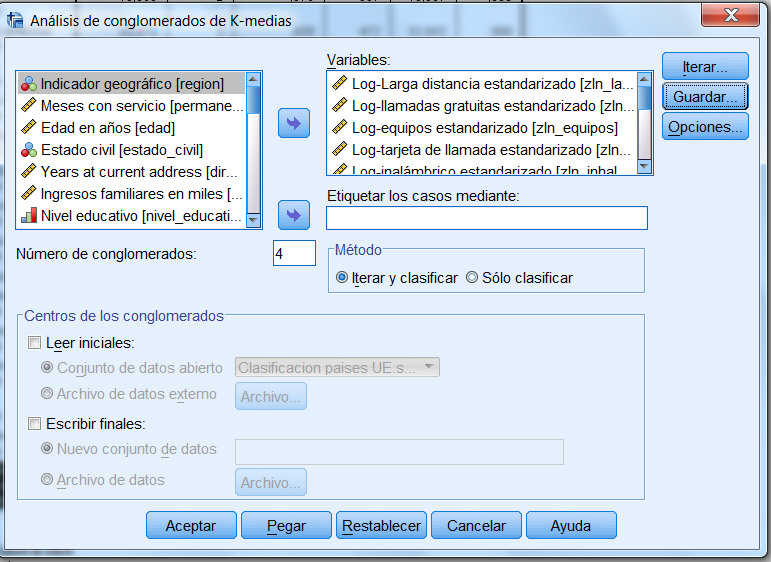
En primer lugar, vamos a guardar el conglomerado de pertenencia y la distancia desde centro del conglomerado y para ello, en el cuadro de diálogo de Análisis de conglomerados de K-medias, ponemos 4 en Número de clusters
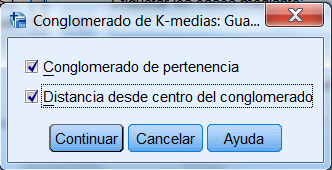
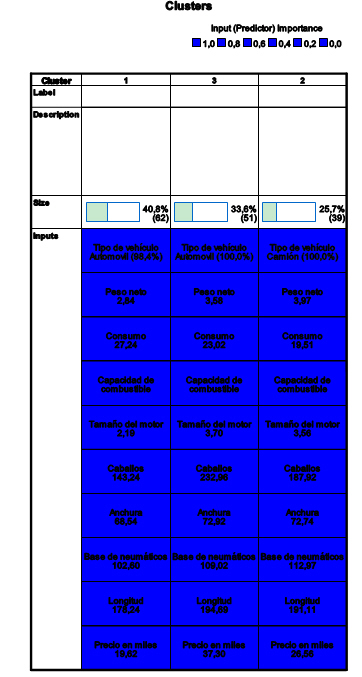
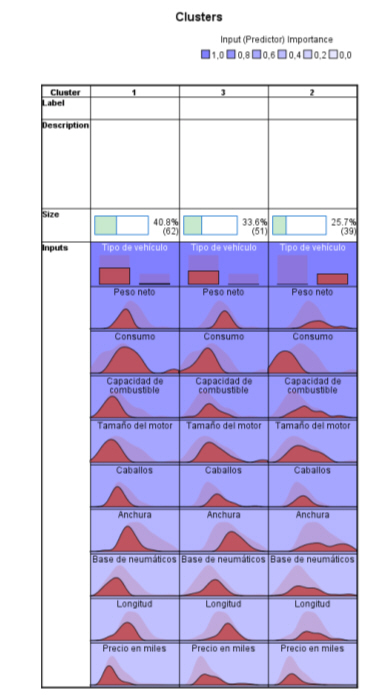
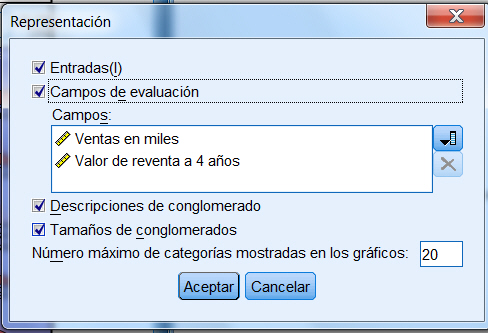
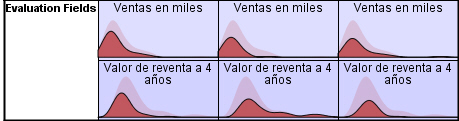
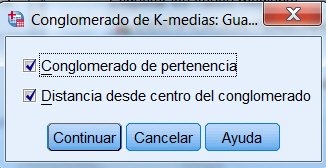
Y pulsamos Guardar… y elegir Conglomerado de pertenencia y Distancia desde centro del conglomerado
Mediante esta opción se guarda en el archivo de datos información de clasificación para cada caso como nuevas variables para que puedan ser utilizadas en análisis subsiguientes.
Conglomerado de pertenencia. Crea una nueva variable en el Editor de datos (con nombre QCL_#) cuyos valores indican el conglomerado final al que pertenece cada caso. Los valores de la nueva variable van desde 1 hasta el número de conglomerados. Esta información es útil, por ejemplo, para construir un diagrama de dispersión con marcas distintas para los casos pertenecientes a distintos conglomerados, o para llevar a cabo un análisis discriminante con intención de identificar la importancia relativa de cada variable en la diferenciación entre conglomerados.
Distancia desde el centro del conglomerado. Crea una variable en el Editor de datos (con nombre QCL_#) cuyos valores indican la distancia euclídea existente entre cada caso y el centro del conglomerado al que ha sido asignado.
Pulsar Continuar y Aceptar. SPSS crea dos nuevas variables en el editor de datos: Las variables QCL_1 (conglomerado de pertenencia) y QCL_2 (distancia desde el centro del conglomerado).
Con el nuevo archivo de datos vamos a realizar el gráfico Diagrama de cajas (boxplot). Para ello seleccionamos en el menú principal Gráficos/Generador de gráficos… y en la salida correspondiente
Hacer clic en la ficha Galería, seleccionar Diagrama de caja de la lista de tipos de gráficos ,
Arrastrar y soltar el icono Boxplot simple en la ventana superior.
Arrastrar y soltar la variable QCL_2 (distancia desde el centro del conglomerado) en el eje y.
Arrastrar y soltar QCL_1 (conglomerado de pertenencia) sobre el eje x .
Pulsar Aceptar para crear el gráfico de caja .
Este gráfico nos ayuda a encontrar los valores extremos dentro de los grupos. Vemos que en el grupo 2 hay una gran variabilidad, pero todas las distancias están dentro de lo razonable.
Supuesto práctico 7
-
Aplicar conglomerados de K-medias al caso de 4 clusters
-
Analizar los resultados obtenidos con 4 clusters y compararlos con los obtenidos para el caso de 3 clusters. ¿Qué solución piensas que es la mejor?
En las salidas del clúster de k-medias tenemos las siguientes tablas
Esta tabla muestra que un grupo importante se pierde en la solución de tres clusters.
Los miembros del clúster 1 (propensos a comprar por Internet, utilizar larga distancia y líneas múltiples) y el clúster 2 (es un grupo muy poco consumidor). Ambos clusters proceden en gran parte del grupo 3 en la solución de tres clusters que era un grupo de clientes que gastaban muy poco y no compraban muchos servicios. Por lo tanto, en la solución de tres clusters se perdería el clúster 1, cuyos miembros son altamente propensos a comprar servicios relacionados con Internet, esto los constituye como un grupo distinto y posiblemente rentable.
Los grupos 3 y 4 parecen corresponder a los grupos 1 y 2 de la solución de tres clusters.
Los miembros del grupo 3 son grandes consumidores y los miembros del grupo 4 son propensos a comprar los servicios de identificador de llamadas, llamada en espera, desvío de llamadas, llamadas a 3.
Las distancias entre los grupos no han cambiado en gran medida.
-
Grupos 1 y 2 son los más similares, lo cual tiene sentido, ya que se combinaron
-
Grupos 2 y 3 son los más disímiles, ya que representan el comportamiento de gastos opuestos en la solución de tres clusters
-
El grupo 4 es igualmente de similar a los otros grupos.
Casi el 25 % de los casos pertenecen al grupo recientemente creado de clientes “e- servicios”, Clúster 1 con 236 casos, lo cual es muy significativo para sus beneficios.
Con el análisis de conglomerados de k-medias, en un inicio se agrupan los clientes en tres grupos. Sin embargo, esta solución no fue muy satisfactoria, por lo que se volvió a ejecutar el análisis con cuatro grupos, cuyos resultados fueron mejores. En el el análisis de conglomerados con tres clusters un grupo “Internet” potencialmente rentable se perdió.
Este ejemplo pone de relieve el carácter exploratorio del análisis de conglomerados, ya que es imposible determinar el “mejor” número de grupos hasta que se haya ejecutado el análisis y se hayan examinado las soluciones.
Análisis clúster en dos etapas
El procedimiento Análisis de conglomerados en dos fases es una herramienta de exploración diseñada para descubrir las agrupaciones naturales (o conglomerados) de un conjunto de datos que, de otra manera, no sería posible detectar. El algoritmo que emplea este procedimiento incluye una serie de funciones que lo hacen diferente de las técnicas de conglomeración tradicionales:
-
Tratamiento de variables categóricas y continuas. Al suponer que las variables son independientes, es posible aplicar una distribución normal multinomial conjunta en las variables continuas y categóricas.
-
Selección automática del número de conglomerados. Mediante la comparación de los valores de un criterio de selección del modelo para diferentes soluciones de conglomeración, el procedimiento puede determinar automáticamente el número óptimo de conglomerados.
-
Escalabilidad. Mediante la construcción de un árbol de características de conglomerados (CF) que resume los registros, el algoritmo en dos fases puede analizar archivos de datos de gran tamaño.
El árbol de características de conglomerados y la solución final pueden depender del Orden de los casos. Para minimizar los efectos del orden estos deben ordenarse aleatoriamente. También se pueden obtener varias soluciones distintas con los casos ordenados en distintos órdenes aleatorios para comprobar la estabilidad de una solución determinada. En situaciones en que esto resulta difícil debido a unos tamaños de archivo demasiado grandes, se pueden sustituir varias ejecuciones por una muestra de casos ordenados con distintos órdenes aleatorios.
Supuestos. La medida de la distancia de la verosimilitud supone que las variables del modelo de conglomerados son independientes. Además, se supone que cada variable continua tiene una distribución normal y que cada variable categórica tiene una distribución multinomial.
Las comprobaciones empíricas internas indican que este procedimiento es bastante robusto frente a las violaciones tanto del supuesto de independencia como de las distribuciones, pero aún así es preciso tener en cuenta hasta qué punto se cumplen estos supuestos.
Los procedimientos que se pueden utilizar para comprobar si se cumplen estos supuesto son los siguientes:
-
Correlaciones bivariadas para comprobar la independencia de dos variables continuas.
-
Tablas de contingencia para comprobar la independencia de dos variables categóricas.
-
El procedimiento de medias para comprobar la independencia entre una variable continua y una variable categórica.
-
El procedimiento de exploración para comprobar la normalidad de una variable continua.
-
La prueba de Chi-cuadrado para comprobar si una variable categórica sigue una distribución multinomial.
Procedimiento de clúster en dos etapas
Está basado en un algoritmo que produce resultados óptimos si todas las variables son independientes, las variables continuas están normalmente distribuidas y las variables categóricas son multinomiales. Pero es un procedimiento que funciona razonablemente bien en ausencia de estos supuestos.
La solución final depende del orden de entrada de los datos, para minimizar el efecto deberíamos ordenar el fichero de forma aleatoria.
Algoritmo del procedimiento. Los dos pasos de este procedimiento se pueden resumir como sigue:
- Primer paso: formación de preclúster de los casos originales. Estos son clusters de los datos originales que se utilizarán en lugar de las filas del fichero original para realizar los clusters jerárquicos en el segundo paso. Todos los casos pertenecientes a un mismo preclúster se tratan como una entidad sencilla.
El procedimiento se inicia con la construcción de un árbol de características del Clúster (CF). El árbol comienza colocando el primer caso en la raíz del árbol en un nodo de hoja que contiene información de la variable sobre ese caso. Cada caso sucesivamente se añade a continuación a un nodo existente o forma un nuevo nodo, basado en la similaridad con los nodos existentes y utilizando medidas de distancias como el criterio de similaridad. Un nodo que contiene varios casos contiene un resumen de información sobre esos casos. Por lo tanto, el árbol CF proporciona un resumen del archivo de datos.
- Segundo paso: Los nodos de las hojas del árbol CF se agrupan utilizando un algoritmo de agrupamiento aglomerativo. El clúster se puede utilizar para producir un rango de soluciones. Para determinar el número de clusters óptimo, cada una de estas soluciones de clúster se compara utilizando el Criterio Bayesiano de Schwarz (BIC) o el Criterio de Información de Akaike (AIC) como criterio de agrupamiento.
Supuesto práctico 8
Utilizamos de nuevo el archivo de datos ventas_vehículos.sav que contiene estimaciones de ventas, listas de precios y especificaciones físicas hipotéticas de varias marcas y modelos de vehículos.
El archivo de datos ventas_vehículos.sav está formado por las siguientes variables:
Variables tipo cadena: marca (Fabricante); modelo
Variables tipo numérico: ventas (en miles); reventa (Valor de reventa en 4 años); tipo (Tipo de vehículo: Valores: {0, Automóvil; 1, Camión}); precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo).
Para obtener un análisis de conglomerados en dos etapas, seleccionar en el menú principal: Analizar/Clasificar/Conglomerado de bietápico… y se muestra el cuadro de diálogo del Análisis de conglomerados en dos fases
Medida de distancia. Especifica la medida de similaridad entre dos clusters
-
Log-verosimilitud. La medida de la verosimilitud realiza una distribución de probabilidad entre las variables. Las variables continuas se supone que tienen una distribución normal, mientras que las variables categóricas se supone que son multinomiales. Se supone que todas las variables son independientes. Esta medida de distancia se debe utilizar en datos mixtos. La distancia entre los dos clusters dependerá del decremento en el log-verosimilitud cuando ambas se combinan en un único clúster.
- Euclídea. La medida euclídea es la distancia según una “línea recta” entre dos conglomerados. Sólo se puede utilizar cuando todas las variables son continuas.
Número de conglomerados. Esta opción permite especificar el número deseado de clusters o dejar que el algoritmo seleccione ese número
- Determinar automáticamente. El procedimiento determinará automáticamente el número “óptimo” de conglomerados, utilizando el criterio especificado en Criterio de conglomeración. Criterio Bayesiano de Schwarz (BIC) o el Criterio de información Akaike (AIC).
-
Especificar número fijo. Permite fijar el número de conglomerados de la solución. Debe ser un número entero positivo para especificar el número máximo de conglomerados que el procedimiento debe tener en cuenta.
Recuento de variables continuas. Proporciona un resumen de las especificaciones acerca de la tipificación de variables continuas realizadas en el cuadro de diálogo Opciones.
Criterio de conglomeración. Mediante esta opción el algoritmo de conglomeración determina el número de conglomerados. Se puede especificar tanto el criterio de información bayesiano (BIC) como el criterio de información de Akaike (AIC).
En este supuesto práctico se selecciona para el campo Variables categóricas: La variable tipo (Tipo de vehículo) y para el campo Variables Continuas: precio; motor; CV; pisada; ancho; largo; peso_neto; depósito y mpg.
Se pulsa Opciones
Tratamiento de valores atípicos. Permite tratar los valores atípicos de manera especial durante la formación de clúster si se llena el árbol de características de los clusters (CF). Este árbol se considera lleno si no puede aceptar ningún caso más en un nodo hoja y no hay ningún nodo hoja que se pueda dividir.
Realizar tratamiento de ruido:
- Si selecciona esta opción y el árbol CF se llena, se hará volver a crecer después de colocar los casos existentes en hojas poco densas, en una hoja de “ruido”. Se considera que una hoja es poco densa si contiene un número de casos inferior a un determinado porcentaje de casos del máximo tamaño de hoja. Tras volver a hacer crecer el árbol, los valores atípicos se colocarán en el árbol CF en caso de que sea posible. Si no es así, se descartarán los valores atípicos.
- Si no selecciona esta opción y el árbol CF se llena, se hará volver a crecer utilizando un umbral del cambio en distancia mayor. Tras la conglomeración final, los valores que no se puedan asignar a un conglomerado se considerarán como valores atípicos. Al conglomerado de valores atípicos se le asigna un número de identificación de –1 y no se incluirá en el recuento del número de conglomerados.
Asignación de memoria. Permite especificar la cantidad máxima de memoria en megabytes (MB) que puede utilizar el algoritmo de conglomeración. Si el procedimiento supera este máximo, utilizará el disco para almacenar la información que no se pueda colocar en la memoria. Especificar un número mayor o igual que 4.
- Consultar con el administrador del sistema si desea conocer el valor máximo que puede especificar en su sistema.
- Si este valor es demasiado bajo, es posible que el algoritmo no consiga obtener el número correcto o deseado de conglomerados.
Tipificación de variables. El algoritmo de conglomeración trabaja con variables continuas tipificadas. Todas las variables continuas que no estén tipificadas deben dejarse como variables en la lista Para tipificar. Para ahorrar algún tiempo y trabajo para el ordenador, se puede seleccionar todas las variables continuas que ya haya tipificado como variables en la lista Asumidas como tipificadas.
Pulsar Avanzado>>
Criterios de ajuste del árbol CF. Los siguientes ajustes del algoritmo de conglomeración se aplican específicamente al árbol de características de conglomerados (CF) y deberán cambiarse con cuidado:
- Umbral del cambio en distancia inicial. Éste es el umbral inicial que se utiliza para hacer crecer el árbol CF. Si se ha insertado una determinada hoja en el árbol CF que produciría una densidad inferior al umbral, la hoja no se dividirá. Si la densidad supera el umbral, se dividirá la hoja.
- Nº máximo de ramas (por nodo hoja). Número máximo de nodos filiales que puede tener una hoja.
- Máxima profundidad de árbol. Número máximo de niveles que puede tener un árbol CF.
- Máximo número posible de nodos. Indica el número máximo de nodos del árbol CF que puede generar potencialmente el procedimiento, de acuerdo con la función (bd+1 – 1) / (b – 1), donde b es el número máximo de ramas y d es la profundidad máxima del árbol. Tener en cuenta que un árbol CF excesivamente grande puede agotar los recursos del sistema y afectar negativamente al rendimiento del procedimiento. Como mínimo, cada nodo requiere 16 bytes.
Actualización del modelo de conglomerados. Este grupo permite importar y actualizar un modelo de conglomerados generado en un análisis anterior. El archivo de entrada contiene el árbol CF en formato XML. A continuación, se actualizará el modelo con los datos existentes en el archivo activo. Se debe seleccionar los nombres de las variables en el cuadro de diálogo principal en el mismo orden en que se especificaron en el análisis anterior. El archivo XML permanecerá inalterado, a no ser que se escriba específicamente la nueva información del modelo en el mismo nombre de archivo.
Si se ha especificado una actualización del modelo de conglomerados, se utilizarán las opciones pertenecientes a la generación del árbol CF que se especificaron para el modelo original. Concretamente, se utilizarán los ajustes del modelo guardado acerca de la medida de distancia, el tratamiento del ruido, la asignación de memoria y los criterios de ajuste del árbol CF, por lo que se ignorarán todos los ajustes de estas opciones que se hayan especificado en los cuadros de diálogo.
Nota: Al realizar una actualización del modelo de conglomerados, el procedimiento supone que ninguno de los casos seleccionados en el conjunto de datos activo se utilizó para crear el modelo de conglomerados original. El procedimiento también supone que los casos utilizados en la actualización del modelo proceden de la misma población que los casos utilizados para crear el modelo; es decir, se supone que las medias y las varianzas de las variables continuas y los niveles de las variables categóricas son los mismos en ambos conjuntos de casos. Si los conjuntos de casos “nuevo” y “antiguo” proceden de poblaciones heterogéneas, se deberá ejecutar el procedimiento Análisis de conglomerados en dos fases para los conjuntos combinados de casos para obtener los resultados óptimos.
Se pulsa Resultados
Resultado del visor de salida. Proporciona opciones para la presentación los resultados
Gráficos y tablas. El resultado gráfico incluye un gráfico de calidad del clúster, de tamaño de conglomerado, de importancia de la variable, de cuadrícula de comparación de conglomerados e información de la casilla. Las tablas incluyen un resumen del modelo y una cuadrícula de conglomerados por funciones.
Campos de evaluación. Calcula los datos del clúster de las variables que no se han utilizado en su creación. Los campos de evaluación se pueden mostrar junto con las características de entrada del visor de modelos seleccionándolas en el cuadro de diálogo. Los campos con valores perdidos se ignoran.
Archivo de datos de trabajo. Guarda las variables en el conjunto de datos activo.
-
Crear variable del conglomerado de pertenencia. Esta variable contiene un número de identificación de conglomerado para cada caso. El nombre de esta variable es tsc_n, donde nes un número entero positivo que indica el ordinal de la operación de almacenamiento del conjunto de datos activo realizada por este procedimiento en una determinada sesión.
Archivos XML. El modelo de conglomerados final y el árbol CF son dos tipos de archivos de resultados que se pueden exportar en formato XML.
-
Exportar modelo final. También se puede exportar el modelo de conglomerado final al archivo especificado en formato XML (PMML). Se puede utilizar este archivo de modelo para aplicar la información del modelo a otros archivos de datos para puntuarlo.
-
Exportar árbol CF. Esta opción permite guardar el estado actual del árbol de conglomerados y actualizarlo más tarde utilizando nuevos datos.
Se selecciona Ventas en miles (ventas) y Valor de reventa a los 4 años (reventa) como Campos de evaluación:
Estos dos campos de evaluación elegidos, ventas y reventas no se han utilizado para crear los clusters, pero ayudarán a comprender mejor los grupos creados con este procedimiento. Pulsar Continuar y Aceptar. Se muestra la siguiente salida
El resumen del modelo incluye una tabla que contiene la siguiente información:
-
Algoritmo. El algoritmo de clúster utilizado, en este caso, “Dos fases”.
-
Características de entrada. El número de variables utilizadas (continuas y categóricas), también conocidos como entradas o predictores.
-
Conglomerados. Número de conglomerados de la solución.
Y muestra un gráfico de calidad del clúster que es una medida de silueta de la cohesión y separación de los clusters sombreada para indicar resultados pobres, correctos o buenos. Esta gráfica permite comprobar rápidamente si la calidad es insuficiente, en cuyo caso se puede optar por volver al nodo de modelado para cambiar los ajustes del modelo de conglomerado para producir mejores resultados.
Los resultados serán pobres, correctos o buenos de acuerdo con el trabajo de Kaufman y Rousseeuw (1990) sobre la interpretación de estructuras de conglomerados. Un resultado “bueno” indica que los datos reflejan una evidencia razonable o sólida de que existe una estructura de clusters, de acuerdo con la valoración Kaufman y Rousseeuw; una resultado “correcto” indica que esa evidencia es débil, y un resultado “pobre” significa que, según esa valoración, no hay evidencias obvias. Las medias de medida de silueta, en todos los registros, (B−A)/max(A,B), donde A es la distancia del registro al centro de su conglomerado y B es la distancia del registro al centro del conglomerado más cercano al que no pertenece.
Un coeficiente de silueta de 1 podría implicar que todos los casos están ubicados directamente en los centros de sus conglomerados. Un valor de −1 significaría que todos los casos se encuentran en los centros de conglomerado de otro conglomerado. Un valor de 0 implica, de media, que los casos están equidistantes entre el centro de su propio conglomerado y el siguiente conglomerado más cercano.
En nuestro ejemplo, la tabla con el resumen del modelo de clúster indica que se han formado 3 clusters con las diez características de entrada (variables categóricas y numéricas) seleccionadas y el gráfico de calidad del clúster indica que el resultado es correcto.
Haciendo doble Clik sobre la gráfica de la figura anterior se muestra en el Visor de modelos una vista interactiva del modelo utilizado
El Visor de clusters se compone de dos paneles, la vista principal en la parte izquierda y la vista relacionada o auxiliar de la derecha.
Vista principal. Hay dos vistas principales:
-
Resumen del modelo (predeterminado).
-
Conglomerados.
Vista auxiliar. Hay cuatro vistas relacionadas/auxiliares:
-
Importancia del predictor.
-
Tamaños de conglomerados (predeterminado).
-
Distribución de casillas.
-
Comparación de conglomerados.
Por defecto se muestra Tamaños de conglomerados mediante un gráfico de sectores que contiene cada clúster. Cada sector contiene la frecuencia en porcentaje de cada clúster. Pasando con el ratón por encima de los sectores del diagrama se muestra el número de registros asignados a cada clúster.
El 40,8% (62) de los registros fueron asignados al primer clúster, el 25,7% (39) al segundo y el 33,6% (51) al tercero.
Esta salida también muestra una tabla con la siguiente información sobre el tamaño de los clusters:
-
El tamaño del clúster más pequeño (recuento y porcentaje)
-
El tamaño del clúster mayor (recuento y porcentaje)
-
La proporción entre el tamaño del mayor clúster y el del menor
En la salida de la figura de la Vista principal del Visor de Clusters, en la barra de herramienta, se selecciona Conglomerados y se muestra la siguiente salida
Se muestra una tabla que contiene la siguiente información:
-
Clúster. Número de clusters creados por el algoritmo
-
Etiqueta. Etiquetas aplicadas a cada clúster (por defecto está en blanco). Pulsando dos veces sobre la casilla se puede introducir la etiqueta para describir el contenido del clúster
-
Descripción. Sobre el contenido del clúster (por defecto está en blanco). Pulsando dos veces en la casilla se puede introducir la descripción
-
Tamaño. Contiene el recuento de casos del clúster, porcentaje del tamaño y un gráfico mostrando el porcentaje
-
Entradas. De forma predeterminada los predictores o entradas individuales se muestran ordenados por Importancia global. Dicha importancia global de la característica se indica por el color sombreado del fondo de la casilla, siendo más oscuro cuanto más importante sea la característica. Situando el ratón en las casillas se muestra el nombre/etiqueta de la característica y el valor de importancia de la casilla. Dicha información depende del tipo de característica y el tipo de vista. También se pueden ordenar las características por Importancia dentro del clúster, por Nombre y por Orden de los datos. Estas formas clasificación de las características se realiza mediante los cuatro botones Clasificar características de la barra de herramientas.
En la Vista principal de los Conglomerados se puede seleccionar varias formas de mostrar la información de conglomerados:
-
Transponer conglomerados y características
-
Clasificar características
-
Clasificar conglomerados
-
Seleccionar contenido de las casillas.
Transponer conglomerados y características
Por defecto los conglomerados aparecen como columnas y las características aparecen como filas. Para invertir esta visualización, se pulsa el botón Transponer conglomerados y entradas. Esta opción es útil cuando hay muchos clusters y de esta forma se reduce la cantidad de desplazamiento horizontal necesario para visualizar los datos.
Clasificar características
-
Importancia global. Las características se clasifican en orden descendente de importancia global y el orden de clasificación es el mismo entre los distintos conglomerados. Si hay características que empatan en valores de importancia, éstas se muestran en orden de clasificación ascendente según el nombre.
-
Importancia dentro del conglomerado. Las características se clasifican con respecto de su importancia para cada conglomerado. Si hay características que empatan en valores de importancia, éstas se muestran en orden de clasificación ascendente según el nombre. Si esta opción está seleccionada, el orden de clasificación suele variar en los diferentes conglomerados.
-
Nombre. Las características se clasifican por nombre en orden alfabético.
-
Orden de los datos. Las características se clasifican por orden en el conjunto de datos.
Clasificar conglomerados
Los tres botones de Clasificar conglomerados de la barra de herramientas permiten ordenar los clusters por tamaño descendente (opción por defecto), por nombre en orden alfabético o, si se han creado etiquetas, por orden de etiqueta alfanumérico. Las características con la misma etiqueta se clasifican por nombre de conglomerado. Si los conglomerados se clasifican por etiqueta y se modifica la etiqueta de un conglomerado, el orden de clasificación se actualiza automáticamente.
Contenido de casilla
Los cuatro botones Casillas de la barra de herramientas permiten cambiar la visualización del contenido de las casillas y campos de evaluación.
-
Las casillas muestran los centros de conglomerados. Por defecto, las casillas muestran nombres/etiquetas de las características y la tendencia central para cada combinación de conglomerado/característica. La media se muestra para los campos continuos y la moda con el porcentaje de categoría para los campos categóricos.
-
Las casillas muestran las distribuciones absolutas. Muestra nombres/etiquetas de las características y distribuciones absolutas de las características de cada conglomerado. En el caso de las funciones categóricas, la visualización muestra gráficos de barras superpuestas con las categorías ordenadas en orden ascendente de valores de datos. En las características continuas, la visualización muestra un gráfico de densidad suave que utiliza los mismos puntos finales e intervalos para cada conglomerado. La visualización en color rojo oscuro muestra la distribución de conglomerados, mientras que la más clara representa los datos generales.
-
Las casillas muestran las distribuciones relativas. Muestra los nombres/etiquetas de características y las distribuciones relativas en las casillas. En general, las visualizaciones son similares a las mostradas para las distribuciones absolutas, sólo que en su lugar se muestran distribuciones relativas. La visualización en color rojo oscuro muestra la distribución de conglomerados, mientras que la más clara representa los datos generales.
-
Las casillas muestran la información básica. Si hay muchos conglomerados, puede resultar difícil ver todos los detalles sin desplazarse. Para reducir la cantidad de desplazamiento, seleccionar esta vista para cambiar la visualización a una versión más compacta de la tabla.
La salida de la tabla de Conglomerados muestra, de forma predeterminada, los clusters ordenados de izquierda a derecha por el tamaño, siendo la clasificación 1, 3, 2
Las medias de los clusters sugieren que los grupos están bien separados.
-
En el clúster 1, el 98.4% de los vehículos son automóviles y se caracterizan por ser baratos, pequeños y consumir poco combustible.
-
En el clúster 2, el 100% de los vehículos son camiones (columna 3) y se caracterizan por tener un precio moderado, son pesados y disponen de un tanque de combustible grande.
-
En el clúster 3, el 100% de los vehículos son automóviles y se caracterizan por ser caros, grandes y moderadamente eficientes en el consumo de combustible.
Situando el ratón en las casillas se muestra información sobre esa característica
Las medias de los clusters (para las variables continuas) y las modas (para las variables categóricas) son útiles, pero sólo dan información de los centros de los conglomerados. Para obtener una visualización de la distribución de los valores de cada campo de clúster, hacer clic en la barra de herramientas de la salida de Clasificar conglomerados y elegir Las casillas muestran las distribuciones absolutas y se muestra la siguiente salida
En el gráfico se aprecia un cierto solapamiento entre los clusters 1 y 3 (columnas 1 y 2) en las características de Peso neto, Tamaño del motor y Capacidad de combustible. Respecto de los clusters 3 y 2 (columnas 2 y 3) observamos que los vehículos con el tamaño del motor más grande están en el clúster 3 mientras que los vehículos con más Capacidad de combustible pertenecen al clúster 2.
La información de los campos de evaluación se muestra haciendo clic en el botón Representación(D) de la barra de herramientas de la salida de Clasificar conglomerados y seleccionando en la salida resultante Campos de evaluación
Se pulsa Aceptar y se muestran los campos de evaluación a continuación de la tabla clúster
La distribución de las ventas es similar en los clusters con la salvedad de que los clusters 1 y 2 (columnas 1 y 3) tienen colas más largas que el clúster 3 (columna 2).
La distribución del valor de reventa a 4 años es muy similar en los tres clusters, sin embargo los clusters 2 y 3 (columnas 2 y 3) se centran en un valor más alto que el clúster 1 y respecto a la asimetría el clúster 3 tiene una cola más larga que cualquiera de los otros dos clusters.
La salida de la ventana Representación se utiliza para controlar la visualización de los clusters:
-
Entradas. Está seleccionado por defecto. Para ocultar todas las características de entrada, se cancela la selección de la casilla de verificación.
-
Campos de evaluación. Seleccionar los campos de evaluación (campos que no se usan para crear el modelo de conglomerado, sino que se envían al visor de modelos para evaluar los conglomerados) que desea mostrar, ya que ninguno se muestra de forma predeterminada. Nota: Esta casilla de verificación no está disponible si no hay ningún campo de evaluación disponible.
-
Descripciones de conglomerados. Está seleccionado por defecto. Para ocultar todas las casillas de descripción de conglomerado, cancelar la selección de la casilla de verificación.
-
Tamaños de conglomerados Está seleccionado por defecto. Para ocultar todas las casillas de tamaño de conglomerado, cancelar la selección de la casilla de verificación.
-
Número máximo de categorías. Especificar el número máximo de categorías que se mostrarán en gráficos de características categóricas. El valor predeterminado es 20.
Otra forma de comparar los clusters es mediante el gráfico que se obtiene seleccionado las tres columnas de los clusters mediante Control+Click en la barra de herramientas de la Vista auxiliar y seleccionando Comparación de conglomerados en el menú desplegable de Ver de la barra de herramientas del Visor de resultados y se muestra la siguiente salida
Este gráfico muestra las características en las filas y conglomerados en las columnas. Esta visualización ayuda a entender mejor los factores de los que se componen los conglomerados, y permite ver las diferencias entre los conglomerados no sólo con respecto a los datos generales, sino entre sí.
Pulsando las teclas Ctrl+Clik en la figura anterior se seleccionan los clusters que se desean visualizar, en la parte superior de la columna del conglomerado (en el panel principal Conglomerados).
Nota: Se pueden seleccionar hasta cinco conglomerados para que se muestren. Los conglomerados se muestran en el orden en que se seleccionan, mientras que el orden de los campos viene determinado por la opción Clasificar características por. Si dentro de Clasificar característica se selecciona Importancia dentro del conglomerado, los campos siempre se clasifican por importancia general.
En esta salida también se muestran unos gráficos de las distribuciones generales de cada característica:
-
Las características categóricas aparecen como gráficos de puntos, donde el tamaño del punto indica la categoría más frecuente (moda) para cada conglomerado (por característica).
-
Las características continuas se muestran como diagramas de caja, que muestran las medianas globales y las amplitudes intercuartiles.
La salida de la figura anterior muestra diagramas de caja para los conglomerados seleccionados:
-
En las características continuas hay marcadores de puntos cuadrados y líneas horizontales que indican el rango de mediana e intercuartil de cada conglomerado.
-
Cada conglomerado viene representado por un color distinto, que se muestra en la parte superior de la vista.
Estos gráficos confirman, en general lo que hemos visto en los anteriores. Este gráfico puede ser especialmente útil cuando hay muchos clusters y se desea compara sólo algunos de ellos.
Es interesante estudiar la importancia del predictor de conglomerados, para ello se selecciona en la barra de herramientas de Vista auxiliar, Importancia del predictor y se obtiene el siguiente gráfico
Esta gráfica muestra la importancia relativa de cada característica en la estimación del modelo.
Ejercicios
Ejercicios Guiados
| A continuación se va a proceder a iniciar una aplicación Java, comprueba que tengas instalada la Máquina Virtual Java para poder ejecutar aplicaciones en Java.Si no tienes instalada la Máquina Virtual Java (Java Runtime Environment – JRE) pincha en uno de los enlaces para descargarla: |
| Instalación directa de la JRE 7 para WindowsPágina oficial de Sun Microsystems, descarga de la JRE para cualquier plataforma |
| Si ya tienes instalada la Máquina Virtual Java pincha en el siguiente enlace para proceder a la ejecución de los ejercicios guiados | Ejercicio 1 |
IMPORTANTE: Si al descargar el archivo *.JAR del ejercicio tu gestor de descargas intenta guardarlo como *.ZIP debes cambiar la extensión a .JAR para poder ejecutarlo.
Enunciado del Ejercicio 1
Realizamos un estudio sobre las pequeñas medianas empresas del sector textil, para ello disponemos de la situación de 12 empresas en 2013 con respecto a los criterios: Personal Especializado, Estudio distribución de Planta, Estudio distribución de Servicios y Aplicación de Sistema de Calidad. Los datos se muestran en la siguiente tabla
Ejercicios Propuestos
Ejercicio Propuesto 1 (Clasificación de países de la UE con datos binarios)
Los datos corresponden a la situación de 6 países europeos en 1996 con respecto a los 4 criterios exigidos por la UE para entrar en la Unión Monetaria: Inflación, Interés, Déficit Público y Deuda Pública y vienen dados en la tabla siguiente:
El objetivo es encontrar grupos de países que muestren un comportamiento similar con respecto a las variables analizadas.
Este es un ejemplo en el que todas las variables son binarias de forma que, 1 significa que el país sí satisfacía el criterio exigido y 0 que no lo satisfacía.
En este caso todas las variables son binarias simétricas y se puede utilizar como medida de distancia la distancia euclídea al cuadrado.
-
La matriz de distancias e interpretación de la misma
- Utilizar un análisis de conglomerados jerárquico aglomerativo con enlace completo para clasificar los países de la UE según las variables Inflación, Interés, Déficit Público y Deuda Pública, con el objetivo de encontrar grupo de países con comportamiento similares.
Ejercicio Propuesto 2
Se desea determinar los segmentos de mercado de un determinado producto en una ciudad pequeña basándose únicamente en la lealtad a las marcas y la lealtad a las tiendas. Para ello se selecciona una muestra de 10 encuestados sobre los que se miden las dos variables lealtad a la tienda (tienda) y lealtad a la marca (marca) en una escala de 0 a 10. Los datos se muestran en la siguiente tabla
Se pide:
-
Realizar un diagrama de dispersión y estudiar los grupos más homogéneos
- Realizar un análisis de conglomerados.
Ejercicio Propuesto 3
El archivo de datos jóvenes.sav contiene información sobre 14 jóvenes respecto a su edad, estudios, hábitos de lectura, fútbol, cine, teatro, concierto, tv, ámbito familiar…
Se desea clasificar a los 14 jóvenes encuestados por el número de veces que van anualmente al fútbol (fútbol), la paga semanal que reciben (paga) y el número de horas semanales que ven la televisión (tv)
Se pide:
-
Realizar un diagrama de dispersión 3-D para mostrar la distribución de los datos y estudiar los posibles grupos que se pueden hacer
- Utilizar un análisis clúster jerárquico. (Etiquetar los casos mediante Identificación personal, id )
- Método: Vecino más lejano; Medida: Intervalo- Distancia euclidea al cuadrado; Transformar valores: Estandarizar las variables (puntuaciones Z)
- Obtener el Historial de conglomeración, Matriz de distancia, Dendograma y en Témpanos: Todos los conglomerados
- Analizar las tablas obtenidas y sacar conclusiones
-
Guardar un rango de soluciones de 3 o 4 clusters
- Repetir el proceso anterior con el Método de Ward
- Guardar un rango de soluciones de 3 o 4 clusters
- Repetir el proceso anterior con el Método de Conglomeración: Agrupación de medianas
- Obtener conclusiones ¿Nº de clustes? ¿Método de conglomeración?
Nota: Para realizar el apartado 1.
- Seleccionar en el menú principal Gráficos/Cuadro de diálogo antiguos/Diagrama/Puntos
- Selecciona Dispersión 3D
- Eje Y: futbol; Eje X: paga; Eje Z: tv; Etiquetar los casos mediante Identificación personal, id
- Opciones: Mostrar el gráfico con las etiquetas de caso
El archivo de datos jóvenes.sav contiene 14 datos y está formado por las siguientes variables:
Variables tipo cadena: id (Identificación personal).
Variables tipo numérico: centro (Tipo de centro de estudios {1, público}…), estudios (Estudios que cursa {1, EGB}…); estupadr (Estudios del padre {1, Sin estudios}…); estumadr (Estudios de la madre {1, Sin estudios}..); paga (Paga semanal en ptas/100); numher (Nº hermanos incluido sujeto); edad ; califest (Calificación media en estudios); lect ( Libros leídos anualmente); cine (Asistencia anual al cine); fútbol (Asistencia anual al futbol); conciert (Asistencia anual conciertos); tv (Horas semanales tv); sexo ({1, hombre}…); hábitat ({1, rural}…); lectp (Segunda tasa de lectura); univ (¿Deseas acceder a la universidad? {1, sí}…); gustcine (Te gusta ir al cine… {1, solo}…); tipocine (Tipo de película que te gusta {1, amor}…); violen (Nivel de rechazo a la violencia {1, activo}…); impdin (Importancia das al dinero {1, muy poca}..); impest (Importancia de estudios {1, muy poca}…); ingr (Ingresos mensuales {1, <100}…); físico (Importancia al físico {1, muy poca}…); depor (interés deporte {1,muy poca}…)
Ejercicio Propuesto 4
Utilizamos de nuevo el archivo de datos ventas_vehículos.sav que contiene estimaciones de ventas, listas de precios y especificaciones físicas hipotéticas de varias marcas y modelos de vehículos. Se desea hacer un estudio de mercado para poder determinar las posibles competencias para sus vehículos, para ello agrupamos las marcas de los coches según los datos disponibles, hábitos de consumo, sexo, edad, nivel de ingresos, etc. de los clientes. Las empresas de coches adaptan sus estrategias de desarrollo de productos y de marketing en función de cada grupo de consumidores para aumentar las ventas y el nivel de fidelidad a la marca.
Realizar este ejercicio para el caso de 3 clusters utilizando únicamente el 20 % de los casos de la muestra. Analizar los resultados y compararlos con los obtenidos en el Supuesto práctico 5 para el caso de 2 clusters. ¿Qué solución piensas que es la mejor?
Nota: El archivo de datos ventas_vehículos .sav contiene 157 datos y está formado por las siguientes variables:
Variables tipo cadena: marca (Fabricante); modelo
Variables tipo numérico: ventas (en miles); reventa (Valor de reventa en 4 años); tipo (Tipo de vehículo: Valores: {0, Automóvil; 1, Camión}); precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo).
Ejercicio Propuesto 5
Utilizar de nuevo el archivo de datos jóvenes.sav que contiene información sobre 14 jóvenes.
Se pide:
-
Tipificar las variables fútbol, paga y tv
-
Realizar un análisis de conglomerados de k-medias con tres conglomerados según las variables tipificadas fútbol, paga y tv (Zpaga, Zfútbol y Ztv). Etiquetar los casos mediante Identificación personal, id.
-
Usar medias actualizadas. Calcular los centros de conglomerados iniciales, Tabla Anova, Información del conglomerado para cada caso
-
Guardar Conglomerado de pertenencia y distancia desde centro del conglomerado
- Resumen de los resultados obtenidos. Interpretar la solución.
-
Ejercicio Propuesto 1 (Clasificación de países de la UE con datos binarios) (Resuelto)
Los datos corresponden a la situación de 6 países europeos en 1996 con respecto a los 4 criterios exigidos por la UE para entrar en la Unión Monetaria: Inflación, Interés, Déficit Público y Deuda Pública y vienen dados en la tabla siguiente:
El objetivo es encontrar grupos de países que muestren un comportamiento similar con respecto a las variables analizadas.
Este es un ejemplo en el que todas las variables son binarias de forma que, 1 significa que el país sí satisfacía el criterio exigido y 0 que no lo satisfacía.
En este caso todas las variables son binarias simétricas y se puede utilizar como medida de distancia la distancia euclídea al cuadrado.
Se pide:
-
La matriz de distancias e interpretación de la misma
- Utilizar un análisis de conglomerados jerárquico aglomerativo con enlace completo para clasificar los países de la UE según las variables Inflación, Interés, Déficit Público y Deuda Pública, con el objetivo de encontrar grupo de países con comportamiento similares.
Solución:
-
La matriz de distancias e interpretación de la misma
En este caso todas las variables son binarias simétricas y se puede utilizar como medida de distancia la distancia euclídea al cuadrado.
Así, por ejemplo, la distancia entre España y Francia es 1 puesto que solamente difieren en un criterio: el de la deuda pública que Francia satisfacía y España no.
2. Utilizar un análisis de conglomerados jerárquico aglomerativo con enlace completo (Vecino más lejano) para clasificar los países de la UE según las variables Inflación, Interés, Déficit Público y Deuda Pública, con el objetivo de encontrar grupo de países con comportamiento similares.
Encontrar grupos de paises que tienen comportamiento similares.
Ejercicio Propuesto 2 (Resuelto)
Se desea determinar los segmentos de mercado de un determinado producto en una ciudad pequeña basándose únicamente en la lealtad a las marcas y la lealtad a las tiendas. Para ello se selecciona una muestra de 10 encuestados sobre los que se miden las dos variables lealtad a la tienda (tienda) y lealtad a la marca (marca) en una escala de 0 a 10. Los datos se muestran en la siguiente tabla
Se pide:
-
Realizar un diagrama de dispersión y estudiar los grupos más homogéneos
- Realizar un análisis de conglomerados.
Solución:
-
Realizar un diagrama de dispersión y estudiar los grupos más homogéneos
Los grupos más homogéneos parecen ser tres formados por: (C, I, J, E, D, B); (H, G, F) y (A)
2. Realizar un análisis de conglomerados comparando diversos métodos, distintas medidas de similitud.
La solución más apropiada se puede observar en el dendograma y es la formada por los grupos: (A); (F, H G) y (I, C, B, D, J, E).
Repetir el análisis con otra medida de similitud y otro procedimiento y comparar los resultados.
Ejercicio Propuesto 3 (Resuelto)
El archivo de datos jóvenes.sav contiene información sobre 14 jóvenes respecto a su edad, estudios, hábitos de lectura, fútbol, cine, teatro, concierto, tv, ámbito familiar…
Se desea clasificar a los 14 jóvenes encuestados por el número de veces que van anualmente al fútbol (fútbol), la paga semanal que reciben (paga) y el número de horas semanales que ven la televisión (tv)
Se pide:
-
Realizar un diagrama de dispersión 3-D para mostrar la distribución de los datos y estudiar los posibles grupos que se pueden hacer
- Utilizar un análisis clúster jerárquico. (Etiquetar los casos mediante Identificación personal, id )
- Método: Vecino más lejano; Medida: Intervalo- Distancia euclidea al cuadrado; Transformar valores: Estandarizar las variables (puntuaciones Z)
- Obtener el Historial de conglomeración, Matriz de distancia, Dendograma y en Témpanos: Todos los conglomerados
- Analizar las tablas obtenidas y sacar conclusiones
-
Guardar un rango de soluciones de 3 o 4 clusters
- Repetir el proceso anterior con el Método de Ward
- Guardar un rango de soluciones de 3 o 4 clusters
- Repetir el proceso anterior con el Método de Conglomeración: Agrupación de medianas
- Obtener conclusiones ¿Nº de clustes? ¿Método de conglomeración?
Nota: Para realizar el apartado 1.
- Seleccionar en el menú principal Gráficos/Cuadro de diálogo antiguos/Diagrama/Puntos
- Selecciona Dispersión 3D
- Eje Y: futbol; Eje X: paga; Eje Z: tv; Etiquetar los casos mediante Identificación personal, id
- Opciones: Mostrar el gráfico con las etiquetas de caso
El archivo de datos jóvenes.sav contiene 14 datos y está formado por las siguientes variables:
Variables tipo cadena: id (Identificación personal).
Variables tipo numérico: centro (Tipo de centro de estudios {1, público}…), estudios (Estudios que cursa {1, EGB}…); estupadr (Estudios del padre {1, Sin estudios}…); estumadr (Estudios de la madre {1, Sin estudios}..); paga (Paga semanal en ptas/100); numher (Nº hermanos incluido sujeto); edad ; califest (Calificación media en estudios); lect ( Libros leídos anualmente); cine (Asistencia anual al cine); fútbol (Asistencia anual al futbol); conciert (Asistencia anual conciertos); tv (Horas semanales tv); sexo ({1, hombre}…); hábitat ({1, rural}…); lectp (Segunda tasa de lectura); univ (¿Deseas acceder a la universidad? {1, sí}…); gustcine (Te gusta ir al cine… {1, solo}…); tipocine (Tipo de película que te gusta {1, amor}…); violen (Nivel de rechazo a la violencia {1, activo}…); impdin (Importancia das al dinero {1, muy poca}..); impest (Importancia de estudios {1, muy poca}…); ingr (Ingresos mensuales {1, <100}…); físico (Importancia al físico {1, muy poca}…); depor (interés deporte {1,muy poca}…).
Solución:
-
Realizar un diagrama de dispersión 3-D para mostrar la distribución de los datos y estudiar los posibles grupos que se pueden hacer
Los grupos más similares parecen ser tres formados por: (B, H, K, M, E); (F, A, C, I, D) y (G, J, N, L)
- Utilizar un análisis clúster jerárquico. (Etiquetar los casos mediante Identificación personal, id )
- Método: Vecino más lejano; Medida: Intervalo- Distancia euclidea al cuadrado; Transformar valores: Estandarizar las variables (puntuaciones Z)
- Obtener el Historial de conglomeración, Matriz de distancia, Dendograma y en Témpanos: Todos los conglomerados
- Analizar las tablas obtenidas y sacar conclusiones
Los individuos que guardan menor distancia son el tercero (C) y el noveno (I) con una distancia de (0.0000) y son los primeros que se unen en un mismo clúster. Lo siguientes serán el segundo (B) y el octavo (H) (guardan aproximadamente la misma distancia, 0.0000)
 Los Coeficientes (niveles de fusión) se han calculado mediante el método del vecino más lejano y utilizando como distancia la euclídea al cuadrado. Se puede observar como va aumentando la variabilidad dentro de los conglomerados conforme se van agrandando.
Los Coeficientes (niveles de fusión) se han calculado mediante el método del vecino más lejano y utilizando como distancia la euclídea al cuadrado. Se puede observar como va aumentando la variabilidad dentro de los conglomerados conforme se van agrandando.
- El la primera etapa había 13 clusters ((3, 9) ; (4); (7); (10); (14); (2); (8); (5); (11); (13); (1); (6) y (12)).
- En la segunda etapa había 12 clusters ((3, 9) ; (2, 8); (4); (7); (10); (14); (5); (11); (13); (1); (6) y (12)).
- El primer salto grande se produce entre las etapas novena y décima (coeficiente = 6.0009) siendo 4 el número de clusters ((3, 9, 4) ; (2, 8, 5, 11, 13); (7, 10, 14) y (1, 6, 12)).
- El siguiente salto se produce entre las etapas once y doce y los clusters formados son: ((3, 9, 4, 7, 10, 14, 2, 8, 5, 11, 13) y (1, 6, 12)) y la última etapa que engloba a los catorce jóvenes.
El dendograma muestra cómo se van formando la clasificación jerárquica de los individuos, si consideramos un corte entre la distancia 20 y 25, se formarían dos clusters: Clúster 1: (C, I, D, G J, N, B, H, E. K, M); Clúster 2: (A, F , L)
El diagrama de témpanos vertical muestra la clasificación de individuos dependiendo del número de clusters que consideremos (cada fila de la tabla). Por filas se van rellenando en otro color y se deja un hueco cuando se cambia de clúster. Por ejemplo, si consideramos 4 clusters, la clasificación sería:
- Clúster 1: N, J G
- Clúster 2: D, I, C
- Cúster 3: M, K, E, H, B
- Clúster 4: L, F, A
Ante la pregunta ¿Qué número de clusters vamos a considerar? El criterio que podemos utilizar es elegir el número de clusters observando los niveles de fusión y teniendo en cuenta el diagrama de dispersión de los individuos. Así el rango de soluciones puede ser 3 0 4 clusters (Coeficientes: 0.104 y 0.349).
 Se muestra la tabla de conglomerados de pertenencia con la clasificación de los 14 individuos para los casos elegidos de 3 y 4 clusters. Así:
Se muestra la tabla de conglomerados de pertenencia con la clasificación de los 14 individuos para los casos elegidos de 3 y 4 clusters. Así:
- Tres clusters: Clúster 1: A, F, L; Clúster 2: B, E, H, K, M; Clúster 3: C, D, G, I, J, N
- Cuatro clusters: Clúster 1: A, F, L; Clúster 2: B, E, H, K, M; Clúster 3: C, D, I; Clúster 4: G, J, N
7. Repetir el proceso anterior con el Método de Ward
Se añaden al fichero de datos las variables CLU4_2 y CLU3_2 que definen 4 clusters y 3 clusters, respectivamente, mediante el método de Ward
Se muestra la tabla de conglomerados de pertenencia con la clasificación de los 14 individuos para los casos elegidos de 3 y 4 clusters, mediante el método de Ward.
8. Guardar un rango de soluciones de 3 o 4 clusters
9. Repetir el proceso anterior con el Método de Conglomeración: Agrupación de medianas
 Se añaden al fichero de datos las variables CLU4_3 y CLU3_3 que definen 4 clusters y 3 clusters, respectivamente, mediante el método de medianas
Se añaden al fichero de datos las variables CLU4_3 y CLU3_3 que definen 4 clusters y 3 clusters, respectivamente, mediante el método de medianas
Se muestra la tabla de conglomerados de pertenencia con a clasificación de los 14 individuos para los casos elegidos de 3 y 4 clusters, mediante el método de medianas
10. Obtener conclusiones ¿Nº de clusters? ¿Método de conglomeración?
Resumen de los resultados obtenidos mediante el análisis clúster Jerárquico y los métodos de aglomeración: Vecino más lejano, Método Ward y Vinculación de medianas
-
El método del Vecino más lejano y el método de Ward proporcionan resultados idénticos y respecto al método de la mediana parece representar peor los datos observados.
-
De las dos soluciones de tres y cuatro clusters nos decidimos por la solución de tres clusters.
En primer lugar tipificamos las variables paga, futbol, tv. Para ello seleccionamos en el menú principal Analizar/Estadísticos descriptivos/Descriptivos… y el editor de datos muestra tres nuevas variables: Zpaga, Z fútbol y Ztv
Se realiza un Análisis de conglomerados de K- medias
Se elige una clasificación en 3 conglomerados y se pulsa
-
Iterar… donde se solicita Usar medias actualizadas para que el procedimiento vaya actualizando cada vez las medias de los clusters
-
Opciones: Centros de conclomerados iniciales, Tabla ANOVA e Información del conglomerado para cada caso
-
Guardar: Conglomerados de pertenecia y Distancia desde centro del conglomerado
Se han creado dos nuevas variables en el editor de datos:
- QCL_1: Codificación que indica la pertenencia a cada clúster
- QCL_2: Codificación que indica la distancia euclidea entre cada caso y el centro del cluster utilizado paraclasificar ese caso.
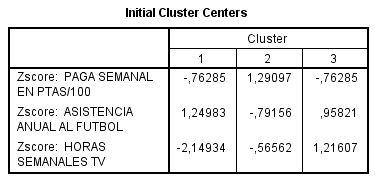 Tabla de los centros iniciales de los clusters que muestra las medias de los clusters iniciales. Por defecto se selecciona entre los datos un número de casso debidamente espaciados igual al número de conglomerados.
Tabla de los centros iniciales de los clusters que muestra las medias de los clusters iniciales. Por defecto se selecciona entre los datos un número de casso debidamente espaciados igual al número de conglomerados.
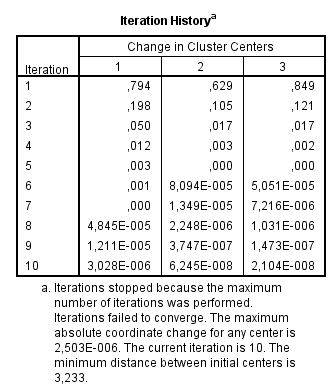 El historial de las iteraciones muestra las medias (centros) de los clusters en cada caso. El método para en 10 pasos sin alcanzar el criterio de convergencia
El historial de las iteraciones muestra las medias (centros) de los clusters en cada caso. El método para en 10 pasos sin alcanzar el criterio de convergencia
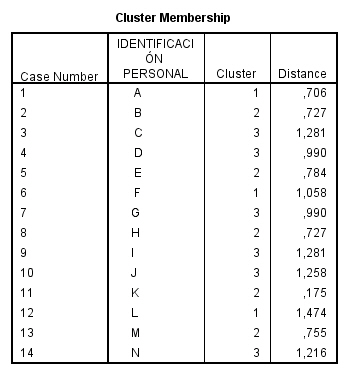 Pertenencia a los conglomerados muestra la solución final de la clasificación en 3 clusters
Pertenencia a los conglomerados muestra la solución final de la clasificación en 3 clusters
Ejercicio Propuesto 4 (Resuelto)
Utilizamos de nuevo el archivo de datos ventas_vehículos.sav que contiene estimaciones de ventas, listas de precios y especificaciones físicas hipotéticas de varias marcas y modelos de vehículos. Se desea hacer un estudio de mercado para poder determinar las posibles competencias para sus vehículos, para ello agrupamos las marcas de los coches según los datos disponibles, hábitos de consumo, sexo, edad, nivel de ingresos, etc. de los clientes. Las empresas de coches adaptan sus estrategias de desarrollo de productos y de marketing en función de cada grupo de consumidores para aumentar las ventas y el nivel de fidelidad a la marca.
Realizar este ejercicio para el caso de 3 clusters utilizando únicamente el 20 % de los casos de la muestra y centrándonos en dos variables de interés peso neto y tamaño del motor. Analizar los resultados y compararlos con los obtenidos en el Supuesto práctico 5 para el caso de 2 clusters. ¿Qué solución piensas que es la mejor?
Nota: El archivo de datos ventas_vehículos .sav contiene 157 datos y está formado por las siguientes variables:
Variables tipo cadena: marca (Fabricante); modelo
Variables tipo numérico: ventas (en miles); reventa (Valor de reventa en 4 años); tipo (Tipo de vehículo: Valores: {0, Automóvil; 1, Camión}); precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo).
Solución
El archivo ventas_vehículos.sav contiene 157 datos Para hacer más comprensible la representación gráfica de los resultados, vamos a comenzar utilizando únicamente el 20 % de los casos de la muestra.
Para ello, en el menú principal seleccionar: Datos/Seleccionar casos
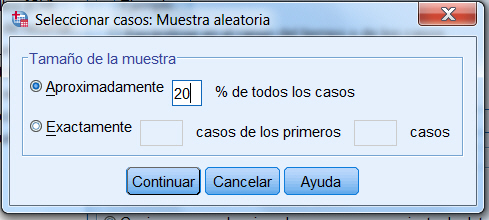 Realizamos un gráfico de dispersión para ver la distancia entre los casos en las dos variables motor y peso. Para ello, seleccionamos en el menú principal Gráficos/Generador de gráficos…
Realizamos un gráfico de dispersión para ver la distancia entre los casos en las dos variables motor y peso. Para ello, seleccionamos en el menú principal Gráficos/Generador de gráficos…
En la ventana Galería, en Elija entre, seleccionamos Dispersión/…
Arrastramos el gráfico de Dispersión simple a la ventana de presentación preliminar del gráfico
Desplazamos la variable peso (peso total del vehículo en kg) al eje abscisas y la Tamaño del motor al eje de ordenadas
Pulsar Aceptar y se muestra el siguiente gráfico 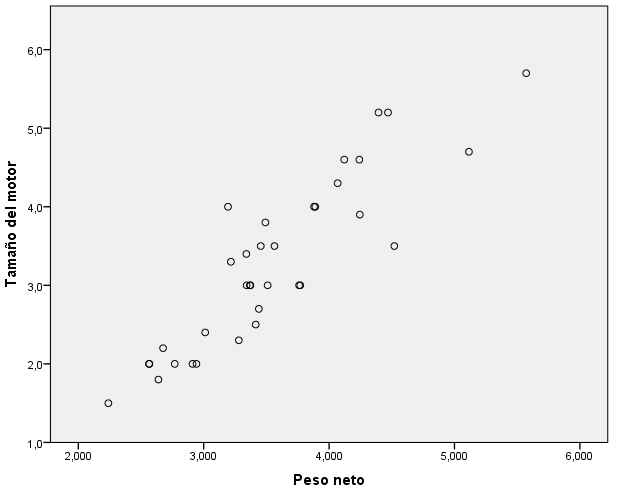
En el diagrama de dispersión están representados los valores Peso y Tamaño motor de los 36 casos seleccionados. Se puede apreciar que:
- Hay dos grupos, un grupo de vehículos relativamente numeroso con peso y tamaño de motor ambos reducidos y otro grupo más disperso de vehículos de mayor peso y mayor motor.
- O bien tres grupos, un grupo de vehículos con peso y tamaño de motor ambos reducidos, un segundo grupo con ambas variables de tamaño mediano y un tercer grupo, menos numeroso y mas disperso, de vehículos de mayor peso y mayor motor.
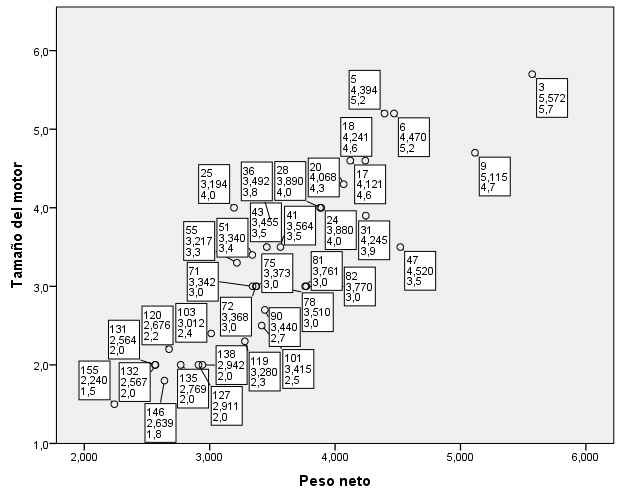 Se han identificado, mediante el número de caso, los dos vehículos aparentemente más alejados entre sí (el caso 3 (Tamaño motor (5.7), Peso (5.572)) y el caso 155 (Tamaño motor (2.240), Peso (1.5))). La nube de puntos, por tanto, incita a pensar que existen al menos dos grupos naturales de casos.
Se han identificado, mediante el número de caso, los dos vehículos aparentemente más alejados entre sí (el caso 3 (Tamaño motor (5.7), Peso (5.572)) y el caso 155 (Tamaño motor (2.240), Peso (1.5))). La nube de puntos, por tanto, incita a pensar que existen al menos dos grupos naturales de casos.
Para clasificar los casos en tres grupos:
Seleccionar en el cuadro de diálogo de Análisis de conglomerados de K-medias la opción Sólo Clasificar. Trasladar las variables motor y peso_neto a la lista Variables. Elegir como Número de conglomerados: 3 y como Método: Sólo clasificar
 Aceptando estas selecciones, el Visor ofrece los resultados
Aceptando estas selecciones, el Visor ofrece los resultados
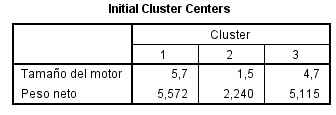 Esta tabla contiene los centros iniciales de tres clusters en las dos variables de clasificación utilizadas (motor y peso).
Esta tabla contiene los centros iniciales de tres clusters en las dos variables de clasificación utilizadas (motor y peso).
- Clúster 1: (Tamaño motor (5.7), Peso (5.572)) es el caso 3
- Clúster 2: (Tamaño motor (1.5), Peso (2.240))es el caso 155
- Clúster 3: (Tamaño motor (4.7), Peso (5.115)) es el caso 9
Una vez seleccionados los centros de los conglomerados, cada caso es asignado al conglomerado de cuyo centro se encuentra más próximo y comienza un proceso de ubicación iterativa de los centros. En la primera iteración se reasignan los casos por su distancia al nuevo centro y, tras la reasignación, se vuelve a actualizar el valor del centro. En la siguiente iteración se vuelven a reasignar los casos y a actualizar el valor del centro. Etc.
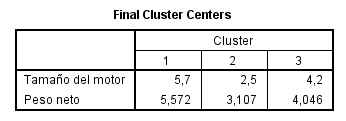 Esta tabla muestra los centros de los conglomerados finales es decir, los centros de los conglomerados tras el proceso de actualización iterativa. Comparando los centros finales (tras la iteración) de esta tabla con los centros iniciales (antes de la iteración) se puede apreciar:
Esta tabla muestra los centros de los conglomerados finales es decir, los centros de los conglomerados tras el proceso de actualización iterativa. Comparando los centros finales (tras la iteración) de esta tabla con los centros iniciales (antes de la iteración) se puede apreciar:
- Un desplazamiento del centro del conglomerado 2 hacia la parte superior del plano definido por las dos variables de clasificación
- Un desplazamiento del centro del conglomerado 3 hacia la parte inferior.
Para interpretar mejor los resultados añadimos una tabla con resumen descrptivo
- El primer conglomerado está formado vehículos de tamaño gran tamaño de motor y mucho peso
- El segundo conglomerado está formado por vehículos de tamaño de pequeño y peso pequeño
- El tercer conglomerado está formado por vehículos de tamaño de mediano y peso mediano.
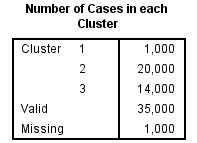 Por último, esta tabla informa sobre el Número de casos asignado a cada conglomerado. En nuestro ejemplo, los tamaños de los tres conglomerados son bastantes diferentes. Por ejemplo, el clúster 1 está formado por un caso: (Tamaño motor (5.7), Peso (5.572)) se trata de un Cadillac que es el coche, de nuestra muestra, que tiene mayor peso y mayor tamaño de motor.
Por último, esta tabla informa sobre el Número de casos asignado a cada conglomerado. En nuestro ejemplo, los tamaños de los tres conglomerados son bastantes diferentes. Por ejemplo, el clúster 1 está formado por un caso: (Tamaño motor (5.7), Peso (5.572)) se trata de un Cadillac que es el coche, de nuestra muestra, que tiene mayor peso y mayor tamaño de motor.
Para mostrar el Historial de iteraciones seleccionar en cuadro de diálogo de Análisis de conglomerados de K-medias la opción Iterar y Clasificar
El subcuadro de diálogo Iterar permite controlar algunos detalles relacionados con el proceso de iteración utilizado para el cálculo de los centroides finales. Se puede determinar el número máximo de iteraciones o bien fijar un criterio de convergencia mayor que cero y menor que uno.
Dejamos el número de iteraciones máximas que viene por defecto, 10, seleccionamos Usar medias actualizadas y pulsamos Continuar y Aceptar
 Comprobamos que no se alcanza la convergencia por lo que aumentamos las Iteraciones máximas a 30 y se muestra el siguiente Historial de iteraciones
Comprobamos que no se alcanza la convergencia por lo que aumentamos las Iteraciones máximas a 30 y se muestra el siguiente Historial de iteraciones
Esta tabla resume el historial de iteraciones (21 en nuestro ejemplo) con indicación del cambio (desplazamiento) experimentado por cada centro en cada iteración. Puede observarse que, conforme avanzan las iteraciones, el desplazamiento de los centros se va haciendo más y más pequeño, hasta llegar a la 21 iteración, en la que ya no existe desplazamiento alguno.
El proceso de iteración se detiene, por defecto, cuando se alcanzan 10 iteraciones o cuando de una iteración a otra no se produce ningún cambio en la ubicación de los centroides (cambio = 0). En nuestro ejemplo, el proceso ha finalizado antes de alcanzar 21 iteraciones donde no se produce ningún cambio.
Ejercicio Propuesto 5 (Resuelto)
Utilizar de nuevo el archivo de datos jóvenes.sav que contiene información sobre 14 jóvenes.
Se pide:
-
Tipificar las variables fútbol, paga y tv
-
Realizar un análisis de conglomerados de k-medias con tres conglomerados según las variables tipificadas fútbol, paga y tv (Zpaga, Zfútbol y Ztv). Etiquetar los casos mediante Identificación personal, id.
-
Usar medias actualizadas. Calcular los centros de conglomerados iniciales, Tabla Anova, Información del conglomerado para cada caso
- Guardar Conglomerado de pertenencia y distancia desde centro del conglomerado
- Resumen de los resultados obtenidos. Interpretar la solución.
Solución
1. Tipificar las variables fútbol, paga y tv
Seleccionar en el menú principal Analizar/Estadísticos descriptivos/Descriptivos. Seleccionar las variables fútbol, paga y tv y elegir Guardar valores tipificados como variables.
 Pulsar Aceptar. En el editor de datos se han creado 3 nuevas variables Zpaga, Zfútbol y Ztv, que contienen los valores tipificados de las variables correspondientes
Pulsar Aceptar. En el editor de datos se han creado 3 nuevas variables Zpaga, Zfútbol y Ztv, que contienen los valores tipificados de las variables correspondientes
2. Realizar un análisis de conglomerados de k-medias con tres conglomerados según las variables tipificadas fútbol, paga y tv (Zpaga, Zfútbol y Ztv). Etiquetar los casos mediante Identificación personal, id.
- Conglomerado 1: G(10 (paga semanal), 1 (asistencia anual al futbol) y 22 (horas semanales de tv))
- Conglomerado 2: F (10 paga, 8 futbol y 5 tv)
- Conglomerado B o H (25 paga, 5 futbol y 17 tv)
- Conglomerado 1: entre 10 y 11 (paga semanal), 2 (asistencia anual al futbol) y entre 18 y 22 (horas semanales de tv)
- Conglomerado 2: entre 11 y 25 paga, 5 futbol y entre 5 y 9 tv
- Conglomerado 3: más de 10 de paga, entre 2 y 5 futbol y entre 18 y 22 tv
- Conglomerado 1: entre 10 y 11 (paga semanal), entre 5 y 7 (asistencia anual al futbol) y entre 10 y 13 (horas semanales de tv)
- Conglomerado 2: entre 10 y 11 paga, 2 futbol y entre 18 y 22 tv
- Conglomerado 3: 25 de paga, entre 2 y 5 futbol y 16 tv
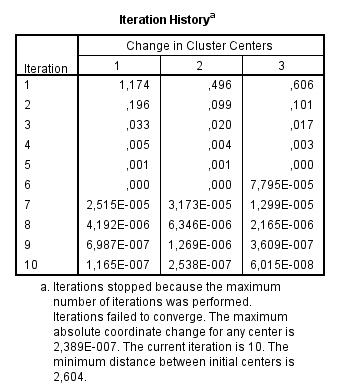 Comprobamos que no se alcanza la convergencia por lo que aumentamos la s iteraciones máximas a 25 y se muestra el siguiente Historial de iteraciones
Comprobamos que no se alcanza la convergencia por lo que aumentamos la s iteraciones máximas a 25 y se muestra el siguiente Historial de iteraciones Esta tabla resume el historial de iteraciones (24 en nuestro ejemplo) con indicación del desplazamiento experimentado por cada centro en cada iteración. Puede observarse que, conforme avanzan las iteraciones, el desplazamiento de los centros se va haciendo más y más pequeño. Hasta llegar a la iteración 24 que ya no existe desplazamiento alguno.
Esta tabla resume el historial de iteraciones (24 en nuestro ejemplo) con indicación del desplazamiento experimentado por cada centro en cada iteración. Puede observarse que, conforme avanzan las iteraciones, el desplazamiento de los centros se va haciendo más y más pequeño. Hasta llegar a la iteración 24 que ya no existe desplazamiento alguno.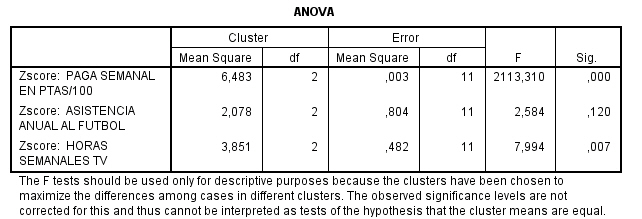
La tabla ANOVA indica qué variables contribuyen más a la solución de clúster. La variable Paga es la que ocasiona la mayor separación entre los clusters y la que proporciona menos separación es la Asistencia anual al futbol