CATÁLISIS

Capitulo 24 Catálisis del libro Fisicoquímica para Farmacia y Biologia, editado por Masson-Salvat Medicina, 1992, pags 637-681.

Con permiso de los autores: G. Roig y F. J. Burguillo Muñoz.

Adaptación realizada por Ana María Lara Porras para personas con dificultad visual

24.1. GENERALIDADES

Las velocidades de muchas reacciones químicas se ven modificadas por la presencia de alguna sustancia que permanece inalterada al final del proceso. Ejemplos de tales reacciones son la conversión del almidón en azúcares, cuya velocidad de transformación se ve afectada por ácidos; la descomposición del peróxido de hidrógeno, afectada por los iones férricos; la formación de amoníaco en presencia de platino poroso. En 1836, el químico J. J. Berzelius denominó estas reacciones como procesos catalizados. En 1895, F. W. Ostwald definió un catalizador como cualquier sustancia que altera la velocidad de una reacción química sin modificación alguna de los factores energéticos de la reacción. Otra definición es la que dice que un catalizador altera la velocidad de una reacción química y es a la vez reactivo y producto de la reacción. Quizás una definición más apropiada sea: «Un catalizador es una sustancia que acelera la velocidad de una reacción sin modificar la variación global de energía de Gibbs normal de la reacción».

Las catálisis pueden ser de diversos tipos. Se llama catálisis homogénea cuando el catalizador y el sistema reactivo forman un sistema homogéneo con: una sola fase, como se ha observado en algunas reacciones en fase gas y en disolución, entre las que se destaca la llamada catálisis ácido-base. Este tipo de catálisis suele ser poco específica y de orden 1 respecto del catalizador. Se llama catálisis heterogénea cuando el catalizador forma una fase distinta al sistema reactivo, como ocurre con los catalizadores sólidos, que incrementan la velocidad de reacciones en fase gas o, a veces, en disolución. Este tipo de catálisis es más específica y la velocidad de las reacciones es función de la superficie y no de la masa del catalizador. Existe también otro importante tipo de catálisis, la denominada catálisis en-zimática, que se produce, sobre todo, en reacciones de tipo bioquímico, por la acción de las enzimas, que son proteínas que normalmente forman una disolución coloidal dentro del sistema reactivo. Asimismo, un fenómeno frecuente en las reacciones de disolución es la denominada autocatálisis, cuando el catalizador viene a ser uno de los productos de la reacción. En este caso, la reacción comienza lentamente, para ir acelerándose a medida que aumenta la concentración del catalizador. Los fenómenos de catálisis y, por tanto, el poder atribuir a una especie o especies la propiedad de catalizador, dependen de una serie de características que se especifican a continuación.

a) Normalmente se ha podido hablar de que el catalizador no participa en lareacción porque, como idea base, se puede establecer que el catalizador se recupera sin haberse consumido al completarse la reacción. Sin embargo, el catalizador sí participa en la reacción, interviene en su mecanismo y se regenera de nuevo.

b) En las reacciones catalizadas, pequeñas cañtidades de catalizador pueden producir un efecto considerable sobre una gran cantidad de reactivos. Esta propiedad es muy destacada en la catálisis enzimática y se manifiesta también en la catálisis heterogénea, pero no es regla general en muchos casos de catálisis homogénea. Casi siempre el efecto del catalizador se manifiesta sobre los valores de las constantes de velocidad. Y es muy frecuente que este efecto sea proporcional a la concentración del catalizador, esto es, que la velocidad de la reacción catalizada viene a ser proporcional a esta concentración

\( v = k [C] \hspace{2 cm}  \)  [24.1]

donde k es función de la concentración del reactivo. En este caso, la velocidad de la reacción en ausencia del catalizador ha de ser cero. Sin embargo, hay muchos ejemplos en los que es necesario introducir un término adicional, independiente de la concentración del catalizador, a la ecuación de velocidad, de modo que

\( v =  k [C] + v_{0} \hspace{2 cm} \)  [24.2]

Es decir, la reacción no catalizada, a concentración cero del catalizador, posee una velocidad \(  v_0 \) .

c) Los catalizadores incrementan la velocidad de reacción, pero no son capaces de provocar o de iniciar esa reacción. El catalizador normalmente contribuye a facilitar la evolución de la reacción mediante un mecanismo diferente que sólo debe superar una barrera de potencial de menor altura. Y ello sin influir sobre el valor de potencial de reacción que depende sólo de las energías de Gibbs de reactivos y productos de la reacción.

d) Por razón semejante, los catalizadores tampoco pueden hacer variar el yalor de la constante de equilibrio de una reacción, porque como no influyen sobre el valor de la variación de la energía de Gibbs o potencial de reacción, no modifican el valor de la constante termodinámica de equilibrio.

Debido a que la constante de equilibrio K es el cociente entre las constantes de velocidad de las reacciones directa e inversa (\( K = k_1/k_{-1} \) ), un catalizador, por tanto, debe afectar en la misma proporción tanto la velocidad de la reacción directa como la de la reacción inversa.

e) La acción de los catalizadores puede ser general o específica. La primera para los catalizadores que actúan sobre muchas reacciones, las cuales pueden ser, o no, semejantes tanto química como cinéticamente. Y aunque este comportamiento sea frecuente con los catalizadores homogéneos, lo más habitual es que su acción sea muy específica y sólo sean efectivos frente a una determinada reacción. Esta característica es muy propia de los catalizadores heterogéneos y más de las enzimas.

24.2. MECANISMO GENERAL DE CATÁLISIS

Si bien por definición la cantidad y calidad de un catalizador deben permanecer inalteradas al final de la reacción, sin embargo, el catalizador se ve indudablemente implicado en el proceso químico. En el caso de un único reactivo, se puede formar un complejo entre ese reactivo (el sustrato) y el catalizador. Si existe más de un sustrato, el complejo puede involucrar a una o más moléculas de sustrato ligadas al catalizador. Estos complejos se forman únicamente como intemediatos y se descomponen para dar lugar a los productos de la reacción, regenerándose la molécula del catalizador.

En algunos casos, como en muchas reacciones superficiales y enzimáticas, este complejo es de adición, pudiéndose escribir la reacción global como:

\( C + S =  CS \hspace{2cm}  (I)   \)

\(  CS \rightarrow  X + C  \hspace{2cm}   (II) \)

donde C es el catalizador, S el sustrato, CS el complejo de adición y X el producto.

En otros casos, como en la catálisis por ácidos y bases y por algunas enzimas, el complejo no es de adición del catalizador y del sustrato, sino que se forma junto con alguna otra sustancia W. En este caso, el esquema de la reacción global podría ser

\( C +S  =  J+W   \hspace{2cm}   (III) \)

\(  J  \rightarrow  X + C  \hspace{2cm}   (IV) \)

Existen dos posibilidades importantes en relación a la estabilidad del complejo intermedio J, y las leyes cinéticas que se obtengan han de depender notablemente de la hipótesis asumida a este respecto. En un caso, el complejo se puede volver a convertir en el catalizador y el sustrato a una velocidad que sea significativamente mayor que la velocidad a la que tiene lugar la reacción (IV) para dar los productos finales. La velocidad global de la reacción se puede calcular obteniendo la concentración de J a partir del equilibrio (I11), multiplicándola por la constante de velocidad de la reacción (IV). Puesto que este planteamiento corresponde al concepto de Arrhenius de una reacción química implicando el equilibrio entre los reactivos y el complejo activado, a los complejos en este tipo de catálisis se les denomina con frecuencia complejos de Arrhenius.

La segunda posibilidad es que el complejo intermedio reaccione para dar los productos finales a una velocidad comparable con la velocidad de la reacción inversa (III). De este modo, la concentración de J se puede considerar prácticamente constante durante el curso de la reacción y, por ello, el tratamiento del estado estacionario se puede aplicar en rigor. A un complejo de este tipo se le suele denominar como complejo de Van’t Hoff.

La energía de activación de una reacción catalizada suele ser menor que la de la misma reacción no catalizada: En otras palabras, el catalizador generalmente trabaja permitiendo que la reacción ocurra por otra ruta que posea una barrera de energía menor. Este hecho se muestra esquemáticamente en la figura 24-1. Los in-hibidores no trabajarían provocando que la reacción ocurriera por una ruta de mayor energía: esto no reduciría la velocidad, ya que la reacción seguiría ocurriendo á través de otro mecanismo alternativo. Así pues, los inhibidores actúan destruyendo el catalizador presente, o bien eliminando los intennediatos de la reacción.

Los procesos de catálisis pueden presentarse, dentro del esquema general de mecanismo propuesto, en todo tipo de reacciones homogéneas y heterogéneas, tanto en fase gas como en fase condensada o en disolución. Entre las reacciones homogéneas catalizadas, por su carácter más relevante ya que suelen ser reacciones que se presentan en la práctica de preparación y tratamiento de los productos de interés farmacéutico, la atención se va a centrar preferentemente en las reacciones de catálisis homogénea en disolución, que se exponen a continuación.

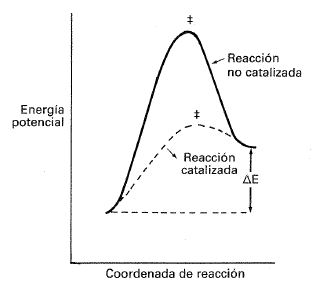
Fig. 24-1. Disminución de la barrera de energía potencial mediante un catalizador.

24.3. TIPOS DE CATÁLISIS HOMOGÉNEA EN DISOLUCIÓN

Son muy numerosas las reacciones químicas inorgánicas y orgánicas en disolución en las que se ha comprobado que determinadas especies, también disueltas en el mismo sistema homogéneo en que ocurre la reacción, pueden contribuir a incrementar de forma notable su velocidad, a consecuencia de un típico proceso de catálisis homogénea.

Los procesos de catálisis homogénea en disolución pueden corresponder a uno de los cuatro tipos característicos siguientes.

a) Catálisis por transferencia de electrones. En ella los catalizadores son generalmente especies iónicas que corresponden a alguno de los diversos grados de oxidación de un determinado elemento.

b) Catálisis específica ácido-base. En ella los catalizadores son propiamente los iones \( H^{+} \) u \( OH^{-} \), procedentes de la ionización de ácidos y bases, sin que los respectivos aniones de estos ácidos o los cationes de estas bases presenten capacidad catalítica.

c) Catálisis general ácido-base. Es la producida por procesos de transferencia de protones entre los catalizadores que se han de considerar como ácidos o bases de Brünsted, frente al sustrato que tiene carácter de base o de ácido de Briinsted.

d) Catálisis electrofílica y nucleofílica. Es la producida mediante procesos de formación de uniones dativas, cuando los catalizadores tienen el carácter de bases o, a veces, de ácidos de Lewis, y las moléculas del sustrato actúan como ácidos o bases de Lewis. Dentro de este tipo de catálisis se debe incluir la que producen ciertos iones metálicos con capacidad para formar complejos con las moléculas del sustrato, que actúan de ligandos, o la catálisis debida a ciertas moléculas con defecto o exceso de electrones, capacitadas también para formar enlaces de estos tipos.

24.4. CATÁLISIS POR TRANSFERENCIA DE ELECTRONES

Ya se han comentado las reacciones de transferencia de carga entre iones, debida a los electrones, que corresponden a estequiometrías del tipo

\( A^{Z_{A}} +   B^{Z_{B}}  \rightarrow  A^{Z_{A}+1} + A^{Z_{B} -1} \hspace{2cm}    \)  [24.3]

considerando los posibles tipos de mecanismos que pueden presentarse, según evolucionen a través de complejos de esfera interna o externa, en los que juegan importante papel las moléculas del disolvente que forman las esferas de solvatación e incluso otras especies iónicas presentes en el sistema. En estas circunstancias, es posible la participación de especies iónicas determinadas, distintas de reactivos o productos, que actúen como catalizadores favoreciendo la evolución de la reacción. Normalmente se trata de iones de un elemento, que puede presentar distintos grados de oxidación, algunos de los cuales pueden ser inestables o poco estables en el seno de la disolución y en las condiciones en que transcurre la reacción. Tal ocurre con la reacción redox.

\(   V^{3+} + Fe^{3+}  \rightarrow V^{4+} + Fe^{2+}   \hspace{2cm}    \)  [24.4]

que es catalizada por los iones \( Cu^{2+} \), con lo que se ha demostrado que entonces la Ia velocidad de reacción resulta ser proporcional a las concentraciones de los iones \( V^{3+} \) y \( Cu^{2+}\) e independiente de la concentración de los iones \( Fe^{3+} \). Este hecho se explica mediante el mecanismo en dos etapas,

        \( I) \hspace{1cm}  V^{3+} + CU^{2+} \rightarrow V^{4+} + Cu^{+}  \hspace{.5cm}  (lenta)    \hspace{2cm}   \) [24.5]

     \( II) \hspace {1cm} Cu^{+} + Fe^{3+} \rightarrow Cu^{2+} + Fe^{2+} \hspace{.5cm} (rápida) \hspace{2cm}     \)  [24.6]

y es, por tanto, I) el paso determinante de la velocidad de reacción. La reacción directa [24.4] presenta dificultades para la formación del complejo de transición y para la reorganización de los solvatos en los iones productos y, por ello, requiere una apreciable activación. La forma más inestable del ion  \( Cu^{+}  \) reduce la barrera de potencial y es la razón de este efecto catalítico.

24.5. CATÁLISIS ÁCIDO-BASE

a. Catálisis específica y general. La catálisis homogénea en fase líquida más importante es la catálisis ácido-base. Un número considerable de reacciones químicas están catalizadas por ácidos y bases. Cuando se da esta catálisis en solución acuosa, los efectos más importantes son los provocados por los iones hidronio o hidroxilo de la solución. Si estos son los únicos efectos, es decir, si estos dos tipos de iones son los únicos catalizadores efectivos presentes, la catálisis ácido-base se denomina específica.

Si estas reacciones se llevan a cabo en un medio ácido fuerte, la concentración de iones hidroxilo resulta tan insignificante que dejan de ejercer una acción catalítica apreciable, con lo que el único catalizador efectivo es el ion hidronio. Así pues, la ecuación de velocidad en este caso queda:

\( v = k_{H^{+}} [H_{3}O^{+}] [S]    \hspace{2cm}    \)  [24.7]

donde \( k_{H^{+}} \) es la constante catalítica para estos iones. De forma semejante, en soluciones muy básicas la única especie catalítica eficaz son los iones hidroxilo, con lo que en este caso la correspondiente ecuación de velocidad resultaría igual a:

\( v = k_{OH^{-}} [OH^{-}][S]   \hspace{2cm}    \)  [24.8]

donde \( k_{OH^{-}} \) es la constante catalítica para estos iones. El valor de las constantes catalíticas se puede determinar midiendo las velocidades en soluciones ácidas y/o básicas a varias concentraciones de iones \( H_{3}O^{+} \) y/o \( OH^{-}\) y de S (sustrato).

En el caso general en el que la catálisis puedan efectuarla simultáneamente los iones hidronio e hidroxilo, y en que la reacción pueda ocurrir también espontáneamente (en ausencia de catalizador alguno), su constante de velocidad de primer orden, \( v/[S] \) sería

\( k = k_{0} + k_{H^{+}} [H_{3}O^{+}] + k_{OH^{-}} [OH^{-}] = k_{0} + k_{H^{+}} [H_{3}O^{+}] + \displaystyle \frac{ k_{OH^{-}}. k_{W}}{[H_{3}O^{+}]}    \hspace{2cm}    \)  [24.9]

Una representación del logaritmo de la constante de velocidad frente al pH de la solución aparece recogida en la figura 24-2, observándose regiones de catálisis por iones hidronio e hidroxilo, separadas por una región en la que la proporción de catálisis es despreciable frente a la reacción espontánea. A concentraciones ácidas suficientemente altas, \(k =  k_{H^{+}} [H_{3}O^{+}] \), con lo que

\( \log k = \log k_{H^{+}} + \log [H^{+}]  = \log k_{H^{+}}- pH   \hspace{2cm} \)     [24.10]

Así, en una disolución suficientemente ácida la representación de log k frente al pH es una línea recta de pendiente -1. De forma análoga, en una disolución suficientemente básica, \( k = k_{OH^{-}} K_{w}/[H_{3}O^{+}] \), de donde:

\( \log k = \log (k_{OH^{-}}K_W)- \log [H_{3}O^{+}] = \log (k_{OH^{-}} K_{W}) + pH    \hspace{2cm}   \)  [24.11]

con lo que la correspondiente representación \(  \log k \)  frente al pH es una línea recta de pendiente igual a +1.

La velocidad en la región intermedia es igual a \( k_{o}[S] \) y \(  k_o \) se puede determinar directamente a partir de la velocidad en esta zona. Si la velocidad de la reacción espontánea es suficientemente pequeña, la parte horizontal de la curva no aparece y los dos limbos se insertan bruscamente (fig. 24-2 b, curva I). Si bien \( k_{H^{+}} \)  o \( k_{OH^{-}} \) son despreciables, los limbos correspondientes de la curva no aparecen (fig. 24-2 b, curvas II y DI).

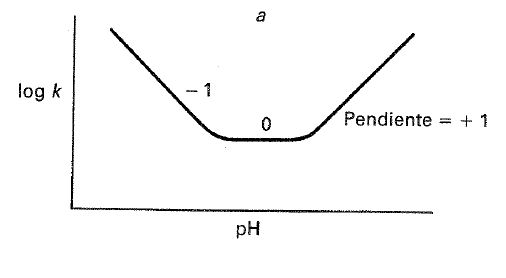
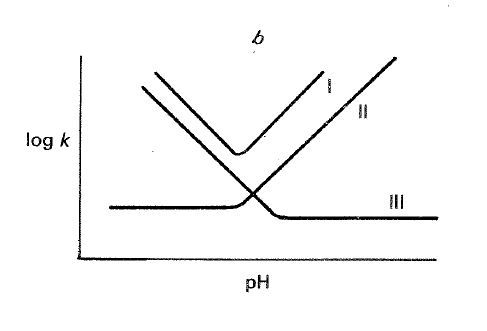
Fig. 24-2. a) Representación de log k frente al pH para una reacción catalizada por \( H^{+} \) y por  \( OH^{-} \), y para la no catalizada. b) Distintas variantes de la representación.

La catálisis ácido-base implica la transferencia de un protón a o desde una molécula de sustrato. Por ello, es de esperar que esta catálisis pueda también verse afectada por otros ácidos y bases distintos de \( H_{3}O^{+} \) y \( OH^{-} \). Este hecho se ha podido comprobar experimentalmente y entonces la catálisis ácido-base se denomina general.

Supongamos que en la solución hay un ácido HA, su base conjugada \( A^{-} \), los iones hidronio e hidroxilo, la constante de velocidad en este caso general podrá tener la forma

\( k = k_{O} + k_{H^{+}} [H_{3}O^{+}] + k_{OH^{-}}[OH^{-}] + k_{HA} [HA] + k_{A^{-}}[A^{-}]  \hspace{2cm}   \) [24.12]

En un caso experimental como este habría que calcular cinco constantes, lo cual puede hacerse variando sistemáticamente las concentraciones de las especies.

b. Efecto salino secundario. En la catálisis ácido-base, se debe tener en cuenta el efecto que la fuerza iónica ejerce sobre la disociación de ácidos y bases débiles, lo que se denomina efecto salino secundario. El grado de disociación de un ácido débil varía al variar la concentración de sales en disolución, y puesto que la velocidad de reacción depende de la concentración de ion hidrógeno, que a su vez procede de la disociación del ácido, es evidente que la velocidad de reacció dependerá de la concentración de sal.

La teoría del efecto salino secundario se puede desarrollar con ayuda de la teoría de Debye-Hückel. Supongamos que se tiene un ácido \( HA^{z} \) en equilibrio con su base conjugada \( A^{z-1} \),

\( HA^{z}   =  H^{+} + A^{z-1} \)

Despejando \( [H^{+}] \) en función de la \( K \) de disociación, de las concentraciones del ácido y de su base conjugada y de los coeficientes de actividad, tomando logaritmos y aplicando la ley límite de Debye-Hückel a los coeficientes de actividad, resulta:

\( \log [H^{+}] = \log K_{a} + \log \displaystyle \frac{[HA^{z}]}{[A^{z-1}]}-  2A(z — 1)I^{1/2} \hspace{2cm}   \)  [24.13]

El efecto salino secundario puede aumentar o disminuir la constante de velocidad, dependiendo del signo de z. Si z vale cero, que es el caso más común, el aumentar l aumenta \( [H^{+}] \) y, por tanto, la velocidad.

c. Mecanismos. Los mecanismos de una catálisis ácida en soluciones acuosas suponen usualmente dos etapas: la primera en la que tiene lugar una transferencia protónica al sustrato S, y la segunda, una transferencia protónica desde el sustracto protonado \( SH^{+} \). La transferencia protónica inicial puede partir de un ion hidronio \( H_{3}O^{+} \) o de alguna otra especie ácida presente, representada por \( BH^{+} \). En la segunda, la transferencia protónica desde \( SH^{+}\) puede ser a una molécula de agua o alguna especie básica B presente. La especie a la que \( SH^{+} \) transfiere el protón, en la segunda etapa es de importancia primordial en cuanto se refiere a las leyes cinéticas que se derivan. Si la transferencia es a una molécula de disolvente, es decir, si el proceso es

\( SH^{+}+ H_{2}O \rightarrow S + H_{3}O^{+} \)

se dice que el mecanismo es protolítico. Si por el contrario, la transferencia protónica en la segunda etapa es a una molécula de soluto

\( SH^{+} +B \rightarrow  S + BH^{+} \)

el mecanismo se llama prototrópico. En este último caso se da catálisis general. Sin embargo, en el caso de un mecanismo protolítico, la catálisis puede ser específica o general, según las circunstancias.

d. Relaciones de Briinsted-Pedersen. En toda reacción en la que se produce catálisis ácida o básica generales existen dos parámetros susceptibles de determinación experimental: la constante de velocidad de la reacción catalizada \( k_{C} \), y la constante de equilibrio \( K_{A} \) o \( K_{B} \), correspondientes a la ionización del ácido o base catalizadores. Comprobada una relación de proporcionalidad entre \( k_{C}\) y  [AH] o [B], se pueden deducir los factores catalíticos

\( ka=  \displaystyle \frac{kc}{AH} \hspace{2cm}   kb = \displaystyle \frac{kc}{B} \hspace{2cm} \)    [24.14]

Bremsted y Pedersen sugirieron que para una determinada reacción catalizada por una serie de ácidos, los factores catalíticos están relacionados con las constantes de equilibrio por las ecuaciones

\( k_{a}= C_{a} K_{A}^{\alpha} \hspace{2cm}   k_{b} = C_{b}K_{B}^{\beta}  \hspace{2cm} \)  [24.15]

o en sus formas logarítmicas

\( \log k_{a}= \log C_{a}+ \alpha \log K_{A} \hspace{2cm}    \)  [24.16]

\( \log k_{b} = \log  C_{b} + \beta \log K_{B}  \hspace{2cm} \)  [24.17]

en las que los parámetros \( C_{a}, \alpha \) y \( C_{b}, \beta \) permiten estos ajustes lineales que se conocen como relaciones de Bffinsted-Pedersen, consecuencia de la existencia de relaciones entre energías de Gibbs y energías de Gibbs de activación, y de que los factores catalíticos engloban constantes de velocidad y de equilibrio.

La comprobación de las relaciones de Brbnsted-Pedersen se ha logrado en numerosas reacciones catalizadas por diversos ácidos o por diversas bases, según mecanismos de catálisis ácida o básica generales. La figura 24-3 muestra el ejemplo de la catálisis ácida general en la reacción de deshidratación del dihidrato del acetaldehído con disolvente acetona.

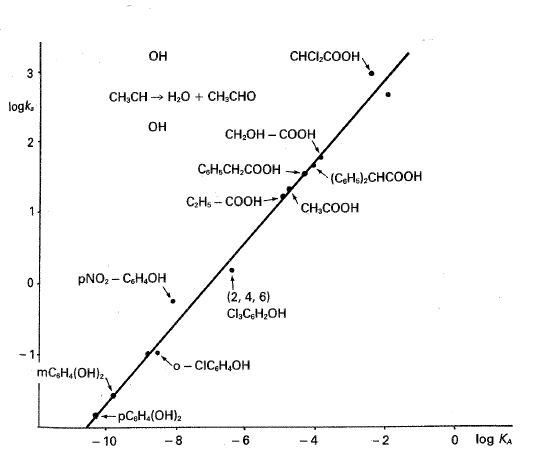
Fig. 24-3. Representación del logaritmo del factor catalítico frente al logaritmo de las constantes de ionización para la catálisis ácida general de la reacción de deshidratación del dihidrato de acetaldehído (Brónsted y Pedersen).

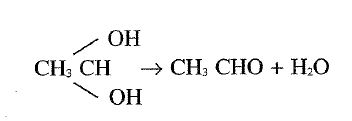Fórmula 24.18

El cumplimiento de las relaciones de Brünsted-Pedersen es una prueba determinante de la existencia de catálisis ácida o básica generales.

e. Funciones de acidez. En disoluciones diluidas de ácidos, la mejor medida de la acidez es el pH. Sin embargo, el pH es de poco valor en soluciones más concentradas, donde los coeficientes de actividad llegan a diferir significativamente de la unidad, por lo que entonces la fuerza del ácido se habrá de medir a través de las funciones de acidez determinables experimentalmente por medio de medidas espectrofotométricas de las concentraciones de las dos formas de ciertos indicadores.

La función de acidez mejor conocida, \( H_{0} \), se basa en el equilibrio

\(  B + H^{+} = BH^{+}   \hspace{2cm}  \) [24.19]

siendo la correspondiente constante de equilibrio

\( K = \displaystyle \frac{ [BH^{+}] }{[B][H^{+}]} \displaystyle \frac{ \gamma_{BH^{+}}}{\gamma_{B} \gamma_{H^{+}}} \hspace{2cm}  \) [24.20]

donde \( \gamma \) y son los correspondientes coeficientes de actividad. Si \( BH^{+} \) y B son las especies que pueden distinguirse espectrofotométricamente, se podrá medir el cociente \( [BH^{+}]/[B] \), y en soluciones más diluidas también puede medirse K. Tomando logaritmos y reorganizando,

\( \log K –  \log  \displaystyle \frac{[BH^{+}]}{[B]} = – \log (a_{H^{+}}) \displaystyle \frac{\gamma_{B}}{\gamma_{BH^{+}}}   \hspace{2cm}  \) [24.21]

Hammen definió como función de acidez \( H_{0} \)

\( H_{0} = –  \log (a_{H^{+}}) \displaystyle \frac{\gamma_{B}}{\gamma_{BH^{+}}}   \hspace{2cm}  \) [24.22]

El significado de la función se desprende de su correlación con las velocidades de reacción en el caso de un proceso en que haya un preequilibrio del mismo tipo de la reacción [24.19]. Supongamos que una reacción transcurre según el mecanismo

\( X + H^{+} = XH^{+}  \hspace{2cm}   (rápida) \)

\( XH^{+} —> Productos  \hspace{2cm}  (lenta) \)

Como la segunda etapa es lenta y la velocidad que determina la del proceso global es proporcional a la concentración de complejo activado \( XH^{+} \) correspondiente a dicha etapa, el coeficiente de velocidad de primer orden \( v/[X] \), es:

\( k= k^{ \neq} K_{x}^{ \neq} K_{x} \displaystyle \frac{ \gamma_{x}}{  \gamma_{\neq}} a_{H^{+}}   \hspace{2cm}  \) [24.23]

\( \log k = \log  (k^{7} K_{x}^{7} K_{x}) + \log  (a_{H^{+}}) \displaystyle \frac{ \gamma_{x}}{\gamma^{\neq}}    \hspace{2cm}  \) [24.24]

Las relaciones \(  \displaystyle \frac{\gamma_{B}}{\gamma_{BH^{+}}} \) y \( \displaystyle \frac{ \gamma_{x}}{\gamma_{ \neq}}  \) deben variar de forma semejante, una a la otra, por lo que si se comparan las ecuaciones [24.21] y [24.24], es de esperar que haya una correlación entre \(  log k \)  y \(  H_0 \) , de modo que al representar uno frente al otro debe salir una línea recta de pendiente -1. Esta relación se ha observado en muchas ocasiones y va en apoyo del mecanismo propuesto.

Se ha definido otra función de acidez, \( H_{R} \) , con referencia al equilibrio

\(  ROH + H^{+} =  R^{+} +H_{2}0    \hspace{2cm}  \) [24.25]

en el que se forma una molécula de agua al producirse la ionización. La constante de equilibrio es

\( K=  \displaystyle \frac{a_{R^{+}} a_{H_{2}O}}{a_{ROH}a_{H^{+}}}=  \displaystyle \frac{a_{H_{2}O}[R^{+}] \gamma_{R^{+}}}{a_{H^{+}}[ROH] \gamma_{ROH}} \hspace{2cm}  \) [24.26]

Y separando las magnitudes determinables experimentalmente de las que no lo son,

 

\( \log K – \log \displaystyle \frac{[R^{+}]}{[ROH]} = – \log \displaystyle \frac{a_{H^{+}} \gamma_{ROH}}{a_{H_{2}O} \gamma_{R^{+}}}  \hspace{2cm}  \) [24.27]

siendo

\( H_{R}= – \log \displaystyle \frac{a_{H^{+}} \gamma_{ROH}}{a_{H_{2}O} \gamma_{R^{+}}}  \hspace{2cm}  \)    [24.28]

Es de esperar una correlación entre esta función de acidez y la constante de velocidad si la reacción procede por un mecanismo del tipo

\( ZOH + H^{+} = Z^{+} + H_{2}O \hspace{2cm} \)  Rápida

\( Z^{+} \rightarrow Productos \hspace{2cm} \)  Lenta

en el que el coeficiente de velocidad de primer orden, igual a u/[ZOH] es ahora

\(  k = k^{7} K_{z}^{7} K_{z} \displaystyle \frac{\gamma_{ZOH}}{\gamma^{ \neq}} \displaystyle \frac{a_{H^{+}}}{a_{H_{2}O}} \hspace{2cm}  \)    [24.29]

es decir

\(  \log k = log (k^{ \neq} K_{z}^{ \neq} K_{z}) + \log \displaystyle \frac{a_{H^{+}}\gamma_{ZOH}}{a_{H_{2}O} \gamma^{ \neq}} \hspace{2cm}  \)    [24.30]

La comparación de las ecuaciones [24.27] y [24.30] muestra que cabe esper la existencia de una correlación entre \( log k \)  y  \( H_{R} \)  cuando se dé este mecanismo.

Una buena correlación lineal entre el logaritmo de una constante de velocid y una función de acidez constituye una prueba a favor de un determinado tipo mecanismo.

24.6. CATÁLISIS ELECTROFÍLICA Y NUCLEOFÍLICA

Otras especies que se comportan como ácidos o bases de Lewis pueden actuar con mecanismos que se asemejan a los de la catálisis ácido-base. Las bases de Lewis (con pares electrónicos compensados no enlazantes) pueden intercambiar con los ácidos de Lewis (con defecto electrónico) los pares electrónicos no enlazantes, y utilizarlos para la formación de enlaces dativos, en los que el dador es la base el aceptor el ácido.

Tienen carácter de ácidos de Lewis especies como \( BF_{3} \), \(  AICI_{3} \), \(  ZnCI_{2} \),…, y muchos iones e iones complejos de los metales de transición (con las capas 3d, 4d o 5d de su envoltura electrónica incompletas). Tienen carácter de bases de Lewis agua, amoniaco, imidazol, acetona, etc., o sustancias orgánicas con enlaces fuertes en los enlaces múltiples. También pueden actuar como ácidos y bases Lewis los disolventes no prótidos.

Estos procesos catalíticos se inician con las reacciones de formación de 1os complejos sustrato-catalizador a través de enlaces dativos

Catálisis con ácidos de Lewis o electrofílica:

\( S: + A  = S:A \)

Catálisis con bases de Lewis o nucleofílica:

\(  S + :B =   S:B \)

y suelen finalizar con la regeneración del catalizador A o :B.

24.7. CATÁLISIS HETEROGÉNEA

En este tipo de catálisis, la especie o mezcla que produce el incremento de la velocidad de una determinada reacción pertenece a una fase distinta a la del sistema reactivo y la acción de estos catalizadores heterogéneos tiene lugar en las interfacies que separan la fase de la que forman parte los reactivos, y muchas veces los productos, de la fase que forma o contiene al catalizador. Los procesos por catálisis heterogénea se producen en sistemas reactivos gaseosos, mientras el catalizador es un bloque sólido compacto o poroso, o está dividido en pequeñas porciones para incrementar la extensión de la interfase gas-sólido. Esta forma de catálisis heterogénea es la más frecuente, la mejor estudiada desde los puntos de vista experimental y teórico; y la que mayor importancia tiene en la práctica, puesto que constituye el método que ha hecho posibles y rentables muchos procesos de síntesis y transformación de interés en el campo de la industria química. Ejemplos como la síntesis del ácido sulfúrico, amoníaco o ácido nítrico, la hidrogenación del carbono para la preparación de carburantes líquidos o los procesos de cracking de hidrocarburos pesados, son muestra de procesos logrados una vez descubiertos los catalizadores heterogéneos apropiados a cada una de estas reacciones.

Sin embargo, también pueden producirse catálisis heterogéneas cuando el sistema es líquido y el catalizador sólido, tanto cuando se trate de reactivos orgánicos, como cuando intervengan disoluciones en las que estén presentes especies iónicas.

Como en las otras formas de procesos catalíticos, la catálisis heterogénea debe iniciarse por la reacción entre el catalizador y uno o varios reactivos, para la formación de los complejos sustrato-catalizador. Pero estos complejos se localizan en la interfase y resultan de procesos de adsorción, preferentemente quimioadsorción de los reactivos sustratos en la superficie del catalizador. El papel de la adsorción en los procesos de catálisis heterogénea es primordial y viene a constituir la base de todos los mecanismos catalíticos. En razón a estas uniones de los sustratos, que son las especies que se adsorben, y el catalizador, que es el adsorbente, resulta un compuesto superficial, o adsorbato, de estequiometría no definida, pero que es la causa de que se produzca una considerable disminución de la energía de activación y con ello el incremento de la velocidad.

Actúan como catalizadores heterogéneos muchos metales, sobre todo de transición, en su estado metal o elemento libre y otras sustancias sólidas, que normalmente son óxidos metálicos. Por el efecto de la quimioadsorción, se forman en el adsorbato enlaces que pueden ser de diversos tipos como Pt-H,  Ni-H, etc., de carácter preferentemente covalente, o uniones como del tipo enlace de hidrógeno, entre iones \( O^{2-} \) de la red cristalina del óxido y compuestos con grupos polares -OH,  \( -NH_{2} \), etc.

La acción de los catalizadores heterogéneos es puramente superficial y está comprobado que su actividad catalítica aumenta con la suPerficie del catalizador. Por esta razón, todo aquello que contribuya a incrementar su superficie permite mayor capacidad catalítica a igual de masa de catalizador. Esta es la explicación de la destacada actividad de los materiales porosos, como el gel de sílice o la conocida esponja de platino.

Y por la misma razón, cuando algunas especies extrañas se adsorben sobre el catalizador y forman adsorbatos más estables que los que puedan formar los sustratos, la actividad catalítica disminuye o incluso puede desaparecer. Las sustancias que provocan estos efectos son los venenos de los catalizadores, y entre ellos se incluyen especies inorgánicas como \( CI_{2}, Br_{2}, I_{2}, CO, SH_{2}, S_{2}C, PH_{3}, As_{2}O_{3} \), etc., u orgánicas como HCN, tiofeno (\( C_{4}H_{4}S \)), mercaptanos, etc. Algunos de estos venenos inhabilitan a los catalizadores de forma permanente, sin que sea posible sil: recuperación. Son los venenos irreversibles, como \( SH_{2} \) o \( PH_{3} \) para con el platino.z En cambio, los venenos reversibles permiten la regeneración del catalizador, después de un tratamiento térmico o químico adecuados. Tal ocurre, por ejemplo, con el platino envenenado con \(  CO \) o \( S_{2}C \) . La acción de estos venenos debe considerarse como un efecto de inhibición.

Otras veces son los productos de las reacciones los que inhiben la acción del catalizador, lo que se supone que es debido a que después de formarse en la superficie, permanecen retenidos en la misma algún tiempo, bloqueando una parte de la misma, que queda inactiva a efectos catalíticos. Si estas uniones se hacen permanentes o de desorción muy lenta, pueden incluso comportarse como auténticos venenos del catalizador. Sin embargo, la acción de los venenos e inhibidores no siempre es perjudicial. En algunas ocasiones se ha utilizado para favorecer la acción encauzante de una determinada reacción. Por ejemplo, se conoce que el óxido de torio puede provocar a la vez la deshidratación a olefinas o la deshidrogenación a aldehídos o cetonas de algunos alcoholes. Pero si previamente se trata e catalizador con vapor de agua, sus moléculas bloquean por enlaces de hidrógeno; los iones \( O^{2-} \) de la red e inhiben el proceso de deshidratación, dejando casi libres los átomos de torio, lo que es posible puesto que se trata de un elemento de elevado volumen atómico, para que sólo se realice la reacción de deshidrogenación.

a. Etapas de un proceso de catálisis heterogénea. La reacción catalizadw ocurre propiamente en la interfase entre el sistema gaseoso reactivo y el catalizador sólido. Para que una reacción de esta naturaleza pueda producirse se han de cubrir los siguientes procesos o etapas:

1.° Transporte de los reactivos hasta la interfase.

2.° Difusión de las moléculas de los sustratos a través de la capa de paso.

3.° Adsorción de los sustratos sobre el catalizador.

4.° Reacción de superficie.

5.° Desorción de los productos de reacción.

6.° Difusión de los productos a través de la capa de paso.

7.° Transporte de los productos hasta el seno de la fase gas.

Se trata de una sucesión de procesos, y determinará la velocidad de reacción el más lento o los más lentos de todos ellos. Normalmente los procesos 1.° y 7.° suelen ser rápidos. Además, se pueden favorecer mediante una adecuada agitación o circulación del sistema gaseoso, de forma que se facilite su homogeneización. Pero esto no evita los procesos de difusión 2.° y 6.°, porque en las inmediaciones de la interfase son más intensas las interacciones entre las moléculas de la fase fluida y los átomos o iones situados en la superficie del sólido, que siempre tienen carácter más o menos insaturado, en razón a sus posiciones superficiales. En estas inmediaciones se forma siempre una capa de moléculas del fluido, en cierto modo inmovilizadas, que no se altera aún con fuerte agitación. En esa capa, de un espesor de pocos \( \dot {A} \), existe un gradiente de concentración de las especies que han de atravesarla, bien en el sentido fase gas a superficie, o bien en sentido contrario, cuyo desplazamiento corresponde siempre a un típico fenómeno de difusión.

Cuando es el proceso 2.°, el más lento y el que determina la velocidad de reacción, se dice que el proceso total está controlado por difusión.

El proceso 3.° suele ser, normalmente, muy rápido, porque el equilibrio de adsorción se establece en un tiempo muy corto y se mantiene a lo largo de todo el proceso de reacción. Pero conviene puntualizar que este proceso es sólo de hecho instantáneo, cuando se trata de fisiadsorción, pero tiene una evolución de tipo cinético si lo que se produce es una quimioadsorción. La velocidad de quimiadsor-ción se incrementa con la temperatura, según una ley de variación semejante a la prevista por la Ecuación de Arrhenius para las reacciones químicas. Es en esta etapa donde se forma el complejo sustrato-catalizador, por lo que la quimioadsorción es de hecho una etapa necesaria para que sea efectiva la catálisis heterogénea. No se excluyen, pese a todo, algunas excepciones poco frecuentes, en las que parece que la acción catalítica es posible con sólo fisiadsorción. La adsorción va siempre acompañada de desprendimiento de calor, determinable mediante la correspondiente entalpía de adsorción \(  \Delta H_{ad} \), que será, por tanto, negativa. Pero es muy típico de los procesos de quimioadsorción que la entalpía de adsorción sea menos negativa y la energía de activación de adsorción más positiva, a medida que la concentración superficial es mayor, hecho relacionado con la no homogeneidad de la superficie.

El proceso 5.° de desorción también suele ser rápido y nunca determinante de la velocidad de reacción. Pero no es instantáneo, sino a veces incluso más bien lento, lo que es motivo de retrasos, porque parte de la superficie del catalizador queda bloqueada temporalmente por las moléculas de los productos de reacciones todavía no desorbidos, con posibles efectos de inhibición e incluso de envenenamiento, a lo que se ha aludido ya en la sección precedente.

Por último, el proceso 4.° es propiamente el de reacción, porque en él se produce la transformación de los reactivos en productos. Este proceso puede ser realizado exclusivamente por el sustrato quimioadsorbido, cuando se trata de su descomposición en especies más sencillas; puede ocurrir entre el sustrato adsorbido y moléculas de los otros reactivos, a medida que van llegando de la fase gaseosa a la superficie, o pueden interaccionar en la misma superficie dos o más reactivos, cuando todos éstos han sido previamente adsorbidos. Esto es causa de que existan diferentes tipos de mecanismos de catálisis heterogénea. Cuando cualquiera de estas etapas sea la que determina la velocidad, se dice que la catálisis está controlada por reacción. También son posibles situaciones intermedias con lo que la velocidad queda controlada por difusión y reacción, con mayor o menor contribución de cada una.

De forma general, es fácil distinguir cuándo una reacción está controlada por difusión o por reacción, porque, como es sabido, la difusión es un proceso que requiere una energía de activación muy baja, inferior normalmente a \( 5 \hspace{.2cm} kJ \hspace{.2cm}  mol^{-1}\), mientras las reacciones superficiales se producen siempre por encima de los \( 10 \hspace{.2cm} a \hspace{.2cm} 20 \hspace{.2cm} kJ \hspace{.2cm} mol^{-1} \) , en los ejemplos más favorables. El efecto que producen estas energías de activación sobre las constantes de velocidad \( k_{c} \), se puede representar con ecuaciones análogas a la de Arrhenius

\( k_{c} = A  \exp { \left ( – \displaystyle \frac{E_{a}}{RT} \right ) }  \hspace{.5cm} o \hspace{.5cm}  \ln {k_{c}} = \ln {A} – \displaystyle \frac {Ea}{RT}  \hspace{2cm}  \)    [24.31]

de forma que las representaciones gráficas de \( \ln {k_{c}} \), frente a 1/T deben conducir a líneas rectas de pendiente negativa, y de los valores de estas pendientes deducir los de las energías de activación. Si la reacción está controlada por difusión, la pendiente debe ser muy pequeña, de forma que la recta será casi paralela al eje de abscisas. Si la reacción está controlada por la reacción superficial, la pendiente será mayor. Y si la reacción no está catalizada y se produce preferentemente en la fase gas, la pendiente ha de ser mucho mayor, por ser mucho mayor la energía de activación.

b. Tipos de catalizadores heterogéneos. Las reacciones susceptibles de ser catalizadas heterogéneamente pueden clasificarse en:

i. De oxi-reducción. En estas reacciones se da la transferencia electrónica de un reactivo a otro a través del catalizador, el cual debe ser capaz de aceptar o ceder con facilidad los electrones.

Catalizadores de este tipo son los metales de transición (platino, níquel, cobre, paladio, cobalto, hierro, plata, etc.) u óxidos semiconductores ( \( Cr_{2}O_{3}, V_{2}O_{5}, MnO, ZnO, NiO \), etc.).

Entre las reacciones de este tipo de mayor importancia industrial están:

– Hidrogenaciones, catalizadas principalmente por metales, como la síntesis del amoníaco (Haber-Bosch), la hidrogenación de las parafinas inferiores en superiores, etc.

– Deshidrogenaciones, catalizadas principalmente por óxidos, como la obtención de olefinas a partir de parafinas, la del tolueno a partir de heptano, etc.

– De oxidación, catalizadas principalmente por óxidos, como la oxidación del \( SO_{2}\) a \( SO_{3} \) (ácido sulfúrico), del \( NH_{3} \) a NO (base de la síntesis del ácido nítrico), etc.

• De polimerización de olefinas.

ii. Ácido-base de Lewis. Como catalizadores se utilizan ácidos y bases de Lewis como la sílice (\( SiO_{2} \)), la alúmina (\( AI_{2}O_{3}) , P_{2}O_{5}, MnO_{2} \), etc. Las reacciones así catalizadas más notables son:

– De hidratación, como la del acetileno a acetaldehído, de olefinas a alcoholes, etc.

– De deshidratación, como las de condensación de alcoholes con \(NH_{3} \) para dar aminas, etc.

– De isomerización de hidrocarburos.

– De adición para obtener derivados halogenados a partir de olefinas, por ejemplo.

– De craqueo del petróleo para obtener hidrocarburos bajos a partir de altos.

c) Energía de activación de las reacciones heterocatalizadas. El efecto energético de los catalizadores heterogéneos sobre la energía de activación de la reacción se puede interpretar con un esquema como el de la figura 24-4, que se fundamenta en las ideas de la Teoría del estado de transición también aplicable a las reacciones catalizadas.

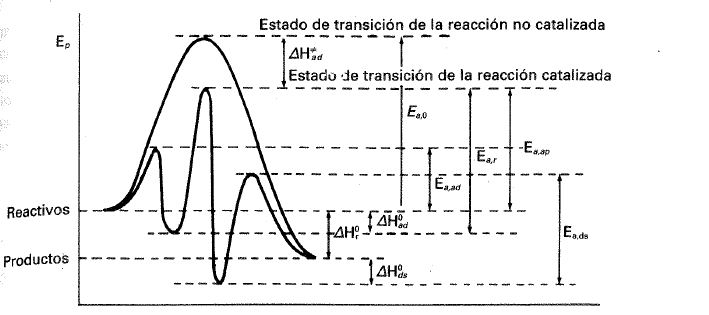
Fig. 24-4. Barreras de potencial en una reacción catalizada heterogéneamente.

Coordenadas de reacción

\(  \hspace{2cm} \Delta H_{r}^{0} = \) Entalpía de reacción < 0

\( \hspace{2cm} \Delta H_{ad}^{0} = \) Entalpía de adsorción del sustrato

\( \hspace{2cm} \Delta H_{ad}^{\neq} = \) Entalpía de adsorción

\( \hspace{2cm} \Delta H_{ds}^{0} = \) Entalpía de desorción de los productos de la reacción

\(   \hspace{2cm} E_{a0} = \) Energía de activación de la reacción no catalizada, en la fase de gaseosa

\(  \hspace{2cm}  E_{a, ad} = \) Energía de activación de adsorción del sustrato

 \( \hspace{2cm} E_{a,v} = \) Energía de activación verdadera

\(  \hspace{2cm}  E_{a, ap} = \) Energía de activación aparente

\(  \hspace{2cm}  E_{a, ds} = \) Energía de activación de desorción

Como se puede observar, la energía de activación de la reacción catalizada es inferior a la de la reacción no catalizada en la fase gas, lo que se ha comprobado de forma general. Pero conviene distinguir entre lo que se denomina energía de activación verdadera y energía de activación aparente, \(  E_{a, ap} \). Esta última se deduce directamente del estudio le la velocidad de reacción a diferentes temperaturas, una vez comprobado el cumplimiento de la ecuación de Arrhenius. Esta energía de activación representa la diferencia entre el estado inicial del sistema y el estado de transición, que se supone adsorbido también en la superficie del catalizador. En la misma figura 24-4 puede advertirse que,

\(  E_{a, 0} – E_{a, ap} = – \Delta H_{ad}^{ \neq} \hspace{2cm}  \)    [24.32]

y de esta forma se pueden estimar las entalpías de adsorción del estado de transición. Se comprueba que el efecto acelerante de los catalizadores heterogéneos se debe a la adsorción del estado de transición en la superficie del catalizador.

En cambio, la energía de activación verdadera, \( E_{a}\), \( \nu \), se refiere a la diferencia entre el nivel energético alcanzado una vez formado el adsorbato sustrato-catalizador y el estado de transición de la reacción catalizada. Asimismo,

\( E_{a,} \nu   = E_{a, ap}- \Delta H_{ad}^{0}   \hspace{2cm}  \)    [24.33]

de forma que, conocido experimentalmente  \( E_{a, ap} \) y \( \Delta H_{ad}^{0}  \), es posible la estimación de esta energía de activación verdadera.

En relación a los distintos tipos de cinéticas formales que pueden presentar las. reacciones catalizadas heterogéneamente, se podrán deducir las correspondientes ecuaciones de velocidad como consecuencia lógica del tipo de mecanismo cinético que presenten, y que, como se ha comentado, incluyen o pueden incluir procesos de difusión, adsorción y reacción suficientemente tratados en este texto.

24.8. BIOCATÁLISIS O CATÁLISIS ENZIMÁTICA

a. Características de la catálisis enzimática. Las reacciones catalizadas por enzimas se caracterizan generalmente por cuatro aspectos:

i. El incremento de velocidad es enorme (del orden de  \( 10^{6} \) a \( 10^{12} \) veces).

ii. Presentan una especificidad alta, entendiendo por especificidad que la enzima es capaz de catalizar selectivamente la reacción de ciertos compuestos llamados sustratos; sin embargo no actúa frente. a otras moléculas.

iii. Tienen carácter de catálisis microheterogénea, en el sentido de que, si bien es formalmente homogénea, el catalizador es una macromolécula que posee algunos puntos activos en los que se cataliza la reacción de manera análoga a como ocurre en la catálisis heterogénea.

iv. Presentan un pH óptimo y una temperatura óptima.

En la actualidad, es bien conocido que todas las enzimas estan formadas por moléculas de proteína. Asimismo, una enzima puede tener uno o más sitios activos donde la reacción con el sustrato tiene lugar. Un sitio activo suele contener solamente unos pocos residuos de aminoácidos, sin embargo el resto de la molécula de proteína se requiere para mantener la integridad de la estructura tridimensional: Se ha propuesto que la especificidad de una enzima se puede explicar en términos de la teoría llave-cerradura. Así, el sitio activo se supone que tiene una estructura rígida, como si fuese una cerradura, mientras que la molécula de sustrato tiene la estructura complementaria y funcionaría como una llave (fig. 24-5). En ciertos asr, pectos esta teoría ha sido modificada para tener en cuenta la flexibilidad de las proteínas en disolución y para explicar los fenómenos de cooperatividad, no obstante, puede ser en principio un símil adecuado.

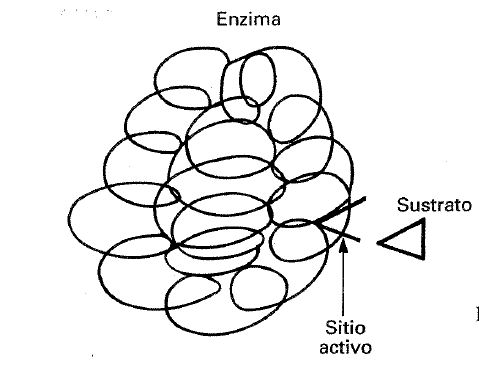Fig. 24-5. Esquema de la unión de un sustrato al sitio activo de una enzima.

A continuación se van a exponer las bases matemáticas del tratamiento de la cinética enzimática.

b. Análisis de los datos en cinética enzimática. En cinética enzimática se prefiere utilizar el método diferencial de las velocidades iniciales en lugar del método de integración. Las razones son varias: puede haber cambio de pH, darse un fenómeno de inhibición por producto, etc., pero la más importante es que las reac-ciotes enzimáticas normalmente no tienen un orden sencillo, sino que presentan ecuaciones de velocidad complejas.

Para analizar esta última causa imaginemos, por ejemplo, una serie de experimentos cinéticos en los que mantenemos la concentración de enzima constante pero variamos la concentración inicial de sustrato (fig. 24-6 a, 24-6 b y 24-6 c):

i. Si la concentración de sustrato es baja, la reacción parece comportarse como de orden 1, y si aplicáramos el método de integración a la curva cinética observaríamos una tendencia hacia el orden 1 (fig. 24-6 a).

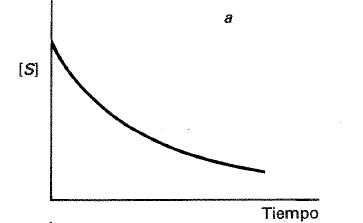
Fig. 24-6. Curvas cinéticas para una reacción catalizada por una enzima a tres concentraciones de sustrato iniciales. Fig. 24-6 a) Concentración inicial de sustrato baja, la reacción se comporta aparentemente como de orden 1.

ii. Si la concentración de sustrato es alta, la reacción parece comportarse como de orden O (fig. 24-6 b).

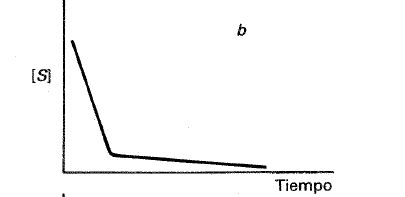
Fig. 24-6. Curvas cinéticas para una reacción catalizada por una enzima a tres concentraciones de sustrato iniciales. Fig. 24-6 b) Concentración inicial de sustrato alta, la reacción se comporta como de orden 0.

iii. Para concentraciones de sustrato intermedias el método de integración no revelaría ni como aproximado, ningún orden (ni 1 ni 0) sino la necesidad de una ecuación de velocidad compleja (fig. 24-6 c).

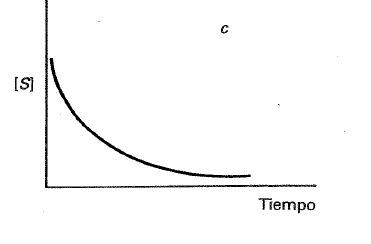Fig. 24-6. Curvas cinéticas para una reacción catalizada por una enzima a tres concentraciones de sustrato iniciales. Fig. 24-6c) Concentración inicial de sustrato intermedia, la reacción parece tener una ecuación de velocidad compleja.

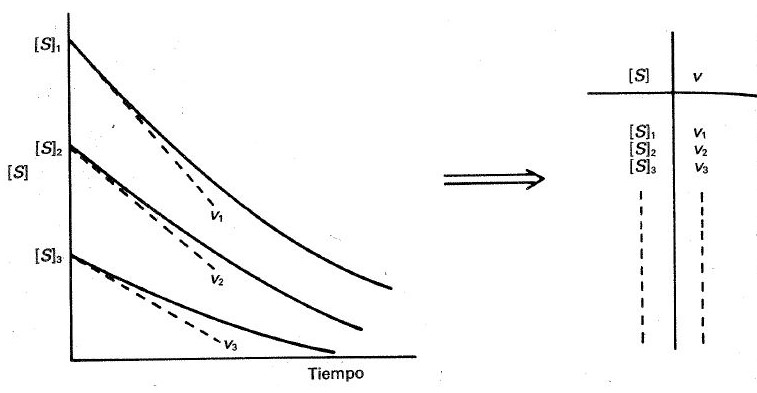
Fig. 24-7. Determinación de la velocidad inicial a diferentes concentraciones iniciales de sustrato; ν es la pendiente cambiada de signo de la línea discontinua, que es la tangente a la curva cinética a tiempo 0.

Para evitar estos problemas los estudios de cinética enzimática se llevan a cabo midiendo las velocidades iniciales a distintas concentraciones de sustrato. Esto es fácil, ya que una representación de la concentración de sustrato frente al tiempo da generalmente una línea recta en al menos el primer 5-10 % de reacción, de forma que, hallando la pendiente de estos tramos rectos iniciales, se obtendrán las velocidades iniciales a las distintas concentraciones de sustrato (fig. 24-7). Viniendo estas velocidades en unidades de concentración/tiempo, por ejemplo µmol de sustrato/l/min, y las concentraciones de sustrato en mol/l.

Si hacemos estas medidas para un margen amplio de sustrato (p. ej., \( 10^{-5} \) M- \(10^{-3} \) M) y representamos los resultados, tendremos en muchos casos un comportamiento como el de la figura 24-8. Es decir, al principio la velocidad se incrementa ta notablemente con el aumento de [S] y al final se va estabilizando en un valor constante mediante un comportamiento de tipo asintótico.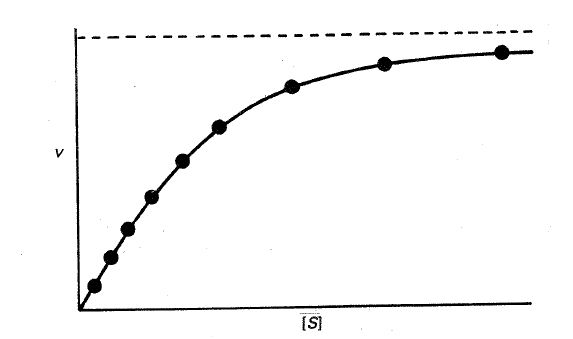

Fig. 24-8. Representación de la velocidad inicial de reacción frente a la concentración de sustrato para una reacción catalizada por una enzima.

Matemáticamente esta curva está representada por la ecuación de una hipérbola rectangular:

\( v = \displaystyle \frac{a [S] }{ b + [S] } \hspace{2cm}  \)    [24.35]

Esta sería, pues, la ecuación empírica de velocidad, donde a y b son parámetros. Conocido este comportamiento experimental, el siguiente paso será proponer los mecanismos adecuados que puedan explicar esta ecuación de velocidad.

c. Mecanismo de Michaelis-Menten bajo la aproximación del equilibrio rápido. En 1913, Michaelis y Menten propusieron un mecanismo para explicar la dependencia de la velocidad inicial con la concentración de sustrato. El esquema que ellos consideraron fue el siguiente:form

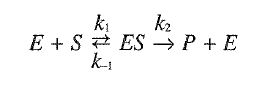donde E y S son la enzima y el sustrato, ES es un complejo enzima-sustrato y P es el producto formado. La enzima E que se libera en la ruptura del complejo ES vuelve a iniciar la ruta de nuevo.

Las concentraciones de la enzima y el sus/ato inmediatamente después de empezar la reacción serán:

\( [E] = [E]_{0} — [ES] \)

\( [S] = [S]_{0} — [ES] \)

Sin embargo, las condiciones experimentales generalmente son tales que:

\( [S]_{0}  \gg  [E]_{0} \)

por lo que

\( [S]_{0} \gg [ES] \)

y por tanto

\( [S] \cong  [S]_{0} \)

Michaelis y Menten asumieron que \( k_{-1} \gg  k_{2} \), por lo que el primer paso (formación del complejo ES) se puede tratar como un proceso de equilibrio rápido. La constante de equilibrio para la disociación de este complejo viene dada por:

\(  K_{S} = k_{-1}/k_{1}  =  [E] [S] / [ES]  \hspace{2cm}  \)    [24.36]

Teniendo ahora en cuenta el siguiente balance de materia

\(  [E]_0 = [E] + [ES] \)

se deduce que

\(  [E] = [E]_0 – [ES] \)

de manera que al sustituir [E] en la ecuación [24.36] queda:

\(  K_S =\left ( [E]_0 – [ES] \right ) [S] / [ES] \)

de donde

\( K_S [ES] = [E]_0 [S] — [ES][S] \)

y por tanto

\( [ES] = \left ( [E]_0 [S] \right ) / \left ( K_S + [S] \right ) \)

Y como la velocidad de reacción viene dada por

\( \nu = – \left ( d[S] / dt \right ) = \left ( d[P]/ dt \right ) = k_2 [ES] \)

se tiene que

\( \nu = \displaystyle \frac {k_2 [E]_0 [S]}{K_{S} + [S]} \hspace{2cm}  \)    [24.37]

que vemos que tiene la misma forma de hipérbola rectangular que la ecuación empírica de velocidad [24.35]

\( \nu = \displaystyle \frac {a[S]}{b+[S] } \)

donde

\( a = k_2 [E]_0  \hspace{1cm}  \) y  \( \hspace{1cm} b = K_s \)

Para comprender el significado físico de la ecuación [24.37] veamos algunos casos límites de ésta:

i. A concentraciones bajas de sustrato, cuando \( [S]  \ll  K_S \), entonces la ecuación se reduce a

\( \nu \cong (k_2 / K_S) [E]_0 [S] \)

de forma que la reacción es de orden 1 respecto a [S] ya que

\( \nu =  cte [S]  \hspace{1cm}  \) (orden 1)

comportamiento que puede apreciarse en la figura 24-9.

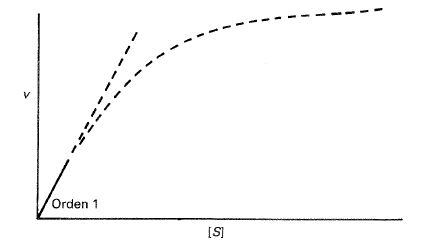
Fig. 24-9. Representación de la velocidad inicial frente a la concentración de sustrato para una reacción que obedece la ecuación [24.37]. A concentraciones bajas de sustrato (línea continua) la velocidad es directamente proporcional a la concentración de sustrato.

ii. A concentraciones altas de sustrato se tiene que:

\(  [S] \gg K_S  \Rightarrow  \nu  \cong k_2 [E]_0 \)

y entonces la ecuación de velocidad se hace de orden 0 respecto al sustrato, alcanzándose un valor máximo de velocidad que ya no se ve incrementado por sucesivos aumentos de [S] (fig. 24-10); es decir, en estas condiciones todas las moléculas de enzima se encuentran prácticamente bajo la forma de complejo ES.

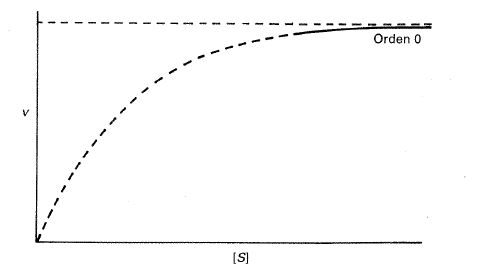
Fig. 24-10. Representación de la velocidad inicial frente a la concentración de sustrato para una reacción que obedece la ecuación [24.37]. A concentraciones altas de sustrato (línea continua) la velocidad se mantiene constante (orden O).

Se dice entonces que la enzima se encuentra saturada por sustrato. Este valor máximo es:

\( \nu = k_2 [E]_0 \equiv  V_{max} \)

con lo cual la ecuación de [24.37] queda:

\( \nu = \displaystyle \frac { V_{max}  \cdotp  [S]}{ K_S + [S] }\hspace{2cm}  \)    [24.38]

esta expresión recibe el nombre de ecuación de Michaelis-Menten y presenta dos parámetros: \( V_{max} \), conocido como velocidad máxima, y \( K_S \), conocido como constante de disociación del complejo ES.

d. Mecanismo de Michaelis-Menten bajo la aproximación del estado estacionario. Formalmente el mecanismo es idéntico al anterior:

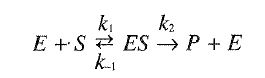
En 1925 Briggs y Haldane demostraron que no es necesario hacer la suposición de Michaelis y Menten según la cual la enzima y el sustrato se encuentran en equilibrio termodinámico. Postularon en su lugar que, al poco tiempo de mezclar la enzima y el sustrato, la concentración del complejo enzima-sustrato alcanzará

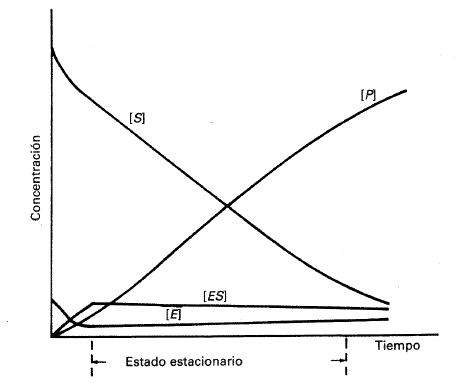
Fig. 24-11. Simulación por ordenador de la concentración de las diferentes especies de una reacción enzimática frente al tiempo. Se supone que la reacción sigue el mecanismo:

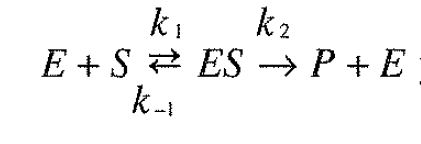
y que los valores de \( k_1, k_{-1} \)  y \( k_2 \) son comparables.

un valor constante, de forma que se puede aplicar el tratamiento del estado estacionario, el cual se define como aquel en que la concentración de ES permanece prácticamente constante. La figura 24-11 muestra la variación a lo largo del tiempo de las diferentes especies participantes en la reacción y pone de manifiesto la situación del estado estacionario.

Bajo la hipótesis del estado estacionario, se tiene que

\( d [ES] / dt  \cong 0 = k_1 [E] [S] –  k_{-1} [ES] – k_2 [ES] \)

y considerando de nuevo el balance de materia

\( [E]_0 = [E] + [ES] \)

resulta que

\( 0 = k_1 \left ( [E]_0 – [ES] \right ) [S] – k_{-1} [ES] –  k_2 [ES] \)

que, resolviendo para [ES], queda

\( k_1 [E]_0 [S] = k_1 [ES][S] + k_{-1} [ES] _2 [ES] \)

\( [ES] = k_1 [E]_0 [S]/  \left ( k_1 [S] + k_{-1} + k_2 \right ) \)

De nuevo, como \( \nu= k_2 [ES] \), tenemos ahora que

\( \nu = k_2 k_1 [E]_0 [S] / \left ( k_{-1} + k_2 + k_1 [S] \right ) \)

dividiendo ahora numerador y denominador por \( k_{-1} \) nos queda

\( \nu = \displaystyle \frac { k_2 [E]_0[S] }{\displaystyle \frac {k_{-1} + k_2}{k_1} + [S]} \)

y llamando ahora constante de Michaelis al término \( (k_{-1}+ k_2)/k_1 \), se tiene que

\( \nu = \displaystyle \frac { k_2 [E]_0[S] }{K_M + [S]} \)

y haciendo \(  k_2[E]_0 = V_{max} \), igual que antes, resulta que

\( \nu = \displaystyle \frac {V_{max} \cdotp  [S] }{K_M + [S] } \hspace{2cm}  \)    [24.39]

ecuación llamada también de Michaelis-Menten y que presenta los parámetros \( V_{max} \) (velocidad máxima) y \( K_M \) (constante de Michaelis). La forma de esta ecuación es la misma que la deducida originariamente por Michaelis y Menten [24.38], sólo que ahora \( K_M  \neq  K_S \) a menos que \( k_{-1} \gg k_2 \) en cuyo caso \( K_M \) y \( K_S \), coincidirían. Por tanto, la \( K_M \) en rigor no es la constante termodinámica de equilibrio para la disociación del complejo enzima-sustrato; desafortunadamente, sin embargo, algunas veces se le asimila este significado y se suele pensar en términos de que a una \( K_M \) alta (disociación alta) corresponde una baja afinidad del sustrato por la enzima, y viceversa, que a una \( K_M \) baja (disociación baja) corresponde una gran afinidad del sustrato por la enzima.

En resumen, pues, el tratamiento del estado estacionario es el más general para el mecanismo de Michaelis-Menten y debe preferirse frente al tratamiento del equilibrio rápido, el cual por otra parte no es sino un caso particular del primero cuando se cumple que \( k_{-1} \gg k_2 \).

e. Determinación gráfica de los parámetros \( K_M \) y \( V_{max} \) Existen diferentes representaciones gráficas que permiten obtener los parámetros \( K_M \) y \( V_{max} \), de la ecuación de Michaelis-Menten. A continuación se describirán los procedimientos más usuales.

i. Representación directa. Como \( \nu =  V_{max} \cdotp [S] / (K_{M} + [S]) \), la representación de \( \nu \) frente a [S] nos proporciona la gráfica de la figura 24-12.

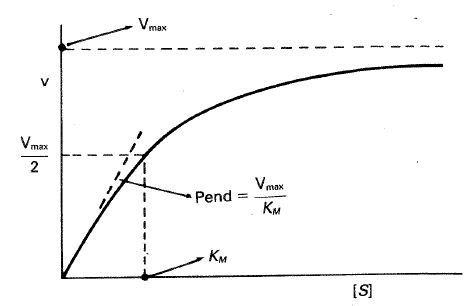Fig. 24-12. Representación de la velocidad inicial (υ) frente a la concentración de sustrato ([S]) para una reacción que obedece la ecuación de Michaelis-Menten.

Como se deduce fácilmente de la ecuación el valor de la asíntota cuando \(   [S]  \rightarrow  \infty \)  es igual al valor de \( V_{max} \) y la pendiente a la curva en el origen es igual \( V_{max}/ K_{M} \). Por último, cuando la velocidad inicial es igual a la mitad de la velocidad máxima, tenemos que

\( V_{max} / 2 = \displaystyle \frac {V_{max} [S] }{ K_{M} + [S]}   \)

de donde:

\( K_{M} = [S] \)

Esta representación no parece muy adecuada para la determinación de los parámetros, debido á la dificultad práctica de trazar una asíntota a la curva. Por eso, se han propuesto algunas formas de linealizar la ecuación de Michaelis-Menten que se exponen a continuación.

ii. Representación doble inversa (o de Lineweaver-Burk). Tornando inversos en la ecuación de Michaelis-Menten queda:

\( \displaystyle \frac {1}{\nu} = \displaystyle \frac {1}{V_{max}} + \displaystyle \frac {K_{M}}{V_{max}} \cdotp \displaystyle \frac {1}{[S]} \hspace{2cm}  \)    [24.40]

Así, una representación de \( 1/ \nu \) frente a \( 1/[S] \) (fig. 24-13) da una línea recta de ordenada en el origen \( 1/V_{max} \) y de pendiente \( K_{M} / V_{max} \). Por otra parte cuando \(  (1/ \nu) = 0 \) (abscisa en el origen), entonces:

\(  \displaystyle \frac {1}{[S]} = –  \displaystyle \frac {1}{K_{M}} \)

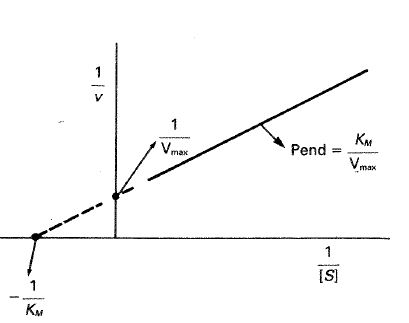
Fig. 24-13. Representación de 1/ υ  frente a 1/[S] según el método de Liriewea-ver-Burk.

iii. Representación de Eadie-Hofstee. Si en la ecuación doble inversa  [24.40] multiplicamos por  \(  \nu \cdotp V_{max} \)  nos queda:

\(  \displaystyle \frac {\nu \cdotp V_{max} }{ \nu} = \displaystyle \frac {\nu \cdotp V_{max}}{ V_{max}} + \displaystyle \frac {\nu \cdotp V_{max} K_{M}}{ V_{max}} \cdotp \displaystyle \frac {1}{[S]} \hspace{2cm}  \)    [24.41]

de donde

\(  V_{max} = \nu + \nu \cdotp K_{M} \displaystyle \frac {1}{[S]} \)

y por tanto

\(  \nu = V_{max} – K_{M }   \displaystyle \frac {\nu}{[S]} \)

Según esta transformación, si representamos \( \nu \) frente a \( \nu / [S] \) (fig. 24-14) obtendremos una línea recta de ordenada en el origen \( V_{max} \) y de pendiente \( – K_{M} \). La abcisa en el origen vale  \( V_{max}/ K_{M} \).

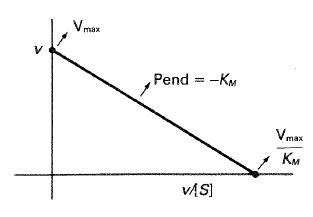24-14. Representación de υ y frente a υ/[S] según el método de Eadie-Hofstee.

iv. Representación de Hanes. Multiplicando en la ecuación doble inversa [24.40] por [S] nos queda:

\(  \displaystyle \frac {[S]}{\nu} = \displaystyle \frac {K_{M}}{V_{max}} + \displaystyle \frac {1}{V_{max}} \cdotp [S] \hspace{2cm}  \)    [24.42]

de manera que si representamos \(  [S] / \nu \) frente a \(  [S] \)  se obtendrá una recta de ordenada en el origen \(  K_{M}/V_{max} \) y de pendiente \(  1/V_{max} \)  (fig. 24-15). La abscisa en el origen vale \(  – K_{M} \) .

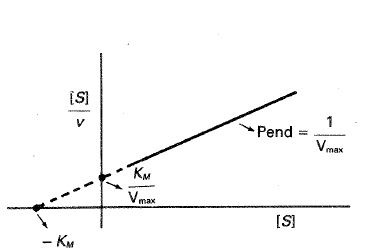
Fig. 24-15. Representación de [S] /υ  frente a [S] según el método de Hanes.

Si cada punto experimental se hubiese obtenido como el valor medio de cinco réplicas, tendríamos entonces que cada valor de \( \nu \) llevaría asociada su desviación estándar: \( \nu_{media} \pm \sigma \), con lo que las representaciones nos quedarían como en la figura 24-16, donde se han simulado datos por ordenador para una enzima de \( V_{max} = 10 \) y \( K_{M} =  5 \cdotp 10^{-5} \), con 10 puntos espaciados logarítmicamente entre \( 10^{-5} \) y \(10^{-3}  M \) en sustrato, y donde las barras de error corresponden a unas desviaciones estándar de \(  \pm 0,10 \nu \).

Aunque la representación doble inversa es la más utilizada en los estudios cinéticos, en realidad no es la mejor gráfica ya que distribuye los puntos de una manera poco uniforme y además tiende a dar más importancia a los puntos de menor concentración en sustrato, que son los más inexactos. La representación de Eadie-Hofstee distribuye más uniformemente los puntos y es la más aconsejable, sobre todo para detectar posibles desviaciones de la linealidad. La representación de Hanes no distribuye tan uniformemente los puntos como la de Eadie-Hofstee, pero es mejor que la de Lineweaver-Burk porque da más importancia a los puntos de mayor concentración, que son los más exactos (fig. 24-16).

 

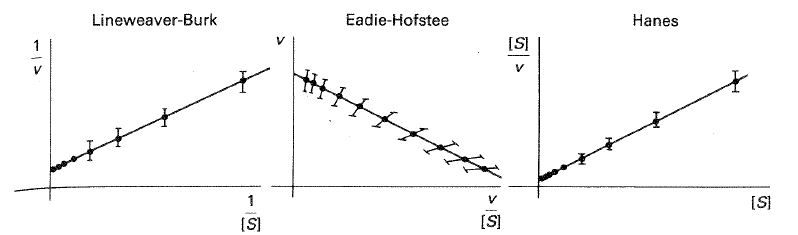
Fig. 24-16. Representación de unos datos simulados según las linealizaciones de Lineweaver-Burk, Eadie-Hofstee y Hanes. La simulación corresponde a una enzima de \( K_{M} = 5 \cdotp 10^{-5} , V_{max}  = 10 \) y se han obtenido 10 puntos espaciados logarítmicamente entre \( 10^{-5} \) y \( 10^{-3} M \). Cada punto lleva barras de error que corresponden a  \( \pm 0.10 \nu \).

f. Unidades de los parámetros \(V_{max} \) y \( K_{M} \). Como se acaba de ver, la ecuación de Michaelis-Menten queda

\( \nu =  V_{max} \displaystyle \frac {[S]}{K_{M} + [S]} \)

donde \( V_{max} \) representa la velocidad máxima alcanzable, es decir, la velocidad cuando la concentración total de enzima se encuentra formando el complejo ES. Como tal velocidad que es, vendrá expresada en las unidades en que se expresa la velocidad \( \nu \), bien en (μmol/l)/s, en (μmol/l)/min, (mol/l)/s,… etc.

Por otra parte:

\( V_{max}  = k_{2} [E]_{0} \)

de donde

\( k_{2} = \displaystyle \frac {V_{max }}{[E]_{0}} \)

esta constante \( k_{2} \) es llamada número de recambio (turnover number) y normalmente se expresa en \(  s^{-1} \):

\( k_2 (s^{-1}) = V_{max} \displaystyle \frac {(mol/l)/s}{ [E]_{0}(mo1/1)} \)

El nombre de «número de recambio» (turnover number) viene a significar el número de veces que la enzima actúa por segundo, o, lo que es lo mismo, cuántas veces pasa a través del complejo ES y es regenerada (turn over) al liberarse el producto. En otras palabras, el número de recambio es el número de moléculas de sustrato transformadas por segundo por una sola molécula de enzima, eso si bajo condiciones tales que la enzima esté completamente saturada con sustrato. Los números de recambio de la mayoría de las enzimas para sus sustratos fisiológicos caen en el intervalo de 1 a \( 10^{5}s^{-1}\). Como se deduce de su determinación, \(  k_2 \) sólo se puede evaluar si se conoce perfectamente \( [E]_{0} \) (\(  V_{max} \) se determina gráficamente), lo que supone saber su concentración en mol/1 (por tanto es necesario conocer la masa molecular de la enzima); es decir, supone trabajar con enzimas puras y bien caracterizadas. En caso contrario \( [E]_{0} \) es una cantidad desconocida, cosa frecuente en la práctica, ya que es difícil obtener enzimas muy purificadas. Por esta razón, muchas veces en lugar de utilizarse el número de recambio, lo que se maneja es la llamada actividad específica \(  (A_{esp}) \) que se expresa como:

\( A_{esp} \left (  \displaystyle \frac {\mu mol }{min \cdotp mgE}  \right ) =  \displaystyle \frac {\nu \left (  \displaystyle \frac {\mu mol/l}{min} \right )}{[E]_0 \left (   \displaystyle \frac {mgE}{l} \right )} \hspace{2cm}  \)    [24.43]

donde υ es la velocidad de reacción en unas condiciones estándar de pH, temperatura y concentración saturante de sustrato, \( [E]_0 \) es la concentración de enzima y mgE significa miligramos de enzima. También se puede expresar la actividad específica en forma de unidades/mgE, donde una unidad (U) se define como la cantidad de enzima que cataliza la transformación de 1 μmol de sustrato en productos en 1 minuto, bajo condiciones estándar, es decir:

\( A_{esp} \left (  \displaystyle \frac {\mu mol }{min \cdotp mgE}  \right ) \hspace{2cm} \)  \(  \hspace{2cm} A_{esp} \left ( \displaystyle \frac {U}{mgE} \right ) \)

La Unión Internacional de Bioquímica ha recomendado una nueva unidad, el katal (kat), que es la cantidad de enzima que cataliza la transformación de 1 mol de sustrato en productos en un segundo, bajo condiciones estándar. El factor de conversión es 1 kat = \( 6  \cdotp 10^{7} \) unidades.

En cuanto a \( K_M \), vimos que venía dada por \( K_M = (k_{-1} + k{2})(k_1 \), expresándose normalmente en unidades de mol/l (como se deduce fácilmente recordando que \( K_M \) es la concentración de sustrato para la que la velocidad es la \( V_{max}/2 \), o también poniendo las unidades correspondientes para \( k_{-1}, k_2 \) y \( k_1 \) y simplificando). Los valores de \( K_M \) para la mayoría de las enzimas están entre \( 10^{-2} \) y \( 10^{-7} M \).

Ejercicio 24.1. La reacción de hidrólisis del p-nitrofenil fosfato es catalizada por la enzima fosfatasa alcalina de E. coli:

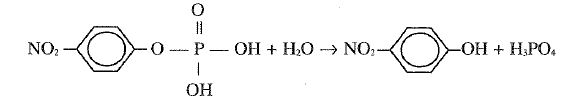
Para el cálculo de los parámetros cinéticos se realizaron experimentos a distintas concentraciones de sustrato, obteniéndose los siguientes resultados:

\(   \begin{array}{lccccccc} \\ [S] / 10^{-5} M: &   0,70 &  1,00 &  2,00 &  4,00 &  7,00  &  10,0 &  20,0 \\ \\ \nu / – \displaystyle \frac {\mu mol/l}{min}: &    0,430 &  0,560 &  0,830  & 1,09 &  1,27 &  1,35 &  1,49 \\  \end{array}  \)

Determínese la constante de Michaelis, la velocidad máxima y el número de recambio, sabiendo que la concentración de enzima empleada fue de 0,036 μg/ml y que su masa molecular es de 86000.

Resolución:

a) Si utilizamos la representación de Lineweaver-Btuic tenemos que:

\( \displaystyle \frac {1}{ \nu}= \displaystyle \frac {1}{V_{max}} + \displaystyle \frac {K_{M}}{V_{max}} \cdotp \displaystyle \frac {1}{[S]} \)

de manera que hay que representar 1/υ frente a 1/[S]. De la ordenada en el origen se calculará \( 1/V_{max} \)  y de la pendiente \( K_{M}/V_{max} \). Para ello se construye la tabla de dobles inversos y se representa (figura 24-17):

\(   \begin{array}{lccccccc} \\  (1/[S])/10^{4}M^{-1}:  & 14,3 &  10,0 &  5,00 & 2,50  & 1,43 & 1,00 &  0,500 \\ \\ \displaystyle \frac {1/ \nu}{ 10^{-1} (\mu mol /l)^{-1} min}:  &  23,3   & 17,9  & 12,0 &  9,2 &  7,9 &  7,4 &  6,7 \\  \end{array}  \)

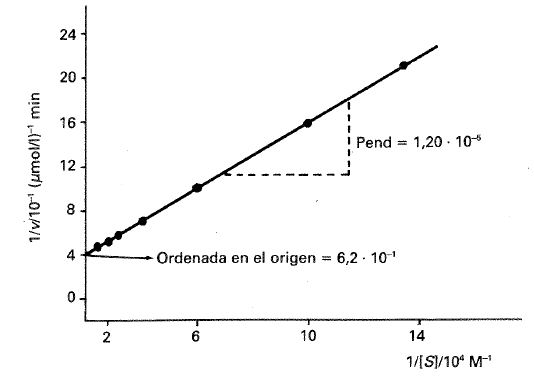
Fig. 24-17. Representación de Lineweaver-Burk para los datos del ejercicio 24.1.

Determinando gráficamente la ordenada en el origen y la pendiente obtenemos:

Ordenada en el origen \( = 0,62 (\mu mol/l)^{-1}min \)

Pendiente  \( = 1,20 \cdotp 10^{-5} (\mu mol/l)^{-1}min/M^{-1} \)

de donde

\(  1/ V_{max} = 0,62 (\mu mol/l)^{-1}min   \Rightarrow  V_{max} = 1,6 (\mu mol/l)/min \)

\(  \displaystyle \frac { K_M}{V_{max}}=  1,20 \cdotp 10^{-5} (\mu mol/l)^{-1} min M^{-1} \Rightarrow  K_M  = 1,9 \cdotp  10^{-5} M \)

y para el cálculo del número de recambio hacemos

como \( V_{max} = k_2 [E_0]  \rightarrow k_2 = V_{max}/ [E_0] \)

y por tanto

\(  k_2 = \displaystyle \frac {1,6 \displaystyle \frac {\mu mol/l }{min} \cdotp 10^{-6} \displaystyle \frac {mol }{\mu mol} } { \left ( 0,036 \displaystyle \frac {mg }{l} \cdotp 10^{-3} \displaystyle \frac {g }{mg} \right ) / 86000 \displaystyle \frac {g }{mol}} = 4 \cdotp 10^{3} min^{-1} \)

pero como normalmente \( k_2 \), se expresa en \( s^{-1} \) queda

\( k_2 = 4 \cdotp 10^{3} \displaystyle \frac {1}{min} \cdotp \displaystyle \frac {1}{60 s/min}= 70 s^{-1} \)

b) Si en lugar de la representación de Lineweaver-Burk utilizáramos la de Eadie-Hofstee, tendríamos

\( \nu =  V_{max} – K_M \displaystyle \frac {\nu}{[S]} \)

de manera que al representar y frente a v/[S] se obtiene una línea recta de cuya ordenada en el origen se calcula la \( V_{max} \) y, de la pendiente, la \(  K_M \) . Para ello se construye la tabla apropiada y se representa (figura 24-18):

\(   \begin{array}{lccccccc} \\  \nu / 10^{-1} (\mu mol/l) min: & 4,30 & 5,60 &  8,30 & 10,9 & 12,7 & 13,5 & 14,9 \\ \\ (\nu / [S]) / 10^{-4} (\mu mol/l) min^{-1} \mu^{-1}: &  6,14 &  5,60 & 4,15 &  2,72 & 1,81 &  1,35 &  0,75 \\  \end{array}  \)

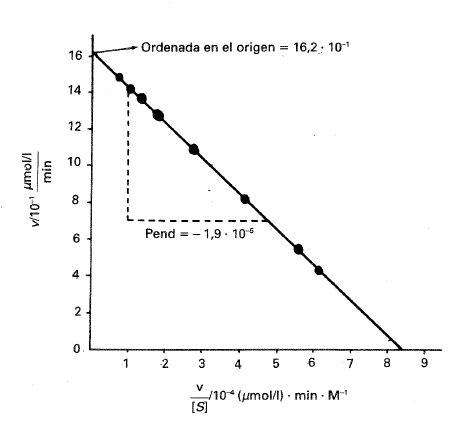
Fig. 24-18. Representación según la linealización de Eadie-Hosftee para los datos del ejercicio 24.1.

Determinando gráficamente la ordenada en el origen y la pendiente obtenemos

Ordenada en el origen \( = 1,62 (\mu mol/l)/min, \hspace{.3cm} \) luego \( \hspace{.3cm}V_{max} = 1.62 (\mu mol/l)/min \)

  Pendiente \( =- 1,9 \cdotp 10^{-5} M \hspace{.3cm} \) luego \( \hspace{.3cm} K_M = 1,9  \cdotp 10^{-5} M \)

Como puede apreciarse, los valores de \( V_{max} \)  y \( K_M \) han salido idénticos a los calculados por la representación de Lineweaver-Burk; la razón es que, en este caso, los puntos experimentales se ajustan , muy bien a la línea recta en ambas linealizaciones, por lo que no se aprecian diferencias significativas; no obstante, ya se ha comentado que la representación de Eadie-Hofstee es más aconsejable que la de Lineweaver-Burk, porque deja los puntos mejor espaciados, como puede apreciarse si se comparan las figuras 24-17 y 24-18.

24.9. INHIBICIÓN DE LA CATÁLISIS ENZIMÁTICA

Un inhibidor es una sustancia que, cuando interactúa con una enzima, origina una disminución de la actividad catalítica.

En la naturaleza existen muchos inhibidores de enzimas que tienen como misión controlar el metabolismo dentro de la célula. Por ejemplo, la actividad de muchas enzimas es regulada por un mecanismo de tipo retroalimentario o feedback, por el cual el producto final de una ruta metabólica actúa como inhibidor específico de la primera enzima de la cadena:

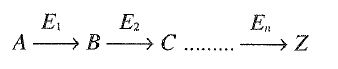
Desde un punto de vista farmacéutico, son de gran importancia también los inhibidores sintéticos, como ocurre en la actualidad con algunos fármacos. Además, los inhibidores son una poderosa herramienta en el estudio de los mecanismos de reacción enzimáticos, naturaleza del sitio activo…, etc.

Hay dos tipos de inhibidores: reversibles e irreversibles. En la inhibición reversible se forma un complejo de adición, no covalente, entre la enzima y el inhibidor, existiendo un equilibrio entre la enzima y el inhibidor. Por su parte en la inhibición irreversible se forma un enlace covalente entre la enzima y el inhibidor, la inhibición aumenta progresivamente con el paso del tiempo y se puede alcanzar una inhibición completa si la concentración del inhibidor irreversible supera la de la enzima.

a. Tipos de inhibición reversible. Existen principalmente cuatro tipos de inhibición reversible que se discuten a continuación.

i. Inhibición cómpetitiva. El sustrato y el inhibidor compiten por el mismo sitio activo de la enzima, las reacciones que se producen son

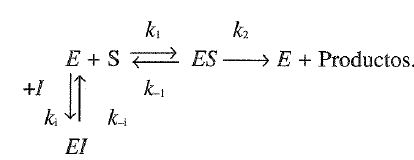
El complejo EI no forma productos, es lo que se llama un complejo no reactivo (dead end).

Aplicando ahora el tratamiento del estado estacionario a ES y EI, y considerando de nuevo el balance de materia

\( [E]_0 = [E] + [ES] + [EI] \)

se llega a la siguiente ecuación de velocidad

\( \nu = \displaystyle \frac {V_{max} \cdotp [S]}{K_M \left ( 1+ \displaystyle \frac {[I]}{K_I } \right ) + [S]} \hspace{2cm}  \)    [24.44]

donde \( K_I \) es la constante de disociación del complejo EI:

\( K_I = k_{-i}/k_i \)

, y \( K_M \) y \( V_{max} \) tienen el significado habitual: \( K_M = (k_{-1} + k_2)/k_1 \),  \( \hspace{.3 cm} V_{max} = k_2 [E]_{0} \).

Como puede observarse, la forma de ecuación de velocidad es de tipo Michaelis-Menten, que en general podríamos escribir denominando los parámetros como aparentes (ap) en la forma:

\( \nu = \displaystyle \frac  {V_{max}^{ap} [S] }{K_{M}^{ap} + [S]} \)

siendo para este caso

\( V_{max}^{ap} = V_{max} \)

\( K_{M}^{ap} = K_{M} \left (     1 + \displaystyle \frac  { [I]}{K_I} \right )  \)

En definitiva, la presencia del inhibidor competitivo deja la \( V_{max} \) inalterada y multiplica la \( K_M \) por el factor  \( (1 + ([I]/K_I)) \).

El comportamiento gráfico de esta ecuación de velocidad se puede deducir de forma análoga a lo ya visto para la ecuación de Michaelis-Menten, como se detalla a continuación. Aunque ya se ha comentado que la representación de Eadie-Hofstee es mejor que la de Lineweaver-Burk (doble inversa), esta última se utiliza más en los estudios de inhibición.

— Representación directa. Una representación de \( \nu \) y frente a [S] según la ecuación [24.44] aparece en la figura 24-19. Como puede verse en esta figura, la \( V_{max} \) no se modifica (esto es lógico si pensamos en términos topológicos del mecanismo, ya que un exceso de sustrato desplazaría toda la enzima del complejo EI para formar ES). Por su parte la \( K_{M}^{ap} \) varía con la concentración de inhibidor.

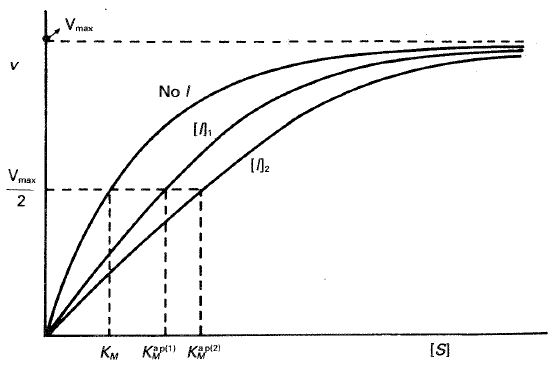
Fig. 24-19. Representación de υ frente a [S] para una inhibición competitiva.

— Representación doble inversa. Tornando inversos en la ecuación anterior [24.44] queda la siguiente expresión:

\( \displaystyle \frac {1 }{\nu}=  \displaystyle \frac {1}{V_{max}} + \displaystyle \frac {K_M}{V_{max}} \left (  1+ \displaystyle \frac {[I]}{k_I}  \right ) \cdotp \displaystyle \frac {1}{[S]} \hspace{2cm}  \)    [24.45]

de manera que al representar 1/υ frente a 1/[S] se obtendrán líneas rectas de la misma ordenada en el origen \( 1/V_{max} \) y de pendiente  \( (K_M/ V_{max}) (1 + [I]/ K_I) \) que se incrementa con la concentración de inhibidor, comportamiento que puede apreciarse en la figura 24-20.

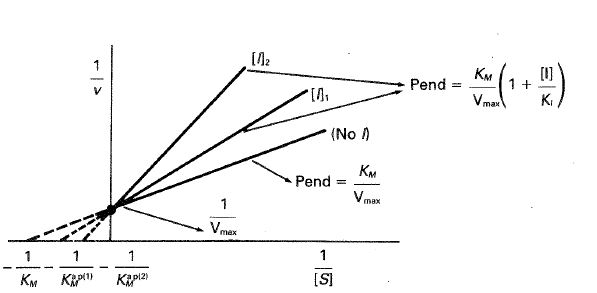
Fig. 24-20. Representación de Lineweaver-Burk para una inhibición competitiva.

Un ejemplo de inhibición competitiva podría ser la reacción de deshidrogena-ción del succínico:

Se da una inhibición competitiva en presencia de ácido malónico (\( COOH-CH_2-COOH \)); esta inhibición se origina debido a la gran semejanza entre succínico y malónico. Algo análogo ocurre con el ácido oxálico (COOH-COOH) que actúa también como inhibidor competitivo.

ii. Inhibición no competitiva clásica. En este tipo de inhibición se admite que el inhibidor, I, puede formar complejos tanto con la enzima libre (E) como con el complejo enzima-sustrato (ES); el mecanismo sería el siguiente:

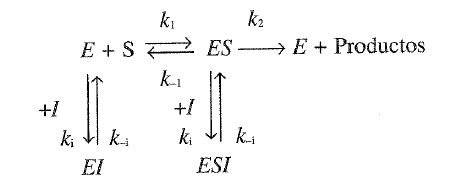
Suponemos que la constante de disociación (\( K_I= k_{-i}/k_i \)) es la misma para la disociación del complejo El que para la del complejo ESI. Por otra parte, El y ESI serían complejos del tipo que hemos llamado no reactivo (dead end). Aplicando de nuevo el tratamiento del estado estacionario, la ecuación de velocidad que se obtiene es

\( \nu = \displaystyle \frac {\displaystyle \frac {V_{max} }  {\left ( 1 + [I]/K_I \right )} \cdotp [S] } {K_M + [S]} \hspace{2cm}  \)    [24.46]

Esta ecuación es de la forma

\( \nu = \displaystyle \frac { V_{max}^{ap} [S]}{K_{M}^{ap} + [S]} \)

que comparada con

\( \nu = \displaystyle \frac { V_{max} [S]}{K_{M}+ [S]} \)

queda

\( V_{max}^{ap} = V_{max} \displaystyle \frac { 1}{1 + \displaystyle \frac { [I]}{K_I}} \)

y

\( K_{M}^{ap} \equiv K_M \)

Es decir, en este tipo de inhibición se modifica la \( V_{max}\) pero la \(  K_M \) permanece inalterada.

—Representación directa. La representación de \( \nu \) frente a [S] según la ecuación [24.46] conduce a los resultados de la figura 24-21, donde puede apreciarse como la \( V_{max} \) disminuye a medida que aumenta la concentración de inhibidor, mientras que la \( K_M \) no se ve influida por la concentración de inhibidor.

—Representación doble inversa. Tomando inversos en la ecuación [24.46] queda:

\( \displaystyle \frac {1}{ \nu} = \displaystyle \frac {1}{V_{max}} \left (  1 + \displaystyle \frac {[I]}{k_I}\right ) + \displaystyle \frac {K_M}{V_{max}} \left ( 1 +  \displaystyle \frac { [I]}{K_I} \right ) \cdotp \displaystyle \frac {1}{[S]} \hspace{2cm}  \)    [24.47]

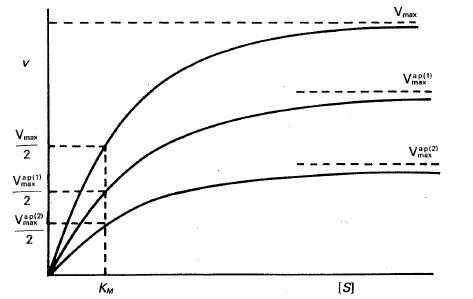
Fig. 24-21. Representación de ν frente a 1/[S] para una inhibición no competitiva clásica.

de manera que al representar 1/ν frente a 1/[S] se obtiene el comportamiento que aparece en la figura 24-22, es decir que todas las rectas tienen pendientes y ordenadas en el origen que aumentan con la concentración de inhibidor y que convergen en un mismo punto sobre el eje 1/[S].

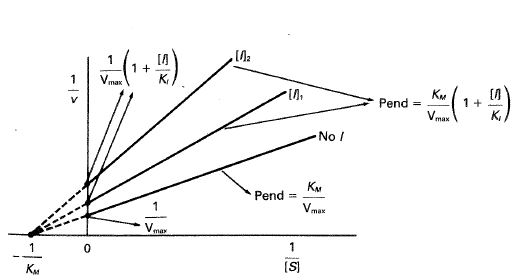
Fig. 24-22. Representación de Lineweaver-Burk para una inhibición no competitiva clásica.

Ejemplos de inhibiciones no competitivas clásicas son las reacciones reversibles entre los grupos sulfhidrilos de los residuos de cisteína y los iones de los metales pesados:

\( 2- SH + H_{g}^{2+} = -S-H_g – S- + 2 H^{+} \)

iii. Inhibición acompetitiva. El modelo para esta inhibición asume que el inhibidor I puede combinarse solamente con el complejo enzima-sustrato, quedando el siguiente mecanismo de reacción

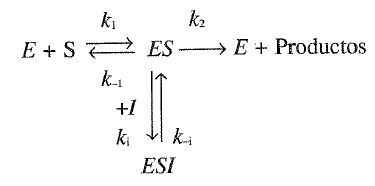
La ecuación de velocidad que se obtiene aplicando el tratamiento del estado estacionario es:

\( \nu = \displaystyle \frac {\displaystyle \frac {V_{max} }  {\left ( 1 + [I]/K_I \right )} \cdotp [S] }    { \displaystyle \frac{K_M}{\left ( 1 + [I]/K_I \right )} + [S]}   \hspace{2cm}  \)    [24.48]

donde \( K_I = k_{-I}/k_i \) es la constante de disociación del complejo ESI. Esta ecuación tiene la forma:

\( \nu = \displaystyle \frac{ V_{max}^{ap}  [S]}{K_{M}^{ap} + [S]} \)

de donde

\( V_{max}^{ap} = V_{max}  \displaystyle \frac {1}{1+[I]/K_I} \)

y

\( K_M^{ap} = K_M  \displaystyle \frac {1}{1+[I]/K_I} \)

y también

\( \displaystyle \frac{V_{max}^{ap}}{k_M^{ap}} = \displaystyle \frac{V_{max}}{K_M} \)

Es decir, se modifica la \(  V_{max} \) y la \(  K_M \) pero no el cociente \(  V_{max} / K_M \)

– Representación directa: la representación de υ frente a [S] según la ecuación [24.48] conduce a los resultados de la figura 24-23, donde puede apreciarse cómo varía la \( V_{max} \) y la \(  K_M \) en presencia del inhibidor.

– Representación doble inversa: tomando inversos en la ecuación [24.48] queda

\( \displaystyle \frac{1}{\nu} = \displaystyle \frac {1}{V_{max}} \left ( 1 + \displaystyle \frac {[I]}{K_I} \right ) + \displaystyle \frac {K_M}{V_{max}} \cdotp \displaystyle \frac{1}{[S]} \hspace{2cm}  \)    [24.49]

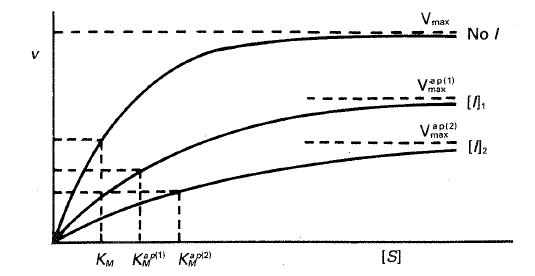
Fig. 24-23. Representación de υ frente a ES] para una inhibición acompetitiva.

de manera que al representar 1/υ frente a 1/[S] se obtiene el comportamiento que nos aparece en la figura 24-24. Como ya se ha podido comprobar, el cociente \( K_M/V_{max} \) permanece inalterado, por esta razón las rectas resultan paralelas en esta representación.

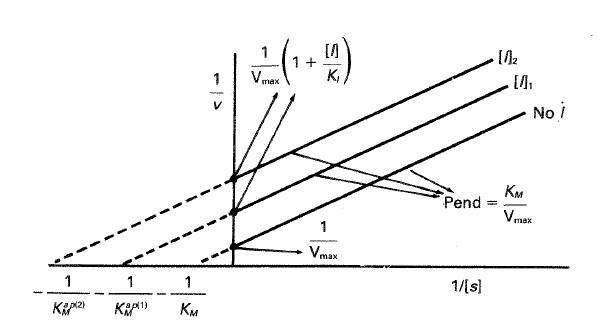
Fig. 24-24. Representación de Lineweaver-Burk para una inhibición acompetitiva.

Ejemplos de inhibición acompetitiva son la inhibición de pepsín-peptidasa por hidracina, la inhibición de arilsulfatasa por cianuro oihidracina, y la inhibición de algunas deshidrogenasas por cianuro, hidroxilamina o tioles.

iv. Inhibición no competitiva mezclada (o inhibición mezclada). En la inhibición no competitiva clásica se hizo una suposición bastante restrictiva, según la cual \( K_I \), era la misma para la unión del inhibidor tanto a la enzima libre (E) como al complejo enzima-sustrato (ES). Un mecanismo más general sería suponer que son distintas:

que da una ecuación de velocidad de estado estacionario:

\( \nu =  \displaystyle \frac {\displaystyle \frac {V_{max} }  {\left ( 1 + [I]/K_I^{´} \right )} \cdotp [S] }    { K_M \cdotp \displaystyle \frac {\left ( 1 + [I]/K_I \right )} {\left ( 1 + [I]/K_I^{´} \right )} + [S]}   \hspace{2cm}  \)    [24.50]

donde \(  K_I \) y \( K_I^{´} \) son las constantes de disociación de El y ESI. Esta ecuación es de la forma

\( \nu  =  \displaystyle \frac {V_{max}^{ap} \cdotp [S]} { K_M^{ap} + [S]} \)

Es decir, ahora tanto \( V_{max} \) como \( K_M \) y el cociente  \( V_{max}/K_M \) se ven alterados:

\( V_{max}^{ap} = V_{max} \left ( 1 / \left ( 1 + [I] / K_I^{´} \right ) \right ) \)

\( K_{M}^{ap}= K_M \left ( \left ( 1 + [I] / K_I \right ) / \left (1 + [I] / K_{I}^{´} \right) \right ) \)

\( V_{max}^{ap} / k_M^{ap} = \left ( V_{max} /K_M \right ) / \left ( 1 + [I]/ K_I \right ) \)

En la inhibición mezclada, \( V_{max} \) siempre disminuye a medida que la concentración de inhibidor aumenta, mientras que la variación de \( K_M \) depende de los valores relativos de \( K_I \) y \( K_I^{´} \): si \( K_I < K_I^{´} \) entonces  \( K _M^{ap} \) aumenta en presencia del inhibidor, y viceversa, si  \( K_I > K_I^{´} \), \( K_M^{ap} \) disminuye en presencia del inhibidor.

– Representación directa. La representación de \( \nu \) frente a [S] según la ecuación [24.50] y para el caso \( K_I < K_I^{´} \) conduce al comportamiento observado en la figura 24-25. El caso \( K_I >  K_I^{´} \) sería análogo pero con \( K_M^{ap} \) disminuyendo con la concentración de inhibidor.

– Representación doble inversa. Tomando inversos en la ecuación [24.50], queda

\( \displaystyle \frac{1}{\nu} = \displaystyle \frac {1}{V_{max}} \left ( 1 + \displaystyle \frac {[I]}{K_I^{´}} \right ) + \displaystyle \frac {K_M}{V_{max}} \left ( 1 +  \displaystyle \frac{1}{[K_I]} \right )  \displaystyle \frac{1}{[S]} \hspace{2cm}  \)    [24.51]

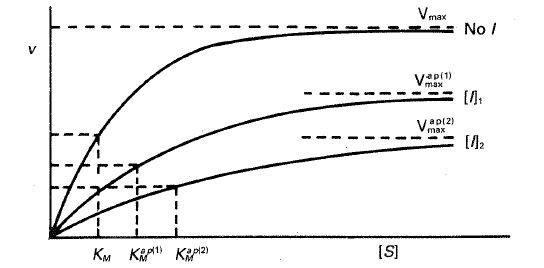
Fig. 24-25. Representación de υ frente a [S] para una inhibición mezclada en la que

 

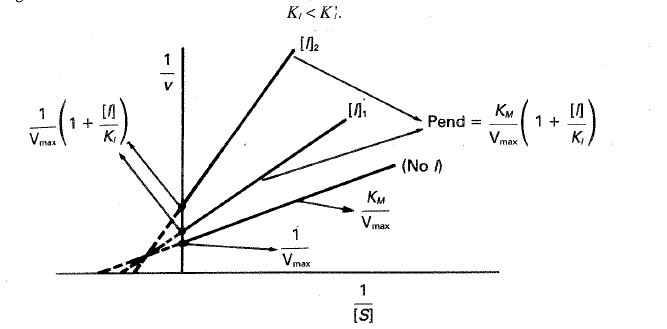
Fig. 24-26. Representación de Lineweaver-Burk para una inhibición mezclada en la que  \( K_I < K_I^{´} \). Obsérvese cómo las líneas tienen su intersección por encima del eje 1/[S].

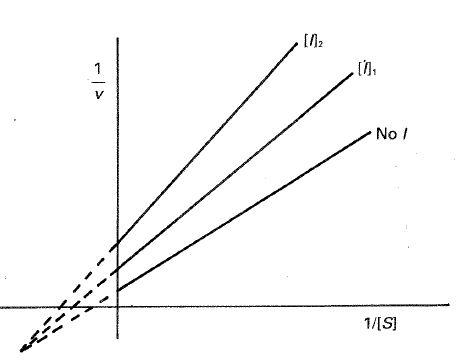
Fig. 24-27. Representación de Line-weaver-Burk   para una inhibición mezdada en la que \( K_I > K_I^{´} \).

Obsérvese cómo las líneas se interseccionan por debajo del eje 1/[S] de manera que al representar 1/υ frente a 1/[S] para el caso de \( K_I < K_I^{´} \) obtendremos los resultados de la figura 24-26, en la que puede observarse cómo las líneas rectas se interseccionan por encima del eje 1/[S]. Por el contrario si \( K_I > K_I^{´} \), las líneas rectas se interseccionan por debajo del eje 1/[S] (fig. 24-27).

b. Inhibición irreversible. En este caso, el inhibidor forma una unión covalente con la molécula de enzima, modificando de forma permanente un grupo funcional necesario para la catálisis. Ahora el inhibidor no se puede separar por técnicas de diálisis o similares como ocurre en la inhibición reversible.

La efectividad de un inhibidor irreversible no se determina por la constante de equilibrio sino por la constante de velocidad a la que se produce la unión.

Un ejemplo puede ser la inhibición de la acetilcolinesterasa por diisopropil-fluorofosfato (gas nervioso utilizado en la guerra). La acetilcolina es un neuro-transmisor que actúa como mensajero entre el nervio y la céhila del músculo y debe ser destruido una vez que ha desempeñado su misión, pues de lo contrario se presentarían convulsiones. La destrucción de la acetilcolina se lleva a cabo por la siguiente reacción de hidrólisis catalizada por la enzima acetilcolinesterasa:

\( CH_3-COO-CH_2-N(CH_3)_3 + H_2O \rightarrow  HOCH_2-CH_2-N(CH_3)_3 + CH_3 – COOH \)

\( \hspace{2cm} \) acetilcolina  \( \hspace{4 cm} \) colina

La inhibición irreversible por diisopropilfluorofosfato se produce mediante la formación de un enlace covalente entre el átomo de fósforo y el oxígeno hidroxílico de un residuo de la enzima:

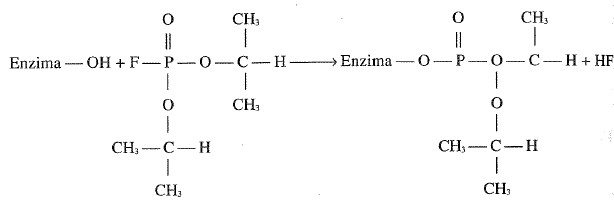
El estudio cinético de estos inhibidores irreversibles se hace de manera convencional según el método de integración; para ello se admite que la concentración inicial de enzima (\( [E]_0 \)) es proporcional a  \( \nu_0 \) y la concentración de enzima a un tiempo t ([E]) es proporcional a \( \nu_t \). Un mecanismo sencillo podría ser el siguiente:

\(    \begin{array}{ccc}  \\ & k & \\ E+I & \rightarrow & E-I \\ \end{array}  \)

el cual sigue una cinética de pseudoprimer orden respecto a E, cuando la concentración de inhibidor está en exceso:

\(  \nu = k [I][E] \Rightarrow \nu = k^{´}[E] \)

que tiene corno ecuación integrada la siguiente:

\(  \ln \displaystyle \frac {\nu_0}{\nu_t} = k^{´}t \)

que usualmente se maneja como:

\(  \ln \displaystyle \frac {\nu_t}{\nu_0} = – k^{´}t \)

De manera que al representar \( \ln ( \nu / \nu_0 ) \) frente a t debe dar una línea recta que pasa por el origen y de cuya pendiente negativa se obtiene \( k^{´} \). Como por otra parte \( k^{´} = k [I] \), se determina finalmente el valor de k a partir de la concentración del inhibidor.

Ejercicio 24.2. Un determinado compuesto es un inhibidor de una enzima hidrolítMa. Para determinar la naturaleza de tal inhibición se han medido las velocidades iniciales de la hidrólisis enzimática a diferentes concentraciones de sustrato, en ausencia de inhibidor (experimento A), en presencia de inhibidor a concentración 2.50 mM (experimento B) y a 5.60 mM (experimento C). En la tabla correspondiente se recogen los resultados. Las velocidades de reacción se expresan en μmoles/l de sustrato hidrolizados por minuto. Determínese el tipo de inhibición y la correspondiente \( K_I \)

   \(   \begin{array}{cccc} & & \nu /(( \mu mol/l)/min)  \\ \hline  [S]/M & A & B & C \\ \hline  12,5 &  1,68  & 1,04 &  0,70 \\  15,0 &  1,89 &  1,20 &  0,83 \\  20,0  &  2,27 &  1,50 &  1,05 \\  25,0  &  2,60  & 1,75 &  1,25 \\  40,0  & 3,22 &  2,35 &  1,75 \\  60,0 &  3,77 &  2,94 &  2,27 \\   100,0 &  4,35 &  3,57 &  2,94 \\ \end{array} \)

Resolución. Utilizando la representación de Lineweaver-Burk tendríamos que representar 1/υ frente a 1/(S), obteniéndose la gráfica de la figura 24-28. Observando dicha representación se aprecia cómo los datos se ajustan a tres rectas que se interseccionan en el eje de ordenadas, por lo que se concluye que el tipo de inhibición es el de inhibición competitiva. Como es sabido, dicha inhibición presenta la siguiente ecuación de velocidad:

   \( \nu = \displaystyle \frac {V_{max} \cdotp [S]}{K_M \left (  1 +  \displaystyle \frac {I}{K_I} \right ) + [S]}    \)

que, puesta bajo la forma doble inversa, queda

\(   \displaystyle \frac {1} {\nu} = \displaystyle \frac {1} {V_{max}} + \displaystyle \frac {K_M}{V_{max}} \left ( 1 + \displaystyle \frac {[I]}{K_I} \right ) \cdotp \displaystyle \frac {1}{[S]}  \)

de manera que al representar \(  1/\nu \)  frente a \(  1/[S] \)  a las diferentes concentraciones de inhibidor se obtendrán líneas rectas de ordenada en el origen \( 1/V_{max} \) y de pendientes \( (K_M /V_{max}) \cdotp  (1 + [I]/ K_I)  \); precisamente del valor de estas pendientes se obtendrá el valor de \( K_I \). Para ello, lo primero que necesitamos es determinar los valores de \( K_M \) y \( V_{max} \) para esta reacción enzimática; esto se consigue a partir de la recta correspondiente al experimento A, es decir en ausencia de inhibidor, caso en el cual se cumple la ecuación de Michaelis-Menten cuyo doble inverso sabemos que es:

\(   \displaystyle \frac {1} {\nu} = \displaystyle \frac {1} {V_{max}} + \displaystyle \frac {K_M}{V_{max}}  \cdotp \displaystyle \frac {1}{[S]}  \)

 

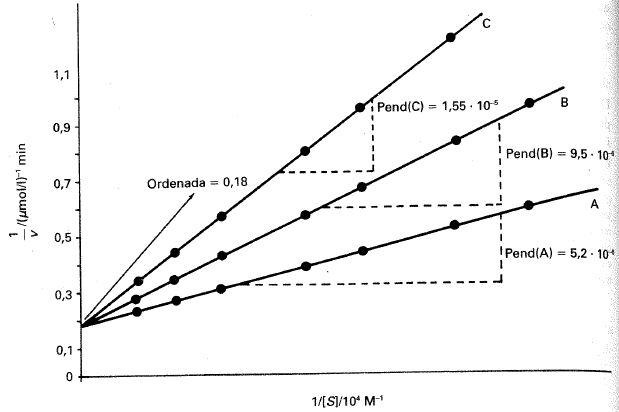
Fig. 24-28. Representación de Lineweaver-Burk para los datos del ejercicio 24.2.

De forma que, determinando la ordenada en el origen y la pendiente de esta recta, tenemos

ordenada en el origen  \(  =  0,18 \left ( \displaystyle \frac{\mu mol/l}{min}   \right )^{-1}   \Rightarrow    \displaystyle \frac{1}{V_{max}} = 0,18 \left ( \displaystyle \frac{\mu mol/l}{min}   \right )^{-1} \Rightarrow V_{max} = 6   \displaystyle \frac{\mu mol/l}{min} \)

pendiente(A) \( = 5,2 \cdotp 10^{-6}   \left ( \displaystyle \frac{\mu mol/l}{min}   \right )^{-1} /M^{-1}\Rightarrow     \displaystyle \frac {K_M}{V_{max}} = 5,2  \cdotp 10^{-6} \left ( \displaystyle \frac{\mu mol/l}{min}   \right )^{-1} /M^{-1}  \)

de donde

\( K_M= 2,9  \cdotp 10^{-5} M \)

Ahora con estos valores de \( K_M \) y \( V_{max} \) y las pendientes de las rectas correspondientes a los experimentos B y C deducimos el valor de \( K_I \).

Para el experimento B:

Pend(B) \( = 9,5  \cdotp 10^{-6 } \left ( \displaystyle \frac{\mu mol/l}{min}   \right )^{-1} / M^{-1} \)

\(  \displaystyle \frac {K_M}{V_{max}} \left ( 1 + \displaystyle \frac {[I]}{K_I} \right ) = 9, 5 \cdotp 10^{-6} \left ( \displaystyle \frac {\mu mol/l}{min} \right )  / M^{-1} \)

sustituyendo ahora los valores de \(  K_M \)  y \(  V_{max} \)  y tomando la \( [I] \) como \(  2,50 \cdotp 10^{-3} M \) se obtiene:

\(  K_I =3,0  \cdotp 10^{-3}M \)

Análogamente tendremos que para el experimento C:

Pend(C)  \(  = 1,55 \cdotp 10^{-5} \left ( \displaystyle \frac{\mu mol/l}{min}   \right )^{-1} / M^{-1} \)

y tomando ahora para \(  [I] \)  el valor respectivo de \(  5,60 \cdotp 10^{-3} M \)  se obtiene:

\(  K_I =2,8 \cdotp 10^{-3} M \)

De donde el valor medio de \(  K_I \)  resulta  \( 2,9 \cdotp 10^{-3} M \)  (fig. 24-28).