ESTADÍSTICA DESCRIPTIVA: REPRESENTACIONES GRÁFICAS
Objetivos
- Calcular medidas de posición, de dispersión y de forma de un conjunto de datos
- Obtener representaciones gráficas que resuman desde el punto de vista estadístico un conjunto de datos
- Detectar valores fuera de rango en un conjunto de datos.
Estadísticos descriptivos con R-Commander
Los estadísticos descriptivos con R-Commander se obtienen seleccionando Estadísticos/Resúmenes.
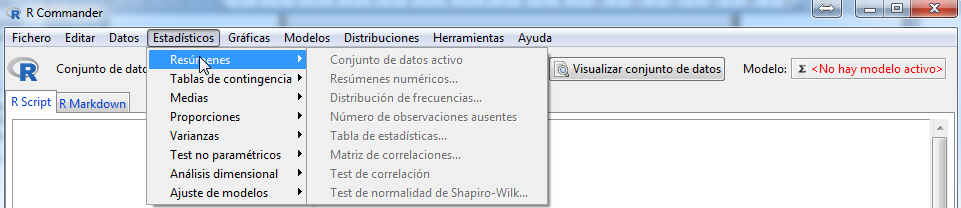 Figura 1: Estadísticos/Resúmenes
Figura 1: Estadísticos/Resúmenes
La salida presenta diversas opciones: Conjunto de datos activo, Resúmenes numéricos, Distribución de frecuencias,………
Para poder ejecutar alguna de estas opciones es necesario que haya un conjunto de datos activo.
Medidas de Posición, Dispersión y Forma
Para calcular las características de posición, dispersión y forma, debe haber un conjunto de datos activo. Lo primero que debemos hacer, si no hay un conjunto de datos activo, es cargar los datos que vamos a utilizar.
Vamos a calcular características de posición, dispersión y forma más comunes, (media, mediana, percentiles, desviación típica y coeficiente de asimetría y curtosis), mediante el siguiente ejemplo
Ejemplo
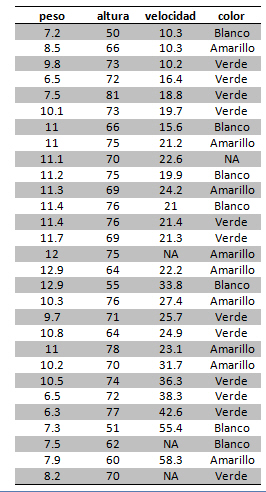
En la siguiente tabla se recogen 29 datos sobre el peso, altura, velocidad y color
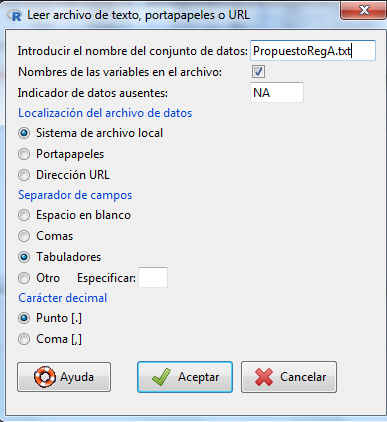
Los datos del ejemplo están en el fichero misdatos.txt. Para importar los datos con R-Commander, seleccionamos: Datos/ Importar datos/ desde archivo de texto, portapapeles o URL…. En la ventana resultante añadimos el nombre del fichero: misdatos y pulsamos Aceptar. Se muestra la siguiente salida
 Figura 2: Importar archivo misdatos.txt
Figura 2: Importar archivo misdatos.txt
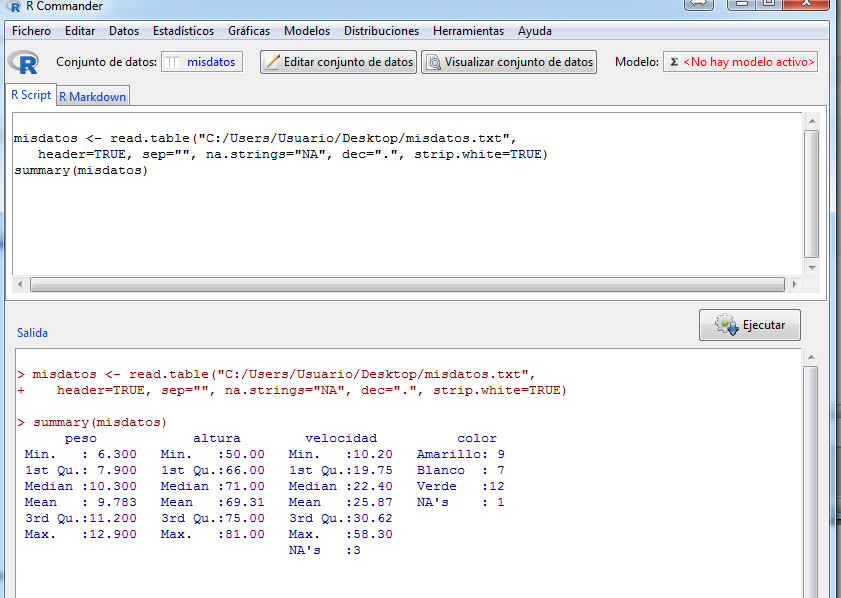
- Conjunto de datos activo: Seleccionando Estadísticos/Resúmenes/ Conjunto de datos activos obtenemos un resumen de los estadísticos descriptivos elementales de todas las variables del conjunto de datos activo. Se muestra la siguiente salida
De cada variable se muestra el valor mínimo, el máximo, el primer, segundo, tercer cuartil y la media. Observemos la sintaxis del comando
> summary (misdatos)
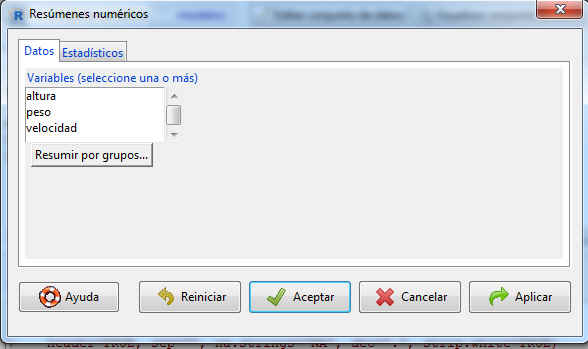
- Resúmenes Numéricos: Seleccionando Estadísticos/Resúmenes/ Resúmenes numéricos se muestra la siguiente pantalla
Esta salida tiene dos opciones: Datos y Estadísticos.
1. Datos: En esta ventana tenemos que elegir una o varias variables del conjunto de datos (elegimos por ejemplo, altura).
- Si pulsamos Aceptar la salida presenta un resumen con los principales estadísticos descriptivos.
- Si pulsamos Aplicar, además de presentar el resumen con los principales estadísticos permanece en la ventana de Resúmenes numéricos (Figura 4) esperando una nueva instrucción.
Por defecto calculará la media, desviación típica y los cuantiles de la variable seleccionada
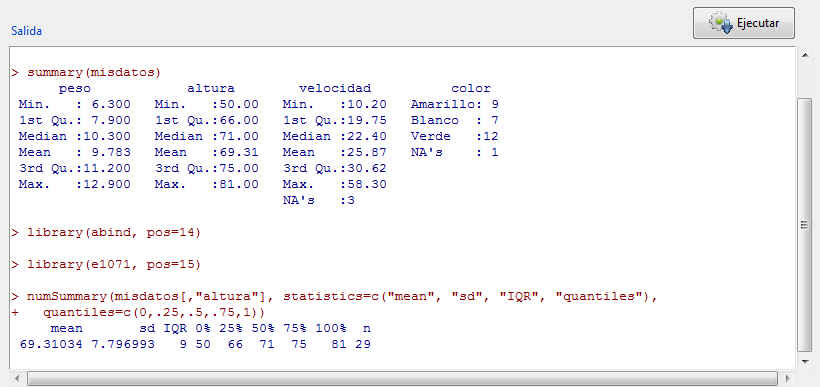 Figura 5: Resúmenes numéricos de la variable Altura
Figura 5: Resúmenes numéricos de la variable Altura
Observemos las librerias utilizadas y la sintaxis del comando
> library(abind, pos=14)
> library(e1071, pos=15)
> numSummary(misdatos[,”altura”], statistics=c(“mean”, “sd”, “IQR”, “quantiles”), quantiles=c(0,.25,.5,.75,1))
2. Estadísticos: Si en la pantalla de la Figura 4 pulsamos estadísticos se muestra la siguiente pantalla
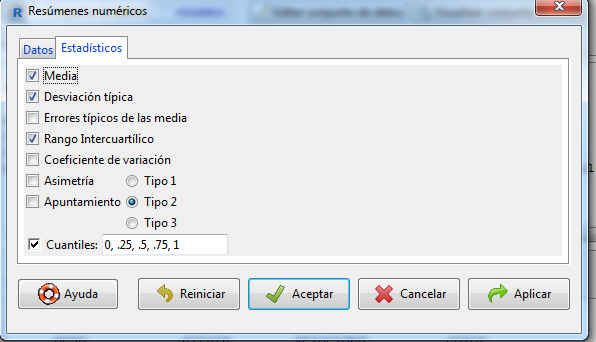 Figura 6: Resúmenes numéricos/Estadísticos
Figura 6: Resúmenes numéricos/Estadísticos
Elegimos todos los estadísticos y se muestra la siguiente salida
 Figura 7: Estadísticos descriptivos de la variable Altura
Figura 7: Estadísticos descriptivos de la variable Altura
En el apartado Apuntamiento se muestran tres tipos algoritmos para calcular la curtosis (Para ver que hace esta función en cada uno de ellos ponemos en la consola de R ?kurtosis).
> ?kurtosis
y se muestra la siguiente descripción
 Figura 8: Tres tipos algoritmos para calcular la curtosis
Figura 8: Tres tipos algoritmos para calcular la curtosis
3. Resúmenes por grupos: Seleccionando Estadísticos/Resúmenes/ Resúmenes numéricos se obtienen los estadísticos descriptivos desglosados por grupos. En la ventana resultante pulsamos Resumir por grupos… y se muestra la siguiente salida
 Figura 9: Estadísticos descriptivos por grupo
Figura 9: Estadísticos descriptivos por grupo
Muestra la variable color, que es la única variable cualitativa en el fichero de datos, pulsamos Aceptar y se muestra la siguiente pantalla
 Figura 10: Estadísticos descriptivos agrupados
Figura 10: Estadísticos descriptivos agrupados
En esta ventana tenemos que elegir una o varias variables del conjunto de datos (elegimos por ejemplo, altura) y pulsamos Aceptar
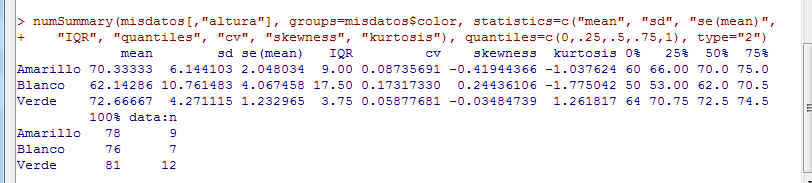 Figura 11: Estadísticos descriptivos agrupados por color
Figura 11: Estadísticos descriptivos agrupados por color
4. Tablas estadísticas: Seleccionamos Estadísticos/Resúmenes/Tablas estadísticas…
 Figura 12: Tablas estadísticas
Figura 12: Tablas estadísticas
Seleccionamos los factores y todas las variables y pulsamos Aceptar
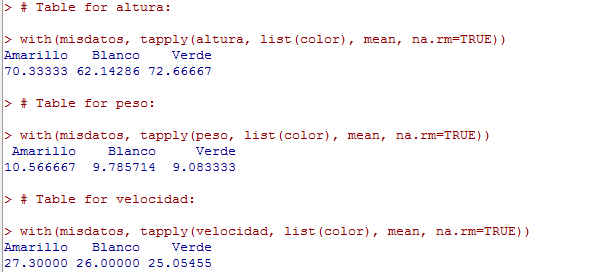 Figura 13: Tablas estadísticas de las variables del fichero misdatos
Figura 13: Tablas estadísticas de las variables del fichero misdatos
Distribuciones de Frecuencias
Para obtener la distribución de frecuencias de una o varias variables de un conjunto de datos, seleccionamos Estadísticos/Resúmenes/ Distribución de frecuencias y se muestra la siguiente pantalla
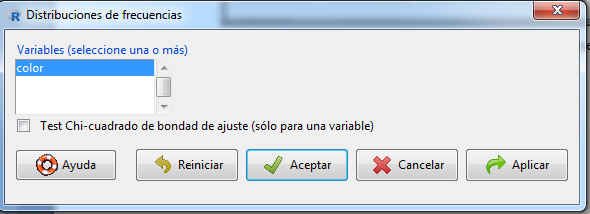 Figura 14: Distribución de frecuencias
Figura 14: Distribución de frecuencias
R-Commander sólo realiza tablas de frecuencias para las variables discretas que se han definido como factores y para las variables cualitativas. En este caso sólo se muestra la variable color.
Si marcamos la variable color y pulsamos Aceptar. Se muestra la siguiente salida,
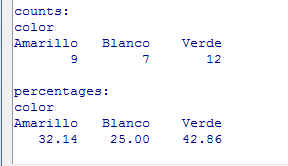 Figura 15: Distribución de frecuencias de la variable color
Figura 15: Distribución de frecuencias de la variable color
Counts muestra la frecuencia absoluta y Percentages muestra la frecuencia relativa de cada una de las variedades del color.
Representaciones gráficas en R-Commander
R-Commander ofrece una gran variedad de gráfico. Atendiendo al tipo de datos vamos a utilizar varios tipos de gráficos.
- Variables cualitativas o variables cuantitativas de tipo discreto: Se pueden considerar gráficos de sectores o gráficos de barras
- Variables cuantitativas: Los gráficos que se suelen emplear con más frecuencia son el histograma, el diagrama de tallos y hojas y el diagrama de caja y bigotes.
En primer lugar realizaremos las representaciones gráficas para las variables cualitativas (Diagrama de barras y gráfico de sectores) y a continuación las representaciones gráficas de las variables cuantitativas (Histograma, diagrama de tallos y hojas y diagrama de cajas y bigotes)
Diagrama de Barras y Diagrama de Sectores
Diagrama de barras
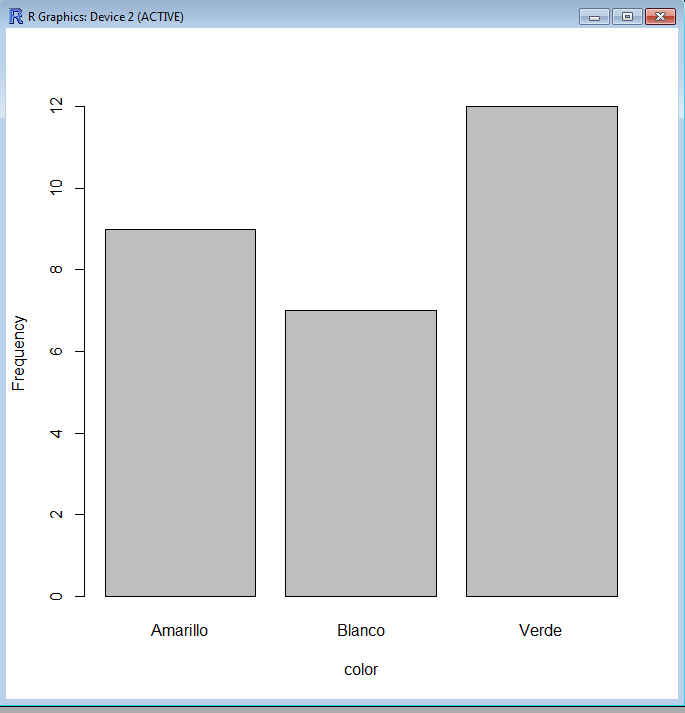
Seleccionamos Gráficas/ Gráfica de barras y se muestra la siguiente pantalla
En la ventana Variable (elegir una), sólo está la variable color que es la única variable cualitativa del archivo de datos. Se elige color y pulsa Aceptar
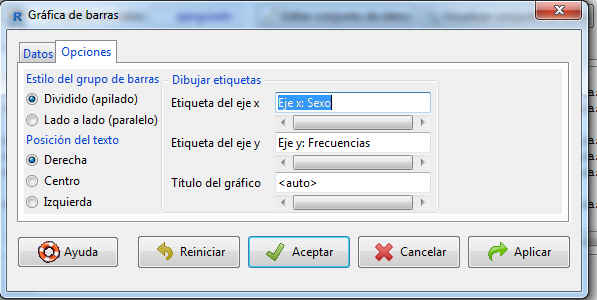
Si en la pantalla de la Figura 16 pulsamos Opciones, se muestra la siguiente pantalla
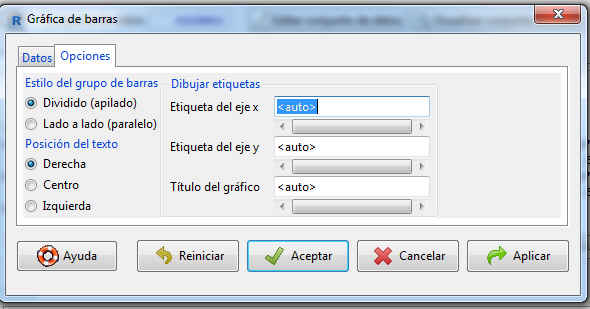 Figura 18: Gráfica de barras: Opciones
Figura 18: Gráfica de barras: Opciones
En esta pantalla se pueden poner las etiquetas de los ejes, título para el gráfico, posición del texto…..
Gráfico de sectores
Seleccionamos Gráficas/ Gráfica de sectores
 Figura 19: Gráfica de sectores
Figura 19: Gráfica de sectores
En la parte Dibujar etiquetas hemos dejado los valores por defecto, pero podríamos modificarlos. Pulsamos Aceptar
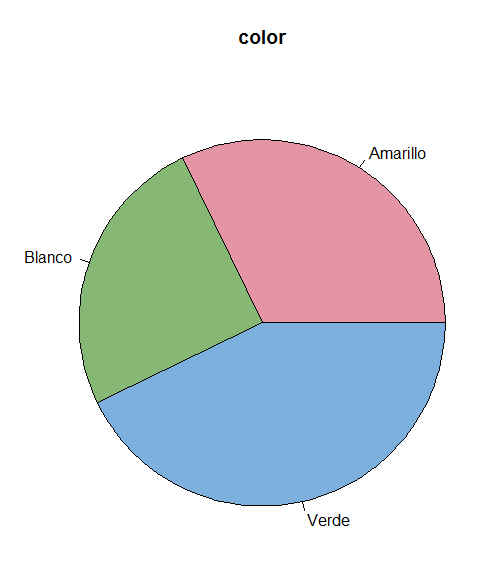 Figura 20: Gráfica de sectores: Variable color
Figura 20: Gráfica de sectores: Variable color
En el que vemos la distribución que tienen cada una de las categorías de la variable color, siendo la categoría Verde la que tiene un mayor porcentaje.
Histograma
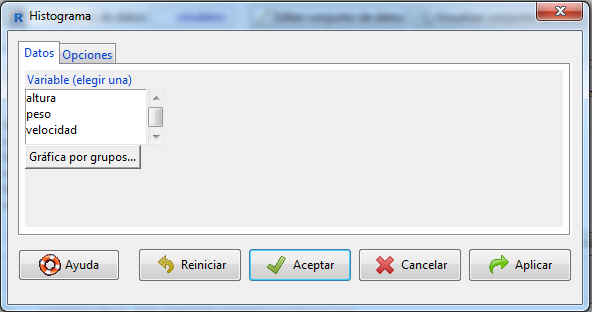
Seleccionamos: Gráficas/Histograma
Esta ventana, como en las anteriores, muestra dos submenús: Datos y Opciones.
Datos: En este submenú podemos ver las distintas variables de nuestro conjunto de datos (Figura 21)
Opciones:
- Opciones gráfica: Número de intervalos/clases del histograma
- Escala de los ejes: Se puede elegir entre frecuencias, porcentajes o densidades
- Dibujar etiquetas: En esta opción se puede poner nombre al eje x, al eje y, y al título del gráfico.
 Figura 22: Histograma. Opciones
Figura 22: Histograma. Opciones
Elegimos la variable altura y dejamos todas las opciones por defecto
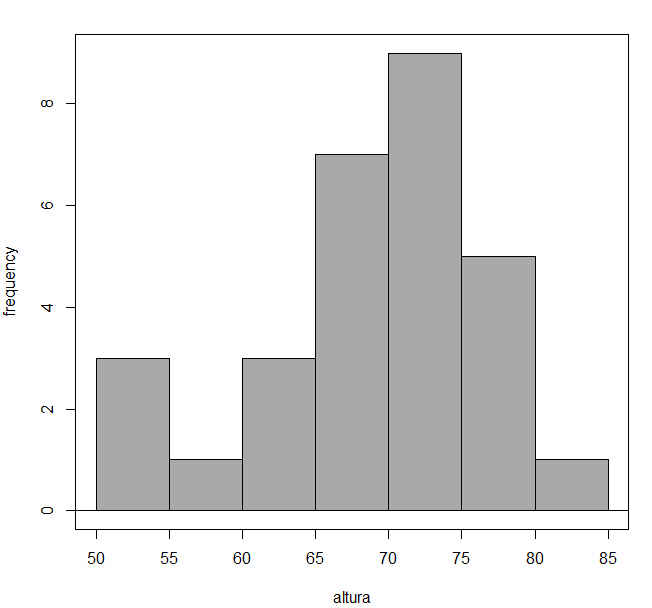 Figura 23: Histograma. Variable: Altura
Figura 23: Histograma. Variable: Altura
Gráfico de tallos y hojas
Se selecciona Gráficas/Gráfica de tallos y hojas
 Figura 24: Gráfica de tallos y hojas
Figura 24: Gráfica de tallos y hojas
Seleccionamos la variable altura, dejamos todas las demas opciones por defecto y pulsamos Aceptar. Se muestra la siguiente salida
 Figura 25: Gráfica de tallos y hojas. (Variable Altura)
Figura 25: Gráfica de tallos y hojas. (Variable Altura)
Diagrama de cajas
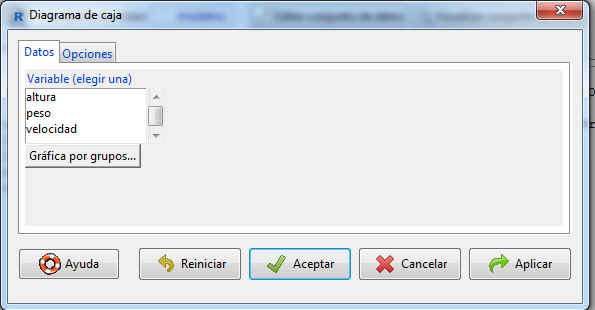
Seleccionamos Gráficas/Diagrama de Caja
La ventana muestra dos submenús: Datos y Opciones.
Datos: En este submenú podemos ver las distintas variables del conjunto de datos.
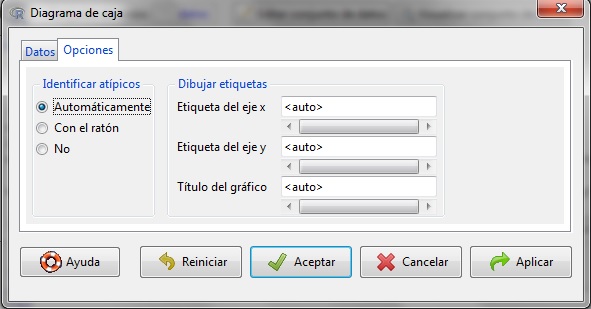
Opciones:
- Identificar atípicos: Da la opción de mostrarlos automáticamente, cuando pase el ratón por encima o no mostrarlos
- Dibujar etiquetas: En esta opción podemos poner nombre al eje x, al eje y, y al título del gráfico.
Figura 27: Diagrama de caja: Opciones
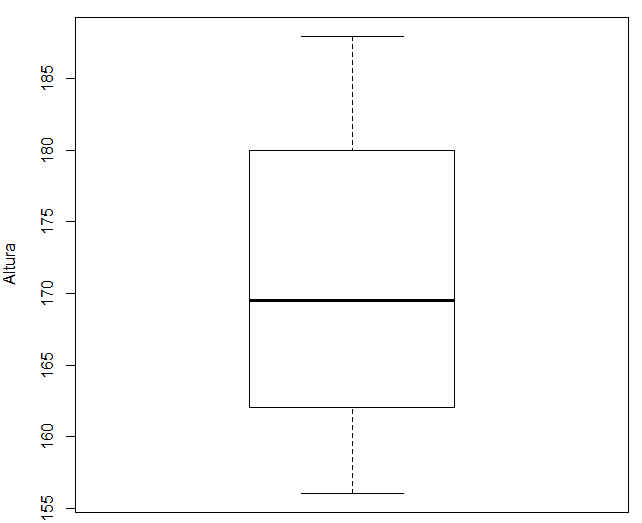
Si seleccionamos la variable altura y dejamos todo lo demás por defecto, muestra el siguiente gráfico
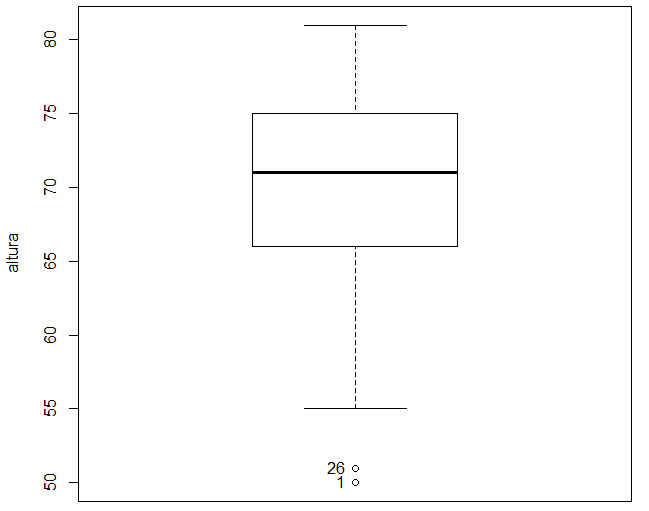 Figura 28: Diagrama de caja (Variable Altura)
Figura 28: Diagrama de caja (Variable Altura)
En este gráfico podemos apreciar dos valores atípicos, los puntos 26 y 1.
Si pulsamos,en la salida de la figura 26, Gráfica por grupos…
 Figura 29: Diagrama de caja por grupos
Figura 29: Diagrama de caja por grupos
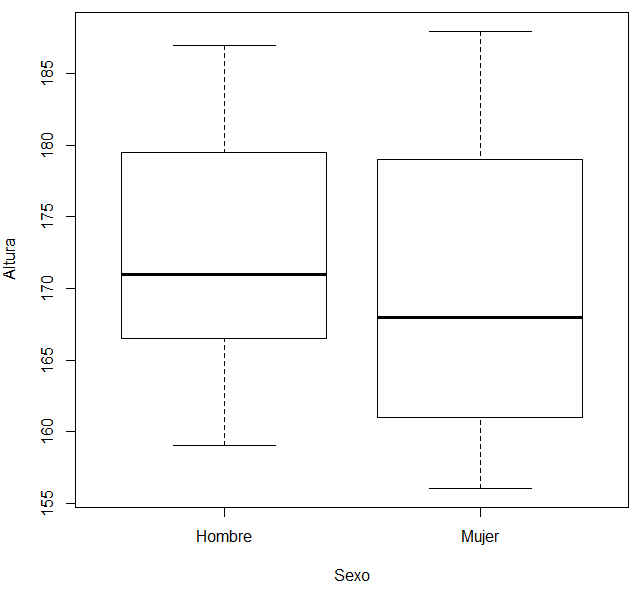
Seleccionamos color, pulsamos Aceptar se muestra el siguiente diagrama de cajas con bigotes
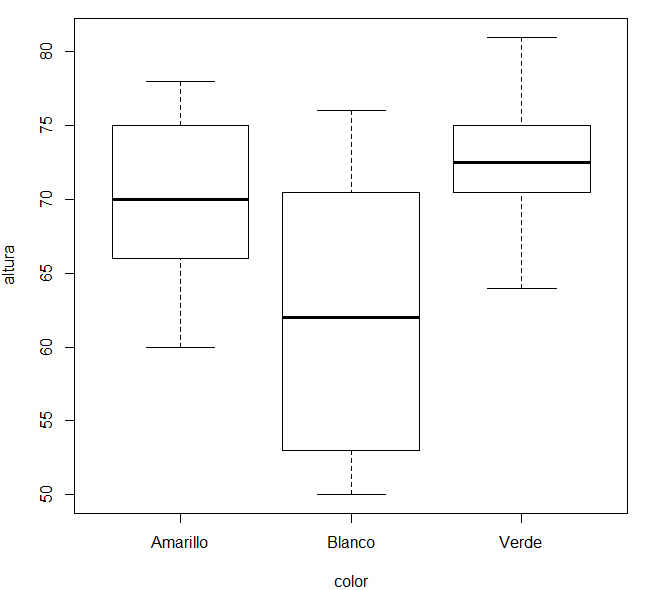 Figura 30: Diagrama de caja por grupos (Variable Altura)
Figura 30: Diagrama de caja por grupos (Variable Altura)
Ejercicios
Ejercicios Guiados
Ejercicio guiado
Considérese el siguiente conjunto de datos que contiene información acerca del sexo, la edad, el peso y la altura de 30 personas:
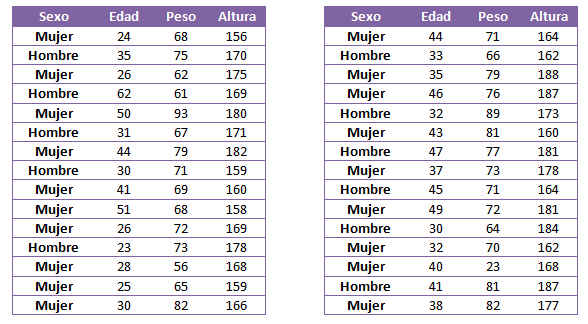 Tabla2. Datos del Ejercicio Guiado 1
Tabla2. Datos del Ejercicio Guiado 1
Se pide:
a) Elabora un fichero de texto que contengan la información de la tabla anterior. Utiliza el tabulador para separar la información referente a cada variable. Guárdalos en el escritorio y nombralos ejerguiado.txt e impórtalos
b) Calcula la edad media de los individuos de la muestra y su mediana. ¿Es homogénea la variable edad? ¿Y simétrica?
c) Calcula el porcentaje de hombres y mujeres que hay en la muestra y haz un gráfico de sectores con el título “Gráfico de sectores para la variable sexo”
d) Realiza un diagrama de barras de la variable sexo
e) Realiza un histograma con la variable altura y añades los títulos a los ejes
f) ¿Existen valores atípicos en alguna de las variables?
Ejercicio Guiado (Resuelto)
a) Elabora un fichero de texto que contengan la información de la tabla anterior. Utiliza el tabulador para separar la información referente a cada variable. Guárdalos en el escritorio, nombralos ejerguiado.txt e impórtalos
Una vez creado el fichero de datos vamos a importarlos, para ello seleccionamos Datos/ Importar datos/ desde archivo de texto, portapapeles o URL…. En la ventana resultante añadimos el nombre del fichero: Ejerguiado
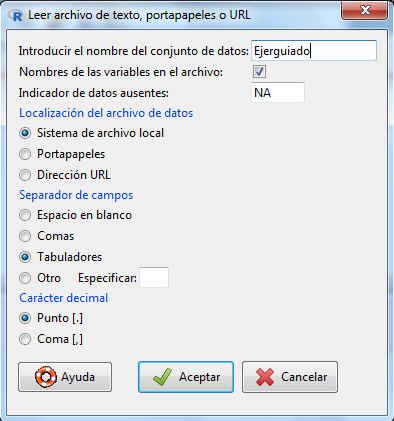 Figura 31: Importar archivo de texto
Figura 31: Importar archivo de texto
Pulsamos Aceptar. Se muestra la siguiente salida
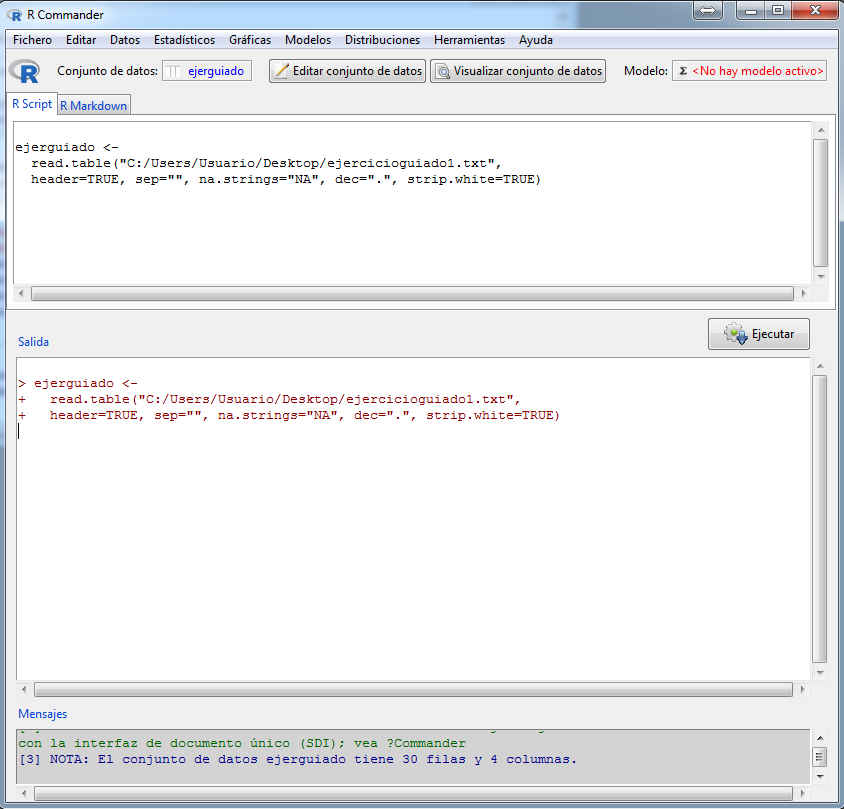 Figura 32: Archivo de texto activo
Figura 32: Archivo de texto activo
b) Calcula la edad media de los individuos de la muestra y su mediana. Proporciona, al menos, dos medidas que indiquen la dispersión de esta variable. Estudia la asimetría y la curtosis de la variable edad
Para calcular la media y la mediana, seleccionamos Estadísticos/ Resúmenes/Conjunto de datos activo y se muestra la siguiente salida
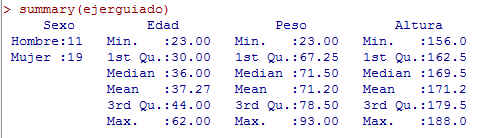 Figura 33: Resúmenes numéricos
Figura 33: Resúmenes numéricos
La edad media y mediana son respectivamente, 37.27 y 36
Como medidas de dispersión, se van a calcular la desviación típica y el recorrido intercuartílico, para ello, seleccionamos Estadísticos/ Resúmenes/Resúmenes numéricos
En la ventana datos, seleccionamos la variable edad
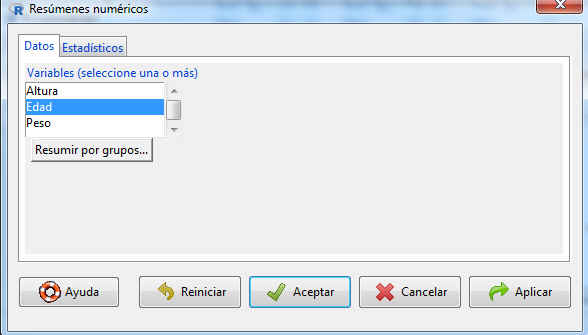 Figura 34: Resúmenes numéricos: Datos
Figura 34: Resúmenes numéricos: Datos
En la ventana estadísticos, seleccionamos todos los estadísticos
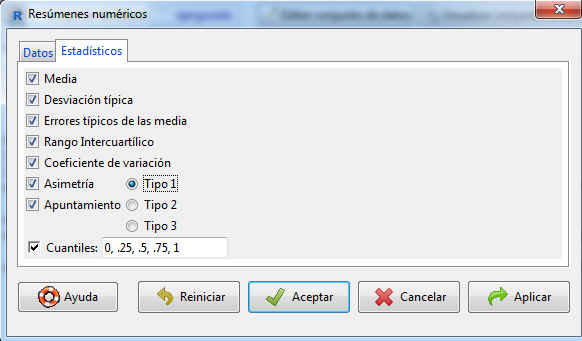 Figura 35: Resúmenes numéricos: Estadísticos
Figura 35: Resúmenes numéricos: Estadísticos
 Figura 36: Resúmenes numéricos: (Variable Edad)
Figura 36: Resúmenes numéricos: (Variable Edad)
Desviación típica = 9.544
Recorrido intercuartílico = 14
Coeficiente de asimetría = 0.4777. La distribución de la variable edad es asimétrica positiva.
Coeficiente de curtosis = -0.3113. La distribución de la variable edad es menos apuntada que la distribución Normal. Es decir, es una distribución platicúrtica.
c) Calcula el porcentaje de hombres y mujeres que hay en la muestra y haz un gráfico de sectores con el título “Gráfico de sectores para la variable sexo”
Para obtener la distribución de frecuencias de una o varias variables de un conjunto de datos, seleccionamos Estadísticos/Resúmenes/Distribución de frecuencias
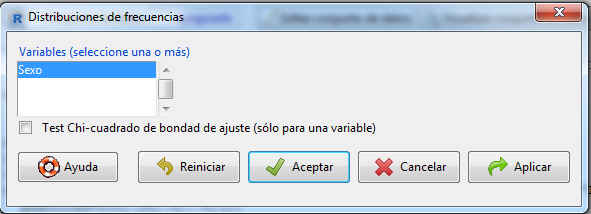 Figura 37: Distribución de frecuencias (Variable: Sexo)
Figura 37: Distribución de frecuencias (Variable: Sexo)
La pantalla sólo muestra la variable sexo, ya que la distribución de frecuencias sólo tiene sentido en las variables cualitativas.
 Figura 38: Porcentajes de hombres y mujeres
Figura 38: Porcentajes de hombres y mujeres
El porcentaje de hombres es 36.67 y el de mujeres 63.33
Para obtener el gráfico de sectores seleccionamos Gráficas/Gráfica de sectores
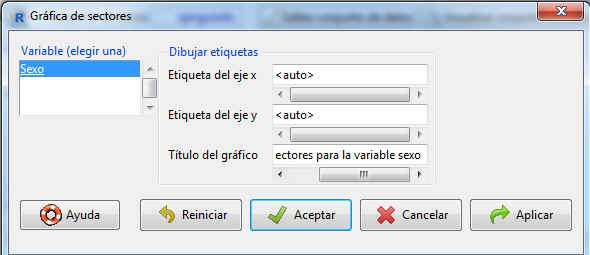 Figura 39: Gráfico de sectores
Figura 39: Gráfico de sectores
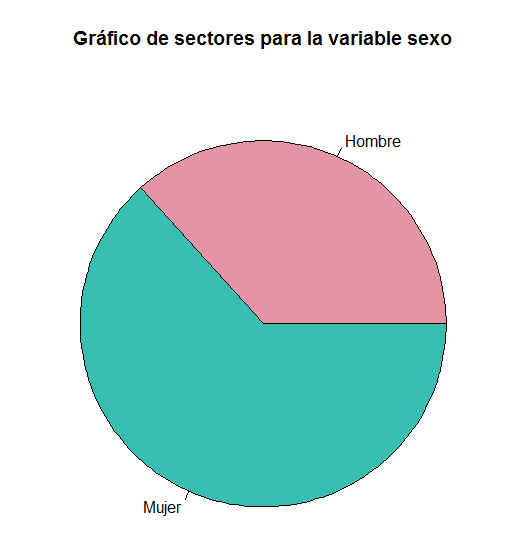 Figura 40: Gráfico de sectores (Variable: sexo)
Figura 40: Gráfico de sectores (Variable: sexo)
d) Realiza un diagrama de barras de la variable sexo
Seleccionamos Gráficas/Gráfica de barras
Pulsar Aceptar
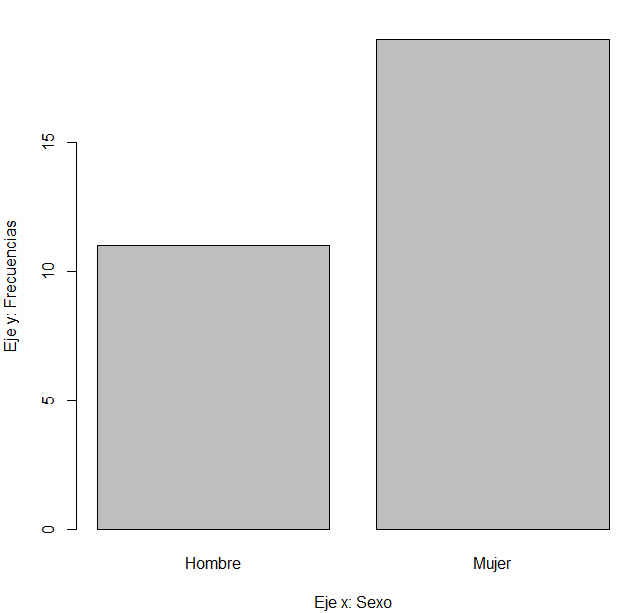 Figura 42: Gráfico de barras (Variable: sexo)
Figura 42: Gráfico de barras (Variable: sexo)
e) Realiza un histograma con la variable altura y añades los títulos a los ejes
Seleccionamos Gráficas/ Histograma
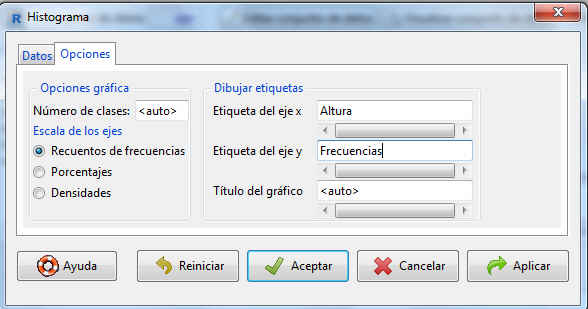 Figura 44: Histograma. Opciones
Figura 44: Histograma. Opciones
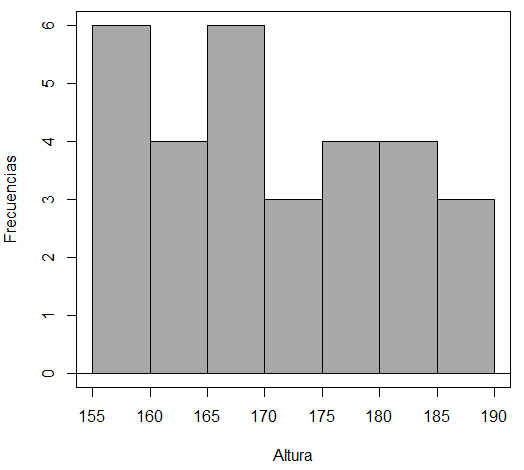 Figura 45: Histograma. (Variable: Altura)
Figura 45: Histograma. (Variable: Altura)
f) ¿Existen valores atípicos en alguna de las variables?
Para comprobar si hay valores atípicos en la distribución de la variable Altura realizamos un gráfico de cajas con bigotes, para ello seleccionamos Gráficas/Diagrama de Caja
Podemos realizar el gráfico de cajas para la variable altura, sin tener cuenta los grupos (Opción por defecto) o teniendo encuenta los grupos, para ello seleccionamos Gráfica por grupos…
 Figura 47: Diagrama de cajas (Variable por grupo)
Figura 47: Diagrama de cajas (Variable por grupo)
Figura 48: Diagrama de cajas (Variable: Altura)
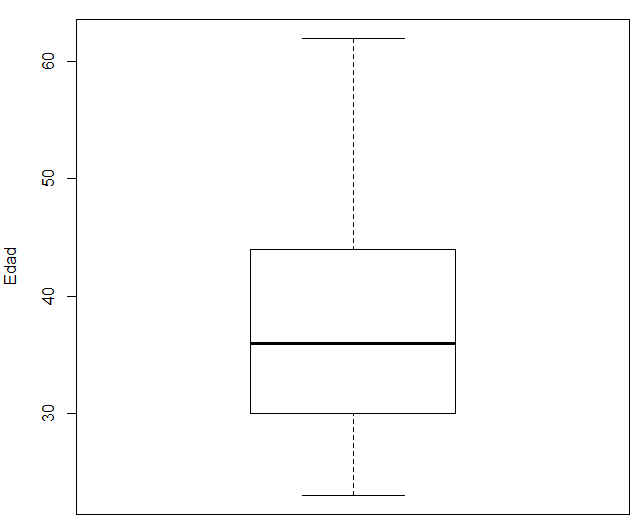
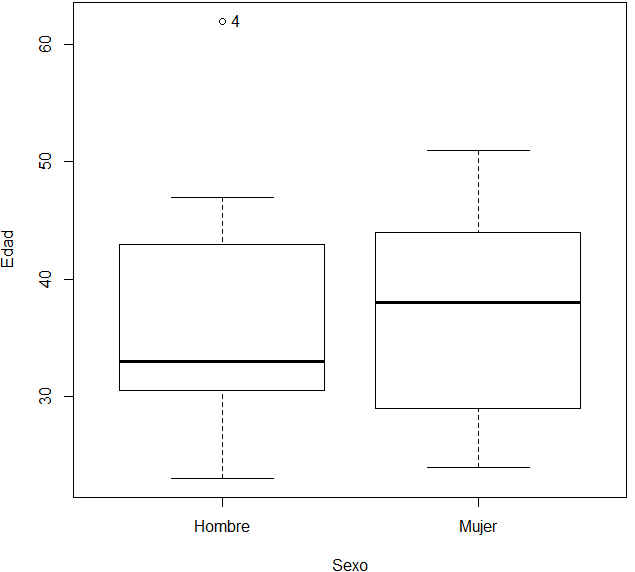
Figura 49: Diagrama de cajas (Variable: Edad)
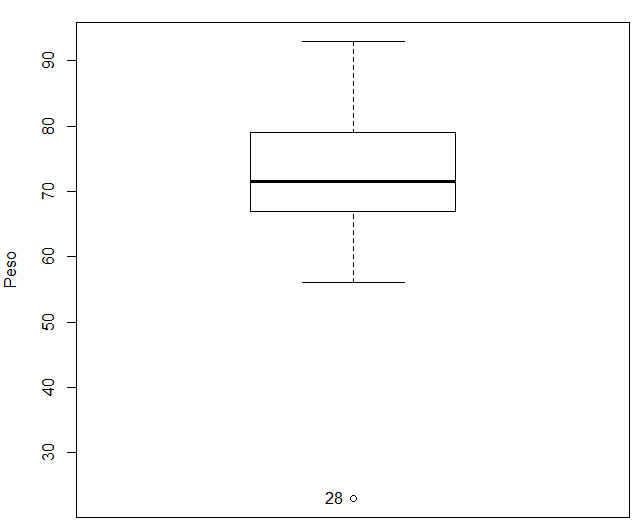
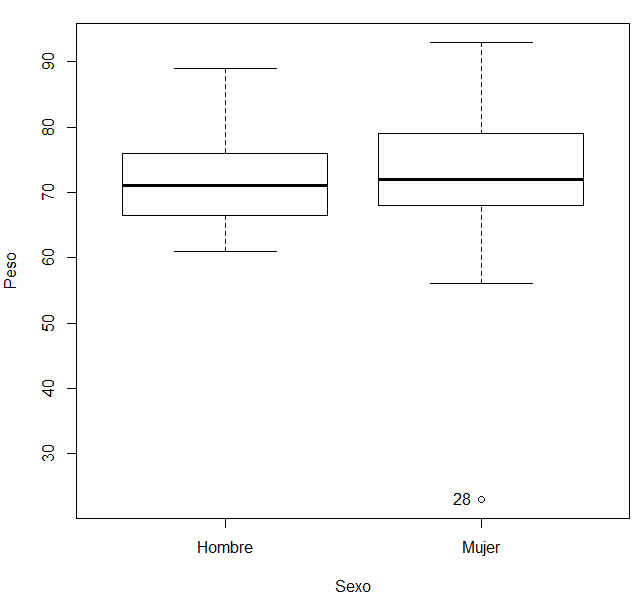
Figura 50: Diagrama de cajas (Variable: Peso)
Los valores atípicos son: El punto 4 en la variable Edad (Hombre). El punto 28 en la variable Peso y ese punto corresponde a la mujer.
Ejercicios Propuestos
Ejercicio Propuesto
Las siguientes tablas recogen información sobre el diámetro, la altura, el volumen del tronco y la variedad de distintos cerezos en dos regiones distintas:
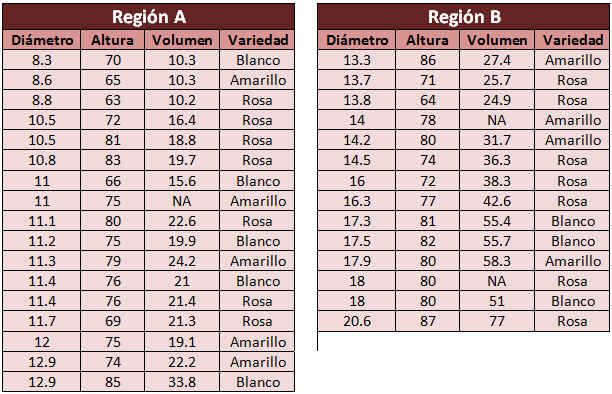 Tabla3. Datos del Ejercicio Propuesto 1
Tabla3. Datos del Ejercicio Propuesto 1
Se pide:
a) Elabora dos ficheros de texto que contengan la información de la tabla anterior. Utiliza el tabulador para separar la información referente a cada variable. Guárdalos en el escritorio y llámalos PropuestoRegA.txt y PropuestoRegB.txt e impórtalos
b) Calcula el diámetro medio de los datos en la Región A y su mediana. ¿Es simétrica la distribución de estos datos? ¿Donde es más homogéneo el diámetro en la Región A o en la Región B?
c) Calcula el porcentaje de cada unas de las variedades que hay en la Región A y haz un gráfico de sectores con el título Gráfico de sectores para la variable: Variedad
d) Realiza un histograma con la variable volumen y añades los títulos a los ejes
e) ¿Existen valores atípicos en alguna de las variables?
Ejercicio Propuesto (Resuelto)
a) Elabora dos ficheros de texto que contengan la información de la tabla anterior. Utiliza el tabulador para separar la información referente a cada variable. Guárdalos en el escritorio y llámalos PropuestoRegA.txt y PropuestoRegB.txt e impórtalos
b) Calcula el diámetro medio de los datos en la Región A y su mediana. ¿Es simétrica la distribución de estos datos? ¿Donde es más homogéneo el diámetro en la Región A o en la Región B?
 Figura 52: Resumen estadístico (Variable: diámetro en la Región A)
Figura 52: Resumen estadístico (Variable: diámetro en la Región A)
La media es 10.905888 y la mediana 11.1
La distribución de los datos de la variable diámetro es asimétrica negativa (-0.6142051)
 Figura 53: Resumen estadístico (Variable: diámetro en la Región B)
Figura 53: Resumen estadístico (Variable: diámetro en la Región B)
Es más homogénea la distribución del diámetro en la Región A ya que el coeficiente de variación de Pearson es menor (CV (Región A) = 0.1201; CV (Región B)=0.1375).
c) Calcula el porcentaje de cada unas de las variedades que hay en la Región A y haz un gráfico de sectores con el título Gráfico de sectores para la variable: Variedad
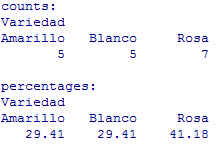 Figura 54: Distribución de frecuencias de la variable: Variedad
Figura 54: Distribución de frecuencias de la variable: Variedad
El porcentaje de la Variedad Amarillo es 29.41, de Blanco 29.41 y de Rosa 41.18.
 Figura 55: Gráfico de sectores para la variable: Variedad
Figura 55: Gráfico de sectores para la variable: Variedad
d) Realiza un histograma con la variable volumen y añades los títulos a los ejes
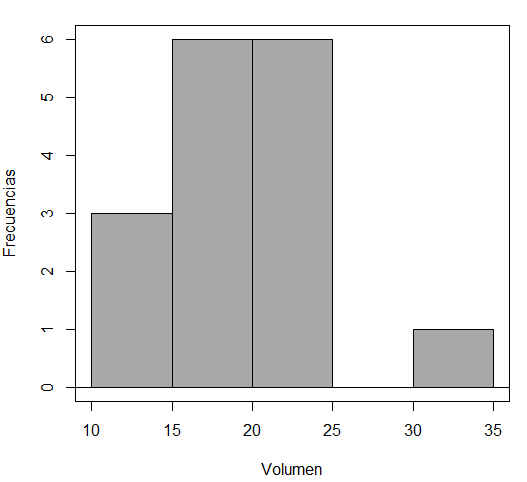 Figura 56: Histograma (Variable: Volumen)
Figura 56: Histograma (Variable: Volumen)
e) ¿Existen valores atípicos en alguna de las variables?
Valores atípicos hay en las variables Diámetro (los puntos: 1, 3 y 17) y en la variable Volumen (el punto 17)
Solución del Ejercicio Propuesto
Autores: Beatriz Cobo Rodríguez y Ana María Lara Porras. Universidad de Granada. (2016)