COMPARACIONES MÚLTIPLES

Introducción

En este capítulo explicaremos algunas técnicas para analizar con mayor detalle los datos de un experimento, con posterioridad a la realización del Análisis de la Varianza. Si dicho análisis confirma la existencia de diferencias significativas entre los tratamientos, es conveniente investigar qué medias son distintas. Para ello, emplearemos diversas técnicas cuyo objeto es identificar qué tratamientos son estadísticamente diferentes y en cuánto oscila el valor de esas diferencias. Consideraremos su aplicación únicamente al modelo de efectos fijos.

El uso de estas técnicas, en algunos casos, está supeditado al resultado del análisis de la varianza; en otros casos, las técnicas pueden emplearse directamente sin haber realizado previamente dicho análisis. Este conjunto de técnicas se engloba bajo la denominación de contrastes para comparaciones múltiples ya que su objetivo fundamental es comparar entre sí medias de tratamientos o grupos de ellas.

En primer lugar estudiamos un procedimiento intuitivo y cualitativo basado en la representación gráfica de los datos del experimento. Depués del método gráfico consideramos la técnica de comparación por parejas introducida por Fisher en 1935. Dicha técnica, denominada método de la diferencia mínima significativa o método LSD (Least Significant Difference), se basa en la construcción de tests de hipótesis para la diferencia de cualquier par de medias.

Cuando el número posibles de comparaciones es elevado, la aplicación reiterada de este procedimiento, para un nivel de significación α dado, puede conducir a un número grande de rechazos de la hipótesis nula aunque no existan diferencias reales. El intento de paliar el problema de los falsos rechazos justifica la introducción de otros procedimientos para comparaciones múltiples. Entre estos métodos se estudia primero el basado en la Desigualdad de Bonferroni. A continuación se aborda otra forma de solventar las deficiencias mencionadas anteriormente, basada en el rango estudentizado, que da lugar al Método de la diferencia significativa honesta propuesto por Tukey o método HSD (Honestly Significant Difference) y a los Procedimientos de rangos múltiples de Newman-Keuls y Duncan.

Finalmente se estudia el Procedimiento general de Scheffé, basado en la construcción de intervalos de confianza simultáneos para todas las posibles diferencias de medias y que permite su extensión a comparaciones más generales denominadas contrastes.

Posteriormente se justifica qué procedimientos pueden ser adecuados para cada situación y cuáles son las condiciones experimentales que los hacen recomendables.

Otro problema de índole diferente, también ligado a las comparaciones múltiples, consiste en las Comparaciones de distintos tratamientos con un control que suele emplearse en determinados campos de investigación, por ejemplo en estudios epidemiológicos. Dicho problema se aborda mediante el contraste de Dunnett.

Comparaciones múltiples de medias

Al estudiar el comportamiento de los tratamientos de un factor, mediante un análisis de la varianza, el único objetivo es saber si, globalmente, dichos tratamientos difieren significativamente entre sí. Ahora estamos interesados, una vez aceptada la existencia de diferencias entre los efectos del factor, en conocer qué tratamientos concretos producen mayor efecto o cuáles son los tratamientos diferentes entre sí. En estas misma condiciones, puede ser útil también realizar comparaciones adicionales entre grupos de medias de los tratamientos.

Antes de seguir con el desarrollo de esta sección, remitimos al lector al Capítulo 1, donde presentamos el modelo de efectos fijos definido por la ecuación

\(  y_{ij}=μ_{i}+u_{ij} \hspace{4cm} [2.1] \)

Antes de estudiar analíticamente las distintas formas de comparar efectos, es conveniente examinar de forma cualitativa su comportamiento. Esto se efectúa de forma gráfica y constituye el primer método que pasamos a desarrollar.

Comparaciones gráficas de medias

Al igual que en el capítulo anterior vamos a concretar toda la explicación sobre un determinado ejemplo. En este caso, vamos a considerar el Ejemplo 1-1.

Para ese ejemplo obtuvimos, véase Tabla 1-6, que el rendimiento de la semilla de algodón depende significativamente del tipo de fertilizante utilizado. Pero esta conclusión no nos informa nada sobre una serie de preguntas tales como: ¿Producen algunos fertilizantes el mismo rendimiento?, en el caso de que dos fertilizantes produzcan distinto rendimiento ¿entre qué valores oscila esa diferencia?, etc. Una primera respuesta a estas preguntas se puede realizar de forma gráfica.

\(  \begin{array}{| c| c|c|c|c|} \hline Fuentes \hspace{.2cm}  de  &   Suma   \hspace{.2cm}  de        &              Grados \hspace{.2cm} de  &   Cuadrados &  F_{exp} \\  variación      &  cuadrados    &    libertad  &  medios &   \\ \hline  Entre \hspace{.2cm} grupos  &   439.88 &   4   & 109.97  &  23.55 \\ \hline Dentro \hspace{.2cm} de \hspace{.2cm} grupos  &  98.00   & 21   &  4.67 & \\ \hline TOTAL &  537.88 &  25 & & \\ \hline  \end{array}  \)

Tabla 1-6. Análisis de la varianza para los datos del Ejemplo 1-1

En primer lugar haremos unas consideraciones generales antes de estudiar el ejemplo de referencia. Para ello, consideremos el modelo equilibrado con \( n \) observaciones por nivel y sean \( \overline {y}_{1.}, \overline {y}_{2.}, \cdots, \overline {y}_{I.} \) las medias muestrales de los correspondientes tratamientos. Bajo las hipótesis del modelo, cualquier promedio \( \overline {y}_{i.} \) de un tratamiento se distribuirá alrededor de su media \( μ_{i} \) con una desviación estándar \( σ/\sqrt {n} \). En consecuencia, si aceptamos que las medias de los distintos niveles de un factor son todas idénticas, entonces las medias muestrales \(  \overline {y}_{i.}, i=1,2, \cdots I \), se comportarán como un conjunto de \( I \) observaciones tomadas al azar de una misma distribución normal con media \( μ \) y desviación estándar \( σ/ \sqrt{n} \).

Supongamos que dibujamos la función de densidad de una distribución normal “deslizante” e imaginemos que situamos dicha distribución sobre los puntos que representan las medias de los tratamientos. Procediendo de esta manera y teniendo en cuenta los distintos comportamientos de los efectos, podemos distinguir dos casos relevantes:

a) Los efectos de los tratamientos son iguales entre sí.

Entonces, al deslizar la distribución a lo largo del eje OX, es probable que exista alguna posición para la cual todos los valores \( \overline {y}_{i.}\) sean compatibles con dicha distribución; es decir, sean una muestra aleatoria de la misma distribución.

b) Los efectos de los tratamientos no son iguales.

Entonces al deslizar la distribución a lo largo del eje OX, es improbable que exista alguna posición para la cual todos los valores \( \overline {y}_{i.}\) sean compatibles con dicha distribución. En este caso, es posible que existan situaciones que permitan detectar niveles del factor que producen respuestas medias diferentes; concretamente, éstos se identifican por medio de aquellos valores \( \overline {y}_{i.}\) que están muy distanciados de los otros.

Como generalmente \( σ^{2} \) es desconocida estimamos su valor por medio de la varianza residual \( \widehat {S}_{R}^{2} \) y, en lugar de la distribución normal, hay que emplear una distribución \( t \) deslizante con factor de escala \(\sqrt { \widehat {S}_{R}^{2}/n } \) y con los grados de libertad correspondientes a dicha varianza residual. Para dibujar dicha distribución \( t \) utilizamos la Tabla correspondiente de la t de Student, que muestra el valor de la función de densidad, para determinadas abscisas, de una distribución t de Student con grados de libertad dados. Para obtener la distribución con factor de escala hay que multipicar las correspondientes abscisas por dicho factor de escala y representar sus valores frente a las correspondientes ordenadas.

Este método se ilustra en la Figura 2-1 donde se distinguen varios casos:

a) Las cinco medias pueden considerarse como una muestra aleatoria de la misma distribución

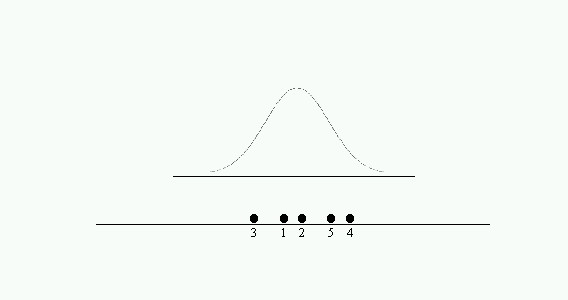Figura 2-1a

b) Al deslizar la distribución de referencia a lo largo del eje horizontal, nos permite detectar grupos homogéneos. Así, deducimos que las medias 2, 4 y 5 son probablemente mayores que 1 y 3 y que no hay distinción entre las medias de cada uno de los grupos.

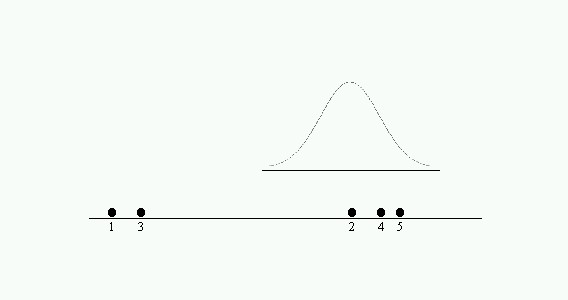
Figura 2-1b

c) Podemos deslizar la distribución de referencia de forma que abarque a las cinco medias, pero no parece razonable concluir que las cinco medias sean compatibles con la misma población.

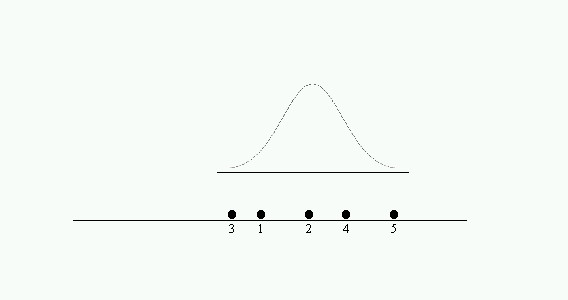
Figura 2-1c

En estos casos parece razonable que el resultado que proporciona el análisis de la varianza sea aceptar la hipótesis \( H_0 \) en el primer caso y rechazarla en los otros dos.

Este procedimiento gráfico se ha desarrollado para el caso en que todos los tamaños muestrales sean iguales. Sin embargo, de forma aproximada, se puede aplicar también cuando las diferencias entre los tamaños muestrales no sean muy grandes. En tal caso, debe usarse

\( \displaystyle \sqrt  { \displaystyle \frac {\widehat {S}_{R}^{2}} {n} }\)

como factor de escala, siendo \( n \) el tamaño medio de las muestras, \( \overline {n}= \displaystyle \frac{1} {I} \sum_{i}n_{i} \).

La aplicación de este método a nuestro ejemplo de referencia se muestra en la Figura 2-2

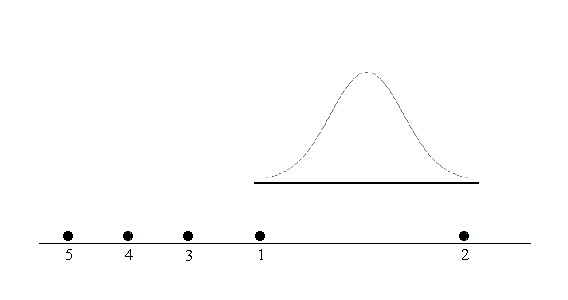
Figura 2-2: Comparación gráfica de los tratamientos del Ejemplo 1-1

En dicho ejemplo, como la varianza es desconocida y los tamaños muestrales son distintos, el factor de escala es igual a

\( \displaystyle \sqrt { \displaystyle \frac { \widehat{S}_{R}^{2}} {n}}= \displaystyle \sqrt { \displaystyle \frac { 4.67} {26/5}}=0.947 \)

Para construir la distribución deslizante, como el número de grados de libertad de la varianza residual es 21, tomamos los valores de la correspondiente fila de la Tabla ordenadas de la distribución t, obteniendo:

\(  \begin{array}{c ccccc}  \\     Abcisa  &   0 &   0.5  &  1.0 &   1.5  &  2.0 \\
Ordenada  &  0.394  &  0.346  &  0.236  &  0.129  &  0.058 \\
Abcisa \times 0.947  &  0   & 0.473  &  0.947 &   1.420  &  1.894 \\ \end{array}  \)

Para dibujar la distribución de referencia, se elige un origen arbitrario, que debe estar próximo a las medias, nosotros hemos considerado como origen \( μ \). A continuación se representan las ordenadas de los puntos \( μ \pm 0, μ \pm 0.473, μ \pm 0.947, μ \pm 1.420, μ \pm 1.894 \) que se unen en una línea continua, con lo que esbozamos la distribución de referencia. El deslizamiento de la distribución de referencia a lo largo del eje horizontal permite obtener las siguientes conclusiones:

• Las cinco medias no son iguales entre sí. No es posible situar la distribución de referencia en ninguna posición de forma que las abarque a todas
•  Los fertilizantes (5 y 4), (4 y 3) y (3 y 1) tienen un rendimiento similar y el fertilizante 2 tiene un rendimiento distinto de los otros cuatro.

Este procedimiento de comparación gráfica de las medias de los tratamientos mediante una distribución de referencia, es un método aproximado pero eficaz en muchos problemas de comparaciones múltiples. En las siguientes secciones se describen otros métodos estadísticos más rigurosos para realizar comparaciones múltiples. En primer lugar se abordan métodos creados específicamente para comparar por parejas los efectos de tratamientos, de entre ellos, comenzaremos con los basados en la distribución t.

Comparaciones basadas en la distribución t

Las pruebas estadísticas para comparaciones múltiples más frecuentemente utilizadas se basan en la distribución t de Student. Supongamos que interesa comparar por parejas los efectos de I tratamientos. Es decir, nos interesa contrastar cualquier hipótesis de la forma

\(  \begin{array}{ ll}  \\     H_0  \equiv &   μ_{i}=μ_{j} \\ H_1 \equiv &    μ_{i} \neq μ_{j} \\ \end{array}  \hspace {4cm} [2.2] \)

La técnica más antigua y popular para efectuar estas comparaciones múltiples es el procedimiento LSD, (Least Significant Difference), que pasamos a estudiar a continuación.

Contraste de la Mínima Diferencia Significativa (LSD)

Este procedimiento fué sugerido por Fisher en 1935 y es el primer método de comparaciones múltiples que vamos a utilizar. Dicho procedimiento consiste en una prueba de hipótesis por parejas basada en la distribución t.

Este método debe aplicarse cuando previamente se haya rechazado la hipótesis nula del test F del análisis de la varianza. Para ello, se determina el siguiente estadístico

\( t= \displaystyle \frac { \overline {y}_{i.}- \overline {y}_{j.}} { \sqrt { \widehat {S}_{R}^{2} \left ( \displaystyle \frac {1}{n_{i}}+ \displaystyle \frac {1} {n_{j}} \right ) }} \hspace{2cm} [2.3] \)

que, por las hipótesis del modelo de ecuación ([1.1]), sigue una distribución t de Student con N-I grados de libertad.

Por lo tanto, se concluye que la pareja de medias \( μ_{i} \) y \( μ_{j} \) son estadísticamente diferentes si

\( ∣ \overline {y}_{i.}- \overline {y}_{j.}∣>LSD \hspace{2cm} [2.4] \)

donde la cantidad LSD, denominada mínima diferencia significativa, viene dada por

\( LSD=t_{α/2;N-I} \displaystyle  \sqrt { \widehat{S}_{R}^{2} \left ( \displaystyle  \frac {1} {n_{i}}+ \displaystyle  \frac {1} {n_{j}} \right ) } \hspace{2cm} [2.5] \)

siendo

∗ \(  n_{i} \) y \(  n_{j} \) el número de observaciones correspondiente a cada media

∗ \(  N-I \) el número de grados de libertad de la varianza residual

∗ \( t_{α/2;N-I} \) el valor crítico de la distribución \( t \) con \( N-I \) grados de libertad que deja una probabilidad a su derecha igual a \( α/2 \).

Si el diseño es balanceado, el valor de LSD se reduce a

\( LSD=t_{α/2;N-I} \displaystyle \sqrt { \displaystyle \frac {2 \widehat {S}_{R}^{2}} {n} }  \hspace{2cm} [2.6] \)

El procedimiento LSD es sencillo de utilizar; se puede aplicar tanto en modelos equilibrados como no-equilibrados. Además proporciona también intervalos de confianza para diferencias de medias. Dichos intervalos son de la forma

\(  \left (( \overline {y}_{i.}- \overline {y}_{j.}) – LSD \hspace{.4cm} , \hspace {.4cm} (\overline {y}_{i.}- \overline {y}_{j.})+LSD \right ) \hspace{2cm} [2.7] \)

Comentarios

C1) Un problema que presenta la aplicación de este procedimiento, para un número relativamente grande de tratamientos, es que el número de posibles falsos rechazos de la hipótesis nula puede ser elevado aunque no existan diferencias reales. Así, por ejemplo, si \( I \) es igual a 10, hay  \(  { 10 \choose  2}=45  \) posibles parejas de comparaciones. Si tomamos \( α=0.05 \), entonces el número esperado de falsos rechazos será

\(  0.05 \times 45=2.25 \)

supuesta independencia estadística entre los distintos contrastes.

Otra forma de enfocar este problema es comprobando que la utilización reiterada de este procedimiento conduce a que la probabilidad de que se rechace al menos una de las posibles comparaciones sea bastante alta. En efecto, bajo la hipótesis nula

\( Pr[Rechazar \hspace{.2cm} al  \hspace{.2cm}menos \hspace{.2cm} una \hspace{.2cm}comparación]=  1-Pr[aceptar \hspace{.2cm} todas]= 1-(1-0.05)^{45}  \simeq 0.90 \)

El intento de paliar este problema justifica la introducción de otros procedimientos para comparaciones múltiples.

C2) Puede suceder que el método LSD falle al aceptar que todas las parejas son iguales, a pesar de que el estadístico F del análisis de la varianza resulte significativo; ésto es debido a que la prueba F considera simultáneamente todas las posibles comparaciones entre las medias de los tratamientos y no sólo las comparaciones por parejas.

A fín de ilustrar este procedimiento, consideramos el ejemplo de referencia. Así, para un nivel de significación del 5%, el valor de LSD es

\( LSD=t_{0.025;21} \displaystyle \sqrt  {\widehat {S}_{R}^{2} \left ( \displaystyle \frac {1}{n_{i}}+ \displaystyle \frac {1} {n_{j}} \right ) }= 2.080 \sqrt {4.67} \displaystyle \sqrt { \displaystyle \frac {1} {n_{i}}+ \displaystyle \frac {1} {n_{j}} } =4.49 \displaystyle \sqrt { \displaystyle \frac {1} {n_{i}}+ \displaystyle \frac {1} {n_{j}} } \)

Por tanto, dos medias difieren significativamente entre sí, si el valor absoluto de la diferencia de sus promedios muestrales es mayor que el valor LSD. Recordemos que, en este ejemplo de referencia, los valores de los cinco promedios de los tratamientos son:

\(  \overline {y}_{1.}=50 \hspace{.2cm},   \hspace{.2cm} \overline {y}_{2.}=57 \hspace{.2cm}, \hspace{.2cm} \overline {y}_{3.}=48 \hspace{.2cm}, \hspace{.2cm} \overline {y}_{4.}=47 \hspace{.2cm}, \hspace{.2cm} \overline {y}_{5.}=45 \)

Para la aplicación de este procedimiento es recomendable ordenar las medias de menor a mayor. Una vez ordenadas se comparan la \( 1^{a} \) y la \( 2^{a} \):

a) Si hay diferencia significativa entre ellas, también la habrá entre la \( 1^{a} \)  y todas las demás.

b) Si no hay diferencia significativa entre ellas, se compara la \(  1^{a} \) con la  \( 3^{a} \)  y siguientes hasta encontrar la primera diferencia significativa.

De forma similar se realiza la comparación de la \( 2^{a} \) media con todas las demás y así sucesivamente se haría con las restantes medias.

Por lo tanto,

\( 1^{o})  \) Ordenamos las medias de menor a mayor.

\(  \overline {y}_{5.}=45  \hspace{.2cm},   \hspace{.2cm} \overline {y}_{4.}=47  \hspace{.2cm},   \hspace{.2cm} \overline {y}_{3.}=48  \hspace{.2cm},   \hspace{.2cm} \overline {y}_{1.}=50  \hspace{.2cm},   \hspace{.2cm} \overline {y}_{2.}=57 \)

\( 2^{o})  \) Comparamos las medias \( 1^{a} \)  y \(  2^{a} \)

\( LSD=4.49 \sqrt {1/6+1/4}=2.898 \hspace{.6cm}   ;  \hspace{.6cm}   \mid \overline {y}_{5.}- \overline {y}_{4.} \mid    = \mid 45-47 \mid    =2 \)

Como no hay diferencia significativa entre ellas, se compara la \( 1^{a} \)  y \(  3^{a} \)

\( LSD=4.49 \sqrt {1/6+1/5}=2.718 \hspace{.6cm}   ;  \hspace{.6cm}   \mid \overline {y}_{5.}- \overline {y}_{3.} \mid    = \mid 45-48 \mid    =3 \)

Al haber diferencia significativa entre ellas, también la hay entre la \( 1^{a} \) y la \( 4^{a} \) y entre la \( 1^{a} \) y la  \( 5^{a}\).

\( 3^{o}) \) Comparamos las medias \( 2^{a} \) y \( 3^{a}\).

\( LSD=4.49 \sqrt {1/4+1/5}=3.011 \hspace{.6cm}   ;  \hspace{.6cm}   \mid \overline {y}_{4.}- \overline {y}_{3.} \mid    = \mid 47-48 \mid    = -1 \)

Como no hay diferencia significativa entre ellas comparamos la \( 2^{a} \) y \( 4^{a}\)

\( LSD=4.49 \sqrt {1/4+1/6}= 2.898 \hspace{.6cm}   ;  \hspace{.6cm}   \mid \overline {y}_{4.}- \overline {y}_{1.} \mid    = \mid 47- 50 \mid    = 3 \)

Al haber diferencia significativa entre ellas, también la hay entre la  \( 2^{a} \) y \( 5^{a}\)

\( 4^{o})  \) Comparamos las medias \( 3^{a} \) y \( 4^{a}\)

\( LSD=4.49 \sqrt {1/5+1/6}=2.718 \hspace{.6cm}   ;  \hspace{.6cm}   \mid \overline {y}_{3.}- \overline {y}_{1.} \mid    = \mid 48- 50 \mid    = 2 \)

No hay diferencia significativa, por lo tanto comparamos la \( 3^{a} \) con la  \( 5^{a}\)

\( LSD=4.49 \sqrt {1/5+1/5}=2.839 \hspace{.6cm}   ;  \hspace{.6cm}   \mid \overline {y}_{3.}- \overline {y}_{2.} \mid    = \mid 48- 57 \mid    = 9 \)

Hay diferencia significativa.

\( 5^{o})  \) Comparamos las medias \( 4^{a} \) y \( 5^{a}\)

\( LSD=4.49 \sqrt {1/6+1/5}=2.718 \hspace{.6cm}   ;  \hspace{.6cm}   \mid \overline {y}_{1.}- \overline {y}_{2.} \mid    = \mid 50- 57 \mid    = 7 \)

Hay diferencia significativa.

Normalmente el resultado de las comparaciones por parejas se suele representar en forma gráfica, como se muestra a continuación

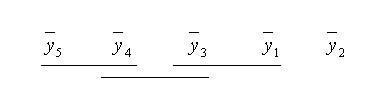
Figura 2-3

En dicha representación los valores de las medias de los tratamientos aparecen en orden creciente y se subrayan aquellos grupos de medias que resultan equivalentes. Esta representación gráfica es muy fácil de interpretar y es la utilizada por la mayoría de los paquetes estadísticos.

En la siguiente sección se describe el método de Bonferroni, que presenta una solución al problema de los falsos rechazos planteado en el método LSD.

Método de Bonferroni

En este procedimiento se fija un nivel de significación \( α \) que se reparte entre cada una de las comparaciones consideradas y se utiliza la desigualdad de Bonferroni

 \( Pr \left ( \displaystyle  \bigcup_{m=1}^{M}A_{m} \right ) \leq  \displaystyle \sum_{m=1}^{M}Pr(A_{m}) \hspace{2cm} [2.8] \)

Consideremos que queremos realizar estimación por intervalos para las  \( M=(I/2)  \) comparaciones posibles, cada una al nivel de significación  \( α^{*}=α/M  \); esto da origen a \( M  \) intervalos de confianza que contienen a cada una de las posibles diferencias  \( μ_{i}-μ_{j}  \) con probabilidad  \( 1-α^{*}  \). Llamando  \( C_{m}  \) al intervalo  \( m-ésimo  \) se tiene que

\( Pr \left [μ_{1m}-μ_{2m} \in C_{m} \right ]=1-α^{*} \hspace{2cm} m=1,2, \cdots , M \)

siendo \( μ_{1m} \) y \( μ_{2m} \) la primera y segunda media de la correspondiente comparación, donde supondremos que  \( 1 \leq 1m < 2m  \leq I \).

Aplicando la desigualdad de Bonferroni, (expresión ([2.8])), se tendrá

\( Pr \left ( \displaystyle  \bigcap_{m=1}^{M}C_{m} \right )=1-Pr \left (\displaystyle  \bigcup_{m=1}^{M} \overline {C}_{m} \right ) \geq 1- \displaystyle  \sum_{m=1}^{M}Pr( \overline {C}_{m})=1- \displaystyle  \sum_{m=1}^{M}α^{*} \)

notamos por \(  \overline {C}_{m} \) al complementario del intervalo \( C_{m} \) .

Teniendo en cuenta este resultado y si queremos garantizar un nivel de significación \( α \) para el conjunto de las M comparaciones por parejas, o un nivel de confianza \( 1-α \) para el conjunto de intervalos, basta tomar

\(  α^{*}= \displaystyle \frac {α}{M} \)

Con ello, evidentemente, la probabilidad de que todos los intervalos, \( C_{m} \), contengan a la correspondiente diferencia de medias, será al menos \( 1-α \). Así pues, los intervalos quedarán en la forma

\(  \overline {y}_{1m.}-\overline {y}_{2m.} \pm t_{α/2M} \displaystyle \sqrt { \widehat {S}_{R}^{2}\left ( \displaystyle \frac {1}{n_{1m}}+ \displaystyle \frac {1}{n_{2m}} \right) }  \hspace{2cm} [2.9] \)

donde \( \overline {y}_{1m.}, \overline {y}_{2m.} \)  y \(  n_{1m}, n_{2m} \), son las medias y los tamaños muestrales correspondientes a la comparación m-ésima.

Denotamos por \( θ_{m}=μ_{1m}-μ_{2m} \hspace{.2cm}, \hspace{.4cm} m=1,2, \cdots ,M \), una de las \( M \) comparaciones lineales por parejas de medias, para las cuales interesa contrastar \(  H_0 \equiv θ_{m}=0 \) frente \(  H_1 \equiv θ_{m} \neq 0 \).

Entonces, se rechaza \(  H_0 \) si

\(  ∣θ_{m}∣>B_{m} \)

y se acepta en caso contrario.

Donde

\(  B_{m}=t_{α/2M} \displaystyle  \sqrt { \widehat {S}_{R}^{2} \left ( \displaystyle \frac {1}{n_{1m}}+ \displaystyle \frac {1}{n_{2m}} \right) }  \hspace{2cm} [2.10] \)

En el caso del modelo equilibrado los valores de \( B_{m} \) coinciden, dichos valores se denotan por BSD y tienen la siguiente expresión

\(  BSD=t_{α/2M}\displaystyle  \sqrt { \widehat {S}_{R}^{2} \left ( \displaystyle \frac {1}{n}+ \displaystyle \frac {1}{n} \right) }  \hspace{2cm} [2.11] \)

siendo \( n \) el número de observaciones de cada grupo y \(  t_{α/2M} \) el valor crítico de la distribución \( t \), con el mismo número de grados de libertad que la varianza residual, que deja una probabilidad \( α/2M \) a su derecha.

Para ilustrar este método consideramos el ejemplo de referencia. Puesto que es un modelo no-equilibrado, los valores de los estadísticos de contraste vendrán dados por la siguiente expresión

\(  B_{m}=t_{ \frac {0.025}{10};21} \displaystyle  \sqrt { (4.67) \left( \displaystyle \frac {1}{n_{1m}}+ \displaystyle \frac {1}{n_{2m}} \right) } \hspace{1.5cm} m=1,2, \cdots,10 \)

Así, por ejemplo, si comparamos

∗ 5 vs 4, el valor de \(  B_{m}\)  es

\(  B_1=t_{\frac {0.025}{10};21}\displaystyle  \sqrt { (4.67) \left( \displaystyle \frac {1}{6}+ \displaystyle \frac {1}{4 } \right) }=(3.135)(1.394)=4.370 \)

Entonces, como

\(  ∣ \overline {y}_{5.}- \overline {y}_{4.}∣=2<B_1 \)

las medias 5 y 4 no son significativamente distintas

∗ 5 vs 3, el valor de \( B_{m} \) es

\( B_2= t_{\frac {0.025}{10};21} \displaystyle  \sqrt { (4.67) \left( \displaystyle \frac {1}{6}+ \displaystyle \frac {1}{5 } \right) }=(3.135)(1.308)=4.100 \)

Entonces, como

\( ∣ \overline {y}_{5.}- \overline {y}_{3.}∣=3<B_2 \)

las medias 5 y 3 no son significativamente distintas.

Nota:  Se utiliza “i vs j”, (i versus j), para denotar la comparación de \( μ_{i} \) frente a \( μ_{j} \).

El resultado de las comparaciones por parejas realizadas con este procedimiento se muestra, en forma gráfica, a continuación

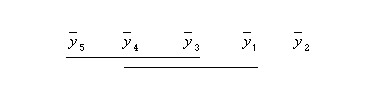Figura 2-4

Seguidamente presentamos los contrastes de rangos múltiples. Dichos contrastes se basan en la distribución del rango estudentizado y se distinguen tres métodos debidos respectivamente a Tukey, Duncan-Newman y Keuls.

Tests de rangos múltiples

Estos contrastes se basan en la distribución del rango estudentizado, cuya definición se realiza en términos del número de grupos que hay que comparar y de los grados de libertad del estimador de la varianza.

Estos procedimientos, al igual que el procedimiento de Bonferroni, permiten superar las dificultades que surgen al aumentar el número de grupos a comparar y no poderse controlar los falsos rechazos de la hipótesis nula. Los métodos resultantes, en términos generales, son conservadores; es decir, la probabilidad real de rechazar la hipótesis nula cuando es cierta es menor que el nivel de significación α fijado.

Para definir el recorrido o rango estudentizado, supongamos que disponemos de k observaciones independientes \( y_1,y_2, \cdots ,y_{k} \) de una distribución Normal con media \( μ \) y varianza \( σ^{2} \). Supongamos que disponemos, también, de un estimador \( S^{2} \) de \( σ^{2} \) que tiene \( ν \) grados de libertad y es independiente de las \( y_{i} \). Sea \( R \) el rango de este conjunto de observaciones,

\( R=max(y_{i})-min(y_{i}) \hspace {2cm} [2.12] \)

Bajo estas condiciones, se define el rango estudentizado como el cociente

\( \displaystyle  \frac {max(y_{i})-min(y_{i}) } {S}= \displaystyle \frac {R} {S} \hspace {2cm} [2.13] \)

que se denota por \( q_{k,ν} \). La distribución de este estadístico, que depende de los parámetros \( k \) y \( ν \), ha sido tabulada y los valores críticos se presentan la Tabla del rango estudentizado.

Método de Tukey (Honestly-significant-difference)

Este procedimiento se va a desarrollar considerando en primer lugar el caso del modelo unifactorial equilibrado. En este modelo vamos a construir intervalos de confianza con coeficiente de confianza conjunto \( 1-α \) para todas las posibles comparaciones por parejas asociadas a los \( I \) niveles, es decir las \(  { I \choose  2} \) comparaciones por parejas.

El nivel de confianza conjunto \( 1-α \) indica que de cada 100 muestras en \( (1-α) \times 100  \) de ellas, cada uno de los intervalos contiene a su correspondiente diferencia de medias. Por tanto el nivel de confianza de cada uno de los intervalos será al menos \( 1-α \).

Para construir dichos intervalos consideramos las desviaciones

\(  ( \overline {y}_{1.}-μ₁),( \overline {y}_{2.}-μ₂), \cdots ,(\overline {y}_{I.}-μ_{I}) \hspace{2cm} [2.14]  \)

Estas desviaciones son variables aleatorias independientes normalmente distribuidas con media 0 y varianza \( σ^{2}/n \). Además \(  \widehat {S}_{R}^{2}/n \) es un estimador de \( σ^{2}/n \) que es independiente de dichas desviaciones. Entonces, de la definición de rango estudentizado, se sigue que

\(  \displaystyle  \frac {max( \overline {y}_{i.}-μ_{i})-min( \overline {y}_{i.}-μ_{i})} { \left ( \displaystyle  \frac { \widehat {S}_{R}^{2}} {n} \right )^{1/2}  } \rightarrow q_{I,N-I} \hspace {2cm} [2.14] \)

donde

• \( N-I \) es el número de grados de libertad asociado a \( \widehat {S}_{R}^{2} \)
• \( max( \overline {y}_{i.}-μ_{i}) \) es la desviación mayor
• \(  min(\overline {y}_{i.}-μ_{i}) \) es la desviación menor.

Entonces se verifica que

\( Pr \left [ \displaystyle  \frac {max( \overline {y}_{i.}-μ_{i})-min( \overline {y}_{i.}-μ_{i})} { \left ( \displaystyle  \frac { \widehat {S}_{R}^{2}} {n} \right )^{1/2}  } \leq q_{α;I,N-I}\right ] =1-α \hspace {2cm} [2.16] \)

Consideramos, a continuación, la siguiente desigualdad generada para todas las parejas de medias de tratamientos \( i \) y \( j \)

\(  \left |( \overline {y}_{i.}-μ_{i})-( \overline {y}_{j.}-μ_{j}) \right |   \leq max ( \overline {y}_{i.}-μ_{i})-min( \overline {y}_{j.}-μ_{j}) \hspace {2cm} [2.17] \)

Puesto que la desigualdad ([2.17]) se verifica para todas las parejas \( μ_{i} \) y \( μ_{j} \), se sigue de ([2.16]) que

\( Pr \left [  \left | \displaystyle \frac {( \overline {y}_{i.}-μ_{i})-( \overline {y}_{j.}-μ_{j}) } { \left (  \displaystyle \frac { \widehat {S}_{R}^{2}} {n} \right )^{1/2}} \right |  \leq q_{α;I,N-I} \right ]=1-α  \hspace {2cm} [2.18] \)

incluye todos los pares \( I(I-1)/2 \) de comparaciones entre los \( I \) niveles del factor.

Reordenando la desigualdad ([2.18]) obtenemos los límites de confianza, al nivel de confianza conjunto \( 1-α \), para todas las \( (I/2) \) comparaciones por parejas de las \( I \) medias, dados por

\( ( \overline {y}_{i.}- \overline {y}_{j.})-HSD \leq μ_{i}-μ_{j} \leq ( \overline {y}_{i.}- \overline {y}_{j.})+HSD \hspace {2cm} [2.19] \)

donde

\( HSD=q_{α;I,N-I}\displaystyle \sqrt { \displaystyle \frac { \widehat {S}_{R}^{2}} {n } \)

Si el intervalo ([2.19]) no contiene el 0 se concluye que las medias \(  μ_{i}\) y \(  μ_{j} \) difieren significativamente entre sí.

El coeficiente de confianza  \( 1-α \) indica que de cada \( 100 \) muestras en \( (1-α) \times 100 \) de ellas se determinará correctamente cuales de las \( (I/2) \) comparaciones por parejas de medias son significativas.

Por tanto, el método de Tukey resuelve el contraste

\( H_0:μ_{i}=μ_{j} \hspace {2cm} vs \hspace {2cm} H_1:μ_{i} \neq μ_{j} \)

de la siguiente manera

Si   \(  \left | \overline {y}_{i.}- \overline {y}_{j.} \right | \leq  HSD   \Rightarrow  \)   Aceptar    \( H_0 \)

Si  \(   \left | \overline {y}_{i.}- \overline {y}_{j.} \right | > HSD    \Rightarrow  \)    Rechazar     \( H_0 \)

En el caso de que el modelo no sea equilibrado se emplea el ajuste de Tukey-Kramer, que consiste en reemplazar \( n \) por la media armónica, \( n_{h} \), de los tamaños de los grupos, es decir

\(  n_{h}= \displaystyle \frac {2} { \displaystyle \sum_{i=1}^{2} \displaystyle \frac {1} {n_{i}}} \hspace {2cm} [2.20] \)

Para ilustrar el uso de este procedimiento consideremos el ejemplo de referencia. En este caso hay que usar \(  q_{0.05;5,21}=4.22 \) como base para determinar el valor crítico y, en consecuencia, ningún par de medias se declara significativamente diferente, salvo que \(  ∣y_{i.}-y_{j.}∣ \) exceda a

\(  HSD=(4.22) \displaystyle \sqrt { \displaystyle \frac { \widehat {S}_{R}^{2}} {n_{h}} }=(4.22) \displaystyle \sqrt { \displaystyle \frac {4.67} {2} \left ( \displaystyle \frac {1} {n_{i}}+ \displaystyle \frac {1} {n_{j}} \right ) } \)

Con esta prueba se obtienen los mismos resultados que con el procedimiento de Bonferroni.

El segundo procedimiento de comparaciones múltiples considerado en esta sección es el test de rango múltiple de Duncan. Es un procedimiento iterativo en el cual se intenta comprobar la igualdad de medias basándose en las más extremas. Es similar al procedimiento HSD de Tukey excepto que el nivel de significación varía de unas comparaciones a otras.

Test de rango múltiple de Duncan

El contraste de Duncan utiliza, como el HSD de Tukey, la distribución del recorrido estudentizado. Se diferencia de ese test en que su aplicación es secuencial, en el sentido de no utilizar un único valor crítico para todas las diferencias de medias, como el de Tukey, sino un valor crítico que depende del número de medias comprendido entre las dos medias que se comparan, habiendo ordenado previamente las medias en orden creciente.

Consideremos, en primer lugar, el modelo equilibrado y después generalizaremos para el caso no-equilibrado.

Se acepta que no hay diferencia significativa entre la media mayor y la media menor de \( p \) medias, \( y_{i.} \) e \( y_{j.} \), si se verifica

\(  \left | \overline {y}_{i.}- \overline {y}_{j.} \right | \leq R_{p} \hspace {2cm} [2.21] \)

y serán consideradas iguales también todas las medias comprendidas entre ellas. En la expresión ([2.21]), el valor de  \( R_{p} \) es

\(  R_{p}=q_{α_{p};p,N-I} \displaystyle \sqrt { \displaystyle \frac { \widehat {S}_{R}^{2}} {n} } \hspace {2cm} p=2,3,⋯,I  \hspace {2cm} [2.22] \)

donde

• \(  q_{α_{p};p,N-I} \) es el punto crítico del rango estudentizado basado en la comparación de la media mayor y la menor de \( p \) medias. Los valores críticos \( q_{α_{p};p,ν} \), para \( p=2,3, \cdots ,I \), se presentan en la Tabla de valores críticos de rangos múltiple de Duncan para los niveles de significación de comparaciones individuales \( α=0.01 \) y \( α=0.05 \)
• \( \widehat {S}_{R}^{2} \) es la varianza residual con \( N-I \) grados de libertad
• \( α_{p} \) es el nivel de significación conjunto relativo a \( p \) medias consecutivas; es decir, es la probabilidad de rechazar erróneamente al menos una de las \( p-1 \) comparaciones independientes asociadas a las medias consideradas. Dicho nivel de significación está relacionado con el nivel de significación \( α \), de una comparación individual, a través de la ecuación

\( α_{p}=1-(1-α)^{p-1} \hspace {2cm} [2.23] \)

Para la aplicación del test de rango múltiple de Duncan, una vez que las medias estén en orden ascendente, se calculan las diferencias entre las medias, comenzando por el valor más pequeño frente al más alto de las \( p=I \) medias de los tratamientos, comparando esta diferencia con el valor \( R_{I} \) en la ecuación ([2.22]) con un nivel de significación \( α_{I} \). Si esas dos medias no se consideran significativamente diferentes, entonces el contraste se termina y se concluye que ninguna de las medias son significativamente diferentes entre sí al nivel de significación \( α_{I} \). Esto es equivalente a no rechazar \( H_0:μ_1=μ_2= \cdots =μ_{I} \). Si las dos medias extremas son significativamente diferentes, el contraste continúa.

En el siguiente paso se calcula la diferencia entre el valor más pequeño y el segundo valor más grande y esta diferencia se compara con \( R_{I-1}\). Si este contraste no es estadísticamente significativo, la prueba cesa en esta comparación y sólo las dos medias extremas se consideran significativamente diferentes. Si este contraste es estadísticamente significativo, la prueba continúa hasta encontrar la primera pareja de medias que no sea significativamente distinta. A continuación, se calcula la diferencia entre la segunda media más pequeña y la más grande y se compara con \( R_{I-1} \). Este proceso continúa hasta que se han considerado las diferencias entre todas las \( I(I-1)/2 \) posibles parejas.

Para modelos no-equilibrados, la expresión de \( R_{p} \) es

\(  R_{p}=q_{α_{p};p,N-I} \displaystyle \sqrt { \displaystyle \frac { \widehat {S}_{R}^{2}} {n_{h}} } \hspace {2cm} p=2,3,\cdots ,I \hspace {2cm} [2.24] \)

donde \( n_{h} \) es la media armónica dada por la expresión ([2.20]).

Comentario

La probabilidad de rechazar erróneamente al menos una hipótesis nula es decir, la probabilidad de detectar incorrectamente como significativa la diferencia entre dos medias de un grupo de tamaño p, es el nivel de significación conjunto \( α_{p} \) relacionado con el nivel de significación \( α \) por medio de la expresión ([2.23]).

Por ejemplo, si \( α=0.05 \), entonces

• Si comparamos parejas de medias adyacentes, el nivel de significación conjunto es

\( α_2=1-(1-0.05)^{2-1}=0.05 \)

que lógicamente coincide con el nivel de significación \( α \).

• Si comparamos parejas de medias separadas por una media, el nivel de significación conjunto es

\( α_3=1-(1-0.05)^{3-1}=0.10 \)

• Si comparamos parejas de medias separadas por dos medias, el nivel de significación conjunto es

\( α_4=1-(1-0.05)^{4-1}=0.142 \)

Observamos que al aumentar \( p \), aumenta el nivel de significación conjunto.

Para ilustrar la prueba de intervalos múltiples de Duncan consideramos el ejemplo de referencia. Recuérdese que \(  \widehat {S}_{R}^{2}=4.67 \) con 21 grados de libertad. Ordenando las medias de los tratamientos en orden ascendente, se tiene

\( \overline {y}_{5.}=45 \hspace {2cm}   \overline {y}_{4.}=47  \hspace {2cm}  \overline {y}_{3.}=48    \hspace {2cm} \overline {y}_{1.}=50  \hspace {2cm}  \overline {y}_{2.}=57 \)

Utilizando la Tabla de amplitudes significativas https://wpd.ugr.es/~bioestad/wp-content/uploads/Tabla-VII.pdf de Duncan, para 21 grados de libertad y α=0.05, se obtienen los puntos críticos del rango estudentizado:

  \(  q_2=q(0.05;2,21)=2.94    \hspace {2cm}  q_3=q(0.05;3,21)=3.09 \)
\( q_4=q(0.05;4,21)=3.17   \hspace {2cm}   q_5=q(0.05;5,21)=3.24  \)

Al hacer las comparaciones se obtiene:

5 vs 2

\(  q_5  \displaystyle \sqrt {2.33 \left ( \displaystyle \frac {1}{6} + \displaystyle \frac {1} {5} \right) }  = 2.994,  \hspace{.4cm}  \left | \overline {y}_{5.}- \overline {y}_{2.} \right |    =12    >2.994 \hspace{.4cm}(*) \)

5 vs 1

\(  q_4  \displaystyle \sqrt {2.33 \left ( \displaystyle \frac {1}{6} + \displaystyle \frac {1} {6} \right) }  = 2.793,  \hspace{.4cm}  \left | \overline {y}_{5.}- \overline {y}_{1.} \right |    =5    >2.793 \hspace{.4cm}(*)  \)

5 vs 3

\(  q_3  \displaystyle \sqrt { 2.33 \left ( \displaystyle \frac {1}{6} + \displaystyle \frac {1} {5} \right) }  = 2.856,  \hspace{.4cm}  \left | \overline {y}_{5.}- \overline {y}_{3.} \right |    =3    >2.856 \hspace{.4cm}(*)  \)

5 vs 4

\(  q_2 \displaystyle \sqrt {2.33 \left ( \displaystyle \frac {1}{6} + \displaystyle \frac {1} {4} \right) }  = 2.896,  \hspace{.4cm}  \left | \overline {y}_{5.}- \overline {y}_{4.} \right |    = 2    <2.896 \)

4 vs 2

\(  q_4  \displaystyle \sqrt { 2.33 \left ( \displaystyle \frac {1}{4} + \displaystyle \frac {1} {5} \right) }  = 3.245,  \hspace{.4cm}  \left | \overline {y}_{4.}- \overline {y}_{2.} \right |    = 10    >3.245 \hspace{.4cm}(*)  \)

4 vs 1

\(  q_3 \displaystyle \sqrt { 2.33 \left ( \displaystyle \frac {1}{4} + \displaystyle \frac {1} {6} \right) }  = 3.044,  \hspace{.4cm}  \left | \overline {y}_{4.}- \overline {y}_{1.} \right |    =  3    <3.044 \)

4 vs 3

\(  q_2 \displaystyle \sqrt {2.33 \left ( \displaystyle \frac {1}{4} + \displaystyle \frac {1} {5} \right) }  = 3.010,  \hspace{.4cm}  \left | \overline {y}_{4.}- \overline {y}_{3.} \right  |      =1    <3.010 \)

3 vs 2

\(  q_3 \displaystyle \sqrt {2.33 \left ( \displaystyle \frac {1}{5} + \displaystyle \frac {1} {5} \right) }  = 2.983,  \hspace{.4cm}  \left | \overline {y}_{3.}- \overline {y}_{2.} \right |    = 9    > 2.983  \hspace{.4cm}(*)  \)

3 vs 1

\(  q_2 \displaystyle \sqrt { 2.33 \left ( \displaystyle \frac {1}{5} + \displaystyle \frac {1} {6} \right) }  = 2.717,  \hspace{.4cm}  \left | \overline {y}_{3.}- \overline {y}_{1.} \right |       = 2    <2.717 \)

donde * denota que la correspondiente diferencia de medias es significativa.

Test de Newman-Keuls

Este contraste fué desarrollado por Newman en 1939 y ampliado por Keuls en 1952, se suele denominar contraste de Newman-Keuls. Al igual que el contraste de Duncan, es un procedimiento iterativo y, desde el punto de vista operacional, es similar a dicho método.

En el procedimiento de Newman-Keuls, los valores con los que se comparan las sucesivas diferencias de medias vienen dados por

 \(  K_{p}=q_{α;p,N-I} \displaystyle \sqrt { \displaystyle \frac { \widehat {S}_{R}^{2}} {n_{h}}} \hspace {2cm} p=2,3, \cdots,I  \hspace {2cm} [2.25] \)

donde

∗  \( q_{α;p,N-I}  \) es el punto crítico del rango estudentizado, definido en ([2.13]). En la Tabla: Percentiles del rango estudentizado se recogen los valores críticos de dicha distribución

∗ \( \widehat {S}_{R}^{2} \) es la varianza residual con \( N-I \) grados de libertad

∗ \( n_{h} \) es la media armónica, dada en la ecuación ([2.20]), que se utiliza cuando los tamaños de las muestras son desiguales. En el caso del modelo equilibrado el valor de la media armónica \( n_{h} \) coincide con el tamaño \( n \) de las muestras.

En este método las medias más extremas de un grupo de \( p \) medias, incluidas ambas, se comparan con \( K_{p} \) exactamente de la misma forma que en la prueba de intervalos múltiples de Duncan.

Comentarios

C1) El contraste de Newman-Keuls es más conservador que el de Duncan en el sentido de que el error de tipo I es menor

C2) En el contraste de Newman-Keuls el nivel de significación es α, en cambio en el contraste de Duncan es \( α_{p} \), cuyo valor cambia dependiendo del número de medias comprendidas entre las que se comparan. Por lo tanto, la potencia de la prueba de Newman-Keuls es menor que la del procedimiento de Duncan porque generalmente \( α \) es menor que \( α_{p} \). Podemos comparar los valores de las Tablas Percentiles del rango estudentizado y de rangos múltiple de Duncan para comprobar que el procedimiento de Newman-Keuls conduce a una prueba menos eficaz que la de los intervalos múltiples de Duncan. Se observa que para \( p>2 \), siempre

\( q_{α;p,N-I}>q_{α_{p};p,N-I}  \hspace {2cm} [2.26] \)

Así, por ejemplo, considerando los grados de libertad correspondientes al ejemplo de referencia y tomando 0.05 como nivel de significación α, tenemos la siguiente tabla

\(  \begin{array}{| c| c|c|c|c|} \hline p   & 2  &  3  &  4 &   5 \\ \hline
q_{α_{p};p,ν} &   2.94  &  3.09  &  3.17 &   3.24 \\ \hline
q_{α;p,ν}  &  2.94  &  3.57  &  3.94  &   4.22 \\ \hline   \end{array}  \)

donde se comprueba que, efectivamente, para p>2 se verifica la desigualdad dada en ([2.26]).

En otras palabras, es “más difícil” declarar que dos medias son significativamente diferentes al utilizar la prueba de Newman-Keuls que cuando se usa el procedimiento de Duncan.

Para ilustrar este procedimiento se utiliza el ejemplo de referencia y se comprueba que los resultados coinciden con los obtenidos por los métodos de Bonferroni y Tukey.

Hasta ahora hemos tratado únicamente comparaciones por parejas de niveles de un factor; es decir, hemos considerado hipótesis del tipo

\(  \begin{array}{ ll}  \\     H_0  \equiv &   μ_{j}=μ_{k} \\ H_1 \equiv &    μ_{j} \neq μ_{k} \\ \end{array}   \)

De forma equivalente, estas hipótesis se pueden reescribir como

\(  \begin{array}{ ll}  \\     H_0  \equiv &   μ_{j} – μ_{k} = 0 \\ H_1 \equiv &    μ_{j} – μ_{k} \neq 0  \\ \end{array}   \)

que son casos particulares de hipótesis de la forma

\(  \begin{array}{ ll}  \\     H_0  \equiv &   \displaystyle \sum_{i=1}^{I}a_{i}μ_{i}=0 \\
H_1 \equiv &  \displaystyle  \sum_{i=1}^{I}a_{i}μ_{i} \neq 0 \\ \end{array}   \)

donde todos los \( a_{i} \) son nulos excepto \(  a_{j}=1 \) y  \( a_{k}=-1 \). Además, se verifica la propiedad de que \( \sum_{i}a_{i}=0 \). Todo esto nos da pie a introducir el concepto de contraste.

Contrastes

Se denomina contraste a toda combinación lineal \(  C  \), de los parámetros del modelo de análisis de la varianza, de la forma

\(  C=a_1μ_1+a_2μ_2+ \cdots +a_{I}μ_{I}=\displaystyle  \sum_{i=1}^{I}a_{i}μ_{i}  \hspace {2cm} [2.27] \)

tal que los coeficientes verifiquen

\(  \displaystyle  \sum_{i=1}^{I}a_{i}=0 \hspace {2cm} [2.28] \)

Ejemplo de contrastes distintos a las comparaciones por parejas son, entre otros,

\( μ_1- \displaystyle  \frac {μ_2+μ_3} {2}  \hspace {2cm} [2.29] \)

\( μ_1+μ_4-(μ_2+μ_3)  \hspace {2cm} [2.30] \)

∗ Si se acepta que el primer contraste es cero se afirma que la media del nivel 1 del factor es igual al promedio de las medias de los niveles 2 y 3

∗ Si se acepta que el segundo contraste es cero se afirma que las medias de los niveles 1 y 4, consideradas en grupo, son iguales a las medias de los niveles 2 y 3, también consideradas en grupo.

La combinación lineal de la forma ([2.27]) también se puede expresar en función de los efectos del factor

\( C= \displaystyle  \sum_{i=1}^{I}a_{i}μ_{i}= \displaystyle  \sum_{i=1}^{I}a_{i}(μ+τ_{i})=μ \displaystyle  \sum_{i=1}^{I}a_{i}+ \displaystyle  \sum_{i=1}^{I}a_{i}τ_{i}= \displaystyle  \sum_{i=1}^{I}a_{i}τ_{i} \hspace {2cm} [2.31] \)

ya que \( \displaystyle  \sum_{i=1}^{I}a_{i}=0 \).

Dado que un contraste es una función de los parámetros del modelo, que son desconocidos, su valor se podrá estimar utilizando los estimadores de los parámetros que intervienen. Concretamente, se puede demostrar que el estimador óptimo de un contraste viene dado por la misma combinación lineal de los estimadores de los parámetros que intervienen; es decir

\(  \widehat {C}= \displaystyle  \sum_{i=1}^{I}a_{i}\widehat {μ}_{i}= \displaystyle  \sum_{i=1}^{I}a_{i} \overline {y}_{i.} \)

que también se puede escribir como la misma combinación lineal de los estimadores de los \( τ_{i}\); es decir,

\(  \widehat {C} =\displaystyle  \sum_{i=1}^{I}a_{i} \widehat {τ}_{i} \hspace {2cm} [2.32] \)

En efecto

\(  \widehat {C}=\displaystyle  \sum_{i=1}^{I}a_{i} \widehat {μ}_{i}=\displaystyle  \sum_{i=1}^{I}a_{i}(\widehat {μ}_{i}- \widehat {μ}+ \widehat {μ})= \displaystyle  \sum_{i=1}^{I}a_{i}(\widehat {μ}_{i}-\widehat {μ})+\displaystyle  \sum_{i=1}^{I}a_{i} \widehat {μ}= \displaystyle  \sum_{i=1}^{I}a_{i} \widehat {τ}_{i} \hspace {2cm} [2.33] \)

Si consideramos el contraste ([2.29]), la combinación líneal \(  \overline {y}_{1.}-(\overline {y}_{2.}+ \overline {y}_{3.})/2 \), es el estimador de ese contraste. Para evitar coeficientes fraccionarios es común reescribir esa combinación como

\(  2 \overline {y}_{1.}-(\overline {y}_{2.}+ \overline {y}_{3.})  \hspace {2cm} [2.34] \)

De la misma forma, un estimador del contraste dado en ([2.30]) es

\(  (\overline {y}_{1.}+ \overline {y}_{4.})-(\overline {y}_{2.}+ \overline {y}_{3.}) \hspace {2cm} [2.35] \)

Como disponemos de un estimador para cada contraste y conocemos la distribución en el muestreo de los estimadores de los parámetros del modelo, podemos conocer también la distribución del estimador de un contraste y realizar inferencia estadística sobre el mismo. Para ello, vamos a mostrar algunas propiedades de dichos estimadores.

Propiedades de los estimadores de los contrastes

\( 1^{a})  \)  \( \widehat {C} \) es un estimador insesgado de \( C \). En efecto

\(  E \{ \widehat {C}\}=E \left [ \displaystyle  \sum_{i=1}^{I}a_{i} \widehat {μ}_{i} \right ]=E \left [ \displaystyle  \sum_{i=1}^{I}a_{i} \overline {y}_{i.} \right ]= \displaystyle  \sum_{i=1}^{I}a_{i}E[ \overline {y}_{i.}]= \displaystyle  \sum_{i=1}^{I}a_{i}μ_{i} \hspace {2cm} [2.36] \)

puesto que \(  \overline {y}_{i.} \) son variables aleatorias con media \( μ_{i}\).

\( 2^{a}) \)  La varianza de \( \widehat {C} \) es \( σ^{2} \sum_{i} \displaystyle \frac {a_{i}^{2}} {n_{i}} \). En efecto

\( σ^{2} \{ \widehat {C} \}=Var \left [ \displaystyle \sum_{i=1}^{I}a_{i} \overline {y}_{i.}\right ]= \displaystyle \sum_{i=1}^{I}a_{i}^{2}Var [ \overline {y}_{i.}]= \displaystyle \sum_{i=1}^{I}a_{i}^{2} \displaystyle \frac {σ^{2}} {n_{i}}=σ^{2} \displaystyle \sum_{i=1}^{I} \displaystyle \frac {a_{i}^{2}} {n_{i}}  \hspace {2cm} [2.37] \)

puesto que \( \overline {y}_{i.} \) son variables aleatorias independientes con varianza \( σ^{2}/n_{i} \).

Por tanto, un estimador de la varianza de \( \widehat {C} \) es

\( S^{2} \{ \widehat {C} \}= \widehat {S}_{R}^{2} \displaystyle \sum_{i=1}^{I} \displaystyle \frac {a_{i}^{2}} {n_{i}}  \hspace {2cm} [2.38] \)

donde \( \widehat {S}_{R}^{2} \), es la varianza residual.

\( 3^{a}) \) \( \widehat {C} \) se distribuye según una Normal al ser una combinación lineal de variables aleatorias Normales independientes. Además, por las propiedades  \( 1^{a} \) y \( 2^{a}\), su media es \( C \) y su desviación típica es \( σ  \{ \widehat {C} \} \). En otras palabras,

\( \widehat {C} \rightarrow N(C,σ  \{ \widehat {C} \}) \)

Por tanto, al considerar la estimación de \( σ  \{\widehat {C} \} \) en función de \( \widehat {S}_{R}^{2} \), se verifica que el cociente

\(  \displaystyle \frac {\widehat {C}-C } {S \{\widehat {C} \}} \rightarrow  t_{N-I}  \hspace {2cm} [2.39] \)

Consecuentemente, podemos efectuar la estimación por intervalos de un contraste \( C \) al nivel de confianza \(1-α \), que vienen dados por la expresión

\( \widehat {C} \pm t_{α/2;N-I}S \{\widehat {C}\}  \hspace {2cm} [2.40] \)

En el ejemplo de referencia y considerando el contraste dado en ([2.29]),

\( C=2μ_1-(μ_2+μ_3) \)

se tiene que:

\( 1^{a}) \) La estimación puntual de \( C \) es

\( \widehat {C} =2 \overline {y}_{1.}-( \overline {y}_{2.}+ \overline {y}_{3.})=2(50)-(57+48)=-5 \)

\( 2^{a}) \) La estimación de la varianza muestral de \( \widehat {C} \) es

\( S^{2} \{ \widehat {C}\}= \widehat {S}_{R}^{2} \displaystyle  \sum_{i=1}^{I} \displaystyle  \frac {a_{i}^{2}} {n_{i}}=4.67(1.067)=4.982 \)

donde \( a_1=2, a_2=a_3=-1 \) y

\( \displaystyle  \sum_{i=1}^{I} \displaystyle  \frac {a_{i}^{2}} {n_{i}}= \displaystyle  \frac {4} {6}+ \displaystyle  \frac {1} {5}+ \displaystyle  \frac {1} {5}= \displaystyle  \frac {16} {15}=1.067 \)

Los límites de confianza para \( C  \), al nivel confianza del 95%, son

\( \widehat {C}\pm t_{α/2;N-I} \displaystyle \sqrt {S^{2}\{\widehat {C}} \}=-5 \pm 2.08(2.23)=-5 \pm 4.63 \)

por lo tanto el intervalo de confianza correspondiente es \( (-9.67-0.37) \).

En los procedimientos de comparaciones múltiples de los efectos del factor interesa manejar únicamente contrastes independientes. Dicha independencia se garantiza al considerar la ortogonalidad entre contrastes, que pasamos a definir a continuación.

Contrastes ortogonales

Decimos que dos contrastes \( C_1= \displaystyle \sum_{i}a_{i} \overline {y}_{i.} \) y \( C_2= \displaystyle \sum_{i}b_{i} \overline {y}_{i.} \) son ortogonales si verifican que

\( \displaystyle \sum_{i=1}^{I}a_{i}b_{i}=0 \hspace {2cm} [2.41] \)

Nota: Aunque \( \widehat {C}= \displaystyle \sum_{i}a_{i} \overline {y}_{i.} \) es un estimador del contraste \( C= \displaystyle \sum_{i}a_{i}μ_{i} \), nos referiremos a él como contraste y lo denotaremos por \( C \).

De la misma forma, se dice que tres o más contrastes son mutuamente ortogonales si todas las posibles parejas de contrastes son ortogonales.

Los coeficientes de contrates ortogonales se pueden elegir de muchas formas para un conjunto dado de tratamientos. Generalmente la naturaleza del experimento sugiere las comparaciones que pueden ser más interesantes.

Para ilustrar los contrastes ortogonales, consideremos el ejemplo de referencia y recordemos que los tamaños de muestras correspondientes a cada uno de los 5 tipos de fertilizantes son: 6, 5, 5, 4, y 6. Supongamos que los contrastes más apropiados son:

\( 1) \) \( C_1=μ_1-μ_3 \)

\( 2) \) \( C_2=-μ_1-μ_3+μ_4+μ_5 \)

\( 3) \) \( C_3=μ_4-μ_5 \)

\( 4) \) \( C_4=-μ_1+4μ_2-μ_3-μ_4-μ_5 \)

Los coeficientes en estas comparaciones expresadas en forma tabular serían

\(  \begin{array}{| c| c  |} \hline  &  Respuesta \hspace {.2cm} media \hspace {.2cm} del \hspace {.2cm} nivel \hspace {.2cm} del \hspace {.2cm} factor     \\ \hline Contraste    &  μ_1 \hspace {1cm}   μ_2 \hspace {1cm}   μ_3  \hspace {1cm} μ_4 \hspace {1cm}   μ_5 \\ \hline  C_1   & \hspace {.95 cm}  1   \hspace {1.3 cm}   0   \hspace {.98 cm}   -1   \hspace {1.3 cm}   0   \hspace {1.3 cm}   0 \\ \hline  C_2  &   \hspace {.94 cm} – 1   \hspace {1.2 cm} 0   \hspace {1.2 cm}   -1  \hspace {1.1 cm}   1  \hspace {1.1 cm}   1 \\ \hline
C_3   &   \hspace {.97 cm} 0  \hspace {1.4 cm}   0   \hspace {1.4 cm}   0  \hspace {1.5 cm}   1  \hspace {.94 cm}   -1 \\ \hline  C_4   &  \hspace {.95 cm} -1   \hspace {1cm}   4   \hspace {.96 cm}   -1  \hspace {.90 cm}    -1  \hspace {.90 cm}   -1 \\ \hline   \end{array}   \)

Tabla 2-1

Obsérvese que la suma de los coeficientes de cada fila es cero indicando que cada \( C_{i} \) es un contraste. Además, es inmediato comprobar que los productos dos a dos de los coeficientes de los contrastes suman cero indicando que los contrastes son mutuamente ortogonales. En efecto, comprobemos, por ejemplo, que los contrastes \( C_1 \) y \( C_2 \) son ortogonales

\( (1)(-1)+(0)(0)+(-1)(-1)+(0)(1)+(0)(1) = 0  \)

Veamos a continuación las expresiones para las sumas de cuadrados asociadas a un contraste cualquiera, tanto en el caso equilibrado como en el caso no-equilibrado.

En el diseño no-equilibrado se puede demostrar que al contraste \( C=∑_{i}a_{i}μ_{i} \) se le puede asociar una suma de cuadrados dada por

\( SSC= \displaystyle \frac { \left ( \displaystyle \sum_{i = 1}^{I}a_{i} \overline {y}_{i.} \right )^{2}} { \displaystyle \sum_{i=1}^{I} \displaystyle \frac {a_{i}^{2}} {n_{i}}}  \hspace {2cm} [2.42] \)

y por lo tanto, la expresión de la suma de cuadrados en el modelo equilibrado es

\( SSC= \displaystyle \frac {n \left ( \displaystyle \sum_{i=1}^{I} a_{i}y_{i.} \right )^{2}} { \displaystyle \sum_{i=1}^{I}a_{i}^{2}} \hspace {2cm} [2.43] \)

teniendo estas sumas de cuadrados un grado de libertad.

Por tanto, para comprobar las hipótesis del contraste

\(  \begin{array}{c c } \\
H_0 \equiv  &  \displaystyle \sum_{i=1}^{I}a_{i}μ_{i}=0 \\ H_1 \equiv  &  \displaystyle  \sum_{i=1}^{I}a_{i}μ_{i} \neq 0  \\ \end{array}    \hspace {2cm} [2.44] \)

basta comparar la suma de cuadrados asociada al contraste con el cuadrado medio del error. Entonces, el cociente \( SSC/ \widehat {S}_{R}^{2} \) es el estadístico de contraste que, bajo la hipótesis nula, sigue una distribución \( F_{1,N-I}\).

A continuación vamos a realizar las sumas de cuadrados asociadas a los contrastes para el ejemplo de referencia. Supongamos que efectuamos los contrastes ortogonales expuestos en la Tabla 2-1. Dichos contrastes junto con sus estimaciones puntuales y su suma de cuadrados asociada se muestran en la siguiente tabla

\(  \begin{array}{| l| l| l  |} \hline Hipótesis &   Estimaciones &    S. \hspace {.2cm} Cuadrados \\ \hline
H_0 \equiv μ_1=μ_3 &     C_1=2   &  SSC_1=10.89 \\ \hline
H_0 \equiv μ_1+μ_3=μ_4+μ_5 &    C_2=-6   &  SSC_2 = 45.97 \\ \hline
H_0 \equiv μ_4=μ_5 &    C_3=2  &  SSC_3=9.61 \\ \hline
H_0 \equiv 4μ_2=μ_1+μ_3+μ_4+μ_4  &    C_4=38   &  SSC_4 =362.35 \\ \hline   \end{array}   \)

Tabla 2-2

Donde

\(  C_1=(1)(  \overline {y}_{1.})+(-1)( \overline {y}_{3.})=50-48=2 \)

\(  C_2=(-1)( \overline {y}_{1.}+ \overline {y}_{3.})+(1)( \overline {y}_{4.}+ \overline {y}_{5.})=-(50+48)+(47+45)=-6 \)

\( C_3=(1)(\overline {y}_{4.})+(-1)( \overline {y}_{5.})=47-45=2 \)

\( C_4=(-1)( \overline {y}_{1.}+ \overline {y}_{3.}+ \overline {y}_{4.}+ \overline {y}_{5.})+4(1) \overline {y}_{2.}=-50-48-47-45+4(57)=38 \)

\(  SSC_1 = \displaystyle \frac {(2)^{2}} { \displaystyle \frac {(1)^{2}} {6} + \displaystyle {(-1)^{2} }{5}}=10.89 \)

\( SSC_2= \displaystyle \frac{(-6)^{2}} {(-1)^{2} \left ( \displaystyle \frac {1} {6}+ \displaystyle \frac {1} {5} \right )+(1)^{2} \left ( \displaystyle \frac {1} {4}+ \displaystyle \frac {1} {6} \right ) }=45.97 \)

\( SSC_3=  \displaystyle  \frac {(2)^{2}} { \displaystyle \frac{(1)^{2}} {4}+ \displaystyle  \frac {(-1)^{2}} {6} }=9.61 \)

\( SSC_4= \displaystyle  \frac {(38)^{2}} {(-1)^{2} \left ( \displaystyle  \frac {1} {6}+ \displaystyle \frac {1} {5}+ \displaystyle  \frac {1} {4}+ \displaystyle  \frac {1}  {6} \right)+ \displaystyle \frac {(4)^{2}} {5} }=362.35 \)

Teniendo en cuenta que el valor de la varianza residual es 4.67, con 21 grados de libertad, obtenemos los siguientes valores para los estadísticos de contraste \( F(C_1) \) , \( F(C_2) \), \( F(C_3) \) y \( F(C_4) \),

\( F(C_1)_{(exp)}=   \displaystyle  \frac {SSC_1} {\widehat {S}_{R}^{2}}= \displaystyle  \frac  {10.89 } {4.67}=2.33 \)

\( F(C_2)_{(exp)}=    \displaystyle  \frac {SSC_2 } {\widehat {S}_{R}^{2}}= \displaystyle  \frac {45.97} {4.67}=9.84 \)

\( F(C_3)_{(exp)}=    \displaystyle  \frac {SSC_3} {\widehat {S}_{R}^{2}}= \displaystyle  \frac {9.61 } {4.67}=2.05 \)

\( F(C_4)_{(exp)}=   \displaystyle  \frac {SSC_4} { \widehat {S}_{R}^{2}}=\displaystyle  \frac {362.35} {4.67}=77.59 \)

Si realizamos el contraste al nivel de significación del 5% y puesto que \( F_{0.05;1,21}=4.32 \), se concluye que \( μ_1=μ_3 \hspace{.2cm}, \hspace{.2cm} μ_4=μ_5 \) y en los otros dos contrastes se rechaza la hipótesis nula.

Generalmente las sumas de cuadrados de los contrastes y las pruebas correspondientes se incorporan a la Tabla ANOVA, de la siguiente forma:

\(  \begin{array}{| l| l| l  |l|l|l|} \hline
F. V.  &  S.C. &   G.L.  &  M. C.  &  F_{exp}  &  F_{α} \\ \hline
Entre \hspace {.2cm}  grupos &   439.88   &  4  &  109.97  &  23.56  &  2.84  \\ \hline
\hspace {1cm} C_1:μ_1=μ_3  &  10.89  &  1  &  10.89  &  2.33  &  4.32  \\ \hline  \hspace {1cm} C_2:μ_1+μ_3=μ_4+μ_5 &   45.97  &  1 &   45.97  &  9.84  &  4.32 \\ \hline  \hspace {1cm} C_3:μ_4=μ_5 &    9.61 &   1  &  9.61  &  2.05  &  4.32 \\ \hline  \hspace {1cm} C_4:4μ_2=μ_1+μ_3+μ_4+μ_5  &    362.35  &  1  &  362.35  &  77.59  &  4.32 \\ \hline
Interna  &  98.00 &   21  &  4.67 & & \\ \hline  TOTAL &   537.88 &   25 & & & \\ \hline   \end{array}   \)

Tabla 2-3

Comentarios sobre el nivel de significación

Cuando se realizan comparaciones múltiples una cuestión importante es la elección del nivel de significación de los tests o el nivel de confianza para la estimación por intervalos. Puesto que varios tests o varias estimaciones por intervalos se hacen sobre el mismo conjunto de datos, es necesario distinguir entre dos probabilidades de error. Describimos esas tasas de error de Tipo I para contrastes de hipótesis, pero igualmente se haría para intervalos de confianza.

– Tasa de error individual o para una pareja, \( α \), es la probabilidad de rechazar erróneamente la hipótesis nula de una única comparación entre una pareja de efectos o medias. Esencialmente indica el nivel de significación asociado a un solo test estadístico de la forma,

\(  \begin{array}{ll} H_0 \equiv &   μ_{i}=μ_{j} \\  H_1 \equiv  & μ_{i} \neq μ_{j} \\    \end{array}   \hspace {2cm} [2.45] \)

– Tasa de error global o del experimento, \( α^{∗} \), es la probabilidad de rechazar erróneamente por lo menos una hipótesis nula al realizar las \( I-1 \) comparaciones independientes relativas a \( I \) medias sobre el mismo conjunto de datos. Esta tasa de error puede ser mucho mayor que la tasa de error individual.

Ambas tasas de error están relacionadas por las siguientes expresiones

\( α^{*}=1-(1-α)^{I-1}  \hspace {2cm} [2.46] \)

\( α=1-(1-α^{*})^{1/(I-1)}  \hspace {2cm} [2.47] \)

Estas fórmulas no son estrictamente válidas cuando hay implicados contrastes no-ortogonales. En estas situaciones, sin embargo, pueden utilizarse dichas ecuaciones obteniéndose resultados aproximados. En tales casos, la tasa global puede ser mayor que la indicada por la ecuación ([2.46]).

Para la ilustración numérica, tomemos como nivel de significación individual 0.05 y como valor de \( I \), 5. Si las 5 medias poblacionales son iguales, la probabilidad de rechazar incorrectamente una o más de las 4 comparaciones ortogonales es \( α^{*}=1-(1-0.05)^{4}=0.1854 \). Es decir, la tasa de error global es casi 4 veces mayor que la tasa individual. Por otra parte, si tomamos \( α^{*} \) igual a 0.05, entonces \( α=1-(1-0.05)^{0.25}=0.01274 \). Observamos que una tasa de error del experimento igual a 0.05 es mucho más exigente que una tasa de error individual de 0.05.

Aunque el experimentador se interesa en controlar todas las tasas de error y niveles de confianza, es importante subrayar que el objetivo principal de los procedimientos de comparaciones múltiples es informarse lo más posible sobre las poblaciones, procesos o fenómenos que intervienen en el experimento. Fijar unas tasas de error pequeñas no es el único propósito de un experimento, es sólamente una medida del grado de exigencia o rigor de la metodología estadística empleada.

En muchos experimentos el investigador no sabe a priori los contrastes que le interesa realizar, siendo después de un análisis preliminar de los datos cuando se descubren las comparaciones de interés.

Método de Scheffé para comparaciones múltiples

Scheffé (1953) propuso un método para realizar cualquier contraste entre medias de tratamientos. Dicho procedimiento no requiere que el modelo sea equilibrado.

Sea una familia de contrastes de la forma

\( C= \displaystyle \sum_{i}a_{i}μ_{i}  \hspace {2cm} [2.48] \)

el objetivo de este procedimiento es decidir, para cada uno de estos contrastes, entre las hipótesis

\(  \begin{array}{ll} H_0 \equiv &   C = 0 \\  H_1 \equiv  & C \neq 0 \\    \end{array}   \hspace {2cm} [2.49] \)

El método de Scheffé está basado en la construcción de intervalos de confianza para todos los posibles contrastes de la forma ([2.49]). Estos intervalos tienen un nivel de confianza simultáneo \( 1-α \), es decir, la probabilidad de que todos los intervalos sean correctos simultáneamente es igual a \( 1-α \). Scheffé demostró que dichos intervalos de confianza tienen la siguiente expresión

\( \widehat {C}  \pm S \{ \widehat {C}\}\sqrt {(I-1)F_{α;I-1,N-I}}  \hspace {2cm} [2.50] \)

donde las cantidades que intervienen son:

∙  \( \widehat {C}  \) es el estimador insesgado de \( C \)

∙  \( S \{ \widehat {C} \} \) es el estimador de la desviación típica del contraste

\( S \{ \widehat {C}\} = \displaystyle  \sqrt { \widehat {S}_{R}^{2} \displaystyle  \sum_{i=1}^{I} \displaystyle  \frac {a_{i}^{2}} {n_{i}} } \hspace {2cm} [2.51] \)

siendo \(  \widehat {S}_{R}^{2} \) la varianza residual con \(  N-I \) grados de libertad.

Por consiguiente, se rechaza la hipótesis \( H_0 \) sobre un contraste \( C \) si el intervalo de confianza para \(  C \)

\(  \widehat  {C} -S \{ \widehat {C} \}\sqrt { (I-1)F_{α;I-1,N-I} } \hspace {.2cm}, \hspace {.2cm} \widehat {C}+S \{ \widehat {C} \} \sqrt { (I-1)F_{α;I-1,N-I} }  \hspace {2cm} [2.52] \)

no incluye al cero, es decir, si

\(  \left | \widehat {C} \right |>S \{ \widehat {C} \} \sqrt {(I-1)F_{α;I-1,N-I}}  \hspace {2cm} [2.53] \)

Para ilustrar el procedimiento, consideramos el ejemplo de referencia y suponemos que los contrastes de interés son

\( C_2=μ_1+μ_3-μ_4-μ_5 \)

y

\( C_3=μ_4-μ_5 \)

Las estimaciones numéricas de estos contrastes son

\( \widehat { C_2 }=    \overline { y}_{1.}+ \overline {y}_{3.}- \overline {y}_{4.}- \overline {y}_{5.}=50+48-47-45=6 \)

\( \widehat {C_3}=     \overline {y}_{4.}- \overline {y}_{5.}=47-45=2 \)

y sus errores típicos, determinados usando la ecuación ([2.51]), son

\(  S \{\widehat {C_2} \}= \displaystyle  \sqrt { \widehat {S}_{R}^{2} \displaystyle \sum_{i=1}^{5} \displaystyle  \frac {a_{i}^{2}} {n_{i}}}= \displaystyle  \sqrt {4.67 \left ( \displaystyle  \frac {1} {6}+ \displaystyle  \frac {1} {5}+ \displaystyle  \frac {1}{4}+ \displaystyle  \frac {1}{6} \right ) }=1.912 \)

y

\(  S \{ \widehat {C_3} \}= \displaystyle  \sqrt { \widehat {S}_{R}^{2} \displaystyle \sum_{i=1}^{5} \displaystyle  \frac {a_{i}^{2}} {n_{i}}}= \displaystyle  \sqrt {4.67 \left ( \displaystyle  \frac {1} {4}+ \displaystyle  \frac {1} {6} \right ) }=1.394 \)

Por lo tanto, los intervalos de confianza son, respectivamente

\(  \begin{array}{ll} \\   I_2=  &  \left (\widehat {C_2}-S \{ \widehat {C_2} \} \sqrt {(I-1)F_{0.05;I-1,N-I}} \hspace{.2cm}, \hspace{.2cm} \widehat {C_2}+S \{ \widehat {C_2} \} \sqrt {(I-1)F_{0.05;I-1,N-I}} \right )= \\  & = (6-1.912 \sqrt {4F_{0.05;4,21}} \hspace {.2cm}, \hspace {.2cm} 6+1.912 \sqrt {4F_{0.05;4,21} })=(-0.44,12.44) \\    \end{array}    \)

\(  \begin{array}{ll} \\   I_2=  &  \left (\widehat {C_3}-S \{ \widehat {C_3} \} \sqrt {(I-1)F_{0.05;I-1,N-I}} \hspace{.2cm}, \hspace{.2cm} \widehat {C_3}+S \{ \widehat {C_3} \} \sqrt {(I-1)F_{0.05;I-1,N-I}} \right )= \\  & = (2 -1.394 \sqrt {4F_{0.05;4,21}} \hspace {.2cm}, \hspace {.2cm} 2+1.394 \sqrt {4F_{0.05;4,21} })=(-2.69, 6.69) \\    \end{array}    \)

Puesto que los intervalos \( I_2 \) e \( I_3 \) contienen al 0, se concluye que tanto \( C_2=  μ_1+μ_3-μ_4-μ_5 \), como \( C_3=μ_4-μ_5 \) no son significativamente distintos de cero. En otras palabras, existe evidencia para concluir, por una parte que las medias de los tratamientos uno y tres, tomadas como grupo, no difieren significativamente de las medias de los tratamientos cuatro y cinco, también tomadas como grupo y por otra parte que no existe diferencia significativa entre los tratamientos cuatro y cinco.

Comparaciones entre los métodos

En diversos textos se encuentran comentarios sobre las comparaciones entre los distintos métodos; entre otras referencias, se recomienda consultar Neter at al. (1990) y Mason at al. (1989). A continuación, presentamos aquí un resumen de ambos estudios.

∗ Cuando sólo se hacen comparaciones por parejas, el método de Tukey conduce a límites de confianza más estrechos que el método de Scheffé, por lo cual el método de Tukey encontrará más diferencias significativas, siendo en este caso el método preferido. En cambio cuando los contrastes son más complicados que la diferencia de medias, es el método de Scheffé el que tiene límites de confianza más estrechos.

∗ El método de Bonferroni es preferido al de Scheffé cuando el número de contrastes es igual o menor que el número de niveles del factor.

∗ Cuando el número de comparaciones por parejas es muy grande no se debe utilizar el método de Bonferroni, ya que el nivel de significación de cada comparación puede llegar a ser demasiado pequeño para considerarse de utilidad. En estas situaciones los tests de rangos múltiples como Tukey, Newman-Keuls y Duncan ofrecen una solución de compromiso entre la tasa de error global deseada y una tasa de error individual demasiado pequeña y por tanto inaceptable. Estos métodos son preferidos en el sentido de producir intervalos de confianza más estrechos.

∗ El método LSD de Fisher es el que proporciona más diferencias significativas; a continuación, le siguen los métodos de Duncan y Tukey. Eligiremos uno u otro dependiendo del riesgo que estemos dispuestos a correr al aceptar más o menos diferencias significativas. Es decir, a aceptar como significativas diferencias que no lo sean (situación no conservadora), o a aceptar menos diferencias significativas de las que realmente existan (situación conservadora). Cramer y Swanson (1973), realizaron estudios de simulación por el método de Montecarlo de los que concluyeron que el procedimiento LSD es una prueba muy eficiente para detectar diferencias verdaderas entre las medias si se aplica después que la prueba F del análisis de la varianza resultó significativa al 5 %. También concluyeron que el procedimiento de intervalos múltiples de Duncan es un buen método para detectar diferencias reales.

∗ El procedimiento de Tukey tiene un error tipo I menor que los correspondientes errores de los tests de Newman-Keuls y de Duncan; es decir, es un test más conservador. En consecuencia, el procedimiento de Tukey tiene menos potencia que los procedimientos de Newman-Keuls o de Duncan.

∗ Si se desea controlar la tasa de error individual, los métodos LSD de Fisher y de Duncan resultan apropiados. Facilitan más protección de los errores de Tipo I que los otros métodos y son menos conservadores que los procedimientos basados en la elección de la tasa de global.

∗ Si se desea controlar la tasa de error global, los métodos más útiles incluyen el test de Bonferroni y procedimiento de Tukey. Ambas técnicas tienen fuertes defensores. El test de Bonferroni tiene la ventaja de utilizar un estadístico t, siendo su principal desventaja, cuando se realizan un gran número de comparaciones, que el nivel de significación individual se hace demasiado pequeño.

Existen otros procedimientos para hacer comparaciones múltiples. Algunos de ellos están designados para casos especiales, tales como para comparar tratamientos experimentales con un tratamiento control.

Comparaciones de tratamientos con un Control

Estamos ante el caso de un experimento en el que uno de los tratamientos es un control y el experimentador puede estar interesado en comparar los restantes tratamientos con este control. Por tanto, sólo deben realizarse I-1 comparaciones. Un procedimiento que realiza dichas comparaciones fué desarrollado por Dunnett (1964).

Supongamos que el control es el tratamiento I. Entonces se desean probar las hipótesis

\(  \begin{array}{ll} H_0 \equiv &   μ_{i}=μ_{j} \\  H_1 \equiv  & μ_{i} \neq μ_{j} \\    \end{array}   \hspace {2cm} [2.54] \)

El procedimiento de Dunnett es una modificación de la prueba \( t \). Para cada hipótesis se calculan las diferencias que se observan entre las medias muestrales

\(  \left | \overline {y}_{i.}- \overline {y}_{I.} \right | \hspace{2cm} i=1,2, \cdots , I-1  \)

La pareja de medias \( μ_{i} \) y \( μ_{I} \) se consideran diferentes, a un nivel de significación conjunto \( α \) asociado a las \( I-1\) comparaciones, si

\(  \left | \overline {y}_{i.}- \overline {y}_{I.} \right | >d_{α;I-1,N-I} \displaystyle  \sqrt { \widehat {S}_{R}^{2} \left (  \displaystyle  \frac {1} {n_{i}} + \displaystyle  \frac {1} {n_{I}} \right ) } \hspace {2cm} [2.55] \)

en donde la cantidad \(  d_{α;I-1,N-I} \)  se obtiene a partir de la Tabla: Valores críticos para la prueba de Dunnett.

Para ilustrar la prueba de Dunnett, consideramos el ejemplo de referencia y aunque en el desarrollo teórico hemos dicho que el control es el último tratamiento, la posición que ocupe el control es arbitraria, por ello, en este ejemplo vamos a considerar que es la primera posición, el tratamiento 1. En dicho ejemplo, \( I=5 \),  \( ν=21 \) y para un nivel de significación del 5% el valor de \( d_{0.05;4,21} \) es 2.64. Por tanto, las diferencias críticas y observadas son, respectivamente,

2 vs 1:    \(  d_{0.05;4,21} \displaystyle  \sqrt {4.67 \left ( \displaystyle  \frac {1} {5} + \displaystyle  \frac {1} {6} \right) }=3.454  \hspace{4cm}   \left | \overline {y}_{2.}- \overline {y}_{1.} \right |=    7* \)

3 vs 1:   \(  d_{0.05;4,21} \displaystyle  \sqrt {4.67 \left ( \displaystyle  \frac {1} {5} + \displaystyle  \frac {1} {6} \right) }=3.454  \hspace{4cm}   \left | \overline {y}_{3.}- \overline {y}_{1.} \right |=   2 \)

4 vs 1:   \(  d_{0.05;4,21} \displaystyle  \sqrt {4.67 \left ( \displaystyle  \frac {1} {4} + \displaystyle  \frac {1} {6} \right) }=3.682  \hspace{4cm}   \left | \overline {y}_{4.}- \overline {y}_{1.} \right |=    3 \)

5 vs 1:   \(  d_{0.05;4,21} \displaystyle  \sqrt {4.67 \left ( \displaystyle  \frac {1} {6} + \displaystyle  \frac {1} {6} \right) }=3.293 \hspace{4cm}   \left | \overline {y}_{5.}- \overline {y}_{1.} \right |=    5* \)

Observamos que las parejas de medias 2 vs 1 y 5 vs 1 resultan significativamente diferentes.

Al comparar tratamientos con un control es conveniente tomar más observaciones para el tratamiento de control que para los otros tratamientos. Como norma general, se debe verificar que la razón \( n_{I}/n_{i}\) sea aproximadamente igual a la raíz cuadrada del número total de tratamientos. Es decir,

 \( \displaystyle \frac {n_{I}} {n_{i}} \approx \sqrt {I } \)

Tratamiento mediante ordenador

1. Realizamos los contrastes de comparaciones múltiples con el paquete estadístico R

Al igual que en el tema anterior vamos a concretar toda la explicación sobre un determinado ejemplo. Continuamos con el Ejemplo 1.1

Ejemplo 1.1

Una compañía algodonera, interesada en maximizar el rendimiento de la semilla de algodón, desea comprobar si dicho rendimiento depende del tipo de fertilizante utilizado para tratar la planta. A su disposición tiene 5 tipos de fertilizantes. Para comparar su eficacia fumiga, con cada uno de los fertilizantes, un cierto número de parcelas de terreno de la misma calidad y de igual superficie. Al recoger la cosecha se mide el rendimiento de la semilla, obteniéndose las siguientes observaciones que se muestran en la Tabla 1

\(  \begin{array}{| c| cccccc|} \hline  Fertilizantes & & & Rendimiento &&& \\ \hline     1 &   51 &   49  &  50  &  49  &  51  &  50 \\  2  &  56 &   60  &  56   & 56  &  57 &  \\ 3  &  48 &   50   & 53 &   44  &  45 & \\ 4 &  47  &  48  &  49  &  44 & & \\
5 &  43 &   43  &  46  &  47  &  45  &  46 \\ \hline   \end{array}  \)

Tabla 1. Datos del Ejmplo 1.1

¿El rendimiento de la semilla de algodón depende del tipo de fertilizante utilizado?

Nota: La ruta hasta llegar al fichero varía en función del ordenador. Utilizar la orden setwd() para situarse en el directorio de trabajo

> setwd(“C:/Users/Usuario/Desktop/Datos”)
> datos <- read.table(“Ejemplo1-1.txt”, header = TRUE)
>  datos$Fertilizantes <- factor(datos$Fertilizantes)
> anova <- aov(Observaciones ~ Fertilizantes, data = datos)
> summary(anova)
Df Sum Sq Mean Sq F value   Pr(>F)    
Fertilizantes  1  203.5  203.46    14.6 0.000827 ***
Residuals     24  334.4   13.93                     
—
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Comprobamos que, a un nivel de significación del 5 %, el rendimiento de la semilla de algodón difiere significativamente dependiendo del tipo de fertilizante utilizado. Igualmente ocurriría al nivel de significación del 1%, o incluso a un nivel de significación mucho más pequeño.

Sabemos que globalmente los tratamientos difieren significativamente entre sí. Una vez aceptada la existencia de diferencias entre los efectos del factor, nuestro objetivo es conoce qué tratamientos concretos producen mayor efecto o cuáles son los tratamientos diferentes entre sí.

Comenzamos instalando algunos paquetes que vamos a necesitar para la realización de los contrastes de comparaciones múltiple

# INSTALAR LOS SIGUIENTE PAQUETES

> install.packages(“gplots”)
> install.packages(“agricolae”)
> install.packages(“multcomp”)
> install.packages(“lawstat”)
> library(agricolae)
> library(gplots)
> library(multcomp)
> library(lawstat)

#MOSTRAR MEDIAS

> tapply(datos$Observaciones,datos$Fertilizantes,mean, na.rm=TRUE)
1  2  3  4  5
50 57 48 47 45

# MOSTRAR DESVIACIONES TÍPICA

> tapply(datos$Observaciones,datos$Fertilizantes, sd, na.rm=TRUE)
1         2         3         4         5
0.8944272 1.7320508 3.6742346 2.1602469 1.6733201

# COMPARACIONES GRAFICAS DE MEDIAS

> boxplot(Observaciones ~ Fertilizantes , data = datos)

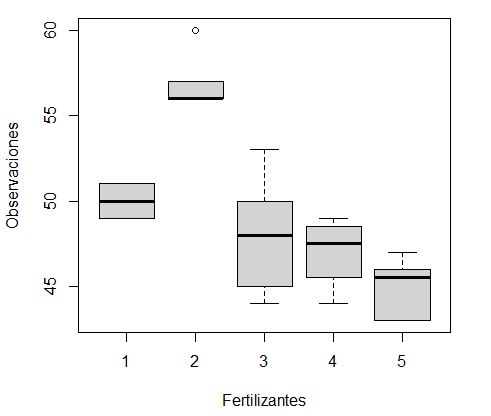
Observamos que las cajas correspondientes a los tratamientos 3 y 4 están prácticamente superpuestas, de hecho el valor mediano del tratamiento 3 (línea negra dentro de las cajas) está a un nivel interno dentro de la caja del tratamiento 4. Este criterio se utiliza para comparar grupos y en este caso nos indica que hay homogeneidad o que no hay diferencias significativas en ese grupo de medias.

Observamos que el tratamiento 2 tiene una distribución superior a los demás, por lo que concluimos que el rendimiento de la semilla de algodón es mucho mayor con el tratamiento 2. Observando el gráfico podemos deducir que el tratamiento 2 difiere significativamente de los demás tratamientos y que el tratamiento 1 difiere significativamente de los tratamientos 4 y 5.

Recordar que los procedimiento de comparaciones gráficas son métodos aproximados.

> plotmeans(Observaciones ~ Fertilizantes , data = datos)

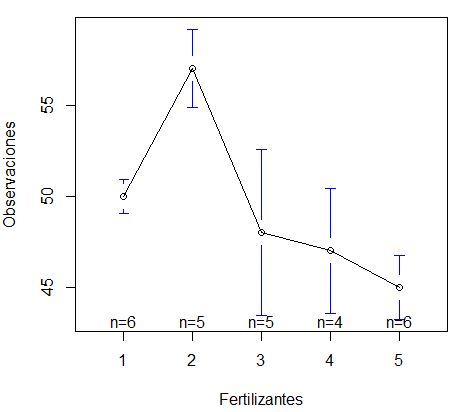
#Tukey

> Tukey <- HSD.test(anova,”Fertilizantes”, group = TRUE)
> Tukey
$statistics
   MSerror Df     Mean       CV
  13.93439 24 49.34615 7.564682
$parameters
   test        name.t ntr StudentizedRange alpha
  Tukey Fertilizantes   5         4.166314  0.05
$means
  Observaciones       std r Min Max   Q25  Q50   Q75
1            50 0.8944272 6  49  51 49.25 50.0 50.75
2            57 1.7320508 5  56  60 56.00 56.0 57.00
3            48 3.6742346 5  44  53 45.00 48.0 50.00
4            47 2.1602469 4  44  49 46.25 47.5 48.25
5            45 1.6733201 6  43  47 43.50 45.5 46.00
$comparison
NULL
$groups
  Observaciones groups
2            57      a
1            50      b
3            48      b
4            47      b
5            45      b
attr(,”class”)

[1] “group”

Esta salida muestra que el tratamiento 2 difiere significativamente de los demás y que no hay diferencias significativas entre los tratamientos 1, 3, 4 y 5

Otra forma de realizar el contraste HSD es utilizando las siguientes instrucciones

> regresion<-lm(Observaciones ~ Fertilizantes , data = datos)
> regresion
Call:
lm(formula = Observaciones ~ Fertilizantes, data = datos)

Coefficients:
   (Intercept)  Fertilizantes2  Fertilizantes3  Fertilizantes4  Fertilizantes5  
            50               7              -2              -3              -5 
> summary(regresion)
Call:
lm(formula = Observaciones ~ Fertilizantes, data = datos)
Residuals:
Min     1Q Median     3Q    Max
-4     -1      0      1      5
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)     50.0000     0.8819  56.695  < 2e-16 ***
Fertilizantes2   7.0000     1.3081   5.351 2.63e-05 ***
Fertilizantes3  -2.0000     1.3081  -1.529 0.141203
Fertilizantes4  -3.0000     1.3944  -2.151 0.043236 *
Fertilizantes5  -5.0000     1.2472  -4.009 0.000636 ***
—
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.16 on 21 degrees of freedom
Multiple R-squared:  0.8178,    Adjusted R-squared:  0.7831
F-statistic: 23.57 on 4 and 21 DF,  p-value: 1.649e-07

> confint(regresion)
2.5 %     97.5 %
(Intercept)    48.165953 51.8340470
Fertilizantes2  4.279669  9.7203313
Fertilizantes3 -4.720331  0.7203313
Fertilizantes4 -5.899883 -0.1001170
Fertilizantes5 -7.593734 -2.4062658

> HSD.test(regresion,”Fertilizantes”, group=TRUE,console=TRUE)

Study: regresion ~ “Fertilizantes”
HSD Test for Observaciones
Mean Square Error:  4.666667
Fertilizantes,  means
Observaciones       std r Min Max
1            50 0.8944272 6  49  51
2            57 1.7320508 5  56  60
3            48 3.6742346 5  44  53
4            47 2.1602469 4  44  49
5            45 1.6733201 6  43  47
Alpha: 0.05 ; DF Error: 21
Critical Value of Studentized Range: 4.212995
Groups according to probability of means differences and alpha level( 0.05 )
Treatments with the same letter are not significantly different.
Observaciones groups
2            57      a
1            50      b
3            48     bc
4            47     bc
5            45      c

> plot(HSD.test(anova,”Fertilizantes”))

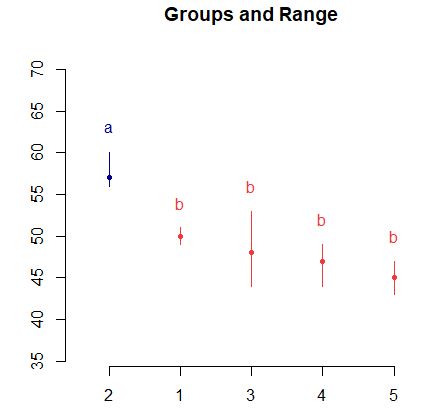
En esta gráfica se observa, al igual que en el contrate que el tratamiento 2 difiere significativamente de los demás

#Bonferroni

> pairwise.t.test(datos$Observaciones,datos$Fertilizantes,p.adj=”bonferroni”)
   Pairwise comparisons using t tests with pooled SD
data:  datos$Observaciones and datos$Fertilizantes
              1            2             3               4      
2       0.00026       –              –               –      
3      1.00000    1.6e-05       –                –      
4      0.43236    8.1e-06    1.00000       –      
5      0.00636    8.6e-08    0.32244    1.00000
P value adjustment method: bonferroni

Las salidas del test de Bonferroni son las significaciones entre tratamientos. Observamos los p-valores del tratamiento 2 con cada uno de los demás tratamientos son menores que 0.05 y también el p-valor del tratamiento 1 y 5 (P_valor= 0.00636 )

# LSD

> LSD.test(regresion,”Fertilizantes”, group=TRUE,p.adj=”bonferroni”,console=TRUE)
Study: regresion ~ “Fertilizantes”
LSD t Test for Observaciones
P value adjustment method: bonferroni
Mean Square Error:  4.666667
Fertilizantes,  means and individual ( 95 %) CI
Observaciones       std r      LCL      UCL Min Max
1            50 0.8944272 6 48.16595 51.83405  49  51
2            57 1.7320508 5 54.99090 59.00910  56  60
3            48 3.6742346 5 45.99090 50.00910  44  53
4            47 2.1602469 4 44.75376 49.24624  44  49
5            45 1.6733201 6 43.16595 46.83405  43  47
Alpha: 0.05 ; DF Error: 21
Critical Value of t: 3.135206
Groups according to probability of means differences and alpha level( 0.05 )
Treatments with the same letter are not significantly different.
Observaciones groups
2            57      a
1            50      b
3            48     bc
4            47     bc
5            45      c

> LSD.test(anova,”Fertilizantes”,p.adj=”none”,console=TRUE)
Study: anova ~ “Fertilizantes”
LSD t Test for Observaciones
Mean Square Error:  4.666667
Fertilizantes,  means and individual ( 95 %) CI
Observaciones       std r      LCL      UCL Min Max
1            50 0.8944272 6 48.16595 51.83405  49  51
2            57 1.7320508 5 54.99090 59.00910  56  60
3            48 3.6742346 5 45.99090 50.00910  44  53
4            47 2.1602469 4 44.75376 49.24624  44  49
5            45 1.6733201 6 43.16595 46.83405  43  47
Alpha: 0.05 ; DF Error: 21
Critical Value of t: 2.079614
Groups according to probability of means differences and alpha level( 0.05 )
Treatments with the same letter are not significantly different.
Observaciones groups
2            57      a
1            50      b
3            48     bc
4            47     cd
5            45      d

Esta salida muestra que el tratamiento 2 difiere de los otros cuatro y que el tratamiento 1 difiere de los tratamientos 4 y 5.

# Scheffe

> scheffe.test(regresion,”Fertilizantes”, group=TRUE,console=TRUE)
Study: regresion ~ “Fertilizantes”
Scheffe Test for Observaciones
Mean Square Error  : 4.666667
Fertilizantes,  means
Observaciones       std r Min Max
1            50 0.8944272 6  49  51
2            57 1.7320508 5  56  60
3            48 3.6742346 5  44  53
4            47 2.1602469 4  44  49
5            45 1.6733201 6  43  47
Alpha: 0.05 ; DF Error: 21
Critical Value of F: 2.8401
Groups according to probability of means differences and alpha level( 0.05 )
Means with the same letter are not significantly different.
Observaciones groups
2            57      a
1            50      b
3            48     bc
4            47     bc
5            45      c

# Student-Newman-Keuls

> ajuste.SNK = SNK.test(anova ,”Fertilizantes”)
> ajuste.SNK
$statistics
MSerror Df     Mean       CV
4.666667 21 49.34615 4.377741
$parameters
test        name.t ntr alpha
SNK Fertilizantes   5  0.05
$snk
NULL
$means
Observaciones       std r Min Max   Q25  Q50   Q75
1            50 0.8944272 6  49  51 49.25 50.0 50.75
2            57 1.7320508 5  56  60 56.00 56.0 57.00
3            48 3.6742346 5  44  53 45.00 48.0 50.00
4            47 2.1602469 4  44  49 46.25 47.5 48.25
5            45 1.6733201 6  43  47 43.50 45.5 46.00
$comparison
NULL
$groups
Observaciones groups
2            57      a
1            50      b
3            48     bc
4            47     bc
5            45      c
attr(,”class”)
[1] “group”

# Dunnett

Recordar que el objetivo de este contraste es que uno de los tratamientos sea un control y el experimentador está interesado en comparar los restantes tratamientos con este control.

Supongamos que el tratamiento control va a ser el tratamiento 1

> install.packages (“DunnettTests”)
> install.packages(“DescTools”)
> library (DunnettTests)
> library (DescTools)

> Dunnett <- DunnettTest(Observaciones ~ Fertilizantes , data = datos, control=”1″, conf.level=0.9)
> Dunnett
Dunnett’s test for comparing several treatments with a control :  
    90% family-wise confidence level
$`1`
    diff    lwr.ci     upr.ci    pval    
2-1    7  3.973286 10.0267138 9.4e-05 ***
3-1   -2 -5.026714  1.0267138  0.3866    
4-1   -3 -6.226488  0.2264877  0.1359    
5-1   -5 -7.885858 -2.1141417  0.0022 **
—
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1

Observamos que las parejas de medias 2 vs 1 y 5 vs 1 resultan significativamente diferentes.

> summary(Dunnett)
Length Class  Mode
1         16     -none- numeric
data.name  1     -none- character

> plot(Dunnett)

> Dunnet <- glht(anova, linfct=mcp(Fertilizantes=”Dunnett”))
> Dunnet
  General Linear Hypotheses
Multiple Comparisons of Means: Dunnett Contrasts
Linear Hypotheses:
           Estimate
2 – 1 == 0        7
3 – 1 == 0       -2
4 – 1 == 0       -3
5 – 1 == 0       -5

> confint(Dunnet)
Simultaneous Confidence Intervals
Multiple Comparisons of Means: Dunnett Contrasts
Fit: aov(formula = Observaciones ~ Fertilizantes, data = datos)
Quantile = 2.6522
95% family-wise confidence level
 Linear Hypotheses:
           Estimate lwr     upr    
2 – 1 == 0  7.0000   3.5306 10.4694
3 – 1 == 0 -2.0000  -5.4694  1.4694
4 – 1 == 0 -3.0000  -6.6984  0.6984
5 – 1 == 0 -5.0000  -8.3079 -1.6921

> summary(Dunnet)
         Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Dunnett Contrasts

Fit: aov(formula = Observaciones ~ Fertilizantes, data = datos)
Linear Hypotheses:
           Estimate Std. Error t value Pr(>|t|)    
2 – 1 == 0    7.000      1.308   5.351  < 0.001 ***
3 – 1 == 0   -2.000      1.308  -1.529  0.38667    
4 – 1 == 0   -3.000      1.394  -2.151  0.13607    
5 – 1 == 0   -5.000      1.247  -4.009  0.00228 **
—
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported — single-step method)

#CONTRASTES ORTOGONALES

> contrastes<-rbind(c(3,-2,3,-2,-2),c(-1,-1,4,-1,-1),c(2,2,2,-3,-3),c(1,1,0,0,-2))
> contrastes
[,1] [,2] [,3] [,4] [,5]
[1,]    3   -2    3   -2   -2
[2,]   -1   -1    4   -1   -1
[3,]    2    2    2   -3   -3
[4,]    1    1    0    0   -2

> comparaciones<-glht(anova, linfct=mcp(Fertilizantes=contrastes))
> comparaciones
General Linear Hypotheses
Multiple Comparisons of Means: User-defined Contrasts
Linear Hypotheses:
       Estimate
1 == 0       -4
2 == 0       -7
3 == 0       34
4 == 0       17
> summary(comparaciones)
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: User-defined Contrasts
Fit: aov(formula = Observaciones ~ Fertilizantes, data = datos)
Linear Hypotheses:
       Estimate Std. Error t value Pr(>|t|)    
1 == 0   -4.000      5.188  -0.771    0.828    
2 == 0   -7.000      4.311  -1.624    0.312    
3 == 0   34.000      5.299   6.416   <0.001 ***
4 == 0   17.000      2.196   7.742   <0.001 ***
—
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported — single-step method)

Hemos realizado los contrastes ortogonales

\(  \begin{array}{| l| l| l  |} \hline Hipótesis &   Estimaciones &    P-valor \\ \hline
H_0 \equiv 3μ_1-2μ_2 + 3μ_3-2μ_4-2 μ_5=0 &     C_1=-4   &  0.828 \\ \hline
H_0 \equiv -μ_1- μ_2+4μ_3-μ_4-μ_5 =0 &    C_2=-7   &  0.312 \\ \hline
H_0 \equiv 2μ_1+2μ_2+2μ_3-3μ_4-3μ_5=0 &    C_3=34  &  0.001 * \\ \hline
H_0 \equiv μ_1+μ_2-2μ_5=0  &    C_4=17   &  0.001 * \\ \hline   \end{array}   \)

Se concluye que \( 3μ_1 + 3μ_3 = 2μ_2+2μ_4+2 μ_5 \) y \( 4μ_3 = μ_1+μ_2 + μ_4 + μ_5 \) y en los otros dos contrastes se rechaza la hipótesis nula.

Sentencias utilizadas para la realización de los contrastes de comparaciones múltiples y contrastes ortogonales

> install.packages(“agricolae”)
> install.packages(“gplots”)
> install.packages(“multcomp”)
> install.packages(“lawstat”)
> install.packages (“DunnettTests”)
> install.packages(“DescTools”)

> library(agricolae)
> library(gplots)
> library(multcomp)
> library(lawstat)
> library (DunnettTests)
> library (DescTools)

> setwd(“C:/Users/Usuario/Desktop/Datos”)
> datos <- read.table(“Ejemplo1-1.txt”, header = TRUE)
> datos$Fertilizantes <- factor(datos$Fertilizantes)
> anova <- aov(Observaciones ~ Fertilizantes, data = datos)
> summary(mod)

# MOSTRAR MEDIAS
> tapply(datos$Observaciones,datos$Fertilizantes,mean, data = datos)
# MOSTRAR DESVIACIONES TÍPICA
> tapply(datos$Observaciones,datos$Fertilizantes, sd, na.rm=TRUE)
# COMPARACIONES GRAFICAS DE MEDIAS
> boxplot(Observaciones ~ Fertilizantes , data = datos)
> plotmeans(Observaciones ~ Fertilizantes , data = datos)
#COMPARACIONES MULTIPLES
#Tukey
> Tukey <- HSD.test(anova,”Fertilizantes”, group = TRUE)
> Tukey
> regresion<-lm(Observaciones ~ Fertilizantes , data = datos)
> regresion
> summary(regresion)
> confint(regresion)
> HSD.test(regresion,”Fertilizantes”, group=TRUE,console=TRUE)
> plot(HSD.test(anova,”Fertilizantes”))
#Bonferroni
> pairwise.t.test(datos$Observaciones,datos$Fertilizantes,p.adj=”bonferroni”)
#LSD
> LSD.test(regresion,”Fertilizantes”, group=TRUE,p.adj=”bonferroni”,console=TRUE)
> LSD.test(anova,”Fertilizantes”,p.adj=”none”,console=TRUE)
#Scheffe
> scheffe.test(regresion,”Fertilizantes”, group=TRUE,console=TRUE)
# Student-Newman-Keuls
> ajuste.SNK <- SNK.test(anova ,”Fertilizantes”)
> ajuste.SNK
# Dunnett
>Dunnett <- DunnettTest(Observaciones ~ Fertilizantes , data = datos, control=”1″, conf.level=0.9)
>Dunnett
>summary(Dunnett)
>plot(Dunnett)

>Dunnet <- glht(anova, linfct=mcp(Fertilizantes=”Dunnett”))
>Dunnet
>summary(Dunnet)
>confint(Dunnet)

#CONTRASTES ORTOGONALES
>contrastes<-rbind(c(3,-2,3,-2,-2),c(-1,-1,4,-1,-1),c(2,2,2,-3,-3),c(1,1,0,0,-2))
>comparaciones<-glht(anova, linfct=mcp(Fertilizantes=contrastes))
>summary(comparaciones)

2. Realizamos el análisis de la varianza unifactorial con la libreria BrailleR de R

Recordar que cada vez que iniciemos R hay que conectar la biblioteca a nuestro espacio de trabajo mediante la sentencia

> library(“BrailleR”)

The BrailleR.View option has been set to TRUE.
Consult the help page for GoSighted() to see how settings can be altered.
You may wish to use the GetGoing() function as a quick way of getting started.
Attaching package: ‘BrailleR’
The following objects are masked from ‘package:graphics’:
    boxplot, hist
The following object is masked from ‘package:utils’:
    history
The following objects are masked from ‘package:base’:
    grep, gsub

> datos$Fertilizantes<-factor(datos$Fertilizantes)
> OneFactor (“Observaciones”, “Fertilizantes”, Data = datos)

Se muestra la siguiente salida

• Group Summaries (Explicado en el Tema 1)
• Comparative boxplots (En este caso no incluye este gráfico porque el tamaño de uno de los grupos es demasiado pequeño)
• Comparative dotplots (Está explicado en OneFactor.html)
• One-way Analysis of Variance
• Gráfico de los residuos (Estudiaremos en el tema 3)
• Tests for homogeneity of Variance (Estudiaremos en el Tema 3)
• Tukey Honestly Significant Difference test

El test de Tukey muestra las parejas de tratamientos estadísticamente significativas al nivel de significación del 5%.

Observamos que el tratamiento 2 difiere significativamente del 1, 3, 4 y 5 y que 1 tratamiento difiere significativamente del tratamiento 5.

La salida también muestra una gráfica con los intervalos de confianza, según Tukey, para las parejas de medias.

Autora: Ana María Lara Porras. Universidad de Granada

Diseño estadístico de experimentos. Análisis de la varianza. Grupo Editorial Universitario