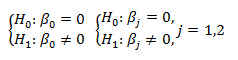REGRESIÓN Y CORRELACIÓN
Objetivos
- Ajustar modelos de regresión lineal simple y múltiple estimando los valores de sus parámetros
- Obtener información adicional sobre los modelos de regresión (contrastes de significación de los parámetros, test de bondad de ajuste,…)
- Contrastar las hipótesis del modelo de regresión lineal
- Ajustar un modelo de regresión cuadrático
- Estudiar la correlación entre variables
.
Regresión
Cuando se trabaja con un conjunto de varias variables es habitual encontrar relaciones entre ellas, de manera que el valor de una de ellas (a la que se denomina variable dependiente) puede predecirse a partir de los valores de otra u otras variables (que reciben el nombre de variables independientes). El principal objetivo de la regresión es encontrar la función que mejor capte la relación entre la variable dependiente y las independientes.
Generalmente se supone que la relación que guardan la variable dependiente y las independientes es lineal. En estos casos, se utlizan los modelos de regresión lineal. Aunque las relaciones lineales aparecen de forma frecuente, también es posible considerar otro tipo de relación entre las variables, que se modelizan mediante otros modelos de regresión, como pueden ser, por ejemplo, el modelo de regresión cuadrático o parabólico, el modelo de regresión hiperbólico.
Correlación
La correlación está íntimamente ligada con la regresión en el sentido de que se centra en el estudio del grado de asociación entre variables. Por lo tanto, una variable independiente que presente un alto grado de correlación con una variable dependiente será muy útil para predecir los valores de ésta última. Cuando la relación entre las variables es lineal, se habla de correlación lineal. Una de las medidas más utilizadas para medir la correlación lineal entre variables es el coeficiente de correlación lineal de Pearson.
En esta práctica se mostrará cómo ajustar un modelo de regresión con R-Commander, prestando especial atención a los modelos de regresión lineal. Además, mostraremos como calcular e interpretar algunas medidas de correlación.
Regresión lineal simple
La regresión lineal simple supone que los valores de la variable dependiente, a los que llamaremos yi, pueden escribirse en función de los valores de una única variable independiente, los cuales notaremos por xi, según el siguiente modelo lineal:
Estudiaremos la regresión lineal simple mediante un ejemplo, para ello vamos a trabajar con la base de datos empleados.xls que contiene una serie de variables medidas en los empleados de una empresa.
Ejemplo 1
La base de datos empleados.xls contiene información de la edad, altura, peso y sexo de 100 empleados de una empresa.
En primer lugar, importamos los datos de Excel desde R-Commander, para ello seleccionamos: Datos/Importar datos/desde un archivo de Excel
Se muestra la siguiente ventana donde introducimos el nombre del conjunto de datos
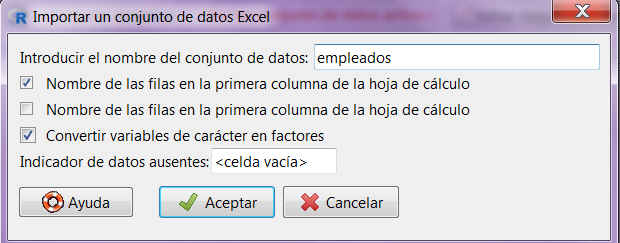Fig. 1: Importar un conjunto de datos Excel
Una vez elegidas las opciones pulsamos Aceptar, se selecciona el archivo empleados.xls. Y se muestra la siguiente pantalla
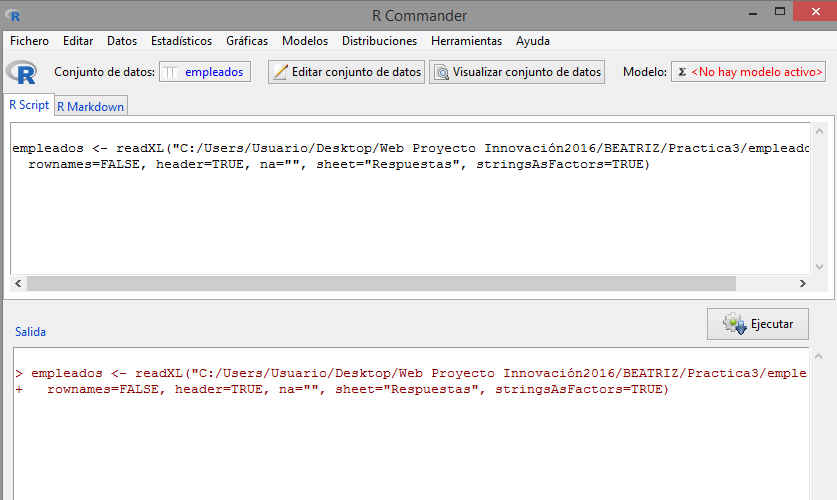Fig. 2: Seleccionar el archivo empleados.xls
En este caso, R-Commander detecta automáticamente los nombres de las variables.
Visualizamos el archivo pulsando Visualizar conjunto de datos.
Guardamos el archivo con el nombre empleados.RData, para ello seleccionamos: Datos/Conjunto de datos activo/Guardar el conjunto de datos activo.
Supongamos que nuestro objetivo es determinar el peso de un individuo a partir de su altura o, lo que es lo mismo, supongamos que la variable dependiente es peso y que la variable independiente es altura. Para ello, con el fichero de datos empleados.RData, vamos a obtener un modelo de regresión lineal para predecir el peso en función de la altura.
Habitualmente, al iniciar un estudio de regresión lineal simple se suelen representar los valores de la variable dependiente y de la variable independiente de forma conjunta mediante un diagrama de dispersión para determinar si la relación existente entre ambas puede considerarse lineal, y por tanto, tiene sentido plantear un modelo de regresión lineal simple.
Para realizar un diagrama de dispersión en R-Commander, seleccionamos Graficas/Gráfica XY e introducimos como variable explicativa la variable Altura y como variable explicada el Peso.
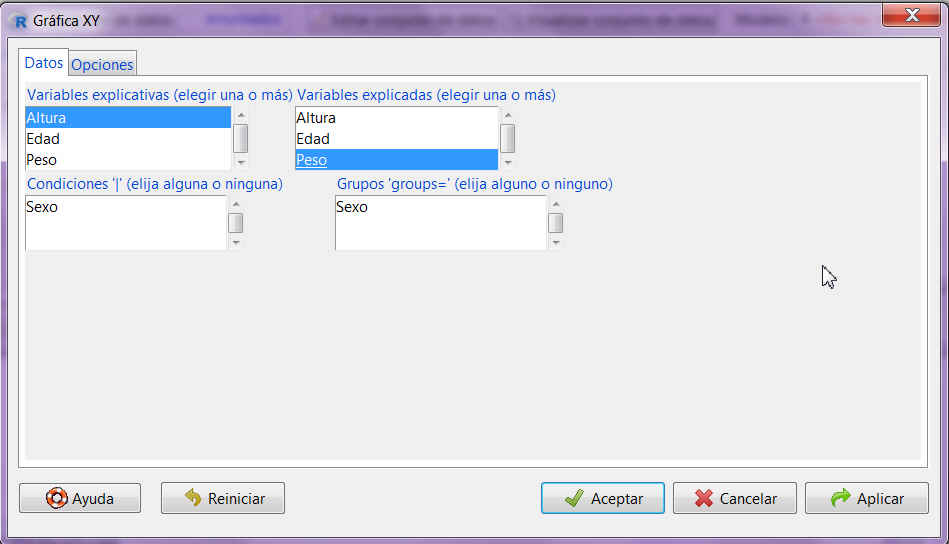Fig. 3: Seleccionamos Graficas/Gráfica XY
Pulsamos Aceptar
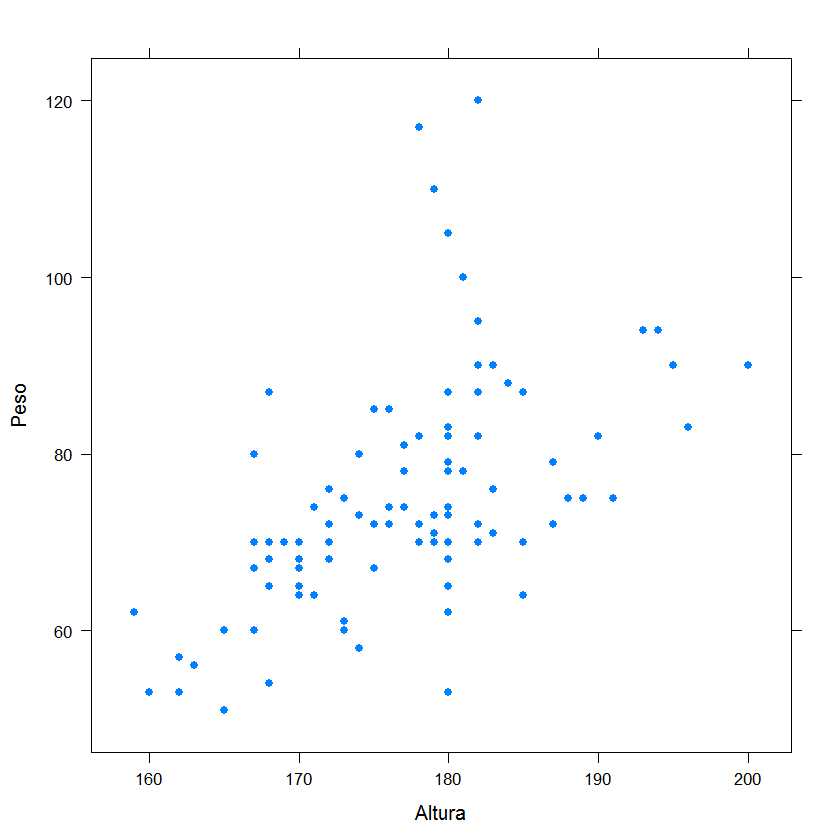Fig. 4: Diagrama de Dispersión (Peso en función de la Altura)
La forma de la nube puede indicarnos si existe una relación más o menos intensa entre dos variables. A la vista del gráfico de dispersión, se puede asumir un cierto grado de relación lineal entre ambas variables, por lo que procedemos al ajuste del modelo lineal.
El modelo de regresión lineal simple para predecir el peso en función de la altura es:
Para llevar a cabo esta regresión, seleccionamos Estadísticos/Ajuste de modelos/Regresión lineal
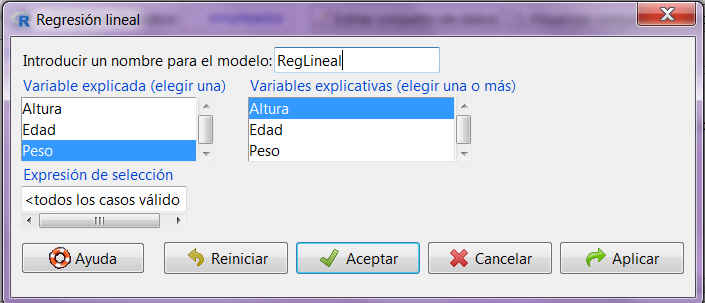Fig. 5: Estadísticos/Ajuste de modelos/Regresión lineal
Se pulsa Aceptar y se muestra la siguiente salida
> RegLineal <- lm(Peso~Altura, data=empleados)
> summary(RegLineal)
Call:
lm(formula = Peso ~ Altura, data = empleados)
Residuals:
Min 1Q Median 3Q Max
-24.363 -6.546 -1.678 4.557 41.374
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -78.9797 24.1051 -3.276 0.00146 **
Altura 0.8686 0.1360 6.385 5.92e-09 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 11.06 on 97 degrees of freedom
Multiple R-squared: 0.2959, Adjusted R-squared: 0.2886
F-statistic: 40.76 on 1 and 97 DF, p-value: 5.922e-09
Esta salida, de R-Commander, contiene una información muy completa sobre el análisis.
La salida que muestra la función lm y summary incluye: información sobre los residuos (en el apartado Residuals), las estimaciones para los parámetros, en nuestro caso 
y 
, el coeficiente de determinación R² para estudiar la bondad de ajuste del modelo, los valores de los estadísticos de contrastes y los p-valores correspondientes.
En la tabla Coefficients encontramos los valores de los parámetros junto a su error estándar. Cada parámetro aparece acompañado del valor de un estadístico t de Student y un p-valor que sirven para contrastar la significación del parámetro en cuestión, es decir, para resolver los siguientes contrastes de hipótesis de los coeficientes
Lo que se pretende mediante estos contrastes es determinar si los efectos de la constante y de la variable independiente son realmente importantes para explicar la variable dependiente o si, por el contario, pueden considerarse nulos.
En nuestro ejemplo, los p-valores que nos ayudan a resolver estos contrastes son 0.000146 y 5.29e-09, ambos menores que 0.05. Así, considerando un nivel del significación del 5%, rechazamos la hipótesis nula en ambos contrastes, de manera que podemos suponer ambos parámetros significativamente distintos de 0.
Por tanto, el modelo lineal puede escribirse del siguiente modo:
Estos dos parámetros pueden interpretarse del siguiente modo: -78.9797 es el valor del peso para una persona de altura 0, lo cual no tiene sentido. De hecho, en multitud de ocasiones la interpretación del parámetro no es relevante y todo el interés recae sobre la interpretación del resto de parámetros. El que sea igual a 0.8686 nos indica que, por término medio, cada centímetro de incremento en la altura de una persona supone un incremento de 0.8686 kg. en su peso.
Analizamos, a continuación, la información sobre los residuos (en el apartado Residuals). Los Residuos se definen como la diferencia entre el verdadero valor de la variable dependiente y el valor que pronostica el modelo de regresión. Cuanto más pequeños sean estos residuos mejor será el ajuste del modelo a los datos y más acertadas serán las predicciones que se realicen a partir de dicho modelo. El error estándar de los residuos indica la dispersión de los valores de los residuos. Representa una medida de la parte de la variabilidad de la variable dependiente que no es explicada por la recta de regresión. En general, cuanto mejor es el ajuste, más pequeño es este error típico. En este caso el error estándar de los residuos tiene un valor de 11.06
Por último, en la parte final de la salida, encontramos el valor de R² (Multiple R-squared) y de R² ajustado (Adjusted R-squared), que son indicadores de la bondad del ajuste de nuestro modelo a los datos. R² oscila entre 0 y 1, de manera que, valores de R² próximos a 1 indican un buen ajuste del modelo lineal a los datos. Por otro lado, R² ajustado es similar a R², pero penaliza la introducción en el modelo de variables independientes poco relevantes para explicar la variable dependiente. Por tanto, R² ajustado <= R². En nuestro ejemplo, R² = 0.2959 y R² ajustado = 0.2886.
Respecto a la bondad del ajuste, el coeficiente de determinación R² tiene un valor de 0.2959, indica que el 29.59% de toda la variabilidad que tiene el fenómeno relativo al peso puede ser explicado por la altura.
El coeficiente de correlación lineal es R = √R² = 0.5439. Sabiendo que la correlación oscila entre -1 y +1, podemos ver el grado de asociación entre las variables y el sentido negativo o positivo de esa asociación. Cuanto más se aproxime a -1 o +1 la asociación es más intensa y más débil a medida que se aproxime a cero. En este caso, podemos decir que tiene dependencia positiva pero débil.
La última línea de la salida incluye un estadístico F de Snedecor y el p-valor correspondiente que se utilizan para resolver el siguiente contraste de regresión
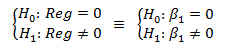Este procedimiento es a menudo considerado como un test global de idoneidad del modelo y se conoce habitualmente como contraste ómnibus. Mediante este contraste se comprueba si, de forma global, el modelo lineal es apropiado para modelizar los datos. En nuestro ejemplo, se muestra un valor del estadístico de contraste F de 40.76 con un p_valor = 5.922e-9. Deduciendo que a un nivel de significación del 5%, (p_valor < 0.05), rechazamos la hipótesis nula, y podemos cocluir que el modelo lineal es adecuado para nuestro conjunto de datos.
Una vez que tenemos ajustado el modelo podemos realizar predicciones, en este caso vamos a calcular una predicción para el caso de un individuo que mide 173cm
Esto lo podemos hacer de 2 formas diferentes:
1. Directamente en la ventana de instrucciones de R introduciendo manualmente los valores de la ecuación; es decir, tecleando
> Altura=173
> Peso_nuevo=-78.9797+0.8686*Altura
> Peso_nuevo
[1] 71.2881
o bien en R Script, tecleamos
Altura=173
Peso_nuevo=-78.9797+0.8686*Altura
Peso_nuevo
y pulsamos Ejecutar
R-Commander muestra la siguiente salida
> Altura=173
> Peso_nuevo=-78.9797+0.8686*Altura
> Peso_nuevo
[1] 71.2881
2. Usando el comando predict
> predict(RegLineal,data.frame(Altura=173))
1
71.28329
Para saber la exactitud de las predicción podemos solicitar intervalos alrededor de su predicción.
> predict(RegLineal,data.frame(Altura=173),interval=”confidence”)
fit lwr upr
1 71.28329 68.82657 73.74001
A continuación vamos a representar el modelo ajustado a la nube de puntos (e incluir una línea suavizada, lowess line), para ello en la ventana de R escribimos
> plot(empleados$Altura, empleados $Peso, main=”Nube de puntos y ajuste”, xlab=”Altura”, ylab=”Peso”)
> abline(lm(empleados $Peso ~ empleados $Altura), col=”red”)
> lines(lowess(empleados $Altura, empleados $Peso), col=”blue”)
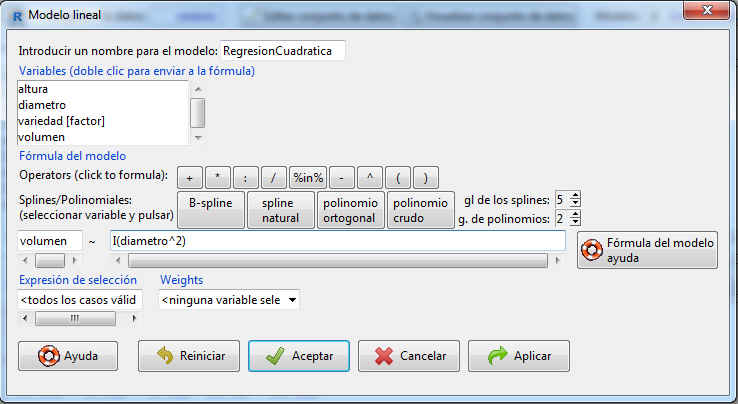
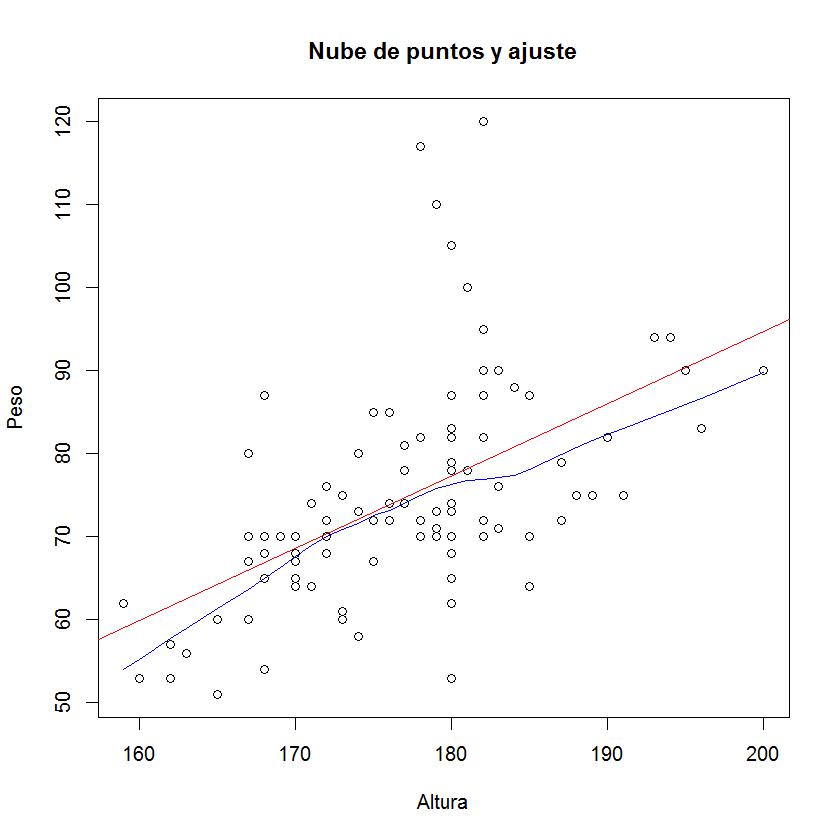Fig. 6: Nube de puntos y ajuste
O bien escribimos en R Script
plot(empleados$Altura, empleados $Peso, main=”Nube de puntos y ajuste”, xlab=”Altura”, ylab=”Peso”)
abline(lm(empleados $Peso ~ empleados $Altura), col=”red”)
lines(lowess(empleados $Altura, empleados $Peso), col=”blue”)
Pulsamos Ejecutar
Introduciendo la siguiente orden, podemos ver el ajuste por sexos
scatterplot(Peso ~ Altura | Sexo, xlab=”Altura”, ylab=”Peso”, data=empleados)
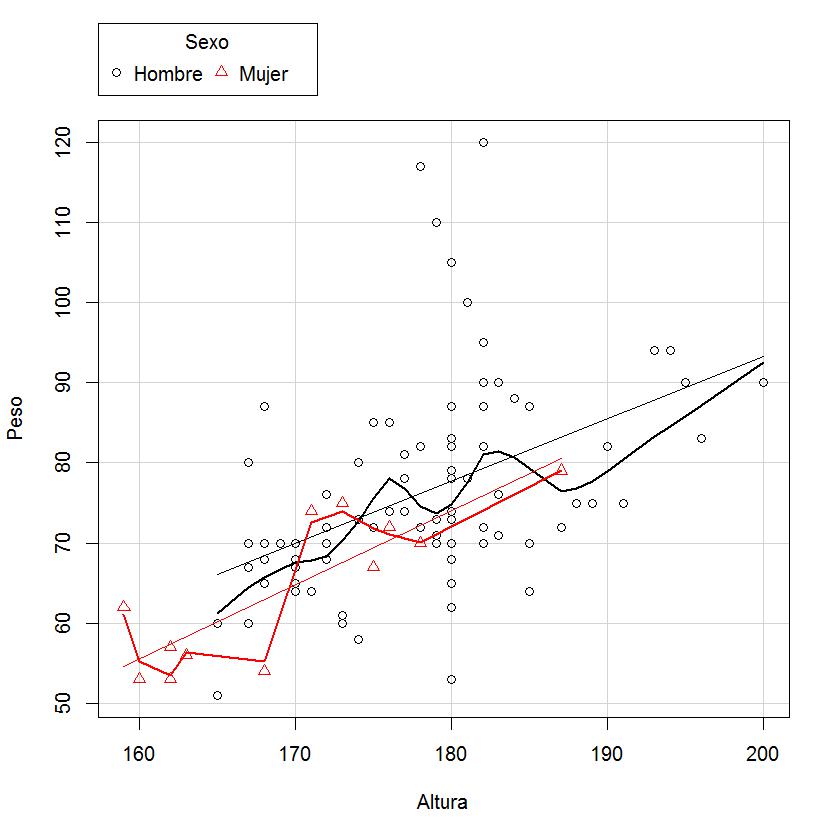Fig. 7: Nube de puntos y ajuste por sexos
Regresión lineal múltiple
En ocasiones, se dispone de más de una variable independiente, por lo que en lugar de un modelo de regresión lineal simple hay que considerar un modelo de regresión lineal múltiple. Un modelo de regresión lineal múltiple con un número genérico, p, de variables independientes puede escribirse del siguiente modo:
Para ajustar este tipo de modelos mediante R-commander, seleccionamos en el menú Estadísticos/Ajuste de modelos/Modelo lineal. Donde las variables explicativas incluso pueden ser cualitativas (factores) que se convertirán a variables dicotómicas.
Ejemplo 2
Utilizamos el mismo archivo de datos que en el ejemplo1: empleados.RData
Vamos a ajustar el Peso en función de la Altura y la Edad.
En este caso tenemos el siguiente modelo de regresión
Seleccionamos: Estadísticos/Ajuste de modelos/Modelo lineal
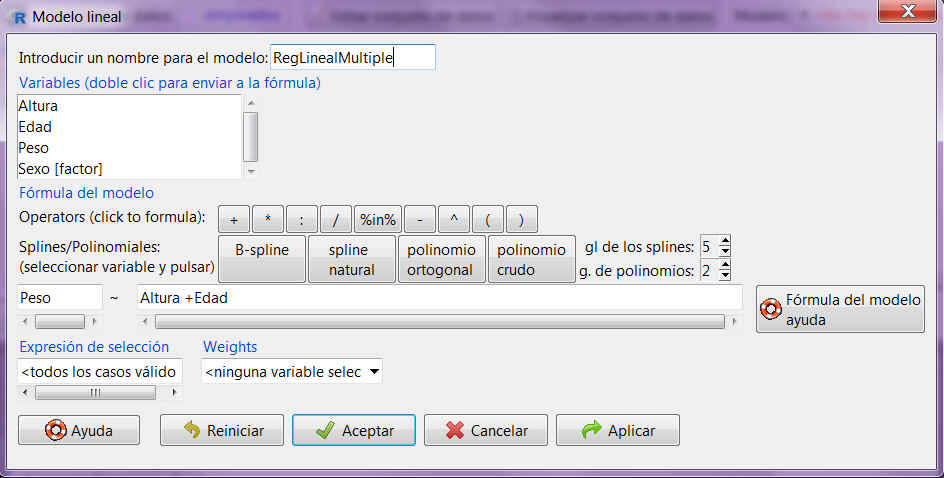Fig. 8: Estadísticos/Ajuste de modelos/Modelo lineal
En la ventana resultante:
Introducir un nombre para el modelo: RegLinealMultiple
Introducir en la primera casilla Peso y en la siguiente Altura + Edad. Para ello selecciona la variable y pulsa dos veces
Pulsar Aceptar y se muestra la siguiente salida
> RegLinealMultiple <- lm(Peso ~ Altura +Edad, data=empleados)
> summary(RegLinealMultiple)
Call:
lm(formula = Peso ~ Altura + Edad, data = empleados)
Residuals:
Min 1Q Median 3Q Max
-22.638 -6.517 -1.072 4.590 40.441
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -86.8216 23.7088 -3.662 0.00041 ***
Altura 0.8377 0.1332 6.289 9.43e-09 ***
Edad 0.6490 0.2628 2.470 0.01528 *
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 10.78 on 96 degrees of freedom
Multiple R-squared: 0.338, Adjusted R-squared: 0.3242
F-statistic: 24.5 on 2 and 96 DF, p-value: 2.526e-09
Tanto la interpretación como la comprobación de la significación de los parámetros se realizan de forma similar al caso en que se cuenta con una única variable independiente. Igualmente, la validación se lleva a cabo del mismo modo que para la regresión lineal simple.
Contraste de regresión
En este caso el p-valor obtenido es 2.526e-9, por lo tanto a un nivel de significación del 5%, rechazamos la hipótesis nula, y se concluye que existe relación lineal entre las variables
Contrastes sobre coeficientes de regresión individuales
Los p_valores de la constante (0.00041), la altura ( 9.43e-9) y la edad (0.01528) son menores que 0.05. Por lotanto, para un nivel de significación del 5% rechazamos las hipótesis nulas planteadas.
El modelo de regresión lineal múltiple puede expresarse de la siguiente manera:
El error estándar de los residuos tiene un valor de 10.78
Respecto a la bondad del ajuste, el coeficiente de determinación R² tiene un valor de 0.338, indica que el 33.8% de toda la variabilidad que tiene el fenómeno relativo al peso puede ser explicado por la altura y la edad.
El coeficiente de correlación lineal R = √R² = 0.5813. En este caso, podemos decir que tiene dependencia positiva pero débil.
Otros modelos de regresión
Con R-Commander también se pueden realizar modelos “linealizables”, como por ejemplo, el modelo exponencial Y=exp(a+b*X), el modelo logarítmico Y=a+b*ln(X) o modelo multiplicativo Y =a*X^ b entre otros.
Ejemplo 3
Ajustar la variable Peso y la variable Altura mediante un modelo exponencial, para ello hemos de hacer las transformaciones oportunas para linealizar la función
En este caso el modelo de regresión tiene la siguiente ecuación
Seleccionamos en el menú de R-Commander: Estadísticos/Ajuste de modelos/Modelo lineal
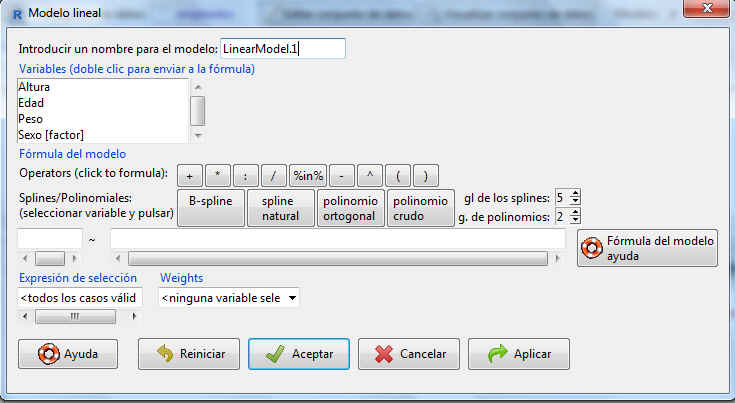Fig. 9: Estadísticos/Ajuste de modelos/Modelo lineal
Rellenar las casillas de nombre para el modelo y selección de variables como muestra la siguiente figura
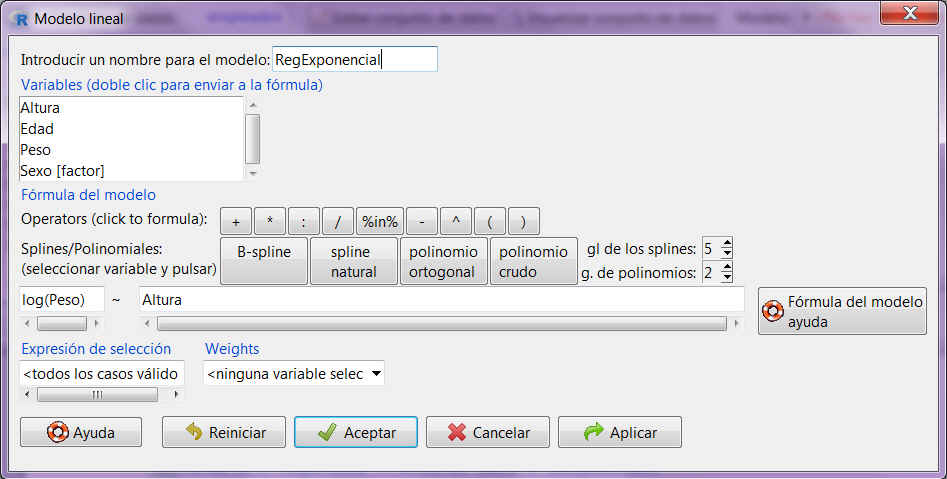Fig. 10: Estadísticos/Ajuste de modelos/Modelo lineal (RegExponencial)
Se muestra la siguiente salida
> RegExponencial <- lm(log(Peso) ~ Altura, data=empleados)
> summary(RegExponencial)
Call:
lm(formula = log(Peso) ~ Altura, data = empleados)
Residuals:
Min 1Q Median 3Q Max
-0.36521 -0.08462 -0.01195 0.06924 0.45044
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.196035 0.302042 7.271 9.19e-11 ***
Altura 0.011886 0.001705 6.973 3.80e-10 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 0.1386 on 97 degrees of freedom
Multiple R-squared: 0.3339, Adjusted R-squared: 0.327
F-statistic: 48.62 on 1 and 97 DF, p-value: 3.799e-10
Contraste de regresión
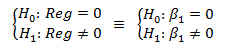En este caso obtenemos un valor del estadístico F de 48.62 con un p-valor de 3.799e-10: por lo tanto rechazamos la hipótesis nula, y se concluye que existe relación lineal entre las variables
Contrastes sobre coeficientes de regresión individuales
Los p_valores de la constante (9.19e-11) y de la altura (3.8e-10); nos indican que se rechazan las hipótesis nulas planteadas.
La recta ajustada aparece especificada a través de sus dos coeficientes: el término independiente o intercept y la pendiente de la recta
El error estándar de los residuos tiene un valor de 0.1386
Respecto a la bondad del ajuste, el coeficiente de determinación R² tiene un valor de 0.3339, indica que el 33.39% de toda la variabilidad que tiene el fenómeno relativo al logaritmo del peso puede ser explicado por la altura.
El coeficiente de correlación lineal R es 0.5778. Podemos decir que tiene dependencia positiva, pero débil.
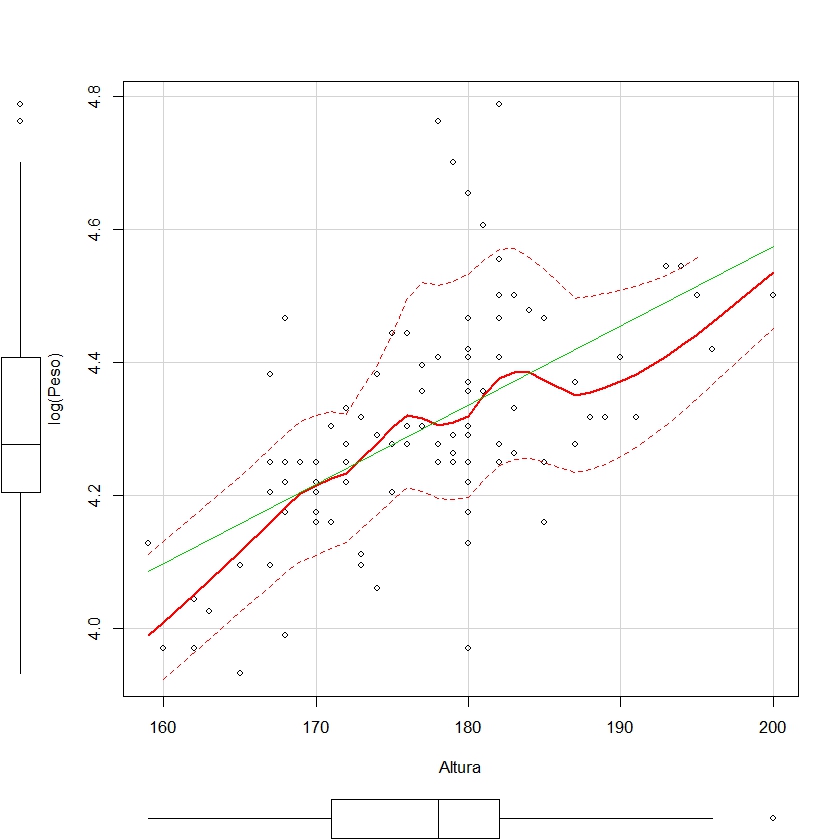
A continuación vamos a representar el ajuste realizado mediante la función scatterplot. Para ello, escribimos en R Script
scatterplot(log(Peso)~Altura, reg.line=lm, xlab=”Altura”, ylab=”log(Peso)”, data=empleados)
y pulsamos Ejecutar
Ejercicios
Ejercicios Guiados
Ejercicio guiado
El conjunto de datos cerezos.txt contiene información relativa al diametro, altura, volumen y variedad de cerezos
Se pide
a) Importar cerezos.txt
b) Realizar el diagrama de dispersión del volumen en función del diámetro
c) Ajustar el modelo de regresión lineal volumen en función del diámetro. Representar la recta ajustada
d) Ajustar el modelo de regresión : 
f) Determinar el volumen de un cerezo cuyo diámtero valga 10 y calcular el intervalo de confianza para el valor ajustado.
Ejercicio Guiado (Resuelto)
a) Importar cerezos.txt
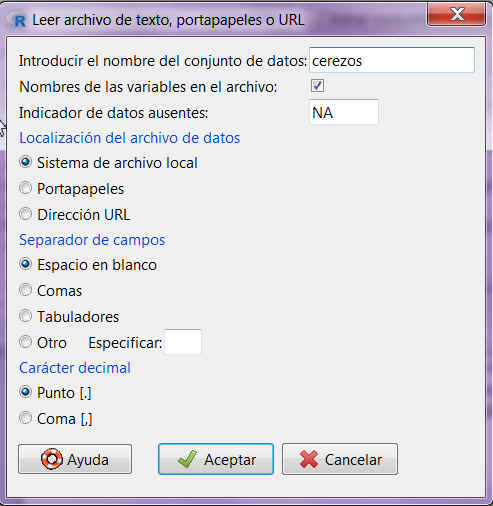
Seleccionar en el menú principal de R-Commander: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
En la ventana correspondiente al nombre del conjunto de datos introducir: cerezos
Pulsar Aceptar
La pantalla de salida muestra
> cerezos <- read.table(“C:/Users/Usuario/Desktop/cerezos.txt”, header=TRUE, sep=””, na.strings=”NA”, dec=”.”, strip.white=TRUE)
b) Realizar el diagrama de dispersión del volumen en función del diámetro
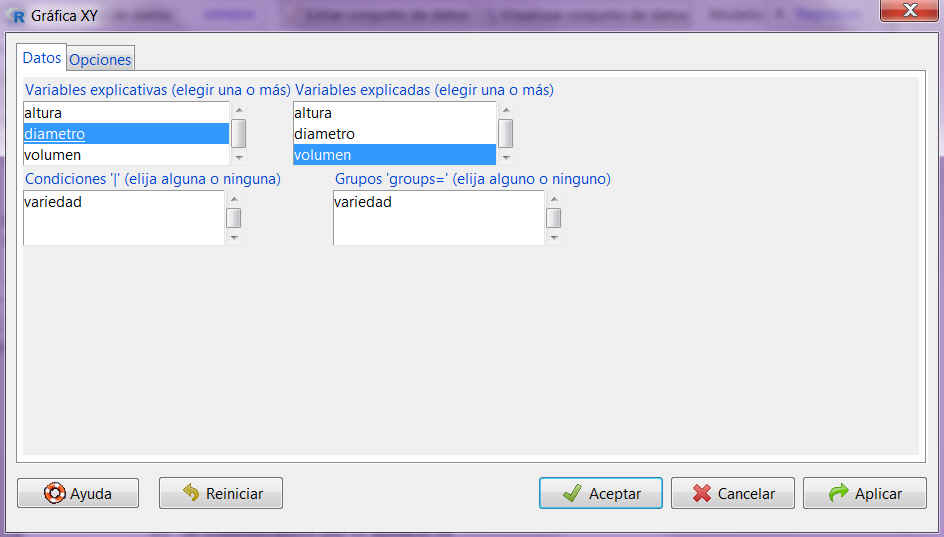
Seleccionamos: Gráficas/Gráfica XY. En la ventana resultante seleccionamos diámetro como variable explicativa y volumen como variable explicada
Fig. 13: Gráfica XY
Pulsamos Aceptar y se muestra la siguiente gráfica
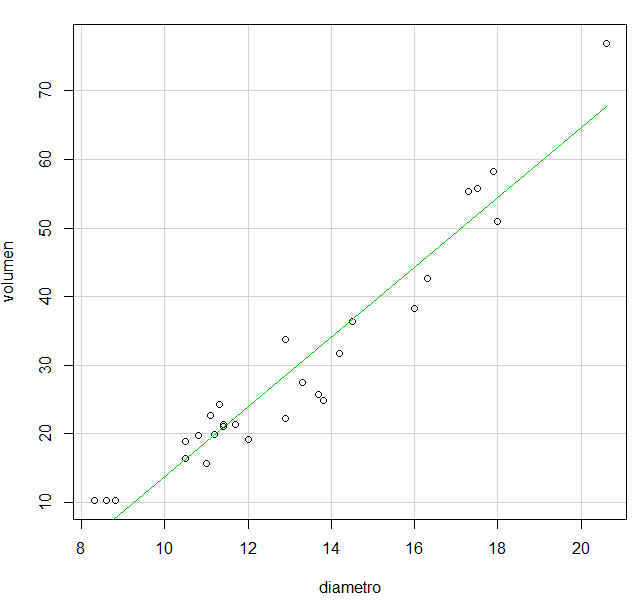
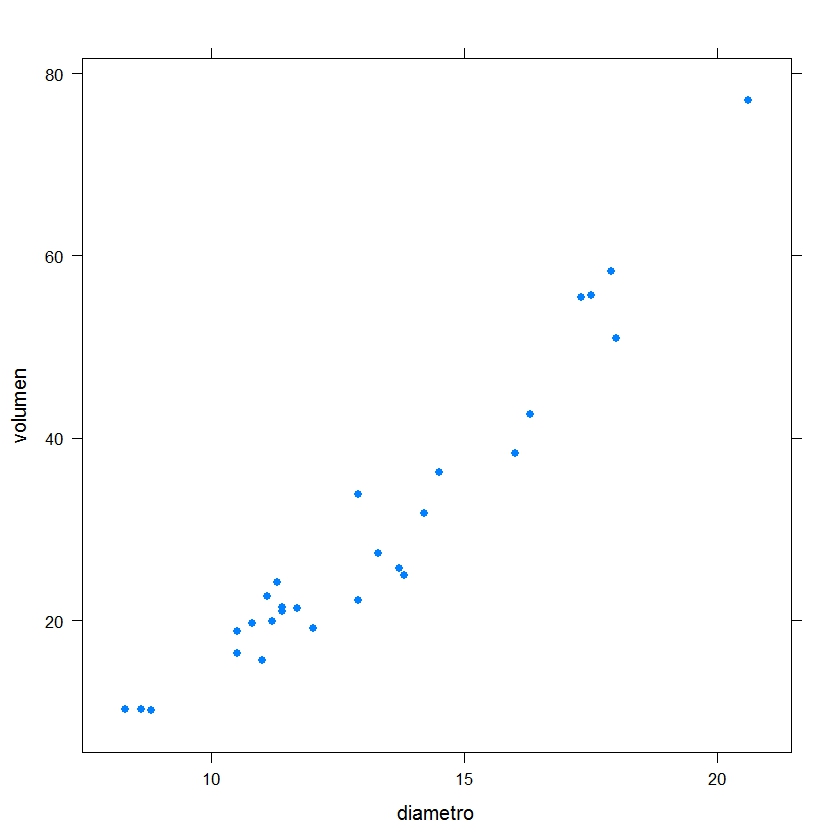Fig. 14: Gráfica XY (Volumen en función de diámetro)
c) Ajustar el modelo de regresión lineal volumen en función del diámetro. Representar la recta ajustada
Seleccionamos: Estadísticos/Ajuste de modelos/Regresión lineal y en la ventana resultante seleccionamos diámetro como variable explicativa y volumen como variable explicada
Fig. 15: Regresión lineal (Volumen en función de diámetro)
Se pulsa Aceptar y se muestra la siguiente salida
> RegModel.1 <- lm(volumen~diametro, data=cerezos)
> summary(RegModel.1)
Call:
lm(formula = volumen ~ diametro, data = cerezos)
Residuals:
Min 1Q Median 3Q Max
-8.2235 -3.3178 0.1068 3.6941 9.2076
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -37.2339 3.6829 -10.11 1.69e-10 ***
diametro 5.0984 0.2731 18.67 < 2e-16 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 4.47 on 26 degrees of freedom
(3 observations deleted due to missingness)
Multiple R-squared: 0.9306, Adjusted R-squared: 0.9279
F-statistic: 348.5 on 1 and 26 DF, p-value: < 2.2e-16
Analizamos la salida
Contraste de regresión
En este caso obtenemos un p_valor = 2.2e-16, por lo que rechazamos la hipótesis nula, y se concluye que existe relación lineal entre las variables
Contrastes sobre coeficientes de regresión individuales
Los p_valores de la constante (1.69e-10) y el diámetro (2e-16); indican que rechazamos las hipótesis nulas planteadas.
La recta ajustada es la siguiente
El error estándar de los residuos tiene un valor de 4.47
Respecto a la bondad del ajuste, el coeficiente de determinación que tiene un valor de 0.9306, indica que el 93.06% de toda la variabilidad que tiene el fenómeno relativo al volumen puede ser explicado por el diámetro.
El coeficiente de correlación lineal es 0.9646761, indica que hay una dependencia positiva muy fuerte.
Para realizar el diagrama de dispresión y la recta ajustada, seleccionamos en el menú principal Gráficas/Diagrama de dispersión
Fig. 16: Diagrama de dispersión
seleccionamos las variables (variable x: diámetro; variable y: volumen) y pulsamos Opciones
Fig. 17: Diagrama de dispersión: Opciones
donde elegimos Línea de mínimos cuadrados y pulsamos Aceptar
Fig. 18: Línea de mínimos cuadrados
R- Commander muestra el siguiente código
> scatterplot(volumen~diametro, reg.line=lm, smooth=FALSE, spread=FALSE, boxplots=FALSE, span=0.5, ellipse=FALSE, levels=c(.5, .9), data=cerezos)
También se puede realizar el diagrama de dispersión y la recta ajustada, escribiendo en R Script
plot(cerezos$diametro,cerezos$volumen)
abline(lm(cerezos$volumen~cerezos$diametro), col=”red”)
y pulsar Ejecutar
d) Ajustar el modelo de regresión :
Seleccionamos: Estadísticos/ Ajuste de modelos/ Modelo lineal
Fig. 19: Modelo Lineal
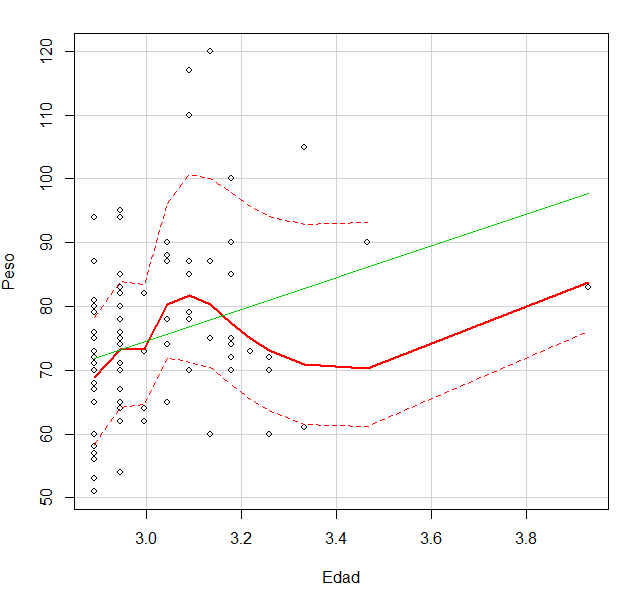
En la pestaña de introducir un nombre para el modelo tecleamos RegresionCuadratica
Pulsando volumen, se muestra en la primera casilla y pulsando diametro se muestra en la segunda casilla donde añadimos ^ 2 y la función I() de la siguiente forma: I(diametro)^2.
Nota: Las fórmulas pueden contener además de los nombres de variables y factores también expresiones aritméticas. Por ejemplo: en (y) ~ a + x^2, para que en R no haya confusión entre la aritmética y el uso del operador simbólico, se utiliza la función I () . Esta función se puede utilizar para poner entre paréntesis aquellas porciones de una fórmula en la que los operadores se utilizan en su sentido aritmético. Por ejemplo, en la fórmula y ~ a + I (b + c), el término b + c, debe interpretarse como la suma de b y c.
Pulsamos Aceptar y se muestra la siguiente salida
> RegresionCuadratica <- lm(volumen ~ I(diametro^2), data=cerezos)
> summary(RegresionCuadratica)
Call:
lm(formula = volumen ~ I(diametro^2), data = cerezos)
Residuals:
Min 1Q Median 3Q Max
-6.3589 -2.5674 0.4634 2.3956 6.9430
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.626980 1.508094 -2.405 0.0236 *
I(diametro^2) 0.183186 0.007476 24.504 <2e-16 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 3.456 on 26 degrees of freedom
(3 observations deleted due to missingness)
Multiple R-squared: 0.9585, Adjusted R-squared: 0.9569
F-statistic: 600.5 on 1 and 26 DF, p-value: < 2.2e-16
Contraste de regresión
En este caso obtenemos un p_valor = 2.2e-16, por lo que rechazamos la hipótesis nula, y se concluye que existe relación lineal entre las variables
Contrastes sobre coeficientes de regresión individuales
Los p_valores de la constante (0.0236) y el diámetro (2e-16); indican que rechazamos las hipótesis nulas planteadas.
La recta ajustada aparece especificada a través de sus coeficientes:
El error estándar de los residuos tiene un valor de 3.456
Respecto a la bondad del ajuste, el coeficiente de determinación que tiene un valor de 0.9585, indica que el 95.85% de toda la variabilidad que tiene el fenómeno relativo al volumen puede ser explicado por el cuadrado del diámetro.
El coeficiente de correlación lineal es 0.9569, indica que hay una dependencia positiva muy fuerte.
e) Determinar el volumen de un cerezo cuyo diámetro valga 10 y calcular el intervalo de confianza para el valor ajustado.
predict(RegresionCuadratica,data.frame(diametro=10))
1
14.6916
predict(RegresionCuadratica,data.frame(diametro=10),interval=”confidence”)
fit lwr upr
1 14.6916 12.85213 16.53106
El volumen de un cerezo de diámetro 10 es: 14.6916.
El intervalo de confianza para el valor ejustado es: (12.85213. 16.53106)
Ejercicios Propuestos
Ejercicio Propuesto1
El conjunto de datos empleados.xls, contiene información relativa a la altura, edad y peso de los ampleados de una empresa.
a) Importar el archivo de datos empleados.xls
b) Realizar el diagrama de dispersión del peso en función de la edad
c) Ajustar el modelo de regresión lineal peso en función de la edad. Representar la recta ajustada
d) Realizar una regresión logarítmica considerando que el peso de los empleados depende de la edad.
e) Realiza el gráfico con la función scatterplot
f) Realizar el modelo exponencial y comparar ambos modelos
g) Ajustar el Peso en función de la Edad y el cuadrado de la Altura
Ejercicio Propuesto2
Se realiza un estudio para investigar la relación entre el nivel de humedad del suelo y la tasa de mortalidad en lombrices. La tasa de mortalidad, Y, es la proporción de lombrices de tierra que mueren tras un periodo de dos semanas; el nivel de humedad, X, viene medido en milímetros de agua por centímetro cuadrado de suelo. Los datos se muestran en la siguiente tabla.
Tabla 1: Datos ejercico propuesto 2
Se pide:
a) ¿Muestran los datos una tendencia lineal?
b) Determinar la recta de regresión Y/X, el grado de asociación lineal entre la tasa de mortalidad y el nivel de humedad y la bondad del ajuste realizado en la recta de regresión. ¿Cuánto explica el modelo?
c) Predecir el nivel de humedad del suelo si la tasa de mortalidad de las lombrices es 0.7
d) Determinar el coeficiente de correlación lineal de las rectas de regresión Y/X y X/Y
e) Ajustar los datos mediante una regresión curvilínea
d) ¿Qué ajuste es mejor ¿Lineal? ¿Curvilíneo?
Ejercicio Propuesto 1(Resuelto)
a) Importar el archivo de datos empleados.xls
Fig. 20: Importar conjunto de datos Excel
b) Realizar el diagrama de dispersión del peso en función de la edad
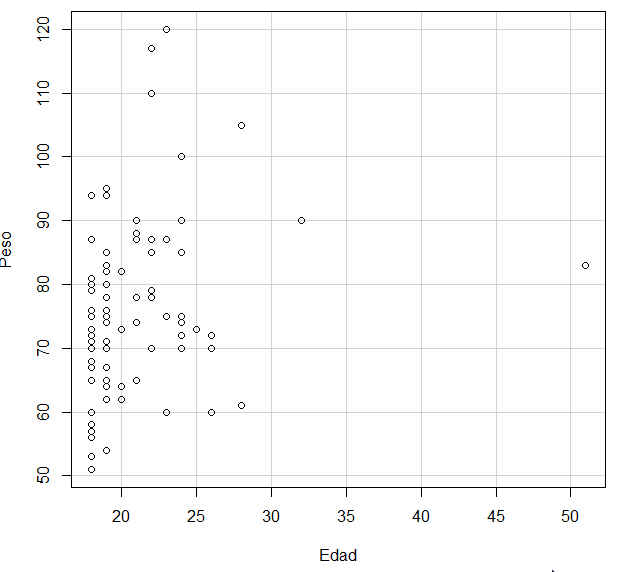Fig. 21: Diagrama de dispersión
c) Ajustar el modelo de regresión lineal peso en función de la edad. Representar la recta ajustada
> RegLineal <- lm(Peso~Edad, data=empleados)
> summary(RegLineal)
Call:
lm(formula = Peso ~ Edad, data = empleados)
Residuals:
Min 1Q Median 3Q Max
-21.735 -7.648 -1.735 7.548 43.244
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 58.2563 6.4725 9.001 1.93e-14 ***
Edad 0.8043 0.3093 2.601 0.0108 *
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 12.75 on 97 degrees of freedom
Multiple R-squared: 0.06519, Adjusted R-squared: 0.05556
F-statistic: 6.765 on 1 and 97 DF, p-value: 0.01075
d) Realizar una regresión logarítmica considerando que el peso de los empleados depende de la edad
> RegresionLogaritmica <- lm(Peso ~ log(Edad), data=empleados)
> summary(RegresionLogaritmica)
Call:
lm(formula = Peso ~ log(Edad), data = empleados)
Residuals:
Min 1Q Median 3Q Max
-21.850 -8.205 -1.695 7.519 42.043
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.02984 24.25558 -0.001 0.99902
log(Edad) 24.87238 8.05582 3.088 0.00263 **
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 12.58 on 97 degrees of freedom
Multiple R-squared: 0.08948, Adjusted R-squared: 0.08009
F-statistic: 9.533 on 1 and 97 DF, p-value: 0.002632
e) Realiza el gráfico con la función scatterplot
f) Realizar el modelo exponencial y comparar ambos modelos
> RegresionExponencial <- lm(log(Peso) ~ Edad, data=empleados)
> summary(RegresionExponencial)
Call:
lm(formula = log(Peso) ~ Edad, data = empleados)
Residuals:
Min 1Q Median 3Q Max
-0.34202 -0.09341 -0.00804 0.11019 0.46197
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.087817 0.083397 49.016 <2e-16 ***
Edad 0.010335 0.003985 2.594 0.011 *
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 0.1642 on 97 degrees of freedom
Multiple R-squared: 0.06486, Adjusted R-squared: 0.05521
F-statistic: 6.727 on 1 and 97 DF, p-value: 0.01097
Por lo tanto el modelo logarítmico explica una mayor variabilidad de los datos.
g) Ajustar el Peso en función de la Edad y el cuadrado de la Altura
> RegresionEdadPeso <- lm(Peso ~ Edad + I(Altura^2), data=empleados)
> summary(RegresionEdadPeso)
Call:
lm(formula = Peso ~ Edad + I(Altura^2), data = empleados)
Residuals:
Min 1Q Median 3Q Max
-22.447 -6.903 -0.934 4.543 40.593
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.204e+01 1.256e+01 -0.958 0.3402
Edad 6.580e-01 2.635e-01 2.497 0.0142 *
I(Altura^2) 2.335e-03 3.752e-04 6.222 1.28e-08 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 10.82 on 96 degrees of freedom
Multiple R-squared: 0.3338, Adjusted R-squared: 0.32
F-statistic: 24.05 on 2 and 96 DF, p-value: 3.405e-09
Solución del Ejercicio Propuesto1
Ejercicio Propuesto 2 (Resuelto)
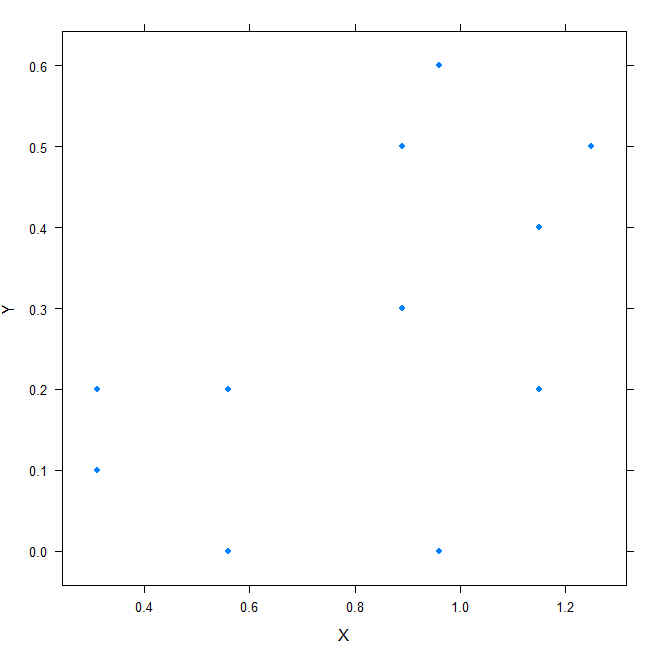
a) ¿Muestran los datos una tendencia lineal?
b) Determinar la recta de regresión Y/X, el grado de asociación lineal entre la tasa de mortalidad (Y) y el nivel de humedad (X) y la bondad del ajuste realizado en la recta de regresión. ¿Cuánto explica el modelo?
> RegresionLinealYX <- lm(Y~X, data=Lombrices)
> summary(RegresionLinealYX)
Call:
lm(formula = Y ~ X, data = Lombrices)
Residuals:
Min 1Q Median 3Q Max
-0.31865 -0.09465 0.01005 0.08927 0.28135
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.009771 0.153945 0.063 0.951
X 0.321749 0.175600 1.832 0.100
Residual standard error: 0.1848 on 9 degrees of freedom
Multiple R-squared: 0.2717, Adjusted R-squared: 0.1908
F-statistic: 3.357 on 1 and 9 DF, p-value: 0.1001
c) Predecir el nivel de humedad del suelo si la tasa de mortalidad de las lombrices es 0.7
> RegresionLinealXY <- lm(X~Y, data=Lombrices)
> summary(RegresionLinealXY)
Call:
lm(formula = X ~ Y, data = Lombrices)
Residuals:
Min 1Q Median 3Q Max
-0.44586 -0.16474 -0.02698 0.23304 0.39414
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.5870 0.1547 3.794 0.00426 **
Y 0.8444 0.4608 1.832 0.10013
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 0.2993 on 9 degrees of freedom
Multiple R-squared: 0.2717, Adjusted R-squared: 0.1908
F-statistic: 3.357 on 1 and 9 DF, p-value: 0.1001
> 0.5870+0.7*0.8444
[1] 1.17808
d) Ajustar los datos mediante una regresión curvilínea
> ModeloCuadratico <- lm(Y ~ X +I(X^2), data=Lombrices)
> summary(ModeloCuadratico)
Call:
lm(formula = Y ~ X + I(X^2), data = Lombrices)
Residuals:
Min 1Q Median 3Q Max
-0.31177 -0.10136 0.01473 0.07647 0.28823
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.06094 0.37424 0.163 0.875
X 0.15643 1.10411 0.142 0.891
I(X^2) 0.10922 0.71902 0.152 0.883
Residual standard error: 0.1957 on 8 degrees of freedom
Multiple R-squared: 0.2738, Adjusted R-squared: 0.09222
F-statistic: 1.508 on 2 and 8 DF, p-value: 0.2781
d) ¿Qué ajuste es mejor ¿Lineal? ¿Curvilíneo?
Es mejor el ajuste cuadrático
Solución del ejercicio Propuesto 2
Autores: Beatriz Cobo Rodríguez y Ana María Lara Porras. Universidad de Granada. (2016)