CONTRASTES DE HIPÓTESIS
Objetivos
- Realizar contrastes de hipótesis paramétricos para la media de una población normal.
- Realizar contrastes de hipótesis paramétricos para comparar dos medias de variables normales en muestras independientes y en muestras apareadas.
- Realizar contrastes de hipótesis para comparar dos proporciones.
- Realizar contrastes de hipótesis no-paramétricos de independencia para variables cualitativas.
- Realizar contrastes de hipótesis no-paramétricos de bondad de ajuste de distribuciones.
- Realizar contrastes de hipótesis no-paramétricos de aleatoriedad.
- Realizar contrastes de hipótesis no-paramétricos de dos muestras independientes y de dos muestras relacionadas.
- APÉNDICE: Introducción al Análisis de datos categóricos: Tablas de Contingencia
Conceptos básicos
Contraste de hipótesis. Un contraste de hipótesis es un proceso estadístico mediante el cual se investiga si una propiedad que se supone que cumple una población es compatible con lo observado en una muestra de dicha población. Es un procedimiento que permite elegir una hipótesis de trabajo de entre dos posibles y antagónicas.
Hipótesis Estadística. Todo contraste de hipótesis se basa en la formulación de dos hipótesis exhaustivas y mutuamente exclusivas:
- Hipótesis nula (H0)
- Hipótesis alternativa (H1)
La hipótesis H0 es la que se desea contrastar. Consiste generalmente en una afirmación concreta sobre la forma de una distribución de probabilidad o sobre el valor de alguno de los parámetros de esa distribución. El nombre de “nula” significa “sin valor, efecto o consecuencia”, lo cual sugiere que H0 debe identificarse con la hipótesis de no cambio (a partir de la opinión actual); no diferencia, no mejora, etc. H0 representa la hipótesis que mantendremos a no ser que los datos indiquen su falsedad, y puede entenderse, por tanto, en el sentido de “neutra”. La hipótesis H0 nunca se considera probada, aunque puede ser rechazada por los datos. Por ejemplo, la hipótesis de que dos poblaciones tienen la misma media puede ser rechazada fácilmente cuando ambas difieren mucho, analizando muestras suficientemente grandes de ambas poblaciones, pero no puede ser “demostrada” mediante muestreo, puesto que siempre cabe la posibilidad de que las medias difieran en una cantidad lo suficientemente pequeña para que no pueda ser detectada, aunque la muestra sea muy grande. Dado que descartaremos o no la hipótesis nula a partir de muestras obtenidas (es decir, no dispondremos de información completa sobre la población), no será posible garantizar que la decisión tomada sea la correcta.
La hipótesis H1 es la negación de la nula. Incluye todo lo que H0 excluye.
¿Qué asignamos como H0 y H1 ?
La hipótesis H0 asigna un valor específico al parámetro en cuestión y por lo tanto “el igual” siempre forma parte de H0.
La idea básica de la prueba de hipótesis es que los hechos tengan probabilidad de rechazar H0. La hipótesis H0 es la afirmación que podría ser rechazada por los hechos. El interés del investigador se centra, por lo tanto, en la H1.
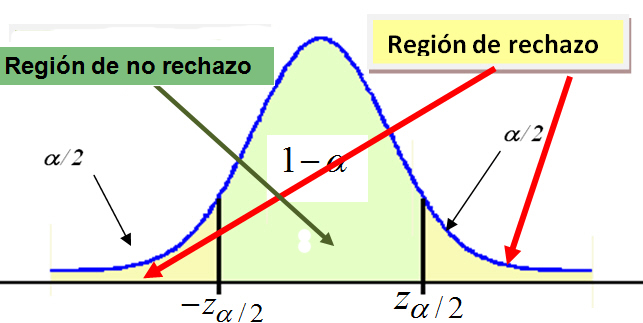
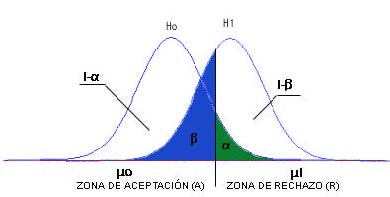
La regla de decisión. Es el criterio que vamos a utilizar para decidir si la hipótesis nula planteada debe o no ser rechazada. Este criterio se basa en la partición de la distribución muestral del estadístico de contraste en dos regiones o zonas mutuamente excluyentes: Región crítica o región de rechazo y Región de no-rechazo.
Región de no-rechazo. Es el área de la distribución muestral que corresponde a los valores del estadístico de contraste próximos a la afirmación establecida en H0. Es decir, los valores del estadístico de contraste que nos conducen a decidir H0. Es por tanto, el área correspondiente a los valores del estadístico de contraste que es probable que ocurran si H0 es verdadera. Su probabilidad se denomina nivel de confianza y se representa por 1 – α .
Región de rechazo o región crítica. Es el área de distribución muestral que corresponde a los valores del estadístico de contraste que se encuentran tan alejados de la afirmación establecida en H0, que es muy poco probable que ocurran si H0 es verdadera. Su probabilidad se denomina nivel de significación o nivel de riesgo y se representa con la letra α .
Ya definidas las dos zonas, la regla de decisión consiste en rechazar H0 si el estadístico de contraste toma un valor perteneciente a la zona de rechazo, o mantener H0 si el estadístico de contraste toma un valor perteneciente a la zona de no-rechazo.
El tamaño de las zonas de rechazo y no-rechazo se determina fijando el valor de α, es decir, fijando el nivel de significación con el que se desea trabajar. Se suele tomar un 1% o un 5%.
La forma de dividir la distribución muestral en zona de rechazo y de no-rechazo depende de si el contraste es bilateral o unilateral. La zona crítica debe situarse donde puedan aparecer los valores muestrales incompatibles con H0.
Estadístico de contraste. Un estadístico de contraste es un resultado muestral que cumple la doble condición de:
- Proporcionar información empírica relevante sobre la afirmación propuesta en la H0.
- Poseer una distribución muestral conocida
Tipos de contrastes.
Contrastes paramétricos: Conocida una v.a. con una determinada distribución, se establecen afirmaciones sobre los parámetros de dicha distribución.
Contrastes no paramétricos: Las afirmaciones establecidas no se hacen en base a la distribución de las observaciones, que a priori es desconocida .
Tipos de hipótesis del contraste.
Hipótesis simples: La hipótesis asigna un único valor al parámetro desconocido, H: θ = θ0
Hipótesis compuestas: La hipótesis asigna varios valores posibles al parámetro desconocido, H: θ ∈ ( θ1 , θ2 )
La Reglas de decisión.
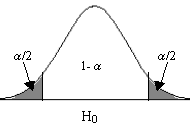
- Contrastes bilaterales: Si la hipótesis alternativa da lugar a una región crítica “a ambos lados” del valor del parámetro, diremos que el test es bilateral o de dos colas.
Se rechaza H0 si el estadístico de contraste cae en la zona crítica, es decir, si el estadístico de contraste toma un valor tan grande o tan pequeño que la probabilidad de obtener un valor tan extremo o más que el encontrado es menor que α /2.
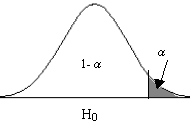
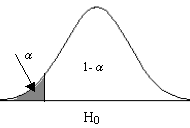
- Contraste unilateral: Si la hipótesis alternativa da lugar a una región crítica “a un solo lado del valor del parámetro”, diremos que el test es unilateral o de una sola cola
Se rechaza H0 si el estadístico de contraste cae en la zona crítica, es decir, si toma un valor tan grande que la probabilidad de obtener un valor como ese o mayor es menor que α .
|
Contraste bilateral H0 = θ = θ0 H1 = θ ≠ θ0 |
Contraste unilateral: Cola a la derecha H0 = θ ≤ θ0 H1 =θ > θ0 |
Contraste unilateral: Cola a la izquierda H0 = θ ≥ θ0 H1 = θ < θ0 |
La decisión:
Planteada la hipótesis, formulados los supuestos, definido el estadístico de contraste y su distribución muestral, y establecida la regla de decisión, el paso siguiente es obtener una muestra aleatoria de tamaño n, calcular el estadístico de contraste y tomar una decisión:
- Si es estadístico de contraste cae en la zona crítica se rechaza H0.
- Si es estadístico cae en la zona de no rechazo se mantiene H0.
Si rechazamos Ho afirmamos que la hipótesis es falsa, es decir, que afirmamos con una probabilidad α de equivocarnos, que hemos conseguido probar que esa hipótesis es falsa. Por el contrario, si no la rechazamos, no estamos afirmando que la hipótesis sea verdadera. Simplemente que no tenemos evidencia empírica suficiente para rechazarla y que se considera compatible con los datos.
Como conclusión, si se mantiene o no se rechaza H0, nunca se puede afirmar que es verdadera.
Errores de Tipo I y II.
-
Error de tipo I: Se comete cuando se decide rechazar la hipótesis nula H0 que en realidad es verdadera. La probabilidad de cometer ese error es α.
P[ Rechazar H0 / H0 es verdadera ] = α
-
Error de tipo II: Se comete cuando se decide no rechazar la hipótesis nula H0 que en realidad es falsa. La probabilidad de cometer ese error es β .
P[ No rechazar H0 / H0 es falsa ] = β
Por tanto,
- 1 – α es la probabilidad de tomar una decisión correcta cuando H0 es verdadera.
- 1 – β es la probabilidad de tomar una decisión correcta cuando H0 es falsa.
El siguiente cuadro resume las ideas:
- La dificultad al usar un procedimiento basado en datos muestrales es que debido a la variabilidad de muestreo, puede resultar una muestra no representativa, y por tanto, resultaría un rechazo erróneo de H0.
- La probabilidad de cometer un error de tipo I con nuestra decisión es una probabilidad conocida, pues el valor de α lo fija el propio investigador.
- Sin embargo, la probabilidad de cometer un error de tipo II, β , es un valor desconocido que depende de tres factores:
-
- La hipótesis H1 que consideremos verdadera.
- El valor de α .
- El tamaño del error típico (desviación típica) de la distribución muestral utilizada para efectuar el contraste.
-
Relaciones entre los errores de Tipo I y II. El estudio de las relaciones entre los errores lo realizamos mediante el contraste de hipótesis:
Para ello utilizamos la información muestral proporcionada por el estadístico media muestral ![]()
-
Cualquier valor atribuido a μ1 en H1 (siempre mayor a μ0) generará distribuciones muestrales distintas para la media muestral. Aunque todas tendrán la misma forma, unas estarán más alejadas que otras de la curva de H0, es decir, unas serán distintas de otras únicamente en el valor asignado a μ1 .
- Cuanto mayor es α , menor es β . Se relacionan de forma inversa.
-
Para una distancia dada entre μ0 y μ1 , el solapamiento entre las curvas correspondientes a uno y otro parámetro será tanto mayor cuanto mayor sea el error típico de la distribución muestral representada por esas curvas (cuanto mayor es el error típico de una distribución, más ancha es esa distribución). Y cuanto mayor sea el solapamiento, mayor será el valor de β .
En lugar de buscar procedimientos libres de error, debemos buscar procedimientos para los que no sea probable que ocurran ningún tipo de estos errores. Esto es, un buen procedimiento es aquel para el que es pequeña la probabilidad de cometer cualquier tipo de error. La elección de un valor particular de corte de la región de rechazo fija las probabilidades de errores tipo I y tipo II.
Debido a que H0 especifica un valor único del parámetro, hay un solo valor de α . Sin embargo, hay un valor diferente de β por cada valor del parámetro recogido en H1 .
En general, un buen contraste o buena regla de decisión debe tender a minimizar los dos tipos de error inherentes a toda decisión. Como α queda fijado por el investigador, trataremos de elegir una región donde la probabilidad de cometer el error de tipo II sea la menor .
Usualmente, se diseñan los contrastes de tal manera que la probabilidad a sea el 5% (0,05), aunque a veces se usan el 10% (0,1) o 1% (0,01) para adoptar condiciones más relajadas o más estrictas.
Potencia de un contraste. Es la probabilidad de decidir H1 cuando ésta es cierta
P[ decidir H1 / H1 es verdadera ] = 1 – β
El concepto de potencia se utiliza para medir la bondad de un contraste de hipótesis. Cuanto más lejana se encuentra la hipótesis H1 de H0 menor es la probabilidad de incurrir en un error tipo II y, por consiguiente, la potencia tomará valores más próximos a 1.
Si la potencia en un contraste es siempre muy próxima a 1 entonces se dice que el estadístico de contraste es muy potente para contrastar H0 ya que en ese caso las muestras serán, con alta probabilidad, incompatibles con H0 cuando H1 sea cierta.
Por tanto puede interpretarse la potencia de un contraste como su sensibilidad o capacidad para detectar una hipótesis alternativa. La potencia de un contraste cuantifica la capacidad del criterio utilizado para rechazar H0 cuando esta hipótesis sea falsa
Es deseable en un contraste de hipótesis que las probabilidades de ambos tipos de error fueran tan pequeñas como fuera posible. Sin embargo, con una muestra de tamaño prefijado, disminuir la probabilidad del error de tipo I, α, conduce a incrementar la probabilidad del error de tipo II, β. El recurso para aumentar la potencia del contraste, esto es, disminuir la probabilidad de error de tipo II, es aumentar el tamaño muestral lo que en la práctica conlleva un incremento de los costes del estudio que se quiere realizar
El concepto de potencia nos permite valorar cual entre dos contrastes con la misma probabilidad de error de tipo I, α, es preferible. Se trata de escoger entre todos los contrastes posibles con α prefijado aquel que tiene mayor potencia, esto es, menor probabilidad β de incurrir en el error de tipo II. En este caso el Lema de Neyman-Pearson garantiza la existencia de un contraste de máxima potencia y determina cómo construirlo.
Potencia de un contraste de hipótesis
Contrastes de hipótesis paramétricos
El propósito de los contrastes de hipótesis es determinar si un valor propuesto (hipotético) para un parámetro u otra característica de la población debe aceptarse como plausible con base en la evidencia muestral.
Podemos considerar las siguientes etapas en la realización de un contraste:
-
-
El investigador formula una hipótesis sobre un parámetro poblacional, por ejemplo que toma un determinado valor
-
Selecciona una muestra de la población
-
Comprueba si los datos están o no de acuerdo con la hipótesis planteada, es decir, compara la observación con la teoría
- Si lo observado es incompatible con lo teórico entonces el investigador puede rechazar la hipótesis planteada y proponer una nueva teoría
- Si lo observado es compatible con lo teórico entonces el investigador puede continuar como si la hipótesis fuera cierta.
-
Los contrastes de hipótesis que construye SPSS son los proporcionados por las Pruebas T, estas son de tres tipos: Prueba T para una muestra, Prueba T para muestras independientes y Prueba T para muestras relacionadas
Contrastes de hipótesis para la media de una población normal
El objetivo es probar uno de los siguientes contrastes de hipótesis con respecto de μ
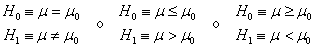
donde μ0 es un valor conocido dado de antemano. Para ello se toma una m.a.s. concreta x1, x2, …, xn cuya media valdrá: ![]() .
.
Se distinguen dos situaciones: a) Varianza poblacional conocida y b) varianza poblacional desconocida. El programa SPSS sólo resuelve el segundo caso.
En el caso de varianza poblacional desconocida, el estadístico de contraste que se utiliza sigue una distribución t_Student y, bajo la hipótesis nula H0:μ = μ0 dicho estadístico tiene la siguiente expresión:
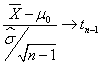
Fijado un nivel de significación α
a) Para la hipótesis alternativa H1:μ ≠ μ0 la correspondiente región de no rechazo es (- tα/2;n-1, tα/2;n-1) y el estadístico de contraste adopta la forma
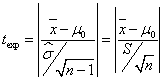
y se utiliza la siguiente regla de decisión
![]()
b) Para la hipótesis alternativa H1:μ > μ0 la correspondiente región de no rechazo es (-∞, tα;n-1) y el estadístico de contraste adopta la forma
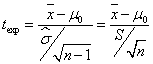
y se utiliza la siguiente regla de decisión ![]()
c) Para la hipótesis alternativa H1:μ < μ0 la correspondiente región de no rechazo es (- tα;n-1,∞), el estadístico de contrate es el anterior y se adopta la siguiente regla de decisión
![]()
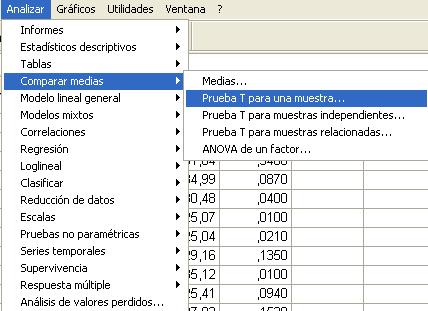
El procedimiento que utiliza SPSS es la Prueba T para una muestra que contrasta si la media de una población difiere de una constante especificada. Para obtener una Prueba T para una muestra se elige, en el menú principal, Analizar/Comparar medias/Prueba T para una muestra…
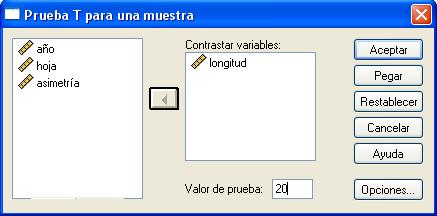
En la salida correspondiente se selecciona una o más variables cuantitativas para contrastarlas con el mismo valor supuesto.
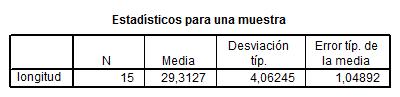
Por ejemplo, en la siguiente salida se muestra un contraste para el caso en que la media de la variable longitud sea igual a 20 (Valor de prueba: 20)
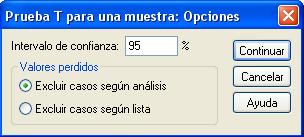
Pulsando Opciones… se puede elegir el nivel de confianza.
Se pulsa Continuar y Aceptar. Se obtiene un resumen estadístico para la muestra y la salida del procedimiento.
Esta salida muestra el tamaño muestral, la media, la desviación típica y error típico de la media.
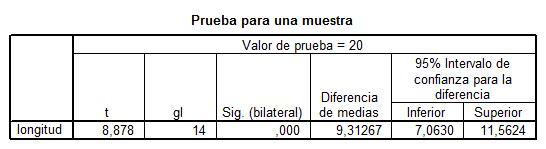
Esta salida muestra los resultados del contraste de la t de Student con un intervalo de confianza para la diferencia entre el valor observado y el valor teórico (contrastado). Cada una de las columnas de la tabla muestra:
- t = 8,878: El valor experimental del estadístico de contraste
- gl = 14: Los grados de libertad
- Sig.= 0,000: El p-valor o nivel crítico del contraste
- Diferencia de medias = 9.31267: Es la diferencia entre la media teórica (20) y la media observada (29.3127)
- 95% Intervalo de confianza = (7.063, 11.5624): Es el intervalo de confianza para la diferencia entre la media teórica y la media observada al nivel de confianza del 95%.
Supuesto práctico 1
Se realiza un experimento para estudiar el nivel (en minutos) que se requiere para que la temperatura del cuerpo de un lagarto del desierto alcance los 45º partiendo de la temperatura normal de su cuerpo mientras está en la sombra. Se obtuvieron las siguientes observaciones: 10.1 ; 12.5 ; 12.2 ; 10.2 ; 12.8 ; 12.1 ; 11.2 ; 11.4 ; 10.7 ; 14.9 ; 13.9 ; 13.3. Se pide:
a) Hallar estimaciones puntuales de la media y la varianza
b) Supóngase que la variable X: “Tiempo en alcanzar los 45º sigue una ley Normal
b1) ¿Puede concluirse que el tiempo medio requerido para alcanzar la dosis letal es de 15 minutos?
b2) ¿Puede concluirse que el tiempo medio requerido para alcanzar la dosis letal es inferior a 13 minutos?
Solución
a) Hallar estimaciones puntuales de la media y la varianza b1) ¿Puede concluirse que el tiempo medio requerido para alcanzar la dosis letal es de 15 minutos?.
b1) ¿Puede concluirse que el tiempo medio requerido para alcanzar la dosis letal es de 15 minutos?.
Se realiza el siguiente contraste de hipótesis: ![]()
El procedimiento que utiliza SPSS es la Prueba T para una muestra que contrasta si la media de una población difiere de una constante especificada. Para obtener una Prueba T para una muestra se elige, en el menú principal. Analizar/Comparar medias/Prueba T para una muestra… En la salida correspondiente se selecciona tiempo para la Variable para contrastar y el valor de la prueba se pone 15
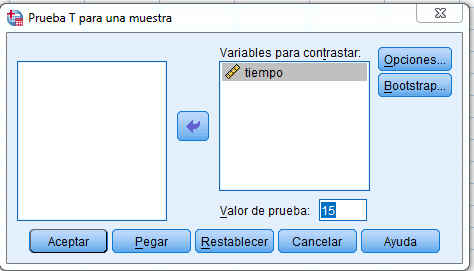
Se pulsa Aceptar y se obtiene la siguiente salida
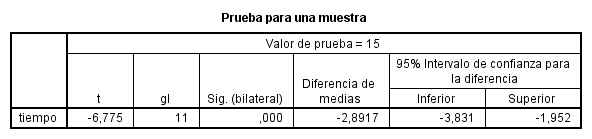
El valor del estadístico de contraste experimental, -6.775, deja a la derecha una área menor que 0.000 < 0.025. Por lo tanto se rechaza la hipótesis nula de que el tiempo medio requerido para alcanzar la dosis letal es de 15 minutos.
b2) ¿Puede concluirse que el tiempo medio requerido para alcanzar la dosis letal es inferior a 13 minutos?
Se realiza el siguiente contraste de hipótesis: ![]()
Se selecciona en el menú principal, Analizar/Comparar medias/Prueba T para una muestra. En la salida correspondiente se selecciona tiempo para la Variable para contrastar y el valor de la prueba se pone 13
Se pulsa Aceptar y se obtiene la siguiente salida
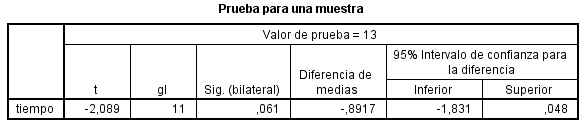
El valor del estadístico de contraste experimental, -2.089, deja a la derecha una área 0.030 < 0.05. Por lo tanto se rechaza la hipótesis nula y se concluye que el tiempo medio requerido para alcanzar la dosis letal es inferior a 13 minutos.
Contrastes de hipótesis para dos muestras independientes
De un modo general, dos muestras se dice que son independientes cuando las observaciones de una de ellas no condicionan para nada a las observaciones de la otra, siendo dependientes en caso contrario. En realidad, el tipo de dependencia que se considera a estos efectos es muy especial: cada dato de una muestra tiene un homónimo en la otra, con el que está relacionada, de ahí el nombre alternativo de muestras apareadas. Por ejemplo, supongamos que se quiere estudiar el efecto de un medicamento, sobre la hipertensión, a un grupo de 20 individuos. El experimento se podría planificar de dos formas:
-
Aplicando el medicamento a 10 de estos individuos y dejando sin tratamiento al resto. Transcurrido un tiempo se miden las presiones sanguíneas de ambos grupos y se contrasta la hipótesis H0: µ1= µ2 vs H1: µ1 <>µ2 para evaluar si las medias son iguales o no. Como las muestras están formadas por individuos distintos sin relación entre sí, se dirá que son muestras independientes.
-
Aplicando el medicamento a los 20 individuos disponibles y anotando su presión sanguínea antes y después de la administración del mismo. En este caso los datos vienen dados por parejas, presión antes y después y tales datos están relacionados entre sí. Las muestras son apareadas.
El paquete estadístico SPSS realiza el procedimiento Prueba T para muestras independientes; en este procedimiento se compara la media de dos poblaciones normales e independientes. Para realizar dicho contraste los sujetos deben asignarse aleatoriamente a las dos poblaciones, de forma que cualquier diferencia en la respuesta sea debida al tratamiento (o falta de tratamiento) y no a otros factores.
El procedimiento Prueba T para muestras independientes mediante SPSS contrasta si la diferencia de las medias de dos poblaciones normales e independientes difiere de una constante especificada.El objetivo es probar uno de los siguientes contrastes de hipótesis![]() conocidas las medias muestrales y los tamaños muestrales.
conocidas las medias muestrales y los tamaños muestrales.
Para obtener una Prueba T para muestras independiente se selecciona, en el menú principal, Analizar/Comparar medias/Prueba T para muestras independientes…
Se accede a la siguiente ventana
donde se puede seleccionar una o más variables cuantitativas y se calcula una Prueba T diferente para cada variable. Por ejemplo, en esta salida se selecciona la variable asimetría.
A continuación se selecciona una sola variable de agrupación, en nuestro caso, la variable Parte y se pulsa Definir Grupos para especificar los códigos de los grupos que se quieran comparar. Vamos a contrastar la igualdad de medias de la variable asimetría según la variable Parte (Canopy, Sprouts)
Pulsando Definir Grupos… se muestra la siguiente pantalla
donde se especifican el número de grupos que se quieren comparar.
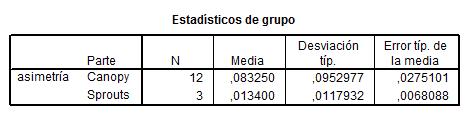
Se pulsa Continuar y después Aceptar y se obtienen las siguientes pantallas que muestran un resumen estadístico para las dos muestras y la salida del procedimiento.
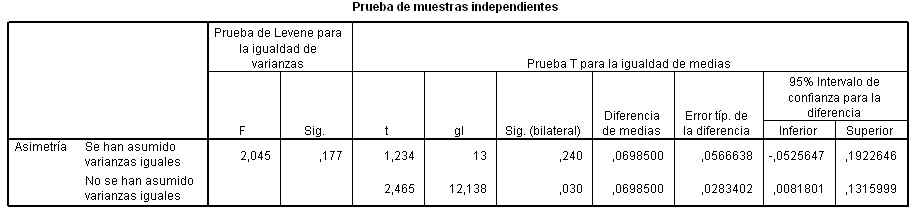
Para realizar un contraste de diferencia de medias de dos poblaciones independientes hay que contrastar previamente las varianzas de dichas poblaciones.
Esta salida nos muestra el valor experimental del estadístico de contraste (Fexp = 2.045), este valor deja a la derecha un área igual a 0.176 (Sig.= 0.176), por lo tanto no se puede rechazar la hipótesis nula de igualdad de varianzas.
A continuación se realiza el contraste para la diferencia de medias suponiendo que las varianzas son iguales. La tabla nos muestra el valor experimental del estadístico de contraste (texp = 1.233) y el p-valor = 0.240 (Sig.= 0.240), por lo tanto no se puede rechazar la hipótesis nula de igualdad de medias. También, se puede concluir el contraste observando que el intervalo de confianza para la diferencia de medias (-0.05256, 0.192264) contiene al cero.
Supuesto práctico 2
Se quieren comparar dos poblaciones de ranas pipiens aisladas geográficamente. Para ello se toman dos muestras de ambas poblaciones de tamaño 12 y 10 y se les mide la longitud del cuerpo expresado en milímetros.
Población 1: 20,1; 22,5; 22,2 ; 30,2 ; 22,8 ; 22,1 ; 21,2 ; 21,4 ; 20,7 ; 24,9 ; 23,9 ; 23,3
Población 2: 25,3 ; 31,2 ; 22,4 ; 23,1 ; 26,4 ; 28,2 ;21,3 ;31,1 ;26,2 ;21,4
Contrastar la hipótesis de igualdad de medias a un nivel de significación del 1%. (Suponiendo que la longitud se distribuya según una Normal).
Solución
Sean las variables aleatorias
X: “Longitud del cuerpo de ranas 1”; X→ N(μX, σX)
Y: “Longitud del cuerpo de ranas 2”; X→ N(μY, σY)
Se pide el siguiente contraste![]()
Para realizar un contraste de muestras independientes los datos se deben introducir en el Editor de SPSS de la siguiente forma: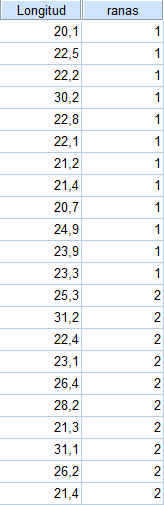
A continuación se selecciona, en el menú principal, Analizar/Comparar medias/Prueba T para muestras independientes y se obtiene la siguiente salida
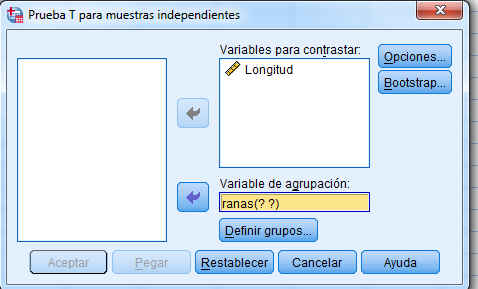
Se pulsa Definir grupos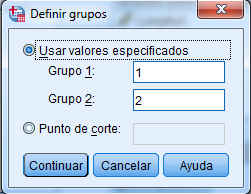
donde se especifican el número de grupos que se quieren comparar. Se pulsa Continuar y Opciones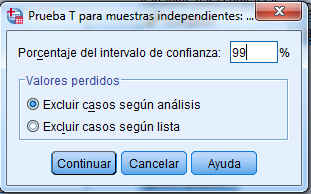
La casilla de porcentaje del intervalo de confianza se rellena con 99. Se pulsa Continuar y Aceptar y se obtiene el siguiente resultado Para realizar un contraste de diferencia de medias de dos poblaciones independientes hay que contrastar previamente las varianzas de dichas poblaciones.
Para realizar un contraste de diferencia de medias de dos poblaciones independientes hay que contrastar previamente las varianzas de dichas poblaciones.
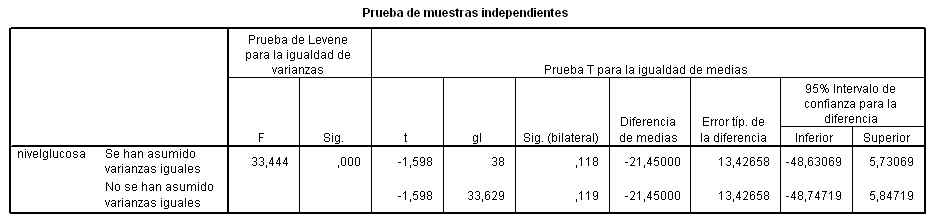
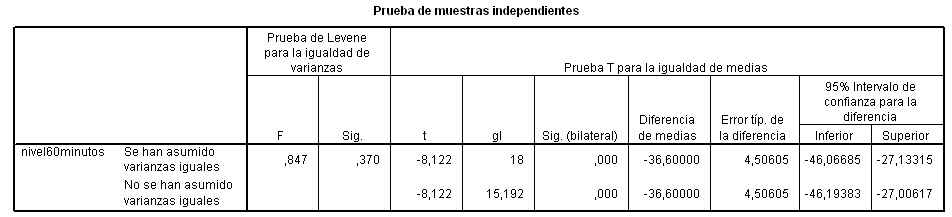
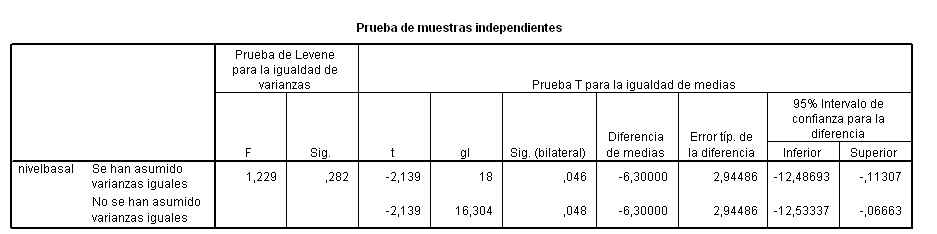
Esta salida nos muestra el valor experimental del estadístico de contraste (Fexp = 2.110), este valor deja a la derecha un área igual a 0.162 (Sig.= 0.162), por lo tanto no se puede rechazar la hipótesis nula de igualdad de varianzas.
A continuación se realiza el contraste para la diferencia de medias suponiendo que las varianzas son iguales. La tabla nos muestra el valor experimental del estadístico de contraste (texp = -2.010) y el p-valor = 0.0508 (Sig.= 0.058), por lo tanto no se puede rechazar la hipótesis nula de igualdad de medias. También, se puede concluir el contraste observando que el intervalo de confianza para la diferencia de medias (-5.5399, 0.1032) contiene al cero.
Contrastes de hipótesis para muestras apareadas
En las muestras apareadas, cada observación de una muestra está emparejado con una observación de la otra muestra, por lo tanto consideramos parejas de valores (x, y).
El paquete estadístico SPSS realiza el procedimiento Prueba T para muestras apareadas; en este procedimiento se comparan las medias de dos variables de un solo grupo. Calcula las diferencias entre los valores de cada caso, Di = Xi– Yi y contrasta si la media difiere de cero.Es decir, contrastar la hipótesis nula H0: μX-μY = 0 es equivalente a contrastar H0: μD =0
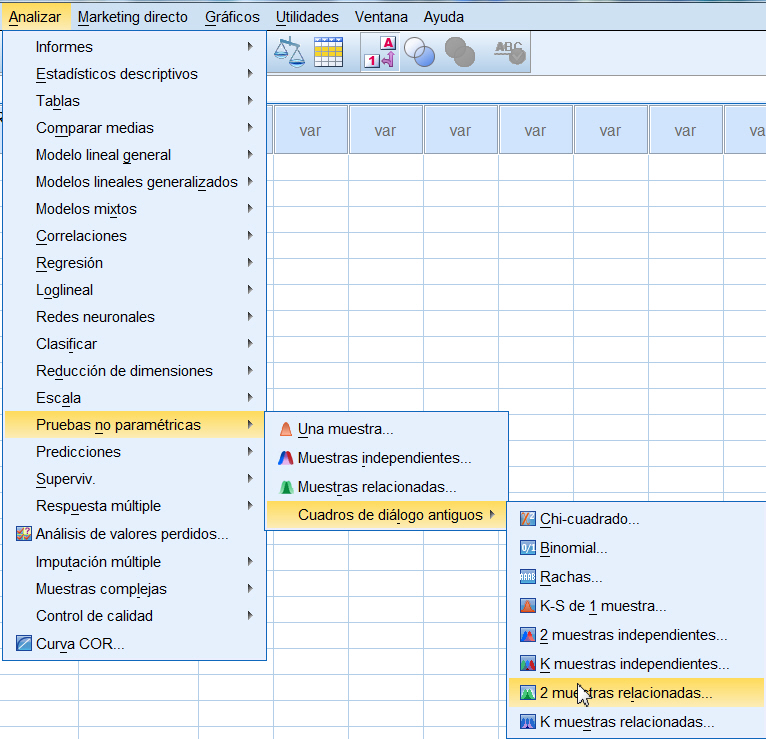
Para obtener una Prueba T para muestras relacionadas se elige en los menús Analizar/Comparar medias/Prueba T para muestras relacionadas…
Se accede a la siguiente ventana
donde se selecciona un par de variables pulsando en cada una de ellas. La primera variable aparecerá en la sección Selecciones actuales como Variable 1 y la segunda aparecerá como Variable 2. Una vez seleccionado el par de variables, en nuestro caso Asim95 y Asim97, se pulsa el botón de flecha para moverlas a la ventana de Variables relacionadas. Se puede realizar el contraste para más de una pareja de variables simultáneamente.
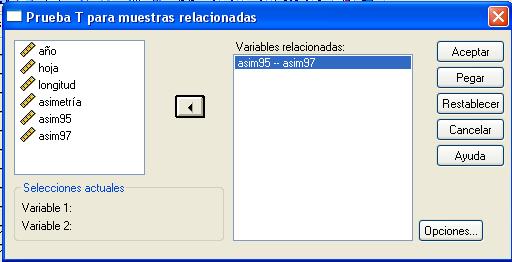 Al pulsar Continuar y después Aceptar se obtiene un resumen estadístico para las dos muestras y la salida del procedimiento.
Al pulsar Continuar y después Aceptar se obtiene un resumen estadístico para las dos muestras y la salida del procedimiento.
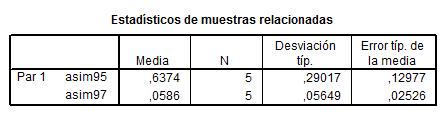 Para cada variable se presenta la media, tamaño de la muestra, desviación típica y error típico de la media.
Para cada variable se presenta la media, tamaño de la muestra, desviación típica y error típico de la media.
 Esta salida muestra para cada pareja de variables: el número de datos, el coeficiente de correlación y el p-valor asociado al contraste H0: r = 0 frente a H1: r <> 0. El coeficiente de correlación es igual a -0.681, por lo tanto las variables están relacionadas en sentido inverso, cuando una crece la otra decrece. Observando el p-valor (0.206) deducimos que no se puede rechazar la hipótesis nula (H0: r = 0) por lo tanto no existe correlación entre las variables. (La correlación no es significativa).
Esta salida muestra para cada pareja de variables: el número de datos, el coeficiente de correlación y el p-valor asociado al contraste H0: r = 0 frente a H1: r <> 0. El coeficiente de correlación es igual a -0.681, por lo tanto las variables están relacionadas en sentido inverso, cuando una crece la otra decrece. Observando el p-valor (0.206) deducimos que no se puede rechazar la hipótesis nula (H0: r = 0) por lo tanto no existe correlación entre las variables. (La correlación no es significativa).
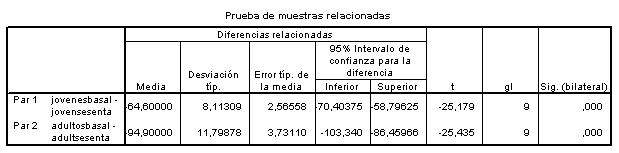
 Esta salida muestra el valor experimental del estadístico de contraste (t = 3.908) y el p-valor igual a 0.017, por lo tanto se debe rechazar la hipótesis nula de igualdad de medias.
Esta salida muestra el valor experimental del estadístico de contraste (t = 3.908) y el p-valor igual a 0.017, por lo tanto se debe rechazar la hipótesis nula de igualdad de medias.
Supuesto práctico 3
Se realiza un estudio, en el que participan 10 individuos, para investigar el efecto del ejercicio físico en el nivel de colesterol en plasma. Antes del ejercicio se tomaron muestras de sangre para determinar el nivel de colesterol de cada individuo. Después, los participantes fueron sometidos a un programa de ejercicios. Al final de los ejercicios se tomaron nuevamente muestras de sangre y se obtuvo una segunda lectura del nivel de colesterol. Los resultados se muestran a continuación.
Nivel previo: 182; 230; 160; 200; 160; 240; 260; 480; 263; 240
Nivel posterior: 190; 220; 166; 150; 140; 220; 156; 312; 240; 250
Se quiere saber si el ejercicio físico ha reducido el nivel de colesterol para un nivel de confianza del 95%.
Solución
Se pide el siguiente contraste
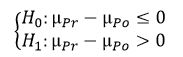
Para realizar un contraste de muestras apareadas los datos se deben introducir en el Editor de SPSS de la siguiente forma: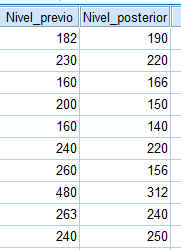
A continuación se selecciona, en el menú principal, Analizar/Comparar medias/Prueba T para muestras relacionadas y se obtiene la siguiente salida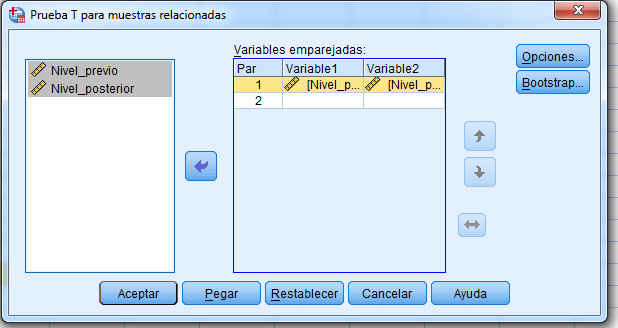
donde se selecciona el par de variables pulsando en cada una de ellas, se pulsa el botón de flecha para moverlas a la ventana de Variables relacionadas. Se pulsa Aceptar y se obtiene las siguientes salidas

Esta salida muestra para cada pareja de variables: el número de datos, (N = 10) el coeficiente de correlación (0.816) y el p-valor (0.004) asociado al contraste H0: r = 0 frente a H1: r <> 0. El coeficiente de correlación es igual a 0.816, por lo tanto las variables están relacionadas en sentido directo, cuando una crece la otra también crece. Observando el p-valor (0.004) deducimos que se puede rechazar la hipótesis nula (H0: r = 0) por lo tanto existe correlación entre las variables. (La correlación es significativa).
 Esta salida muestra el valor experimental del estadístico de contraste (t = 2.053) y Sig. (bilateral) es 0.070. En nuestro caso es un contraste unilateral por lo tanto el valor de Sig es 0.035 menor que 0.05, y se debe rechazar la hipótesis nula.
Esta salida muestra el valor experimental del estadístico de contraste (t = 2.053) y Sig. (bilateral) es 0.070. En nuestro caso es un contraste unilateral por lo tanto el valor de Sig es 0.035 menor que 0.05, y se debe rechazar la hipótesis nula.
Contrastes de hipótesis para el parámetro p de una distribución Binomial
El contraste de hipótesis para el parámetro p (proporción de éxitos) de una distribución Binomial se basa en la distribución del estadístico muestral ![]() para un tamaño muestral n suficientemente grande.
para un tamaño muestral n suficientemente grande.
Denotando por p y ![]() las proporciones de éxitos de la población y de dicha muestra, respectivamente, se verifica que
las proporciones de éxitos de la población y de dicha muestra, respectivamente, se verifica que 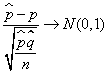 El objetivo es probar uno de los siguientes contrastes
El objetivo es probar uno de los siguientes contrastes![]() a) Para la hipótesis alternativa H1:p ≠ p0 la correspondiente región de no rechazo es (- zα/2, zα/2) y el estadístico de contraste bajo la hipótesis nula H0:p = p0 adopta la siguiente expresión
a) Para la hipótesis alternativa H1:p ≠ p0 la correspondiente región de no rechazo es (- zα/2, zα/2) y el estadístico de contraste bajo la hipótesis nula H0:p = p0 adopta la siguiente expresión 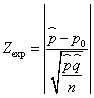 b) Para la hipótesis alternativa H1:p > p0 la correspondiente región de no rechazo es (-∞, zα)
b) Para la hipótesis alternativa H1:p > p0 la correspondiente región de no rechazo es (-∞, zα)
c) Para la hipótesis alternativa H1:p < p0 la correspondiente región de no rechazo es (-zα, ∞, ).
En los casos b) y c) el estadístico de contraste adopta la siguiente expresión 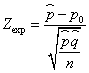
El paquete estadístico SPSS realiza el procedimiento Binomial, para ello se selecciona en el menú principal, Analizar/Cuadros de diálogos antiguos/Binomial
Supuesto práctico 4
Se ignora la proporción de familias numerosas y con el fin de determinar dicha proporción se toma una muestra de 800 familias siendo la proporción observada de 0.18. Se puede afirmar que la proporción de familias numerosas es 0.20.
Solución
Se pide realizar el siguiente contraste H0: P = 0.20 frente a la alternativa H1: p≠20.
Según el enunciado de una muestra de 800 familias la proporción observada de familias numerosas es 0.18. Por lo tanto 144 familias son numerosas y 656 no lo son.
Introducimos los datos en SPSS
Ponderamos los datos, para ello seleccionamos Datos/Ponderar casos
En la ventana resultante ponderamos los casos mediante la variable frecuencia y pulsamos Aceptar.
A continuación realizamos el contraste, para ello seleccionamos en el menú principal, Analizar/Pruebas no parámetricas/Cuadros de diálogos antiguos/Binomial. En la ventana resultante introducimos familias en Lista Contrastar variables: y en Proporción de prueba ponemos 0.20
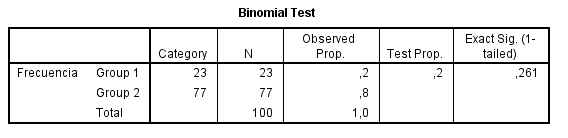
Pulsamos Aceptar y obtenemos al siguiente salida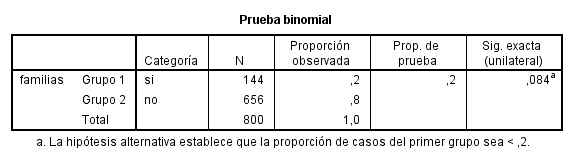 El p-valor de la prueba (Sig. exacta (unilateral)) es 0.084 mayor que 0.05. Por lo tanto no se rechaza la Hipótesis nula. Se puede afirmar que la proporción de familias numerosas es 0.20.
El p-valor de la prueba (Sig. exacta (unilateral)) es 0.084 mayor que 0.05. Por lo tanto no se rechaza la Hipótesis nula. Se puede afirmar que la proporción de familias numerosas es 0.20.
Contrastes de hipótesis para dos proporciones independientes. Muestras grandes
El contraste de hipótesis para la comparación de dos proporciones independientes se basa en la distribución aproximada de un estadístico muestral que requiere muestras grandes.
Supongamos dos muestras aleatorias de tamaños nX y nY, suficientemente grandes y denotamos por ![]() las proporciones de éxitos de cada una de las poblaciones y de dichas muestras, respectivamente. Se verifica que
las proporciones de éxitos de cada una de las poblaciones y de dichas muestras, respectivamente. Se verifica que 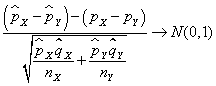 Fijado un nivel de significación α, la región de no rechazo para el contraste bilateral es (- zα/2, zα/2) y el estadístico de contraste, bajo la hipótesis nula H0: pX– pY=(pX– pY)0 , adopta la forma
Fijado un nivel de significación α, la región de no rechazo para el contraste bilateral es (- zα/2, zα/2) y el estadístico de contraste, bajo la hipótesis nula H0: pX– pY=(pX– pY)0 , adopta la forma 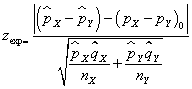 El paquete estadístico SPSS no incluye el cálculo de dicho estadístico pero permite el cálculo de otros cuatro estadísticos para muestras grandes y el estadístico exacto de Fisher para muestras pequeñas.
El paquete estadístico SPSS no incluye el cálculo de dicho estadístico pero permite el cálculo de otros cuatro estadísticos para muestras grandes y el estadístico exacto de Fisher para muestras pequeñas.
El contraste de comparación de dos proporciones es un caso particular del contraste de homogeneidad de dos muestras de una variable cualitativa cuando ésta sólo presenta dos modalidades. Por ello, el procedimiento que vamos a realizar es el análisis de una tabla de contingencia 2×2.
Para obtener el procedimiento Tablas de contingencia se elige en los menús Analizar/Estadísticos descriptivos/Tablas de contingencia…
En la ventana emergente se seleccionan las variables dicotómicas que se van a contrastar. Por ejemplo, en la siguiente salida se muestra el procedimiento de Tablas de contingencia en el que se comparan las variables Sexo y Fumador, para ello se han seleccionado la variable Sexo y mediante el botón de flecha se ha pasado al campo Filas: y la variable Fumador que se ha pasado al campo Columnas: (Se desea comparar la proporción de fumadores en los grupos (hombres y mujeres)).
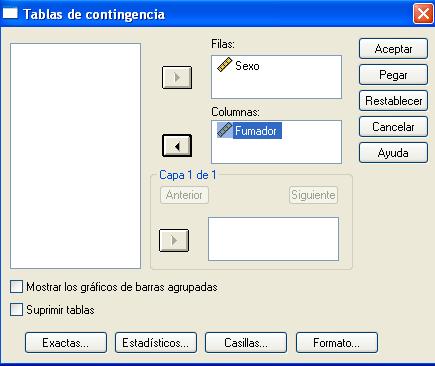 Se pulsa el botón Casillas… y se selecciona en Frecuencias (Observadas) y en Porcentajes (Fila)
Se pulsa el botón Casillas… y se selecciona en Frecuencias (Observadas) y en Porcentajes (Fila)
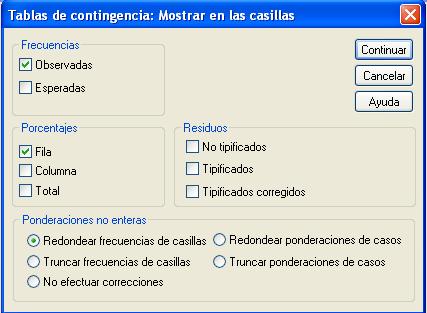 Se pulsa Continuar y en la pantalla correspondiente se pulsa el botón Estadísticos… y se selecciona Chi-cuadrado
Se pulsa Continuar y en la pantalla correspondiente se pulsa el botón Estadísticos… y se selecciona Chi-cuadrado
 Se pulsa Continuar y Aceptar. Se muestran la Tabla de contingencia y los contrastes Chi-cuadrado
Se pulsa Continuar y Aceptar. Se muestran la Tabla de contingencia y los contrastes Chi-cuadrado
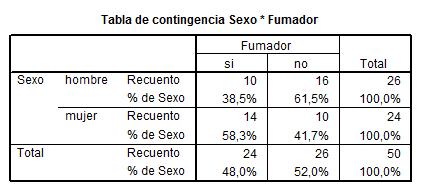 Cada casilla de esta tabla muestra la frecuencia observada y el porcentaje que ésta representa sobre el total de la fila enla tabla de contingencia Sexo * Fumador. Las proporciones muestrales que vamos a comparar son 10/26 y 14/24. Para ello se realiza un contraste bilateral para evaluar si existen diferencias significativas entre ambas proporciones muestrales (H0: p1 – p2=0 frente a H1: p1 – p2 <>0)
Cada casilla de esta tabla muestra la frecuencia observada y el porcentaje que ésta representa sobre el total de la fila enla tabla de contingencia Sexo * Fumador. Las proporciones muestrales que vamos a comparar son 10/26 y 14/24. Para ello se realiza un contraste bilateral para evaluar si existen diferencias significativas entre ambas proporciones muestrales (H0: p1 – p2=0 frente a H1: p1 – p2 <>0)
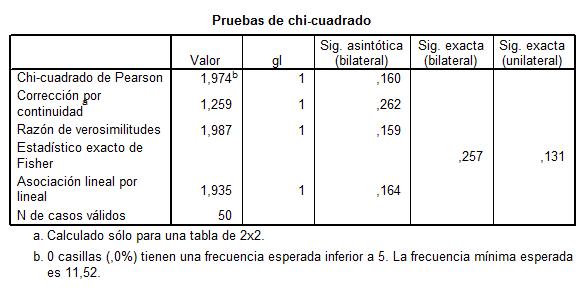 Esta tabla muestra los resultados de cinco estadísticos para la comparación de ambas proporciones. Generalmente, en el caso de muestras grandes se elige el estadístico Corrección por continuidad. Dicho estadístico calcula el estadístico Chi-cuadrado con la corrección por continuidad de Yates. En nuestro caso, el valor de dicho estadístico es 1.259 y el p-valor asociado es 0.262 (Sig. asintótica bilateral) por lo tanto no se debe rechazar la Hipótesis nula, es decir las diferencias observadas entre las proporciones de fumadores en los dos grupos no son estadísticamente significativas.
Esta tabla muestra los resultados de cinco estadísticos para la comparación de ambas proporciones. Generalmente, en el caso de muestras grandes se elige el estadístico Corrección por continuidad. Dicho estadístico calcula el estadístico Chi-cuadrado con la corrección por continuidad de Yates. En nuestro caso, el valor de dicho estadístico es 1.259 y el p-valor asociado es 0.262 (Sig. asintótica bilateral) por lo tanto no se debe rechazar la Hipótesis nula, es decir las diferencias observadas entre las proporciones de fumadores en los dos grupos no son estadísticamente significativas.
En el caso de muestras pequeñas, se decide a partir del Estadístico exacto de Fisher.

Supuesto práctico 5
Se sospecha que añadiendo al tratamiento habitual para la curación de una enfermedad un medicamento A, se consigue mayor número de curaciones. Tomamos dos grupos de enfermos de 100 individuos cada uno. A un grupo se le suministra el medicamento A y se curan 60 enfermos y al otro no se le suministra, curándose 55 enfermos. ¿Es efectivo el tratamiento A en la curación de la enfermedad?
Solución
Se pide realizar el siguiente contraste de hipótesis![]() Se introducen los datos en SPSS
Se introducen los datos en SPSS Se ponderan los casos
Se ponderan los casos Se pulsa Aceptar.
Se pulsa Aceptar.
Como hemos dicho anteriormente, el paquete estadístico SPSS no incluye el cálculo de dicho estadístico pero permite el cálculo de otros cuatro estadísticos para muestras grandes y el estadístico exacto de Fisher para muestras pequeñas.
El contraste de comparación de dos proporciones es un caso particular del contraste de homogeneidad de dos muestras de una variable cualitativa cuando ésta sólo presenta dos modalidades. Por ello, el procedimiento que vamos a realizar es el análisis de una tabla de contingencia 2×2.
Para obtener el procedimiento Tablas de contingencia se elige en los menús Analizar/Estadísticos descriptivos/Tablas de contingencia…
Se pulsa el botón Casillas… y se selecciona en Frecuencias (Observadas) y en Porcentajes (Columna)
Se pulsa Continuar y en la salida correspondiente se pulsa Estadísticos, donde se elige Chi-cuadrado
Se pulsa Continuar y Aceptar y se muestran las siguientes salidas 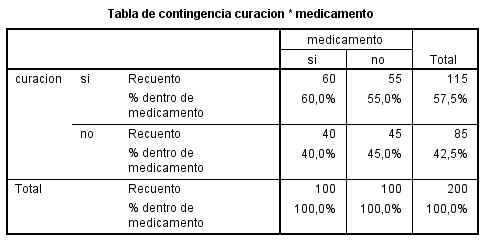
Cada casilla de esta tabla muestra la frecuencia observada y el porcentaje que ésta representa sobre el total de la columna en la tabla de contingencia Curación * Medicamento. Las proporciones muestrales que vamos a comparar son 60/100 y 55/100 . Para ello se realiza un contraste bilateral para evaluar si existen diferencias significativas entre ambas proporciones muestrales (H0: pX – pY<=0 frente a H1: pX – pY >0).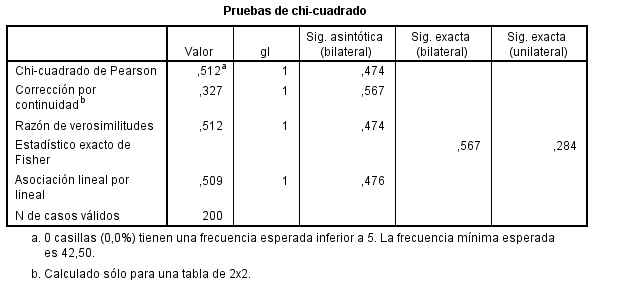
Esta tabla muestra los resultados de cinco estadísticos para la comparación de ambas proporciones. Generalmente, en el caso de muestras grandes se elige el estadístico Corrección por continuidad. Dicho estadístico calcula el estadístico Chi-cuadrado con la corrección por continuidad de Yates. En nuestro caso, el valor de dicho estadístico es 0.327 y el p-valor asociado es 0.567 (Sig. asintótica bilateral) por lo tanto no se debe rechazar la Hipótesis nula. Podemos afirmar que el medicamento A no consigue un mayor número de curaciones.
Contrastes de hipótesis no paramétricos
En la sesión anterior hemos estudiado contrastes de hipótesis acerca de parámetros poblacionales, tales como la media y la varianza, de ahí el nombre de contrastes paramétricos. En estadística paramétrica se trabaja bajo el supuesto de que las poblaciones poseen distribuciones conocidas, donde cada función de distribución teórica depende de uno o más parámetros poblacionales. Sin embargo, en muchas situaciones, es imposible especificar la forma de la distribución poblacional. El proceso de obtener conclusiones directamente de las observaciones muestrales, sin formar los supuestos con respecto a la forma matemática de la distribución poblacional se llama teoría no paramétrica.
En esta sesión vamos a realizar procedimientos que no exigen ningún supuesto, o muy pocos acerca de la familia de distribuciones a la que pertenece la población, y cuyas observaciones pueden ser cualitativas o bien se refieren a alguna característica ordenable. Estos procedimientos reciben el nombre de Contrastes de hipótesis no paramétricos.
Así, uno de los objetivos de esta sesión es el estudio de contrates de hipótesis para determinar si una población tiene una distribución teórica específica. La técnica que nos introduce a estudiar esas cuestiones se llama Contraste de la Chi-cuadrado para la Bondad de Ajuste. Una variación de este contraste se emplea para resolver los Contrastes de Independencia. Tales contrastes pueden utilizarse para determinar si dos características (por ejemplo preferencia política e ingresos) están relacionadas o son independientes. Y, por último estudiaremos otra variación del contraste de la bondad de ajuste llamado Contraste de Homogeneidad. Tal contraste se utiliza para estudiar si diferentes poblaciones, son similares (u homogéneas) con respecto a alguna característica. Por ejemplo, queremos saber si las proporciones de votantes que favorecen al candidato A, al candidato B o los que se abstuvieron son las mismas en dos ciudades.
El procedimiento Prueba de la Chi-cuadrado
Hemos agrupado los procedimientos en los que el denominador común a todos ellos es que su tratamiento estadístico se aborda mediante la distribución Chi-cuadrado. El procedimiento Prueba de Chi-cuadrado tabula una variable en categorías y calcula un estadístico de Chi-cuadrado. Esta prueba compara las frecuencias observadas y esperadas en cada categoría para contrastar si todas las categorías contienen la misma proporción de valores o si cada categoría contiene una proporción de valores especificada por el usuario.
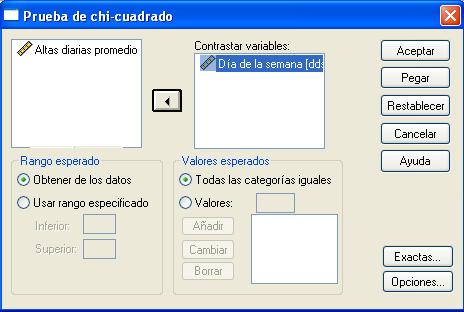
Para obtener una prueba de Chi-cuadrado se eligen en los menús Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/Chi-cuadrado…
En la salida correspondiente se selecciona una o más variables de contraste. Cada variable genera una prueba independiente.
Por ejemplo, en la siguiente salida se muestra una Prueba de Chi-cuadrado en la que la variable a contrastar es Día de la semana (Se desea saber si el número de altas diarias de un hospital difiere dependiendo del día de la semana)
Se pulsa Opciones… para obtener estadísticos descriptivos, cuartiles y controlar el tratamiento de los datos perdidos
 Al pulsar Continuar y Aceptar se muestran las siguientes salidas
Al pulsar Continuar y Aceptar se muestran las siguientes salidas
En esta salida se muestra:
- N observado: Muestra la frecuencia observada para cada fila (día). Se observa, en esta tabla, que el número de altas diariasde un total de 589 altas por semana es: 44 el domingo, 78 el lunes etc.
- N esperado: Muestra el valor esperado para cada fila (suma de las frecuencias observadas dividida por el número de filas). En este ejemplo hay 589 altas observadas por semana, resultando alrededor de 84 altas por día.
- Residual: Muestra el residuo (frecuencia observada menos el valor esperado). La tabla muestra que el domingo hay muchas menos altas de pacientes que el viernes. De lo que parece deducirse que todos los días de la semana no tienen la misma proporción de altas de pacientes.
Por último la siguiente salida muestra el resultado del contraste Chi-cuadrado
 El valor experimental del estadístico de contraste de Chi-cuadrado es igual a 29.389 y el p-valor asociado es menor que 0.001 (Sig = 0.000), por lo tanto se rechaza la hipótesis nula. En consecuencia, el número de altas en los pacientes difiere dependiendo del día de la semana.
El valor experimental del estadístico de contraste de Chi-cuadrado es igual a 29.389 y el p-valor asociado es menor que 0.001 (Sig = 0.000), por lo tanto se rechaza la hipótesis nula. En consecuencia, el número de altas en los pacientes difiere dependiendo del día de la semana.
Supuesto práctico 6
Lanzamos un dado 720 veces y obtenemos los resultados que se muestran en la tabla.

Contrastar la hipótesis de que el dado está bien construido.
Solución
Introducimos los datos en SPSS 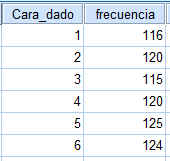 Ponderamos los casos
Ponderamos los casos
Pulsamos Aceptar.
Para obtener una prueba de Chi-cuadrado se eligen en los menús Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/Chi-cuadrado… Y en la ventana resultante, pasamos Cara_dado a la Lista Contratrar variables
Pulsamos Aceptar y obtenemos la siguiente salida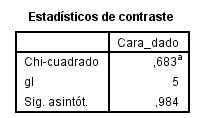 El valor experimental del estadístico de contraste de Chi-cuadrado es igual a 0.683 y el p-valor asociado es 0.984 (mayor que 0.05), por lo tanto no se rechaza la hipótesis nula. En consecuencia, el dado está bien construido
El valor experimental del estadístico de contraste de Chi-cuadrado es igual a 0.683 y el p-valor asociado es 0.984 (mayor que 0.05), por lo tanto no se rechaza la hipótesis nula. En consecuencia, el dado está bien construido
Contrastes de Independencia: Procedimiento Tablas de contingencia
El procedimiento Tablas de contingencia proporciona una serie de pruebas y medidas de asociación para tablas de doble clasificación.
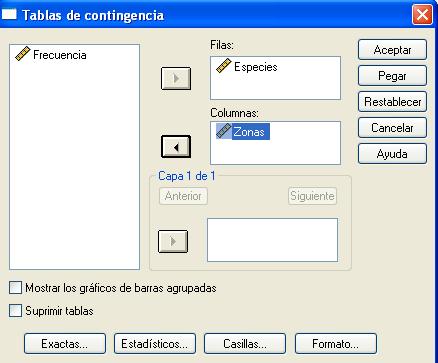
Para obtener tablas de contingencia se selecciona, en el menú principal, Analizar/Estadísticos descriptivos/Tablas de contingencia…
 En el cuadro de diálogo resultante se especifican las variables que forman la tabla. Una de las variables se introduce en Filas: y la otra variable se introduce en Columnas:
En el cuadro de diálogo resultante se especifican las variables que forman la tabla. Una de las variables se introduce en Filas: y la otra variable se introduce en Columnas:
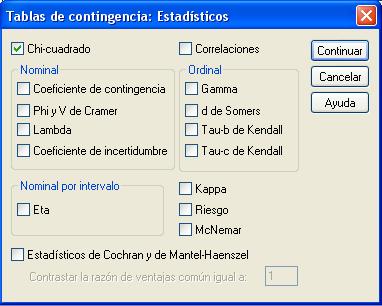
En este cuadro de diálogo se pulsa el botón Estadísticos… y se accede a otra ventana donde se especifican los valores numéricos que se desea obtener. Se selecciona Chi-cuadrado
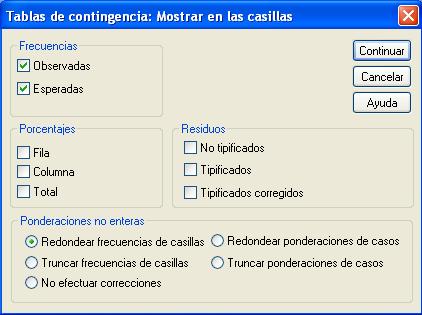
Se pulsa Continuar y se selecciona Casillas… para obtener frecuencias observadas y esperadas, porcentajes y residuos
Se pulsa Continuar y se selecciona Formato para especificar el orden de las categorías (ascendente o descendente)
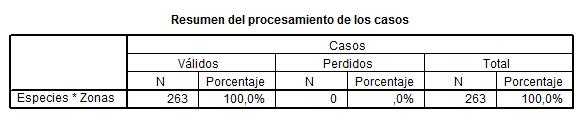
Se pulsa Continuar y Aceptar. Se muestran las siguientes salidas
- 263: Número de datos válidos con los que se trabaja, es el 100% de los datos
- 0: número de datos no válidos
La siguiente salida nos muestra la Tabla de Contingencia de las variables seleccionadas
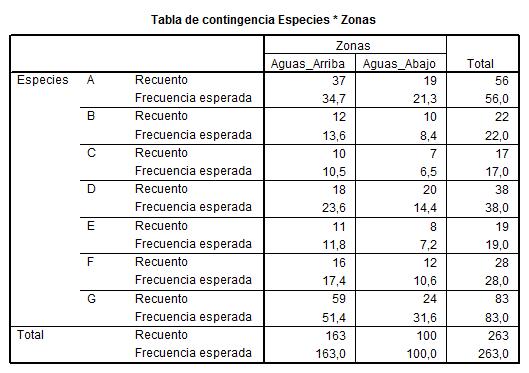 Por último muestra el resultado del contraste de hipótesis.
Por último muestra el resultado del contraste de hipótesis.
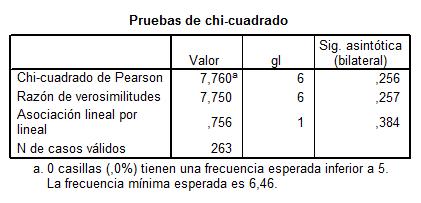 El p-valor (Sig = 0.256) indica que no debe rechazarse la hipótesis de independencia.
El p-valor (Sig = 0.256) indica que no debe rechazarse la hipótesis de independencia.
Supuesto práctico 7
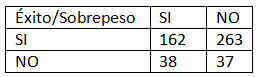
Se realiza una investigación para determinar si hay alguna asociación entre el peso de un estudiante y un éxito precoz en la escuela. Se selecciona una muestra de 50 estudiantes y se clasifica a cada uno según dos criterios, el peso y el éxito en la escuela. Los datos se muestran en la tabla adjunta
Solución
Introducimos los datos en SPSS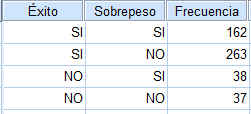 Ponderamos los casos
Ponderamos los casos
Pulsamos Aceptar.
Para obtener tablas de contingencia se selecciona, en el menú principal, Analizar/Estadísticos descriptivos/Tablas de contingencia… En la ventana resultante introducimos Éxito en Filas y Sobrepeso en Columnas y pulsamos Aceptar
Y se muestran las siguientes salidas:
La Tabla de Contingencia de las variables Éxito * Sobrepeso
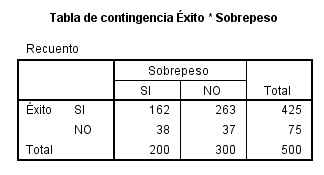
El resultado del contraste de hipótesis.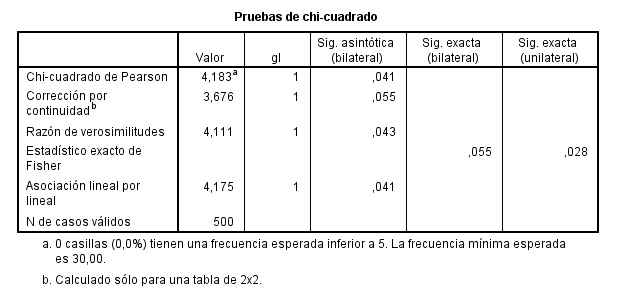
El p-valor (Sig = 0.041) indica que se debe rechazar la hipótesis de independencia. Por lo tanto La obesidad y la precocidad en la escuela no son independientes.
Otros contrastes no paramétricos
El procedimiento Prueba binomial
El procedimiento Prueba binomial compara las frecuencias observadas de las dos categorías de una variable dicotómica con las frecuencias esperadas en una distribución binomial con un parámetro de probabilidad especificado. Por defecto, el parámetro de probabilidad para ambos grupos es 0.5. Se puede cambiar el parámetro de probabilidad en el primer grupo. Siendo la probabilidad en el segundo grupo igual a uno menos la probabilidad del primer grupo.
Si las variables no son dicotómicas se debe especificar un punto de corte. Mediante el punto de corte se divide la variable en dos grupos, el formado por los casos mayores o iguales que el punto de corte y el formado por los casos menores que el punto de corte.
Para obtener una Prueba binomial se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo atiguos/Binomial…
En la salida correspondiente se selecciona una o más variables de contraste numéricas.
 Se deja la opción por defecto Contrastar proporción: 0.50. (Queremos ver si el porcentaje de mujeres en un determinado estudio es del 50%, es decir, queremos contrastar H0: p = 0.5 frente a H1: p <> 0.5). En esta ventana se pulsa el botón Opciones… y se accede a otra ventana para obtener estadísticos descriptivos, cuartiles y controlar el tratamiento de los datos perdidos.
Se deja la opción por defecto Contrastar proporción: 0.50. (Queremos ver si el porcentaje de mujeres en un determinado estudio es del 50%, es decir, queremos contrastar H0: p = 0.5 frente a H1: p <> 0.5). En esta ventana se pulsa el botón Opciones… y se accede a otra ventana para obtener estadísticos descriptivos, cuartiles y controlar el tratamiento de los datos perdidos.
Se pulsa Aceptar y se muestra la siguiente salida
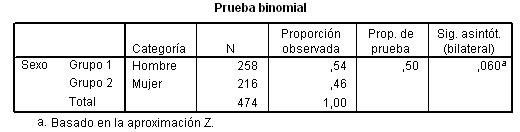 SPSS realiza un contraste bilateral. De un total de 474 personas se observa que el 54 % son hombres y el 46% son mujeres. El p-valor del contraste (Sig. asintót. bilateral) es 0.06, nos indica que no debe rechazarse la hipótesis nula.
SPSS realiza un contraste bilateral. De un total de 474 personas se observa que el 54 % son hombres y el 46% son mujeres. El p-valor del contraste (Sig. asintót. bilateral) es 0.06, nos indica que no debe rechazarse la hipótesis nula.
Este procedimiento permite dicotomizar una variable continua. Por ejemplo, queremos saber si el 30% de las personas de un estudio son menores de 25 años. Para resolverlo, en el campo Definir la dicotomía pondríamos en el Punto de corte: el valor de 25 y en el campo Contrastar proporción: pondríamos 0.30.
Supuesto práctico 8
Entre los pacientes con cáncer de pulmón, el 90% o más muere generalmente en el espacio de tres años. Como resultado de nuevas formas de tratamiento, se cree que esta tasa se ha reducido. En un reciente estudio sobre 150 paciente diagnosticados de cáncer de pulmón, 128 murieron en el espacio de tres años. ¿Se puede afirmar que realmente ha disminuido la tasa de mortalidad?
Solución
Hay que realizar el siguiente contraste de hipótesis: H0: p ≥ 0.90 frente a H1: p < 0.90
Introducimos los datos en SPSS
Ponderamos los casos
Pulsamos Aceptar.
Para obtener una Prueba binomial se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo atiguos/Binomial… En la salida correspondiente insertamos CáncerPulmón en la ventana Lista Contrastar variables y en Proporción de prueba ponemos 0.90
Pulsamos Aceptar
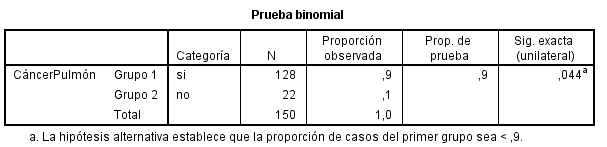
SPSS realiza un contraste bilateral. De un total de 150 pacientes con cáncer de pulmón se observa que el 90 % murieron en el espacio de tres años. El p-valor del contraste (Sig. asintót. unilateral) es 0.044, que nos indica que debe rechazarse la hipótesis nula. Por lo tanto se puede afirmar que ha disminuido la tasa de mortalidad.
Contraste de aleatoriedad. Test de Rachas
El procedimiento Prueba de Rachas contrasta si es aleatorio el orden de aparición de los valores de una variable. Se puede utilizar para determinar si la muestra fue extraída de manera aleatoria.
Una racha es una secuencia de observaciones similares, una sucesión de símbolos idénticos consecutivos. Ejemplo: + + – – – + – – + + + + – – – (6 rachas). Una muestra con un número excesivamente grande o excesivamente pequeño de rachas sugiere que la muestra no es aleatoria.
Para obtener una Prueba de Rachas se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/Rachas…
En la salida correspondiente se selecciona una o más variables de contraste numéricas.
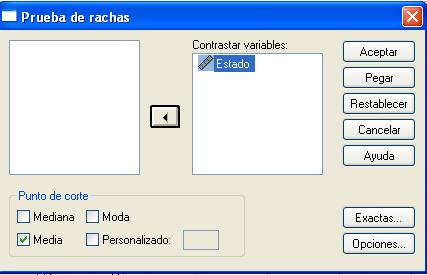
En el campo Punto de corte se especifica un punto de corte para dicotomizar las variables seleccionadas. Se puede utilizar como punto de corte los valores observados para la media, la mediana o la moda, o bien un valor especificado. Los casos con valores menores que el punto de corte se asignarán a un grupo y los casos con valores mayores o iguales que el punto de corte se asignarán a otro grupo. Se lleva a cabo una prueba para cada punto de corte seleccionado. En esta ventana se pulsa el botón Opciones… y se accede a otra ventana para obtener estadísticos descriptivos, cuartiles y controlar el tratamiento de los datos perdidos.
Se pulsa Aceptar y se obtiene la salida del procedimiento
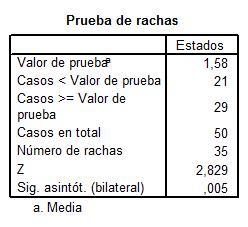
En esta salida se muestran los siguientes valores:
-
Valor de la prueba = 1.58: Es el punto de corte para dicotomizar la variable seleccionada. En esta tabla el punto de corte es la media muestral
-
Casos < Valor de prueba = 21: De los 50 casos contrastados, 21 de ellos tienen valores menores que la media. Los consideramos los casos negativos
-
Casos > Valor de prueba = 29: De los 50 casos contrastados, 29 de ellos tienen valores mayores que la media. Los consideramos los casos positivos
-
Número de rachas = 35: Una racha se define como una secuencias de casos al mismo lado del punto de corte (sucesión de símbolos idénticos consecutivos)
-
Z = 2.829: Valor experimental del estadístico de contraste
-
Sig. Asintót (bilateral) = 0.005: El p-valor o nivel crítico del contraste, que nos indica el rechazo de la hipótesis de aleatoriedad.
Supuesto práctico 9
Se realiza un estudio sobre el tiempo en horas de un tipo determinado de escáner antes de la primera avería. Se ha observado una muestra de 10 escáner y se ha anotado el tiempo de funcionamiento en horas: 18.21; 2.36; 17.3; 16.6; 4.70; 3.63; 15.56; 7.35; 9.78; 14.69. Se puede considerar aleatoriedad en la muestra
Solución
Se introducen los datos en SPSS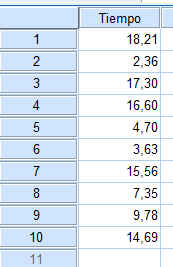
Para obtener una Prueba de Rachas se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/Rachas…. Se introduce Tiempo en el ventana Lista Contrastar variables
Se pulsa Aceptar
y se obtiene el siguiente resultado
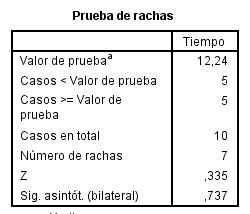 En esta salida se muestran los siguientes valores:
En esta salida se muestran los siguientes valores:
-
Valor de la prueba = 12.24: Es el punto de corte para dicotomizar la variable seleccionada. En esta tabla el punto de corte es la mediana
-
Casos < Valor de prueba = 5: De los 10 casos, 5 de ellos tienen valores menores que la mediana. Los consideramos los casos negativos
-
Casos > Valor de prueba = 5: De los 10 casos, 5 de ellos tienen valores mayores que la mediana. Los consideramos los casos positivos
-
Número de rachas = 7: Una racha se define como una secuencias de casos al mismo lado del punto de corte (sucesión de símbolos idénticos consecutivos)
-
Z = 0.335: Valor experimental del estadístico de contraste
-
Sig. Asintót (bilateral) = 0.737: El p-valor o nivel crítico del contraste, que nos indica que no se debe rechazar la hipótesis de aleatoriedad
Contraste sobre bondad de ajuste: Procedimiento Prueba de Kolmogorov-Smirnov
Mediante el contraste de bondad de ajuste de Kolmogorv-Smirnov se prueba si los datos de una muestra proceden, o no, de una determinada distribución de probabilidad. Lo que se hace es comparar la función de distribución acumulada que se calcula a partir de los datos de la muestra con la función de distribución acumulada teórica de la distribución con la que se compara.
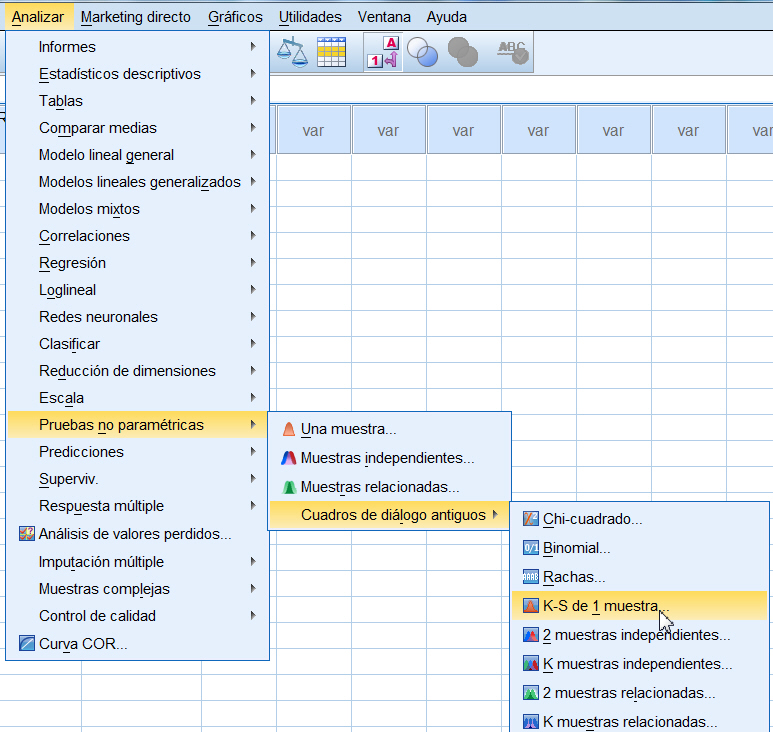
Para obtener una Prueba de Kolmogorov-Smirnov se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/K-S de 1 muestra…
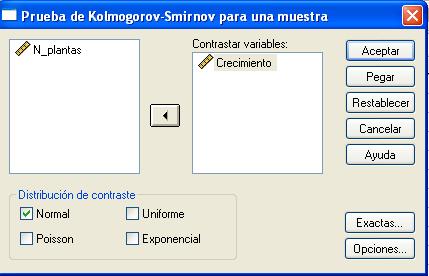
Se muestra la siguiente ventana
En esta salida se puede elegir una o más variables de contraste numéricas, cada variable genera una prueba independiente. Elegiremos la variable Crecimiento, una vez seleccionada la variable se pasa al campo Contrastar variable: mediante el botón de flecha o pulsando dos veces en la variable
Se selecciona la distribución a la que queremos ajustar los datos en el campo Distribución de contraste. En esta ventana se pulsa el botón Opciones… y se accede a otra ventana para obtener estadísticos descriptivos, cuartiles y controlar el tratamiento de los datos perdidos
Se pulsa Aceptar y se obtiene la salida del procedimiento
 En esta salida se muestran los siguientes valores:
En esta salida se muestran los siguientes valores:
- 104: Número de observaciones del fichero de datos
- 3.63: Número medio de plantas
- 1.435: Desviación típica del número de plantas
- 0.183: Diferencia mayor encontrada entre el valor teórico de la distribución normal y el valor observado
- 0.123: Diferencia positiva mayor encontrada entre la distribución teórica y la distribución empírica
- -0.183: Diferencia negativa mayor encontrada entre la distribución teórica y la distribución empírica
- 1.871: Valor experimental del estadístico de contraste
- 0.002: p-valor asociado al contraste
El p-valor (Sig. Asintót (bilateral) = 0.002) indica que debe rechazarse la hipótesis H0 de normalidad, de forma que no se admite que la distribución de los datos sea de tipo Normal.
Supuesto práctico 10
A lo largo de 540 días se anota el número de accidentes mortales de tráfico que se producen en una ciudad, obteniéndose los resultados de la tabla adjunta

¿Se ajustan los datos a una Poisson?
Solución
Se introducen los datos en SPSS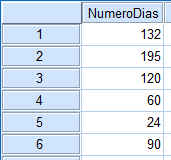
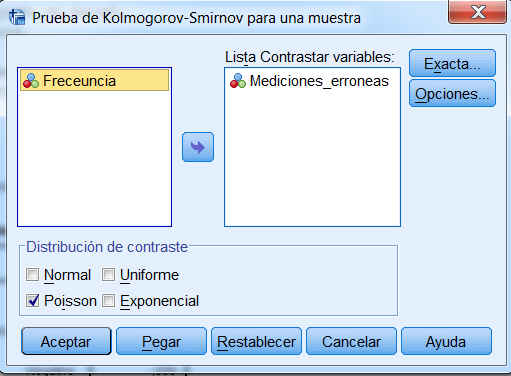
Para obtener una Prueba de Kolmogorov-Smirnov se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/K-S de 1 muestra… Se introduce NumeroDias en el ventana Lista Contrastar variables
Se pulsa Aceptar y se obtiene la siguiente salida
En esta salida se muestran los siguientes valores:
- 6: Número de observaciones del fichero de datos
- 103.5: Número medio de accidentes
- 0.440: Diferencia mayor encontrada entre el valor teórico de la distribución de Poisson y el valor observado
- 0.401: Diferencia positiva mayor encontrada entre la distribución teórica y la distribución empírica
- -0.440: Diferencia negativa mayor encontrada entre la distribución teórica y la distribución empírica
- 1.077: Valor experimental del estadístico de contraste
- 0.197: p-valor asociado al contraste
El p-valor (Sig. Asintót (bilateral) = 0.197) indica que no debe rechazarse la hipótesis H0 (los datos se distribuyen según una Poisson), de forma que se admite que la distribución del número de accidentes mortales sea de tipo Poisson.
Pruebas para dos muestras independientes
El procedimiento Pruebas para dos muestras independientes compara dos grupos de casos existentes en una variable y comprueba si provienen de la misma población (homogeneidad). Estos contrastes, son la alternativa no paramétrica de los tests basados en el t de Student, sirven para comparar dos poblaciones independientes. SPSS dispone de cuatro pruebas para realizar este contraste.
- La prueba U de Mann-Whitney es la más conocida de la pruebas para dos muestras independientes. Es equivalente a la prueba de la suma de rangos de Wilcoxon y a la prueba de Kruskal-Wallis para dos grupos. Requiere que las dos muestras probadas sean similares en la forma y contrasta si dos poblaciones muestreadas son equivalentes en su posición.
- La prueba Z de Kolmogorov-Smirnov y la prueba de rachas de Wald-Wolfowitz son pruebas más generales que detectan las diferencias entre las posiciones y las formas de las distribuciones. La prueba de Kolmogorov-Smirnov se basa en la diferencia máxima absoluta entre las funciones de distribución acumulada observadas para ambas muestras. Cuando esta diferencia es significativamente grande, se consideran diferentes las dos distribuciones.
- La prueba de rachas de Wald-Wolfowitz combina y ordena las observaciones de ambos grupos. Si las dos muestras proceden de una misma población, los dos grupos deben dispersarse aleatoriamente en la ordenación de los rangos.
- La prueba de reacciones extremas de Moses presupone que la variable experimental afectará a algunos sujetos en una dirección y a otros en dirección opuesta. La prueba contrasta las respuestas extremas comparándolas con un grupo control.
Para obtener Pruebas para dos muestras independientes, se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/2 muestras independientes…
 Se muestra la siguiente ventana
Se muestra la siguiente ventana
 En esta salida se puede elegir una o más variables de contraste numéricas. Se elige la variable Tiempo, una vez seleccionada la variable se pasa al campo Contrastar variable: mediante el botón de flecha o pulsando dos veces en la variable. Se selecciona una variable de agrupación, en nuestro caso la variable es Grupo (Se desea saber si las persona fumadoras tardan más tiempo en dormirse que las no fumadoras)
En esta salida se puede elegir una o más variables de contraste numéricas. Se elige la variable Tiempo, una vez seleccionada la variable se pasa al campo Contrastar variable: mediante el botón de flecha o pulsando dos veces en la variable. Se selecciona una variable de agrupación, en nuestro caso la variable es Grupo (Se desea saber si las persona fumadoras tardan más tiempo en dormirse que las no fumadoras)
 Se pulsa Definir grupos…, para dividir el archivo en dos grupos o muestras, y emerge la siguiente ventana
Se pulsa Definir grupos…, para dividir el archivo en dos grupos o muestras, y emerge la siguiente ventana
 Para segmentar el archivo en dos grupos o muestras se introduce un valor entero para el Grupo 1 y un valor entero para el Grupo 2. Así, en los campos Grupo 1 y Grupo 2 se ponen los valores con los que están codificados Fumador (con 1) y NoFumador (con 2), respectivamente. Como indica la siguiente salida
Para segmentar el archivo en dos grupos o muestras se introduce un valor entero para el Grupo 1 y un valor entero para el Grupo 2. Así, en los campos Grupo 1 y Grupo 2 se ponen los valores con los que están codificados Fumador (con 1) y NoFumador (con 2), respectivamente. Como indica la siguiente salida
Se pulsa Continuar y como está marcado por defecto el test U de Mann-Whitney se pulsa Aceptar y se obtiene las siguientes salidas
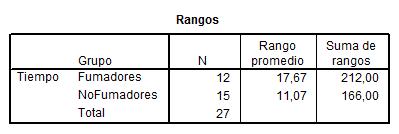 Las observaciones de ambos grupos se combinan para formar una sola muestra, se ordenan linealmente y se les asigna un rango, asignándose el rango promedio en caso de producirse empate, conservando su identidad como grupo. El estadístico W de Wilcoxon (Wm) es la suma de los rangos asociados con las observaciones que originariamente constituyen la muestra menor (Fumadores). Se realiza está elección ya que se piensa que si la población de Fumadores está situada por debajo de la población de NoFumadores, entonces los rangos menores tenderán a asociarse con los valores de los Fumadores. Ello producirá un valor pequeño para el estadístico Wm. Si es cierto lo contrario (la población de Fumadores está situada por encima de la población de NoFumadores) entonces los rangos mayores se encontrarán entre los Fumadores, dando lugar a un valor grande del estadístico Wm. De esta forma, se rechaza H0 si el valor observado Wm fuera demasiado pequeño o demasiado grande para que se debiera al azar.
Las observaciones de ambos grupos se combinan para formar una sola muestra, se ordenan linealmente y se les asigna un rango, asignándose el rango promedio en caso de producirse empate, conservando su identidad como grupo. El estadístico W de Wilcoxon (Wm) es la suma de los rangos asociados con las observaciones que originariamente constituyen la muestra menor (Fumadores). Se realiza está elección ya que se piensa que si la población de Fumadores está situada por debajo de la población de NoFumadores, entonces los rangos menores tenderán a asociarse con los valores de los Fumadores. Ello producirá un valor pequeño para el estadístico Wm. Si es cierto lo contrario (la población de Fumadores está situada por encima de la población de NoFumadores) entonces los rangos mayores se encontrarán entre los Fumadores, dando lugar a un valor grande del estadístico Wm. De esta forma, se rechaza H0 si el valor observado Wm fuera demasiado pequeño o demasiado grande para que se debiera al azar.
Si las diferencias entre los grupos se deben al azar, el rango promedio de los dos grupos debería ser aproximadamente igual. En la salida anterior se observa que hay una diferencia de alrededor de siete minutos (Rango promedio de Fumadores es 17.67 el de los NoFumadores es 11.07). Siendo mayor el tiempo que tarda en dormirse los Fumadores.
En la siguiente salida se muestran los valores experimentales de los estadísticos de contrastes y el p-valor asociado
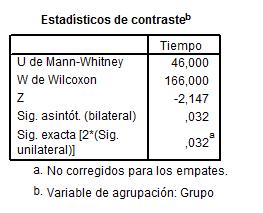 SPSS calcula dos estadísticos: U de Mann-Whitney y W de Wilcoxon, como ambos estadísticos son equivalentes SPSS muestra un único valor de p-valor (Sig). Además, en el cálculo de dicho p-valor aplica una aproximación a la distribución normal, la cual sólo es válida para muestras grandes.
SPSS calcula dos estadísticos: U de Mann-Whitney y W de Wilcoxon, como ambos estadísticos son equivalentes SPSS muestra un único valor de p-valor (Sig). Además, en el cálculo de dicho p-valor aplica una aproximación a la distribución normal, la cual sólo es válida para muestras grandes.
El estadístico U de Mann-Whitney, como el de W de Wilcoxon, dependen de las observaciones de los dos grupos linealmente ordenadas. El estadístico U es el número de veces que un valor de los Fumadores precede al de los NoFumadores. El Estadístico U será grande si la población de los Fumadores está situada por encima de la población de los NoFumadores y será pequeño si sucede lo contario.
El estadístico de contraste Wm es la suma de los rangos asociados a los Fumadores. Como sospechamos que los Fumadores tardan más tiempo en quedarse dormidos que los NoFumadores, se rechaza la Hipótesis nula de que no existen diferencias entre los dos grupos si el valor de Wm es demasiado pequeño para que se deba al azar.
El p-valor asociado al contraste, 0.032, nos conduce a rechazar la hipótesis nula de que no existe diferencias entre los dos grupos y concluimos que los Fumadores tienden a tardar más tiempo en quedarse dormidos que los NoFumadores.
Supuesto práctico 11
En unos grandes almacenes se realiza un estudio sobre el rendimiento de ventas de los vendedores. Para ello, se observa durante 10 dias, el número de ventas de dos vendedores
Vendedor A: 10 40 60 15 70 90 30 32 22 13
Vendedor B: 45 60 35 30 30 15 50 20 32 9
Solución
Se introducen los datos en SPSS
Para obtener Pruebas para dos muestras independientes, se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/2 muestras independientes… En la salida correspondiente, se elige la variable Ventas y se pasa al campo Lista Contrastar variable: Se selecciona una variable de agrupación, en nuestro caso la variable es Vendedores (Se desea saber si el rendimiento de ambos vendedores es independiente del producto de venta).
Para segmentar el archivo en dos grupos o muestras se introduce un valor entero para el Grupo 1 y un valor entero para el Grupo 2. Así, en los campos Grupo 1 y Grupo 2 se ponen los valores con los que están codificados Vendedor 1 (con 1) y Vendedor 2 (con 2), respectivamente. Como indica la siguiente salida
Se pulsa Continuar y como está marcado por defecto el test U de Mann-Whitney se pulsa Aceptar y se obtiene las siguientes salidas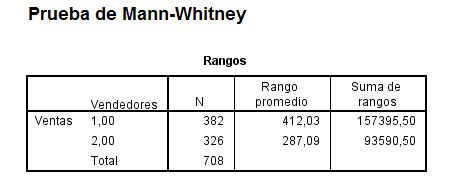
Las observaciones de ambos grupos se combinan para formar una sola muestra, se ordenan linealmente y se les asigna un rango, asignándose el rango promedio en caso de producirse empate, conservando su identidad como grupo. El estadístico W de Wilcoxon (Wm) es la suma de los rangos asociados con las observaciones que originariamente constituyen la muestra menor (Vendedor 2). Se realiza está elección ya que se piensa que si la población de número de ventas del Vendedor 2 está situada por debajo de la población número de ventas del Vendedor1, entonces los rangos menores tenderán a asociarse con los valores del número de ventas del Vendedor 2. Ello producirá un valor pequeño para el estadístico Wm. Si es cierto lo contrario (la población número de ventas del Vendedor 2 está situada por encima de la población número de ventas del Vendedor 1) entonces los rangos mayores se encontrarán entre el número de ventas del Vendedor 2, dando lugar a un valor grande del estadístico Wm. De esta forma, se rechaza H0 si el valor observado Wm fuera demasiado pequeño o demasiado grande para que se debiera al azar.
Si las diferencias entre los grupos se deben al azar, el rango promedio de los dos grupos debería ser aproximadamente igual. En la salida anterior se observa que hay una diferencia de alrededor de 125 (Rango promedio de Ventas del Vendedor 1 es 412.03 el del Vendedor 2 es 287.09). Siendo mayor el promedio del Vendedor 1.
En la siguiente salida se muestran los valores experimentales de los estadísticos de contrastes y el p-valor asociado
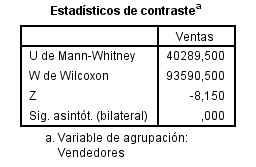
SPSS calcula dos estadísticos: U de Mann-Whitney y W de Wilcoxon, como ambos estadísticos son equivalentes SPSS muestra un único valor de p-valor (Sig). Además, en el cálculo de dicho p-valor aplica una aproximación a la distribución Normal, la cual sólo es válida para muestras grandes.
El estadístico U de Mann-Whitney, como el de W de Wilcoxon, dependen de las observaciones de los dos grupos linealmente ordenadas. El estadístico U es el número de veces que un valor del número de ventas del Vendedor 2 precede al del Vendedor 1. El Estadístico U será grande si la población de ventas del Vendedor 2 está situada por encima de la población ventas del Vendedor 1 y será pequeño si sucede lo contario.
El p-valor asociado al contraste, 0.000, nos conduce a rechazar la hipótesis nula de que no existe diferencias entre los dos grupos y concluimos que el número de Ventas del Vendedor 1 es mayor que las del Vendedor 2.
Procedimiento Pruebas para dos muestras relacionadas
Estas pruebas comparan las distribuciones de dos poblaciones relacionadas. Se supone que la distribución de población de las diferencias emparejadas es simétrica.
SPSS dispone de cuatro pruebas para realizar este contraste, la prueba de signos, la prueba de Wilcoxon de los rangos con signo, la prueba de McNemar y la prueba de homogeneidad marginal. La prueba apropiada depende del tipo de datos:
- Datos continuos, se utiliza la prueba de signos o la prueba de Wilcoxon de los rangos con signo. La prueba de los signos calcula las diferencias entre las dos variable y clasifica las diferencias como positivas, negativas o empatadas. Si las dos variables tienen una distribución similar, el número de diferencias positivas y negativas no difiere de forma significativa. La prueba de Wilcoxon de los rangos con signo tiene en cuenta la información del signo de las diferencias y de la magnitud de las diferencias entre los pares. Dado que esta prueba incorpora más información acerca de los datos, es más potente que la prueba de los signos.
-
Datos binarios, se utiliza la prueba de McNemar, dicha prueba se usa normalmente cuando las medidas están repetidas, es decir la respuesta de cada sujeto se obtiene dos veces, una antes y otra después de que ocurra un evento especificado. Esta prueba determina si la tasa de respuesta inicial (antes del evento) es igual a la tasa de respuesta final (después del evento). Es útil para detectar cambios en la respuesta en los diseños del tipo antes-después.
-
Datos categóricos, se utiliza la prueba de homogeneidad marginal. Es una extensión de la prueba de McNemar a partir de la respuesta binaria a la respuesta multinomial. Contrasta los cambios de respuesta, utilizando la distribución de Chi-cuadrado y es útil para detectar cambios de respuesta en diseños antes-después.
Para obtener pruebas para dos muestras relacionadas se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/2 muestras relacionadas…
Se muestra la siguiente ventana
 En esta salida se puede elegir una o más variables de contraste numéricas. Para ello, se pulsa en cada una de las variables. La primera de ellas aparecerá en la sección Selecciones actuales como Variable1, se pulsa en la variable Crudo; la segunda variable aparecerá como Variable2, se pulsa en la variable Cocido. A continuación se pulsa en el botón de flecha para incluir las variables en la campo Contrastar pares: Se pulsa Aceptar y se muestra la siguiente salida
En esta salida se puede elegir una o más variables de contraste numéricas. Para ello, se pulsa en cada una de las variables. La primera de ellas aparecerá en la sección Selecciones actuales como Variable1, se pulsa en la variable Crudo; la segunda variable aparecerá como Variable2, se pulsa en la variable Cocido. A continuación se pulsa en el botón de flecha para incluir las variables en la campo Contrastar pares: Se pulsa Aceptar y se muestra la siguiente salida
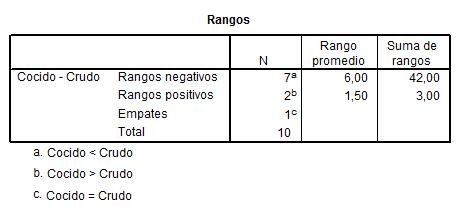 En el text de Wilcoxon, los rangos están basados en el valor absoluto de la diferencia entre las dos variables contrastadas. El signo de la diferencia es usado para clasificar los casos en uno o tres grupos: diferencia menor que 0 (rangos negativos), mayor que cero (rangos positivos) o igual a cero (empates). Los casos de empates son ignorados
En el text de Wilcoxon, los rangos están basados en el valor absoluto de la diferencia entre las dos variables contrastadas. El signo de la diferencia es usado para clasificar los casos en uno o tres grupos: diferencia menor que 0 (rangos negativos), mayor que cero (rangos positivos) o igual a cero (empates). Los casos de empates son ignorados
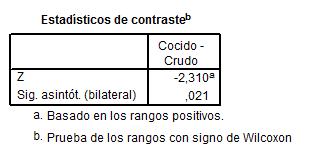 El p-valor asignado al contraste 0.021 (Sig asintótica bilateral) nos indica que se debe rechazar la hipótesis nula de que no existen diferencias entre los dos grupos.
El p-valor asignado al contraste 0.021 (Sig asintótica bilateral) nos indica que se debe rechazar la hipótesis nula de que no existen diferencias entre los dos grupos.
Ejercicios
Ejercicios Guiados
| Instalación directa de la JRE 6 para Windows Página oficial de Sun Microsystems, descarga de la JRE para cualquier plataforma |
|
Si ya tienes instalada la Máquina Virtual Java pincha en el siguiente enlace para proceder a la ejecución de los ejercicios guiados
|
Ejercicio1 |
IMPORTANTE: Si al descargar el archivo *.JAR del ejercicio tu gestor de descargas intenta guardarlo como *.ZIP debes cambiar la extensión a .JAR para poder ejecutarlo.
Enunciado del Ejercicio 1
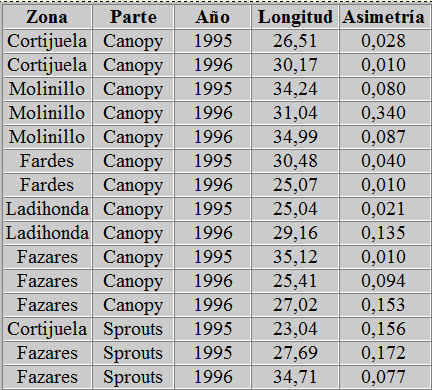
En 5 zonas de la provincia de Granada (Ladihonda y Fazares, zonas muy secas y Cortijuela, Molinillo y Fardes, zonas húmedas) se hacen una serie de mediciones sobre las hojas de las encinas a lo largo de 3 años consecutivos: 1995, muy seco y 1996 y 1997, muy lluviosos.
El objetivo es medir la simetría fluctuante en dichas hojas como indicador de stress en la planta. Bajo condiciones de stress (sequía, herbivoría, limitación por nutrientes…), la hipótesis es que la asimetría aumente. Contamos con la siguiente información:
- Localización árboles: 5 zonas, dos en zonas muy secas (Hoya Guadix-Baza, Ladihonda y Fazares) y tres en zonas con mayor precipitación (Cortijuela, Molinillo, Fardes). En esta última, Fardes, son árboles situados en la ladera de un río (presumiblemente poco afectados por años más o menos secos).
- Años de climatología diferente: 1995 año muy seco y años 1996 y 1997, años muy lluviosos.
- Situación de la hoja: Canopy (copa de los árboles) y Sprouts (rebrotes, hojas nuevas que salen desde la parte inferior del tronco).
Disponemos de un total de 2101 casos, cedidos por el Departamento de Ecología de la Universidad de Granada (España), de los que hemos seleccionado aleatoriamente una muestra de tamaño 15 que se presenta en la siguiente tabla:
Se pide:
a) ¿Se puede admitir que la longitud de las hojas de encina se distribuye normalmente?
b) ¿Se puede admitir que la longitud media de las hojas es igual a 30 cm a un nivel de significación del 5%?
c) Suponiendo que la asimetría de las hojas sigan una distribución Normal; comprobar mediante un contraste de hipótesis si existen diferencias significativas en la asimetría de las hojas teniendo en cuenta la situación de la hoja en el árbol.
d) A un nivel de significación del 5%, ¿es representativo el ajuste lineal entre la longitud y la asimetría? ¿Cuál sería la expresión del modelo? ¿Cuánto explica el modelo?
Enunciado del Ejercicio 2
Se realiza un estudio para investigar el efecto del ejercicio físico sobre el nivel de triglicéridos, en el que participaron once individuos. Antes del ejercicio se tomaron muestras de sangre para determinar el nivel de triglicéridos de cada participante. Después, los individuos fueron sometidos a un programa físico que se centraba en carreras y marchas diarias. Al final del periodo de ejercicios, se tomaron nuevamente muestras de sangre y se obtuvo una segunda lectura del nivel de triglicéridos en sangre.Los datos se muestran en la siguiente tabla
 Se pensó que el programa de ejercicios físicos podría reducir del nivel de triglicéridos en sangre. ¿Sostienen estos datos el argumento de los investigadores? (Supóngase normalidad).
Se pensó que el programa de ejercicios físicos podría reducir del nivel de triglicéridos en sangre. ¿Sostienen estos datos el argumento de los investigadores? (Supóngase normalidad).
Enunciado del Ejercicio 3
Se realiza un estudio para investigar el efecto de la presencia de una gran planta industrial sobre la población de invertebrados en un río que atraviesa la planta. Se tomaron muestras de siete especies de invertebrados en dos zonas del río: antes de la planta “Aguas arriba” y después de la planta “Aguas abajo”. Los datos se muestran en la siguiente tabla
Se pide:
a) ¿Se puede admitir que el tipo de especies de vertebrados está relacionado con la situación respecto de la planta de “Aguas arriba del río”?
b) ¿Se puede admitir relación entre la situación respecto a la planta de la zona del río y el tipo de especies halladas en ella?
Enunciado del Ejercicio 4
Se quiere estudiar si el 85% de los niños con dolor torácico tienen un ecocardiograma normal. Para ello, se toma una muestra de 139 niños con dolor torácico, de ellos 123 presentan un ecocardiograma normal. ¿Apoyan los datos la hipótesis?
Enunciado del Ejercicio 5
En un proceso de producción de unas píldoras que se fabrican secuencialmente, la periodicidad de rachas de píldoras defectuosas puede ser significativa de la falta de aleatoriedad en la producción y sugeriría la revisión del proceso. Se desea saber si en el proceso de fabricación de las píldoras, la obtención de éstas en mal estado se produce de manera aleatoria. Para ello se anota el estado de 17 píldoras obtenidas en la cadena de producción a una determinada hora:
B: Buen estado D: Defectuosa
B D B D B B B D D B D B D D B D B
Enunciado del Ejercicio 6
En un estudio sobre el hábito de fumar y sus efectos sobre las pautas del sueño, una de las variables importantes es el tiempo que se tarda en quedarse dormido. Se extrae una muestra, de tamaño 8, de la población de fumadores y otra independiente, de tamaño 10, de la población de no fumadores. Se obtienen los siguientes datos:
¿Indican estos datos que los fumadores tienden a tardar más tiempo en quedarse dormidos que los no fumadores?
Enunciado del Ejercicio 7
En un estudio sobre los efectos del ejercicio físico en pacientes con enfermedad coronaria, se mide el máximo de oxígeno consumido por cada paciente, antes de comenzar el entrenamiento. Después de seis meses de hacer ejercicio con bicicleta tres veces por semana, se midió nuevamente el oxígeno consumido por cada persona y se obtuvieron los siguientes resultados.
¿Se puede concluir que, al nivel de significación del 5%, el ejercicio tiende a aumentar el máximo de oxígeno admitido por los pacientes?
Ejercicios Propuestos
Ejercicio Propuesto 1
En una unidad de investigación hospitalaria se está realizando un estudio para conocer si la tolerancia a la glucosa en sujetos sanos tiende a decrecer con la edad. Para ello se realizó un test oral de glucosa a dos muestras de pacientes sanos, unos jóvenes y otros adultos. El test consistió en medir el nivel de glucosa en sangre en el momento de la ingestión (nivel basal) de 100 grs. de glucosa y a los 60 minutos de la toma. Los resultados fueron los siguientes
Jóvenes
Adultos
Responder a las siguientes cuestiones
a) ¿Los niveles de glucosa en sangre en el momento de la ingestión (nivel basal) siguen una distribución normal en las dos poblaciones?
b) ¿Se puede admitir que el nivel medio de glucosa en sangre en el momento de la ingestión en los jóvenes es menor que 85?
c)¿Se detecta una variación significativa del nivel de glucosa en sangre en cada grupo?
d) Estudiar donde es mayor la concentración de glucosa en sangre:
d1) ¿La concentración de glucosa es mayor en adultos que en jóvenes?
d2) ¿La concentración de glucosa es mayor a los 60 minutos en adultos que en jóvenes?
d3) ¿La concentración de glucosa es mayor en el momento de la ingestión en adultos que en jóvenes
e) A un nivel de significación del 5%,
e1) ¿Es representativo el ajuste lineal, en los jóvenes, entre el nivel de glucosa en sangre en el momento de la ingestión (nivel basal) y a los 60 minutos? ¿Cuál sería la expresión del modelo?¿Cuánto explica el modelo?
e2) ¿Es representativo el ajuste lineal, en los adultos, entre el nivel de glucosa en sangre en el momento de la ingestión (nivel basal) y a los 60 minutos? ¿Cuál sería la expresión del modelo?¿Cuánto explica el modelo? e3) ¿Es representativo el ajuste lineal entre los jóvenes y los adultos?
Ejercicio Propuesto 2
Continuando con el estudio de la asimetría en la hoja de la encina, (Ejercicio guiado 1) se ha detectado la presencia de Agallas en Encina (pequeñas agallas en el envés de una hoja de encina causadas por el díptero Dryomyia lichtensteini) tanto en las zonas secas como en las zonas con mayor precipitación.
a) En las dos zonas muy secas (Ladihonda y Fazares) se pretende comprobar si determinado tratamiento, aplicado durante un mes, ayuda a reducir la presencia de dichas agallas. Para ello, se realiza un estudio a 10 encinas, en las que se selecciona aleatoriamente 10 hojas y se registra el promedio de agallas presentes antes del tratamiento y después del tratamiento (se supone normalidad). Los resultados se muestran a continuación:
b)Se quiere estudiar la asociación entre el nivel de dióxido de sulfúrico del aire y el número medio de Agallas en Encina en las zonas de los árboles de Molinillo. Se elige una muestra de 10 zonas de las que se sabe que tienen una alta concentración de dióxido de sulfúrico, 10 zonas que se sabe que tienen un nivel normal y 10 zonas que tienen una baja concentración. Dentro de cada zona se seleccionan aleatoriamente 20 encinas y se determina para cada encina el promedio de agallas en las hojas. Sobre esta base se clasifica cada encina según tenga un recuento bajo, normal o alto de agallas. Se obtienen los datos que se muestran en la siguiente tabla
Ejercicio Propuesto 3
Se asegura que la quinta parte de cierto tipo de empresas químicas utilizan gasoil para su funcionamiento. Para contrastar esta afirmación se toma una muestra aleatoria de 100 empresas y se obtiene que 23 de ellas utiliza este combustible. Resolver el contraste a un nivel de significación 0.01.
Ejercicio Propuesto 4
En un laboratorio se observó el número de partículas a emitidas por una sustancia radioactiva a intervalos iguales de tiempo. La información se muestra en la siguiente tabla:
¿Se puede considerar al nivel de significación 0.01 que los datos se ajustan a una distribución de Poisson?
Ejercicio Propuesto 5
Se quiere estudiar si el número de bacterias que aparecen en un determinado cultivo al cabo de una semana es aleatorio o por el contrario habría que suponer que hay algo en el cultivo que propicia el desarrollo de tales bacterias. Para ello, se sometió el cultivo a 10 semanas de observación y se obtuvieron los siguientes resultados: 498, 490, 510, 505, 495, 496, 497, 501, 502, 520.
Ejercicio Propuesto 6
En un determinado hospital se están realizando diversos estudios comparativos, con el objetivo de estudiar el número pacientes que llegan, durante una semana al hospital, para ser diagnosticado y el número de enfermos con un tipo de carcinoma que reciben una determinada terapia. Para ello se dispone de la siguiente información:
Se pide, a un nivel de confianza del 5%:
- Estudiar si el porcentaje de hombres que llegan, durante una semana al hospital, para ser diagnosticado es del 52%.
- Comparar la proporción de mujeres con carcinoma que reciben o no reciben la terapia.
Ejercicio Propuesto 1(Resuelto)
En una unidad de investigación hospitalaria se está realizando un estudio para conocer si la tolerancia a la glucosa en sujetos sanos tiende a decrecer con la edad. Para ello se realizó un test oral de glucosa a dos muestras de pacientes sanos, unos jóvenes y otros adultos. El test consistió en medir el nivel de glucosa en sangre en el momento de la ingestión (nivel basal) de 100 grs. de glucosa y a los 60 minutos de la toma. Los resultados fueron los siguientes
Jóvenes
Adultos
Responder a las siguientes cuestiones
a) ¿Los niveles de glucosa en sangre en el momento de la ingestión (nivel basal) siguen una distribución normal en las dos poblaciones?
b) ¿Se puede admitir que el nivel medio de glucosa en sangre en el momento de la ingestión en los jóvenes es menor que 85?
c)¿Se detecta una variación significativa del nivel de glucosa en sangre en cada grupo?
d) Estudiar donde es mayor la concentración de glucosa en sangre:
d1) ¿La concentración de glucosa es mayor en adultos que en jóvenes?
d2) ¿La concentración de glucosa es mayor a los 60 minutos en adultos que en jóvenes?
d3) ¿La concentración de glucosa es mayor en el momento de la ingestión en adultos que en jóvenes
e) A un nivel de significación del 5%,
e1) ¿Es representativo el ajuste lineal, en los jóvenes, entre el nivel de glucosa en sangre en el momento de la ingestión (nivel basal) y a los 60 minutos? ¿Cuál sería la expresión del modelo?¿Cuánto explica el modelo?
e2) ¿Es representativo el ajuste lineal, en los adultos, entre el nivel de glucosa en sangre en el momento de la ingestión (nivel basal) y a los 60 minutos? ¿Cuál sería la expresión del modelo?¿Cuánto explica el modelo? e3) ¿Es representativo el ajuste lineal entre los jóvenes y los adultos?
Solución:
a) ¿Los niveles de glucosa en sangre en el momento de la ingestión (nivel basal) siguen una distribución normal en las dos poblaciones?
Se debe contrastar si la distribución de nivel de glucosa para los jóvenes y los adultos en el momento de la ingestión (nivel basal) sigue una distribución normal. Para ello, una vez introducidos los datos en SPSS, se contrasta la normalidad mediante el contraste de Kolmogorov-Smirnov.
Se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/K-S de 1 muestra… y se obtiene la siguiente salida
De los resultados deducimos
- p-valor=0.968, que a un nivel de significación del 5 % no se debe rechazar la hipótesis nula, por tanto se concluye que la distribución de nivel basal de glucosa para los adultos sigue una distribución normal.
- p-valor=0.953, que a un nivel de significación del 5 % no se debe rechazar la hipótesis nula, por tanto se concluye que la distribución de nivel basal de glucosa para los jóvenes sigue una distribución normal.
b) ¿Se puede admitir que el nivel medio de glucosa en sangre en el momento de la ingestión en los jóvenes es menor que 85?
Este apartado se resuelve mediante un contraste unilateral (en este caso de cola a la izquierda) para la media de una población normal. Para ello, se selecciona Analizar/Comparar medias/Prueba T de una muestra…
SPSS muestra la siguiente salida: En esta tabla se observa que el valor del estadístico (t = -1.128) deja a la derecha un p-valor (Sig. (bilateral)) de 0.289. Para resolver el contraste de una cola el p-valor asociado al contraste será la mitad del p-valor mostrado en la tabla. Es decir el p-valor es 0.1445 mayor que el nivel de significación 0.05. Por lo tanto, no se debe rechazar la hipótesis nula y concluimos que el nivel basal medio de glucosa en los jóvenes no es menor que 85.
En esta tabla se observa que el valor del estadístico (t = -1.128) deja a la derecha un p-valor (Sig. (bilateral)) de 0.289. Para resolver el contraste de una cola el p-valor asociado al contraste será la mitad del p-valor mostrado en la tabla. Es decir el p-valor es 0.1445 mayor que el nivel de significación 0.05. Por lo tanto, no se debe rechazar la hipótesis nula y concluimos que el nivel basal medio de glucosa en los jóvenes no es menor que 85.
c) ¿Se detecta una variación significativa del nivel de glucosa en sangre en cada grupo?
Se pretende comprobar si, como muestran los datos, los niveles de glucosa en sangre son distintos para cada grupo en el momento de la ingestión y a los 60 minutos. Se realiza un contraste de medias de variables normales en muestras apareadas. Para realizar este contraste mediante SPSS se selecciona, en el menú principal, Analizar/Comparar medias/Prueba T para muestras relacionadas… y se obtiene la siguiente salida
De los resultados deducimos
- p-valor < 0,001, que a un nivel de significación del 5 % se debe rechazar la hipótesis nula y por tanto hay diferencias significativas en el nivel de glucosa de los jóvenes en el momento de la ingestión y a los 60 minutos.
- p-valor< 0,001, que a un nivel de significación del 5 % se debe rechazar la hipótesis nula y por tanto hay diferencias significativas en el nivel de glucosa de los adultos en el momento de la ingestión y a los 60 minutos.
d) Estudiar donde es mayor la concentración de glucosa en sangre:
d1) ¿La concentración de glucosa es mayor en adultos que en jóvenes?
Se trata de un contraste unilateral (de cola a la izquierda) para la diferencia de medias de dos muestras independientes, H0: µ1 >= µ2 (La concentración media de glucosa es menor o igual en adultos que en jóvenes) frente a la alternativa H1: µ1 < µ2 (la concentración media de glucosa es mayor en adultos que en jóvenes). Para resolverlo mediante SPSS se selecciona, en el menú principal: Analizar/Comparar medias/Prueba T para muestras independientes… y se obtiene la siguiente salida
De los resultados deducimos
- p-valor < 0,001, que a un nivel de significación del 5 % se debe rechazar la hipótesis nula de igualdad de varianzas.
- texp = -1,598, y el p-valor asociado será la mitad del obtenido para el contraste bilateral, es decir, p-valor = 0,0595, que a un nivel de significación del 5 % no se debe rechazar la hipótesis nula y por tanto la concentración de glucosa en sangre de los jóvenes es mayor que la de los adultos.
d2) ¿La concentración de glucosa es mayor a los 60 minutos en adultos que en jóvenes?
Se trata de un contraste unilateral (de cola a la izquierda) para la diferencia de medias de dos muestras independientes, H0: µ1 >= µ2 (La concentración media de glucosa es menor o igual a los 60 minutos en adultos que en jóvenes) frente a la alternativa H1: µ1 < µ2 (la concentración media de glucosa es mayor a los 60 minutos en adultos que en jóvenes). Para resolverlo mediante SPSS se selecciona, en el menú principal: Analizar/Comparar medias/Prueba T para muestras independientes y se obtiene la siguiente salida
De los resultados deducimos
- p-valor = 0,370, que a un nivel de significación del 5 % no se debe rechazar la hipótesis nula de igualdad de varianzas.
- texp = -8,122, y el p-valor asociado será la mitad del obtenido para el contraste bilateral, es decir, p-valor < 0,0005, que a un nivel de significación del 5 % se debe rechazar la hipótesis nula y por tanto el nivel de glucosa en sangre de los adultos a los 60 minutos de la toma es mayor que la de los jóvenes.
d3) ¿La concentración de glucosa es mayor en el momento de la ingestión en adultos que en jóvenes?
Se trata de un contraste unilateral (de cola a la izquierda) para la diferencia de medias de dos muestras independientes, H0: µ1 >= µ2 (La concentración media de glucosa en el momento de la ingestión es menor o igual en adultos que en jóvenes) frente a la alternativa H1: µ1 < µ2 (la concentración media de glucosa en el momento de la ingestión es mayor en adultos que en jóvenes). Para resolverlo mediante SPSS se selecciona, en el menú principal: Analizar/Comparar medias/Prueba T para muestras independientes… y se obtiene la siguiente salida
De los resultados deducimos
- p-valor = 0,282, que a un nivel de significación del 5 % no se debe rechazar la hipótesis nula de igualdad de varianzas.
- texp = -2,139, y el p-valor asociado será la mitad del obtenido para el contraste bilateral, es decir, p-valor = 0,023, que a un nivel de significación del 5 % se debe rechazar la hipótesis nula y por tanto el nivel de glucosa en sangre en el momento de la ingestión es menor en los jóvenes que en los adultos.
e) A un nivel de significación del 5%,
e1) ¿Es representativo el ajuste lineal, en los jóvenes, entre el nivel de glucosa en sangre en el momento de la ingestión (nivel basal) y a los 60 minutos? ¿Cuál sería la expresión del modelo?¿Cuánto explica el modelo?
Para comprobar si es representativo, mediante SPSS, el ajuste lineal pedido se selecciona en el menú principal, Analizar/Regresión/Lineal… y se analiza la siguiente salida de SPSS
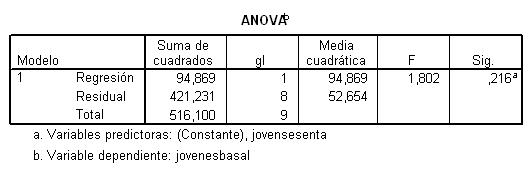 El p-valor igual a 0,216 nos indica que no se debe rechazar la hipótesis nula de que el coeficiente de regresión es 0 y por tanto no se debe predecir el nivel basal de glucosa de los jóvenes a partir del nivel a los 60 minutos.
El p-valor igual a 0,216 nos indica que no se debe rechazar la hipótesis nula de que el coeficiente de regresión es 0 y por tanto no se debe predecir el nivel basal de glucosa de los jóvenes a partir del nivel a los 60 minutos.
Para obtener la expresión del modelo se selecciona la siguiente salida de SPSS
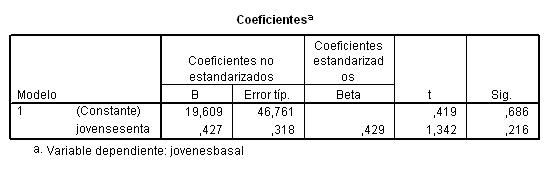 La expresión del modelo es: y = 19.609 + 0.427x, donde
La expresión del modelo es: y = 19.609 + 0.427x, donde
- y: nivel basal de glucosa de los jóvenes
- x: nivel de glucosa de los jóvenes a los 60 minutos
Para saber cuánto explica el modelo la siguiente tabla muestra el coeficiente de determinación R2 = 0,184, este valor indica que el modelo explica el 18,4 % de la variación del nivel basal de glucosa en los jóvenes.
 e2) A un nivel de significación del 5% ¿Es representativo el ajuste lineal, en los adultos, entre el nivel de glucosa en sangre en el momento de la ingestión (nivel basal) y a los 60 minutos en los adultos? ¿Cuál sería la expresión del modelo?¿Cuánto explica el modelo?
e2) A un nivel de significación del 5% ¿Es representativo el ajuste lineal, en los adultos, entre el nivel de glucosa en sangre en el momento de la ingestión (nivel basal) y a los 60 minutos en los adultos? ¿Cuál sería la expresión del modelo?¿Cuánto explica el modelo?
Para comprobar si es representativo, mediante SPSS, el ajuste lineal pedido se selecciona en el menú principal, Analizar/Regresión/Lineal… y se analiza la siguiente salida de SPSS
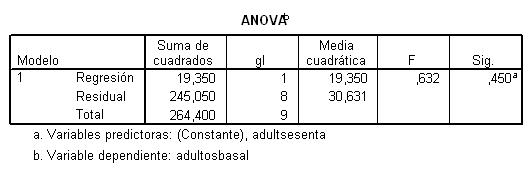 El p-valor igual a 0,450 nos indica que no se debe rechazar la hipótesis nula de que el coeficiente de regresión es 0 y por tanto no se debe predecir el nivel basal de glucosa de los adultos a partir del nivel a los 60 minutos.
El p-valor igual a 0,450 nos indica que no se debe rechazar la hipótesis nula de que el coeficiente de regresión es 0 y por tanto no se debe predecir el nivel basal de glucosa de los adultos a partir del nivel a los 60 minutos.
Para obtener la expresión del modelo se selecciona la siguiente salida de SPSS
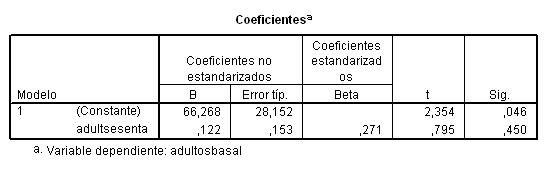 La ecuación del modelo está dada por: y = 66.268 + 0.122x, donde
La ecuación del modelo está dada por: y = 66.268 + 0.122x, donde
- y: nivel basal de glucosa de los adultos
- x: nivel de glucosa de los adultos a los 60 minutos
¿Cuánto explica el modelo?
 El coeficiente de determinación R2 = 0,073 indica que el modelo explica el 7,3 % de la variación del nivel basal de glucosa en los adultos.
El coeficiente de determinación R2 = 0,073 indica que el modelo explica el 7,3 % de la variación del nivel basal de glucosa en los adultos.
e3) A un nivel de significación del 5% ¿Es representativo el ajuste lineal entre los jóvenes y los adultos?
Se selecciona, en el menú principal, Analizar/Regresión/Lineal… y se analiza la siguiente salida de SPSS
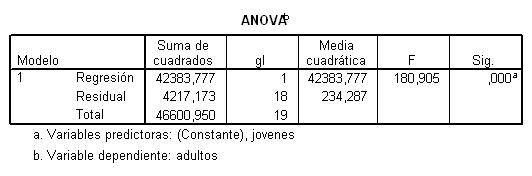 El p-valor menor que 0,001 nos indica que se debe rechazar la hipótesis nula de que el coeficiente de regresión es 0 y por tanto se puede predecir el nivel de glucosa de los adultos a partir del nivel de glucosa de los jóvenes.
El p-valor menor que 0,001 nos indica que se debe rechazar la hipótesis nula de que el coeficiente de regresión es 0 y por tanto se puede predecir el nivel de glucosa de los adultos a partir del nivel de glucosa de los jóvenes.
Para obtener la expresión del modelo se considera la siguiente salida de SPSS
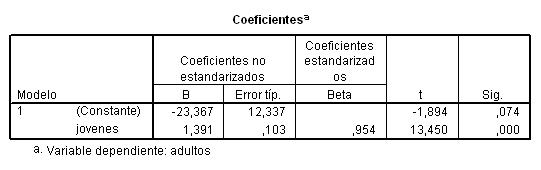 La expresión del modelo es: y = -23.367 + 1.391x, donde
La expresión del modelo es: y = -23.367 + 1.391x, donde
- y: nivel de glucosa de los adultos
- x: nivel de glucosa de los jóvenes
¿Cuánto explica el modelo?
 El coeficiente de determinación R2 = 0,91 indica que el modelo explica el 91 % de la variación del nivel de glucosa en los adultos. El ajuste realizado es bueno.
El coeficiente de determinación R2 = 0,91 indica que el modelo explica el 91 % de la variación del nivel de glucosa en los adultos. El ajuste realizado es bueno.
Ejercicio Propuesto 2 (Resuelto)
Continuando con el estudio de la asimetría en la hoja de la encina, (Ejercicio guiado 1) se ha detectado la presencia de Agallas en Encina (pequeñas agallas en el envés de una hoja de encina causadas por el díptero Dryomyia lichtensteini) tanto en las zonas secas como en las zonas con mayor precipitación.
a) En las dos zonas muy secas (Ladihonda y Fazares) se pretende comprobar si determinado tratamiento, aplicado durante un mes, ayuda a reducir la presencia de dichas agallas. Para ello, se realiza un estudio a 10 encinas, en las que se selecciona aleatoriamente 10 hojas y se registra el promedio de agallas presentes antes del tratamiento y después del tratamiento (se supone normalidad). Los resultados se muestran a continuación:
b)Se quiere estudiar la asociación entre el nivel de dióxido de sulfúrico del aire y el número medio de Agallas en Encina en las zonas de los árboles de Molinillo. Se elige una muestra de 10 zonas de las que se sabe que tienen una alta concentración de dióxido de sulfúrico, 10 zonas que se sabe que tienen un nivel normal y 10 zonas que tienen una baja concentración. Dentro de cada zona se seleccionan aleatoriamente 20 encinas y se determina para cada encina el promedio de agallas en las hojas. Sobre esta base se clasifica cada encina según tenga un recuento bajo, normal o alto de agallas. Se obtienen los datos que se muestran en la siguiente tabla
Solución:
a) En las dos zonas muy secas (Ladihonda y Fazares) se pretende comprobar si determinado tratamiento, aplicado durante un mes, ayuda a reducir la presencia de dichas agallas. Para ello, se realiza un estudio a 10 encinas, en las que se selecciona aleatoriamente 10 hojas y se registra el promedio de agallas presentes antes del tratamiento y después del tratamiento (se supone normalidad).
Para comprobar la efectividad del tratamiento aplicado de la forma especificada (antes-después) se realiza un contraste unilateral (de cola a la derecha) de diferencias de medias de variables normales en muestras apareadas, H0: µ1 <= µ2 (El número medios de agallas antes del tratamiento es menor o igual que después de haberlo aplicado) frente a la alternativa H1: µ1> µ2; (El número medios de agallas antes del tratamiento es mayor que después de haberlo aplicado). Para ello, se selecciona, en el menú principal, Analizar/Comparar medias/Prueba T para muestras relacionadas. Se obtiene la siguiente pantalla
texp = 3.031 y el p-valor asociado será la mitad del obtenido para el contraste bilateral, es decir, p-valor < 0,007, que a un nivel de significación del 5 % se debe rechazar la hipótesis nula, por lo tanto el tratamiento durante un mes ayuda a reducir la presencia de Agallas en Encina.
b) Se quiere estudiar la asociación entre el nivel de dióxido de sulfúrico del aire y el número medio de Agallas en Encina en la zona de los árboles de Molinillo.
Para estudiar la asociación entre el promedio de Agallas en Encina y el nivel de S02 se realiza un contraste de independencia mediante el contrate no-paramétrico de Chi-cuadrado. Para ello se elige, en el menú principal, Analizar/Estadísticos descriptivos/Tablas de contingencia… Se muestra la siguiente salida
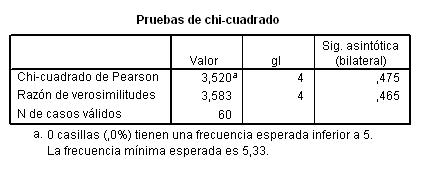 El p-valor es igual a 0.475 por lo que no se puede rechazar la hipótesis de independencia.
El p-valor es igual a 0.475 por lo que no se puede rechazar la hipótesis de independencia.
Ejercicio Propuesto 3 (Resuelto)
Se asegura que la quinta parte de cierto tipo de empresas químicas utilizan gasoil para su funcionamiento. Para contrastar esta afirmación se toma una muestra aleatoria de 100 empresas y se obtiene que 23 de ellas utiliza este combustible. Resolver el contraste a un nivel de significación 0.01.
Solución:
Para contrastar si la proporción de empresas químicas que utilizan gasoil para su funcionamiento es del 20% (quinta parte de las 100 empresas), tenemos que realizar el siguiente contraste de hipótesis: H0: p = 0.2 frente a H1: p <> 0.2. Para ello, una vez definidas las variables e introducidos los datos
Se selecciona Datos/Ponderar casos… Se elige Ponderar casos mediante. A continuación se introduce la variable Frecuencia en el campo Variable de ponderación:
Para realizar el contraste se elige, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/Binomial…
El contraste que vamos a realizar es H0: p = 0.2 frente a H1: p <> 0.2, siendo p la proporción (20%) de empresas químicas que utilizan gasoil para su funcionamiento. Para ello, en el campo Contrastar proporción: se pone el valor 0.2
Se pulsa Aceptar y se muestra el resultado de la prueba binomial
La proporción observada de empresas químicas que utilizan gasoil para su funcionamiento es 0.2 y el p-valor correspondiente (Sig. Asintót. (unilateral)) es 0.261. Por lo tanto no se debe rechazar la hipótesis nula, es decir no se debe rechazar que la quinta parte de cierto tipo de empresas químicas utilizan gasoil para su funcionamiento.
Ejercicio Propuesto 4 (Resuelto)
En un laboratorio se observó el número de partículas a emitidas por una sustancia radioactiva a intervalos iguales de tiempo. La información se muestra en la siguiente tabla:
¿Se puede considerar al nivel de significación 0.01 que los datos se ajustan a una distribución de Poisson?
Solución
Para comprobar si el número de partículas emitidas por una sustancia radioactiva se ajustan a una distribución de Poisson, se realiza un contraste no-paramétrico de Bondad de ajuste. (H0: Los datos se ajustan a una Poisson H1: Los datos no se ajustan a una Poisson). Para ello se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/K-S de una muesta… donde se selecciona en Poisson Distribución de contraste.
Se obtiene la siguiente salida
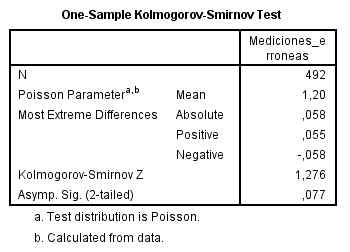 Mediante el contraste de Kolmogorov-Smirnov para una muestra se obtiene el valor de Zexp (1.276), dicho valor deja a la derecha un área de 0.077, mayor que el nivel de significación 0.01, por lo tanto no debe rechazarse la hipótesis nula. Se puede admitir que si el número de partículas emitidas por una sustancia radioactiva se ajustan a una distribución de Poisson
Mediante el contraste de Kolmogorov-Smirnov para una muestra se obtiene el valor de Zexp (1.276), dicho valor deja a la derecha un área de 0.077, mayor que el nivel de significación 0.01, por lo tanto no debe rechazarse la hipótesis nula. Se puede admitir que si el número de partículas emitidas por una sustancia radioactiva se ajustan a una distribución de Poisson
Ejercicio Propuesto 5 (Resuelto)
Se quiere estudiar si el número de bacterias que aparecen en un determinado cultivo al cabo de una semana es aleatorio o por el contrario habría que suponer que hay algo en el cultivo que propicia el desarrollo de tales bacterias. Para ello, se sometió el cultivo a 10 semanas de observación y se obtuvieron los siguientes resultados: 498, 490, 510, 505, 495, 496, 497, 501, 502, 520.
Solución
Para comprobar si el número de bacterias que aparecen en un determinado cultivo al cabo de una semana es aleatorio, se realiza un contraste no-paramétrico de aleatoriedad. (H0: Hay aleatoriedad frente a H1: No hay aleatoriedad). Para ello se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/Rachas… Se obtiene la siguiente salida
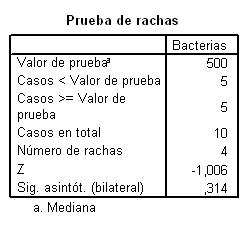 Mediante la Prueba de rachas se obtiene el valor de Zexp (-1.006), dicho valor deja a la derecha un área de 0.314, mayor que el nivel de significación 0.05, por lo tanto no debe rechazarse la hipótesis nula de aleatoriedad.
Mediante la Prueba de rachas se obtiene el valor de Zexp (-1.006), dicho valor deja a la derecha un área de 0.314, mayor que el nivel de significación 0.05, por lo tanto no debe rechazarse la hipótesis nula de aleatoriedad.
Ejercicio Propuesto 6 (Resuelto)
En un determinado hospital se están realizando diversos estudios comparativos, con el objetivo de estudiar el número pacientes que llegan, durante una semana al hospital, para ser diagnosticado y el número de enfermos con un tipo de carcinoma que reciben una determinada terapia. Para ello se dispone de la siguiente información:
![]()
Se pide, a un nivel de confianza del 5%:
- Estudiar si el porcentaje de hombres que llegan, durante una semana al hospital, para ser diagnosticado es del 52%.
- Comparar la proporción de mujeres con carcinoma que reciben o no reciben la terapia.
Solución:
a) Estudiar si el porcentaje de hombres que llegan, durante una semana al hospital, para ser diagnosticado es del 52%.
Para resolver este apartado, se realiza un contraste para la proporción de una distribución Binomial. Es decir, se quiere contrastar H0: p = 0.52 frente a H1: p <> 0.52. Siendo p la proporción de hombres.
Para obtener una Prueba binomial, mediante SPSS, se selecciona en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/Binomial
La pantalla de resultados de este procedimiento se presenta en la tabla de la Prueba binomial
 Se observa que la proporción muestral de hombres es 0.55 y que el p-valor (Sig. exacta (unilateral)) es de 0.483, por lo tanto no se debe rechazar la hipótesis nula.
Se observa que la proporción muestral de hombres es 0.55 y que el p-valor (Sig. exacta (unilateral)) es de 0.483, por lo tanto no se debe rechazar la hipótesis nula.
b) Comparar la proporción de mujeres con carcinoma que reciben la terapia
Para evaluar si existen diferencias significativas entre la proporción muestral de mujeres que reciben la terapia y la proporción muestral que no la reciben, se realiza un contraste bilateral con las siguientes hipótesis estadísticas: H0: p1 = p2 (proporciones iguales) frente a H1: p1 <>p2 (proporciones distintas).
El contraste de comparación de dos proporciones es un caso particular del contraste de homogeneidad de dos muestras de una variable cualitativa cuando ésta sólo presenta dos modalidades. (Ver Contrastes de hipótesis para dos proporciones independientes. Muestras grandes en la “Introducción” de la Práctica 6). Por ello, el procedimiento que vamos a realizar es el análisis de una tabla de contingencia 2×2.
Para obtener el procedimiento Tablas de contingencia se elige en los menús Analizar/Estadísticos descriptivos/Tablas de contingencia…
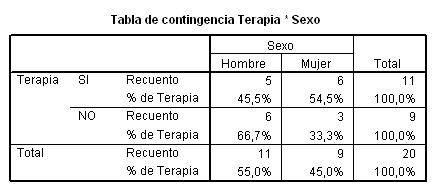 La tabla de contingencia muestra la tabla de frecuencias conjuntas. En cada casilla aparece, además de la frecuencia observada, el porcentaje que ésta representa sobre el total de la fila. Así las proporciones muestrales que vamos a comparar son: 3/9 y 6/11.
La tabla de contingencia muestra la tabla de frecuencias conjuntas. En cada casilla aparece, además de la frecuencia observada, el porcentaje que ésta representa sobre el total de la fila. Así las proporciones muestrales que vamos a comparar son: 3/9 y 6/11.
La siguiente salida de SPSS muestra la tabla Pruebas de chi-cuadrado
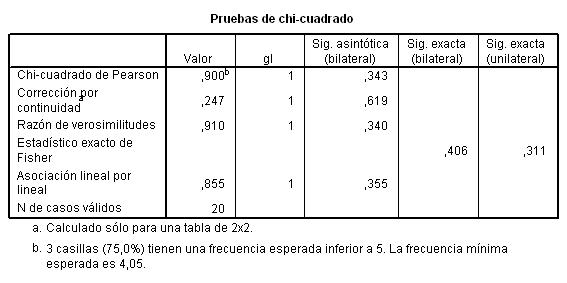 Esta tabla presenta los resultados de cinco estadísticos para la comparación de ambas proporciones. Generalmente, en el caso de muestras grandes se elige el estadístico Corrección por continuidad. Dicho estadístico calcula el estadístico Chi-cuadrado con la corrección por continuidad de Yates. En el caso de muestras pequeñas, se decide a partir del Estadístico exacto de Fisher. El valor p de la prueba exacta de Fisher es 0.406 (Sig. exacta (bilateral)). Comparando este valor con el nivel de significación establecido del 5% se concluye que no se debe rechazar la hipótesis nula, es decir las diferencias observadas entre ambas proporciones no son estadísticamente significativas.
Esta tabla presenta los resultados de cinco estadísticos para la comparación de ambas proporciones. Generalmente, en el caso de muestras grandes se elige el estadístico Corrección por continuidad. Dicho estadístico calcula el estadístico Chi-cuadrado con la corrección por continuidad de Yates. En el caso de muestras pequeñas, se decide a partir del Estadístico exacto de Fisher. El valor p de la prueba exacta de Fisher es 0.406 (Sig. exacta (bilateral)). Comparando este valor con el nivel de significación establecido del 5% se concluye que no se debe rechazar la hipótesis nula, es decir las diferencias observadas entre ambas proporciones no son estadísticamente significativas.
APÉNDICE
Introducción al Análisis de datos categóricos: Tablas de Contingencia
Las variables categóricas o cualitativas son aquellas cuyos valores son un conjunto de cualidades no cuantificables (no numéricas) que reciben el nombre de categorías o modalidades.
Las variables categóricas se clasifican en:
Variables cualitativas ordinales: Son aquellas en las que se pueden ordenar sus distintas modalidades. Es decir, es posible establecer relaciones de orden entre las categoría. (Ejemplo: el rango militar, la clase social, el nivel de estudios)
Variables cualitativas nominales: Son aquellas en las que no se puede definir un orden natural entre sus categorías. (Ejemplo: el color del pelo, el color de los ojos, la raza, la religión).
Variables cualitativas por Intervalo: Proceden de variables cuantitativas agrupadas en intervalos. Estas variables pueden tratarse como ordinales pero en éstas se pueden calcular distancias numéricas entre dos niveles de la escala ordinal. (Ejemplos: el sueldo, la edad, los días del mes, el nivel de presión sanguínea. Son ejemplos de variables que se pueden agrupar por intervalos).
El conjunto de técnicas estadísticas específicas para el estudio de la asociación entre variables cualitativas recibe el nombre de Análisis de Datos Categóricos o Cualitativos.
Tablas de Contingencia
Una tabla de contingencia es una tabla bidimensional en la que las variables objeto de estudio no son cuantitativas.
Una tabla de doble entrada para las variables X e Y con p filas y k columnas se muestra a continuación
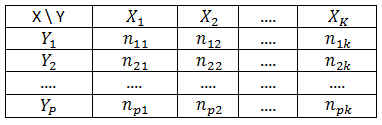
nij: expresa la frecuencia absoluta observada en las modalidades Xi e Yj
El objetivo es estudiar las posibles relaciones entre las dos variables cualitativas, este estudio se realiza mediante la tabla de contingencia.
Ejemplo 1: Se realiza un estudio en 20 individuos que se clasificaron según el sexo (hombre, mujer) y su deseo de asistir o no a un festival de música. La tabla de contingencia para estudiar las posibles relaciones entre las dos variables se muestra a continuación
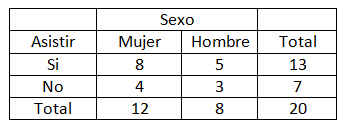
Ejemplo 2: Se realiza un estudio sobre las relaciones entre la opinión sobre la prohibición de fumar en lugares públicos y el hecho de ser fumador o no. Para ello se seleccionan 350 personas de las cuales 140 son fumadores.
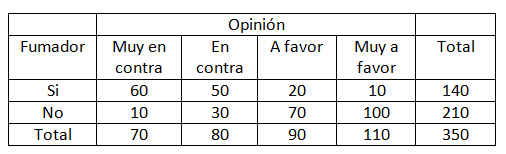
Hemos dicho anteriormente, que el objetivo es estudiar las posibles relaciones entre las dos variables cualitativas y para ello estudiamos, en primer lugar, la independencia de variables categóricas y a continuación la asociación de variables categóricas.
Independencia de variables categóricas
Relizamos el siguiente contraste![]() dicho contraste se resuelve mediante el siguiente estadístico propuesto por Pearson:
dicho contraste se resuelve mediante el siguiente estadístico propuesto por Pearson: 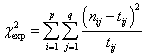 con
con ![]()
dicho estadístico, bajo la hipótesis nula, se distribuye según una ![]() ; donde p es el número de filas y q el número de columnas.
; donde p es el número de filas y q el número de columnas.
Supuesto práctico 11
Los datos sobre 20 individuos que se clasificaron según el sexo (hombre, mujer) y su deseo de asistir o no a un festival de música se muestran en la siguiente tabla de contingencia .

Razonar, con una significacción del 5%, si el hecho de ser hombre o mujer está relacionado con asistir o no a un festival de música.
Solución
Vamos a realizar el siguinte contraste ![]() Para ello, utilizamos el procedimiento Tablas de contingencia que proporciona una serie de pruebas y medidas de asociación para tablas de doble clasificación.
Para ello, utilizamos el procedimiento Tablas de contingencia que proporciona una serie de pruebas y medidas de asociación para tablas de doble clasificación.
En primer lugar se definen las variables Sexo y Asistir y se introducen los datos en SPSS como se muestra en la siguiente figura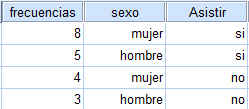
A continuación, ponderamos los casos mediante la variable frecuencias, para ello seleccionamos Datos/Ponderar casos y se muestra la siguiente salida
Pulsamos Ponderar casos mediante y pasamos frecuencias a la celda Variable de frecuencia. Pulsamos Aceptar
A continuación, para realizar el contraste de independencia se selecciona, en el menú principal, Analizar/Estadísticos descriptivos/Tablas de contingencia…
Se muestra la siguiente salida
Se pulsa Estadísticos y se selecciona Chi-cuadrado y Correlaciones
Se pulsa Continuar y Aceptar y se muestran las siguientes salidas:
En primer lugar, el programa proporciona la tabla de contingencia que relaciona el sexo con el hecho de asistir o no al festival.
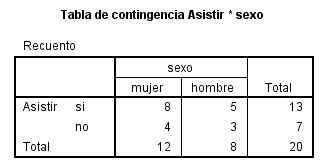
A continuación se realiza el contraste de hipótesis de independencia:
H0: Sexo y Asisitir al festival son independientes
H1: Sexo y Asisitir al festival no son independientes
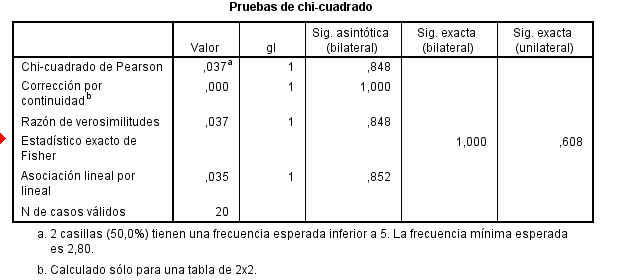
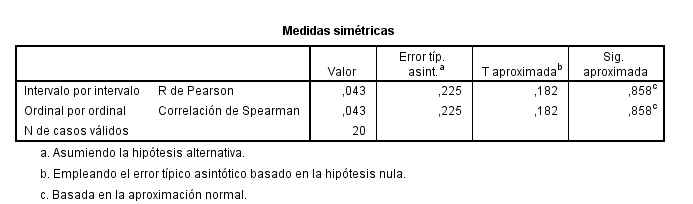
Corrección por continuidad de Yates (1934)
Consiste en restar (0,5) puntos a |nij-eij| en la expresión del estadístico χ2, de la siguiente forma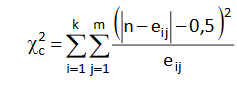 Algunos autores sugieren, que con muestras pequeñas, esta corrección permite que el estadístico χ2 se ajuste mejor a las probabilidades de la distribución χ2 , pero no existe un consenso generalizado sobre la utilización de esta corrección.
Algunos autores sugieren, que con muestras pequeñas, esta corrección permite que el estadístico χ2 se ajuste mejor a las probabilidades de la distribución χ2 , pero no existe un consenso generalizado sobre la utilización de esta corrección.
Razón de verosimilitud Chi‐cuadrado
Se obtiene mediante la siguiente expresión: 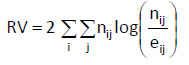 (Fisher, 1924; Neyman y Pearson, 1928)
(Fisher, 1924; Neyman y Pearson, 1928)
Este estadístico es asintóticamente equivalente a χ2 (se distribuye y se interpreta igual) y es muy utilizado para estudiar la relación entre variables categóricas, particularmente en el contexto de los modelos log‐lineales.
Si RV < χ2α;(k-1).(m-1) entonces X e Y no son independientes al nivel α
Si RV ≥ χ2α;(k-1).(m-1) entonces X e Y son independientes al nivel α
Se acepta la hipótesis nula cuando la significación de RV (Sig. asintótica) es mayor que 0,05.
La aplicación de los dos estadísticos (χ2 ,RV) suelen conducir a la misma conclusión. En los casos en que no se produzca esta coincidencia, se elige el estadístico con una significación (probabilidad asociada) menor.
Señalar que, en el ejemplo, la razón de verosimilitudes (RV) es 0.037, tiene asociada una probabilidad (Sig. asintótica) de 0,848 que como es mayor que 0,05, conduce a no rechazar la hipótesis de independencia.
Correlaciones
El coeficiente de correlación de Spearman también es una medida de asociación lineal, pero para variables ordinales.
Ambos coeficientes son de poca utilidad en el estudio de las pautas de relación presentes en una tabla de contingencia.
Medidas de asociación de variables categóricas
Sean X e Y dos características, cualitativas o cuantitativas, con i = 1, …, p y j = 1, …q modalidades o categorías, respectivamente, presentadas en una tabla pxq.
Medidas de asociación: Chi-cuadrado
La medida de asociación más usada en la práctica es la medida Chi-cuadrado 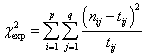
Medida resumen que compara los valores (nij) observados en la tabla, con los que teóricamente se obtendría (tij), en el supuesto de que las variables X e Y fuesen independientes.
El estadístico Chi-cuadrado permite contrastar la hipótesis de independencia de X e Y, basándose en el conocimiento del comportamiento de Chi-cuadrado bajo la hipótesis de independencia: Modelo Chi-cuadrado con (p-1)(q-1) grados de libertad.
Los valores teóricos tij se obtienen mediante: ![]()
Este estadístico toma valores comprendidos entre:
- 0 y N para tablas de contingencia 2×2
- 0 y N*mín{p-1, q-1}, para tablas de contingencia pxq para p,q ≥ 2.
El valor 0 indica que el numerador de la expresión anterior es nulo ((nij–tij)=0), por tanto las frecuencias observadas coinciden con las que habría si las variables fuesen independientes; de donde se admite la independencia de X e Y. El hecho de que sus valores dependan tanto del número de elementos de la tabla (N), como del nº de filas y columnas, hace difícil su interpretación e impracticable la comparación entre tablas.
Después de analizar si existe relación o no entre las variables objeto de estudio, cabe preguntarse ¿cuál es la intensidad de esa relación?.
Entre las medidas utilizada en escala nominal (aquellas variables en las que no se puede definir un orden natural entre sus categorias), distinguiremos ls siguientes:
- Coeficiente Phi (Φ)
- Coeficiente de contingencia o C de Pearson
- Coeficiente V de Cramer
- Coeficiente Lambda (λ)
- Coeficiente de incertidumbre
- Coeficiente Q de Yule
Coeficiente de Contingencia o C de Pearson
El coeficiente de contingencia C es una medida del grado de asociación de dos variables cualitativas en escala nominal. 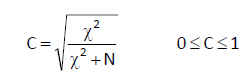
- Si C = 0 ⇒ Independencia entre las variables
- Si C = 1⇒ Asociación perfecta
Este coeficiente solamente se utiliza cuando las tablas de contingencia tienen la misma dimensión.
En una tabla de contingencia 2×2 el coeficiente C de Pearson toma valores comprendidos entre 0 y ![]()
- Si C=
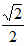 ⇒ Asociación perfecta
⇒ Asociación perfecta - Si C = 0 ⇒ Independencia entre las variables
En una tabla de contingencia (k x k) el valor máximo que toma el coeficiente es 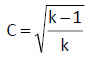
Coeficiente Q de YULE
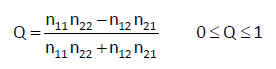
Coeficiente Phi (Φ)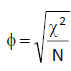
- En las tablas de contingencia (2 x 2), el coeficiente Phi adopta valores entre 0 y 1, y su valor es idéntico al del coeficiente de correlación de Pearson.
- En las tablas en las que una de las variables tiene más de dos niveles, Phi puede tomar valores mayores que 1 (pues el valor de χ2 puede ser mayor que el tamaño muestral).
Coeficiente V de Cramer
El coeficiente V de Cramer incluye una ligera modificación del coeficiente Phi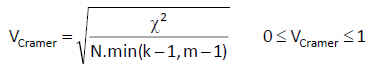 En las tablas de contingencia (2 x 2), los coeficientes V de Cramer y Phi (φ) son idénticos.
En las tablas de contingencia (2 x 2), los coeficientes V de Cramer y Phi (φ) son idénticos.
El problema de este estadístico es que tiende a subestimar el grado de asociación entre las variables.
El coeficiente de contingencia o C de Perason, el coeficiente Phi y el coeficiente V de Cramer, son medidas basadas en Chi‐cuadrado, y que intentan corregir el valor del estadístico χ2 para hacerle tomar un valor entre 0 y 1, y para minimizar el efecto del tamaño de la muestra sobre la cuantificación del grado de asociación (Pearson, 1913;Cramer, 1946).
Coeficiente Lambda (λ) de Goodman y Kruskall
Es un coeficiente que no depende de la χ2 .
- Si Y es la variable dependiente y X la independiente entonces se evalúa la capacidad de X para predecir Y mediante:
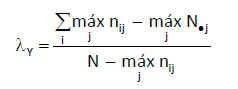
- Si Y es la variable independiente y X la dependiente entonces se evalúa la capacidad de Y para predecir X mediante:
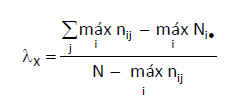
Los valores del coeficiente Lambda están comprendidos entre 0 y 1 para tablas pxq, con p, q ≥ 2; 0 ≤ (λx, λy) ≤ 1.
Valores próximos a 0 implican baja asociación y valores próximos a 1 denotan fuerte asociación. Sin embargo un valor de 0 no implica independencia entre los atributos
Dos variables son independientes cuando λ = 0 , pero λ = 0 no implica independencia estadística.
Los valores que pueden tomar los coeficientes los resumimos en las siguientes tablas
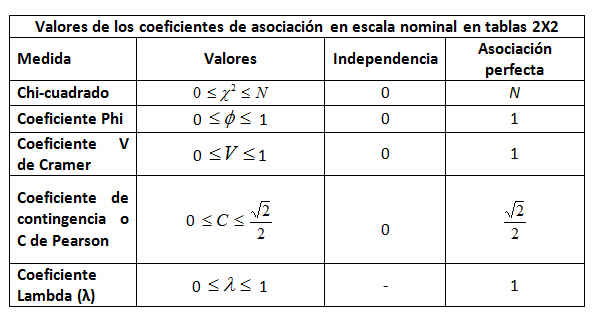

Supuesto práctico 12
Se realiza un estudio sobre las relaciones entre la opinión sobre la prohibición de fumar en lugares públicos y el hecho de ser fumador o no. Para ello se seleccionan 350 personas de las cuales 140 son fumadores.

Solución
Realizamos en primer lugar el contraste de independencia sobre sexo y opinión
H0: Sexo y Opinión son independientes
H1: Sexo y Opinión no son independientes
Para ello, en primer lugar introducimos los datos en SPSS
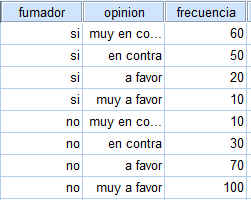
Poderamos los casos mediante la variable frecuencia y pulsamos Aceptar
A continuación, para realizar el contraste de independencia se selecciona, en el menú principal, Analizar/Estadísticos descriptivos/Tablas de contingencia…
Se pulsa Estadísticos y en la ventana correspondiente se elige Chi-cuadrado 
Pulsamos Continuar y Aceptar y se muestra la siguiente salida 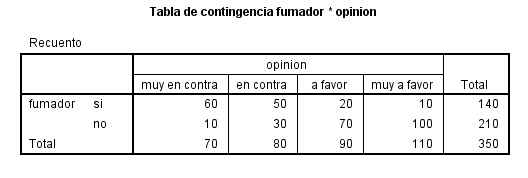
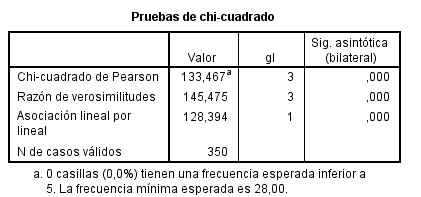
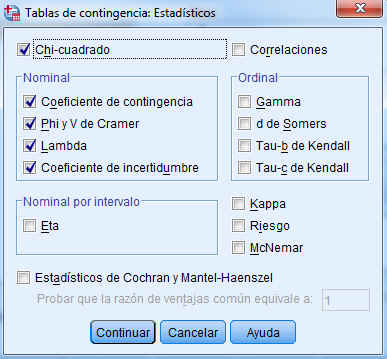
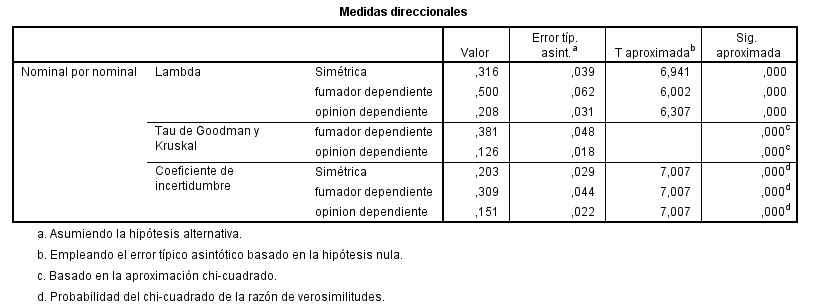
Cada medida (Lambda, Tau de Goodman‐Kruskall, Coeficiente de incertidumbre) figura acompañada de su nivel crítico (Sig. aproximada), que como es pequeño, menor que 0,05, conduce a rechazar la hipótesis nula de independencia, concluyendo que las variables en estudio están relacionadas.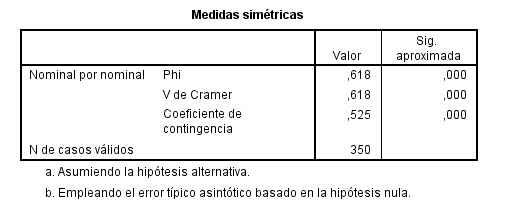
En el análisis de Medidas Simétricas se encuentran las medidas nominales, que son aquella que permiten contrastar la independencia sin decir nada sobre la fuerza de asociación entre las variables, informan únicamente del grado de asociación existente, no de la dirección o de la naturaleza de tal asociación. Son medidas basadas en el estadístico chi‐cuadrado: Phi, V de Cramer y el Coeficiente de Contingencia.
Las medidas de asociación en escala nominal, en las tablas pxq , con p, q ≥2 , en este caso tablas 2×4
- El coeficiente de contingencia o C de Pearson varía entre 0 y 1/√2. El valor que muestra la salida de SPSS es 0.525, próximo a 1/√2. Se puede considerar que la asociación entre las variables es alta
- El coeficiente Phi y el coeficiente V de Cramer varían todos entre 0 y 1. Los valores que muestra la salida de SPSS son: 0.618, 0.618. Se puede considerar que la asociación entre las variables es alta
Por tanto, podemos afirmar que sexo y opinión tienen una asociación alta.
Medidas de asociación en escala ordinal
Las medidas de asociación en escala ordinal son una serie de medidas de asociación que permite aprovechar la información ordinal que las medidas diseñadas para datos nominales no analizan.
Con datos ordinales tiene sentido hablar de dirección de la relación:
- Una dirección positiva indica que los valores altos de una variable se asocian con los valores altos de la otra variable, y los valores bajos con valores bajos.
- Una dirección negativa indica que los valores altos de una variable se asocian con los valores bajos de la otra, y los valores bajos con los valores altos.
Muchas de las medidas de asociación diseñadas para estudiar la relación entre variables ordinales se basan en el concepto de concordancia (inversión) y discordancia (no‐inversión).
- Concordancia o no‐inversión (C): Cuando los dos valores de un caso en ambas variables son mayores (o menores) que los dos valores de otro caso. Cuando predominan las concordancias, la relación es positiva, a medida que aumentan (o disminuyen) los valores de una de las variables, aumentan (o disminuyen) los de la otra. Llamaremos C al número de concordancias
- Discordancia o inversión (D). Cuando el valor de un caso en una de las variables es mayor que el del otro caso, y en la segunda variable el valor del segundo caso es mayor que el del primero. Cuando predominan las discordancias, la relación es negativa, a medida que aumentan (o disminuyen) los valores de una de las variables, disminuyen (o aumentan) los de la otra. Llamaremos D al número de discordancias
- Empate (E). Cuando los dos casos tienen valores idénticos en una o en las dos variables. Hay tres tipos de empates:
- EX: Empate en la variable X y no en la variable Y. Llamaremos EX al número empates en la variable X (tomando a Y como independiente)
- EY: Empate en la variable Y y no en la variable X. Llamaremos EY al número empates en la variable Y (tomando a X como independiente)
- EXY: Empate en ambas variables. Llamaremos EXY al número empates en ambas variables.
Todas las medidas de asociación mencionadas, utilizan en el numerador la diferencia entre el número de discordancias y concordancias resultantes de comparar cada caso con cada caso, diferenciándose en el tratamiento dado a los empates.
Denotamos por T el número total de pares de valores sin repeticiones y N el número total de casos. La siguiente expresión permite calcular T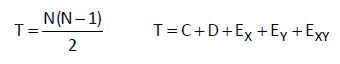 Coeficiente Gamma (γ) de Goodman y Kruskal
Coeficiente Gamma (γ) de Goodman y Kruskal
El coeficiente Gamma es uno de los coeficientes más conocidos, para este coeficiente los empates son irrelevantes, se basa en la relación que siguen los rangos de los dos atributos
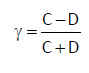 -1 ≤ γ ≤ 1
-1 ≤ γ ≤ 1
- γ = − 1: La asociación entre las variables es perfecta y negativa
- γ = 1: La asociación entre las variables es perfecta y positiva
- γ = 0: Hay independencia entre las variables
Coeficiente d de Somers
Este coeficiente, a diferencia de los anteriores, considera que las variables pueden ser simétricas o dependientes.
- En el caso de que las variables sean simétricas, el estadístico d de Somers coincide con la Tau‐b de Kendall.
- En caso de que las variables sean dependientes, el estadístico d de Somers se diferencia del estadístico Gamma en que incluye los empates de la variable que considera dependiente, lo que da lugar a tres índices (dos asimétricos y uno simétrico):
- Cuando la variable independiente es Y y siendo Ex los empates en la variable X
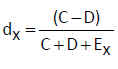
- Cuando la variable independiente es X y siendo Ey los empates en la variable Y
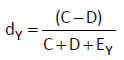
- Versión simétrica para X e Y
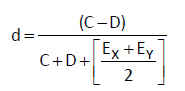 -1 ≤ d ≤ 1
-1 ≤ d ≤ 1 - d = -1 : La asociación entre las variables es perfecta y negativa
- d = 0: Independencia entre las variables
- |d| → 1: Asociación a medida
- d = 1 : La asociación entre las variables es perfecta y positiva
- Cuando la variable independiente es Y y siendo Ex los empates en la variable X
Coeficiente de Concordancia TAU‐b de Kendall (τb)
El coeficiente Tau-b de Kendall utiliza el mismo criterio que el coeficiente d de Sommer simétrica, si bien utiliza la media geométrica en lugar de la media aritmética
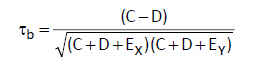
En las tablas de contingencia cuadradas y si ninguna frecuencia marginal vale cero, entonces el coeficiente TAU-b de Kendall toma valores entre [‐1, 1].
Coeficiente de Concordancia TAU‐c de Kendall (τc)
Este coeficiente utiliza el mínimo de filas y de columnas
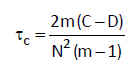
Siendo: m = mín{nº filas, nº columnas} y -1 ≤ τc ≤ 1
Los valores de estas cuatro medidas de asociación de variables en escala ordinal están comprendidos entre [‐1, 1]
-1 ≤ γ, d, τb, τc ≤ 1
En general para estas medidas
- Cuanto más próximos estén los valores de estas medidas a 0 más débil será la asociación entre las variables.
- Cuanto más cercanos a 1 (o a -1) sean los valores de todas estas medidas mayor será la asociación positiva (negativa) entre las variables.
Los valores que pueden tomar los coeficientes los resumimos en la siguiente tabla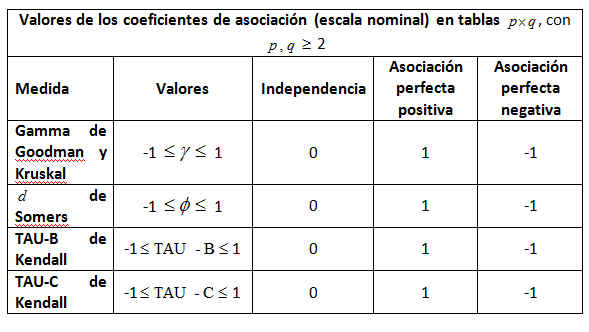
Nota:
- En tablas no cuadradas la medida TAU-B de Kendall no alcanza los límites.
- Si las variables son independientes entonces γ = 0, sin embargo el recíproco no es cierto.
- |γ| =1 no implica asociación perfecta.
Supuesto práctico 13
Se realiza un estudio sobre la práctica deportiva y la sensación de bienestar. Se desea saber si hay asociación entre ambas variables. La práctica deportiva se clasifica en (Poca, Moderada, Alta y Muy Alta) y la sensación de bienestar se clasifica en (Poca, Moderada y Alta). Para dicho estudio se selecciona una muestra aleatoria de 500 sujetos. Los datos se muestran en la siguiente tabla.
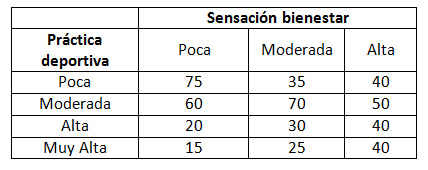
Realizar los contrastes necesarios y calcular e interpretar las medidas de asociación.
Solución
Se introducen los datos en SPSS
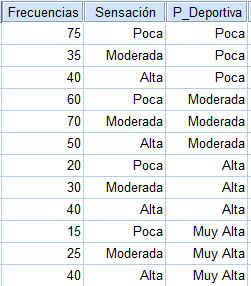
Se ponderan los casos
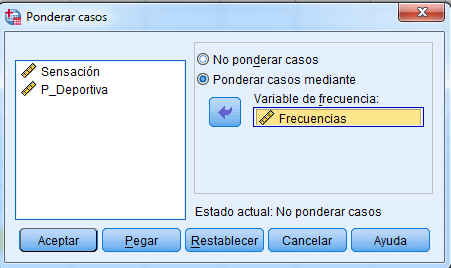
A continuación, para realizar el contraste de independencia se selecciona, en el menú principal, Analizar/Estadísticos descriptivos/Tablas de contingencia…
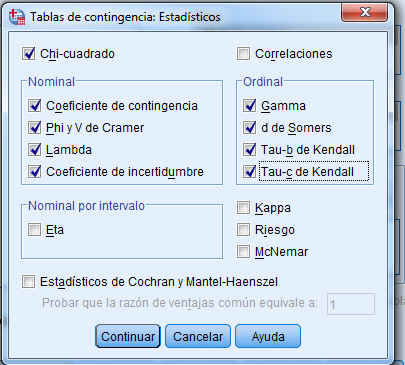
Se pulsa Continuar y Aceptar. Se muestran las siguientes salidas
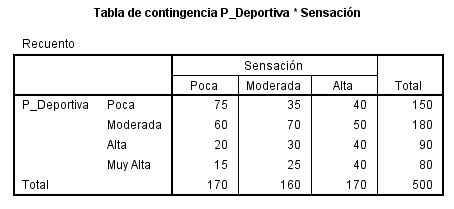
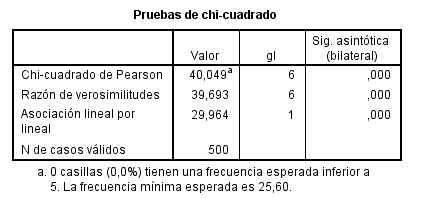
Realizamos en primer lugar el contraste de independencia sobre Sensación de bienestar y Práctica deportiva
H0: Sensación de bienestar y Práctica deportiva son independientes
H1: Sensación de bienestar y Práctica deportiva no son independientes
Estadístico de contraste (observado) es 40.049, el cual, en la distribución χ2 de Pearson tiene 6 grados de libertad (gl = 6) , tiene asociada una probabilidad Sig. asintótica (Significación asintótica) de 0,000. Puesto que esta probabilidad (denominada nivel crítico o nivel de significación observado) es muy pequeño, mucho menor que el nivel de significación del 5%, lo que conduce al rechazo de la hipóetsis nula y concluimos que las variables analizadas no son independientes y por lo tanto tienen cierta asociación.
Estadístico de contraste (observado) dela razón de verosimilitudes (RV) es 39.693, tiene asociada una probabilidad (Sig. asintótica ) de 0,000 que como es menor que 0,05, conduce a rechazar la hipótesis nula, concluyendo que existe dependencia entre las variables analizadas.
Señalamos, que en caso de ambos estadísticis tengan distinta Sig. asintótica, se elige el estadístico con menor Sig. asintótica.
A continuación vamos a estudiar el grado de asociación entre ambas variables.
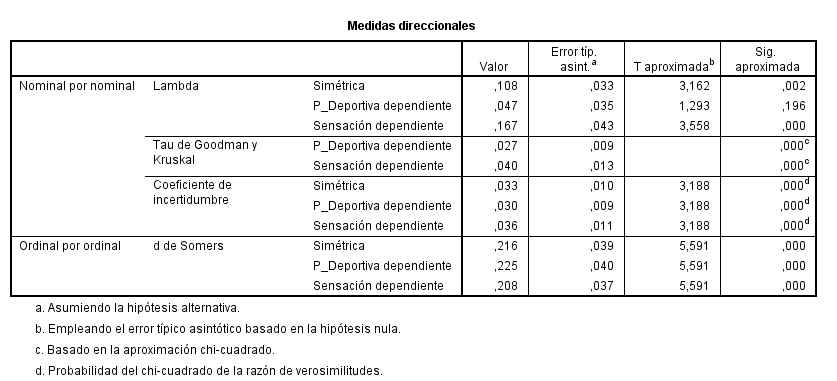
En el análisis de Medidas Direccionales se encuentran las medidas nominales (lambda, Tau de Goodman y Kruskal, coeficiente de incertidumbre), medidas ordinales (d de Somers).
- Las medidas nominales permiten contrastar la independencia sin decir nada sobre la fuerza de asociación entre las variables, informan únicamente del grado de asociación existente, no de la dirección o de la naturaleza de tal asociación.
- Las medidas ordinales recogen la dirección de la asociación de las variables: una relación positiva indica que los valores altos de una variable se asocian con los valores altos de la otra variable, y los valores bajos con los valores bajos; una relación negativa indica que los valores altos de una variable se asocian con los valores bajos de la otra variable, y los valores bajos con los valore altos.
Cada medida de asociación en la tabla (Lambda, Tau de Goodman‐Kruskall, Coeficiente de incertidumbre) se muestra acompañada de su nivel crítico (Sig. aproximada = 0.002, 0.000, 0.000, respectivamente), que al ser menores que 0,05, conduce a rechazar la hipótesis nula de independencia, concluyendo que las variables en estudio (Sensación de bienestar y Práctica deportiva) están relacionadas.
Junto al valor concreto adoptado por cada medida de asociación nominal por nominal (0.108, 0.027 y 0.033) se muestra su valor estandarizado (T aproximada), que se obtiene dividiendo el valor de la medida entre su error típico (calculado éste suponiendo independencia entre las variables.
La tabla también muestra el error típico de cada medida calculado sin suponer independencia (Error típico asintótico).
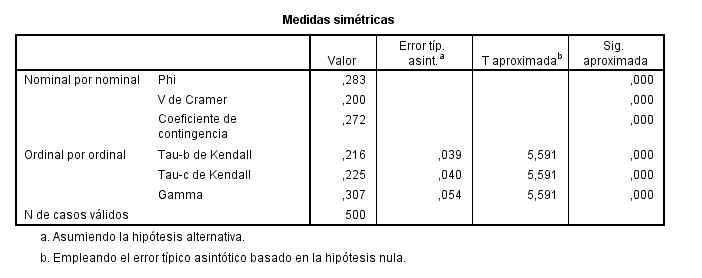
En el análisis de Medidas Simétricas se encuentran las medidas nominales, medidas ordinales.
Las medidas nominales que muestra esta tabla son medidas basadas en el estadístico chi‐cuadrado: Phi, V de Cramer y el Coeficiente de Contingencia.
Las medidas ordinales se basan en el concepto de concordancias (o inversión) y discordancias ( o no inversión). Utilizan en el numerador la diferencia entre el número de concordancias o inversiones y discordancias o no‐inversiones resultantes de comparar cada caso con otro, diferenciándose en el tratamiento dado a los empates. son: Tau-b de Kendall, Tau-c de Kendall y Gamma
Cada coeficiente de asociación se muestra con su correspondiente nivel crítico (Sig. aproximada, todos 0.0000), puesto que estos niveles críticos son menores que 0,05, se rechaza la hipótesis nula de independencia, afirmando que las variables (Sensación de bienestar y Práctica deportiva) están relacionadas.
Al lado del valor de cada coeficiente se encuentra su valor estandarizado (T aproximada: valor del coeficiente dividido por su error típico), así como el error típico del valor de cada coeficiente obtenido sin suponer independencia (Error típico asintótico).
Y como el valor concreto adoptado por estas medidas (0.283, 0.2, 0.272, 0.216, 0.225 y 0.307) es positivo (relación positiva entre la Sensación de bienestar y la Práctica deportiva ), se puede interpretar que a una mayor
Práctica deportiva le corresponde una mejor Sensación de bienestar. El grado de asociación entre las variables es bajo.
Ejercicios Propuestos
Se realiza un estudio sobre la posible relación que hay entre la edad de las mujeres y su grado de aceptación de una ley sobre interrupción del embarazo. Para ello se ha realizado una encuesta sobre 450 mujeres cuyos resultados se adjuntan en la tabla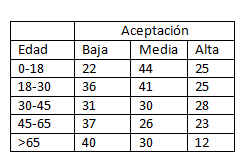
Solución
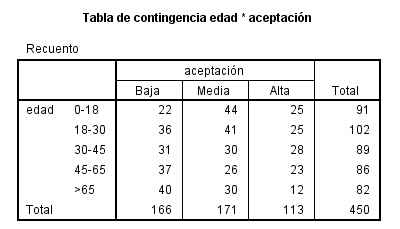
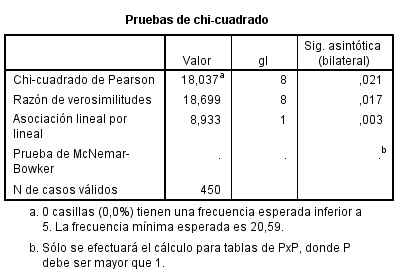
El valor del estadístico de contraste (observado) de18.037, sigue una distribución χ2 con 8 grados de libertad (gl = 8) y tiene asociada una probabilidad (Significación asintótica) de 0,021. Puesto que esta probabilidad (denominada nivel crítico o nivel de significación observada) es pequeña (menor que 0,05), se decide rechazar la hipótesis nula, indicando que hay evidencia de asociación entre el grado de aceptación del aborto y la edad de las mujeres.
El valor de la Razón de verosimilitudes (RV) es 18.699, tiene asociada una probabilidad (Sig. asintótica) de 0,017 menor que 0,05, indica que hay evidencia de asociación entre el grado de aceptación del aborto y la edad de las mujeres.
Los estadísticos (χ2 ,RV) llevan a la misma conclusión, en caso contrario, se elige el estadístico con menor Sig. asintótica.
El valor del estadístico Asociación lineal por lineal tiene un valor de 8.933 con un nivel crítico de (0.003 < 0,05), por lo que se rechaza la hipótesis nula de independencia, llegando a la misma conclusión que con los estadísticos anteriores.
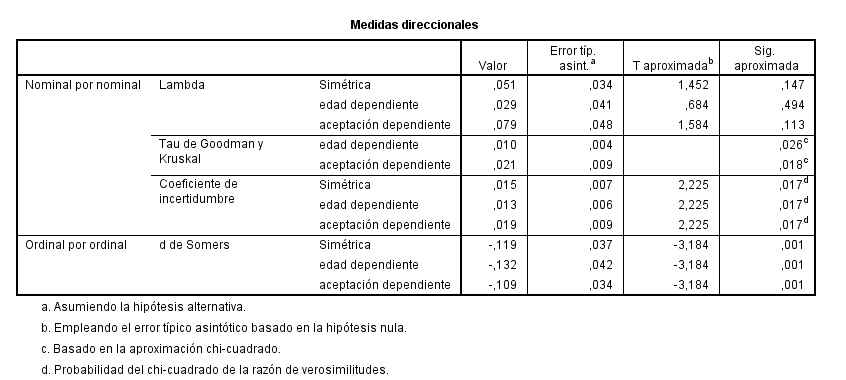
Los valores obtenidos de Lambda, Tau de Goodman y Kruskall, Coeficiente de incertidumbre, y d de Somers (como medidas nominales cuantifican el grado de asociación) indican una asociación baja entre la edad de las mujeres y la aceptación del aborto.
Cada medida acompañada de un nivel crítico (Sig. aproximada), que en los casos que es menor que 0,05, (Tau de Goodman y Kruskal, Coeficiente de incertidumbre d de Somers) conducen a rechazar la hipótesis nula de independencia y concluir que las variables (edad de las mujeres, aceptación del aborto) están asociadas.
Observamos que cada coeficiente tiene un valor cuando se considera una de las variables independiente. Así por ejemplo el coeficiente Tau de Goodman y Kruskall tiene:
- El valor 0,010 cuando considera la variable “Aceptación del aborto” como independiente. La interpretación es la siguiente: Conociendo la edad de la mujer consultada (filas), se reduce en un 1% la probabilidad de cometer un error al predecir su aceptación al aborto (columnas). Esto significa que la edad de la mujer no tiene capacidad predictiva sobre la aceptación del aborto.
- El valor 0,021 cuando considera la variable “Edad de la mujer” como independiente. La interpretación es la siguiente: Conociendo el grado de aceptación del aborto por parte de las mujeres, se reduce en un 21% la probabilidad de cometer un error al predecir la edad de la mujer. Esto significa que el grado de aceptación del aborto no tiene capacidad para predecir la edad de la mujer que tiene ese grado de aceptación de la ley sobre el aborto.
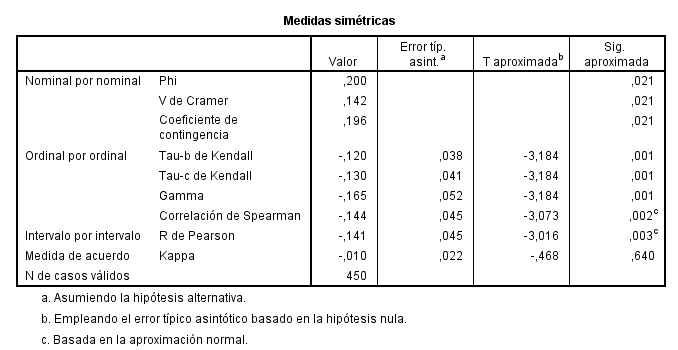
El valor de cada coeficiente aparece acompañado de su correspondiente nivel crítico (Sig. aproximada), que permite tomar una decisión sobre la hipótesis nula de independencia. Puesto que estos niveles críticos son menores que 0,05, se puede afirmar que hay relación entre la aceptación del aborto y la edad de las mujeres.
- los valores obtenidos de los Coeficientes Phi, V de Cramer y de Contingencia (como medidas nominales cuantifican el grado de asociación) indican una asociación baja entre la edad de las mujeres y la aceptación del aborto.
- los valores obtenidos de los Coeficientes Tau‐b de Kendall, Tau‐c de Kendall, Gamma y Correlación de Spearman (como medidas ordinales indican además el tipo de asociación) presentan una asociación baja negativa, es decir, que el grado de aceptación del aborto disminuye al aumentar la edad.
Se concluye, que existe evidencia de asociación entre el grado de aceptación del aborto y la edad de las mujeres, disminuyendo el grado de aceptación al aumentar la edad.
El ministerio de sanidad está interesado en conocer si hay relación entre el motivo de la consulta de los usuarios y el centro hospitalario al que recurren. Para ello, clasifican el motivo de la consulta en 7 grupos y realizan el estudio en 5 centros similares. Los 7 motivos de consulta se clasificaron en los siguientes grupos: (1) Medicina preventiva; (2) Enfermedades alérgicas; (3) Enfermedades respiratorias de vías altas; (4) Enfermedades respiratorias de vías bajas; (5) Enfermedades agudas; (6) Enfermedades crónicas; (7) Intoxicaciones. Los datos se muestran en la siguiente tabla
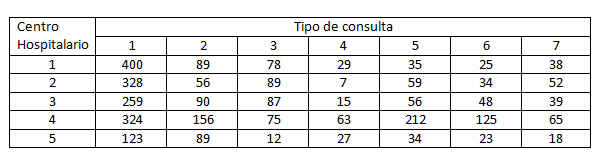
Solución
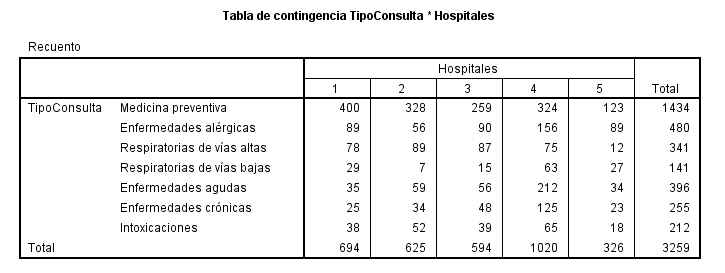
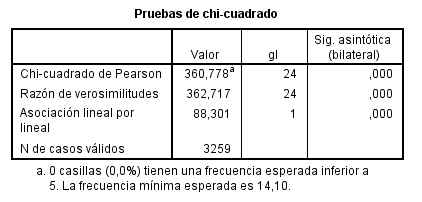
El valor del estadístico de contraste (observado) Chi-cuadrado de Pearson es 360.778, tiene asociado una probabilidad (Significación asintótica) de 0.000. Puesto que esta probabilidad es pequeña (menor que 0,05), se decide rechazar la hipótesis nula, indicando que hay evidencia de asociación entre el centro hospitalario y el tipo de consulta.
El valor del estadístico la Razón de verosimilitudes (RV) es 362.717, tiene asociada una probabilidad (Sig. asintótica) de 0,000 , que como es menor que 0,05, indica que hay evidencia de asociación entre las dos variables analizadas.
Los estadísticos (χ2 ,RV) llevan a la misma conclusión, en caso contrario, se elige el estadístico con menor Sig. asintótica.
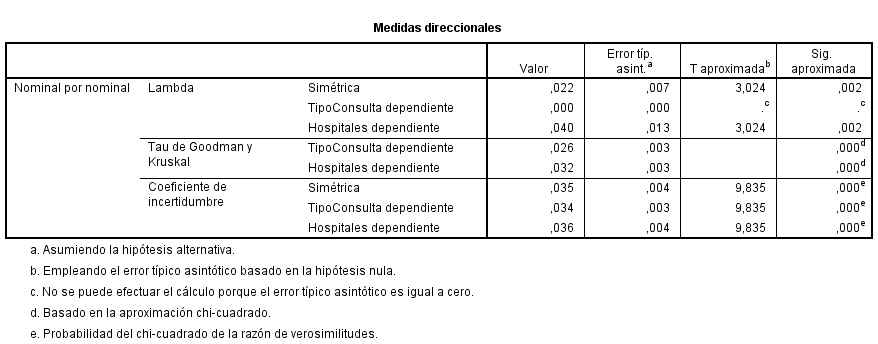
Los valores obtenidos de Lambda, Tau de Goodman y Kruskall, Coeficiente de incertidumbre (como medidas nominales cuantifican el grado de asociación, la capacidad de hacer pronósticos de una variable respecto de la otra). Indican una asociación baja entre el centro hospitalario y el tipo de consulta, es decir, la capacidad de hacer pronósticos de una variable respecto de la otra es realmente escasa.
Cada medida acompañada de un nivel crítico (Sig. aproximada), en todos los casos es menor que 0.05, conduce a rechazar la hipótesis nula de independencia y concluir que las variables (centro hospitalario, tipo de de la consulta) están asociadas.
El valor 0,026 del coeficiente Tau de Goodman y Kruskall, considera la variable “Centro hospitalario” como independiente, tiene la siguiente interpretación: Conociendo el centro hodpitalario, se reduce en un 2,6% la probabilidad de cometer un error al predecir el tipo de consulta. Esto significa que el centro hospitalario no tiene capacidad predictiva sobre el tipo de consulta.
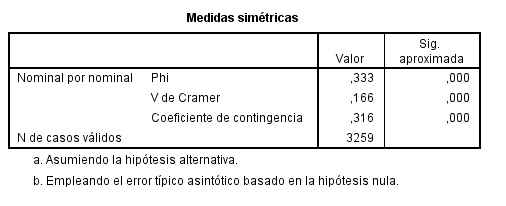 El valor de cada coeficiente aparece acompañado de su correspondiente nivel crítico (Sig. aproximada), que permite tomar una decisión sobre la hipótesis nula de independencia. Puesto que estos niveles críticos son menores que 0,05, se puede afirmar que hay asociación entre el centro hospitalario y el tipo de las consultas.
El valor de cada coeficiente aparece acompañado de su correspondiente nivel crítico (Sig. aproximada), que permite tomar una decisión sobre la hipótesis nula de independencia. Puesto que estos niveles críticos son menores que 0,05, se puede afirmar que hay asociación entre el centro hospitalario y el tipo de las consultas.
Los valores obtenidos del Coeficiente de clos coeficientes Phi, V de Cramer y de Contingencia (como medidas nominales cuantifican el grado de asociación) indican una asociación baja entre el centro hospitalario y el tipo de la consulta.
En definitiva, se puede concluir que el centro hospitalario y el tipo de consulta están relacionados, pero en ningún caso se podría considerar un claro factor de pronóstico sobre las consultas.
Se realiza un estudio para analizar si existe asociación entre los ingresos de un grupo de 132 trabajadores de varias empresas y su nivel de estudios. Se clasifica el salario que reciben en tres categorías: (Salarios están entre 700 y 999 euros; Salarios entre 1000 y 1500 euros y Salarios mayores de 1500 euros). El nivel de estudios se mide en tres categorías (estudios básicos, secundarios y universitarios). Los datos del ejercicio se recogen en la siguiente tabla:
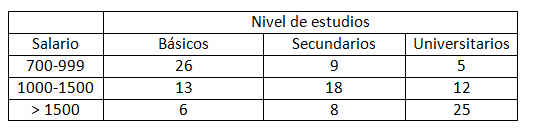
Solución
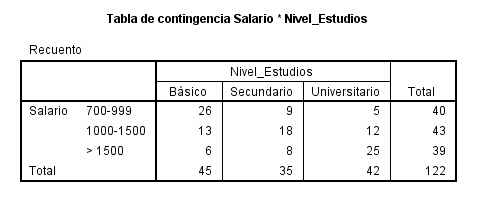
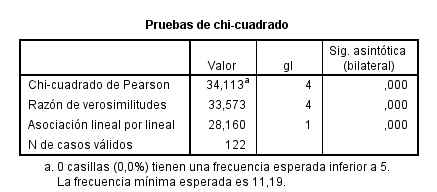
El valor del estadístico de contraste (observado) Chi-cuadrado de Pearson es 34.113, tiene asociado una probabilidad (Significación asintótica) de 0.000. Puesto que esta probabilidad es pequeña (menor que 0,05), se decide rechazar la hipótesis nula, indicando que hay evidencia de asociación entre el Nivel de estudios y el salario.
El valor del estadístico la Razón de verosimilitudes (RV) es 33.573, tiene asociada una probabilidad (Sig. asintótica) de 0,000, que como es menor que 0,05, indica que hay evidencia de asociación entre las dos variables analizadas.
Los estadísticos (χ2 ,RV) llevan a la misma conclusión, en caso contrario, se elige el estadístico con menor Sig. asintótica.
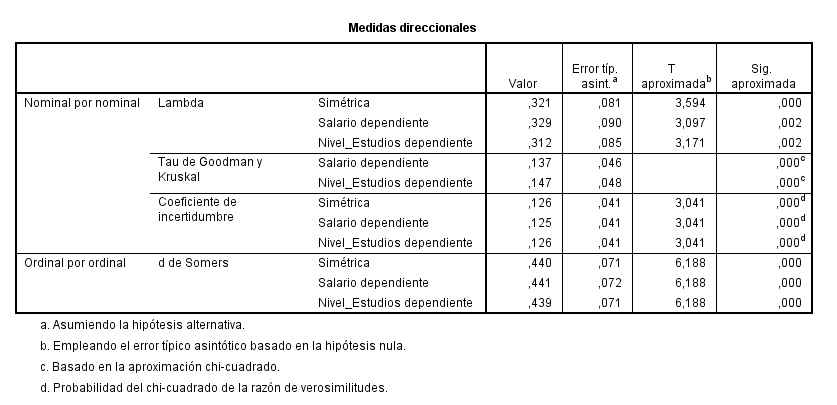
En el análisis de Medidas Direccionales se encuentran las medidas nominales (Lambda, Tau de Goodman y Kruskal, Coeficiente de incertidumbre), medidas ordinales (d de Somers).
- Las medidas nominales permiten contrastar la independencia sin decir nada sobre la fuerza de asociación entre las variables, informan únicamente del grado de asociación existente, no de la dirección o de la naturaleza de tal asociación.
- Las medidas ordinales recogen la dirección de la asociación de las variables: una relación positiva indica que los valores altos de una variable se asocian con los valores altos de la otra variable, y los valores bajos con los valores bajos; una relación negativa indica que los valores altos de una variable se asocian con los valores bajos de la otra variable, y los valores bajos con los valore altos.
Cada medida de asociación en la tabla (Lambda, Tau de Goodman‐Kruskall, Coeficiente de incertidumbre) se muestra acompañada de su nivel crítico (Sig. aproximada = 0.000), que al ser menor que 0,05, conduce a rechazar la hipótesis nula de independencia, concluyendo que las variables en estudio están relacionadas.
Junto al valor concreto adoptado por cada medida de asociación nominal por nominal (0.321, 0.137 y 0.126) se muestra su valor estandarizado (T aproximada), que se obtiene dividiendo el valor de la medida entre su error típico (calculado éste suponiendo independencia entre las variables).
La tabla también muestra el error típico de cada medida calculado sin suponer independencia (Error típico asintótico).
Observamos que cada coeficiente tiene un valor cuando se considera una de las variables independiente. Así por ejemplo el coeficiente Tau de Goodman y Kruskall tiene:
- El valor 0,137 cuando considera la variable “Nivel de estudios” como independiente. La interpretación es la siguiente: Conociendo el tipo de salario consultada (filas), se reduce en un 13.7% la probabilidad de cometer un error al predecir su nivel de estudios. Esto significa que el tipo de salario no tiene capacidad predictiva sobre el nivel de estudios.
- El valor 0,147 cuando considera la variable “Tipo de salario” como independiente. La interpretación es la siguiente: Conociendo el Nivel de estudios, se reduce en un 14.7% la probabilidad de cometer un error al predecir el tipo de salario. Esto significa que el Nivel de estudios de la persona no tiene capacidad para predecir el tipo de salario que percibe.
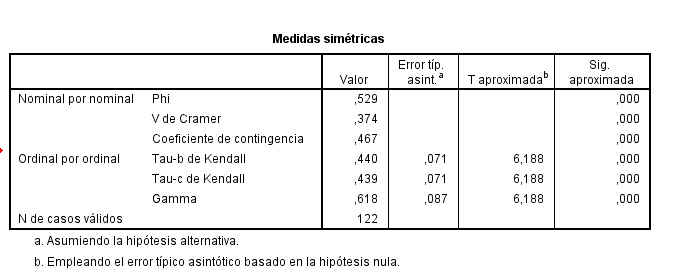
El valor de cada coeficiente aparece acompañado de su correspondiente nivel crítico (Sig. aproximada), que permite tomar una decisión sobre la hipótesis nula de independencia. Puesto que estos niveles críticos son menores que 0,05, se puede afirmar que hay relación entre el tipo de Salario y el Nivel de estudios.
- los valores obtenidos de los Coeficientes Phi, V de Cramer y de Contingencia (como medidas nominales cuantifican el grado de asociación) indican una asociación aceptable entre ambas variables.
- los valores obtenidos de los Coeficientes Tau‐b de Kendall, Tau‐c de Kendall, Gamma y Correlación de Spearman (como medidas ordinales indican además el tipo de asociación) presentan una asociación media y positiva, es decir, que el tipo de salario aumenta con el nivel de estudios.
Se concluye, que existe evidencia de asociación entre el tipo de salario y el nivel de estudios, aumentando el tipo de salario cuando aumenta el nivel de estudios. Teniendo ambas variable un grado medio de asociación.