DISTRIBUCIONES DE PROBABILIDAD: BINOMIAL, POISSON Y NORMAL

Objetivos

• • Seleccionar la distribución de probabilidad para modelizar un experimento aleatorio
  • Calcular probabilidades de las distribuciones Binomial,  Poisson y Normal
  • Calcular cuantiles
  • Generar valores aleatorios de una distribución determinada.

---

Introducción

En la teoría de la probabilidad existen muchos modelos teóricos que resultan de utilidad en una gran variedad de situaciones prácticas, ya que sirven para modelizar gran número de situaciones reales. Estas distribuciones o modelos de probabilidad se dividen en dos grandes grupos dependiendo del tipo de la variable que modelizan. Así, distinguimos entre distribuciones de probabilidad discretas, si la variable aleatoria que modelizan es de naturaleza discreta y distribuciones de probabilidad continuas, cuando la variable aleatoria es continua.

Existen muchas distribuciones de probabilidad pero, dado el carácter introductorio de esta práctica, nos limitaremos a estudiar la distribución binomial y la distribución de Poisson como ejemplos de distribuciones discretas y la distribución Normal para ilustrar las distribuciones continuas.

En esta práctica calcularemos las probabilidades asociadas a sucesos aleatorios a través de R-Commander, obtendremos valores relevantes (como, por ejemplo, valores de la función masa de probabilidad (o función de densidad), de la función de distribución o cuantiles) de las distribuciones de probabilidad mencionadas anteriormente y extraeremos muestras aleatorias de tales distribuciones.

 Todas las opciones relativas a las distribuciones de probabilidad se encuentran en el menú Distribuciones de R-Commander.

Figura 1: Distribuciones en R Commander

R-Commander agrupa las distribuciones de probabilidad en discretas y continuas, de  manera que lo primero que debemos hacer es identificar el grupo al que pertenece la distribución con la que queremos trabajar. La siguiente tabla recoge las distribuciones discretas y continuas que se utilizan con más frecuencia.

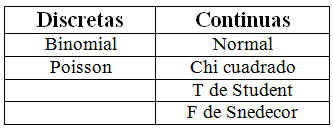Tabla 1. Clasificación de las distribuciones de probabilidad mas frecuentes

Distribuciones discretas

Seleccionamos en el menú principal: Distribuciones/Distribuciones discretas y se muestran las siguientes distribuciones: Binomial, Poisson, Geométrica, Hipergeométrica y Binomial negativa. Seleccionando una de ellas accedemos a su menú para ver las opciones disponibles. Así, para cualquiera de las distribuciones de probabilidad discretas estas opciones son:

Figura 2: Distribuciones/Distribuciones discretas

• Cuantiles: Calcula los cuantiles (cuartiles, deciles, percentiles, …) de la distribución.
• Probabilidades acumuladas: Calcula valores de la función de distribución.
• Probabilidades: Calcula valores de la función masa de probabilidad.
• Gráfica de la distribución: Representa gráficamente la función masa de probabilidad o la función de distribución.
• Muestra de una distribución: Extrae una muestra aleatoria de valores de la distribución.

Veamos el funcionamiento de cada una de estas opciones mediante supuestos resueltos

Distribución Binomial

Consideremos repeticiones independientes de un experimento aleatorio con dos posibles resultados a los cuales nos referiremos genéricamente como “éxito” y “fracaso”. El éxito ocurre con una probabilidad \(  p \) y el fracaso, por tanto, con una probabilidad \(  q = 1-p \).

En este contexto, interesa estudiar el número de éxitos en estas repeticiones del experimento aleatorio y, para ello, se define la siguiente variable aleatoria,  X = “Número de éxitos en  ensayos independientes con probabilidad de éxito constante p ”.

Entonces decimos que \(  X \) sigue una distribución binomial de parámetros \(  n \) y \(  p \), y lo representamos como \(  X \rightarrow B (n,p ) \).

La distribución binomial es una distribución de probabilidad discreta, mide el número de éxitos en una secuencia de \(  n \) ensayos independientes, con una probabilidad fija \(  p \) de ocurrencia de éxitos entre los ensayos.

Es evidente que los posibles valores que puede tomar la variable aleatoria (o, lo que es lo mismo, el número de ensayos exitosos de los que se realizan) son los valores comprendidos entre 0 y n.

A continuación vamos a definir y calcular:

1. La probabilidad de que la variable aleatoria X tome cada valor concreto o, equivalentemente, el valor de la función masa de probabilidad en cada uno de estos puntos
2. La probabilidad que acumula cada uno de los valores de la variable aleatoria X, es decir, el valor de la función de distribución en cada punto de la variable
3. Cuantiles de la distribución binomial
4. Valores aleatorios de la distribución binomial.

Función masa de probabilidad

La función masa de probabilidad de una variable aleatoria discreta, la cual suele representarse por \(  p_i \), es una función que asigna una determinada probabilidad a cada uno de los puntos de la variable.

\(  p_i  = P [ X = x_i ] \)

En R Commander, los valores de la función masa de probabilidad de una variable con distribución binomial se obtienen seleccionando en el menú principal: Distribuciones/Distribuciones discretas/Distribución binomial/Probabilidades binomiales.

Función de distribución

La función de distribución evaluada en un punto \( x_i \) x_i de una variable aleatoria discreta se denota por \(  F(x_i) \) y viene dada por

\(  F(x_i) = P[X \leq x_i] = P [X = 0] + P [X  = 1] + \cdots + P [X = x_i] \) 

 

En R Commander, los valores de la función masa de probabilidad de una variable con distribución binomial se obtienen seleccionando en el menú principal: Distribuciones/Distribuciones discretas/Distribución binomial/Cuantiles binomiales acumuladas.

Cuantiles de la distribución binomial

Por definición, el cuantil de orden α  de una distribución de probabilidad es aquel valor de la distribución que deja a su izquierda una proporción de valores α (o, equivalentemente, un porcentaje del \(  (α \times100)%  \)).  Esto es, el cuantil de orden \(  α \), será aquel valor \(  k \) tal que

\(  P[ X \leq  k ] = α \)

En R Commander, los valores de los cuantiles de una variable con distribución binomial se obtienen seleccionando en el menú principal: Distribuciones/Distribuciones discretas/Distribución binomial/Probabilidades binomiales acumuladas.

Generar valores aleatorios de la distribución binomial

Por último, calcular muestras de valores aleatorios generados a partir de una distribución binomial. Esta opción puede resultar de mucho interés en experimentos de simulación en los que se conoce de antemano que la variable de interés sigue una distribución binomial.

En R Commander, los valores los valores generados aleatoriamente de una variable con distribución binomial se obtienen seleccionando en el menú principal: Distribuciones/Distribuciones discretas/Distribución binomial/Muestra de una distribución binomial.

Supuesto Práctico 1

Supongamos una variable aleatoria, X, que sigue una distribución binomial de parámetros n = 10 y  p = 0.4;  \( X \rightarrow B(10, 0.4) \) 

a) Representar las gráficas de la función masa de probabilidad y de la función de distribución de la variable X

b) Calcula las siguientes probabilidades: \( P[ X  ≤  7 ]  ; P[ 2 <  X  ≤  5 ] ; P[ X  ≥  4 ]  \)

c) Calcula los cuantiles asociados a las siguientes probabilidades: 0.1, 0.5 y 0.75

d) Extraer dos muestras aleatorias de elementos de esta distribución de probabilidad, una de tamaño 10 y otra de tamaño 20. Llamar a las muestras “MBinom1” y “MBinom2”.

Solución

a) Representar las gráficas de la función masa de probabilidad y de la función de distribución de la variable X

Seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/ Gráfica de la distribución binomial tal y como muestra la siguiente imagen

 Figura 3: Distribuciones/Distribuciones discretas/ Gráfica de la distribución binomial

 Y se muestra la siguiente pantalla

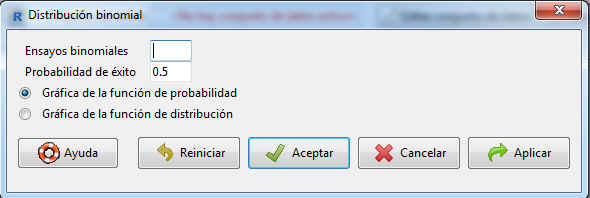Figura 4: Gráfica de la función de probabilidad de una distribución binomial

En esta salida, introducimos los parámetros de la distribución: Ensayos binomiales, 10; Probabilidad de éxito, 0.4 y seleccionamos Gráfica de la función de probabilidad

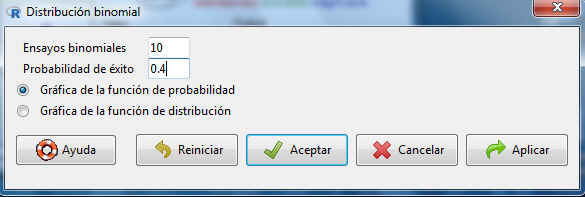Figura 5: Gráfica de la función de probabilidad de una distribución B(10, 0.4)

 Pulsamos Aceptar y se muestra la Gráfica de la función de probabilidad de una B(10, 0.4)

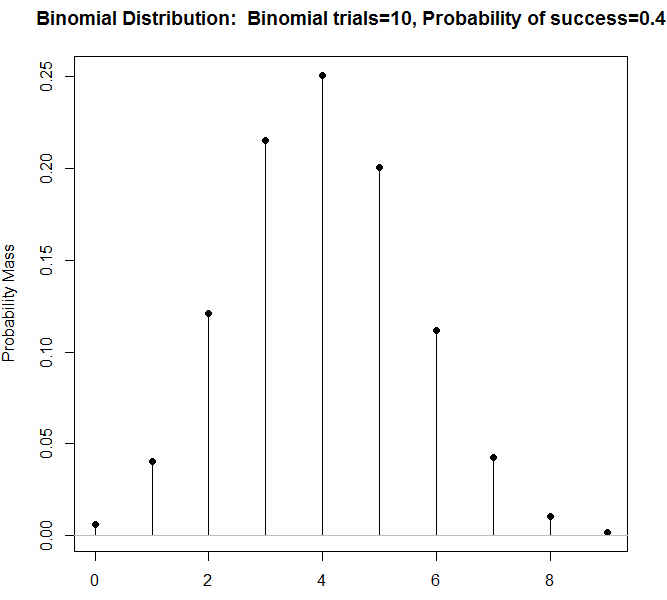 Figura 6: Gráfica de la función de probabilidad

 En la salida de la figura 5, seleccionamos Gráfica de la función de distribución y pulsamos Aceptar

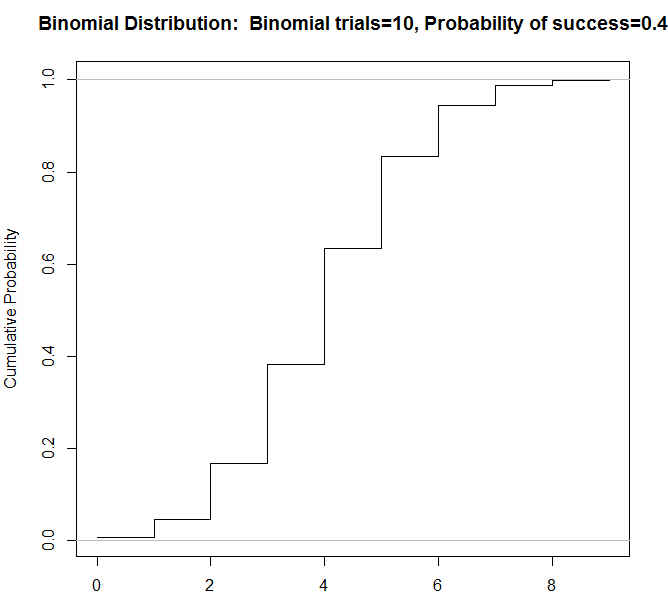Figura 7: Gráfica de la función de la función de distribución

b) Calcula las siguientes probabilidades:  \( P[ X  ≤  7 ]  ; P[ 2 <  X  ≤  5 ] ; P[ X  ≥  4 ]  \)

b1)  \( P[ X  ≤  7 ]  \) 

 Hay dos formas de calcular esta probabilidad. Por un lado, dado que nos encontramos ante una distribución de probabilidad discreta, sabemos que:

 \(  P[X ≤ 7] = P[X   =0] + P[X= 1]  + \cdots +  P[X =7 ]   \)

De este modo, podemos utlizar la función masa de probabilidad para calcular de forma separada cada una de estas probabilidades para después sumarlas y obtener así la probabilidad que buscamos. Para ello, seleccionamos en el menú principal Distribuciones/Distribuciones discretas/ Probabilidades binomiales

Figura 8: Distribuciones/Distribuciones discretas/ Probabilidades binomiales

 Y en la salida resultante, ponemos 4 en Ensayos binomiales y 0.4 en Probabilidad de éxito

Figura 9: Cálculo de \( P[ X  ≤  7 ]  \) de una B(10, 4)

Pinchamos en Aceptar y obtenemos las probabilidades puntuales de la distribución:

> local({
+   .Table <- data.frame(Probability=dbinom(0:10, size=10, prob=0.4))
+   rownames(.Table) <- 0:10
+   print(.Table)
+ })
Probability
0  0.0060466176
1  0.0403107840
2  0.1209323520
3  0.2149908480
4  0.2508226560
5  0.2006581248
6  0.1114767360
7  0.0424673280
8  0.0106168320
9  0.0015728640
10 0.0001048576

La probabilidad que nos piden, por tanto, es:

\(   \begin{array}{ll} P[X  ≤  7] = P[X  = 0] + P[X = 1]  + \cdots +  P[X = 7 ]  = & \\  =  0.0060466176 + 0.0403107840 + 0.1209323520 + 0.2149908480 + & \\ + 0.2508226560 + 0.2006581248 + 0.1114767360 + 0.0424673280 = 0.9877054 & \end {array} \)

Una segunda forma de obtener esta probabilidad es teniendo en cuenta que \( P[X  ≤  7]  = F(7) \), donde F(7) representa la función de distribución. Por tanto, podemos calcular esta probabilidad accediendo a la opción  Probabilidades binomiales acumuladas que está dentro del menú de la distribución binomial. Para ello, seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución binomial/Probabilidades binomiales acumuladas

Figura 10: Distribuciones/Distribuciones discretas/Distribución binomial/Probabilidades binomiales acumuladas

Y se muestra la siguiente pantalla

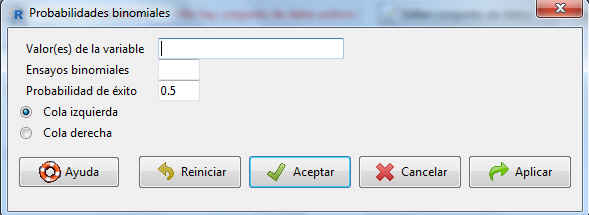Figura 11: Pantalla de las probabilidades binomiales acumuladas

En la salida resultante, en Valor(es) de la variable, insertamos el valor de la variable hasta el cual queremos acumular la probabilidad (en nuestro caso, el 7), indicamos los parámetros de la distribución (Ensayos binomiales = 10 y Probabilidad de éxito = 0.4) y señalamos si queremos probabilidades acumuladas con cola a la izquierda (es decir, del tipo \(  P[X  ≤  x] \)) o con cola a la derecha (del tipo \(  P[X  > x] \)).

Figura 12: Cálculo de la Probabilidades binomiales acumulada \(  P[X  ≤  7] \) de un B(10, 0.4)

Pulsamos Aceptar y se obtiene la siguiente salida

> pbinom(c(7), size=10, prob=0.4, lower.tail=TRUE)
[1] 0.9877054

\(  P[X  ≤  7]  = F(7) = 0.9877054 \)

b2) \(  P[ 2 <  X  ≤  5 ] \) 

Para calcular esta probabilidad, tenemos que tener en cuenta que, en este caso, \(  P[ 2 <  X  ≤  5 ] = P[ 3 ≤  X  ≤  5 ] \). Al igual que en el caso anterior, tenemos dos vías de calcular esta probabilidad, una basada en los valores de la función masa de probabilidad y otra basada en la función de distribución.

 La primera forma se basa en las probabilidades puntuales de la distribución que calculamos en el apartado anterior.

Así, resulta evidente que:

\(   \begin{array}{ll} P[ 3 ≤  X  ≤  5 ] = P[ X   = 3] + P[X = 4]  +  P[X = 5]   =  & \\   0.2149908480 +  0.2508226560 +  0.2006581248 = 0.6664716 & \end {array} \)

De forma alternativa, podemos usar la función de distribución para obtener el valor de esta probabilidad sabiendo que:

\(  P[ 2 <  X  ≤  5 ] = P[ 3 ≤  X  ≤  5 ] =   P[ X  ≤  5 ] – P[ X ≤ 2 ] = F(5) – F(2) \) 

Por tanto, la probabilidad que buscamos se puede calcular como la diferencia entre dos valores de la función de distribución. Calculemos en primer lugar el valor de F(5) . Como ya hicimos en el caso anterior, tenemos que entrar en el menú Probabilidades binomiales acumuladas e indicar los parámetros de la distribución y los valores hasta los cuales queremos acumular. Para ello, en Valor(es) de la variable insertamos 5 y 2; en Ensayos binomiales ponemos 10 y en Probabilidad de éxito ponemos 0.4

Figura 13: Cálculo de la Probabilidades binomiales acumulada \(  P[ 2 <  X  ≤  5 ] \)

Pulsamos Aceptar y se obtiene la siguiente salida

> pbinom(c(5,2), size=10, prob=0.4, lower.tail=TRUE)
[1] 0.8337614 0.1672898
La diferencia entre ambos números nos da la probabilidad que buscamos

\(   \begin{array}{ll}  P[ 2 <  X  ≤  5 ] = P[ 3 ≤  X  ≤  5 ] =  & \\  = P[ X  ≤  5 ] – P[ X ≤ 2 ] = F(5) – F(2) = 0.8337614 – 0.1672898 = 0.6664716 & \end {array} \)

b3) \(  P[X ≥ 4] \) 

Para obtener esta probabilidad podemos recurrir de nuevo a las probabilidades puntuales que hemos calculado en los apartados anteriores, ya que

\(   \begin{array}{ll}  P[X ≥ 4] = P[X = 4]  +  P[X = 5]  + ….+ P[X = 10] =  & \\  = 0.2508226560 + 0.2006581248 + 0.1114767360 +  0.0424673280 +  & \\ + 0.0106168320 + 0.0015728640 + 0.0001048576 =  0.6177194 & \end {array} \)

Hay que tener en cuenta que, si la variable tuviera un número infinito de posibles valores, no podríamos considerar este primer método, ya que tendríamos que sumar las probabilidades de infinitos valores.

 Al igual que en los dos casos anteriores, podemos calcular esta probabilidad a partir de un valor de la función de distribución sin más que tener en cuenta que

\(  P[X ≥ 4] = 1 – P[X ≤ 3] = 1 – F(3) \)

Vamos a calcular el valor de esta probabilidad acumulada, entrando de nuevo al menú Probabilidades binomiales acumuladas dentro de la distribución binomial

Figura 14: Cálculo de la Probabilidades binomiales acumulada \(  P[   X  \geq  4 ] = 1 – P[X \leq 3] \)  

Y en la salida correspondiente, en Valor(es) de la variable insertamos el valor 3; Ensayos binomiales ponemos 10 y en Probabilidad de éxito ponemos 0.4 y pulsamos Aceptar

Se obtiene la siguiente salida

> pbinom(c(3), size=10, prob=0.4, lower.tail=TRUE)
[1] 0.3822806

Por tanto, la probabilidad que buscamos es

\(  P[X ≥ 4] = 1 – P[X ≤ 3] = 1 – F(3) = 1 – 0.3822806 = 0.6177194 \)

Igualmente, podríamos haber obtenido este valor directamente considerando colas a la derecha en la función de distribución. Hay que tener en cuenta que cuando marcamos cola derecha estamos calculando \( P[X > x] \) por lo que \( P[X ≥ 4] = P[X > 3] \). Para ello en la salida de Probabilidades binomiales, en Valor(es) de la variable insertamos el valor 3; Ensayos binomiales ponemos 10 y en Probabilidad de éxito ponemos 0.4 y seleccionamos Cola derecha.

Figura 15: Cálculo de la Probabilidades binomiales acumulada \(  P[   X  \geq  4 ] = P[X > 3] \)   

Pulsamos Aceptar y se obtiene la siguiente salida

> pbinom(c(3), size=10, prob=0.4, lower.tail=FALSE)
[1] 0.6177194

\(  P[X ≥ 4] = P[X > 3] = 0.6177194 \)

c) Calcula los cuantiles asociados a las siguientes probabilidades: 0.1, 0.5 y 0.75

En este caso, nos piden los valores de la variable que dejan a su izquierda probabilidades acumuladas de 0.1, 0.5 y 0.75. Para calcular estos valores tenemos que acceder al submenú Cuantiles binomiales dentro del menú de la distribución binomial. Para ello, seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución binomial/Cuantiles binomiales

Figura 16: Distribuciones/Distribuciones discretas/Distribución binomial/Cuantiles binomiales

 y se muestra la siguiente salida

Figura 17: Cuantiles binomiales

En la pantalla resultante, tenemos que indicar, además de los parámetros de la distribución, las probabilidades para el cálculo de los cuantiles asociados. Podemos insertar más de una probabilidad, separándolas por comas. De esta forma, en Probabilidades ponemos 0.1, 0.5,  0.75, en Ensayos binomiales, 10, en Probabilidad de éxito, 0.4

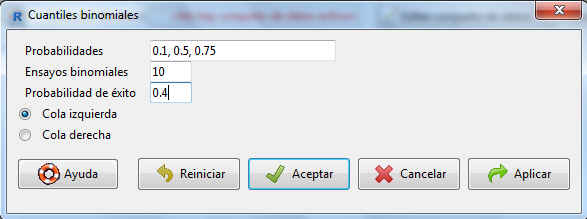Figura 18: Cálculo de cuantiles binomiales asociados a las probabilidades 0.1, 0.5 y 0.75

 Pulsamos Aceptar y se muestra la siguiente salida

> qbinom(c(0.1,0.5,0.75), size=10, prob=0.4, lower.tail=TRUE)
[1] 2 4 5

Los cuantiles asociados a las siguientes probabilidades 0.1, 0.5 y 0.75 son 2, 4 y 5 respectivamente

Estos cuantiles, 0.1, 0.5 y 0.75  deben coincidir con aquellos que dejan unas probabilidades de 0.9, 0.5 y 0.25 en la cola derecha de la distribución. Para ello, en la pantalla de los Cuantiles, introducimos en Probabilidades, 0.9, 0.5, 0.25 y seleccionamos Cola derecha

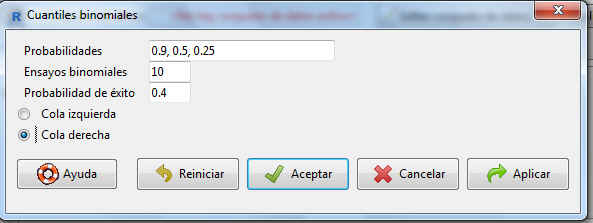Figura 19: Cálculo de cuantiles binomiales a las probabilidades 0.9, 0.5 y 0.25

Pulsamos Aceptar y se muestra la siguiente salida

> qbinom(c(0.9,0.5,0.25), size=10, prob=0.4, lower.tail=FALSE)
[1] 2 4 5

d) Extraer dos muestras aleatorias de elementos de esta distribución de probabilidad, una de tamaño 10 y otra de tamaño 20. Llamar a las muestras “MBinom1” y “MBinom2”.

Para extraer muestras aleatorias de una distribución binomial, accedemos a la opción Muestra de una distribución binomial, dentro del menú de la distribución. Para ello, seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución binomial/Muestra de una distribución binomial

Figura 20: Distribuciones/Distribuciones discretas/Distribución binomial/Muestra de una distribución binomial

Y se muestra la siguiente pantalla

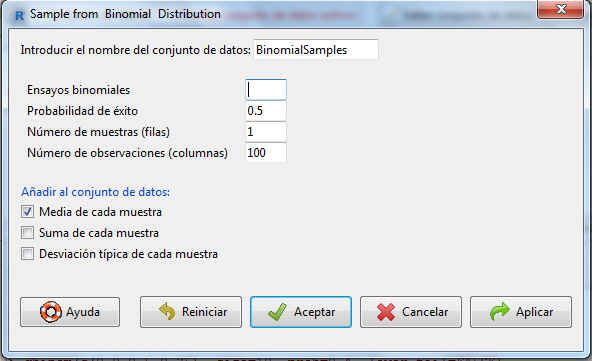Figura 21: Muestra de una distribución binomial

A continuación, introducimos el nombre que le queremos dar a la muestra que se va a generar e indicamos los parámetros de la distribución. Así, en Introducir el nombre del conjunto de datos ponemos MBinom1, en Ensayos binomiales, 10; en Probabilidad de éxito, 0.4. También indicamos en Número de muestras (filas) cuántas muestras queremos generar y en Número de observaciones (columnas) el número de elementos que tendrá cada una de esas muestras. Hay que tener en cuenta que, si generamos más de una muestra al mismo tiempo, todas tendrán el mismo número de elementos. Por lo tanto, como las dos muestras que nos piden generar tienen distinto número de observaciones, tendremos que generarlas de forma independiente. En esta primera muestra indicamos 1 para el Número de muestras (filas) y 10 para Número de observaciones (columnas)

Por último, el programa nos permite calcular algunos estadísticos descriptivos sobre las muestras generadas, como son la media, la desviación típica y la suma de los elementos de cada muestra.

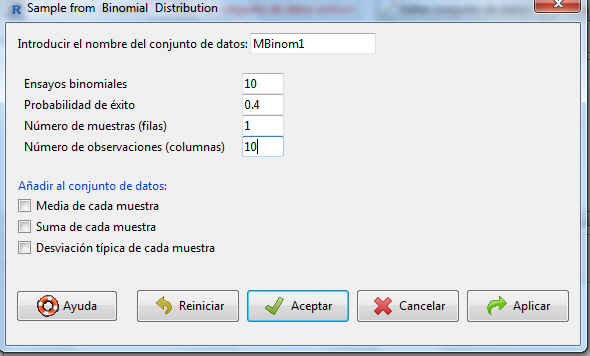Figura 22: Cálculo de la muestra 1 de una distribución binomial

Pulsamos Aceptar y Editar conjunto de datos. Se muestra la siguiente salida

Figura 23: Editor de datos de la muestra 1 (MBinom1)

Como resultado, obtenemos un data frame con la primera muestra que buscábamos, para ello pulsamos Visualizar conjunto de datos

Figura 24:  Data frame de la muestra 1 (MBinom1)

Para obtener la segunda muestra de valores aleatorios, repetimos el proceso, ajustando el número de observaciones y el nombre de la muestra. En la casilla Introducir el nombre del conjunto de datos ponemos MBinom2, en Ensayos binomiales, 10; en Probabilidad de éxito, 0.4, Número de muestras (filas), 1, en Número de observaciones (columnas), 20.

Figura 25: Cálculo de la muestra 2 de una distribución binomial

Pulsamos Aceptar y Visualizar conjunto de datos y obtenemos un segundo data frame de nombre Mbinom2 con los datos de la nueva muestra

Figura 26:  Data frame de la muestra 2 (MBinom2)

Distribución de Poisson

La distribución de Poisson es una distribución de probabilidad discreta que modeliza la probabilidad de que ocurra un determinado número de eventos durante cierto período de tiempo. A modo de ejemplo, la distribución de Poisson se utiliza frecuentemente para contar el número de llamadas que una centralita telefónica recibe por unidad de tiempo o el número de clientes que llegan a un determinado establecimiento en un período de tiempo dado.

A diferencia de la distribución binomial, la cual necesita dos parámetros para ser correctamente identificada, la distribución de Poisson se define a partir de un único parámetro, que suele notarse por λ. Generalmente, el parámetro λ representa el número medio de sucesos que ocurren por unidad de tiempo. Entonces, podemos definir la variable aleatoria  X = “Número de sucesos aleatorios que ocurren en un determinado periodo de tiempo” e identificar su distribución, \(  X \rightarrow P(λ) \). Los posibles valores que puede tomar una variable con distribución de Poisson van desde 0 a infinito.

Puesto que la distribución de Poisson también es una distribución discreta, los valores que podemos calcular son los mismos que ya estudiamos para la distribución binomial. Por lo tanto, para la distribución de Poisson obtendremos valores de la función masa de probabilidad, de la función de distribución y de los cuantiles. También generaremos muestras de valores aleatorios que siguen distribuciones de Poisson.

El tratamiento computacional con R Commander de la distribución de Poisson es similar al que hemos empleado con la distribución binomial. Para ello, seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson

Función masa de probabilidad

Seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson

Función de distribución

Seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson acumuladas

Cuantiles de la distribución de Poisson

Seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Cuantiles de Poisson

Generar valores aleatorios de la distribución de Poisson

Seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Muestra aleatoria  de una distribución de Poisson.

Supuesto Práctico 2

Supongamos una variable aleatoria, X, que sigue una distribución de Poisson con media 5, \(  X \rightarrow P(5) \).

a) Representar las gráficas de la función masa de probabilidad y de la función de distribución de la variable

b) Calcular las siguientes probabilidades: \( P[X ≤ 2] ; P[2 ≤ X ≤ 4]; P[X > 4] \) 

c) Calcular los cuantiles asociados a las siguientes probabilidades: 0.3 y 0.5

d) Extraer una muestra aleatoria de elementos de esta distribución de probabilidad de tamaño 10 y calcular su media.

Solución

a) Representar las gráficas de la función masa de probabilidad y de la función de distribución de la variable

Para ello, seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Gráfica de la distribución de Poisson

Figura 27: Distribuciones/Distribuciones discretas/Distribución de Poisson/Gráfica de la distribución de Poisson

y se muestra la siguiente pantalla

Figura 28: Obtención de la gráfica de la función de distribución de Poisson

En esta pantalla, se introduce el valor de la media y se selecciona entre Gráfica de la función de probabilidad y Gráfica de la función de distribución.

En primer lugar vamos a representar gráficamente la función de probabilidad de una distribución de Poisson de media 5, para ello en Media introducimos 5 y seleccionamos Gráfica de la función de probabilidad

Figura 29:  Obtención de la gráfica de la función de probabilidad de una P(5)

 Pulsamos Aceptar y se muestra la siguiente gráfica

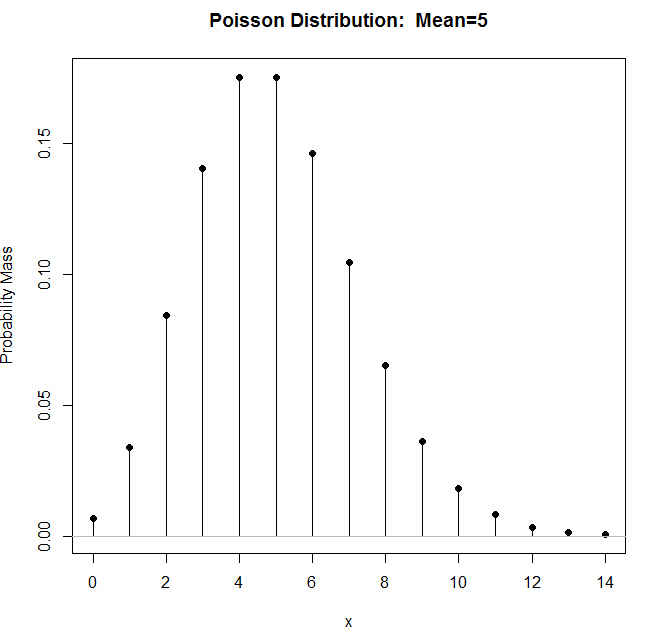Figura 30:  Gráfica de la función de probabilidad de P(5)

A continuación realizamos la gráfica de la función de distribución y para ello en la pantalla de la figura 29, seleccionamos Gráfica de la función de distribución

Figura 31:  Obtención de la gráfica de la función de distribución de una P(5)

Se pulsa Aceptar y se obtiene la siguiente gráfica

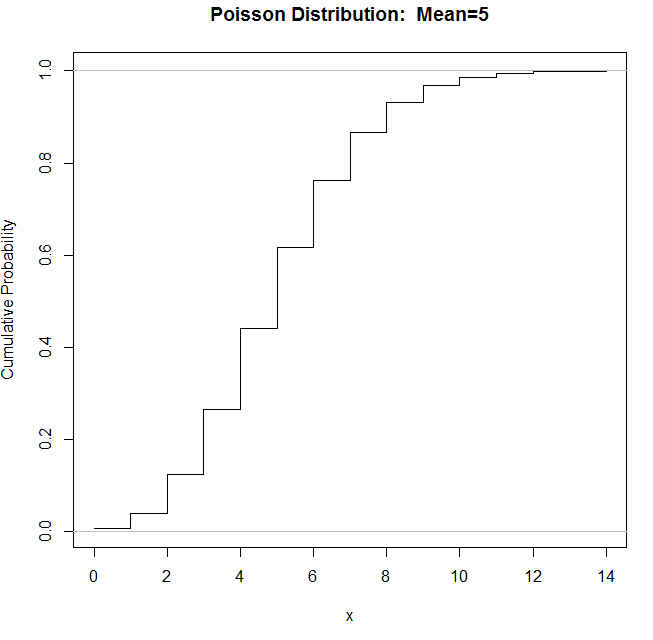Figura 32:  Gráfica de la función de distribución de una P(5)

b) Calcula las siguientes probabilidades: \( P[X ≤ 2] ; P[2 ≤ X ≤ 4]; P[X > 4] \)  

b1)  \( P[X ≤ 2] \) 

Al igual que en el caso de la distribución binomial, en la distribución de Poisson existen dos formas de calcular esta probabilidad. Por un lado, dado que nos encontramos ante una distribución de probabilidad discreta, sabemos que

\(  P[X ≤ 2] = P[X = 0] + P[X = 1] + P[X = 2] \)

De este modo, podemos usar la función masa de probabilidad para calcular de forma separada cada una de estas probabilidades para después sumarlas y obtener así la probabilidad que buscamos. Para ello, seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson

Figura 33: Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson

 Se muestra la siguiente pantalla

Figura 34: Cálculo de la probabilidad de la distribución de Poisson

Introducimos el valor de la media de la distribución (5)

Figura 35: Cálculo de la probabilidad de la distribución de Poisson de media 5

Se pulsa Aceptar y obtenemos las probabilidades puntuales de la distribución de Poisson de media 5

> local({
+   .Table <- data.frame(Probability=dpois(0:14, lambda=5))
+   rownames(.Table) <- 0:14
+   print(.Table)
+ })
Probability
0  0.0067379470
1  0.0336897350
2  0.0842243375
3  0.1403738958
4  0.1754673698
5  0.1754673698
6  0.1462228081
7  0.1044448630
8  0.0652780393
9  0.0362655774
10 0.0181327887
11 0.0082421767
12 0.0034342403
13 0.0013208616
14 0.0004717363

La probabilidad pedida es:

\(   \begin{array}{ll} P[X ≤ 2] = P[X = 0] + P[X = 1] + P[X = 2] = & \\  =0.0067379470 + 0.0336897350 + 0.0842243375 = 0.124652 & \end {array} \)

Una segunda forma de obtener esta probabilidad es teniendo en cuenta que \( P[X ≤ 2] = F(2) \), donde \(  F \) representa la función de distribución. Por tanto, podemos calcular esta probabilidad accediendo a la opción  Probabilidades de Poisson acumuladas. Para ello, seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson acumuladas

Figura 36: Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson acumuladas

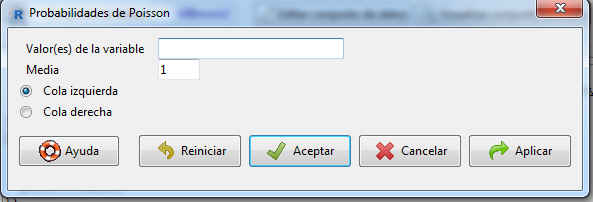Figura 37: Cálculo de la probabilidad de la distribución de Poisson (Probabilidades acumuladas)

Introducimos el valor de la variable, 2:  y la media, 5 y seleccionamos Cola izquierda

Figura 38: Cálculo \( P[X ≤ 2] \)  distribución de Poisson (Probabilidades acumuladas)

Se pulsa Aceptar y se obtiene la siguiente probabilidad

> ppois(c(2), lambda=5, lower.tail=TRUE)
[1] 0.124652

b2)  \( P[2 ≤ X ≤ 4] \) 

En este caso utilizaremos los valores de la función masa de probabilidad calculados en el apartado anterior 

\(   \begin{array}{ll} P[2 ≤ X ≤ 4] =  P[ X = 2] + P[ X = 3] + P[ X = 4] = & \\  = 0.0842243375 + 0.1403738958 + 0.1754673698 = 0.4000656 & \end {array} \)

b3)  \( P[X > 4] \) 

Calcularemos esta probabilidad a partir de un valor de la función de distribución.

Vamos a calcular el valor de esta probabilidad acumulada, seleccionando de nuevo en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson acumuladas.

En la pantalla resultante seleccionamos: Valor(es) de la variable = 4; Media= 5, y Cola derecha

Figura 39: Cálculo \( P[X > 4 ] \) distribución de Poisson (Probabilidades acumuladas)

Se obtiene la siguiente salida

> ppois(c(4), lambda=5, lower.tail=FALSE)
[1] 0.5595067

Por tanto, la probabilidad que buscamos es:  \( P[X  > 4] = F(4) = 0.5595067  \)

c) Calcula los cuantiles asociados a las siguientes probabilidades: 0.3 y 0.5

En este caso, nos piden los valores de la variable que dejan a su izquierda probabilidades acumuladas de 0.3 y 0.5. Para calcular estos valores tenemos que acceder al submenú Cuantiles de Poisson. Para ello, seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Cuantiles de Poisson

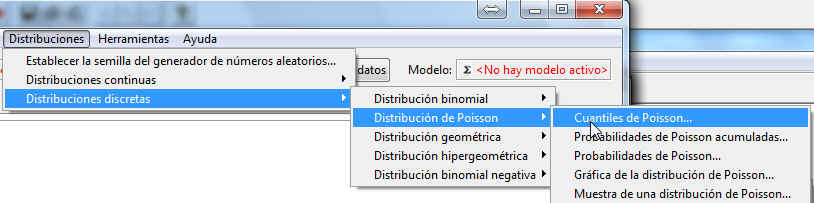Figura 40: Distribuciones/Distribuciones discretas/Distribución de Poisson/Cuantiles de Poisson

En la pantalla resultante tenemos que indicar, las probabilidades para el cálculo de los cuantiles asociados y el valor de la media de la distribución. Podemos indicar más de una probabilidad, separándolas por comas. Por tanto insertamos los valores: Probabilidades  = 0.3, 0.5; Media = 5 y Cola izquierda

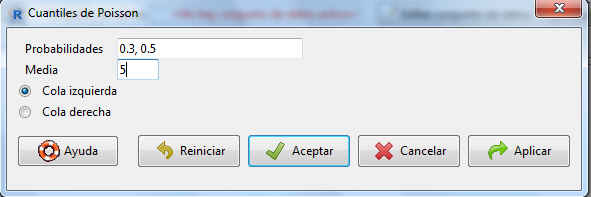Figura 41: Cálculo de los Cuantiles de Poisson

Se pulsa Aceptar y se obtiene la siguiente salida

> qpois(c(0.3,0.5), lambda=5, lower.tail=TRUE)
[1] 4 5

d) Extraer una muestra aleatoria de elementos de esta distribución de probabilidad de tamaño 10 y calcular su media

Para extraer muestras aleatorias de una distribución de Poisson, accedemos a la opción Muestra de una distribución de Poisson, dentro del menú de la distribución. Para ello, seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Muestra de una distribución de Poisson

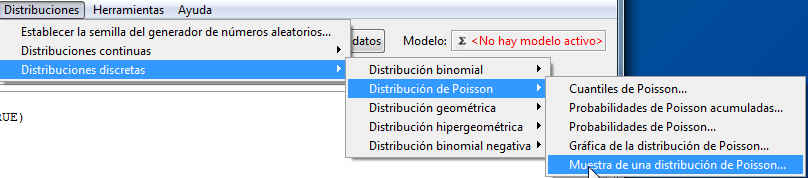Figura 42: Distribuciones/Distribuciones discretas/Distribución de Poisson/Muestra de una distribución de Poisson

En la pantalla resultante, introducimos el nombre que le queremos dar a la muestra que se va a generar, MPoisson, y la media de la distribución, 5.También indicamos en Número de muestras (filas) cuántas muestras queremos generar, en nuestro caso 1, y en Número de observaciones (columnas) el número de elementos que tendrá nuestra muestra, 10.

Por último, el programa nos permite calcular algunos estadísticos descriptivos sobre las muestras generadas, en este caso nos interesa conocer la media

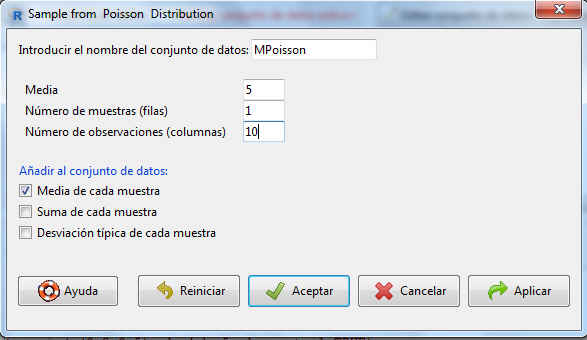Figura 43: Cálculo de una muestra de tamaño 10 de una distribución de Poisson

Pulsamos Aceptar y a continuación la pestaña Visualizar conjunto de dato y como resultado, obtenemos un data frame con la muestra que buscábamos.

Figura 44:  Muestra de tamaño 10 de una distribución de Poisson

La muestra está formada por los elementos {2, 8, 4, 5, 4, 8, 2, 6, 5, 5} y la media vale 4.9

Distribuciones continuas

Seleccionamos en el menú principal: Distribuciones/Distribuciones continuas y se muestran las distribuciones Normal, Poisson, t, Chi-cuadrado, F, exponencial, uniforme, beta, Cauchy, logística, lognormal, gamma, Weibull y Gumbel.

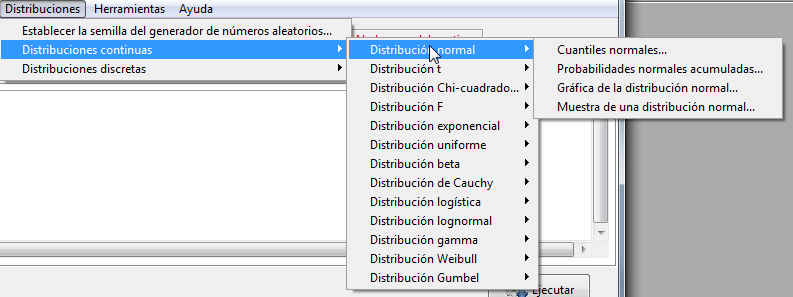Figura 45: Distribuciones/Distribuciones continuas

Seleccionando una de ellas accedemos a su menú para ver las opciones disponibles. Así, para cualquiera de las distribuciones de probabilidad continuas estas opciones son:

• Cuantiles: Calcula los cuantiles (cuartiles, deciles, percentiles, …) de la distribución
• Probabilidades acumuladas: Calcula valores de la función de distribución
• Gráfica de la distribución: Representa gráficamente la función de densidad o la función de distribución.
• Muestra de la distribución: Extrae una muestra aleatoria de valores de la distribución.

Distribución Normal

La distribución Normal es la más importante y de mayor uso de las distribuciones continuas, debido a la gran cantidad de fenómenos aleatorios que modeliza. Esta distribución también se conoce como gaussiana o de Gauss, en honor a su descubridor. La distribución Normal viene identificada por dos parámetros, \( \mu \) y \( σ \), que coinciden con la media y la desviación típica de la distribución. Cuando una variable aleatoria, \( X \), siga una distribución normal lo notaremos \( X \rightarrow N(μ, σ) \).

El tratamiento computacional con R Commander de la distribución Normal en particular, y de cualquier distribución de probabilidad continua en general, es similar al que se utiliza con las distribuciones discretas. La principal salvedad se encuentra en la función masa de probabilidad. Esta función es la equivalente para la distribución normal a la probabilidades acumuladas en las distribuciones binomal y de Poisson. Recordemos que las funciones masa de probabilidad devuelven la probabilidad puntual para cada uno de los valores posibles que puede tomar una variable con distribución binomial y de Poisson. Pero el cálculo de probabilidades en valores concretos en una distribución continua no tiene sentido, ya que dicha probabilidad vale 0. Por todo ello, la opción de probabilidades acumuladas en la distribución Normal,  devuelve el valor de la función de densidad en un punto (o puntos) determinado.

Supuesto Práctico 3

Consideremos una variable aleatoria Y  que sigue una distribución Normal con media 20 y con desviación típica 2, es decir,  \( Y → N(20, 2) \). Se pide: 

 a) Representar gráficamente las funciones de densidad y de distribución de la variable \( Y → N(20, 2)  \) 

b) Calcular las siguientes probabilidades:   \( P[Y  ≤ 12]; P[18 < Y ≤  20]; P[Y  ≥  21]  \) 

c) Calcula los tres cuartiles de la distribución

d) Obtener dos muestras aleatorias de valores de la distribución de tamaño 12 y las medias de cada muestra

Solución

a) Representar gráficamente las funciones de densidad y de distribución de la variable \( Y → N(20, 2)  \) 

Para obtener las representaciones gráficas de las funciones de densidad y de distribución, tenemos que seleccionar en el menú principal Distribución/Distribuciones continuas/ Distribución Normal/ Gráfica de la distribución normal

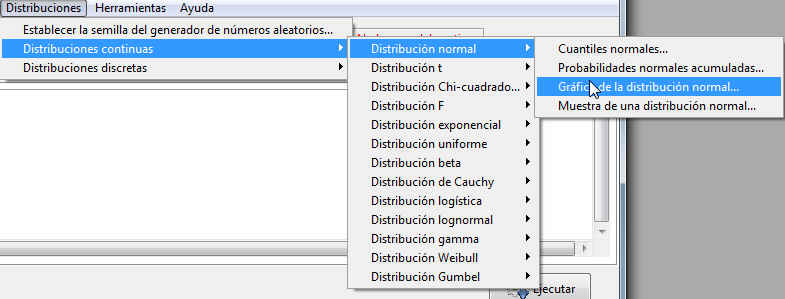Figura 46: Distribuciones/Distribuciones continuas/Distribución normal/Gráfica de la distribución normal

En la pantalla correspondiente poner Media = 20, Desviación típica = 2 y elegir Gráfica de la función de densidad

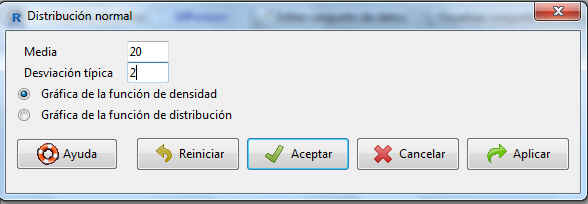Figura 47: Pantalla para representar la función de densidad

pulsar Aceptar y se muestra la siguiente gráfica

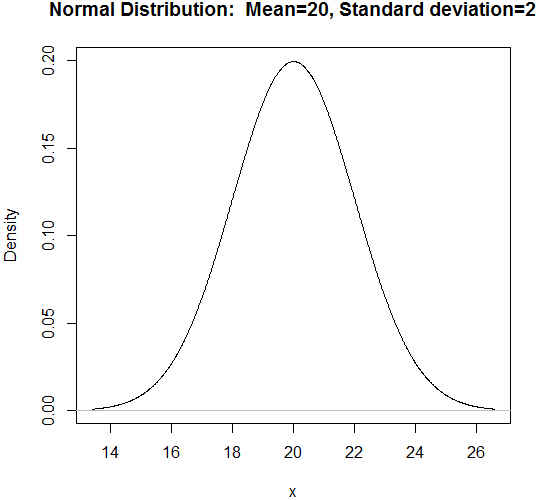Figura 48: Gráfica de la función de densidad de N(20, 2)

En la pantalla de la Figura 47, elegir Gráfica de la función de distribución

 Figura 49: Pantalla para representar la función de distribución

Se pulsa Aceptar y se muestra la siguiente gráfica

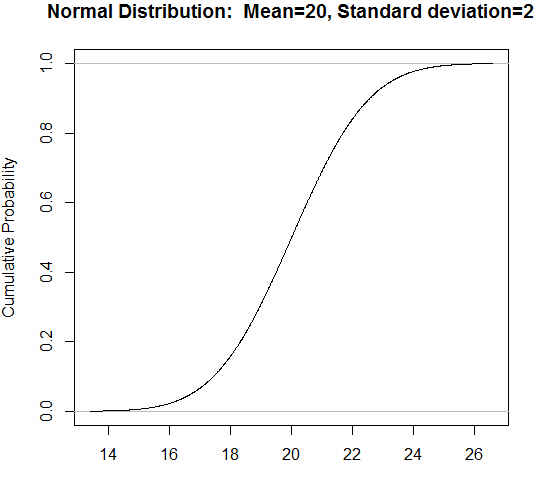Figura 50: Gráfica de la función de distribución de N(20, 2)

b) Calcular las siguientes probabilidades:  \( P[Y  ≤ 12]; P[18 < Y ≤  20]; P[Y  ≥  21]  \) 

A diferencia con el caso discreto, en donde las probabilidades se pueden calcular en base a la función masa de probabilidad o la función de distribución, en el caso continuo el cálculo de probabilidades se hace únicamente a partir de la función de distribución. De este modo, para el cálculo de la probabilidad que nos piden resulta esencial conocer que la función de distribución de una variable representa la probabilidad acumulada hasta un determinado valor de dicha variable. Por tanto, si llamamos  a la función de distribución de la variable Y tenemos que \( P[Y  ≤ y] = F(y) \), de manera que la probabilidad que queremos calcular no es más que el valor de la función de distribución en el punto y.

Para calcular valores de la función de distribución dada una distribución normal tenemos que seleccionar, en el menú principal, Distribución/Distribuciones continuas/ Distribución Normal/ Probabilidades normales acumuladas.

Figura 51: Distribución/Distribuciones continuas/ Distribución Normal/ Probabilidades normales acumuladas

y se obtiene la siguiente pantalla

Figura 52:  Cálculo de Probabilidades normales acumuladas

b1)  \( P[Y  ≤ 12] \)

En la pantalla resultante, introducimos los parámetros de la distribución y el valor de la variable hasta la cual queremos acumular la probabilidad. También es muy importante tener en cuenta si queremos que el programa nos devuelva probabilidades acumuladas por la cola izquierda (es decir, del tipo \( P[Y  ≤ y] \) ) o por la cola derecha (que serán del tipo \( P[Y  \geq y] \)).

Así para calcular \( P[Y  ≤ 12] \) de una  \( N(20, 2)  \). Sustituimos:  Valores de la variable = 12; Media = 20; Desviación típica = 2 y elegimos cola de la izquierda

Figura 53: Cálculo de \( P[Y  ≤ 12 ] \)

Después de Aceptar, obtenemos la probabilidad  que buscamos, que en este caso es 0.00003161

> pnorm(c(12), mean=20, sd=2, lower.tail=TRUE)
[1] 3.167124e-05

b2) \( P[18 < Y ≤  20] \)

El cálculo de esta segunda probabilidad también se hace basándose en valores de la función de distribución. Para escribir esta probabilidad en términos de la función de distribución de la variable tenemos que tener en cuenta que

 \( P[18 < Y ≤  20] = P[18 ≤ Y ≤  20] = P[ Y ≤  20] – P[ Y ≤  18] = F(20) – F(18) \)

Consecuentemente, necesitamos obtener los valores de la función de distribución evaluados en los puntos 20 y 18. Para ello, en la pantalla resultante de Distribución/Distribuciones continuas/ Distribución Normal/ Probabilidades normales acumuladas, seleccionamos:

Valores de la variable = 20, 18; Media = 20; Desviación típica = 2 y elegimos cola de la izquierda

Figura 54: Cálculo de  \( P[18 < Y ≤  20] \)

El programa nos permite calcular de forma conjunta los dos valores que necesitamos. Al Aceptar, obtenemos dichos valores: 0.5000000 y 0.1586553

> pnorm(c(20,18), mean=20, sd=2, lower.tail=TRUE)
[1] 0.5000000 0.1586553

La diferencia entre ambos valores nos proporciona la probabilidad que buscamos

\(   \begin{array}{ll} P[18 < Y ≤  20] = P[18 ≤ Y ≤  20] = & \\  =  P[ Y ≤  20] – P[ Y ≤  18] = F(20) – F(18) = 0.5000000 –  0.1586553 = 0.3413447 & \end {array} \)

b3) \( P[Y  ≥  21] \)

Esta probabilidad también se puede expresar en términos de la función de distribución sin más que hacer la transformación

\(  P[Y  ≥  21] = 1 – P[Y  ≤  21 ] = 1 – F(21)  \)

Vamos a calcular, por tanto, el valor de la función de distribución evaluado en el punto 21. Para ello en la pantalla resultante de Distribución/Distribuciones continuas/ Distribución Normal/ Probabilidades normales acumuladas, seleccionamos:

Valores de la variable = 21; Media = 20; Desviación típica = 2 y elegimos cola de la izquierda

Figura 55: Cálculo de  \( P[Y  ≥  21] = 1 – P[Y  ≤  21 ] \)

Pulsamos Aceptar y se obtiene el siguiente resultado

> pnorm(c(21), mean=20, sd=2, lower.tail=TRUE)
[1] 0.6914625

La probabilidad que buscamos, por tanto, es

\(  P[Y  ≥  21] = 1 – P[Y  ≤  21 ] = 1 – F(21) = 1- 0.6914625 = 0.3085375 \)

Igualmente, podríamos haber obtenido esta probabilidad directamente sin necesidad de ningún cálculo adicional indicando al programa que calculara la probabilidad acumulada en la cola derecha de la distribución, en lugar de en la cola izquierda.

Para ello, en la pantalla resultante de Distribución/Distribuciones continuas/ Distribución Normal/ Probabilidades normales acumuladas, seleccionamos:

Valores de la variable = 21; Media = 20; Desviación típica = 2 y elegimos cola de la derecha

Figura 56: Cálculo de  \(  P[Y  ≥  21] \)

Se pulsa Aceptar y se obtiene el siguiente resultado

> pnorm(c(21), mean=20, sd=2, lower.tail=FALSE)
[1] 0.3085375

\( P[Y  ≥  21] = 0.3085375 \)

c) Calcula los tres cuartiles de la distribución

Los cuartiles de una distribución son los valores de la variable que dejan por debajo suyo (es decir, a su izquierda) el 25%, el 50% y el 75% de los valores de la variable. Para calcularlos, tenemos que  que seleccionar, en el menú principal, Distribución/Distribuciones continuas/ Distribución Normal/Cuantiles normales

Figura 57: Distribución/Distribuciones continuas/ Distribución Normal/Cuantiles normales

En la pantalla resultante, introducimos los valores de las probabilidades junto con los parámetros de la distribución. De nuevo, es importante tener en cuenta si queremos operar con valores acumulados por la izquierda o por la derecha. Seleccionamos:

Probabilidades = 0.25, 0.5, 0.75; Media = 20; Desviación típica = 2 y elegimos cola de la izquierda

Figura 58: Cálculo de los cuartiles 0.25, 0.5 y 0.75 de una N(20, 2)

Pulsando Aceptar obtenemos los tres cuartiles de la distribución

> qnorm(c(0.25,0.5,0.75), mean=20, sd=2, lower.tail=TRUE)
[1] 18.65102 20.00000 21.34898

Los tres cuartiles de la distribución son: 18.65102,  20.00000 y 21.34898

d) Obtener dos muestras aleatorias de valores de la distribución de tamaño 12 y las medias de cada muestra

Para generar muestras aleatorias de una distribución normal seleccionamos en el menú principal, Distribución/Distribuciones continuas/ Distribución Normal/Muestra de una distribución normal

Figura 59: Distribución/Distribuciones continuas/ Distribución Normal/Muestra de una distribución Normal

Y se obtiene la siguiente pantalla

Figura 60: Cálculo de muestras aleatorias de un distribución Normal

En el cuadro de diálogo que aparece indicamos:

El nombre del data frame en el que se almacenarán las muestras (Introducir el nombre del conjunto de datos: Muestras Normales), así como los parámetros de la distribución (Media = 20; Desviación típica = 2), el número de muestras a generar (Número de muestras = 2) y el número de elementos de las mismas (Número de observaciones = 12). Adicionalmente, podemos incluir algunos valores descriptivos para cada muestra.

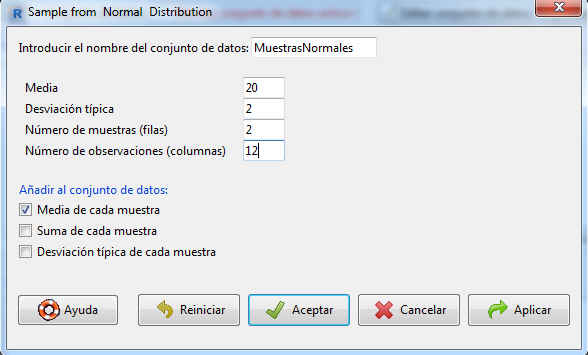Figura 61: Cálculo de dos muestras aleatorias de valores de la distribución N(20, 2) de tamaño 12

Pulsamos Aceptar y Visualizar conjunto de datos y se muestra el contenido de la variable MuestrasNormales que almacena las dos muestras que buscamos.

Figura 62: Dos muestras aleatorias de valores de la distribución N(20, 2) de tamaño 12

---

---

---

Ejercicios

Ejercicios Guiados

Ejercicio Guiado1

Se pretende comprobar la efectividad de una determinada vacuna contra la gripe. Para ello se administra dicha vacuna a un grupo de 15 pacientes. La probabilidad de que el paciente vacunado contraiga la gripe es 0.3. Calcular las siguientes probabilidades:

a) Ningún paciente contraiga la gripe

b) Más de dos pacientes contraigan la gripe

c) Contraigan la gripe entre tres y cinco pacientes, ambos inclusive

d) Generar una muestra aleatoria con 20 de valores de una distribución Binomial de parámetros n = 10 y prob = 0.2 y la media de la muestra

Ejercicio Guiado2

En un servicio de urgencias de un determinado hospital se sabe que por término medio llegan diez pacientes durante una hora. Calcular la probabilidad de que:

a) Lleguen exactamente cinco pacientes en una hora

b) Lleguen menos de quince pacientes en una hora

c) Lleguen más de cuatro y menos de ocho pacientes en una hora

d) Generar una muestra de tamaño 5 para una distribución de Poisson de parámetro media igual a 30.

Ejercicio Guiado3

Se ha estudiado el nivel de glucosa en sangre en ayunas en un grupo de diabéticos. Esta variable se supone que sigue una distribución Normal, con media 106 mg/100 ml y desviación típica 8 mg/100 ml.
Se pide:

a) Obtener la probabilidad de que el nivel de glucosa en sangre en un diabético sea inferior a 120 mg/100 ml

b) ¿Qué porcentaje de diabéticos tienen niveles de glucosa en sangre comprendidos entre 90 y 130 mg/100 ml?

c) Hallar el valor de la variable caracterizado por la propiedad de que el 25% de todos los diabéticos tiene un nivel de glucosa en ayunas inferior a dicho valor

d) Generar una muestra de tamaño 12 para la una distribución Normal con media igual a 5 y desviación típica igual a 3.

---

Ejercicio Guiado 1 (Resuelto)

Se pretende comprobar la efectividad de una determinada vacuna contra la gripe. Para ello se administra dicha vacuna a un grupo de 15 pacientes. La probabilidad de que el paciente vacunado contraiga la gripe es 0.3. Calcular las siguientes probabilidades:

a) Ningún paciente contraiga la gripe

b) Más de dos pacientes contraigan la gripe

c) Contraigan la gripe entre tres y cinco pacientes, ambos inclusive

d) Generar una muestra aleatoria con 20 de valores de una distribución Binomial de parámetros n = 10 y prob = 0.2 y la media de la muestra

---

Solución:

Definimos la variable aleatoria X = “Nº de pacientes vacunados que contraen la gripe de un grupo de 15 pacientes”. Esta variable aleatoria tiene una distribución Binomial de parámetros n = 15 y p = 0.3. \( (X  → B (15, 0.3)) \)

a) Ningún paciente contraiga la gripe

Seleccionamos en el menú principal Distribuciones/Distribuciones discretas/ Probabilidades binomiales

Figura 63: Distribuciones/Distribuciones discretas/ Probabilidades binomiales

 Y en la salida resultante, ponemos 15 en Ensayos binomiales y 0.3 en Probabilidad de éxito

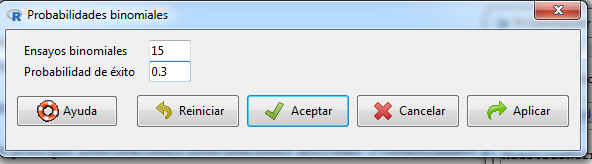Figura 64: Cálculo de probabilidades binomiales n = 15 y p = 0.3. \( (X  → B (15, 0.3)) \)

Pinchamos en Aceptar y obtenemos las probabilidades puntuales de la distribución:

> local({
+   .Table <- data.frame(Probability=dbinom(0:15, size=15, prob=0.3))
+   rownames(.Table) <- 0:15
+   print(.Table)
+ })
Probability
0  4.747562e-03
1  3.052004e-02
2  9.156011e-02
3  1.700402e-01
4  2.186231e-01
5  2.061304e-01
6  1.472360e-01
7  8.113003e-02
8  3.477001e-02
9  1.159000e-02
10 2.980287e-03
11 5.805754e-04
12 8.293934e-05
13 8.202792e-06
14 5.022117e-07
15 1.434891e-08

Por tanto,

\( P[Ningún  \hspace{.2cm} paciente \hspace{.2cm} contraiga \hspace{.2cm} la \hspace{.2cm} gripe] = P[X = 0] = 0.004747562  \)

b) Más de dos pacientes contraigan la gripe

\(  P[Más \hspace{.2cm} de \hspace{.2cm} dos \hspace{.2cm} pacientes \hspace{.2cm} contraigan \hspace{.2cm} la gripe] = P[X > 2] \)

Para resolverlo, seleccionamos en el menú principal Distribuciones/Distribuciones discretas/ Probabilidades binomiales acumuladas y en la pantalla resultante indicamos: Valores de la variable = 2; Ensayos binomiales = 15; Probabilidad de éxito = 0.3 y elegimos cola de la derecha

Figura 65: Cálculo de P[X > 2] de una B(15, 0.3)

Pulsamos Aceptar y se muestra el siguiente resultado

> pbinom(c(2), size=15, prob=0.3, lower.tail=FALSE)
[1] 0.8731723

\(  P[Más \hspace{.2cm} de \hspace{.2cm} dos \hspace{.2cm} pacientes \hspace{.2cm} contraigan \hspace{.2cm} la \hspace{.2cm} gripe] = P[X > 2] = 0.8731723 \)

c) Contraigan la gripe entre tres y cinco pacientes, ambos inclusive

\(   \begin{array}{ll} P[Contraigan \hspace{.2cm} la \hspace{.2cm} gripe \hspace{.2cm} entre \hspace{.2cm} 3 \hspace{.2cm} y \hspace{.2cm} 5 \hspace{.2cm} pacientes] = P[3 ≤ X ≤ 5] = P[X ≤ 5] – P[X < 3 ] = & \\ =   P[X ≤ 5] – P[X ≤ 2] = F(5) – F(2) & \end {array} \)

Para resolverlo, seleccionamos en el menú principal Distribuciones/Distribuciones discretas/ Probabilidades binomiales acumuladas y en la pantalla resultante indicamos: Valores de la variable = 5, 2; Ensayos binomiales = 15; Probabilidad de éxito = 0.3 y elegimos cola de la izquierda

Figura 66: Cálculo de \( P[3 ≤ X ≤ 5] \)

Pulsamos Aceptar y se muestra el siguiente resultado

> pbinom(c(5,2), size=15, prob=0.3, lower.tail=TRUE) 
[1] 0.7216214 0.1268277

\(   \begin{array}{ll} P[Contraigan \hspace{.2cm} la \hspace{.2cm} gripe \hspace{.2cm} entre  \hspace{.2cm} 3 \hspace{.2cm} y  \hspace{.2cm} 5 \hspace{.2cm} pacientes] = P[3 ≤ X ≤ 5] = P[X ≤ 5] – P[X < 3 ] = & \\ =  P[X ≤ 5] – P[X ≤ 2] = F(5) – F(2) = 0.7216214 – 0.1268277 = 0.5947937 & \end {array} \)

d) Generar una muestra aleatoria con 20 de valores de una distribución Binomial de parámetros n = 10 y prob = 0.2 y la media de la muestra

Para generar una muestra aleatoria seleccionamos en el menú principal Distribuciones/Distribuciones discretas/Muestras de una distribución binomial y en la pantalla resultante indicamos el nombre que le queremos dar a la muestra que se va a generar y los parámetros de la distribución. Así, en Introducir el nombre del conjunto de datos ponemos MBinom3, en Ensayos binomiales, 10; en Probabilidad de éxito, 0.2. También indicamos en Número de muestras (filas) cuántas muestras queremos generar, 1 y en Número de observaciones (columnas) el número de elementos que tendrá cada una de esas muestras, 20 y elegimos cola de la izquierda

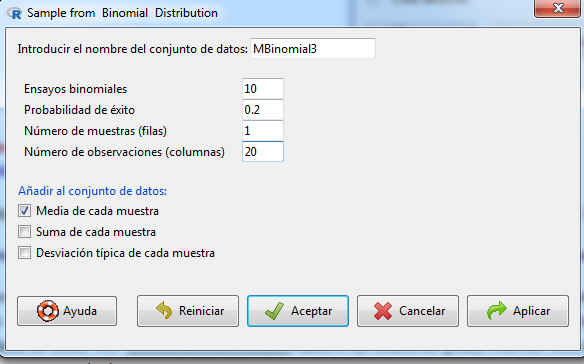Figura 67: Generar una muestra aleatoria con 20 de valores de una distribución B (10, 0.2)

Pulsamos Aceptar y Visualizar conjunto de datos. Se muestra el siguiente resultado

Figura 68: Muestra aleatoria con 20 de valores de una distribución B (10, 0.2)

---

Ejercicio Guiado 2 (Resuelto)

En un servicio de urgencias de un determinado hospital se sabe que por término medio llegan diez pacientes durante una hora. Calcula la probabilidad de que:

a) Lleguen exactamente cinco pacientes en una hora

b) Lleguen menos de cinco pacientes en una hora

c) Lleguen más de cuatro y menos de ocho pacientes en una hora

d) Generar una muestra de tamaño 5 para una distribución de Poisson de parámetro media igual a 30 y obtener la media de dicha muestra

---

Solución:

Definimos la variable aleatoria X = “Nº de pacientes que acuden al servicio de urgencias de un hospital en una hora”. Esta variable sigue una distribución Poisson de parámetro \( λ = 10 \) ; \( X → P(10) \)

a) Lleguen exactamente cinco pacientes en una hora

Hay que calcular la probabilidad de que la variable aleatoria X tome exactamente el valor 5

\( P[Lleguen \hspace{.2cm} exactamente \hspace{.2cm} cinco \hspace{.2cm} pacientes \hspace{.2cm} en \hspace{.2cm} una \hspace{.2cm} hora] = P[X = 5] \)

Es decir, el valor de la función masa de probabilidad de la variable aleatoria X en el punto 5. Para ello seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson.

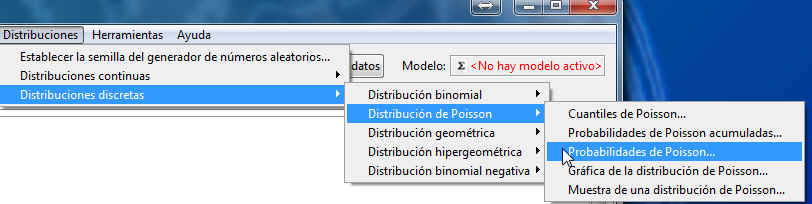Figura 69: Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson

En la pantalla resultante seleccionamos: Media = 10

Figura 70: Cálculo de P[X = 5] de una distribución de P(10)

Pulsamos Aceptar y se obtiene el siguiente resultado

> local({
+   .Table <- data.frame(Probability=dpois(0:14, lambda=10))
+   rownames(.Table) <- 0:14
+   print(.Table)
+ })

Probability
0  4.539993e-05
1  4.539993e-04
2  2.269996e-03
3  7.566655e-03
4  1.891664e-02
5  3.783327e-02
6  6.305546e-02
7  9.007923e-02
8  1.125990e-01
9  1.251100e-01
10 1.251100e-01
11 1.137364e-01
12 9.478033e-02
13 7.290795e-02
14 5.207710e-02

\( P[Lleguen \hspace{.2cm} exactamente \hspace{.2cm} cinco \hspace{.2cm} pacientes \hspace{.2cm} en \hspace{.2cm} una \hspace{.2cm} hora] = P[X = 5] = 0.0378332 \)

b) Lleguen menos de cinco pacientes en una hora

\( P[Lleguen \hspace{.2cm} menos \hspace{.2cm} de \hspace{.2cm} cinco \hspace{.2cm} pacientes \hspace{.2cm} en \hspace{.2cm} una \hspace{.2cm} hora] = P[X < 5] =P[X ≤ 4] \)

Se puede obtener mediante la función masa de probabilidad o la función de distribución.

En el caso de la función masa de probabilidad

\(   \begin{array}{ll} P[Lleguen \hspace{.2cm} menos \hspace{.2cm} de \hspace{.2cm} cinco \hspace{.2cm} pacientes \hspace{.2cm} en \hspace{.2cm} una \hspace{.2cm} hora] = P[X < 5] =P[X ≤ 4] =  & \\  =  P[X = 0] + P[X = 1] + P[X = 2] + P[X = 3] + P[X = 4] = 0.000045 + 0.000 & \end {array} \)

En el caso de la función de distribución

\(  P[Lleguen \hspace{.2cm} menos \hspace{.2cm} de \hspace{.2cm} cinco \hspace{.2cm} pacientes \hspace{.2cm} en \hspace{.2cm} una \hspace{.2cm} hora] = P[X < 5] =P[X ≤ 4] = F(4) \)

Para ello, seleccionamos en el menú principal Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson acumuladas

Figura 71: Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson acumuladas

y en la pantalla resultante insertamos en Valores de la variable, 4; Media, 10 y elegimos cola de la izquierda

Figura 72: Cálculo de \( P[X < 5] = P[X ≤ 4] = F(4) \) de una distribución de P(10)

Se pulsa Aceptar y se obtiene la siguiente salida

> ppois(c(4), lambda=10, lower.tail=TRUE)
[1] 0.02925269

\(  P[Lleguen \hspace{.2cm} menos \hspace{.2cm} de \hspace{.2cm} cinco \hspace{.2cm} pacientes \hspace{.2cm} en \hspace{.2cm} una \hspace{.2cm} hora] = P[X < 5] =P[X ≤ 4] = F(4) = 0.02925269 \)

c) Lleguen más de cuatro y menos de ocho pacientes en una hora

\(   \begin{array}{ll}  P[Lleguen \hspace{.2cm} más \hspace{.2cm} de \hspace{.2cm} cuatro \hspace{.2cm} y \hspace{.2cm} menos \hspace{.2cm} de \hspace{.2cm} ocho \hspace{.2cm} pacientes] = P[4 < X < 8] =  & \\  = P[X < 8] – P[X ≤ 4] = P[X ≤ 7] – P[X ≤ 4] = F(7) – F(4) & \end {array} \)

Para ello, seleccionamos en el menú principal Distribuciones/Distribuciones discretas/Distribución de Poisson/Probabilidades de Poisson acumuladas y en la pantalla resultante insertamos en Valores de la variable, 7, 4; Media, 10 y elegimos cola de la izquierda

Figura 73: Cálculo de \( P[4 < X < 8] \) de una distribución de P(10)

Pulsamos Aceptar y se obtiene la siguiente salida

> ppois(c(7,4), lambda=10, lower.tail=TRUE)
[1] 0.22022065 0.02925269

\( P[Lleguen  \hspace{.2cm} más  \hspace{.2cm} de  \hspace{.2cm} cuatro  \hspace{.2cm} y  \hspace{.2cm} menos  \hspace{.2cm} de  \hspace{.2cm} 8] = P[X ≤ 7] – P[X ≤ 4] = 0.22022065 – 0.02925269 =  0.1909 \)

d) Generar una muestra de tamaño 5 para una distribución de Poisson de parámetro media igual a 30 y obtener la media de dicha muestra

Para extraer muestras aleatorias de una distribución de Poisson, accedemos a la opción Muestra de una distribución de Poisson, dentro del menú de la distribución. Para ello, seleccionamos en el menú principal: Distribuciones/Distribuciones discretas/Distribución de Poisson/Muestra de una distribución de Poisson

Figura 74: Distribuciones/Distribuciones discretas/Distribución de Poisson/Muestra de una distribución de Poisson

En la pantalla resultante, introducimos el nombre que le queremos dar a la muestra que se va a generar, MuestraPoisson3, y la media de la distribución, 30.También indicamos en Número de muestras (filas) cuántas muestras queremos generar, en nuestro caso 1, y en Número de observaciones (columnas) el número de elementos que tendrá nuestra muestra, 5.

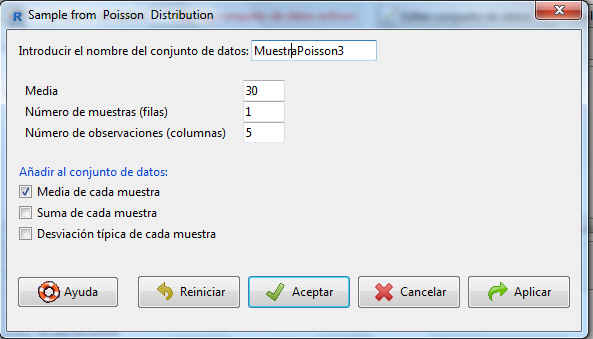Figura 75 : Cálculo de una muestra de tamaño 5 para una distribución de P(30)

Se pulsa Aceptar y Visualizar conjunto de datos y se obtiene la siguiente salida

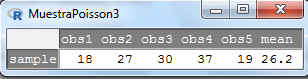Figura 76: Muestra de tamaño 5 para una distribución de P(30)

---

Ejercicio Guiado 3 (Resuelto)

Se ha estudiado el nivel de glucosa en sangre en ayunas en un grupo de diabéticos. Esta variable se supone que sigue una distribución Normal, con media 106 mg/100 ml y desviación típica 8 mg/100 ml.
Se pide:

a) Obtener la probabilidad de que el nivel de glucosa en sangre en un diabético sea inferior a 120 mg/100 ml

b) ¿Qué porcentaje de diabéticos tienen niveles de glucosa en sangre comprendidos entre 90 y 130 mg/100 ml?

c) Hallar el valor de la variable caracterizado por la propiedad de que el 25% de todos los diabéticos tiene un nivel de glucosa en ayunas inferior a dicho valor

d) Generar una muestra de tamaño 12 para la una distribución Normal con media igual a 5 y desviación típica igual a 3   calcular la media de la muestra

---

Solución:

Se define la variable, X = “Nivel de glucosa en sangre en un diabético”. Esta variable tiene distribución Normal con media 106 y desviación típica 8; \( X → N(106, 8) \)

a) Obtener la probabilidad de que el nivel de glucosa en sangre en un diabético sea inferior a 120 mg/100 ml

 \(  P[Nivel  \hspace{.2cm}  de  \hspace{.2cm}  glucosa  \hspace{.2cm}  sea  \hspace{.2cm}  inferior  \hspace{.2cm}  a 120] = P[X < 120] = F(120)  \)

Calculamos la probabilidad pedida utilizando la función de distribución. Para calcular valores de la función de distribución dada una distribución normal tenemos que seleccionar, en el menú principal, Distribución/Distribuciones continuas/ Distribución Normal/ Probabilidades normales acumuladas.

Figura 77: Distribución/Distribuciones continuas/ Distribución Normal/ Probabilidades normales acumuladas

En la pantalla resultante, introducimos los parámetros de la distribución y el valor de la variable hasta la cual queremos acumular la probabilidad. También es muy importante tener en cuenta si queremos que el programa nos devuelva probabilidades acumuladas por la cola izquierda (es decir, del tipo \( P[Y  ≤ y] \)) o por la cola derecha (que serán del tipo \( P[Y ≥ y] \) ).

Así para calcular \( P[X  < 120] \) de una \( N(106, 8) \). Sustituimos: Valores de la variable = 120; Media = 106; Desviación típica = 8 y elegimos cola de la izquierda

Figura 78: Cálculo de \( P[X  < 120] \) de una \( N(106, 8) \)

Se pulsa Aceptar y se obtiene la siguiente salida

> pnorm(c(120), mean=106, sd=8, lower.tail=TRUE)
[1] 0.9599408

b) ¿Qué porcentaje de diabéticos tienen niveles de glucosa en sangre comprendidos entre 90 y 130 mg/100 ml?

\( \begin{array}{ll} P[Niveles \hspace{.2cm} comprendidos \hspace{.2cm} entre \hspace{.2cm} 90 \hspace{.2cm} y \hspace{.2cm} 130]  = P[90 ≤ X ≤ 130] = & \\  = P[X ≤ 130] – P[X ≤ 90] = F(130)- F(90) & \end {array} \)

Utilizamos de nuevo la función de distribución. Para ello seleccionamos, en el menú principal, Distribución/Distribuciones continuas/ Distribución Normal/ Probabilidades normales acumuladas. Y en la pantalla resultante sustituimos: Valores de la variable = 90, 130; Media = 106; Desviación típica = 8 y elegimos cola de la izquierda

Figura 79: Cálculo de \( P[90 ≤ X ≤ 130] \) de una \( N(106, 8) \)

Se pulsa Aceptar y se obtiene la siguiente salida

> pnorm(c(90,130), mean=106, sd=8, lower.tail=TRUE)
[1] 0.02275013 0.99865010

Por lo tanto,

\( \begin{array}{ll} P[Niveles \hspace{.2cm} comprendidos \hspace{.2cm} entre \hspace{.2cm} 90 \hspace{.2cm} y \hspace{.2cm} 130] = P[X <= 130] – P[X ≤ 90]  = & \\  = 0.99865010 – 0.02275013 = 0.97589997 & \end {array} \)

c) Hallar el valor de la variable caracterizado por la propiedad de que el 25% de todos los diabéticos tiene un nivel de glucosa en ayunas inferior a dicho valor

Se pide calcular un valor de la distribución de X,  tal que \( P[X < x] = 0.25 \)
El valor que tenemos que calcular es el cuantil 25. Para calcularlo, tenemos que seleccionar, en el menú principal, Distribución/Distribuciones continuas/ Distribución Normal/Cuantiles normales

Figura 80: Distribución/Distribuciones continuas/ Distribución Normal/Cuantiles normales

En la pantalla resultante, introducimos los valores de las probabilidades junto con los parámetros de la distribución. De nuevo, es importante tener en cuenta si queremos operar con valores acumulados por la izquierda o por la derecha. Seleccionamos: Probabilidades = 0.25; Media = 106; Desviación típica = 8 y elegimos cola de la izquierda

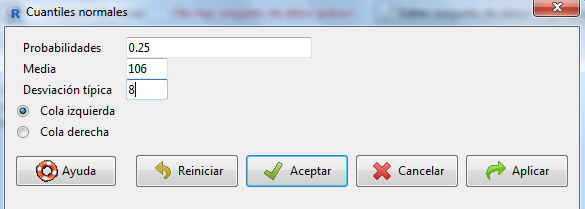Figura 81: Cálculo del cuartil 0.25 de una N(106,8)

Pulsando Aceptar se obtiene el cuantil 25 de la distribución

> qnorm(c(0.25), mean=106, sd=8, lower.tail=TRUE)
[1] 100.6041

d) Generar una muestra de tamaño 12 para la una distribución Normal con media igual a 5 y desviación típica igual a 3 y  calcular la media de la muestra

Para generar muestras aleatorias de una distribución normal seleccionamos en el menú principal, Distribución/Distribuciones continuas/ Distribución Normal/Muestra de una distribución normal

Figura 82: Distribución/Distribuciones continuas/ Distribución Normal/Muestra de una distribución normal

En el cuadro de diálogo que aparece indicamos:

El nombre del data frame en el que se almacenarán las muestras (Introducir el nombre del conjunto de datos: MuestraNormal1), así como los parámetros de la distribución (Media = 106; Desviación típica = 8), el número de muestras a generar (Número de muestras = 1) y el número de elementos de las mismas (Número de observaciones = 12). Adicionalmente, podemos incluir algunos valores descriptivos para cada muestra.

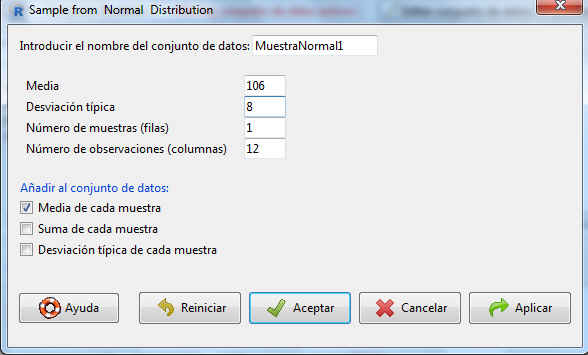Figura 83: Cálculo de una muestra aleatoria de valores de la distribución N(106, 8) de tamaño 12

Pulsamos Aceptar y Visualizar conjunto de datos y se muestra el contenido de la variable MuestraNormal1 que almacena las dos muestras que buscamos.

Figura 84: Muestra aleatoria de valores de la distribución N(106, 8) de tamaño 12

---

---

Ejercicios Propuestos

Ejercicio Propuesto 1

A un examen se han presentado un total de 100 alumnos y la probabilidad de aprobar el examen es de 0.8. Calcular las siguiente probabilidades

a) Que aprueben el examen exactamente 70 alumnos

b) Que aprueben el examen como máximo 60 alumnos

c) Que aprueben el examen entre 60 y 70 alumnos (ambos inclusive)

 d) Calcular el valor de la variable tal que deja a su derecha un 25% de las observaciones

 e) Generar una muestra de 25 valores aleatorios de esta distribución y calcular su media

---

Ejercicio Propuesto 2

Una empresa electrónica observa que el número de componentes que fallan antes de cumplir 100 horas de funcionamiento es una variable aleatoria de Poisson. Si el número promedio de estos fallos es ocho,

 a)  ¿Cuál es la probabilidad de que falle un componente?

b)  ¿Cuál es la probabilidad de que fallen no más de dos componentes?

c  ¿Cuál es la probabilidad de que fallen por lo menos diez?

d)  Obtener la mediana de la variable

e) Generar una muestra de 10 valores aleatorios de la distribución y calcular su desviación típica.

---

Ejercicio Propuesto 3

Los pesos de 2000 alumnos presentan una distribución normal de media 65 kg y desviación típica 8 kg. Calcula la probabilidad de que un alumno elegido al azar pese:

a) Más de 61 kg.

b) Entre 63 y 69 kg.

c) Menos de 70 kg.

d) El peso máximo del 15% de los alumnos que menos pesan

e) Representa la función de distribución.

---

Ejercicio Propuesto 1 (Resuelto)

A un examen se han presentado un total de 100 alumnos y la probabilidad de aprobar el examen es de 0.8. Calcular las siguientes probabilidades

En primer lugar, definimos la variable aleatoria X  = “Número de alumnos que aprueban el examen de los 100 que se presentan”.

A partir de la información que nos proporciona el enunciado podemos afirmar que \( X→B(100, 0.8) \).

a) Que exactamente 70 alumnos aprueben el examen

En este apartado nos piden la probabilidad de que la variable aleatoria tome, exactamente, un valor o, lo que es lo mismo, el valor de la función masa de probabilidad evaluada en el punto \( x_i = 70 \). Debemos, por tanto, calcular \( p_{70} = P[X=70] \)

\( P[X=70] = 5.189643e^{-03} \)

b) Que aprueben el examen como máximo 60 alumnos

En este caso, la probabilidad que nos piden calcular es \( P[X ≤ 60] \). Sabemos que la función de distribución evaluada en un punto \( x_i \), se define como \( F(x_i) = P[X \leq x_i] \). Por lo que vamos a calcular \( P[X ≤ 60] = F(60) \).

\( P[X ≤ 60] = F(60) = 3.60842e^{-06} \)

c) Que entre 60 y 70 alumnos (ambos inclusive) aprueben el examen

En esta ocasión, nos piden calcular la probabilidad del intervalo \( P[60 ≤ X ≤ 70 ] \), que puede reescribirse como

\( P[60 ≤ X ≤ 70 ] = P[ X ≤ 70 ] – P[ X  < 60 ] = P [X ≤ 70 ] – P[ X ≤ 59 ] = F(70) – F(59) \)

Por lo que el cálculo de dicha probabilidad se reduce al cálculo del valor de la función de distribución en los puntos 70 y 59.

 \( P[60 ≤ X ≤ 70 ] = 1.124898e^{-02} –  1.292184e^{-06} = 0.01124769 \)

d) Calcular el valor de la variable tal que deja a su derecha un 25% de las observaciones

El valor de la variable  que deja a su derecha un 25% de las observaciones es el mismo que deja a su izquierda el 75% restante. Por tanto, debemos calcular el cuantil de orden 0.75 de una distribución binomial de parámetros 100 y 0.8.

El valor de la variable que deja a su derecha el 25% de las observaciones es 83

 e) Generar una muestra de 25 valores aleatorios de esta distribución y calcular su media

Nota: Dado el carácter aleatorio de los valores generados en este apartado, dichos valores pueden no coincidir con los suyos

Figura 85: Muestra aleatoria de valores de la distribución B(100, 0.8) de tamaño 25

Podemos ver, en la Figura 85, que el valor de la media de la muestra generada es 80.04

Solución del Ejercicio Propuesto 1

---

Ejercicio Propuesto 2 (Resuelto)

Una empresa electrónica observa que el número de componentes que fallan antes de cumplir 100 horas de funcionamiento es una variable aleatoria de Poisson. Si el número promedio de estos fallos es ocho,

En primer lugar, definimos la variable aleatoria X  = “Número de componentes que fallan antes de cumplir 100 horas de funcionamiento”.

A partir de la información que nos proporciona el enunciado podemos afirmar que \(  X→P(8) \).

a) ¿Cuál es la probabilidad de que falle un componente?

En este apartado nos piden la probabilidad de que la variable aleatoria tome, exactamente, un valor o, lo que es lo mismo, el valor de la función masa de probabilidad evaluada en el punto \( x_i = 1 \). Debemos, por tanto, calcular \( p_1 =  P[X = 1] \)

\( P[X = 1] = 0.0026837010 \)

b) ¿Cuál es la probabilidad de que fallen no más de dos componentes?

En este caso, la probabilidad que nos piden calcular es \( P[X ≤ 2] \). Sabemos que la función de distribución evaluada en un punto  se define como \( F(x_i) = P[X ≤ x_i] \). Por lo que vamos a calcular \( P[X ≤ 2] = F(2) \)

 \( P[X ≤ 2] = 0.01375397 \)

c) ¿Cuál es la probabilidad de que fallen por lo menos diez?

La probabilidad que nos piden calcular en este caso es \( P[X ≥ 10] \). Por lo tanto, sabiendo que la probabilidad puede expresarse como \( P[X ≥ 10] = 1 – P[X < 10] = 1 – P[X ≤ 9] = 1 – F(9) \). Tenemos que calcular

\( P[X ≥ 10] = 1 – F(9) = 0.7166243 \)

d) Obtener la mediana de la variable

La mediana de una variable aleatoria es el valor de la variable que deja a su izquierda el 50% de las observaciones, quedando el 50% restante a la derecha de tal valor. De aquí se deduce que la mediana de una variable coincide con el cuantil de orden 0.5 de la variable.

El valor de la variable que deja a su izquierda el 50% de las observaciones es 8.
e) Generar una muestra de 10 valores aleatorios de la distribución y calcular su desviación típica.

Nota: Dado el carácter aleatorio de los valores generados en este apartado, dichos valores pueden no coincidir con los suyos

Figura 86: Muestra aleatoria de valores de la distribución P(8) de tamaño 10

Podemos ver, en la Figura 86, que la desviación típica de la muestra generada es 4.25

Solución del Ejercicio Propuesto 2

---

Ejercicio Propuesto 3 (Resuelto)

Los pesos de 2000 soldados presentan una distribución normal de media 65 kg y desviación típica 8 kg. Calcula la probabilidad de que un soldado elegido al azar pese:

a) Más de 61 kg

La probabilidad que nos piden calcular en este caso es\(  P[X ≥ 61] \). Por lo tanto, sabiendo que la probabilidad puede expresarse como \( P[X ≥ 61] = 1 – P[X≤ 61] \). Tenemos que calcular

\( P[X ≥ 61] = 1 – P[X ≤ 61] = 1 – F(61) = 1 – 0.3085375 = 0.6914625 \)

b) Entre 63 y 69 kg

Nos piden calcular \( P[63 ≤ X≤ 69] \) . Esta probabilidad puede reescribirse como

\( P[63 ≤ X≤ 69] = P[X≤ 69] – P[ X≤ 63] = F(69) – F(63) = 0.6914625 – 0.4012937 = 0.2901688 \)

c) Menos de 70 kg

La probabilidad de que el estudiante pese menos de 70 kg se puede escribir como \( P[X ≤ 70] \). Esto es, la probabilidad coincide con el valor de la función de distribución evaluada en el punto 70.

\( P[X ≤ 70] = F(70) = 0.7340145 \)

d) El peso máximo del 15% de los alumnos que menos pesan

En este caso buscamos el valor de la variable que deja a su izquierda el 15% de las observaciones, es decir, buscamos el valor del cuantil 0.15.

El valor de la variable que deja a su izquierda el 15% de las observaciones es 56.70

e) Representa la función de distribución

Figura 87: Gráfica de la función de distribución de una N(65, 8)

Solución del Ejercicio Propuesto 3

Autores: Beatriz Cobo Rodríguez y Ana María Lara Porras. Universidad de Granada. (2016)

Reformulado con MathML en 2021 por Ana María Lara Porras