ANÁLISIS DE LA VARIANZA UNIFACTORIAL

Objetivos

Identificar un diseño unifactorial
Realizar un análisis de la varianza de una vía
Emitir juicios sobre la validación del modelo en vista de los gráficos residuales.
Contrastar la igualdad de varianzas a partir del test de Bartlett
Aplicar los procedimientos de comparaciones múltiples

Introducción

El análisis de la varianza o abreviadamente (ANOVA por sus siglas en inglés ANalysis Of VAriance) es una técnica que se basa en analizar la variabilidad (varianza) de los datos. Con la información sobre la variabilidad dentro de los grupos y entre los grupos se intenta dilucidar si existe una diferencia significativa en la posición central (media) de los grupos considerados. Este procedimiento estadístico permite dividir la variabilidad observada en componentes independientes que pueden atribuirse a diferentes causas de interés.

El análisis de la varianza fue desarrollado por Fisher en 1925 con el objetivo de comparar entre sí varios grupos o tratamientos mediante la descomposición de la variabilidad total de un experimento en componentes independientes que puedan atribuirse a distintas causas. Esencialmente este análisis determina si la discrepancia entre las medias de los tratamientos es mayor de lo que podría esperarse razonablemente de la discrepancia existente dentro de los tratamientos.

Es una de las técnicas más utilizadas en investigación y experimentación.

Utilidad:

Abordamos el problema de conocer si existen diferencias significativas en las medias de varios grupos.
Tenemos que tener al menos una variable o factor que indique en qué grupo estamos observando (hombres/mujeres, diferentes nacionalidades, grupos de edad, nivel de estudios, etc.).
Tenemos que tener observaciones numéricas para cada uno de los individuos de cada grupo.
Nuestro objetivo es comparar más de dos grupos entre sí para saber si tienen valores medios diferentes o no.

Formulación del problema:

A partir de una variable $ Y $ denominada variable respuesta que se ha observado bajo $ I $ tratamientos de clasificación (variable factor), se pretende contrastar si el factor tiene un efecto significativo sobre la variable respuesta.
Equivalentemente se trata de contrastar si las medias de $ Y $ bajo cada tratamiento son iguales.

La tabla de observaciones es

TRATAMIENTOS

$ \begin{array} {|c|c|c|c|c|c|} \hline 1 & 2 & \cdots & j & \cdots & I \\ \hline y_{11} & y_{12} & \cdots & y_{1j} & \cdots & y_{1I} \\ \hline y_{21} & y_{22} & \cdots & y_{2j} & \cdots & y_{2I} \\ \hline \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \hline y_{i1} & y_{i2} & \cdots & y_{ij} & \cdots & y_{iI} \\ \hline \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \hline y_{n_11} & y_{n_22} & \cdots & y_{n_ij} & \cdots & y_{n_kI} \\ \hline \end{array} $

Tabla 1: Tabla de observaciones

Al total de observaciones lo notamos como: $ N=\sum_{i=1}^{n_k}n_i $

Planteamiento del modelo

Para desarrollar esta sección consideramos como ejemplo ilustrativo la situación de la compañía algodonera. A lo largo de las sucesivas secciones, seguiremos haciendo referencia a este ejemplo. Dicha situación daría lugar, con unos datos concretos, al siguiente enunciado:

Supuesto práctico

Un ingeniero de desarrollo de productos desea maximizar la resistencia a la tensión de una nueva fibra sintética que se utilizará para fabricar camisas. Por experiencia, parece que la resistencia (o fortaleza) se ve influida por el porcentaje de algodón presente en la fibra. También se sospecha que valores elevados de porcentaje de algodón repercuten negativamente en otras cualidades de calidad que se desean (por ej. que la fibra pueda recibir un tratamiento de planchado permanente). Ante esta situación, el ingeniero decide tomar cinco muestras para diferentes niveles de porcentaje de algodón y medir la fortaleza de las fibras así producidas. Los resultados de las mediciones se resumen en la siguiente tabla:

$ \begin{array} {|c|c|} \hline \% \hspace{.2cm} algodón & Fortaleza \hspace{.2cm} de \hspace{.2cm} las \hspace{.2cm} fibras \\ \hline 15 \% & 7 \hspace{1cm} 7 \hspace{1.2cm} 15 \hspace{1cm} 11 \hspace{1.2cm} 9 \\ \hline 20 \% & 12 \hspace{1cm} 17 \hspace{1cm} 12 \hspace{1cm} 18 \hspace{1cm} 18 \\ \hline 25\% & 14 \hspace{1cm} 18 \hspace{1cm} 18 \hspace{1cm} 19 \hspace{1cm} 19 \\ \hline 30 \% & 19 \hspace{1cm} 25 \hspace{1cm} 22 \hspace{1cm} 19 \hspace{1cm} 23 \\\hline 35 \% & 7 \hspace{1cm} 10 \hspace{1.2cm} 11 \hspace{1cm} 15 \hspace{1cm} 11 \\ \hline \end{array} $

Tabla 2: Tabla de datos del Supuesto Práctico1

El Análisis de la Varianza nos ayudará a responder las siguientes cuestiones:

¿Influye el porcentaje de algodón en la fortaleza de la fibra fabricada?
Si es así, ¿qué niveles de porcentaje de algodón son similares y cuáles no?

En el ejemplo disponemos de una colección de 25 unidades experimentales y queremos estudiar el efecto de la fortaleza de las fibras sintéticas para la fabricación de camisas según el porcentaje de algodón que contengan las mismas. Es decir, estamos interesados en contrastar el efecto de un factor, que se presenta con cinco niveles, sobre la variable respuesta.

Nos interesa saber si la fortaleza de las fibras sintéticas para la fabricación de camisas es igual según los cinco porcentajes de algodón de las mismas, para ello realizamos el siguiente contraste de hipótesis:

$ H_0: \mu_1=\mu_2=\mu_3=\mu_4=\mu_5=\mu \hspace{.6cm} $ vs $ H_1: \mu_i \neq \mu_j \hspace{.4cm} $ para algún $ i \neq j $

Expresión 1: Contraste de hipótesis

Es decir, contrastamos que no hay diferencia en las medias de los cinco tratamientos frente a la alternativa de que al menos una media difiere de otra.

La hipótesis nula, $ H_0 $, indica que los valores medios son iguales en todos los grupos, es decir NO HAY DIFERENCIAS SIGNIFICATIVAS.
La hipótesis alternativa, $ H_1 $, indica que al menos dos grupos tienen medias significativamente distintas, es decir SÍ HAY DIFERENCIAS SIGNIFICATIVAS.
Por tanto, el resultado del contraste se interpretará como:
- Si es posible rechazar $ H_0 $, las medias de las $ I $ poblaciones no son todas iguales entre sí o el efecto de los tratamientos sobre la respuesta es distinguible estadísticamente.
- Si no puede rechazarse $ H_0 $, cualquier desviación observada en la respuesta se debe al error aleatorio y no a causa de un cambio en el tratamiento.

En este modelo, que estudia el efecto que produce un solo factor en la variable respuesta, la asignación de las unidades experimentales a los distintos niveles del factor se debe realizar de forma completamente al azar. Este modelo, junto con este procedimiento de asignación, recibe el nombre de Diseño Completamente Aleatorizado y está basado en el modelo estadístico de Análisis de la Varianza de un Factor o una Vía. Esta técnica estadística, Análisis de la Varianza de un factor, se utiliza cuando se tienen que comparar más de dos grupos y la variable respuesta es una variable numérica. Para aplicar este diseño adecuadamente las unidades experimentales deben ser lo más homogéneas posible.

Todo este planteamiento se puede formalizar de manera general para cualquier experimento unifactorial. Supongamos un factor con $ I $ niveles y para el nivel i-ésimo se obtienen $ n_{i} $ observaciones de la variable respuesta. Entonces podemos postular el siguiente modelo:

$ y_{ij} = \mu + \tau_{i} + u_{ij} \hspace {.1cm} , \hspace {.1cm} i=1, \cdots, I \hspace {.1cm} ; j = 1, \cdots , n_{i} $

Expresión 2: Ecuación del modelo unifactorial

donde:

$ y_{ij} $ : observación j de la variable respuesta bajo el tratamiento i
$ \mu $: Es un efecto constante, común a todos los niveles del factor, denominado media global.

$ \tau_{i} $: Efecto sobre la variable respuesta debido al tratamiento i-ésimo (lo que se desvía la media de la variable respuesta en el grupo j-ésimo con respecto a $ \mu $)

$ u_{ij} $: Son variables aleatorias que engloban un conjunto de factores, cada uno de los cuales influye en la respuesta sólo en pequeña magnitud pero que de forma conjunta debe tenerse en cuenta. Es decir, se pueden interpretar como las variaciones causadas por todos los factores no analizados y que dentro del mismo tratamiento variarán de unos elementos a otros. Reciben el nombre de perturbaciones o error experimental.

$ \mu_i = \mu + \tau_{i} \hspace {.3cm} $ es la media de la variable respuesta en el grupo i-ésimo

El ANOVA se basa en la descomposición de la variación total de los datos con respecto a la media global (SCT), que bajo el supuesto de que $ H_0 $ es cierta, es una estimación de la varianza obtenida a partir de toda la información muestral, en dos partes:

$ SCT = SCTr + SCR $

Donde:

Variación Total: $ SCT $ es la suma de cuadrados total o variabilidad total de $ Y $

$ SCT= \displaystyle \sum_{i=1}^I\sum_{j=1}^{n_i}\left(y_{ij}-\bar{y}_{..}\right)^2 $

Expresión 3: Suma de cuadrados Total

Variación Inter-grupos: $ SCTr $ es la suma de cuadrados entre tratamientos o variabilidad explicada,

$ SCTr= \displaystyle \sum_{i=1}^I n_i \left(\bar{y}_{i.}-\bar{y}_{..}\right)^2 $

Expresión 4: Suma de cuadrados entre Tratamientos

Variación Intra-grupos: $ SCR $ o $ SCE $ es la suma de cuadrados dentro de los tratamientos, variabilidad no explicada o residual

$ SCR= \displaystyle \sum_{i=1}^I\sum_{j=1}^{n_i}\left(y_{ij}-\bar{y}_{i.} \right)^2 $

Expresión 5: Suma de cuadrados Residual

Variación dentro de las muestras (SCR) o Intra-grupos, cuantifica la dispersión de los valores de cada muestra con respecto a sus correspondientes medias.
Variación entre muestras (SCTr) o Inter-grupos, cuantifica la dispersión de las medias de las muestras con respecto a la media global.

Cuando la hipótesis nula es cierta, $ SCTr/k-1 $ y $ SCR/N-k $ son dos estimadores insesgados de la varianza poblacional y el cociente entre ambos se distribuye según una F de Snedecor con $ k-1 $ grados de libertad en el numerador y $ N-k $ grados de libertad en el denominador. Por lo tanto, si $ H_0 $ es cierta es de esperar que el estadístico $ Fexp $ que se calcula como el cociente entre ambas estimaciones será aproximadamente igual a 1, de forma que se rechazará $ H_0 $si dicho cociente difiere significativamente de 1, es decir, si $ F_{exp}\geq F_{k-1,N-k;1-\alpha} $. Según el p-valor, se rechaza $ H_0 $ si $ p-valor\leq\alpha $, donde $ p-valor=P[F_{k-1,N-k}\geq F_{exp}]$.

En el Supuesto práctico:

La fortaleza de las fibras es una variable numérica
El porcentaje de algodón es una variable categórica que divide a los individuos en grupos

Con el paquete BrailleR, el ANOVA se realiza utilizando la función OneFactor cuya sintaxis es la siguiente:

OneFactor(Response, Factor, Data = NULL, HSD = TRUE, AlphaE = 0.05)

donde

Response: Nombre de la variable continua dependiente
Factor: Variable factor de agrupación
Data: La base de datos que contiene la variable respuesta y la variable factor
HSD: Valor lógico: ¿Debe ser evaluado el método de Tukey HSD para el conjunto de datos?
AlphaE: Probabilidad del error Tipo I para el cálculo del método de Tukey.

En primer lugar, cargamos el paquete BrailleR

> library(“BrailleR”)

almacenamos los datos de las dos variables en dos vectores:

> algodon=factor(c(rep(“15%”,5), rep(“20%”,5), rep(“25%”,5), rep(“30%”,5), rep(“35%”,5)),levels = c(“15%”, “20%”, “25%”, “30%”, “35%”))
> algodon
[1] 15% 15% 15% 15% 15% 20% 20% 20% 20% 20% 25% 25% 25% 25% 25% 30% 30% 30% 30%
[20] 30% 35% 35% 35% 35% 35%
Levels: 15% 20% 25% 30% 35%
> fortaleza=c(7, 7, 15, 11, 9, 12, 17, 12, 18, 18, 14, 18, 18, 19, 19, 19, 25, 22, 19, 23, 7, 10, 11, 15, 11)
> fortaleza
[1] 7 7 15 11 9 12 17 12 18 18 14 18 18 19 19 19 25 22 19 23 7 10 11 15 11

Agrupamos las 2 variables en un data frame, al que vamos a llamar fibra:
> fibra = data.frame (algodon, fortaleza)

Comprobemos que los datos se han guardado correctamente.

> head(fibra)
algodon fortaleza
1 15% 7
2 15% 7
3 15% 15
4 15% 11
5 15% 9
6 20% 12

Realizamos el ANOVA pedido mediante la función OneFactor, indicándole al programa en principio que no nos muestre el Test post-hoc.
> OneFactor(“fortaleza”, “algodon”, fibra, HSD = FALSE)

Muestra una salida en html: Fortaleza.Algodon-OneFactor

Analysis of the Fibra data, using Fortaleza as the response variable and Algodon as the single grouping factor.

Prepared by BrailleR

Muestra:

Una tabla resumen que incluye para cada grupo la media, la desviación típica, el número de datos y el error estándar
Diagramas de caja y bigotes comparativos para cada grupo
Gráfico de puntos comparativos para cada grupo
Análisis de la varianza de un factor
Dos tests de homogeneidad de varianzas

A continuación, se muestra y se detalla cada resultado, excepto el 5 que se verá posteriormente:

Una tabla resumen que incluye para cada grupo la media, la desviación típica, el número de datos y el error estándar

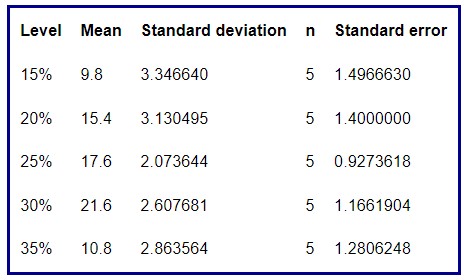
2. Diagramas de caja y bigotes comparativos para cada grupo

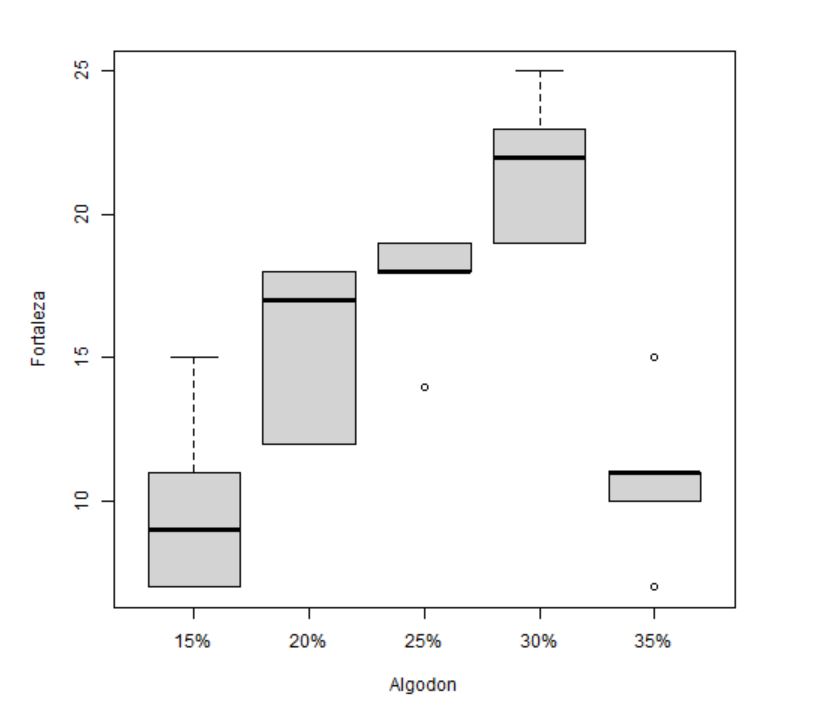Este tipo de representación permite identificar de forma preliminar si existen asimetrías, datos atípicos o diferencia de varianzas. Además, se puede tener una idea intuitiva de si las medias difieren unas de otras o no.

En general no se ve claramente si los datos son simétricos o no.
En los diferentes porcentajes de algodón se detectan algunos valores atípicos que habrá que estudiar con detalle por si fuese necesario eliminarlos.
El tamaño de las cajas parece diferente para cada grupo por lo que podría incumplirse la hipótesis de homocedasticidad. Lo confirmaremos posteriormente gráfica y analíticamente.
Se puede intuir que existirá diferencia de medias.

3. Gráfico de puntos comparativos para cada grupo

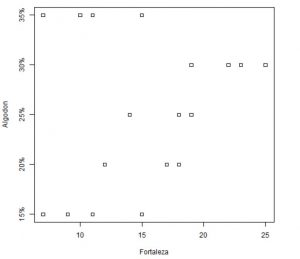
Al igual que en el diagrama de caja y bigotes, se puede tener una idea intuitiva de si las medias difieren unas de otras o no. Obteniendo las mismas conclusiones que con el gráfico anterior.

Análisis de la varianza de un factor

Df Sum Sq Mean Sq F value Pr(>F)

algodon 4 475.8 118.94 14.76 9.13e-06 ***

Residuals 20 161.2 8.06

—

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1

Esta es la tabla ANOVA que nos proporciona un p-valor=9.13e-06 por lo que se rechaza la hipótesis nula, esto quiere decir que existen diferencias significativas entre la fortaleza de las fibras sintéticas según el porcentaje de algodón de las mismas (al menos en dos de ellos).

Comparaciones múltiples

Si un Análisis de Varianza resulta significativo, implica que al menos dos de las medias comparadas son significativamente distintas entre sí, pero no se indica cuáles.
Para identificarlas hay que comparar dos a dos las medias de todos los grupos introducidos en el análisis mediante un test que compare 2 grupos, a esto se le conoce como análisis post-hoc. Hay varios métodos, el que nosotros usaremos se denomina Método de Tukey HSD.

En el Supuesto práctico:

Añadimos a la función anterior el test post-hoc de la siguiente forma:

> OneFactor(“fortaleza”, “algodon”, fibra)

Esta función nos devuelve otra salida en htmlFortaleza.Algodon-OneFactor1

Test post-hoc mediante el método de Tukey Honestly Significant Difference

Tukey multiple comparisons of means

95% family-wise confidence level

factor levels have been ordered

Fit: aov(formula = fortaleza ~ algodon, data = fibra)

$algodon

diff lwr upr p adj

35%-15% 1.0 -4.3729583 6.372958 0.9797709

20%-15% 5.6 0.2270417 10.972958 0.0385024

25%-15% 7.8 2.4270417 13.172958 0.0025948

30%-15% 11.8 6.4270417 17.172958 0.0000190

20%-35% 4.6 -0.7729583 9.972958 0.1162970

25%-35% 6.8 1.4270417 12.172958 0.0090646

30%-35% 10.8 5.4270417 16.172958 0.0000624

25%-20% 2.2 -3.1729583 7.572958 0.7372438

30%-20% 6.2 0.8270417 11.572958 0.0188936

30%-25% 4.0 -1.3729583 9.372958 0.2101089

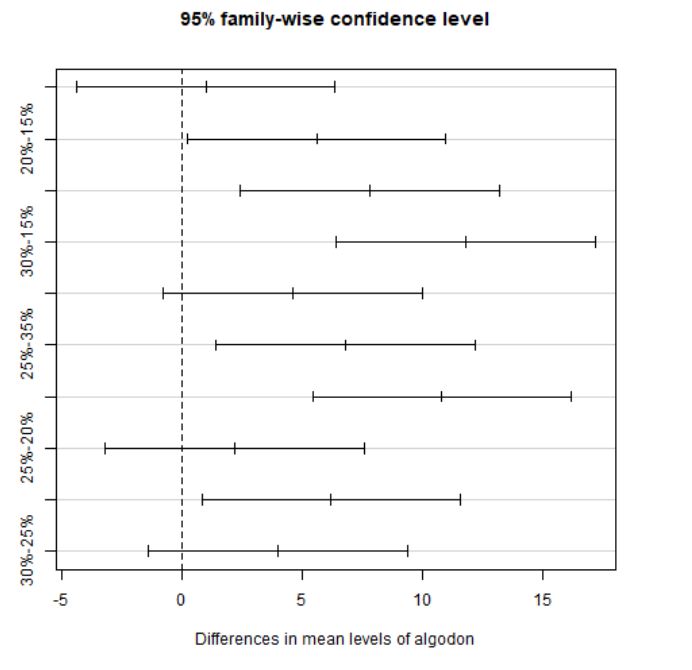
Los intervalos de confianza permiten estimar entre qué límites se encuentra la verdadera diferencia entre las medias de los grupos. Estos intervalos permiten tomar decisiones sobre si dos promedios difieren o no significativamente (dependiendo de que el intervalo incluya o no el valor cero). Además, se puede ver la diferencia significativa observando el p-valor asociado a cada comparación.

35% y 15%: Puesto que p-valor=0.9797709, no podemos rechazar $ H_0 $, es decir, no hay diferencias significativas en la fortaleza de las fibras sintéticas para hacer camisas según si los porcentajes de algodón de las mismas son 35% y 15%.
20% y 15%: Puesto que p-valor=0.0385024, se rechaza $ H_0 $, es decir, existen diferencias significativas la fortaleza de las fibras sintéticas para hacer camisas según si los porcentajes de algodón de las mismas son 20% y 15%.
25% y 15%: Puesto que p-valor=0.0025948, se rechaza $ H_0 $, es decir, existen diferencias significativas la fortaleza de las fibras sintéticas para hacer camisas según si los porcentajes de algodón de las mismas son 25% y 15%.
30% y 15%: Puesto que p-valor=0.0000190, se rechaza $ H_0 $, es decir, existen diferencias significativas la fortaleza de las fibras sintéticas para hacer camisas según si los porcentajes de algodón de las mismas son 30% y 15%.
20% y 35%: Puesto que p-valor=0.1162970, no podemos rechazar $ H_0 $, es decir, no hay diferencias significativas en la fortaleza de las fibras sintéticas para hacer camisas según si los porcentajes de algodón de las mismas son 20% y 35%.
25% y 35%: Puesto que p-valor=0.0090646, se rechaza $ H_0 $, es decir, existen diferencias significativas la fortaleza de las fibras sintéticas para hacer camisas según si los porcentajes de algodón de las mismas son 25% y 35%.
30% y 35%: Puesto que p-valor=0.0000624, se rechaza $ H_0 $, es decir, existen diferencias significativas la fortaleza de las fibras sintéticas para hacer camisas según si los porcentajes de algodón de las mismas son 30% y 35%.
25% y 20%: Puesto que p-valor=0.7372438, no podemos rechazar $ H_0 $, es decir, no hay diferencias significativas en la fortaleza de las fibras sintéticas para hacer camisas según si los porcentajes de algodón de las mismas son 25% y 20%.
30% y 20%: Puesto que p-valor=0.0188936, se rechaza $ H_0 $, es decir, existen diferencias significativas la fortaleza de las fibras sintéticas para hacer camisas según si los porcentajes de algodón de las mismas son 30% y 20%.
30% y 25%: Puesto que p-valor=0.2101089, no podemos rechazar $ H_0 $, es decir, no hay diferencias significativas en la fortaleza de las fibras sintéticas para hacer camisas según si los porcentajes de algodón de las mismas son 30% y 25%.

En definitiva, existen diferencias significativas en la fortaleza de las fibras sintéticas para hacer camisas entre los siguientes porcentajes de algodón: el 15% con respecto al 20%, 25% y 30%; el 20% con respecto al 30%; y el 35% con respecto al 25% y el 30%. Entre el resto de porcentajes de algodón no existen diferencias significativas.

Hipótesis

Para poder aplicar la técnica ANOVA se tienen que cumplir las siguientes hipótesis:

Normalidad de las observaciones:

$ H_0: y_{ij} \rightarrow N \left(\mu_{ij}, \sigma_j \right), \hspace {.2cm} i=1,\ldots,I, \hspace {.2cm} j=1,\ldots,n_k $

Homocedasticidad (igualdad de varianzas):

$ H_0: \sigma_1^2=\sigma_2^2=\cdots=\sigma_I^2=\sigma^2 $

Observaciones independientes:

$ H_0: $ muestras independientes

Residuos con media cero

Si no se cumplen estas cuatro suposiciones, estamos usando una técnica que no es apropiada, por lo que no estaremos seguros de que los resultados sean válidos.

Siguiendo con el Supuesto práctico:

Para comprobar la idoneidad del modelo propuesto, la salida de la función OneFactor muestra los gráficos:

Valores ajustados frente a residuos
Gráfico Q-Q de normalidad
Valores ajustados frente a raíz cuadrada de los residuos estandarizados (en valor absoluto)
Residuos estandarizados frente a leverages

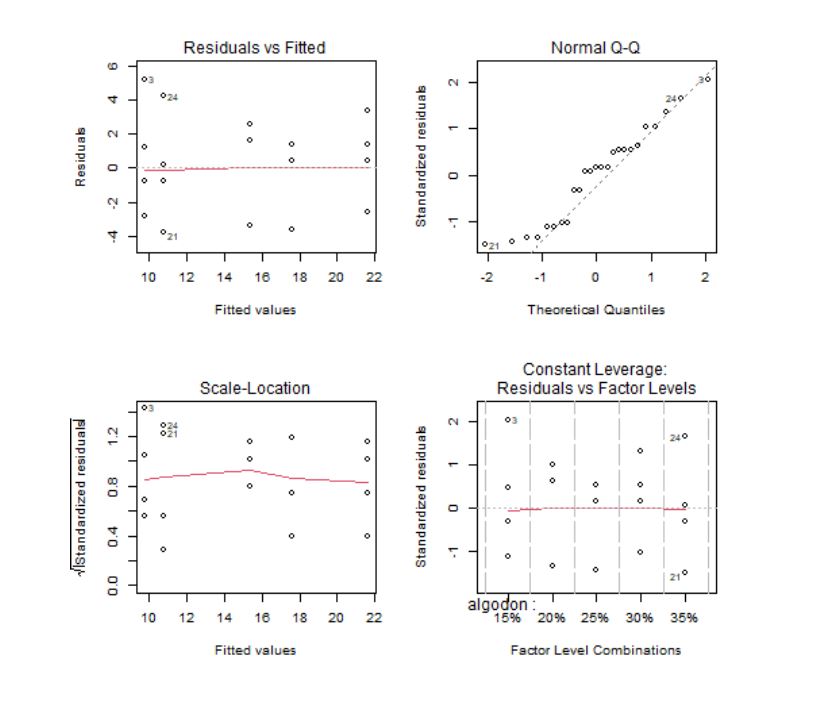
Los gráficos 1 y 3 se utilizan para contrastar gráficamente si la media de los residuos es cero y la homocedasticidad de los residuos. La idea intuitiva para que se cumplan estas hipótesis es que no se observe ningún patrón ni forma de embudo. Además, en el gráfico 3 se usa como regla general que cualquier punto por encima de 2 en el eje Y sugeriría heterogeneidad de varianza.

El gráfico Q-Q, por su parte, se utiliza para contrastar la normalidad de los residuos. Lo deseable es que los residuos estandarizados estén lo más cerca posible a la diagonal punteada que aparece en el gráfico.

El gráfico de Leverage para cada grupo frente a los residuos estandarizados se utiliza para detectar valores atípicos. En caso de detectarse alguna observación fuera del rango [-2,2] debe estudiarse este punto de forma aislada para detectar, por ejemplo, si la elevada importancia de esa observación se debe a un error.

Los gráficos confirman que los residuos tienen media cero, son homocedásticos, con distribución normal y sin valores atípicos. La hipótesis de independencia es intrínseca al diseño del experimento, por tanto, se supone que las observaciones son independientes ya que se están considerando distintos porcentajes de algodón.

Dos tests de homogeneidad de varianzas

Vamos a confirmar la homocedasticidad mediante dos métodos analíticos. El test de homogeneidad de varianzas de Bartlett permite contrastar la igualdad de varianzas en 2 o más poblaciones sin necesidad de que el tamaño de los grupos sea el mismo. Es más sensible que el test de Levene a la falta de normalidad, pero si se está seguro de que los datos provienen de una distribución normal, es la mejor opción. El test de homogeneidad de varianzas de Fligner-Killeen es un test no paramétrico que compara las varianzas basándose en la mediana. Es también una alternativa cuando no se cumple la condición de normalidad en las muestras.

El test de homogeneidad de varianzas de Bartlett

Bartlett test of homogeneity of variances

data: fortaleza by algodon

Bartlett’s K-squared = 0.93309, df = 4, p-value = 0.9198

Considerando como nivel de significación 0.05, y observando el p-valor=0.9198 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

El test de homogeneidad de varianzas de Fligner-Killeen

Fligner-Killeen test of homogeneity of variances

data: fortaleza by algodon

Fligner-Killeen:med chi-squared = 1.7265, df = 4, p-value = 0.7859

Considerando como nivel de significación 0.05, y observando el p-valor=0.7859 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

Resumiendo, los pasos a seguir en un contraste ANOVA son:

Se recogen los datos asegurándonos de que sean independientes, es decir, que las observaciones no se vean afectadas unas por otras.
Realizamos el contraste de hipótesis y ponemos la conclusión en cuarentena.
Comprobamos que efectivamente se están cumpliendo las hipótesis de partida
1. En caso de que se cumplan: nuestra conclusión es válida, ya podemos quitarle la cuarentena.
2. En caso de que no se cumplan: nuestra conclusión no sabemos si es válida, podemos hacer algo para que se cumplan:
  1. Si no podemos defender la normalidad a veces basta con tomar más datos.
  2. Si la naturaleza de la variable no es de tipo normal, mejor usar otra técnica, por ejemplo, técnicas no paramétricas (Kruskal-Wallis).
  3. Si observamos falta de independencia hay que repetir el experimento entero cuidando que no haya interacción.
  4. Si observamos falta de homocedasticidad podría arreglarse transformando la variable (por ejemplo, usando la función logaritmo) o, en el caso de que haya el mismo número de observaciones en los grupos, no es algo grave y los resultados son consistentes.

Ejercicios

Ejercicios Guiados

Ejercicio guiado 1

Se realiza un estudio de diversas especies de pájaros que son de similar naturaleza y comparten un medio común. El canto de cada especie tiene un conjunto de rasgos distintivos que permite reconocerla. Una característica investigada es la duración del canto en segundos. Se estudian tres especies; el towhee, el cuelliamarillo común, y el malviz pardo. Se obtuvieron los siguientes datos:

$ \begin{array} {|c|c|} \hline Especie & Duración \hspace {.2cm} del \hspace {.2cm} canto \\ \hline Towee & 1.11 \hspace{1cm} 1.23 \hspace{0.7cm} 0.91 \hspace{0.7cm} 0.95 \hspace{0.7cm} 0.99 \hspace{0.7cm} 1.08 \hspace{0.7cm} 1.18 \hspace{0.7cm} 1.20 \\ \hline Cuelliamarillo & 2.17 \hspace{1cm} 1.85 \hspace{0.7cm} 1.99 \hspace{0.7cm} 1.74 \hspace{0.7cm} 1.54 \hspace{0.7cm} 1.86 \hspace{0.7cm} 1.87 \hspace{0.7cm} 2.04 \\ \hline Malviz & 0.42 \hspace{1cm} 0.93 \hspace{0.7cm} 0.77 \hspace{0.7cm} 0.37 \hspace{0.7cm} 0.50 \hspace{0.7cm} 0.48 \hspace{0.7cm} 0.68 \hspace{0.7cm} 0.69 \\ \hline \end{array} $

Tabla 3: Datos del Ejercicio Guiado 1

¿Existen diferencias significativas entre las duraciones medias de los cantos de las tres especies de pájaros?, en caso afirmativo, ¿entre qué especies de pájaros? Utilice un nivel de significación del 5%. Además, estudiar las hipótesis del modelo: homocedasticidad, independencia y normalidad.

Ejercicio guiado 2

En una academia de inglés, se pretende realizar un estudio sobre la velocidad de lectura de 400 estudiantes que han recibido clases de 4 instructores diferentes. Para ello se mide el tiempo, en segundos, que tardan en realizar una primera lectura después de una semana de clase.

¿Existen diferencias significativas en la velocidad media de lectura de los alumnos según cada uno de los instructores?, en caso afirmativo, ¿entre qué instructores? Utilice un nivel de significación del 5%. Además, estudiar las hipótesis del modelo: homocedasticidad, independencia y normalidad.

Los datos están en el fichero lectura.txt.

Ejercicio guiado 3

En el paquete WRS2 de R se dispone de la siguiente base de datos goggles. Este conjunto de datos trata sobre los efectos del alcohol a la hora de elegir pareja en clubes nocturnos. Se supone que después de consumir alcohol, las percepciones subjetivas del atractivo físico se volverían más inexactas (efecto “gafas de cerveza”). Se consideran 48 participantes: 24 hombres y 24 mujeres. El investigador eligió 3 grupos de 8 participantes en un club nocturno. Un grupo no consumió alcohol, un grupo consumió 2 pintas y otro grupo consumió 4 pintas. Al final de la velada, el investigador tomó una fotografía de la persona con la que el participante estaba charlando. Posteriormente, jueces independientes evaluaron el atractivo de la persona en la foto con una puntuación entre 0 y 100.

¿Existen diferencias significativas en el atractivo de la persona elegida por los participantes según la cantidad de alcohol consumida?, en caso afirmativo, ¿entre qué cantidades? Utilice un nivel de significación del 5%. Además, estudiar las hipótesis del modelo: homocedasticidad, independencia y normalidad.

Ejercicio Guiado 1 (Resuelto)

Tabla 3: Datos del Ejercicio Guiado 1

Nos interesa saber si las diferentes especies de pájaros influyen significativamente en la duración del canto de los mismos

La duración del canto es una variable numérica
La especie es una variable categórica que divide a los individuos en grupos

Nuestro contraste de hipótesis es:

$ \begin{array} { c} H_0: \mu_1=\mu_2=\mu_3=\mu \\ H_1: \exists i,j;\, i\neq j / \mu_i\neq \mu_j \end{array} $

Es decir,

$ H_0 $: La duración media del canto es la misma para las tres especies

$ H_1 $: La duración media del canto es diferente según la especie

En primer lugar, cargamos el paquete BrailleR

> library(“BrailleR”)

vamos a almacenar los datos de las dos variables en dos vectores:

> especie = factor(c(rep(“Towee”,8), rep(“Cuelliamarillo”,8), rep(“Malviz”,8)),levels = c(“Towee”, “Cuelliamarillo”, “Malviz”))
> duracion=c(1.11,1.23,0.91,0.95,0.99,1.08,1.18,1.29, 2.17,1.85,1.99,1.74,1.54,1.86,1.87,2.04, 0.42,0.93,0.77,0.37,0.50,0.48,0.68,0.69)

Agrupamos las 2 variables en un data frame, al que vamos a llamar Datos:

> Datos = data.frame (especie, duracion)

Comprobemos que los datos se han guardado correctamente.

> head(Datos)
especie duracion
1 Towee 1.11
2 Towee 1.23
3 Towee 0.91
4 Towee 0.95
5 Towee 0.99
6 Towee 1.08

Realizamos el ANOVA pedido mediante la función OneFactor. En este ejemplo, vamos a indicarle al programa que no nos muestre el Test post-hoc. En el caso de que nos salgan diferencias significativas en el ANOVA, lo añadiremos posteriormente.

> OneFactor(“duracion”, “especie”, Datos, HSD = FALSE)

Muestra una salida en html:Duracion.Especie-OneFactor

Analysis of the Datos data, using Duracion as the response variable and Especie as the single grouping factor.

Prepared by BrailleR

Muestra:

Una tabla resumen que incluye para cada grupo la media, la desviación típica, el número de datos y el error estándar
Diagramas de caja y bigotes comparativos para cada grupo
Gráfico de puntos comparativos para cada grupo
Análisis de la varianza de un factor
Dos tests de homogeneidad de varianzas

A continuación, se muestra y se detalla cada resultado:

Una tabla resumen que incluye para cada grupo la media, la desviación típica, el número de datos y el error estándar

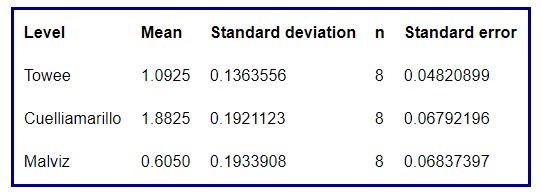
Tabla 4: Resumen para cada especie

2. Diagramas de caja y bigotes comparativos para cada grupo

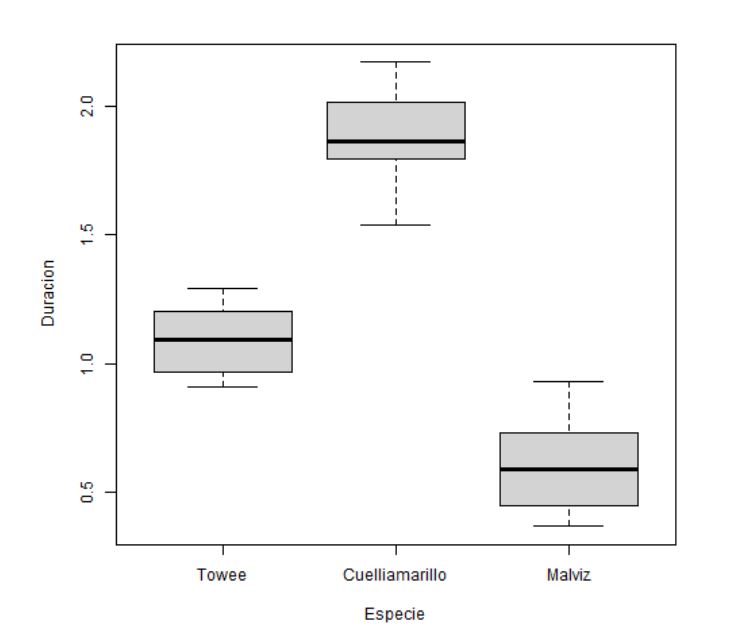
Figura 1: Diagrama de caja y bigotes para cada especie

Los grupos Towee y Malviz parecen seguir una distribución simétrica, mientras que en el grupo Cuelliamarillo no se ve claramente tal simetría.
No se detectan valores atípicos.
El tamaño de las cajas es similar para todos los niveles por lo que no hay indicios de falta de homocedasticidad.
Se puede intuir que existirá diferencia de medias.

3. Gráfico de puntos comparativos para cada grupo

Figura 2: Gráfico de puntos para cada especie

Al igual que en el diagrama de caja y bigotes, se puede tener una idea intuitiva de si las medias difieren unas de otras o no. Obteniendo las mismas conclusiones que con el gráfico anterior.

Análisis de la varianza de un factor

Df Sum Sq Mean Sq F value Pr(>F)

especie 2 6.65 3.325 107.4 9.39e-12 ***

Residuals 21 0.65 0.031

—

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1

Esta es la tabla ANOVA que nos proporciona un p-valor=9.39e-12 por lo que se rechaza la hipótesis nula, esto quiere decir que existen diferencias significativas entre las duraciones medias de los cantos de las tres especies de pájaros (al menos en dos de ellos).

Al existir diferencias significativas, tiene sentido realizar las comparaciones de medias dos a dos, con el objetivo de encontrar entre qué dos medias hay diferencias significativas. Para ello se realiza un análisis post-hoc, mediante el método Tukey HSD.

Previamente, se comprueba gráficamente si se cumplen las hipótesis del modelo:

Para comprobar la idoneidad del modelo propuesto, la salida de la función OneFactor muestra los gráficos:

Valores ajustados frente a residuos
Gráfico Q-Q de normalidad
Valores ajustados frente a raíz cuadrada de los residuos estandarizados (en valor absoluto)
Residuos estandarizados frente a leverages

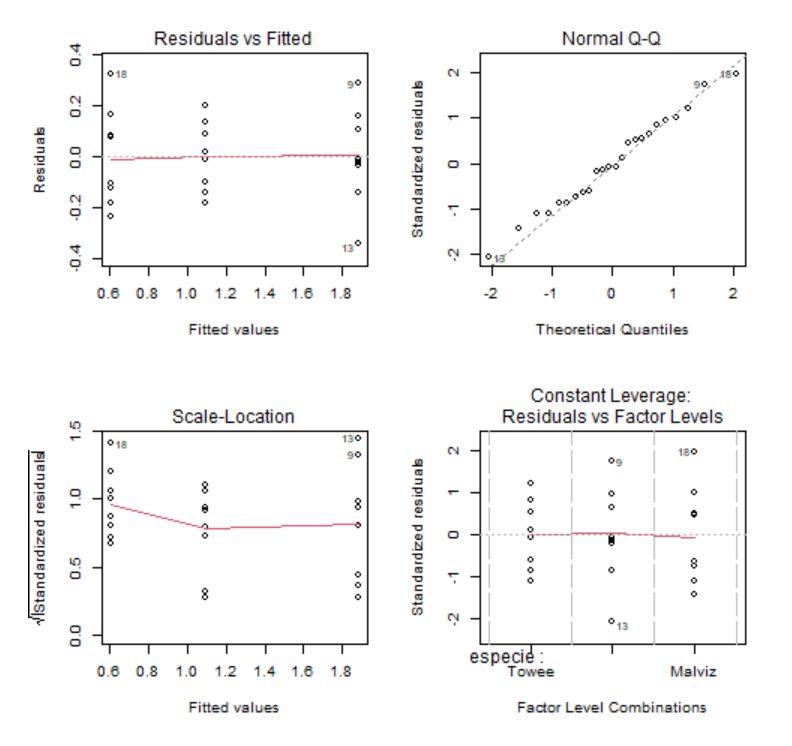
Figura 3: Gráficos de comprobación de las hipótesis

Dos tests de homogeneidad de varianzas

El test de homogeneidad de varianzas de Bartlett

Bartlett test of homogeneity of variances

data: duracion by especie

Bartlett’s K-squared = 0.9602, df = 2, p-value = 0.6187

Considerando como nivel de significación 0.05, y observando el p-valor=0.6187 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

El test de homogeneidad de varianzas de Fligner-Killeen

Fligner-Killeen test of homogeneity of variances

data: duracion by especie

Fligner-Killeen:med chi-squared = 0.85016, df = 2, p-value = 0.6537

Considerando como nivel de significación 0.05, y observando el p-valor=0.6537 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

Ahora vamos a añadir a la función el test post-hoc de la siguiente forma:

> OneFactor(“duracion”, “especie”, Datos)

Esta nos devuelve todo lo anterior junto con lo que se especifica a continuación: Duracion.Especie-OneFactor

Test post-hoc mediante el método de Tukey Honestly Significant Difference

Tukey multiple comparisons of means

95% family-wise confidence level

factor levels have been ordered

Fit: aov(formula = duracion ~ especie, data = Datos)

$especie

diff lwr upr p adj

Towee-Malviz 0.4875 0.2657232 0.7092768 4.86e-05

Cuelliamarillo-Malviz 1.2775 1.0557232 1.4992768 0.00e+00

Cuelliamarillo-Towee 0.7900 0.5682232 1.0117768 0.00e+00

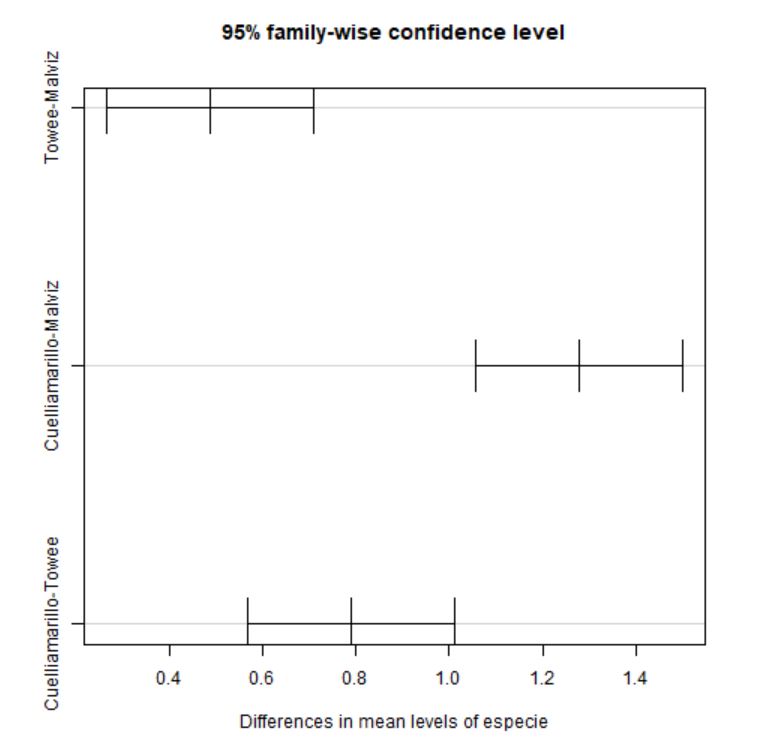
Figura 4: Intervalos de confianza de la diferencia de medias para cada par de especies

Towee y Malviz: Puesto que p-valor=4.86e-05, se rechaza $ H_0 $, es decir, existen diferencias significativas entre en tiempo medio de canto entre las especies Towee y Cuelliamarillo.
Cuelliamarillo y Malviz: Puesto que p-valor=0, se rechaza $ H_0 $, es decir, existen diferencias significativas entre en tiempo medio de canto entre las especies Cuelliamarillo y Malviz.
Cuelliamarillo y Towee: Puesto que p-valor=0, se rechaza $ H_0 $, es decir, existen diferencias significativas entre en tiempo medio de canto entre las especies Cuelliamarillo y Towee.

En definitiva, existen diferencias significativas entre el tiempo medio de canto entre las tres especies de pájaros.

Se pueden deducir las mismas conclusiones, observando que los intervalos de confianza, tanto analítica como gráficamente no contienen al cero.

Ejercicio Guiado 2 (Resuelto)

Los datos están en el fichero lectura.txt.

Nos interesa saber si los diferentes instructores influyen significativamente en el tiempo medio de lectura de los alumnos tras una semana de clase.

El tiempo de lectura es una variable numérica
El instructor es una variable categórica que divide a los individuos en grupos

El contraste de hipótesis correspondiente es:

$ \begin{array} { c} H_0: \mu_1=\mu_2=\mu_3=\mu_4 = \mu \\ H_1: \exists i,j;\, i\neq j / \mu_i\neq \mu_j \end{array} $

Es decir,

$ H_0 $ : La velocidad media es la misma para los cuatro instructores

$ H_1 $ : La velocidad media es diferente según el instructor

En primer lugar, cargamos el paquete BrailleR

> library(“BrailleR”)

> setwd(“C:/Users/Usuario/Desktop/datos/”) # cambiar al directorio de trabajo donde están los datos

Leemos los datos y los llamamos “lectura”

> lectura=read.table(“lectura.txt”, header=T, sep=””)

Comprobemos que los datos se han guardado correctamente

> head(lectura)
observacion tiempo_primeralectura Instructor
1 1 80.48 Instructor 1
2 2 84.53 Instructor 2
3 3 77.76 Instructor 3
4 4 86.50 Instructor 4
5 5 90.40 Instructor 1
6 6 6 98.26 Instructor 2

Transformamos la variable Instructor en factor

> lectura$Instructor=as.factor(lectura$Instructor)

> OneFactor(“tiempo_primeralectura”, “Instructor”, lectura, HSD = FALSE)

Muestra una salida en html:

Analysis of the Lectura data, using Tiempo_primeralectura as the response variable and Instructor as the single grouping factor.

Prepared by BrailleR

Muestra:

Una tabla resumen que incluye para cada grupo la media, la desviación típica, el número de datos y el error estándar
Diagramas de caja y bigotes comparativos para cada grupo
Gráfico de puntos comparativos para cada grupo
Análisis de la varianza de un factor
Dos tests de homogeneidad de varianzas

A continuación, se muestra y se detalla cada resultado:

Una tabla resumen que incluye para cada grupo la media, la desviación típica, el número de datos y el error estándar

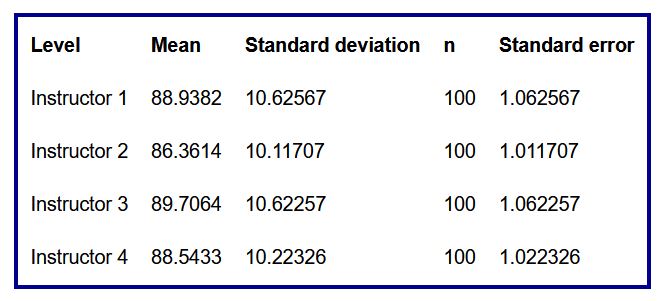
Tabla 5: Resumen para cada instructor

2. Diagramas de caja y bigotes comparativos para cada grupo

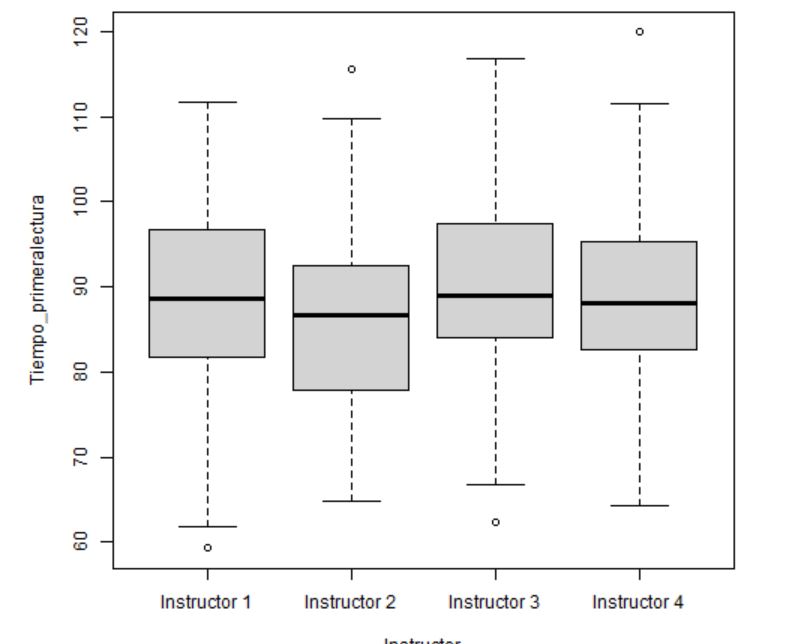
Figura 5: Diagrama de caja y bigotes para cada instructor

En este caso, los 4 grupos parecen seguir una distribución simétrica.
En los diferentes instructores se detectan algunos valores atípicos que habrá que estudiar con detalle por si fuese necesario eliminarlos.
El tamaño de las cajas es similar para todos los niveles por lo que no hay indicios de falta de homocedasticidad.
A simple vista no parece que vaya a haber diferencia de medias.

3. Gráfico de puntos comparativos para cada grupo

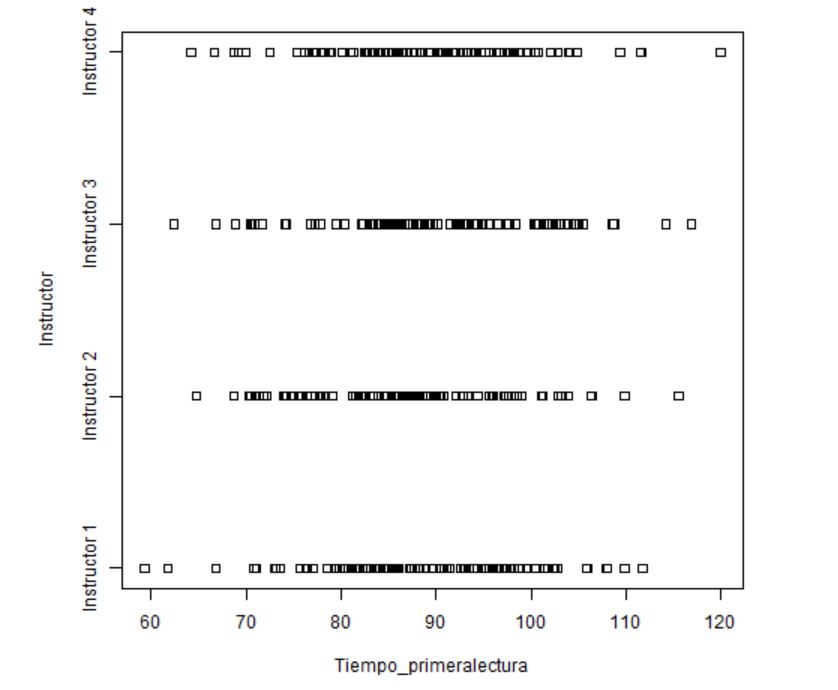
Figura 6: Gráfico de puntos para cada instructor

Al igual que en el diagrama de caja y bigotes, se puede tener una idea intuitiva de si las medias difieren unas de otras o no. Obteniendo las mismas conclusiones que con el gráfico anterior.

Análisis de la varianza de un factor

Df Sum Sq Mean Sq F value Pr(>F)

Instructor 3 617 205.7 1.902 0.129

Residuals 396 42829 108.2

Esta es la tabla ANOVA que nos proporciona un p-valor=0.129 por lo que no tenemos evidencia muestral para rechazar la hipótesis nula, esto quiere decir que no hay diferencias significativas en el tiempo de la primera lectura considerando los distintos instructores.

Al no existir diferencias significativas, no tiene sentido realizar las comparaciones de medias dos a dos, es decir, el análisis post-hoc.

A continuación, se comprueba gráficamente si se cumplen las hipótesis del modelo:

Para comprobar la idoneidad del modelo propuesto, la salida de la función OneFactor muestra los gráficos:

Valores ajustados frente a residuos
Gráfico Q-Q de normalidad
Valores ajustados frente a raíz cuadrada de los residuos estandarizados (en valor absoluto)
Residuos estandarizados frente a leverages

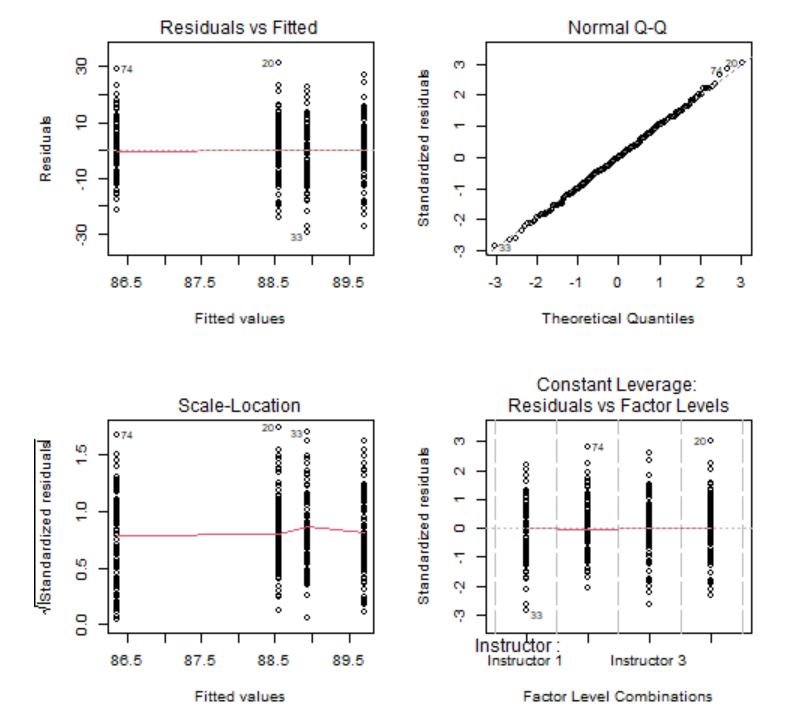
Figura 7: Gráficos de comprobación de las hipótesis

Los gráficos confirman que los residuos tienen media cero, son homocedásticos y con distribución normal. Sin embargo, se detectan algunos valores atípicos que habría que analizar de manera individual por si fuera necesario eliminarlos del modelo. La hipótesis de independencia es intrínseca al diseño del experimento, por tanto, se supone que las observaciones son independientes ya que se están considerando alumnos que han recibido clases de instructores diferentes.

Dos tests de homogeneidad de varianzas

Vamos a confirmar la homocedasticidad mediante dos métodos analíticos.

El test de homogeneidad de varianzas de Bartlett

Bartlett test of homogeneity of variances

data: tiempo_primeralectura by Instructor

Bartlett’s K-squared = 0.38638, df = 3, p-value = 0.943

Considerando como nivel de significación 0.05, y observando el p-valor=0.943 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

El test de homogeneidad de varianzas de Fligner-Killeen

Fligner-Killeen test of homogeneity of variances

data: tiempo_primeralectura by Instructor

Fligner-Killeen:med chi-squared = 1.3492, df = 3, p-value = 0.7175

Considerando como nivel de significación 0.05, y observando el p-valor=0.7175 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

Ejercicio Guiado 3 (Resuelto)

Nos interesa saber si las diferentes cantidades de alcohol consumido influyen significativamente en el grado de atractivo de la persona elegida.

La puntuación que mide el grado de atractivo es una variable numérica
La cantidad de alcohol consumido (clasificado en Nada, 2 Pintas, 4 Pintas) es una variable categórica que divide a los individuos en grupos

Nuestro contraste de hipótesis es:

$ \begin{array} { c} H_0: \mu_1=\mu_2=\mu_3= \mu \\ H_1: \exists i,j;\, i \neq j / \mu_i \neq \mu_j \end{array} $

Es decir,

$ H_0 $ : La puntuación media es la misma para todas las cantidades de alcohol consumidas

$ H_1 $ : La puntuación media es diferente para todas las cantidades de alcohol consumidas

En primer lugar, cargamos el paquete BrailleR

> library(“BrailleR”)

El paquete de R donde se encuentran los datos se instala (si es la primera vez que se usa) y se carga

> install.packages(“WRS2”)

> library(WRS2)

Leemos los datos

> data(“goggles”)

Observamos los datos

> head(goggles)

gender alcohol attractiveness
1 Female None 65
2 Female None 70
3 Female None 60
4 Female None 60
5 Female None 60
6 Female None 55

Transformamos la variable alcohol en factor

> goggles$alcohol=as.factor(goggles$alcohol)

[1] None None None None None None None None 2 Pints
[10] 2 Pints 2 Pints 2 Pints 2 Pints 2 Pints 2 Pints 2 Pints 4 Pints 4 Pints
[19] 4 Pints 4 Pints 4 Pints 4 Pints 4 Pints 4 Pints None None None
[28] None None None None None 2 Pints 2 Pints 2 Pints 2 Pints
[37] 2 Pints 2 Pints 2 Pints 2 Pints 4 Pints 4 Pints 4 Pints 4 Pints 4 Pints
[46] 4 Pints 4 Pints 4 Pints
Levels: None 2 Pints 4 Pints

> OneFactor(“attractiveness”, “alcohol”, goggles, HSD = FALSE)

Muestra una salida en html:

Analysis of the Goggles data, using Attractiveness as the response variable and Alcohol as the single grouping factor.

Prepared by BrailleR

Muestra:

Una tabla resumen que incluye para cada grupo la media, la desviación típica, el número de datos y el error estándar
Diagramas de caja y bigotes comparativos para cada grupo
Gráfico de puntos comparativos para cada grupo
Análisis de la varianza de un factor
Dos tests de homogeneidad de varianzas

A continuación, se muestra y se detalla cada resultado:

Una tabla resumen que incluye para cada grupo la media, la desviación típica, el número de datos y el error estándar

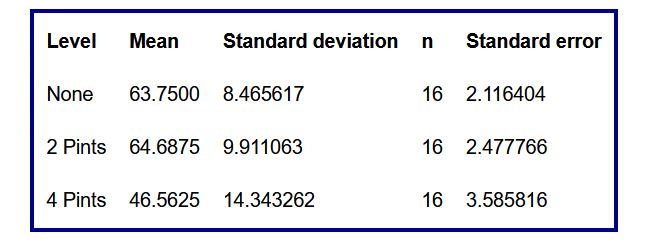
Tabla 6: Resumen según el consumo de alcohol

The ratio of the largest group standard deviation to the smallest is 1.69

Diagramas de caja y bigotes comparativos para cada grupo

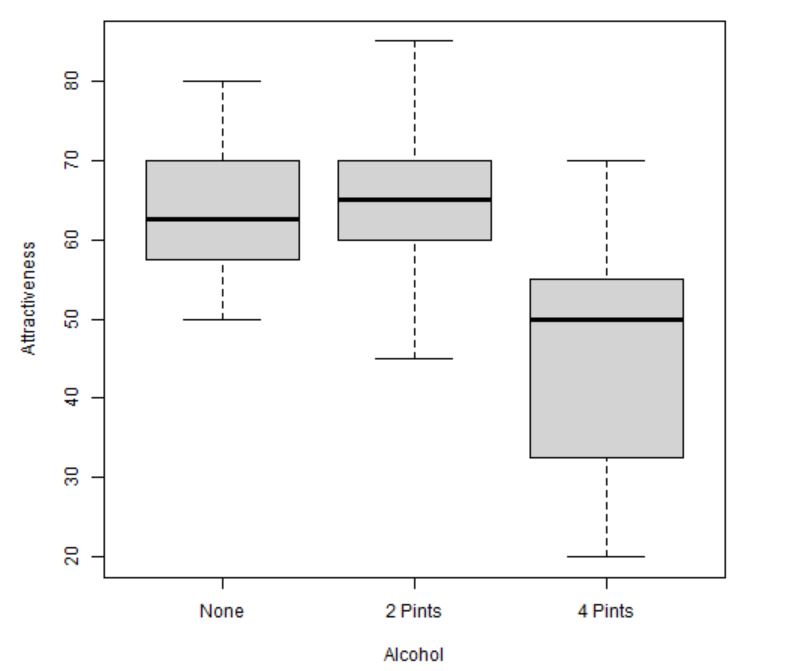
Figura 8: Diagrama de caja y bigotes según el consumo de alcohol

Los grupos de Nada y 2 Pintas parecen seguir una distribución más o menos simétrica, mientras que en el grupo de 4 Pintas la distribución parece asimétrica. Lo comprobaremos posteriormente gráficamente.
No se detectan valores atípicos.
El tamaño de las cajas es similar para los dos primeros grupos. Sin embargo, hay bastante diferencia con respecto al tamaño del tercer grupo, por lo que podría incumplirse la hipótesis de homocedasticidad. Lo confirmaremos posteriormente gráfica y analíticamente.
Se puede intuir que existirá diferencia de medias entre los grupos Nada y 2 Pintas con respecto al de 4 Pintas.

3. Gráfico de puntos comparativos para cada grupo

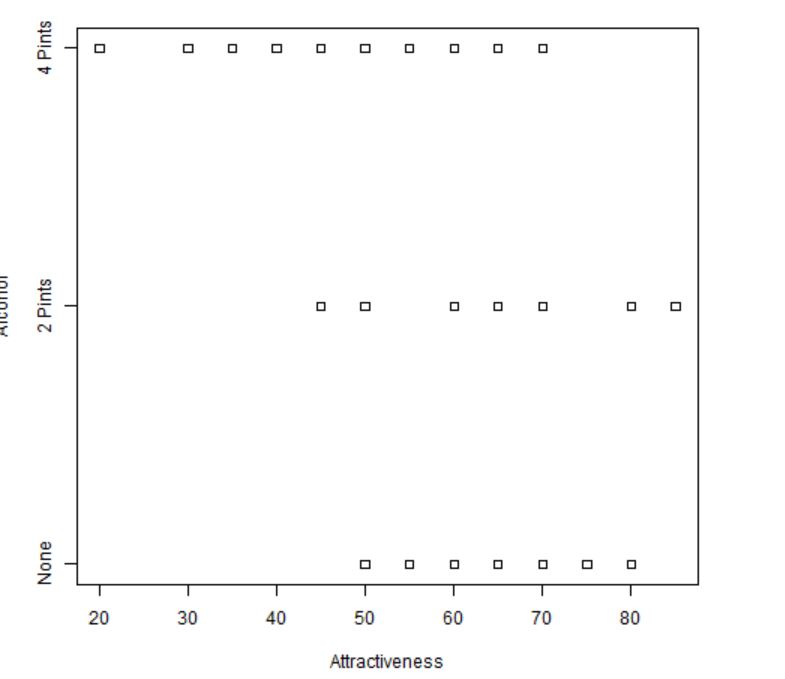
Figura 9: Gráfico de puntos según el consumo de alcohol

Al igual que en el diagrama de caja y bigotes, se puede tener una idea intuitiva de si las medias difieren unas de otras o no. Obteniendo las mismas conclusiones que con el gráfico anterior.

4. Análisis de la varianza de un factor

Df Sum Sq Mean Sq F value Pr(>F)

alcohol 2 3332 1666.1 13.31 2.88e-05 ***

Residuals 45 5634 125.2

—

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1

Esta es la tabla ANOVA que nos proporciona un p-valor=2.88e-05 por lo que se rechaza la hipótesis nula, esto quiere decir que existen diferencias significativas en el atractivo de la persona elegida por los participantes según la cantidad de alcohol consumida (al menos en dos grupos).

Previamente, se comprueba gráficamente si se cumplen las hipótesis del modelo:

Para comprobar la idoneidad del modelo propuesto, la salida de la función OneFactor muestra los gráficos:

Valores ajustados frente a residuos
Gráfico Q-Q de normalidad
Valores ajustados frente a raíz cuadrada de los residuos estandarizados (en valor absoluto)
Residuos estandarizados frente a leverages

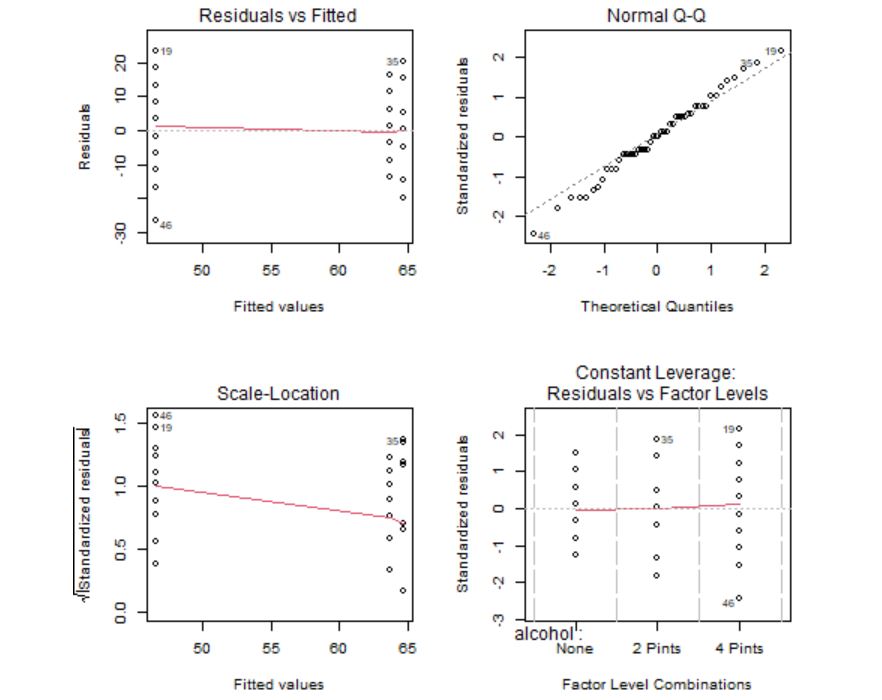
Figura 10: Gráficos de comprobación de las hipótesis

Los gráficos confirman que los residuos tienen media cero, son homocedásticos y con distribución normal. Sin embargo, se detectan algunos valores atípicos que habría que analizar de manera individual por si fuera necesario eliminarlos del modelo. La hipótesis de independencia es intrínseca al diseño del experimento, por tanto, se supone que las observaciones son independientes ya que se están considerando jueces independientes que evaluaron el atractivo de la persona en la foto y la división por grupos se realizó de manera independiente.

Dos tests de homogeneidad de varianzas

Vamos a confirmar la homocedasticidad mediante dos métodos analíticos.

El test de homogeneidad de varianzas de Bartlett

Bartlett test of homogeneity of variances

data: attractiveness by alcohol

Bartlett’s K-squared = 4.4295, df = 2, p-value = 0.1092

Considerando como nivel de significación 0.05, y observando el p-valor=0.1092 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

El test de homogeneidad de varianzas de Fligner-Killeen

Fligner-Killeen test of homogeneity of variances

data: attractiveness by alcohol

Fligner-Killeen:med chi-squared = 4.3876, df = 2, p-value = 0.1115

Considerando como nivel de significación 0.05, y observando el p-valor=0.1115 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

Ahora vamos a añadir a la función el test post-hoc de la siguiente forma:

> OneFactor(“attractiveness”, “alcohol”, goggles)

Muestra una salida en html: Esta salida nos devuelve todo lo anterior junto con lo que se especifica a continuación:

Analysis of the Goggles data, using Attractiveness as the response variable and Alcohol as the single grouping factor.

Prepared by BrailleR

Test post-hoc mediante el método de Tukey Honestly Significant Difference

Tukey multiple comparisons of means

95% family-wise confidence level

factor levels have been ordered

Fit: aov(formula = attractiveness ~ alcohol, data = goggles)

$alcohol

diff lwr upr p adj

None-4 Pints 17.1875 7.599346 26.77565 0.0002283

2 Pints-4 Pints 18.1250 8.536846 27.71315 0.0001067

2 Pints-None 0.9375 -8.650654 10.52565 0.9695381

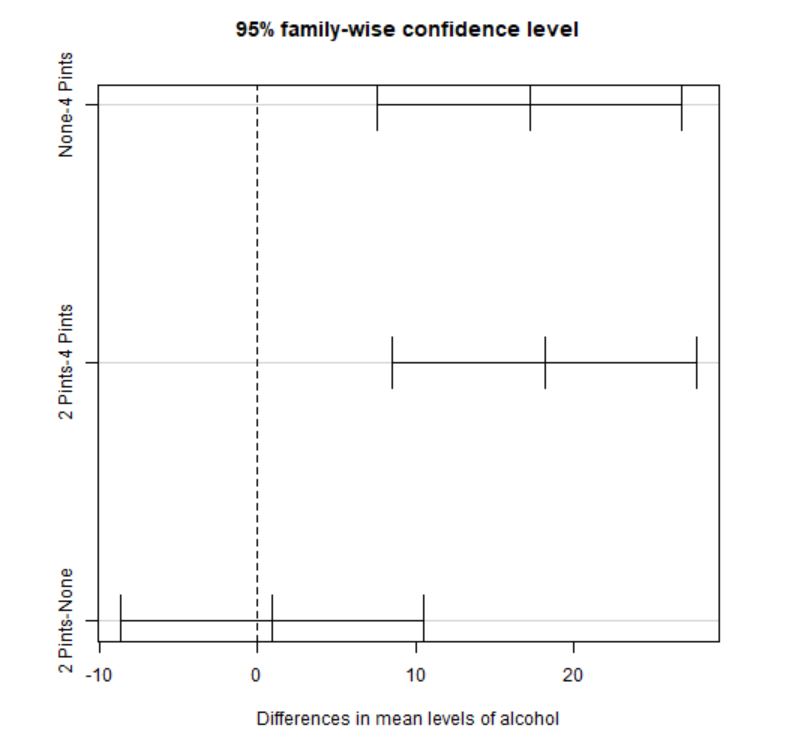
Figura 11: Intervalos de confianza de la diferencia de medias para cada par de grupos

Nada y 4 Pintas: Puesto que p-valor=0.0002283, se rechaza $ H_0 $, es decir, existen diferencias significativas en el atractivo de la persona elegida por los participantes según si los participantes no consumen alcohol o consumen 4 Pintas.
2 Pintas y 4 Pintas: Puesto que p-valor=0.0001067, se rechaza $ H_0 $, es decir, existen diferencias significativas en el atractivo de la persona elegida por los participantes según si los participantes consumen 2 Pintas o consumen 4 Pintas.
2 Pintas y Nada: Puesto que p-valor=0.9695381, no podemos rechazar $ H_0 $, es decir, no hay diferencias significativas en el atractivo de la persona elegida por los participantes según si los participantes consumen 2 Pintas o no consumen alcohol.

Se pueden deducir las mismas conclusiones, observando que los dos primeros intervalos de confianza, tanto analítica como gráficamente no contienen al cero y el tercer intervalo sí que lo contiene.

Ejercicios Propuestos

Ejercicio Propuesto1

Se realiza un estudio con el objetivo de conocer si hay colores que sean más atractivos que otros para los insectos. Para ello se diseñaron trampas con los siguientes colores: azul, verde, blanco y amarillo. Se cuantificó el número de insectos que quedaban atrapados:

$ \begin{array} {|c|c|} \hline Color & Número \hspace {.2cm} de \hspace {.2cm} insectos \hspace {.2cm} atrapados \\ \hline Azul & 16 \hspace{0.7cm} 11 \hspace{0.7cm} 20 \hspace{0.7cm} 21 \hspace{0.7cm} 14 \hspace{0.7cm} 7 \\ \hline Verde & 37 \hspace{0.7cm} 32 \hspace{0.7cm} 15 \hspace{0.7cm} 25 \hspace{0.7cm} 39 \hspace{0.7cm} 41 \\ \hline Blanco & 21 \hspace{0.7cm} 12 \hspace{0.7cm} 14 \hspace{0.7cm} 17 \hspace{0.7cm} 13 \hspace{0.7cm} 17 \\ \hline Amarillo & 45 \hspace{0.7cm} 59 \hspace{0.7cm} 48 \hspace{0.7cm} 46 \hspace{0.7cm} 38 \hspace{0.7cm} 47 \\ \hline \end{array} $

Tabla 7: Datos del Ejercicio Propuesto 1

Existen diferencias significativas entre el número de insectos atrapados según el color de las trampas? Utilice un nivel de significación del 5%.
En caso afirmativo en el apartado anterior, ¿entre qué colores? Utilice un nivel de significación del 5%.

3. Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.

Ejercicio Propuesto 2

Se pretende estudiar la acción que ejercen tres tipos de levadura distintos en el proceso de fermentación del vino, para ello se desea conocer cómo es la cantidad de levadura en 1 mm³ de vino contadas según los tres tipos distintos de levadura, que son Kloeckera, Pichia y Mycoderma al finalizar todo el proceso. Se toman 10 muestras aleatorias de 1 mm³ a cada una de las tres especies, y se toma el recuento de la cantidad de levadura:

$ \begin{array} {|c|c|} \hline Tipo & Cantidad \hspace {.2cm} de \hspace {.2cm} levadura \\ \hline Kloeckera & 279 \hspace{0.7cm} 301 \hspace{0.7cm} 337 \hspace{0.7cm} 287 \hspace{0.7cm} 331 \hspace{0.7cm} 297 \hspace{0.7cm} 326 \hspace{0.7cm} 297 \hspace{0.7cm} 304 \hspace{0.7cm} 294 \\ \hline Pichia & 204 \hspace{1cm} 177 \hspace{0.7cm} 212 \hspace{0.7cm} 224 \hspace{0.7cm} 197 \hspace{0.7cm} 220 \hspace{0.7cm} 198 \hspace{0.7cm} 211 \hspace{0.7cm} 187 \hspace{0.7cm} 229 \\ \hline Mycoderma & 190 \hspace{1cm} 200 \hspace{0.7cm} 220 \hspace{0.7cm} 180 \hspace{0.7cm} 160 \hspace{0.7cm} 169 \hspace{0.7cm} 203 \hspace{0.7cm} 230 \hspace{0.7cm} 186 \hspace{0.7cm} 198 \\ \hline \end{array} $

Tabla 8: Datos del Ejercicio Propuesto 2

¿Influye el tipo de levadura en el proceso de fermentación del vino? Utilice un nivel de significación del 5%.

2. En caso afirmativo en el apartado anterior, ¿entre qué tipos? Utilice un nivel de significación del 5%.

3. Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.

Ejercicio Propuesto 3

Se quiere estudiar el efecto a distintas dosis de un medicamento que está en proceso de experimentación para combatir al parásito Sparicotyle chrysophrii, que comúnmente se encuentra en las branquias de las doradas (Sparus aurata) criadas en acuicultura. Para ello, se tomaron 30 doradas parasitadas al azar, y se dividieron en 3 grupos de 10 individuos cada uno. El primer grupo llamado Control no fue medicado, pero a los dos restantes se les suministró el medicamento en dosis distintas. Tras una semana de tratamiento, se contabilizó el número de parásitos existentes en cada individuo, obteniendo los resultados siguientes:

$ \begin{array} {|c|c|} \hline Grupo & Número \hspace {.2cm} de \hspace {.2cm} parásitos \\ \hline Control & 50 \hspace{0.7cm} 65 \hspace{0.7cm} 60 \hspace{0.7cm} 46 \hspace{0.7cm} 38 \hspace{0.7cm} 29 \hspace{0.7cm} 61 \hspace{0.7cm} 85 \hspace{0.7cm} 62 \hspace{0.7cm} 40 \\ \hline 50 \hspace {.2cm} mg & 20 \hspace{1cm} 59 \hspace{0.7cm} 64 \hspace{0.7cm} 61 \hspace{0.7cm} 28 \hspace{0.7cm} 47 \hspace{0.7cm} 29 \hspace{0.7cm} 41 \hspace{0.7cm} 60 \hspace{0.7cm} 57 \\ \hline 125 \hspace{0.3cm} mg & 30 \hspace{1cm} 45 \hspace{0.7cm} 52 \hspace{0.7cm} 46 \hspace{0.7cm} 31 \hspace{0.7cm} 21 \hspace{0.7cm} 34 \hspace{0.7cm} 32 \hspace{0.7cm} 51 \hspace{0.7cm} 36 \\ \hline \end{array} $

Tabla 9: Datos del Ejercicio Propuesto 3

¿Existen diferencias significativas en la cantidad de parásitos según la dosis del medicamento suministrada? Utilice un nivel de significación del 5%.

2. En caso afirmativo en el apartado anterior, ¿entre qué dosis? Utilice un nivel de significación del 5%.

3. Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.

Ejercicio Propuesto 1 (Resuelto)

Tabla 7: Datos del Ejercicio Propuesto 1

¿Existen diferencias significativas entre el número de insectos atrapados según el color de las trampas? Utilice un nivel de significación del 5%.

2. En caso afirmativo en el apartado anterior, ¿entre qué colores? Utilice un nivel de significación del 5%.

3. Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.

Solución

¿Existen diferencias significativas entre el número de insectos atrapados según el color de las trampas? Utilice un nivel de significación del 5%.

Nos interesa saber si el color de las trampas influye significativamente en el número de insectos atrapados

El número de insectos atrapados es una variable numérica

El color de las trampas es una variable categórica que divide a los individuos en grupos

Nuestro contraste de hipótesis es:

$ \begin{array} { c} H_0: \mu_1=\mu_2=\mu_3= \mu_4 = \mu \\ H_1: \exists i,j;\, i \neq j / \mu_i \neq \mu_j \end{array} $

Es decir,

$ H_0 $ : El número de insectos atrapados es el mismo para los cuatro colores de trampas

$ H_1 $ : El número de insectos atrapados es diferente según el color de las trampas

Análisis de la varianza de un factor

Df Sum Sq Mean Sq F value Pr(>F)

color 3 4218 1406 30.55 1.15e-07 ***

Residuals 20 920 46

—

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1

Esta es la tabla ANOVA que nos proporciona un p-valor=1.15e-07 por lo que se rechaza la hipótesis nula, esto quiere decir que existen diferencias significativas entre el número de insectos atrapados según el color de las trampas (al menos en dos de ellos).

2. En caso afirmativo en el apartado anterior, ¿entre qué colores? Utilice un nivel de significación del 5%.

Se realiza un análisis post-hoc, mediante el método Tukey HSD. Añadimos a la función el test post-hoc de la siguiente forma:

> OneFactor(“atrapados”, “color”, Datos)

Test post-hoc mediante el método de Tukey Honestly Significant Difference

Tukey multiple comparisons of means

95% family-wise confidence level

factor levels have been ordered

Fit: aov(formula = atrapados ~ color, data = Datos)

$color

diff lwr upr p adj

Blanco-Azul 0.8333333 -10.129663 11.79633 0.9964823

Verde-Azul 16.6666667 5.703670 27.62966 0.0020222

Amarillo-Azul 32.3333333 21.370337 43.29633 0.0000004

Verde-Blanco 15.8333333 4.870337 26.79633 0.0032835

Amarillo-Blanco 31.5000000 20.537004 42.46300 0.0000006

Amarillo-Verde 15.6666667 4.703670 26.62966 0.0036170

Dos tests de homogeneidad de varianzas

Vamos a confirmar la homocedasticidad mediante dos métodos analíticos.

El test de homogeneidad de varianzas de Bartlett

Bartlett test of homogeneity of variances

data: atrapados by color

Bartlett’s K-squared = 5.2628, df = 3, p-value = 0.1535

Considerando como nivel de significación 0.05, y observando el p-valor=0.1535 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

El test de homogeneidad de varianzas de Fligner-Killeen

Fligner-Killeen test of homogeneity of variances

data: atrapados by color

Fligner-Killeen:med chi-squared = 3.7498, df = 3, p-value = 0.2898

Considerando como nivel de significación 0.05, y observando el p-valor=0.2898 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

Solución al Ejercicio Propuesto 1

Ejercicio Propuesto 2 (Resuelto)

Tabla 8: Datos del Ejercicio Propuesto 2

¿Influye el tipo de levadura en el proceso de fermentación del vino? Utilice un nivel de significación del 5%.

2. En caso afirmativo en el apartado anterior, ¿entre qué tipos? Utilice un nivel de significación del 5%.

3. Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.

Solución

¿Influye el tipo de levadura en el proceso de fermentación del vino? Utilice un nivel de significación del 5%.

Nos interesa saber si el tipo de levadura influye significativamente en la cantidad de levadura en 1 mm³ de vino

La cantidad de levadura en 1 mm³ de vino es una variable numérica

El tipo de levadura es una variable categórica que divide a los individuos en grupos

Nuestro contraste de hipótesis es:

$ \begin{array} { c} H_0: \mu_1=\mu_2=\mu_3= \mu \\ H_1: \exists i,j;\, i \neq j / \mu_i \neq \mu_j \end{array} $

Es decir,

$ H_0 $ : La cantidad de levadura en 1 mm3 es la misma para los tres tipos

$ H_1 $ : La cantidad de levadura en 1 mm3 es diferente según el tipo

Realizamos el ANOVA pedido mediante la función OneFactor sin que nos muestre el Test post-hoc.

Análisis de la varianza de un factor

Df Sum Sq Mean Sq F value Pr(>F)

tipo 2 75028 37514 101 2.92e-13 ***

Residuals 27 10027 371

—

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1

Esta es la tabla ANOVA que nos proporciona un p-valor=2.92e-13 por lo que se rechaza la hipótesis nula, esto quiere decir que existen diferencias significativas en la cantidad de levadura en 1 mm³ de vino según el tipo de la misma (al menos en dos de ellos). Esto es, el tipo de levadura influye en el proceso de fermentación del vino.

2. En caso afirmativo en el apartado anterior, ¿entre qué tipos? Utilice un nivel de significación del 5%.

Se realiza un análisis post-hoc, mediante el método Tukey HSD. Añadimos a la función el test post-hoc de la siguiente forma:

Test post-hoc mediante el método de Tukey Honestly Significant Difference

Tukey multiple comparisons of means

95% family-wise confidence level

factor levels have been ordered

Fit: aov(formula = cantidad ~ tipo, data = levadura)

$tipo

diff lwr upr p adj

Pichia-Mycoderma 12.3 -9.068645 33.66864 0.3415057

Kloeckera-Mycoderma 111.7 90.331355 133.06864 0.0000000

Kloeckera-Pichia 99.4 78.031355 120.76864 0.0000000

3. Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.

Para comprobar la idoneidad del modelo propuesto, la salida de la función OneFactor muestra los gráficos:

Valores ajustados frente a residuos

Gráfico Q-Q de normalidad

Valores ajustados frente a raíz cuadrada de los residuos estandarizados (en valor absoluto)

Residuos estandarizados frente a leverages

Dos tests de homogeneidad de varianzas

Vamos a confirmar la homocedasticidad mediante dos métodos analíticos.

El test de homogeneidad de varianzas de Bartlett

Bartlett test of homogeneity of variances

data: cantidad by tipo

Bartlett’s K-squared = 0.58681, df = 2, p-value = 0.7457

Considerando como nivel de significación 0.05, y observando el p-valor=0.7457 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

El test de homogeneidad de varianzas de Fligner-Killeen

Fligner-Killeen test of homogeneity of variances

data: cantidad by tipo

Fligner-Killeen:med chi-squared = 0.48253, df = 2, p-value = 0.7856

Considerando como nivel de significación 0.05, y observando el p-valor=0.7856 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

Solución al Ejercicio Propuesto 2

Ejercicio Propuesto 3 (Resuelto)

Tabla 9: Datos del Ejercicio Propuesto 3

Existen diferencias significativas en la cantidad de parásitos según la dosis del medicamento suministrada? Utilice un nivel de significación del 5%.

2. En caso afirmativo en el apartado anterior, ¿entre qué dosis? Utilice un nivel de significación del 5%.

3. Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.

Solución

1. ¿Existen diferencias significativas en la cantidad de parásitos según la dosis del medicamento suministrada? Utilice un nivel de significación del 5%.

Nos interesa saber si el control y las distintas dosis de medicamento influyen significativamente en el número de parásitos existentes en las branquias de las doradas

El número de parásitos por individuo es una variable numérica

La dosis de medicamento suministrada es una variable categórica que divide a los individuos en grupos

Nuestro contraste de hipótesis es:

$ \begin{array} { c} H_0: \mu_1=\mu_2=\mu_3= \mu \\ H_1: \exists i,j;\, i \neq j / \mu_i \neq \mu_j \end{array} $

Es decir,

$ H_0 $ : El número de parásitos en las branquias de las doradas es el mismo para los tres grupos

$ H_1 $ : El número de parásitos en las branquias de las doradas es diferente según el grupo

Realizamos el ANOVA pedido mediante la función OneFactor sin que nos muestre el Test post-hoc.

Muestra una salida en html:

Analysis of the Medicamento data, using Parasitos as the response variable and Grupo as the single grouping factor.

Prepared by BrailleR

Esta es la tabla ANOVA que nos proporciona un p-valor=0.0674 por lo que no tenemos evidencia muestral para rechazar la hipótesis nula, esto quiere decir que no hay diferencias significativas en la cantidad de parásitos según la dosis del medicamento suministrada.

2. En caso afirmativo en el apartado anterior, ¿entre qué dosis? Utilice un nivel de significación del 5%.

3. Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.

Dos tests de homogeneidad de varianzas

Vamos a confirmar la homocedasticidad mediante dos métodos analíticos.

El test de homogeneidad de varianzas de Bartlett

Bartlett test of homogeneity of variances

data: parasitos by grupo

Bartlett’s K-squared = 2.168, df = 2, p-value = 0.3382

Considerando como nivel de significación 0.05, y observando el p-valor=0.3382 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

El test de homogeneidad de varianzas de Fligner-Killeen

Fligner-Killeen test of homogeneity of variances

data: parasitos by grupo

Fligner-Killeen:med chi-squared = 2.2805, df = 2, p-value = 0.3197

Considerando como nivel de significación 0.05, y observando el p-valor=0.3197 no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que la varianza permanece constante entre grupos.

Solución al Ejercicio Propuesto 2

Versión de R utilizada: 4.2.2

Versión de RStudio utilizada: 2022.07.2

Versión Package BrailleR utilizada: 0.32.1

Autores: Irene García Garrido, Antonio Jesús López Montoya y Ana María Lara Porras. Universidad de Granada. (2023)

Estadística

Universidad de Granada

Práctica 4

ANÁLISIS DE LA VARIANZA UNIFACTORIAL

Objetivos

Introducción

Planteamiento del modelo

Supuesto práctico

Analysis of the Fibra data, using Fortaleza as the response variable and Algodon as the single grouping factor.

Prepared by BrailleR

Ejercicios

Ejercicios Guiados

Ejercicio guiado 1

Ejercicio guiado 2

Ejercicio guiado 3

Ejercicio Guiado 1 (Resuelto)

Analysis of the Datos data, using Duracion as the response variable and Especie as the single grouping factor.

Prepared by BrailleR

Ejercicio Guiado 2 (Resuelto)

Analysis of the Lectura data, using Tiempo_primeralectura as the response variable and Instructor as the single grouping factor.

Prepared by BrailleR

Ejercicio Guiado 3 (Resuelto)

Analysis of the Goggles data, using Attractiveness as the response variable and Alcohol as the single grouping factor.

Prepared by BrailleR

Analysis of the Goggles data, using Attractiveness as the response variable and Alcohol as the single grouping factor.

Prepared by BrailleR

Ejercicios Propuestos

Ejercicio Propuesto1

Ejercicio Propuesto 2

Ejercicio Propuesto 3

Ejercicio Propuesto 1 (Resuelto)

Solución

Ejercicio Propuesto 2 (Resuelto)

Solución

Ejercicio Propuesto 3 (Resuelto)

Solución

Analysis of the Medicamento data, using Parasitos as the response variable and Grupo as the single grouping factor.

Prepared by BrailleR