Métodos de regresión

REGRESIÓN Y CORRELACIÓN

Objetivos

• Ajustar modelos de regresión lineal simple y múltiple estimando los valores de sus parámetros
• Obtener información adicional sobre los modelos de regresión (contrastes de significación de los parámetros, test de bondad de ajuste,…)
• Contrastar las hipótesis del modelo de regresión lineal
• Ajustar un modelo de regresión cuadrático
• Estudiar la correlación entre variables.

---

Regresión

El objetivo del Análisis de regresión es determinar una función matemática sencilla que describa el comportamiento de una variable dados los valores de otra u otras variables. En el Análisis de regresión simple, se pretende estudiar y explicar el comportamiento de una variable que notamos y, y que llamaremos variable explicada, variable dependiente o variable de interés, a partir de otra variable, que notamos x, y que llamamos variable explicativa, variable independiente o variable de predicción. El principal objetivo de la regresión es encontrar la función que mejor explique la relación entre la variable dependiente y las independientes.

Para cumplir dicho objetivo, el primer paso que debe realizar el investigador, es representar las observaciones de ambas variables en un gráfico llamado diagrama de dispersión o nube de puntos. A partir de esta representación el investigador puede especificar la forma funcional de la función de regresión.

A menudo se supone que la relación que guardan la variable dependiente y las independientes es lineal. En estos casos, se utlizan los modelos de regresión lineal. Aunque las relaciones lineales aparecen de forma frecuente, también es posible considerar otro tipo de relación entre las variables, que se modelizan mediante otros modelos de regresión, como pueden ser el modelo de regresión cuadrático o parabólico o el modelo de regresión hiperbólico.

Teoría de la Regresión: Consiste en la búsqueda de una “función” que exprese lo mejor posible el tipo de relación entre dos o más variables.

Correlación

La correlación está íntimamente ligada con la regresión en el sentido de que se centra en el estudio del grado de asociación entre variables. Por lo tanto, una variable independiente que presente un alto grado de correlación con una variable dependiente será muy útil para predecir los valores de ésta última. Cuando la relación entre las variables es lineal, se habla de correlación lineal. Una de las medidas más utilizadas para medir la correlación lineal entre variables es el coeficiente de correlación lineal de Pearson.

Teoría de la Correlación: Estudia el grado de dependencia entre las variables, es decir su objetivo es medir el grado de ajuste existente entre la función teórica (función ajustada) y la nube de puntos.

En esta práctica se mostrará cómo ajustar un modelo de regresión con RStudio, prestando especial atención a los modelos de regresión lineal. Además, enseñaremos como calcular e interpretar algunas medidas de correlación.

Regresión lineal simple

La regresión lineal simple supone que los valores de la variable dependiente, a los que llamaremos y_i, pueden escribirse en función de los valores de una única variable independiente, los cuales notaremos por x_i, según el siguiente modelo lineal:

dondey , son los parámetros desconocidos que vamos a estimar.

Habitualmente, al iniciar un estudio de regresión lineal simple se suelen representar los valores de la variable dependiente y de la variable independiente de forma conjunta mediante un diagrama de dispersión para determinar si realmente existe una relación lineal entre ambas. Para realizar un diagrama de dispersión en R y RStudio utilizaremos la orden plot

 > plot(x,y)

donde x e y son los valores de las variables independiente y dependiente, respectivamente. En caso de que en el diagrama de dispersión se aprecie un patrón lineal entre las dos variables, se podrá asumir una cierta relación lineal entre ambas variables y se procederá a ajustar el modelo de regresión lineal simple.

Después de comprobar gráficamente la relación lineal entre las variables, el siguiente paso es la estimación de los valores de los parámetrosy  que aparecen en la fórmula (1) a partir de un conjunto de datos. Para ello, podemos utilizar la función lm de R, cuya sintaxis es la siguiente

>  lm(formula, data)

donde formula indica la relación que guardan la variable dependiente y la variable independiente.

Por ejemplo:

> lm(formula = y  ~ x, data=midataset)

Algunas peculiaridades sobre este argumento:

•  Las partes izquierda (variable dependiente) y derecha (variable independiente) de la fórmula vienen separadas por el símbolo ~ , que puede escribirse con la secuencia de comandos Alt + 126.
• Por defecto, la función devuelve un valor para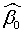. En determinadas ocasiones, interesa que dicho valor sea igual a 0, lo cual se indica en la fórmula del siguiente modo:

> lm(formula = y  ~0 +  x, data=midataset)

•  data es el conjunto de datos en el que se encuentran las variables que se utilizan en la fórmula. Este argumento es optativo, aunque es muy recomendable usarlo para una mayor claridad en la fórmula. Para ver la diferencia, observemos las siguientes llamadas a la función lm:

> lm(formula = y  ~ x, data=midataset)

> lm(formula =midataset$y  ~ midataset$x)

 Ambas llamadas son equivalentes, pero en la primera de ellas se aprecia mucho mejor cuál es la expresión que indica la relación entre las variables.

Ejemplo 1

La siguiente tabla muestra información  sobre la edad y la presión sanguínea de 10 mujeres:

Tabla1: Datos del Ejemplo 1

En primer lugar, vamos a almacenar los datos de las dos variables en dos vectores. Para ello, en primer lugar abrimos un nuevo Script en el Editor de datos de RStudio, seleccionando File/New File/R Script (o las teclas Ctrl + Shift + N) y escribimos

edad <- c(56, 42, 72,  36, 63, 47, 55, 47, 38, 42)
presion <- c(148, 126, 159, 118, 149, 130, 151, 142, 114, 141)
edad
presion

Seleccionanos las sentencias y  pulsamos la tecla Run o bien Ctrl + Enter y se muestran las siguientes órdenes en la Consola de RStudio

> edad <- c(56, 42, 72, 36, 63, 47, 55, 47, 38, 42)
> presion <- c(148, 126, 159, 118, 149, 130, 151, 142, 114, 141)
> edad
[1] 56 42 72 36 63 47 55 47 38 42
> presion
[1] 148 126 159 118 149 130 151 142 114 141

Otra opción es:

> setwd(“F:/Desktop/EJEMPLOSRS3”)
> datos <- read.table(“F:/Desktop/EJEMPLOSRS3/ejemplo1.txt”, header = TRUE)
> datos 
edad Presión
1   56    148
2   42    126
3   72   159
4   36   118
5   63   149
6   47   130
7   55   151
8   47  142
9   38  114
10  42 141

Supongamos que nuestro objetivo es determinar la edad de una mujer a partir de su presión sanguínea o, lo que es lo mismo, supongamos que la variable dependiente es edad y que la variable independiente es presión. Vamos a representar el diagrama de dispersión de las dos variables para determinar si la relación existente entre ambas puede considerarse lineal, y por tanto, tiene sentido plantear un modelo de regresión lineal simple.

> plot(presion, edad)

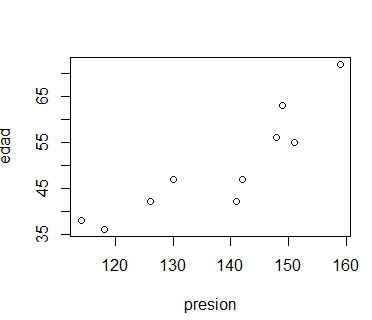Figura 1: Diagrama de Dispersión

A la vista del gráfico de dispersión, se puede asumir un cierto grado de relación lineal entre ambas variables, por lo que procedemos al ajuste del modelo lineal.

> reg_lin <- lm(edad ~ presion)
> reg_lin

Call:
lm(formula = edad ~ presion)

Coefficients:
(Intercept) presion
-43.5440 0.6774

Por defecto, la salida que muestra la función lm incluye únicamente las estimaciones para los parámetros, en nuestro caso y . Por tanto, el modelo lineal puede escribirse del siguiente modo:

edad_i = -43.5440 + 0.6774 presion_i

Estos dos parámetros pueden interpretarse del siguiente modo: –43.5440  es el valor de la edad para una persona de  presión sanguínea 0, lo cual no tiene sentido. De hecho, en multitud de ocasiones la interpretación del parámetro   no es relevante y todo el interés recae sobre la interpretación del resto de parámetros.

El parámetro es igual a 0.6774  indica que, por término medio, cada mmHg (milímetros de mercurio) de incremento en la presión sanguínea de una persona supone un incremento de 0.6774. en su edad.

Podemos obtener más información sobre el modelo de regresión que hemos calculado aplicando la función summary al objeto que contiene los datos de la regresión, al cual hemos llamado reg_lin en este ejemplo.

> summary(reg_lin)

Call:
lm(formula = edad ~ presion)

Residuals:
Min 1Q Median 3Q Max
-9.9676 -2.9835 -0.0973 3.8623 7.8394

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -43.5440 17.6126 -2.472 0.038571 *
presion 0.6774 0.1271 5.328 0.000704 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.742 on 8 degrees of freedom
Multiple R-squared: 0.7802, Adjusted R-squared: 0.7527
F-statistic: 28.39 on 1 and 8 DF, p-value: 0.000704

Esta salida contiene una información más completa sobre el análisis. Así, por ejemplo, encontramos información sobre los residuos (en el apartado Residuals), que se definen como la diferencia entre el verdadero valor de la variable dependiente y el valor que pronostica el modelo de regresión. Cuanto más pequeños sean estos residuos mejor será el ajuste del modelo a los datos y más acertadas serán las predicciones que se realicen a partir de dicho modelo.

En la tabla Coefficients encontramos los valores de los parámetros que aparecían en la salida por defecto junto a su error estándar. Cada parámetro aparece acompañado del valor de un estadístico t de Student y un p-valor que sirven para contrastar la significación del parámetro en cuestión, es decir, para resolver los siguientes contrastes de hipótesis:

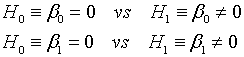Lo que se pretende mediante estos contrastes, es determinar si los efectos de la constante y de la variable independiente son realmente importantes para explicar la variable dependiente o si, por el contario, pueden considerarse nulos.

En nuestro ejemplo, los p-valores que nos ayudan a resolver estos contrastes son 0.038571 y 0.000704 ambos menores que 0.05. Así, considerando un nivel del significación del 5%, rechazamos la hipótesis nula en ambos contrastes, de manera que podemos suponer ambos parámetros significativamente distintos de 0.

Por último, en la parte final de la salida, encontramos el valor de R² (Multiple R-squared) y de R² ajustado (Adjusted R-squared), que son indicadores de la bondad del ajuste de nuestro modelo a los datos. R² oscila entre 0 y 1, de manera que, valores de R² próximos a 1 indican un buen ajuste del modelo lineal a los datos. Por otro lado, R² ajustado es similar a R², pero penaliza la introducción en el modelo de variables independientes poco relevantes a la hora de explicar la variable dependiente. Por tanto, R² ajustado <=  R². En nuestro ejemplo, R² = 0.7802 y R² ajustado = 0.7527, por lo que podemos concluir que el modelo lineal se ajusta de forma aceptable a nuestros datos. La última línea de la salida incluye un estadístico F de Snedecor y el p-valor correspondiente que se utilizan para resolver el siguiente contraste:

que se conoce habitualmente como contraste ómnibus. Mediante este contraste se comprueba si, de forma global, el modelo lineal es apropiado para modelizar los datos. En nuestro ejemplo, el p-valor asociado a este contraste es inferior a 0.05 por lo que, al 5% de significación podemos rechazar la hipótesis nula y afirmar que, efectivamente, el modelo lineal es adecuado para nuestro conjunto de datos.

R y RStudio nos permiten dibujar la recta de regresión lineal sobre el diagrama de dispersión mediante la orden abline. De este modo podemos visualizar la distancia existente entre los valores observados y los valores que el modelo pronostica (esto es, los residuos).

> plot(presion, edad)

> abline(reg_lin) 

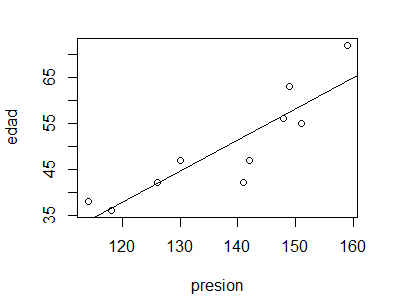Figura 2: Diagrama de Dispersión y recta de regresión

Un aspecto importante cuando se trabaja con modelos de regresión lineal es la comprobación de las hipótesis que deben de cumplirse para poder utilizar este tipo de modelos. Estas suposiciones hacen referencia a los residuos y pueden resumirse en los siguientes puntos:

• Normalidad de los residuos
• Independencia de los residuos
• Homocedasticidad (igualdad de las varianzas de los residuos)
• Linealidad de los residuos

Al aplicar la función plot sobre el objeto que contiene la información del modelo obtenemos 4 gráficos que nos ayudan para la validación del modelo. Estos gráficos son:

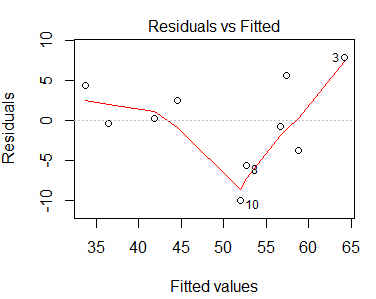
• Valores predichos frente a residuos
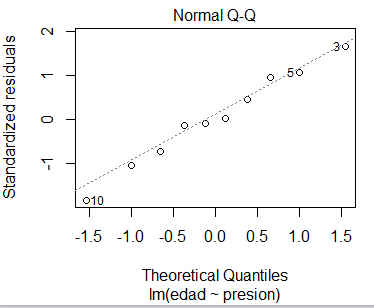
• Gráfico Q-Q de normalidad
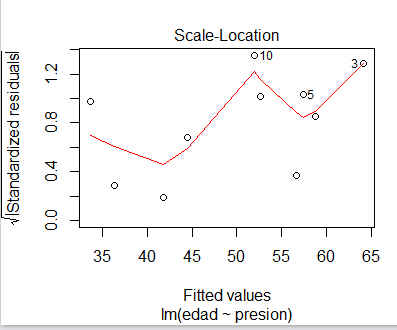
• Valores predichos frente a raíz cuadrada de los residuos estandarizados (en valor absoluto)
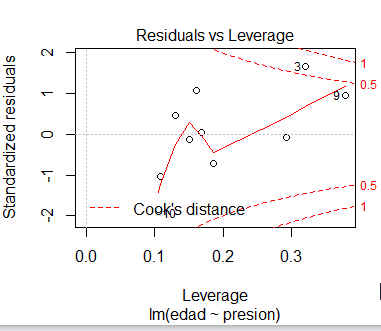
• Residuos estandarizados frente a leverages
  

> plot(reg_lin)
Hit <Return> to see next plot:

Nota: Para pasar de un gráfico al siguiente basta con hacer Clik con el ratón o presionar Enter sobre el gráfico en cuestión

   
   

Figura 3,4,5 y 6: Gráficos para la validación del modelo

Los gráficos 4 y 6 se utilizan para contrastar gráficamente la independencia, la homocedasticidad y la linealidad de los residuos. Idealmente, los residuos deben estar aleatoriamente distribuidos a lo largo del gráfico, sin formar ningún tipo de patrón.

El gráfico Q- Q, (Gráfico 5) por su parte, se utiliza para contrastar la normalidad de los residuos. Lo deseable es que los residuos estandarizados estén lo más cerca posible a la línea punteada que aparece en el gráfico.

El gráfico de residuos estandarizados frente a leverages (Gráfico 3) se utiliza para detectar puntos con una influencia importante en el cálculo de las estimaciones de los parámetros. En caso de detectarse algún punto fuera de los límites que establecen las líneas discontinuas debe estudiarse este punto de forma aislada para detectar, por ejemplo, si la elevada importancia de esa observación se debe a un error.

Los gráficos parecen indicar que los residuos son aleatorios, independientes y homocedásticos. Sin embargo, no parece que los residuos sigan una distribución Normal. Vamos a confirmar si esto es así mediante métodos analíticos.

Para comprobar la normalidad, aplicaremos a los residuos el test de normalidad de Kolmogorov-Smirnov, que en R y Rstudio se calcula a través de la función ks.test, cuya sintaxis es la siguiente:

 ks.test (x, distrib)

donde

• x es un vector numérico con los datos a los que vamos a aplicar el test (en nuestro caso, los residuos)
• distrib indica la distribución de referencia que se usará en el contraste (en nuestro caso, la distribución Normal, por lo que distrib = pnorm)

Al realizar un análisis de regresión lineal, R y RStudio guardan automáticamente los residuos en el objeto que almacena la información de la regresión (y que nosotros hemos llamado reg_lin). Para acceder a estos residuos, escribiremos $residuals a continuación del nombre del objeto que contiene la información del análisis. Por tanto, podemos realizar el contraste de Kolmogorov-Smirnov del siguiente modo:

> ks.test(reg_lin$residuals, “pnorm”)

One-sample Kolmogorov-Smirnov test

data: reg_lin$residuals
D = 0.3935, p-value = 0.06608
alternative hypothesis: two-sided

Los resultados del test nos confirman lo que se intuía en el gráfico Q-Q: a un 10% de significación los residuos no siguen una distribución normal, puesto que el p-valor que se obtiene (0.06608) es menor que 0.1. Sin embargo para una significación del 5% no se debe rechazar la hipótesis nula.

Por último, contrastemos la independencia de los residuos mediante el test de Durbin-Watson. La función que calcula este test se llama dwtest y se encuentra dentro del paquete lmtest. Por lo que lo primero que tenemos que hacer es instalar y cargar dicho paquete. Puedes encontrar más información sobre la instalación y cargas de paquetes en la práctica 2.

Para ello elegir en el menú principal Tools/Install Packages

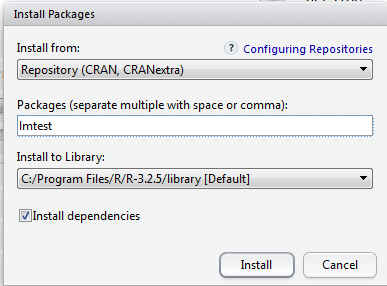Figura 7: Tools/Install Packages

En la consola de RStudio se muestra

> install.packages(“lmtest”)
trying URL ‘https://cran.rstudio.com/bin/windows/contrib/3.2/lmtest_0.9-34.zip’
Content type ‘application/zip’ length 283498 bytes (276 KB)
downloaded 276 KB

package ‘lmtest’ successfully unpacked and MD5 sums checked

The downloaded binary packages are in
C:\Users\Usuario\AppData\Local\Temp\RtmpMtPgAz\downloaded_packages

A continuación se debe Cargar el paquete, para ello desde el panel de paquetes simplemente se selecciona dicho paquete

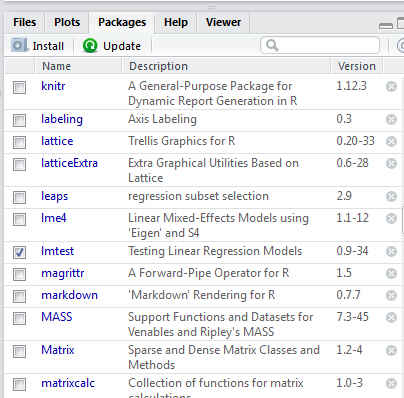Figura 8: Cargar el paquete lmtest

En la consola de RStudio se muestra
> library(“lmtest”, lib.loc=”C:/Program Files/R/R-3.2.5/library”)
Loading required package: zoo

Attaching package: ‘zoo’

The following objects are masked from ‘package:base’:

as.Date, as.Date.numeric

También se puede utilizar las instrucciones

> install.packages(“lmtest”)   #Instalación del paquete

> library(lmtest)  #Carga del paquete

Ahora ya podemos utilizar la función dwtest, cuya sintaxis es

dwtest (formula)

donde

• formula indica la relación que guardan la variable dependiente y la independiente, y debe coincidir con la que se ha empleado en la función lm.
  

> dwtest(edad~presion)

Durbin-Watson test

data: edad ~ presion
DW = 1.9667, p-value = 0.5879
alternative hypothesis: true autocorrelation is greater than 0

En este caso, con un p-valor de 0.5879 no podemos rechazar la hipótesis de que los residuos son independientes.

Regresión lineal múltiple

El modelo de regresión múltiple es la extensión a k variables explicativas del modelo de regresión simple. En general, una variable de interés y depende de varias variables x₁, x₂, …, x_k y no sólo de una única variable de predicción x. Por ejemplo, para estudiar la contaminación atmosférica, parece razonable considerar más de una variable explicativa, como pueden la temperatura media anual,  el número de fábricas, el número de habitantes, etc. Además de las variables observables, la variable de interés puede depender de otras desconocidas para el investigador. Un modelo de regresión representa el efecto de estas variables en lo que se conoce como error aleatorio o perturbación.

Un modelo de regresión teórico en el que las variables se pueden relacionar mediante una función de tipo lineal, podemos expresarlo de la siguiente forma:

Figura 9: Expresión del modelo de regresión múltiple

donde

• y es la variable de interés que vamos a predecir, también llamada variable respuesta o variable dependiente

• x₁, x₂, …, x_k  son  variables independientes, explicativas o de predicción

•  β₁, β₂, …, β_k son los parámetros desconocidos que vamos a estimar

•  ε es el error aleatorio o perturbación, que representa el efecto de todas las variables que pueden afectar a la variable dependiente y no están incluidas en el modelo de regresión.

En R y Rstudio, el paso de un modelo de regresión lineal simple a un modelo de regresión lineal múltiple es muy sencillo: basta con añadir variables independientes al argumento formula de la función lm separadas por el signo +. Veamos un ejemplo:

Ejemplo 2

Se desea conocer el gasto de alimentación mensual de una familia en función del ingreso mensual, el tamaño de la familia y el número de hijos en la universidad. Los datos se muestran en la tabla adjunta

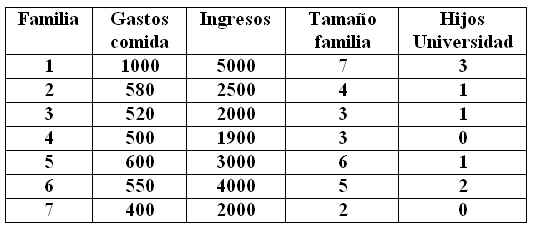Tabla 2: Gastos de alimentación mensual

Vamos a ajustar un nuevo modelo de regresión lineal múltiple que explique el gasto de alimentación mensual en función de las variables descritas anteriormente. En primer lugar, vamos a crear cuatro vectores numéricos, uno para cada variable

> gastos <- c(1000, 580, 520, 500, 600, 550, 400)
> ingresos <- c(50000, 2500, 2000, 1900, 3000, 4000, 2000)
> tamaño <- c(7, 4, 3, 3, 6, 5, 2)
> hijosU <- c(3,1,1,0,1,2,0)

Y vamos a agrupar la información relativa a las 4 variables de las que disponemos en un data frame al que pondremos por nombre datos2:

> datos2 <- data.frame(gastos, ingresos, tamaño, hijosU)

Comprobemos que, efectivamente, el data frame que hemos creado contiene la información sobre las 4 variables:
> datos2

gastos ingresos tamaño hijosU
1 1000 50000 7 3
2 580 2500 4 1
3 520 2000 3 1
4 500 1900 3 0
5 600 3000 6 1
6 550 4000 5 2
7 400 2000 2 0
A continuación ajustamos el modelo de regresión lineal múltiple

> reg_lin_mul <- lm(gastos ~ ingresos + tamaño + hijosU)
> summary(reg_lin_mul)

Call:
lm(formula = gastos ~ ingresos + tamaño + hijosU)

Residuals:
1 2 3 4 5 6 7
1.216 48.164 29.125 15.209 -10.134 -35.402 -48.178

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.590e+02 6.291e+01 5.706 0.0107 *
ingresos 7.247e-03 1.802e-03 4.021 0.0276 *
tamaño 3.734e+01 2.046e+01 1.825 0.1655
hijosU 5.359e+00 4.061e+01 0.132 0.9034
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 48.57 on 3 degrees of freedom
Multiple R-squared: 0.9677, Adjusted R-squared: 0.9353
F-statistic: 29.93 on 3 and 3 DF, p-value: 0.009772

En Coefficients se muestran los parámetros estimados de regresión β₀ = 3.590e, β_{01/sub>=7.247e, β2 =  3.734e y β3 =  5.359e
La ecuación de regresión ajustada está dada por:}

gastos_i = 3.590e⁰² + 7.247e^-03 * ingresos_i + 3.734e⁰¹ * tamaño_i + 5.359 *hijosU_i .

• Los gastos estimados son iguales a 3.590e⁰² euros (constantes las demás variables)
• Por cada mil euros de ingresos, los gastos aumentan en 7.247e^-03, supuesto que permanecen constantes las otras variables.
• Por cada aumento del tamaño de la familia en un familiar, los gastos estimados aumentan en 3.734e⁰¹e, suponiendo que se mantienen constantes las otras variables
• Por cada aumento del número de hijos estudiando en la Universidad, los gastos estimados aumentan en 5.359, suponiendo que se mantienen constantes las otras variables

Tanto la interpretación como la comprobación de la significación de los parámetros se realizan de forma similar al caso en que se cuenta con una única variable independiente. Igualmente, la validación se lleva a cabo del mismo modo que para la regresión lineal simple.

El p-valor asociado al contraste (0.009772) es menor que a = 0.05 , por lo que rechazamos la hipótesis nula. Esto implica que al menos una de las variables independientes contribuye de forma significativa a la explicación de la variable respuesta.

Para las variables tamaño familiar  y número de hijos en la Universidad, los p-valores son 0.1655 y 0.9034, respectivamente. Ambos mayores que 0.05, por lo que no rechazamos la hipótesis nula de significación de ambas variables. Estas variables no son válidas para predecir los gastos alimentación mensual de una familia y por tanto se pueden eliminar del modelo.

Con respecto a las representaciones gráficas, se pueden representar gráficos de dispersión de la variable dependiente con respecto a cada una de las variables independientes mediante el comando plot, como se ha mostrado anteriormente.

Correlación lineal

Para calcular el coeficiente de correlación lineal entre dos variables en R y RStudio utilizan la orden cor, cuya sintaxis es la siguiente:

cor (x, y, method = c(“pearson” “kendall”, “spearman”))

donde

• x hace referencia a la primera de las variables
• y hace referencia a la segunda de las variables
• method indica el método que se va a utilizar para calcular el coeficiente de correlación lineal. Las posibles opciones son: pearson (método que se considera por defecto), kendall y spearman. Puedes encontrar más información sobre estos 3 métodos de cálculo del coeficiente de correlación lineal en el siguiente enlace: http://www.napce.org/documents/research-design-yount/22_correlation_4th.pdf

Ejemplo 3

Vamos a calcular el coeficiente de correlación lineal de Pearson entre las variables gastos e ingresos:
> cor(gastos, ingresos)
[1] 0.9465675

El 94.65% de los gastos de alimentación mensual de una familia es explicada por sus ingresos mensuales.

También es posible calcular de forma simultánea la correlación entre un conjunto de variables almacenada en un data frame. Por ejemplo:

> cor(datos2)

              gastos   ingresos   tamaño        hijosU
gastos 1.0000000 0.9465675 0.8457301 0.8627733
ingresos 0.9465675 1.0000000 0.6886470 0.7885404
tamaño 0.8457301 0.6886470 1.0000000 0.8416254
hijosU 0.8627733 0.7885404 0.8416254 1.0000000

En este caso, en lugar de un único valor numérico, la función cor devuelve una matriz simétrica con las correlaciones entre las variables.

Habitualmente, se está interesado en contrastar si la correlación lineal entre pares de variables puede considerarse 0 o no. Es decir, se quiere resolver el contraste

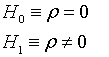donde ρ representa el coeficiente de correlación lineal. Este contraste se resuelve en R y Rstudio usando la función cor.test

cor.test(x, y, alternative = c(“two.sided”, “less”, “greater”), method = c(“pearson”, “kendall”, “spearman”), conf.level = 0.95)

donde

• x, y, method son los mismos parámetros que se usan en la función cor
• alternative indica cuál va a ser la hipótesis alternativa del contraste. Por defecto se considera que la hipótesis alternativa es  (two.sided), aunque también pueden considerarse las hipótesis alternativas  (less) o  (greater).
• conf.level indica el nivel de confianza que se usará en el contraste (por defecto, 0.95)

En el Ejemplo 3 vamos a contrastar la significación de la correlación entre las variables gastos e ingresos:

> cor.test (gastos, ingresos)

Pearson’s product-moment correlation
data: gastos and ingresos
t = 6.5629, df = 5, p-value = 0.001231
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.6738267 0.9922965
sample estimates:
cor
0.9465675

El p-valor asociado a este contraste es de 0.001231 < 0.05, por lo que rechazamos la hipótesis de que la correlación lineal entre estas dos variables sea 0.

Otros modelos de regresión: regresión cuadrática

Aunque los modelos de regresión lineal (tanto simple como múltiple) funcionan bien en una amplia mayoría de situaciones, en ocasiones es necesario considerar modelos más complejos para conseguir un mejor ajuste a los datos.

Un ejemplo de este tipo de modelos es la regresión cuadrática. El modelo más sencillo de regresión cuadrática es el siguiente:

Para ajustar un modelo de regresión cuadrático en R y RStudio basta con indicar en el argumento formula de la función lm que una de las variables independientes está elevada al cuadrado mediante el símbolo ^2.

Ejemplo 4

Calcular los valores de las estimaciones , y    en el modelo de regresión:

> lm(formula = gastos ~ ingresos + tamaño^2)

Call:
lm(formula = gastos ~ ingresos + tamaño^2)

Coefficients:
(Intercept) ingresos tamaño
3.562e+02 7.374e-03 3.915e+01

gastos = 3.562e+02 + 7.374e-03 * ingresos + 3.915e+01 * tamaño²

---

---

---

Ejercicios

Ejercicios Guiados

Ejercicio guiado

Una empresa fabricante de cereales está interesada en conocer cómo afecta a las ventas del producto, la publicidad en la televisión, en la radio y en los periódicos. Para ello, realiza un estudio de los gastos mensuales (en miles de euros) correspondientes a los últimos 20 meses. Estos datos se presentan en la siguiente tabla.

 Tabla3: Datos del Ejemplo Guiado 1

a) Crea 4 vectores numéricos, de manera que cada uno contenga los datos de una columna y un data frame llamado Cereales con los 4 vectores que acabas de crear

b) Representa el diagrama de dispersión de las ventas y la publicidad en tv

c) Escribe la recta de regresión lineal que surge de considerar las ventas como variable dependiente y la publicidad en tv como variable independiente

d) ¿Son significativos los dos parámetros anteriores? ¿Qué puede decirse del ajuste del modelo a los datos?

e) ¿Cuál sería la recta de regresión en el caso de que se considere un modelo de regresión lineal simple sin constante?

f) Calcula el coeficiente de correlación lineal de Pearson entre ambas variables. ¿Es significativa esta correlación?

g) ¿Cuál sería la recta de regresión lineal si se incluye la publicidad en radio como variable independiente?

h) Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación

i) Contrastar la significación del modelo propuesto

j) ¿Puede eliminarse alguna variable del modelo? Realiza los contrastes de significación individuales

k) Coeficiente de determinación

---

Ejercicio Guiado (Resuelto)

a) Crea 4 vectores numéricos, de manera que cada uno contenga los datos de una columna y un data frame llamado Cereales con los 4 vectores que acabas de crear

> ventas <- c(10,12,11,13,12,14,16,12,14,11,10,19,8.5,8,9,13,16,18,20,22)

> tv <- c(13,14,15,17,17.5,13,14.5,9,8,9,8,10,17,18,18.5,19,20,20,13,14)

> radio <-c(56,55,60,65,69,67,68,67,97,66,65,60,70,110,75,80,85,90,56,55)

> periodicos <- c(40,40,42,50,40,44,40,44,46,46,45,110,30,50,45,40,80,90,90, 110)

> cereales <- data.frame(ventas, tv, radio, periodicos)

Comprobemos que los datos se han guardado correctamente

> cereales

  ventas tv radio periodicos
1    10.0 13.0    56         40
2    12.0 14.0    55         40
3    11.0 15.0    60         42
4    13.0 17.0    65         50
5    12.0 17.5    69         40
6    14.0 13.0    67         44
7    16.0 14.5    68         40
8    12.0  9.0    67         44
9    14.0  8.0    97         46
10   11.0  9.0    66         46
11   10.0  8.0    65         45
12   19.0 10.0    60        110
13    8.5 17.0    70         30
14    8.0 18.0   110         50
15    9.0 18.5    75         45
16   13.0 19.0    80         40
17   16.0 20.0    85         80
18   18.0 20.0    90         90
19   20.0 13.0    56         90
20   22.0 14.0    55        110

Otra opción es, Seleccionar en el menú principal: Session/Set Working Directory/Choose Directory (Ctrl+Shift+H) y en la Consola de RStudio se muestra la siguiente orden:

> setwd(“F:/Desktop/EJEMPLOSRS3”)

A continuación leemos el fichero utilizando read.table
> cereales <- read.table(“F:/Desktop/EJEMPLOSRS3/cereales.txt”, header = TRUE).

b) Representa el diagrama de dispersión de las ventas y la publicidad en tv

> plot(cereales$ventas, cereales$tv)

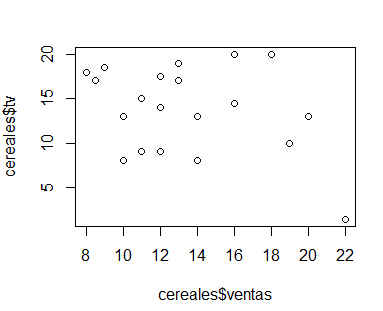Figura 10: Diagrama de Dispersión

c) Escribe la recta de regresión lineal que surge de considerar las  ventas como variable dependiente y la publicidad en tv como  variable independiente

> reg_lin <- lm(ventas ~ tv, data = cereales)
> reg_lin

Call:
  lm(formula = ventas ~ tv, data = cereales)

Coefficients:
  (Intercept)           tv  
14.02705     -0.04188

Por tanto, la recta de regresión es:

ventas_i = 14.0275 -0.04188 tv_i

d) ¿Son significativos los dos parámetros anteriores? ¿Qué puede decirse del ajuste del modelo a los datos?

> summary(reg_lin)

Call:
  lm(formula = ventas ~ tv, data = cereales)

Residuals:
  Min      1Q  Median      3Q     Max
-5.2732 -2.8582 -0.8046  2.6378  8.5593

Coefficients:
  Estimate Std. Error t value Pr(>|t|)    
(Intercept) 14.02705    3.47625   4.035 0.000777 ***
  tv          -0.04188    0.23342  -0.179 0.859609    
—
  Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.063 on 18 degrees of freedom
Multiple R-squared:  0.001785,    Adjusted R-squared:  -0.05367
F-statistic: 0.03219 on 1 and 18 DF,  p-value: 0.8596

Los p-valores asociados al contraste t de Student para ambos parámetros (0.000777 y 0.859609). El intercepto tiene un p-valor menor que 0.05, por lo es significativamente distintos de 0 y  el p-valor correspondiente al parámetro publicidad en tv tiene un p-valor mayor que 0.05, por lo tanto no es significativamente distintos de 0.

Por otra parte, el valor de R² (0.001785) nos lleva a concluir que el ajuste del modelo a los datos es muy malo.

e) ¿Cuál sería la recta de regresión en el caso de que se considere un modelo de regresión lineal simple sin constante?

> reg_lin2 <- lm(ventas ~ 0 + tv, data = cereales)
> reg_lin2

Call:
  lm(formula = ventas ~ 0 + tv, data = cereales)

Coefficients:
  tv  
0.8673

En este caso, el modelo sería:   ventas_i = 0.8673 tv_i

f) Calcula el coeficiente de correlación lineal de Pearson entre ambas variables. ¿Es significativa esta correlación?

> cor.test(cereales$ventas, cereales$tv)

Pearson’s product-moment correlation

data:  cereales$ventas and cereales$tv
t = -0.17942, df = 18, p-value = 0.8596
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.4758758  0.4078947
sample estimates:
cor
-0.04225282

Puesto que el p-valor del contraste es de 0.8596 y, por lo tanto, mayor que 0.05, podemos concluir que la correlación no es significativa, y podría considerarse 0.

g) ¿Cuál sería la recta de regresión lineal si se incluye la publicidad en radio como variable independiente?

> reg_lin_mul <- lm(ventas ~ tv + radio, data = cereales)
> reg_lin_mul

Call:
lm(formula = ventas ~ tv + radio, data = cereales)

Coefficients:
(Intercept)           tv        radio
17.38543      0.03823     -0.06370

En este caso, la recta de regresión lineal múltiple podría escribirse como: ventas_i = 17.38543 + 0.03823 tv_i – 0.06370 radio_i

h) Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación

> reg_lin_mul2 <- lm(ventas ~ tv + radio + periodicos, data = cereales)
> reg_lin_mul2

Call:
lm(formula = ventas ~ tv + radio + periodicos, data = cereales)

Coefficients:
(Intercept)           tv        radio   periodicos
8.775929    -0.008508    -0.038358     0.133460

La ecuación de la recta de regresión ajustada es: ventas_i = 8.775929 – 0.008508 tv_i  – 0.038358 radio_i + 0.133460 periodicos_i

Las ventas estimadas son de 8775.929 euros si no se produce inversión en ninguno de los tres tipos de publicidad.

Por cada mil euros invertidos en publicidad en televisión las ventas esperadas disminuyen en 8.508 euros, supuesto que permanecen constantes las otras variables

Por cada mil euros invertidos en publicidad en radio las ventas esperadas disminuyen en 38.358 euros, supuesto que permanecen constantes las otras variables

Por cada mil euros invertidos en publicidad en periódicos las ventas esperadas aumentan en 133.460 euros, supuesto que permanecen constantes las otras variables.

A la vista de estos resultados parece únicamente recomendable la publicidad en periódicos.

i) Contrastar la significación del modelo propuesto

> summary(reg_lin_mul2)

Call:
  lm(formula = ventas ~ tv + radio + periodicos, data = cereales)

Residuals:
  Min      1Q  Median      3Q     Max
-3.0764 -1.5515  0.0564  0.9941  4.6174

Coefficients:
  Estimate Std. Error t value Pr(>|t|)    
(Intercept)  8.775929   2.967301   2.958  0.00926 **
  tv          -0.008508   0.133711  -0.064  0.95005    
radio       -0.038358   0.036079  -1.063  0.30349    
periodicos   0.133460   0.020365   6.554 6.64e-06 ***
  —
  Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.187 on 16 degrees of freedom
Multiple R-squared:  0.7428,    Adjusted R-squared:  0.6946
F-statistic:  15.4 on 3 and 16 DF,  p-value: 5.61e-05

 Mediante los contrastes de hipótesis:

podemos determinar si los efectos de la constante y de las variables independientes son realmente importantes para explicar la variable dependiente o si, por el contario, pueden considerarse nulos.

En nuestro ejemplo, el p-valor 5.61e-05 es menor que 0.05. Considerando un nivel del significación del 5%, rechazamos la hipótesis nula, de manera que podemos suponer que al menos una de las variables independiente contribuye de forma significativa a la explicación de la variable respuesta.

j) ¿Puede eliminarse alguna variable del modelo? Realiza los contrastes de significación individuales 

Realizamos tres contrastes de hipótesis, uno para cada coeficiente de cada variable explicativa

Los p-valores asociados a cada uno de los contrastes de las variable independientes son 0.95005, 0.30349 y 6.64e-06 para publicidad en tv, radio y periódicos, respectivamente. Los p-valores para publicidad en tv y en radio son mayores que 0.05, por lo que no rechazamos la hipótesis nula de significación de ambas variables. Estas variables no son válidas para predecir las ventas de cereales y por tanto las eliminamos del estudio

k) Coeficiente de determinación

El coeficiente de determinación es igual a 0.7428 y el coeficiente de determinación corregido es  0.6946. En este caso no se aprecian grandes diferencias entre ambos coeficientes. El 74.28% de la variación en las ventas de cereales se explican por su relación lineal con el modelo propuesto. Este valor del 74.28% lo podemos considerar satisfactorio.

Solución:

ventas <- c(10,12,11,13,12,14,16,12,14,11,10,19,8.5,8,9,13,16,18,20,22)
tv <- c(13,14,15,17,17.5,13,14.5,9,8,9,8,10,17,18,18.5,19,20,20,13,14)
radio <-c(56,55,60,65,69,67,68,67,97,66,65,60,70,110,75,80,85,90,56,55)
periodicos <- c(40,40,42,50,40,44,40,44,46,46,45,110,30,50,45,40,80,90,90, 110)
cereales <- data.frame(ventas, tv, radio, periodicos)
cereales
plot(cereales$ventas,cereales$tv)
reg_lin <- lm(ventas ~ tv, data = cereales)
reg_lin
summary(reg_lin)
reg_lin2 <- lm(ventas ~ 0 + tv, data = cereales)
reg_lin2
cor(cereales$ventas, cereales$tv)
cor.test(cereales$ventas, cereales$tv)
reg_lin_mul <- lm(ventas ~ tv + radio, data = cereales)
reg_lin_mul
reg_lin_mul2 <- lm(ventas ~ tv + radio + periodicos, data = cereales)
reg_lin_mul2
summary(reg_lin_mul2)

---

---

Ejercicios Propuestos

Ejercicio Propuesto

Con el objetivo de realizar un estudio de mercado sobre el precio de los pisos, se seleccionan de forma aleatoria una muestra estratificada representativa de los distintos barrios de una ciudad. Los datos sobre el precio de los pisos en miles de euros, la superficie en m² y la antigüedad del inmueble en años, se muestran en la siguiente tabla.

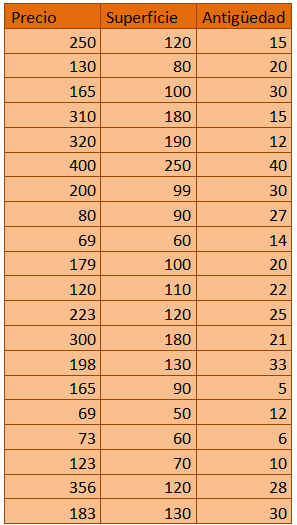
 Tabla4. Datos del Ejemplo Propuesto 1

Se pide:

a) Crear un data frame de nombre pisos que almacene los datos del ejemplo propuesto

b) Dibujar el diagrama de dispersión de las variables precio y superficie y determinar si puede existir una cierta relación lineal entre ambas

c) ¿Cuál es la recta de regresión lineal simple que considera a la precio como variable dependiente y a la superficie como variable independiente? Interpreta los parámetros de esa recta

d) ¿Son significativos estos parámetros? ¿Qué puede decirse del ajuste del modelo a los datos?

e) ¿Cuál es la correlación lineal de Pearson entre ambas variables? ¿Es significativa?

f) ¿Cuál es la recta de regresión lineal si se considera también como variable independiente la antigüedad?

g) Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación

h) Contrastar la significación del modelo propuesto

i) ¿Puede eliminarse alguna variable del modelo? Razona la respuesta

j) Coeficiente de determinación y de determinación corregido. Interpretación

k) Calcular los valores de las estimaciones , y    en el modelo de regresión: 

---

Ejercicio Propuesto (Resuelto)

 a) Crear un data frame de nombre pisos que almacene los datos del ejemplo propuesto

> pisos

precio superficie antiguedad
1     250        120         15
2     130         80         20
3     165        100         30
4     310        180         15
5     320        190         12
6     400        250         40
7     200         99         30
8      80         90         27
9      69         60         14
10    179        100         20
11    120        110         22
12    223        120         25
13    300        180         21
14    198        130         33
15    165         90          5
16     69         50         12
17     73         60          6
18    123         70         10
19    356        120         28
20    183        130         30

b) Dibujar el diagrama de dispersión de las variables precio y superficie y determinar si puede existir una cierta relación lineal entre ambas

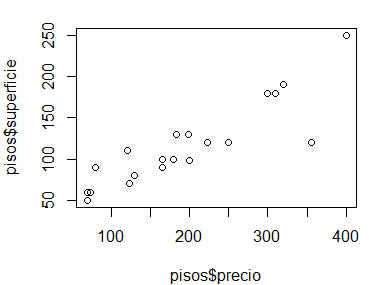
En el gráfico se aprecia un cierto patrón lineal entre las variables, aunque esto debe confirmarse mediante métodos analíticos.

c) ¿Cuál es la recta de regresión lineal simple que considera a la precio como variable dependiente y a la superficie como variable independiente? Interpreta los parámetros de esa recta

Call:
lm(formula = precio ~ superficie, data = pisos)

Coefficients:
(Intercept) superficie
-7.813 1.747

La recta de regresión lineal simple es: precio = -7.813 + 1.747 superficie

Los dos parámetros de la recta se interpretan del siguiente modo: -7.8136 es el precio esperado para un piso que tiene 0 de superficie (que no tiene ningún sentido). Por otra parte, por cada metro cuadrado de incremento en la superficie de un piso, se espera un aumento en el precio del piso de 1747 euros.

d) ¿Son significativos estos parámetros? ¿Qué puede decirse del ajuste del modelo a los datos?

Call:
lm(formula = precio ~ superficie, data = pisos)

Residuals:
Min 1Q Median 3Q Max
-69.436 -25.020 -3.061 12.960 154.147

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.8131 27.5629 -0.283 0.78
superficie 1.7472 0.2181 8.012 2.4e-07 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 47.92 on 18 degrees of freedom
Multiple R-squared: 0.781, Adjusted R-squared: 0.7688
F-statistic: 64.19 on 1 and 18 DF, p-value: 2.399e-07

Considerando un nivel de significación del 5%, sólo es significativamente distintos de 0 el parámetro superficie, ya que su p-valor (2.4e-07 ) es inferior a  0.05.

El ajuste del modelo a los datos es aceptable, ya que el valor de R² es de 0.781

e) ¿Cuál es la correlación lineal de Pearson entre ambas variables? ¿Es significativa?

Pearson’s product-moment correlation

data:  pisos$precio and pisos$superficie
t = 8.012, df = 18, p-value = 2.399e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7245916 0.9534095
sample estimates:
     cor
0.883743

El coeficiente de correlación lineal de Pearson entre las dos variables es de 0.883743

Con un p-valor de 2.399e-07 < 0.05, rechazamos la hipótesis de que el coeficiente de correlación lineal de Pearson entre ambas variables pueda considerarse 0.

f) ¿Cuál es la recta de regresión lineal si se considera también como variable independiente la antigüedad?

Call:
  lm(formula = precio ~ antiguedad, data = pisos)

Coefficients:
  (Intercept)   antiguedad  
110.423        4.107 

En este caso, la recta de regresión lineales: precio = 110.423 + 4.107 antiguedad

g) Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación

Call:
  lm(formula = precio ~ superficie + antiguedad, data = pisos)

Coefficients:
  (Intercept)   superficie   antiguedad  
-6.82133      1.75516     -0.09239 

En este caso, la recta de regresión lineal múltiple es: precio = -6.82133 + 1.75516 superficie – 0.09239 antiguedad

h) Contrastar la significación del modelo propuesto

Coefficients:
  Estimate Std. Error t value Pr(>|t|)    
(Intercept) -6.82133   31.73892  -0.215    0.832    
superficie   1.75516    0.25176   6.972 2.25e-06 ***
  antiguedad  -0.09239    1.32791  -0.070    0.945    
—
  Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 49.3 on 17 degrees of freedom
Multiple R-squared:  0.7811,    Adjusted R-squared:  0.7553
F-statistic: 30.32 on 2 and 17 DF,  p-value: 2.47e-06

El único parámetro significativamente distinto de cero es superficie (P-valor = 2.25e-06)

i) ¿Puede eliminarse alguna variable del modelo? Razona la respuesta

Se puede eliminar la variable antiguedad ya que su p-valor  es 0.945 > α = 0.05, por lo que no rechazamos la hipótesis nula de significación de dicha variable. Esta variable no es válida para predecir el precio de los pisos

j) Coeficiente de determinación y de determinación corregido. Interpretación

El coeficiente de determinaciónes 0.7811 y el de determinación corregido es 0.7553. No se aprecian grandes diferencias entre ambos coeficientes.

El 78.11% de la variación en el precio de los pisos se explican por su relación lineal con el modelo propuesto. El valor de este coeficiente es satisfactorio.

k) Calcular los valores de las estimaciones , y    en el modelo de regresión: 

Call:
  lm(formula = precio ~ superficie + antiguedad^2, data = pisos)

Coefficients:
  (Intercept)   superficie   antiguedad  
-6.82133      1.75516     -0.09239 

En este caso, el modelo de regresión cuadrático puede escribirse del siguiente modo:

precio = -6.82133 + 1.75516 superficie – 0.09239 antiguedad

 

Solución del Ejercicio Propuesto

Autora: Ana María Lara Porras. Universidad de Granada. (2017)