INTERVALOS DE CONFIANZA

Objetivos

- Calcular e interpretar intervalos de confianza para la media en una población Normal con varianza conocida
- Calcular e interpretar intervalos de confianza para la media en una población Normal con varianza desconocida
- Calcular e interpretar intervalos de confianza para la proporción
- Calcular e interpretar intervalos de confianza para la diferencia de medias en dos poblaciones normales independientes con varianzas desconocidas
  - Suponiendo que las varianzas, aun siendo desconocidas, son iguales en las dos poblaciones
  - Suponiendo que las varianzas son diferentes en las dos poblaciones
Calcular e interpretar intervalos de confianza para la diferencia de medias en dos poblaciones normales relacionadas
Calcular e interpretar intervalos de confianza para la diferencia de proporciones.

Introducción

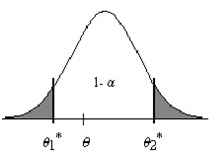
El objetivo de la estimación mediante intervalos de confianza o estimación confidencial es la determinación de dos valores, $ \theta_{1}^{*} $ y $ \theta_{2}^{*} $, que verifiquen $ \theta_{1}^{*} < \theta_{2}^{*} $, tales que, al constituirse en intervalo $ ( \theta_{1}^{*} , \theta_{2}^{*} ) $ contengan, con una probabilidad prefijada, el verdadero valor del parámetro que deseamos estimar. De forma gráfica, un intervalo de confianza puede representarse del siguiente modo:

Figura 1: Representación gráfica de un I.C.

$ P [ \theta_{1}^{*} \leq \theta \leq \theta_{2}^{*}] = 1-\alpha $, para algún $ \alpha > 0 $, entonces se puede decir que $ \theta_{1}^{*} $ y $ \theta_{2}^{*} $determinan un intervalo que tiene la probabilidad $ 1 – α $ de contener al parámetro poblacional $ \theta $

donde

$ 1 – \alpha $: Recibe el nombre de coeficiente de confianza o nivel de confianza. Es la probabilidad de que el intervalo de confianza contenga el verdadero valor del parámetro poblacional $ θ $
$ \alpha $: Es un valor comprendido entre 0 y 1, $ 0 < α < 1 $, (usualmente próximo a 0), que indica el riesgo de que el intervalo de confianza no contenga el valor del parámetro poblacional a estimar, $ θ $. Por lo que $ α $ recibe el nombre de riesgo del error del intervalo, nivel del error del intervalo o nivel de significación del intervalo.
$ \theta _{1}^{*} $ y $ \theta _{2}^{*} $: Son los valores que delimitan el intervalo de confianza y reciben el nombre de límite superior y límite inferior del intervalo, respectivamente. La diferencia entre el límite superior y el límite inferior de un intervalo, $ \theta _{2}^{*} – \theta _{1}^{*} $ se conoce como amplitud del intervalo.

Para la construcción de un intervalo de confianza, lo deseable es maximizar el nivel de confianza asociado al intervalo o equivalentemente minimizar el nivel de significación y conseguir una amplitud lo más pequeña posible.

Intervalo de confianza para la media en una población normal con varianza conocida

El intervalo de confianza para la media de una variable continua con el valor de la varianza de dicha variable conocida en toda la población es el intervalo menos usual.

Para estimar la media poblacional $ \mu $ de una población Normal de media $ \mu $ (desconocida) y de varianza $ \sigma^{2} $ (conocida), $ N(\mu, \sigma^{2}) $, se selecciona una muestra aleatoria $ X_1, X_2, \cdots, X_n $; de tamaño $ n $ de valores de una variable aleatoria de esta población y se calcula su media muestral, como mejor estimador puntual de $ \mu $. La construcción del intervalo de confianza se hace tomando como base este estimador. Para calcular un intervalo de confianza para $ \mu $ partimos de la variable aleatoria

$ Z= \displaystyle \frac {\overline{X}-μ }{ σ / \sqrt {n}} $

Expresión 1: Expresión de la variable aleatoria

que sigue una distribución normal de media 0 y desviación típica 1. Buscamos los cuantiles de esta distribución tales que

$ P \left [ – z_{1- α/2} \leq \displaystyle \frac {\overline{X}-μ }{σ / \sqrt {n}} \leq z_{1-α/2} \right] = 1-α $

Expresión 2: Obtención del cuantil z_{{1 – α/2}}

O, equivalentemente,

- $ P \left [ \overline {X} – z_{1-α/2} \displaystyle \frac { σ} { \sqrt{n }} \leq μ \leq \overline {X} + z_{1-α/2} \displaystyle \frac { σ} { \sqrt{n}} \right] = 1-α $
  
  Expresión 3: Obtención del cuantil z_{{1 – α/2}}

Por lo tanto, el intervalo de confianza que debemos calcular es

$ \left [ \overline {X} – z_{1-α/2} \displaystyle \frac { \sigma} { \sqrt{n}} , \overline {X} + z_{1-α/2} \displaystyle \frac { \sigma} { \sqrt{n}} \right] $

Expresión 4: Intervalo de confianza (varianza conocida)

Nota: R-Commander no calcula este tipo de intervalos, por lo que tendremos que realizarlo mediante código

Supuesto Práctico 1

El archivo empleados.xls nos informa de la edad, altura, peso, sexo y posesión de coche de 100 empleados de una empresa. Suponiendo la normalidad de la variable Altura, calcular el intervalo de confianza sobre la altura media poblacional a un 95% de confianza, sabiendo que la varianza poblacional es 6.

Solución

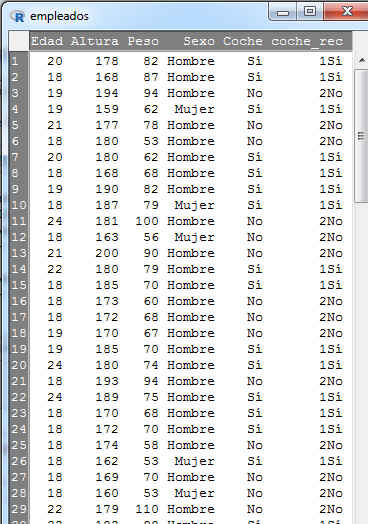
Vamos a trabajar con la base de datos empleados.xls que contiene las variables edad, altura, peso, sexo y posesión de coche, medidas en los empleados de una empresa.

Recordemos, que para poder utilizar R Commander hemos de instalar y cargar el paquete Rcmdr, que no viene incluido por defecto en R. Como dicho paquete ya está instalado, únicamente tenemos que cargarlo. Para ello, en el menú principal se selecciona Paquetes/Cargar paquete.. y en la ventana que se despliega, se selecciona el paquete Rcmdr y se pulsa Ok.

Una vez activado R Commander, pasamos a importar datos de Excel a R-Commander mediante el Menú: Datos/Importar datos/desde un archivo de Excel.

Se muestra la siguiente ventana, donde en Introducir el nombre del conujto de datos ponemos empleados

Se pulsa Aceptar y se selcciona el fichero

Pulsamos Abrir

Seleccionamos Visualizar conjunto de datos y se muestra

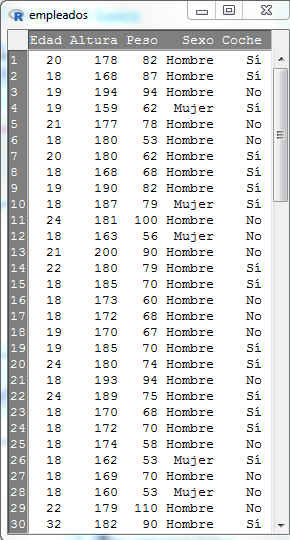
A continuación guardamos el archivo (Datos/Conjunto de datos activo/Guardar el conjunto de datos activo)

como fichero Empleados.RData.

Introducimos en R los datos, que proporciona el enunciado, relativos al nivel de significación y la varianza poblacional de la variable.

alpha<- 0.05 (Pulsamos Ejecutar)
varianza <- 7.5 (Pulsamos Ejecutar)

Calculamos por separado cada uno de los elementos restantes que necesitamos para obtener el intervalo de confianza.

n <- nrow(empleados)
media <- mean(empleados$Altura)
cuantil<- qnorm(1-alpha/2)

Los seleccionamos todos y pulsamos Ejecutar

Por último, calculamos los extremos inferior y superior del intervalo de acuerdo

lim_inferior<-media -cuantil * sqrt(varianza) / sqrt(n)
lim_inferior

[1] 176.4605

lim_superior<- media + cuantil * sqrt(varianza) / sqrt(n)
lim_superior

[1] 177.5395

Por lo que el intervalo de confianza que buscamos es (176.4605, 177.5395).

Intervalo de confianza para la media en una población normal con varianza desconocida

Supongamos, en este caso, que la varianza poblacional de la variable de interés es desconocida. Nuestro objetivo sigue siendo el cálculo de un intervalo de confianza para la media de dicha variable.

Supongamos una muestra aleatoria $ X_1, X_2, \cdots, X_n $; de tamaño $ n $ de valores de la variable aleatoria que sigue una distribución Normal de media $ \mu $ y de varianza $ \sigma^{2} $, ambas desconocidas. Para calcular un intervalo de confianza, en este caso, partimos de la variable aleatoria

$ T= \displaystyle \frac {\overline{X}-μ }{s / \sqrt {n}} $

Expresión 5: Expresión de la variable aleatoria

que sigue una distribución t de Student con n-1 grados de libertad. En la fórmula anterior, s hace referencia a la cuasidesviación típica muestral.

Tenemos que buscar dos valores de esta distribución tales que

$ P \left [ – t_{1- α/2} \leq \displaystyle \frac {\overline{X}-μ }{s / \sqrt {n}} \leq t_{1-α/2} \right] = 1-α $

Expresión 6: Obtención del cuantil $ t_{1- α/2} $

Al operar algebraicamente, se obtiene que

$ P \left [ \overline {X} – t_{1-α/2} \displaystyle \frac { s} { \sqrt{n }} \leq μ \leq \overline {X} + t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} \right] =1-α $

Expresión 7: Obtención del cuantil $ t_{1- α/2} $

por lo que el intervalo de confianza que buscamos es

$ \left [ \overline {X} – t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} , \overline {X} + t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} \right] $

Expresión 8: Expresión del Intervalo de confianza (varianza desconocida)

Para calcular un intervalo de confianza para la media de una población normal con varianza desconocida mediante R-Commander, seleccionamos en el menú principal: Estadísticos/ Medias/ Test t para una muestra

Nota: Mediante esta opción también se resuelven contrastes de hipótesis, como veremos en la práctica siguiente.

Supuesto Práctico 2

Considerando el conjunto de datos de empleados.xls y asumiendo que la variable que mide la altura de los empleados sigue una distribución Normal con varianza desconocida. Calcular un intervalo de confianza a un nivel de confianza del 90% para la altura media poblacional.

Solución

Accedemos al menú Test t para una muestra, seleccionando en el menú principal: Estadísticos/ Medias/ Test t para una muestra.

Se mostrrá el siguiente cuadro de diálogo

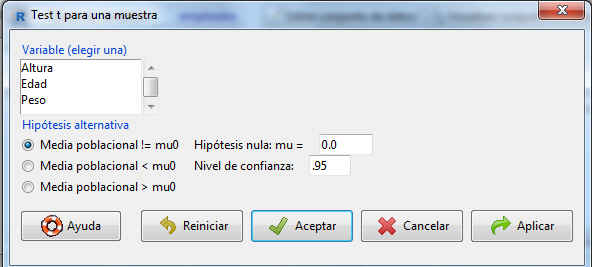
En la parte superior izquierda se muestra una lista con todas las variables cuantitativas del archivo de datos que son susceptibles de ser contrastadas, de la cual debemos elegir exclusivamente una.

A continuación se muestran diversas Hipótesis alternativas así como el nivel de confianza. En este caso queremos obtener un intervalo de confianza, por lo que dejamos marcada la opción por defecto Media poblacional!=mu0 y como Hipótesis nula: mu=0.0. Lo único que tenemos que cambiar es el nivel de confianza (el valor se introduce en tanto por uno). Nivel de confianza: .90.

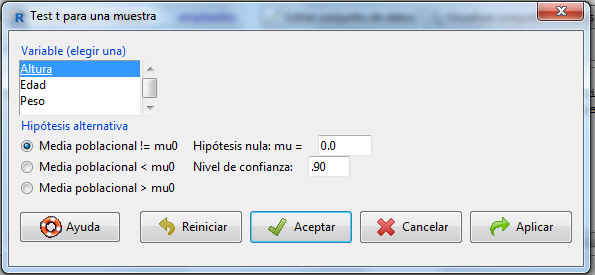
Presionamos Aceptar, y la salida que nos muestra el programa es la siguiente:

One Sample t-test
data: Altura
t = 214.41, df = 98, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
90 percent confidence interval:
175.6292 178.3708
sample estimates:
mean of x
177

De toda la información que devuelve, sólo nos interesa la relativa al intervalo de confianza. El resto hace referencia a los contrastes de hipótesis.

90 percent confidence interval:
175.6292 178.3708

El intervalo de confianza pedido es (175.6292, 178.3708).

Intervalo de confianza para la proporción

Dada una variable aleatoria $ X $ con distribución de probabilidad binomial de parámetros $ n $ y $ \pi $, esto es, $ X \rightarrow B(n, π) $; con $ \pi $ desconocido. El objetivo es determinar un intervalo de confianza para el parámetro $ \pi $. Para ello, se extrae una muestra aleatoria $ X_1, X_2, \cdots, X_n $ de tamaño $ n $ de dicha distribución. Sea $ p $ la proporción muestral. Entonces, se sabe que el estadístico

$ Z = \displaystyle \frac { p – \pi} { \displaystyle \sqrt { \displaystyle \frac { p(1-p)} {n} } } $

Expresión 10: Expresión de la variable aleatoria

sigue una distribución normal de media 0 y desviación típica 1. Por ello, calcular el intervalo de confianza para la proporción consiste en obtener los cuantiles de la distribución normal tales que

$ P \left [ -z_{1-α/2} \leq \displaystyle \frac {p – \pi } { \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}}} \leq z_{1-α/2} \right ]=1-α $

Expresión 11: Obtención del cuantil z_{{1 – α/2}}

O, equivalentemente,

$ P \left [ p -z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \leq \pi \leq p + z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \right ]=1-α $

Expresión 12: Obtención del cuantil z_{{1 – α/2}}

Por lo tanto, el intervalo de confianza que debemos calcular es

$ \left [ p -z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}}, p + z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \right ] $

Expresión 13: Intervalo de confianza para la proporción

Para calcular un intervalo de confianza para la proporción de una población normal mediante R-Commander, seleccionamos en el menú principal: Estadísticos/Proporciones/ Test de proporciones para una muestra.

Supuesto Práctico 3

A partir del conjunto de datos de empleados.xls, obtener un intervalo de confianza al 95% para la proporción de empleados varones en la población.

Solución

Accedemos al menú Test de proporciones para una muestra de R-Commander, seleccionando en el menú principal: Estadísticos/Proporciones/ Test de proporciones para una muestra.

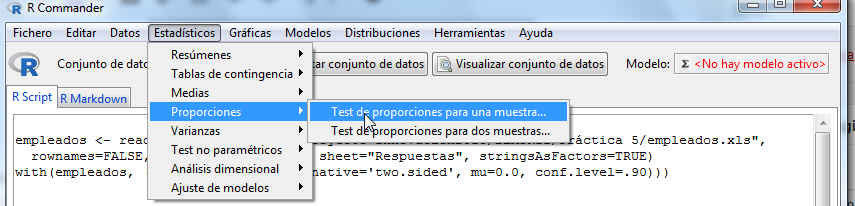
Se muestra el siguiente cuadro de diálogo

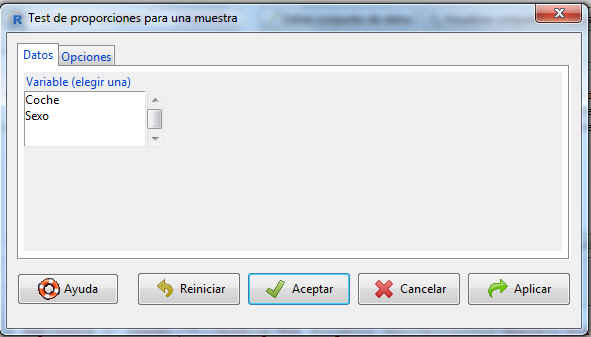
En la pestaña Datos del cuadro de diálogo, se muestra una lista con todas las variables cualitativas que pueden utilizarse en este tipo de contrastes, de entre las cuales tenemos que elegir una. En este caso elegimos Sexo.

Una vez elegido Sexo, pulsamos la pestana Opciones

En la pestaña Opciones dejamos los valores que vienen por defecto, ya que el nivel de confianza es el pedido por el enunciado, 0.95. Pulsamos Aceptar y se muestra la siguiente salida

Frequency counts (test is for first level):
Sexo
Hombre Mujer
    87     12
    1-sample proportions test without continuity correction
data: rbind(.Table), null probability 0.5
X-squared = 56.818, df = 1, p-value = 4.78e-14
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.7999934 0.9292845
sample estimates:
        p
0.8787879

Analicemos las salidas que proporciona el programa

Frequency counts (test is for first level):
Sexo
Hombre Mujer
87 12

En primer lugar, se muestra una tabla con las frecuencias absolutas de cada categoría de la variable cualitativa. Es muy importante tener en cuenta que R-Commander realiza el contraste de hipótesis, y por lo tanto el intervalo, para la primera categoría de la variable.

Para R-Commander la primera categoría de una variable es la que primero aparece siguiendo el orden alfabético, en caso de que las categorías vengan dadas por cadenas de caracteres, o aquella con el número más bajo, en caso de que las categorías se identifiquen mediante un código numérico.

En este ejemplo, las dos posibles opciones para la variable Sexo son “Hombre” y “Mujer”, por lo que la primera de las categorías para R-Commander es “Hombre”. Dado que la hipótesis que se ha planteado se ha hecho sobre los hombres no es necesario hacer ninguna modificación.

Si, por el contrario, la hipótesis del problema se hubiera planteado sobre las mujeres, deberíamos hacer una recodificación previa de la variable para situar la categoría “Mujer” como la primera.

En la segunda parte se muestran los resultados del contraste de hipótesis, que analizaremos en la práctica sobre Contrastes de Hipótesis.

Y por último,muestra el resultado del intervalo de confianza pedido

95 percent confidence interval:
0.7999934 0.9292845

Por lo que el intervalo de confianza, a un nivel de confianza del 95% para la proporción de empleados varones en la población es (0.7999934, 0.9292845).

Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes

Consideramos dos variables aleatorias independientes $ X_1, X_2, \cdots, X_n $ e $ Y_1, Y_2, \cdots Y_n $ con distribuciones normales de parámetros $ (\mu_1, \sigma_1) $ y $ (\mu_2, \sigma_2) $, respectivamente, de las que vamos a tomar muestras aleatorias independientes de tamaños $ n_1 $ y $ n_2 $, respectivamente.

Nuestro objetivo, en este caso, es obtener un intervalo de confianza para la diferencia de las medias de ambas distribuciones, es decir, para $ \mu_1- \mu_2 $. Pero previo al cálculo de este intervalo, debemos determinar si las varianzas de ambas distribuciones o, equivalentemente, sus desviaciones típicas, $ \sigma_1 $ y $ \sigma_2 $, aun siendo desconocidas, pueden asumirse iguales o no. El cálculo del intervalo de confianza se realiza de forma diferente dependiendo El cálculo del intervalo de confianza se realiza de forma diferente dependiendo de si las varianzas (desviaciones típicas) pueden asumirse iguales o no.

En primer lugar determinemos el Intervalo de confianza para el cociente de varianzas

Intervalo de confianza para el cociente de varianzas en dos poblaciones normales independientes

Para decidir si las varianzas de las dos distribuciones pueden asumirse iguales o no construiremos un intervalo de confianza para el cociente de ambos valores, esto es, para $ \sigma_1^{2}/\sigma_2^{2} $. En este caso, partimos de la variable aleatoria

$ F= \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \displaystyle \frac {\sigma_{2}^{2}} {\sigma_{1}^{2}} $

Expresión 14: Expresión de la variable aleatoria para el cociente de varianzas

que sigue una distribución F de Snedecor con $ n_{1} – 1 $ grados de libertad en el numerador y $ n_{2} – 1 $ grados de libertad en el denominador. Los valores $ s_{1}^{2} $ y $ s_{2}^{2} $_, en la expresión anterior, hacen referencia a las cuasivarianzas muestrales de la variable en el primer y el segundo grupo, respectivamente. Buscamos los valores de la variable F tales que

$ \left [ F_{n_{1}-1,n_{2}-1, α/2} \leq \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \displaystyle \frac {\sigma_{2}^{2}} {\sigma_{1}^{2}} \leq F_{n_{1}-1,n_{2}-1, 1-α/2} \right ] = 1- \alpha $

Expresión 15: Obtención de los cuantiles F_{{ α/2}} y F_{{1 – α/2}}

O, equivalentemente,

$ \left [ \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1,1- α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \leq \displaystyle \frac {\sigma_{1}^{2}} {\sigma_{2}^{2}} \leq \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}, α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \right ] = 1- \alpha $

Expresión 16: Obtención de los cuantiles F_{{ α/2}} y F_{{1 – α/2}}

De modo que el intervalo de confianza que buscamos es el formado por

$ \left ( \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1, 1-α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}}, \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1, α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \right ) $

Expresión 17: Intervalo de confianza para el cociente de varianzas

Para calcular el intervalo de confianza para el cociente de varianzas en R-Commander, seleccionamos en el menú principal: Estadísticos/ Varianzas/ Test F para dos varianzas

Una vez calculado el intervalo de confianza, si el valor 1 está incluido en dicho intervalo, podremos afirmar que las varianzas (y, consecuentemente, las desviaciones típicas) de ambas distribuciones pueden considerarse iguales. Si el 1 queda fuera del intervalo obtenido, las varianzas de las dos distribuciones se considerarán diferentes.

Supuesto Práctico 4

Continuando con los datos del archivo empleados.xls y asumiendo que el peso en hombres y el peso en mujeres se distribuyen según distribuciones normales con medias y varianzas desconocidas. Calcular un intervalo de confianza a un nivel de confianza del 95% para el cociente de varianzas en ambas poblaciones. ¿Puede asumirse que ambas varianzas son iguales?

Solución

Accedemos a Test F para dos varianzas, de R-Commander, seleccionando en el menú principal: Estadísticos/ Varianzas/ Test F para dos varianzas

Se muestra el siguiente cuadro de diálogo

La pestaña Datos muestra dos listas de variables.

La lista de Grupos, muestra todas las variables cualitativas del fichero de datos. En esta lista tenemos que seleccionar cuál es la variable que nos va a dividir la muestra de observaciones en dos submuestras independientes. En nuestro caso, al tratar con hombres y mujeres, seleccionamos el Sexo del empleado como variable de agrupación.
La lista de Variable explicativa, muestra todas las variables cuantitativas del fichero de datos. Señalamos la variable principal sobre la cual se va a llevar a cabo el contraste (en nuestro caso, Peso).

Seleccionamos la pestaña Opciones

En la pestaña Opciones podemos personalizar el contraste. Como en este caso sólo nos interesa el intervalo de confianza, sólo hemos de mirar el nivel de confianza. Por defecto es 0.95, por lo que no cambiamos ninguna de las opciones de esta pestaña y mantenemos las opciones por defecto. Pulsamos Aceptar y se muestra la siguiente salida

F test to compare two variances
data: Peso by Sexo
F = 1.814, num df = 86, denom df = 11, p-value = 0.2752
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.6112226 3.8937784
sample estimates:
ratio of variances
1.813982

Esta salida, muestra que el intervalo de confianza para el cociente de las varianzas es (0.6112226, 3.8937784).

La interpretación del intervalo de confianza puede servirnos para concluir acerca de la igualdad de las varianzas. En este ejemplo, dicho intervalo es (0.6112226, 3.8937784) que, como podemos comprobar incluye al 1 entre sus posibles valores. Esto implica que a un nivel de confianza del 95% se puede suponer que el cociente entre las dos varianzas puede tomar el valor 1 o, lo que es lo mismo, que las dos varianzas son iguales.

Una vez se ha determinado la igualdad (o desigualdad) de las varianzas de ambas distribuciones, procedemos a calcular el intervalo de confianza para la diferencia de las medias propiamente dicho.

a) Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes cuando las varianzas poblacionales son desconocidas pero supuestas iguales

Si la varianzas poblacionales son desconocidas pero supuestas iguales, se parte de la variable aleatoria

$ T= \displaystyle \frac { ( \overline {X}_1- \overline {X}_2)-(μ_{1}-μ_{2}) } { \displaystyle \sqrt {\displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}}+ \displaystyle \frac {1} {n_{2}} } } $

Expresión18: Expresión de la variable aleatoria para la diferencia de medias (varianzas iguales)

la cual se distribuye según una t de Student con $ n_1+n_2-2 $ grados de libertad. El cálculo del intervalo de confianza para la diferencia de medias se realiza obteniendo los valores de la distribución t de Student con $ n_1+n_2-2 $ grados de libertad que verifican

$ \left [-t_{n_1+n_2-2,1-\alpha/2} \leq \displaystyle \frac { ( \overline {X}_1- \overline {X}_2)-(μ_{1}-μ_{2}) } { \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}}+ \displaystyle \frac {1} {n_{2}} } } \leq t_{n_1+n_2-2,1-\alpha/2} \right ] = 1- \alpha $

Expresión 19: Obtención del cuantil t_{{1 – α/2}}

Al operar algebraicamente, tenemos que

$ \begin{array} {c} P \left [ ( \overline {X}_1- \overline {X}_2) -t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} \leq (μ_{1}-μ_{2}) \leq \\ \leq ( \overline {X}_1- \overline {X}_2) + t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} \right ] = 1- \alpha \\ \end{array} $

Expresión 20: Obtención del cuantil t_{{1 – α/2}}

De modo que el intervalo de confianza que buscamos es

$ \begin{array} {c} \left ( ( \overline {X}_1- \overline {X}_2) -t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} , \\ ( \overline {X}_1- \overline {X}_2) + t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} \right ) \\ \end{array} $

Expresión 21: Intervalo de confianza para la diferencia de medias (varianzas iguales)

b) Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes cuando las varianzas poblacionales son desconocidas, distintas y tamaños muestrales grandes

Si las varianzas de las poblaciones son desconocidas y, además, distintas y tamaños muestrales grandes, se sigue un procedimiento similar al que acabamos de describir en el caso de igualdad de varianzas para la obtención del intervalo de confianza, partiendo de una variable aleatoria.

$ Z = \displaystyle \frac { (\overline {X}_1 – \overline {X}_2) (\mu_1- \mu_2) } { \displaystyle \sqrt{\displaystyle \frac {s_1^{2}}{n_1} + \displaystyle \frac {s_2^{2}}{n_2} } } $

Expresión 22: Expresión de la variable aleatoria para la diferencia de medias (varianzas distintas y tamaños muestrales grandes)

De modo que el intervalo de confianza que buscamos es

$ (\overline {X}_1 – \overline {X}_2) – z_{1-\alpha/2} \displaystyle \sqrt{ \displaystyle \frac {s_1^{2}}{n_1} + \displaystyle \frac {s_2^{2}}{n_2} }, (\overline {X}_1 – \overline {X}_2) + z_{1-\alpha/2} \displaystyle \sqrt{ \displaystyle \frac {s_1^{2}}{n_1} + \displaystyle \frac {s_2^{2}}{n_2} } $

Expresión 23: Intervalo de confianza para la diferencia de medias (varianzas distintas y tamaños muestrales grandes)

Para calcular un intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes, tanto si las varianzas de la variable son iguales en los dos grupos como si no en R-Commander. Seleccionamos en el menú principal: Estadísticos/Medias/ Test t para muestras independientes.

La interpretación del intervalo de confianza resultante nos permitirá determinar si las medias poblacionales de las dos distribuciones pueden suponerse iguales o no. Así, si el intervalo contiene al valor 0, dichas medias podrán asumirse iguales. En cualquier otro caso, concluiremos que las medias son distintas en ambas distribuciones.

Supuesto Práctico 5

Sabiendo que las varianzas son iguales (Supuesto práctico 4), obtener un intervalo de confianza al 95% para la diferencia del peso medio entre hombres y mujeres. ¿Puede suponerse que el peso medio entre hombres y mujeres es igual?

Solución

Para obtener el Test t para muestras independientes con R-Commander. Seleccionamos en el menú principal: Estadísticos/Medias/ Test t para muestras independientes.

Se muestra el siguiente cuadro de diálogo

La pestaña Datos muestra dos listas de variables. Como ya se ha comentado con anterioridad, en la lista de la izquierda (Grupos) tenemos que escoger la variable a partir de la cual se formarán los dos grupos de observaciones, seleccionamos Sexo. En la de la derecha (Variable explicada) seleccionamos la variable cuya diferencia de medias en las poblaciones queremos estudiar, seleccionamos Peso.

Seleccionamos Opciones

La pestaña muestra todas las opciones del contraste que podemos modificar. En nuestro caso como sólo buscamos el intervalo de confianza, especificamos el nivel de confianza que se va a asumir al calcular el intervalo e indicamos si las varianzas de las dos poblaciones pueden suponerse iguales o no. En nuestro caso suponemos que las varianzas son iguales

Cuando hemos seleccionado las variables adecuadas y hemos marcado las opciones que nos interesan, pulsamos en Aceptar, de manera que en la consola se muestra la siguiente salida

Two Sample t-test
data: Peso by Sexo
t = 3.0597, df = 97, p-value = 0.002865
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
4.167581 19.556557
sample estimates:
mean in group Hombre mean in group Mujer
76.19540 64.33333

El intervalo de confianza que se incluye entre los resultados es:

95 percent confidence interval:
4.167581 19.556557

Se puede afirmar que el intervalo de confianza a un 95% de confianza para la diferencia de las medias del peso medio para hombres y mujeres es (4.167581, 19.556557). Como el 0 no está dentro de este intervalo, no tenemos suficiente evidencia muestral para decir que el peso medio de hombres y mujeres sea el mismo.

Intervalo de confianza para la diferencia de medias en dos poblaciones normales relacionadas

Sean $ X_1,X_2, \cdots, X_n $ e $ Y_1,Y_2, \cdots, Y_n $ dos muestras aleatoria de tamaño $ n $ y relacionadas, de tal forma que la primera procede de una población $ N (\mu_1, \sigma_1) $ y la segunda de una población $ N (\mu_2, \sigma_2) $ .

Antes de proporcionar el intervalo para la diferencia de medias de estas dos poblaciones, se hace necesario indicar qué se entiende por muestras relacionadas. Se dicen que dos muestras $ X_1,X_2, \cdots, X_n $ e $ Y_1,Y_2, \cdots, Y_n $ están relacionadas o apareadas cuando los datos de las muestras vienen por parejas, uno de cada una de ellas, de manera que cada individuo proporciona dos observaciones.

Para calcular un intervalo de confianza para la diferencia de medias en dos poblaciones normales relacionadas en R-Commander. Seleccionamos en el menú principal: Estadísticos/Medias/ Test t para datos relacionados.

Supuesto Práctico 6

Se desea evaluar la eficacia de un fármaco para la reducción del nivel de glucosa en pacientes. Para ello, se selecciona una muestra de 10 pacientes a los que se les mide su nivel de glucosa en sangre antes y después del suministro del medicamento. Los resultados aparecen recogidos en la siguiente tabla:

$ \begin{array} {|c|c|c|c|c|c|c|} \hline Antes & 72.0 & 73.5 & 70.0 & 71.5 & 76.0 & 80.5 \\ \hline Después & 73.0 & 74.5 & 74.0 & 74.5 & 75.0 & 82.0 \\ \hline \end{array} $

Tabla 1: Datos del supuesto práctico 6

Calcular el intervalo de confianza para la diferencia de medias al 90%. ¿Son iguales los niveles medios de glucosa antes y después del medicamento?

Solución

En primer lugar, debemos crear un nuevo conjunto de datos con la información que nos proporciona la tabla. El conjunto de datos estará formado por dos variables con los niveles de glucosa antes y después de la aplicación del fármaco. Organizamos los datos en un fichero .txt (supuesto6.txt)

A continuación seleccionamos en el menú principal: Datos/Importar datos/desde archivo de texto

Se muestra la siguiente pantalla

Introducimos el nombre del conjunto de datos (supuesto6) y pulsamos Aceptar. En la ventana resultante elegimos el fichero supuesto6 y pulsamos Abrir.

Seleccionamos Visualizar conjunto de datos y se muestra

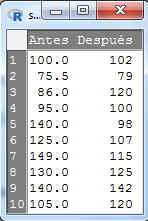
A continuación, accedemos al menú Test t para datos relacionados en R-Commander. Seleccionamos en el menú principal: Estadísticos/Medias/ Test t para datos relacionados

Se muestra la siguiente pantalla

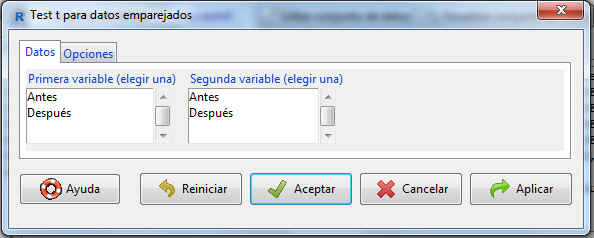
La pestaña Datos muestra dos listas de variables cada una de las cuales incluye todas las variables cuantitativas que son susceptibles de ser analizadas. Seleccionamos, en nuestro caso, Antes y Después

Es importante destacar que, a diferencia del caso de muestras independientes, cuando trabajamos con muestras pareadas no necesitamos una variable de agrupación, sino que debemos seleccionar las dos variables a analizar de forma separada.

En la pestaña Opciones personalizamos el contraste conforme al problema que estemos resolviendo. Como en este caso sólo nos interesa el intervalo de confianza, introducimos el valor del nivel de confianza dado en el enunciado.

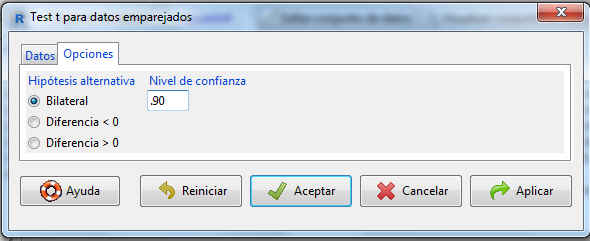
Si hacemos clic en Aceptar, el programa nos devuelve la siguiente salida:

Paired t-test
data: Antes and Después
t = 0.52714, df = 9, p-value = 0.6108
alternative hypothesis: true difference in means is not equal to 0
90 percent confidence interval:
-9.290501 16.790501
sample estimates:
mean of the differences
3.75

En la segunda parte de los resultados se incluye el intervalo de confianza al 90% para la diferencia de las medias de la variable glucosa, que es (-9.290501, 16.790501). Este intervalo incluye el valor 0, lo que significa que el 0 es un valor posible para la diferencia entre las medias. Por ello, concluimos que puede asumirse que la diferencia entre dichas medias es 0, o dicho de otro modo, que ambos niveles medios de glucosa son iguales.

Intervalo de confianza para la diferencia de dos proporciones

Vamos a construir un intervalo de confianza para la diferencia de proporciones $ \pi_1-\pi_2 $. Para ello, consideramos dos muestras aleatorias $ X_1, X_2, \cdots, X_{n_{1}} $ e $ Y_1, Y_2, \cdots, Y_{n_{2}} $ de tamaño $ n_1 $ y $ n_2 $, independientes entre sí, extraídas de poblaciones con distribuciones binomiales $ B (1, \pi_1) $ y $ B (1, \pi_2) $, respectivamente.

Construimos, a continuación, un intervalo de confianza para la diferencia de proporciones $ \pi_1-\pi_2 $. Para ello, partimos de la variable aleatoria

$ Z = \displaystyle \frac { ( p_1 – p_2 ) -(\pi_1-\pi_2) } { \displaystyle \sqrt { \displaystyle \frac { p_1(1-p_1)}{n_1} + \displaystyle \frac {p_2 (1-p_2)}{n_2} }} $

Expresión 24: Expresión de la variable aleatoria (diferencia de dos proporciones)

con $ p_1 $ y $ p_2 $ las proporciones de individuos que presentan la característica de interés en la primera y la segunda muestra, respectivamente. Esta variable aleatoria sigue una distribución normal de media 0 y desviación típica 1, por lo que debemos calcular los valores de la distribución normal estándar que verifican que

$ P \left [- z_{1-\alpha/2} \leq \displaystyle \frac { ( p_1 – p_2 ) -(\pi_1-\pi_2) } { \displaystyle \sqrt { \displaystyle \frac { p_1(1-p_1)}{n_1} + \displaystyle \frac {p_2 (1-p_2)}{n_2} }} \leq z_{1-\alpha/2} \right ] = 1- \alpha $

Expresión 25: Obtención del cuantil z_{{1 – α/2}}

O, lo que es lo mismo

$ \begin{array} {c} P \left [(p_1-p_2) – z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}} \leq \pi_1 – \pi_2 \leq \\ \leq (p_1-p_2) + z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}} \right ] = 1-\alpha \\ \end{array} $

Expresión 26: Obtención del cuantil z_{{1 – α/2}}

De modo que el intervalo de confianza buscado es

$ \left [(p_1-p_2) – z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}}, (p_1-p_2) + z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}} \right ] $

Expresión 27: Intervalo de confianza para la diferencia de dos proporciones

Para calcular un intervalo de confianza para la diferencia de dos proporciones con R-Commander. Se selecciona en el menú principal: Estadísticos/Proporciones/ Test de proporciones para dos muestras.F

Si el intervalo de confianza resultante incluye al 0 entre sus posibles valores, la diferencia entre ambas proporciones poblaciones podrá considerarse nula lo que equivale a decir que ambas proporciones son iguales.

Supuesto Práctico 7

A partir del conjunto de datos empleados.xls, obtener un intervalo de confianza al 85% para la diferencia entre la proporción de empleados hombres y mujeres que tienen coche. ¿Pueden considerarse ambas proporciones iguales?

Solución

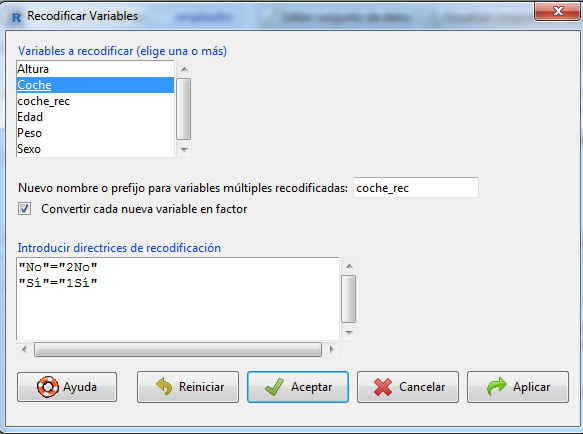
Dado que la hipótesis se ha planteado sobre la proporción de hombres y mujeres que tienen coche, es necesario recodificar la variable coche. Para ello seleccionamos Datos/Modificar variables del conjunto de datos activo/Recodificar variables

Se muestra la siguiente pantalla

En esta pantalla:

Se selecciona Coche en Variables a recodificar
En Nuevo nombre o prefijo para variables múltiples recodificadas hemos puesto como nombre de la variable: coche_rec
En la ventana Introducir directrices de recodificación: “No”=”2No” y “Sí”=”1Sí”

Se pulsa Aceptar. Seleccionando Visualizar conjunto de datos activos se muestra el archivo de datos resultantes

Accedemos al menú Test de proporciones para dos muestras de R-Commander, seleccionando en el menú principal: Estadísticos/Proporciones/ Test de proporciones para dos muestras

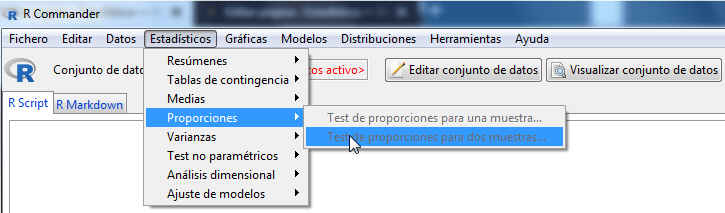
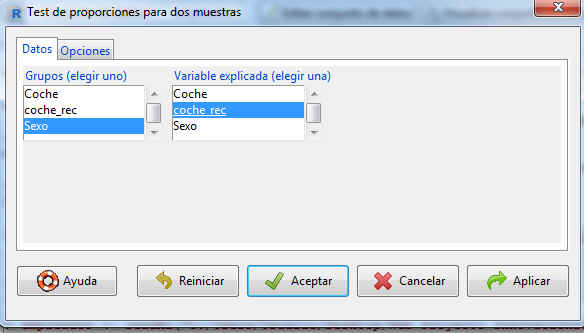
Se muestra la siguiente pantalla

La pestaña Datos muestra dos listas con las variables cualitativas que incluye el conjunto de datos. De la primera lista seleccionamos la variable de agrupación (en nuestro caso es el Sexo, ya que distinguimos entre hombres y mujeres) y de la segunda, la variable de interés (que es, si el empleado tiene coche, coche_rec).

Pulsamos la pestaña Opciones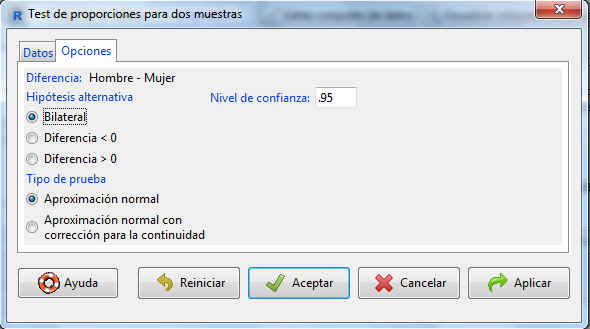En la pestaña Opciones indicamos el nivel de confianza propuesto en el enunciado, 85%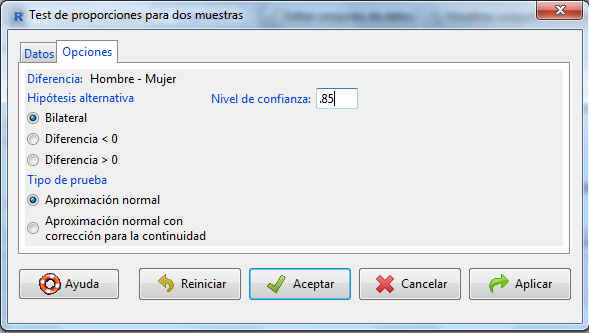Se pulsa Aceptar y R-Commander muestra la siguiente salida

Percentage table:
coche_rec
Sexo      1Sí 2No Total Count
Hombre 52.9 47.1   100    87
Mujer 50.0 50.0   100    12
2-sample test for equality of proportions without continuity correction
data: .Table
X-squared = 0.03492, df = 1, p-value = 0.8518
alternative hypothesis: two.sided
95 percent confidence interval:
-0.2729805 0.3304517
sample estimates:
prop 1    prop 2
0.5287356 0.5000000

El intervalo de confianza pedido al 85% de confíanza es (-0.2729805, 0.3304517). El 0 está dentro de este intervalo, por lo que podemos concluir que las proporciones de hombre y mujeres que tienen coche coinciden.

Ejercicios

Ejercicios Guiados

Ejercicio Guiado1

En la base de datos universidad.txt tenemos información sobre las variables, Coeficiente intelectual y Asistir a clase de estadística de dos grupos de alumnos, dependiendo del turno de clase en el que se encuentren. El turno de mañana se define como A y el de tarde como B.

$ \begin{array} {|c|c|c|c|} \hline Sujeto & Grupo & C.L. & Estadística \\ \hline 1 & A & 101 & Sí \\ \hline 2 & B & 103 & Sí \\ \hline 3 & A & 98 & NO \\ \hline 4 & A & 105 & Sí \\ \hline 5 & B & 99 & NO \\ \hline \end{array} $

Tabla 2: Datos del Ejercicio guiado 1

Se pide:

a) Obtener un intervalo de confianza a un nivel del 99% para el cociente intelectual medio, sabiendo que la varianza poblacional es igual a 3

b) Obtener un intervalo de confianza a un nivel del 95% para el cociente intelectual medio

c) Obtener un intervalo de confianza a un nivel del 98% para la diferencia media de cociente intelectual entre el grupo A y B. ¿Puede suponerse que el cociente intelectual medio entre ambos grupos es igual?

d) Obtener un intervalo de confianza a un nivel del 90% para la proporción de alumnos en el grupo A. Y un intervalo de confianza al 90% para la proporción de alumnos en el grupo B

e) Obtener un intervalo de confianza a un nivel del 93% para la diferencia entre la proporción de alumnos en el grupo A y B que tienen clase de estadística.

Ejercicio Guiado 2

En un hospital se elige una muestra de pacientes y se les mide la tasa cardíaca por la mañana (TCM) y a última hora de la tard (TCT).

$ \begin{array} {|c|c|c|} \hline Sujeto & TCM & TCT \\ \hline 1 & 58 & 65 \\ \hline 2 & 72 & 72 \\ \hline 3 & 64 & 73 \\ \hline 4 & 68 & 80 \\ \hline 5 & 67 & 63 \\ \hline \end{array} $

Tabla 3: Datos del Ejercicio guiado 2

Estudiar mediante un intervalo de confianza al 99% si, por término medio, la tasa cardíaca es igual por la mañana y a última hora de la tarde.

Ejercicio Guiado 3

Una determinada empresa quiere saber si su nuevo producto tendrá más aceptación en la población de hombres o entre las mujeres. Para ello, considera una muestra aleatoria de 38 hombres y 62 mujeres, observando que sólo a 15 hombres y 33 mujeres les había gustado su producto. Construir un intervalo de confianza al 99% de confianza para la diferencia de proporciones de hombres y mujeres a los que les gusta el producto. ¿Puede suponerse que el producto gusta por igual en hombres y mujeres?

Ejercicio Guiado 4

En una experiencia genética se extraen 20 moscas de una caja experimental y se mide la longitud del ala de cada una. Se obtuvieron los siguientes valores:

93, 90, 97, 90, 93, 91, 96, 94, 91, 91, 88, 93, 95, 91, 89, 92, 87, 88, 90, 86

Suponiendo que la longitud del ala sigue una distribución Normal. Construir un intervalo de confianza al 99% de confianza para

a) La media μ

b) La varianza σ²

Ejercicio Guiado 1 (Resuelto)

Tabla 2: Datos del Ejercicio guiado 1

Se pide:

a) Obtener un intervalo de confianza a un nivel del 99% para el cociente intelectual medio, sabiendo que la varianza poblacional es igual a 3

b) Obtener un intervalo de confianza a un nivel del 95% para el cociente intelectual medio

d) Obtener un intervalo de confianza a un nivel del 90% para la proporción de alumnos en el grupo A. Y un intervalo de confianza al 90% para la proporción de alumnos en el grupo B

e) Obtener un intervalo de confianza a un nivel del 93% para la diferencia entre la proporción de alumnos en el grupo A y B que no tienen clase de estadística.

Solución:

En primer lugar debemos importar el archivo de datos universidad.txt.

Para ello, seleccionamos en el menú principal: Datos/Importar datos/desde archivo de texto

Se muestra la siguiente pantalla

donde, en Introducir el nombre del conjunto de datos escribimos universidad y pulsamos Aceptar. En el directorio seleccionamos el archivo universida.txt y pulsamos abrir.

R-Commander muestra el archivo universidad en Conjunto de datos

Pulsamos Visualizar conjunto de datos y se muestra

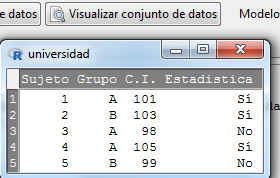a) Obtener un intervalo de confianza a un nivel del 99% para el cociente intelectual medio, sabiendo que la varianza poblacional es igual a 3

En este caso nos encontramos ante un intervalo de confianza sobre la media de una población normal con varianza conocida, por lo que hay que calcularlo mediante código

Introducimos en R Commander los datos relativos al nivel de significación y la varianza poblacional de la variable que proporciona el enunciado.

alpha<- 0.01
varianza <- 3

Calculamos por separado cada uno de los elementos restantes que necesitamos para obtener el intervalo de confianza.

n <- nrow(universidad)
media <- mean(universidad$C.I.)
cuantil<- qnorm(1 – alpha/2)

Por último, calculamos los extremos inferior y superior del intervalo
lim_inferior<-media – cuantil * sqrt(varianza) / sqrt(n)
lim_inferior

[1] 99.20477

lim_superior<- media + cuantil * sqrt(varianza) / sqrt(n)
lim_superior

[1] 103.1952

Por lo que el intervalo de confianza que buscamos es (99.20477, 103.1952).

Nota: Recordar que para que se ejecute una instrucción hay que pulsar Ejecutar

b) Obtener un intervalo de confianza a un nivel del 95% para el cociente intelectual medio

En este caso nos encontramos ante un intervalo de confianza sobre la media de una población normal con varianza desconocida. Para realizarlo con R-Commander, seleccionamos en el menú principal: Estadísticos/Medias/ Test t para una muestra

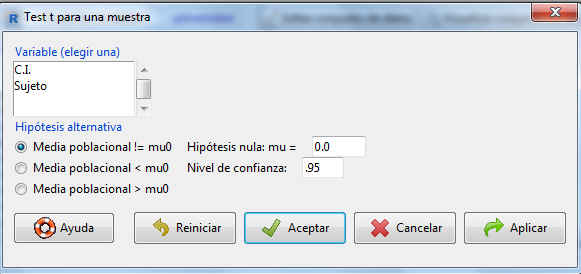
En la parte superior izquierda aparece una lista con todas las variables cuantitativas del archivo de datos que son susceptibles de ser contrastadas, de la cual debemos elegir exclusivamente una. Elegimos C.I

El resto de opciones las dejamos por defecto, ya que el enunciado nos pide el intervalo de confianza al 95%.

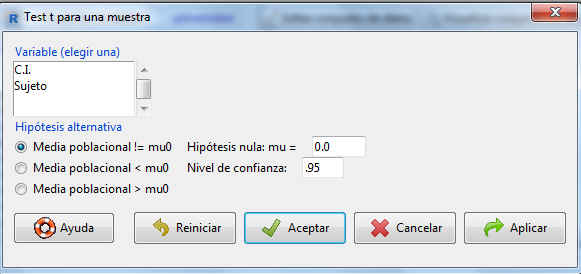
Pulsamos Aceptar y se muestra la siguiente salida

One Sample t-test
data: C.I.
t = 79.024, df = 4, p-value = 1.537e-07
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
97.64442 104.75558
sample estimates:
mean of x
101.2

Por lo que el intervalo de confianza es (97.64442, 104.75558).

En este caso nos encontramos ante un intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes.

En primer lugar tenemos que saber si las varianzas de ambas distribuciones son iguales. Para ello, seleccionamos en R-Commander: Estadísticos/ Varianzas/ Test F para dos varianzas. Se muestra la siguiente pantalla

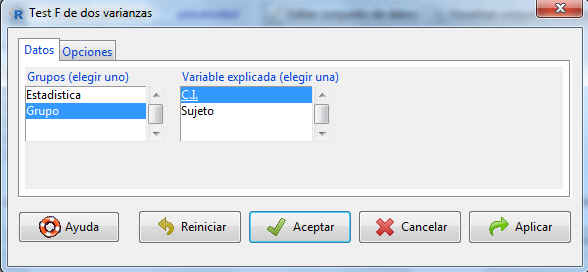
La pestaña Datos muestra dos listas de variables. La lista de la izquierda (Grupos) incluye todas las variables cualitativas del fichero de datos. En esta lista tenemos que seleccionar cuál es la variable que nos va a dividir la muestra de observaciones en dos submuestras independientes. En nuestro caso, Grupo. En la lista de la derecha se incluyen las variables cuantitativas del fichero de datos. Aquí tenemos que señalar la variable principal sobre la cual se va a llevar a cabo el contraste (en nuestro caso, C.I.). Seleccionamos Opciones

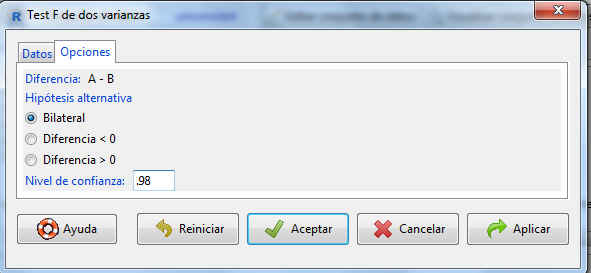
En la pestaña Opciones podemos personalizar el contraste. Como en este caso sólo nos interesa el intervalo de confianza, sólo hemos de mirar el nivel de confianza. Por defecto es 0.95, por lo que lo cambiamos a 0.98. Pulsamos Aceptar y se muestra la siguiente salida.

F test to compare two variances
data: C.I. by Grupo
F = 1.5417, num df = 2, denom df = 1, p-value = 0.9897
alternative hypothesis: true ratio of variances is not equal to 1
98 percent confidence interval:
3.083642e-04 1.518580e+02
sample estimates:
ratio of variances
1.541667

El intervalo de confianza para el cociente de las varianzas, (3.083642e-04, 1.518580e+02). Dicho intervalo incluye al 1 entre sus posibles valores. Esto implica que a un nivel de confianza del 98% se puede suponer que el cociente entre las dos varianzas puede tomar el valor 1 o, lo que es lo mismo, que las dos varianzas son iguales.

Una vez se ha determinado la igualdad de las varianzas de ambas distribuciones, procedemos a calcular el intervalo de confianza para la diferencia de las medias cuando las varianzas poblacionales son iguales. Para ello, seleccionamos en R-Commander: Estadísticos/Medias/Test t para muestras independientes

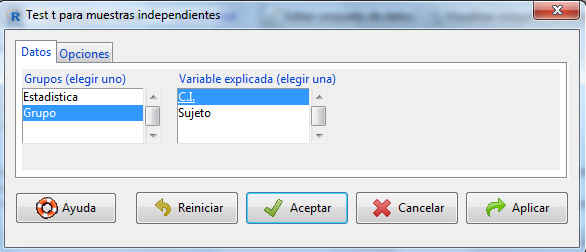
La pestaña Datos muestra dos listas de variables. Como ya se ha comentado con anterioridad, en la lista de la izquierda (Grupos) tenemos que escoger la variable a partir de la cual se formarán los dos grupos de observaciones, en nuestro caso Grupo. En la de la derecha (Variable explicada) seleccionamos la variable cuya diferencia de medias en las poblaciones queremos estudiar, en nuestro cado C.I.. Pulsamos Opciones

La pestaña Opciones muestra todas las opciones del contraste que podemos modificar. En nuestro caso como sólo buscamos el intervalo de confianza, especificamos el nivel de confianza que se va a asumir al calcular el intervalo (98%) e indicamos si las varianzas de las dos poblaciones pueden suponerse iguales o no, en nuestro caso Sí.

Una vez que hemos seleccionado las variables adecuadas y hemos marcado las opciones que nos interesan, pulsamos en Aceptar, de manera que en la consola aparece una salida como esta:

Two Sample t-test
data: C.I. by Grupo
t = 0.11066, df = 3, p-value = 0.9189
alternative hypothesis: true difference in means is not equal to 0
98 percent confidence interval:
-13.34472 14.01139
sample estimates:
mean in group A mean in group B
101.3333 101.0000

El intervalo de confianza a un 98% de confianza para la diferencia de las medias del cociente intelectual entre el grupo A y el B es (-13.34472, 14.01139). Como el 0 está dentro de este intervalo, tenemos suficiente evidencia muestral para decir que el cociente intelectual medio del grupo A y B son iguales.

d) Obtener un intervalo de confianza a un nivel del 90% para la proporción de alumnos en el grupo A. Y un intervalo de confianza al 90% para la proporción de alumnos en el grupo B

En este caso nos encontramos ante un intervalo de confianza para la proporción.

Obtener un intervalo de confianza a un nivel del 90% para la proporción de alumnos en el grupo A.

Dado que la hipótesis que se ha planteado se ha hecho sobre el grupo A, no es necesario hacer ninguna recodificación de la variable. Seleccionamos: Estadísticos/Proporciones/Test de proporciones para una muestra

La pestaña Variable muestra una lista con todas las variables cualitativas que pueden utilizarse en este tipo de contrastes, de entre las cuales tenemos que elegir una. En este caso elegimos la variable Grupo.

En la pestaña Opciones modificamos el valor del nivel de confianza a un 90%.

Cuando presionamos el botón Aceptar, obtenemos los resultados del análisis, que son los que se muestran a continuación:

Por lo que el intervalo de confianza, a un nivel de confianza del 90% para la proporción de estudiantes en el grupo A es (0.2724832, 0.8572935).

Obtener un intervalo de confianza a un nivel del 90% para la proporción de alumnos en el grupo B.

Dado que la hipótesis que se ha planteado se ha hecho sobre el grupo B es necesario hacer una recodificación de la variable. Para ello seleccionamos Datos/Modificar variables del conjunto de datos activo/Recodificar variables

Se muestra la siguiente pantalla

En la casilla: Nuevo nombre o prefijo para la variable múltiple recodificadas ponemos Grupo_rec.

Una forma de recodificar la variable es ponerle un número delante del carácter. De este modo la primera categoría de la variable es aquella con el número más bajo, en este caso la B.

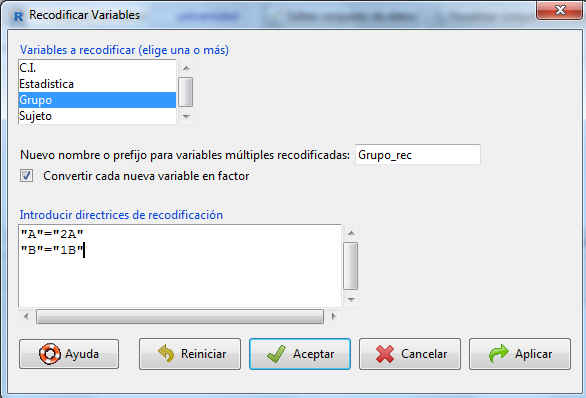
Tras la recodificación la base de datos quedará

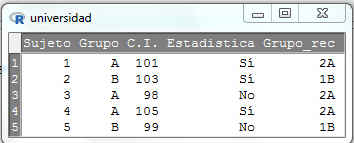
Una vez recodificada la variable, pasamos a calcular el intervalo de confianza. En este caso nos encontramos ante un intervalo de confianza para la proporción. Seleccionamos: Estadísticos/Proporciones/Test de proporciones para una muestra. Se muestra la siguiente pantalla

En la pestaña Opciones modificamos el valor del nivel de confianza a un 90%.

Cuando presionamos el botón Aceptar, obtenemos los resultados del análisis, que son los que se muestran a continuación:

1-sample proportions test without continuity correction
data: rbind(.Table), null probability 0.5
X-squared = 0.2, df = 1, p-value = 0.6547
alternative hypothesis: true p is not equal to 0.5
90 percent confidence interval:
0.1427065 0.7275168
sample estimates:
p
0.4
Por lo que el intervalo de confianza, a un nivel de confianza del 90% para la proporción de estudiantes en el grupo B es (0.1427065, 0.7275168).

e) Obtener un intervalo de confianza a un nivel del 93% para la diferencia entre la proporción de alumnos en el grupo A y B que no tienen clase de estadística.

Dado que la hipótesis que se ha planteado se ha hecho sobre los alumnos que no tienen clase de estadística no es necesario hacer una recodificación de la variable Estadística. En este caso nos encontramos ante un intervalo de confianza para la diferencia de dos proporciones. Seleccionamos: Estadísticos/Proporciones/Test de proporciones para dos muestras. Se muestra la siguiente pantalla

La pestaña Datos muestra dos listas con las variables cualitativas que incluye el conjunto de datos. De la primera lista seleccionamos la variable de agrupación (en nuestro caso es el Grupo) y de la segunda, la variable de interés (Estadística). Pulsamos Opciones

Ya en la segunda pestaña (Opciones) indicamos el nivel de confianza propuesto en el enunciado, 93%. Pulsamos Aceptar y se muestra la siguiente salida

2-sample test for equality of proportions without continuity correction
data: .Table
X-squared = 0.13889, df = 1, p-value = 0.7094
alternative hypothesis: two.sided
93 percent confidence interval:
-0.9750999 0.6417665
sample estimates:
prop 1 prop 2
0.3333333 0.5000000

Por último, el programa devuelve el intervalo de confianza al 93% de confíanza, (-0.9750999, 0.6417665). El 0 está dentro de este intervalo, por lo que podemos concluir que las proporciones de alumnos en ambos grupos que no tienen clase de estadística coinciden.

Ejercicio Guiado 2 (Resuelto)

En un hospital se elige una muestra de pacientes y se les mide la tasa cardíaca por la mañana (TCM) y a última hora de la tard (TCT).
$ \begin{array} {|c|c|c|} \hline Sujeto & TCM & TCT \\ \hline 1 & 58 & 65 \\ \hline 2 & 72 & 72 \\ \hline 3 & 64 & 73 \\ \hline 4 & 68 & 80 \\ \hline 5 & 67 & 63 \\ \hline \end{array} $
Tabla 3 : Datos del Ejercicio guiado 2

Estudiar mediante un intervalo de confianza al 99% si, por término medio, la tasa cardíaca es igual por la mañana y a última hora de la tarde.

Solución:

En primer lugar debemos importar el archivo de datos tcardiaca.txt.

Para ello, seleccionamos en el menú principal: Datos/Importar datos/desde archivo de texto

Se muestra la siguiente pantalla

donde, en Introducir el nombre del conjunto de datos escribimos tcardiaca y pulsamos Aceptar. En el directorio seleccionamos el archivo tcardiaca.txt y pulsamos abrir.

R-Commander muestra el archivo tcardiaca en Conjunto de datos

Puslsamos Visualizar conjunto de datos y se muestra

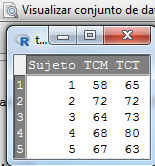
En este caso nos encontramos ante un intervalo de confianza para la diferencia medias en dos poblaciones normales relacionadas. Seleccionamos: Estadísticos/Medias/Test t para datos relacionados. Se muestra la siguiente pantalla

La pestaña Datos muestra dos listas de variables cada una de las cuales incluye todas las variables cuantitativas que son susceptibles de ser analizadas. Seleccionamos en cada lista la variable que nos interese (TCM y TCT en nuestro caso).

Pulsamos Opciones

En la pestaña Opciones podemos personalizar el contraste. Como en este caso sólo nos interesa el intervalo de confianza, introducimos el valor del nivel de confianza dado en el enunciado (99%). Si hacemos clic en Aceptar, el programa nos devuelve la siguiente salida:

Paired t-test
data: TCM and TCT
t = -1.6236, df = 4, p-value = 0.1798
alternative hypothesis: true difference in means is not equal to 0
99 percent confidence interval:
-18.411312 8.811312
sample estimates:
mean of the differences
-4.8

En la segunda parte de los resultados se incluye el intervalo de confianzaal 99% para la diferencia de las medias de la variable tasa cardíaca, que es (-18.411312, 8.811312). Este intervalo incluye el valor 0, lo que significa que el 0 es un valor posible para la diferencia entre las medias. Por ello, concluimos que puede asumirse que la diferencia entre dichas medias es 0, o dicho de otro modo, que ambas tasas cardíacas son iguales.

Ejercicio Guiado 3 (Resuelto)

Una determinada empresa quiere saber si su nuevo producto tendrá más aceptación en la población de hombres o entre las mujeres. Para ello, considera una muestra aleatoria de 38 hombres y 62 mujeres, observando que sólo a 15 hombres y 33 mujeres les había gustado su producto. Construir un intervalo de confianza al 99% de confianza para la diferencia de proporciones de hombres y mujeres a los que les gusta el producto. ¿Puede suponerse que el producto gusta por igual en hombres y mujeres?

Solución:

En primer lugar debemos importar el archivo de datos empresa.xls

Para ello, seleccionamos en el menú principal: Datos/Importar datos/desde un archivo de Excel

Se pulsa Aceptar. En el directorio seleccionamos el archivo empresa.xls y pulsamos abrir.

Se selecciona Visualizar conjunto de datos

Dado que la hipótesis que se ha planteado se ha hecho la diferencia entre mujeres y hombres a los que les gusta el producto, es necesario hacer una recodificación de la variable Producto. Para ello seleccionamos Datos/Modificar variables del conjunto de datos activo/Recodificar variables
En la pantalla resultante:
En la casilla: Nuevo nombre o prefijo para la variable múltiple recodificadas ponemos Producto_rec.

Una forma de recodificar la variable es ponerle un número delante del carácter. De este modo la primera categoría de la variable es aquella con el número más bajo, en este caso Sí
Se pulsa Aceptar y se muestra el siguiente conjunto de datos
A continuación realizamos un intervalo de confianza para la diferencia de dos proporciones. Seleccionamos: Estadísticos/Proporciones/Test de proporciones para dos muestras. Se muestra la siguiente pantalla
La pestaña Datos muestra dos listas con las variables cualitativas que incluye el conjunto de datos. De la primera lista seleccionamos la variable de agrupación (en nuestro caso es el Sexo) y de la segunda, la variable de interés (Producto_rec).
Pulsamos Opciones

En la pestaña Opciones podemos personalizar el contraste. Como en este caso sólo nos interesa el intervalo de confianza, introducimos el valor del nivel de confianza dado en el enunciado (99%). Si hacemos clic en Aceptar, el programa nos devuelve la siguiente salida:
Percentage table:
Producto_rec
Sexo      1Sí 2No Total Count
Hombre 39.5 60.5   100    38
Mujer 53.2 46.8   100    62
2-sample test for equality of proportions without continuity correction
data: .Table
X-squared = 1.7851, df = 1, p-value = 0.1815
alternative hypothesis: two.sided
99 percent confidence interval:
-0.3989753 0.1239329
sample estimates:
prop 1    prop 2
0.3947368 0.5322581

Según los resultados, el intervalo de confianza para la diferencia de proporciones que buscamos es ( -0.3989753 0.1239329), el cual incluye al 0, por lo que se puede afirmar que el producto gusta por igual entre hombres y mujeres.

Ejercicio Guiado 4 (Resuelto)

En una experiencia genética se extraen 20 moscas de una caja experimental y se mide la longitud del ala de cada una. Se obtuvieron los siguientes valores:

93, 90, 97, 90, 93, 91, 96, 94, 91, 91, 88, 93, 95, 91, 89, 92, 87, 88, 90, 86

Suponiendo que la longitud del ala sigue una distribución Normal. Construir un intervalo de confianza al 99% de confianza para

a) La media μ

b) La varianza σ²

Solución:

En primer lugar debemos importar el archivo de datos moscas.txt

Para ello, seleccionamos en el menú principal: Datos/Importar datos/desde un archivo de texto

Se pulsa Aceptar. En el directorio seleccionamos el archivo moscas.txt y pulsamos abrir

Se selecciona Visualizar conjunto de datos

a) Construir un intervalo de confianza al 99% de confianza para la media μ

Hay que obtener un intervalo de confianza cuando la varianza poblacional es desconocida

Accedemos al menú Test t para una muestra, seleccionando en el menú principal: Estadísticos/ Medias/ Test t para una muestra.

Se mostrrá el siguiente cuadro de diálogo

En la parte superior izquierda se muestra una lista con todas las variables cuantitativas del archivo de datos que son susceptibles de ser contrastadas, de la cual debemos elegir exclusivamente una.

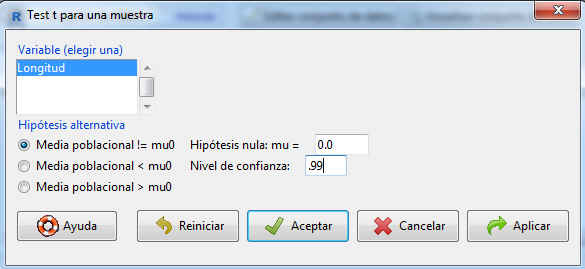
Presionamos Aceptar, y la salida que nos muestra el programa es la siguiente:

One Sample t-test
data: Longitud
t = 139.01, df = 19, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
99 percent confidence interval:
89.37195 93.12805
sample estimates:
mean of x
91.25

El intervalo de confianza para la longitud media de las alas al 99% de confianza, es (89.37195, 93.12805)

b) Construir un intervalo de confianza para la varianza σ² al 99% de confianza.

El intervalo de confianza que debemos calcular es

$ \left ( \displaystyle \frac {(n-1) \sigma^{2}}{ \chi^{2}_{1- \alpha/2, n-1 }}, \displaystyle \frac {(n-1) \sigma^{2}}{ \chi^{2}_{\alpha/2, n-1 } } \right ) $

Expresión 28: Expresión del Intervalo de confianza para la varianza (media conocida)

Nota: R-Commander no incluye una función específica para el cálculo de intervalos de confianza en este tipo de situaciones. Por lo tanto calcularemos el intervalo de la siguiente forma

> n <- length(longitud)
> varianza <- var(longitud)
> L1 <- (n – 1) * varianza / qchisq(1-alpha / 2,n – 1)
> L2 <- (n – 1) * varianza / qchisq(alpha /2,n – 1)
> IC <- c(L1,L2)
> IC

[1] 4.244179 23.926166

El intervalo pedido es: (4.244179, 23.926166)

Ejercicios Propuestos

Ejercicio Propuesto 1

En la tabla siguiente se muestran los salarios mensuales en euros de 10 trabajadores de Madrid y Barcelona.

$ \begin{array} {|c|c|c|} \hline Trabajador & Ciudad & Salario \\ \hline 1 & Madrid & 1800 \\ \hline 2 & Madrid & 2000 \\ \hline 3 & Barcelona & 2100 \\ \hline 4 & Madrid & 2300 \\ \hline 5 & Barcelona & 1900 \\ \hline 6 & Barcelona & 2500 \\ \hline 7 & Madrid & 1900 \\ \hline 8 & Madrid & 2300 \\ \hline 9 & Madrid & 2500 \\ \hline 10 & Barcelona & 1800 \\ \hline \end{array} $

Tabla 4 : Datos del Ejercicio propuesto 1

Se pide:

a) Obtener un intervalo de confianza a un nivel del 89% para el salario medio entre ambas ciudades

b) Obtener un intervalo de confianza a un nivel del 90% para la diferencia media de salarios entre ambas ciudades. ¿Se pueden considerar iguales?

c) Obtener un intervalo de confianza a un nivel del 90% para la proporción de trabajadores en Barcelona.

Ejercicio Propuesto 2

Para comprobar si un determinado fertilizante puede mejorar la producción de manzanas, se selecciona una muestra aleatoria simple de 10 árboles. En la tabla siguiente se muestra el peso (en Kgr) de manzanas por árbol recogidas antes y después del tratamiento

$ \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 1 & 1 & 0.5 & 1 & 2 & 2 & 1.2 & 2.5 & 1.2 & 1.3 \\ \hline Después & 1.5 & 2 & 1.2 & 1 & 2.8 & 1.5 & 1 & 2 & 2.3 & 2.5 \\ \hline \end{array} $

Tabla 5: Datos del Ejercicio propuesto 2

Obtener un intervalo de confianza al 98% para la diferencia de los pesos medios producida antes y después del tratamiento.

Ejercicio Propuesto 3

En una muestra aleatoria de 150 personas con pelo oscuro se encontró que 90 de ellas tenían los ojos azules. Construir un intervalo de confianza al 95% para la proporción de individuos que teniendo pelo oscuro en la población posee ojos azules. ¿Son compatibles estos resultados con la suposición de que dicha proporción vale 2/3).

Ejercicio Propuesto 4

En una piscifactoría se desea comparar el porcentaje de peces adultos que miden menos de 20 cm con los que miden más de 40 cm. Para ello, se toma una muestra de 200 peces observando que 40 de ellos miden menos de 20 cm y una muestra de 200 peces de los que 57 miden más de 40 cm. Halla un intervalo de confianza para:

a) La diferencia de proporciones de peces adultos que miden más de 40 cm con los que miden menos de 20 cm al nivel de confianza del 0.95
a) La diferencia de proporciones de peces adultos que miden menos de 20 cm con los que miden más de 40 cm al nivel de confianza del 0.95

Ejercicio Propuesto 1 (Resuelto)

En la tabla siguiente se muestran los salarios mensuales en euros de 10 trabajadores de Madrid y Barcelona.

$ \begin{array} {|c|c|c|} \hline Trabajador & Ciudad & Salario \\ \hline 1 & Madrid & 1800 \\ \hline 2 & Madrid & 2000 \\ \hline 3 & Barcelona & 2100 \\ \hline 4 & Madrid & 2300 \\ \hline 5 & Barcelona & 1900 \\ \hline 6 & Barcelona & 2500 \\ \hline 7 & Madrid & 1900 \\ \hline 8 & Madrid & 2300 \\ \hline 9 & Madrid & 2500 \\ \hline 10 & Barcelona & 1800 \\ \hline \end{array} $

Tabla 4: Datos del Ejercicio propuesto 1

Se pide:

a) Obtener un intervalo de confianza a un nivel del 89% para el salario medio entre ambas ciudades

b) Obtener un intervalo de confianza a un nivel del 90% para la diferencia media de salarios entre ambas ciudades. ¿Se pueden considerar iguales?

c) Obtener un intervalo de confianza a un nivel del 90% para la proporción de trabajadores en Barcelona.

Solución:

En primer lugar debemos importar el archivo de datos salario.xls

Para ello, seleccionamos en el menú principal: Datos/Importar datos/desde un archivo de Excel.

a) Obtener un intervalo de confianza a un nivel del 89% para el salario medio entre ambas ciudades

One Sample t-test
data: Salario
t = 24.473, df = 9, p-value = 1.521e-09
alternative hypothesis: true mean is not equal to 0
89 percent confidence interval:
1957.145 2262.855
sample estimates:
mean of x
2110

Por lo que el intervalo de confianza es (1957.145, 2262.855).

b) Obtener un intervalo de confianza a un nivel del 90% para la diferencia media de salarios entre ambas ciudades. ¿Se pueden considerar iguales?

En este caso nos encontramos ante un intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes.

En primer lugar, comprobamos si las varianzas de ambas distribuciones son iguales.

Se muestra la siguiente salida

F test to compare two variances
data: Salario by Ciudad
F = 1.2835, num df = 3, denom df = 5, p-value = 0.7512
alternative hypothesis: true ratio of variances is not equal to 1
90 percent confidence interval:
0.2372666 11.5686088
sample estimates:
ratio of variances
1.283482

El intervalo de confianza para el cociente de las varianzas es (0.2372666, 11.5686088). Dicho intervalo incluye al 1 entre sus posibles valores. Esto implica que a un nivel de confianza del 90% se puede suponer que el cociente entre las dos varianzas puede tomar el valor 1 o, lo que es lo mismo, que las dos varianzas son iguales.

Una vez se ha determinado la igualdad de las varianzas de ambas distribuciones, procedemos a calcular el intervalo de confianza para la diferencia de las medias propiamente dicho.

Se muestra la siguiente salida

Two Sample t-test
data: Salario by Ciudad
t = -0.31443, df = 8, p-value = 0.7612
alternative hypothesis: true difference in means is not equal to 0
90 percent confidence interval:
-403.3204 286.6537
sample estimates:
mean in group Barcelona mean in group Madrid
2075.000 2133.333

El intervalo de confianza a un 90% de confianza para la diferencia de las medias de salarios entre ambas ciudades es (-403.3204, 286.6537). Como el 0 está dentro de este intervalo, tenemos suficiente evidencia muestral para decir que los salarios en ambas ciudades son iguales.

c) Obtener un intervalo de confianza a un nivel del 90% para la proporción de trabajadores en Barcelona.

En este caso nos encontramos ante un intervalo de confianza para la proporción.

Dado que la hipótesis que se ha planteado se ha hecho sobre Barcelona, no es necesario hacer ninguna recodificación de la variable.

Se muestra la siguiente salida

Frequency counts (test is for first level):
Ciudad
Barcelona    Madrid
        4         6
    1-sample proportions test without continuity correction
data: rbind(.Table), null probability 0.5
X-squared = 0.4, df = 1, p-value = 0.5271
alternative hypothesis: true p is not equal to 0.5
90 percent confidence interval:
0.1942270 0.6483614
sample estimates:
p
0.4

Por lo que el intervalo de confianza, a un nivel de confianza del 90% para la proporción de trabajadores en Barcelona es (0.1942270, 0.6483614).

Solución del Ejercicio propuesto 1

Ejercicio Propuesto 2 (Resuelto)

Tabla 5: Datos del Ejercicio propuesto 2

Obtener un intervalo de confianza al 98% para la diferencia de los pesos medios producida antes y después del tratamiento.

Solución:

En primer lugar se importa el archivo de datos manzanas.xls,

El intervalo de confianza al 98% para la diferencia de los pesos medios producida antes y después del tratamiento

Paired t-test
data: Antes and Después
t = -2.1262, df = 9, p-value = 0.0624
alternative hypothesis: true difference in means is not equal to 0
98 percent confidence interval:
-1.0006005 0.1406005
sample estimates:
mean of the differences
-0.43

En la segunda parte de los resultados se incluye el intervalo de confianzaal 98% para la diferencia de las medias los pesos, que es (-1.0006005, 0.1406005). Este intervalo incluye el valor 0, lo que significa que el 0 es un valor posible para la diferencia entre las medias. Por ello, concluimos que puede asumirse que la diferencia entre dichas medias es 0, o dicho de otro modo, que ambos pesos son iguales.

Solución del Ejercicio propuesto 2

Ejercicio Propuesto 3 (Resuelto)

Solución:

En primer lugar debemos importar el archivo de datos propuesto3.xls

Frequency counts (test is for first level):
Azules_R
1Sí 2No
90 60
1-sample proportions test without continuity correction

data: rbind(.Table), null probability 0.5
X-squared = 6, df = 1, p-value = 0.01431
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.5200492 0.6749568
sample estimates:
p
0.6

El intervalo de confianza para la proporción de individuos que teniendo pelo oscuro en la población posee ojos azules, a un nivel del 95%, es (0.5200492, 0.6749568). Este resultado si es compatible con la suposición de que dicha proporción vale 2/3, ya que 2/3 pertenece al intervalo.

Solución del Ejercicio propuesto 3

Ejercicio Propuesto 4 (Resuelto)

a) La diferencia de proporciones de peces adultos que miden más de 40 cm con los que miden menos de 20 cm al nivel de confianza del 0.95
b) La diferencia de proporciones de peces adultos que miden menos de 20 cm con los que miden más de 40 cm al nivel de confianza del 0.95

Solución:

En primer lugar debemos importar el archivo de datos propuesto4.xls

a) La diferencia de proporciones de peces adultos que miden más de 40 cm con los que miden menos de 20 cm al nivel de confianza del 0.95

Percentage table:
           resultado_rec
medida       1Sí 2No Total Count
masde40   28.5 71.5   100   200
menosde20 20.0 80.0   100   200
    2-sample test for equality of proportions without continuity correction
data: .Table
X-squared = 3.9332, df = 1, p-value = 0.04734
alternative hypothesis: two.sided
95 percent confidence interval:
0.001410925 0.168589075
sample estimates:
prop 1 prop 2
0.285 0.200

Intervalo de confianza para la diferencia de proporciones entre los peces adultos que miden más de 40 cm y los que miden menos de 20 cm al 95% (0.001410925, 0.168589075)

b) La diferencia de proporciones de peces adultos que miden menos de 20 cm con los que miden más de 40 cm al nivel de confianza del 0.95

Percentage table:
            resultado_rec
medida_rec    1Sí 2No Total Count
1menosde20 20.0 80.0   100   200
2masde40   28.5 71.5   100   200
    2-sample test for equality of proportions without continuity correction
data: .Table
X-squared = 3.9332, df = 1, p-value = 0.04734
alternative hypothesis: two.sided
95 percent confidence interval:
-0.168589075 -0.001410925
sample estimates:
prop 1 prop 2
0.200 0.285

Intervalo de confianza para la diferencia de proporciones entre los peces adultos que miden menos de 20 cm y los que miden más de 40 cm al 95% ( -0.168589075, -0.001410925).

Solución del Ejercicio propuesto 4

Autoras: Beatriz Cobo Rodríguez y Ana María Lara Porras. Universidad de Granada. (2017).

Reformulado con MathML en 2021 por Ana María Lara Porras

Práctica 5

INTERVALOS DE CONFIANZA

Objetivos

Introducción

Intervalo de confianza para la media en una población normal con varianza conocida

Supuesto Práctico 1

Solución

Intervalo de confianza para la media en una población normal con varianza desconocida

Supuesto Práctico 2

Solución

Intervalo de confianza para la proporción

Supuesto Práctico 3

Solución

Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes

Intervalo de confianza para el cociente de varianzas en dos poblaciones normales independientes

Supuesto Práctico 4

Solución

a) Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes cuando las varianzas poblacionales son desconocidas pero supuestas iguales

b) Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes cuando las varianzas poblacionales son desconocidas, distintas y tamaños muestrales grandes

Supuesto Práctico 5

Solución

Intervalo de confianza para la diferencia de medias en dos poblaciones normales relacionadas

Supuesto Práctico 6

Solución

Intervalo de confianza para la diferencia de dos proporciones

Supuesto Práctico 7

Solución

Ejercicios

Ejercicios Guiados

Ejercicio Guiado1

Ejercicio Guiado 2

Ejercicio Guiado 3

Ejercicio Guiado 4

Ejercicio Guiado 1 (Resuelto)

Solución:

Ejercicio Guiado 2 (Resuelto)

Solución:

Ejercicio Guiado 3 (Resuelto)

Solución:

Ejercicio Guiado 4 (Resuelto)

Solución:

Ejercicios Propuestos

Ejercicio Propuesto 1

Ejercicio Propuesto 2

Ejercicio Propuesto 3

Ejercicio Propuesto 4

Ejercicio Propuesto 1 (Resuelto)

Solución:

Ejercicio Propuesto 2 (Resuelto)

Solución:

Ejercicio Propuesto 3 (Resuelto)

Solución:

Ejercicio Propuesto 4 (Resuelto)

Solución: