MÉTODOS DE ANÁLISIS MULTIVARIANTE: ANÁLISIS CLÚSTER
Objetivos
- Identificar grupos de objetos homogéneos.
- Determinar el criterio de similitud.
- Distinguir los Métodos de clasificación Jerárquicos y los Métodos de clasificación No-Jerárquicos o Repartición.
- Plantear y aplicar el Análisis Clúster Jerárquico.
- Distinguir los Métodos Jerárquicos Aglomerativos y los Métodos Jerárquicos Divisivos.
- Entender y aplicar el proceso algorítmico del Análisis Clúster Jerárquico Aglomerativo.
- Saber construir una matriz de distancias.
- Representar e Interpretar un dendograma.
- Plantear y aplicar el Análisis Clúster de K medias.
- Entender y aplicar el proceso algorítmico del Análisis Clúster de K medias.
- Plantear y aplicar el Análisis Clúster en dos etapas o bietápico.
Introducción al Análisis Clúster
El análisis clúster, también llamado análisis de conglomerados, es una técnica estadística multivariante que tiene por objeto formar grupos de individuos. Estos grupos reciben el nombre de clústers o conglomerados; de ahí el nombre de la técnica. Los individuos que conforman cada uno de los grupos que resultan de la aplicación de un análisis clúster son muy similares entre sí y, a la vez, muy diferentes a los individuos que conforman el resto de grupos.
- El objetivo del Análisis Clúster es formar grupos de objetos de manera que, por un lado, los objetos pertenecientes a un mismo grupo sean muy semejantes entre sí y, por otro lado, los objetos pertenecientes a grupos diferentes sean lo más heterogéneos posible entre sí
La formación de los grupos se realiza en función de la similitud o de la distancia que existe entre los individuos calculada a partir de un conjunto de variables numéricas. La obtención de dichos clústers depende del criterio o distancia considerados, por ejemplo, una baraja de carta española se podría dividir de distintas formas: en dos clústers (figuras y números), en cuatro clústers (los cuatro palos), en ocho clústers (los cuatro palos y según sean figuras o números). Es decir, el número de clústers depende de lo que consideremos como similar.
El análisis clúster es una tarea de clasificación. Por ejemplo
- Clasificar grupos de consumidores respecto a sus preferencias en nuevos productos
- Clasificar las entidades bancarias donde sería más rentable invertir
- Clasificar las estrellas del cosmos en función de su luminosidad
- Identificar si hay grupos de municipios en una determinada comunidad con una tendencia similar en el consumo de agua con el fin de identificar buenas prácticas para la sostenibilidad y zonas problemáticas por alto consumo.
El análisis Clúster es una técnica exploratoria puesto que para realizar el proceso de clasificación no utiliza ningún tipo de modelo estadístico.
Como se puede comprender fácilmente el análisis clúster tiene una extraordinaria importancia en la investigación científica, en cualquier rama del saber. La clasificación es uno de los objetivos fundamentales de la Ciencia y en la medida en que el análisis clúster nos proporciona los medios técnicos para realizarla, se nos hará imprescindible en cualquier investigación. Es muy importante que el analista tenga conocimientos del problema a analizar, ya que de otra forma el resultado del análisis de los datos se puede convertir en una disección de los mismos en vez de una clasificación representativa en conglomerados
Planteamiento del problema
Supongamos que partimos de una muestra \( X \) formada por n individuos y para cada uno de ellos se miden p variables, \( X_1,X_2, \cdots, X_p \) (p variables numéricas observadas en n objetos o individuos). Donde \( x_{ij} \) representa el valor de la la variable \( X_{j} \) para el i -ésimo individuo \( i= 1,2, \cdots, n \); \( j=1,2, \cdots, p \).
Toda la información recogida en la muestra puede resumirse en la siguiente matriz:
\( X = \left( \begin{matrix} x_{11} & x_{12} & \dots & x_{1j} & \dots & x_{1p} \\ x_{21} & x_{22} & \dots & x_{2j} & \dots & x_{2p} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_{i1} & x_{i2} & \dots & x_{ij} & \dots & x_{ip} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_{n1} & x_{n2} & \dots & x_{nj} & \dots & x_{np} \end{matrix} \right) \)
La i-ésima fila de la matriz X contiene los valores de cada variable para el i-ésimo individuo, mientras que la j-ésima columna muestra los valores pertenecientes a la j-ésima variable a lo largo de todos los individuos de la muestra. Es decir, donde cada fila recoge las observaciones para un individuo y cada columna recoge las observaciones para una variable.
Se trata, fundamentalmente, de resolver el siguiente problema: Dado un conjunto de n individuos caracterizados por la información de p variables \( X_{j} \), \( ( j=1,2, \cdots, p) \), nos planteamos clasificarlos de manera que los individuos pertenecientes a un grupo (clúster) (y siempre con respecto a la información disponible de las variables) sean lo más similares posibles entre sí y los distintos grupos sean entre ellos tan disimilares como sea posible.
El proceso completo puede estructurarse de acuerdo con el siguiente esquema:
-
Partimos de un conjunto de n individuos de los que se dispone de una información cifrada por un conjunto de p variables (una matriz de datos de n individuos y p variables).
-
Establecemos un criterio de similaridad y construimos una matriz de similaridades que nos permita relacionar la semejanza de los individuos entre sí. Para medir lo similares (o disimilares) que son los individuos existe una gran cantidad de índices de similaridad y de disimilaridad o divergencia. Todos ellos tienen propiedades y utilidades distintas y habrá que ser consciente de ellas para su correcta aplicación.
-
Elegimos un algoritmo de clasificación para determinar la estructura de agrupación de los individuos.
-
Especificamos esa estructura mediante diagramas arbóreos.
El análisis clúster: Técnica de agrupación de variables y de casos
-
Como técnica de agrupación de variables, el análisis clúster es similar al análisis factorial. Pero, mientras que el análisis factorial es poco flexible en algunos de sus supuestos (linealidad, normalidad, variables cuantitativas, etc.) y estima de la misma manera la matriz de distancias, el análisis clúster es menos restrictivo en sus supuestos (no exige linealidad, ni simetría, permite variables categóricas, etc.) y admite varios métodos de estimación de la matriz de distancias.
-
Como técnica de agrupación de casos, el análisis clúster es similar al análisis discriminante. Pero mientras que el análisis discriminante se centra en la agrupación de variables, es decir efectúa la clasificación tomando como referencia un criterio o variable dependiente (los grupos de clasificación), el análisis clúster se centra en agrupar objetos, es decir permite detectar el número óptimo de grupos y su composición únicamente a partir de la similaridad existente entre los casos; además, el análisis de clúster no asume ninguna distribución específica para las variables.
Inconvenientes del Análisis Clúster: Es un análisis descriptivo, a teórico y no inferencial. Habitualmente se utiliza como una técnica exploratoria que no ofrece soluciones únicas, las soluciones dependen de las variables consideradas y del método de análisis clúster utilizado.
Aplicabilidad: Las técnicas de análisis clúster han sido tradicionalmente utilizadas en muchas disciplinas, por ejemplo, Astronomía (Clúster = galaxia, súper galaxias, etc.), Marketing (segmentación de mercados, investigación de mercados), Psicología, Biología (Taxonomía. Microarrays), Ciencias Ambientales (Clasificación de ríos para establecer tipologías según la calidad de las aguas), Sociología, Economía, Ingeniería, ….
JAIN and DUBES (1988) definen el Análisis de Clúster como una herramienta de exploración de datos que se complementa con técnicas de visualización de los mismos.
Resumiendo
-
El objetivo del Análisis Clúster es obtener grupos de objetos de forma que, por un lado, los objetos pertenecientes a un mismo grupo sean muy semejantes entre sí y, por el otro, los objetos pertenecientes a grupos diferentes tengan un comportamiento distinto con respecto a las variables analizadas.
-
Es una técnica exploratoria puesto que la mayor parte de las veces no utiliza ningún tipo de modelo estadístico para llevar a cabo el proceso de clasificación.
-
Conviene estar siempre alerta ante el peligro de obtener, como resultado del análisis, no una clasificación de los datos sino una disección de los mismos en distintos grupos. El conocimiento que el analista tenga acerca del problema decidirá que grupos obtenidos son significativos y cuáles no.
-
Una vez establecidas las variables y los objetos a clasificar el siguiente paso consiste en establecer una medida de proximidad o de distancia entre ellos que cuantifique el grado de similaridad entre cada par de objetos.
- Las medidas de proximidad, similitud o semejanza miden el grado de semejanza entre dos objetos de forma que, cuanto mayor (menor) es su valor, mayor (menor) es el grado de similaridad existente entre ellos y mayor (menor) es la probabilidad de que los métodos de clasificación los asignen en el mismo grupo.
-
Las medidas de disimilitud, desemejanza o distancia miden la distancia entre dos objetos de forma que, cuanto mayor (menor) sea su valor, más (menos) diferentes son los objetos y menor (mayor) es la probabilidad de que los métodos de clasificación los asignen en el mismo grupo.
Técnicas de clasificación
Se distinguen dos grandes categorías de métodos clústers, dos procedimientos distintos para la clasificación de los individuos en grupos o, equivalentemente, para la formación de los grupos. En concreto: Procedimientos jerárquicos y Procedimientos no-jerárquicos
- Procedimientos Jerárquicos: En cada paso del algoritmo sólo un objeto cambia de grupo y los grupos están anidados en los de pasos anteriores. Si un objeto ha sido asignado a un grupo ya no cambia más de grupo. La clasificación resultante tiene un número creciente de clases anidadas.
- Procedimientos No jerárquico o Repartición: Comienzan con una solución inicial, un número de grupos g fijado de antemano y agrupa los objetos para obtener los g grupos.
Procedimientos jerárquicos
Son procedimientos iterativos en los que, en cada paso o iteración, se produce un único cambio en las agrupaciones motivado por la asignación de un individuo a un grupo. Una vez que un individuo es asignado a un grupo, se mantiene en el mismo grupo hasta el final de procedimiento.
Este procedimiento intenta identificar grupos relativamente homogéneos de casos basándose en las variables seleccionadas. Se utiliza cuando no se conoce el número de clusters a priori y cuando el número de objetos no es muy grande. Al trabajar con variables que pueden venir dadas en diferentes unidades de medida, el escalamiento de las variables es un aspecto importante, ya que las diferentes escalas en que están medidas las variables pueden afectar a las soluciones de conglomeración. Si las variables muestran grandes diferencias en el escalamiento (por ejemplo, una variable se mide en dólares y la otra se mide en años), se debe considerar la posibilidad de estandarizarlas.
Los métodos jerárquicos se subdividen a su vez en aglomerativos y divisivos (o disociativos):
- Los procedimientos jerárquicos aglomerativos parten de una situación inicial en la que hay tantos grupos como individuos componen la muestra. En cada paso, se fusionan los dos grupos más similares (o, equivalentemente, los dos grupos menos disimilares o menos distantes). A continuación, se vuelve a calcular el grado de similaridad entre grupos. El procedimiento termina con un único grupo formado por todos los individuos de la muestra. En este tipo de procedimientos, cuando dos grupos se fusionan permanecerán unidos hasta el final del proceso.
- Los procedimientos jerárquicos divisivos (o disociativos) parten de una situación inicial en la que hay un único grupo que incluye a todos los individuos de la muestra. En cada paso, se divide en dos al grupo más heterogéneo, esto es, el grupo cuyos elementos sean menos similares o estén más distantes. A continuación, se vuelve a calcular el grado de similaridad dentro de cada grupo. El procedimiento termina con tantos grupos (de un individuo cada uno) como individuos compongan la muestra.
Independientemente del proceso de agrupamiento, hay diversos criterios para ir formando los clústers; todos estos criterios se basan en una matriz de distancias o similitudes.
Algunos de los métodos jerárquicos aglomerativos más usados son:
- Método del enlace simple o del vecino más próximo. En este método se asume que la distancia o similitud entre dos grupos viene dada por la mínima distancia (o máxima similitud) entre sus individuos (entre sus individuos más cercanos).
- Método del enlace completo o del vecino más lejano. En este método se asume que la distancia o similitud entre dos grupos viene dada por la máxima distancia (o mínima similitud) entre sus individuos (entre sus individuos más lejanos).
- Método del promedio entre grupos. En este método se asume que la distancia o similitud entre dos grupos viene dada por la media de las distancias (o de las similitudes) entre los individuos de ambos grupos.
- Método del promedio ponderado entre grupos. Variación del método anterior, en el que cada individuo tiene un peso asignado.
- Método del centroide. Este método mide la proximidad entre grupos calculando la distancia entre sus centroides, teniendo en cuenta los tamaños de los grupos.
- Método de la mediana. Este método mide la proximidad entre grupos calculando la distancia entre sus centroides, teniendo en cuenta los tamaños de los grupos. Este método mide la proximidad entre grupos calculando la distancia entre sus centroides, sin tener en cuenta los tamaños de los grupos.
- Método de Ward. Este método se unen grupos de manera que se minimiza la varianza dentro cada uno de ellos, por lo que se maximiza la homogeneidad dentro de cada grupo.
Jerárquicos aglomerativos:
- Método del Linkage Simple, Enlace Simple o Vecino más próximo
- Método del Linkage Completo, Enlace Completo o Vecino más alejado
- Método del Promedio entre grupos
- Método del Centroide
- Método del la Mediana
- Método de Ward
Jerárquicos divisivos o disociativos
- Método del Linkage Simple
- Método del Linkage Completo
- Método del Promedio entre grupos
- Método del Centroide
- Método del la Mediana
- Análisis de Asociación
Procedimientos no jerárquicos (o de partición o reparto)
Este tipo de procedimientos parten de una solución inicial con un número de clústers determinado de antemano, (requiere conocer el número de clústers a priori) y se agrupan los objetos para obtener esos grupos. Es decir, se elige una partición de los individuos conformada por un número de grupos determinado y se van intercambiando los individuos entre grupos para obtener una partición mejor, entendida como aquella con mayor similitud (o menor distancia) entre los miembros de los grupos. El clúster no jerárquico sólo puede ser aplicado a variables cuantitativas.
El método de análisis clúster no jerárquico más utilizado es el de las k-medias.
Análisis de conglomerados de K medias
En el análisis clúster de k-medias se asignan los individuos a un número fijo de grupos, en base a los valores de un conjunto de variables que deben ser cuantitativas. Cada individuo debe pertenecer a un grupo y solo a uno. Esta técnica es especialmente útil cuando se quiere clasificar un gran número de casos. De forma general, este método se basa en el siguiente algoritmo:
- Fijar, aleatoriamente, los centroides de los k clústers (k debe ser fijado de antemano).
- Asignar cada unidad a un clúster, en base a un determinado criterio.
- Recalcular los centroides de los clústers.
Los pasos 2 y 3 se repiten iterativamente hasta que se satisface un criterio de parada como, por ejemplo, que no se produzca ninguna reasignación, es decir, que los clústers obtenidos en dos iteraciones consecutivas sean los mismos.
En este método, la medida de distancia o de similaridad entre los casos se calcula utilizando la distancia euclídea. Es muy importante el tipo de escala de las variables, si las variables tienen diferentes escalas (por ejemplo, una variable se expresa en dólares y otra en años), los resultados podrían ser equívocos. En estos casos, se debería considerar la estandarización de las variables antes de realizar el análisis de conglomerados de k-medias.
Este procedimiento supone que se ha seleccionado el número apropiado de conglomerados y que se han incluido todas las variables relevantes. Si se ha seleccionado un número inapropiado de conglomerados o se han omitido variables relevantes, los resultados podrían ser equívocos.
El método suele ser muy sensible a la solución inicial dada por lo que es conveniente utilizar una que sea buena o probar con varias soluciones iniciales. Una forma de construir una solución inicial apropiada es mediante una clasificación obtenida por un algoritmo jerárquico.
Proceso que se debe seguir en un análisis clúster
Paso 1: Selección de variables
De forma previa a la aplicación de la técnica en sí hay que prestar atención a las variables que se van a considerar para la formación de los clústers. Hay que asegurarse, por ejemplo, de seleccionar exclusivamente aquellas variables que realmente caracterizan a los individuos que se van a agrupar y que pueden tener relevancia a la hora de la formación de los clústers.
La clasificación dependerá de las variables elegidas. Introducir variables irrelevantes aumenta la posibilidad de errores. También hay que tener en cuenta el número de variables.
- Seleccionar sólo aquellas variables que caracterizan los objetos que se van agrupando, y referentes a los objetivos del análisis clúster que se va a realizar
- Si el número de variables es muy grande es aconsejable realizar previamente un Análisis de Componentes Principales para reducir la dimensionalidad y resumir la información del conjunto de variables.
Paso 2: Detección y eliminación de valores atípicos.
El análisis clúster es muy sensible a la presencia de individuos con características muy diferentes a las del grueso del grupo. En general, estos individuos tienden a ser asignados a un grupo exclusivo que no comparten con ningún otro individuo, lo cual dificulta la interpretación de los resultados.
Paso 3. Selección del método para determinar la distancia o disimilitud entre individuos dependiendo de si los datos con cuantitativos o cualitativos
- Datos métricos: Para datos de naturaleza cuantitativa, se suelen emplear métodos basados en la correlación así como medidas de distancia. Medidas de correlación y medidas de distancia
- Datos no métricos: Si los datos son cualitativos, se utilizan técnicas basadas en la asociación. Medidas de asociación.
Paso 4: Decisión sobre la estandarización de los datos.
Si las variables a partir de las cuales se van a formar los grupos vienen dadas en unidades de medida muy dispares o si la magnitud de sus valores es muy dispar, se recomienda la estandarización de los datos antes de llevar a cabo el análisis clúster. Hay que tener en cuenta que el orden de las similitudes puede variar bastante con tan solo un cambio de escala en una de las variables, por lo que la tipificación solo se realizará cuando resulte necesaria.
Paso 5: Aplicación de la técnica e interpretación de los resultados.
Por último, se aplica el análisis clúster. Para ello, se ha de elegir el procedimiento que se va a emplear así como el número de clústers con el que nos quedaremos.
- El procedimiento que se va a emplear (jerárquicos o no jerárquicos)
- Número de clústers: Regla de parada. Existen diversos métodos de determinación del número de clústers, algunos están basados en reconstruir la matriz de distancias original, otros en los coeficientes de concordancia de Kendall y otros realizan análisis de la varianza entre los grupos obtenidos. Aunque no existe un criterio universalmente aceptado para determinar el número final de clústers, se suele hacer en función de las distancias de formación de los grupos, localizando en qué iteraciones del método utilizado dichas distancias dan grandes saltos
- Adecuación del modelo. Comprobar que el modelo no ha definido clúster con un solo objeto, clúster con tamaños desiguales,…
Análisis clúster en R
Con el programa R, podemos realizar un número casi ilimitado de tipos de análisis clúster.
En esta práctica vamos a estudiar tres tipos de métodos de análisis clúster:
- Análisis de conglomerados de bietápico
- Análisis de conglomerados de K medias
- Análisis de conglomerados jerárquicos.
Análisis de conglomerados de bietápico
El clúster en dos etapas está pensado para minería de datos, es decir para estudios con un número de individuos grande que pueden tener problemas de clasificación con los otros procedimientos. Se puede utilizar tanto cuando el número de clúster es conocido a priori y cuando es desconocido. Permite trabajar conjuntamente con variables de tipo mixto (cualitativas y cuantitativas).
Análisis de conglomerados de K medias
Es un método de clasificación No Jerárquico (Repartición). El número de clusters que se van a formar es fijado de antemano (requiere conocer el número de clústers a priori) y se agrupan los objetos para obtener esos grupos. Comienzan con una solución inicial y los objetos se reagrupan de acuerdo con algún criterio de optimalidad. El clúster no jerárquico sólo puede ser aplicado a variables cuantitativas. Este procedimiento puede analizar archivos de datos grandes.
Análisis de conglomerados jerárquicos
En el método de clasificación Jerárquico en cada paso del algoritmo sólo un objeto cambia de grupo y los grupos están anidados en los pasos anteriores. Si un objeto ha sido asignado a un grupo ya no cambia más de grupo. El método jerárquico es idóneo para determinar el número óptimo de conglomerados existente en los datos y el contenido de los mismos. Se utiliza cuando no se conoce el número de clusters a priori y cuando el número de objetos no es muy grande. Permite trabajar conjuntamente con variables de tipo mixto (cualitativas y cuantitativas). Siempre que todas las variables sean del mismo tipo, el procedimiento Análisis de Conglomerados Jerárquico podrá analizar variables de intervalo (continuas), de recuento o binarias.
Los tres métodos de análisis que vamos a estudiar son de tipo aglomerativo, en el sentido de que, partiendo del análisis de los casos individuales, intentan ir agrupando casos hasta llegar a la formación de grupos o conglomerados homogéneos.
Todos los métodos de análisis clúster son métodos exploratorios de datos
- Para cada conjunto de datos podemos tener diferentes agrupaciones, dependiendo del método
- Lo importante es identificar una solución que nos enseñe cosas relevantes de los datos.
En esta práctica estudiamos primero el Análisis clúster Jerárquico, seguido del Análisis Clúster de K medias y por último el Análisis Clúster en dos etapas.
Antes de comenzar a realizar un análisis clúster, primero explicaremos qué paquetes vamos a utilizar a lo largo de la práctica.
- Paquete “MVA”. Este paquete incorpora la función hclust, la más importante función para el análisis cluster.
- Paquete “foreign”. Este paquete sirve para leer datos .sav, datos con formato tipo SPSS.
- Paquete “vegan”. Este paquete amplia el paquete MVA permitiendo calcular otros tipos de matrices de distancias.
Vamos a proceder a instalarlos todos.
> install.packages(“foreign”)
> install.packages(“MVA”)
> install.packages(“vegan”)
Vamos a cargarlos todos en la librería.
> library(“foreign”)
> library(“MVA”)
> library(“vegan”)
Análisis clúster jerárquico
Este procedimiento intenta identificar grupos relativamente homogéneos de casos (o de variables) basándose en las características seleccionadas. Permite trabajar conjuntamente con variables de tipo mixto (cualitativas y cuantitativas), siendo posible analizar las variables brutas o elegir de entre una variedad de transformaciones de estandarización. Se utiliza cuando no se conoce el número de clústers a priori y cuando el número de objetos no es muy grande. Como hemos dicho anteriormente, los objetos de análisis de agrupamiento jerárquico pueden ser casos o variables, dependiendo de si desea clasificar los casos o examinar las relaciones entre las variables.
Al trabajar con variables que pueden ser cuantitativas, binarias o datos de recuento (frecuencias), el escalamiento de las variables es un aspecto importante, ya que las diferentes escalas en que están medidas las variables pueden afectar a las soluciones de conglomeración. Si las variables muestran grandes diferencias en el escalamiento (por ejemplo, una variable se mide en dólares y la otra se mide en años), se debe considerar la posibilidad de estandarizarlas. Esto puede llevarse a cabo automáticamente mediante el propio procedimiento Análisis de conglomerados jerárquico.
Estudiaremos fundamentalmente los Métodos Jerárquicos Aglomerativos. En estos métodos se utilizan diversos criterios para determinar, en cada paso del algoritmo, qué grupos se deben unir.
- Enlace simple o vecino más próximo: Mide la proximidad entre dos grupos calculando la distancia entre sus objetos más próximos o la similitud entre sus objetos más semejantes
- Enlace completo o vecino más alejado: Mide la proximidad entre dos grupos calculando la distancia entre sus objetos más lejanos o la similitud entre sus objetos menos semejantes
- Enlace medio entre grupos: Mide la proximidad entre dos grupos calculando la media de las distancias entre objetos de ambos grupos o la media de las similitudes entre objetos de ambos grupos
- Enlace medio dentro de los grupos: Mide la proximidad entre dos grupos con la distancia media existente entre los miembros del grupo unión de los dos grupos
- Métodos del centroide y de la mediana: Ambos métodos miden la proximidad entre dos grupos calculando la distancia entre sus centroides. Los dos métodos difieren en la forma de calcular los centroides: Método de Ward
- El método del centroide utiliza las medias de todas las variables
- En el método de la mediana, el nuevo centroide es la media de los centroides de los grupos que se unen
Comparación de los diversos métodos aglomerativos
- El enlace simple conduce a clústers encadenados
- El enlace completo conduce a clústers compactos
- El enlace completo es menos sensible a outliers que el enlace simple
- El método de Ward y el método del enlace medio son los menos sensibles a outliers
- El método de Ward tiene tendencia a formar clústers más compactos y de igual tamaño y forma en comparación con el enlace medio
- Todos los métodos salvo el método del centroide satisfacen la desigualdad ultramétrica
\( d_{ut} \leq min (d_{ur}, d_{us} ) \hspace {.2cm}; \hspace{.2cm}t =r \cup s \)
Decisiones que hay que tomar para hacer un clúster
- Elegir el método clúster que se va a utilizar
- Decidir si se estandarizan los datos
- Seleccionar la forma de medir la distancia/disimilitud entre los individuos
- Elegir un criterio para unir grupos, distancia entre grupos.
Proceso que se debe seguir en un Análisis Clúster Jerárquico Aglomerativo
Paso 1: Selección de las variables. Se recomienda que las variables sean del mismo tipo (continuas, categóricas,..)
Paso 2: Detección de valores atípicos. El análisis clúster es muy sensible a la presencia de objetos muy diferentes del resto (valores atípicos).
Paso 3: Elección de una medida de similitud entre objetos y obtención de la matriz de distancias. Mediante estas medidas se determinan los clusters iniciales.
Paso 4: Buscar los clústers más similares
Paso 5: Unir estos dos clústers en un nuevo clúster que tenga al menos dos objetos, de forma que el número de clúster decrece en una unidad.
Paso 6: Calcular la distancia entre este clúster y el resto. Los distintos métodos para el cálculo de las distancias entre los clústers producen distintas agrupaciones, por lo que no existe una agrupación única.
Paso 7: Repetir desde el paso 4 hasta que todos los objetos estén en un único clúster.
El proceso de agrupación jerárquico se puede resumir gráficamente mediante una representación gráfica en forma de árbol que recibe el nombre de Dendograma. Los objetos similares se enlazan y su posición en el diagrama está determinada por el nivel de similitud/disimilitud entre los objetos.
Vamos a realizar el proceso descrito y para ello utilizamos un ejemplo sencillo. Dicho ejemplo está formado por 5 objetos (A, B, C, D, E) y 2 variables \( (X_1, X_2 ) \). Los datos se presentan en la siguiente tabla
\( \begin{array} {|c|c|c|} \hline Objetos/individuos & X_1 & X_2 \\ \hline A & 1 & 1 \\ \hline B & 2 & 1 \\ \hline C & 4 & 5 \\ \hline D & 7 & 7 \\ \hline E & 5 & 7 \\ \hline \end{array} \)
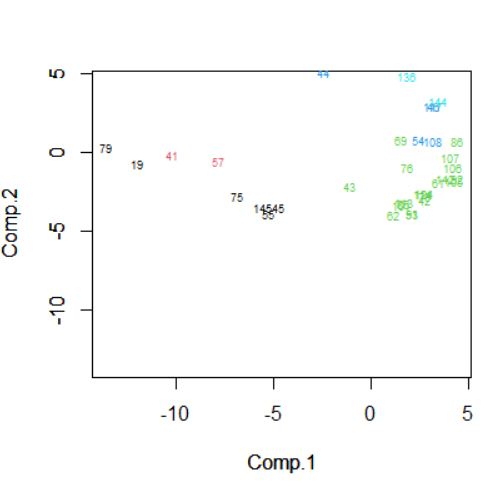
Paso 1 y 2: Para detectar valores atípicos podemos representar los puntos en el plano
En este caso no detectamos valores atípicos, no hay ningún valor que sea muy distinto de los demás.
Paso 3: La medida de distancia que vamos a tomar entre los objetos va a ser la distancia euclídea cuya expresión es:
\( d(P_1, P_2) = \displaystyle \sqrt {(x_2-x_1)^{2} + (y_2-y_1)^{2} } \)
Así, por ejemplo, la distancia entre el clúster A y el clúster B es:
\( d(A, B) = \displaystyle \sqrt {(2-1)^{2} + (1-1)^{2}} = 1 \)
Realizamos la distancia euclídea entre todos los puntos y obtenemos la siguiente matriz de distancias euclídeas entre los objetos
\( \begin{array} {|c|c|c|c|c|c|} \hline & A & B & C & D & E \\ \hline A & 0 & & & & \\ \hline B & 1 & 0 & & & \\ \hline C & 5 & 4.5 & 0 & & \\ \hline D & 8.5 & 7.8 & 3.6 & 0 & \\ \hline E & 7.2 & 6.7 & 2.2 & 2 & 0 \\ \hline \end{array} \)
Nota: Estamos realizando el método jerárquico aglomerativo, por lo que inicialmente tenemos 5 clústers, uno por cada uno de los objetos a clasificar.
Paso 4: Observamos en la matriz de distancias cuales son los objetos más similares, en nuestro ejemplo son el A y B que tienen la distancia menor (1).
Paso 5: Fusionamos los clusters más similares construyendo un nuevo clúster que contiene A y B. Se han formado los clusters: AB, C, D y E.
Paso 6: Calculamos la distancia entre el clúster AB y los objetos C, D y E. Para medir esta distancia tomamos como representante del clúster AB el centroide, es decir, el punto que tiene como coordenadas las medias de los valores de las componentes de las variables, es decir, las coordenadas de AB son: ((1+2)/2 , (1+1)/2) = (1.5, 1). La tabla de datos es la siguiente
\( \begin{array} {|c|c|c|} \hline Cluster & X_1 & X_2 \\ \hline AB & 1.5 & 1 \\ \hline C & 4 & 5 \\ \hline D & 7 & 7 \\ \hline E & 5 & 7 \\ \hline \end{array} \)
Paso 7: Repetimos desde el paso 4 hasta que todos los objetos estén en un único clúster
Paso 4: A partir de estos datos calculamos de nuevo la matriz de distancias
\( \begin{array} {|c|c|c|c|c|} \hline & AB & C & D & E \\ \hline AB & 0 & & & \\ \hline C & 4.7 & 0 & & \\ \hline D & 8.1 & 3.6 & 0 & \\ \hline E & 6.9 & 2.2 & 2 & 0 \\ \hline \end{array} \)
Paso 5: Los clusters más similares son el D y E con una distancia de 2, que se fusionan en un nuevo clúster DE. Se han formado tres clusters AB, C, DE
Paso 6: Calculamos el centroide del nuevo clúster que es el punto (6,7) y formamos de nuevo la tabla de datos
\( \begin{array} {|c|c|c|} \hline Cluster & X_1 & X_2 \\ \hline AB & 1.5 & 1 \\ \hline C & 4 & 5 \\ \hline DE & 6 & 7 \\ \hline \end{array} \)
Paso 4: A partir de estos datos calculamos de nuevo la matriz de distancias
\( \begin{array} {|c|c|c|c|} \hline & AB & C & DE \\ \hline AB & 0 & & \\ \hline C & 4.7 & 0 & \\ \hline DE & 7.5 & 2.8 & 0 \\ \hline \end{array} \)
Paso 5: Los clusters más similares son el C y DE con una distancia de 2.8, que se fusionan en un nuevo clúster CDE. Se han formado dos clusters AB y CDE
Paso 6. Calculamos el centroide del nuevo clúster ((4+5+7)/3 , (5+7+7)/3) = (5.3, 6.3) y formamos de nuevo la tabla de datos
\( \begin{array} {|c|c|c|} \hline Cluster & X_1 & X_2 \\ \hline AB & 1.5 & 1 \\ \hline CDE & 5.3 & 6.3 \\ \hline \end{array} \)
Paso 4 : A partir de estos datos calculamos de nuevo la matriz de distancias
\( \begin{array} {|c|c|c|} \hline & AB & CDE \\ \hline AB & 0 & \\ \hline CDE & 6.4 & 0 \\ \hline \end{array} \)
En este último paso tenemos solamente dos clusters con distancia 6.4 que se fusionarán en un único clúster en el paso siguiente terminando el proceso.
A continuación vamos a representar gráficamente el proceso de fusión mediante un dendograma
A continuación mostramos varias soluciones, para ello cortamos el dendograma por medio de líneas horizontales, así por ejemplo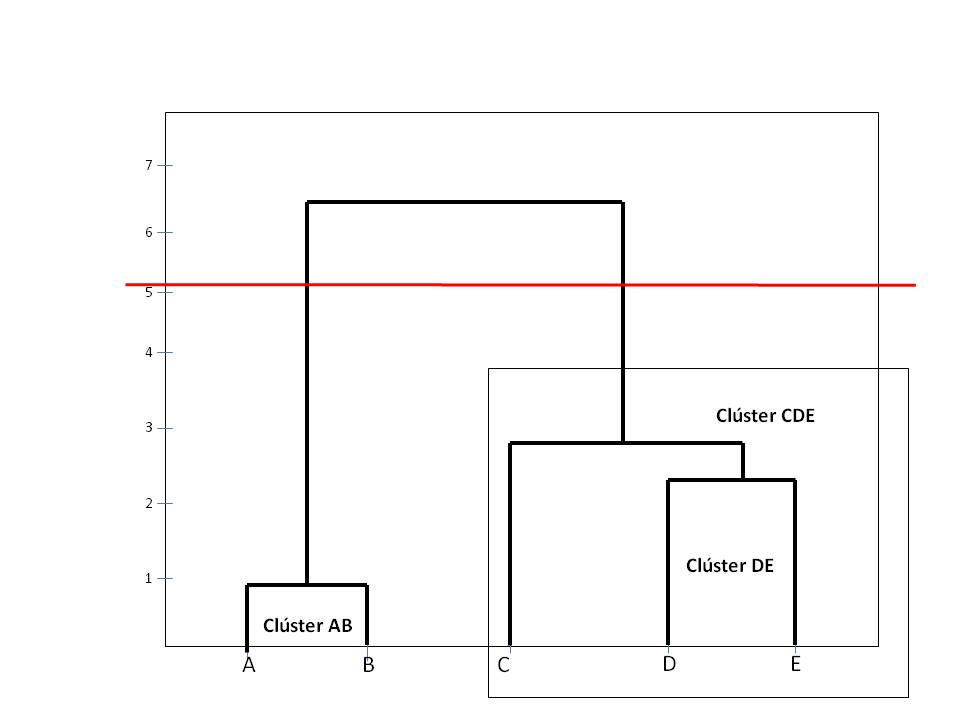
En la figura anterior se muestran 2 clústers: AB y CDE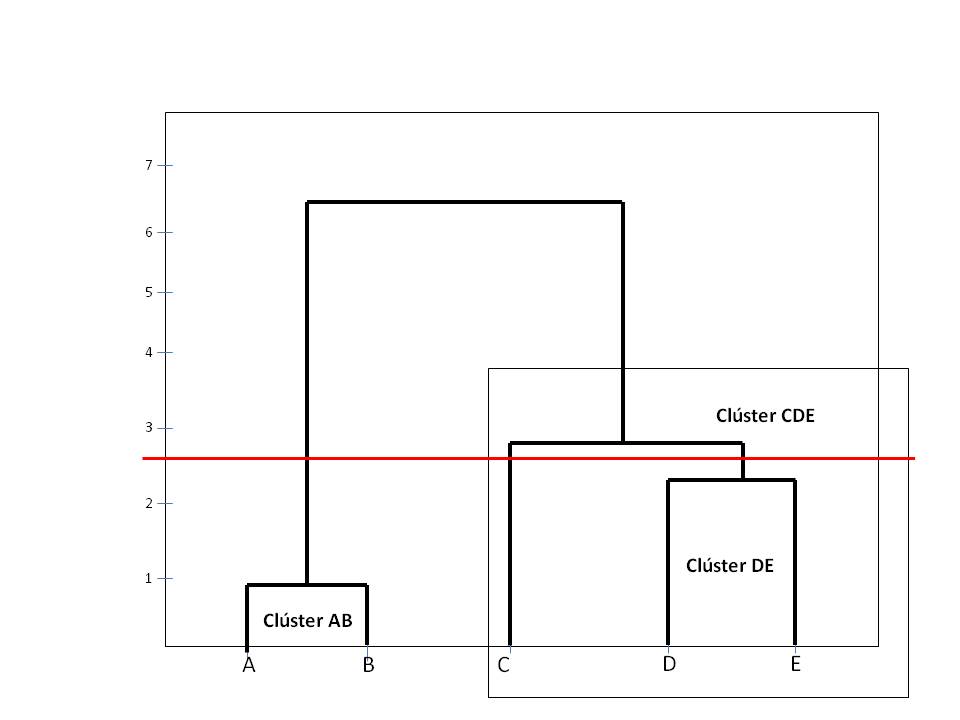
En esta figura la línea de corte nos muestra 3 clústers: AB, C y DE
El número de clústers depende del sitio donde cortemos el dendograma, por lo tanto la decisión sobre el número óptimo de clústers es subjetiva. Es conveniente elegir un número de clústers que sepamos interpretar. Para interpretar los clúster podemos utilizar:
- ANOVA
- Análisis factorial
- Análisis discriminante
- …
- Sentido común
Para decidir el número de clústers nos puede ser de gran utilidad representar los distintos pasos del algoritmo y las distancias a la que se produce la fusión de los clústers. En los primeros pasos el salto de las distancias es pequeño, mientras que esas diferencias van aumentando en los sucesivos pasos. Podemos elegir como punto de corte aquel donde comienzan a producirse saltos más bruscos. En nuestro ejemplo, el salto brusco se produce entre etapas 3 y 4, por lo tanto son dos el número de clústers óptimo.
Comentarios sobre el clúster jerárquico
-
Realizar el clúster jerárquico en conjunto de datos grande es problemático ya que un árbol con más de 50 individuos es difícil de representar e interpretar.
-
Una desventaja general es la imposibilidad de reasignar los individuos a los clústers en los casos en que la clasificación haya sido dudosa en las primeras etapas del análisis.
-
Debido a que el análisis clúster implica la elección entre diferentes medidas y procedimientos, con frecuencia es difícil juzgar la veracidad de los resultados.
-
Se recomienda comparar los resultados con diferentes métodos de conglomerados. Soluciones similares generalmente indican la existencia de una estructura en los datos. Soluciones muy diferentes probablemente indican una estructura pobre.
-
En último caso, la validez de los clústers se juzga mediante una interpretación cualitativa que puede ser subjetiva.
-
El número de clústers depende del sitio donde cortemos el dendograma.
Supuesto práctico 1
Los fabricantes de automóviles deben adaptar sus estrategias de desarrollo de productos y de marketing en función de cada grupo de consumidores para aumentar las ventas y el nivel de fidelidad a la marca. La tarea de agrupación de los coches según variables que describen los hábitos de consumo, sexo, edad, nivel de ingresos, etc. de los clientes puede ser en gran medida automática utilizando el análisis de clúster.
Se desea hacer un estudio de mercado sobre las preferencias de los consumidores al adquirir un vehículo, para ello disponemos una base de datos, ventas_vehículos.sav de automóviles y camiones en los que figura una serie de variables como el fabricante, modelo, ventas, etc.
El archivo de datos contiene 157 datos y está formado por las siguientes variables:
Variables tipo cadena: marca (Fabricante); modelo
Variables tipo numérico: ventas (en miles); reventa (Valor de reventa en 4 años); tipo (Tipo de vehículo: Valores: {0, Automóvil; 1, Camión}); precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo).
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
Nota: La ruta hasta llegar al fichero varía en función del ordenador. Utilizar la orden setwd() para situarse en el directorio de trabajo
> setwd(“C:/Users/Usuario/Desktop/Datos”)
Mediante la función read.spss leemos los datos que están en un archivo .sav. Para poder utilizar esta función debemos instalar el paquete foreign.
Para ello, seleccionar Paquetes/Instalar paquetes y de la lista escoger foreign. O bien utilizar la siguiente orden
> install.packages(“foreign”)
A continuación debemos cargar el paquete, para ello se seleccionan Paquetes/cargar paquete y de la lista escoger foreign. O bien utilizar la siguiente orden
> library(foreign)
> datos<- read.spss(“ventas-vehiculos.sav”,use.value.labels=TRUE, max.value.labels=TRUE, to.data.frame=TRUE, sep)
re-encoding from CP1252
> datos
marca modelo ventas reventa tipo precio motor CV pisada ancho largo peso_neto deposito mpg
1 Acura Integra 16.919 16.360 0 21.500 1.8 140 101.2 67.3 172.4 2.639 13.2 28.0
2 Acura TL 39.384 19.875 0 28.400 3.2 225 108.1 70.3 192.9 3.517 17.2 25.0
3 Acura CL 14.114 18.225 0 NA 3.2 225 106.9 70.6 192.0 3.470 17.2 26.0
4 Acura RL 8.588 29.725 0 42.000 3.5 210 114.6 71.4 196.6 3.850 18.0 22.0
5 Audi A4 20.397 22.255 0 23.990 1.8 150 102.6 68.2 178.0 2.998 16.4 27.0
6 Audi A6 18.780 23.555 0 33.950 2.8 200 108.7 76.1 192.0 3.561 18.5 22.0
7 Audi A8 1.380 39.000 0 62.000 4.2 310 113.0 74.0 198.2 3.902 23.7 21.0
8 BMW 323i 19.747 NA 0 26.990 2.5 170 107.3 68.4 176.0 3.179 16.6 26.1
9 BMW 328i 9.231 28.675 0 33.400 2.8 193 107.3 68.5 176.0 3.197 16.6 24.0
10 BMW 528i 17.527 36.125 0 38.900 2.8 193 111.4 70.9 188.0 3.472 18.5 24.8
11 Buick Century 91.561 12.475 0 21.975 3.1 175 109.0 72.7 194.6 3.368 17.5 25.0
12
Nota: La función read.spss se utiliza para leer archivos .sav. Los otros dos argumentos son para darle formato de data frame.
El estudio de mercado lo queremos realizar sólo en automóviles de mayor venta y para ello vamos a utilizar el procedimiento Análisis de conglomerados jerárquico para agrupar los automóviles de mayor venta en función de sus precios, fabricante, modelo y propiedades físicas.
En primer lugar restringiremos el archivo de datos sólo a los automóviles de los que se vendieron al menos 100.000 unidades. Para ello seleccionamos los casos que cumplan esa condición mediante la siguiente fórmula:
>datos100k <- subset(datos, subset =datos$ventas>100 & datos$tipo==0)
La función subset filtramos los datos, poniendo las condiciones de selección en el segundo argumento.
> datos100k
marca modelo ventas reventa tipo precio motor CV pisada ancho largo peso_neto deposito mpg
20 Chevrolet Cavalier 145.519 9.250 0 13.260 2.2 115 104.1 67.9 180.9 2.676 14.3 27
21 Chevrolet Malibu 135.126 11.225 0 16.535 3.1 170 107.0 69.4 190.4 3.051 15.0 25
28 Chevrolet Impala 107.995 NA 0 18.890 3.4 180 110.5 73.0 200.0 3.389 17.0 27
48 Ford Mustang 113.369 12.760 0 21.560 3.8 190 101.3 73.1 183.2 3.203 15.7 24
50 Ford Taurus 245.815 10.055 0 17.885 3.0 155 108.5 73.0 197.6 3.368 16.0 24
51 Ford Focus 175.670 NA 0 12.315 2.0 107 103.0 66.9 174.8 2.564 13.2 30
58 Honda Civic 199.685 9.850 0 12.885 1.6 106 103.2 67.1 175.1 2.339 11.9 32
59 Honda Accord 230.902 13.210 0 15.350 2.3 135 106.9 70.3 188.8 2.932 17.1 27
120 Pontiac Grand Am 131.097 10.290 0 19.720 3.4 175 107.0 70.4 186.3 3.091 15.2 25
137 Toyota Corolla 142.535 10.025 0 13.108 1.8 120 97.0 66.7 174.0 2.420 13.2 33
138 Toyota Camry 247.994 13.245 0 17.518 2.2 133 105.2 70.1 188.5 2.998 18.5 27
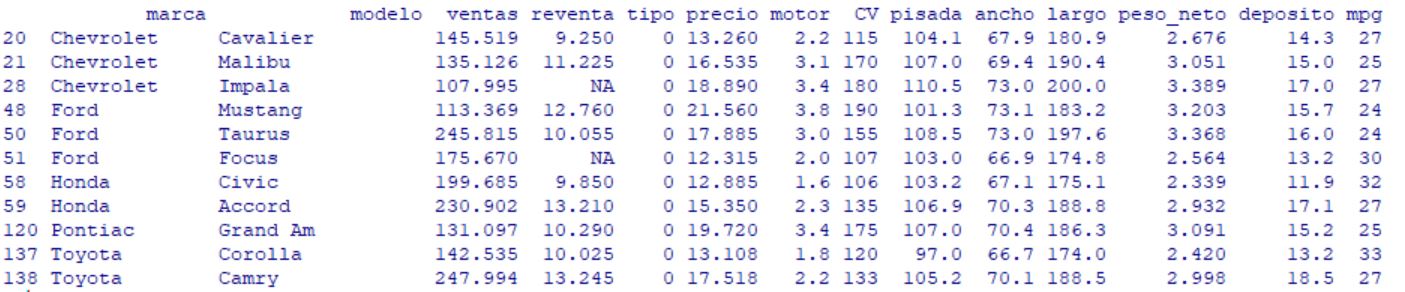
Al leer los datos vemos que se han colado una serie de espacios en las variables “marca” y “modelo”. Para corregirlo utilizamos la función gsub, que funciona sustituyendo lo que pongas en el primer argumento por lo que pones en el segundo. En este caso un espacio por nada.
> datos100k$marca= gsub(” “,””,datos100k$marca)
> datos100k$modelo= gsub(” “,””,datos100k$modelo)
Mostramos la matriz de datos correcta
> datos100k
marca modelo ventas reventa tipo precio motor CV pisada ancho largo peso_neto deposito mpg
20 Chevrolet Cavalier 145.519 9.250 0 13.260 2.2 115 104.1 67.9 180.9 2.676 14.3 27
21 Chevrolet Malibu 135.126 11.225 0 16.535 3.1 170 107.0 69.4 190.4 3.051 15.0 25
28 Chevrolet Impala 107.995 NA 0 18.890 3.4 180 110.5 73.0 200.0 3.389 17.0 27
48 Ford Mustang 113.369 12.760 0 21.560 3.8 190 101.3 73.1 183.2 3.203 15.7 24
50 Ford Taurus 245.815 10.055 0 17.885 3.0 155 108.5 73.0 197.6 3.368 16.0 24
51 Ford Focus 175.670 NA 0 12.315 2.0 107 103.0 66.9 174.8 2.564 13.2 30
58 Honda Civic 199.685 9.850 0 12.885 1.6 106 103.2 67.1 175.1 2.339 11.9 32
59 Honda Accord 230.902 13.210 0 15.350 2.3 135 106.9 70.3 188.8 2.932 17.1 27
120 Pontiac GrandAm 131.097 10.290 0 19.720 3.4 175 107.0 70.4 186.3 3.091 15.2 25
137 Toyota Corolla 142.535 10.025 0 13.108 1.8 120 97.0 66.7 174.0 2.420 13.2 33
138 Toyota Camry 247.994 13.245 0 17.518 2.2 133 105.2 70.1 188.5 2.998 18.5 27
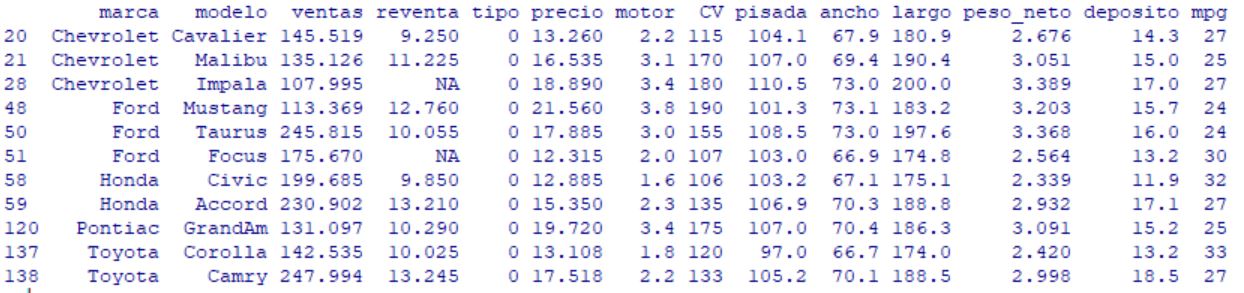
A continuación vamos a elegir las variables para hacer el análisis clúster.
Variables: precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo).
> x <- datos100k[,c(“precio”,”motor”,”CV”,”pisada”,”ancho”,”largo”,”peso_neto”,”deposito”,”mpg” )]
> x
precio motor CV pisada ancho largo peso_neto deposito mpg
20 13.260 2.2 115 104.1 67.9 180.9 2.676 14.3 27
21 16.535 3.1 170 107.0 69.4 190.4 3.051 15.0 25
28 18.890 3.4 180 110.5 73.0 200.0 3.389 17.0 27
48 21.560 3.8 190 101.3 73.1 183.2 3.203 15.7 24
50 17.885 3.0 155 108.5 73.0 197.6 3.368 16.0 24
51 12.315 2.0 107 103.0 66.9 174.8 2.564 13.2 30
58 12.885 1.6 106 103.2 67.1 175.1 2.339 11.9 32
59 15.350 2.3 135 106.9 70.3 188.8 2.932 17.1 27
120 19.720 3.4 175 107.0 70.4 186.3 3.091 15.2 25
137 13.108 1.8 120 97.0 66.7 174.0 2.420 13.2 33
138 17.518 2.2 133 105.2 70.1 188.5 2.998 18.5 27
Como las variables se miden en unidades diferentes vamos a normalizar la variable con Media 0 y Varianza 1. Para ello usamos la función scale. Elegimos True tanto para centrar como para escalar. También renombramos a las filas como el nombre de sus modelos.
> X.scale<- scale(x, center = T, scale = T)
> row.names(X.scale)<- datos100k$modelo
> round(X.scale,3)
precio motor CV pisada ancho largo peso_neto deposito mpg
Cavalier -0.963 -0.562 -0.942 -0.209 -0.772 -0.511 -0.648 -0.455 -0.118
Malibu 0.083 0.648 0.833 0.567 -0.165 0.563 0.382 -0.097 -0.769
Impala 0.835 1.051 1.156 1.503 1.290 1.648 1.310 0.924 -0.118
Mustang 1.688 1.588 1.479 -0.958 1.331 -0.251 0.799 0.260 -1.094
Taurus 0.514 0.513 0.349 0.968 1.290 1.377 1.252 0.413 -1.094
Focus -1.265 -0.831 -1.200 -0.503 -1.176 -1.200 -0.955 -1.016 0.857
Civic -1.083 -1.368 -1.232 -0.450 -1.096 -1.166 -1.573 -1.680 1.508
Accord -0.296 -0.428 -0.296 0.540 0.199 0.382 0.055 0.975 -0.118
GrandAm 1.100 1.051 0.995 0.567 0.239 0.100 0.492 0.005 -0.769
Corolla -1.012 -1.100 -0.780 -2.108 -1.257 -1.291 -1.351 -1.016 1.833
Camry 0.397 -0.562 -0.361 0.085 0.118 0.348 0.236 1.689 -0.118
attr(,”scaled:center”)
precio motor CV pisada ancho largo peso_neto deposito mpg
16.275091 2.618182 144.181818 104.881818 69.809091 185.418182 2.911909 15.190909 27.363636
attr(,”scaled:scale”)
precio motor CV pisada ancho largo peso_neto deposito mpg
3.1303620 0.7440674 30.9865073 3.7381327 2.4728342 8.8457694 0.3642111 1.9588030 3.0748245
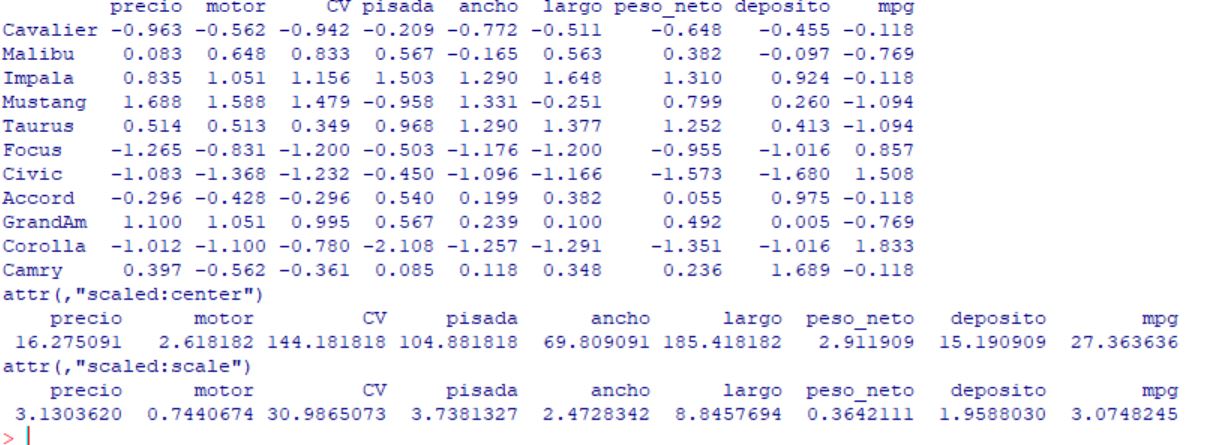
Con esta estructura en el data.frame podemos realizar el análisi clúster
En primer lugar vamos a calcular la matriz de distancias.
Las medidas que podemos elegir para la matriz de distancias son “euclidean”, “maximum”,”manhattan”, “canberra”,”binary” o “minkowski“.
Nosotros vamos a usar la distancia euclídea.
> dmx <- dist(X.scale[, colnames(x)], method = “euclidean”)
> dmx
Cavalier Malibu Impala Mustang Taurus Focus Civic Accord GrandAm Corolla
Malibu 3.072816
Impala 5.274025 2.708019
Mustang 5.110737 3.084236 3.526982
Taurus 4.418552 2.122562 1.618253 3.224947
Focus 1.522351 4.323238 6.447844 6.136681 5.743645
Civic 2.518551 5.107705 7.099278 6.849459 6.472819 1.256555
Accord 2.391317 2.102429 3.297454 4.134429 2.650065 3.652378 4.447080
GrandAm 3.812895 1.274623 2.532611 2.185040 2.190572 4.956890 5.681518 2.727180
Corolla 3.063649 5.408865 7.389655 6.598459 6.831109 2.002918 1.915638 4.783256 5.896650
Camry 3.030349 2.642446 3.450847 3.988278 2.915417 4.201357 4.992374 1.122524 2.927103 5.048393
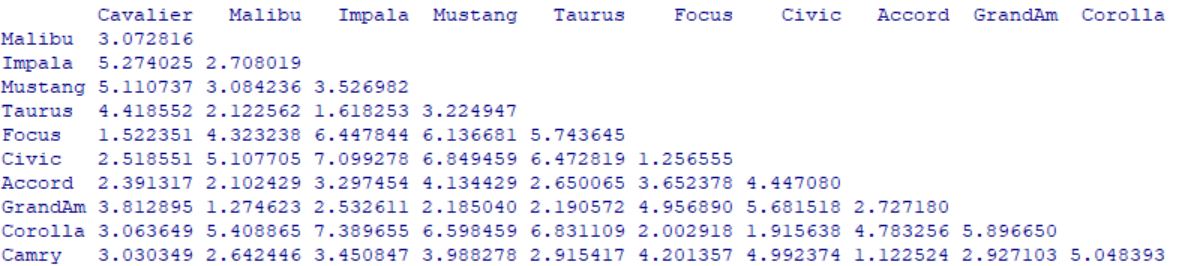
> round(dmx,3)
Cavalier Malibu Impala Mustang Taurus Focus Civic Accord GrandAm Corolla
Malibu 3.073
Impala 5.274 2.708
Mustang 5.111 3.084 3.527
Taurus 4.419 2.123 1.618 3.225
Focus 1.522 4.323 6.448 6.137 5.744
Civic 2.519 5.108 7.099 6.849 6.473 1.257
Accord 2.391 2.102 3.297 4.134 2.650 3.652 4.447
GrandAm 3.813 1.275 2.533 2.185 2.191 4.957 5.682 2.727
Corolla 3.064 5.409 7.390 6.598 6.831 2.003 1.916 4.783 5.897
Camry 3.030 2.642 3.451 3.988 2.915 4.201 4.992 1.123 2.927 5.048
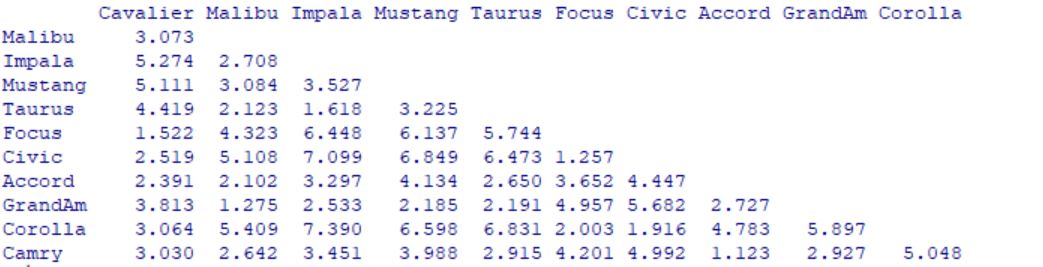
Hermos obtenido nuestra matriz de distancias. A continuación vamos a realizar el análisis clúster. Y para ello vamos a elegir el método de conglomeración.
Método de conglomeración. Los métodos de enlace (linkage) utilizan la proximidad entre pares de individuos para unir grupos de individuos. Existen diversas formas de medir la distancia entre clúster que producen diferentes agrupaciones y diferentes dendogramas. No hay un criterio para seleccionar cual es el algoritmo mejor. La decisión es normalmente subjetiva y depende del método que mejor refleje los propósitos de cada estudio en particular.
- Vinculación inter-grupos. “average”. Media Intergrupos
- Vinculación intra-grupos. “mcquitty”. Media Intragrupos
- Vecino más próximo. “single”. Enlace sencillo (salto mínimo). Utiliza la mínima distancia/disimilitud entre dos individuos de cada grupo (útil para identificar atípicos). Conduce a clusters encadenados
- Vecino más lejano. “complete”. Enlace completo (salto máximo). Utiliza la máxima distancia/disimilitud entre dos individuos de cada grupo. Conduce a clusters compactos
- Agrupación de centroides. “centroid”. Utiliza la distancia/disimilitud entre los centros de los grupos
- Agrupación de medianas. “median”. Utiliza la mediana de las distancias/disimilitud entre todos los individuos de los dos grupos
- Método de Ward. “ward.D” o “ward.D2”. Tiene tendencia a formar clusters más compactos y de igual tamaño y forma, en comparación con el enlace medio
Para más información sobre los distintos métodos escribir “?hclust” en la consola.
Vamos a elegir como método Vecino más próximo. Es decir, “single”.
> cs <- hclust(dmx^2, method = “single”)
> cs
Call:
hclust(d = dmx^2, method = “single”)
Cluster method : single
Distance : euclidean
Number of objects: 11
De esta forma elegimos el método, y como la distancia que queremos es la euclídea al cuadrado. elevamos nuestra matriz de distancias a 2.
A continuación construimos el dendrograma.
> plot(cs)
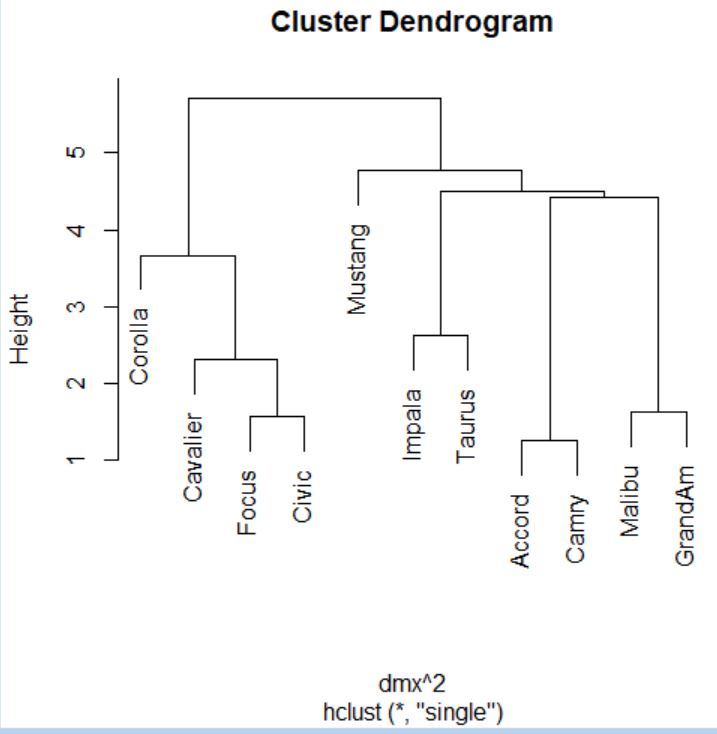
> abline(h=4.85, col=”red”)
Cortamos donde más nos interese, en este caso por ejemplo en el 4.85.
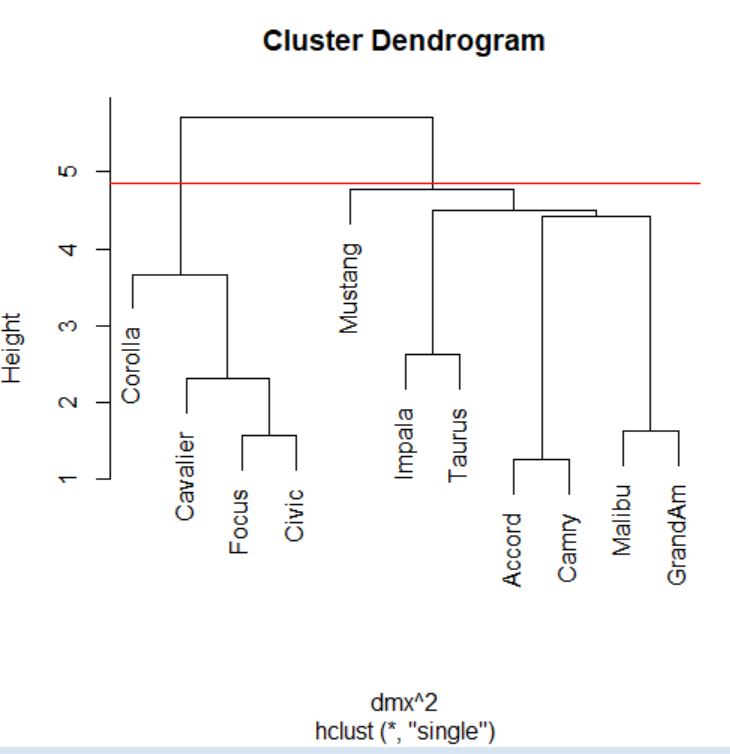
Dendrograma. Es una representación gráfica en forma de árbol, en el que los clusters están representados mediante trazos verticales (horizontales) y las etapas de fusión mediante trazos horizontales (verticales). La separación entre las etapas de fusión es proporcional a la distancia a la que están los grupos que se funden en esa etapa. Es un resumen gráfico de la solución de clúster. Los casos (marcas de coche) se encuentran a lo largo del eje vertical izquierdo. El eje horizontal muestra la distancia entre los grupos cuando se unieron (de 0 a 5.71).
Analizar el árbol de clasificación para determinar el número de grupos es un proceso subjetivo. En general, se comienza por buscar “huecos” entre uniones a lo largo del eje horizontal. De derecha a izquierda hay un hueco en el 4.8, que divide los coches en dos grupos:
- Un grupo está formado por los modelos: Accord, Camry, Malibu, Grand Am, Impala, Taurus, Mustang y
- el otro grupo está formado por los modelos: Focus, Civic, Cavalier y Corolla.
Con el siguiente código podemos ver donde se han ido formando los clústers.
> cs$height
[1] 1.260060 1.578930 1.624664 2.317551 2.618741 3.669669 4.420208 4.505270
[9] 4.774399 5.718398
Realizamos el Historial de conglomeración
> cs$merge
[,1] [,2]
[1,] -8 -11
[2,] -6 -7
[3,] -2 -9
[4,] -1 2
[5,] -3 -5
[6,] -10 4
[7,] 1 3
[8,] 5 7
[9,] -4 8
[10,] 6 9
El Historial de conglomeración es una tabla que muestra un resumen numérico de la solución del método clúster utilizado. El Historial muestra los casos o conglomerados combinados en cada etapa, las distancias entre los casos o los conglomerados que se combinan (Coeficientes), así como el último nivel del proceso de conglomeración en el que cada caso (o variable) se unió a su conglomerado correspondiente. Cuando se combinan dos clusters, R asigna al nuevo clúster la etiqueta menor entre las que tienen los clusters que se combinan.
En nuestro ejemplo, en la primera etapa se unen los casos 8 y 11 (Accord (8), Camry (11)) porque son los que tienen la distancia más pequeña (1.260). El grupo creado por 8 y 11 aparece de nuevo en la etapa 7 donde se une al clúster 2 (formado en la etapa 3). Por lo tanto en esta etapa se unen los grupos creados en las etapas 1 y 3 y el grupo resultante formado por 8, 11, 2 y 9 aparece en la siguiente etapa la 8.
Si hay muchos casos la tabla es bastante larga, pero suele ser más fácil de estudiar la columna de coeficientes para distinguir grandes distancias que analizar el dendrograma. Cuando se observa un salto inesperado en el coeficiente de distancia, la solución antes de ese hueco indica una buena elección de conglomerados.
Las mayores diferencias en la columna de los coeficientes se producen entre las etapas 5 y 6, lo que indica una solución de 6-clúster ((8, 11); (2,9); (3, 5); (4); (6, 7, 1); (10)) y entre las etapas 9 y 10, lo que indica una solución de 2-clúster. Estos son los mismos que los resultados del dendrograma.
En este estudio no hemos podido obtener unas conclusiones sólidas sobre la agrupación de los automóviles de mayor venta en función de sus precios, fabricante, modelo y propiedades físicas. Puede deberse a que hemos utilizado como método de clúster el Vecino más próximo que, aunque es aconsejable para examinar los grados de similitud es pobre en la construcción de los distintos grupos. Por ello, debemos volver a realizar de nuevo el análisis utilizando otro método de conglomerado.
Supuesto práctico 2
Se desea hacer un estudio de mercado sobre las preferencias de los consumidores al adquirir un vehículo, como en el supuesto práctico 1. Para ello, disponemos de un conjunto de datos, que se encuentra en el fichero ventas_vehiculos.txt.
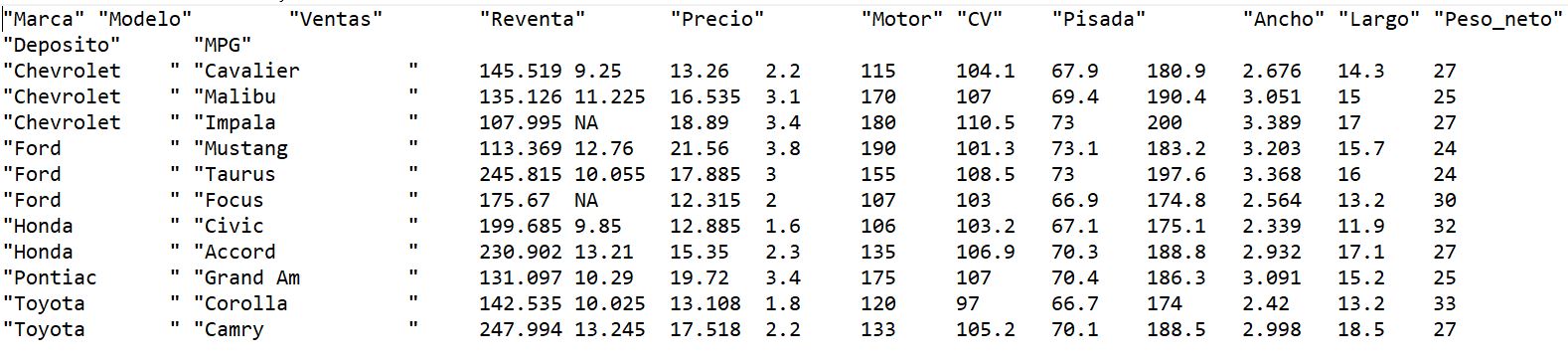
Tabla1: Datos del Supuesto práctico 2
El fichero contiene 11 datos, cada uno de ellos correspondiente a un vehículo. Para cada vehículo se han recogido las siguientes variables:
- Marca del automóvil.
- Modelo del automóvil.
- Ventas. Número de vehículos vendidos durante un determinado año, en miles de unidades.
- Reventa. Precio de reventa en 4 años, en miles de euros.
- Precio. Precio de venta, en miles de euros.
- Motor. Tamaño del motor.
- CV. Caballos de potencia.
- Pisada. Base de los neumáticos.
- Ancho. Anchura del vehículo.
- Largo. Longitud del vehículo.
- Peso_neto. Peso neto del vehículo.
- Depósito. Capacidad del depósito de combustible.
- MPG. Millas por galón, medida de consumo del vehículo.
En primer lugar, debemos importar en R los datos de los vehículos. Para ello, utilizamos la orden read.table.
> setwd(“C:/Users/Usuario/Desktop/Datos”) # Nos situamos en el directorio donde se encuentra el fichero de datos
> datos <- read.table(“ventas_vehiculos.txt”, header = TRUE)
Cuando las variables vienen dadas en diferentes unidades de medida, se recomienda escalar los datos, para que la formación de los clústers no se vea afectada por dichas unidades de medida. Para escalar un conjunto de datos, se utiliza la función scale. Esta función solo puede aplicarse sobre las variables del conjunto de datos que sean de tipo numérico.
> datos[3:13] <- scale(datos[3:13])
A continuación, antes de realizar el análisis clúster en sí, es necesario calcular la distancia entre las observaciones. Para ello, se utiliza la función de R dist. La sintaxis de esta función es la siguiente:
dist(x, method = “euclidean”, p = 2)
donde
- x es una matriz numérica o un data frame.
- method indica el método que se empleará para calcular las distancias entre individuos. Las posibles opciones son “euclidean”, para la distancia euclídea (por defecto); “maximum”, para la distancia máxima; “manhattan”, para la distancia Manhattan; “canberra”, para la distancia Canberra y “minkowski”, para la distancia de Minkowski.
- p es un valor numérico que se indica el valor de p, en el caso de que se seleccione la distancia de Minkowski en el argumento method.
Utilizaremos la función dist para calcular las distancias entre las observaciones de la muestra a partir de algunas de las variables de las que se dispone. En nuestro caso, utilizaremos las variables Precio, Motor, CV, Pisada, Ancho, Largo, Peso_neto, Deposito y MPG y usaremos la distancia euclídea.
> attach(datos)
> variables <- data.frame (Precio, Motor, CV, Pisada, Ancho, Largo, Peso_neto, Deposito, MPG)
> distancias <- dist(variables, method = “euclidean”)
> distancias
1 2 3 4 5 6 7 8 9 10
2 3.072816
3 5.274025 2.708019
4 5.110737 3.084236 3.526982
5 4.418552 2.122562 1.618253 3.224947
6 1.522351 4.323238 6.447844 6.136681 5.743645
7 2.518551 5.107705 7.099278 6.849459 6.472819 1.256555
8 2.391317 2.102429 3.297454 4.134429 2.650065 3.652378 4.447080
9 3.812895 1.274623 2.532611 2.185040 2.190572 4.956890 5.681518 2.727180
10 3.063649 5.408865 7.389655 6.598459 6.831109 2.002918 1.915638 4.783256 5.896650
11 3.030349 2.642446 3.450847 3.988278 2.915417 4.201357 4.992374 1.122524 2.927103 5.048393
Una vez obtenidas las distancias, pasamos a realizar el análisis clúster propiamente dicho utilizando la función hclust de R. La sintaxis de esta función es la siguiente:
hclust(d, method = “complete”)
donde
- d es la matriz que proporciona la función dist.
- method indica el método que se empleará para conformar los clústers. Las posibles opciones son “ward.D”, “ward.D2”, dos variaciones del método de Ward; “single”, para el método del enlace simple; “complete”, para el método del enlace completo (por defecto); “average”, para el método del promedio entre grupos; “mcquitty”, para el método del promedio ponderado entre grupos; “median”, para el método de la mediana y “centroid”, para el método del centroide.
Utilizaremos la función hclust para llevar a cabo el análisis clúster y el método del enlace completo (o del vecino más lejano) como método de formación de los grupos de observaciones.
> cluster <- hclust(distancias, method = “complete”)
> cluster
Call:
hclust(d = distancias, method = “complete”)
Cluster method : complete
Distance : euclidean
Number of objects: 11
La función hclust devuelve varios elementos. Los más interesantes son el historial de aglomeración y las distancias de aglomeración, que se pueden consultar accediendo a los componentes merge y height, respectivamente, del objeto generado por hclust. Para acceder a dichos componentes, se indica el nombre del objeto generado por hclust (cluster, en nuestro caso), seguido del símbolo del dólar ($) y del nombre del componente.
> cluster$merge
[,1] [,2]
[1,] -8 -11
[2,] -6 -7
[3,] -2 -9
[4,] -3 -5
[5,] -10 2
[6,] 3 4
[7,] -1 1
[8,] -4 6
[9,] 5 7
[10,] 8 9
El historial de aglomeración indica qué dos elementos se funden en cada etapa del procedimiento de agrupamiento. Estos elementos pueden ser dos unidades individuales, dos grupos o una unidad individual y un grupo. En el historial de aglomeración, los números negativos indican unidades individuales y los números positivos indican grupos formados previamente.
En concreto, la interpretación del historial de aglomeración anterior es la que sigue:
- En la primera etapa se unen en un grupo las unidades individuales 8 y 11 (los números indican la posición dentro del fichero de datos).
- En la segunda etapa se unen en un grupo las unidades individuales 6 y 7.
- En la tercera etapa se unen en un grupo las unidades individuales 2 y 9.
- En la cuarta etapa se unen en un grupo las unidades individuales 3 y 5.
- En la quinta etapa se unen en un grupo la unidad individual 10 y el grupo formado en la etapa 2 (esto es, el grupo formado por las unidades 6 y 7).
- En la sexta etapa se unen en un grupo los grupos formados en la etapa 3 (esto es, el formado por las unidades 2 y 9) y en la etapa 4 (esto es, el formado por las unidades 3 y 5).
- En la séptima etapa se unen en un grupo la unidad individual 1 y el grupo formado en la etapa 1 (esto es, el grupo formado por las unidades 8 y 11).
- En la octava etapa se unen en un grupo la unidad individual 4 y el grupo formado en la etapa 6 (esto es, el grupo formado por las unidades 2, 3, 5 y 9).
- En la novena etapa se unen en un grupo los grupos formados en la etapa 5 (esto es, el formado por las unidades 6, 7 y 10) y en la etapa 7 (esto es, el formado por las unidades 1, 8 y 11).
- Por último, en la décima etapa se unen en un grupo los grupos formados en la etapa 8 (esto es, el formado por las unidades (2, 3, 4, 5 y 9) y en la etapa 9 (esto es, el formado por las unidades 1, 6, 7, 8, 10 y 11).
> cluster$height
[1] 1.122524 1.256555 1.274623 1.618253 2.002918 2.708019 3.030349 3.526982
[9] 5.048393 7.389655
Como ya hemos comentado, el componente height incluye las distancias a las que se producen las uniones entre unidades y/o grupos en cada etapa. Así, a modo de ejemplo, en nuestro caso podemos concluir que, en la primera etapa, las unidades 8 y 11 están separadas por una distancia de 1.1225 unidades. También sabemos que los grupos que se unen en la décima etapa están separados por una distancia de 7.3896 unidades.
El proceso de agrupamiento de las unidades y de los grupos se suele visualizar a través de un gráfico conocido como dendrograma. Para realizar un dendrograma basta con utilizar la función plot, pasándole como argumento el objeto generado por la función hclust (cluster, en nuestro caso).
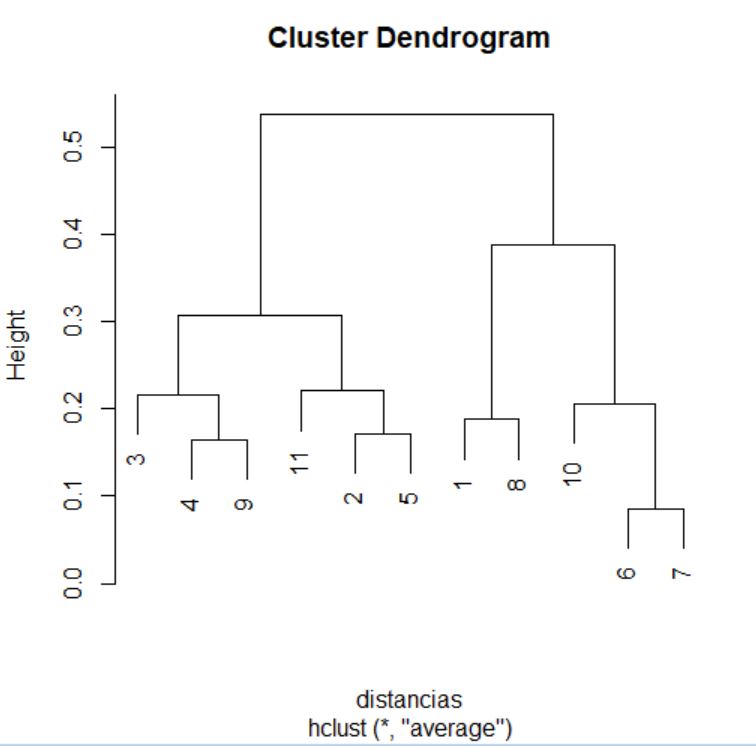
> plot(cluster)
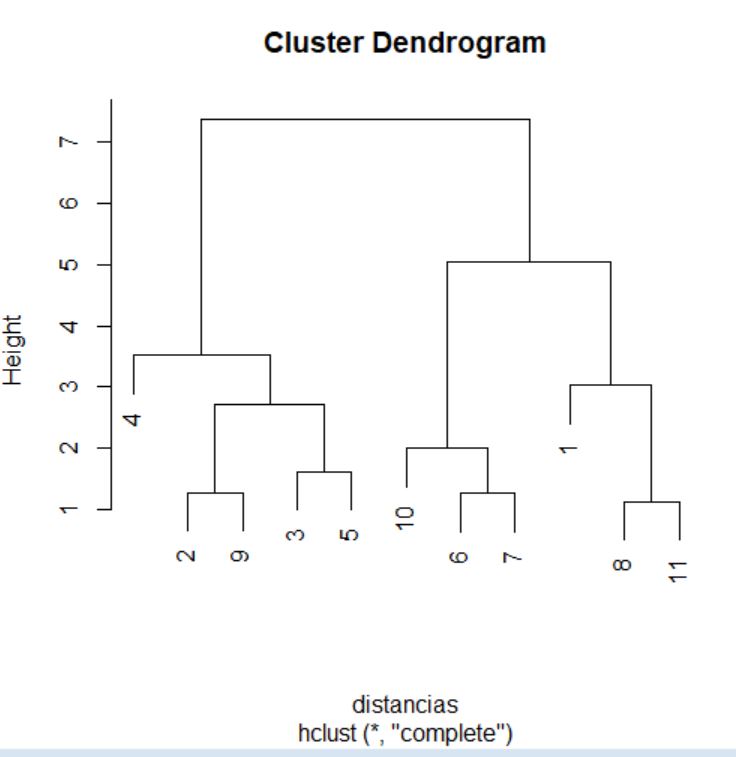
El dendrograma, en este caso, se interpreta desde abajo hacia arriba. Si se desea, para facilitar la interpretación, se pueden incluir las etiquetas de los individuos mediante el argumento label en la llamada a la función plot.
> plot(cluster, labels = datos$Modelo)
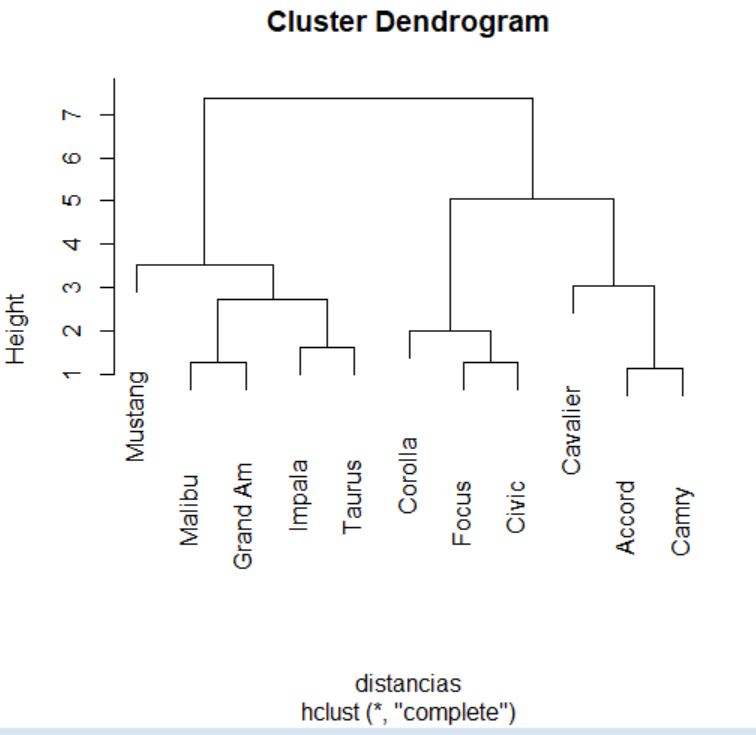
Supuesto práctico 3: Análisis clúster jerárquico divisivo o disociativo en R
A partir de los datos del supuesto práctico 1, realizar un análisis clúster divisivo o disociativo.
Todos los métodos que ofrece la función hclust son de tipo aglomerativo. Para hacer un análisis clúster jerárquico divisivo se utiliza la función diana, que pertenece al paquete que se llama cluster. Por lo tanto, el primer paso consiste en instalar y cargar el paquete cluster.
> install.packages(“cluster”)
> library(cluster)
A continuación, se importan los datos y se escalan las variables numéricas del conjunto de datos, tal y como se hizo en el supuesto práctico anterior.
> datos <- read.table(“ventas_vehiculos.txt”, header = TRUE)
> datos[3:13] <- scale(datos[3:13])
El siguiente paso es calcular la matriz de distancias, usando la función dist. De nuevo, volveremos a utilizar la distancia euclídea.
> variables <- data.frame (Precio, Motor, CV, Pisada, Ancho, Largo, Peso_neto, Deposito, MPG)
> distancias <- dist(variables, method = “euclidean”)
1 2 3 4 5 6 7 8 9 10
2 3.072816
3 5.274025 2.708019
4 5.110737 3.084236 3.526982
5 4.418552 2.122562 1.618253 3.224947
6 1.522351 4.323238 6.447844 6.136681 5.743645
7 2.518551 5.107705 7.099278 6.849459 6.472819 1.256555
8 2.391317 2.102429 3.297454 4.134429 2.650065 3.652378 4.447080
9 3.812895 1.274623 2.532611 2.185040 2.190572 4.956890 5.681518 2.727180
10 3.063649 5.408865 7.389655 6.598459 6.831109 2.002918 1.915638 4.783256 5.896650
11 3.030349 2.642446 3.450847 3.988278 2.915417 4.201357 4.992374 1.122524 2.927103 5.048393
Ahora ya podemos utilizar la función diana del paquete cluster. La sintaxis de esta función es la que sigue:
diana(x, diss, metric = “euclidean”)
donde
- x es, bien una matriz de distancias (como la que proporciona la función dist), o bien un data frame con los valores de las variables a partir de las cuales se realizará el análisis clúster. Estas variables han de ser numéricas.
- diss es un valor lógico. Si este parámetro es igual a TRUE, indica que el parámetro x es una matriz de distancias. Si este parámetro es igual a FALSE, indica que el parámetro x es un data frame con valores de las variables.
- metric es una cadena de caracteres usada para calcular la distancia entre observaciones, solo en el caso en que x contenga los valores de las variables. Los posibles valores para este parámetro son “euclidean”, para la distancia euclídea (valor por defecto) y “manhattan”, para la distancia Manhattan.
> cluster <- diana(distancias, diss = TRUE)
Merge:
[,1] [,2]
[1,] -8 -11
[2,] -6 -7
[3,] -2 -9
[4,] -3 -5
[5,] -1 2
[6,] 5 -10
[7,] 3 -4
[8,] 4 1
[9,] 7 8
[10,] 6 9
Order of objects:
[1] 1 6 7 10 2 9 4 3 5 8 11
Height:
[1] 2.518551 1.256555 3.063649 7.389655 1.274623 3.084236 4.134429 1.618253 3.450847 1.122524
Divisive coefficient:
[1] 0.7636703
Available components:
[1] “order” “height” “dc” “merge” “diss” “call”
Como ocurría en el supuesto anterior, el objeto que devuelve la función diana contiene algunos componentes interesantes. De hecho, los nombres de los componentes que nos interesan son merge y height que, como en el caso anterior, indican el historial de disociación y las distancias de disociación, respectivamente. Comencemos por obtener el historial de disociación.
> cluster$merge
[,1] [,2]
[1,] -8 -11
[2,] -6 -7
[3,] -2 -9
[4,] -3 -5
[5,] -1 2
[6,] 5 -10
[7,] 3 -4
[8,] 4 1
[9,] 7 8
[10,] 6 9
En este caso, i-ésima fila de la matriz anterior indica el desagrupamiento que sea realiza en la etapa \( n_i \) del proceso. Por lo tanto, conviene interpretar el historial de disociación a partir de la última hasta la primera fila de la matriz que lo contiene. De nuevo, valores negativos en la matriz indican unidades individuales y los números positivos indican grupos de individuos. La interpretación del historial de disociación anterior es la siguiente:
- En la primera etapa (que corresponde con la décima fila de la matriz) se divide el conjunto total de observaciones en dos grupos: el que se volverá a dividir según lo indicado en la fila 6 de la matriz y el que se volverá a dividir según lo indicado en la fila 9 de la matriz.
- En la segunda etapa (que corresponde con la novena fila de la matriz) uno de los grupos generados en el paso anterior se vuelve a dividir en otros dos: el que se volverá a dividir según lo indicado en la fila 7 de la matriz y el que se volverá a dividir según lo indicado en la fila 8 de la matriz.
- En la tercera etapa (que corresponde con la octava fila de la matriz) uno de los grupos generados en el paso anterior se vuelve a dividir en otros dos: el que se volverá a dividir según lo indicado en la fila 4 de la matriz y el que se volverá a dividir según lo indicado en la fila 1 de la matriz.
- En la cuarta etapa (que corresponde con la séptima fila de la matriz) uno de los grupos generados en la segunda etapa se vuelve a dividir en un grupo que se volverá a dividir según lo indicado en la fila 3 de la matriz y una unidad individual (en concreto, la que ocupa la posición 4 en el fichero de datos).
- …
- Por último, en la décima etapa (que corresponde con la primera fila de la matriz) se dividen las unidades individuales 8 y 11, las cuales permanecían unidas hasta este momento.
Consultemos las distancias a las que se separan cada uno de los grupos.
> cluster$height
[1] 2.518551 1.256555 3.063649 7.389655 1.274623 3.084236 4.134429 1.618253 3.450847 1.122524
La primera división se produce a una distancia de 2.5185 unidades (entendiendo como distancia la mayor de las distancias entre dos unidades del conjunto de datos). Después, el resto de unidades se asigna al grupo del que se encuentra menos distante. La segunda división entre grupos se produce a una distancia de 1.2565 unidades.
Al igual que con los métodos aglomerativos, en este caso es posible representar un dendrograma para visualizar el proceso de división del conjunto de datos. Para ello, de nuevo, debemos utilizar la función plot pasándole como argumento el objeto generado por la función diana.
> plot(cluster)
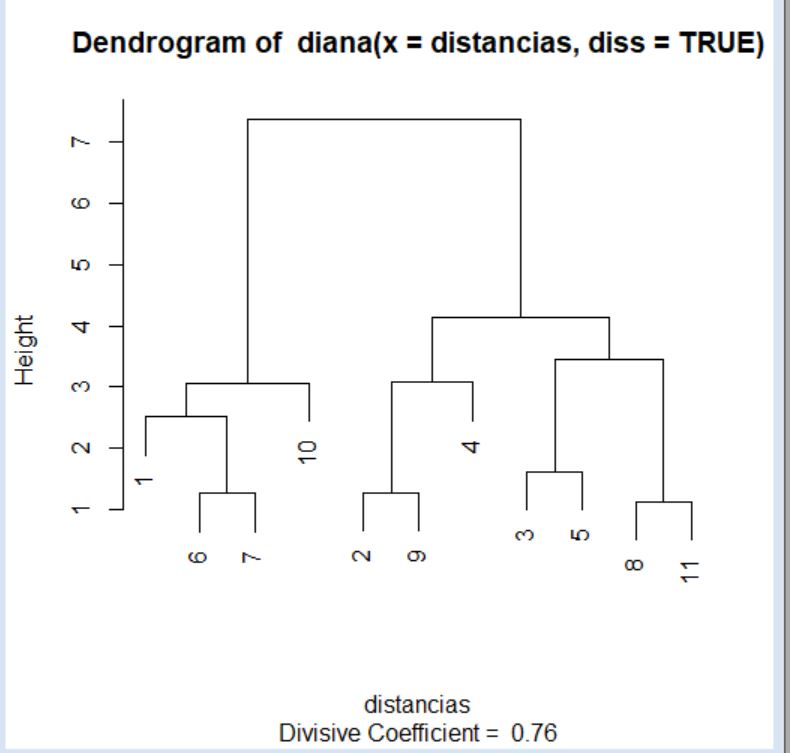
La interpretación de este dendrograma se realiza desde arriba hacia abajo. Si comparamos este dendrograma con el del supuesto práctico anterior observamos importantes diferencias, por lo que la elección del método para la creación de los clústers (aglomerativo o divisivo) puede condicionar los resultados de forma notable.
Supuesto práctico 4: Análisis clúster jerárquico en R con variables dicotómicas
Realizamos un estudio sobre las pequeñas y medianas empresas del sector textil. En el estudio se recoge información sobre si 12 empresas disponen de los siguientes servicios: Personal Especializado, Estudio de distribución de Planta, Estudio de distribución de Servicios y Aplicación de Sistema de Calidad. Si la empresa dispone del servicio en cuestión, la variable correspondiente toma el valor 1 y, si no dispone de él, la variable toma el valor 0.
Realizar un análisis clúster jerárquico aglomerativo utilizando el método del enlace simple (o del vecino más próximo).
Los datos se encuentran en el fichero empresas.txt.
Comenzamos importando los datos del fichero empresas.txt en R.

Tabla 2: Datos del Supuesto Práctico 3
Comenzamos importando los datos del fichero empresas.txt en R.
> datos <- read.table(“empresas.txt”, header = TRUE
A continuación, guardamos en un data frame las variables a partir de las cuales generaremos los grupos.
> attach(datos)
> variables <- data.frame(Personal_Especializado, Distribucion_Planta, Distribucion_Servicios, Sistema_Calidad)
Calculamos las distancias entre empresas mediante la función dist, teniendo en cuenta que la distancia a usar es la binaria, dado el carácter dicotómico de las variables.
> distancias <- dist(variables, method = “binary”)
Por último, llamamos a la función hclust, pasando como argumento la matriz de distancias que acabamos de calcular y el método que se ha de utilizar para la formación de los conglomerados.
> cluster <- hclust(distancias, method = “single”)
> cluster
Call:
hclust(d = distancias, method = “single”)
Cluster method : single
Distance : binary
Number of objects: 12
Consultemos ahora el historial de conglomeración, accediendo al componente merge del objeto que ha generado la función hclust.
> cluster$merge
[,1] [,2]
[1,] -3 -5
[2,] -8 1
[3,] -11 2
[4,] -12 3
[5,] -2 -6
[6,] -1 5
[7,] -7 6
[8,] -4 7
[9,] -9 8
[10,] -10 9
[11,] 4 10
Este historial se interpreta de la misma manera que el del supuesto práctico 1, por lo que podemos decir que las unidades que se unen en el primer paso son las situadas en la posición 3 y 5 del fichero. En el segundo paso, se unen el grupo formado en el paso anterior con la unidad situada en la posición 8 del fichero. El proceso continúa hasta que en el undécimo y último paso se fusionan los grupos generados en la etapa 4 y en la etapa 10 del procedimiento.
Veamos ahora las distancias a las que se producen los agrupamientos. Para ello, accedemos al componente height del objeto cluster.
> cluster$height
[1] 0.0000000 0.0000000 0.0000000 0.0000000 0.2500000 0.3333333 0.3333333
[8] 0.5000000 0.5000000 0.5000000 1.0000000
Terminemos este ejemplo graficando el dendrograma asociado mediante la orden plot.
> plot(cluster)
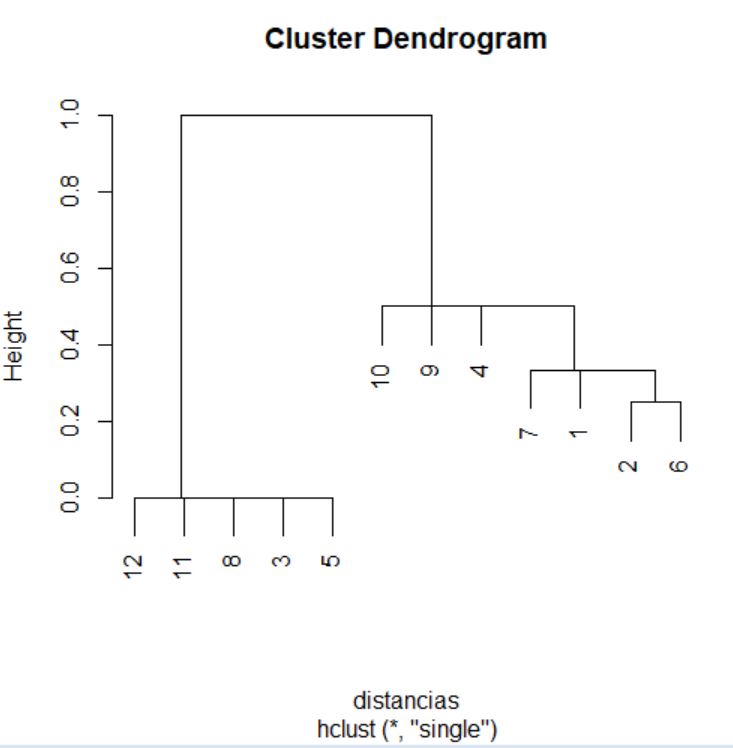
Supuesto práctico 5: Análisis clúster jerárquico en R con variables mixtas
Los ejemplos que se han realizado hasta ahora realizaban los clúster a partir de un conjunto de variables las cuales eran, o todas numéricas o todas dicotómicas. En la práctica, los grupos en un análisis clúster suelen crear a partir de conjuntos de variables en los que aparecen ambos tanto unas como otras de forma simultánea. Como ejemplo tenemos este supuesto práctico:
Se dispone de una versión ampliada del conjunto de datos utilizado en el supuesto 1, la cual, además de las variables numéricas del conjunto original, contiene las siguientes variables:
- Tipo del automóvil: manual (0) o automático (1).
- Combustible del automóvil: gasolina (0) o diesel (1).
Realizar un análisis de conglomerados jerárquico utilizando el método el promedio entre grupos a partir de todas las variables numéricas y de las dos variables dicotómicas que se acaban de presentar.
Los datos se encuentran en el fichero ventas_vehiculos_ext.txt.
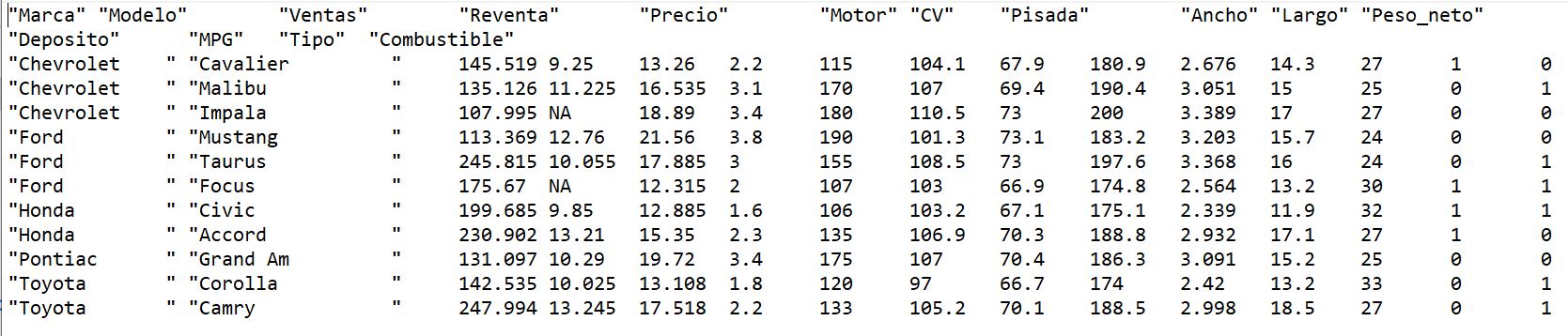
Tabla3: Datos del Supuesto Práctico 4
Recordar que el fichero con el que se trabaja debe estar situado en el directorio de trabajo
> setwd(“C:/Users/Usuario/Desktop/Datos”) # Nos situamos en el directorio donde se encuentra el fichero de datos
> datos <- read.table(“ventas_vehiculos_ext.txt”, header = TRUE) # Importamos los datos
Creamos un data frame con las variables que utilizaremos para formar los clústers.
> attach(datos)
> variables <- data.frame (Precio, Motor, CV, Pisada, Ancho, Largo, Peso_neto, Deposito, MPG, Tipo, Combustible)
> variables
Precio Motor CV Pisada Ancho Largo Peso_neto Deposito MPG Tipo Combustible
1 13.260 2.2 115 104.1 67.9 180.9 2.676 14.3 27 1 0
2 16.535 3.1 170 107.0 69.4 190.4 3.051 15.0 25 0 1
3 18.890 3.4 180 110.5 73.0 200.0 3.389 17.0 27 0 0
4 21.560 3.8 190 101.3 73.1 183.2 3.203 15.7 24 0 0
5 17.885 3.0 155 108.5 73.0 197.6 3.368 16.0 24 0 1
6 12.315 2.0 107 103.0 66.9 174.8 2.564 13.2 30 1 1
7 12.885 1.6 106 103.2 67.1 175.1 2.339 11.9 32 1 1
8 15.350 2.3 135 106.9 70.3 188.8 2.932 17.1 27 1 0
9 19.720 3.4 175 107.0 70.4 186.3 3.091 15.2 25 0 0
10 13.108 1.8 120 97.0 66.7 174.0 2.420 13.2 33 0 1
11 17.518 2.2 133 105.2 70.1 188.5 2.998 18.5 27 0 1
No es posible utilizar la función dist para calcular las distancias entre los vehículos, puesto que los distintos tipos de distancia que nos ofrece esta función sólo son válidas cuando todas las variables son numéricas o cuando todas son dicotómicas. En el caso de que el conjunto de datos esté constituido por variables de ambos tipos, se recomienda utilizar una distancia alternativa, conocida como distancia de Gower. Para calcular distancias entre individuos en R mediante el método de Gower se debe utilizar la función daisy, que forma parte del paquete cluster. La sintaxis de esta función es la siguiente:
daisy(x, metric = “euclidean”, type)
donde
- x es, bien una matriz o bien un data frame con los valores de las variables a partir de las cuales se realizará el análisis clúster.
- metric es una cadena de caracteres usada para calcular la distancia entre observaciones. Los posibles valores para este parámetro son “euclidean”, para la distancia euclídea (valor por defecto), “manhattan”, para la distancia Manhattan y “gower” para la distancia de Gower. Si el data frame contiene variables no numéricas, la función utiliza la distancia de Gower de forma automática.
- type es una lista en donde hay que indicar la posición de las variables dicotómicas, indicando si son simétricas (symm) o asimétricas (asymm).
Calculemos las distancias de Gower para los vehículos de nuestro conjunto de datos.
> distancias <- daisy(variables, metric = “gower”, type = list(symm = c(10,11))) # puede necesitar instalar algún paquete
> distancias
Dissimilarities :
1 2 3 4 5 6 7 8 9 10
2 0.44709986
3 0.54744953 0.32257190
4 0.51578552 0.33991073 0.24003425
5 0.57774205 0.17137419 0.21213172 0.31665610
6 0.21521619 0.48049787 0.76266573 0.71618690 0.61114007
7 0.27957459 0.54485627 0.82702412 0.78323890 0.67549846 0.08604171
8 0.18762940 0.34288988 0.36257495 0.44359489 0.42041568 0.40284560 0.46720399
9 0.41140477 0.17479442 0.19277213 0.16511631 0.27877349 0.62662096 0.69097936 0.29359948
10 0.39215788 0.46479887 0.74696672 0.67759227 0.59544106 0.20985336 0.20281705 0.56896478 0.61092196
11 0.39412986 0.18860741 0.37646017 0.43248658 0.25248272 0.42752787 0.49188627 0.24976927 0.30538679 0.41182887
Metric : mixed ; Types = I, I, I, I, I, I, I, I, I, S, S
Number of objects : 11
En este caso, hemos indicado que las variables de las columnas 10 (Tipo) y 11 (Combustible) son variables dicotómicas simétricas, es decir, variables en las cuales no hay preferencia por qué valor se codifique como 0 y cuál se codifique como 1.
Una vez calculadas las distancias, procedemos a llamar a la función hclust, tal y como lo hemos hecho en ejemplos anteriores.
> cluster <- hclust(distancias, method = “average”)
> cluster
Call:
hclust(d = distancias, method = “average”)
Cluster method : average
Number of objects: 11
A continuación, accedemos al historial de conglomeración, consultando el componente merge del objeto que nos ha devuelto la función hclust.
> cluster$merge
[,1] [,2]
[1,] -6 -7
[2,] -4 -9
[3,] -2 -5
[4,] -1 -8
[5,] -10 1
[6,] -3 2
[7,] -11 3
[8,] 6 7
[9,] 4 5
[10,] 8 9
El historial de conglomeración se interpreta del mismo modo que en ejemplos anteriores. Así, podemos decir que en el primer paso se agrupan los vehículos situados en las posiciones 6 y 7 del conjunto de datos. Del mismo modo, en la segunda etapa se unen en un grupo las observaciones situadas en las posiciones 4 y 9 del conjunto de datos. El proceso de agrupación continúa hasta que, en el décimo paso, se aúnan los grupos formados en las etapas 8 y 9 del proceso.
Vamos a consultar ahora las distancias a las que se producen los agrupamientos. Para ello, accedemos al componente height del objeto cluster.
> cluster$height
[1] 0.08604171 0.16511631 0.17137419 0.18762940 0.20633520 0.21640319 0.22054506 0.30657465 0.38766051 0.53840428
En este ejemplo, los primeros vehículos que se unen están separados por una distancia de 0,08604 unidades, mientras que el último agrupamiento se produce a una distancia de 0,5384 unidades.
Para terminar, representamos el dendrograma asociado.
> plot(cluster)
Análisis clúster de k-medias
Análisis clúster de K-medias es una herramienta diseñada para asignar los casos a un número fijo de grupos, cuyas características no se conocen, pero se basan en un conjunto de variables que deben ser cuantitativas. Es muy útil cuando se quiere clasificar un gran número de casos. Es un método de agrupación de casos que se basa en las distancias existentes entre ellos en un conjunto de variables cuantitativas. Este método de aglomeración no permite agrupar variables. El objetivo de optimalidad que se persigue es “maximizar la homogeneidad dentro de los grupos.”
Es el método que se usa más habitualmente, es fácil de programar y da resultados razonables. Tiene por objetivo separar las observaciones en K clúster, de manera que cada dato pertenezca a un grupo y sólo a uno. El algoritmo busca con un método iterativo:
-
Los centroides (medias, medianas,… ) de los K clusters
-
Asigna cada individuo a un clúster.
El algoritmo requiere que se especifique el número de conglomerados, también se puede especificar los centros iniciales de los clusters si conoce de antemano dicha información.
En este método, la medida de distancia o de similaridad entre los casos se calcula utilizando la distancia euclídea. Es muy importante el tipo de escala de las variables, si las variables tienen diferentes escalas (por ejemplo, una variable se expresa en dólares y otra en años), los resultados podrían ser equívocos. En estos casos, se debería considerar la estandarización de las variables antes de realizar el análisis de conglomerados de k-medias.
Este procedimiento supone que se ha seleccionado el número apropiado de conglomerados y que se han incluido todas las variables relevantes. Si se ha seleccionado un número inapropiado de conglomerados o se han omitido variables relevantes, los resultados podrían ser equívocos.
Existen varias formas de implementarlo pero todas ellas siguen, básicamente, los siguientes pasos:
-
Paso 1. Se toman al azar k clusters iniciales y se calculan los centroides (medias) de los clusters
-
Paso 2. Se calcula la distancia euclídea de cada observación a los centroides de los clusters y se reasigna cada observación al grupo más próximo formando los nuevos clusters que se toman en lugar de los primeros como una mejor aproximación de los mismos
-
Paso 3. Se calculan los centroides de los nuevos clusters
-
Paso4. Se repiten los pasos 2) y 3) hasta que se satisfaga un criterio de parada como, por ejemplo, no se produzca ninguna reasignación, es decir, los clusters obtenidos en dos iteraciones consecutivas son los mismos.
El método suele ser muy sensible a la solución inicial dada por lo que es conveniente utilizar una que sea buena. Una forma de construirla es mediante una clasificación obtenida por un algoritmo jerárquico.
Como aclaración, vamos a realizar el procedimiento para el caso de dos variables \( X_1 \) y \( X_2 \) y cuatro elementos A, B, C. D. Los datos son los siguientes:
\( \begin{array} {|c|c|c|} \hline & X_1 & X_2 \\ \hline A & 6 & 3 \\ \hline B & -2 & 1 \\ \hline C & 2 & 3 \\ \hline D & -2 & -1 \\ \hline \end{array} \)
Se quiere agrupar estas observaciones en dos clusters (k = 2)
Paso 1. De forma arbitraria se agrupan las observaciones en dos clusters (AB) y (CD) y se calculan los centroides de cada clúster
\( \begin{array} {|ccc|} \hline & Cluster (AB) & \\ \hline \bar {x_1} & & \bar{x_2} \\ \hline (6-2)/2=2 & & (3+1)/2=2 \\ \hline \end{array} \) \( \hspace{.3cm} \begin{array} {|ccc|} \hline & Cluster (CD) & \\ \hline \bar {x_1} & & \bar{x_2} \\ \hline (2-2)/2=0 & & (3-1)/2=1 \\ \hline \end{array} \)
Paso 2. Calculamos la distancia euclídea de cada observación a los centroides de los clusters y reasignamos cada una de estas observaciones al clúster que esté más próximo
\( d^{2} (A,(AB)) = (6-2)^{2} + (3-2)^{2} = 17 \hspace{2 cm} d^{2} (A,(CD)) = (6-0)^{2} + (3-1)^{2} = 40 \)
Como A está más próximo al clúster (AB) que al clúster (CD), no se reasigna
\( d^{2} (B,(AB)) = (-2-2)^{2} + (1-2)^{2} = 17 \hspace{2 cm} d^{2} (B,(CD)) = (-2-0)^{2} + (1-1)^{2} = 4 \)
Como B está más próximo al clúster (CD) que al clúster (AB), se reasigna al clúster (CD) formando el clúster (BCD).
A continuación se calculan los centroides de los nuevos clusters
\( \begin{array} {|ccc|} \hline & Cluster (A) & \\ \hline \bar {x_1} & & \bar{x_2} \\ \hline 6 & & 3 \\ \hline \end{array} \) \( \hspace{.3cm} \begin{array} {|ccc|} \hline & Cluster (BCD) & \\ \hline \bar {x_1} & & \bar{x_2} \\ \hline \displaystyle \frac{-2+2-2}{3} = -0.7 & & \displaystyle \frac{1+3-1}{3}= 1\\ \hline \end{array} \)
Paso 3. Se repite el paso 2 calculando las distancias de cada observación a los centroides de los nuevos clusters para ver si se producen cambios de nuevas reasignaciones
\( \begin{array} {|c|c|c|} \hline & Cluster (A) & Cluster (BCD) \\ \hline A & 0 & (6+0.7)^{2} + (3-1)^{2} = 48.89 \\ \hline B & (-2 -6)^{2} + (1-3)^{2} = 20 & (-2+0.7)^{2} + (1-1)^{2} = 1.69 \\ \hline C & (2-6)^{2} + (3-3)^{2} = 16 & (2+0.7)^{2} + (3-1)^{2} = 11.29 \\ \hline D & (-2-6)^{2} + (-1-3)^{2}= 32 & (-2+0.7)^{2} + (-1-1.5)^{2} = 5.69\\ \hline \end{array} \)
Como no se producen cambios en las ubicaciones de los clusters, la solución para k=2 clusters es: Clúster 1: (A) y Clúster 2: (BCD).
Existe la posibilidad de utilizar esta técnica de manera exploratoria, clasificando los casos e iterando para encontrar la ubicación de los centroides, o sólo como técnica de clasificación, clasificando los casos a partir de centroides conocidos. Cuando se utiliza como técnica exploratoria, es habitual que se desconozca el número idóneo de conglomerados, (como el ejemplo numérico que hemos hecho), por lo que es conveniente repetir el análisis con distinto número de conglomerados y comparar las soluciones obtenidas; en estos casos también se puede utilizar el método análisis de conglomerados jerárquico con una submuestra de casos.
Por último hay que interpretar la clasificación obtenida, ello requiere, en primer lugar, un conocimiento suficiente del problema analizado. Hay que estar abierto a la posibilidad de que no todos los grupos obtenidos tienen por qué ser significativos. Algunas ideas que pueden ser útiles en la interpretación de los resultados son las siguientes:
-
-
Realizar ANOVAS y MANOVAS para ver qué grupos son significativamente distintos y en qué variables lo son.
-
Realizar Análisis Discriminante.
-
Realizar un Análisis Factorial o de Componentes Principales para representar gráficamente los grupos obtenidos y observar las diferencias existentes entre ellos.
-
Calcular perfiles medios por grupos y compararlos.
-
Conviene hacer notar, finalmente, que es una técnica eminentemente exploratoria cuya finalidad es sugerir ideas al analista a la hora de elaborar hipótesis y modelos que expliquen el comportamiento de las variables analizadas identificando grupos homogéneos de objetos. Los resultados del análisis deberían tomarse como punto de partida en la elaboración de teorías que expliquen dicho comportamiento
Un buen análisis de clúster es:
-
Eficiente. Utiliza el menor número de grupos posibles.
-
Efectivo. Captura todas las agrupaciones estadísticamente y comercialmente importante. Por ejemplo, un clúster con cinco clientes puede ser estadísticamente diferente, pero no es muy rentable.
Supuesto práctico 6
A partir de los datos del supuesto práctico 2, realizar un análisis clúster no jerárquico utilizando el algoritmo de las k-medias.
Los fabricantes de automóviles deben adaptar sus estrategias de desarrollo de productos y de marketing en función de cada grupo de consumidores para aumentar las ventas y el nivel de fidelidad a la marca. La tarea de agrupación de los coches según variables que describen los hábitos de consumo, sexo, edad, nivel de ingresos, etc. de los clientes puede ser en gran medida automática utilizando el análisis de clúster.
Se desea hacer un estudio de mercado sobre las preferencias de los consumidores al adquirir un vehículo. Para ello, disponemos de un conjunto de datos, que se encuentra en el fichero ventas_vehiculosR.txt.
Comenzamos importando los datos del fichero de texto ventas_vehiculos.txt y escalando sus variables numéricas.
> datos <- read.table(“ventas_vehiculos.txt”, header = TRUE)
> datos[3:13] <- scale(datos[3:13])
> datos[3:13]
Ventas Reventa Precio Motor CV Pisada
1 -0.47598937 -1.17923440 -0.96317643 -0.5620214 -0.9417589 -0.20914671
2 -0.67386911 0.07892235 0.08302845 0.6475464 0.8332072 0.56664168
3 -1.19043557 NA 0.83533760 1.0507356 1.1559283 1.50293802
4 -1.08811615 1.05678089 1.68827410 1.5883213 1.4786494 -0.95818379
5 1.43361771 -0.66641608 0.51428847 0.5131500 0.3491256 0.96791154
6 0.09807702 NA -1.26505845 -0.8308142 -1.1999358 -0.50341128
7 0.55531574 -0.79700957 -1.08297088 -1.3683999 -1.2322079 -0.44990863
8 1.14967847 1.34344952 -0.29552202 -0.4276250 -0.2963167 0.53989036
9 -0.75058011 -0.51671135 1.10048265 1.0507356 0.9945678 0.56664168
10 -0.53280387 -0.68552732 -1.01173312 -1.0996071 -0.7803983 -2.10849072
11 1.47510525 1.36574597 0.39704963 -0.5620214 -0.3608609 0.08511785
Ancho Largo Peso_neto Deposito MPG
1 -0.7720254 -0.51077319 -0.64772634 -0.454823228 -0.1182625
2 -0.1654340 0.56318653 0.38189645 -0.097462120 -0.7687061
3 1.2903854 1.64845109 1.30992979 0.923569615 -0.1182625
4 1.3308248 -0.25076189 0.79923689 0.259898987 -1.0939279
5 1.2903854 1.37713495 1.25227092 0.413053748 -1.0939279
6 -1.1764197 -1.20036837 -0.95524034 -1.016390682 0.8574030
7 -1.0955409 -1.16645385 -1.57301402 -1.680061310 1.5078466
8 0.1985208 0.38230910 0.05516282 0.974621202 -0.1182625
9 0.2389603 0.09968813 0.49172288 0.004641053 -0.7687061
10 -1.2572986 -1.29080708 -1.35061549 -1.016390682 1.8330684
11 0.1176420 0.34839459 0.23637643 1.689343417 -0.1182625
A continuación, se procede a realizar el análisis clúster utilizando la función kmeans de R. Esta función forma parte del paquete base de R, por lo que no es necesario instalar ningún paquete adicional. Su sintaxis es la que sigue:
kmeans(x, centers, nstart = 1, algorithm = “Hartigan-Wong”)
donde
- x es una matriz numérica con los datos de las variables que usarán para generar los clústers.
- centers es, bien un número que indica el número de clústers a generar, o bien el conjunto de los centroides iniciales de los clústers.
- nstart es un número que indica el número de soluciones iniciales a partir de las cuales se aplicará el algoritmo. Después, el propio algoritmo se quedará con la más conveniente. El valor de este parámetro solamente se tiene en cuenta si el parámetro centers es un número.
- algorithm es una cadena de caracteres que indica el algoritmo a utilizar para la clasificación. Las posibles opciones son “Hartigan-Wong” (opción por defecto), “Lloyd”, “Forgy” (ambas denotan el algoritmo de Lloyd-Forgy) y “MacQueen”. Las principales diferencias entre estos algoritmos estriban en el criterio para la asignación de los individuos a los grupos y la frecuencia de actualización de los centroides de los grupos. En la página https://towardsdatascience.com/three-versions-of-k-means-cf939b65f4ea puede consultarse más información sobre las diferencias entre estos algoritmos.
Volviendo a nuestro ejemplo, seleccionamos las variables numéricas que emplearemos para generar los grupos de vehículos.
> attach(datos)
The following objects are masked from datos (pos = 8):
Ancho, CV, Deposito, Largo, Marca, Modelo, Motor, MPG, Peso_neto,
Pisada, Precio, Reventa, Ventas
> variables <- data.frame (Precio, Motor, CV, Pisada, Ancho, Largo, Peso_neto, Deposito, MPG)
> variables
Precio Motor CV Pisada Ancho Largo
1 -0.96317643 -0.5620214 -0.9417589 -0.20914671 -0.7720254 -0.51077319
2 0.08302845 0.6475464 0.8332072 0.56664168 -0.1654340 0.56318653
3 0.83533760 1.0507356 1.1559283 1.50293802 1.2903854 1.64845109
4 1.68827410 1.5883213 1.4786494 -0.95818379 1.3308248 -0.25076189
5 0.51428847 0.5131500 0.3491256 0.96791154 1.2903854 1.37713495
6 -1.26505845 -0.8308142 -1.1999358 -0.50341128 -1.1764197 -1.20036837
7 -1.08297088 -1.3683999 -1.2322079 -0.44990863 -1.0955409 -1.16645385
8 -0.29552202 -0.4276250 -0.2963167 0.53989036 0.1985208 0.38230910
9 1.10048265 1.0507356 0.9945678 0.56664168 0.2389603 0.09968813
10 -1.01173312 -1.0996071 -0.7803983 -2.10849072 -1.2572986 -1.29080708
11 0.39704963 -0.5620214 -0.3608609 0.08511785 0.1176420 0.34839459
Peso_neto Deposito MPG
1 -0.64772634 -0.454823228 -0.1182625
2 0.38189645 -0.097462120 -0.7687061
3 1.30992979 0.923569615 -0.1182625
4 0.79923689 0.259898987 -1.0939279
5 1.25227092 0.413053748 -1.0939279
6 -0.95524034 -1.016390682 0.8574030
7 -1.57301402 -1.680061310 1.5078466
8 0.05516282 0.974621202 -0.1182625
9 0.49172288 0.004641053 -0.7687061
10 -1.35061549 -1.016390682 1.8330684
11 0.23637643 1.689343417 -0.1182625
Ralizamos la llamada a la función kmeans. Supondremos que queremos generar dos clústers y probaremos con 5 soluciones iniciales distintas. Utilizaremos el algoritmo de Lloyd-Forgy.
> cluster <- kmeans (variables, centers = 2, nstart = 5, algorithm = “Lloyd”)
> cluster
K-means clustering with 2 clusters of sizes 7, 4
Cluster means:
Precio Motor CV Pisada Ancho Largo Peso_neto Deposito MPG
1 0.6175627 0.5515489 0.5934715 0.4672796 0.6144692 0.5954861 0.6466566 0.5953808 -0.5828651
2 -1.0807347 -0.9652106 -1.0385752 -0.8177393 -1.0753211 -1.0421006 -1.1316490 -1.0419165 1.0200139
Clustering vector:
[1] 2 1 1 1 1 2 2 1 1 2 1
Within cluster sum of squares by cluster:
[1] 23.484815 6.826719
(between_SS / total_SS = 66.3 %)
Available components:
[1] “cluster” “centers” “totss” “withinss” “tot.withinss” “betweenss” “size”
[8] “iter” “ifault”
Al inicio de la salida se indica el número de clústers generados (2, tal y como habíamos indicado) y el tamaño de cada uno de ellos (7 y 4 unidades, respectivamente). Para conocer qué unidades componen cada clúster, es necesario mirar la sección Clustering vector, en donde, siguiendo el orden en el que aparecen las unidades en el fichero de datos, se les asigna un número que indica el clúster al que pertenece cada una. Así, en nuestro caso el primer clúster estaría formado por los vehículos situados en las posiciones 2, 3, 4, 5, 8, 9 y 11 del conjunto de datos, mientras que el segundo clúster lo conformarían los vehículos situados en las posiciones 1, 6, 7 y 10 del fichero.
En Cluster means encontramos los centroides de los dos grupos que se han formado expresados como coordenadas con tantos componentes como variables haya. Por último, en la sección Within cluster sum of squares by cluster aparece la suma de cuadrados de cada grupo. Esta suma de cuadrados es una medida de la homogeneidad de cada grupo, por lo que interesan valores pequeños. En nuestro ejemplo, podemos concluir que el segundo grupo es mucho más homogéneo que el primero. Por otra parte, el porcentaje between_SS / total_SS es una medida que indica cómo de diferentes son los clústers creados, por lo que, en este caso, conviene obtener valores altos.
Veamos si se obtienen diferencias cuando se emplean los algoritmos de MacQueen o de Hartigan-Wong a la hora de la realización de los clústers.
> cluster <- kmeans (variables, centers = 2, nstart = 5, algorithm = “MacQueen”)
> cluster
K-means clustering with 2 clusters of sizes 7, 4
Cluster means:
Precio Motor CV Pisada Ancho Largo Peso_neto Deposito MPG
1 0.6175627 0.5515489 0.5934715 0.4672796 0.6144692 0.5954861 0.6466566 0.5953808 -0.5828651
2 -1.0807347 -0.9652106 -1.0385752 -0.8177393 -1.0753211 -1.0421006 -1.1316490 -1.0419165 1.0200139
Clustering vector:
[1] 2 1 1 1 1 2 2 1 1 2 1
Within cluster sum of squares by cluster:
[1] 23.484815 6.826719
(between_SS / total_SS = 66.3 %)
Available components:
[1] “cluster” “centers” “totss” “withinss” “tot.withinss” “betweenss” “size”
[8] “iter” “ifault”
> cluster <- kmeans (variables, centers = 2, nstart = 5, algorithm = “Hartigan-Wong”)
> cluster
K-means clustering with 2 clusters of sizes 4, 7
Cluster means:
Precio Motor CV Pisada Ancho Largo Peso_neto Deposito MPG
1 -1.0807347 -0.9652106 -1.0385752 -0.8177393 -1.0753211 -1.0421006 -1.1316490 -1.0419165 1.0200139
2 0.6175627 0.5515489 0.5934715 0.4672796 0.6144692 0.5954861 0.6466566 0.5953808 -0.5828651
Clustering vector:
[1] 1 2 2 2 2 1 1 2 2 1 2
Within cluster sum of squares by cluster:
[1] 6.826719 23.484815
(between_SS / total_SS = 66.3 %)
Available components:
[1] “cluster” “centers” “totss” “withinss” “tot.withinss” “betweenss” “size”
[8] “iter” “ifault”
En nuestro ejemplo, las soluciones que proporcionan los métodos de MacQueen y de Hartigan-Wong son idénticas a la que se ha obtenido aplicando el método de Lloyd-Forgy, aunque podría no ser así.
Los resultados de los dos últimos algoritmos podrían también ser:
> cluster <- kmeans (variables, centers = 2, nstart = 5, algorithm = “MacQueen”)
> cluster
K-means clustering with 2 clusters of sizes 4, 7
Cluster means:
Precio Motor CV Pisada Ancho Largo Peso_neto
1 -1.0807347 -0.9652106 -1.0385752 -0.8177393 -1.0753211 -1.0421006 -1.1316490
2 0.6175627 0.5515489 0.5934715 0.4672796 0.6144692 0.5954861 0.6466566
Deposito MPG
1 -1.0419165 1.0200139
2 0.5953808 -0.5828651
Clustering vector:
[1] 1 2 2 2 2 1 1 2 2 1 2
Within cluster sum of squares by cluster:
[1] 6.826719 23.484815
(between_SS / total_SS = 66.3 %)
> cluster <- kmeans (variables, centers = 2, nstart = 5, algorithm = “Hartigan-Wong”)
> cluster
K-means clustering with 2 clusters of sizes 7, 4
Cluster means:
Precio Motor CV Pisada Ancho Largo Peso_neto
1 0.6175627 0.5515489 0.5934715 0.4672796 0.6144692 0.5954861 0.6466566
2 -1.0807347 -0.9652106 -1.0385752 -0.8177393 -1.0753211 -1.0421006 -1.1316490
Deposito MPG
1 0.5953808 -0.5828651
2 -1.0419165 1.0200139
Clustering vector:
[1] 2 1 1 1 1 2 2 1 1 2 1
Within cluster sum of squares by cluster:
[1] 23.484815 6.826719
(between_SS / total_SS = 66.3 %)
Respecto a las diferencias, los resultados son exactamente los mismos (mismos centroides, misma distribución por clústers…), pero intercambiando el clúster 1 por el clúster 2. Esto ocurre porque las soluciones iniciales que se cogen (que vienen dadas por el argumento nstart) son aleatorias. Dependiendo de estas soluciones, asigna la denominación de clúster 1 y de clúster 2 a uno u otro grupo.
Análisis clúster de bietápico en R
El análisis clúster bietápico o en dos etapas es una técnica estadística muy útil para realizar grupos de observaciones cuando el tamaño de la muestra de la que se dispone es grande. En R, la función create_profiles_cluster, contenida en el paquete que se denomina prcr realiza el análisis clúster bietápico. Esta función actúa del siguiente modo: en el primer paso, realiza un análisis de conglomerados jerárquico, que mejora o ajusta en un segundo paso, en el que aplica una conglomeración según el algoritmo de las k-medias. La sintaxis de la función es la siguiente:
create_profiles_cluster(df, …, n_profiles, to_center = FALSE, to_scale = FALSE, distance_metric = “squared_euclidean”, linkage = “complete”)
donde
- df es un data frame con variables continuas.
- … son las variables, sin comillas y separadas por comas, a partir de las cuales se realizará la conglomeración.
- n_profiles es un número que indica el número conglomerados que se formarán.
- to_center es un valor lógico que indica si las variables deben centrarse para que su media sea 0. Por defecto, toma el valor FALSE, pero es recomendable cambiar su valor a TRUE cuando las variables continuas vienen dadas en unidades de medida muy dispares.
- to_scale es un valor lógico que indica si las variables deben escalarse para que su desviación típica sea 1. Por defecto, toma el valor FALSE, pero es recomendable cambiar su valor a TRUE cuando las variables continuas vienen dadas en unidades de medida muy dispares.
- distance_metric es una cadena de caracteres que indica la distancia que se usa en la conglomeración jerárquica. Por defecto, la distancia que se considera es la euclídea, pero puede indicarse cualquier otra distancia compatible con la función dist.
- linkage es una cadera de caracteres que indica el método de aglomeración en la conglomeración jerárquica. Por defecto, el método de conglomeración que se considera es el del enlace completo, pero puede indicarse cualquier otro método compatible con la función hclust.
Supuesto práctico 7
A partir del conjunto de datos birth.death.rates.1966 contenido en el paquete cluster.datasets, realizar un análisis clúster bietápico utilizando la distancia euclídea y el método del enlace simple. Considerar 2 clústers.
De no haberlo hecho con anterioridad, hay que instalar este paquete usando la orden
> install.packages(“cluster.datasets”)
Y a continuación, es necesario cargarlo mediante la orden
> library(cluster.datasets)
Una vez cargado el paquete, podemos acceder al conjunto de datos al que nos hemos referido anteriormente ejecutando la orden
> data(birth.death.rates.1966)
Consultamos las primeras líneas del conjunto de datos, para echar un vistazo a las variables que las componen usando la función head.
> head(birth.death.rates.1966)
country birth death
1 Algeria 36.4 14.6
2 Congo 37.3 8.0
3 Egypt 42.1 15.3
4 Ghana 55.8 25.6
5 Ivory Coast 56.1 33.1
6 Malagasy 41.8 15.8
El conjunto de datos contiene las tasas de nacimiento y muerte de 70 países de todo el mundo en el año 1966.
A continuación, instalamos y cargamos el paquete prcr, que es el que contiene la función que lleva a cabo el análisis clúster bietápico.
> install.packages(“prcr”)
> library(prcr)
A continuación llamamos a la función create_profiles_cluster, indicando el número de clústers a generar y el método de conglomeración para la etapa jerárquica de conglomeración. En este caso, al tratarse de tasas, no será necesario el centrado y el escalado de las variables.
> cluster <- create_profiles_cluster(birth.death.rates.1966, birth, death, n_profiles = 2, linkage = “single”)
Prepared data: Removed 0 incomplete cases
Hierarchical clustering carried out on: 70 cases
K-means algorithm converged: 1 iteration
Clustered data: Using a 2 cluster solution
Calculated statistics: R-squared = 0.717
Automáticamente, la función devuelve información sobre la preparación de los datos y las dos etapas de conglomeración. También devuelve una medida R2 que es útil para la comparación entre modelos con distinto número de clústers.
Podemos consultar a qué cluster ha quedado asignado cada individuo accediendo al elemento cluster de la variable en la que hemos almacenado el resultado del análisis.
> cluster$cluster
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 1 2 1 1 2 2 1 2 2 1 1 1 1 1 1 1 2 2 2 1 1 1 1
[42] 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
Para caracterizar los dos clústers resultantes del análisis, podemos llamar a la función plot_profiles, también incluida en el paquete prcr, cuyo único argumento es la variable en la que se ha almacenado el resultado del análisis clúster bietápico, a las que hemos llamado cluster en nuestro ejemplo.
> plot_profiles(cluster)
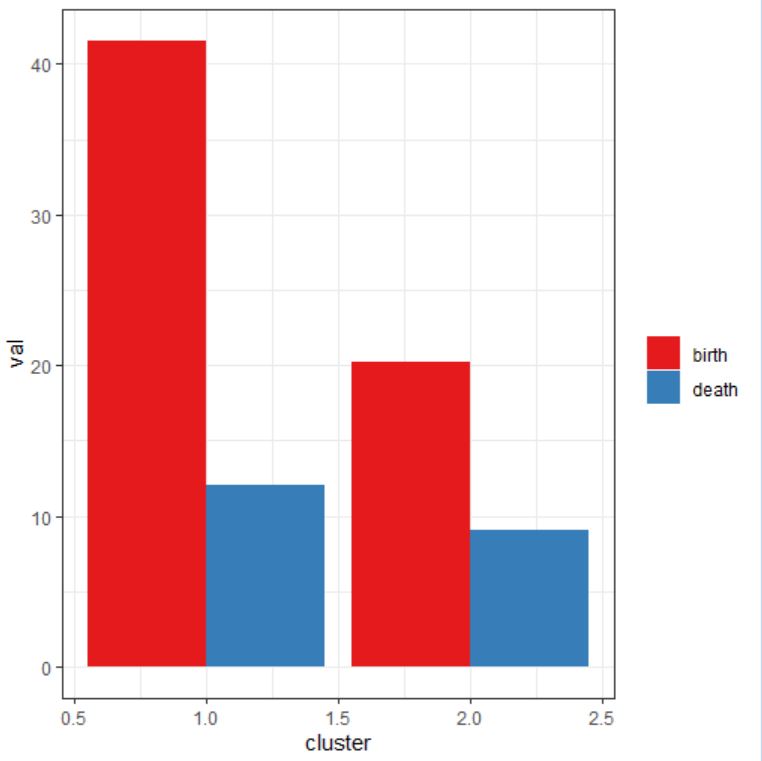
El gráfico muestra el promedio de las variables usadas para la conglomeración en cada uno de los dos clústers formados. Así, se aprecia que los países que conforman el primer clústers se caracterizan por tener unas tasas de nacimiento y muerte mayores, en promedio, que las de los países del segundo clúster.
Supuesto práctico 8
Utilizamos de nuevo el archivo de datos Ventas-vehículos.sav que contiene estimaciones de ventas, listas de precios y especificaciones físicas de varias marcas y modelos de vehículos. Como se ha detallado en el Supuesto Práctico 1
Variables tipo numérico: ventas (en miles); reventa (Valor de reventa en 4 años); tipo (Tipo de vehículo: Valores: {0, Automóvil; 1, Camión}); precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo).
> setwd(“C:/Users/Usuario/Desktop/Datos”) # En primer lugar nos situaremos en el directorio de trabajo
> library(“foreign”) # para leer un archivo .sav hay que instalar y cargar el paquete foreign. Como dicho paquete ya se instaló cada vez que se abra R hay que cargarlo
> datos<- read.spss(“Ventas-vehiculos.sav”,use.value.labels=TRUE, max.value.labels=TRUE, to.data.frame=TRUE, sep) #abrimos el archivo en SPSS, activamos los argumentos escribiendo “=TRUE” y le ponemos de nombre.
re-encoding from CP1252
El archivo Ventas-vehículos.sav contiene 157 datos Para hacer más comprensible la representación gráfica de los resultados, vamos a comenzar utilizando únicamente el 20 % de los casos de la muestra. Para ello vamos a instalar el paquete “dplyr”.
> install.packages(“dplyr”)
> library(“dplyr”)
El muestreo lo vamos a realizar utilizando la función “sample_frac”. Simplemente introducimos el data frame donde queremos hacer el muestreo y en el segundo argumento ponemos el peso.
> datos20 <- sample_frac(datos, 0.2)
> datos20
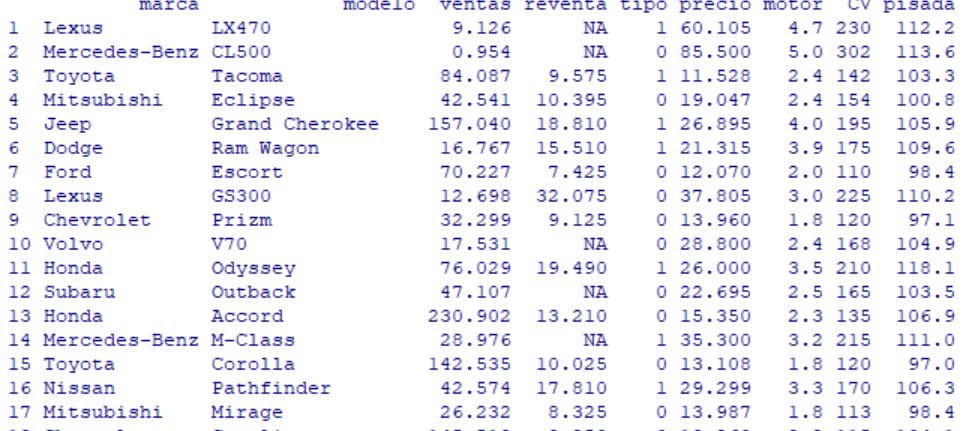
Ya tenemos nuestra muestra de 31 casos.
Vamos a comenzar representando la distancia existente entre los casos en dos variables de interés, hemos elegido la variable peso y la variable Tamaño del motor.
> x <- datos20[,c(“motor”,”peso_neto” )]
> x
motor peso_neto
1 4.7 5.401
2 5.0 4.115
3 2.4 2.580
4 2.4 2.910
5 4.0 3.880
6 3.9 4.245
7 2.0 2.468
8 3.0 3.638
9 1.8 2.398
10 2.4 3.259
11 3.5 4.288
12 2.5 3.415
13 2.3 2.932
14 3.2 4.387
15 1.8 2.420
16 3.3 3.947
17 1.8 2.250
18 2.2 2.676
19 2.7 2.778
20 2.4 2.958
21 3.9 4.298
22 2.7 3.452
23 5.2 4.470
24 3.0 3.294
25 4.0 3.876
26 4.6 4.808
27 3.0 3.761
28 2.3 3.250
29 2.0 2.853
30 2.0 2.626
31 5.0 4.125
A continuación representamos el gráfico. Mediante la función plot lo dibujamos y con la función text mostramos las etiquetas de los casos.
> plot(x)
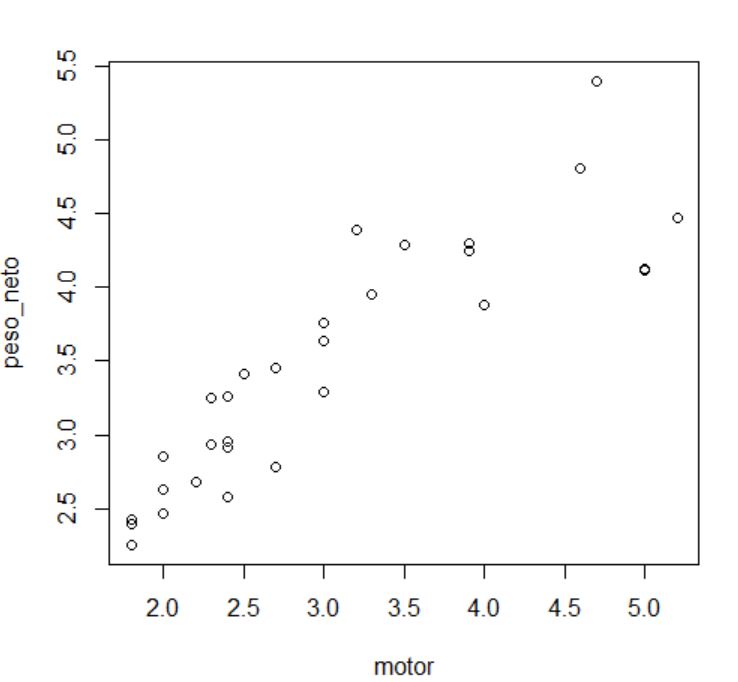
> text(x, cex=0.8)
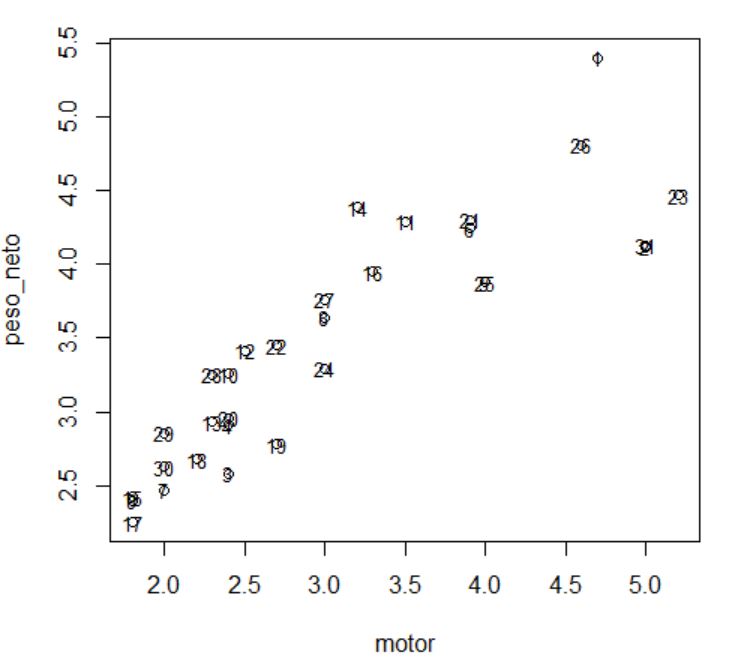
En el diagrama de dispersión están representados los valores Peso y Tamaño motor de los 31 casos seleccionados. Se puede apreciar que existe un grupo de vehículos relativamente numeroso con peso y tamaño de motor reducidos y otro grupo más disperso de vehículos de mayor peso y mayor motor.
Se han identificado, mediante el número de caso, los dos vehículos aparentemente más alejados entre sí. La nube de puntos, por tanto, incita a pensar que existen al menos dos grupos naturales de casos.
Para clasificar los casos en dos grupos:
Calculamos la matriz de distancias usando la distancia euclíeda al cuadrado.
> X.scale=scale(x, center = T, scale = T)
> X.scale
motor peso_neto
[1,] 1.56005908 2.38371341
[2,] 1.84622376 0.79121565
[3,] -0.63387016 -1.10962732
[4,] -0.63387016 -0.70097704
[5,] 0.89234149 0.50020712
[6,] 0.79695326 0.95219910
……………………………………
…………………………………….
[30,] -1.01542307 -1.05266395
[31,] 1.84622376 0.80359899
> dmx <- dist(X.scale[, colnames(x)], method = “euclidean”)
> dmx
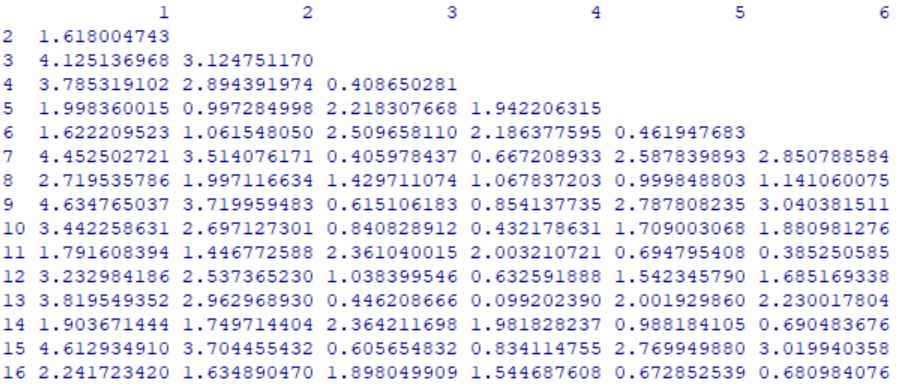
Una vez calculada la matriz de distancias, usamos la función kmeans, donde ponemos como argumento el nº de clústers que queremos obtener. Los asignamos a una variable nueva y lo juntamos con nuestro data frame x.
> c2 <- kmeans(dmx^2, 2)
> c2
K-means clustering with 2 clusters of sizes 12, 19
Cluster means:
1 2 3 4 5 6 7
1 2.687151 1.319047 8.2236302 6.6295866 0.9903831 0.7461069 10.2903123
2 14.702436 8.907523 0.6284961 0.4280488 4.2398051 5.2022665 0.8835422
8 9 10 11 12 13 14 15
1 2.665441 11.529492 5.3071529 1.096942 4.5198978 6.8703355 1.561751 11.400551
2 1.546247 1.157782 0.5794489 4.396034 0.7856492 0.4270397 4.274928 1.121748
16 17 18 19 20 21 22 23
1 1.596854 12.435491 8.4139450 6.3308822 6.4255490 0.7382233 3.840003 1.61970
2 2.786568 1.438774 0.5548919 0.5758992 0.4267161 5.4182029 0.931335 11.37668
24 25 26 27 28 29 30 31
1 3.5664349 0.9958055 1.176976 2.431367 5.671707 8.3308193 9.4311572 1.312913
2 0.9945231 4.2283354 10.353346 1.831605 0.571331 0.5499117 0.6916242 8.943619
Clustering vector:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
1 1 2 2 1 1 2 2 2 2 1 2 2 1 2 1 2 2 2 2 1 2 1 2 1 1
27 28 29 30 31
2 2 2 2 1
Within cluster sum of squares by cluster:
[1] 3181.877 2409.506
(between_SS / total_SS = 65.3 %)
Available components:
[1] “cluster” “centers” “totss” “withinss” “tot.withinss”
[6] “betweenss” “size” “iter” “ifault”
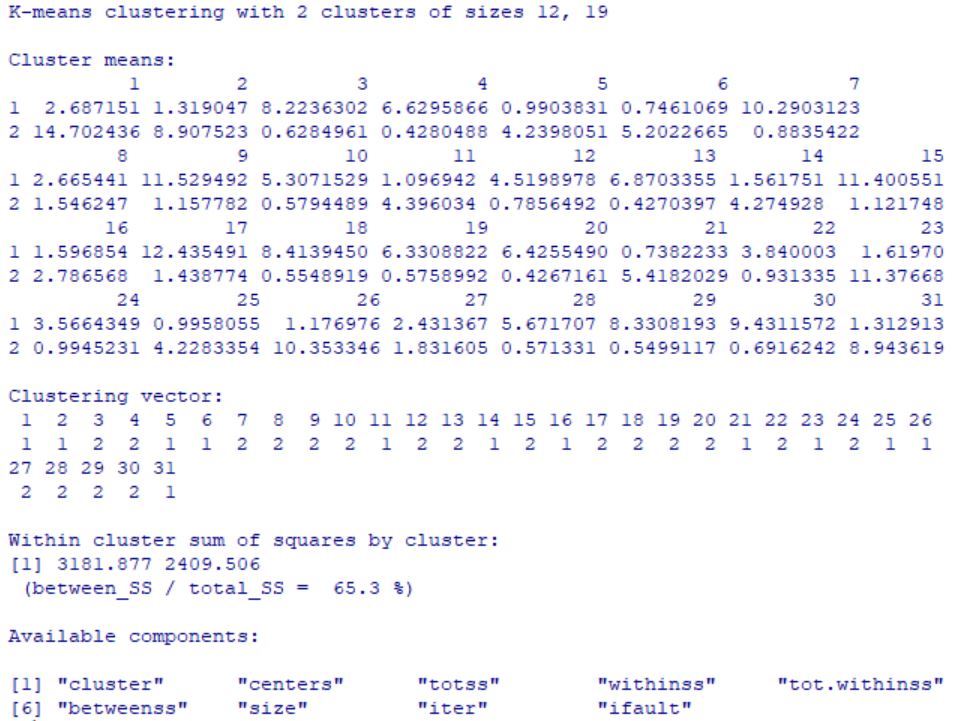
> asignacion<-data.frame(c2$cluster)
> asignacion
c2.cluster
1 1
2 1
3 2
4 2
5 1
6 1
7 2
8 2
9 2
10 2
11 1
12 2
13 2
14 1
15 2
16 1
17 2
18 2
19 2
20 2
21 1
22 2
23 1
24 2
25 1
26 1
27 2
28 2
29 2
30 2
31 1
> x <- cbind(x,asignacion)
> x
motor peso_neto c2.cluster
1 4 .7 5.401 1
2 5.0 4.115 1
3 2.4 2.580 2
4 2.4 2.910 2
5 4 .0 3.880 1
6 3.9 4.245 1
7 2.0 2.468 2
8 3.0 3.638 2
9 1.8 2.398 2
10 2.4 3.259 2
11 3.5 4.288 1
12 2.5 3.415 2
13 2.3 2.932 2
14 3.2 4.387 1
15 1.8 2.420 2
16 3.3 3.947 1
17 1.8 2.250 2
18 2.2 2.676 2
19 2.7 2.778 2
20 2.4 2.958 2
21 3.9 4.298 1
22 2.7 3.452 2
23 5.2 4.470 1
24 3.0 3.294 2
25 4.0 3.876 1
26 4.6 4.808 1
27 3.0 3.761 2
28 2.3 3.250 2
29 2.0 2.853 2
30 2.0 2.626 2
31 5.0 4.125 1
A continuación realizamos el gráfico donde ponemos en cada color cada uno de los clusters.
> plot(x$motor, x$peso_neto, col=x$c2.cluster)
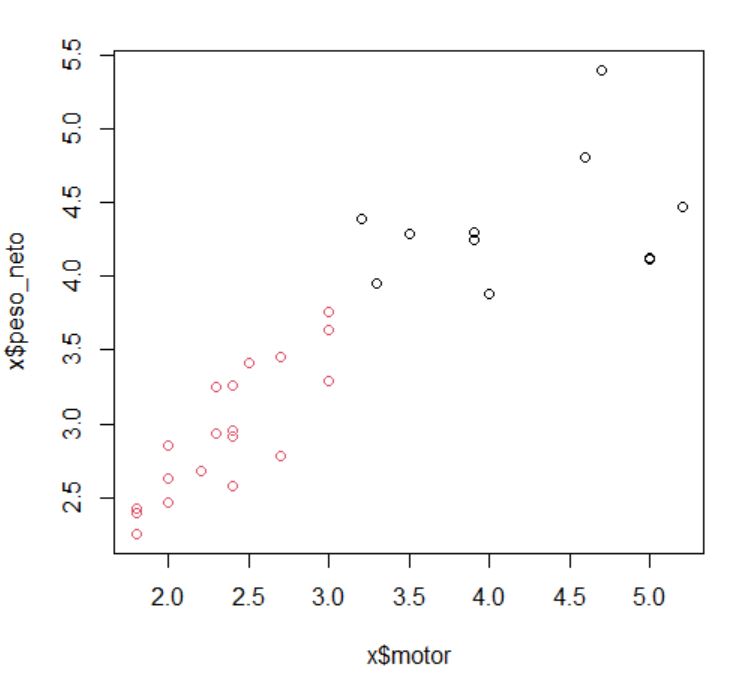
> text(x, cex=0.8, col=”black”)
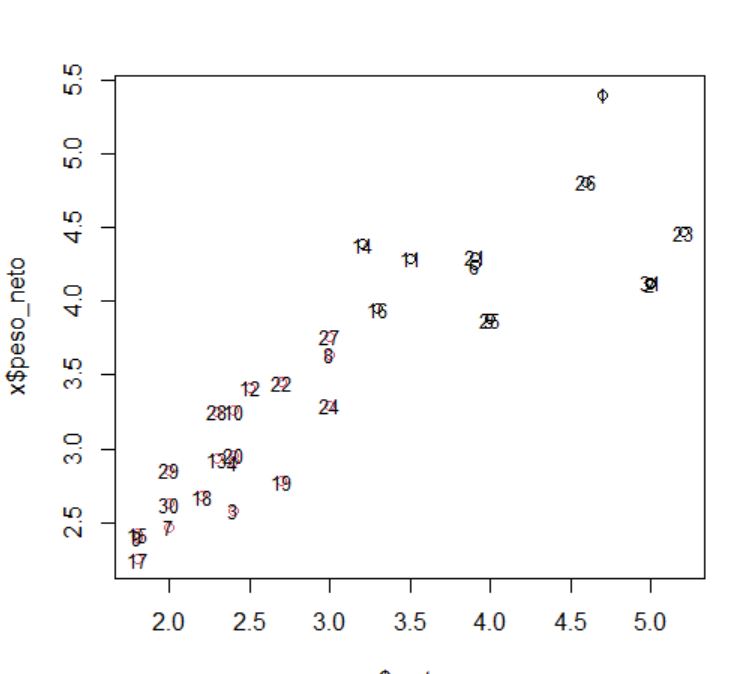
> dim(x)
[1] 31 3
> dim(datos)
[1] 157 14
Supuesto práctico 9
> datos<- read.spss(“Ventas-vehiculos.sav”,use.value.labels=TRUE, max.value.labels=TRUE, to.data.frame=TRUE, sep)
re-encoding from CP1252
Realizamos el muestreo
> library(“dplyr”)
> datos40 <- sample_frac(datos, 0.4)
> datos40$marca= gsub(” “,””,datos40$marca)
> datos40$modelo= gsub(” “,””,datos40$modelo)
Vamos a comenzar representando la distancia existente entre los casos en dos variables de interés, hemos vuelto a elegir la variable peso y la variable Tamaño del motor.
Elegimos las variables y las transformamos
> x <- datos40[,c(“motor”,”peso_neto” )]
> X.scale=scale(x, center = T, scale = T)
Como distancia, esta vez vamos a usar la distancia “manhattan” que es mayor que la euclídea pero más real. Calculamos la matriz de distancias
> dmx <- dist(X.scale[, colnames(x)], method = “manhattan”)
Vamos a dibujar el gráfico para ver como están representados los puntos.
> plot(x)
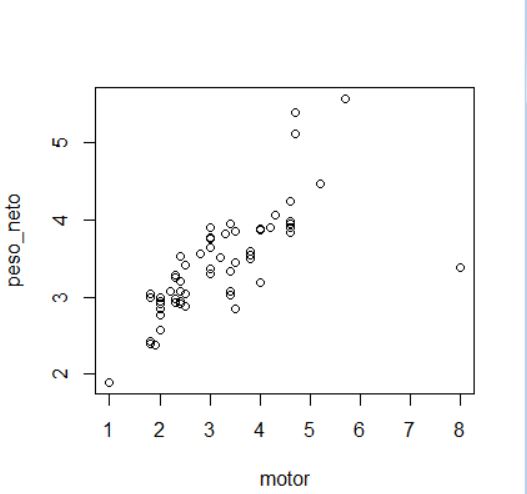
> text(x, cex=0.8, col=”red”)
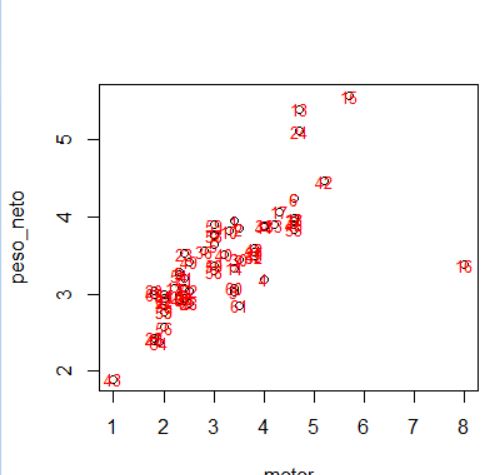
Podemos hacernos una idea de los distintos grupos que se formarán.
Una vez calculada la matriz de distancias, usamos la función kmeans, donde ponemos como argumento el nº de clústers que queremos obtener. Los asignamos a una variable nueva y lo juntamos con nuestro data frame x.
> c <- kmeans(dmx, 4)
> ca <- hclust(dmx)
> ca
Call:
hclust(d = dmx)
Cluster method : complete
Distance : manhattan
Number of objects: 63
> c$size # Para ver el tamaño de los cuatro clústers.[1] 5 9 24 25
> asignacion<-data.frame(c$cluster)
> x <- cbind(x,asignacion)
Volvemos a dibujar la misma gráfica esta vez agrupando los clústers por colores.
> plot(x$motor, x$peso_neto, col=x$c.cluster)
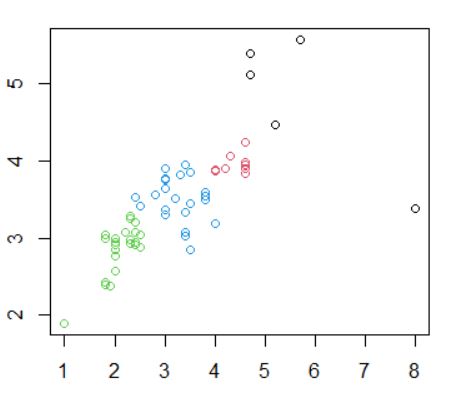 > text(x, cex=0.8, col=”grey”)
> text(x, cex=0.8, col=”grey”)
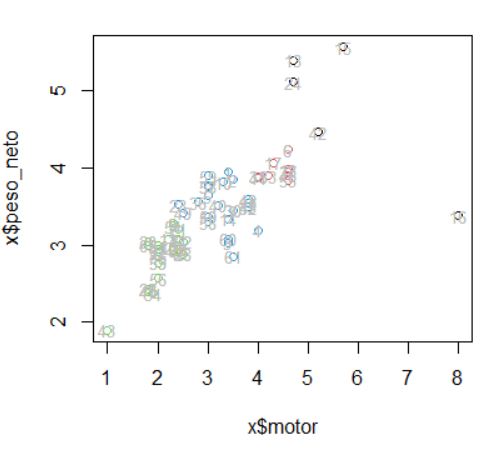
Y para conocer que individuos forman los clústers, por ejemplo todos los individuos que forman el clúster 2
> x2 <- subset(x, subset = x$c.cluster==2)
> x2
motor peso_neto c.cluster
6 4.6 4.241 2
17 4.3 4.068 2
18 4.6 3.978 2
31 4.0 3.890 2
33 4.2 3.902 2
37 4.6 3.958 2
44 4.0 3.876 2
46 4.6 3.908 2
55 4.6 3.843 2
> c
K-means clustering with 4 clusters of sizes 5, 9, 24, 25
Otro modo gráfico de inspeccionar la estructura de conglomerados que va formándose en cada paso es mediante el diagrama horizontal llamado bannerplot que es similar a un gráfico de barras. Para realizar el gráfico bannerplot es necesario instalar el paquete “cluster”
> install.packages(“cluster”)
Vamos a cargarlos todos en la librería.
> library(“cluster”)
> bannerplot(ca)
> plot(ca)
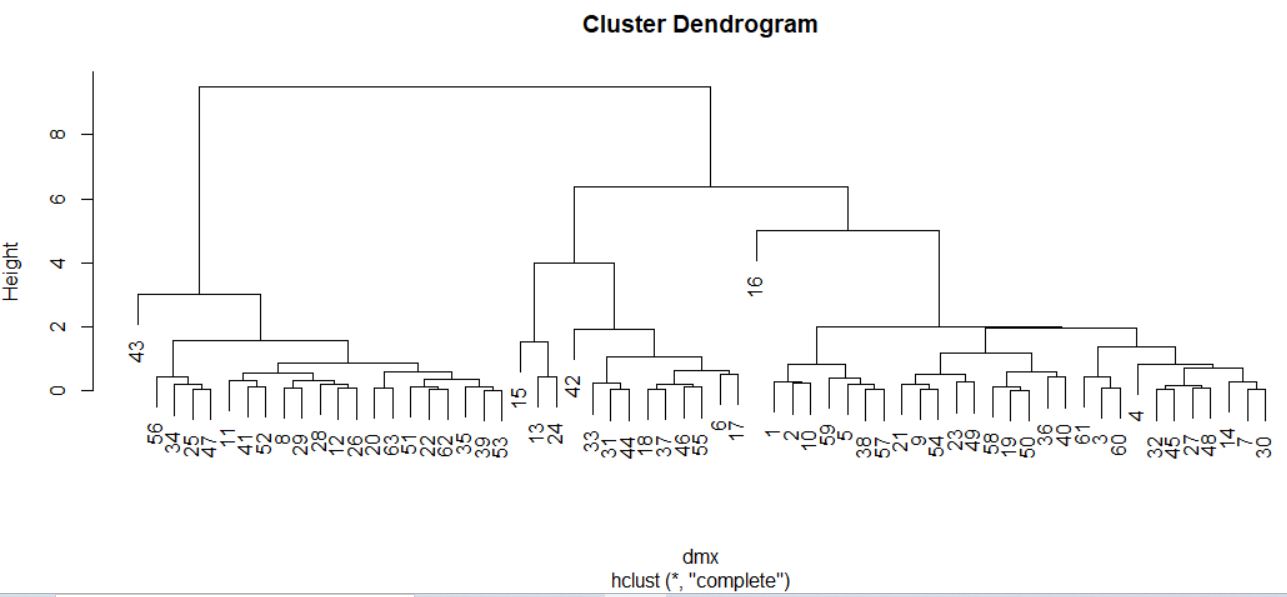
Supuesto práctico 10
En este supuesto práctico vamos a utilizar de nuevo el archivo de datos ventas_vehículos.sav que contiene estimaciones de ventas, listas de precios y especificaciones físicas hipotéticas de varias marcas y modelos de vehículos. En este caso queremos agrupar los camiones en función de sus variables de potencia: motor, CV, pisada y peso.
> library(“dplyr”)
> datos<- read.spss(“Ventas-vehiculos.sav”, use.value.labels = TRUE, max.value.labels =TRUE, to.data.frame=TRUE, sep)
re-encoding from CP1252
Seleccionamos los datos y las variables:
> autos <- subset(datos, subset = datos$tipo==0)
> camiones <- subset(datos, subset = datos$tipo==1)
> camiones <- camiones[,c(“motor”, “CV”, “pisada”, “peso_neto”)]
Y lo dibujamos para ver los datos
> plot(camiones)
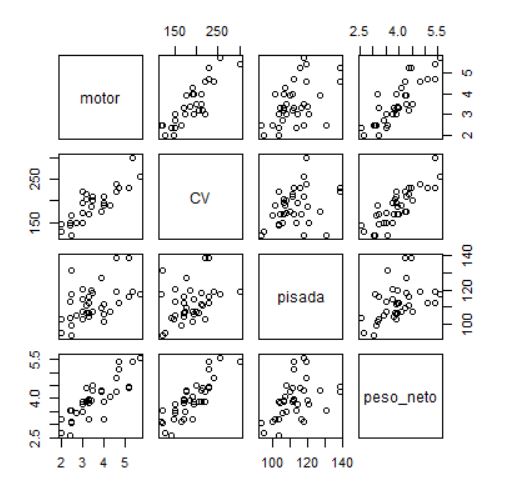 > camiones
> camiones
motor CV pisada peso_neto
19 5.7 255 117.5 5.572
34 NA NA NA NA
41 5.2 230 138.7 4.470
42 3.9 175 109.6 4.245
43 3.9 175 127.2 4.298
44 2.5 120 131.0 3.557
45 5.2 230 115.7 4.394
46 2.4 150 113.3 3.533
53 4.0 210 111.6 3.876
54 3.0 150 120.7 3.761
55 4.6 240 119.0 4.808
56 2.5 119 117.5 3.086
57 4.6 220 138.5 4.241
Observamos tanto en el gráfico como en los datos que hay un valor perdido, el 34, lo eliminamos
> camiones <- camiones[-2,]
Calculamos la matriz de distancias. Para ello vamos a tipificar los datos.
> x.scale <- scale(camiones, center = T, scale = T)
> x.scale
motor CV pisada peso_neto
19 2.28031886 1.72663870 0.50058896 2.357946581
41 1.75730995 1.09739719 2.63161026 0.770520878
42 0.39748677 -0.28693413 -0.29351803 0.446409460
43 0.39748677 -0.28693413 1.47563172 0.522755705
44 -1.06693818 -1.67126544 1.85760724 -0.544651232
45 1.75730995 1.09739719 0.31965319 0.661043244
46 -1.17153997 -0.91617563 0.07840550 -0.579223117
53 0.50208856 0.59400398 -0.09247828 -0.085133266
54 -0.54392927 -0.91617563 0.82225255 -0.250790213
55 1.12969925 1.34909379 0.65136877 1.257408254
56 -1.06693818 -1.69643510 0.50058896 -1.223124468
57 1.12969925 0.84570059 2.61150628 0.440647479
………………………………………………………………………..
attr(,”scaled:center”)
motor CV pisada peso_neto
3.5200 186.4000 112.5200 3.9351
attr(,”scaled:scale”)
motor CV pisada peso_neto
0.9560067 39.7303733 9.9482816 0.6942057
Vamos a calcular la distancia euclídea de los datos:
> dm1 <- dist(x.scale, method = “euclidean”)
Y a continuación vamos a formar los clústers, vamos a utilizar el método del promedio “average”:
> ca=hclust(dm1, method = “average”)
> ca
Call:
hclust(d = dm1, method = “average”)
Cluster method : average
Distance : euclidean
Number of objects: 40
Dibujamos en dendrograma:
> plot(ca)
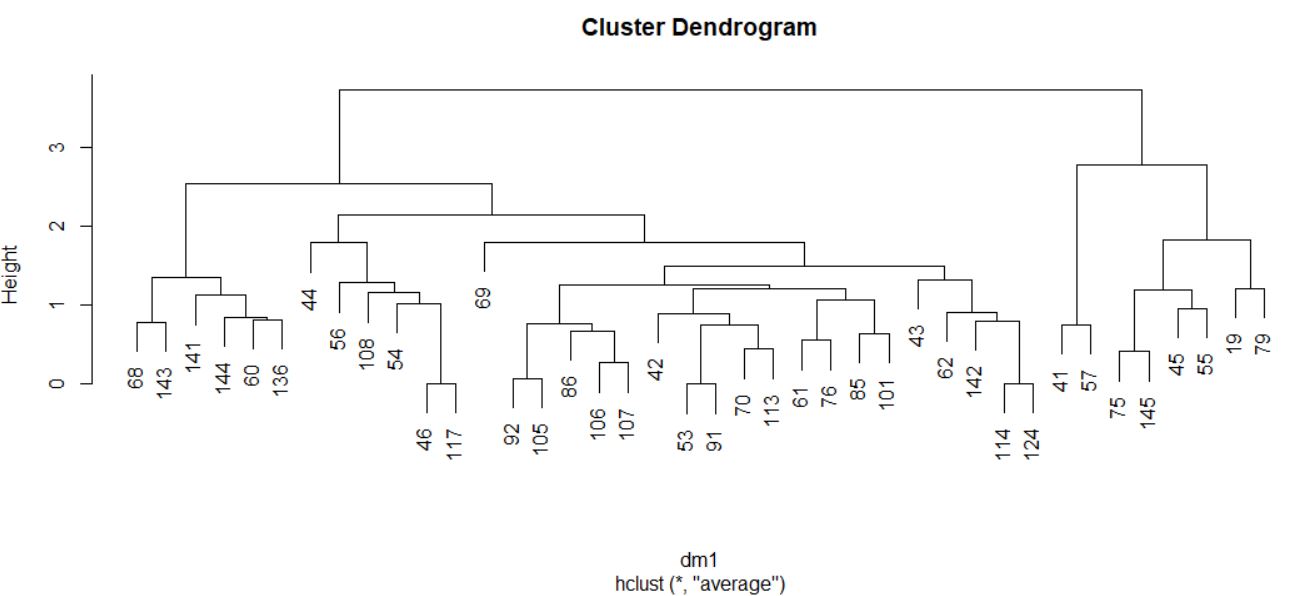
Estos son los clúsers que se formarían naturalmente. Imaginemos ahora que queremos cortar a la altura de 1.85 que nos dará un número particular de grupos.
> abline(h=1.85, col=”red”)
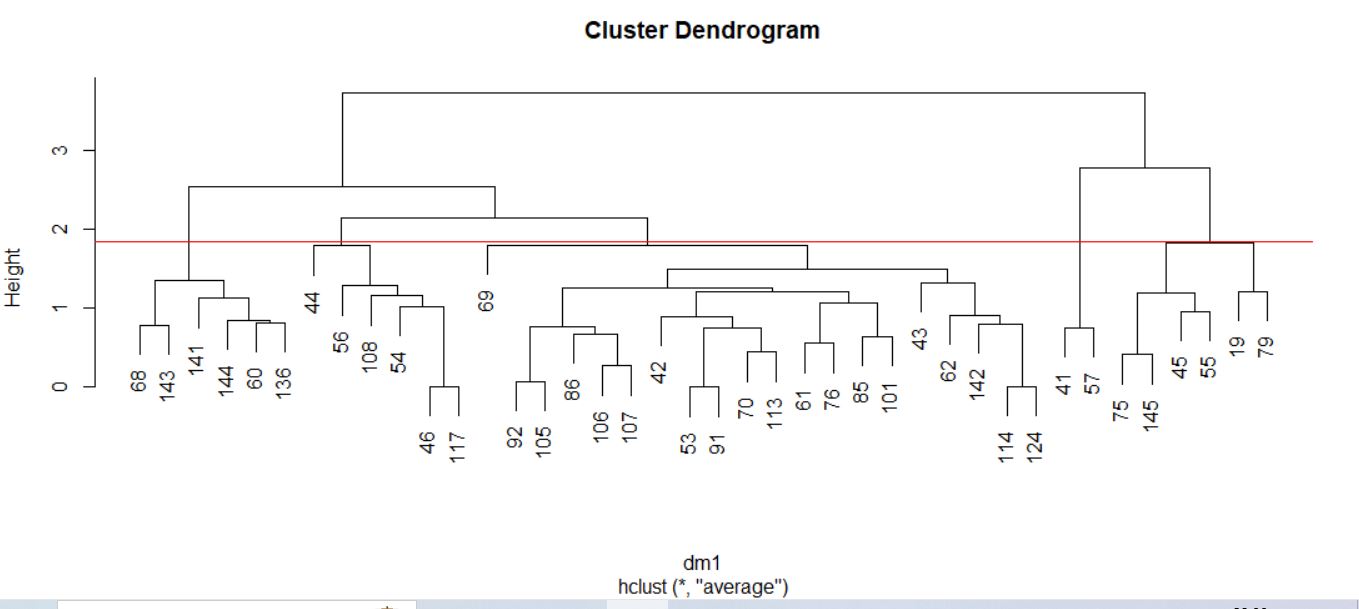
Vamos a representar la solución gráficamente, como tenemos 4 variables dibujamos las dos primeras componentes principales y etiquetando los puntos para identificar la solución clúster.
Realizamos entonces un ACP sobre la matriz de distancias. Para ello utilizamos la variable princomp.
> camiones_cp <- princomp(dm1, cor=T)
Formamos los clústers. Como hemos cortado en 1.85 se han formado 5 clústers
> lab <- cutree(ca, h=1.85)
> lab
19 41 42 43 44 45 46 53 54 55 56 57 60 61 62 68 69 70 75 76
1 2 3 3 4 1 4 3 4 1 4 2 5 3 3 5 3 3 1 3
79 85 86 91 92 101 105 106 107 108 113 114 117 124 136 141 142 143 144 145
1 3 3 3 3 3 3 3 3 4 3 3 4 3 5 5 3 5 5 1
Vamos a crear el marco del dibujo. En el eje X ponemos el rango de la primera componente y en el eje Y la segunda
> xlim<-range(camiones_cp$scores[,1])
> xlim
[1] -13.581699 4.425607
> ylim<-range(camiones_cp$scores[,2])
> ylim
[1] -3.980300 9.638053
> plot(camiones_cp$scores[,1:2], type=”n”, xlim=xlim, ylim= xlim)
A continuación ponemos el texto. El número representa el individuo que es y el color el clúster al que pertenece.
> text(camiones_cp$scores[,1:2], labels = rownames(camiones), cex = 0.6, col=lab)
Ejercicios
Ejercicios Guiados
Ejercicio Guiado 1
Los datos corresponden a la situación de 6 países europeos en 1996 con respecto a los 4 criterios exigidos por la UE para entrar en la Unión Monetaria: Inflación, Interés, Déficit Público y Deuda Pública y vienen dados en la tabla siguiente:
\( \begin{array} {|c|c|c|c|c|} \hline Pais & Inflación & Interes & Deficit & Deuda \\ \hline Alemania & 1 & 1 & 1 & 0 \\ \hline España & 1 & 1 & 1 & 0 \\ \hline Francia & 1 & 1 & 1 & 1 \\ \hline Grecia & 0 & 0 & 0 & 1 \\ \hline Italia & 1 & 1 & 0 & 0 \\ \hline Reino Unido & 1 & 1 & 0 & 1 \\ \hline \end{array} \)
Tabla: Datos del Ejercicio Guiado 1.doc
El objetivo es encontrar grupos de países que muestren un comportamiento similar con respecto a las variables analizadas.
Este es un ejemplo en el que todas las variables son binarias de forma que, 1 significa que el país si satisfacía el criterio exigido y 0 que no lo satisfacía.
En este caso todas las variables son binarias simétricas y se pueden utilizar como medida de distancia la distancia euclídea al cuadrado.
\( \displaystyle \sum_{i=1}^{n} (x_{ri}-x{si})^{2} \)
Se pide:
- La matriz de distancias e interpretación de la misma.
- Utilizar un análisis de conglomerados jerárquico aglomerativo con enlace completo para clasificar los países de la UE según las variables Inflación, Interés, Déficit Público y Deuda Pública, con el objetivo de encontrar grupo de países que muestren un comportamiento similar con respecto a los criterios analizados.
- Repetir el ejercicio introduciendo los datos como vectores y utilizando la distancia binaria
Ejercicio Guiado 2
Se desea determinar los segmentos de mercado de un determinado producto en una ciudad pequeña basándose únicamente en la lealtad a las marcas y la lealtad a las tiendas. Para ello se selecciona una muestra de 10 encuestados sobre los que se miden las dos variables lealtad a la tienda (tienda) y lealtad a la marca (marca) en una escala de 0 a 10. Los datos se muestran en la siguiente tabla
Encuestado
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Variable & A & B & C & D & E & F & G & H & I & J \\ \hline Tienda & 2 & 5 & 3 & 4 & 6 & 9 & 8 & 7 & 4 & 5 \\ \hline Marca & 2 & 9 & 5 & 8 & 7 & 3 & 4 & 5 & 6 & 7 \\ \hline \end{array} \)
Tabla: Datos del Ejercicio Guiado 2.docx
Se pide:
-
Realizar un diagrama de dispersión y estudiar los grupos más homogéneos
- Realizar un análisis de conglomerados.
Ejercicio Guiado 3
El archivo de datos jóvenes.sav contiene información sobre 14 jóvenes respecto a su edad, estudios, hábitos de lectura, fútbol, cine, teatro, concierto, tv, ámbito familiar…
Se desea clasificar a los 14 jóvenes encuestados por el número de veces que van anualmente al fútbol (fútbol), la paga semanal que reciben (paga) y el número de horas semanales que ven la televisión (tv)
Se pide:
-
Realizar un diagrama de dispersión 3-D para mostrar la distribución de los datos y estudiar los posibles grupos que se pueden hacer
- Utilizar un análisis clúster jerárquico.
- Método: centroide; Medida: Intervalo- Distancia euclidea al cuadrado; Transformar valores: Estandarizar las variables
- Obtener el Historial de conglomeración, Matriz de distancia, Dendograma y en Témpanos: Todos los conglomerados
- Analizar las tablas obtenidas y sacar conclusiones
-
Repetir el anterior proceso con el método de ward
- Repetir el proceso anterior con el Método de Conglomeración: Agrupación de medianas
- Obtener conclusiones ¿Nº de clustes? ¿Método de conglomeración?
El archivo de datos jóvenes.sav contiene 14 datos y está formado por las siguientes variables:
Variables tipo cadena: id (Identificación personal).
Variables tipo numérico: centro (Tipo de centro de estudios {1, público}…), estudios (Estudios que cursa {1, EGB}…); estupadr (Estudios del padre {1, Sin estudios}…); estumadr (Estudios de la madre {1, Sin estudios}..); paga (Paga semanal en ptas/100); numher (Nº hermanos incluido sujeto); edad ; califest (Calificación media en estudios); lect ( Libros leídos anualmente); cine (Asistencia anual al cine); fútbol (Asistencia anual al futbol); conciert (Asistencia anual conciertos); tv (Horas semanales tv); sexo ({1, hombre}…); hábitat ({1, rural}…); lectp (Segunda tasa de lectura); univ (¿Deseas acceder a la universidad? {1, sí}…); gustcine (Te gusta ir al cine… {1, solo}…); tipocine (Tipo de película que te gusta {1, amor}…); violen (Nivel de rechazo a la violencia {1, activo}…); impdin (Importancia das al dinero {1, muy poca}..); impest (Importancia de estudios {1, muy poca}…); ingr (Ingresos mensuales {1, <100}…); físico (Importancia al físico {1, muy poca}…); depor (interés deporte {1,muy poca}…)
Ejercicio Guiado 4
A partir del conjunto de datos acidosis.patients contenido en el paquete cluster.datasets, realizar un análisis clúster jerárquico aglomerativo utilizando el método del enlace simple y considerando la distancia euclídea.
Ejercicio Guiado 5
A partir del conjunto de datos acidosis.patients contenido en el paquete cluster.datasets, realizar un análisis clúster no jerárquico utilizando el procedimiento de las k-medias y el algoritmo de Hartigan-Wong. Considerar 3 clústers.
Ejercicio Guiado 6
A partir del conjunto de datos all.mammals.milk.1956 contenido en el paquete cluster.datasets, realizar un análisis clúster jerárquico aglomerativo utilizando el método del enlace completo y considerando la distancia de Minkowski.
Ejercicio Guiado 1 (Resuelto)
Los datos corresponden a la situación de 6 países europeos en 1996 con respecto a los 4 criterios exigidos por la UE para entrar en la Unión Monetaria: Inflación, Interés, Déficit Público y Deuda Pública y vienen dados en la tabla siguiente:
\( \begin{array} {|c|c|c|c|c|} \hline Pais & Inflación & Interes & Deficit & Deuda \\ \hline Alemania & 1 & 1 & 1 & 0 \\ \hline España & 1 & 1 & 1 & 0 \\ \hline Francia & 1 & 1 & 1 & 1 \\ \hline Grecia & 0 & 0 & 0 & 1 \\ \hline Italia & 1 & 1 & 0 & 0 \\ \hline Reino Unido & 1 & 1 & 0 & 1 \\ \hline \end{array} \)
Tabla: Datos del Ejercicio Guiado 1.doc
El objetivo es encontrar grupos de países que muestren un comportamiento similar con respecto a las variables analizadas.
Este es un ejemplo en el que todas las variables son binarias de forma que, 1 significa que el país si satisfacía el criterio exigido y 0 que no lo satisfacía.
En este caso todas las variables son binarias simétricas y se pueden utilizar como medida de distancia la distancia euclídea al cuadrado.
\( \displaystyle \sum_{i=1}^{n} (x_{ri}-x{si})^{2} \)
Se pide:
- La matriz de distancias e interpretación de la misma.
- Utilizar un análisis de conglomerados jerárquico aglomerativo con enlace completo para clasificar los países de la UE según las variables Inflación, Interés, Déficit Público y Deuda Pública, con el objetivo de encontrar grupo de países que muestren un comportamiento similar con respecto a los criterios analizados.
- Repetir el ejercicio introduciendo los datos como vectores y utilizando la distancia binaria
Solución
Antes de comenzar con la resolución del ejercicio vamos a introducir los datos
> setwd(“C:/Users/Usuario/Desktop/Datos”) # situarnos en el directorio de trabajo
> library(haven) # importar y exportar datos .sav
> paises <- read_sav(“paises.sav”)
> paises
Pais Inflación Interés Déficit Deuda
1 Alemania 1 1 1 0
2 España 1 1 1 0
3 Francia 1 1 1 1
4 Grecia 0 0 0 1
5 Italia 1 1 0 0
6 Reino Unido 1 1 0 1
> rownames(paises)<-paises[,1]
> rownames(paises)
[1] “Alemania” “España” “Francia” “Grecia” “Italia”
[6] “Reino Unido”
> paises<-paises[,-1]
> paises
Inflación Interés Déficit Deuda
Alemania 1 1 1 0
España 1 1 1 0
Francia 1 1 1 1
Grecia 0 0 0 1
Italia 1 1 0 0
Reino Unido 1 1 0 1
1. La matriz de distancias e interpretación de la misma.
> dis<-dist(paises[,-1])
> dis
Alemania España Francia Grecia Italia
España 0.000000
Francia 1.000000 1.000000
Grecia 1.732051 1.732051 1.414214
Italia 1.000000 1.000000 1.414214 1.414214
Reino Unido 1.414214 1.414214 1.000000 1.000000 1.000000
Esta matriz muestra la distancia que existe entre los países dadas las variables. En la diagonal principal (que no muestra R) se encuentra formada por valores 0
Así, por ejemplo, la distancia entre España y Francia es 1 puesto que solamente difieren en un criterio: el de la deuda pública que Francia satisfacía y España no.
2. Utilizar un análisis de conglomerados jerárquico aglomerativo con enlace completo para clasificar los países de la UE según las variables Inflación, Interés, Déficit Público y Deuda Pública, con el objetivo de encontrar grupo de países con comportamiento similares.
> x<-hclust(dis)
> x
Call:
hclust(d = dis)
Cluster method : complete
Distance : euclidean
Number of objects: 6
> x$merge
[,1] [,2]
[1,] -1 -2
[2,] -3 1
[3,] -4 -6
[4,] -5 2
[5,] 3 4
> plot(x)
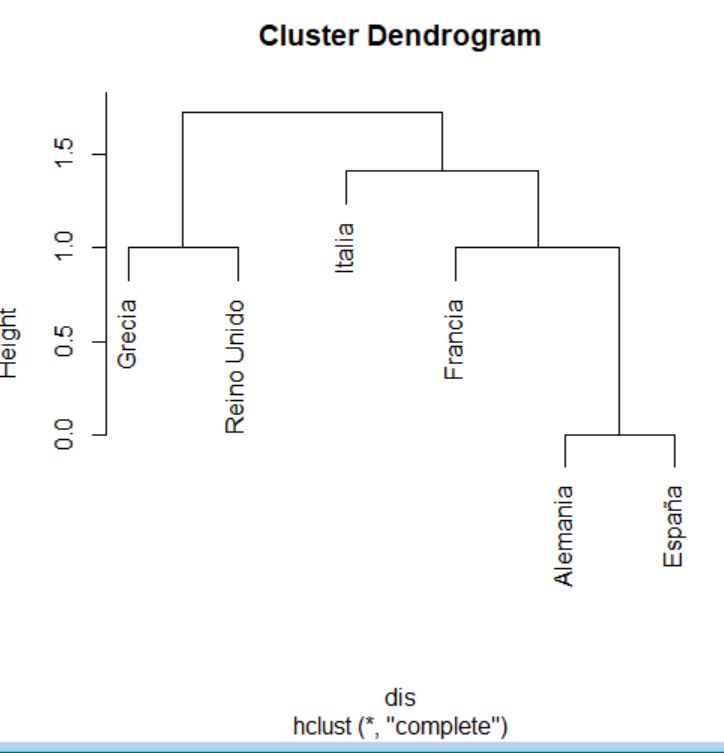
3. Repetir el ejercicio introduciendo los datos como vectores y utilizando la distancia binaria
Comenzamos, en primer lugar, generando las 5 variables que conforman el conjunto de datos y aunándolas en un data frame.
> Pais <- c(“Alemania”, “España”, “Francia”, “Grecia”, “Italia”, “Reino Unido”)
> Inflacion <- c(1, 1, 1, 0, 1, 1)
> Interes <- c(1, 1, 1, 0, 1, 1)
> Deficit <- c(1, 1, 1, 0, 0, 0)
> Deuda <- c(0, 0, 1, 0, 0, 1)
> datos <- data.frame(Pais, Inflacion, Interes, Deficit, Deuda)
> datos
Pais Inflacion Interes Deficit Deuda
1 Alemania 1 1 1 0
2 España 1 1 1 0
3 Francia 1 1 1 1
4 Grecia 0 0 0 0
5 Italia 1 1 0 0
6 Reino Unido 1 1 0 1
A continuación, almacenamos en un nuevo data frame las variables a partir de las cuales se generarán los grupos.
> attach(datos)
The following objects are masked _by_ .GlobalEnv:
Deficit, Deuda, Inflacion, Interes, Pais
> variables <- data.frame(Inflacion, Interes, Deficit, Deuda)
> variables
Inflacion Interes Deficit Deuda
1 1 1 1 0
2 1 1 1 0
3 1 1 1 1
4 0 0 0 0
5 1 1 0 0
6 1 1 0 1
El siguiente paso es calcular las distancias entre los países en función a las variables de las que se dispone información. Para ello, realizaremos una llamada a la función dist. Como las variables son de tipo dicotómico, indicaremos que la distancia a emplear es la binaria.
> distancias <- dist(variables, method = “binary”)
> distancias
1 2 3 4 5
2 0.0000000
3 0.2500000 0.2500000
4 1.0000000 1.0000000 1.0000000
5 0.3333333 0.3333333 0.5000000 1.0000000
6 0.5000000 0.5000000 0.2500000 1.0000000 0.3333333
A continuación llamamos a la función hclust, pasando la matriz de distancias que acabamos de calcular e indicando el método para la generación de los grupos de países, que en este caso será el de enlace completo.
> cluster <- hclust(distancias, method = “single”)
> cluster
Call:
hclust(d = distancias, method = “single”)
Cluster method : single
Distance : binary
Number of objects: 6
Analicemos las salidas que proporciona la función clúster. Como en ejemplos anteriores, nos centraremos en el historial de conglomeración y en las distancias de conglomeración. Para consultar el historial de conglomeración, accedemos al componente merge del objeto cluster que ha generado la función hclust.
> cluster$merge
[,1] [,2]
[1,] -1 -2
[2,] -3 1
[3,] -6 2
[4,] -5 3
[5,] -4 4
Al interpretar el historial de conglomeración se aprecia que los dos primeros países que se funden en un grupo son los situados en las posiciones 1 y 2 del conjunto de datos, esto es Alemania y España. En el segundo paso, al grupo formado por Alemania y España se incorpora el país situado en la posición 3 del conjunto de datos, Francia. A continuación, en el tercer paso, a este grupo de 3 países se incorpora el país situado en la sexta posición del fichero de datos, Reino Unido. En el cuarto paso, al grupo de 4 países se incorpora el país situado en la posición 5 del fichero de datos, Italia. Ya en el último paso, se incorpora a este grupo de 5 países el último de ellos, el situado en la posición 4 del conjunto de datos, que es Grecia.
Veamos ahora a qué distancia se produce cada uno de los agrupamientos. Para ello, consultamos el componente height del objeto cluster.
> cluster$height
[1] 0.0000000 0.2500000 0.2500000 0.3333333 1.0000000
Finalicemos el ejemplo dibujando el dendrograma asociado, incluyendo los nombres de los países como etiquetas de las observaciones.
> plot(cluster, labels = Pais)
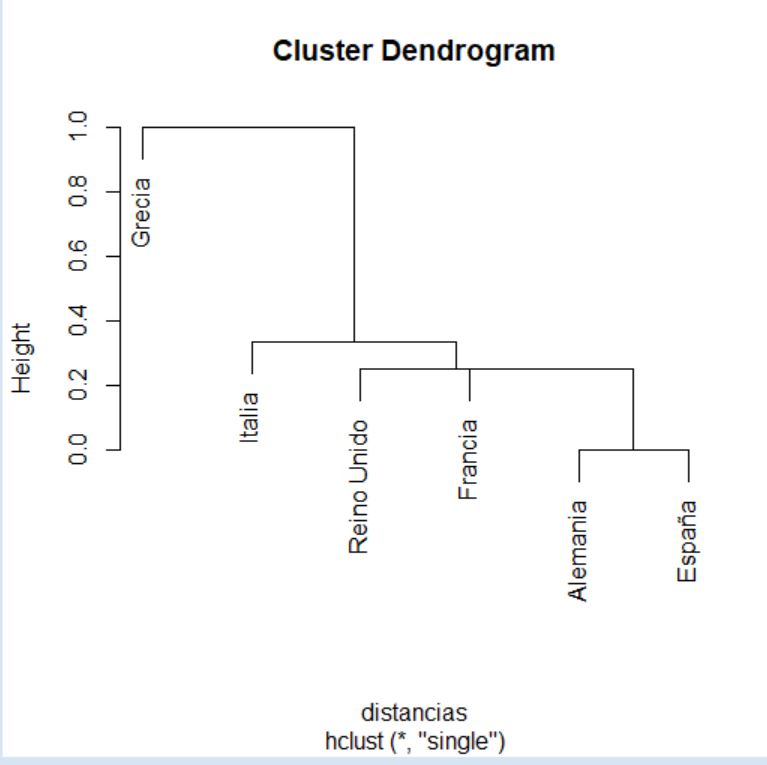
Ejercicio Guiado 2 (Resuelto)
Se desea determinar los segmentos de mercado de un determinado producto en una ciudad pequeña basándose únicamente en la lealtad a las marcas y la lealtad a las tiendas. Para ello se selecciona una muestra de 10 encuestados sobre los que se miden las dos variables lealtad a la tienda (tienda) y lealtad a la marca (marca) en una escala de 0 a 10. Los datos se muestran en la siguiente tabla
Encuestado
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Variable & A & B & C & D & E & F & G & H & I & J \\ \hline Tienda & 2 & 5 & 3 & 4 & 6 & 9 & 8 & 7 & 4 & 5 \\ \hline Marca & 2 & 9 & 5 & 8 & 7 & 3 & 4 & 5 & 6 & 7 \\ \hline \end{array} \)
Tabla: Datos del Ejercicio Guiado 2.docx
Se pide:
-
Realizar un diagrama de dispersión y estudiar los grupos más homogéneos
- Realizar un análisis de conglomerados.
Solución
Se comienza introduciendo los datos con los siguientes comandos
> datos<-matrix(c(2,5,3,4,6,9,8,7,4,5,2,9,5,8,7,3,4,5,6,7),byrow=TRUE,ncol = 10)
> datos
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 2 5 3 4 6 9 8 7 4 5
[2,] 2 9 5 8 7 3 4 5 6 7
> dimnames(datos)<-list(Variable=c(‘Tienda’,’Marca’),Encuestado=c(‘A’,’B’,’C’,’D’,’E’,’F’,’G’,’H’,’I’,’J’))
> datos
Encuestado
Variable A B C D E F G H I J
Tienda 2 5 3 4 6 9 8 7 4 5
Marca 2 9 5 8 7 3 4 5 6 7
- Realizar un diagrama de dispersión y estudiar los grupos más homogéneos
El diagrama de dispersión se obtiene con los siguientes comandos:
> plot(datos[1,],datos[2,],type = ‘n’)
> text(datos[1,],datos[2,], col=’red’, labels=colnames(datos))
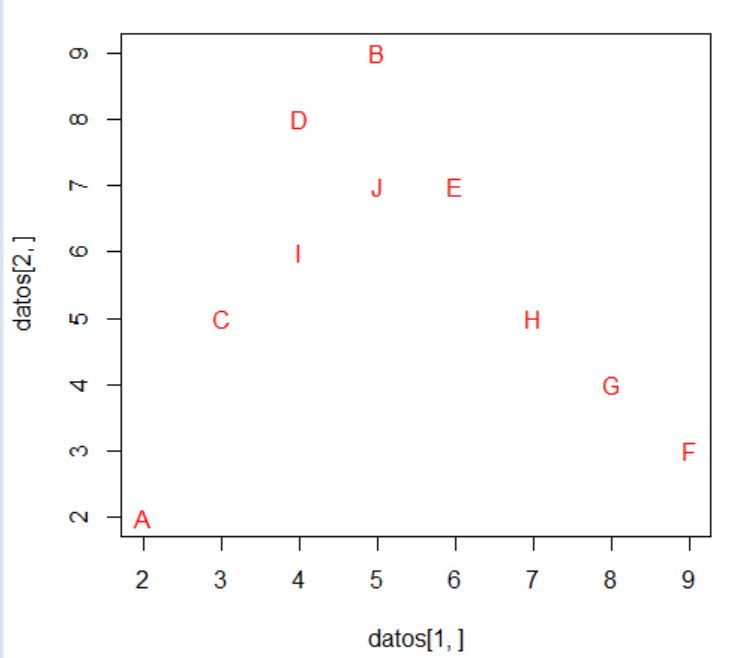
Se observa en el gráfico anterior que los grupos más homogéneos parece ser tres, formados por: (C, I, J, E, D, B) , (H, G, F) y (A)
2.Realizar un análisis de conglomerados.
> dis<-dist(t(datos))
> dis
A B C D E F G H
B 7.615773
C 3.162278 4.472136
D 6.324555 1.414214 3.162278
E 6.403124 2.236068 3.605551 2.236068
F 7.071068 7.211103 6.324555 7.071068 5.000000
G 6.324555 5.830952 5.099020 5.656854 3.605551 1.414214
H 5.830952 4.472136 4.000000 4.242641 2.236068 2.828427 1.414214
I 4.472136 3.162278 1.414214 2.000000 2.236068 5.830952 4.472136 3.162278
J 5.830952 2.000000 2.828427 1.414214 1.000000 5.656854 4.242641 2.828427
I
B
C
D
E
F
G
H
I
J 1.414214
> y<-hclust(dis)
> y
Call:
hclust(d = dis)
Cluster method : complete
Distance : euclidean
Number of objects: 10
> y$merge
[,1] [,2]
[1,] -5 -10
[2,] -2 -4
[3,] -3 -9
[4,] -6 -7
[5,] 1 2
[6,] -8 4
[7,] -1 3
[8,] 6 7
[9,] 5 8
> plot(y)
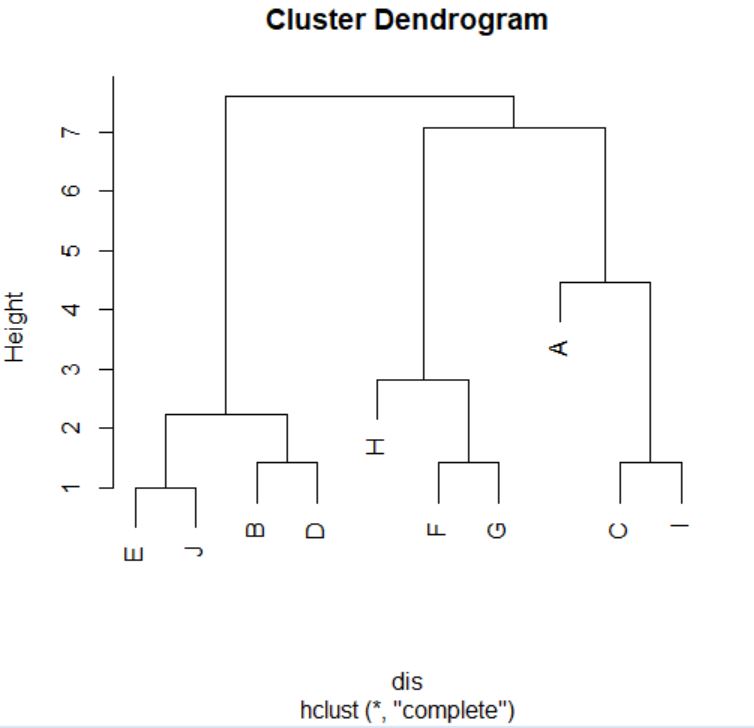
Repetir el análisis con otra medida de similitud y otro procedimiento y comparar los resultados.
Ejercicio Guiado 3 (Resuelto)
El archivo de datos jóvenes.sav contiene información sobre 14 jóvenes respecto a su edad, estudios, hábitos de lectura, fútbol, cine, teatro, concierto, tv, ámbito familiar…
Se desea clasificar a los 14 jóvenes encuestados por el número de veces que van anualmente al fútbol (fútbol), la paga semanal que reciben (paga) y el número de horas semanales que ven la televisión (tv)
Se pide:
-
Realizar un diagrama de dispersión 3-D para mostrar la distribución de los datos y estudiar los posibles grupos que se pueden hacer
- Utilizar un análisis clúster jerárquico.
- Método: centroide; Medida: Intervalo- Distancia euclidea al cuadrado; Transformar valores: Estandarizar las variables
- Obtener el Historial de conglomeración, Matriz de distancia, Dendograma y en Témpanos: Todos los conglomerados
- Analizar las tablas obtenidas y sacar conclusiones
-
Repetir el anterior proceso con el método de ward
- Repetir el proceso anterior con el Método de Conglomeración: Agrupación de medianas
- Obtener conclusiones ¿Nº de clustes? ¿Método de conglomeración?
Solución
Antes de todo se comienza leyendo los datos. Debidos a que las variables se encuentran en medidas distintas lo mejor sería estandarizar las variables, pues de esta forma se reduce el error cometido. Como existen valores NA, estos serán tomados como 0.
> setwd(“C:/Users/Usuario/Desktop/Datos”) # situarnos en el directorio de trabajo
> library(haven) # importar y exportar datos .sav
> jovenes <- read_sav(“jovenes.sav”)
> jovenes<-as.data.frame(jovenes)
> rownames(jovenes)<-jovenes$id
> jovenes<-jovenes[,-1]
> jovenes<-replace(jovenes,is.na(jovenes),0)
> jovenes<-scale(jovenes,center = TRUE,scale = TRUE)
> jovenes<-replace(jovenes,is.na(jovenes),0)
> jovenes<-as.data.frame(jovenes)
- Realizar un diagrama de dispersión 3-D para mostrar la distribución de los datos y estudiar los posibles grupos que se pueden hacer
El paquete rgl nos permite visualizar el diagrama de dispersión en 3-D. Abrirá una ventana con el gráfico el cual se puede mover.
> library(“rgl”)
> plot3d(c(jovenes$fútbol,jovenes$paga,jovenes$tv))
Error in rgl.texts(x = 0.5, y = -0.1695, z = -0.1695, text = “c(jovenes$fútbol, jovenes$paga, jovenes$tv)”, :
text 1 contains unsupported character
> text3d(c(jovenes$fútbol,jovenes$paga,jovenes$tv), text=rownames(jovenes), adj=1.3)
> decorate3d(xlab = “Futbol”,ylab = “Paga”,zlab = “TV”)

Los grupos más similares parecen ser tres formados por: (D, B, A, F,G,J), (E,K,N,C) y (H,M)
2. Utilizar un análisis clúster jerárquico.
3. Método: centroide; Medida: Intervalo- Distancia euclidea al cuadrado; Transformar valores: Estandarizar las variables
4. Obtener el Historial de conglomeración, Matriz de distancia, Dendograma y en Témpanos: Todos los conglomerados
5. Analizar las tablas obtenidas y sacar conclusiones
> dis<-dist(jovenes)^2
> z<-hclust(dis)
> z$merge
[,1] [,2]
[1,] -6 -8
[2,] -4 -5
[3,] -9 -10
[4,] -7 1
[5,] -13 -14
[6,] -11 -12
[7,] 3 5
[8,] 2 4
[9,] -1 -2
[10,] 6 7
[11,] -3 10
[12,] 8 9
[13,] 11 12
> plot(z)
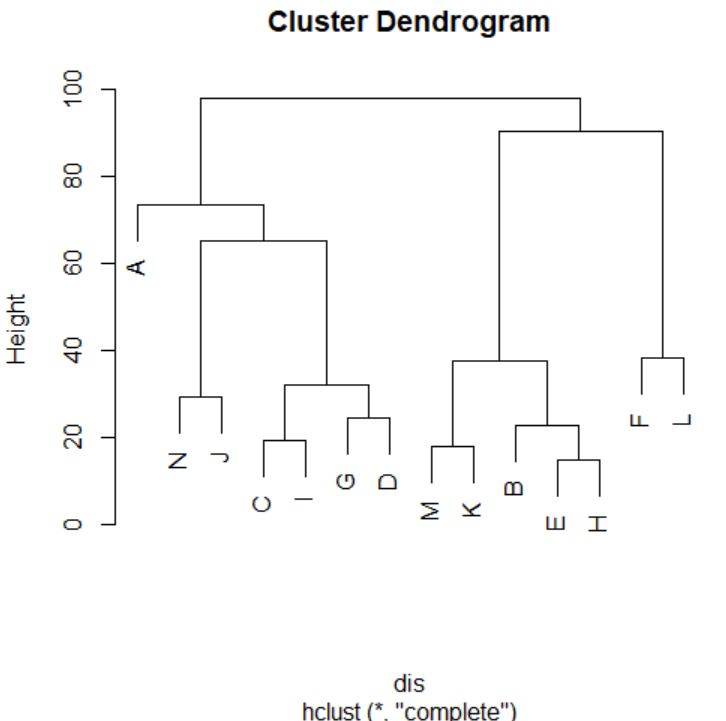
El dendograma muestra cómo se van formando la clasificación jerárquica de los individuos, si consideramos un corte entre la distancia 80 y 100, se formarían dos clusters: Clúster 1: (A, N, J, C, I, G, D); Clúster 2: (M, K, B, E, I , F, L)
6. Repetir el anterior proceso con el método de ward
> x<-hclust(dis,method = “ward.D”)
> x$merge
[,1] [,2]
[1,] -6 -8
[2,] -4 -5
[3,] -9 -10
[4,] -7 1
[5,] -13 -14
[6,] -11 -12
[7,] 3 5
[8,] -1 -2
[9,] 2 4
[10,] -3 8
[11,] 6 7
[12,] 10 11
[13,] 9 12
> plot(x)
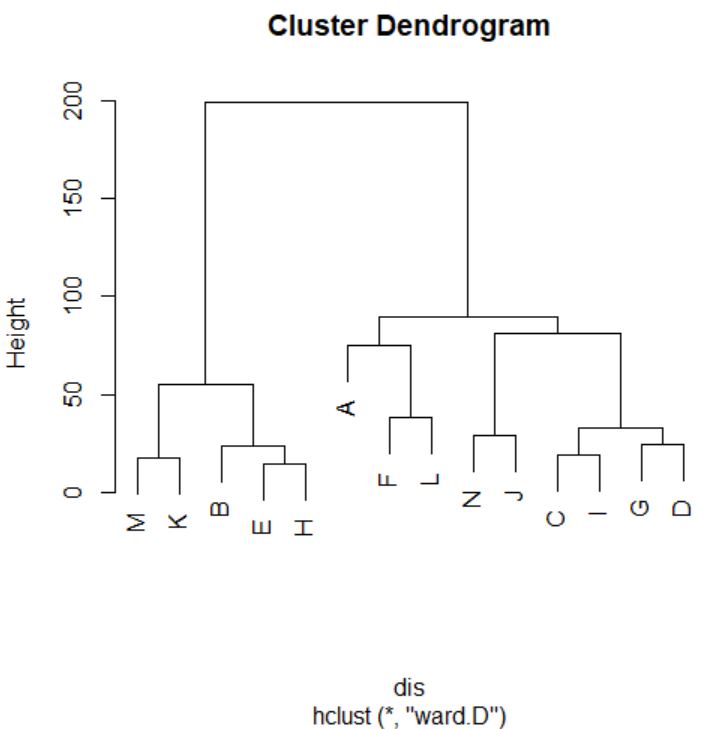
Si consideramos un corte entre la distancia 100 y 150, se formarían dos clusters: Clúster 1: (M, K, B, E, I ); Clúster 2: (A, F, L, N, J, C, I, G, D)
7. Repetir el proceso anterior con el Método de Conglomeración: Agrupación de medianas
> y<-hclust(dis,method = “median”)
> y$merge
[,1] [,2]
[1,] -6 -8
[2,] -7 1
[3,] -4 -5
[4,] -9 -10
[5,] -14 4
[6,] -13 5
[7,] -11 3
[8,] 2 7
[9,] 6 8
[10,] -12 9
[11,] -1 -2
[12,] 10 11
[13,] -3 12
> plot(y)
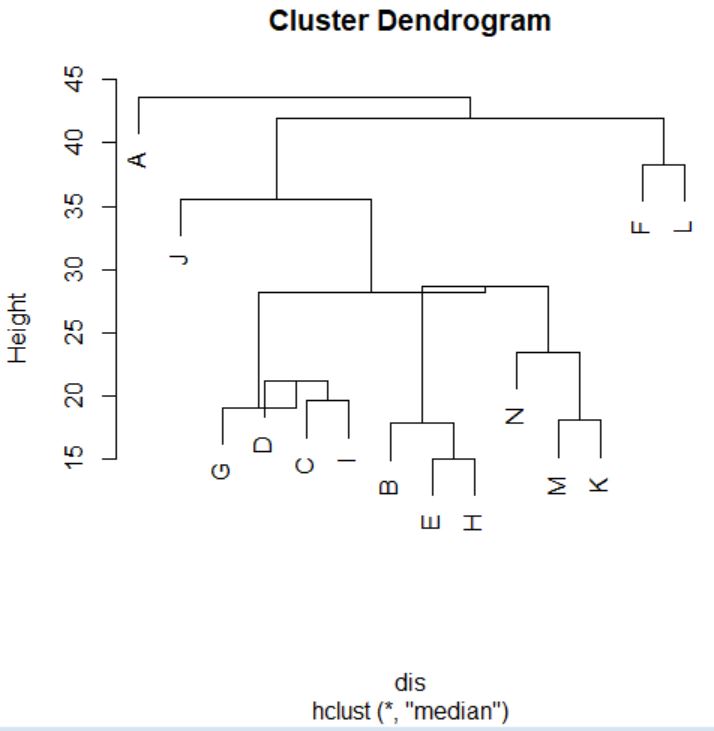
8. Obtener conclusiones ¿Nº de clustes? ¿Método de conglomeración?
Los clusters que se forman son:
(A,(N,J),((C,I),(G,D))
((F,L),((M,K),(B,(E,H))))
Ejercicio Guiado 4 (Resuelto)
A partir del conjunto de datos acidosis.patients contenido en el paquete cluster.datasets, realizar un análisis clúster jerárquico aglomerativo utilizando el método del enlace simple y considerando la distancia euclídea.
Solución
De no haberlo hecho con anterioridad, hay que instalar este paquete usando la orden
> install.packages(“cluster.datasets”)
Y a continuación, es necesario cargarlo mediante la orden
> library(cluster.datasets)
Una vez cargado el paquete, podemos acceder al conjunto de datos al que nos hemos referido anteriormente ejecutando la orden
> data(acidosis.patients)
Consultamos las primeras líneas del conjunto de datos, para echar un vistazo a las variables que las componen usando la función head.
> head(acidosis.patients)
ph.cerebrospinal.fluid ph.blood hco3.cerebrospinal.fluid hco3.blood
1 39.8 38.0 22.2 23.2
2 53.7 37.2 18.7 18.5
3 47.3 39.8 23.3 22.1
4 41.7 37.6 22.8 22.3
5 44.7 38.5 24.8 24.4
6 47.9 39.8 22.0 23.3
co2.cerebrospinal.fluid co2.blood
1 38.8 36.5
2 45.1 28.3
3 48.2 36.4
4 41.6 34.6
5 48.5 38.8
6 46.2 38.5
El conjunto de datos está compuesto por 6 variables, todas ellas cuantitativas, por lo que tiene sentido utilizar la distancia euclídea para calcular la separación o distancia entre cada observación.
> distancias <- dist(acidosis.patients, method = “euclidean”)
Como sabemos, la función dist devuelve como resultado una matriz triangular inferior con las distancias entre observaciones. Esta matriz será el primer argumento que pasaremos a la función hclust, que será la que ejecute el análisis cluster. Como segundo argumento, indicaremos el método de agrupamiento que, según el enunciado del ejercicio, será el del enlace simple.
> cluster <- hclust(distancias, method = “single”)
> cluster
Call:
hclust(d = distancias, method = “single”)
Cluster method : single
Distance : euclidean
Number of objects: 40
La función hclust devuelve varios elementos. Vamos a consultar, en primer lugar, el historial de conglomeración.
> cluster$merge
[,1] [,2]
[1,] -18 -21
[2,] -22 1
[3,] -7 -39
[4,] -23 2
[5,] -12 -19
[6,] -3 -6
[7,] -38 6
[8,] -4 -35
[9,] -1 8
[10,] -17 7
Se muestran los 10 primeros pasos del historial de conglomeración (de los 39 que lo componen). De acuerdo a lo indicado en el primer paso, los dos primeros individuos que se unen son el número 18 y el número 21. Esto es, estos dos individuos son los más próximos entre sí o, equivalentemente, aquellos que están separados por una menor distancia. A continuación, en el segundo paso, el grupo formado en el paso 1 se fusiona con el individuo número 22. En el tercero de los pasos, se unen los individuos 7 y 39 y, en el cuarto, a este grupo se le incorpora el individuo 23. De este modo se puede seguir interpretando el historial de conglomeración.
Para conocer las distancias a las que se producen las uniones entre dos individuos, entre un grupo de individuos previamente formado y un nuevo individuo o entre dos grupos de individuos, accedemos al elemento height del objeto que devuelve hclust.
> cluster$height
[1] 2.102380 2.487971 2.539685 2.776689 2.903446 3.449638 3.730952
[8] 3.853570 4.048456 4.244997 4.267318 4.346263 4.442972 4.601087
[15] 4.673329 4.694678 4.778075 4.907138 4.930517 5.584801 5.682429
[22] 5.715768 5.830094 5.905083 5.915235 6.059703 6.597727 6.853466
[29] 7.117584 7.144228 7.766595 9.647279 11.657187 12.024142 12.499600
[36] 12.744803 13.145722 13.661991 23.841141
La primera de las fusiones entre individuos (que, recordemos, es la que se produce entre los individuos 18 y 21) se produce a una distancia de 2.10 unidades. Dicho de otra forma, la distancia euclídea entre ambos individuos es de 2.10 unidades. La segunda fusión (la que une el grupo formado por los individuos 18 y 21 con el individuo número 22) se produce a una distancia de 2.48 unidades. El resto de datos se interpretan de igual forman e indican las distancias a las que se producen las fusiones en cada uno de los pasos del historial de conglomeración.
Para terminar, representamos el dendrograma, para visualizar el proceso de conglomeración.
> plot(cluster)
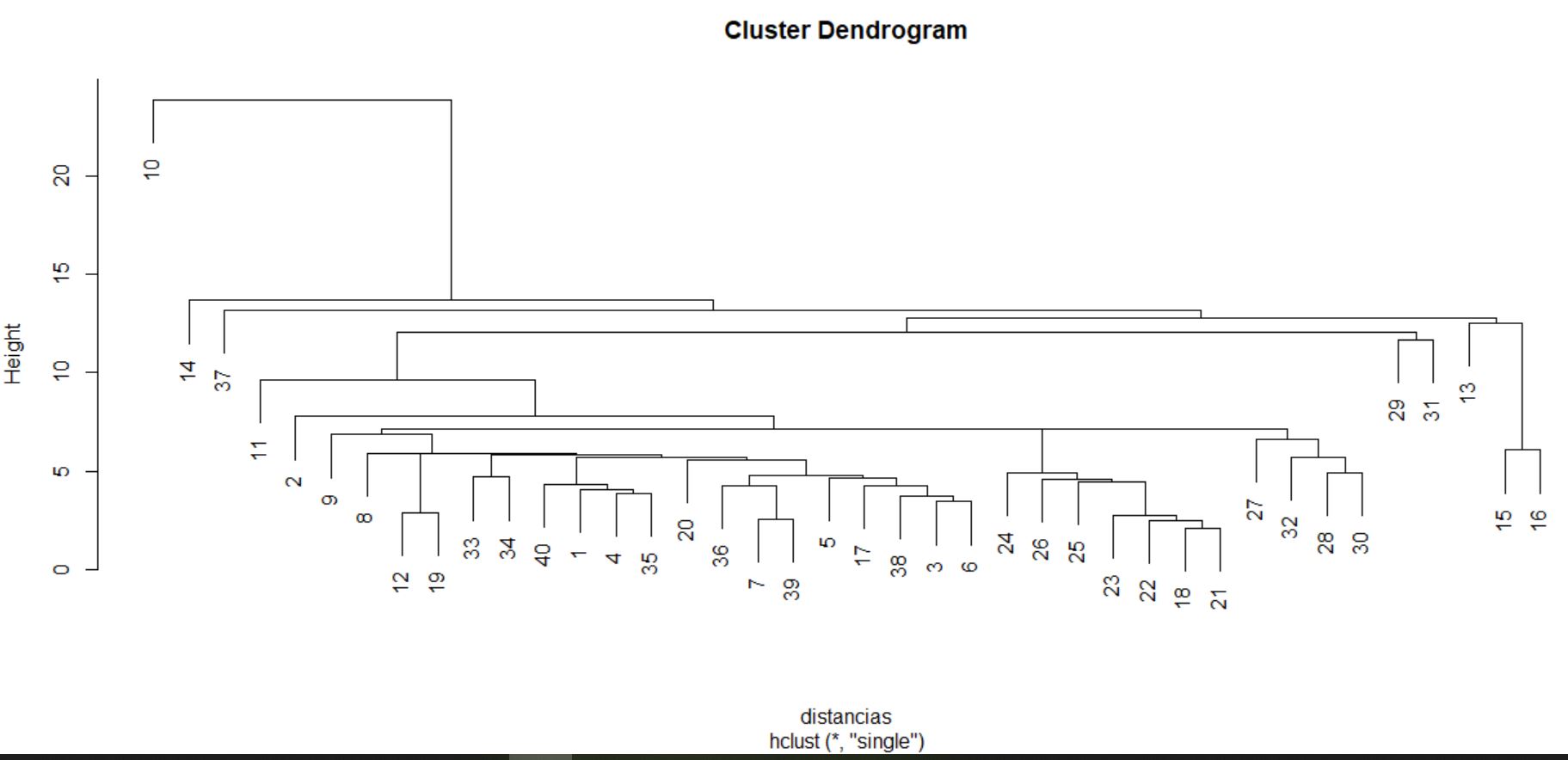
Ejercicio Guiado 5 (Resuelto)
A partir del conjunto de datos acidosis.patients contenido en el paquete cluster.datasets, realizar un análisis clúster no jerárquico utilizando el procedimiento de las k-medias y el algoritmo de Hartigan-Wong. Considerar 3 clústers.
Solución
De no haberlo hecho con anterioridad, hay que instalar este paquete usando la orden
> install.packages(“cluster.datasets”)
Y a continuación, es necesario cargarlo mediante la orden
> library(cluster.datasets)
Una vez cargado el paquete, podemos acceder al conjunto de datos al que nos hemos referido anteriormente ejecutando la orden
> data(acidosis.patients)
Consultamos las primeras líneas del conjunto de datos, para echar un vistazo a las variables que las componen usando la función head.
> head(acidosis.patients)
ph.cerebrospinal.fluid ph.blood hco3.cerebrospinal.fluid hco3.blood
1 39.8 38.0 22.2 23.2
2 53.7 37.2 18.7 18.5
3 47.3 39.8 23.3 22.1
4 41.7 37.6 22.8 22.3
5 44.7 38.5 24.8 24.4
6 47.9 39.8 22.0 23.3
co2.cerebrospinal.fluid co2.blood
1 38.8 36.5
2 45.1 28.3
3 48.2 36.4
4 41.6 34.6
5 48.5 38.8
6 46.2 38.5
A continuación llamamos a la función kmeans, que será la que ejecute el análisis cluster mediante el procedimiento de las k medias. Como parámetros, recibirá el conjunto de datos, el número de clústers, el número de soluciones iniciales y el nombre del algoritmo a emplear.
> cluster <- kmeans (acidosis.patients, centers = 3, nstart = 5, algorithm = “Hartigan-Wong”)
> cluster
K-means clustering with 3 clusters of sizes 22, 13, 5
Cluster means:
ph.cerebrospinal.fluid ph.blood hco3.cerebrospinal.fluid hco3.blood
1 46.76818 37.80455 21.34545 22.05455
2 50.17692 41.37692 26.40000 29.35385
3 43.96000 58.52000 12.76000 8.38000
co2.cerebrospinal.fluid co2.blood
1 43.34091 33.42273
2 57.56154 48.26154
3 24.20000 18.98000
Clustering vector:
[1] 1 1 1 1 1 1 1 1 1 3 1 1 3 3 3 3 1 2 1 1 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1
[39] 1 1
Within cluster sum of squares by cluster:
[1] 1684.718 1341.880 1066.188
(between_SS / total_SS = 74.6 %)
Available components:
[1] “cluster” “centers” “totss” “withinss” “tot.withinss”
[6] “betweenss” “size” “iter” “ifault”
También la salida puede ser:
K-means clustering with 3 clusters of sizes 13, 22, 5
Cluster means:
ph.cerebrospinal.fluid ph.blood hco3.cerebrospinal.fluid hco3.blood
1 50.17692 41.37692 26.40000 29.35385
2 46.76818 37.80455 21.34545 22.05455
3 43.96000 58.52000 12.76000 8.38000
co2.cerebrospinal.fluid co2.blood
1 57.56154 48.26154
2 43.34091 33.42273
3 24.20000 18.98000
Clustering vector:
[1] 2 2 2 2 2 2 2 2 2 3 2 2 3 3 3 3 2 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2
[39] 2 2
Within cluster sum of squares by cluster:
[1] 1341.880 1684.718 1066.188
(between_SS / total_SS = 74.6 %)
Como le hemos pedido, la función kmeans devuelve 3 clústers de tamaños 13, 22 y 5. Justo después, se muestran los centroides de los 3 clústers en función de las 6 variables consideradas.
A continuación, se indica a qué clúster pertenece cada uno de los individuos del conjunto de datos. Así, por ejemplo, se aprecia que los 9 primeros individuos forman parte del segundo clúster, mientras que el décimo individuo pertenece al clúster número 3.
Para terminar, se muestran las sumas de cuadrados intra-cluster, que son ciertamente elevadas, lo cual sugiere la necesidad de aumentar el número de clústers considerados. También se muestra el porcentaje between_SS / total_SS, que es una medida que indica cómo de diferentes son los clústers creados.
Ejercicio Guiado 6 (Resuelto)
A partir del conjunto de datos all.mammals.milk.1956 contenido en el paquete cluster.datasets, realizar un análisis clúster jerárquico aglomerativo utilizando el método del enlace completo y considerando la distancia de Minkowski.
Solución
De no haberlo hecho con anterioridad, hay que instalar este paquete usando la orden
> install.packages(“cluster.datasets”)
Y a continuación, es necesario cargarlo mediante la orden
> library(cluster.datasets)
Una vez cargado el paquete, podemos acceder al conjunto de datos al que nos hemos referido anteriormente ejecutando la orden
> data(all.mammals.milk.1956)
El conjunto de datos contiene información sobre los componentes de la leche de 25 mamíferos. En concreto, las variables que contiene son, además del nombre del animal, los porcentajes de leche, proteínas, grasas, lactosa y minerales que contiene su leche. Podemos visualizar las primeras filas del conjunto de datos utilizando la función head.
> head(all.mammals.milk.1956)
name water protein fat lactose ash
1 Horse 90.1 2.6 1.0 6.9 0.35
2 Orangutan 88.5 1.4 3.5 6.0 0.24
3 Monkey 88.4 2.2 2.7 6.4 0.18
4 Donkey 90.3 1.7 1.4 6.2 0.40
5 Hippo 90.4 0.6 4.5 4.4 0.10
6 Camel 87.7 3.5 3.4 4.8 0.71
A continuación, calculamos las distancias entre los individuos del conjunto de datos usando la función dist. Previo a ello vamos a crear un nuevo data frame que contenga exclusivamente las variables numéricas del conjunto.
> variables <- all.mammals.milk.1956[,-1]
> distancias <- dist(variables, method = “minkowski”)
Una vez que hemos calculado las distancias entre los mamíferos de acuerdo a las 5 variables numéricas recogidas en el conjunto de datos, procedemos a realizar el análisis clúster. Para ello, utilizamos la función hclust.
> cluster <- hclust(distancias, method = “complete”)
> cluster
Call:
hclust(d = distancias, method = “complete”)
Cluster method : complete
Distance : minkowski
Number of objects: 25
En primer lugar, consultemos el historial de conglomeración accediendo al elemento merge del objeto cluster.
> cluster$merge
[,1] [,2]
[1,] -4 -13
[2,] -11 -16
[3,] -2 -3
[4,] -21 -22
[5,] -6 -12
[6,] -1 1
[7,] -15 5
[8,] -8 2
[9,] -23 4
[10,] -9 -14
[11,] 8 10
[12,] 3 6
[13,] -7 7
[14,] -19 -20
[15,] -10 11
[16,] -5 12
[17,] 13 16
[18,] -17 14
[19,] -24 -25
[20,] -18 9
[21,] 15 17
[22,] 18 20
[23,] 21 22
[24,] 19 23
Los dos primeros individuos que se fusionan son los que ocupan las posiciones 4 y 13 dentro del conjunto de datos. Esto equivale a decir que la composición de la leche de los mamíferos situados en las posiciones 4 y 13 (el burro y la mula) son las más parecidas. A continuación, forman un grupo independiente del anterior los individuos situados en las posiciones 11 y 16 del conjunto (que son el zorro y la oveja, respectivamente). Siguiendo este procedimiento, se pueden interpretar el resto de pasos del historial de conglomeración.
Una vez revisado el historial de conglomeración, veamos las distancias a las que se producen las fusiones entre individuos consultando el contenido del elemento height del objeto cluster.
> cluster$height
[1] 0.9137286 1.2043255 1.2056533 1.2922848 1.5126467 1.7275416
[7] 2.1702765 2.1914607 2.2918333 2.5243811 3.2973323 3.3274765
[13] 3.6796739 3.7509999 4.5322070 4.7594643 6.3292970 7.0270904
[19] 7.3744424 10.9575727 13.1765891 16.5669098 33.9413096 60.7368093
Los 24 valores numéricos que muestra height se corresponden con las distancias a las que se produce cada fusión en cada paso del historial de conglomeración. Así, podemos concluir que la distancia de Minkowski que separa al burro de la mula (las observaciones 4 y 13, que se fusionan en el primer paso del historial de conglomeración) en cuanto a diferencias en la composición de su leche es de 0,9137 unidades. Igualmente, esta distancia es de 1,2043 unidades para el zorro y la oveja.
Para finalizar, mostramos el dendrograma asociado a este análisis clúster, en el que incluiremos el nombre de cada animal para facilitar su interpretación.
> plot(cluster, labels = all.mammals.milk.1956$name)
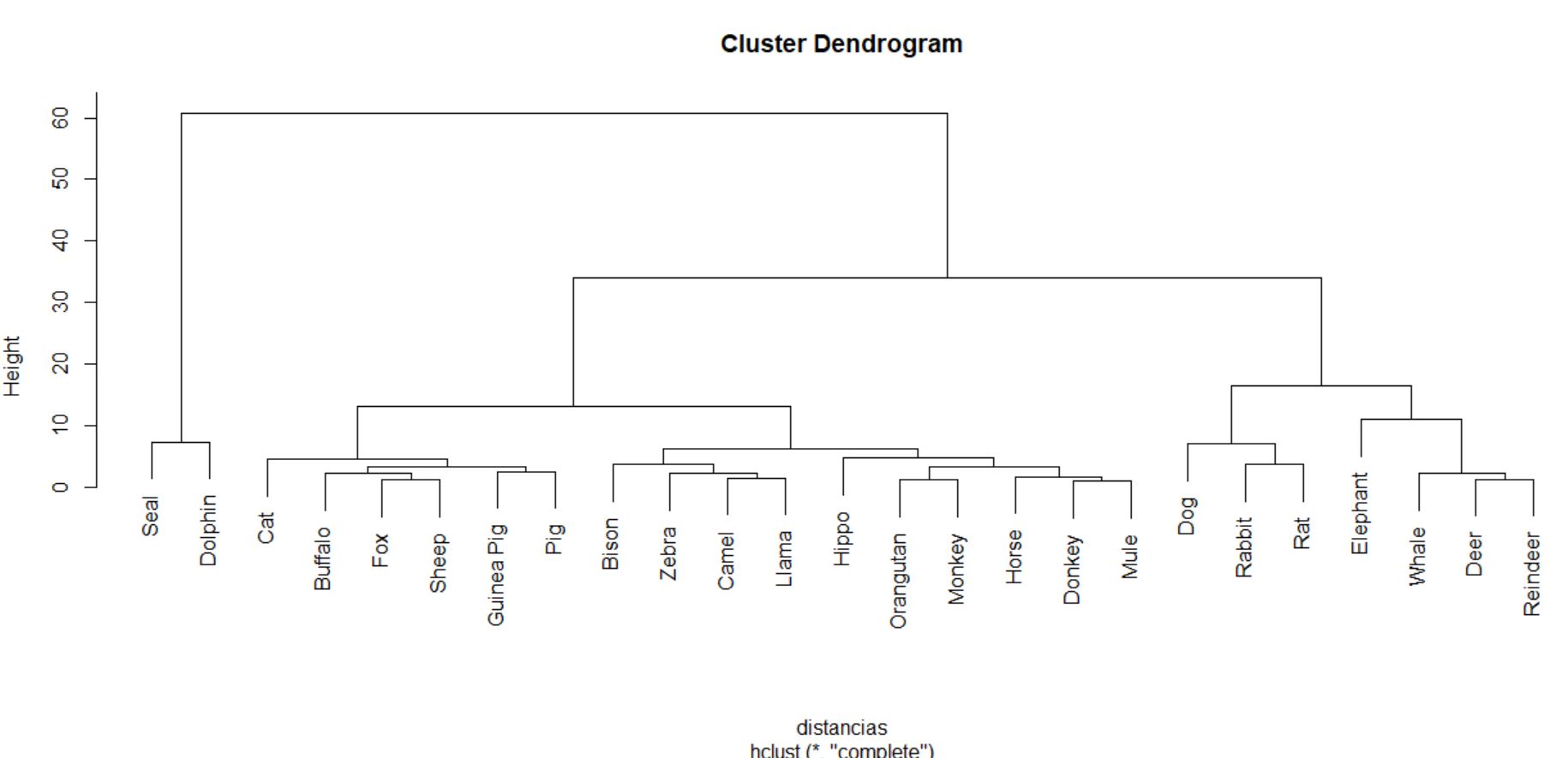
Ejercicios Propuestos
Ejercicio Propuesto 1
Utilizamos de nuevo el archivo de datos ventas_vehículos.sav que contiene estimaciones de ventas, listas de precios y especificaciones físicas hipotéticas de varias marcas y modelos de vehículos. Se desea hacer un estudio de mercado para poder determinar las posibles competencias para sus vehículos, para ello agrupamos las marcas de los coches según los datos disponibles, hábitos de consumo, sexo, edad, nivel de ingresos, etc. de los clientes. Las empresas de coches adaptan sus estrategias de desarrollo de productos y de marketing en función de cada grupo de consumidores para aumentar las ventas y el nivel de fidelidad a la marca.
Se pide:
a) Utilizar un análisis clúster jerárquico
b) Método de conglomerado, el Vecino más lejano
Nota: El archivo de datos ventas_vehículos .sav contiene 157 datos y está formado por las siguientes variables:
Variables tipo cadena: marca (Fabricante); modelo
Variables tipo numérico: ventas (en miles); reventa (Valor de reventa en 4 años); tipo (Tipo de vehículo: Valores: {0, Automóvil; 1, Camión}); precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo).
Ejercicio Propuesto2
Una compañía de telecomunicaciones realiza un estudio con el fin de reducir el abandono de sus clientes. Para ello dispone de un archivo de datos, donde cada caso corresponde a un cliente distinto del que registra diversa información demográfica y del uso del servicio. El objetivo es segmentar su base de clientes por patrones de uso del servicio. Si los clientes se pueden clasificar por el uso, la empresa puede ofrecer paquetes más atractivos para sus clientes. Las variables que indican el uso y no uso de los servicios están contenidas en el archivo Telecomunicaciones1.sav o Teleconunicaciones1.dat
El archivo de datos telecomunicaciones1.dat contiene 1000 datos y está formado por las siguientes variables: región, permanencia, edad, estado_civil, dirección, ingresos_familiares, nivel_educativo, empleo, género, n-pers_hogar, llamadas_gratuitas, alquiler_equipo, tarjeta_llamada, inalámbrico, larga_distancia_mes, llamadas_gratuitas_mes, equipo_mes, tarjeta_mes, inalámbrico_mes, líneas_múltiples, mensaje_voz, servicio_busca, internet, identificador_llamada, desvío_llamadas, llamada_a_tres, facturación_electrónica.
Se pide:
a) Utilizar el procedimiento Análisis de conglomerados jerárquico para estudiar las relaciones entre los distintos servicios.
b) Realizar de nuevo el estudio con la medida de distanciade Jaccard y comparar los resultados.
Ejercicio Propuesto 3
El fichero de datos Localidades.txt incluye información sobre los servicios de los que disponen (señalados con un 1) y no disponen (señalados con un 0) una muestra de 10 localidades españolas de menos de 1.000 habitantes. Realizar un análisis clúster jerárquico aglomerativo utilizando el método del promedio entre grupos y considerando la distancia adecuada.
Ejercicio Propuesto 4
A partir del conjunto de datos ohio.croplands.1949 contenido en el paquete cluster.datasets, realizar un análisis clúster jerárquico divisivo considerando la distancia Manhattan.
Ejercicio Propuesto 1 (Resuelto)
Utilizamos de nuevo el archivo de datos ventas_vehículos.sav que contiene estimaciones de ventas, listas de precios y especificaciones físicas hipotéticas de varias marcas y modelos de vehículos. Se desea hacer un estudio de mercado para poder determinar las posibles competencias para sus vehículos, para ello agrupamos las marcas de los coches según los datos disponibles, hábitos de consumo, sexo, edad, nivel de ingresos, etc. de los clientes. Las empresas de coches adaptan sus estrategias de desarrollo de productos y de marketing en función de cada grupo de consumidores para aumentar las ventas y el nivel de fidelidad a la marca.
Se pide:
a) Utilizar un análisis clúster jerárquico
b) Método de conglomerado, el Vecino más lejano
Nota: El archivo de datos ventas_vehículos .sav contiene 157 datos y está formado por las siguientes variables:
Variables tipo cadena: marca (Fabricante); modelo
Variables tipo numérico: ventas (en miles); reventa (Valor de reventa en 4 años); tipo (Tipo de vehículo: Valores: {0, Automóvil; 1, Camión}); precio (en miles); motor (Tamaño del motor); CV (Caballos); pisada (Base de neumáticos); ancho (Anchura); largo (Longitud); peso_neto (Peso neto); depósito (Capacidad de combustible); mpg (Consumo).
Solución
> setwd(“C:/Users/Usuario/Desktop/Datos”) # situarnos en el directorio de trabajo
> library(foreign) # importar y exportar datos .sav
> datos<- read.spss(“Ventas-vehiculos.sav”,use.value.labels=TRUE, max.value.labels=TRUE, to.data.frame=TRUE, sep)
a) Utilizar un análisis clúster jerárquico
b) Método de conglomerado, el Vecino más lejano
En primer lugar restringiremos el archivo de datos sólo a los automóviles de los que se vendieron al menos 100.000 unidades. Para ello seleccionamos los casos que cumplan esa condición mediante la siguiente fórmula:
> datos100k <- subset(datos, subset =datos$ventas>100 & datos$tipo==0)
La función subset filtramos los datos, poniendo las condiciones de selección en el segundo argumento.
> datos100k$marca= gsub(” “,””,datos100k$marca)
> datos100k$modelo= gsub(” “,””,datos100k$modelo)
> x <- datos100k[,c(“precio”,”motor”,”CV”,”pisada”,”ancho”,”largo”,”peso_neto”,”deposito”,”mpg” )]
> x
precio motor CV pisada ancho largo peso_neto deposito mpg
20 13.260 2.2 115 104.1 67.9 180.9 2.676 14.3 27
21 16.535 3.1 170 107.0 69.4 190.4 3.051 15.0 25
28 18.890 3.4 180 110.5 73.0 200.0 3.389 17.0 27
48 21.560 3.8 190 101.3 73.1 183.2 3.203 15.7 24
50 17.885 3.0 155 108.5 73.0 197.6 3.368 16.0 24
51 12.315 2.0 107 103.0 66.9 174.8 2.564 13.2 30
58 12.885 1.6 106 103.2 67.1 175.1 2.339 11.9 32
59 15.350 2.3 135 106.9 70.3 188.8 2.932 17.1 27
120 19.720 3.4 175 107.0 70.4 186.3 3.091 15.2 25
137 13.108 1.8 120 97.0 66.7 174.0 2.420 13.2 33
138 17.518 2.2 133 105.2 70.1 188.5 2.998 18.5 27
> X.scale<- scale(x, center = T, scale = T)
> row.names(X.scale)<- datos100k$modelo
> dmx <- dist(X.scale[, colnames(x)], method = “euclidean”)
En este caso seleccionamos el método “complete” en la función hclust.
la solución es:
Call:
hclust(d = dmx^2, method = “complete”)
Cluster method : complete
Distance : euclidean
Number of objects: 11
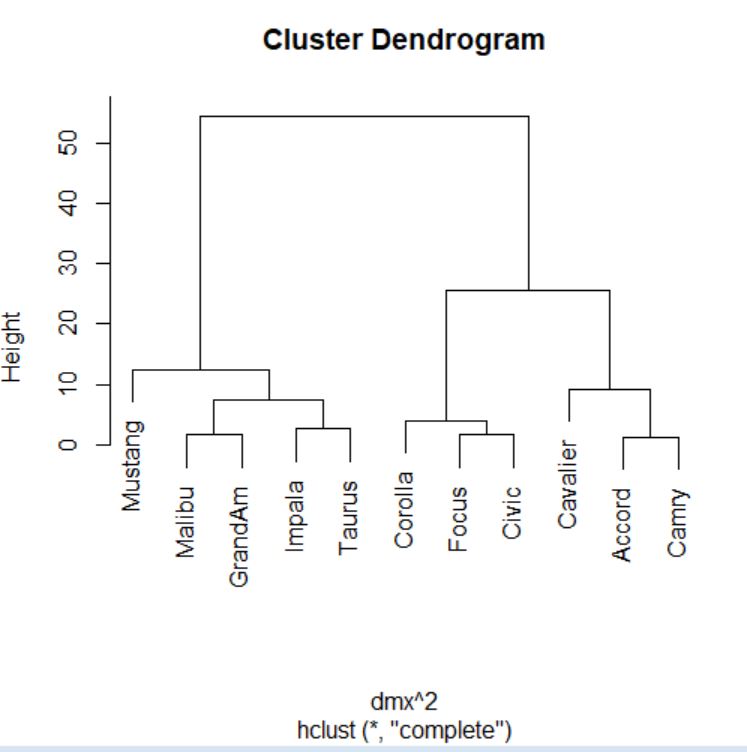
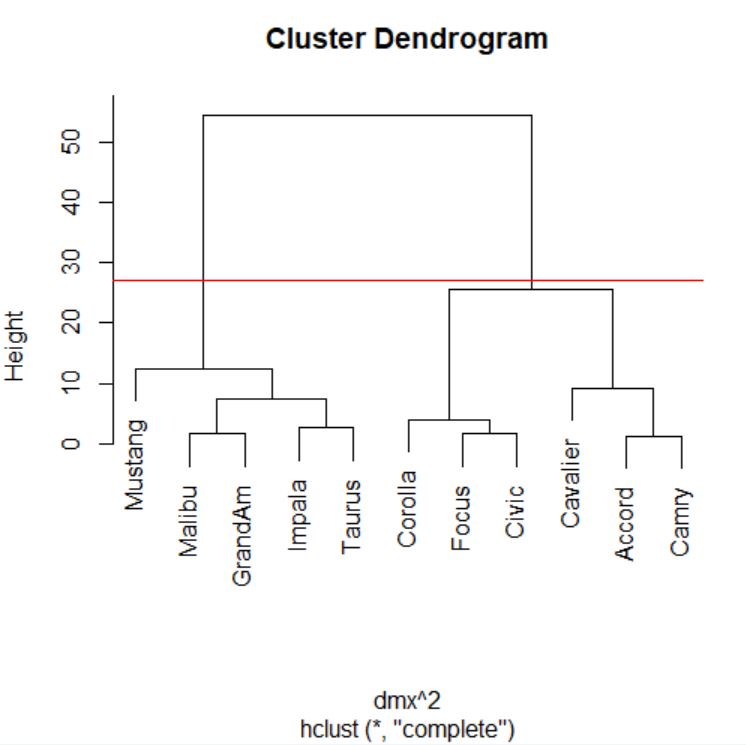
> cc$height
[1] 1.260060 1.578930 1.624664 2.618741 4.011680 7.333368 9.183015
[8] 12.439603 25.486274 54.606994
> cc$merge
[,1] [,2]
[1,] -8 -11
[2,] -6 -7
[3,] -2 -9
[4,] -3 -5
[5,] -10 2
[6,] 3 4
[7,] -1 1
[8,] -4 6
[9,] 5 7
[10,] 8 9
Ejercicio Propuesto 1 Resuelto
Ejercicio Propuesto 2 (Resuelto)
Una compañía de telecomunicaciones realiza un estudio con el fin de reducir el abandono de sus clientes. Para ello dispone de un archivo de datos, donde cada caso corresponde a un cliente distinto del que registra diversa información demográfica y del uso del servicio. El objetivo es segmentar su base de clientes por patrones de uso del servicio. Si los clientes se pueden clasificar por el uso, la empresa puede ofrecer paquetes más atractivos para sus clientes. Las variables que indican el uso y no uso de los servicios están contenidas en el archivo Telecomunicaciones1.sav o Teleconunicaciones1.dat
El archivo de datos telecomunicaciones1.dat contiene 1000 datos y está formado por las siguientes variables: región, permanencia, edad, estado_civil, dirección, ingresos_familiares, nivel_educativo, empleo, género, n-pers_hogar, llamadas_gratuitas, alquiler_equipo, tarjeta_llamada, inalámbrico, larga_distancia_mes, llamadas_gratuitas_mes, equipo_mes, tarjeta_mes, inalámbrico_mes, líneas_múltiples, mensaje_voz, servicio_busca, internet, identificador_llamada, desvío_llamadas, llamada_a_tres, facturación_electrónica.
Se pide:
a) Utilizar el procedimiento Análisis de conglomerados jerárquico para estudiar las relaciones entre los distintos servicios.
b) Realizar de nuevo el estudio con la medida de distanciade Jaccard y comparar los resultados.
Solución
> setwd(“C:/Users/Usuario/Desktop/Datos”)
> datos <- read.table(“Telecomunicaciones1.dat”, header = TRUE)
A continuación, filtramos las variables que queremos elegir:
Variables: Servicio de llamadas gratuitas, Alquiler de equipo, Servicio de tarjeta de llamada, Servicio inalámbrico, Líneas múltiples, mensajes de voz, servicio de busca, internet, Identificador de llamadas, llamadas en espera, Desvío de llamadas, llamadas a tres, Facturación electrónica
> datos

Ya tenemos el data frame con las variables que nos interesan. A continuación calculamos la matriz de distancias:
a) Utilizar el procedimiento Análisis de conglomerados jerárquico para estudiar las relaciones entre los distintos servicios.
Elegimos como medida la binaria, y como método Vinculación inter-grupos, es decir “average”. Los datos los metemos como su tabla traspuesta ya que se van a aglomerar las variables en vez de los casos
hclust(d = dmx, method = “average”)
Cluster method : average
Distance : binary
Number of objects: 13
Ya podemos dibujar nuestro dendrograma.
> cl$height
[1] 0.3116197 0.3264605 0.3321387 0.3440881 0.3991507 0.3994253 0.4368252 0.4458629 0.4632616 0.5989666 0.5996411 0.6844400
> cl$merge
[,1] [,2]
[1,] -1 -10
[2,] -9 -11
[3,] 1 2
[4,] -12 3
[5,] -2 -8
[6,] -4 -7
[7,] -13 5
[8,] -3 4
[9,] -6 6
[10,] 8 9
[11,] -5 7
[12,] 10 11
> plot(cl)
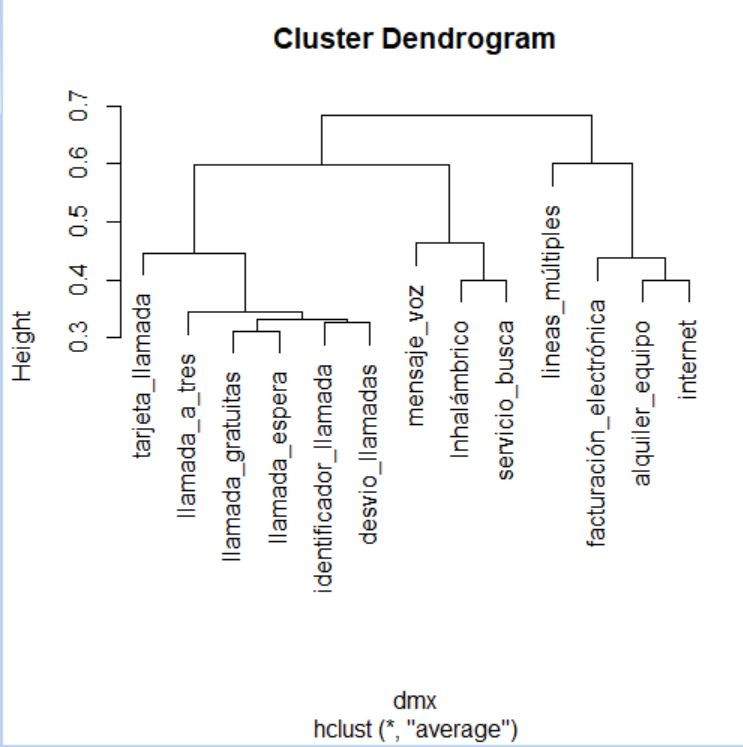
> abline(h=.65, col=”red”)
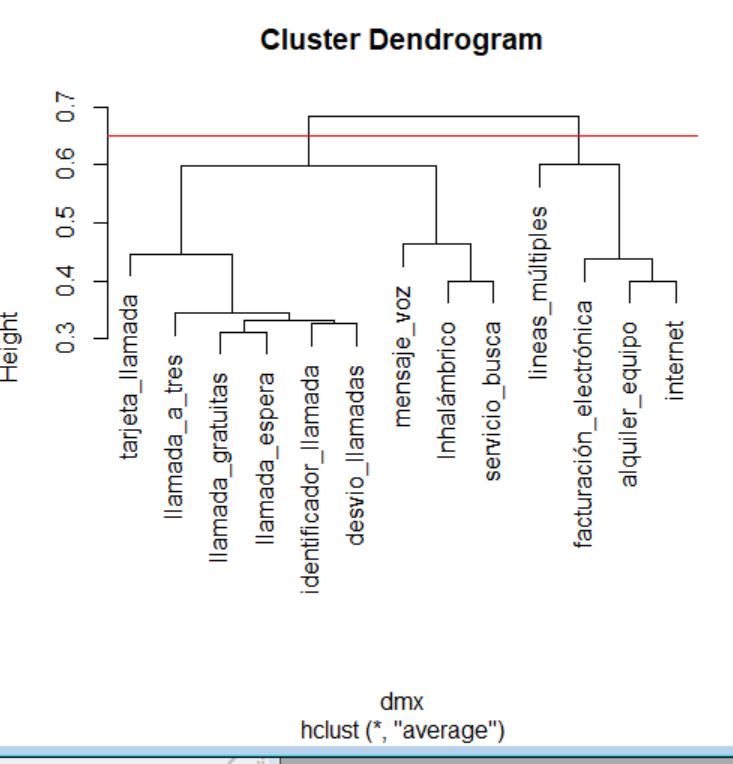
b) Realizar de nuevo el estudio con la medida de distanciade Jaccard y comparar los resultados.
Para ejecutar un análisis de conglomerados con la medida de distanciade Jaccard, utilizamos la función “vegdist”. Para ello, instalamos y cargamos el paquete “vegan”.
> install.packages(“vegan”)
> library(“vegan”)
> dmx2 <- vegdist(t(datos), method = “jaccard”, binary=T)
Call:
hclust(d = dmx2, method = “average”)
Cluster method : average
Distance : binary jaccard
Number of objects: 13
[1] 0.3116197 0.3264605 0.3321387 0.3440881 0.3991507 0.3994253 0.4368252 0.4458629
[9] 0.4632616 0.5989666 0.5996411 0.6844400
[,1] [,2]
[1,] -1 -10
[2,] -9 -11
[3,] 1 2
[4,] -12 3
[5,] -2 -8
[6,] -4 -7
[7,] -13 5
[8,] -3 4
[9,] -6 6
[10,] 8 9
[11,] -5 7
[12,] 10 11
> abline(h=.65, col=”red”)
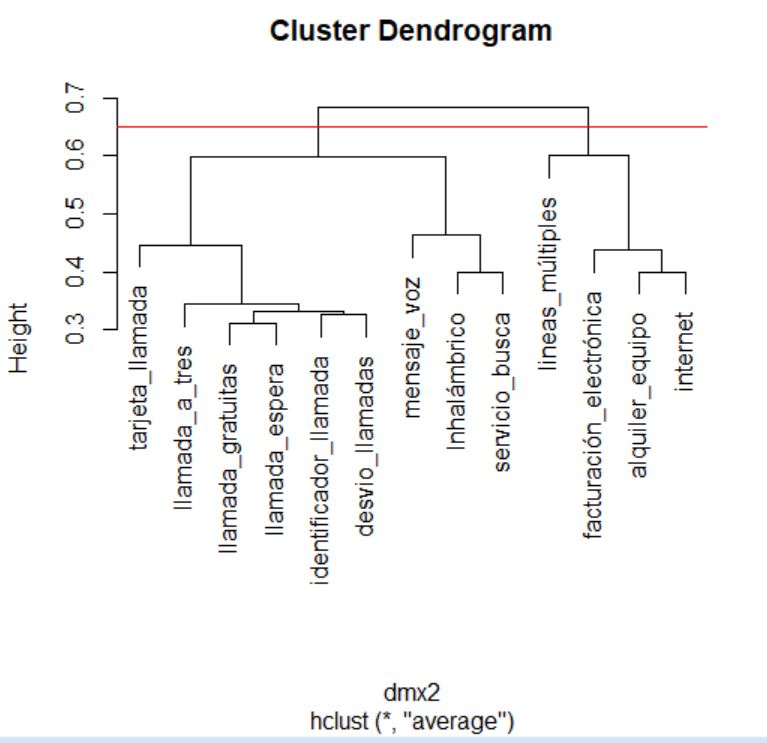
Ejercicio Propuesto 2 Resuelto
Ejercicio Propuesto 3 (Resuelto)
El fichero de datos Localidades.txt incluye información sobre los servicios de los que disponen (señalados con un 1) y no disponen (señalados con un 0) una muestra de 10 localidades españolas de menos de 1.000 habitantes. Realizar un análisis clúster jerárquico aglomerativo utilizando el método del promedio entre grupos y considerando la distancia adecuada.
Solución
> Localidades <- read.table(“Localidades.txt”, header = TRUE)
> Localidades
Localidad Consultorio Cine Teatro Parada.Bus Parada.Taxi Banco Biblioteca
1 1 1 0 1 1 0 1 0
2 2 0 1 0 1 1 0 0
3 3 0 0 0 1 0 1 1
4 4 1 0 1 1 1 1 0
5 5 0 1 0 1 1 0 1
6 6 1 0 1 0 0 1 0
7 7 1 1 0 1 0 0 0
8 8 0 0 0 1 1 0 1
9 9 1 1 0 1 0 1 1
10 10 0 0 0 1 1 0 1
Supermercado
1 1
2 0
3 1
4 0
5 1
6 1
7 1
8 0
9 0
10 0
Como ya nos adelantaba el enunciado, todas las variables que componen el conjunto de datos son de tipo dicotómico y toman únicamente los valores 0 y 1. Consecuentemente, para calcular la distancia entre cada para de individuos (de localidades, en este caso) usaremos la distancia binaria. De forma previa al cálculo de estas distancias crearemos un data frame, que llamaremos distancias, y contendrá únicamente las variables dicotómicas del conjunto de datos.
A continuación, llamamos a la función hclust, indicando como argumentos la matriz de distancias que devuelve la función dist así como el método de aglomeración.
> cluster <- hclust(distancias, method = “average”)
> cluster
Call:
hclust(d = distancias, method = “average”)
Cluster method : average
Distance : binary
Number of objects: 10
Consultemos, en primer lugar, el historial de conglomeración del análisis, que está contenido en el elemento merge del objeto cluster.
[,1] [,2]
[1,] -8 -10
[2,] -1 -6
[3,] -2 -5
[4,] -4 2
[5,] 1 3
[6,] -3 -9
[7,] -7 6
[8,] 4 7
[9,] 5 8
Según lo mostrado en el historial de conglomeración, las localidades más similares en lo que a servicios se refiere son la 8 y la 10 y, en consecuencia, son las primeras que se unen en un grupo. A continuación, las localidades 1 y 6 hacen lo propio, pero en una agrupación independiente a la anterior. El resto de pasos del historial de conglomeración se interpreta del mismo modo.
Las distancias a las que se producen las fusiones entre localidades se pueden consultar accediendo al elemento height del objeto cluster.
[1] 0.0000000 0.2000000 0.4000000 0.4166667 0.4500000 0.5000000 0.5833333
[8] 0.6243386 0.7424107
Así, se puede apreciar que la primera fusión entre localidades se produce a una distancia de 0 unidades; la segunda, a una distancia de 0.2 unidades; la tercera, a una distancia de 0.4 unidades y así, sucesivamente.
Por último, graficamos el dendrograma asociado al proceso de formación de clústers.
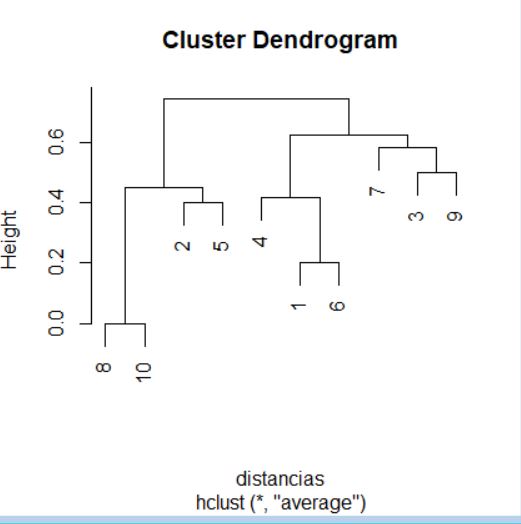
Ejercicio Propuesto 4 Resuelto
A partir del conjunto de datos ohio.croplands.1949 contenido en el paquete cluster.datasets, realizar un análisis clúster jerárquico divisivo considerando la distancia Manhattan.
Solución
De no haberlo hecho con anterioridad, hay que instalar y cargar el paquete cluster.datasets
Una vez cargado el paquete, podemos acceder al conjunto de datos al que nos hemos referido anteriormente ejecutando la orden
> data(ohio.croplands.1949)
El conjunto de datos contiene información sobre los porcentajes de terreno dedicados a diferentes cultivos en 15 condados de Ohio, en Estados Unidos. Para asegurarnos de que la lectura del conjunto de datos ha sido correcta, consultamos las primeras observaciones ejecutando la orden head.
> head(ohio.croplands.1949)
county corn mixed wheat oats barley soy hay
1 Adams 42.41 0.21 22.47 1.07 0.37 0.62 27.80
2 Allen 34.43 0.13 23.76 18.35 0.11 12.18 15.31
3 Ashtabula 22.88 0.24 13.52 15.67 0.02 1.30 38.89
4 Athens 26.61 0.18 8.89 3.42 0.05 0.71 53.91
5 Delaware 33.52 0.13 17.60 11.33 0.16 11.82 22.69
6 Clinton 48.45 0.24 29.50 3.10 0.25 2.72 9.85
A continuación, instalamos (de no haberlo hecho antes) y cargamos el paquete cluster, que es el que contiene la función diana, la que realiza el análisis clúster jerárquico divisivo.
Antes de llamar a la función diana, calcularemos las distancias de Manhattan entre individuos, previa creación de un data frame, que llamaremos distancias, que contenga únicamente las variables numéricas del conjunto de datos.
> distancias <- dist(variables, method = “manhattan”)
Ahora sí, realizamos la llamada a la función diana, asignando el valor TRUE al argumento diss para indicar que el primer argumento de la función es una matriz de distancias.
> cluster
Merge:
[,1] [,2]
[1,] -3 -8
[2,] -2 -9
[3,] -7 -11
[4,] 2 -13
[5,] -6 -10
[6,] 3 -15
[7,] -1 -14
[8,] -4 6
[9,] 1 -12
[10,] 4 -5
[11,] 7 5
[12,] 9 8
[13,] 11 10
[14,] 13 12
Order of objects:
[1] 1 14 6 10 2 9 13 5 3 8 12 4 7 11 15
Height:
[1] 18.84 35.30 12.04 57.20 7.28 11.57 25.45 89.20 4.87 24.71 52.24 21.38
[13] 8.87 14.09
Una vez que se ha ejecutado la función diana, podemos acceder al historial de conglomeración.
> cluster$merge
[,1] [,2]
[1,] -3 -8
[2,] -2 -9
[3,] -7 -11
[4,] 2 -13
[5,] -6 -10
[6,] 3 -15
[7,] -1 -14
[8,] -4 6
[9,] 1 -12
[10,] 4 -5
[11,] 7 5
[12,] 9 8
[13,] 11 10
[14,] 13 12
En el caso del análisis clúster jerárquico divisivo, la interpretación del historial de conglomeración comienza por el final. Así, el paso notado con el número 14 será el primero que se interprete. En este caso, la información de este paso indica que, en primer lugar, el total del conjunto de datos se divide en dos grupos: uno, el que se volverá a dividir en el paso notado con el número 13 en el historial de conglomeración (que será el 2º paso a interpretar), y otro, que será el que se volverá a dividir en el paso notado con el número 12 en el historial de conglomeración (que será el 3er paso a interpretar). A continuación, según lo especificado en el paso notado con el número 13, uno de los grupos surgidos de la división en el paso anterior vuelve a dividirse en dos: uno, el que se volverá a dividir en el paso notado con el número 11 dentro del historial de conglomeración, y otro, el que se volverá a dividir en el paso notado con el número 10 dentro del historial de conglomeración. Del mismo modo pueden interpretarse el resto de pasos del historial de conglomeración.
A continuación, se muestran las distancias a las que se producen las divisiones o disociaciones entre grupos.
[1] 18.84 35.30 12.04 57.20 7.28 11.57 25.45 89.20 4.87 24.71 52.24 21.38
[13] 8.87 14.09
Por último, se puede obtener el dendrograma con la representación gráfica del proceso de división de los individuos del conjunto de datos.
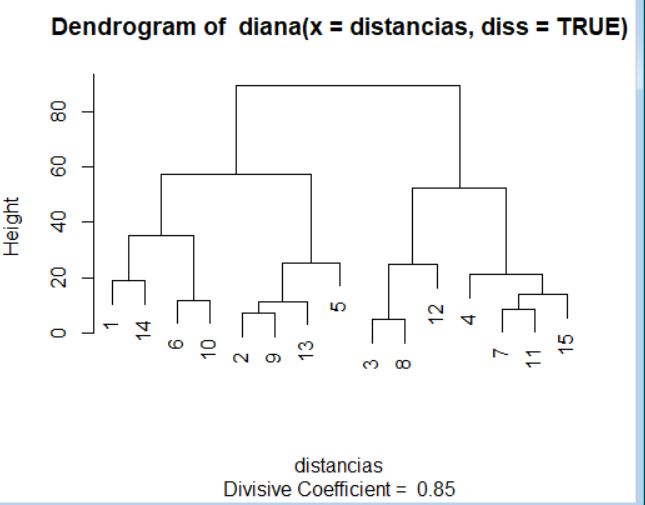
Ejercicio Propuesto 4 Resuelto
Autores: Felícita Doris Miranda Huaynalaya y Ana María Lara Porras. Universidad de Granada. (2023)