INTERVALOS DE CONFIANZA
Objetivos
- Calcular e interpretar intervalos de confianza para la media en una población Normal con varianza conocida
- Calcular e interpretar intervalos de confianza para la media en una población Normal con varianza desconocida
- Calcular e interpretar intervalos de confianza para la proporción
- Calcular e interpretar intervalos de confianza para la diferencia de medias en dos poblaciones normales independientes con varianzas desconocidas, pero supuestas iguales en las dos poblaciones
- Calcular e interpretar intervalos de confianza para la diferencia de medias en dos poblaciones normales independientes con varianzas desconocidas, pero supuestas iguales
- Calcular e interpretar intervalos de confianza para la diferencia de medias en dos poblaciones normales relacionadas
- Calcular e interpretar intervalos de confianza para la diferencia de proporciones.
Introducción
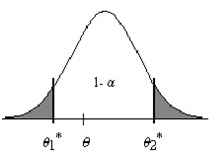
El objetivo de la estimación mediante intervalos de confianza o estimación confidencial es la determinación de dos valores, \( \theta_{1}^{*} \) y \( \theta_{2}^{*} \), que verifiquen \( \theta_{1}^{*} < \theta_{2}^{*} \), tales que, al constituirse en intervalo \( ( \theta_{1}^{*} , \theta_{2}^{*} ) \) contengan, con una probabilidad prefijada, el verdadero valor del parámetro que deseamos estimar. De forma gráfica, un intervalo de confianza puede representarse del siguiente modo:
donde
- \( 1 – \alpha \): Recibe el nombre de coeficiente de confianza o nivel de confianza. Es la probabilidad de que el intervalo de confianza contenga el verdadero valor del parámetro poblacional \( θ \)
- \( \alpha \): Es un valor comprendido entre 0 y 1, \( 0 < α < 1 \), (usualmente próximo a 0), que indica el riesgo de que el intervalo de confianza no contenga el valor del parámetro poblacional a estimar, \( θ \). Por lo que \( α \) recibe el nombre de riesgo del error del intervalo, nivel del error del intervalo o nivel de significación del intervalo.
- \( \theta _{1}^{*} \) y \( \theta _{2}^{*} \): Son los valores que delimitan el intervalo de confianza y reciben el nombre de límite superior y límite inferior del intervalo, respectivamente. La diferencia entre el límite superior y el límite inferior de un intervalo, \( \theta _{2}^{*} – \theta _{1}^{*} \) se conoce como amplitud del intervalo.
Para la construcción de un intervalo de confianza, lo deseable es maximizar el nivel de confianza asociado al intervalo o equivalentemente minimizar el nivel de significación y conseguir una amplitud lo más pequeña posible.
Intervalo de confianza para la media en una población normal con varianza conocida
El intervalo de confianza para la media de una variable continua con el valor de la varianza de dicha variable conocida en toda la población es es el intervalo menos usual.
Para estimar la media poblacional \( \mu \) de una población Normal de media \( \mu \) (desconocida) y de varianza \( \sigma^{2} \) (conocida), \( N(\mu, \sigma^{2}) \), se selecciona una muestra aleatoria \( X_1, X_2, \cdots, X_n \); de tamaño \( n \) de valores de una variable aleatoria de esta población y se calcula su media muestral, como mejor estimador puntual de \( \mu \). La construcción del intervalo de confianza se hace tomando como base este estimador. Para calcular un intervalo de confianza para \( \mu \) partimos de la variable aleatoria
\( Z= \displaystyle \frac {\overline{X}-μ }{ σ / \sqrt {n}} \)
Expresión 1: Expresión de la variable aleatoria
que sigue una distribución normal de media 0 y desviación típica 1. Buscamos los cuantiles de esta distribución tales que
\( P \left [ – z_{1- α/2} \leq \displaystyle \frac {\overline{X}-μ }{σ / \sqrt {n}} \leq z_{1-α/2} \right] = 1-α \)
Expresión 2: Obtención del cuantil z{1 – α/2}
O, equivalentemente,
\( P \left [ \overline {X} – z_{1-α/2} \displaystyle \frac { σ} { \sqrt{n }} \leq μ \leq \overline {X} + z_{1-α/2} \displaystyle \frac { σ} { \sqrt{n}} \right] = 1-α \)
Expresión 3: Obtención del cuantil z{1 – α/2}
Por lo tanto, el intervalo de confianza que debemos calcular es
\( \left [ \overline {X} – z_{1-α/2} \displaystyle \frac { \sigma} { \sqrt{n}} , \overline {X} + z_{1-α/2} \displaystyle \frac { \sigma} { \sqrt{n}} \right] \)
Expresión 4: Intervalo de confianza (varianza conocida)
Nota: R y RStudio no incluyen una función específica para el cálculo de este tipo de intervalos de confianza. Aun así, pueden calcularse de una forma muy sencilla como se muestra en el siguiente ejemplo.
Supuesto Práctico 1
De una cierta población se ha extraído una muestra de 64 individuos, cuyo valor medio es 1012. Se sabe por otras experiencias del mismo tipo, que la desviación típica vale 25. Hallar intervalos de confianza para el valor medio de la población a los niveles de confianza del 0.95 y 0.99.
Solución
Iniciamos un nuevo Script en RStudio donde introducimos los datos relativos a la media, varianza, tamaño muestral y nivel de significación que proporciona el enunciado.
> alpha<- 0.05
> n = 64
> varianza <- 625
> media <- 1012
> cuantil<- qnorm(1 – alpha/2)
Una vez introducidos los datos del enunciado, pasamos a calcular los extremos inferior y superior del intervalo de acuerdo a la expresión que se vio anteriormente:
> lim_inf<-media – cuantil * sqrt(varianza) / sqrt(n)
> lim_inf
[1] 1005.875
> lim_sup<- media + cuantil * sqrt(varianza) / sqrt(n)
> lim_sup
[1] 1018.125
Por tanto, se tiene el 95% de confianza de que el intervalo [1005.875, 1018.125] contenga el valor medio de la población
P[1005.875 ≤ μ ≤ 1018.125 ] = 0.95
Para el nivel de confianza del 0.99, lo único que tenemos que cambiar es el valor de α
> alpha<- 0.01
> cuantil<- qnorm(1 – alpha/2)
> lim_inf<-media – cuantil * sqrt(varianza) / sqrt(n)
> lim_inf
[1] 1003.951
> lim_sup<- media + cuantil * sqrt(varianza) / sqrt(n)
> lim_sup
[1] 1020.049
Por tanto, el intervalo de confianza para el valor medio de la población al nivel de confianza del 0.99 es [1003.951, 1020.049]
P[1003.951 ≤ μ ≤ 1020.049 ] = 0.99
Intervalo de confianza para la media en una población normal con varianza desconocida
Supongamos, en este caso, que la varianza poblacional de la variable de interés es desconocida. Nuestro objetivo sigue siendo el cálculo de un intervalo de confianza para la media de dicha variable.
Supongamos una muestra aleatoria \( X_1, X_2, \cdots, X_n \); de tamaño \( n \) de valores de la variable aleatoria que sigue una distribución Normal de media \( \mu \) y de varianza \( \sigma^{2} \), ambas desconocidas. Para calcular un intervalo de confianza, en este caso, partimos de la variable aleatoria
\( T= \displaystyle \frac {\overline{X}-μ }{s / \sqrt {n}} \)
Expresión 5: Expresión de la variable aleatoria
que sigue una distribución \( t \) de Student con \( n-1 \) grados de libertad. En la fórmula anterior, \( s \) hace referencia a la cuasidesviación típica muestral.
Tenemos que buscar dos valores de esta distribución tales que
\( P \left [ – t_{1- α/2} \leq \displaystyle \frac {\overline{X}-μ }{s / \sqrt {n}} \leq t_{1-α/2} \right] = 1-α \)
Expresión 6: Obtención del cuantil \( t_{1- α/2} \)
Al operar algebraicamente, se obtiene que
\( P \left [ \overline {X} – t_{1-α/2} \displaystyle \frac { s} { \sqrt{n }} \leq μ \leq \overline {X} + t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} \right] =1-α \)
Expresión 7: Obtención del cuantil \( t_{1- α/2} \)
por lo que el intervalo de confianza que buscamos es
\( \left [ \overline {X} – t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} , \overline {X} + t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} \right] \)
Expresión 8: Expresión del Intervalo de confianza (varianza desconocida)
La función de R t.test calcula intervalos de confianza en este contexto. Esta función también se utiliza para resolver contrastes de hipótesis, como veremos en la práctica 6. La sintaxis de la función t.test es la siguiente:
t.test(x, conf.level = 0.95)
donde
- x: Vector numérico con los valores de la variables de interés
- conf.level: Valor numérico que indica el nivel de confianza, en tanto por uno, al que se construirá el intervalo. Si omitimos este parámetro en la llamada a la función, los intervalos de confianza se calculan a un nivel de confianza del 95%.
Veamos el funcionamiento de la función t.test mediante un ejemplo.
Supuesto Práctico 2
En una muestra de 9 preparados de jugo de tomate se ha obtenido una media de 21 mg/100 cc y una cuasidesviación típica de 2.45 mg/100 cc. Supuesto que el contenido de vitamina C del jugo de tomate se distribuye según una distribución Normal de varianza desconocida. Se pide:
a) Estimar el contenido medio de vitamina C del jugo de tomate
b) Calcular el intervalo de confianza al 98 %
a) El estimador pedido es la media muestral, 21
b)
Al no disponer de un vector numérico con los valores de la variable de interés, para resolver el ejemplo recurriremos a utilizar la expresión del intervalo de confianza para este caso
\( \left [ \overline {X} – t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} , \overline {X} + t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} \right] \)
Expresión 9: Expresión del Intervalo de confianza (varianza desconocida)
En primer lugar, introducimos los datos del ejemplo
> alpha<- 0.02
> n = 9
> cuasi <- 2.45
> media <- 21
La función que devuelve resultados de los cuantiles de la t-Student es:
qt(p, df, ncp, lower.tail = T)
donde:
- p: Vector de probabilidades
- df: Grados de libertad
- lower.tail: Parámetro booleano, si es TRUE (por defecto), las probabilidades son P[X ≤ x], de lo contrario, P [X > x].
> cuantil<- qt((1 – alpha/2), 8, lower.tail = T)
> lim_inf<-media – cuantil * cuasi / sqrt(n)
> lim_inf
[1] 18.63456
> lim_sup<- media + cuantil * cuasi / sqrt(n)
> lim_sup
[1] 23.36544
P[18.63456 ≤ μ ≤ 23.36544] = 0.98
Por lo tanto, hay un 98% de confianza de que el intervalo [18.63456, 23.36544] contenga el contenido medio en vitamina C del jugo de tomate.
Supongamos el mismo ejemplo pero en el caso de disponer de los datos de los 9 preparados en contenido de vitamina C del jugo de tomate. Los datos se muestran en el fichero tomate.txt
Solución
En primer lugar nos situamos en el directorio de trabajo. En el Script de RStudio escribimos
> setwd(“F:/Desktop/EJEMPLOSRS5”)
> datos1 <- read.table(“tomate.txt”, header = TRUE)
> datos1
Contenido
1 24
2 20
3 21
4 19
5 22
6 23
7 16
8 23
9 21
Partiendo del conjunto de datos del Supuesto Práctico 2, el cual se había importado y almacenado en una variable de nombre datos1, vamos a calcular el intervalo de confianza que nos piden. Para ello, basta con realizar la siguiente llamada a la función t.test
>t.test(datos1$Contenido, conf.level = 0.98)
data: datos1$Contenido
t = 25.72, df = 8, p-value = 5.601e-09
alternative hypothesis: true mean is not equal to 0
98 percent confidence interval:
18.63505 23.36495
sample estimates:
mean of x
21
De toda la información que devuelve la función t.test, sólo nos interesa la relativa al intervalo de confianza. El resto hace referencia a los contrastes de hipótesis que, como hemos comentado, se estudiarán en la práctica 6.
98 percentconfidenceinterval:
18.63505 23.36495
Por lo tanto, el intervalo de confianza para el contenido medio en vitamina C en el jugo de tomate a un nivel de confianza del 98% es ( 18.63505 23.36495).
Intervalo de confianza para la proporción
Dada una variable aleatoria \( X \) con distribución de probabilidad binomial de parámetros \( n \) y \( \pi \), esto es, \( X \rightarrow B(n, π) \); con \( \pi \) desconocido. El objetivo es determinar un intervalo de confianza para el parámetro \( \pi \). Para ello, se extrae una muestra aleatoria \( X_1, X_2, \cdots, X_n \) de tamaño \( n \) de dicha distribución. Sea \( p \) la proporción muestral. Entonces, se sabe que el estadístico
\( Z = \displaystyle \frac { p – \pi} { \displaystyle \sqrt { \displaystyle \frac { p(1-p)} {n} } } \)
Expresión 10: Expresión de la variable aleatoria
sigue una distribución normal de media 0 y desviación típica 1. Por ello, calcular el intervalo de confianza para la proporción consiste en obtener los cuantiles de la distribución normal tales que
\( P \left [ -z_{1-α/2} \leq \displaystyle \frac {p – \pi } { \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}}} \leq z_{1-α/2} \right ]=1-α \)
Expresión 11: Obtención del cuantil z{1 – α/2}
O, equivalentemente,
\( P \left [ p -z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \leq \pi \leq p + z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \right ]=1-α \)
Expresión 12: Obtención del cuantil z{1 – α/2}
Por lo tanto, el intervalo de confianza que debemos calcular es
\( \left [ p -z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}}, p + z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \right ] \)
Expresión 13: Intervalo de confianza para la proporción
La función que calcula este intervalo de confianza en R es prop.test. Sus argumentos son los siguientes
prop.test(x, n, conf.level = 0.95)
donde
- x: Valor numérico que indica el número de elementos del grupo que presentan la característica de interés.
- n: Valor numérico que indica el número total de elementos del grupo.
- conf.level: Valor numérico que indica el nivel de confianza, en tanto por uno, al que se construirá el intervalo. Si omitimos este parámetro en la llamada a la función, los intervalos de confianza se calculan a un nivel de confianza del 95%.
Vamos a aplicar la función prop.test a los datos sobre las flexiones realizadas por los alumnos que hemos utilizado en los ejemplos anteriores.
Supuesto Práctico 3
En una muestra de 900 personas con pelo oscuro se encontró que 150 de ellas tenían los ojos azules. Construir un intervalo de confianza al 95% para la proporción de individuos que teniendo el pelo oscuro posee los ajos azules. ¿Son compatibles estos resultados con la suposición de que dicha proporción vale 1/4?
Solución
Para el cálculo del intervalo de confianza utilizamos la función prop.test
De las 900 personas que conforman la muestra, 150 tienen los ojos azules. Por lo que la llamada a prop.test sería la siguiente:
>prop.test(150,900)
1-sample proportions test with continuity correction
data: 150 out of 900, null probability 0.5
X-squared = 398.67, df = 1, p-value < 2.2e-16
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.1432251 0.1930061
sample estimates:
p
0.1666667
Como el nivel de confianza para este intervalo es el 95% no ha sido necesario incluir el argumento conf.level en la llamada a prop.test, puesto que este es el nivel de confianza por defecto.
De nuevo, los resultados de la función incluyen mucha más información aparte de la relativa al intervalo de confianza. Por ahora, nos centraremos únicamente en esta última.
95 percentconfidenceinterval:
0.1432251 0.1930061
Por lo que el intervalo de confianza, a un nivel de confianza del 95% para la proporción de personas con los ojos azules en la población es (0.1432251 0.1930061).
Este resultado no es compatible la suposición de que dicha proporción vale 1/4, ya que 1/4 no pertenece al intervalo (0.1432251 0.1930061).
Resolvamos este ejercicio utilizando la expresión del intervalo de confianza para la proporción
\( \left [ p -z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}}, p + z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \right ] \)
Expresión 14: Intervalo de confianza para la proporción
Solución
Intervalo de confianza, a un nivel de confianza del 95% para la proporción de alumnos varones en la población
> alpha<- 0.05
> n = 900
> p = 150/900
> cuantil<- qnorm(1 – alpha/2)
> lim_inf<-p – cuantil * sqrt (p*(1 – p)) / sqrt (n)
> lim_inf
[1] 0.1423188
> lim_sup<-p + cuantil * sqrt (p*(1 – p)) / sqrt (n)
> lim_sup
[1] 0.1910145
Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes
Consideramos dos variables aleatorias independientes \( X_1 \) y \( X_2 \) con distribuciones normales de parámetros \( (\mu_1, \sigma_1) \) y \( (\mu_2, \sigma_2) \), respectivamente, de las que vamos a tomar muestras aleatorias independientes de tamaños \( n_1 \) y \( n_2 \), respectivamente.
Nuestro objetivo, en este caso, es obtener un intervalo de confianza para la diferencia de las medias de ambas distribuciones, es decir, para μ1 – μ2. Pero previo al cálculo de este intervalo, debemos determinar si las varianzas de ambas distribuciones o, equivalentemente, sus desviaciones típicas, σ1 y σ2, aun siendo desconocidas, pueden asumirse iguales o no. El cálculo del intervalo de confianza se realiza de forma diferente dependiendo de si las varianzas (desviaciones típicas) pueden asumirse iguales o no.
En primer lugar determinemos el Intervalo de confianza para el cociente de varianzas
Intervalo de confianza para el cociente de varianzas en dos poblaciones normales independientes
Para decidir si las varianzas de las dos distribuciones pueden asumirse iguales o no construiremos un intervalo de confianza para el cociente de ambos valores, esto es, para \( \sigma_1^{2}/\sigma_2^{2} \). En este caso, partimos de la variable aleatoria
\( F= \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \displaystyle \frac {\sigma_{2}^{2}} {\sigma_{1}^{2}} \)
Expresión 15: Expresión de la variable aleatoria para el cociente de varianzas
que sigue una distribución F de Snedecor con \( n_{1} – 1 \) grados de libertad en el numerador y \( n_{2} – 1 \) grados de libertad en el denominador. Los valores \( s_{1}^{2} \) y \( s_{2}^{2} \), en la expresión anterior, hacen referencia a las cuasivarianzas muestrales de la variable en el primer y el segundo grupo, respectivamente. Buscamos los valores de la variable F tales que
\( \left [ F_{n_{1}-1,n_{2}-1, α/2} \leq \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \displaystyle \frac {\sigma_{2}^{2}} {\sigma_{1}^{2}} \leq F_{n_{1}-1,n_{2}-1, 1-α/2} \right ] = 1- \alpha \)
Expresión 16: Obtención de los cuantiles F{ α/2} y F{1 – α/2}
O, equivalentemente,
\( \left [ \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1,1- α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \leq \displaystyle \frac {\sigma_{1}^{2}} {\sigma_{2}^{2}} \leq \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1, α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \right ] = 1- \alpha \)
Expresión 17: Obtención de los cuantiles F{ α/2} y F{1 – α/2}
De modo que el intervalo de confianza que buscamos es el formado por
\( \left ( \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1, 1-α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}}, \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1, α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \right ) \)
Expresión 18: Intervalo de confianza para el cociente de varianzas
En R, la función var.test se encarga de calcular este intervalo. Sus parámetros son los siguientes:
var.test(x, y, conf.level = 0.95)
siendo
- x : Vector numérico con los datos de la variable de interés en el primer grupo o muestra
- y : Vector numérico con los datos de la variable de interés en el segundo grupo o muestra
- conf.level: Valor numérico que indica el nivel de confianza, en tanto por uno, al que se construirá el intervalo. Si omitimos este parámetro en la llamada a la función, los intervalos de confianza se calculan a un nivel de confianza del 95%.
Una vez calculado el intervalo de confianza, si el valor 1 está incluido en dicho intervalo, podremos afirmar que las varianzas (y, consecuentemente, las desviaciones típicas) de ambas distribuciones pueden considerarse iguales. Si el 1 queda fuera del intervalo obtenido, las varianzas de las dos distribuciones se considerarán diferentes.
Supuesto Práctico 4
La siguiente tabla proporciona datos sobre la precipitación total registrada en 11 estaciones meteorológicas de dos provincias españolas. Suponiendo independencia y normalidad. Calcular un intervalo de confianza a un nivel de confianza del 80% para el cociente de varianzas en ambas poblaciones. ¿Puede asumirse que ambas varianzas son iguales?
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Prov_A & 100 & 89 & 84 & 120 & 130 & 105 & 60 & 70 & 90 & 108 & 130 \\ \hline Prov_B & 120 & 115 & 96 & 115 & 140 & 120 & 75 & 90 & 108 & 130 & 135 \\ \hline \end{array} \)
Tabla 1: Datos del Supuesto práctico 4
Solución
En primer lugar determinamos el intervalo de confianza para el cociente de varianzas, para ello utilizamos la función var.test. Lo primero que tenemos que hacer para aplicar la función var.test es separar en dos variables los datos relativos a las precipitaciones realizadas en cada provincia.
> Prov_A <- c(100, 89, 84, 120, 130, 105, 60, 70, 90, 108, 130)
> Prov_B <- c(120, 115, 96, 115, 140, 120, 75, 90, 108, 130, 135)
> Prov_A
[1] 100 89 84 120 130 105 60 70 90 108 130
> Prov_B
[1] 120 115 96 115 140 120 75 90 108 130 135
A continuación, utilizamos la función var.test tal y como se indica a continuación:
>var.test(Prov_A, Prov_B, conf.level = 0.80)
F test to compare two variances
data: Prov_A and Prov_B
F = 1.3474, num df = 10, denom df = 10, p-value = 0.6462
alternative hypothesis: true ratio of variances is not equal to 1
80 percent confidence interval:
0.5801448 3.1295847
sample estimates:
ratio of variances
1.347447
Analizando la información relativa al intervalo de confianza que se incluye en la salida de var.test, podemos afirmar que el intervalo de confianza a un nivel de confianza del 80% para el cociente de las varianzas de las dos distribuciones es (0.5801448, 3.1295847). Este intervalo de confianza contiene al valor 1, por lo que se puede suponer que las varianzas de las dos distribuciones son idénticas.
Una vez se ha determinado la igualdad (o desigualdad) de las varianzas de ambas distribuciones, procedemos a calcular el intervalo de confianza para la diferencia de las medias.
a) Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes cuando las varianzas poblacionales son desconocidas pero supuestas iguales
Si la varianzas poblacionales son desconocidas pero supuestas iguales, se parte de la variable aleatoria
\( T= \displaystyle \frac { ( \overline {X}_1- \overline {X}_2)-(μ_{1}-μ_{2}) } { \displaystyle \sqrt {\displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}}+ \displaystyle \frac {1} {n_{2}} } } \)
Expresión19: Expresión de la variable aleatoria para la diferencia de medias (varianzas iguales)
la cual se distribuye según una t de Student con \( n_1+n_2-2 \) grados de libertad. El cálculo del intervalo de confianza para la diferencia de medias se realiza obteniendo los valores de la distribución t de Student con \( n_1+n_2-2 \) grados de libertad que verifican
\( \left [-t_{n_1+n_2-2,1-\alpha/2} \leq \displaystyle \frac { ( \overline {X}_1- \overline {X}_2)-(μ_{1}-μ_{2}) } { \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}}+ \displaystyle \frac {1} {n_{2}} } } \leq t_{n_1+n_2-2,1-\alpha/2} \right ] = 1- \alpha \)
Expresión 20: Obtención del cuantil t{1 – α/2}
Al operar algebraicamente, tenemos que
\( \begin{array} {c} P \left [ ( \overline {X}_1- \overline {X}_2) -t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} \leq (μ_{1}-μ_{2}) \leq \\ \leq ( \overline {X}_1- \overline {X}_2) + t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} \right ] = 1- \alpha \\ \end{array} \)
Expresión 21: Obtención del cuantil t{1 – α/2}
De modo que el intervalo de confianza que buscamos es
\( \begin{array} {c} \left ( ( \overline {X}_1- \overline {X}_2) -t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} , \\ ( \overline {X}_1- \overline {X}_2) + t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} \right ) \\ \end{array} \)
Expresión 22: Intervalo de confianza para la diferencia de medias (varianzas iguales)
b) Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes cuando las varianzas poblacionales son desconocidas, distintas y tamaños muestrales grandes
Si las varianzas de las poblaciones son desconocidas y, además, distintas y tamaños muestrales grandes, se sigue un procedimiento similar al que acabamos de describir en el caso de igualdad de varianzas para la obtención del intervalo de confianza, partiendo de una variable aleatoria.
\( Z = \displaystyle \frac { (\overline {X}_1 – \overline {X}_2) (\mu_1- \mu_2) } { \displaystyle \sqrt{\displaystyle \frac {s_1^{2}}{n_1} + \displaystyle \frac {s_2^{2}}{n_2} } } \)
Expresión 23: Expresión de la variable aleatoria para la diferencia de medias (varianzas distintas y tamaños muestrales grandes)
De modo que el intervalo de confianza que buscamos es
\( (\overline {X}_1 – \overline {X}_2) – z_{1-\alpha/2} \displaystyle \sqrt{ \displaystyle \frac {s_1^{2}}{n_1} + \displaystyle \frac {s_2^{2}}{n_2} }, (\overline {X}_1 – \overline {X}_2) + z_{1-\alpha/2} \displaystyle \sqrt{ \displaystyle \frac {s_1^{2}}{n_1} + \displaystyle \frac {s_2^{2}}{n_2} } \)
Expresión 24: Intervalo de confianza para la diferencia de medias (varianzas distintas y tamaños muestrales grandes)
En R, la función t.test (que fue introducida y utilizada con anterioridad) se encarga de proporcionar intervalos de confianza para la diferencia de medias, tanto si las varianzas de la variable son iguales en los dos grupos como si no. Los parámetros de t.test presentan algunos cambios cuando la función se utiliza en un contexto de dos poblaciones:
t.test (x, y, var.equal = FALSE, conf.level = 0.95)
En este caso:
-
- x: Vector numérico que incluye los valores de la variable de interés en el primer grupo o muestra
- y: Vector numérico que incluye los datos de la variable de interés en el segundo grupo o muestra
- var.equal: Es un argumento lógico que indica si las varianzas de la variable en los dos grupos o muestras puede suponerse igual o no. Para establecer el valor de este parámetro nos basamos en la interpretación del intervalo de confianza que proporciona la función var.test. Por defecto, la función considera que las varianzas en los dos grupos son distintas.
La interpretación del intervalo de confianza resultante permitirá determinar si las medias poblacionales de las dos distribuciones pueden suponerse iguales o no. Así, si el intervalo contiene al valor 0, dichas medias podrán asumirse iguales. En cualquier otro caso, concluiremos que las medias son distintas en ambas distribuciones.
Supuesto Práctico 5
En vista de los resultados obtenidos en el supuesto práctico 4, y suponiendo que las precipitaciones registradas en 11 estaciones meteorológicas de dos provincias españolas se distribuyen de acuerdo a variables normales de medias y varianzas desconocidas. Obtener un intervalo de confianza al 80% para la diferencia del número medio de precipitaciones entre las dos provincias. ¿Puede suponerse que el número medio de precipitaciones de las dos provincias es igual?
Solución
Dado que en el supuesto práctico 4 se concluyó la igualdad de las varianzas del número de precipitaciones entre las dos provincias, debemos establecer a TRUE el valor del parámetro var.equal cuando realicemos la llamada a la función t.test.
> Prov_A <- c(100, 89, 84, 120, 130, 105, 60, 70, 90, 108, 130)
> Prov_B <- c(120, 115, 96, 115, 140, 120, 75, 90, 108, 130, 135)
> t.test(Prov_A, Prov_B, conf.level = 0.80, var.equal = TRUE)
Two Sample t-test
data: Prov_A and Prov_B
t = -1.5755, df = 20, p-value = 0.1308
alternative hypothesis: true difference in means is not equal to 0
80 percent confidence interval:
-26.446718 -2.280555
sample estimates:
mean of x mean of y
98.72727 113.09091
Atendiendo la información sobre el intervalo de confianza que se incluye entre los resultados
80 percent confidence interval:
-26.446718 -2.280555
Se puede afirmar que el intervalo de confianza a un 80% de confianza para la diferencia de las medias del número medio de precipitaciones entre las dos provincias es: ( -26.446718 , -2.280555). Como el 0 no está dentro de este intervalo, no se puede decir que ambas medias son idénticas.
Intervalo de confianza para la diferencia de medias en dos poblaciones normales relacionadas
Consideremos dos muestras aleatorias \( X_1,X_2, \cdots, X_n \) e \( Y_1,Y_2, \cdots, Y_n \) de tamaño \( n \) y relacionadas, de tal forma que la primera procede de una población \( N (\mu_1, \sigma_1) \) y la segunda de una población \( N (\mu_2, \sigma_2) \)
Antes de proporcionar el intervalo para la diferencia de medias de estas dos poblaciones, se hace necesario indicar qué se entiende por muestras relacionadas. Se dicen que dos muestras \( X_1,X_2, \cdots, X_n \) e \( Y_1,Y_2, \cdots, Y_n \) están relacionadas o apareadas cuando los datos de las muestras vienen por parejas, uno de cada una de ellas, de manera que cada individuo proporciona dos observaciones.
En los casos de muestras relacionadas, se utiliza nuevamente la función t.test para la obtención de intervalos de confianza, pero se ha de indicar que los datos que reciben como parámetros provienen de muestras relacionadas incluyendo en la llamada a la función el argumento lógico paired, cuyo valor debe establecerse a TRUE.
t.test (x, y, paired = TRUE, conf.level = 0.95)
Supuesto Práctico 6
Se desea comprobar el efecto de un fertilizante sobre la producción de los árboles frutales. Para ello se seleccionan aleatoriamente un grupo de 10 árboles y se toman los datos de la producción antes y después de tratar a los árboles con el fertilizante. Obtener un intervalo de confianza al 99% de confianza para la diferencia de medias de la producción antes y después.
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 25 & 20 & 25 & 28 & 30 & 30 & 26 & 15 & 18 & 22 \\ \hline Después & 30 & 25 & 28 & 29 & 30 & 31 & 24 & 22 & 25 & 27 \\ \hline \end{array} \)
Tabla 2: Tabla de datos del supuesto práctico 6
Solución
Como puede observarse, los datos vienen por parejas: producción antes y después (dos datos por árbol). Parece lógico que los datos se encuentren relacionados entre sí.
En primer lugar, vamos a introducir los datos en el Script de RStudio. Para ello definimos dos vectores
> Antes <- c(25, 20, 25, 28, 30, 30, 26, 15, 18, 22)
> Despues <- c(30, 25, 28, 29, 30, 31, 24, 22, 25, 27)
A partir de estos datos, vamos a aplicar la función t.test, para obtener el intervalo de confianza que buscamos.
>t.test(Antes, Despues, paired = TRUE, conf.level = 0.99)
Paired t-test
data: Antes and Despues
t = -3.2812, df = 9, p-value = 0.009511
alternative hypothesis: true difference in means is not equal to 0
99 percent confidence interval:
-6.36939969 -0.03060031
sample estimates:
mean of the differences
-3.2
Según los datos que se incluyen en la salida de la función, el intervalo de confianza al 99% de confianza para la diferencia de las medias es (-6.36939969, -0.03060031). Como el 0 no está contenido dentro de este intervalo, podemos afirmar que la diferencia entre las producciones medias de los árboles antes y después de seguir el tratamiento con el fertilizante es no nula o, equivalentemente, que ambos producciones medias no pueden suponerse iguales.
Intervalo de confianza para la diferencia de dos proporciones
Vamos a construir un intervalo de confianza para la diferencia de proporciones \( \pi_1-\pi_2 \). Para ello, consideramos dos muestras aleatorias \( X_1, X_2, \cdots, X_{n_{1}} \) e \( Y_1, Y_2, \cdots, Y_{n_{2}} \) de tamaño \( n_1 \) y \( n_2 \), independientes entre sí, extraídas de poblaciones con distribuciones binomiales \( B (1, \pi_1) \) y \( B (1, \pi_2) \), respectivamente.
Construimos, a continuación, un intervalo de confianza para la diferencia de proporciones \( \pi_1-\pi_2 \). Para ello, partimos de la variable aleatoria
\( Z = \displaystyle \frac { ( p_1 – p_2 ) -(\pi_1-\pi_2) } { \displaystyle \sqrt { \displaystyle \frac { p_1(1-p_1)}{n_1} + \displaystyle \frac {p_2 (1-p_2)}{n_2} }} \)
Expresión 25: Expresión de la variable aleatoria (diferencia de dos proporciones)
con \( p_1 \) y \( p_2 \) las proporciones de individuos que presentan la característica de interés en la primera y la segunda muestra, respectivamente. Esta variable aleatoria sigue una distribución normal de media 0 y desviación típica 1, por lo que debemos calcular los valores de la distribución normal estándar que verifican que
\( P \left [- z_{1-\alpha/2} \leq \displaystyle \frac { ( p_1 – p_2 ) -(\pi_1-\pi_2) } { \displaystyle \sqrt { \displaystyle \frac { p_1(1-p_1)}{n_1} + \displaystyle \frac {p_2 (1-p_2)}{n_2} }} \leq z_{1-\alpha/2} \right ] = 1- \alpha \)
Expresión 26: Obtención del cuantil z{1 – α/2}
O, lo que es lo mismo
\( \begin{array} {c} P \left [(p_1-p_2) – z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}} \leq \pi_1 – \pi_2 \leq \\ \leq (p_1-p_2) + z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}} \right ] = 1-\alpha \\ \end{array} \)
Expresión 27: Obtención del cuantil z{1 – α/2}
De modo que el intervalo de confianza buscado es
\( \left [(p_1-p_2) – z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}}, (p_1-p_2) + z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}} \right ] \)
Expresión 28: Intervalo de confianza para la diferencia de dos proporciones
Para calcular este intervalo en R o RStudio utilizaremos de nuevo la función prop.test, pero teniendo en cuenta que ahora contamos con dos muestras en lugar de una. Esto afecta (mínimamente) a la manera de definir los parámetros. La sintaxis de la función sigue siendo la misma:
prop.test(x, n, conf.level = 0.95)
donde:
- x: Vector de dimensión 2 que indica el número de elementos en cada grupo que presentan la característica de interés.
- n: Vector numérico de dimensión 2 que indica el número total de elementos del grupo.
- conf.level: Valor numérico que indica el nivel de confianza, en tanto por uno, al que se construirá el intervalo. Si omitimos este parámetro en la llamada a la función, los intervalos de confianza se calculan a un nivel de confianza del 95%.
Si el intervalo de confianza resultante incluye al 0 entre sus posibles valores, la diferencia entre ambas proporciones poblaciones podrá considerarse nula lo que equivale a decir que ambas proporciones son iguales.
Supuesto Práctico 7
Se realiza un estudio sobre en un grupo de personas de las que se les anota el número de Km en una caminata, el sexo y si hacen o no deporte. Para realizar dicho estudio se toma una muestra de 55 personas. Calcular un intervalo de confianza al 92% para la diferencia entre la proporción de hombres y de mujeres que practican deporte ¿Puede considerarse que ambas proporciones son iguales? Los datos correspondientes están en el fichero supuesto7.txt
Solución
En primer lugar, nos situamos en el directorio de trabajo
> setwd(“F:/Desktop/EJEMPLOSRS5”)
A continuación, sino tenemos importado el fichero de datos, debemos importarlo. Para ello, utilizamos la orden read.table
> datos <- read.table(“supuesto7.txt”, header = TRUE)
> datos
Km Sexo Deporte
1 10 H 0
2 21 H 0
3 13 M 1
4 3 M 0
5 11 H 0
6 26 H 0
7 10 H 0
8 3 M 1
9 5 M 1
10 8 M 0
11 6 M 1
12 28 M 1
13 16 H 0
14 12 M 1
15 14 M 0
16 10 H 1
………………………….
Una vez importado el fichero de datos, utilizamos el comando table para determinar cuántos hombres y cuantas mujeres practican deporte.
> table(datos$Sexo, datos$Deporte)
0 1
H 23 8
M 9 15
En total, 8 de los 31 hombres y 15 de las 24 mujeres muestreados practican deporte. Vamos a crear dos vectores con esta información:
- vector_Deport: Total de hombres y mujeres que practican deporte
- vector_Sexo:Total de hombres y mujeres en la muestra.
> vector_Deporte<- c(8, 15)
> vector_Deporte
[1] 8 15
> vector_Sexo<- c(31, 24)
> vector_Sexo
[1] 31 24
Es muy importante que los valores se introduzcan en el mismo orden en los dos vectores. A continuación podemos utilizar la función prop.test con estos dos vectores como argumentos.
> prop.test(vector_Deporte, vector_Sexo, conf.level = 0.92)
2-sample test for equality of proportions with continuity correction
data: vector_Deporte out of vector_Sexo
X-squared = 6.0536, df = 1, p-value = 0.01388
alternative hypothesis: two.sided
92 percent confidence interval:
-0.6249422 -0.1089287
sample estimates:
prop 1 prop 2
0.2580645 0.6250000
Según la salida de la función prop.test, el intervalo de confianza al 92% de confianza es (-0.6249422, -0.1089287). El 0 no está dentro de este intervalo, por lo que podemos concluir que las proporciones de hombres y mujeres que hacen deporte no coinciden.
Ejercicios
Ejercicios Guiados
Ejercicio Guiado1
La concentración media de dióxido de carbono en el aire en una cierta zona no es habitualmente mayor que 335 ppmv (partes por millon en volumen). Se sospecha que esta concentración es mayor en la capa de aire más próxima a la superficie. Se ha analizado el aire en 20 puntos elegidos aleatoriamente a una misma altura cerca del suelo, resultando los siguientes datos: 332, 320, 312, 270, 330, 354, 356, 310, 341, 313, 223, 224, 305, 321, 325, 333, 332, 345, 312, 331.
Construir un intervalo de confianza al 98% de confianza:
a) Si la concentración de dióxido de carbono se distribuye según una Normal de desviación típica σ = 120 ppmv
b) Si la concentración de dióxido de carbono se distribuye según una Normal de desviación típica desconocida.
Ejercicio Guiado 2
Con el fin de estudiar el efecto de los rayos X sobre la viabilidad huevo-larva en Tribolium casteneum, se irradiaron 1000 huevos de los que resultaron 572 larvas. Calcular un intervalo de confianza para la proporción de larvas en huevos irradiados al nivel de confianza del 95%.
Ejercicio Guiado 3
Para realizar un estudio de la concentración de una hormona en una solución vamos a utilizar dos métodos. Disponemos de 10 dosis preparadas en el laboratorio y medimos la concentración de cada una con los dos métodos. Se obtienen los siguientes resultados:
Suponiendo normalidad e independencia. Se pide:
a) Calcular un intervalo de confianza al nivel 0.9 para el cociente de varianzas
b) Calcular un intervalo de confianza al nivel 0.9 para la diferencia de concentraciones medias.
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Dosis & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline Método \hspace{.1cm} A & 10.7 & 11.2 & 15.3 & 14.9 & 13.9 & 15 & 15.6 & 15.7 & 14.3 & 10.8 \\ \hline Método \hspace{.1cm} B & 11.1 & 11.4 & 15 & 15.1 & 14.3 & 15.4 & 15.4 & 16 & 14.3 & 11.2 \\ \hline \end{array} \)
Tabla 3: Datos del Ejercicio guiado 3
Ejercicio Guiado 4
En una unidad del sueño se está probando con un nuevo somnífero. Para comprobar su eficacia se toman 10 individuos al azar, un día no se les suministra el somnífero y se les comprueba el número de horas de sueño, al día siguiente se les suministra y se vuelve a comprobar las horas de sueño. Los resultados entes y después del tratamiento han sido los siguientes:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 7.3 & 8.2 & 6.3 & 5.2 & 6.9 & 5.8 & 5.3 & 7.1 & 6.9 & 8.1 \\ \hline Después & 8.2 & 7.9 & 6.4 & 5.1 & 7.1 & 6.3 & 5.9 & 8.2 & 7.1 & 7.7 \\ \hline \end{array} \)
Tabla 4: Datos del Ejercicio guiado 4
Calcular un intervalo de confianza, al 96% de confianza para la diferencia del número medio de horas de sueño antes y después del tratamiento.
Ejercicio Guiado 5
Unos estudios sobre las ranas tigres en dos regiones de Méjico tienen como objetivo comparar las proporciones de dichas ranas en cada una de las regiones. Para ello se toma una muestra al azar de 100 ranas observando que 5 son ranas tigres en la zona A, mientras que de una muestra de 150 ranas en la zona B, 9 son ranas tigres. Construir un intervalo de confianza al 95% y al 98% para la diferencia entre las verdaderas proporciones de ranas tigres en la dos regiones. ¿Puede suponerse que la proporción de ranas tigres es igual en ambas regiones?
Ejercicio Guiado 6
Para estudiar la audiencia de un programa de televisión, se ha medido el número de personas que ven el programa en diferentes días. Los datos del número de personas (en miles) son los siguientes: 521, 742, 593, 635, 788, 717, 606, 639, 666, 624. Suponiendo normalidad. Se pide:
a) Obtener estimaciones puntuales de la audiencia media y de la varianza
b) Construir un intervalo de confianza para la audiencia media
c) Construir un intervalo de confianza para la varianza.
Ejercicio Guiado 1 (Resuelto)
La concentración media de dióxido de carbono en el aire en una cierta zona no es habitualmente mayor que 335 ppmv (partes por millon en volumen). Se sospecha que esta concentración es mayor en la capa de aire más próxima a la superficie. Se ha analizado el aire en 20 puntos elegidos aleatoriamente a una misma altura cerca del suelo, resultando los siguientes datos: 332, 320, 312, 270, 330, 354, 356, 310, 341, 313, 223, 224, 305, 321, 325, 333, 332, 345, 312, 331.
Construir un intervalo de confianza al 95% y 98% de confianza:
a) Si la concentración de dióxido de carbono se distribuye según una Normal de desviación típica σ = 120 ppmv
b) Si la concentración de dióxido de carbono se distribuye según una Normal de desviación típica desconocida.
Solución:
En primer lugar, introducimos, en un vector, los datos de las 20 concentraciones observadas y en segundo lugar introducimos el dato relativo al nivel de significación
>concentraciones<- c(332, 320, 312, 270, 330, 354, 356, 310, 341, 313, 223, 224, 305, 321, 325, 333, 332, 345, 312, 331)
>alpha<- 0.05
a) Si la concentración de dióxido de carbono se distribuye según una Normal de desviación típica σ = 120 ppmv
Tenemos que obtener un intervalo de confianza para la media con varianza conocida
\( \left [ \overline {X} – z_{1-α/2} \displaystyle \frac { \sigma} { \sqrt{n}} , \overline {X} + z_{1-α/2} \displaystyle \frac { \sigma} { \sqrt{n}} \right] \)
Expresión 29: Expresión del Intervalo de confianza para la media (varianza conocida)
En este primer caso, y dado que conocemos la desviación típica poblacional, debemos calcular manualmente los límites inferior y superior del intervalo.
Así, calculamos la media muestral y el cuantil que intervienen en dicho intervalo.
> n <- length(concentraciones)
> media <- mean(concentraciones)
>cuantil<- qnorm(1 – alpha/2)
Introducimos el dato de la desviación típica
>desv_tipica<- 120
A continuación calculamos el límite inferior y superior del intervalo pedido.
>lim_inf<- media – cuantil * desv_tipica / sqrt(n)
>lim_inf
[1] 261.8586
>lim_sup<- media + cuantil * desv_tipica / sqrt(n)
>lim_sup
[1] 367.0414
Por lo que el intervalo de confianza al 95% para la concentración de dióxido de carbono es (261.8586 , 367.0414).
>alpha<- 0.02
>cuantil<- qnorm(1 – alpha/2)
>lim_inf<- media – cuantil * desv_tipica / sqrt(n)
>lim_inf
[1] 252.0275
>lim_sup<- media + cuantil * desv_tipica / sqrt(n)
>lim_sup
[1] 376.8725
Por lo que el intervalo de confianza al 98% para la concentración de dióxido de carbono es (252.0275 , 376.8725).
b) Si la concentración de dióxido de carbono se distribuye según una Normal de desviación típica desconocida.
Hay que obtener un intervalo de confianza cuando la desviación típica es desconocida. Para ello, usamos la función t.test
>t.test(concentraciones)
One Sample t-test
data: concentraciones
t = 38.589, df = 19, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
297.3944 331.5056
sample estimates:
mean of x
314.45
> t.test(concentraciones, conf.level = 0.98)
One Sample t-test
data: concentraciones
t = 38.589, df = 19, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
98 percent confidence interval:
293.7563 335.1437
sample estimates:
mean of x
314.45
En este segundo caso, el intervalo de confianza para la concentración de dióxido de carbono, al 95% y 98% de confianza, es (297.3944, 331.5056) y (293.7563, 335.1437), respectivamente
Ejercicio Guiado2 (Resuelto)
Con el fin de estudiar el efecto de los rayos X sobre la viabilidad huevo-larva en Tribolium casteneum, se irradiaron 1000 huevos de los que resultaron 572 larvas. Calcular un intervalo de confianza para la proporción de larvas en huevos irradiados al nivel de confianza del 95%.
Solución:
Para obtener un intervalo de confianza para la proporción poblacional, se utiliza la función prop.test. Disponemos tanto del número de huevos que presentan la característica de interés (de los que resultaron larvas) como del número total de huevos en la muestra, de manera que podemos realizar la llamada a la función tal y como sigue:
>prop.test(572, 1000)
1-sample proportions test with continuity correction
data: 572 out of 1000, null probability 0.5
X-squared = 20.449, df = 1, p-value = 6.124e-06
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.5406126 0.6028273
sample estimates:
p
0.572
El intervalo de confianza para la proporción poblacional de huevos conformes al 95% de confianza es (0.5406126, 0.6028273).
Ejercicio Guiado3 (Resuelto)
Para realizar un estudio de la concentración de una hormona en una solución vamos a utilizar dos métodos. Disponemos de 10 dosis preparadas en el laboratorio y medimos la concentración de cada una con los dos métodos. Se obtienen los siguientes resultados:
Suponiendo normalidad e independencia. Se pide:
a) Calcular un intervalo de confianza al nivel 0.9 para el cociente de varianzas
b) Calcular un intervalo de confianza al nivel 0.9 para la diferencia de concentraciones medias.
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Dosis & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline Método \hspace{.1cm} A & 10.7 & 11.2 & 15.3 & 14.9 & 13.9 & 15 & 15.6 & 15.7 & 14.3 & 10.8 \\ \hline Método \hspace{.1cm} B & 11.1 & 11.4 & 15 & 15.1 & 14.3 & 15.4 & 15.4 & 16 & 14.3 & 11.2 \\ \hline \end{array} \)
Tabla 3: Datos del Ejercicio guiado 3
Solución:
En primer lugar introducimos, en el Script de RStudio, en dos vectores los los datos:
> MetodoA <- c(10.7, 11.2, 15.3, 14.9, 13.9, 15, 15.6, 15.7, 14.3, 10.8)
> MetodoB <- c(11.1, 11.4, 15, 15.1, 14.3, 15.4, 15.4, 16, 14.3, 11.2)
a) Calcular un intervalo de confianza al nivel 0.9 para el cociente de varianzas
Para calcular el intervalo de confianza para el cociente de varianza utilizamos la función var.test.
>var.test(MetodoA, MetodoB, conf.level = 0.90)
F test to compare two variances
data: MetodoA and MetodoB
F = 1.1229, num df = 9, denom df = 9, p-value = 0.8657
alternative hypothesis: true ratio of variances is not equal to 1
90 percent confidence interval:
0.3532441 3.5696591
sample estimates:
ratio of variances
1.122925
Según los resultados de var.test, el intervalo de confianza al 90% de confianza para el cociente de las varianzas de la variable en ambos métodos es ( 0.3532441, 3.5696591), que contiene al 1. Por tanto, podemos asumir que ambas varianzas son iguales en ambos métodos.
b) Calcular un intervalo de confianza al nivel 0.9 para la diferencia de concentraciones medias.
En el apartado anterior hemos obtenido que las varianzas son iguales en los dos métodos, por lo tanto, tenemos que obtener un intervalo de confianza para la diferencia de medias de dos poblaciones cuando las varianzas de ambas poblaciones son iguales. Para ello, utilizamos la función t.test y ponemos var.equal = TRUE
>t.test(MetodoA, MetodoB, var.equal = TRUE, conf.level = 0.90)
Two Sample t-test
data: MetodoA and MetodoB
t = -0.20323, df = 18, p-value = 0.8412
alternative hypothesis: true difference in means is not equal to 0
90 percent confidence interval:
-1.715841 1.355841
sample estimates:
mean of x mean of y
13.74 13.92
El intervalo de confianza, al 90% de confianza, para la diferencia de medias de las concentraciones de un hormona en ambos métodos es ( -1.715841, 1.355841), que ontiene al 0, por lo que podemos concluir que la cantidad media de concentración de una hormona en una solución en ambos métodos es la misma.
Ejercicio Guiado 4 (Resuelto)
En una unidad del sueño se está probando con un nuevo somnífero. Para comprobar su eficacia se toman 10 individuos al azar, un día no se les suministra el somnífero y se les comprueba el número de horas de sueño, al día siguiente se les suministra y se vuelve a comprobar las horas de sueño. Los resultados entes y después del tratamiento han sido los siguientes:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 7.3 & 8.2 & 6.3 & 5.2 & 6.9 & 5.8 & 5.3 & 7.1 & 6.9 & 8.1 \\ \hline Después & 8.2 & 7.9 & 6.4 & 5.1 & 7.1 & 6.3 & 5.9 & 8.2 & 7.1 & 7.7 \\ \hline \end{array} \)
Tabla 4: Datos del Ejercicio guiado 4
Calcular un intervalo de confianza, al 96% de confianza para la diferencia del número medio de horas de sueño antes y después del tratamiento.
Solución:
En primer lugar introducimos los datos, en el Script RStudio, en dos vectores.
> Antes <- c(7.3, 8.2, 6.3, 5.2, 6.9, 5.8, 5.3, 7.1, 6.9, 8.1)
> Despues<- c(8.2, 7.9, 6.4, 5.1, 7.1, 6.3, 5.9, 8.2, 7.1, 7.7)
Estos datos son un claro ejemplo de datos pareados, ya que a los mismos individuos se les ha comprobado las horas de sueño antes y después del tratamiento. Por lo que tenemos que obtener un intervalo de confianza para la diferencia de medias de dos poblaciones normales relacionadas. Para ello, realizamos la llamada a la función t.test, sin olvidar indicar mediante el parámetro paired la relación que existe entre los conjuntos de datos.
>t.test(Antes, Despues, paired = TRUE, conf.level = 0.96)
Paired t-test
data: Antes and Despues
t = -1.7925, df = 9, p-value = 0.1066
alternative hypothesis: true difference in means is not equal to 0
96 percent confidence interval:
-0.65464846 0.09464846
sample estimates:
mean of the differences
-0.28
El intervalo de confianza, al 96% de confianza, para la diferencia del número medio de horas de sueño antes y después del tratamiento es ( -0.65464846 0.09464846). Este intervalo contiene al 0, por lo que podemos concluir que el número de horas de sueño antes y después del tratamiento pueden considerarse iguales, poniendo así en duda la efectividad del somnífero.
Ejercicio Guiado 5 (Resuelto)
Unos estudios sobre las ranas tigres en dos regiones de Méjico tienen como objetivo comparar las proporciones de dichas ranas en cada una de las regiones. Para ello se toma una muestra al azar de 100 ranas observando que 5 son ranas tigres en la zona A, mientras que de una muestra de 150 ranas en la zona B, 9 son ranas tigres. Construir un intervalo de confianza al 95% y al 98% para la diferencia entre las verdaderas proporciones de ranas tigres en la dos regiones. ¿Puede suponerse que la proporción de ranas tigres es igual en ambas regiones?
Solución:
En este caso debemos utilizar la función prop.test para calcular el intervalo de confianza para la diferencia de proporciones. Pero primero, debemos crear un vector que indique el número de ranas tigres en cada región así como un segundo vector con el número total de ranas en cada región.
>ranastigres<- c(5, 9)
>ranas<- c(100, 150)
Una vez hecho esto, llamamos a la función prop.test, indicando el nivel de confianza adecuado.
>prop.test(ranastigres, ranas)
2-sample test for equality of proportions with continuity correction
data: ranastigres out of ranas
X-squared = 0.0031527, df = 1, p-value = 0.9552
alternative hypothesis: two.sided
95 percent confidence interval:
-0.07550922 0.05550922
sample estimates:
prop 1 prop 2
0.05 0.06
Según los resultados que proporciona prop.test, el intervalo de confianza para la diferencia de proporciones que buscamos es (-0.07550922, 0.05550922), que contiene al 0, por lo que se puede afirmar que la proporción de ranas tigres es igual en ambas regiones con una confianza del 95%.
> prop.test(ranastigres, ranas, conf.level = 0.98)
2-sample test for equality of proportions with continuity correction
data: ranastigres out of ranas
X-squared = 0.0031527, df = 1, p-value = 0.9552
alternative hypothesis: two.sided
98 percent confidence interval:
-0.08619733 0.06619733
sample estimates:
prop 1 prop 2
0.05 0.06
El intervalo de confianza al 98% es ( -0.08619733, 0.06619733), que como el caso anterior contiene al cero y por lo tanto se se puede afirmar que la proporción de ranas tigres es igual en ambas regiones con una confianza del 98%.
Ejercicio Guiado 6 (Resuelto)
Para estudiar la audiencia de un programa de televisión, se ha medido el número de personas que ven el programa en diferentes días. Los datos del número de personas (en miles) son los siguientes: 521, 742, 593, 635, 788, 717, 606, 639, 666, 624. Suponiendo normalidad. Se pide:
a) Obtener estimaciones puntuales de la audiencia media y de la varianza
b) Construir un intervalo de confianza al 98% para la audiencia media
c) Construir un intervalo de confianza al 95% para la varianza.
Solución:
a) Obtener estimaciones puntuales de la audiencia media y de la varianza
En primer lugar introducimos los datos en el Script de RStudio
> datos <- c(521, 742, 593, 635, 788, 717, 606, 639, 666, 624)
> datos
[1] 521 742 593 635 788 717 606 639 666 624
Estimación puntual de la media
> media <- mean(datos)
> media
[1] 653.1
Estimación puntual de la varianza
> varianza <- var(datos)
> varianza
[1] 6111.656
b) Construir un intervalo de confianza al 98% para la audiencia media
Para construir un intervalo de confianza para la media con varianza desconocida utilizamos la función t.test(x, conf.level = 0.98)
> t.test(datos, conf.level = 0.98)
One Sample t-test
data: datos
t = 26.418, df = 9, p-value = 7.709e-10
alternative hypothesis: true mean is not equal to 0
98 percent confidence interval:
583.3491 722.8509
sample estimates:
mean of x
653.1
El intervalo pedido es (583.3491, 722.8509)
c) Construir un intervalo de confianza al 95% para la varianza
El intervalo de confianza que debemos calcular es
\( \left ( \displaystyle \frac {(n-1) \sigma^{2}}{ \chi^{2}_{1- \alpha/2, n-1 }}, \displaystyle \frac {(n-1) \sigma^{2}}{ \chi^{2}_{alpha/2, n-1 } } \right ) \)
Expresión 30: Expresión del Intervalo de confianza para la varianza (media conocida)
Nota: R no incluye una función específica para el cálculo de intervalos de confianza en este tipo de situaciones. Por lo tanto calcularemos el intervalo de la siguiente forma
> n <- length(datos)
> alfa <- 0.05
> L1 <- (n – 1) * varianza / qchisq(1-alfa / 2,n – 1)
> L2 <- (n – 1) * varianza / qchisq(alfa /2,n – 1)
> IC <- c(L1,L2)
> IC
[1] 2891.53 20369.25
El intervalo de confianza pedido es: (20369.25, 2891.53)
Ejercicios Propuestos
Ejercicio Propuesto 1
Una compañía contrata 10 tubos con filamentos del tipo A y 12 tubos con filamentos del tipo B. Las duraciones medias observadas se muestran en la siguiente tabla:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline Tipo \hspace{.1cm} A & 1614 & 1094 & 1293 & 1643 & 1466 & 1270 & 1340 & 1380 & 1081 & 1497 & \\ \hline Tipo \hspace{.1cm} B & 1383 & 1138 & 1092 & 1143 & 1017 & 1061 & 1627 & 1021 & 1711 & 1065 & 1162 & 1698 \\ \hline \end{array} \)
Tabla 5: Datos del Ejercicio propuesto 1
Obtener los siguientes intervalos de confianza a un nivel del 99%
a) Para la duración media de los tubos
a1) del tipo A si la desviación típica σ = 203.25
a2) del tipo B si la desviación típica σ = 272.56
b) Para la duración media de los tubos del tipo A y de los tubos del tipo B
c) Para la diferencia entre las duraciones medias de los tubos del tipo A y del tipo B.
Ejercicio Propuesto 2
Se diseñó un programa de ejercicios regulares, moderadamente activos, para someter a individuos que habían sufrido previamente un infarto, para comprobar si el programa podría beneficiar a estos pacientes. Se eligieron al azar once individuos que habían sufrido previamente un infarto. A estos individuos se les determinó, antes de empezar el programa, la capacidad de trabajo de cada uno midiendo el tiempo que tardó en alcanzar una frecuencia de 160 latidos por minuto mientras caminaba sobre una cinta sin fin. Después de 25 semanas de ejercicio controlado, se repitieron las medidas a los mismos individuos en la cinta sin fin y se registró el tiempo para cada sujeto. En la siguiente tabla se muestra el tiempo que tarda cada individuo antes y después del experimento
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 7.3 & 8.9 & 8.4 & 9.6 & 6.5 & 7.8 & 9.2 & 10.2 & 6.7 & 6.9 \\ \hline Después & 4.5 & 5.7 & 7.8 & 7.3 & 3.5 & 5.3 & 6.4 & 7.2 & 6.9 & 5.6 \\ \hline \end{array} \)
Tabla 6: Datos del Ejercicio propuesto 2
Obtener un intervalo de confianza al 98% para la diferencia de los tiempos medios que tardan los sujetos sobre la cinta sin fin antes y después del experimento.
Ejercicio Propuesto 3
En una piscifactoría hay una proporción desconocida de peces de una especie A. Para obtener información sobre la proporción se sacan 145 peces de los cuales 29 son del tipo A. Estimar dicha proporción mediante un intervalo de confianza al nivel de confianza 0.95. ¿Son compatibles estos resultados con la suposición de que dicha proporción vale 1/5?
Ejercicio Propuesto 4
Se estudian dos procedimientos de fabricación de pistones. Una muestra al azar de 100 pistones producidos por el primer procedimiento contiene 5 defectuosos mientras que una muestra de 150 pistones fabricados con el segundo procedimiento contiene 9 defectuosos. Construir un intervalo de confianza al 99% para la diferencia entre las verdaderas proporciones de defectuosos en los dos procedimientos.
Ejercicio Propuesto 1(Resuelto)
Una compañía contrata 10 tubos con filamentos del tipo A y 12 tubos con filamentos del tipo B. Las duraciones medias observadas se muestran en la siguiente tabla:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline Tipo \hspace{.1cm} A & 1614 & 1094 & 1293 & 1643 & 1466 & 1270 & 1340 & 1380 & 1081 & 1497 & \\ \hline Tipo \hspace{.1cm} B & 1383 & 1138 & 1092 & 1143 & 1017 & 1061 & 1627 & 1021 & 1711 & 1065 & 1162 & 1698 \\ \hline \end{array} \)
Tabla 5: Datos del Ejercicio propuesto 1
Obtener los siguientes intervalos de confianza a un nivel del 99%
a) Para la duración media de los tubos
a1) del tipo A si la desviación típica σ = 203.25
a2) del tipo B si la desviación típica σ = 272.56
b) Para la duración media de los tubos del tipo A y de los tubos del tipo B
c) Para la diferencia entre las duraciones medias de los tubos del tipo A y del tipo B.
Solución:
a) Obtener un intervalo de confianza a un nivel del 99%
a1) Para la duración media de los tubos del tipo A si la desviación típica σ = 203.25
a2) Para la duración medialos tubos del tipo B si la desviación típica σ = 272.56.
a1) El intervalo de confianza al 99% para la duración media de los tubos del tipo A es (1202.243 1533.357).
a2) El intervalo de confianza al 99% para la duración media de los tubos del tipo B es (1057.164, 1462.503).
b) Para la duración media de los tubos del tipo A y de los tubos del tipo B
Intervalo pedido para el tipo A: (1169.235, 1566.365)
Intervalo pedido para el tipo B: (1017.253, 1502.414)
c) Para la diferencia entre las duraciones medias de los tubos del tipo A y del tipo B.
El intervalo de confianza resultante es (-183.0579, 398.9913), dicho intervalo contiene al 0, por lo que podemos concluir que la duración de los filamentos del tipo A y B es la misma.
Solución del Ejercicio propuesto 1
Ejercicio Propuesto 2 (Resuelto)
Se diseñó un programa de ejercicios regulares, moderadamente activos, para someter a individuos que habían sufrido previamente un infarto, para comprobar si el programa podría beneficiar a estos pacientes. Se eligieron al azar once individuos que habían sufrido previamente un infarto. A estos individuos se les determinó, antes de empezar el programa, la capacidad de trabajo de cada uno midiendo el tiempo que tardó en alcanzar una frecuencia de 160 latidos por minuto mientras caminaba sobre una cinta sin fin. Después de 25 semanas de ejercicio controlado, se repitieron las medidas a los mismos individuos en la cinta sin fin y se registró el tiempo para cada sujeto. En la siguiente tabla se muestra el tiempo que tarda cada individuo antes y después del experimento
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 7.3 & 8.9 & 8.4 & 9.6 & 6.5 & 7.8 & 9.2 & 10.2 & 6.7 & 6.9 \\ \hline Después & 4.5 & 5.7 & 7.8 & 7.3 & 3.5 & 5.3 & 6.4 & 7.2 & 6.9 & 5.6 \\ \hline \end{array} \)
Tabla 6: Datos del Ejercicio propuesto 2
Obtener un intervalo de confianza al 98% para la diferencia de los tiempos medios que tardan los sujetos sobre la cinta sin fin antes y después del experimento.
Solución:
El intervalo de confianza para la diferencia de los tiempos medios que tardan los sujetos sobre la cinta sin fin antes y después del experimento, a un nivel del 98%, es (1.092016, 3.167984). Como el intervalo de confianza no contiene el 0 podemos deducir que existen diferencias significativas entre las medias. Se puede apreciar que el tiempo que tardan en la cinta sin fin es menor después del tratamiento.
Solución del Ejercicio Propuesto 2
Ejercicio Propuesto 3 (Resuelto)
En una piscifactoría hay una proporción desconocida de peces de una especie A. Para obtener información sobre la proporción se sacan 145 peces de los cuales 29 son del tipo A. Estimar dicha proporción mediante un intervalo de confianza al nivel de confianza 0.95 ¿Son compatibles estos resultados con la suposición de que dicha proporción vale 1/5?
Solución:
El intervalo de confianza pedido es (0.1400633, 0.2762259). Este resultado si es compatible con la suposición de que dicha proporción vale 1/5, ya que 1/5 pertenece al intervalo.
Solución del Ejercicio Propuesto 3
Ejercicio Propuesto 4 (Resuelto)
Se estudian dos procedimientos de fabricación de pistones. Una muestra al azar de 100 pistones producidos por el primer procedimiento contiene 5 defectuosos mientras que una muestra de 150 pistones fabricados con el segundo procedimiento contiene 9 defectuosos. Construir un intervalo de confianza al 99% para la diferencia entre las verdaderas proporciones de defectuosos en los dos procedimientos.
Solución:
El intervalo de confianza para la diferencia de proporciones de los dos procedimientos al 99% es (-0.09347518 0.07347518).
Solución del Ejercicio Propuesto 4
Autora: Ana María Lara Porras. Universidad de Granada. (2017).
Reformulado con MathML en 2021 por Ana María Lara Porras