INTERVALOS DE CONFIANZA
Objetivos
- Calcular e interpretar intervalos de confianza para la media en una población Normal con varianza conocida
- Calcular e interpretar intervalos de confianza para la media en una población Normal con varianza desconocida
- Calcular e interpretar intervalos de confianza para la proporción
- Calcular e interpretar intervalos de confianza para la diferencia de medias en dos poblaciones normales independientes con varianzas desconocidas
Suponiendo que las varianzas, aun siendo desconocidas, son iguales en las dos poblaciones
Suponiendo que las varianzas son diferentes en las dos poblaciones - Calcular e interpretar intervalos de confianza para la diferencia de medias en dos poblaciones normales relacionadas
- Calcular e interpretar intervalos de confianza para la diferencia de proporciones.
Introducción
El objetivo de la estimación mediante intervalos de confianza o estimación confidencial es la determinación de dos valores, \( \theta_{1}^{*} \) y \( \theta_{2}^{*} \), que verifiquen \( \theta_{1}^{*} < \theta_{2}^{*} \), tales que, al constituirse en intervalo \( ( \theta_{1}^{*} , \theta_{2}^{*} ) \) contengan, con una probabilidad prefijada, el verdadero valor del parámetro que deseamos estimar. De forma gráfica, un intervalo de confianza puede representarse del siguiente modo:
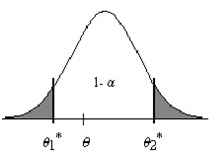 Figura 1: Representación gráfica de un I.C. Figura 1: Representación gráfica de un I.C. |
\( P [ \theta_{1}^{*} \leq \theta \leq \theta_{2}^{*}] = 1-\alpha \), para algún \( \alpha > 0 \), entonces se puede decir que \( \theta_{1}^{*} \) y \( \theta_{2}^{*} \) determinan un intervalo que tiene la probabilidad \( 1 – α \) de contener al parámetro poblacional \( \theta \) |
donde
- \( 1 – \alpha \): Recibe el nombre de coeficiente de confianza o nivel de confianza. Es la probabilidad de que el intervalo de confianza contenga el verdadero valor del parámetro poblacional \( θ \)
- \( \alpha \): Es un valor comprendido entre 0 y 1, \( 0 < α < 1 \), (usualmente próximo a 0), que indica el riesgo de que el intervalo de confianza no contenga el valor del parámetro poblacional a estimar, \( θ \). Por lo que \( α \) recibe el nombre de riesgo del error del intervalo, nivel del error del intervalo o nivel de significación del intervalo.
- \( \theta _{1}^{*} \) y \( \theta _{2}^{*} \): Son los valores que delimitan el intervalo de confianza y reciben el nombre de límite superior y límite inferior del intervalo, respectivamente. La diferencia entre el límite superior y el límite inferior de un intervalo, \( \theta _{2}^{*} – \theta _{1}^{*} \) se conoce como amplitud del intervalo.
Para la construcción de un intervalo de confianza, lo deseable es maximizar el nivel de confianza asociado al intervalo o equivalentemente minimizar el nivel de significación y conseguir una amplitud lo más pequeña posible.
Intervalo de confianza para la media en una población normal con varianza conocida
El intervalo de confianza para la media de una variable continua con el valor de la varianza de dicha variable conocida en toda la población es el intervalo menos usual.
Para estimar la media poblacional \( \mu \) de una población Normal de media \( \mu \) (desconocida) y de varianza \( \sigma^{2} \) (conocida), \( N(\mu, \sigma^{2}) \), se selecciona una muestra aleatoria \( X_1, X_2, \cdots, X_n \); de tamaño \( n \) de valores de una variable aleatoria de esta población y se calcula su media muestral, como mejor estimador puntual de \( \mu \). La construcción del intervalo de confianza se hace tomando como base este estimador. Para calcular un intervalo de confianza para \( \mu \) partimos de la variable aleatoria
\( Z= \displaystyle \frac {\overline{X}-μ }{ σ / \sqrt {n}} \)
Expresión 1: Expresión de la variable aleatoria
que sigue una distribución normal de media 0 y desviación típica 1. Buscamos los cuantiles de esta distribución tales que
\( P \left [ – z_{1- α/2} \leq \displaystyle \frac {\overline{X}-μ }{σ / \sqrt {n}} \leq z_{1-α/2} \right] = 1-α \)
Expresión 2: Obtención del cuantil z{1 – α/2}
O, equivalentemente,
\( P \left [ \overline {X} – z_{1-α/2} \displaystyle \frac { σ} { \sqrt{n }} \leq μ \leq \overline {X} + z_{1-α/2} \displaystyle \frac { σ} { \sqrt{n}} \right] = 1-α \)
Expresión 3: Obtención del cuantil z{1 – α/2}
Por lo tanto, el intervalo de confianza que debemos calcular es
\( \left [ \overline {X} – z_{1-α/2} \displaystyle \frac { \sigma} { \sqrt{n}} , \overline {X} + z_{1-α/2} \displaystyle \frac { \sigma} { \sqrt{n}} \right] \)
Expresión 4: Intervalo de confianza (varianza conocida)
Nota: R no incluye una función específica para el cálculo de intervalos de confianza en este tipo de situaciones. Aun así, pueden calcularse de una forma muy sencilla como se muestra en el siguiente ejemplo.
Supuesto Práctico 1
Con el fin de estudiar el número medio de flexiones continuadas que pueden realizar los alumnos, un profesor de educación física somete a 75 de ellos, elegidos aleatoriamente, a una prueba. El número de flexiones realizado por cada alumno, así como su sexo y si realizan o no deporte se muestran en el fichero Flexiones.txt.
Se sabe que el número de flexiones se distribuye según una Normal de varianza poblacional 7.5. ¿Determinar el intervalo de confianza a un nivel de confianza del 95% para el número medio de flexiones?
Solución
En primer lugar debemos importar, en R, los datos que contienen el número de flexiones realizadas por cada alumno. Para ello, utilizamos la orden read.table
> datos <- read.table(“F:/Flexiones.txt”, header = TRUE)
> datos
Flexiones Sexo Deporte
1 60 H 0
2 41 H 0
3 53 M 1
4 53 M 0
5 41 H 0
6 56 H 0
7 50 H 0
8 53 M 1
9 50 M 1
10 48 M 0
……………………………
A continuación, introducimos en R los datos relativos al nivel de significación y la varianza poblacional de la variable que proporciona el enunciado.
> alpha<- 0.05
> varianza <- 7.5
Calculamos por separado cada uno de los elementos restantes que necesitamos para obtener el intervalo de confianza.
> n <- nrow(datos)
> media <- mean(datos$Flexiones)
>cuantil<- qnorm(1 – alpha/2)
Por último, calculamos los extremos inferior y superior del intervalo de acuerdo a la expresión que se vio anteriormente:
Por tanto:
>lim_inf<-media – cuantil * sqrt(varianza) / sqrt(n)
>lim_inf
[1] 49.48687
>lim_sup<- media + cuantil * sqrt(varianza) / sqrt(n)
>lim_sup
[1] 50.72646
Por lo que el intervalo de confianza que buscamos es (49.48687, 50.72646).
Intervalo de confianza para la media en una población normal con varianza desconocida
Supongamos, en este caso, que la varianza poblacional de la variable de interés es desconocida. Nuestro objetivo sigue siendo el cálculo de un intervalo de confianza para la media de dicha variable.
Supongamos una muestra aleatoria \( X_1, X_2, \cdots, X_n \); de tamaño \( n \) de valores de la variable aleatoria que sigue una distribución Normal de media \( \mu \) y de varianza \( \sigma^{2} \), ambas desconocidas. Para calcular un intervalo de confianza, en este caso, partimos de la variable aleatoria
\( T= \displaystyle \frac {\overline{X}-μ }{s / \sqrt {n}} \)
Expresión 5: Expresión de la variable aleatoria
que sigue una distribución \( t \) de Student con \( n-1 \) grados de libertad. En la fórmula anterior, \( s \) hace referencia a la cuasidesviación típica muestral.
Tenemos que buscar dos valores de esta distribución tales que
\( P \left [ – t_{1- α/2} \leq \displaystyle \frac {\overline{X}-μ }{s / \sqrt {n}} \leq t_{1-α/2} \right] = 1-α \)
Expresión 6: Obtención del cuantil \( t_{1- α/2} \)
Al operar algebraicamente, se obtiene que
\( P \left [ \overline {X} – t_{1-α/2} \displaystyle \frac { s} { \sqrt{n }} \leq μ \leq \overline {X} + t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} \right] =1-α \)
Expresión 7: Obtención del cuantil \( t_{1- α/2} \)
por lo que el intervalo de confianza que buscamos es
\( \left [ \overline {X} – t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} , \overline {X} + t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} \right] \)
Expresión 8: Expresión del Intervalo de confianza (varianza desconocida)
La función de R t.test calcula intervalos de confianza en este contexto. Esta función también se utiliza para resolver contrastes de hipótesis, como veremos en la práctica 6. La sintaxis de la función t.test es la siguiente:
t.test(x, conf.level = 0.95)
donde
- x: Vector numérico con los valores de la variables de interés
- conf.level: Valor numérico que indica el nivel de confianza, en tanto por uno, al que se construirá el intervalo. Si omitimos este parámetro en la llamada a la función, los intervalos de confianza se calculan a un nivel de confianza del 95%.
Veamos el funcionamiento de la función t.test mediante un ejemplo.
Supuesto Práctico 2
Considerando nuevamente el conjunto de datos que se ha presentado en el supuesto práctico 1, relativo a las flexiones de los alumnos. Calcular un intervalo de confianza a un nivel de confianza del 98% para el número medio de flexiones. Suponer en este caso que el número de flexiones se distribuye según una distribución Normal de varianza desconocida.
Solución
Partiendo del conjunto de datos del Supuesto Práctico 1, el cual se había importado y almacenado en una variable de nombre datos, vamos a calcular el intervalo de confianza que nos piden. Para ello, basta con realizar la siguiente llamada a la función t.test
>t.test(datos$Flexiones, conf.level = 0.98)
One Sample t-test
data: datos$Flexiones
t = 72.58, df = 74, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
98 percent confidence interval:
48.46512 51.74822
sample estimates:
mean of x
50.10667
De toda la información que devuelve la función t.test, sólo nos interesa la relativa al intervalo de confianza. El resto hace referencia a los contrastes de hipótesis que, como hemos comentado, se estudiarán en la práctica 6.
98 percentconfidenceinterval:
48.46512 51.74822
Por lo tanto, el intervalo de confianza para el número medio de flexiones a un nivel de confianza del 98% es (48.46512, 51.74822).
Resolvamos el mismo ejemplo pero cuando el enunciado nos muestra la media (50.11), la cuasidesviación típica (5.98) y el tamaño muestral (75). Pero no proporciona los datos.
Solución
Al no disponer de un vector numérico con los valores de la variable de interés, para resolver el ejemplo recurriremos a utilizar la expresión del intervalo de confianza para este caso
\( \left [ \overline {X} – t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} , \overline {X} + t_{1-α/2} \displaystyle \frac { s} { \sqrt{n}} \right] \)
Expresión 9: Expresión del Intervalo de confianza (varianza desconocida)
En primer lugar, introducimos los datos del ejemplo
> alpha<- 0.02
> n = 75
> cuasi <- 5.98
> media <- 50.11
La función que devuelve resultados de los cuantiles de la t-Student es:
qt(p, df, ncp, lower.tail = T)
donde:
- p: Vector de probabilidades
- df: Grados de libertad
- lower.tail: Parámetro booleano, si es TRUE (por defecto), las probabilidades son P[X ≤ x], de lo contrario, P [X > x].
> cuantil<- qt((1 – alpha/2), 8, lower.tail = T)
> lim_inf<-media – cuantil * cuasi / sqrt(n)
> lim_inf
[1] 48.10996
> lim_sup<- media + cuantil * cuasi / sqrt(n)
> lim_sup
[1] 52.11004
P[48.10996 ≤ μ ≤ 52.11004] = 0.98
Por lo tanto, hay un 98% de confianza de que el intervalo [48.10996 , 52.11004] contenga el número medio de flexiones.
Intervalo de confianza para la proporción
Dada una variable aleatoria \( X \) con distribución de probabilidad binomial de parámetros \( n \) y \( \pi \), esto es, \( X \rightarrow B(n, π) \); con \( \pi \) desconocido. El objetivo es determinar un intervalo de confianza para el parámetro \( \pi \). Para ello, se extrae una muestra aleatoria \( X_1, X_2, \cdots, X_n \) de tamaño \( n \) de dicha distribución. Sea \( p \) la proporción muestral. Entonces, se sabe que el estadístico
\( Z = \displaystyle \frac { p – \pi} { \displaystyle \sqrt { \displaystyle \frac { p(1-p)} {n} } } \)
Expresión 10: Expresión de la variable aleatoria
sigue una distribución normal de media 0 y desviación típica 1. Por ello, calcular el intervalo de confianza para la proporción consiste en obtener los cuantiles de la distribución normal tales que
\( P \left [ -z_{1-α/2} \leq \displaystyle \frac {p – \pi } { \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}}} \leq z_{1-α/2} \right ]=1-α \)
Expresión 11: Obtención del cuantil z{1 – α/2}
O, equivalentemente,
\( P \left [ p -z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \leq \pi \leq p + z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \right ]=1-α \)
Expresión 12: Obtención del cuantil z{1 – α/2}
Por lo tanto, el intervalo de confianza que debemos calcular es
\( \left [ p -z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}}, p + z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \right ] \)
Expresión 13: Intervalo de confianza para la proporción
La función que calcula este intervalo de confianza en R es prop.test. Sus argumentos son los siguientes
prop.test(x, n, conf.level = 0.95)
donde
- x: Valor numérico que indica el número de elementos del grupo que presentan la característica de interés.
- n: Valor numérico que indica el número total de elementos del grupo.
- conf.level: Valor numérico que indica el nivel de confianza, en tanto por uno, al que se construirá el intervalo. Si omitimos este parámetro en la llamada a la función, los intervalos de confianza se calculan a un nivel de confianza del 95%.
Vamos a aplicar la función prop.test a los datos sobre las flexiones realizadas por los alumnos que hemos utilizado en los ejemplos anteriores.
Supuesto Práctico 3
A partir del conjunto de datos relativo al número de flexiones y el sexo de los alumnos, obtener un intervalo de confianza al 95% para la proporción de alumnos en la población. Del mismo modo, calcular un intervalo de confianza al 90% para la proporción de alumnas.
Solución
Comenzaremos con el cálculo del intervalo de confianza para los chicos. Para realizar la llamada a la función prop.test necesitamos conocer, además del nivel de confianza, que viene indicado en el enunciado, el número de alumnos varones y el número total de estudiantes en la muestra. Para ello utilizamos la función, de R, table.
>table(datos$Sexo)
H M
43 32
De los 75 estudiantes que conforman la muestra, 43 son chicos. Por lo que la llamada a prop.test sería la siguiente:
>prop.test(43,75)
1-sample proportions test with continuity correction
data: 43 out of 75, null probability 0.5
X-squared = 1.3333, df = 1, p-value = 0.2482
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.4539882 0.6851173
sample estimates:
p
0.5733333
Como el nivel de confianza para este intervalo es el 95% no ha sido necesario incluir el argumento conf.level en la llamada a prop.test, puesto que este es el nivel de confianza por defecto.
De nuevo, los resultados de la función incluyen mucha más información aparte de la relativa al intervalo de confianza. Por ahora, nos centraremos únicamente en esta última.
95 percentconfidenceinterval:
0.4539882 0.6851173
Por lo que el intervalo de confianza, a un nivel de confianza del 95% para la proporción de alumnos varones en la población es (0.4539, 0.6851).
Repitamos el procedimiento para obtener ahora un intervalo de confianza para la proporción de chicas. En este caso, tenemos que tener en cuenta que el número de chicas en la muestra era 32.
>prop.test(32,75, conf.level = 0.90)
1-sample proportions test with continuity correction
data: 32 out of 75, null probability 0.5
X-squared = 1.3333, df = 1, p-value = 0.2482
alternative hypothesis: true p is not equal to 0.5
90 percent confidence interval:
0.3306475 0.5281484
sample estimates:
p
0.4266667
Centrándonos en la parte de la salida que incluye el intervalo de confianza
90 percentconfidenceinterval:
0.3306475 0.5281484
Podemos concluir que el intervalo de confianza, considerando un nivel de confianza del 90%, para la proporción de chicas en la población es (0.3306, 0.5281).
Resolvamos este ejercicio utilizando la expresión del intervalo de confianza para la proporción
\( \left [ p -z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}}, p + z_{1-α/2} \displaystyle \sqrt { \displaystyle \frac {p(1-p)} {n}} \right ] \)
Expresión 14: Intervalo de confianza para la proporción
Solución
Intervalo de confianza, a un nivel de confianza del 95% para la proporción de alumnos varones en la población
> alpha<- 0.05
> n = 75
> p = 43/75
> cuantil<- qnorm(1 – alpha/2)
> lim_inf<-p – cuantil * sqrt (p*(1 – p)) / sqrt (n)
> lim_inf
[1] 0.4613985
> lim_sup<-p + cuantil * sqrt (p*(1 – p)) / sqrt (n)
> lim_sup
[1] 0.6852682
Por lo que el intervalo de confianza, a un nivel de confianza del 95% para la proporción de alumnos varones en la población es (0.4613985, 0.6852682).
Intervalo de confianza, a un nivel de confianza del 90% para la proporción de alumnas en la población
> alpha<- 0.02
> n = 75
> p = 32/75
> cuantil<- qnorm(1 – alpha/2)
> lim_inf<-p – cuantil * sqrt (p*(1 – p)) / sqrt (n)
> lim_inf
[1] 0.2938074
> lim_sup<-p + cuantil * sqrt (p*(1 – p)) / sqrt (n)
> lim_sup
[1] 0.559526
Por lo que el intervalo de confianza, a un nivel de confianza del 90%, para la proporción de chicas en la población es (0.2938074, 0.559526).
Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes
Consideramos dos variables aleatorias independientes \( X_1, X_2, \cdots, X_n \) e \( Y_1, Y_2, \cdots Y_n \) con distribuciones normales de parámetros \( (\mu_1, \sigma_1) \) y \( (\mu_2, \sigma_2) \), respectivamente, de las que vamos a tomar muestras aleatorias independientes de tamaños \( n_1 \) y \( n_2 \), respectivamente.
Nuestro objetivo, en este caso, es obtener un intervalo de confianza para la diferencia de las medias de ambas distribuciones, es decir, para \( \mu_1- \mu_2 \). Pero previo al cálculo de este intervalo, debemos determinar si las varianzas de ambas distribuciones o, equivalentemente, sus desviaciones típicas, \( \sigma_1 \) y \( \sigma_2 \), aun siendo desconocidas, pueden asumirse iguales o no. El cálculo del intervalo de confianza se realiza de forma diferente dependiendo El cálculo del intervalo de confianza se realiza de forma diferente dependiendo de si las varianzas (desviaciones típicas) pueden asumirse iguales o no.
En primer lugar determinemos el Intervalo de confianza para el cociente de varianzas
Intervalo de confianza para el cociente de varianzas en dos poblaciones normales independientes
Para decidir si las varianzas de las dos distribuciones pueden asumirse iguales o no construiremos un intervalo de confianza para el cociente de ambos valores, esto es, para \( \sigma_1^{2}/\sigma_2^{2} \). En este caso, partimos de la variable aleatoria
\( F= \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \displaystyle \frac {\sigma_{2}^{2}} {\sigma_{1}^{2}} \)
Expresión 15: Expresión de la variable aleatoria para el cociente de varianzas
que sigue una distribución F de Snedecor con \( n_{1} – 1 \) grados de libertad en el numerador y \( n_{2} – 1 \) grados de libertad en el denominador. Los valores \( s_{1}^{2} \) y \( s_{2}^{2} \), en la expresión anterior, hacen referencia a las cuasivarianzas muestrales de la variable en el primer y el segundo grupo, respectivamente. Buscamos los valores de la variable F tales que
\( \left [ F_{n_{1}-1,n_{2}-1, α/2} \leq \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \displaystyle \frac {\sigma_{2}^{2}} {\sigma_{1}^{2}} \leq F_{n_{1}-1,n_{2}-1, 1-α/2} \right ] = 1- \alpha \)
Expresión 16: Obtención de los cuantiles F{ α/2} y F{1 – α/2}
O, equivalentemente,
\( \left [ \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1,1- α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \leq \displaystyle \frac {\sigma_{1}^{2}} {\sigma_{2}^{2}} \leq \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1, α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \right ] = 1- \alpha \)
Expresión 17: Obtención de los cuantiles F{ α/2} y F{1 – α/2}
De modo que el intervalo de confianza que buscamos es el formado por
\( \left ( \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1, 1-α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}}, \displaystyle \frac {1}{ F_{n_{1}-1,n_{2}-1, α/2}} \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \right ) \)
Expresión 18: Intervalo de confianza para el cociente de varianzas
En R, la función var.test se encarga de calcular este intervalo. Sus parámetros son los siguientes:
var.test(x, y, conf.level = 0.95)
siendo
- x : Vector numérico con los datos de la variable de interés en el primer grupo o muestra
- y : Vector numérico con los datos de la variable de interés en el segundo grupo o muestra
- conf.level: Valor numérico que indica el nivel de confianza, en tanto por uno, al que se construirá el intervalo. Si omitimos este parámetro en la llamada a la función, los intervalos de confianza se calculan a un nivel de confianza del 95%.
Una vez calculado el intervalo de confianza, si el valor 1 está incluido en dicho intervalo, podremos afirmar que las varianzas (y, consecuentemente, las desviaciones típicas) de ambas distribuciones pueden considerarse iguales. Si el 1 queda fuera del intervalo obtenido, las varianzas de las dos distribuciones se considerarán diferentes.
Supuesto Práctico 4
Continuando con los datos relativos a las flexiones realizadas por un grupo de estudiantes y asumiendo que el número de flexiones que realizan los chicos y las que realizan las chicas se distribuyen según sendas distribuciones normales con medias y varianzas desconocidas. Calcular un intervalo de confianza a un nivel de confianza del 95% para el cociente de varianzas en ambas poblaciones. ¿Puede asumirse que ambas varianzas son iguales?
Solución
En primer lugar determinamos el intervalo de confianza para el cociente de varianzas, para ello utilizamos la función var.test. Lo primero que tenemos que hacer para aplicar la función var.test es separar en dos variables los datos relativos a las flexiones realizadas por los chicos y por las chicas.
>Flexiones.chicos<- datos$Flexiones[datos$Sexo == “H”]
>Flexiones.chicas<- datos$Flexiones[datos$Sexo == “M”]
> Flexiones.chicas
[1] 53 53 53 50 48 50 48 52 54 35 50 41 56 52 56 53 41 48 50 53 54 46 50 41 48
[26] 53 54 60 60 35 48 60
> Flexiones.chicos
[1] 60 41 41 56 50 56 50 50 54 52 48 48 54 53 53 50 52 35 35 48 48 60 56 50 41
[26] 54 54 53 54 50 54 54 53 52 50 52 48 46 53 50 35 50 50
A continuación, utilizamos la función var.test tal y como se indica a continuación:
>var.test(Flexiones.chicos, Flexiones.chicas)
F test to compare two variances
data: Flexiones.chicos and Flexiones.chicas
F = 0.87506, numdf = 42, denomdf = 31, p-value = 0.679
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.4415454 1.6765483
sample estimates:
ratio of variances
0.8750585
Analizando la información relativa al intervalo de confianza que se incluye en la salida de var.test, podemos afirmar que el intervalo de confianza a un nivel de confianza del 95% para el cociente de las varianzas de las dos distribuciones es (0.4415, 1.6765). Este intervalo de confianza contiene al valor 1, por lo que se puede suponer que las varianzas de las dos distribuciones son idénticas.
Una vez se ha determinado la igualdad (o desigualdad) de las varianzas de ambas distribuciones, procedemos a calcular el intervalo de confianza para la diferencia de las medias propiamente dicho.
a) Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes cuando las varianzas poblacionales son desconocidas pero supuestas iguales
Si la varianzas poblacionales son desconocidas pero supuestas iguales, se parte de la variable aleatoria
\( T= \displaystyle \frac { ( \overline {X}_1- \overline {X}_2)-(μ_{1}-μ_{2}) } { \displaystyle \sqrt {\displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}}+ \displaystyle \frac {1} {n_{2}} } } \)
Expresión19: Expresión de la variable aleatoria para la diferencia de medias (varianzas iguales)
la cual se distribuye según una t de Student con \( n_1+n_2-2 \) grados de libertad. El cálculo del intervalo de confianza para la diferencia de medias se realiza obteniendo los valores de la distribución t de Student con \( n_1+n_2-2 \) grados de libertad que verifican
\( \left [-t_{n_1+n_2-2,1-\alpha/2} \leq \displaystyle \frac { ( \overline {X}_1- \overline {X}_2)-(μ_{1}-μ_{2}) } { \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}}+ \displaystyle \frac {1} {n_{2}} } } \leq t_{n_1+n_2-2,1-\alpha/2} \right ] = 1- \alpha \)
Expresión 20: Obtención del cuantil t{1 – α/2}
Al operar algebraicamente, tenemos que
\( \begin{array} {c} P \left [ ( \overline {X}_1- \overline {X}_2) -t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} \leq (μ_{1}-μ_{2}) \leq \\ \leq ( \overline {X}_1- \overline {X}_2) + t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} \right ] = 1- \alpha \\ \end{array} \)
Expresión 21: Obtención del cuantil t{1 – α/2}
De modo que el intervalo de confianza que buscamos es
\( \begin{array} {c} \left ( ( \overline {X}_1- \overline {X}_2) -t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} , \\ ( \overline {X}_1- \overline {X}_2) + t_{n_1+n_2-2,1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac {(n_1-1)s_1^{2}+(n_2-1)s_2^{2}}{n_1+n_2-2} } \displaystyle \sqrt { \displaystyle \frac {1 } {n_{1}} + \displaystyle \frac {1 } {n_{2}}} \right ) \\ \end{array} \)
Expresión 22: Intervalo de confianza para la diferencia de medias (varianzas iguales)
b) Intervalo de confianza para la diferencia de medias en dos poblaciones normales independientes cuando las varianzas poblacionales son desconocidas, distintas y tamaños muestrales grandes
Si las varianzas de las poblaciones son desconocidas y, además, distintas y tamaños muestrales grandes, se sigue un procedimiento similar al que acabamos de describir en el caso de igualdad de varianzas para la obtención del intervalo de confianza, partiendo de una variable aleatoria.
\( Z = \displaystyle \frac { (\overline {X}_1 – \overline {X}_2) (\mu_1- \mu_2) } { \displaystyle \sqrt{\displaystyle \frac {s_1^{2}}{n_1} + \displaystyle \frac {s_2^{2}}{n_2} } } \)
Expresión 23: Expresión de la variable aleatoria para la diferencia de medias (varianzas distintas y tamaños muestrales grandes)
De modo que el intervalo de confianza que buscamos es
\( (\overline {X}_1 – \overline {X}_2) – z_{1-\alpha/2} \displaystyle \sqrt{ \displaystyle \frac {s_1^{2}}{n_1} + \displaystyle \frac {s_2^{2}}{n_2} }, (\overline {X}_1 – \overline {X}_2) + z_{1-\alpha/2} \displaystyle \sqrt{ \displaystyle \frac {s_1^{2}}{n_1} + \displaystyle \frac {s_2^{2}}{n_2} } \)
Expresión 24: Intervalo de confianza para la diferencia de medias (varianzas distintas y tamaños muestrales grandes)
En R, la función t.test (que fue introducida y utilizada con anterioridad) se encarga de proporcionar intervalos de confianza para la diferencia de medias, tanto si las varianzas de la variable son iguales en los dos grupos como si no. Los parámetros de t.test presentan algunos cambios cuando la función se utiliza en un contexto de dos poblaciones:
t.test (x, y, var.equal = FALSE, conf.level = 0.95)
En este caso:
-
- x: Vector numérico que incluye los valores de la variable de interés en el primer grupo o muestra
- y: Vector numérico que incluye los datos de la variable de interés en el segundo grupo o muestra
- var.equal: Es un argumento lógico que indica si las varianzas de la variable en los dos grupos o muestras puede suponerse igual o no. Para establecer el valor de este parámetro nos basamos en la interpretación del intervalo de confianza que proporciona la función var.test. Por defecto, la función considera que las varianzas en los dos grupos son distintas.
La interpretación del intervalo de confianza resultante permitirá determinar si las medias poblacionales de las dos distribuciones pueden suponerse iguales o no. Así, si el intervalo contiene al valor 0, dichas medias podrán asumirse iguales. En cualquier otro caso, concluiremos que las medias son distintas en ambas distribuciones.
Supuesto Práctico 5
En vista de los resultados obtenidos en el supuesto práctico 4, y suponiendo que el número de flexiones que realizan los alumnos y las alumnas se distribuyen de acuerdo a variables normales de medias y varianzas desconocidas, obtener un intervalo de confianza al 95% para la diferencia del número medio de flexiones entre chicos y chicas. ¿Puede suponerse que el número medio de flexiones que realizan los chicos y las chicas es igual?
Solución
Dado que en el supuesto práctico 4 se concluyó la igualdad de las varianzas del número de flexiones que hacen chicos y chicas, debemos establecer a TRUE el valor del parámetro var.equal cuando realicemos la llamada a la función t.test.
> datos <- read.table(“F:/Flexiones.txt”, header = TRUE)
> Flexiones.chicos<- datos$Flexiones[datos$Sexo == “H”]
> Flexiones.chicas<- datos$Flexiones[datos$Sexo == “M”]
>t.test(Flexiones.chicos, Flexiones.chicas, var.equal = TRUE)
Two Sample t-test
data: Flexiones.chicos and Flexiones.chicas
t = -0.06154, df = 73, p-value = 0.9511
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.887271 2.714306
sample estimates:
mean of x mean of y
50.06977 50.15625
Atendiendo la información sobre el intervalo de confianza que se incluye entre los resultados
95 percentconfidenceinterval:
-2.887271 2.714306
Se puede afirmar que el intervalo de confianza a un 95% de confianza para la diferencia de las medias del número de flexiones que hacen chicos y chicas es (-2.8872, 2.7143). Como el 0 está dentro de este intervalo, se puede decir que ambas medias son idénticas.
Intervalo de confianza para la diferencia de medias en dos poblaciones normales relacionadas
Consideremos dos muestras aleatorias \( X_1,X_2, \cdots, X_n \) e \( Y_1,Y_2, \cdots, Y_n \) de tamaño \( n \) y relacionadas, de tal forma que la primera procede de una población \( N (\mu_1, \sigma_1) \) y la segunda de una población \( N (\mu_2, \sigma_2) \)
Antes de proporcionar el intervalo para la diferencia de medias de estas dos poblaciones, se hace necesario indicar qué se entiende por muestras relacionadas. Se dicen que dos muestras \( X_1,X_2, \cdots, X_n \) e \( Y_1,Y_2, \cdots, Y_n \) están relacionadas o apareadas cuando los datos de las muestras vienen por parejas, uno de cada una de ellas, de manera que cada individuo proporciona dos observaciones.
En los casos de muestras relacionadas, se utiliza nuevamente la función t.test para la obtención de intervalos de confianza, pero se ha de indicar que los datos que reciben como parámetros provienen de muestras relacionadas incluyendo en la llamada a la función el argumento lógico paired, cuyo valor debe establecerse a TRUE.
t.test (x, y, paired = TRUE, conf.level = 0.95)
Supuesto Práctico 6
Para estudiar los efectos de un programa de control de peso, el profesor de educación física selecciona aleatoriamente a 6 alumnos y se les toma nota de sus pesos antes y después de pasar por el programa.
\( \begin{array} {|c|c|c|c|c|c|c|} \hline Antes & 72.0 & 73.5 & 70.0 & 71.5 & 76.0 & 80.5 \\ \hline Después & 73.0 & 74.5 & 74.0 & 74.5 & 75.0 & 82.0 \\ \hline \end{array} \)
Tabla 2: Datos del supuesto práctico 6
Construir un intervalo de confianza a un 95% de confianza para la diferencia de medias de los pesos antes y después de seguir el programa.
Solución
Como puede observarse, los datos vienen por parejas: peso antes y después, dos datos por individuo. Parece lógico que los datos se encuentren relacionados entre sí.
En primer lugar, vamos a introducir los datos en R. Para ello definimos dos vectores
> Antes <- c(72.0, 73.5, 70.0, 71.5, 76.0, 80.5)
> Despues<- c(73.0, 74.5, 74.0, 74.5, 75.0, 82.0)
A partir de estos datos, vamos a aplicar la función t.test, para obtener el intervalo de confianza que buscamos.
>t.test(Antes, Despues, paired = TRUE)
Paired t-test
data: Antes and Despues
t = -2.2238, df = 5, p-value = 0.07676
alternativehypothesis: true difference in meansisnotequal to 0
95 percentconfidenceinterval:
-3.4135884 0.2469217
sampleestimates:
mean of thedifferences
-1.583333
Según los datos que se incluyen en la salida de la función, el intervalo de confianza al 95% de confianza para la diferencia de las medias es (-3.4135, 0.2469). Como el 0 está contenido dentro de este intervalo, podemos afirmar que la diferencia entre los pesos medios de los alumnos antes y después de seguir el programa de control de peso es nula o, equivalentemente, que ambos pesos medios pueden suponerse iguales.
Intervalo de confianza para la diferencia de dos proporciones
Vamos a construir un intervalo de confianza para la diferencia de proporciones \( \pi_1-\pi_2 \). Para ello, consideramos dos muestras aleatorias \( X_1, X_2, \cdots, X_{n_{1}} \) e \( Y_1, Y_2, \cdots, Y_{n_{2}} \) de tamaño \( n_1 \) y \( n_2 \), independientes entre sí, extraídas de poblaciones con distribuciones binomiales \( B (1, \pi_1) \) y \( B (1, \pi_2) \), respectivamente.
Construimos, a continuación, un intervalo de confianza para la diferencia de proporciones \( \pi_1-\pi_2 \). Para ello, partimos de la variable aleatoria
\( Z = \displaystyle \frac { ( p_1 – p_2 ) -(\pi_1-\pi_2) } { \displaystyle \sqrt { \displaystyle \frac { p_1(1-p_1)}{n_1} + \displaystyle \frac {p_2 (1-p_2)}{n_2} }} \)
Expresión 25: Expresión de la variable aleatoria (diferencia de dos proporciones)
con \( p_1 \) y \( p_2 \) las proporciones de individuos que presentan la característica de interés en la primera y la segunda muestra, respectivamente. Esta variable aleatoria sigue una distribución normal de media 0 y desviación típica 1, por lo que debemos calcular los valores de la distribución normal estándar que verifican que
\( P \left [- z_{1-\alpha/2} \leq \displaystyle \frac { ( p_1 – p_2 ) -(\pi_1-\pi_2) } { \displaystyle \sqrt { \displaystyle \frac { p_1(1-p_1)}{n_1} + \displaystyle \frac {p_2 (1-p_2)}{n_2} }} \leq z_{1-\alpha/2} \right ] = 1- \alpha \)
Expresión 26: Obtención del cuantil z{1 – α/2}
O, lo que es lo mismo
\( \begin{array} {c} P \left [(p_1-p_2) – z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}} \leq \pi_1 – \pi_2 \leq \\ \leq (p_1-p_2) + z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}} \right ] = 1-\alpha \\ \end{array} \)
Expresión 27: Obtención del cuantil z{1 – α/2}
De modo que el intervalo de confianza buscado es
\( \left [(p_1-p_2) – z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}}, (p_1-p_2) + z_{1-\alpha/2} \displaystyle \sqrt { \displaystyle \frac { p_1( 1 – p_1 )}{n_1} + \displaystyle \frac { p_2 (1-p_2) }{n_2}} \right ] \)
Expresión 28: Intervalo de confianza para la diferencia de dos proporciones
Para calcular este intervalo en R utilizaremos de nuevo la función prop.test, pero teniendo en cuenta que ahora contamos con dos muestras en lugar de una. Esto afecta (mínimamente) a la manera de definir los parámetros. La sintaxis de la función sigue siendo la misma:
prop.test(x, n, conf.level = 0.95)
donde:
- x: Vector de dimensión 2 que indica el número de elementos en cada grupo que presentan la característica de interés.
- n: Vector numérico de dimensión 2 que indica el número total de elementos del grupo.
- conf.level: Valor numérico que indica el nivel de confianza, en tanto por uno, al que se construirá el intervalo. Si omitimos este parámetro en la llamada a la función, los intervalos de confianza se calculan a un nivel de confianza del 95%.
Si el intervalo de confianza resultante incluye al 0 entre sus posibles valores, la diferencia entre ambas proporciones poblaciones podrá considerarse nula lo que equivale a decir que ambas proporciones son iguales.
Supuesto Práctico 7
Retomando el conjunto de datos relativo a las flexiones que realizan un grupo de estudiantes, calcular un intervalo de confianza al 92% para la diferencia entre la proporción de alumnos y de alumnas que practican deporte. ¿Puede considerarse que ambas proporciones son iguales?
Solución
En primer lugar, sino tenemos importado el fichero de datos, debemos importarlo. Para ello, utilizamos la orden read.table
> datos <- read.table(“F:/Flexiones.txt”, header = TRUE)
Una vez importado el fichero de datos, utilizamos el comando table para determinar cuántos chicos y cuantas chicas practican deporte.
>table(datos$Sexo, datos$Deporte)
0 1
H 32 11
M 13 19
En total, 11 de los 43 y 19 de las 32 chicas muestreados practican deporte. Vamos a crear dos vectores con esta información:
- vector_Deport: Total de chicos y chicas que practican deporte
- vector_Sexo: Total de chicos y chicas en la muestra.
> vector_Deporte<- c(11, 19)
> vector_Deporte
[1] 11 19
> vector_Sexo<- c(43, 32)
> vector_Sexo
[1] 43 32
Es muy importante que los valores se introduzcan en el mismo orden en los dos vectores. A continuación podemos utilizar la función prop.test con estos dos vectores como argumentos.
> prop.test(vector_Deporte, vector_Sexo, conf.level = 0.92)
2-sample test for equality of proportions with continuity correction
data: vector_Deporte out of vector_Sexo
X-squared = 7.3787, df = 1, p-value = 0.0066
alternative hypothesis: two.sided
92 percent confidence interval:
-0.5566881 -0.1191840
sample estimates:
prop 1 prop 2
0.255814 0.593750
Según la salida de la función prop.test, el intervalo de confianza al 92% de confianza es (-0.5566, -0.1191). El 0 no está dentro de este intervalo, por lo que podemos concluir que las proporciones de chicos y chicas que hacen deporte no coinciden.
Ejercicios
Ejercicios Guiados
Ejercicio Guiado1
Un fabricante diseña un experimento para estimar la tensión de ruptura media de una fibra. Para ello, observa las tensiones de ruptura, en libras, de 16 hilos de dicha fibra seleccionados aleatoriamente. Las tensiones son 20.8, 20.6, 21.0, 20.9, 19.9, 20.2, 19.8, 19.6, 20.9, 21.1, 20.4, 20.6, 19.7, 19.6, 20.3, 20.7.
Construir un intervalo de confianza al 98% de confianza:
a) Si la tensión de ruptura se distribuye según una normal de desviación típica σ = 0.45 libras
b) Si la tensión de ruptura se distribuye según una normal de desviación típica desconocida.
Ejercicio Guiado 2
En una muestra de 40 alumnos, 25 de ellos están conformes con las decisiones que ha tomado el profesor con respecto a las calificaciones. Calcular un intervalo de confianza, a un 95% de confianza para la proporción de alumnos conforme con el profesor.
Ejercicio Guiado 3
Una agencia estatal vigila la calidad del agua para la cría de peces. Esta agencia desea comparar la cantidad media de cierta sustancia tóxica en dos ríos contaminados por desperdicios industriales. Se seleccionaron 11 muestras en un río y 8 muestras en el otro. Los resultados de los análisis fueron:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|c|} \hline Río1 & 10 & 10 & 12 & 13 & 9 & 8 & 12 & 12 & 10 & 14 & 8 \\ \hline Río2 & 11 & 8 & 9 & 7 & 10 & 8 & 8 & 10 \\ \hline \end{array} \)
Tabla 3: Datos del Ejercicio guiado 3
Si las dos poblaciones son normales e independientes, calcular un intervalo de confianza con nivel de confianza del 90% para la diferencia de las medias poblacionales de cantidad de sustancia tóxica.
Ejercicio Guiado 4
Una empresa farmacéutica está interesada en la investigación preliminar de un nuevo medicamento que parece tener propiedades reductoras del colesterol en la sangre. A tal fin se toma una muestra al azar de 6 personas, y se determina el contenido en colesterol antes y después del tratamiento. Los resultados han sido los siguientes:
\( \begin{array} {|c|c|c|c|c|c|c|} \hline Antes & 217 & 252 & 229 & 200 & 209 & 213 \\ \hline Después & 209 & 241 & 230 & 208 & 206 & 211 \\ \hline \end{array} \)
Tabla 4 : Datos del Ejercicio guiado 4
Calcular un intervalo de confianza, al 96% de confianza para la diferencia del nivel de colesterol medio antes y después del tratamiento.
Ejercicio Guiado 5
Una determinada empresa quiere saber si su nuevo producto tendrá más aceptación en la población adulta o entre los jóvenes. Para ello, considera una muestra aleatoria de 400 adultos y 600 jóvenes, observando que sólo a 100 adultos y 300 jóvenes les había gustado su producto. Construir un intervalo de confianza al 99% de confianza para la diferencia de proporciones de adultos y jóvenes a los que les gusta el producto. ¿Puede suponerse que el producto gusta por igual en adultos y jóvenes?
Ejercicio Guiado 6
En una experiencia genética se extraen 20 moscas de una caja experimental y se mide la longitud del ala de cada una. Se obtuvieron los siguientes valores:
93, 90, 97, 90, 93, 91, 96, 94, 91, 91, 88, 93, 95, 91, 89, 92, 87, 88, 90, 86
Suponiendo que la longitud del ala sigue una distribución Normal. Construir un intervalo de confianza al 99% de confianza para
a) La media μ
b) La varianza σ²
Ejercicio Guiado 1 (Resuelto)
Un fabricante diseña un experimento para estimar la tensión de ruptura media de una fibra. Para ello, observa las tensiones de ruptura, en libras, de 16 hilos de dicha fibra seleccionados aleatoriamente. Las tensiones son 20.8, 20.6, 21.0, 20.9, 19.9, 20.2, 19.8, 19.6, 20.9, 21.1, 20.4, 20.6, 19.7, 19.6, 20.3, 20.7.
Construir un intervalo de confianza al 98% de confianza:
a) Si la tensión de ruptura se distribuye según una normal de desviación típica σ = 0.45 libras
b) Si la tensión de ruptura se distribuye según una normal de desviación típica desconocida.
Solución:
En primer lugar, introducimos, en un vector, los datos de las 16 tensiones observadas y en segundo lugar introducimos el dato relativo al nivel de significación
>tensiones<- c(20.8, 20.6, 21.0, 20.9, 19.9, 20.2, 19.8, 19.6, 20.9, 21.1, 20.4, 20.6, + 19.7, 19.6, 20.3, 20.7)
>alpha<- 0.02
a) Si la tensión de ruptura se distribuye según una normal de desviación típica σ = 0.45
Tenemos que obtener un intervalo de confianza para la media con varianza conocida
\( \left [ \overline {X} – z_{1-α/2} \displaystyle \frac { \sigma} { \sqrt{n}} , \overline {X} + z_{1-α/2} \displaystyle \frac { \sigma} { \sqrt{n}} \right] \)
Expresión 29: Expresión del Intervalo de confianza para la media (varianza conocida)
En este primer caso, y dado que conocemos la desviación típica poblacional de la distribución de la tensión de la fibra, debemos calcular manualmente los límites inferior y superior del intervalo.
Así, calculamos la media muestral y el cuantil que intervienen en dicho intervalo.
> n <- length(tensiones)
> media <- mean(tensiones)
>cuantil<- qnorm(1 – alpha/2)
Introducimos el dato de la desviación típica
>desv_tipica<- 0.45
A continuación calculamos el límite inferior y superior del intervalo pedido.
>lim_inf<- media – cuantil * desv_tipica / sqrt(n)
>lim_inf
[1] 20.11954
>lim_sup<- media + cuantil * desv_tipica / sqrt(n)
>lim_sup
[1] 20.64296
Por lo que el intervalo de confianza para la tensión media de la fibra que buscamos es (20.11954, 20.64296).
b) Si la tensión de ruptura se distribuye según una normal de desviación típica desconocida
Hay que obtener un intervalo de confianza cuando la desviación típica no se conoce. Para ello, usamos la función t.test
>t.test(tensiones, conf.level = 0.98)
OneSample t-test
data: tensiones
t = 155.85, df = 15, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
98 percent confidence interval:
20.04092 20.72158
sample estimates:
mean of x
20.38125
En este segundo caso, el intervalo de confianza para la tensión media de la fibra, al 98% de confianza, es (20.04092, 20.72158).
Ejercicio Guiado2 (Resuelto)
En una muestra de 40 alumnos, 25 de ellos están conformes con las decisiones que ha tomado el profesor con respecto a las calificaciones. Calcular un intervalo de confianza, a un 95% de confianza para la proporción de alumnos conforme con el profesor.
Solución:
Para obtener un intervalo de confianza para la proporción poblacional, se utiliza la función prop.test. Disponemos tanto del número de alumnos que presentan la característica de interés (estar conforme con el profesor) como del número total de alumnos en la muestra, de manera que podemos realizar la llamada a la función tal y como sigue:
>prop.test(25, 40)
1-sample proportions test with continuity correction
data: 25 out of 40, null probability 0.5
X-squared = 2.025, df = 1, p-value = 0.1547
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.4580964 0.7682594
sample estimates:
p
0.625
El intervalo de confianza para la proporción poblacional de alumnos conformes al 95% de confianza es (0.4580, 0.7682).
Ejercicio Guiado3 (Resuelto)
Una agencia estatal vigila la calidad del agua para la cría de peces. Esta agencia desea comparar la cantidad media de cierta sustancia tóxica en dos ríos contaminados por desperdicios industriales. Se seleccionaron 11 muestras en un río y 8 muestras en el otro. Los resultados de los análisis fueron:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|c|} \hline Río1 & 10 & 10 & 12 & 13 & 9 & 8 & 12 & 12 & 10 & 14 & 8 \\ \hline Río2 & 11 & 8 & 9 & 7 & 10 & 8 & 8 & 10 \\ \hline \end{array} \)
Tabla 3: Datos del Ejercicio guiado 3
Si las dos poblaciones son normales e independientes, calcular un intervalo de confianza con nivel de confianza del 90% para la diferencia de las medias poblacionales de cantidad de sustancia tóxica.
Solución:
En primer lugar introducimos los datos en R:
> Rio1 <- c(10, 10, 12, 13, 9, 8, 12, 12, 10, 14, 8)
> Rio2 <- c(11, 8, 9, 7, 10, 8, 8, 10)
Aunque el enunciado nos pide calcular un intervalo de confianza para la diferencia de la cantidad media de sustancia tóxica en ambos ríos, primero debemos obtener un intervalo de confianza para el cociente de las varianzas de la sustancia en ambos ríos, para saber si estas varianzas pueden asumirse iguales o no. Para ello, empleamos la función var.test.
>var.test(Rio1, Rio2, conf.level = 0.90)
F test to compare two variances
data: Rio1 and Rio2
F = 2.1846, numdf = 10, denomdf = 7, p-value = 0.3119
alternative hypothesis: true ratio of variances is not equal to 1
90 percent confidence interval:
0.6007504 6.8498698
sample estimates:
ratio of variances
2.184643
Según los resultados de var.test, el intervalo de confianza al 90% de confianza para el cociente de las varianzas de la variable en ambos ríos es (0.6007, 6.8498), que contiene al 1. Por tanto, podemos asumir que ambas varianzas son iguales en ambos ríos.
Por lo tanto, tenemos que obtener un intervalo de confianza para la diferencia de medias de dos poblaciones cuando las varianzas de ambas poblaciones son iguales. Para ello, utilizamos la función t.test.
>t.test(Rio1, Rio2, var.equal = TRUE, conf.level = 0.90)
Two Sample t-test
data: Rio1 and Rio2
t = 2.2564, df = 17, p-value = 0.0375
alternative hypothesis: true difference in means is not equal to 0
90 percent confidence interval:
0.424258 3.280287
sample estimates:
mean of x mean of y
10.72727 8.87500
El intervalo de confianza, al 90% de confianza, para la diferencia de medias de sustancia tóxica en ambos ríos es (0.4242, 3.2802), que no contiene al 0, por lo que podemos concluir que la cantidad media de tóxico en ambos ríos no es la misma.
Ejercicio Guiado 4 (Resuelto)
Una empresa farmacéutica está interesada en la investigación preliminar de un nuevo medicamento que parece tener propiedades reductoras del colesterol en la sangre. A tal fin se toma una muestra al azar de 6 personas, y se determina el contenido en colesterol antes y después del tratamiento. Los resultados han sido los siguientes:
\( \begin{array} {|c|c|c|c|c|c|c|} \hline Antes & 217 & 252 & 229 & 200 & 209 & 213 \\ \hline Después & 209 & 241 & 230 & 208 & 206 & 211 \\ \hline \end{array} \)
Tabla 4: Datos del Ejercicio guiado 4
Calcular un intervalo de confianza, al 96% de confianza para la diferencia del nivel de colesterol medio antes y después del tratamiento.
Solución:
En primer lugar introducimos los datos en R.
> Antes <- c(217, 252, 229, 200, 209, 213)
> Despues<- c(209, 241, 230, 208, 206, 211)
Estos datos son un claro ejemplo de datos pareados, ya que a los mismos individuos se les ha medido el nivel de colesterol en sangre antes y después del tratamiento. Por lo que tenemos que obtener un intervalo de confianza para la diferencia de medias de dos poblaciones normales relacionadas. Para ello, realizamos la llamada a la función t.test, sin olvidar indicar mediante el parámetro paired la relación que existe entre los conjuntos de datos.
>t.test(Antes, Despues, paired = TRUE, conf.level = 0.96)
Paired t-test
data: Antes and Despues
t = 0.91186, df = 5, p-value = 0.4037
alternative hypothesis: true difference in means is not equal to 0
96 percent confidence interval:
-5.057393 10.057393
sample estimates:
mean of the differences
2.5
El intervalo de confianza, al 96% de confianza, para la diferencia del colesterol medio antes y después del tratamiento es (-5.0573, 10.0573). Este intervalo contiene al 0, por lo que podemos concluir que los niveles medios de colesterol antes y después del tratamiento pueden considerarse iguales, poniendo así en duda la efectividad de dicho tratamiento.
Ejercicio Guiado 5 (Resuelto)
Una determinada empresa quiere saber si su nuevo producto tendrá más aceptación en la población adulta o entre los jóvenes. Para ello, considera una muestra aleatoria de 400 adultos y 600 jóvenes, observando que sólo a 100 adultos y 300 jóvenes les había gustado su producto. Construir un intervalo de confianza al 99% de confianza para la diferencia de proporciones de adultos y jóvenes a los que les gusta el producto. ¿Puede suponerse que el producto gusta por igual en adultos y jóvenes?
Solución:
En este caso debemos utilizar la función prop.test para calcular el intervalo de confianza para la diferencia de proporciones. Pero primero, debemos crear un vector que indique el número de adultos y jóvenes a los que les gusta el producto así como un segundo vector con el número total de adultos y jóvenes encuestados.
>Adul_Jov_Gusta_Producto<- c(100, 300)
>Adul_Jov_Total<- c(400, 600)
Una vez hecho esto, llamamos a la función prop.test, indicando el nivel de confianza adecuado.
>prop.test(Adul_Jov_Gusta_Producto, Adul_Jov_Total, conf.level = 0.99)
2-sample test for equality of proportions with continuity correction
data: Adul_Jov_Gusta_Producto out of Adul_Jov_Total
X-squared = 61.463, df = 1, p-value = 4.512e-15
alternative hypothesis: two.sided
99 percent confidence interval:
-0.3287296 -0.1712704
sample estimates:
prop 1 prop 2
0.25 0.50
Según los resultados que proporciona prop.test, el intervalo de confianza para la diferencia de proporciones que buscamos es (-0.3287, -0.1712), el cual deja fuera al 0, por lo que se puede afirmar que el producto no gusta por igual entre adultos y jóvenes.
Ejercicio Guiado 6 (Resuelto)
En una experiencia genética se extraen 20 moscas de una caja experimental y se mide la longitud del ala de cada una. Se obtuvieron los siguientes valores:
93, 90, 97, 90, 93, 91, 96, 94, 91, 91, 88, 93, 95, 91, 89, 92, 87, 88, 90, 86
Suponiendo que la longitud del ala sigue una distribución Normal. Construir un intervalo de confianza al 99% de confianza para
a) La media μ
b) La varianza σ².
Solución:
En primer lugar introducimos, en un vector, los datos de las 20 concentraciones observadas y en segundo lugar introducimos el dato relativo al nivel de significación
> longitud<- c(93, 90, 97, 90, 93, 91, 96, 94, 91, 91, 88, 93, 95, 91, 89, 92, 87, 88, 90, 86)
> alpha<- 0.01
a) Construir un intervalo de confianza al 99% de confianza para la media μ
Hay que obtener un intervalo de confianza cuando la varianza poblacional es desconocida. Para ello, usamos la función t.test
> t.test(longitud)
One Sample t-test
data: longitud
t = 139.01, df = 19, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
89.87604 92.62396
sample estimates:
mean of x
91.25
El intervalo de confianza para la longitud media de las alas al 99% de confianza, es (89.87604, 92.62396).
a) Construir un intervalo de confianza al 99% de confianza para la varianza σ².
El intervalo de confianza que debemos calcular es
\( \left ( \displaystyle \frac {(n-1) \sigma^{2}}{ \chi^{2}_{1- \alpha/2, n-1 }}, \displaystyle \frac {(n-1) \sigma^{2}}{ \chi^{2}_{\alpha/2, n-1 } } \right ) \)
Expresión 30: Intervalo de confianza para la varianza (media conocida)
Nota: R no incluye una función específica para el cálculo de intervalos de confianza en este tipo de situaciones. Por lo tanto calcularemos el intervalo de la siguiente forma
> n <- length(longitud)
> varianza <- var(longitud)
> L1 <- (n – 1) * varianza / qchisq(1-alpha / 2,n – 1)
> L2 <- (n – 1) * varianza / qchisq(alpha /2,n – 1)
> IC <- c(L1,L2)
> IC
[1] 4.244179 23.926166
El intervalo pedido es: (4.244179, 23.926166)
Ejercicios Propuestos
Ejercicio Propuesto 1
Se desea estudiar si la longitud del pico en una especie de loro es distinta entre los machos y las hembras. Para ello se selecciona una muestra de 14 machos y 12 hembras, cuyos resultados, expresados en milímetros, se muestran en la siguiente tabla:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline Machos & 57 & 58 & 60 & 58 & 61 & 62 & 61 & 59 & 57 & 63 & 58 & 55 & 59 & 60 \\ \hline Hembras & 55 & 56 & 58 & 54 & 53 & 55 & 57 & 53 & 54 & 54 & 55 & 55 & & \\ \hline \end{array} \)
Tabla 5: Datos del Ejercicio propuesto 1
Se pide:
- Obtener un intervalo de confianza a un nivel del 99%
- para la longitud media del pico en los machos
- para la longitud media del pico en las hembras
- Obtener un intervalo de confianza a un nivel del 99% para la diferencia entre la longitud media del pico de los machos y de las hembras.
Ejercicio Propuesto 2
Para comprobar si un determinado pienso puede mejorar la producción de lana de las ovejas, se selecciona una muestra aleatoria simple de 10 ovejas para ser alimentadas con dicho pienso. En la tabla siguiente se muestra el peso (en Kgr) de la lana producida antes y después del experimento
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 10 & 8 & 7 & 5 & 9 & 12 & 10 & 9 & 8 & 8 \\ \hline Después & 10 & 9 & 9 & 7 & 10 & 12 & 11 & 12 & 11 & 10 \\ \hline \end{array} \)
Tabla 6: Datos del Ejercicio propuesto 2
Obtener un intervalo de confianza al 98% para la diferencia de los pesos medios de la lana producida antes y después del experimento.
Ejercicio Propuesto 3
En una muestra aleatoria de 900 personas con pelo oscuro se encontró que 150 de ellas tenían los ojos azules. Construir un intervalo de confianza al 95% para la proporción de individuos que teniendo pelo oscuro en la población posee ojos azules. ¿Son compatibles estos resultados con la suposición de que dicha proporción vale 1/4).
Ejercicio Propuesto 4
En una piscifactoría se desea comparar el porcentaje de peces adultos que miden menos de 20 cm con los que miden más de 40 cm. Para ello, se toma una muestra de 200 peces observando que 40 de ellos miden menos de 20 cm y una muestra de 200 peces de los que 57 miden más de 40 cm. Halla un intervalo de confianza para la diferencia de proporciones al nivel de confianza del 0.95. Realizarlo también para un nivel de confianza del 99%.
Ejercicio Propuesto 1(Resuelto)
Se desea estudiar si la longitud del pico en una especie de loro es distinta entre los machos y las hembras. Para ello se selecciona una muestra de 14 machos y 12 hembras, cuyos resultados, expresados en milímetros, se muestran en la siguiente tabla:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline Machos & 57 & 58 & 60 & 58 & 61 & 62 & 61 & 59 & 57 & 63 & 58 & 55 & 59 & 60 \\ \hline Hembras & 55 & 56 & 58 & 54 & 53 & 55 & 57 & 53 & 54 & 54 & 55 & 55 & & \\ \hline \end{array} \)
Tabla 5: Datos del Ejercicio propuesto 1
Se pide:
- Obtener un intervalo de confianza a un nivel del 99%
- para la longitud media del pico en los machos
- para la longitud media del pico en las hembras
- Obtener un intervalo de confianza a un nivel del 99% para la diferencia entre la longitud media del pico de los machos y de las hembras.
Solución:
1. Obtener un intervalo de confianza a un nivel del 99%
- para la longitud media del pico en los machos
- para la longitud media del pico en las hembras
Los intervalos de confianza para la longitud media del pico de los machos y de las hembras, a un nivel del 99%, son (57.38877, 60.89695) y (53.56729, 56.26604), respectivamente. Como se puede apreciar la longitud del pico en los machos es mayor que en las hembras.
2. Obtener un intervalo de confianza a un nivel del 99% para la diferencia entre la longitud media del pico de los machos y de las hembras.
El intervalo de confianza resultante es (2.135710, 6.316671), dicho intervalo no contiene al 0, por lo que podemos concluir que la longitud del pico de lo machos y de las hembras no es la misma.
Solución del Ejercicio propuesto 1
Ejercicio Propuesto 2 (Resuelto)
Para comprobar si un determinado pienso puede mejorar la producción de lana de las ovejas, se selecciona una muestra aleatoria simple de 10 ovejas para ser alimentadas con dicho pienso. En la tabla siguiente se muestra el peso (en Kgr) de la lana producida antes y después del experimento
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 10 & 8 & 7 & 5 & 9 & 12 & 10 & 9 & 8 & 8 \\ \hline Después & 10 & 9 & 9 & 7 & 10 & 12 & 11 & 12 & 11 & 10 \\ \hline \end{array} \)
Tabla 6 : Datos del Ejercicio propuesto 2
Obtener un intervalo de confianza al 98% para la diferencia de los pesos medios de la lana producida antes y después del experimento.
Solución:
El intervalo de confianza para la diferencia de los pesos medios de la lana producida antes y después del experimento, a un nivel del 98%, es (-2.4637045, -0.5362955). Como el intervalo de confianza no contiene el 0 podemos deducir que existen diferencias significativas entre las medias. Se puede apreciar que el peso de la lana es mayor después del tratamiento.
Solución del Ejercicio Propuesto 2
Ejercicio Propuesto 3 (Resuelto)
En una muestra aleatoria de 900 personas con pelo oscuro se encontró que 150 de ellas tenían los ojos azules. Construir un intervalo de confianza al 95% para la proporción de individuos que teniendo pelo oscuro en la población posee ojos azules. ¿Son compatibles estos resultados con la suposición de que dicha proporción vale 1/4)
Solución:
El intervalo de confianza para la proporción de individuos que teniendo pelo oscuro en la población posee ojos azules, a un nivel del 95%, es (0.1432251, 0.1930061). Este resultado no es compatible con la suposición de que dicha proporción vale 1/4, ya que 1/4 no pertenece al intervalo.
Solución del Ejercicio Propuesto 3
Ejercicio Propuesto 4 (Resuelto)
En una piscifactoría se desea comparar el porcentaje de peces adultos que miden menos de 20 cm con los que miden más de 40 cm. Para ello, se toma una muestra de 200 peces observando que 40 de ellos miden menos de 20 cm y una muestra de 200 peces de los que 57 miden más de 40 cm. Halla un intervalo de confianza para la diferencia de proporciones al nivel de confianza del 0.95. Realizarlo también para un nivel de confianza del 99%.
Solución:
Intervalos de confianza para la diferencia de proporciones entre los peces adultos que miden menos de 20 cm al 95% y 99%, respectivamente : (-0.6035891, -0.4264109) y (-0.6298547, -0.4001453).
Intervalos de confianza para la diferencia de proporciones entre los peces adultos que miden más de 40 cm al 95% y 99%, respectivamente: (0.4264109, 0.6035891) y (0.4001453, 0.6298547).
Intervalos de confianza para la diferencia de proporciones entre los peces adultos que miden menos de 20 cm y los que miden más de 40 cm al 95% y 99%, respectivamente: (-0.173589075, 0.003589075) y (-0.19985467, 0.02985467).
Solución del Ejercicio Propuesto 4
Autores: David Molina Muñoz y Ana María Lara Porras. Universidad de Granada. (2016).
Reformulado con MathML en 2021 por Ana María Lara Porras